Signal and systems. Linear Systems. Luigi Palopoli. Signal and systems p. 1/5
|
|
|
- Elvin Gilmore
- 5 years ago
- Views:
Transcription
1 Signal and systems p. 1/5 Signal and systems Linear Systems Luigi Palopoli
2 Wrap-Up Signal and systems p. 2/5
3 Signal and systems p. 3/5 Fourier Series We have see that is a signal is periodic, it can be conveniently expressed as a Fourier Series: X s(t) = s n e jnωt n= or, if s(t) is real, s(t) = X n=1 2 s n cos(nωt + Φ(s n )) This is essentially a representation of the signal in an appropriate base made of exponential orthonormal functions The convenience of this representation can easily be seen when we process a signal through a linear systems
4 Signal and systems p. 4/5 Fourier Series Because exponential functions are eigenfunctions, the response to a sinusoidal signal is: S e st = H(s)e st, H(s) = R h(t)e st dt S {cos(ωt + φ 0 )} = H(jω) cos(ωt + φ 0 + Φ(H(jω)) S {1} = H(0) Where the last expression is true iff H(s) converges for s = jω. Using the superimposition principle, for a generic periodic signal s(t), we get: S {s(t)} = H(0)s 0 + P n=1 2 s n H(jnω) cos(ωnt + Φ(s n ) + Φ(H(jnω))) The expression above reveals the power of our formalism. By simply knowing H(jω), we are able to compute the response to any periodic signal without solving differential equations. We would like to apply this to non-periodic signals as well.
5 Linear systems: Frequency Domain Signal and systems p. 5/5
6 Nonperiodic signals Signal and systems p. 6/5
7 Signal and systems p. 7/5 Fourier series of a non periodic signal A non-periodic signal can be obtained as the limit of a periodic signal: s(t) = lim T0 rep T0 s(t) where rep T0 s(t) = P h= s(t + ht 0) The coefficients of the periodic signal rept0 s(t) are given by: s n = 1 T 0 Z T0 /2 T 0 /2 = 1 Z T0 /2 X T 0 [rep T0 s(t)]e jnω 0t dt T 0 /2 h= s(t + ht 0 )e jnω 0t dt
8 Signal and systems p. 8/5 Fourier series of a non periodic signal Observing that e j2πnh = 1, we can write s n = 1 Z T0 /2 X T 0 T 0 /2 h= = 1 Z T0 /2 X T 0 = 1 T 0 X = 1 T 0 X T 0 /2 h= Z T0 /2 h= T 0 /2 Z T0 (h+1/2) h= T 0 (h 1/2) = 1 Z s(t )e jnω 0t dt T 0 s(t + ht 0 )e jnω 0t e jω 0nhT 0 dt s(t + ht 0 )e jnω 0(t+hT 0 ) dt s(t + ht 0 )e jnω 0(t+hT 0 ) dt s(t )e jnω 0t dt
9 Signal and systems p. 9/5 Fourier series of a nonperiodic signal Define S(ω) = R s(t)e jωt dt We get: sn = 1 S(nω T 0 ) 0 Notice that two coefficients are spaced out by ω = ω0. Drawing the spectrum in the (ω s n ) plan, the rows s n become closer and closer as T 0 : the spectrum tends to be continuous. Therefore, s n = ω 2π S(n ω) We can write: rept0 s(t) = P n= ω 2π S(n ω)ejnω 0t As T ( ω 0), we get the definition of the integral: s(t) = lim T 0 rep T 0 s(t) = 1 2π Z S(ω)e jω dω
10 Signal and systems p. 10/5 Fourier Transform Starting from the definition of Fourier series (that applies to periodic signal) we have [informally] derived the fourier transform, S(ω) = Z s(t)e jωt dt s(t) = 1 2π Z S(ω)e jωt dω It can be seen that if the signal is absolutely integrable and bounded, (plus other technical mathematical conditions) i.e., R s(t) dt = L <, then the fourier transform exists for almost all ω R also the Fourier is squared -integrable: S(ω) 2 dω < its inverse transform converges to s(t) (in squared error sense) Notice If a signal has finite is absolutely integrable, then it has finite energy: R s(t) 2 dt is finite. The above conditions are only sufficient (we will find the Fourier transform of several signals that do not meet these conditions).
11 Signal and systems p. 11/5 Example Compute the FT of a rectangular impulse: s(t) = AG τ (t) = 8 < A if τ/2 t τ/2 : 0 Otherwise By applying the definition: S(ω) = = A Z Z τ/2 s(t)e jωt dt τ/2 e jωt dt = A 1 jω e jωt τ/2 τ/2 = A 1 jω ( 2j sin(ω τ 2 ) = Aτ 1 ω τ 2 sin(ω τ 2 ) = AτSinc(ω τ 2 )
12 Signal and systems p. 12/5 Example Compute the FT of a dirac impulse: s(t) = δ(t) By applying the definition: S(ω) = = 1 Z δ(t)e jωt dt
13 Signal and systems p. 13/5 Properties of the Fourier transform Linearity: F(u 1 (t)) = U 1 (ω), F(u 2 (t)) = U 2 (ω) F(a 1 u 1 (t) + a 2 u 2 (t)) = a 1 U 1 (ω) + a 2 U 2 (ω) This is a fairly obvious consequence of the linearity of the integral operator. Time shifting: F(u 1 (t)) = U 1 (ω) F(u 1 (t t 0 )) = = Z Z = e jωt 0 U 1 (ω) u 1 (t t 0 )e jωt dt = u 1 (t t 0 )e jω(t t 0) e jωt 0 dt =
14 Signal and systems p. 14/5 Properties of the Fourier transform Shifiting in the frequency domain F(u 1 (t)) = U 1 (ω), F(e jω0t u 1 (t)) = = Z Z = U 1 (ω ω 0 ) e jω 0t u 1 (t)e jωt dt = u 1 (t)e j(ω ω 0)t dt =
15 Signal and systems p. 15/5 Properties of the Fourier transform Time scaling. Assume a positive F(u 1 (t)) = U 1 (ω) F(u 1 (at)) = = Z Z u 1 (at)e jωt dt = 1 a u 1(t )e j ω a t dt = = 1 a U 1( ω a ) For general a we can easily see F(u 1 (t)) = U 1 (ω) F(u 1 (at)) = 1 a U 1( ω a )
16 Properties of the Fourier transform Differentiation in the time domain: F(u 1 (t)) = U 1 (ω), u 1 (t) = 1 2π F( d dt u 1(t)) = F( d dt Z = F( 1 2π Z Z = jωu 1 (ω) U 1 (ω)e jωt dt = U 1 (ω)e jωt dt) = jωu 1 (ω)e jωt dt) = More generally F(u 1 (t)) = U 1 (ω), F( dn u 1 dt n ) = (jω)n U 1 (ω) Signal and systems p. 16/5
17 Signal and systems p. 17/5 Properties of the Fourier transform Duality F(f(t)) = F(ω) F(F(t)) = 2πf( ω) Proof: F(f(t)) = F(ω) f(t) = 1 2π Z F(ω)e jωt dt If we simply swap the two variables t and ω, we find: f(ω) = 1 2π Z F(t)e jωt dt = 1 2π F(F(t)) ω
18 Signal and systems p. 18/5 An example Consider the signal s(t) = 1. This is not absolutely integrable (it does not converge to 0). However, if we apply duality we get: F(δ(t)) = 1 F(1) = 2πδ(ω) This is extremely important because it shows that if we consider generalised functions (δ(.)) we can find the Fourier Transform of function that are not absolutely integrable
19 Signal and systems p. 19/5 Another (important) example Let us consider the signal (non absolutely integrable) 1(t) = 8 < 1 t 0 : 0 Otherwise We can see that: 1(t) = 1 sgn(t) = (1 + sgn(t)) 2 8 < 1 t 0 : 1 Otherwise Function sgn(t) is not an absolutely integrable function, but we can manage it with some trick...
20 Signal and systems p. 20/5 Another (important) example We can write: sgn(t) = lim S α (t) α 0 8 < e αt t 0 S α (t) = : e αt t < 0 Sα (t) is absolutely integrable, hence we can deal with it: F(S α (t)) = = Z Z 0 S α (t)e jωt dt e αt e jωt dt + Z 0 e αt e jωt dt = 1 α jω e(α jω)t 0 1 α + jω e (α+jω)t 0 = 1 α jω + 1 α + jω
21 Signal and systems p. 21/5 Another (important) example Hence: We can conclude: F(sgn(t)) = lim α 0 1 α jω + 1 α + jω = 2 jω F(1(t)) = 1 «2 2 jω + 2πδ(ω) = 1 jω + πδ(ω)
22 Signal and systems p. 22/5 Properties of the Fourier transform Convolution Proof F(u1(t) u2(t)) = F(u 1 (t)) = U 1 (ω), F(u 2 (t)) = U 2 (ω), F(u 1 (t) u 2 (t)) = U 1 (ω)u 2 (ω) = = = Z Z Z Z Z Z u 1 (τ)u 2 (t τ)dτe jωt dt u 1 (τ)u 2 (t τ)dτe jωt dt»z u 1 (τ) = U 1 (ω)u 2 (ω) u 1 (τ)u 1 (ω)e jωτ dτ u 2 (t τ)e jωt dt dτ
23 Signal and systems p. 23/5 Properties of the Fourier transform Product F(u 1 (t)) = U 1 (ω), F(u 2 (t)) = U 2 (ω), F(u 1 (t)u 2 (t)) = 1 2π U 1(ω) U 2 (ω) Proof: It descends from duality + convolution
24 Signal and systems p. 24/5 Properties of the Fourier transform Integration F(u 1 (t)) = U 1 (ω), Z t F( u 1 (τ)dτ) = 1 τ= jω U 1(ω) + πu 1 (0)δ(ω) Proof Z t τ= u 1 (τ)dτ = u 1 (t) 1(t) Z t F( u 1 (τ)dτ) = F (u 1 (t) 1(t)) τ= = ( 1 jω + πδ(ω))u 1(ω) = U 1(ω) jω + πδ(ω))u 1(0)
25 Signal and systems p. 25/5 Example Consider the f(t) = B cos ω0 t F(f(t)) = B 2 F ``e jω0t jω + e 0t We have seen that F(δ(t)) = 1; applying the duality property: F (1) = 2πδ ( ω) Now, we apply frequency shifting property: F `e jω 0t = 2πδ (ω ω 0 ) Therefore, we get: F (B cos ω 0 t) = Bπ (δ(ω ω 0 ) + δ(ω + ω 0 ))
26 Signal and systems p. 26/5 Example We have seen that Let us find: F ( AG τ/2 ) F (AG τ (t)) = AτSinc ( ω τ ) 2 We can apply time scaling rule: F ( AG τ/2 ) = Aτ 2 Sinc ( ω 2 τ ) 2
27 Signal and systems p. 27/5 Spectrum Also for non periodic signals g(t) we can associate a frequency domain spectrum G(ω) It is typically depicted by giving its norm G(ω) and its phase (G(ω)) For real signals the following hold: G(ω) = G( ω), (G(ω)) = (G( ω)) If the signal is even, then G(ω) is real If the signal is odd, then G(ω) is imaginary An interesting example is the following ideal filter. Its spectrum is given by: H(ω) = 1GateB (ω) and (H(ω) = ωt 0
28 Signal and systems p. 28/5 Why is an ideal filter ideal? Consider, for simplicity, t0 = 0 Applying duality, we get: h(t) = 2πBSinc t B 2 As we can see this filter is not a causal system... Therefore the system is not pysically implementable
29 Signal and systems p. 29/5 Fourier Transform of periodic signals We have seen that the fourier transform of a cosine is the sum of two δ The same applies also to other periodic signals For a periodic signal, we have seen that it is possible to write them in terms of Fouries series: X s(t) = s n e jnω 0t n= we have seen that F `ejnω 0 t = 2πδ(ω nω 0 ) Therefore we get: F (s(t)) = X n= 2πs n δ(ω nω 0 )
30 Signal and systems p. 30/5 Fourier Transform of periodic signals What if we construct a periodic repeating a non periodic signal? s(t) = X i= s c (t + it 0 ) The signal can be expressed as s(t) = s c (t) X i= δ(t + it 0 ) We can compute the Fourier series of signal sr (t) = P i= δ(t + it 0): s n = 1 T 0 Z T0 /2 s r (t) = T 0 /2 X n= s n e jnω 0t δ(t)e jnω 0t dt = 1 T 0
31 Signal and systems p. 31/5 Fourier Transform of periodic signals Therefore: s(t) = s c (t) 1 T 0 X n= e jnω 0t Which, corresponds, in the frequency domain, to: S(ω) = S c (ω) 2π T 0 X n= δ(ω nω 0 )
32 Signal and systems p. 32/5 Fourier Transform of periodic signals Example:
33 Mathematical Complements Signal and systems p. 33/5
34 Signal and systems p. 34/5 Discussion We have seen that for signals compying with the following conditions: s(t) limited Finite number of minima and maxima and of singularities Absolutely integrable The Fourier transform exists and the inverxe transform converges to s(t). For these signals we have the Parseval equality: Z s(t) 2 dt = 1 2π Z S(ω) 2 dω We can compute the integral in the easier domain (for instance for a low pass filter it is much easier in the frequency domain)
35 Signal and systems p. 35/5 Discussion If we consider signals with finite power (e.g. periodic signals) we can still compute the fourier transform using generalized functions (δ) We have derived the Fourier transform from the Fourier series, but we also have seen that the Fourier series is a special case of the Fourier transform.
36 Two interesting applications Signal and systems p. 36/5
37 Signal and systems p. 37/5 Amplitude Modulation We want to use the same medium (e.g., the air), to transmit multiple signals (e.g., different channels) Assume that each transmission can have a limited bandwidth One of the oldest ways for doing this was to modulate the amplitude of the signal by multiplying it by a sinusoidal oscillation: x AM (t) = x(t)cos(5t)
38 Signal and systems p. 38/5 Amplitude Modulation 1.0 x(t) K10 K t * cos(5t) K10 K K0.5 K1.0 = x(t)cos(5t) K10 K5 K t 10 K0.4 K0.6
39 Signal and systems p. 39/5 Amplitude Modulation - Frequency domain It is important to see what happens in the frequency domain. Remember cos ω 0 t = ejω 0 t +e jω 0 t 2 Therefore x AM (t) = x(t)cos(ω 0 t) = x(t) ejω0t + e jω 0t 2 X AM (ω) = X(ω ω 0) + X(ω + ω 0 ) 2
40 Signal and systems p. 40/5 Fourier Transform of periodic signals Example:
41 Signal and systems p. 41/5 FDM The idea outlined above can be used to do a Frequency Division Demultiplexing In practice, the spectrum of each singnal is translated to a different frequency range: X i (ω) X i (ω ω i ) In order for the idea to work, the frequency used to translate the signal must be sufficiently spaced out so as to avoid interference: ω i+1 ω > B/2, where B is the bandwidth To demodulate the signal, we first isoltate the part of the spectrum we are interested in, translate the spectrum by ω i and then elimnate spurious component by a low pass filter.
42 FDM Signal and systems p. 42/5
43 FDM - demodulation Signal and systems p. 43/5
44 Sampling Signal and systems p. 44/5
45 Signal and systems p. 45/5 Ideal sampler Ideal sampling can intuitively be seen as generated by multiplying a signal by a sequence of dirac s δ
46 Signal and systems p. 46/5 Properties of δ + f(t)δ(t a)dt = f(a) t δ(τ)dτ = 1 F (δ(t)) = 1 f(t) δ(t t 0 ) = f(t t 0 )
47 Signal and systems p. 47/5 F-trasform of r Using the above properties it is possible to write: F (r (t)) = F r(t) P n= δ(t nt) We can express the sampling signal using the Fourier series: X n= δ(t nt) = 1 T X h= jh 2π e T t Hence F (r (t)) = F r(t) 1 T P t h= ejh2π T Applying the frequency shifting property we get: F (r (t)) = 1 P h= R(ω h 2π T T )
48 Signal and systems p. 48/5 Example R(j ω) 0.5 R * (jω) π /T ω ω
49 Signal and systems p. 49/5 Aliasing The spectrum might be altered (i.e., signal not attainable from samples!) sin(2 π t/3) samples collected with T = 3/ sin(2 π t)
50 Signal and systems p. 50/5 Shannon theorem If the signal has a finite badwidth then the signal can be reconstructed from samples collected with a period such that 1 T 2B Band-limited signals have infinite duration; many signals of interest have infinite bandwidth Typically a low-pass filter is used to de-emphasize higher frequencies
51 Signal and systems p. 51/5 Data Extrapolation If the following hypotheses hold the signal has limited bandwidth B (i.e., the spectrum is not null in the range [ B, B]. the signal is sampled at frequency fs = 1 T 2B then the signal can be reconstructed using an ideal lowpass filter L(s) with L(ω) = 8 < T if ω [ π T, π T ] : 0 elsewhere. Signal l(t) is given by: l(t) = 1 2π Z pi/t pi/t Te jωt dω = sin(πt/t) πt/t = sinc(πt/t)
52 Signal and systems p. 52/5 Data Extrapolation I The reconstructed signal is computed as follows: r(t) = r (t) l(t) = R + r(τ) P δ(τ kt)sinc π(t τ = P + r(kt)sinc π(t kt) T The function sinc is not causal and has infinite duration T dτ = In communication applications The duration problem can be solved truncating the signal The causality problem can be solved introducing a delay and collecting some sample before the reconstruction Not viable in control applications since large delays jeopardise stability
Homework 4. May An LTI system has an input, x(t) and output y(t) related through the equation y(t) = t e (t t ) x(t 2)dt
 Homework 4 May 2017 1. An LTI system has an input, x(t) and output y(t) related through the equation y(t) = t e (t t ) x(t 2)dt Determine the impulse response of the system. Rewriting as y(t) = t e (t
Homework 4 May 2017 1. An LTI system has an input, x(t) and output y(t) related through the equation y(t) = t e (t t ) x(t 2)dt Determine the impulse response of the system. Rewriting as y(t) = t e (t
Fourier transforms. Definition F(ω) = - should know these! f(t).e -jωt.dt. ω = 2πf. other definitions exist. f(t) = - F(ω).e jωt.
 Fourier transforms This is intended to be a practical exposition, not fully mathematically rigorous ref The Fourier Transform and its Applications R. Bracewell (McGraw Hill) Definition F(ω) = - f(t).e
Fourier transforms This is intended to be a practical exposition, not fully mathematically rigorous ref The Fourier Transform and its Applications R. Bracewell (McGraw Hill) Definition F(ω) = - f(t).e
Signals and Systems Spring 2004 Lecture #9
 Signals and Systems Spring 2004 Lecture #9 (3/4/04). The convolution Property of the CTFT 2. Frequency Response and LTI Systems Revisited 3. Multiplication Property and Parseval s Relation 4. The DT Fourier
Signals and Systems Spring 2004 Lecture #9 (3/4/04). The convolution Property of the CTFT 2. Frequency Response and LTI Systems Revisited 3. Multiplication Property and Parseval s Relation 4. The DT Fourier
Signals & Systems. Lecture 5 Continuous-Time Fourier Transform. Alp Ertürk
 Signals & Systems Lecture 5 Continuous-Time Fourier Transform Alp Ertürk alp.erturk@kocaeli.edu.tr Fourier Series Representation of Continuous-Time Periodic Signals Synthesis equation: x t = a k e jkω
Signals & Systems Lecture 5 Continuous-Time Fourier Transform Alp Ertürk alp.erturk@kocaeli.edu.tr Fourier Series Representation of Continuous-Time Periodic Signals Synthesis equation: x t = a k e jkω
Figure 3.1 Effect on frequency spectrum of increasing period T 0. Consider the amplitude spectrum of a periodic waveform as shown in Figure 3.2.
 3. Fourier ransorm From Fourier Series to Fourier ransorm [, 2] In communication systems, we oten deal with non-periodic signals. An extension o the time-requency relationship to a non-periodic signal
3. Fourier ransorm From Fourier Series to Fourier ransorm [, 2] In communication systems, we oten deal with non-periodic signals. An extension o the time-requency relationship to a non-periodic signal
LECTURE 12 Sections Introduction to the Fourier series of periodic signals
 Signals and Systems I Wednesday, February 11, 29 LECURE 12 Sections 3.1-3.3 Introduction to the Fourier series of periodic signals Chapter 3: Fourier Series of periodic signals 3. Introduction 3.1 Historical
Signals and Systems I Wednesday, February 11, 29 LECURE 12 Sections 3.1-3.3 Introduction to the Fourier series of periodic signals Chapter 3: Fourier Series of periodic signals 3. Introduction 3.1 Historical
EE 224 Signals and Systems I Review 1/10
 EE 224 Signals and Systems I Review 1/10 Class Contents Signals and Systems Continuous-Time and Discrete-Time Time-Domain and Frequency Domain (all these dimensions are tightly coupled) SIGNALS SYSTEMS
EE 224 Signals and Systems I Review 1/10 Class Contents Signals and Systems Continuous-Time and Discrete-Time Time-Domain and Frequency Domain (all these dimensions are tightly coupled) SIGNALS SYSTEMS
Review of Fourier Transform
 Review of Fourier Transform Fourier series works for periodic signals only. What s about aperiodic signals? This is very large & important class of signals Aperiodic signal can be considered as periodic
Review of Fourier Transform Fourier series works for periodic signals only. What s about aperiodic signals? This is very large & important class of signals Aperiodic signal can be considered as periodic
Mathematical Foundations of Signal Processing
 Mathematical Foundations of Signal Processing Module 4: Continuous-Time Systems and Signals Benjamín Béjar Haro Mihailo Kolundžija Reza Parhizkar Adam Scholefield October 24, 2016 Continuous Time Signals
Mathematical Foundations of Signal Processing Module 4: Continuous-Time Systems and Signals Benjamín Béjar Haro Mihailo Kolundžija Reza Parhizkar Adam Scholefield October 24, 2016 Continuous Time Signals
IB Paper 6: Signal and Data Analysis
 IB Paper 6: Signal and Data Analysis Handout 5: Sampling Theory S Godsill Signal Processing and Communications Group, Engineering Department, Cambridge, UK Lent 2015 1 / 85 Sampling and Aliasing All of
IB Paper 6: Signal and Data Analysis Handout 5: Sampling Theory S Godsill Signal Processing and Communications Group, Engineering Department, Cambridge, UK Lent 2015 1 / 85 Sampling and Aliasing All of
EE 3054: Signals, Systems, and Transforms Summer It is observed of some continuous-time LTI system that the input signal.
 EE 34: Signals, Systems, and Transforms Summer 7 Test No notes, closed book. Show your work. Simplify your answers. 3. It is observed of some continuous-time LTI system that the input signal = 3 u(t) produces
EE 34: Signals, Systems, and Transforms Summer 7 Test No notes, closed book. Show your work. Simplify your answers. 3. It is observed of some continuous-time LTI system that the input signal = 3 u(t) produces
2.161 Signal Processing: Continuous and Discrete Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu.6 Signal Processing: Continuous and Discrete Fall 008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS
MIT OpenCourseWare http://ocw.mit.edu.6 Signal Processing: Continuous and Discrete Fall 008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS
1.1 SPECIAL FUNCTIONS USED IN SIGNAL PROCESSING. δ(t) = for t = 0, = 0 for t 0. δ(t)dt = 1. (1.1)
 SIGNAL THEORY AND ANALYSIS A signal, in general, refers to an electrical waveform whose amplitude varies with time. Signals can be fully described in either the time or frequency domain. This chapter discusses
SIGNAL THEORY AND ANALYSIS A signal, in general, refers to an electrical waveform whose amplitude varies with time. Signals can be fully described in either the time or frequency domain. This chapter discusses
MEDE2500 Tutorial Nov-7
 (updated 2016-Nov-4,7:40pm) MEDE2500 (2016-2017) Tutorial 3 MEDE2500 Tutorial 3 2016-Nov-7 Content 1. The Dirac Delta Function, singularity functions, even and odd functions 2. The sampling process and
(updated 2016-Nov-4,7:40pm) MEDE2500 (2016-2017) Tutorial 3 MEDE2500 Tutorial 3 2016-Nov-7 Content 1. The Dirac Delta Function, singularity functions, even and odd functions 2. The sampling process and
Series FOURIER SERIES. Graham S McDonald. A self-contained Tutorial Module for learning the technique of Fourier series analysis
 Series FOURIER SERIES Graham S McDonald A self-contained Tutorial Module for learning the technique of Fourier series analysis Table of contents Begin Tutorial c 24 g.s.mcdonald@salford.ac.uk 1. Theory
Series FOURIER SERIES Graham S McDonald A self-contained Tutorial Module for learning the technique of Fourier series analysis Table of contents Begin Tutorial c 24 g.s.mcdonald@salford.ac.uk 1. Theory
Chapter 4 The Fourier Series and Fourier Transform
 Chapter 4 The Fourier Series and Fourier Transform Fourier Series Representation of Periodic Signals Let x(t) be a CT periodic signal with period T, i.e., xt ( + T) = xt ( ), t R Example: the rectangular
Chapter 4 The Fourier Series and Fourier Transform Fourier Series Representation of Periodic Signals Let x(t) be a CT periodic signal with period T, i.e., xt ( + T) = xt ( ), t R Example: the rectangular
Fourier transform representation of CT aperiodic signals Section 4.1
 Fourier transform representation of CT aperiodic signals Section 4. A large class of aperiodic CT signals can be represented by the CT Fourier transform (CTFT). The (CT) Fourier transform (or spectrum)
Fourier transform representation of CT aperiodic signals Section 4. A large class of aperiodic CT signals can be represented by the CT Fourier transform (CTFT). The (CT) Fourier transform (or spectrum)
Signals and Systems. Lecture 14 DR TANIA STATHAKI READER (ASSOCIATE PROFESSOR) IN SIGNAL PROCESSING IMPERIAL COLLEGE LONDON
 Signals and Systems Lecture 14 DR TAIA STATHAKI READER (ASSOCIATE PROFESSOR) I SIGAL PROCESSIG IMPERIAL COLLEGE LODO Introduction. Time sampling theorem resume. We wish to perform spectral analysis using
Signals and Systems Lecture 14 DR TAIA STATHAKI READER (ASSOCIATE PROFESSOR) I SIGAL PROCESSIG IMPERIAL COLLEGE LODO Introduction. Time sampling theorem resume. We wish to perform spectral analysis using
4 The Continuous Time Fourier Transform
 96 4 The Continuous Time ourier Transform ourier (or frequency domain) analysis turns out to be a tool of even greater usefulness Extension of ourier series representation to aperiodic signals oundation
96 4 The Continuous Time ourier Transform ourier (or frequency domain) analysis turns out to be a tool of even greater usefulness Extension of ourier series representation to aperiodic signals oundation
Chapter 4 The Fourier Series and Fourier Transform
 Chapter 4 The Fourier Series and Fourier Transform Representation of Signals in Terms of Frequency Components Consider the CT signal defined by N xt () = Acos( ω t+ θ ), t k = 1 k k k The frequencies `present
Chapter 4 The Fourier Series and Fourier Transform Representation of Signals in Terms of Frequency Components Consider the CT signal defined by N xt () = Acos( ω t+ θ ), t k = 1 k k k The frequencies `present
E2.5 Signals & Linear Systems. Tutorial Sheet 1 Introduction to Signals & Systems (Lectures 1 & 2)
 E.5 Signals & Linear Systems Tutorial Sheet 1 Introduction to Signals & Systems (Lectures 1 & ) 1. Sketch each of the following continuous-time signals, specify if the signal is periodic/non-periodic,
E.5 Signals & Linear Systems Tutorial Sheet 1 Introduction to Signals & Systems (Lectures 1 & ) 1. Sketch each of the following continuous-time signals, specify if the signal is periodic/non-periodic,
DESIGN OF CMOS ANALOG INTEGRATED CIRCUITS
 DESIGN OF CMOS ANALOG INEGRAED CIRCUIS Franco Maloberti Integrated Microsistems Laboratory University of Pavia Discrete ime Signal Processing F. Maloberti: Design of CMOS Analog Integrated Circuits Discrete
DESIGN OF CMOS ANALOG INEGRAED CIRCUIS Franco Maloberti Integrated Microsistems Laboratory University of Pavia Discrete ime Signal Processing F. Maloberti: Design of CMOS Analog Integrated Circuits Discrete
SIGNALS AND SYSTEMS: PAPER 3C1 HANDOUT 6. Dr Anil Kokaram Electronic and Electrical Engineering Dept.
 SIGNALS AND SYSTEMS: PAPER 3C HANDOUT 6. Dr Anil Kokaram Electronic and Electrical Engineering Dept. anil.kokaram@tcd.ie www.mee.tcd.ie/ sigmedia FOURIER ANALYSIS Have seen how the behaviour of systems
SIGNALS AND SYSTEMS: PAPER 3C HANDOUT 6. Dr Anil Kokaram Electronic and Electrical Engineering Dept. anil.kokaram@tcd.ie www.mee.tcd.ie/ sigmedia FOURIER ANALYSIS Have seen how the behaviour of systems
EC Signals and Systems
 UNIT I CLASSIFICATION OF SIGNALS AND SYSTEMS Continuous time signals (CT signals), discrete time signals (DT signals) Step, Ramp, Pulse, Impulse, Exponential 1. Define Unit Impulse Signal [M/J 1], [M/J
UNIT I CLASSIFICATION OF SIGNALS AND SYSTEMS Continuous time signals (CT signals), discrete time signals (DT signals) Step, Ramp, Pulse, Impulse, Exponential 1. Define Unit Impulse Signal [M/J 1], [M/J
Homework 7 Solution EE235, Spring Find the Fourier transform of the following signals using tables: te t u(t) h(t) = sin(2πt)e t u(t) (2)
 Homework 7 Solution EE35, Spring. Find the Fourier transform of the following signals using tables: (a) te t u(t) h(t) H(jω) te t u(t) ( + jω) (b) sin(πt)e t u(t) h(t) sin(πt)e t u(t) () h(t) ( ejπt e
Homework 7 Solution EE35, Spring. Find the Fourier transform of the following signals using tables: (a) te t u(t) h(t) H(jω) te t u(t) ( + jω) (b) sin(πt)e t u(t) h(t) sin(πt)e t u(t) () h(t) ( ejπt e
ANALOG AND DIGITAL SIGNAL PROCESSING CHAPTER 3 : LINEAR SYSTEM RESPONSE (GENERAL CASE)
 3. Linear System Response (general case) 3. INTRODUCTION In chapter 2, we determined that : a) If the system is linear (or operate in a linear domain) b) If the input signal can be assumed as periodic
3. Linear System Response (general case) 3. INTRODUCTION In chapter 2, we determined that : a) If the system is linear (or operate in a linear domain) b) If the input signal can be assumed as periodic
2A1H Time-Frequency Analysis II
 2AH Time-Frequency Analysis II Bugs/queries to david.murray@eng.ox.ac.uk HT 209 For any corrections see the course page DW Murray at www.robots.ox.ac.uk/ dwm/courses/2tf. (a) A signal g(t) with period
2AH Time-Frequency Analysis II Bugs/queries to david.murray@eng.ox.ac.uk HT 209 For any corrections see the course page DW Murray at www.robots.ox.ac.uk/ dwm/courses/2tf. (a) A signal g(t) with period
Introduction to Fourier Transforms. Lecture 7 ELE 301: Signals and Systems. Fourier Series. Rect Example
 Introduction to Fourier ransforms Lecture 7 ELE 3: Signals and Systems Fourier transform as a limit of the Fourier series Inverse Fourier transform: he Fourier integral theorem Prof. Paul Cuff Princeton
Introduction to Fourier ransforms Lecture 7 ELE 3: Signals and Systems Fourier transform as a limit of the Fourier series Inverse Fourier transform: he Fourier integral theorem Prof. Paul Cuff Princeton
ENSC327 Communications Systems 2: Fourier Representations. School of Engineering Science Simon Fraser University
 ENSC37 Communications Systems : Fourier Representations School o Engineering Science Simon Fraser University Outline Chap..5: Signal Classiications Fourier Transorm Dirac Delta Function Unit Impulse Fourier
ENSC37 Communications Systems : Fourier Representations School o Engineering Science Simon Fraser University Outline Chap..5: Signal Classiications Fourier Transorm Dirac Delta Function Unit Impulse Fourier
Review of Discrete-Time System
 Review of Discrete-Time System Electrical & Computer Engineering University of Maryland, College Park Acknowledgment: ENEE630 slides were based on class notes developed by Profs. K.J. Ray Liu and Min Wu.
Review of Discrete-Time System Electrical & Computer Engineering University of Maryland, College Park Acknowledgment: ENEE630 slides were based on class notes developed by Profs. K.J. Ray Liu and Min Wu.
Lecture 7 ELE 301: Signals and Systems
 Lecture 7 ELE 30: Signals and Systems Prof. Paul Cuff Princeton University Fall 20-2 Cuff (Lecture 7) ELE 30: Signals and Systems Fall 20-2 / 22 Introduction to Fourier Transforms Fourier transform as
Lecture 7 ELE 30: Signals and Systems Prof. Paul Cuff Princeton University Fall 20-2 Cuff (Lecture 7) ELE 30: Signals and Systems Fall 20-2 / 22 Introduction to Fourier Transforms Fourier transform as
Communication Theory Summary of Important Definitions and Results
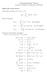 Signal and system theory Convolution of signals x(t) h(t) = y(t): Fourier Transform: Communication Theory Summary of Important Definitions and Results X(ω) = X(ω) = y(t) = X(ω) = j x(t) e jωt dt, 0 Properties
Signal and system theory Convolution of signals x(t) h(t) = y(t): Fourier Transform: Communication Theory Summary of Important Definitions and Results X(ω) = X(ω) = y(t) = X(ω) = j x(t) e jωt dt, 0 Properties
Chap 4. Sampling of Continuous-Time Signals
 Digital Signal Processing Chap 4. Sampling of Continuous-Time Signals Chang-Su Kim Digital Processing of Continuous-Time Signals Digital processing of a CT signal involves three basic steps 1. Conversion
Digital Signal Processing Chap 4. Sampling of Continuous-Time Signals Chang-Su Kim Digital Processing of Continuous-Time Signals Digital processing of a CT signal involves three basic steps 1. Conversion
2.1 Basic Concepts Basic operations on signals Classication of signals
 Haberle³me Sistemlerine Giri³ (ELE 361) 9 Eylül 2017 TOBB Ekonomi ve Teknoloji Üniversitesi, Güz 2017-18 Dr. A. Melda Yüksel Turgut & Tolga Girici Lecture Notes Chapter 2 Signals and Linear Systems 2.1
Haberle³me Sistemlerine Giri³ (ELE 361) 9 Eylül 2017 TOBB Ekonomi ve Teknoloji Üniversitesi, Güz 2017-18 Dr. A. Melda Yüksel Turgut & Tolga Girici Lecture Notes Chapter 2 Signals and Linear Systems 2.1
A system that is both linear and time-invariant is called linear time-invariant (LTI).
 The Cooper Union Department of Electrical Engineering ECE111 Signal Processing & Systems Analysis Lecture Notes: Time, Frequency & Transform Domains February 28, 2012 Signals & Systems Signals are mapped
The Cooper Union Department of Electrical Engineering ECE111 Signal Processing & Systems Analysis Lecture Notes: Time, Frequency & Transform Domains February 28, 2012 Signals & Systems Signals are mapped
e st f (t) dt = e st tf(t) dt = L {t f(t)} s
 Additional operational properties How to find the Laplace transform of a function f (t) that is multiplied by a monomial t n, the transform of a special type of integral, and the transform of a periodic
Additional operational properties How to find the Laplace transform of a function f (t) that is multiplied by a monomial t n, the transform of a special type of integral, and the transform of a periodic
LTI Systems (Continuous & Discrete) - Basics
 LTI Systems (Continuous & Discrete) - Basics 1. A system with an input x(t) and output y(t) is described by the relation: y(t) = t. x(t). This system is (a) linear and time-invariant (b) linear and time-varying
LTI Systems (Continuous & Discrete) - Basics 1. A system with an input x(t) and output y(t) is described by the relation: y(t) = t. x(t). This system is (a) linear and time-invariant (b) linear and time-varying
LINEAR SYSTEMS. J. Elder PSYC 6256 Principles of Neural Coding
 LINEAR SYSTEMS Linear Systems 2 Neural coding and cognitive neuroscience in general concerns input-output relationships. Inputs Light intensity Pre-synaptic action potentials Number of items in display
LINEAR SYSTEMS Linear Systems 2 Neural coding and cognitive neuroscience in general concerns input-output relationships. Inputs Light intensity Pre-synaptic action potentials Number of items in display
Ver Chap Lecture 15- ECE 240a. Q-Switching. Mode Locking. ECE 240a Lasers - Fall 2017 Lecture Q-Switch Discussion
 ing Ver Chap. 9.3 Lasers - Fall 2017 Lecture 15 1 ing ing (Cavity Dumping) 1 Turn-off cavity - prevent lasing 2 Pump lots of energy into upper state - use pulsed pump 3 Turn cavity back on - all the energy
ing Ver Chap. 9.3 Lasers - Fall 2017 Lecture 15 1 ing ing (Cavity Dumping) 1 Turn-off cavity - prevent lasing 2 Pump lots of energy into upper state - use pulsed pump 3 Turn cavity back on - all the energy
ENSC327 Communications Systems 2: Fourier Representations. Jie Liang School of Engineering Science Simon Fraser University
 ENSC327 Communications Systems 2: Fourier Representations Jie Liang School of Engineering Science Simon Fraser University 1 Outline Chap 2.1 2.5: Signal Classifications Fourier Transform Dirac Delta Function
ENSC327 Communications Systems 2: Fourier Representations Jie Liang School of Engineering Science Simon Fraser University 1 Outline Chap 2.1 2.5: Signal Classifications Fourier Transform Dirac Delta Function
Lecture 8 ELE 301: Signals and Systems
 Lecture 8 ELE 30: Signals and Systems Prof. Paul Cuff Princeton University Fall 20-2 Cuff (Lecture 7) ELE 30: Signals and Systems Fall 20-2 / 37 Properties of the Fourier Transform Properties of the Fourier
Lecture 8 ELE 30: Signals and Systems Prof. Paul Cuff Princeton University Fall 20-2 Cuff (Lecture 7) ELE 30: Signals and Systems Fall 20-2 / 37 Properties of the Fourier Transform Properties of the Fourier
7. Find the Fourier transform of f (t)=2 cos(2π t)[u (t) u(t 1)]. 8. (a) Show that a periodic signal with exponential Fourier series f (t)= δ (ω nω 0
![7. Find the Fourier transform of f (t)=2 cos(2π t)[u (t) u(t 1)]. 8. (a) Show that a periodic signal with exponential Fourier series f (t)= δ (ω nω 0 7. Find the Fourier transform of f (t)=2 cos(2π t)[u (t) u(t 1)]. 8. (a) Show that a periodic signal with exponential Fourier series f (t)= δ (ω nω 0](/thumbs/96/126850209.jpg) Fourier Transform Problems 1. Find the Fourier transform of the following signals: a) f 1 (t )=e 3 t sin(10 t)u (t) b) f 1 (t )=e 4 t cos(10 t)u (t) 2. Find the Fourier transform of the following signals:
Fourier Transform Problems 1. Find the Fourier transform of the following signals: a) f 1 (t )=e 3 t sin(10 t)u (t) b) f 1 (t )=e 4 t cos(10 t)u (t) 2. Find the Fourier transform of the following signals:
Solutions to Problems in Chapter 4
 Solutions to Problems in Chapter 4 Problems with Solutions Problem 4. Fourier Series of the Output Voltage of an Ideal Full-Wave Diode Bridge Rectifier he nonlinear circuit in Figure 4. is a full-wave
Solutions to Problems in Chapter 4 Problems with Solutions Problem 4. Fourier Series of the Output Voltage of an Ideal Full-Wave Diode Bridge Rectifier he nonlinear circuit in Figure 4. is a full-wave
2.161 Signal Processing: Continuous and Discrete
 MI OpenCourseWare http://ocw.mit.edu.6 Signal Processing: Continuous and Discrete Fall 8 For information about citing these materials or our erms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSES INSIUE
MI OpenCourseWare http://ocw.mit.edu.6 Signal Processing: Continuous and Discrete Fall 8 For information about citing these materials or our erms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSES INSIUE
Spectral Analysis of Random Processes
 Spectral Analysis of Random Processes Spectral Analysis of Random Processes Generally, all properties of a random process should be defined by averaging over the ensemble of realizations. Generally, all
Spectral Analysis of Random Processes Spectral Analysis of Random Processes Generally, all properties of a random process should be defined by averaging over the ensemble of realizations. Generally, all
Continuous-Time Fourier Transform
 Signals and Systems Continuous-Time Fourier Transform Chang-Su Kim continuous time discrete time periodic (series) CTFS DTFS aperiodic (transform) CTFT DTFT Lowpass Filtering Blurring or Smoothing Original
Signals and Systems Continuous-Time Fourier Transform Chang-Su Kim continuous time discrete time periodic (series) CTFS DTFS aperiodic (transform) CTFT DTFT Lowpass Filtering Blurring or Smoothing Original
2A1H Time-Frequency Analysis II Bugs/queries to HT 2011 For hints and answers visit dwm/courses/2tf
 Time-Frequency Analysis II (HT 20) 2AH 2AH Time-Frequency Analysis II Bugs/queries to david.murray@eng.ox.ac.uk HT 20 For hints and answers visit www.robots.ox.ac.uk/ dwm/courses/2tf David Murray. A periodic
Time-Frequency Analysis II (HT 20) 2AH 2AH Time-Frequency Analysis II Bugs/queries to david.murray@eng.ox.ac.uk HT 20 For hints and answers visit www.robots.ox.ac.uk/ dwm/courses/2tf David Murray. A periodic
2.161 Signal Processing: Continuous and Discrete Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu 2.161 Signal Processing: Continuous and Discrete Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. Massachusetts
MIT OpenCourseWare http://ocw.mit.edu 2.161 Signal Processing: Continuous and Discrete Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. Massachusetts
IB Paper 6: Signal and Data Analysis
 IB Paper 6: Signal and Data Analysis Handout 2: Fourier Series S Godsill Signal Processing and Communications Group, Engineering Department, Cambridge, UK Lent 2015 1 / 1 Fourier Series Revision of Basics
IB Paper 6: Signal and Data Analysis Handout 2: Fourier Series S Godsill Signal Processing and Communications Group, Engineering Department, Cambridge, UK Lent 2015 1 / 1 Fourier Series Revision of Basics
Grades will be determined by the correctness of your answers (explanations are not required).
 6.00 (Fall 20) Final Examination December 9, 20 Name: Kerberos Username: Please circle your section number: Section Time 2 am pm 4 2 pm Grades will be determined by the correctness of your answers (explanations
6.00 (Fall 20) Final Examination December 9, 20 Name: Kerberos Username: Please circle your section number: Section Time 2 am pm 4 2 pm Grades will be determined by the correctness of your answers (explanations
Principles of Communication
 Principles of Communication The communication process: Sources of information, communication channels, modulation process, and communication networks Representation of signals and systems: Signals, Continuous
Principles of Communication The communication process: Sources of information, communication channels, modulation process, and communication networks Representation of signals and systems: Signals, Continuous
EE Homework 13 - Solutions
 EE3054 - Homework 3 - Solutions. (a) The Laplace transform of e t u(t) is s+. The pole of the Laplace transform is at which lies in the left half plane. Hence, the Fourier transform is simply the Laplace
EE3054 - Homework 3 - Solutions. (a) The Laplace transform of e t u(t) is s+. The pole of the Laplace transform is at which lies in the left half plane. Hence, the Fourier transform is simply the Laplace
ECE 3084 QUIZ 2 SCHOOL OF ELECTRICAL AND COMPUTER ENGINEERING GEORGIA INSTITUTE OF TECHNOLOGY APRIL 2, Name:
 ECE 3084 QUIZ 2 SCHOOL OF ELECTRICAL AND COMPUTER ENGINEERING GEORGIA INSTITUTE OF TECHNOLOGY APRIL 2, 205 Name:. The quiz is closed book, except for one 2-sided sheet of handwritten notes. 2. Turn off
ECE 3084 QUIZ 2 SCHOOL OF ELECTRICAL AND COMPUTER ENGINEERING GEORGIA INSTITUTE OF TECHNOLOGY APRIL 2, 205 Name:. The quiz is closed book, except for one 2-sided sheet of handwritten notes. 2. Turn off
LOPE3202: Communication Systems 10/18/2017 2
 By Lecturer Ahmed Wael Academic Year 2017-2018 LOPE3202: Communication Systems 10/18/2017 We need tools to build any communication system. Mathematics is our premium tool to do work with signals and systems.
By Lecturer Ahmed Wael Academic Year 2017-2018 LOPE3202: Communication Systems 10/18/2017 We need tools to build any communication system. Mathematics is our premium tool to do work with signals and systems.
Fourier Series and Fourier Transforms
 Fourier Series and Fourier Transforms EECS2 (6.082), MIT Fall 2006 Lectures 2 and 3 Fourier Series From your differential equations course, 18.03, you know Fourier s expression representing a T -periodic
Fourier Series and Fourier Transforms EECS2 (6.082), MIT Fall 2006 Lectures 2 and 3 Fourier Series From your differential equations course, 18.03, you know Fourier s expression representing a T -periodic
Chapter 5 Frequency Domain Analysis of Systems
 Chapter 5 Frequency Domain Analysis of Systems CT, LTI Systems Consider the following CT LTI system: xt () ht () yt () Assumption: the impulse response h(t) is absolutely integrable, i.e., ht ( ) dt< (this
Chapter 5 Frequency Domain Analysis of Systems CT, LTI Systems Consider the following CT LTI system: xt () ht () yt () Assumption: the impulse response h(t) is absolutely integrable, i.e., ht ( ) dt< (this
Notes 07 largely plagiarized by %khc
 Notes 07 largely plagiarized by %khc Warning This set of notes covers the Fourier transform. However, i probably won t talk about everything here in section; instead i will highlight important properties
Notes 07 largely plagiarized by %khc Warning This set of notes covers the Fourier transform. However, i probably won t talk about everything here in section; instead i will highlight important properties
Fourier Series. Spectral Analysis of Periodic Signals
 Fourier Series. Spectral Analysis of Periodic Signals he response of continuous-time linear invariant systems to the complex exponential with unitary magnitude response of a continuous-time LI system at
Fourier Series. Spectral Analysis of Periodic Signals he response of continuous-time linear invariant systems to the complex exponential with unitary magnitude response of a continuous-time LI system at
Homework 5 EE235, Summer 2013 Solution
 Homework 5 EE235, Summer 23 Solution. Fourier Series. Determine w and the non-zero Fourier series coefficients for the following functions: (a f(t 2 cos(3πt + sin(πt + π 3 w π f(t e j3πt + e j3πt + j2
Homework 5 EE235, Summer 23 Solution. Fourier Series. Determine w and the non-zero Fourier series coefficients for the following functions: (a f(t 2 cos(3πt + sin(πt + π 3 w π f(t e j3πt + e j3πt + j2
Fourier Representations of Signals & LTI Systems
 3. Introduction. A signal can be represented as a weighted superposition of complex sinusoids. x(t) or x[n] 2. LTI system: LTI System Output = A weighted superposition of the system response to each complex
3. Introduction. A signal can be represented as a weighted superposition of complex sinusoids. x(t) or x[n] 2. LTI system: LTI System Output = A weighted superposition of the system response to each complex
Review of Linear Time-Invariant Network Analysis
 D1 APPENDIX D Review of Linear Time-Invariant Network Analysis Consider a network with input x(t) and output y(t) as shown in Figure D-1. If an input x 1 (t) produces an output y 1 (t), and an input x
D1 APPENDIX D Review of Linear Time-Invariant Network Analysis Consider a network with input x(t) and output y(t) as shown in Figure D-1. If an input x 1 (t) produces an output y 1 (t), and an input x
GATE EE Topic wise Questions SIGNALS & SYSTEMS
 www.gatehelp.com GATE EE Topic wise Questions YEAR 010 ONE MARK Question. 1 For the system /( s + 1), the approximate time taken for a step response to reach 98% of the final value is (A) 1 s (B) s (C)
www.gatehelp.com GATE EE Topic wise Questions YEAR 010 ONE MARK Question. 1 For the system /( s + 1), the approximate time taken for a step response to reach 98% of the final value is (A) 1 s (B) s (C)
The Johns Hopkins University Department of Electrical and Computer Engineering Introduction to Linear Systems Fall 2002.
 The Johns Hopkins University Department of Electrical and Computer Engineering 505.460 Introduction to Linear Systems Fall 2002 Final exam Name: You are allowed to use: 1. Table 3.1 (page 206) & Table
The Johns Hopkins University Department of Electrical and Computer Engineering 505.460 Introduction to Linear Systems Fall 2002 Final exam Name: You are allowed to use: 1. Table 3.1 (page 206) & Table
Fourier series. Complex Fourier series. Positive and negative frequencies. Fourier series demonstration. Notes. Notes. Notes.
 Fourier series Fourier series of a periodic function f (t) with period T and corresponding angular frequency ω /T : f (t) a 0 + (a n cos(nωt) + b n sin(nωt)), n1 Fourier series is a linear sum of cosine
Fourier series Fourier series of a periodic function f (t) with period T and corresponding angular frequency ω /T : f (t) a 0 + (a n cos(nωt) + b n sin(nωt)), n1 Fourier series is a linear sum of cosine
Discrete Time Fourier Transform (DTFT)
 Discrete Time Fourier Transform (DTFT) 1 Discrete Time Fourier Transform (DTFT) The DTFT is the Fourier transform of choice for analyzing infinite-length signals and systems Useful for conceptual, pencil-and-paper
Discrete Time Fourier Transform (DTFT) 1 Discrete Time Fourier Transform (DTFT) The DTFT is the Fourier transform of choice for analyzing infinite-length signals and systems Useful for conceptual, pencil-and-paper
Continuous Time Signal Analysis: the Fourier Transform. Lathi Chapter 4
 Continuous Time Signal Analysis: the Fourier Transform Lathi Chapter 4 Topics Aperiodic signal representation by the Fourier integral (CTFT) Continuous-time Fourier transform Transforms of some useful
Continuous Time Signal Analysis: the Fourier Transform Lathi Chapter 4 Topics Aperiodic signal representation by the Fourier integral (CTFT) Continuous-time Fourier transform Transforms of some useful
Laplace Transforms and use in Automatic Control
 Laplace Transforms and use in Automatic Control P.S. Gandhi Mechanical Engineering IIT Bombay Acknowledgements: P.Santosh Krishna, SYSCON Recap Fourier series Fourier transform: aperiodic Convolution integral
Laplace Transforms and use in Automatic Control P.S. Gandhi Mechanical Engineering IIT Bombay Acknowledgements: P.Santosh Krishna, SYSCON Recap Fourier series Fourier transform: aperiodic Convolution integral
Core Concepts Review. Orthogonality of Complex Sinusoids Consider two (possibly non-harmonic) complex sinusoids
 Overview of Continuous-Time Fourier Transform Topics Definition Compare & contrast with Laplace transform Conditions for existence Relationship to LTI systems Examples Ideal lowpass filters Relationship
Overview of Continuous-Time Fourier Transform Topics Definition Compare & contrast with Laplace transform Conditions for existence Relationship to LTI systems Examples Ideal lowpass filters Relationship
2.161 Signal Processing: Continuous and Discrete Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu 2.6 Signal Processing: Continuous and Discrete Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS
MIT OpenCourseWare http://ocw.mit.edu 2.6 Signal Processing: Continuous and Discrete Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSETTS
Chapter 5 Frequency Domain Analysis of Systems
 Chapter 5 Frequency Domain Analysis of Systems CT, LTI Systems Consider the following CT LTI system: xt () ht () yt () Assumption: the impulse response h(t) is absolutely integrable, i.e., ht ( ) dt< (this
Chapter 5 Frequency Domain Analysis of Systems CT, LTI Systems Consider the following CT LTI system: xt () ht () yt () Assumption: the impulse response h(t) is absolutely integrable, i.e., ht ( ) dt< (this
1 Signals and systems
 978--52-5688-4 - Introduction to Orthogonal Transforms: With Applications in Data Processing and Analysis Signals and systems In the first two chapters we will consider some basic concepts and ideas as
978--52-5688-4 - Introduction to Orthogonal Transforms: With Applications in Data Processing and Analysis Signals and systems In the first two chapters we will consider some basic concepts and ideas as
The Laplace Transform
 The Laplace Transform Syllabus ECE 316, Spring 2015 Final Grades Homework (6 problems per week): 25% Exams (midterm and final): 50% (25:25) Random Quiz: 25% Textbook M. Roberts, Signals and Systems, 2nd
The Laplace Transform Syllabus ECE 316, Spring 2015 Final Grades Homework (6 problems per week): 25% Exams (midterm and final): 50% (25:25) Random Quiz: 25% Textbook M. Roberts, Signals and Systems, 2nd
2 Frequency-Domain Analysis
 2 requency-domain Analysis Electrical engineers live in the two worlds, so to speak, of time and frequency. requency-domain analysis is an extremely valuable tool to the communications engineer, more so
2 requency-domain Analysis Electrical engineers live in the two worlds, so to speak, of time and frequency. requency-domain analysis is an extremely valuable tool to the communications engineer, more so
ECE-700 Review. Phil Schniter. January 5, x c (t)e jωt dt, x[n]z n, Denoting a transform pair by x[n] X(z), some useful properties are
![ECE-700 Review. Phil Schniter. January 5, x c (t)e jωt dt, x[n]z n, Denoting a transform pair by x[n] X(z), some useful properties are ECE-700 Review. Phil Schniter. January 5, x c (t)e jωt dt, x[n]z n, Denoting a transform pair by x[n] X(z), some useful properties are](/thumbs/89/98815129.jpg) ECE-7 Review Phil Schniter January 5, 7 ransforms Using x c (t) to denote a continuous-time signal at time t R, Laplace ransform: X c (s) x c (t)e st dt, s C Continuous-ime Fourier ransform (CF): ote that:
ECE-7 Review Phil Schniter January 5, 7 ransforms Using x c (t) to denote a continuous-time signal at time t R, Laplace ransform: X c (s) x c (t)e st dt, s C Continuous-ime Fourier ransform (CF): ote that:
Discrete Time Signals and Systems Time-frequency Analysis. Gloria Menegaz
 Discrete Time Signals and Systems Time-frequency Analysis Gloria Menegaz Time-frequency Analysis Fourier transform (1D and 2D) Reference textbook: Discrete time signal processing, A.W. Oppenheim and R.W.
Discrete Time Signals and Systems Time-frequency Analysis Gloria Menegaz Time-frequency Analysis Fourier transform (1D and 2D) Reference textbook: Discrete time signal processing, A.W. Oppenheim and R.W.
Line Spectra and their Applications
 In [ ]: cd matlab pwd Line Spectra and their Applications Scope and Background Reading This session concludes our introduction to Fourier Series. Last time (http://nbviewer.jupyter.org/github/cpjobling/eg-47-
In [ ]: cd matlab pwd Line Spectra and their Applications Scope and Background Reading This session concludes our introduction to Fourier Series. Last time (http://nbviewer.jupyter.org/github/cpjobling/eg-47-
The Laplace Transform
 The Laplace Transform Generalizing the Fourier Transform The CTFT expresses a time-domain signal as a linear combination of complex sinusoids of the form e jωt. In the generalization of the CTFT to the
The Laplace Transform Generalizing the Fourier Transform The CTFT expresses a time-domain signal as a linear combination of complex sinusoids of the form e jωt. In the generalization of the CTFT to the
Homework 6 Solutions
 8-290 Signals and Systems Profs. Byron Yu and Pulkit Grover Fall 208 Homework 6 Solutions. Part One. (2 points) Consider an LTI system with impulse response h(t) e αt u(t), (a) Compute the frequency response
8-290 Signals and Systems Profs. Byron Yu and Pulkit Grover Fall 208 Homework 6 Solutions. Part One. (2 points) Consider an LTI system with impulse response h(t) e αt u(t), (a) Compute the frequency response
Complex symmetry Signals and Systems Fall 2015
 18-90 Signals and Systems Fall 015 Complex symmetry 1. Complex symmetry This section deals with the complex symmetry property. As an example I will use the DTFT for a aperiodic discrete-time signal. The
18-90 Signals and Systems Fall 015 Complex symmetry 1. Complex symmetry This section deals with the complex symmetry property. As an example I will use the DTFT for a aperiodic discrete-time signal. The
Signals, Systems, and Society. By: Carlos E. Davila
 Signals, Systems, and Society By: Carlos E. Davila Signals, Systems, and Society By: Carlos E. Davila Online: < http://cnx.org/content/col965/.5/ > C O N N E X I O N S Rice University, Houston, Texas
Signals, Systems, and Society By: Carlos E. Davila Signals, Systems, and Society By: Carlos E. Davila Online: < http://cnx.org/content/col965/.5/ > C O N N E X I O N S Rice University, Houston, Texas
ECE 3620: Laplace Transforms: Chapter 3:
 ECE 3620: Laplace Transforms: Chapter 3: 3.1-3.4 Prof. K. Chandra ECE, UMASS Lowell September 21, 2016 1 Analysis of LTI Systems in the Frequency Domain Thus far we have understood the relationship between
ECE 3620: Laplace Transforms: Chapter 3: 3.1-3.4 Prof. K. Chandra ECE, UMASS Lowell September 21, 2016 1 Analysis of LTI Systems in the Frequency Domain Thus far we have understood the relationship between
Ver 3808 E1.10 Fourier Series and Transforms (2014) E1.10 Fourier Series and Transforms. Problem Sheet 1 (Lecture 1)
 Ver 88 E. Fourier Series and Transforms 4 Key: [A] easy... [E]hard Questions from RBH textbook: 4., 4.8. E. Fourier Series and Transforms Problem Sheet Lecture. [B] Using the geometric progression formula,
Ver 88 E. Fourier Series and Transforms 4 Key: [A] easy... [E]hard Questions from RBH textbook: 4., 4.8. E. Fourier Series and Transforms Problem Sheet Lecture. [B] Using the geometric progression formula,
Signals and Systems I Have Known and Loved. Andrew W. Eckford
 Signals and Systems I Have Known and Loved Andrew W. Eckford Department of Electrical Engineering and Computer Science York University, oronto, Ontario, Canada Version: September 2, 216 Copyright c 215
Signals and Systems I Have Known and Loved Andrew W. Eckford Department of Electrical Engineering and Computer Science York University, oronto, Ontario, Canada Version: September 2, 216 Copyright c 215
Unit 2: Modeling in the Frequency Domain Part 2: The Laplace Transform. The Laplace Transform. The need for Laplace
 Unit : Modeling in the Frequency Domain Part : Engineering 81: Control Systems I Faculty of Engineering & Applied Science Memorial University of Newfoundland January 1, 010 1 Pair Table Unit, Part : Unit,
Unit : Modeling in the Frequency Domain Part : Engineering 81: Control Systems I Faculty of Engineering & Applied Science Memorial University of Newfoundland January 1, 010 1 Pair Table Unit, Part : Unit,
The Laplace Transform
 The Laplace Transform Introduction There are two common approaches to the developing and understanding the Laplace transform It can be viewed as a generalization of the CTFT to include some signals with
The Laplace Transform Introduction There are two common approaches to the developing and understanding the Laplace transform It can be viewed as a generalization of the CTFT to include some signals with
FROM ANALOGUE TO DIGITAL
 SIGNALS AND SYSTEMS: PAPER 3C1 HANDOUT 7. Dr David Corrigan 1. Electronic and Electrical Engineering Dept. corrigad@tcd.ie www.mee.tcd.ie/ corrigad FROM ANALOGUE TO DIGITAL To digitize signals it is necessary
SIGNALS AND SYSTEMS: PAPER 3C1 HANDOUT 7. Dr David Corrigan 1. Electronic and Electrical Engineering Dept. corrigad@tcd.ie www.mee.tcd.ie/ corrigad FROM ANALOGUE TO DIGITAL To digitize signals it is necessary
X. Chen More on Sampling
 X. Chen More on Sampling 9 More on Sampling 9.1 Notations denotes the sampling time in second. Ω s = 2π/ and Ω s /2 are, respectively, the sampling frequency and Nyquist frequency in rad/sec. Ω and ω denote,
X. Chen More on Sampling 9 More on Sampling 9.1 Notations denotes the sampling time in second. Ω s = 2π/ and Ω s /2 are, respectively, the sampling frequency and Nyquist frequency in rad/sec. Ω and ω denote,
7 The Waveform Channel
 7 The Waveform Channel The waveform transmitted by the digital demodulator will be corrupted by the channel before it reaches the digital demodulator in the receiver. One important part of the channel
7 The Waveform Channel The waveform transmitted by the digital demodulator will be corrupted by the channel before it reaches the digital demodulator in the receiver. One important part of the channel
Question Paper Code : AEC11T02
 Hall Ticket No Question Paper Code : AEC11T02 VARDHAMAN COLLEGE OF ENGINEERING (AUTONOMOUS) Affiliated to JNTUH, Hyderabad Four Year B. Tech III Semester Tutorial Question Bank 2013-14 (Regulations: VCE-R11)
Hall Ticket No Question Paper Code : AEC11T02 VARDHAMAN COLLEGE OF ENGINEERING (AUTONOMOUS) Affiliated to JNTUH, Hyderabad Four Year B. Tech III Semester Tutorial Question Bank 2013-14 (Regulations: VCE-R11)
Fourier Transform for Continuous Functions
 Fourier Transform for Continuous Functions Central goal: representing a signal by a set of orthogonal bases that are corresponding to frequencies or spectrum. Fourier series allows to find the spectrum
Fourier Transform for Continuous Functions Central goal: representing a signal by a set of orthogonal bases that are corresponding to frequencies or spectrum. Fourier series allows to find the spectrum
The Fourier Transform (and more )
 The Fourier Transform (and more ) imrod Peleg ov. 5 Outline Introduce Fourier series and transforms Introduce Discrete Time Fourier Transforms, (DTFT) Introduce Discrete Fourier Transforms (DFT) Consider
The Fourier Transform (and more ) imrod Peleg ov. 5 Outline Introduce Fourier series and transforms Introduce Discrete Time Fourier Transforms, (DTFT) Introduce Discrete Fourier Transforms (DFT) Consider
Ch.11 The Discrete-Time Fourier Transform (DTFT)
 EE2S11 Signals and Systems, part 2 Ch.11 The Discrete-Time Fourier Transform (DTFT Contents definition of the DTFT relation to the -transform, region of convergence, stability frequency plots convolution
EE2S11 Signals and Systems, part 2 Ch.11 The Discrete-Time Fourier Transform (DTFT Contents definition of the DTFT relation to the -transform, region of convergence, stability frequency plots convolution
16.362: Signals and Systems: 1.0
 16.362: Signals and Systems: 1.0 Prof. K. Chandra ECE, UMASS Lowell September 1, 2016 1 Background The pre-requisites for this course are Calculus II and Differential Equations. A basic understanding of
16.362: Signals and Systems: 1.0 Prof. K. Chandra ECE, UMASS Lowell September 1, 2016 1 Background The pre-requisites for this course are Calculus II and Differential Equations. A basic understanding of
The Continuous-time Fourier
 The Continuous-time Fourier Transform Rui Wang, Assistant professor Dept. of Information and Communication Tongji University it Email: ruiwang@tongji.edu.cn Outline Representation of Aperiodic signals:
The Continuous-time Fourier Transform Rui Wang, Assistant professor Dept. of Information and Communication Tongji University it Email: ruiwang@tongji.edu.cn Outline Representation of Aperiodic signals:
Review: Continuous Fourier Transform
 Review: Continuous Fourier Transform Review: convolution x t h t = x τ h(t τ)dτ Convolution in time domain Derivation Convolution Property Interchange the order of integrals Let Convolution Property By
Review: Continuous Fourier Transform Review: convolution x t h t = x τ h(t τ)dτ Convolution in time domain Derivation Convolution Property Interchange the order of integrals Let Convolution Property By
A.1 THE SAMPLED TIME DOMAIN AND THE Z TRANSFORM. 0 δ(t)dt = 1, (A.1) δ(t)dt =
 APPENDIX A THE Z TRANSFORM One of the most useful techniques in engineering or scientific analysis is transforming a problem from the time domain to the frequency domain ( 3). Using a Fourier or Laplace
APPENDIX A THE Z TRANSFORM One of the most useful techniques in engineering or scientific analysis is transforming a problem from the time domain to the frequency domain ( 3). Using a Fourier or Laplace
Linear systems, small signals, and integrators
 Linear systems, small signals, and integrators CNS WS05 Class Giacomo Indiveri Institute of Neuroinformatics University ETH Zurich Zurich, December 2005 Outline 1 Linear Systems Crash Course Linear Time-Invariant
Linear systems, small signals, and integrators CNS WS05 Class Giacomo Indiveri Institute of Neuroinformatics University ETH Zurich Zurich, December 2005 Outline 1 Linear Systems Crash Course Linear Time-Invariant
Review of Frequency Domain Fourier Series: Continuous periodic frequency components
 Today we will review: Review of Frequency Domain Fourier series why we use it trig form & exponential form how to get coefficients for each form Eigenfunctions what they are how they relate to LTI systems
Today we will review: Review of Frequency Domain Fourier series why we use it trig form & exponential form how to get coefficients for each form Eigenfunctions what they are how they relate to LTI systems
ECEN 420 LINEAR CONTROL SYSTEMS. Lecture 2 Laplace Transform I 1/52
 1/52 ECEN 420 LINEAR CONTROL SYSTEMS Lecture 2 Laplace Transform I Linear Time Invariant Systems A general LTI system may be described by the linear constant coefficient differential equation: a n d n
1/52 ECEN 420 LINEAR CONTROL SYSTEMS Lecture 2 Laplace Transform I Linear Time Invariant Systems A general LTI system may be described by the linear constant coefficient differential equation: a n d n
Sinc Functions. Continuous-Time Rectangular Pulse
 Sinc Functions The Cooper Union Department of Electrical Engineering ECE114 Digital Signal Processing Lecture Notes: Sinc Functions and Sampling Theory October 7, 2011 A rectangular pulse in time/frequency
Sinc Functions The Cooper Union Department of Electrical Engineering ECE114 Digital Signal Processing Lecture Notes: Sinc Functions and Sampling Theory October 7, 2011 A rectangular pulse in time/frequency
