A Bivariate Distribution whose Marginal Laws are Gamma and Macdonald
|
|
|
- Spencer Cole
- 5 years ago
- Views:
Transcription
1 International Journal of Mathematical Analysis Vol. 1, 216, no. 1, HIKARI Ltd, A Bivariate Distribution whose Marginal Laws are Gamma Macdonald Daya K. Nagar, dwin Zarrazola Luz stela Sánchez Instituto de Matematicas Universidad de Antioquia Calle 67, No. 5318, Medellin, Colombia Copyright c 216 Daya K. Nagar, dwin Zarrazola Luz stela Sánchez. This article is distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, reproduction in any medium, provided the original work is properly cited. Abstract Gamma Maconald distributions are associated with gamma extended gamma functions, respectively. In this article, we define a bivariate distribution whose marginal distributions are gamma Macdonald. We study several properties of this distribution. Mathematics Subject Classification: 3399, 65 Keywords: Confluent hypergeometric function; entropy; extended gamma function; gamma distribution; Laguerre polynomial 1 Introduction The gamma function was first introduced by Leonard uler in 1729 as the limit of a discrete expression later as an absolutely convergent improper integral, Γa) = t a 1 exp t) dt, Rea) >. 1) The gamma function has many beautiful properties has been used in almost all the branches of science engineering. Replacing t by z/σ, σ >,
2 456 Daya K. Nagar, dwin Zarrazola Luz stela Sánchez in 1), a more general definition of gamma function can be given as Γa) = σ a z a 1 exp z ) dz, Rea) >. 2) σ In statistical distribution theory, gamma function has been used extensively. Using integr of the gamma function 2), the gamma distribution has been defined by the probability density function p.d.f.) v a 1 exp v/σ), a >, σ >, v >. 3) σ a Γa) We will write V Ga, σ) if the density of V is given by 3). Here, a σ determine the shape scale of the distribution. In 1994, Chaudhry Zubair [3] defined the extended gamma function, Γa; σ), as Γa; σ) = t a 1 exp t σ ) dt, t where σ > a is any complex number. For Rea) > by taking σ =, it is clear that the above extension of the gamma function reduces to the classical gamma function, Γa, ) = Γa). The generalized gamma function extended) has been proved very useful in various problems in engineering physics, see for example, Chaudhry Zubair [2 6]. Using the integr of the extended gamma function, an extended gamma distribution can be defined by the p.d.f. v a 1 exp v σ/v), v >. Γa; σ) The distribution given by the above density will be designated as Ga, σ). By using the definition of the extended gamma function, Chaudhry Zubair [4] have introduced a one parameter Macdonald distribution. By making a slight change in the density proposed by Chaudhry Zubair [4], a three parameter Macdonald distribution Nagar, Roldán-Correa Gupta [7, 8]) is defined by the p.d.f. f M y; α, β, σ) = σ β y β 1 Γα; σ 1 y), y >, σ >, β >, α + β >. Γβ)Γα + β) We will denote it by Y Mα, β, σ). If σ = 1 in the density above, then we will simply write Y Mα, β). By replacing Γα; σ 1 y) by its integral representation, the three parameter Macdonald density can also be written as f M y; α, β, σ) = σ β y β 1 Γβ)Γα + β) exp x y ) x α 1 dx, y >, 4) σx
3 A bivariate distribution whose marginal laws are gamma Macdonald 457 where σ >, β > α + β >. Now, consider two rom variables X Y such that the conditional distribution of Y given X is gamma with the shape parameter β the scale parameter σx the marginal distribution of X is a stard gamma with the shape parameter α + β. That is fy x) = yβ 1 exp y/σx) Γβ)σx) β, y > gx) = xα+β 1 exp x), x >. Γα + β) Then 4) can be written as f M y; α, β, σ) = fy x)gx) dx. Thus, the product fy x)gx) can be used to create a bivariate density with Macdonald stard gamma as marginal densities of Y X, respectively. We, therefore, define the bivariate density of X Y as fx, y; α, β, σ) = xα 1 y β 1 exp x y/σx), x >, y >, 5) σ β Γβ)Γα + β) where β >, α + β > σ >. The distribution defined by the density 5) may be called the Macdonald-gamma distribution. The bivariate distribution defined by the above density has many interesting features. For example, the marginal the conditional distributions of Y are Macdonald gamma, the marginal distribution of X is gamma, the conditional distribution of X given Y is extended gamma. The gamma distribution has been used to model amounts of daily rainfall Aksoy [1]). In neuroscience, the gamma distribution is often used to describe the distribution of inter-spike intervals Robson Troy [9]). The gamma distribution is widely used as a conjugate prior in Bayesian statistics. It is the conjugate prior for the precision i.e. inverse of the variance) of a normal distribution. Further, the fact that marginal distributions are gamma makes this bivariate distribution a potential cidate for many real life problems. In this article, we study distributions defined by the density 5), derive properties such as marginal conditional distributions, moments, entropies, information matrix, distributions of sum quotient.
4 458 Daya K. Nagar, dwin Zarrazola Luz stela Sánchez 2 Properties Let us now briefly discuss the shape of 5). ln fx, y; α, β, σ) with respect to x y are The first order derivatives of f x x, y) = f y x, y) = ln fx, y; α, β, σ) x ln fx, y; α, β, σ) y = α 1 x = β 1 y + y σx 2 1 6) 1 σx 7) respectively. Setting 6) 7) to zero, we note that a, b), a = α + β 2, b = σβ 1)α + β 2) is a stationary point of 5). Computing second order derivatives of ln fx, y; α, β, σ), from 6) 7), we get f xx x, y) = 2 ln fx, y; α, β, σ) = α 1 2y x 2 x 2 σx, 8) 3 f xy x, y) = 2 ln fx, y; α, β, σ) x y = 1 σx 2, 9) f yy x, y) = 2 ln fx, y; α, β, σ) y 2 = β 1 y 2. 1) Further, from 8), 9) 1), we get f xx a, b) = α + 2β 3 α + β 2), f 1 yya, b) = 11) 2 σ 2 β 1)α + β 2) 2 f xx a, b)f yy a, b) [f xy a, b)] 2 = 1 σ 2 β 1)α + β 2) 3. 12) Now, observe that If β > 1 α+β > 2, then f xx a, b)f yy a, b) [f xy a, b)] 2 >, f xx a, b) < f yy a, b) < therefore a, b) is a maximum point. If β < 1 α+β < 2, then f xx a, b)f yy a, b) [f xy a, b)] 2 >, f xx a, b) > f yy a, b) > therefore a, b) is a minimum point. If β < 1 α + β > 2, then f xx a, b)f yy a, b) [f xy a, b)] 2 <, therefore a, b) is a saddle point.
5 A bivariate distribution whose marginal laws are gamma Macdonald 459 A distribution is said to be positively likelihood ratio dependent PLRD) if the density fx, y) satisfies fx 1, y 1 )fx 2, y 2 ) fx 1, y 2 )fx 2, y 1 ) 13) for all x 1 > x 2 y 1 > y 2. In the present case 13) is equivalent to y 1 x 2 + x 1 y 2 x 1 y 1 + x 2 y 2 which clearly holds. Olkin Liu [11] have listed a number of properties of PLRD distributions. By definition, the product moments of X Y associated with 5) are given by X r Y s ) = = σs Γβ + s) Γβ)Γα + β) x α+r 1 y β+s 1 exp x y/σx) dy dx σ β Γβ)Γα + β) x α+β+r+s 1 exp x) dx = σs Γβ + s)γα + β + r + s), 14) Γβ)Γα + β) where both the lines have been derived by using the definition of gamma function. For r = s, the above expression reduces to X s Y s ) = σs Γβ + s), 15) Γβ) which shows that Y/σX has a stard gamma distribution with shape parameter β. Substituting appropriately in 14), means variances of X Y the covariance between X Y are computed as X) = α + β, VarX) = α + β, Y ) = σβα + β), VarY ) = σ 2 βα + β)α + 2β + 1), CovX, Y ) = σβα + β). The correlation coefficient between X Y is given by β ρ X,Y = α + 2β + 1. The variance-covariance matrix Σ of the rom vector X, Y ) whose bivariate density is defined by 5) is given by [ ] 1 σβ Σ = α + β) σβ σ 2 βα + 2β + 1)
6 46 Daya K. Nagar, dwin Zarrazola Luz stela Sánchez Further, the inverse of the covariance matrix is given by Σ 1 = 1 σα + β)α + β + 1) [ ] σα + 2β + 1) βσ The well-known Mahalanobis distance is given by D 2 1 = [σα + 2β + 1)X 2 2XY + Y 2 σα + β)α + β + 1) βσ ] 2σα + β)α + β + 1)X + σα + β) 2 α + β + 1) with D 2 ) = 2 D 4 2 ) = βα + β)α + β + 1) [ ] βα + β)α + β + 4) + 3β + 1)α + β + 2)α + β + 3) From the construction of the bivariate density 5), it is cleat that Y Mα, β, σ), X Gα + β), Y x Gβ, σx) X y Gα, y/σ). Making the transformation S = X + Y R = Y/X + Y ) with the Jacobian Gy, x r, s) = s in 5), the joint density of R S is given by f R,S r, s; α, β, σ) = 1 r)α 1 r β 1 s α+β 1 exp [ s + rs r/σ1 r)], σ β Γβ)Γα + β) where < r < 1 s >. Now, integrating s by using gamma integral, the marginal density of R is derived as f R r; α, β, σ) = 1 r) β 1 r β 1 exp [ r/σ1 r)], < r < 1. σ β Γβ) From the above density it can easily be shown that R/σ1 R) = Y/σX has a stard gamma distribution with shape parameter β. By integrating r, the marginal density of S is derived as f S s; α, β, σ) = sα+β 1 exp s) σ β Γβ)Γα + β) 1 1 r) α 1 r β 1 exp [ ] r rs dr. σ1 r) Now, writing [ ] r exp = 1 r) σ1 r) ) 1 r m L m, σ m=
7 A bivariate distribution whose marginal laws are gamma Macdonald 461 where L m x) is the Laguerre polynomial of degree m, integrating r by using the integral representation of confluent hypergeometric function, we get the marginal density of S as f S s; α, β, σ) = sα+β 1 exp s) ) 1 1 L σ β m 1 r) α+1 1 r β+m 1 exp rs) dr Γβ)Γα + β) σ m= ) = Γα + 1)sα+β 1 exp s) σ β Γβ)Γα + β) m= L m 1 σ 1 F 1 β + m; α + β + m + 1; s), s >, where α + 1 >, β > σ >. 3 Central Moments Γβ + m) Γα + β + m + 1) By definition, the i, j)-th central joint moment of X, Y ) is given by µ ij = [X µ X ) i Y µ Y ) j ]. For different values of i j, expressions for µ ij are given by µ 3 = 2α + β), µ 21 = 2σβα + β), µ 12 = 2σ 2 βα + β)α + 2β + 1), µ 3 = 2σ 3 βα + β)[α + 2β + 1) 2 + β + 1)α + β + 1)], µ 4 = 3α + β)α + β + 2), µ 31 = 3σβα + β)α + β + 2), µ 22 = σ 2 βα + β)[3β + α + β + 1)α + 4β + 6)], µ 13 = 3σ 3 βα + β)[2β + 1)α + β + 1)α + 2β + 2) βα + β)α + 2β + 1)], µ 4 = 3σ 4 βα + β)[2β + 1)α + β + 1)α + 2β + 2)α + 2β + 3) βα + β)α + 2β + 1) 2 ], µ 5 = 4α + β)5α + 5β + 6), µ 41 = 4σβα + β)5α + 5β + 6), µ 32 = 4σ 2 βα + β)[4α α + β + 2)2α + 7β)]. 4 ntropies In this section, exact forms of Rényi Shannon entropies are determined for the bivariate distribution defined in Section 1.
8 462 Daya K. Nagar, dwin Zarrazola Luz stela Sánchez Let X, B, P) be a probability space. Consider a p.d.f. f associated with P, dominated by σ finite measure µ on X. Denote by H SH f) the well-known Shannon entropy introduced in Shannon [13]. It is define by H SH f) = fx) ln fx) dµ. 16) X One of the main extensions of the Shannon entropy was defined by Rényi [12]. This generalized entropy measure is given by where H R η, f) = ln Gη) 1 η Gη) = for η > η 1), 17) X f η dµ. The additional parameter η is used to describe complex behavior in probability models the associated process under study. Rényi entropy is monotonically decreasing in η, while Shannon entropy 16) is obtained from 17) for η 1. For details see Nadarajah Zografos [1], Zografos Nadarajah [15] Zografos [14]. Now, we derive the Rényi the Shannon entropies for the bivariate density defined in 5). Theorem 4.1. For the bivariate distribution defined by the p.d.f. 5), the Rényi the Shannon entropies are given by H R η, f) = 1 [ln Γ[ηβ 1) + 1] + ln Γ[ηα + β 2) + 2] η 1) ln σ 1 η [ηα + 2β 3) + 3] ln η η ln Γβ) η ln Γα + β)] 18) H SH f) = [β 1)ψβ) + α + β 2)ψα + β) ln σ α + 2β) ln Γβ) ln Γα + β)]. 19) Proof. For η > η 1, using the p.d.f. of X, Y ) given by 5), we have Gη) = = [fx, y; α, β, σ)] η dy dx 1 [σ β Γβ)Γα + β)] η Γ[ηβ 1) + 1] = σ η2β 1)+1 η ηβ 1)+1 [Γβ)Γα + β)] η Γ[ηβ 1) + 1]Γ[ηα + β 2) + 2] = σ η 1 η ηα+2β 3)+3 [Γβ)Γα + β)], η x ηα 1) y ηβ 1) exp ηx ηy σx ) dy dx x ηα+β 2)+1 exp ηx) dx
9 A bivariate distribution whose marginal laws are gamma Macdonald 463 where, to evaluate above integrals, we have used the definition of gamma function. Now, taking logarithm of Gη) using 17), we get 18). The Shannon entropy 19) is obtained from 18) by taking η 1 using L Hopital s rule. 5 Fisher Information Matrix In this section we calculate the Fisher information matrix for the bivariate distribution defined by the density 5). The information matrix plays a significant role in statistical inference in connection with estimation, sufficiency properties of variances of estimators. For a given observation vector x, y), the Fisher information matrix for the bivariate distribution defined by the density 5) is defined as 2 ln Lα,β,σ) ) α 2 ) ) 2 ln Lα,β,σ) β α 2 ln Lα,β,σ) σ α ) 2 ln Lα,β,σ) β α 2 ln Lα,β,σ) 2 ln Lα,β,σ) σ β ) β 2 ) 2 ln Lα,β,σ) σ α ) ) 2 ln Lα,β,σ) β σ ) 2 ln Lα,β,σ) σ 2, where Lα, β, σ) = ln fx, y; α, β, σ). Lα, β, σ) is obtained as From 5), the natural logarithm of ln Lα, β, σ) = β ln σ ln Γβ) ln Γα + β) + α 1) ln x + β 1) ln y x y σx, where x > y >. The second order partial derivatives of ln Lα, β, σ) are given by = ψ α 2 1 α + β), β 2 σ 2 α β = ψ 1 β) ψ 1 α + β), = β σ 2 2y σ 3 x, = ψ 1 α + β), =, α σ = 1 β σ σ,
10 464 Daya K. Nagar, dwin Zarrazola Luz stela Sánchez where ψ 1 ) is the trigamma function. Now, noting that the expected value of a constant is the constant itself Y/σX follows a stard gamma distribution with shape parameter β, we have 6 stimation ) = ψ α 2 1 α + β), ) = ψ β 2 1 β) ψ 1 α + β), ) = β σ 2 σ, 2 ) = ψ 1 α + β), α β ) =, α σ ) = 1 β σ σ. The density given by 5) is parameterized by α, β, σ). Here, we consider estimation of these three parameters by the method of maximum likelihood. Suppose x 1, y 1 ),..., x n, y n ) is a rom sample from 5). The loglikelihood can be expressed as: ln Lα, β, σ) = nβ ln σ n ln Γβ) n ln Γα + β) + α 1) + β 1) ln y i x i + y ) i. σx i ln x i The first-order derivatives of this with respect to the three parameters are: ln Lα, β, σ) α = nψα + β) + ln x i,
11 A bivariate distribution whose marginal laws are gamma Macdonald 465 ln Lα, β, σ) β = n ln σ nψβ) nψα + β) + ln Lα, β, σ) σ = nβ σ + 1 σ 2 y i x i. ln y i, The maximum likelihood estimators of α, β, σ), say ˆα, ˆβ, ˆσ), are the simultaneous solutions of the above three equations. It is straightforward to see that ˆβ can be calculated by solving numerically the equation [ ψ ˆβ) ln ˆβ = 1 ) )] yi y i ln ln. n Further, for ˆβ so obtained, ˆσ ˆα can be computed by solving numerically the equations ˆβˆσ = 1 y i n ψˆα + ˆβ) = 1 n x i x i ln x i respectively. Using the expansion of the digamma function, namely, ψz) = ln z z 1 48 z z z 199 ) z + 5 an approximation for ˆβ can be given as ˆβ = 1 [ ] 1 q 2 n q) 1, 1/n where q = n q i/n, q = n q i) 1/n q i = y i /x i, i = 1,..., n. Using this estimate of β, the estimates of σ α are given by [ ˆσ = 2 q q n q) 1/n 1 ˆα = x 1 ] 1 [1 n q)1/n, 2 q respectively, where x = n x i) 1/n. Acknowledgements. The research work of DKN LS was supported by the Sistema Universitario de Investigación, Universidad de Antioquia under the project no. IN1231C. ] x i
12 466 Daya K. Nagar, dwin Zarrazola Luz stela Sánchez References [1] H. Aksoy, Use of gamma distribution in hydrological analysis, Turkish Journal of ngineering nvironmental Sciences, 24 2), [2] M. Aslam Chaudhry Syed M. Zubair, On the decomposition of generalized incomplete gamma functions with applications to Fourier transforms, Journal of Computational Applied Mathematics, ), [3] M. A. Chaudhry S. M. Zubair, Generalized incomplete gamma functions with applications, Journal of Computational Applied Mathematics, ), [4] M. Aslam Chaudhry Syed M. Zubair, xtended gamma digamma functions, Fractional Calculus Applied Analysis, 4 21), no. 3, [5] M. Aslam Chaudhry Syed M. Zubair, xtended incomplete gamma functions with applications, Journal of Mathematical Analysis Applications, ), no. 2, [6] M. Aslam Chaudhry Syed M. Zubair, On an extension of generalized incomplete Gamma functions with applications, Journal of the Australian Mathematical Society Series B)- Applied Mathematics, ), no. 3, [7] Daya K. Nagar, Alejro Roldán-Correa Arjun K. Gupta, xtended matrix variate gamma beta functions, Journal of Multivariate Analysis, ), [8] Daya K. Nagar, Alejro Roldán-Correa Arjun K. Gupta, Matrix variate Macdonald distribution, Communications in Statistics - Theory Methods, ), no. 5, [9] J. G. Robson J. B. Troy, Nature of the maintained discharge of Q, X, Y retinal ganglion cells of the cat, Journal of the Optical Society of America A, ), [1] S. Nadarajah K. Zografos, xpressions for Rényi Shannon entropies for bivariate distributions, Information Sciences, 17 25), no. 2-4,
13 A bivariate distribution whose marginal laws are gamma Macdonald 467 [11] Ingram Olkin Ruixue Liu, A bivariate beta distribution, Statistics & Probability Letters, 62 23), no. 4, [12] A. Rényi, On measures of entropy information, Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics Probability, Vol. I, Univ. California Press, Berkeley, Calif., 1961), [13] C.. Shannon, A mathematical theory of communication, Bell System Technical Journal, ), , [14] K. Zografos, On maximum entropy characterization of Pearson s type II VII multivariate distributions, Journal of Multivariate Analysis, ), no. 1, [15] K. Zografos S. Nadarajah, xpressions for Rényi Shannon entropies for multivariate distributions, Statistics & Probability Letters, 71 25), no. 1, Received: February 23, 216; Published: April 1, 216
Properties and Applications of Extended Hypergeometric Functions
 Ingeniería y Ciencia ISSN:1794-9165 ISSN-e: 2256-4314 ing. cienc., vol. 1, no. 19, pp. 11 31, enero-junio. 214. http://www.eafit.edu.co/ingciencia This a open-access article distributed under the terms
Ingeniería y Ciencia ISSN:1794-9165 ISSN-e: 2256-4314 ing. cienc., vol. 1, no. 19, pp. 11 31, enero-junio. 214. http://www.eafit.edu.co/ingciencia This a open-access article distributed under the terms
The Distributions of Sums, Products and Ratios of Inverted Bivariate Beta Distribution 1
 Applied Mathematical Sciences, Vol. 2, 28, no. 48, 2377-2391 The Distributions of Sums, Products and Ratios of Inverted Bivariate Beta Distribution 1 A. S. Al-Ruzaiza and Awad El-Gohary 2 Department of
Applied Mathematical Sciences, Vol. 2, 28, no. 48, 2377-2391 The Distributions of Sums, Products and Ratios of Inverted Bivariate Beta Distribution 1 A. S. Al-Ruzaiza and Awad El-Gohary 2 Department of
Generalized Extended Whittaker Function and Its Properties
 Applied Mathematical Sciences, Vol. 9, 5, no. 3, 659-654 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.988/ams.5.58555 Generalized Extended Whittaker Function and Its Properties Junesang Choi Department
Applied Mathematical Sciences, Vol. 9, 5, no. 3, 659-654 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.988/ams.5.58555 Generalized Extended Whittaker Function and Its Properties Junesang Choi Department
Chapter 5 continued. Chapter 5 sections
 Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Estimation of the Bivariate Generalized. Lomax Distribution Parameters. Based on Censored Samples
 Int. J. Contemp. Math. Sciences, Vol. 9, 2014, no. 6, 257-267 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ijcms.2014.4329 Estimation of the Bivariate Generalized Lomax Distribution Parameters
Int. J. Contemp. Math. Sciences, Vol. 9, 2014, no. 6, 257-267 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ijcms.2014.4329 Estimation of the Bivariate Generalized Lomax Distribution Parameters
MATH c UNIVERSITY OF LEEDS Examination for the Module MATH2715 (January 2015) STATISTICAL METHODS. Time allowed: 2 hours
 MATH2750 This question paper consists of 8 printed pages, each of which is identified by the reference MATH275. All calculators must carry an approval sticker issued by the School of Mathematics. c UNIVERSITY
MATH2750 This question paper consists of 8 printed pages, each of which is identified by the reference MATH275. All calculators must carry an approval sticker issued by the School of Mathematics. c UNIVERSITY
Joint Distributions. (a) Scalar multiplication: k = c d. (b) Product of two matrices: c d. (c) The transpose of a matrix:
 Joint Distributions Joint Distributions A bivariate normal distribution generalizes the concept of normal distribution to bivariate random variables It requires a matrix formulation of quadratic forms,
Joint Distributions Joint Distributions A bivariate normal distribution generalizes the concept of normal distribution to bivariate random variables It requires a matrix formulation of quadratic forms,
MAS223 Statistical Modelling and Inference Examples
 Chapter MAS3 Statistical Modelling and Inference Examples Example : Sample spaces and random variables. Let S be the sample space for the experiment of tossing two coins; i.e. Define the random variables
Chapter MAS3 Statistical Modelling and Inference Examples Example : Sample spaces and random variables. Let S be the sample space for the experiment of tossing two coins; i.e. Define the random variables
2 Functions of random variables
 2 Functions of random variables A basic statistical model for sample data is a collection of random variables X 1,..., X n. The data are summarised in terms of certain sample statistics, calculated as
2 Functions of random variables A basic statistical model for sample data is a collection of random variables X 1,..., X n. The data are summarised in terms of certain sample statistics, calculated as
Information geometry for bivariate distribution control
 Information geometry for bivariate distribution control C.T.J.Dodson + Hong Wang Mathematics + Control Systems Centre, University of Manchester Institute of Science and Technology Optimal control of stochastic
Information geometry for bivariate distribution control C.T.J.Dodson + Hong Wang Mathematics + Control Systems Centre, University of Manchester Institute of Science and Technology Optimal control of stochastic
A Marshall-Olkin Gamma Distribution and Process
 CHAPTER 3 A Marshall-Olkin Gamma Distribution and Process 3.1 Introduction Gamma distribution is a widely used distribution in many fields such as lifetime data analysis, reliability, hydrology, medicine,
CHAPTER 3 A Marshall-Olkin Gamma Distribution and Process 3.1 Introduction Gamma distribution is a widely used distribution in many fields such as lifetime data analysis, reliability, hydrology, medicine,
Probability and Distributions
 Probability and Distributions What is a statistical model? A statistical model is a set of assumptions by which the hypothetical population distribution of data is inferred. It is typically postulated
Probability and Distributions What is a statistical model? A statistical model is a set of assumptions by which the hypothetical population distribution of data is inferred. It is typically postulated
MULTIVARIATE DISTRIBUTIONS
 Chapter 9 MULTIVARIATE DISTRIBUTIONS John Wishart (1898-1956) British statistician. Wishart was an assistant to Pearson at University College and to Fisher at Rothamsted. In 1928 he derived the distribution
Chapter 9 MULTIVARIATE DISTRIBUTIONS John Wishart (1898-1956) British statistician. Wishart was an assistant to Pearson at University College and to Fisher at Rothamsted. In 1928 he derived the distribution
Bivariate Generalization of The Inverted Hypergeometric Function Type I Distribution
 EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 5, No. 3,, 37-33 ISSN 37-5543 www.ejpam.com Bivariate Generalization of The Inverted Hypergeometric Function Type I Distribution Paula A. Bran-Cardona,
EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 5, No. 3,, 37-33 ISSN 37-5543 www.ejpam.com Bivariate Generalization of The Inverted Hypergeometric Function Type I Distribution Paula A. Bran-Cardona,
Generalized Simpson-like Type Integral Inequalities for Differentiable Convex Functions via Riemann-Liouville Integrals
 International Journal of Mathematical Analysis Vol. 9, 15, no. 16, 755-766 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/1.1988/ijma.15.534 Generalized Simpson-like Type Integral Ineualities for Differentiable
International Journal of Mathematical Analysis Vol. 9, 15, no. 16, 755-766 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/1.1988/ijma.15.534 Generalized Simpson-like Type Integral Ineualities for Differentiable
Parametric Stokes phenomena of Gauss s hypergeometric differential equation with a large parameter
 Parametric Stokes phenomena of Gauss s hypergeometric differential equation with a large parameter Mika TANDA (Kinki Univ) Collaborator :Takashi AOKI (Kinki Univ) Global Study of Differential Equations
Parametric Stokes phenomena of Gauss s hypergeometric differential equation with a large parameter Mika TANDA (Kinki Univ) Collaborator :Takashi AOKI (Kinki Univ) Global Study of Differential Equations
Linear Methods for Prediction
 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
Bayesian inference. Rasmus Waagepetersen Department of Mathematics Aalborg University Denmark. April 10, 2017
 Bayesian inference Rasmus Waagepetersen Department of Mathematics Aalborg University Denmark April 10, 2017 1 / 22 Outline for today A genetic example Bayes theorem Examples Priors Posterior summaries
Bayesian inference Rasmus Waagepetersen Department of Mathematics Aalborg University Denmark April 10, 2017 1 / 22 Outline for today A genetic example Bayes theorem Examples Priors Posterior summaries
Cheng Soon Ong & Christian Walder. Canberra February June 2018
 Cheng Soon Ong & Christian Walder Research Group and College of Engineering and Computer Science Canberra February June 2018 (Many figures from C. M. Bishop, "Pattern Recognition and ") 1of 89 Part II
Cheng Soon Ong & Christian Walder Research Group and College of Engineering and Computer Science Canberra February June 2018 (Many figures from C. M. Bishop, "Pattern Recognition and ") 1of 89 Part II
Statistics STAT:5100 (22S:193), Fall Sample Final Exam B
 Statistics STAT:5 (22S:93), Fall 25 Sample Final Exam B Please write your answers in the exam books provided.. Let X, Y, and Y 2 be independent random variables with X N(µ X, σ 2 X ) and Y i N(µ Y, σ 2
Statistics STAT:5 (22S:93), Fall 25 Sample Final Exam B Please write your answers in the exam books provided.. Let X, Y, and Y 2 be independent random variables with X N(µ X, σ 2 X ) and Y i N(µ Y, σ 2
USEFUL PROPERTIES OF THE MULTIVARIATE NORMAL*
 USEFUL PROPERTIES OF THE MULTIVARIATE NORMAL* 3 Conditionals and marginals For Bayesian analysis it is very useful to understand how to write joint, marginal, and conditional distributions for the multivariate
USEFUL PROPERTIES OF THE MULTIVARIATE NORMAL* 3 Conditionals and marginals For Bayesian analysis it is very useful to understand how to write joint, marginal, and conditional distributions for the multivariate
Solving Homogeneous Systems with Sub-matrices
 Pure Mathematical Sciences, Vol 7, 218, no 1, 11-18 HIKARI Ltd, wwwm-hikaricom https://doiorg/112988/pms218843 Solving Homogeneous Systems with Sub-matrices Massoud Malek Mathematics, California State
Pure Mathematical Sciences, Vol 7, 218, no 1, 11-18 HIKARI Ltd, wwwm-hikaricom https://doiorg/112988/pms218843 Solving Homogeneous Systems with Sub-matrices Massoud Malek Mathematics, California State
Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017
 Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Let X 1, X 2,, X n be a sequence of i.i.d. observations from a
Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Let X 1, X 2,, X n be a sequence of i.i.d. observations from a
Logistic-Modified Weibull Distribution and Parameter Estimation
 International Journal of Contemporary Mathematical Sciences Vol. 13, 2018, no. 1, 11-23 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/ijcms.2018.71135 Logistic-Modified Weibull Distribution and
International Journal of Contemporary Mathematical Sciences Vol. 13, 2018, no. 1, 11-23 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/ijcms.2018.71135 Logistic-Modified Weibull Distribution and
The Expansion of the Confluent Hypergeometric Function on the Positive Real Axis
 Applied Mathematical Sciences, Vol. 12, 2018, no. 1, 19-26 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/ams.2018.712351 The Expansion of the Confluent Hypergeometric Function on the Positive Real
Applied Mathematical Sciences, Vol. 12, 2018, no. 1, 19-26 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/ams.2018.712351 The Expansion of the Confluent Hypergeometric Function on the Positive Real
Asymptotic Variance Formulas, Gamma Functions, and Order Statistics
 Statistical Models and Methods for Lifetime Data, Second Edition by Jerald F. Lawless Copyright 2003 John Wiley & Sons, Inc. APPENDIX Β Asymptotic Variance Formulas, Gamma Functions, and Order Statistics
Statistical Models and Methods for Lifetime Data, Second Edition by Jerald F. Lawless Copyright 2003 John Wiley & Sons, Inc. APPENDIX Β Asymptotic Variance Formulas, Gamma Functions, and Order Statistics
INTRODUCING LINEAR REGRESSION MODELS Response or Dependent variable y
 INTRODUCING LINEAR REGRESSION MODELS Response or Dependent variable y Predictor or Independent variable x Model with error: for i = 1,..., n, y i = α + βx i + ε i ε i : independent errors (sampling, measurement,
INTRODUCING LINEAR REGRESSION MODELS Response or Dependent variable y Predictor or Independent variable x Model with error: for i = 1,..., n, y i = α + βx i + ε i ε i : independent errors (sampling, measurement,
Parameter Estimation
 Parameter Estimation Consider a sample of observations on a random variable Y. his generates random variables: (y 1, y 2,, y ). A random sample is a sample (y 1, y 2,, y ) where the random variables y
Parameter Estimation Consider a sample of observations on a random variable Y. his generates random variables: (y 1, y 2,, y ). A random sample is a sample (y 1, y 2,, y ) where the random variables y
Direct Product of BF-Algebras
 International Journal of Algebra, Vol. 10, 2016, no. 3, 125-132 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ija.2016.614 Direct Product of BF-Algebras Randy C. Teves and Joemar C. Endam Department
International Journal of Algebra, Vol. 10, 2016, no. 3, 125-132 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ija.2016.614 Direct Product of BF-Algebras Randy C. Teves and Joemar C. Endam Department
For iid Y i the stronger conclusion holds; for our heuristics ignore differences between these notions.
 Large Sample Theory Study approximate behaviour of ˆθ by studying the function U. Notice U is sum of independent random variables. Theorem: If Y 1, Y 2,... are iid with mean µ then Yi n µ Called law of
Large Sample Theory Study approximate behaviour of ˆθ by studying the function U. Notice U is sum of independent random variables. Theorem: If Y 1, Y 2,... are iid with mean µ then Yi n µ Called law of
ON THE NORMAL MOMENT DISTRIBUTIONS
 ON THE NORMAL MOMENT DISTRIBUTIONS Akin Olosunde Department of Statistics, P.M.B. 40, University of Agriculture, Abeokuta. 00, NIGERIA. Abstract Normal moment distribution is a particular case of well
ON THE NORMAL MOMENT DISTRIBUTIONS Akin Olosunde Department of Statistics, P.M.B. 40, University of Agriculture, Abeokuta. 00, NIGERIA. Abstract Normal moment distribution is a particular case of well
Statistics, Data Analysis, and Simulation SS 2015
 Statistics, Data Analysis, and Simulation SS 2015 08.128.730 Statistik, Datenanalyse und Simulation Dr. Michael O. Distler Mainz, 27. April 2015 Dr. Michael O. Distler
Statistics, Data Analysis, and Simulation SS 2015 08.128.730 Statistik, Datenanalyse und Simulation Dr. Michael O. Distler Mainz, 27. April 2015 Dr. Michael O. Distler
18 Bivariate normal distribution I
 8 Bivariate normal distribution I 8 Example Imagine firing arrows at a target Hopefully they will fall close to the target centre As we fire more arrows we find a high density near the centre and fewer
8 Bivariate normal distribution I 8 Example Imagine firing arrows at a target Hopefully they will fall close to the target centre As we fire more arrows we find a high density near the centre and fewer
Solution. (i) Find a minimal sufficient statistic for (θ, β) and give your justification. X i=1. By the factorization theorem, ( n
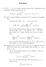 Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Week 10 Worksheet. Math 4653, Section 001 Elementary Probability Fall Ice Breaker Question: Do you prefer waffles or pancakes?
 Week 10 Worksheet Ice Breaker Question: Do you prefer waffles or pancakes? 1. Suppose X, Y have joint density f(x, y) = 12 7 (xy + y2 ) on 0 < x < 1, 0 < y < 1. (a) What are the marginal densities of X
Week 10 Worksheet Ice Breaker Question: Do you prefer waffles or pancakes? 1. Suppose X, Y have joint density f(x, y) = 12 7 (xy + y2 ) on 0 < x < 1, 0 < y < 1. (a) What are the marginal densities of X
t x 1 e t dt, and simplify the answer when possible (for example, when r is a positive even number). In particular, confirm that EX 4 = 3.
 Mathematical Statistics: Homewor problems General guideline. While woring outside the classroom, use any help you want, including people, computer algebra systems, Internet, and solution manuals, but mae
Mathematical Statistics: Homewor problems General guideline. While woring outside the classroom, use any help you want, including people, computer algebra systems, Internet, and solution manuals, but mae
Statistical Methods for Handling Incomplete Data Chapter 2: Likelihood-based approach
 Statistical Methods for Handling Incomplete Data Chapter 2: Likelihood-based approach Jae-Kwang Kim Department of Statistics, Iowa State University Outline 1 Introduction 2 Observed likelihood 3 Mean Score
Statistical Methods for Handling Incomplete Data Chapter 2: Likelihood-based approach Jae-Kwang Kim Department of Statistics, Iowa State University Outline 1 Introduction 2 Observed likelihood 3 Mean Score
Let X and Y denote two random variables. The joint distribution of these random
 EE385 Class Notes 9/7/0 John Stensby Chapter 3: Multiple Random Variables Let X and Y denote two random variables. The joint distribution of these random variables is defined as F XY(x,y) = [X x,y y] P.
EE385 Class Notes 9/7/0 John Stensby Chapter 3: Multiple Random Variables Let X and Y denote two random variables. The joint distribution of these random variables is defined as F XY(x,y) = [X x,y y] P.
Linear Methods for Prediction
 Chapter 5 Linear Methods for Prediction 5.1 Introduction We now revisit the classification problem and focus on linear methods. Since our prediction Ĝ(x) will always take values in the discrete set G we
Chapter 5 Linear Methods for Prediction 5.1 Introduction We now revisit the classification problem and focus on linear methods. Since our prediction Ĝ(x) will always take values in the discrete set G we
Empirical Comparison of ML and UMVU Estimators of the Generalized Variance for some Normal Stable Tweedie Models: a Simulation Study
 Applied Mathematical Sciences, Vol. 10, 2016, no. 63, 3107-3118 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/ams.2016.69238 Empirical Comparison of and Estimators of the Generalized Variance for
Applied Mathematical Sciences, Vol. 10, 2016, no. 63, 3107-3118 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/ams.2016.69238 Empirical Comparison of and Estimators of the Generalized Variance for
Stat 5101 Notes: Brand Name Distributions
 Stat 5101 Notes: Brand Name Distributions Charles J. Geyer February 14, 2003 1 Discrete Uniform Distribution DiscreteUniform(n). Discrete. Rationale Equally likely outcomes. The interval 1, 2,..., n of
Stat 5101 Notes: Brand Name Distributions Charles J. Geyer February 14, 2003 1 Discrete Uniform Distribution DiscreteUniform(n). Discrete. Rationale Equally likely outcomes. The interval 1, 2,..., n of
k-weyl Fractional Derivative, Integral and Integral Transform
 Int. J. Contemp. Math. Sciences, Vol. 8, 213, no. 6, 263-27 HIKARI Ltd, www.m-hiari.com -Weyl Fractional Derivative, Integral and Integral Transform Luis Guillermo Romero 1 and Luciano Leonardo Luque Faculty
Int. J. Contemp. Math. Sciences, Vol. 8, 213, no. 6, 263-27 HIKARI Ltd, www.m-hiari.com -Weyl Fractional Derivative, Integral and Integral Transform Luis Guillermo Romero 1 and Luciano Leonardo Luque Faculty
Stieltjes Transformation as the Iterated Laplace Transformation
 International Journal of Mathematical Analysis Vol. 11, 2017, no. 17, 833-838 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/ijma.2017.7796 Stieltjes Transformation as the Iterated Laplace Transformation
International Journal of Mathematical Analysis Vol. 11, 2017, no. 17, 833-838 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/ijma.2017.7796 Stieltjes Transformation as the Iterated Laplace Transformation
COPYRIGHTED MATERIAL CONTENTS. Preface Preface to the First Edition
 Preface Preface to the First Edition xi xiii 1 Basic Probability Theory 1 1.1 Introduction 1 1.2 Sample Spaces and Events 3 1.3 The Axioms of Probability 7 1.4 Finite Sample Spaces and Combinatorics 15
Preface Preface to the First Edition xi xiii 1 Basic Probability Theory 1 1.1 Introduction 1 1.2 Sample Spaces and Events 3 1.3 The Axioms of Probability 7 1.4 Finite Sample Spaces and Combinatorics 15
Z. Omar. Department of Mathematics School of Quantitative Sciences College of Art and Sciences Univeristi Utara Malaysia, Malaysia. Ra ft.
 International Journal of Mathematical Analysis Vol. 9, 015, no. 46, 57-7 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.1988/ijma.015.57181 Developing a Single Step Hybrid Block Method with Generalized
International Journal of Mathematical Analysis Vol. 9, 015, no. 46, 57-7 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.1988/ijma.015.57181 Developing a Single Step Hybrid Block Method with Generalized
Multiple Random Variables
 Multiple Random Variables This Version: July 30, 2015 Multiple Random Variables 2 Now we consider models with more than one r.v. These are called multivariate models For instance: height and weight An
Multiple Random Variables This Version: July 30, 2015 Multiple Random Variables 2 Now we consider models with more than one r.v. These are called multivariate models For instance: height and weight An
1 Uniform Distribution. 2 Gamma Distribution. 3 Inverse Gamma Distribution. 4 Multivariate Normal Distribution. 5 Multivariate Student-t Distribution
 A Few Special Distributions Their Properties Econ 675 Iowa State University November 1 006 Justin L Tobias (ISU Distributional Catalog November 1 006 1 / 0 Special Distributions Their Associated Properties
A Few Special Distributions Their Properties Econ 675 Iowa State University November 1 006 Justin L Tobias (ISU Distributional Catalog November 1 006 1 / 0 Special Distributions Their Associated Properties
Continuous Random Variables 1
 Continuous Random Variables 1 STA 256: Fall 2018 1 This slide show is an open-source document. See last slide for copyright information. 1 / 32 Continuous Random Variables: The idea Probability is area
Continuous Random Variables 1 STA 256: Fall 2018 1 This slide show is an open-source document. See last slide for copyright information. 1 / 32 Continuous Random Variables: The idea Probability is area
Continuous Random Variables
 1 / 24 Continuous Random Variables Saravanan Vijayakumaran sarva@ee.iitb.ac.in Department of Electrical Engineering Indian Institute of Technology Bombay February 27, 2013 2 / 24 Continuous Random Variables
1 / 24 Continuous Random Variables Saravanan Vijayakumaran sarva@ee.iitb.ac.in Department of Electrical Engineering Indian Institute of Technology Bombay February 27, 2013 2 / 24 Continuous Random Variables
Lecture 25: Review. Statistics 104. April 23, Colin Rundel
 Lecture 25: Review Statistics 104 Colin Rundel April 23, 2012 Joint CDF F (x, y) = P [X x, Y y] = P [(X, Y ) lies south-west of the point (x, y)] Y (x,y) X Statistics 104 (Colin Rundel) Lecture 25 April
Lecture 25: Review Statistics 104 Colin Rundel April 23, 2012 Joint CDF F (x, y) = P [X x, Y y] = P [(X, Y ) lies south-west of the point (x, y)] Y (x,y) X Statistics 104 (Colin Rundel) Lecture 25 April
1. Prove the following properties satisfied by the gamma function: 4 n n!
 Math 205A: Complex Analysis, Winter 208 Homework Problem Set #6 February 20, 208. Prove the following properties satisfied by the gamma function: (a) Values at half-integers: Γ ( n + 2 (b) The duplication
Math 205A: Complex Analysis, Winter 208 Homework Problem Set #6 February 20, 208. Prove the following properties satisfied by the gamma function: (a) Values at half-integers: Γ ( n + 2 (b) The duplication
Dependence. Practitioner Course: Portfolio Optimization. John Dodson. September 10, Dependence. John Dodson. Outline.
 Practitioner Course: Portfolio Optimization September 10, 2008 Before we define dependence, it is useful to define Random variables X and Y are independent iff For all x, y. In particular, F (X,Y ) (x,
Practitioner Course: Portfolio Optimization September 10, 2008 Before we define dependence, it is useful to define Random variables X and Y are independent iff For all x, y. In particular, F (X,Y ) (x,
On Symmetric Bi-Multipliers of Lattice Implication Algebras
 International Mathematical Forum, Vol. 13, 2018, no. 7, 343-350 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/imf.2018.8423 On Symmetric Bi-Multipliers of Lattice Implication Algebras Kyung Ho
International Mathematical Forum, Vol. 13, 2018, no. 7, 343-350 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/imf.2018.8423 On Symmetric Bi-Multipliers of Lattice Implication Algebras Kyung Ho
Probability Distributions
 Probability Distributions Seungjin Choi Department of Computer Science Pohang University of Science and Technology, Korea seungjin@postech.ac.kr 1 / 25 Outline Summarize the main properties of some of
Probability Distributions Seungjin Choi Department of Computer Science Pohang University of Science and Technology, Korea seungjin@postech.ac.kr 1 / 25 Outline Summarize the main properties of some of
Topic 12 Overview of Estimation
 Topic 12 Overview of Estimation Classical Statistics 1 / 9 Outline Introduction Parameter Estimation Classical Statistics Densities and Likelihoods 2 / 9 Introduction In the simplest possible terms, the
Topic 12 Overview of Estimation Classical Statistics 1 / 9 Outline Introduction Parameter Estimation Classical Statistics Densities and Likelihoods 2 / 9 Introduction In the simplest possible terms, the
Bivariate Transformations
 Bivariate Transformations October 29, 29 Let X Y be jointly continuous rom variables with density function f X,Y let g be a one to one transformation. Write (U, V ) = g(x, Y ). The goal is to find the
Bivariate Transformations October 29, 29 Let X Y be jointly continuous rom variables with density function f X,Y let g be a one to one transformation. Write (U, V ) = g(x, Y ). The goal is to find the
One-Step Hybrid Block Method with One Generalized Off-Step Points for Direct Solution of Second Order Ordinary Differential Equations
 Applied Mathematical Sciences, Vol. 10, 2016, no. 29, 142-142 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ams.2016.6127 One-Step Hybrid Block Method with One Generalized Off-Step Points for
Applied Mathematical Sciences, Vol. 10, 2016, no. 29, 142-142 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ams.2016.6127 One-Step Hybrid Block Method with One Generalized Off-Step Points for
A Probability Review
 A Probability Review Outline: A probability review Shorthand notation: RV stands for random variable EE 527, Detection and Estimation Theory, # 0b 1 A Probability Review Reading: Go over handouts 2 5 in
A Probability Review Outline: A probability review Shorthand notation: RV stands for random variable EE 527, Detection and Estimation Theory, # 0b 1 A Probability Review Reading: Go over handouts 2 5 in
A Very Brief Summary of Statistical Inference, and Examples
 A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2008 Prof. Gesine Reinert 1 Data x = x 1, x 2,..., x n, realisations of random variables X 1, X 2,..., X n with distribution (model)
A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2008 Prof. Gesine Reinert 1 Data x = x 1, x 2,..., x n, realisations of random variables X 1, X 2,..., X n with distribution (model)
Ingeniería y Ciencia ISSN: Universidad EAFIT Colombia
 Ingeniería y Ciencia ISSN: 794-965 ingciencia@eafit.edu.co Universidad EAFIT Colombia Zarrazola, Edwin; Nagar, Daya K. Product of independent random variables involving inverted hypergeometric function
Ingeniería y Ciencia ISSN: 794-965 ingciencia@eafit.edu.co Universidad EAFIT Colombia Zarrazola, Edwin; Nagar, Daya K. Product of independent random variables involving inverted hypergeometric function
EEL 5544 Noise in Linear Systems Lecture 30. X (s) = E [ e sx] f X (x)e sx dx. Moments can be found from the Laplace transform as
![EEL 5544 Noise in Linear Systems Lecture 30. X (s) = E [ e sx] f X (x)e sx dx. Moments can be found from the Laplace transform as EEL 5544 Noise in Linear Systems Lecture 30. X (s) = E [ e sx] f X (x)e sx dx. Moments can be found from the Laplace transform as](/thumbs/85/92409620.jpg) L30-1 EEL 5544 Noise in Linear Systems Lecture 30 OTHER TRANSFORMS For a continuous, nonnegative RV X, the Laplace transform of X is X (s) = E [ e sx] = 0 f X (x)e sx dx. For a nonnegative RV, the Laplace
L30-1 EEL 5544 Noise in Linear Systems Lecture 30 OTHER TRANSFORMS For a continuous, nonnegative RV X, the Laplace transform of X is X (s) = E [ e sx] = 0 f X (x)e sx dx. For a nonnegative RV, the Laplace
The Delta Method and Applications
 Chapter 5 The Delta Method and Applications 5.1 Local linear approximations Suppose that a particular random sequence converges in distribution to a particular constant. The idea of using a first-order
Chapter 5 The Delta Method and Applications 5.1 Local linear approximations Suppose that a particular random sequence converges in distribution to a particular constant. The idea of using a first-order
On Generalized Entropy Measures and Non-extensive Statistical Mechanics
 First Prev Next Last On Generalized Entropy Measures and Non-extensive Statistical Mechanics A. M. MATHAI [Emeritus Professor of Mathematics and Statistics, McGill University, Canada, and Director, Centre
First Prev Next Last On Generalized Entropy Measures and Non-extensive Statistical Mechanics A. M. MATHAI [Emeritus Professor of Mathematics and Statistics, McGill University, Canada, and Director, Centre
Bayesian Inference. Chapter 9. Linear models and regression
 Bayesian Inference Chapter 9. Linear models and regression M. Concepcion Ausin Universidad Carlos III de Madrid Master in Business Administration and Quantitative Methods Master in Mathematical Engineering
Bayesian Inference Chapter 9. Linear models and regression M. Concepcion Ausin Universidad Carlos III de Madrid Master in Business Administration and Quantitative Methods Master in Mathematical Engineering
P (x). all other X j =x j. If X is a continuous random vector (see p.172), then the marginal distributions of X i are: f(x)dx 1 dx n
 JOINT DENSITIES - RANDOM VECTORS - REVIEW Joint densities describe probability distributions of a random vector X: an n-dimensional vector of random variables, ie, X = (X 1,, X n ), where all X is are
JOINT DENSITIES - RANDOM VECTORS - REVIEW Joint densities describe probability distributions of a random vector X: an n-dimensional vector of random variables, ie, X = (X 1,, X n ), where all X is are
Statement: With my signature I confirm that the solutions are the product of my own work. Name: Signature:.
 MATHEMATICAL STATISTICS Homework assignment Instructions Please turn in the homework with this cover page. You do not need to edit the solutions. Just make sure the handwriting is legible. You may discuss
MATHEMATICAL STATISTICS Homework assignment Instructions Please turn in the homework with this cover page. You do not need to edit the solutions. Just make sure the handwriting is legible. You may discuss
Research on Independence of. Random Variables
 Applied Mathematical Sciences, Vol., 08, no. 3, - 7 HIKARI Ltd, www.m-hikari.com https://doi.org/0.988/ams.08.8708 Research on Independence of Random Variables Jian Wang and Qiuli Dong School of Mathematics
Applied Mathematical Sciences, Vol., 08, no. 3, - 7 HIKARI Ltd, www.m-hikari.com https://doi.org/0.988/ams.08.8708 Research on Independence of Random Variables Jian Wang and Qiuli Dong School of Mathematics
MAS223 Statistical Inference and Modelling Exercises and Solutions
 MAS3 Statistical Inference and Modelling Exercises and Solutions The exercises are grouped into sections, corresponding to chapters of the lecture notes Within each section exercises are divided into warm-up
MAS3 Statistical Inference and Modelling Exercises and Solutions The exercises are grouped into sections, corresponding to chapters of the lecture notes Within each section exercises are divided into warm-up
Covariance. Lecture 20: Covariance / Correlation & General Bivariate Normal. Covariance, cont. Properties of Covariance
 Covariance Lecture 0: Covariance / Correlation & General Bivariate Normal Sta30 / Mth 30 We have previously discussed Covariance in relation to the variance of the sum of two random variables Review Lecture
Covariance Lecture 0: Covariance / Correlation & General Bivariate Normal Sta30 / Mth 30 We have previously discussed Covariance in relation to the variance of the sum of two random variables Review Lecture
Convex Sets Strict Separation in Hilbert Spaces
 Applied Mathematical Sciences, Vol. 8, 2014, no. 64, 3155-3160 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ams.2014.44257 Convex Sets Strict Separation in Hilbert Spaces M. A. M. Ferreira 1
Applied Mathematical Sciences, Vol. 8, 2014, no. 64, 3155-3160 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ams.2014.44257 Convex Sets Strict Separation in Hilbert Spaces M. A. M. Ferreira 1
4. Distributions of Functions of Random Variables
 4. Distributions of Functions of Random Variables Setup: Consider as given the joint distribution of X 1,..., X n (i.e. consider as given f X1,...,X n and F X1,...,X n ) Consider k functions g 1 : R n
4. Distributions of Functions of Random Variables Setup: Consider as given the joint distribution of X 1,..., X n (i.e. consider as given f X1,...,X n and F X1,...,X n ) Consider k functions g 1 : R n
Inference and Regression
 Inference and Regression Assignment 3 Department of IOMS Professor William Greene Phone:.998.0876 Office: KMC 7-90 Home page:www.stern.nyu.edu/~wgreene Email: wgreene@stern.nyu.edu Course web page: www.stern.nyu.edu/~wgreene/econometrics/econometrics.htm.
Inference and Regression Assignment 3 Department of IOMS Professor William Greene Phone:.998.0876 Office: KMC 7-90 Home page:www.stern.nyu.edu/~wgreene Email: wgreene@stern.nyu.edu Course web page: www.stern.nyu.edu/~wgreene/econometrics/econometrics.htm.
Deccan Education Society s FERGUSSON COLLEGE, PUNE (AUTONOMOUS) SYLLABUS UNDER AUTOMONY. SECOND YEAR B.Sc. SEMESTER - III
 Deccan Education Society s FERGUSSON COLLEGE, PUNE (AUTONOMOUS) SYLLABUS UNDER AUTOMONY SECOND YEAR B.Sc. SEMESTER - III SYLLABUS FOR S. Y. B. Sc. STATISTICS Academic Year 07-8 S.Y. B.Sc. (Statistics)
Deccan Education Society s FERGUSSON COLLEGE, PUNE (AUTONOMOUS) SYLLABUS UNDER AUTOMONY SECOND YEAR B.Sc. SEMESTER - III SYLLABUS FOR S. Y. B. Sc. STATISTICS Academic Year 07-8 S.Y. B.Sc. (Statistics)
Further results involving Marshall Olkin log logistic distribution: reliability analysis, estimation of the parameter, and applications
 DOI 1.1186/s464-16-27- RESEARCH Open Access Further results involving Marshall Olkin log logistic distribution: reliability analysis, estimation of the parameter, and applications Arwa M. Alshangiti *,
DOI 1.1186/s464-16-27- RESEARCH Open Access Further results involving Marshall Olkin log logistic distribution: reliability analysis, estimation of the parameter, and applications Arwa M. Alshangiti *,
ECON 3150/4150, Spring term Lecture 7
 ECON 3150/4150, Spring term 2014. Lecture 7 The multivariate regression model (I) Ragnar Nymoen University of Oslo 4 February 2014 1 / 23 References to Lecture 7 and 8 SW Ch. 6 BN Kap 7.1-7.8 2 / 23 Omitted
ECON 3150/4150, Spring term 2014. Lecture 7 The multivariate regression model (I) Ragnar Nymoen University of Oslo 4 February 2014 1 / 23 References to Lecture 7 and 8 SW Ch. 6 BN Kap 7.1-7.8 2 / 23 Omitted
Random vectors X 1 X 2. Recall that a random vector X = is made up of, say, k. X k. random variables.
 Random vectors Recall that a random vector X = X X 2 is made up of, say, k random variables X k A random vector has a joint distribution, eg a density f(x), that gives probabilities P(X A) = f(x)dx Just
Random vectors Recall that a random vector X = X X 2 is made up of, say, k random variables X k A random vector has a joint distribution, eg a density f(x), that gives probabilities P(X A) = f(x)dx Just
Basics on Probability. Jingrui He 09/11/2007
 Basics on Probability Jingrui He 09/11/2007 Coin Flips You flip a coin Head with probability 0.5 You flip 100 coins How many heads would you expect Coin Flips cont. You flip a coin Head with probability
Basics on Probability Jingrui He 09/11/2007 Coin Flips You flip a coin Head with probability 0.5 You flip 100 coins How many heads would you expect Coin Flips cont. You flip a coin Head with probability
Multivariate Statistics
 Multivariate Statistics Chapter 2: Multivariate distributions and inference Pedro Galeano Departamento de Estadística Universidad Carlos III de Madrid pedro.galeano@uc3m.es Course 2016/2017 Master in Mathematical
Multivariate Statistics Chapter 2: Multivariate distributions and inference Pedro Galeano Departamento de Estadística Universidad Carlos III de Madrid pedro.galeano@uc3m.es Course 2016/2017 Master in Mathematical
Math 3215 Intro. Probability & Statistics Summer 14. Homework 5: Due 7/3/14
 Math 325 Intro. Probability & Statistics Summer Homework 5: Due 7/3/. Let X and Y be continuous random variables with joint/marginal p.d.f. s f(x, y) 2, x y, f (x) 2( x), x, f 2 (y) 2y, y. Find the conditional
Math 325 Intro. Probability & Statistics Summer Homework 5: Due 7/3/. Let X and Y be continuous random variables with joint/marginal p.d.f. s f(x, y) 2, x y, f (x) 2( x), x, f 2 (y) 2y, y. Find the conditional
APPLICATION OF INFORMATION ENTROPY AND FRACTIONAL CALCULUS IN EMULSIFICATION PROCESSES
 14 th European Conference on Mixing Warszawa, 10-13 September 2012 APPLICATION OF INFORMATION ENTROPY AND FRACTIONAL CALCULUS IN EMULSIFICATION PROCESSES Barbara Tal-Figiel Cracow University of Technology,
14 th European Conference on Mixing Warszawa, 10-13 September 2012 APPLICATION OF INFORMATION ENTROPY AND FRACTIONAL CALCULUS IN EMULSIFICATION PROCESSES Barbara Tal-Figiel Cracow University of Technology,
Improvements in Newton-Rapshon Method for Nonlinear Equations Using Modified Adomian Decomposition Method
 International Journal of Mathematical Analysis Vol. 9, 2015, no. 39, 1919-1928 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ijma.2015.54124 Improvements in Newton-Rapshon Method for Nonlinear
International Journal of Mathematical Analysis Vol. 9, 2015, no. 39, 1919-1928 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ijma.2015.54124 Improvements in Newton-Rapshon Method for Nonlinear
Continuous Random Variables and Continuous Distributions
 Continuous Random Variables and Continuous Distributions Continuous Random Variables and Continuous Distributions Expectation & Variance of Continuous Random Variables ( 5.2) The Uniform Random Variable
Continuous Random Variables and Continuous Distributions Continuous Random Variables and Continuous Distributions Expectation & Variance of Continuous Random Variables ( 5.2) The Uniform Random Variable
MATH 38061/MATH48061/MATH68061: MULTIVARIATE STATISTICS Solutions to Problems on Random Vectors and Random Sampling. 1+ x2 +y 2 ) (n+2)/2
 MATH 3806/MATH4806/MATH6806: MULTIVARIATE STATISTICS Solutions to Problems on Rom Vectors Rom Sampling Let X Y have the joint pdf: fx,y) + x +y ) n+)/ π n for < x < < y < this is particular case of the
MATH 3806/MATH4806/MATH6806: MULTIVARIATE STATISTICS Solutions to Problems on Rom Vectors Rom Sampling Let X Y have the joint pdf: fx,y) + x +y ) n+)/ π n for < x < < y < this is particular case of the
A Non-uniform Bound on Poisson Approximation in Beta Negative Binomial Distribution
 International Mathematical Forum, Vol. 14, 2019, no. 2, 57-67 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/imf.2019.915 A Non-uniform Bound on Poisson Approximation in Beta Negative Binomial Distribution
International Mathematical Forum, Vol. 14, 2019, no. 2, 57-67 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/imf.2019.915 A Non-uniform Bound on Poisson Approximation in Beta Negative Binomial Distribution
Introduction to Probability and Stocastic Processes - Part I
 Introduction to Probability and Stocastic Processes - Part I Lecture 2 Henrik Vie Christensen vie@control.auc.dk Department of Control Engineering Institute of Electronic Systems Aalborg University Denmark
Introduction to Probability and Stocastic Processes - Part I Lecture 2 Henrik Vie Christensen vie@control.auc.dk Department of Control Engineering Institute of Electronic Systems Aalborg University Denmark
Exercises and Answers to Chapter 1
 Exercises and Answers to Chapter The continuous type of random variable X has the following density function: a x, if < x < a, f (x), otherwise. Answer the following questions. () Find a. () Obtain mean
Exercises and Answers to Chapter The continuous type of random variable X has the following density function: a x, if < x < a, f (x), otherwise. Answer the following questions. () Find a. () Obtain mean
Stat 5101 Notes: Brand Name Distributions
 Stat 5101 Notes: Brand Name Distributions Charles J. Geyer September 5, 2012 Contents 1 Discrete Uniform Distribution 2 2 General Discrete Uniform Distribution 2 3 Uniform Distribution 3 4 General Uniform
Stat 5101 Notes: Brand Name Distributions Charles J. Geyer September 5, 2012 Contents 1 Discrete Uniform Distribution 2 2 General Discrete Uniform Distribution 2 3 Uniform Distribution 3 4 General Uniform
Joint Probability Distributions and Random Samples (Devore Chapter Five)
 Joint Probability Distributions and Random Samples (Devore Chapter Five) 1016-345-01: Probability and Statistics for Engineers Spring 2013 Contents 1 Joint Probability Distributions 2 1.1 Two Discrete
Joint Probability Distributions and Random Samples (Devore Chapter Five) 1016-345-01: Probability and Statistics for Engineers Spring 2013 Contents 1 Joint Probability Distributions 2 1.1 Two Discrete
On a Type of Para-Kenmotsu Manifold
 Pure Mathematical Sciences, Vol. 2, 2013, no. 4, 165-170 HIKARI Ltd, www.m-hikari.com On a Type of Para-Kenmotsu Manifold T. Satyanarayana Department of Mathematics Pragati Engineering College, Surampalem,
Pure Mathematical Sciences, Vol. 2, 2013, no. 4, 165-170 HIKARI Ltd, www.m-hikari.com On a Type of Para-Kenmotsu Manifold T. Satyanarayana Department of Mathematics Pragati Engineering College, Surampalem,
Stat 5101 Notes: Algorithms (thru 2nd midterm)
 Stat 5101 Notes: Algorithms (thru 2nd midterm) Charles J. Geyer October 18, 2012 Contents 1 Calculating an Expectation or a Probability 2 1.1 From a PMF........................... 2 1.2 From a PDF...........................
Stat 5101 Notes: Algorithms (thru 2nd midterm) Charles J. Geyer October 18, 2012 Contents 1 Calculating an Expectation or a Probability 2 1.1 From a PMF........................... 2 1.2 From a PDF...........................
Dependence. MFM Practitioner Module: Risk & Asset Allocation. John Dodson. September 11, Dependence. John Dodson. Outline.
 MFM Practitioner Module: Risk & Asset Allocation September 11, 2013 Before we define dependence, it is useful to define Random variables X and Y are independent iff For all x, y. In particular, F (X,Y
MFM Practitioner Module: Risk & Asset Allocation September 11, 2013 Before we define dependence, it is useful to define Random variables X and Y are independent iff For all x, y. In particular, F (X,Y
Maximum Likelihood Estimation
 Maximum Likelihood Estimation Assume X P θ, θ Θ, with joint pdf (or pmf) f(x θ). Suppose we observe X = x. The Likelihood function is L(θ x) = f(x θ) as a function of θ (with the data x held fixed). The
Maximum Likelihood Estimation Assume X P θ, θ Θ, with joint pdf (or pmf) f(x θ). Suppose we observe X = x. The Likelihood function is L(θ x) = f(x θ) as a function of θ (with the data x held fixed). The
Chapter 5. Chapter 5 sections
 1 / 43 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
1 / 43 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Random Variables and Their Distributions
 Chapter 3 Random Variables and Their Distributions A random variable (r.v.) is a function that assigns one and only one numerical value to each simple event in an experiment. We will denote r.vs by capital
Chapter 3 Random Variables and Their Distributions A random variable (r.v.) is a function that assigns one and only one numerical value to each simple event in an experiment. We will denote r.vs by capital
Copula Regression RAHUL A. PARSA DRAKE UNIVERSITY & STUART A. KLUGMAN SOCIETY OF ACTUARIES CASUALTY ACTUARIAL SOCIETY MAY 18,2011
 Copula Regression RAHUL A. PARSA DRAKE UNIVERSITY & STUART A. KLUGMAN SOCIETY OF ACTUARIES CASUALTY ACTUARIAL SOCIETY MAY 18,2011 Outline Ordinary Least Squares (OLS) Regression Generalized Linear Models
Copula Regression RAHUL A. PARSA DRAKE UNIVERSITY & STUART A. KLUGMAN SOCIETY OF ACTUARIES CASUALTY ACTUARIAL SOCIETY MAY 18,2011 Outline Ordinary Least Squares (OLS) Regression Generalized Linear Models
General Bayesian Inference I
 General Bayesian Inference I Outline: Basic concepts, One-parameter models, Noninformative priors. Reading: Chapters 10 and 11 in Kay-I. (Occasional) Simplified Notation. When there is no potential for
General Bayesian Inference I Outline: Basic concepts, One-parameter models, Noninformative priors. Reading: Chapters 10 and 11 in Kay-I. (Occasional) Simplified Notation. When there is no potential for
Aalborg Universitet. Published in: IEEE International Conference on Acoustics, Speech, and Signal Processing. Creative Commons License Unspecified
 Aalborg Universitet Model-based Noise PSD Estimation from Speech in Non-stationary Noise Nielsen, Jesper jær; avalekalam, Mathew Shaji; Christensen, Mads Græsbøll; Boldt, Jesper Bünsow Published in: IEEE
Aalborg Universitet Model-based Noise PSD Estimation from Speech in Non-stationary Noise Nielsen, Jesper jær; avalekalam, Mathew Shaji; Christensen, Mads Græsbøll; Boldt, Jesper Bünsow Published in: IEEE
The Linear Chain as an Extremal Value of VDB Topological Indices of Polyomino Chains
 Applied Mathematical Sciences, Vol. 8, 2014, no. 103, 5133-5143 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ams.2014.46507 The Linear Chain as an Extremal Value of VDB Topological Indices of
Applied Mathematical Sciences, Vol. 8, 2014, no. 103, 5133-5143 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ams.2014.46507 The Linear Chain as an Extremal Value of VDB Topological Indices of
Chapter 12 - Lecture 2 Inferences about regression coefficient
 Chapter 12 - Lecture 2 Inferences about regression coefficient April 19th, 2010 Facts about slope Test Statistic Confidence interval Hypothesis testing Test using ANOVA Table Facts about slope In previous
Chapter 12 - Lecture 2 Inferences about regression coefficient April 19th, 2010 Facts about slope Test Statistic Confidence interval Hypothesis testing Test using ANOVA Table Facts about slope In previous
Statistics 351 Probability I Fall 2006 (200630) Final Exam Solutions. θ α β Γ(α)Γ(β) (uv)α 1 (v uv) β 1 exp v }
 Statistics 35 Probability I Fall 6 (63 Final Exam Solutions Instructor: Michael Kozdron (a Solving for X and Y gives X UV and Y V UV, so that the Jacobian of this transformation is x x u v J y y v u v
Statistics 35 Probability I Fall 6 (63 Final Exam Solutions Instructor: Michael Kozdron (a Solving for X and Y gives X UV and Y V UV, so that the Jacobian of this transformation is x x u v J y y v u v
