For iid Y i the stronger conclusion holds; for our heuristics ignore differences between these notions.
|
|
|
- Sherilyn Reed
- 5 years ago
- Views:
Transcription
1 Large Sample Theory Study approximate behaviour of ˆθ by studying the function U. Notice U is sum of independent random variables. Theorem: If Y 1, Y 2,... are iid with mean µ then Yi n µ Called law of large numbers. Strong law Yi P (lim n = µ) = 1 and the weak law that Yi lim P ( µ > ɛ) = 0 n For iid Y i the stronger conclusion holds; for our heuristics ignore differences between these notions. 159
2 Now suppose θ 0 is true value of θ. Then U(θ)/n µ(θ) where [ ] log f µ(θ) =E θ0 (X i, θ) θ log f = (x, θ)f(x, θ 0 )dx θ 160
3 Example: N(µ, 1) data: U(µ)/n = (X i µ)/n = X µ If the true mean is µ 0 then X µ 0 and U(µ)/n µ 0 µ Consider µ < µ 0 : derivative of l(µ) is likely to be positive so that l increases as µ increases. For µ > µ 0 : derivative is probably negative and so l tends to be decreasing for µ > 0. Hence: l is likely to be maximized close to µ 0. Repeat ideas for more general case. Study rv log[f(x i, θ)/f(x i, θ 0 )]. You know the inequality E(X) 2 E(X 2 ) (difference is Var(X) 0.) Generalization: Jensen s inequality: for g a convex function (g 0 roughly) then g(e(x)) E(g(X)) 161
4 Inequality above has g(x) = x 2. Use g(x) = log(x): convex because g (x) = x 2 > 0. We get log(e θ0 [f(x i, θ)/f(x i, θ 0 )] E θ0 [ log{f(x i, θ)/f(x i, θ 0 )}] But [ ] f(xi, θ) E θ0 f(x i, θ 0 ) = = f(x, θ) f(x, θ 0 ) f(x, θ 0)dx = 1 f(x, θ)dx We can reassemble the inequality and this calculation to get E θ0 [log{f(x i, θ)/f(x i, θ 0 )}] 0 162
5 Fact: inequality is strict unless the θ and θ 0 densities are actually the same. Let µ(θ) < 0 be this expected value. Then for each θ we find l(θ) l(θ 0 ) n = log[f(xi, θ)/f(x i, θ 0 )] n µ(θ) This proves likelihood probably higher at θ 0 than at any other single θ. Idea can often be stretched to prove that the mle is consistent; need uniform convergence in θ. 163
6 Definition A sequence ˆθ n of estimators of θ is consistent if ˆθ n converges weakly (or strongly) to θ. Proto theorem: In regular problems the mle ˆθ is consistent. More precise statements of possible conclusions. Use notation N(ɛ) = {θ : θ θ 0 ɛ}. Suppose: ˆθ n is global maximizer of l. ˆθ n,δ maximizes l over N(δ) = { θ θ 0 δ}. A ɛ = { ˆθ n θ 0 ɛ} B δ,ɛ = { ˆθ n,δ θ 0 ɛ} C L = {!θ N(L/n 1/2 ) : U(θ) = 0, U (θ) < 0} 164
7 Theorem: 1. Under conditions I P (A ɛ ) 1 for each ɛ > Under conditions II there is a δ > 0 such that for all ɛ > 0 we have P (B δ,ɛ ) Under conditions III for all δ > 0 there is an L so large and an n 0 so large that for all n n 0, P (C L ) > 1 δ. 4. Under conditions III there is a sequence L n tending to so slowly that P (C Ln ) 1. Point: conditions get weaker as conclusions get weaker. Many possible conditions in literature. See book by Zacks for some precise conditions. 165
8 Asymptotic Normality Study shape of log likelihood near the true value of θ. Assume ˆθ is a root of the likelihood equations close to θ 0. Taylor expansion (1 dimensional parameter θ): U(ˆθ) =0 =U(θ 0 ) + U (θ 0 )(ˆθ θ 0 ) + U ( θ)(ˆθ θ 0 ) 2 /2 for some θ between θ 0 and ˆθ. WARNING: This form of the remainder in Taylor s theorem is not valid for multivariate θ. 166
9 Derivatives of U are sums of n terms. So each derivative should be proportional to n in size. Second derivative is multiplied by the square of the small number ˆθ θ 0 so should be negligible compared to the first derivative term. Ignoring second derivative term get U (θ 0 )(ˆθ θ 0 ) U(θ 0 ) Now look at terms U and U. 167
10 Normal case: U(θ 0 ) = (X i µ 0 ) has a normal distribution with mean 0 and variance n (SD n). Derivative is U (µ) = n. Next derivative U is 0. Notice: both U and U are sums of iid random variables. Let and U i = log f θ (X i, θ 0 ) V i = 2 log f θ 2 (X i, θ) 168
11 In general, U(θ 0 ) = U i has mean 0 and approximately a normal distribution. Here is how we check that: E θ0 (U(θ 0 )) = ne θ0 (U 1 ) log(f(x, θ0 )) = n f(x, θ 0 )dx θ f(x, θ0 )/ θ = n f(x, θ 0 )dx f(x, θ 0 ) f = n θ (x, θ 0)dx = n θ = n θ 1 = 0 f(x, θ)dx θ=θ0 169
12 Notice: interchanged order of differentiation and integration at one point. This step is usually justified by applying the dominated convergence theorem to the definition of the derivative. Differentiate identity just proved: log f (x, θ)f(x, θ)dx = 0 θ Take derivative of both sides wrt θ; pull derivative under integral sign: [ ] log f (x, θ)f(x, θ) dx = 0 θ θ Do the derivative and get 2 log(f) θ 2 f(x, θ)dx log f = (x, θ) f (x, θ)dx θ θ [ log f 2 = (x, θ)] f(x, θ)dx θ 170
13 Definition: The Fisher Information is I(θ) = E θ (U (θ)) = ne θ0 (V 1 ) We refer to I(θ 0 ) = E θ0 (V 1 ) as the information in 1 observation. The idea is that I is a measure of how curved the log likelihood tends to be at the true value of θ. Big curvature means precise estimates. Our identity above is I(θ) = V ar θ (U(θ)) = ni(θ) Now we return to our Taylor expansion approximation U (θ 0 )(ˆθ θ 0 ) U(θ 0 ) and study the two appearances of U. We have shown that U = U i is a sum of iid mean 0 random variables. The central limit theorem thus proves that n 1/2 U(θ 0 ) N(0, σ 2 ) where σ 2 = Var(U i ) = E(V i ) = I(θ). 171
14 Next observe that where again U (θ) = V i V i = U i θ The law of large numbers can be applied to show U (θ 0 )/n E θ0 [V 1 ] = I(θ 0 ) Now manipulate our Taylor expansion as follows n 1/2 (ˆθ θ 0 ) [ Vi n ] 1 Ui n Apply Slutsky s Theorem to conclude that the right hand side of this converges in distribution to N(0, σ 2 /I(θ) 2 ) which simplifies, because of the identities, to N{0, 1/I(θ)}. 172
15 Summary In regular families: assuming ˆθ = ˆθ n is a consistent root of U(θ) = 0. n 1/2 U(θ 0 ) MV N(0, I) where I ij = E θ0 { V1,ij (θ 0 ) } and V k,ij (θ) = 2 log f(x k, θ) θ i θ j If V k (θ) is the matrix [V k,ij ] then nk=1 V k (θ 0 ) n I If V(θ) = k V k (θ) then {V(θ 0 )/n}n 1/2 (ˆθ θ 0 ) n 1/2 U(θ 0 ) 0 in probability as n. 173
16 Also {V(ˆθ)/n}n 1/2 (ˆθ θ 0 ) n 1/2 U(θ 0 ) 0 in probability as n. n 1/2 (ˆθ θ 0 ) {I(θ 0 )} 1 U(θ 0 ) 0 in probability as n. n 1/2 (ˆθ θ 0 ) MV N(0, I 1 ). In general (not just iid cases) I(θ 0 )(ˆθ θ 0 ) N(0, 1) I(ˆθ)(ˆθ θ 0 ) N(0, 1) V (θ 0 )(ˆθ θ 0 ) N(0, 1) V (ˆθ)(ˆθ θ 0 ) N(0, 1) where V = l is the so-called observed information, the negative second derivative of the log-likelihood. Note: If the square roots are replaced by matrix square roots we can let θ be vector valued and get MV N(0, I) as the limit law. 174
17 Why all these different forms? Use limit laws to test hypotheses and compute confidence intervals. Test H o : θ = θ 0 using one of the 4 quantities as test statistic. Find confidence intervals using quantities as pivots. E.g.: second and fourth limits lead to confidence intervals and ˆθ ± z α/2 / I(ˆθ) ˆθ ± z α/2 / V (ˆθ) respectively. The other two are more complicated. For iid N(0, σ 2 ) data we have and V (σ) = 3 X 2 i σ 4 n σ 2 I(σ) = 2n σ 2 The first line above then justifies confidence intervals for σ computed by finding all those σ for which 2n(ˆσ σ) σ z α/2 Similar interval can be derived from 3rd expression, though this is much more complicated. 175
18 Usual summary: mle is consistent and asymptotically normal with an asymptotic variance which is the inverse of the Fisher information. Problems with maximum likelihood 1. Many parameters lead to poor approximations. MLEs can be far from right answer. See homework for Neyman Scott example where MLE is not consistent. 2. Multiple roots of the likelihood equations: you must choose the right root. Start with different, consistent, estimator; apply iterative scheme like Newton Raphson to likelihood equations to find MLE. Not many steps of NR generally required if starting point is a reasonable estimate. 176
19 Finding (good) preliminary Point Estimates Method of Moments Basic strategy: set sample moments equal to population moments and solve for the parameters. Definition: The r th sample moment (about the origin) is 1 n n Xi r i=1 The r th population moment is E(X r ) (Central moments are and 1 n n i=1 (X i X) r E [(X µ) r ]. 177
20 If we have p parameters we can estimate the parameters θ 1,..., θ p by solving the system of p equations: and so on to µ 1 = X µ 2 = X2 µ p = Xp You need to remember that the population moments µ k will be formulas involving the parameters. 178
21 Gamma Example The Gamma(α, β) density is f(x; α, β) = 1 βγ(α) and has and ( ) α 1 [ x exp β µ 1 = αβ µ 2 = α(α + 1)β2. This gives the equations or αβ = X α(α + 1)β 2 = X 2 αβ = X αβ 2 = X 2 X 2. x β ] 1(x > 0) 179
22 Divide the second equation by the first to find the method of moments estimate of β is β = (X 2 X 2 )/X. Then from the first equation get α = X/ β = (X) 2 /(X 2 X 2 ). The method of moments equations are much easier to solve than the likelihood equations which involve the function ψ(α) = d dα log(γ(α)) called the digamma function. 180
23 Score function has components and U β = Xi β 2 nα/β U α = nψ(α) + log(x i ) n log(β). You can solve for β in terms of α to leave you trying to find a root of the equation nψ(α) + log(x i ) n log( X i /(nα)) = 0 To use Newton Raphson on this you begin with the preliminary estimate ˆα 1 = α and then compute iteratively ˆα k+1 = log(x) ψ(ˆα k) log(x)/ˆα k 1/α ψ (ˆα k ) until the sequence converges. Computation of ψ, the trigamma function, requires special software. Web sites like netlib and statlib are good sources for this sort of thing. 181
24 Estimating Equations Same large sample ideas arise whenever estimates derived by solving some equation. Example: large sample theory for Generalized Linear Models. Suppose Y i is number of cancer cases in some group of people characterized by values x i of some covariates. Think of x i as containing variables like age, or a dummy for sex or average income or.... Possible parametric regression model: Y i has a Poisson distribution with mean µ i where the mean µ i depends somehow on x i. 182
25 Typically assume g(µ i ) = β 0 + x i β; g is link function. Often g(µ) = log(µ) and x i β is a matrix product: x i row vector, β column vector. Linear regression model with Poisson errors. Special case log(µ i ) = βx i where x i is a scalar. The log likelihood is simply l(β) = (Y i log(µ i ) µ i ) ignoring irrelevant factorials. The score function is, since log(µ i ) = βx i, U(β) = (Y i x i x i µ i ) = x i (Y i µ i ) (Notice again that the score has mean 0 when you plug in the true parameter value.) 183
26 The key observation, however, is that it is not necessary to believe that Y i has a Poisson distribution to make solving the equation U = 0 sensible. Suppose only that log(e(y i )) = x i β. Then we have assumed that E β (U(β)) = 0 This was the key condition in proving that there was a root of the likelihood equations which was consistent and here it is what is needed, roughly, to prove that the equation U(β) = 0 has a consistent root ˆβ. 184
27 Ignoring higher order terms in a Taylor expansion will give V (β)(ˆβ β) U(β) where V = U. In the mle case we had identities relating the expectation of V to the variance of U. In general here we have Var(U) = x 2 i Var(Y i). If Y i is Poisson with mean µ i (and so Var(Y i ) = µ i ) this is Moreover we have and so Var(U) = x 2 i µ i. V i = x 2 i µ i V (β) = x 2 i µ i. 185
28 The central limit theorem (the Lyapunov kind) will show that U(β) has an approximate normal distribution with variance σ 2 U = x 2 i Var(Y i) and so ˆβ β N(0, σ 2 U /( x 2 i µ i) 2 ) If Var(Y i ) = µ i, as it is for the Poisson case, the asymptotic variance simplifies to 1/ x 2 i µ i. 186
29 Other estimating equations are possible, popular. If w i is any set of deterministic weights (possibly depending on µ i ) then could define U(β) = w i (Y i µ i ) and still conclude that U = 0 probably has a consistent root which has an asymptotic normal distribution. Idea widely used: Example: Generalized Estimating Equations, Zeger and Liang. Abbreviation: GEE. Called by econometricians Generalized Method of Moments. 187
30 An estimating equation is unbiased if E θ (U(θ)) = 0 Theorem: Suppose ˆθ is a consistent root of the unbiased estimating equation U(θ) = 0. Let V = U. Suppose there is a sequence of constants B(θ) such that and let and Then V (θ)/b(θ) 1 A(θ) = V ar θ (U(θ)) C(θ) = B(θ)A 1 (θ)b(θ). C(θ 0 )(ˆθ θ 0 ) N(0, 1) C(ˆθ)(ˆθ θ 0 ) N(0, 1) Other ways to estimate A, B and C lead to same conclusions. There are multivariate extensions using matrix square roots. 188
P n. This is called the law of large numbers but it comes in two forms: Strong and Weak.
 Large Sample Theory Large Sample Theory is a name given to the search for approximations to the behaviour of statistical procedures which are derived by computing limits as the sample size, n, tends to
Large Sample Theory Large Sample Theory is a name given to the search for approximations to the behaviour of statistical procedures which are derived by computing limits as the sample size, n, tends to
Unbiased Estimation. Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others.
 Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Ph.D. Qualifying Exam Friday Saturday, January 3 4, 2014
 Ph.D. Qualifying Exam Friday Saturday, January 3 4, 2014 Put your solution to each problem on a separate sheet of paper. Problem 1. (5166) Assume that two random samples {x i } and {y i } are independently
Ph.D. Qualifying Exam Friday Saturday, January 3 4, 2014 Put your solution to each problem on a separate sheet of paper. Problem 1. (5166) Assume that two random samples {x i } and {y i } are independently
Statistics 3858 : Maximum Likelihood Estimators
 Statistics 3858 : Maximum Likelihood Estimators 1 Method of Maximum Likelihood In this method we construct the so called likelihood function, that is L(θ) = L(θ; X 1, X 2,..., X n ) = f n (X 1, X 2,...,
Statistics 3858 : Maximum Likelihood Estimators 1 Method of Maximum Likelihood In this method we construct the so called likelihood function, that is L(θ) = L(θ; X 1, X 2,..., X n ) = f n (X 1, X 2,...,
Unbiased Estimation. Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others.
 Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Introduction to Estimation Methods for Time Series models Lecture 2
 Introduction to Estimation Methods for Time Series models Lecture 2 Fulvio Corsi SNS Pisa Fulvio Corsi Introduction to Estimation () Methods for Time Series models Lecture 2 SNS Pisa 1 / 21 Estimators:
Introduction to Estimation Methods for Time Series models Lecture 2 Fulvio Corsi SNS Pisa Fulvio Corsi Introduction to Estimation () Methods for Time Series models Lecture 2 SNS Pisa 1 / 21 Estimators:
simple if it completely specifies the density of x
 3. Hypothesis Testing Pure significance tests Data x = (x 1,..., x n ) from f(x, θ) Hypothesis H 0 : restricts f(x, θ) Are the data consistent with H 0? H 0 is called the null hypothesis simple if it completely
3. Hypothesis Testing Pure significance tests Data x = (x 1,..., x n ) from f(x, θ) Hypothesis H 0 : restricts f(x, θ) Are the data consistent with H 0? H 0 is called the null hypothesis simple if it completely
f(x θ)dx with respect to θ. Assuming certain smoothness conditions concern differentiating under the integral the integral sign, we first obtain
 0.1. INTRODUCTION 1 0.1 Introduction R. A. Fisher, a pioneer in the development of mathematical statistics, introduced a measure of the amount of information contained in an observaton from f(x θ). Fisher
0.1. INTRODUCTION 1 0.1 Introduction R. A. Fisher, a pioneer in the development of mathematical statistics, introduced a measure of the amount of information contained in an observaton from f(x θ). Fisher
Expectation Maximization (EM) Algorithm. Each has it s own probability of seeing H on any one flip. Let. p 1 = P ( H on Coin 1 )
 Expectation Maximization (EM Algorithm Motivating Example: Have two coins: Coin 1 and Coin 2 Each has it s own probability of seeing H on any one flip. Let p 1 = P ( H on Coin 1 p 2 = P ( H on Coin 2 Select
Expectation Maximization (EM Algorithm Motivating Example: Have two coins: Coin 1 and Coin 2 Each has it s own probability of seeing H on any one flip. Let p 1 = P ( H on Coin 1 p 2 = P ( H on Coin 2 Select
Chapter 3. Point Estimation. 3.1 Introduction
 Chapter 3 Point Estimation Let (Ω, A, P θ ), P θ P = {P θ θ Θ}be probability space, X 1, X 2,..., X n : (Ω, A) (IR k, B k ) random variables (X, B X ) sample space γ : Θ IR k measurable function, i.e.
Chapter 3 Point Estimation Let (Ω, A, P θ ), P θ P = {P θ θ Θ}be probability space, X 1, X 2,..., X n : (Ω, A) (IR k, B k ) random variables (X, B X ) sample space γ : Θ IR k measurable function, i.e.
Lecture 1: Introduction
 Principles of Statistics Part II - Michaelmas 208 Lecturer: Quentin Berthet Lecture : Introduction This course is concerned with presenting some of the mathematical principles of statistical theory. One
Principles of Statistics Part II - Michaelmas 208 Lecturer: Quentin Berthet Lecture : Introduction This course is concerned with presenting some of the mathematical principles of statistical theory. One
Maximum Likelihood Estimation
 Maximum Likelihood Estimation Assume X P θ, θ Θ, with joint pdf (or pmf) f(x θ). Suppose we observe X = x. The Likelihood function is L(θ x) = f(x θ) as a function of θ (with the data x held fixed). The
Maximum Likelihood Estimation Assume X P θ, θ Θ, with joint pdf (or pmf) f(x θ). Suppose we observe X = x. The Likelihood function is L(θ x) = f(x θ) as a function of θ (with the data x held fixed). The
Maximum Likelihood Estimation
 Chapter 7 Maximum Likelihood Estimation 7. Consistency If X is a random variable (or vector) with density or mass function f θ (x) that depends on a parameter θ, then the function f θ (X) viewed as a function
Chapter 7 Maximum Likelihood Estimation 7. Consistency If X is a random variable (or vector) with density or mass function f θ (x) that depends on a parameter θ, then the function f θ (X) viewed as a function
5.2 Fisher information and the Cramer-Rao bound
 Stat 200: Introduction to Statistical Inference Autumn 208/9 Lecture 5: Maximum likelihood theory Lecturer: Art B. Owen October 9 Disclaimer: These notes have not been subjected to the usual scrutiny reserved
Stat 200: Introduction to Statistical Inference Autumn 208/9 Lecture 5: Maximum likelihood theory Lecturer: Art B. Owen October 9 Disclaimer: These notes have not been subjected to the usual scrutiny reserved
Chapter 4: Asymptotic Properties of the MLE
 Chapter 4: Asymptotic Properties of the MLE Daniel O. Scharfstein 09/19/13 1 / 1 Maximum Likelihood Maximum likelihood is the most powerful tool for estimation. In this part of the course, we will consider
Chapter 4: Asymptotic Properties of the MLE Daniel O. Scharfstein 09/19/13 1 / 1 Maximum Likelihood Maximum likelihood is the most powerful tool for estimation. In this part of the course, we will consider
Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017
 Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Let X 1, X 2,, X n be a sequence of i.i.d. observations from a
Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Let X 1, X 2,, X n be a sequence of i.i.d. observations from a
A Very Brief Summary of Statistical Inference, and Examples
 A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2008 Prof. Gesine Reinert 1 Data x = x 1, x 2,..., x n, realisations of random variables X 1, X 2,..., X n with distribution (model)
A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2008 Prof. Gesine Reinert 1 Data x = x 1, x 2,..., x n, realisations of random variables X 1, X 2,..., X n with distribution (model)
A Very Brief Summary of Statistical Inference, and Examples
 A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2009 Prof. Gesine Reinert Our standard situation is that we have data x = x 1, x 2,..., x n, which we view as realisations of random
A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2009 Prof. Gesine Reinert Our standard situation is that we have data x = x 1, x 2,..., x n, which we view as realisations of random
1 Likelihood. 1.1 Likelihood function. Likelihood & Maximum Likelihood Estimators
 Likelihood & Maximum Likelihood Estimators February 26, 2018 Debdeep Pati 1 Likelihood Likelihood is surely one of the most important concepts in statistical theory. We have seen the role it plays in sufficiency,
Likelihood & Maximum Likelihood Estimators February 26, 2018 Debdeep Pati 1 Likelihood Likelihood is surely one of the most important concepts in statistical theory. We have seen the role it plays in sufficiency,
Statistics. Lecture 2 August 7, 2000 Frank Porter Caltech. The Fundamentals; Point Estimation. Maximum Likelihood, Least Squares and All That
 Statistics Lecture 2 August 7, 2000 Frank Porter Caltech The plan for these lectures: The Fundamentals; Point Estimation Maximum Likelihood, Least Squares and All That What is a Confidence Interval? Interval
Statistics Lecture 2 August 7, 2000 Frank Porter Caltech The plan for these lectures: The Fundamentals; Point Estimation Maximum Likelihood, Least Squares and All That What is a Confidence Interval? Interval
DA Freedman Notes on the MLE Fall 2003
 DA Freedman Notes on the MLE Fall 2003 The object here is to provide a sketch of the theory of the MLE. Rigorous presentations can be found in the references cited below. Calculus. Let f be a smooth, scalar
DA Freedman Notes on the MLE Fall 2003 The object here is to provide a sketch of the theory of the MLE. Rigorous presentations can be found in the references cited below. Calculus. Let f be a smooth, scalar
Chapter 4: Asymptotic Properties of the MLE (Part 2)
 Chapter 4: Asymptotic Properties of the MLE (Part 2) Daniel O. Scharfstein 09/24/13 1 / 1 Example Let {(R i, X i ) : i = 1,..., n} be an i.i.d. sample of n random vectors (R, X ). Here R is a response
Chapter 4: Asymptotic Properties of the MLE (Part 2) Daniel O. Scharfstein 09/24/13 1 / 1 Example Let {(R i, X i ) : i = 1,..., n} be an i.i.d. sample of n random vectors (R, X ). Here R is a response
Lecture 3 September 1
 STAT 383C: Statistical Modeling I Fall 2016 Lecture 3 September 1 Lecturer: Purnamrita Sarkar Scribe: Giorgio Paulon, Carlos Zanini Disclaimer: These scribe notes have been slightly proofread and may have
STAT 383C: Statistical Modeling I Fall 2016 Lecture 3 September 1 Lecturer: Purnamrita Sarkar Scribe: Giorgio Paulon, Carlos Zanini Disclaimer: These scribe notes have been slightly proofread and may have
Stat 5102 Lecture Slides Deck 3. Charles J. Geyer School of Statistics University of Minnesota
 Stat 5102 Lecture Slides Deck 3 Charles J. Geyer School of Statistics University of Minnesota 1 Likelihood Inference We have learned one very general method of estimation: method of moments. the Now we
Stat 5102 Lecture Slides Deck 3 Charles J. Geyer School of Statistics University of Minnesota 1 Likelihood Inference We have learned one very general method of estimation: method of moments. the Now we
Optimization. The value x is called a maximizer of f and is written argmax X f. g(λx + (1 λ)y) < λg(x) + (1 λ)g(y) 0 < λ < 1; x, y X.
 Optimization Background: Problem: given a function f(x) defined on X, find x such that f(x ) f(x) for all x X. The value x is called a maximizer of f and is written argmax X f. In general, argmax X f may
Optimization Background: Problem: given a function f(x) defined on X, find x such that f(x ) f(x) for all x X. The value x is called a maximizer of f and is written argmax X f. In general, argmax X f may
Maximum Likelihood Estimation
 Chapter 8 Maximum Likelihood Estimation 8. Consistency If X is a random variable (or vector) with density or mass function f θ (x) that depends on a parameter θ, then the function f θ (X) viewed as a function
Chapter 8 Maximum Likelihood Estimation 8. Consistency If X is a random variable (or vector) with density or mass function f θ (x) that depends on a parameter θ, then the function f θ (X) viewed as a function
Lecture 17: Likelihood ratio and asymptotic tests
 Lecture 17: Likelihood ratio and asymptotic tests Likelihood ratio When both H 0 and H 1 are simple (i.e., Θ 0 = {θ 0 } and Θ 1 = {θ 1 }), Theorem 6.1 applies and a UMP test rejects H 0 when f θ1 (X) f
Lecture 17: Likelihood ratio and asymptotic tests Likelihood ratio When both H 0 and H 1 are simple (i.e., Θ 0 = {θ 0 } and Θ 1 = {θ 1 }), Theorem 6.1 applies and a UMP test rejects H 0 when f θ1 (X) f
EM Algorithm II. September 11, 2018
 EM Algorithm II September 11, 2018 Review EM 1/27 (Y obs, Y mis ) f (y obs, y mis θ), we observe Y obs but not Y mis Complete-data log likelihood: l C (θ Y obs, Y mis ) = log { f (Y obs, Y mis θ) Observed-data
EM Algorithm II September 11, 2018 Review EM 1/27 (Y obs, Y mis ) f (y obs, y mis θ), we observe Y obs but not Y mis Complete-data log likelihood: l C (θ Y obs, Y mis ) = log { f (Y obs, Y mis θ) Observed-data
STAT 135 Lab 3 Asymptotic MLE and the Method of Moments
 STAT 135 Lab 3 Asymptotic MLE and the Method of Moments Rebecca Barter February 9, 2015 Maximum likelihood estimation (a reminder) Maximum likelihood estimation Suppose that we have a sample, X 1, X 2,...,
STAT 135 Lab 3 Asymptotic MLE and the Method of Moments Rebecca Barter February 9, 2015 Maximum likelihood estimation (a reminder) Maximum likelihood estimation Suppose that we have a sample, X 1, X 2,...,
Fisher Information & Efficiency
 Fisher Information & Efficiency Robert L. Wolpert Department of Statistical Science Duke University, Durham, NC, USA 1 Introduction Let f(x θ) be the pdf of X for θ Θ; at times we will also consider a
Fisher Information & Efficiency Robert L. Wolpert Department of Statistical Science Duke University, Durham, NC, USA 1 Introduction Let f(x θ) be the pdf of X for θ Θ; at times we will also consider a
Linear model A linear model assumes Y X N(µ(X),σ 2 I), And IE(Y X) = µ(x) = X β, 2/52
 Statistics for Applications Chapter 10: Generalized Linear Models (GLMs) 1/52 Linear model A linear model assumes Y X N(µ(X),σ 2 I), And IE(Y X) = µ(x) = X β, 2/52 Components of a linear model The two
Statistics for Applications Chapter 10: Generalized Linear Models (GLMs) 1/52 Linear model A linear model assumes Y X N(µ(X),σ 2 I), And IE(Y X) = µ(x) = X β, 2/52 Components of a linear model The two
Multivariate Analysis and Likelihood Inference
 Multivariate Analysis and Likelihood Inference Outline 1 Joint Distribution of Random Variables 2 Principal Component Analysis (PCA) 3 Multivariate Normal Distribution 4 Likelihood Inference Joint density
Multivariate Analysis and Likelihood Inference Outline 1 Joint Distribution of Random Variables 2 Principal Component Analysis (PCA) 3 Multivariate Normal Distribution 4 Likelihood Inference Joint density
Review and continuation from last week Properties of MLEs
 Review and continuation from last week Properties of MLEs As we have mentioned, MLEs have a nice intuitive property, and as we have seen, they have a certain equivariance property. We will see later that
Review and continuation from last week Properties of MLEs As we have mentioned, MLEs have a nice intuitive property, and as we have seen, they have a certain equivariance property. We will see later that
MISCELLANEOUS TOPICS RELATED TO LIKELIHOOD. Copyright c 2012 (Iowa State University) Statistics / 30
 MISCELLANEOUS TOPICS RELATED TO LIKELIHOOD Copyright c 2012 (Iowa State University) Statistics 511 1 / 30 INFORMATION CRITERIA Akaike s Information criterion is given by AIC = 2l(ˆθ) + 2k, where l(ˆθ)
MISCELLANEOUS TOPICS RELATED TO LIKELIHOOD Copyright c 2012 (Iowa State University) Statistics 511 1 / 30 INFORMATION CRITERIA Akaike s Information criterion is given by AIC = 2l(ˆθ) + 2k, where l(ˆθ)
Statistics Ph.D. Qualifying Exam
 Department of Statistics Carnegie Mellon University May 7 2008 Statistics Ph.D. Qualifying Exam You are not expected to solve all five problems. Complete solutions to few problems will be preferred to
Department of Statistics Carnegie Mellon University May 7 2008 Statistics Ph.D. Qualifying Exam You are not expected to solve all five problems. Complete solutions to few problems will be preferred to
BTRY 4090: Spring 2009 Theory of Statistics
 BTRY 4090: Spring 2009 Theory of Statistics Guozhang Wang September 25, 2010 1 Review of Probability We begin with a real example of using probability to solve computationally intensive (or infeasible)
BTRY 4090: Spring 2009 Theory of Statistics Guozhang Wang September 25, 2010 1 Review of Probability We begin with a real example of using probability to solve computationally intensive (or infeasible)
Hypothesis Testing. A rule for making the required choice can be described in two ways: called the rejection or critical region of the test.
 Hypothesis Testing Hypothesis testing is a statistical problem where you must choose, on the basis of data X, between two alternatives. We formalize this as the problem of choosing between two hypotheses:
Hypothesis Testing Hypothesis testing is a statistical problem where you must choose, on the basis of data X, between two alternatives. We formalize this as the problem of choosing between two hypotheses:
1 One-way analysis of variance
 LIST OF FORMULAS (Version from 21. November 2014) STK2120 1 One-way analysis of variance Assume X ij = µ+α i +ɛ ij ; j = 1, 2,..., J i ; i = 1, 2,..., I ; where ɛ ij -s are independent and N(0, σ 2 ) distributed.
LIST OF FORMULAS (Version from 21. November 2014) STK2120 1 One-way analysis of variance Assume X ij = µ+α i +ɛ ij ; j = 1, 2,..., J i ; i = 1, 2,..., I ; where ɛ ij -s are independent and N(0, σ 2 ) distributed.
Classical Estimation Topics
 Classical Estimation Topics Namrata Vaswani, Iowa State University February 25, 2014 This note fills in the gaps in the notes already provided (l0.pdf, l1.pdf, l2.pdf, l3.pdf, LeastSquares.pdf). 1 Min
Classical Estimation Topics Namrata Vaswani, Iowa State University February 25, 2014 This note fills in the gaps in the notes already provided (l0.pdf, l1.pdf, l2.pdf, l3.pdf, LeastSquares.pdf). 1 Min
Chapter 1: A Brief Review of Maximum Likelihood, GMM, and Numerical Tools. Joan Llull. Microeconometrics IDEA PhD Program
 Chapter 1: A Brief Review of Maximum Likelihood, GMM, and Numerical Tools Joan Llull Microeconometrics IDEA PhD Program Maximum Likelihood Chapter 1. A Brief Review of Maximum Likelihood, GMM, and Numerical
Chapter 1: A Brief Review of Maximum Likelihood, GMM, and Numerical Tools Joan Llull Microeconometrics IDEA PhD Program Maximum Likelihood Chapter 1. A Brief Review of Maximum Likelihood, GMM, and Numerical
Normalising constants and maximum likelihood inference
 Normalising constants and maximum likelihood inference Jakob G. Rasmussen Department of Mathematics Aalborg University Denmark March 9, 2011 1/14 Today Normalising constants Approximation of normalising
Normalising constants and maximum likelihood inference Jakob G. Rasmussen Department of Mathematics Aalborg University Denmark March 9, 2011 1/14 Today Normalising constants Approximation of normalising
Central Limit Theorem ( 5.3)
 Central Limit Theorem ( 5.3) Let X 1, X 2,... be a sequence of independent random variables, each having n mean µ and variance σ 2. Then the distribution of the partial sum S n = X i i=1 becomes approximately
Central Limit Theorem ( 5.3) Let X 1, X 2,... be a sequence of independent random variables, each having n mean µ and variance σ 2. Then the distribution of the partial sum S n = X i i=1 becomes approximately
Statistical Methods for Handling Incomplete Data Chapter 2: Likelihood-based approach
 Statistical Methods for Handling Incomplete Data Chapter 2: Likelihood-based approach Jae-Kwang Kim Department of Statistics, Iowa State University Outline 1 Introduction 2 Observed likelihood 3 Mean Score
Statistical Methods for Handling Incomplete Data Chapter 2: Likelihood-based approach Jae-Kwang Kim Department of Statistics, Iowa State University Outline 1 Introduction 2 Observed likelihood 3 Mean Score
Spring 2012 Math 541B Exam 1
 Spring 2012 Math 541B Exam 1 1. A sample of size n is drawn without replacement from an urn containing N balls, m of which are red and N m are black; the balls are otherwise indistinguishable. Let X denote
Spring 2012 Math 541B Exam 1 1. A sample of size n is drawn without replacement from an urn containing N balls, m of which are red and N m are black; the balls are otherwise indistinguishable. Let X denote
parameter space Θ, depending only on X, such that Note: it is not θ that is random, but the set C(X).
 4. Interval estimation The goal for interval estimation is to specify the accurary of an estimate. A 1 α confidence set for a parameter θ is a set C(X) in the parameter space Θ, depending only on X, such
4. Interval estimation The goal for interval estimation is to specify the accurary of an estimate. A 1 α confidence set for a parameter θ is a set C(X) in the parameter space Θ, depending only on X, such
Qualifying Exam in Probability and Statistics. https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf
 Part : Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Part : Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Testing Hypothesis. Maura Mezzetti. Department of Economics and Finance Università Tor Vergata
 Maura Department of Economics and Finance Università Tor Vergata Hypothesis Testing Outline It is a mistake to confound strangeness with mystery Sherlock Holmes A Study in Scarlet Outline 1 The Power Function
Maura Department of Economics and Finance Università Tor Vergata Hypothesis Testing Outline It is a mistake to confound strangeness with mystery Sherlock Holmes A Study in Scarlet Outline 1 The Power Function
Hypothesis Testing. 1 Definitions of test statistics. CB: chapter 8; section 10.3
 Hypothesis Testing CB: chapter 8; section 0.3 Hypothesis: statement about an unknown population parameter Examples: The average age of males in Sweden is 7. (statement about population mean) The lowest
Hypothesis Testing CB: chapter 8; section 0.3 Hypothesis: statement about an unknown population parameter Examples: The average age of males in Sweden is 7. (statement about population mean) The lowest
Fall 2017 STAT 532 Homework Peter Hoff. 1. Let P be a probability measure on a collection of sets A.
 1. Let P be a probability measure on a collection of sets A. (a) For each n N, let H n be a set in A such that H n H n+1. Show that P (H n ) monotonically converges to P ( k=1 H k) as n. (b) For each n
1. Let P be a probability measure on a collection of sets A. (a) For each n N, let H n be a set in A such that H n H n+1. Show that P (H n ) monotonically converges to P ( k=1 H k) as n. (b) For each n
Linear Methods for Prediction
 Chapter 5 Linear Methods for Prediction 5.1 Introduction We now revisit the classification problem and focus on linear methods. Since our prediction Ĝ(x) will always take values in the discrete set G we
Chapter 5 Linear Methods for Prediction 5.1 Introduction We now revisit the classification problem and focus on linear methods. Since our prediction Ĝ(x) will always take values in the discrete set G we
Generalized Linear Models. Kurt Hornik
 Generalized Linear Models Kurt Hornik Motivation Assuming normality, the linear model y = Xβ + e has y = β + ε, ε N(0, σ 2 ) such that y N(μ, σ 2 ), E(y ) = μ = β. Various generalizations, including general
Generalized Linear Models Kurt Hornik Motivation Assuming normality, the linear model y = Xβ + e has y = β + ε, ε N(0, σ 2 ) such that y N(μ, σ 2 ), E(y ) = μ = β. Various generalizations, including general
Section 8: Asymptotic Properties of the MLE
 2 Section 8: Asymptotic Properties of the MLE In this part of the course, we will consider the asymptotic properties of the maximum likelihood estimator. In particular, we will study issues of consistency,
2 Section 8: Asymptotic Properties of the MLE In this part of the course, we will consider the asymptotic properties of the maximum likelihood estimator. In particular, we will study issues of consistency,
Likelihood-Based Methods
 Likelihood-Based Methods Handbook of Spatial Statistics, Chapter 4 Susheela Singh September 22, 2016 OVERVIEW INTRODUCTION MAXIMUM LIKELIHOOD ESTIMATION (ML) RESTRICTED MAXIMUM LIKELIHOOD ESTIMATION (REML)
Likelihood-Based Methods Handbook of Spatial Statistics, Chapter 4 Susheela Singh September 22, 2016 OVERVIEW INTRODUCTION MAXIMUM LIKELIHOOD ESTIMATION (ML) RESTRICTED MAXIMUM LIKELIHOOD ESTIMATION (REML)
Statistics - Lecture One. Outline. Charlotte Wickham 1. Basic ideas about estimation
 Statistics - Lecture One Charlotte Wickham wickham@stat.berkeley.edu http://www.stat.berkeley.edu/~wickham/ Outline 1. Basic ideas about estimation 2. Method of Moments 3. Maximum Likelihood 4. Confidence
Statistics - Lecture One Charlotte Wickham wickham@stat.berkeley.edu http://www.stat.berkeley.edu/~wickham/ Outline 1. Basic ideas about estimation 2. Method of Moments 3. Maximum Likelihood 4. Confidence
1. Fisher Information
 1. Fisher Information Let f(x θ) be a density function with the property that log f(x θ) is differentiable in θ throughout the open p-dimensional parameter set Θ R p ; then the score statistic (or score
1. Fisher Information Let f(x θ) be a density function with the property that log f(x θ) is differentiable in θ throughout the open p-dimensional parameter set Θ R p ; then the score statistic (or score
Master s Written Examination
 Master s Written Examination Option: Statistics and Probability Spring 016 Full points may be obtained for correct answers to eight questions. Each numbered question which may have several parts is worth
Master s Written Examination Option: Statistics and Probability Spring 016 Full points may be obtained for correct answers to eight questions. Each numbered question which may have several parts is worth
Some explanations about the IWLS algorithm to fit generalized linear models
 Some explanations about the IWLS algorithm to fit generalized linear models Christophe Dutang To cite this version: Christophe Dutang. Some explanations about the IWLS algorithm to fit generalized linear
Some explanations about the IWLS algorithm to fit generalized linear models Christophe Dutang To cite this version: Christophe Dutang. Some explanations about the IWLS algorithm to fit generalized linear
Recall that in order to prove Theorem 8.8, we argued that under certain regularity conditions, the following facts are true under H 0 : 1 n
 Chapter 9 Hypothesis Testing 9.1 Wald, Rao, and Likelihood Ratio Tests Suppose we wish to test H 0 : θ = θ 0 against H 1 : θ θ 0. The likelihood-based results of Chapter 8 give rise to several possible
Chapter 9 Hypothesis Testing 9.1 Wald, Rao, and Likelihood Ratio Tests Suppose we wish to test H 0 : θ = θ 0 against H 1 : θ θ 0. The likelihood-based results of Chapter 8 give rise to several possible
Regression Estimation Least Squares and Maximum Likelihood
 Regression Estimation Least Squares and Maximum Likelihood Dr. Frank Wood Frank Wood, fwood@stat.columbia.edu Linear Regression Models Lecture 3, Slide 1 Least Squares Max(min)imization Function to minimize
Regression Estimation Least Squares and Maximum Likelihood Dr. Frank Wood Frank Wood, fwood@stat.columbia.edu Linear Regression Models Lecture 3, Slide 1 Least Squares Max(min)imization Function to minimize
Chapter 4 HOMEWORK ASSIGNMENTS. 4.1 Homework #1
 Chapter 4 HOMEWORK ASSIGNMENTS These homeworks may be modified as the semester progresses. It is your responsibility to keep up to date with the correctly assigned homeworks. There may be some errors in
Chapter 4 HOMEWORK ASSIGNMENTS These homeworks may be modified as the semester progresses. It is your responsibility to keep up to date with the correctly assigned homeworks. There may be some errors in
MATH4427 Notebook 2 Fall Semester 2017/2018
 MATH4427 Notebook 2 Fall Semester 2017/2018 prepared by Professor Jenny Baglivo c Copyright 2009-2018 by Jenny A. Baglivo. All Rights Reserved. 2 MATH4427 Notebook 2 3 2.1 Definitions and Examples...................................
MATH4427 Notebook 2 Fall Semester 2017/2018 prepared by Professor Jenny Baglivo c Copyright 2009-2018 by Jenny A. Baglivo. All Rights Reserved. 2 MATH4427 Notebook 2 3 2.1 Definitions and Examples...................................
Statistics & Data Sciences: First Year Prelim Exam May 2018
 Statistics & Data Sciences: First Year Prelim Exam May 2018 Instructions: 1. Do not turn this page until instructed to do so. 2. Start each new question on a new sheet of paper. 3. This is a closed book
Statistics & Data Sciences: First Year Prelim Exam May 2018 Instructions: 1. Do not turn this page until instructed to do so. 2. Start each new question on a new sheet of paper. 3. This is a closed book
Mathematical statistics
 October 4 th, 2018 Lecture 12: Information Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation Chapter
October 4 th, 2018 Lecture 12: Information Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation Chapter
Generalized Linear Models I
 Statistics 203: Introduction to Regression and Analysis of Variance Generalized Linear Models I Jonathan Taylor - p. 1/16 Today s class Poisson regression. Residuals for diagnostics. Exponential families.
Statistics 203: Introduction to Regression and Analysis of Variance Generalized Linear Models I Jonathan Taylor - p. 1/16 Today s class Poisson regression. Residuals for diagnostics. Exponential families.
Information in Data. Sufficiency, Ancillarity, Minimality, and Completeness
 Information in Data Sufficiency, Ancillarity, Minimality, and Completeness Important properties of statistics that determine the usefulness of those statistics in statistical inference. These general properties
Information in Data Sufficiency, Ancillarity, Minimality, and Completeness Important properties of statistics that determine the usefulness of those statistics in statistical inference. These general properties
Problem Selected Scores
 Statistics Ph.D. Qualifying Exam: Part II November 20, 2010 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. Problem 1 2 3 4 5 6 7 8 9 10 11 12 Selected
Statistics Ph.D. Qualifying Exam: Part II November 20, 2010 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. Problem 1 2 3 4 5 6 7 8 9 10 11 12 Selected
Generalized Linear Models
 Generalized Linear Models Advanced Methods for Data Analysis (36-402/36-608 Spring 2014 1 Generalized linear models 1.1 Introduction: two regressions So far we ve seen two canonical settings for regression.
Generalized Linear Models Advanced Methods for Data Analysis (36-402/36-608 Spring 2014 1 Generalized linear models 1.1 Introduction: two regressions So far we ve seen two canonical settings for regression.
POLI 8501 Introduction to Maximum Likelihood Estimation
 POLI 8501 Introduction to Maximum Likelihood Estimation Maximum Likelihood Intuition Consider a model that looks like this: Y i N(µ, σ 2 ) So: E(Y ) = µ V ar(y ) = σ 2 Suppose you have some data on Y,
POLI 8501 Introduction to Maximum Likelihood Estimation Maximum Likelihood Intuition Consider a model that looks like this: Y i N(µ, σ 2 ) So: E(Y ) = µ V ar(y ) = σ 2 Suppose you have some data on Y,
Parametric Inference
 Parametric Inference Moulinath Banerjee University of Michigan April 14, 2004 1 General Discussion The object of statistical inference is to glean information about an underlying population based on a
Parametric Inference Moulinath Banerjee University of Michigan April 14, 2004 1 General Discussion The object of statistical inference is to glean information about an underlying population based on a
Optimization. Charles J. Geyer School of Statistics University of Minnesota. Stat 8054 Lecture Notes
 Optimization Charles J. Geyer School of Statistics University of Minnesota Stat 8054 Lecture Notes 1 One-Dimensional Optimization Look at a graph. Grid search. 2 One-Dimensional Zero Finding Zero finding
Optimization Charles J. Geyer School of Statistics University of Minnesota Stat 8054 Lecture Notes 1 One-Dimensional Optimization Look at a graph. Grid search. 2 One-Dimensional Zero Finding Zero finding
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003
 Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Solution-Midterm Examination - I STAT 421, Spring 2012
 Solution-Midterm Examination - I STAT 4, Spring 0 Prof. Prem K. Goel. [0 points] Let X, X,..., X n be a random sample of size n from a Gamma population with β = and α = ν/, where ν is the unknown parameter.
Solution-Midterm Examination - I STAT 4, Spring 0 Prof. Prem K. Goel. [0 points] Let X, X,..., X n be a random sample of size n from a Gamma population with β = and α = ν/, where ν is the unknown parameter.
Ch. 5 Hypothesis Testing
 Ch. 5 Hypothesis Testing The current framework of hypothesis testing is largely due to the work of Neyman and Pearson in the late 1920s, early 30s, complementing Fisher s work on estimation. As in estimation,
Ch. 5 Hypothesis Testing The current framework of hypothesis testing is largely due to the work of Neyman and Pearson in the late 1920s, early 30s, complementing Fisher s work on estimation. As in estimation,
Brief Review on Estimation Theory
 Brief Review on Estimation Theory K. Abed-Meraim ENST PARIS, Signal and Image Processing Dept. abed@tsi.enst.fr This presentation is essentially based on the course BASTA by E. Moulines Brief review on
Brief Review on Estimation Theory K. Abed-Meraim ENST PARIS, Signal and Image Processing Dept. abed@tsi.enst.fr This presentation is essentially based on the course BASTA by E. Moulines Brief review on
Mathematics Ph.D. Qualifying Examination Stat Probability, January 2018
 Mathematics Ph.D. Qualifying Examination Stat 52800 Probability, January 2018 NOTE: Answers all questions completely. Justify every step. Time allowed: 3 hours. 1. Let X 1,..., X n be a random sample from
Mathematics Ph.D. Qualifying Examination Stat 52800 Probability, January 2018 NOTE: Answers all questions completely. Justify every step. Time allowed: 3 hours. 1. Let X 1,..., X n be a random sample from
Some Assorted Formulae. Some confidence intervals: σ n. x ± z α/2. x ± t n 1;α/2 n. ˆp(1 ˆp) ˆp ± z α/2 n. χ 2 n 1;1 α/2. n 1;α/2
 STA 248 H1S MIDTERM TEST February 26, 2008 SURNAME: SOLUTIONS GIVEN NAME: STUDENT NUMBER: INSTRUCTIONS: Time: 1 hour and 50 minutes Aids allowed: calculator Tables of the standard normal, t and chi-square
STA 248 H1S MIDTERM TEST February 26, 2008 SURNAME: SOLUTIONS GIVEN NAME: STUDENT NUMBER: INSTRUCTIONS: Time: 1 hour and 50 minutes Aids allowed: calculator Tables of the standard normal, t and chi-square
Greene, Econometric Analysis (6th ed, 2008)
 EC771: Econometrics, Spring 2010 Greene, Econometric Analysis (6th ed, 2008) Chapter 17: Maximum Likelihood Estimation The preferred estimator in a wide variety of econometric settings is that derived
EC771: Econometrics, Spring 2010 Greene, Econometric Analysis (6th ed, 2008) Chapter 17: Maximum Likelihood Estimation The preferred estimator in a wide variety of econometric settings is that derived
Final Exam. 1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given.
 1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given. (a) If X and Y are independent, Corr(X, Y ) = 0. (b) (c) (d) (e) A consistent estimator must be asymptotically
1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given. (a) If X and Y are independent, Corr(X, Y ) = 0. (b) (c) (d) (e) A consistent estimator must be asymptotically
1 General problem. 2 Terminalogy. Estimation. Estimate θ. (Pick a plausible distribution from family. ) Or estimate τ = τ(θ).
 Estimation February 3, 206 Debdeep Pati General problem Model: {P θ : θ Θ}. Observe X P θ, θ Θ unknown. Estimate θ. (Pick a plausible distribution from family. ) Or estimate τ = τ(θ). Examples: θ = (µ,
Estimation February 3, 206 Debdeep Pati General problem Model: {P θ : θ Θ}. Observe X P θ, θ Θ unknown. Estimate θ. (Pick a plausible distribution from family. ) Or estimate τ = τ(θ). Examples: θ = (µ,
If g is also continuous and strictly increasing on J, we may apply the strictly increasing inverse function g 1 to this inequality to get
 18:2 1/24/2 TOPIC. Inequalities; measures of spread. This lecture explores the implications of Jensen s inequality for g-means in general, and for harmonic, geometric, arithmetic, and related means in
18:2 1/24/2 TOPIC. Inequalities; measures of spread. This lecture explores the implications of Jensen s inequality for g-means in general, and for harmonic, geometric, arithmetic, and related means in
Outline of GLMs. Definitions
 Outline of GLMs Definitions This is a short outline of GLM details, adapted from the book Nonparametric Regression and Generalized Linear Models, by Green and Silverman. The responses Y i have density
Outline of GLMs Definitions This is a short outline of GLM details, adapted from the book Nonparametric Regression and Generalized Linear Models, by Green and Silverman. The responses Y i have density
Delta Method. Example : Method of Moments for Exponential Distribution. f(x; λ) = λe λx I(x > 0)
 Delta Method Often estimators are functions of other random variables, for example in the method of moments. These functions of random variables can sometimes inherit a normal approximation from the underlying
Delta Method Often estimators are functions of other random variables, for example in the method of moments. These functions of random variables can sometimes inherit a normal approximation from the underlying
Lecture 6: Discrete Choice: Qualitative Response
 Lecture 6: Instructor: Department of Economics Stanford University 2011 Types of Discrete Choice Models Univariate Models Binary: Linear; Probit; Logit; Arctan, etc. Multinomial: Logit; Nested Logit; GEV;
Lecture 6: Instructor: Department of Economics Stanford University 2011 Types of Discrete Choice Models Univariate Models Binary: Linear; Probit; Logit; Arctan, etc. Multinomial: Logit; Nested Logit; GEV;
Spring 2012 Math 541A Exam 1. X i, S 2 = 1 n. n 1. X i I(X i < c), T n =
 Spring 2012 Math 541A Exam 1 1. (a) Let Z i be independent N(0, 1), i = 1, 2,, n. Are Z = 1 n n Z i and S 2 Z = 1 n 1 n (Z i Z) 2 independent? Prove your claim. (b) Let X 1, X 2,, X n be independent identically
Spring 2012 Math 541A Exam 1 1. (a) Let Z i be independent N(0, 1), i = 1, 2,, n. Are Z = 1 n n Z i and S 2 Z = 1 n 1 n (Z i Z) 2 independent? Prove your claim. (b) Let X 1, X 2,, X n be independent identically
Nonconcave Penalized Likelihood with A Diverging Number of Parameters
 Nonconcave Penalized Likelihood with A Diverging Number of Parameters Jianqing Fan and Heng Peng Presenter: Jiale Xu March 12, 2010 Jianqing Fan and Heng Peng Presenter: JialeNonconcave Xu () Penalized
Nonconcave Penalized Likelihood with A Diverging Number of Parameters Jianqing Fan and Heng Peng Presenter: Jiale Xu March 12, 2010 Jianqing Fan and Heng Peng Presenter: JialeNonconcave Xu () Penalized
Maximum Likelihood Large Sample Theory
 Maximum Likelihood Large Sample Theory MIT 18.443 Dr. Kempthorne Spring 2015 1 Outline 1 Large Sample Theory of Maximum Likelihood Estimates 2 Asymptotic Results: Overview Asymptotic Framework Data Model
Maximum Likelihood Large Sample Theory MIT 18.443 Dr. Kempthorne Spring 2015 1 Outline 1 Large Sample Theory of Maximum Likelihood Estimates 2 Asymptotic Results: Overview Asymptotic Framework Data Model
Regression Estimation - Least Squares and Maximum Likelihood. Dr. Frank Wood
 Regression Estimation - Least Squares and Maximum Likelihood Dr. Frank Wood Least Squares Max(min)imization Function to minimize w.r.t. β 0, β 1 Q = n (Y i (β 0 + β 1 X i )) 2 i=1 Minimize this by maximizing
Regression Estimation - Least Squares and Maximum Likelihood Dr. Frank Wood Least Squares Max(min)imization Function to minimize w.r.t. β 0, β 1 Q = n (Y i (β 0 + β 1 X i )) 2 i=1 Minimize this by maximizing
Econometrics I, Estimation
 Econometrics I, Estimation Department of Economics Stanford University September, 2008 Part I Parameter, Estimator, Estimate A parametric is a feature of the population. An estimator is a function of the
Econometrics I, Estimation Department of Economics Stanford University September, 2008 Part I Parameter, Estimator, Estimate A parametric is a feature of the population. An estimator is a function of the
Answers to the 8th problem set. f(x θ = θ 0 ) L(θ 0 )
 Answers to the 8th problem set The likelihood ratio with which we worked in this problem set is: Λ(x) = f(x θ = θ 1 ) L(θ 1 ) =. f(x θ = θ 0 ) L(θ 0 ) With a lower-case x, this defines a function. With
Answers to the 8th problem set The likelihood ratio with which we worked in this problem set is: Λ(x) = f(x θ = θ 1 ) L(θ 1 ) =. f(x θ = θ 0 ) L(θ 0 ) With a lower-case x, this defines a function. With
[y i α βx i ] 2 (2) Q = i=1
![[y i α βx i ] 2 (2) Q = i=1 [y i α βx i ] 2 (2) Q = i=1](/thumbs/75/72005858.jpg) Least squares fits This section has no probability in it. There are no random variables. We are given n points (x i, y i ) and want to find the equation of the line that best fits them. We take the equation
Least squares fits This section has no probability in it. There are no random variables. We are given n points (x i, y i ) and want to find the equation of the line that best fits them. We take the equation
Submitted to the Brazilian Journal of Probability and Statistics
 Submitted to the Brazilian Journal of Probability and Statistics Multivariate normal approximation of the maximum likelihood estimator via the delta method Andreas Anastasiou a and Robert E. Gaunt b a
Submitted to the Brazilian Journal of Probability and Statistics Multivariate normal approximation of the maximum likelihood estimator via the delta method Andreas Anastasiou a and Robert E. Gaunt b a
Statistical Inference
 Statistical Inference Robert L. Wolpert Institute of Statistics and Decision Sciences Duke University, Durham, NC, USA. Asymptotic Inference in Exponential Families Let X j be a sequence of independent,
Statistical Inference Robert L. Wolpert Institute of Statistics and Decision Sciences Duke University, Durham, NC, USA. Asymptotic Inference in Exponential Families Let X j be a sequence of independent,
f (1 0.5)/n Z =
 Math 466/566 - Homework 4. We want to test a hypothesis involving a population proportion. The unknown population proportion is p. The null hypothesis is p = / and the alternative hypothesis is p > /.
Math 466/566 - Homework 4. We want to test a hypothesis involving a population proportion. The unknown population proportion is p. The null hypothesis is p = / and the alternative hypothesis is p > /.
Maximum Likelihood. F θ, θ Θ. X 1,..., X n. L(θ) = f(x i ; θ) l(θ) = ln L(θ) = i.i.d. i=1. n ln f(x i ; θ) Sometimes
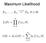 Maximum Likelihood X 1,..., X n i.i.d. F θ, θ Θ L(θ) = n i=1 f(x i ; θ) l(θ) = ln L(θ) = Sometimes n i=1 ln f(x i ; θ) Close your eyes and differentiate? Let X 1,..., X n be a random sample from a Gamma
Maximum Likelihood X 1,..., X n i.i.d. F θ, θ Θ L(θ) = n i=1 f(x i ; θ) l(θ) = ln L(θ) = Sometimes n i=1 ln f(x i ; θ) Close your eyes and differentiate? Let X 1,..., X n be a random sample from a Gamma
6.1 Variational representation of f-divergences
 ECE598: Information-theoretic methods in high-dimensional statistics Spring 2016 Lecture 6: Variational representation, HCR and CR lower bounds Lecturer: Yihong Wu Scribe: Georgios Rovatsos, Feb 11, 2016
ECE598: Information-theoretic methods in high-dimensional statistics Spring 2016 Lecture 6: Variational representation, HCR and CR lower bounds Lecturer: Yihong Wu Scribe: Georgios Rovatsos, Feb 11, 2016
Generalized Linear Models Introduction
 Generalized Linear Models Introduction Statistics 135 Autumn 2005 Copyright c 2005 by Mark E. Irwin Generalized Linear Models For many problems, standard linear regression approaches don t work. Sometimes,
Generalized Linear Models Introduction Statistics 135 Autumn 2005 Copyright c 2005 by Mark E. Irwin Generalized Linear Models For many problems, standard linear regression approaches don t work. Sometimes,
 2018 2019 1 9 sei@mistiu-tokyoacjp http://wwwstattu-tokyoacjp/~sei/lec-jhtml 11 552 3 0 1 2 3 4 5 6 7 13 14 33 4 1 4 4 2 1 1 2 2 1 1 12 13 R?boxplot boxplotstats which does the computation?boxplotstats
2018 2019 1 9 sei@mistiu-tokyoacjp http://wwwstattu-tokyoacjp/~sei/lec-jhtml 11 552 3 0 1 2 3 4 5 6 7 13 14 33 4 1 4 4 2 1 1 2 2 1 1 12 13 R?boxplot boxplotstats which does the computation?boxplotstats
STA216: Generalized Linear Models. Lecture 1. Review and Introduction
 STA216: Generalized Linear Models Lecture 1. Review and Introduction Let y 1,..., y n denote n independent observations on a response Treat y i as a realization of a random variable Y i In the general
STA216: Generalized Linear Models Lecture 1. Review and Introduction Let y 1,..., y n denote n independent observations on a response Treat y i as a realization of a random variable Y i In the general
Estimation and Model Selection in Mixed Effects Models Part I. Adeline Samson 1
 Estimation and Model Selection in Mixed Effects Models Part I Adeline Samson 1 1 University Paris Descartes Summer school 2009 - Lipari, Italy These slides are based on Marc Lavielle s slides Outline 1
Estimation and Model Selection in Mixed Effects Models Part I Adeline Samson 1 1 University Paris Descartes Summer school 2009 - Lipari, Italy These slides are based on Marc Lavielle s slides Outline 1
10-704: Information Processing and Learning Fall Lecture 24: Dec 7
 0-704: Information Processing and Learning Fall 206 Lecturer: Aarti Singh Lecture 24: Dec 7 Note: These notes are based on scribed notes from Spring5 offering of this course. LaTeX template courtesy of
0-704: Information Processing and Learning Fall 206 Lecturer: Aarti Singh Lecture 24: Dec 7 Note: These notes are based on scribed notes from Spring5 offering of this course. LaTeX template courtesy of
