Maximum Likelihood Estimation
|
|
|
- Marjorie Sutton
- 5 years ago
- Views:
Transcription
1 Maximum Likelihood Estimation Assume X P θ, θ Θ, with joint pdf (or pmf) f(x θ). Suppose we observe X = x. The Likelihood function is L(θ x) = f(x θ) as a function of θ (with the data x held fixed). The likelihood function L(θ x) and joint pdf f(x θ) are the same except that f(x θ) is generally viewed as a function of x with θ held fixed, and L(θ x) as a function of θ with x held fixed. f(x θ) is a density in x for each fixed θ. But L(θ x) is not a density (or mass function) in θ for fixed x (except by coincidence). The Maximum Likelihood Estimator (MLE) A point estimator ˆθ = ˆθ(x) is a MLE for θ if L(ˆθ x) = sup θ that is, ˆθ maximizes the likelihood. L(θ x), In most cases, the maximum is achieved at a unique value, and we can refer to the MLE, and write ˆθ(x) = argmax θ L(θ x). (But there are cases where the likelihood has flat spots and the MLE is not unique.)
2 Motivation for MLE s Note: We often write L(θ x) = L(θ), suppressing x, which is kept fixed at the observed data. Suppose x R n. Discrete Case: If f( θ) is a mass function (X is discrete), then L(θ) = f(x θ) = P θ (X = x). L(θ) is the probability of getting the observed data x when the parameter value is θ. Continuous Case: When f( θ) is a continuous density P θ (X = x) = 0, but if B R n is a very, very small ball (or cube) centered at the observed data x, then P θ (X B) f(x θ) Volume(B) L(θ). L(θ) is proportional to the probability the random data X will be close to the observed data x when the parameter value is θ. Thus, the MLE ˆθ is the value of θ which makes the observed data x most probable.
3 To find ˆθ, we maximize L(θ). This is usually done by calculus (finding a stationary point), but not always. If the parameter space Θ contains endpoints or boundary points, the maximum can be achieved at a boundary point without being a stationary point. If L(θ) is not smooth (continuous and everywhere differentiable), the maximum does not have to be achieved at a stationary point. Cautionary Example: Suppose X 1,..., X n are iid Uniform(0, θ) and Θ = (0, ). Given data x = (x 1,..., x n ), find the MLE for θ. L(θ) = n θ 1 I(0 x i θ) = θ n I(0 min x i )I(max x i θ) i=1 = { θ n for θ max x i 0 for 0 < θ < max x i (Draw this!) which is maximized at θ = max x i, which is a point of discontinuity (and certainly not a stationary point). Thus, the MLE is ˆθ = max x i = x (n). Notes: L(θ) = 0 for θ < max x i is just saying that these values of θ are absolutely ruled out by the data (which is obvious). A strange property of the MLE in this example (not typical): P θ (ˆθ < θ) = 1 The MLE is biased; it is always less than the true value.
4 A Similar Example: Let X 1,..., X n be iid Uniform(α, β) and Θ = {(α, β) : α < β}. Given data x = (x 1,..., x n ), find the MLE for θ = (α, β). L(α, β) = n (β α) 1 I(α x i β) i=1 = (β α) n I(α min x i )I(max x i β) { (β α) n for α min x i, max x i β = 0 otherwise which is maximized by making β α as small as possible without entering 0 otherwise region. Clearly, the maximum is achieved at (α, β) = (min x i, max x i ). Thus the MLE is ˆθ = (ˆα, ˆβ) = (min x i, max x i ). Again, P α,β (α < ˆα, ˆβ < β) = 1.
5 Maximizing the Likelihood (one parameter) General Remarks Basic Result: A continuous function g(θ) defined on a closed, bounded interval J attains its supremum (but might do so at one of the endpoints). (That is, there exists a point θ 0 J such that g(θ 0 ) = sup θ J g(θ). ) Consequence: Suppose g(θ) is a continuous, non-negative function defined on an open interval J = (c, d) (where perhaps c = or d = + ). If then g attains its supremum. lim g(θ) = lim g(θ) = 0, θ c θ d Thus, MLE s usually exist when the likelihood function is continuous.
6 Maxima at Stationary Points Suppose the function g(θ) is defined on an interval Θ (which may be open or closed, infinite or finite). If g is differentiable and attains its supremum at a point θ 0 in the interior of Θ, that point must be a stationary point (that is, g (θ 0 ) = 0). (1) If g (θ 0 ) = 0 and g (θ 0 ) < 0, then θ 0 is a local maximum (but might not be the global maximum). (2) If g (θ 0 ) = 0 and g (θ) < 0 for all θ Θ, then θ 0 is a global maximum (that is, it attains the supremum). The condition in (1) is necessary (but not sufficient) for θ 0 to be a global maximum. Condition (2) is sufficient (but not necessary). A function satisfying g (θ) < 0 for all θ Θ is called strictly concave. It lies below any tangent line. Another useful condition (sufficient, but not necessary) is: (3) If g (θ) > 0 for θ < θ 0 and g (θ) < 0 for θ > θ 0, then θ 0 is a global maximum.
7 Maximizing the Likelihood (multi-parameter) Basic Result: A continuous function g(θ) defined on a closed, bounded set J R k attains its supremum (but might do so on the boundary). Consequence: Suppose g(θ) is a continuous, non-negative function defined for all θ R k. If g(θ) 0 as θ, then g attains its supremum. Thus, MLE s usually exist when the likelihood function is continuous. Suppose the function g(θ) is defined on a convex set Θ R k (that is, the line segment joining any two points in Θ lies entirely inside Θ). If g is differentiable and attains its supremum at a point θ 0 in the interior of Θ, that point must be a stationary point: g(θ 0 ) θ i = 0 for i = 1, 2,..., k. Define the gradient vector D and Hessian matrix H: D(θ) = ( g(θ) θ i ) k i=1 (a k 1 vector). H(θ) = ( 2 g(θ) θ i θ j where θ = (θ 1, θ 2,..., θ k ). ) k i,j=1 (a k k matrix).
8 Maxima at Stationary Points (1) If D(θ 0 ) = 0 and H(θ 0 ) is negative definite, then θ 0 is a local maximum (but might not be the global maximum). (2) If D(θ 0 ) = 0 and H(θ) is negative definite for all θ Θ, then θ 0 is a global maximum (that is, it attains the supremum). (1) is necessary (but not sufficient) for θ 0 to be a global maximum. (2) is sufficient (but not necessary). A function for which H(θ) is negative definite for all θ Θ is called strictly concave. It lies below any tangent plane. Positive and Negative Definite Matrices Suppose M is a k k symmetric matrix. Note: Hessian matrices and covariance matrices are symmetric. Definitions: M is positive definite if x Mx > 0 for all x 0 (x R k ). M is negative definite if x Mx < 0 for all x 0. M is non-negative definite (or positive semi-definite) if x Mx 0 for all x R k.
9 Facts: M is p.d. iff all its eigenvalues are positive. M is n.d. iff all its eigenvalues are negative. M is n.n.d. iff all its eigenvalues are non-negative. M is p.d. iff M is n.d. If M is p.d., all its diagonal elements must be positive. If M is n.d., all its diagonal elements must be negative. The determinant of a symmetric matrix is equal to the product of its eigenvalues. 2 2 Symmetric Matrices: ( ) m11 m M = (m ij ) = 12 m 21 m 22 with m 12 = m 21. M = m 11 m 22 m 12 m 21 = m 11 m 22 m A 2 2 matrix is p.d. when the determinant is positive and the diagonal elements are positive. A 2 2 matrix is n.d. when the determinant is positive and the diagonal elements are negative. The bare minimum you need to check: M is p.d. if m 11 > 0 (or m 22 > 0) and M > 0. M is n.d. if m 11 < 0 (or m 22 < 0) and M > 0.
10 Example: Observe X 1,..., X n be iid Gamma(α, β). Preliminaries: (likelihood) L(α, β) = n i=1 x α 1 i e x i/β β α Γ(α). Maximizing L is same as maximizing l = log L given by l(α, β) = (α 1)T 1 T 2 /β nα log β n log Γ(α) where T 1 = i log x i, T 2 = i x i. Note that T = (T 1, T 2 ) is the natural sufficient statistic of this 2pef. l α = T 1 n log β nψ(α) where ψ(α) d dα log Γ(α) = Γ (α) Γ(α) l β = T 2 β nα 2 β = 1 β (T 2 2 nαβ) 2 l α 2 = nψ (α) 2 l = 2T 2 β 2 β 3 2 l α β = n β + nα β 2 = 1 β 3 (2T 2 nαβ)
11 Situation #1: Suppose α = α 0 is known. Find MLE for β. (Drop α from arguments: l(β) = l(α 0, β) etc.) l(β) is continuous and differentiable. l(β) has a unique stationary point: l (β) = l β = 1 β 2 (T 2 nα 0 β) = 0 iff T 2 = nα 0 β iff β = T 2 nα 0 ( β ). Now we check the second derivative. l (β) = 2 l β 2 = 1 β 3 (2T 2 nαβ) = 1 β 3 (T 2 + (T 2 nαβ)). Note l (β ) < 0 since T 2 nα 0 β = 0, but l (β) > 0 for β > 2T 2 /(nα 0 ). Thus, the stationary point satisfies the necessary condition for a global maximum, but not the sufficient condition (i.e., l(β) is not a strictly concave function). How can we be sure that we have found the global maximum, and not just a local maximum? In this case, there is a simple argument: The stationary point β is unique, and l (β) > 0 for β < β, and l (β) < 0 for β > β. This ensures β is the unique global maximizer. Conclusion: ˆβ = T 2 nα 0 is the MLE. (This is a function of T 2, which is a sufficient statistic for β when α is known.)
12 Situation #2: Suppose β = β 0 is known. Find MLE for α. (Drop β from arguments: l(α) = l(α, β 0 ) etc.) Note: l (α) and l (α) involve ψ(α) The function ψ is infinitely differentiable on the interval (0, ), and satisfies ψ (α) > 0 and ψ (α) < 0 for all α > 0. (The function is strictly increasing and strictly concave.) Also lim ψ(α) = and lim ψ(α) =. α 0 + α Thus ψ 1 : R (0, ) exists. (Draw a Picture.) l(α) is continuous and differentiable. l(α) has a unique stationary point: l (α) = T 1 n log β 0 nψ(α) = 0 iff ψ(α) = T 1 /n log β 0 iff α = ψ 1 (T 1 /n log β 0 ) This is the unique global maximizer since l (α) = nψ (α) < 0 for all α > 0. Thus ˆα = ψ 1 (T 1 /n log β 0 ) is the MLE. (This is a function of T 1, which is a sufficient statistic for α when β is known.)
13 Situation #3: Find MLE for θ = (α, β) l(α, β) is continuous and differentiable. A stationary point must satisfy the system of two equations: l α = T 1 n log β nψ(α) = 0 l β = 1 β 2 (T 2 nαβ) = 0 Solving the second equation for β gives β = T 2 nα. Plugging this into the first equation, and rearranging a bit leads to ( ) T 1 n log T2 = ψ(α) log α H(α) n The function H(α) is continuous and strictly increasing from (0, ) to (, 0), so that it has an inverse mapping (, 0) to (0, ). Thus, the solution to the above equation can be written: ( ( )) α = H 1 T1 n log T2. n
14 Thus, the unique stationary point is: Is this the MLE? ˆα = H 1 ( T1 n log ˆβ = T 2 nˆα. Let us examine the Hessian. 2 l 2 l H(α, β) = α 2 α β 2 l 2 l = H(ˆα, ˆβ) = ( T2 n )) α β β 2 nψ n (α) β n 1. β β (2T 3 2 nαβ) nψ n 2ˆα (ˆα) plugging in T 2 n 2ˆα n 3ˆα 3 ˆβ = T 2 T 2 T2 2 nˆα The diagonal elements are both negative, and the determinant is equal to n 4ˆα 2 (ˆαψ (ˆα) 1). T 2 2 This is positive since αψ (α) 1 > 0 for all α > 0. This guarantees that H(ˆα, ˆβ) is negative definite so that (ˆα, ˆβ) is (at least) a local maximum.
1 Likelihood. 1.1 Likelihood function. Likelihood & Maximum Likelihood Estimators
 Likelihood & Maximum Likelihood Estimators February 26, 2018 Debdeep Pati 1 Likelihood Likelihood is surely one of the most important concepts in statistical theory. We have seen the role it plays in sufficiency,
Likelihood & Maximum Likelihood Estimators February 26, 2018 Debdeep Pati 1 Likelihood Likelihood is surely one of the most important concepts in statistical theory. We have seen the role it plays in sufficiency,
1 General problem. 2 Terminalogy. Estimation. Estimate θ. (Pick a plausible distribution from family. ) Or estimate τ = τ(θ).
 Estimation February 3, 206 Debdeep Pati General problem Model: {P θ : θ Θ}. Observe X P θ, θ Θ unknown. Estimate θ. (Pick a plausible distribution from family. ) Or estimate τ = τ(θ). Examples: θ = (µ,
Estimation February 3, 206 Debdeep Pati General problem Model: {P θ : θ Θ}. Observe X P θ, θ Θ unknown. Estimate θ. (Pick a plausible distribution from family. ) Or estimate τ = τ(θ). Examples: θ = (µ,
Statistics 3858 : Maximum Likelihood Estimators
 Statistics 3858 : Maximum Likelihood Estimators 1 Method of Maximum Likelihood In this method we construct the so called likelihood function, that is L(θ) = L(θ; X 1, X 2,..., X n ) = f n (X 1, X 2,...,
Statistics 3858 : Maximum Likelihood Estimators 1 Method of Maximum Likelihood In this method we construct the so called likelihood function, that is L(θ) = L(θ; X 1, X 2,..., X n ) = f n (X 1, X 2,...,
Lecture 4 September 15
 IFT 6269: Probabilistic Graphical Models Fall 2017 Lecture 4 September 15 Lecturer: Simon Lacoste-Julien Scribe: Philippe Brouillard & Tristan Deleu 4.1 Maximum Likelihood principle Given a parametric
IFT 6269: Probabilistic Graphical Models Fall 2017 Lecture 4 September 15 Lecturer: Simon Lacoste-Julien Scribe: Philippe Brouillard & Tristan Deleu 4.1 Maximum Likelihood principle Given a parametric
Stat 5102 Lecture Slides Deck 3. Charles J. Geyer School of Statistics University of Minnesota
 Stat 5102 Lecture Slides Deck 3 Charles J. Geyer School of Statistics University of Minnesota 1 Likelihood Inference We have learned one very general method of estimation: method of moments. the Now we
Stat 5102 Lecture Slides Deck 3 Charles J. Geyer School of Statistics University of Minnesota 1 Likelihood Inference We have learned one very general method of estimation: method of moments. the Now we
For iid Y i the stronger conclusion holds; for our heuristics ignore differences between these notions.
 Large Sample Theory Study approximate behaviour of ˆθ by studying the function U. Notice U is sum of independent random variables. Theorem: If Y 1, Y 2,... are iid with mean µ then Yi n µ Called law of
Large Sample Theory Study approximate behaviour of ˆθ by studying the function U. Notice U is sum of independent random variables. Theorem: If Y 1, Y 2,... are iid with mean µ then Yi n µ Called law of
Chapter 4: Asymptotic Properties of the MLE
 Chapter 4: Asymptotic Properties of the MLE Daniel O. Scharfstein 09/19/13 1 / 1 Maximum Likelihood Maximum likelihood is the most powerful tool for estimation. In this part of the course, we will consider
Chapter 4: Asymptotic Properties of the MLE Daniel O. Scharfstein 09/19/13 1 / 1 Maximum Likelihood Maximum likelihood is the most powerful tool for estimation. In this part of the course, we will consider
Section 8: Asymptotic Properties of the MLE
 2 Section 8: Asymptotic Properties of the MLE In this part of the course, we will consider the asymptotic properties of the maximum likelihood estimator. In particular, we will study issues of consistency,
2 Section 8: Asymptotic Properties of the MLE In this part of the course, we will consider the asymptotic properties of the maximum likelihood estimator. In particular, we will study issues of consistency,
f(x θ)dx with respect to θ. Assuming certain smoothness conditions concern differentiating under the integral the integral sign, we first obtain
 0.1. INTRODUCTION 1 0.1 Introduction R. A. Fisher, a pioneer in the development of mathematical statistics, introduced a measure of the amount of information contained in an observaton from f(x θ). Fisher
0.1. INTRODUCTION 1 0.1 Introduction R. A. Fisher, a pioneer in the development of mathematical statistics, introduced a measure of the amount of information contained in an observaton from f(x θ). Fisher
Infinitely Imbalanced Logistic Regression
 p. 1/1 Infinitely Imbalanced Logistic Regression Art B. Owen Journal of Machine Learning Research, April 2007 Presenter: Ivo D. Shterev p. 2/1 Outline Motivation Introduction Numerical Examples Notation
p. 1/1 Infinitely Imbalanced Logistic Regression Art B. Owen Journal of Machine Learning Research, April 2007 Presenter: Ivo D. Shterev p. 2/1 Outline Motivation Introduction Numerical Examples Notation
Link lecture - Lagrange Multipliers
 Link lecture - Lagrange Multipliers Lagrange multipliers provide a method for finding a stationary point of a function, say f(x, y) when the variables are subject to constraints, say of the form g(x, y)
Link lecture - Lagrange Multipliers Lagrange multipliers provide a method for finding a stationary point of a function, say f(x, y) when the variables are subject to constraints, say of the form g(x, y)
Notes, March 4, 2013, R. Dudley Maximum likelihood estimation: actual or supposed
 18.466 Notes, March 4, 2013, R. Dudley Maximum likelihood estimation: actual or supposed 1. MLEs in exponential families Let f(x,θ) for x X and θ Θ be a likelihood function, that is, for present purposes,
18.466 Notes, March 4, 2013, R. Dudley Maximum likelihood estimation: actual or supposed 1. MLEs in exponential families Let f(x,θ) for x X and θ Θ be a likelihood function, that is, for present purposes,
Graduate Econometrics I: Maximum Likelihood I
 Graduate Econometrics I: Maximum Likelihood I Yves Dominicy Université libre de Bruxelles Solvay Brussels School of Economics and Management ECARES Yves Dominicy Graduate Econometrics I: Maximum Likelihood
Graduate Econometrics I: Maximum Likelihood I Yves Dominicy Université libre de Bruxelles Solvay Brussels School of Economics and Management ECARES Yves Dominicy Graduate Econometrics I: Maximum Likelihood
Fundamentals. CS 281A: Statistical Learning Theory. Yangqing Jia. August, Based on tutorial slides by Lester Mackey and Ariel Kleiner
 Fundamentals CS 281A: Statistical Learning Theory Yangqing Jia Based on tutorial slides by Lester Mackey and Ariel Kleiner August, 2011 Outline 1 Probability 2 Statistics 3 Linear Algebra 4 Optimization
Fundamentals CS 281A: Statistical Learning Theory Yangqing Jia Based on tutorial slides by Lester Mackey and Ariel Kleiner August, 2011 Outline 1 Probability 2 Statistics 3 Linear Algebra 4 Optimization
Expectation Maximization (EM) Algorithm. Each has it s own probability of seeing H on any one flip. Let. p 1 = P ( H on Coin 1 )
 Expectation Maximization (EM Algorithm Motivating Example: Have two coins: Coin 1 and Coin 2 Each has it s own probability of seeing H on any one flip. Let p 1 = P ( H on Coin 1 p 2 = P ( H on Coin 2 Select
Expectation Maximization (EM Algorithm Motivating Example: Have two coins: Coin 1 and Coin 2 Each has it s own probability of seeing H on any one flip. Let p 1 = P ( H on Coin 1 p 2 = P ( H on Coin 2 Select
Optimization. The value x is called a maximizer of f and is written argmax X f. g(λx + (1 λ)y) < λg(x) + (1 λ)g(y) 0 < λ < 1; x, y X.
 Optimization Background: Problem: given a function f(x) defined on X, find x such that f(x ) f(x) for all x X. The value x is called a maximizer of f and is written argmax X f. In general, argmax X f may
Optimization Background: Problem: given a function f(x) defined on X, find x such that f(x ) f(x) for all x X. The value x is called a maximizer of f and is written argmax X f. In general, argmax X f may
Review and continuation from last week Properties of MLEs
 Review and continuation from last week Properties of MLEs As we have mentioned, MLEs have a nice intuitive property, and as we have seen, they have a certain equivariance property. We will see later that
Review and continuation from last week Properties of MLEs As we have mentioned, MLEs have a nice intuitive property, and as we have seen, they have a certain equivariance property. We will see later that
STAT215: Solutions for Homework 2
 STAT25: Solutions for Homework 2 Due: Wednesday, Feb 4. (0 pt) Suppose we take one observation, X, from the discrete distribution, x 2 0 2 Pr(X x θ) ( θ)/4 θ/2 /2 (3 θ)/2 θ/4, 0 θ Find an unbiased estimator
STAT25: Solutions for Homework 2 Due: Wednesday, Feb 4. (0 pt) Suppose we take one observation, X, from the discrete distribution, x 2 0 2 Pr(X x θ) ( θ)/4 θ/2 /2 (3 θ)/2 θ/4, 0 θ Find an unbiased estimator
Parameter Estimation
 Parameter Estimation Consider a sample of observations on a random variable Y. his generates random variables: (y 1, y 2,, y ). A random sample is a sample (y 1, y 2,, y ) where the random variables y
Parameter Estimation Consider a sample of observations on a random variable Y. his generates random variables: (y 1, y 2,, y ). A random sample is a sample (y 1, y 2,, y ) where the random variables y
CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS. W. Erwin Diewert January 31, 2008.
 1 ECONOMICS 594: LECTURE NOTES CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS W. Erwin Diewert January 31, 2008. 1. Introduction Many economic problems have the following structure: (i) a linear function
1 ECONOMICS 594: LECTURE NOTES CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS W. Erwin Diewert January 31, 2008. 1. Introduction Many economic problems have the following structure: (i) a linear function
P n. This is called the law of large numbers but it comes in two forms: Strong and Weak.
 Large Sample Theory Large Sample Theory is a name given to the search for approximations to the behaviour of statistical procedures which are derived by computing limits as the sample size, n, tends to
Large Sample Theory Large Sample Theory is a name given to the search for approximations to the behaviour of statistical procedures which are derived by computing limits as the sample size, n, tends to
Preliminary draft only: please check for final version
 ARE211, Fall2012 CALCULUS4: THU, OCT 11, 2012 PRINTED: AUGUST 22, 2012 (LEC# 15) Contents 3. Univariate and Multivariate Differentiation (cont) 1 3.6. Taylor s Theorem (cont) 2 3.7. Applying Taylor theory:
ARE211, Fall2012 CALCULUS4: THU, OCT 11, 2012 PRINTED: AUGUST 22, 2012 (LEC# 15) Contents 3. Univariate and Multivariate Differentiation (cont) 1 3.6. Taylor s Theorem (cont) 2 3.7. Applying Taylor theory:
DA Freedman Notes on the MLE Fall 2003
 DA Freedman Notes on the MLE Fall 2003 The object here is to provide a sketch of the theory of the MLE. Rigorous presentations can be found in the references cited below. Calculus. Let f be a smooth, scalar
DA Freedman Notes on the MLE Fall 2003 The object here is to provide a sketch of the theory of the MLE. Rigorous presentations can be found in the references cited below. Calculus. Let f be a smooth, scalar
ECE 275A Homework 7 Solutions
 ECE 275A Homework 7 Solutions Solutions 1. For the same specification as in Homework Problem 6.11 we want to determine an estimator for θ using the Method of Moments (MOM). In general, the MOM estimator
ECE 275A Homework 7 Solutions Solutions 1. For the same specification as in Homework Problem 6.11 we want to determine an estimator for θ using the Method of Moments (MOM). In general, the MOM estimator
Maximum Likelihood Estimation
 Maximum Likelihood Estimation Guy Lebanon February 19, 2011 Maximum likelihood estimation is the most popular general purpose method for obtaining estimating a distribution from a finite sample. It was
Maximum Likelihood Estimation Guy Lebanon February 19, 2011 Maximum likelihood estimation is the most popular general purpose method for obtaining estimating a distribution from a finite sample. It was
Maximum Likelihood, Logistic Regression, and Stochastic Gradient Training
 Maximum Likelihood, Logistic Regression, and Stochastic Gradient Training Charles Elkan elkan@cs.ucsd.edu January 17, 2013 1 Principle of maximum likelihood Consider a family of probability distributions
Maximum Likelihood, Logistic Regression, and Stochastic Gradient Training Charles Elkan elkan@cs.ucsd.edu January 17, 2013 1 Principle of maximum likelihood Consider a family of probability distributions
Statistics - Lecture One. Outline. Charlotte Wickham 1. Basic ideas about estimation
 Statistics - Lecture One Charlotte Wickham wickham@stat.berkeley.edu http://www.stat.berkeley.edu/~wickham/ Outline 1. Basic ideas about estimation 2. Method of Moments 3. Maximum Likelihood 4. Confidence
Statistics - Lecture One Charlotte Wickham wickham@stat.berkeley.edu http://www.stat.berkeley.edu/~wickham/ Outline 1. Basic ideas about estimation 2. Method of Moments 3. Maximum Likelihood 4. Confidence
Lecture 1: Entropy, convexity, and matrix scaling CSE 599S: Entropy optimality, Winter 2016 Instructor: James R. Lee Last updated: January 24, 2016
 Lecture 1: Entropy, convexity, and matrix scaling CSE 599S: Entropy optimality, Winter 2016 Instructor: James R. Lee Last updated: January 24, 2016 1 Entropy Since this course is about entropy maximization,
Lecture 1: Entropy, convexity, and matrix scaling CSE 599S: Entropy optimality, Winter 2016 Instructor: James R. Lee Last updated: January 24, 2016 1 Entropy Since this course is about entropy maximization,
Gaussian Graphical Models and Graphical Lasso
 ELE 538B: Sparsity, Structure and Inference Gaussian Graphical Models and Graphical Lasso Yuxin Chen Princeton University, Spring 2017 Multivariate Gaussians Consider a random vector x N (0, Σ) with pdf
ELE 538B: Sparsity, Structure and Inference Gaussian Graphical Models and Graphical Lasso Yuxin Chen Princeton University, Spring 2017 Multivariate Gaussians Consider a random vector x N (0, Σ) with pdf
ARE202A, Fall 2005 CONTENTS. 1. Graphical Overview of Optimization Theory (cont) Separating Hyperplanes 1
 AREA, Fall 5 LECTURE #: WED, OCT 5, 5 PRINT DATE: OCTOBER 5, 5 (GRAPHICAL) CONTENTS 1. Graphical Overview of Optimization Theory (cont) 1 1.4. Separating Hyperplanes 1 1.5. Constrained Maximization: One
AREA, Fall 5 LECTURE #: WED, OCT 5, 5 PRINT DATE: OCTOBER 5, 5 (GRAPHICAL) CONTENTS 1. Graphical Overview of Optimization Theory (cont) 1 1.4. Separating Hyperplanes 1 1.5. Constrained Maximization: One
Introduction to Maximum Likelihood Estimation
 Introduction to Maximum Likelihood Estimation Eric Zivot July 26, 2012 The Likelihood Function Let 1 be an iid sample with pdf ( ; ) where is a ( 1) vector of parameters that characterize ( ; ) Example:
Introduction to Maximum Likelihood Estimation Eric Zivot July 26, 2012 The Likelihood Function Let 1 be an iid sample with pdf ( ; ) where is a ( 1) vector of parameters that characterize ( ; ) Example:
Topic 12 Overview of Estimation
 Topic 12 Overview of Estimation Classical Statistics 1 / 9 Outline Introduction Parameter Estimation Classical Statistics Densities and Likelihoods 2 / 9 Introduction In the simplest possible terms, the
Topic 12 Overview of Estimation Classical Statistics 1 / 9 Outline Introduction Parameter Estimation Classical Statistics Densities and Likelihoods 2 / 9 Introduction In the simplest possible terms, the
x +3y 2t = 1 2x +y +z +t = 2 3x y +z t = 7 2x +6y +z +t = a
 UCM Final Exam, 05/8/014 Solutions 1 Given the parameter a R, consider the following linear system x +y t = 1 x +y +z +t = x y +z t = 7 x +6y +z +t = a (a (6 points Discuss the system depending on the
UCM Final Exam, 05/8/014 Solutions 1 Given the parameter a R, consider the following linear system x +y t = 1 x +y +z +t = x y +z t = 7 x +6y +z +t = a (a (6 points Discuss the system depending on the
Joint work with Nottingham colleagues Simon Preston and Michail Tsagris.
 /pgf/stepx/.initial=1cm, /pgf/stepy/.initial=1cm, /pgf/step/.code=1/pgf/stepx/.expanded=- 10.95415pt,/pgf/stepy/.expanded=- 10.95415pt, /pgf/step/.value required /pgf/images/width/.estore in= /pgf/images/height/.estore
/pgf/stepx/.initial=1cm, /pgf/stepy/.initial=1cm, /pgf/step/.code=1/pgf/stepx/.expanded=- 10.95415pt,/pgf/stepy/.expanded=- 10.95415pt, /pgf/step/.value required /pgf/images/width/.estore in= /pgf/images/height/.estore
Lecture 3 September 1
 STAT 383C: Statistical Modeling I Fall 2016 Lecture 3 September 1 Lecturer: Purnamrita Sarkar Scribe: Giorgio Paulon, Carlos Zanini Disclaimer: These scribe notes have been slightly proofread and may have
STAT 383C: Statistical Modeling I Fall 2016 Lecture 3 September 1 Lecturer: Purnamrita Sarkar Scribe: Giorgio Paulon, Carlos Zanini Disclaimer: These scribe notes have been slightly proofread and may have
Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017
 Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Let X 1, X 2,, X n be a sequence of i.i.d. observations from a
Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Let X 1, X 2,, X n be a sequence of i.i.d. observations from a
Concave and Convex Functions 1
 John Nachbar Washington University March 6, 2017 Concave and Convex Functions 1 1 Basic Definitions Definition 1 Let C R N be convex and let f : C R 1 (a) f is concave iff for any a, b C and any θ [0,
John Nachbar Washington University March 6, 2017 Concave and Convex Functions 1 1 Basic Definitions Definition 1 Let C R N be convex and let f : C R 1 (a) f is concave iff for any a, b C and any θ [0,
Advanced Quantitative Methods: maximum likelihood
 Advanced Quantitative Methods: Maximum Likelihood University College Dublin 4 March 2014 1 2 3 4 5 6 Outline 1 2 3 4 5 6 of straight lines y = 1 2 x + 2 dy dx = 1 2 of curves y = x 2 4x + 5 of curves y
Advanced Quantitative Methods: Maximum Likelihood University College Dublin 4 March 2014 1 2 3 4 5 6 Outline 1 2 3 4 5 6 of straight lines y = 1 2 x + 2 dy dx = 1 2 of curves y = x 2 4x + 5 of curves y
Maximum likelihood estimation
 Maximum likelihood estimation Guillaume Obozinski Ecole des Ponts - ParisTech Master MVA Maximum likelihood estimation 1/26 Outline 1 Statistical concepts 2 A short review of convex analysis and optimization
Maximum likelihood estimation Guillaume Obozinski Ecole des Ponts - ParisTech Master MVA Maximum likelihood estimation 1/26 Outline 1 Statistical concepts 2 A short review of convex analysis and optimization
A Very Brief Summary of Bayesian Inference, and Examples
 A Very Brief Summary of Bayesian Inference, and Examples Trinity Term 009 Prof Gesine Reinert Our starting point are data x = x 1, x,, x n, which we view as realisations of random variables X 1, X,, X
A Very Brief Summary of Bayesian Inference, and Examples Trinity Term 009 Prof Gesine Reinert Our starting point are data x = x 1, x,, x n, which we view as realisations of random variables X 1, X,, X
Maximum Likelihood. F θ, θ Θ. X 1,..., X n. L(θ) = f(x i ; θ) l(θ) = ln L(θ) = i.i.d. i=1. n ln f(x i ; θ) Sometimes
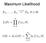 Maximum Likelihood X 1,..., X n i.i.d. F θ, θ Θ L(θ) = n i=1 f(x i ; θ) l(θ) = ln L(θ) = Sometimes n i=1 ln f(x i ; θ) Close your eyes and differentiate? Let X 1,..., X n be a random sample from a Gamma
Maximum Likelihood X 1,..., X n i.i.d. F θ, θ Θ L(θ) = n i=1 f(x i ; θ) l(θ) = ln L(θ) = Sometimes n i=1 ln f(x i ; θ) Close your eyes and differentiate? Let X 1,..., X n be a random sample from a Gamma
MATH Max-min Theory Fall 2016
 MATH 20550 Max-min Theory Fall 2016 1. Definitions and main theorems Max-min theory starts with a function f of a vector variable x and a subset D of the domain of f. So far when we have worked with functions
MATH 20550 Max-min Theory Fall 2016 1. Definitions and main theorems Max-min theory starts with a function f of a vector variable x and a subset D of the domain of f. So far when we have worked with functions
Section 4.2: The Mean Value Theorem
 Section 4.2: The Mean Value Theorem Before we continue with the problem of describing graphs using calculus we shall briefly pause to examine some interesting applications of the derivative. In previous
Section 4.2: The Mean Value Theorem Before we continue with the problem of describing graphs using calculus we shall briefly pause to examine some interesting applications of the derivative. In previous
SOLUTION FOR HOMEWORK 6, STAT 6331
 SOLUTION FOR HOMEWORK 6, STAT 633. Exerc.7.. It is given that X,...,X n is a sample from N(θ, σ ), and the Bayesian approach is used with Θ N(µ, τ ). The parameters σ, µ and τ are given. (a) Find the joinf
SOLUTION FOR HOMEWORK 6, STAT 633. Exerc.7.. It is given that X,...,X n is a sample from N(θ, σ ), and the Bayesian approach is used with Θ N(µ, τ ). The parameters σ, µ and τ are given. (a) Find the joinf
Parameter Estimation for the Beta Distribution
 Brigham Young University BYU ScholarsArchive All Theses and Dissertations 2008-11-20 Parameter Estimation for the Beta Distribution Claire Elayne Bangerter Owen Brigham Young University - Provo Follow
Brigham Young University BYU ScholarsArchive All Theses and Dissertations 2008-11-20 Parameter Estimation for the Beta Distribution Claire Elayne Bangerter Owen Brigham Young University - Provo Follow
1 Convexity, concavity and quasi-concavity. (SB )
 UNIVERSITY OF MARYLAND ECON 600 Summer 2010 Lecture Two: Unconstrained Optimization 1 Convexity, concavity and quasi-concavity. (SB 21.1-21.3.) For any two points, x, y R n, we can trace out the line of
UNIVERSITY OF MARYLAND ECON 600 Summer 2010 Lecture Two: Unconstrained Optimization 1 Convexity, concavity and quasi-concavity. (SB 21.1-21.3.) For any two points, x, y R n, we can trace out the line of
Chapter 4: Asymptotic Properties of the MLE (Part 2)
 Chapter 4: Asymptotic Properties of the MLE (Part 2) Daniel O. Scharfstein 09/24/13 1 / 1 Example Let {(R i, X i ) : i = 1,..., n} be an i.i.d. sample of n random vectors (R, X ). Here R is a response
Chapter 4: Asymptotic Properties of the MLE (Part 2) Daniel O. Scharfstein 09/24/13 1 / 1 Example Let {(R i, X i ) : i = 1,..., n} be an i.i.d. sample of n random vectors (R, X ). Here R is a response
Math (P)refresher Lecture 8: Unconstrained Optimization
 Math (P)refresher Lecture 8: Unconstrained Optimization September 2006 Today s Topics : Quadratic Forms Definiteness of Quadratic Forms Maxima and Minima in R n First Order Conditions Second Order Conditions
Math (P)refresher Lecture 8: Unconstrained Optimization September 2006 Today s Topics : Quadratic Forms Definiteness of Quadratic Forms Maxima and Minima in R n First Order Conditions Second Order Conditions
HT Introduction. P(X i = x i ) = e λ λ x i
 MODS STATISTICS Introduction. HT 2012 Simon Myers, Department of Statistics (and The Wellcome Trust Centre for Human Genetics) myers@stats.ox.ac.uk We will be concerned with the mathematical framework
MODS STATISTICS Introduction. HT 2012 Simon Myers, Department of Statistics (and The Wellcome Trust Centre for Human Genetics) myers@stats.ox.ac.uk We will be concerned with the mathematical framework
A dual form of the sharp Nash inequality and its weighted generalization
 A dual form of the sharp Nash inequality and its weighted generalization Elliott Lieb Princeton University Joint work with Eric Carlen, arxiv: 1704.08720 Kato conference, University of Tokyo September
A dual form of the sharp Nash inequality and its weighted generalization Elliott Lieb Princeton University Joint work with Eric Carlen, arxiv: 1704.08720 Kato conference, University of Tokyo September
Likelihood-Based Methods
 Likelihood-Based Methods Handbook of Spatial Statistics, Chapter 4 Susheela Singh September 22, 2016 OVERVIEW INTRODUCTION MAXIMUM LIKELIHOOD ESTIMATION (ML) RESTRICTED MAXIMUM LIKELIHOOD ESTIMATION (REML)
Likelihood-Based Methods Handbook of Spatial Statistics, Chapter 4 Susheela Singh September 22, 2016 OVERVIEW INTRODUCTION MAXIMUM LIKELIHOOD ESTIMATION (ML) RESTRICTED MAXIMUM LIKELIHOOD ESTIMATION (REML)
Chapter 3. Point Estimation. 3.1 Introduction
 Chapter 3 Point Estimation Let (Ω, A, P θ ), P θ P = {P θ θ Θ}be probability space, X 1, X 2,..., X n : (Ω, A) (IR k, B k ) random variables (X, B X ) sample space γ : Θ IR k measurable function, i.e.
Chapter 3 Point Estimation Let (Ω, A, P θ ), P θ P = {P θ θ Θ}be probability space, X 1, X 2,..., X n : (Ω, A) (IR k, B k ) random variables (X, B X ) sample space γ : Θ IR k measurable function, i.e.
STAT 512 sp 2018 Summary Sheet
 STAT 5 sp 08 Summary Sheet Karl B. Gregory Spring 08. Transformations of a random variable Let X be a rv with support X and let g be a function mapping X to Y with inverse mapping g (A = {x X : g(x A}
STAT 5 sp 08 Summary Sheet Karl B. Gregory Spring 08. Transformations of a random variable Let X be a rv with support X and let g be a function mapping X to Y with inverse mapping g (A = {x X : g(x A}
STAT 513 fa 2018 hw 5
 STAT 513 fa 2018 hw 5 assigned: Thursday, Oct 4th, 2018 due: Thursday, Oct 11th, 2018 1. Let X 11,..., X 1n1 and X 21,..., X 2n2 be independent random samples from the Normal(µ 1, σ 2 ) and Normal(µ 1,
STAT 513 fa 2018 hw 5 assigned: Thursday, Oct 4th, 2018 due: Thursday, Oct 11th, 2018 1. Let X 11,..., X 1n1 and X 21,..., X 2n2 be independent random samples from the Normal(µ 1, σ 2 ) and Normal(µ 1,
Minimax lower bounds I
 Minimax lower bounds I Kyoung Hee Kim Sungshin University 1 Preliminaries 2 General strategy 3 Le Cam, 1973 4 Assouad, 1983 5 Appendix Setting Family of probability measures {P θ : θ Θ} on a sigma field
Minimax lower bounds I Kyoung Hee Kim Sungshin University 1 Preliminaries 2 General strategy 3 Le Cam, 1973 4 Assouad, 1983 5 Appendix Setting Family of probability measures {P θ : θ Θ} on a sigma field
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003
 Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
1 Probability Model. 1.1 Types of models to be discussed in the course
 Sufficiency January 18, 016 Debdeep Pati 1 Probability Model Model: A family of distributions P θ : θ Θ}. P θ (B) is the probability of the event B when the parameter takes the value θ. P θ is described
Sufficiency January 18, 016 Debdeep Pati 1 Probability Model Model: A family of distributions P θ : θ Θ}. P θ (B) is the probability of the event B when the parameter takes the value θ. P θ is described
Advanced Quantitative Methods: maximum likelihood
 Advanced Quantitative Methods: Maximum Likelihood University College Dublin March 23, 2011 1 Introduction 2 3 4 5 Outline Introduction 1 Introduction 2 3 4 5 Preliminaries Introduction Ordinary least squares
Advanced Quantitative Methods: Maximum Likelihood University College Dublin March 23, 2011 1 Introduction 2 3 4 5 Outline Introduction 1 Introduction 2 3 4 5 Preliminaries Introduction Ordinary least squares
Statistics: Learning models from data
 DS-GA 1002 Lecture notes 5 October 19, 2015 Statistics: Learning models from data Learning models from data that are assumed to be generated probabilistically from a certain unknown distribution is a crucial
DS-GA 1002 Lecture notes 5 October 19, 2015 Statistics: Learning models from data Learning models from data that are assumed to be generated probabilistically from a certain unknown distribution is a crucial
Testing Restrictions and Comparing Models
 Econ. 513, Time Series Econometrics Fall 00 Chris Sims Testing Restrictions and Comparing Models 1. THE PROBLEM We consider here the problem of comparing two parametric models for the data X, defined by
Econ. 513, Time Series Econometrics Fall 00 Chris Sims Testing Restrictions and Comparing Models 1. THE PROBLEM We consider here the problem of comparing two parametric models for the data X, defined by
Tangent spaces, normals and extrema
 Chapter 3 Tangent spaces, normals and extrema If S is a surface in 3-space, with a point a S where S looks smooth, i.e., without any fold or cusp or self-crossing, we can intuitively define the tangent
Chapter 3 Tangent spaces, normals and extrema If S is a surface in 3-space, with a point a S where S looks smooth, i.e., without any fold or cusp or self-crossing, we can intuitively define the tangent
Stat 451 Lecture Notes Numerical Integration
 Stat 451 Lecture Notes 03 12 Numerical Integration Ryan Martin UIC www.math.uic.edu/~rgmartin 1 Based on Chapter 5 in Givens & Hoeting, and Chapters 4 & 18 of Lange 2 Updated: February 11, 2016 1 / 29
Stat 451 Lecture Notes 03 12 Numerical Integration Ryan Martin UIC www.math.uic.edu/~rgmartin 1 Based on Chapter 5 in Givens & Hoeting, and Chapters 4 & 18 of Lange 2 Updated: February 11, 2016 1 / 29
V. Graph Sketching and Max-Min Problems
 V. Graph Sketching and Max-Min Problems The signs of the first and second derivatives of a function tell us something about the shape of its graph. In this chapter we learn how to find that information.
V. Graph Sketching and Max-Min Problems The signs of the first and second derivatives of a function tell us something about the shape of its graph. In this chapter we learn how to find that information.
Extreme Abridgment of Boyd and Vandenberghe s Convex Optimization
 Extreme Abridgment of Boyd and Vandenberghe s Convex Optimization Compiled by David Rosenberg Abstract Boyd and Vandenberghe s Convex Optimization book is very well-written and a pleasure to read. The
Extreme Abridgment of Boyd and Vandenberghe s Convex Optimization Compiled by David Rosenberg Abstract Boyd and Vandenberghe s Convex Optimization book is very well-written and a pleasure to read. The
Physics 403. Segev BenZvi. Parameter Estimation, Correlations, and Error Bars. Department of Physics and Astronomy University of Rochester
 Physics 403 Parameter Estimation, Correlations, and Error Bars Segev BenZvi Department of Physics and Astronomy University of Rochester Table of Contents 1 Review of Last Class Best Estimates and Reliability
Physics 403 Parameter Estimation, Correlations, and Error Bars Segev BenZvi Department of Physics and Astronomy University of Rochester Table of Contents 1 Review of Last Class Best Estimates and Reliability
1 Directional Derivatives and Differentiability
 Wednesday, January 18, 2012 1 Directional Derivatives and Differentiability Let E R N, let f : E R and let x 0 E. Given a direction v R N, let L be the line through x 0 in the direction v, that is, L :=
Wednesday, January 18, 2012 1 Directional Derivatives and Differentiability Let E R N, let f : E R and let x 0 E. Given a direction v R N, let L be the line through x 0 in the direction v, that is, L :=
A Very Brief Summary of Statistical Inference, and Examples
 A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2008 Prof. Gesine Reinert 1 Data x = x 1, x 2,..., x n, realisations of random variables X 1, X 2,..., X n with distribution (model)
A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2008 Prof. Gesine Reinert 1 Data x = x 1, x 2,..., x n, realisations of random variables X 1, X 2,..., X n with distribution (model)
ARE211, Fall 2005 CONTENTS. 5. Characteristics of Functions Surjective, Injective and Bijective functions. 5.2.
 ARE211, Fall 2005 LECTURE #18: THU, NOV 3, 2005 PRINT DATE: NOVEMBER 22, 2005 (COMPSTAT2) CONTENTS 5. Characteristics of Functions. 1 5.1. Surjective, Injective and Bijective functions 1 5.2. Homotheticity
ARE211, Fall 2005 LECTURE #18: THU, NOV 3, 2005 PRINT DATE: NOVEMBER 22, 2005 (COMPSTAT2) CONTENTS 5. Characteristics of Functions. 1 5.1. Surjective, Injective and Bijective functions 1 5.2. Homotheticity
The properties of L p -GMM estimators
 The properties of L p -GMM estimators Robert de Jong and Chirok Han Michigan State University February 2000 Abstract This paper considers Generalized Method of Moment-type estimators for which a criterion
The properties of L p -GMM estimators Robert de Jong and Chirok Han Michigan State University February 2000 Abstract This paper considers Generalized Method of Moment-type estimators for which a criterion
EM Algorithm II. September 11, 2018
 EM Algorithm II September 11, 2018 Review EM 1/27 (Y obs, Y mis ) f (y obs, y mis θ), we observe Y obs but not Y mis Complete-data log likelihood: l C (θ Y obs, Y mis ) = log { f (Y obs, Y mis θ) Observed-data
EM Algorithm II September 11, 2018 Review EM 1/27 (Y obs, Y mis ) f (y obs, y mis θ), we observe Y obs but not Y mis Complete-data log likelihood: l C (θ Y obs, Y mis ) = log { f (Y obs, Y mis θ) Observed-data
Graphical Models for Collaborative Filtering
 Graphical Models for Collaborative Filtering Le Song Machine Learning II: Advanced Topics CSE 8803ML, Spring 2012 Sequence modeling HMM, Kalman Filter, etc.: Similarity: the same graphical model topology,
Graphical Models for Collaborative Filtering Le Song Machine Learning II: Advanced Topics CSE 8803ML, Spring 2012 Sequence modeling HMM, Kalman Filter, etc.: Similarity: the same graphical model topology,
Parametric Techniques Lecture 3
 Parametric Techniques Lecture 3 Jason Corso SUNY at Buffalo 22 January 2009 J. Corso (SUNY at Buffalo) Parametric Techniques Lecture 3 22 January 2009 1 / 39 Introduction In Lecture 2, we learned how to
Parametric Techniques Lecture 3 Jason Corso SUNY at Buffalo 22 January 2009 J. Corso (SUNY at Buffalo) Parametric Techniques Lecture 3 22 January 2009 1 / 39 Introduction In Lecture 2, we learned how to
Statistical Inference
 Statistical Inference Robert L. Wolpert Institute of Statistics and Decision Sciences Duke University, Durham, NC, USA. Asymptotic Inference in Exponential Families Let X j be a sequence of independent,
Statistical Inference Robert L. Wolpert Institute of Statistics and Decision Sciences Duke University, Durham, NC, USA. Asymptotic Inference in Exponential Families Let X j be a sequence of independent,
Suppose that f is continuous on [a, b] and differentiable on (a, b). Then
![Suppose that f is continuous on [a, b] and differentiable on (a, b). Then Suppose that f is continuous on [a, b] and differentiable on (a, b). Then](/thumbs/74/71325034.jpg) Lectures 1/18 Derivatives and Graphs When we have a picture of the graph of a function f(x), we can make a picture of the derivative f (x) using the slopes of the tangents to the graph of f. In this section
Lectures 1/18 Derivatives and Graphs When we have a picture of the graph of a function f(x), we can make a picture of the derivative f (x) using the slopes of the tangents to the graph of f. In this section
Lecture Unconstrained optimization. In this lecture we will study the unconstrained problem. minimize f(x), (2.1)
 Lecture 2 In this lecture we will study the unconstrained problem minimize f(x), (2.1) where x R n. Optimality conditions aim to identify properties that potential minimizers need to satisfy in relation
Lecture 2 In this lecture we will study the unconstrained problem minimize f(x), (2.1) where x R n. Optimality conditions aim to identify properties that potential minimizers need to satisfy in relation
Max. Likelihood Estimation. Outline. Econometrics II. Ricardo Mora. Notes. Notes
 Maximum Likelihood Estimation Econometrics II Department of Economics Universidad Carlos III de Madrid Máster Universitario en Desarrollo y Crecimiento Económico Outline 1 3 4 General Approaches to Parameter
Maximum Likelihood Estimation Econometrics II Department of Economics Universidad Carlos III de Madrid Máster Universitario en Desarrollo y Crecimiento Económico Outline 1 3 4 General Approaches to Parameter
STAT 135 Lab 2 Confidence Intervals, MLE and the Delta Method
 STAT 135 Lab 2 Confidence Intervals, MLE and the Delta Method Rebecca Barter February 2, 2015 Confidence Intervals Confidence intervals What is a confidence interval? A confidence interval is calculated
STAT 135 Lab 2 Confidence Intervals, MLE and the Delta Method Rebecca Barter February 2, 2015 Confidence Intervals Confidence intervals What is a confidence interval? A confidence interval is calculated
Concave and Convex Functions 1
 John Nachbar Washington University March 27, 2018 Concave and Convex Functions 1 1 Basic Definitions. Definition 1. Let C R N be non-empty and convex and let f : C R. 1. (a) f is concave iff for any a,
John Nachbar Washington University March 27, 2018 Concave and Convex Functions 1 1 Basic Definitions. Definition 1. Let C R N be non-empty and convex and let f : C R. 1. (a) f is concave iff for any a,
Nonlinear Programming Models
 Nonlinear Programming Models Fabio Schoen 2008 http://gol.dsi.unifi.it/users/schoen Nonlinear Programming Models p. Introduction Nonlinear Programming Models p. NLP problems minf(x) x S R n Standard form:
Nonlinear Programming Models Fabio Schoen 2008 http://gol.dsi.unifi.it/users/schoen Nonlinear Programming Models p. Introduction Nonlinear Programming Models p. NLP problems minf(x) x S R n Standard form:
Linear model A linear model assumes Y X N(µ(X),σ 2 I), And IE(Y X) = µ(x) = X β, 2/52
 Statistics for Applications Chapter 10: Generalized Linear Models (GLMs) 1/52 Linear model A linear model assumes Y X N(µ(X),σ 2 I), And IE(Y X) = µ(x) = X β, 2/52 Components of a linear model The two
Statistics for Applications Chapter 10: Generalized Linear Models (GLMs) 1/52 Linear model A linear model assumes Y X N(µ(X),σ 2 I), And IE(Y X) = µ(x) = X β, 2/52 Components of a linear model The two
Lecture 7 Introduction to Statistical Decision Theory
 Lecture 7 Introduction to Statistical Decision Theory I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw December 20, 2016 1 / 55 I-Hsiang Wang IT Lecture 7
Lecture 7 Introduction to Statistical Decision Theory I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw December 20, 2016 1 / 55 I-Hsiang Wang IT Lecture 7
ExtremeValuesandShapeofCurves
 ExtremeValuesandShapeofCurves Philippe B. Laval Kennesaw State University March 23, 2005 Abstract This handout is a summary of the material dealing with finding extreme values and determining the shape
ExtremeValuesandShapeofCurves Philippe B. Laval Kennesaw State University March 23, 2005 Abstract This handout is a summary of the material dealing with finding extreme values and determining the shape
Notes on Random Vectors and Multivariate Normal
 MATH 590 Spring 06 Notes on Random Vectors and Multivariate Normal Properties of Random Vectors If X,, X n are random variables, then X = X,, X n ) is a random vector, with the cumulative distribution
MATH 590 Spring 06 Notes on Random Vectors and Multivariate Normal Properties of Random Vectors If X,, X n are random variables, then X = X,, X n ) is a random vector, with the cumulative distribution
Machine Learning and Computational Statistics, Spring 2017 Homework 2: Lasso Regression
 Machine Learning and Computational Statistics, Spring 2017 Homework 2: Lasso Regression Due: Monday, February 13, 2017, at 10pm (Submit via Gradescope) Instructions: Your answers to the questions below,
Machine Learning and Computational Statistics, Spring 2017 Homework 2: Lasso Regression Due: Monday, February 13, 2017, at 10pm (Submit via Gradescope) Instructions: Your answers to the questions below,
Random vectors X 1 X 2. Recall that a random vector X = is made up of, say, k. X k. random variables.
 Random vectors Recall that a random vector X = X X 2 is made up of, say, k random variables X k A random vector has a joint distribution, eg a density f(x), that gives probabilities P(X A) = f(x)dx Just
Random vectors Recall that a random vector X = X X 2 is made up of, say, k random variables X k A random vector has a joint distribution, eg a density f(x), that gives probabilities P(X A) = f(x)dx Just
Maximum Likelihood Estimation
 Chapter 8 Maximum Likelihood Estimation 8. Consistency If X is a random variable (or vector) with density or mass function f θ (x) that depends on a parameter θ, then the function f θ (X) viewed as a function
Chapter 8 Maximum Likelihood Estimation 8. Consistency If X is a random variable (or vector) with density or mass function f θ (x) that depends on a parameter θ, then the function f θ (X) viewed as a function
Multiple regression. CM226: Machine Learning for Bioinformatics. Fall Sriram Sankararaman Acknowledgments: Fei Sha, Ameet Talwalkar
 Multiple regression CM226: Machine Learning for Bioinformatics. Fall 2016 Sriram Sankararaman Acknowledgments: Fei Sha, Ameet Talwalkar Multiple regression 1 / 36 Previous two lectures Linear and logistic
Multiple regression CM226: Machine Learning for Bioinformatics. Fall 2016 Sriram Sankararaman Acknowledgments: Fei Sha, Ameet Talwalkar Multiple regression 1 / 36 Previous two lectures Linear and logistic
Generalized Linear Models. Kurt Hornik
 Generalized Linear Models Kurt Hornik Motivation Assuming normality, the linear model y = Xβ + e has y = β + ε, ε N(0, σ 2 ) such that y N(μ, σ 2 ), E(y ) = μ = β. Various generalizations, including general
Generalized Linear Models Kurt Hornik Motivation Assuming normality, the linear model y = Xβ + e has y = β + ε, ε N(0, σ 2 ) such that y N(μ, σ 2 ), E(y ) = μ = β. Various generalizations, including general
Greene, Econometric Analysis (6th ed, 2008)
 EC771: Econometrics, Spring 2010 Greene, Econometric Analysis (6th ed, 2008) Chapter 17: Maximum Likelihood Estimation The preferred estimator in a wide variety of econometric settings is that derived
EC771: Econometrics, Spring 2010 Greene, Econometric Analysis (6th ed, 2008) Chapter 17: Maximum Likelihood Estimation The preferred estimator in a wide variety of econometric settings is that derived
Differentiable Functions
 Differentiable Functions Let S R n be open and let f : R n R. We recall that, for x o = (x o 1, x o,, x o n S the partial derivative of f at the point x o with respect to the component x j is defined as
Differentiable Functions Let S R n be open and let f : R n R. We recall that, for x o = (x o 1, x o,, x o n S the partial derivative of f at the point x o with respect to the component x j is defined as
Hypothesis Testing: The Generalized Likelihood Ratio Test
 Hypothesis Testing: The Generalized Likelihood Ratio Test Consider testing the hypotheses H 0 : θ Θ 0 H 1 : θ Θ \ Θ 0 Definition: The Generalized Likelihood Ratio (GLR Let L(θ be a likelihood for a random
Hypothesis Testing: The Generalized Likelihood Ratio Test Consider testing the hypotheses H 0 : θ Θ 0 H 1 : θ Θ \ Θ 0 Definition: The Generalized Likelihood Ratio (GLR Let L(θ be a likelihood for a random
The outline for Unit 3
 The outline for Unit 3 Unit 1. Introduction: The regression model. Unit 2. Estimation principles. Unit 3: Hypothesis testing principles. 3.1 Wald test. 3.2 Lagrange Multiplier. 3.3 Likelihood Ratio Test.
The outline for Unit 3 Unit 1. Introduction: The regression model. Unit 2. Estimation principles. Unit 3: Hypothesis testing principles. 3.1 Wald test. 3.2 Lagrange Multiplier. 3.3 Likelihood Ratio Test.
Paul Schrimpf. October 18, UBC Economics 526. Unconstrained optimization. Paul Schrimpf. Notation and definitions. First order conditions
 Unconstrained UBC Economics 526 October 18, 2013 .1.2.3.4.5 Section 1 Unconstrained problem x U R n F : U R. max F (x) x U Definition F = max x U F (x) is the maximum of F on U if F (x) F for all x U and
Unconstrained UBC Economics 526 October 18, 2013 .1.2.3.4.5 Section 1 Unconstrained problem x U R n F : U R. max F (x) x U Definition F = max x U F (x) is the maximum of F on U if F (x) F for all x U and
Statistics. Lecture 4 August 9, 2000 Frank Porter Caltech. 1. The Fundamentals; Point Estimation. 2. Maximum Likelihood, Least Squares and All That
 Statistics Lecture 4 August 9, 2000 Frank Porter Caltech The plan for these lectures: 1. The Fundamentals; Point Estimation 2. Maximum Likelihood, Least Squares and All That 3. What is a Confidence Interval?
Statistics Lecture 4 August 9, 2000 Frank Porter Caltech The plan for these lectures: 1. The Fundamentals; Point Estimation 2. Maximum Likelihood, Least Squares and All That 3. What is a Confidence Interval?
N. L. P. NONLINEAR PROGRAMMING (NLP) deals with optimization models with at least one nonlinear function. NLP. Optimization. Models of following form:
 0.1 N. L. P. Katta G. Murty, IOE 611 Lecture slides Introductory Lecture NONLINEAR PROGRAMMING (NLP) deals with optimization models with at least one nonlinear function. NLP does not include everything
0.1 N. L. P. Katta G. Murty, IOE 611 Lecture slides Introductory Lecture NONLINEAR PROGRAMMING (NLP) deals with optimization models with at least one nonlinear function. NLP does not include everything
Lecture 4: Exponential family of distributions and generalized linear model (GLM) (Draft: version 0.9.2)
 Lectures on Machine Learning (Fall 2017) Hyeong In Choi Seoul National University Lecture 4: Exponential family of distributions and generalized linear model (GLM) (Draft: version 0.9.2) Topics to be covered:
Lectures on Machine Learning (Fall 2017) Hyeong In Choi Seoul National University Lecture 4: Exponential family of distributions and generalized linear model (GLM) (Draft: version 0.9.2) Topics to be covered:
Information in Data. Sufficiency, Ancillarity, Minimality, and Completeness
 Information in Data Sufficiency, Ancillarity, Minimality, and Completeness Important properties of statistics that determine the usefulness of those statistics in statistical inference. These general properties
Information in Data Sufficiency, Ancillarity, Minimality, and Completeness Important properties of statistics that determine the usefulness of those statistics in statistical inference. These general properties
Methods of Estimation
 Methods of Estimation MIT 18.655 Dr. Kempthorne Spring 2016 1 Outline Methods of Estimation I 1 Methods of Estimation I 2 X X, X P P = {P θ, θ Θ}. Problem: Finding a function θˆ(x ) which is close to θ.
Methods of Estimation MIT 18.655 Dr. Kempthorne Spring 2016 1 Outline Methods of Estimation I 1 Methods of Estimation I 2 X X, X P P = {P θ, θ Θ}. Problem: Finding a function θˆ(x ) which is close to θ.
Master s Written Examination
 Master s Written Examination Option: Statistics and Probability Spring 016 Full points may be obtained for correct answers to eight questions. Each numbered question which may have several parts is worth
Master s Written Examination Option: Statistics and Probability Spring 016 Full points may be obtained for correct answers to eight questions. Each numbered question which may have several parts is worth
Lecture 1: Introduction
 Principles of Statistics Part II - Michaelmas 208 Lecturer: Quentin Berthet Lecture : Introduction This course is concerned with presenting some of the mathematical principles of statistical theory. One
Principles of Statistics Part II - Michaelmas 208 Lecturer: Quentin Berthet Lecture : Introduction This course is concerned with presenting some of the mathematical principles of statistical theory. One
