Lecture 25: Review. Statistics 104. April 23, Colin Rundel
|
|
|
- Cathleen Elliott
- 5 years ago
- Views:
Transcription
1 Lecture 25: Review Statistics 104 Colin Rundel April 23, 2012
2 Joint CDF F (x, y) = P [X x, Y y] = P [(X, Y ) lies south-west of the point (x, y)] Y (x,y) X Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
3 Joint CDF, cont. The joint Cumulative distribution function follows the same rules as the univariate CDF, Univariate definition: x F (x) = P (X x) = f(z)dz lim F (x) = 0 x lim F (x) = 1 x x y F (x) F (y) Bivariate definition: y x F (x, y) = P (X x, Y y) = f(x, y) dx dy lim F (x, y) = 0 lim x,y F (x, y) = 1 x x,y x, y y F (x, y) F (x, y ) Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
4 Marginal Distributions We can define marginal distributions based on the CDF by setting one of the values to infinity: F (x, ) = P (X x, Y ) = = P (X x) = F X (x) x f(x, y) dy dy F (, y) = P (X, Y y) = = P (Y y) = F Y (y) y f(x, y) dx dy Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
5 Joint pdf Similar to the CDF the probability density function follows the same general rules except in two dimensions, Univariate definition: f(x) 0 for all x f(x) = d dx F (x) f(x)dx = 1 Bivariate definition: f(x, y) 0 for all (x, y) f(x, y) = F (x, y) x y f(x, y) dx dy = 1 Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
6 Marginal pdfs Marginal probability density functions are defined in terms of integrating out one of the random variables. f X (x) = f Y (x) = f(x, y) dy f(x, y) dx Previously we defined independence in terms of E(XY ) = E(X)E(Y ) X and Y are independent. This is equivalent in the joint case of f(x, y) = f X (x)f Y (y) X and Y are independent. Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
7 Probability and Expectation Univariate definition: Bivariate definition: P (X A) = f(x) dx A E[g(X)] = g(x) f(x) dx P (X A, Y B) = f(x, y) dx dy A B E[g(X, Y )] = g(x, y) f(x, y) dx dy Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
8 Bivariate Unit Normal If X and Y have independent unit normal distributions then their joint distribution f(x, y) is given by f(x, y) = φ(x)φ(y) = 1 2π e 1 2 (x2 +y 2 ) Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
9 Rayleigh Distribution The distance from the origin, R, of a point (x, y) derived from X, Y N (0, 1) is called the Rayleigh distribution. f R(r) = re 1 2 r2 F r(r) = r re 1 2 r2 0 = e 1 2 r2 r V ar(r) = 4 π 2 0 dr = 1 e 1 2 r2 E(R) = π 2 Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
10 Sum of Independent Normals Let X N (µ, σ 2 ) and Y N (λ, τ) then M X(t) = exp(µt σ2 t 2 ) M Y (t) = exp(λt τ 2 t 2 ) M X+Y (t) = exp(µt σ2 t 2 ) exp(λt τ 2 t 2 ) = exp((µ + λ)t (σ2 + τ 2 )t 2 Therefore X + Y N (µ + λ, σ 2 + τ 2 ), which can be generalized to any number of normals. Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
11 Operation Distributions If X, Y have a joint density f(x, y), then Z = g(x, Y ) has a density f g(x,y ) (z) which is determined by integrating over all values of X or Y and then considering a change of variables for the other to Z. Distribution of Sums - Z = X + Y : / dz f X+Y (z) = f(x, z/x) dy dx = f(x, z x) dx Distribution of Ratios - Z = Y/X: / dz f Y/X) (z) = f(x, z/x) dy dx = x f(x, zx) dx Product Distribution - Z = XY : / dz f XY (z) = f(x, z/x) dy dx = f(x, z/x)/ x dx Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
12 Conditional Expectation If X and Y are independent random variables then we define the conditional expectation as follows E(X Y = y) = all y xf(x y) dx E(X Y = y) = xf(x y) dx We can think of the conditional expectation as being a function of the random variable Y, thereby making E(X Y ) itself a random variable E(E(X Y )) = E(X) Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
13 Conditional Variance Similar to conditional expectation we can also define conditional variance V ar(y X) = E [(Y E(Y X)) 2 ] X = E(Y 2 X) E(Y X) 2 there is also an equivalent to the law of total probability for expectations, the Law of Total Probability for Variance: V ar(y ) = E[V ar(y X)] + V ar[e(y X)] Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
14 Covariance We have previously discussed Covariance in relation to the variance of the sum of two random variables (Review Lecture 8). V ar(x + Y ) = V ar(x) + V ar(y ) + 2Cov(X, Y ) Specifically, covariance is defined as Cov(X, Y ) = E[(X E(X))(Y E(Y ))] = E(XY ) E(X)E(Y ) this is a generalization of variance to two random variables and generally measures the degree to which X and Y tend to be large (or small) at the same time or the degree to which one tends to be large while the other is small. Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
15 Properties of Covariance Cov(X, Y ) = E[(X µ x )(Y µ y )] = E(XY ) µ x µ y Cov(X, Y ) = Cov(Y, X) Cov(X, Y ) = 0 if X and Y are independent Cov(X, c) = 0 Cov(X, X) = V ar(x) Cov(aX, by ) = ab Cov(X, Y ) Cov(X + a, Y + b) = Cov(X, Y ) Cov(X, Y + Z) = Cov(X, Y ) + Cov(X, Z) Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
16 Correlation Since Cov(X, Y ) depends on the magnitude of X and Y we would prefer to have a measure of association that is not effected by arbitrary changes in the scales of the random variables. The most common measure of linear association is correlation which is defined as ρ(x, Y ) = Cov(X, Y ) σ X σ Y 1 < ρ(x, Y ) < 1 Where the magnitude of the correlation measures the strength of the linear association and the sign determines if it is a positive or negative relationship. Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
17 General Bivariate Normal Let Z 1, Z 2 N (0, 1), which we will use to build a general bivariate normal distribution. f(z 1, z 2 ) = 1 [ 2π exp 1 ] 2 (z2 1 + z2) 2 We want to transform these unit normal distributions to have the follow arbitrary parameters: µ X, µ Y, σ X, σ Y, ρ X = σ X Z 1 + µ X Y = σ Y [ρz ρ 2 Z 2 ] + µ Y [ ( 1 1 (x µx ) 2 f(x, y) = 2πσ X σ Y (1 ρ 2 exp ) 1/2 2(1 ρ 2 ) σ X 2 + (y µ Y ) 2 σ 2 Y 2ρ (x µ )] X ) (y µ Y ) σ X σ Y Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
18 General Bivariate Normal - Marginals and Cov The marginal distributions of X and Y are given by X = σ X Z 1 + µ X = σ X N (0, 1) + µ X = N (µ X, σ 2 X ) Y = σ Y [ρz ρ 2 Z 2 ] + µ Y = σ Y [ρn (0, 1) + 1 ρ 2 N (0, 1)] + µ Y = σ Y [N (0, ρ 2 ) + N (0, 1 ρ 2 )] + µ Y = σ Y N (0, 1) + µ Y = N (µ Y, σ 2 Y ) Cov(X, Y ) = E [(X E(X))(Y E(Y ))] [ = E (σ X Z 1 + µ X µ X )(σ Y [ρz 1 + ] 1 ρ 2 Z 2 ] + µ Y µ Y ) [ = E (σ X Z 1 )(σ Y [ρz 1 + ] 1 ρ 2 Z 2 ]) = σ X σ Y E [ρz ] 1 ρ 2 Z 1 Z 2 = σ X σ Y ρe[z 2 1 ] = σ X σ Y ρ ρ(x, Y ) = Cov(X, Y ) σ X σ Y = ρ Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
19 General Bivariate Normal - Density (Matrix Notation) Obviously, the density for the Bivariate Normal is ugly, and it only gets worse when we consider higher dimensional joint densities of normals. We can write the density in a more compact form using matrix notation, f(x) = 1 [ 2π (det Σ) 1/2 exp 1 ] 2 (x µ)t Σ 1 (x µ) In the bivariate case, ( ) x x = y µ = ( µx µ Y ) ( σ 2 Σ = X ρσ X σ Y ρσ X σ Y σ 2 Y ) Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
20 Conditional Expectation of the Bivariate Normal Using X = µ X + σ X Z 1 and Y = µ Y + σ Y [ρz 1 + (1 ρ 2 ) 1/2 Z 2 ] where Z 1, Z 2 N (0, 1) we can find E(Y X). Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
21 Conditional Expectation of the Bivariate Normal Using X = µ X + σ X Z 1 and Y = µ Y + σ Y [ρz 1 + (1 ρ 2 ) 1/2 Z 2 ] where Z 1, Z 2 N (0, 1) we can find E(Y X). ) ] E[Y X = x] = E [µ Y + σ Y (ρz 1 + (1 ρ 2 ) 1/2 Z 2 X = x ( = E [µ Y + σ Y ρ x µ ) X + (1 ρ 2 ) 1/2 Z 2 X = x] σ X ( = µ Y + σ Y ρ x µ ) X + (1 ρ 2 ) 1/2 E[Z 2 X = x] σ X ( ) x µx = µ Y + σ Y ρ σ X By symmetry, ( ) y µy E[X Y = y] = µ X + σ X ρ σ Y Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
22 Conditional Variance of the Bivariate Normal Using X = µ X + σ X Z 1 and Y = µ Y + σ Y [ρz 1 + (1 ρ 2 ) 1/2 Z 2 ] where Z 1, Z 2 N (0, 1) we can find V ar(y X). Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
23 Conditional Variance of the Bivariate Normal Using X = µ X + σ X Z 1 and Y = µ Y + σ Y [ρz 1 + (1 ρ 2 ) 1/2 Z 2 ] where Z 1, Z 2 N (0, 1) we can find V ar(y X). ) ] V ar[y X = x] = V ar [µ Y + σ Y (ρz 1 + (1 ρ 2 ) 1/2 Z 2 X = x ( = V ar [µ Y + σ Y ρ x µ ) X + (1 ρ 2 ) 1/2 Z 2 X = x] σ X = V ar[σ Y (1 ρ 2 )Z 2 X = x] = σ 2 Y (1 ρ 2 ) By symmetry, V ar[x Y = y] = σ 2 X(1 ρ 2 ) Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
24 Bayesian Inference Bayes Theorem states P (A B) = P (B A)P (A) P (B) We are interested in estimating the model parameters based on the observed data and any prior belief about the parameters, which we setup as follows P (θ X) = P (X θ) P (X) π(θ) P (X θ) π(θ) Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
25 Bayesian Inference - Terminology Elements of the Bayesian Model: π(θ) - Prior distribution - This distribution reflects any preexisting information / belief about the distribution of the parameter(s). P (X θ) - Likelihood / Sampling distribution - Distribution of the data given the parameters, which is the probability model believed to have generated the data. P (X) - Marginal distribution of the data - Distribution of the observed data marginalized over all possible values of the parameter(s). P (θ X) - Posterior distribution - Distribution of the parameter(s) after taking the observed data into account. Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
26 Maximum Likelihood The maximum likelihood estimates parameter(s) by maximizing the likelihood function given the observed data. n L(θ X) = f(x θ) = f(x i θ) i=1 l(θ X) = log L(θ X) = i = 1 n log f(x i θ) The maximum likelihood estimate (estimator), MLE, is therefore given by MLE = ˆθ MLE = arg max θ L(θ X) = arg max θ l(θ X) Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
27 Why use the MLE? The maximum likelihood estimator has the following properties: Consistency - as the sample size tends to infinity the MLE tends to the true value of the parameter(s) Asymptotic normality - as the sample size increases, the distribution of the MLE tends to the normal distribution Efficiency - as the sample size tends to infinity, there are not any other unbiased estimator with a lower mean squared error Common issues: Uniqueness - estimate may not be unique Computation - results may not have a closed form Statistics 104 (Colin Rundel) Lecture 25 April 23, / 24
Covariance. Lecture 20: Covariance / Correlation & General Bivariate Normal. Covariance, cont. Properties of Covariance
 Covariance Lecture 0: Covariance / Correlation & General Bivariate Normal Sta30 / Mth 30 We have previously discussed Covariance in relation to the variance of the sum of two random variables Review Lecture
Covariance Lecture 0: Covariance / Correlation & General Bivariate Normal Sta30 / Mth 30 We have previously discussed Covariance in relation to the variance of the sum of two random variables Review Lecture
Probability Theory and Statistics. Peter Jochumzen
 Probability Theory and Statistics Peter Jochumzen April 18, 2016 Contents 1 Probability Theory And Statistics 3 1.1 Experiment, Outcome and Event................................ 3 1.2 Probability............................................
Probability Theory and Statistics Peter Jochumzen April 18, 2016 Contents 1 Probability Theory And Statistics 3 1.1 Experiment, Outcome and Event................................ 3 1.2 Probability............................................
ENGG2430A-Homework 2
 ENGG3A-Homework Due on Feb 9th,. Independence vs correlation a For each of the following cases, compute the marginal pmfs from the joint pmfs. Explain whether the random variables X and Y are independent,
ENGG3A-Homework Due on Feb 9th,. Independence vs correlation a For each of the following cases, compute the marginal pmfs from the joint pmfs. Explain whether the random variables X and Y are independent,
matrix-free Elements of Probability Theory 1 Random Variables and Distributions Contents Elements of Probability Theory 2
 Short Guides to Microeconometrics Fall 2018 Kurt Schmidheiny Unversität Basel Elements of Probability Theory 2 1 Random Variables and Distributions Contents Elements of Probability Theory matrix-free 1
Short Guides to Microeconometrics Fall 2018 Kurt Schmidheiny Unversität Basel Elements of Probability Theory 2 1 Random Variables and Distributions Contents Elements of Probability Theory matrix-free 1
Multivariate Random Variable
 Multivariate Random Variable Author: Author: Andrés Hincapié and Linyi Cao This Version: August 7, 2016 Multivariate Random Variable 3 Now we consider models with more than one r.v. These are called multivariate
Multivariate Random Variable Author: Author: Andrés Hincapié and Linyi Cao This Version: August 7, 2016 Multivariate Random Variable 3 Now we consider models with more than one r.v. These are called multivariate
STOR Lecture 16. Properties of Expectation - I
 STOR 435.001 Lecture 16 Properties of Expectation - I Jan Hannig UNC Chapel Hill 1 / 22 Motivation Recall we found joint distributions to be pretty complicated objects. Need various tools from combinatorics
STOR 435.001 Lecture 16 Properties of Expectation - I Jan Hannig UNC Chapel Hill 1 / 22 Motivation Recall we found joint distributions to be pretty complicated objects. Need various tools from combinatorics
STT 441 Final Exam Fall 2013
 STT 441 Final Exam Fall 2013 (12:45-2:45pm, Thursday, Dec. 12, 2013) NAME: ID: 1. No textbooks or class notes are allowed in this exam. 2. Be sure to show all of your work to receive credit. Credits are
STT 441 Final Exam Fall 2013 (12:45-2:45pm, Thursday, Dec. 12, 2013) NAME: ID: 1. No textbooks or class notes are allowed in this exam. 2. Be sure to show all of your work to receive credit. Credits are
EEL 5544 Noise in Linear Systems Lecture 30. X (s) = E [ e sx] f X (x)e sx dx. Moments can be found from the Laplace transform as
![EEL 5544 Noise in Linear Systems Lecture 30. X (s) = E [ e sx] f X (x)e sx dx. Moments can be found from the Laplace transform as EEL 5544 Noise in Linear Systems Lecture 30. X (s) = E [ e sx] f X (x)e sx dx. Moments can be found from the Laplace transform as](/thumbs/85/92409620.jpg) L30-1 EEL 5544 Noise in Linear Systems Lecture 30 OTHER TRANSFORMS For a continuous, nonnegative RV X, the Laplace transform of X is X (s) = E [ e sx] = 0 f X (x)e sx dx. For a nonnegative RV, the Laplace
L30-1 EEL 5544 Noise in Linear Systems Lecture 30 OTHER TRANSFORMS For a continuous, nonnegative RV X, the Laplace transform of X is X (s) = E [ e sx] = 0 f X (x)e sx dx. For a nonnegative RV, the Laplace
Multiple Random Variables
 Multiple Random Variables This Version: July 30, 2015 Multiple Random Variables 2 Now we consider models with more than one r.v. These are called multivariate models For instance: height and weight An
Multiple Random Variables This Version: July 30, 2015 Multiple Random Variables 2 Now we consider models with more than one r.v. These are called multivariate models For instance: height and weight An
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003
 Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Math 510 midterm 3 answers
 Math 51 midterm 3 answers Problem 1 (1 pts) Suppose X and Y are independent exponential random variables both with parameter λ 1. Find the probability that Y < 7X. P (Y < 7X) 7x 7x f(x, y) dy dx e x e
Math 51 midterm 3 answers Problem 1 (1 pts) Suppose X and Y are independent exponential random variables both with parameter λ 1. Find the probability that Y < 7X. P (Y < 7X) 7x 7x f(x, y) dy dx e x e
Introduction to Probability and Stocastic Processes - Part I
 Introduction to Probability and Stocastic Processes - Part I Lecture 2 Henrik Vie Christensen vie@control.auc.dk Department of Control Engineering Institute of Electronic Systems Aalborg University Denmark
Introduction to Probability and Stocastic Processes - Part I Lecture 2 Henrik Vie Christensen vie@control.auc.dk Department of Control Engineering Institute of Electronic Systems Aalborg University Denmark
Elements of Probability Theory
 Short Guides to Microeconometrics Fall 2016 Kurt Schmidheiny Unversität Basel Elements of Probability Theory Contents 1 Random Variables and Distributions 2 1.1 Univariate Random Variables and Distributions......
Short Guides to Microeconometrics Fall 2016 Kurt Schmidheiny Unversität Basel Elements of Probability Theory Contents 1 Random Variables and Distributions 2 1.1 Univariate Random Variables and Distributions......
P (x). all other X j =x j. If X is a continuous random vector (see p.172), then the marginal distributions of X i are: f(x)dx 1 dx n
 JOINT DENSITIES - RANDOM VECTORS - REVIEW Joint densities describe probability distributions of a random vector X: an n-dimensional vector of random variables, ie, X = (X 1,, X n ), where all X is are
JOINT DENSITIES - RANDOM VECTORS - REVIEW Joint densities describe probability distributions of a random vector X: an n-dimensional vector of random variables, ie, X = (X 1,, X n ), where all X is are
Notes on Random Processes
 otes on Random Processes Brian Borchers and Rick Aster October 27, 2008 A Brief Review of Probability In this section of the course, we will work with random variables which are denoted by capital letters,
otes on Random Processes Brian Borchers and Rick Aster October 27, 2008 A Brief Review of Probability In this section of the course, we will work with random variables which are denoted by capital letters,
Properties of Summation Operator
 Econ 325 Section 003/004 Notes on Variance, Covariance, and Summation Operator By Hiro Kasahara Properties of Summation Operator For a sequence of the values {x 1, x 2,..., x n, we write the sum of x 1,
Econ 325 Section 003/004 Notes on Variance, Covariance, and Summation Operator By Hiro Kasahara Properties of Summation Operator For a sequence of the values {x 1, x 2,..., x n, we write the sum of x 1,
Problem 1. Problem 2. Problem 3. Problem 4
 Problem Let A be the event that the fungus is present, and B the event that the staph-bacteria is present. We have P A = 4, P B = 9, P B A =. We wish to find P AB, to do this we use the multiplication
Problem Let A be the event that the fungus is present, and B the event that the staph-bacteria is present. We have P A = 4, P B = 9, P B A =. We wish to find P AB, to do this we use the multiplication
Stat 5101 Notes: Algorithms (thru 2nd midterm)
 Stat 5101 Notes: Algorithms (thru 2nd midterm) Charles J. Geyer October 18, 2012 Contents 1 Calculating an Expectation or a Probability 2 1.1 From a PMF........................... 2 1.2 From a PDF...........................
Stat 5101 Notes: Algorithms (thru 2nd midterm) Charles J. Geyer October 18, 2012 Contents 1 Calculating an Expectation or a Probability 2 1.1 From a PMF........................... 2 1.2 From a PDF...........................
Introduction to Computational Finance and Financial Econometrics Probability Review - Part 2
 You can t see this text! Introduction to Computational Finance and Financial Econometrics Probability Review - Part 2 Eric Zivot Spring 2015 Eric Zivot (Copyright 2015) Probability Review - Part 2 1 /
You can t see this text! Introduction to Computational Finance and Financial Econometrics Probability Review - Part 2 Eric Zivot Spring 2015 Eric Zivot (Copyright 2015) Probability Review - Part 2 1 /
STAT/MATH 395 PROBABILITY II
 STAT/MATH 395 PROBABILITY II Bivariate Distributions Néhémy Lim University of Washington Winter 2017 Outline Distributions of Two Random Variables Distributions of Two Discrete Random Variables Distributions
STAT/MATH 395 PROBABILITY II Bivariate Distributions Néhémy Lim University of Washington Winter 2017 Outline Distributions of Two Random Variables Distributions of Two Discrete Random Variables Distributions
ECON 3150/4150, Spring term Lecture 6
 ECON 3150/4150, Spring term 2013. Lecture 6 Review of theoretical statistics for econometric modelling (II) Ragnar Nymoen University of Oslo 31 January 2013 1 / 25 References to Lecture 3 and 6 Lecture
ECON 3150/4150, Spring term 2013. Lecture 6 Review of theoretical statistics for econometric modelling (II) Ragnar Nymoen University of Oslo 31 January 2013 1 / 25 References to Lecture 3 and 6 Lecture
Random Variables and Their Distributions
 Chapter 3 Random Variables and Their Distributions A random variable (r.v.) is a function that assigns one and only one numerical value to each simple event in an experiment. We will denote r.vs by capital
Chapter 3 Random Variables and Their Distributions A random variable (r.v.) is a function that assigns one and only one numerical value to each simple event in an experiment. We will denote r.vs by capital
ECE Lecture #9 Part 2 Overview
 ECE 450 - Lecture #9 Part Overview Bivariate Moments Mean or Expected Value of Z = g(x, Y) Correlation and Covariance of RV s Functions of RV s: Z = g(x, Y); finding f Z (z) Method : First find F(z), by
ECE 450 - Lecture #9 Part Overview Bivariate Moments Mean or Expected Value of Z = g(x, Y) Correlation and Covariance of RV s Functions of RV s: Z = g(x, Y); finding f Z (z) Method : First find F(z), by
More than one variable
 Chapter More than one variable.1 Bivariate discrete distributions Suppose that the r.v. s X and Y are discrete and take on the values x j and y j, j 1, respectively. Then the joint p.d.f. of X and Y, to
Chapter More than one variable.1 Bivariate discrete distributions Suppose that the r.v. s X and Y are discrete and take on the values x j and y j, j 1, respectively. Then the joint p.d.f. of X and Y, to
Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017
 Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Let X 1, X 2,, X n be a sequence of i.i.d. observations from a
Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Let X 1, X 2,, X n be a sequence of i.i.d. observations from a
Lecture 2: Probability
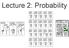 Lecture 2: Probability Statistical Paradigms Statistical Estimator Method of Estimation Output Data Complexity Prior Info Classical Cost Function Analytical Solution Point Estimate Simple No Maximum Likelihood
Lecture 2: Probability Statistical Paradigms Statistical Estimator Method of Estimation Output Data Complexity Prior Info Classical Cost Function Analytical Solution Point Estimate Simple No Maximum Likelihood
conditional cdf, conditional pdf, total probability theorem?
 6 Multiple Random Variables 6.0 INTRODUCTION scalar vs. random variable cdf, pdf transformation of a random variable conditional cdf, conditional pdf, total probability theorem expectation of a random
6 Multiple Random Variables 6.0 INTRODUCTION scalar vs. random variable cdf, pdf transformation of a random variable conditional cdf, conditional pdf, total probability theorem expectation of a random
Lecture 11. Probability Theory: an Overveiw
 Math 408 - Mathematical Statistics Lecture 11. Probability Theory: an Overveiw February 11, 2013 Konstantin Zuev (USC) Math 408, Lecture 11 February 11, 2013 1 / 24 The starting point in developing the
Math 408 - Mathematical Statistics Lecture 11. Probability Theory: an Overveiw February 11, 2013 Konstantin Zuev (USC) Math 408, Lecture 11 February 11, 2013 1 / 24 The starting point in developing the
BASICS OF PROBABILITY
 October 10, 2018 BASICS OF PROBABILITY Randomness, sample space and probability Probability is concerned with random experiments. That is, an experiment, the outcome of which cannot be predicted with certainty,
October 10, 2018 BASICS OF PROBABILITY Randomness, sample space and probability Probability is concerned with random experiments. That is, an experiment, the outcome of which cannot be predicted with certainty,
Chapter 5 continued. Chapter 5 sections
 Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Stat 5101 Notes: Algorithms
 Stat 5101 Notes: Algorithms Charles J. Geyer January 22, 2016 Contents 1 Calculating an Expectation or a Probability 3 1.1 From a PMF........................... 3 1.2 From a PDF...........................
Stat 5101 Notes: Algorithms Charles J. Geyer January 22, 2016 Contents 1 Calculating an Expectation or a Probability 3 1.1 From a PMF........................... 3 1.2 From a PDF...........................
Probability Lecture III (August, 2006)
 robability Lecture III (August, 2006) 1 Some roperties of Random Vectors and Matrices We generalize univariate notions in this section. Definition 1 Let U = U ij k l, a matrix of random variables. Suppose
robability Lecture III (August, 2006) 1 Some roperties of Random Vectors and Matrices We generalize univariate notions in this section. Definition 1 Let U = U ij k l, a matrix of random variables. Suppose
5 Operations on Multiple Random Variables
 EE360 Random Signal analysis Chapter 5: Operations on Multiple Random Variables 5 Operations on Multiple Random Variables Expected value of a function of r.v. s Two r.v. s: ḡ = E[g(X, Y )] = g(x, y)f X,Y
EE360 Random Signal analysis Chapter 5: Operations on Multiple Random Variables 5 Operations on Multiple Random Variables Expected value of a function of r.v. s Two r.v. s: ḡ = E[g(X, Y )] = g(x, y)f X,Y
Chapter 4 Multiple Random Variables
 Review for the previous lecture Definition: n-dimensional random vector, joint pmf (pdf), marginal pmf (pdf) Theorem: How to calculate marginal pmf (pdf) given joint pmf (pdf) Example: How to calculate
Review for the previous lecture Definition: n-dimensional random vector, joint pmf (pdf), marginal pmf (pdf) Theorem: How to calculate marginal pmf (pdf) given joint pmf (pdf) Example: How to calculate
Perhaps the simplest way of modeling two (discrete) random variables is by means of a joint PMF, defined as follows.
 Chapter 5 Two Random Variables In a practical engineering problem, there is almost always causal relationship between different events. Some relationships are determined by physical laws, e.g., voltage
Chapter 5 Two Random Variables In a practical engineering problem, there is almost always causal relationship between different events. Some relationships are determined by physical laws, e.g., voltage
Some Concepts of Probability (Review) Volker Tresp Summer 2018
 Some Concepts of Probability (Review) Volker Tresp Summer 2018 1 Definition There are different way to define what a probability stands for Mathematically, the most rigorous definition is based on Kolmogorov
Some Concepts of Probability (Review) Volker Tresp Summer 2018 1 Definition There are different way to define what a probability stands for Mathematically, the most rigorous definition is based on Kolmogorov
STA 2201/442 Assignment 2
 STA 2201/442 Assignment 2 1. This is about how to simulate from a continuous univariate distribution. Let the random variable X have a continuous distribution with density f X (x) and cumulative distribution
STA 2201/442 Assignment 2 1. This is about how to simulate from a continuous univariate distribution. Let the random variable X have a continuous distribution with density f X (x) and cumulative distribution
Final Exam # 3. Sta 230: Probability. December 16, 2012
 Final Exam # 3 Sta 230: Probability December 16, 2012 This is a closed-book exam so do not refer to your notes, the text, or any other books (please put them on the floor). You may use the extra sheets
Final Exam # 3 Sta 230: Probability December 16, 2012 This is a closed-book exam so do not refer to your notes, the text, or any other books (please put them on the floor). You may use the extra sheets
Practice Examination # 3
 Practice Examination # 3 Sta 23: Probability December 13, 212 This is a closed-book exam so do not refer to your notes, the text, or any other books (please put them on the floor). You may use a single
Practice Examination # 3 Sta 23: Probability December 13, 212 This is a closed-book exam so do not refer to your notes, the text, or any other books (please put them on the floor). You may use a single
LIST OF FORMULAS FOR STK1100 AND STK1110
 LIST OF FORMULAS FOR STK1100 AND STK1110 (Version of 11. November 2015) 1. Probability Let A, B, A 1, A 2,..., B 1, B 2,... be events, that is, subsets of a sample space Ω. a) Axioms: A probability function
LIST OF FORMULAS FOR STK1100 AND STK1110 (Version of 11. November 2015) 1. Probability Let A, B, A 1, A 2,..., B 1, B 2,... be events, that is, subsets of a sample space Ω. a) Axioms: A probability function
Random Variables. Random variables. A numerically valued map X of an outcome ω from a sample space Ω to the real line R
 In probabilistic models, a random variable is a variable whose possible values are numerical outcomes of a random phenomenon. As a function or a map, it maps from an element (or an outcome) of a sample
In probabilistic models, a random variable is a variable whose possible values are numerical outcomes of a random phenomenon. As a function or a map, it maps from an element (or an outcome) of a sample
Continuous Random Variables
 1 / 24 Continuous Random Variables Saravanan Vijayakumaran sarva@ee.iitb.ac.in Department of Electrical Engineering Indian Institute of Technology Bombay February 27, 2013 2 / 24 Continuous Random Variables
1 / 24 Continuous Random Variables Saravanan Vijayakumaran sarva@ee.iitb.ac.in Department of Electrical Engineering Indian Institute of Technology Bombay February 27, 2013 2 / 24 Continuous Random Variables
Bivariate Distributions. Discrete Bivariate Distribution Example
 Spring 7 Geog C: Phaedon C. Kyriakidis Bivariate Distributions Definition: class of multivariate probability distributions describing joint variation of outcomes of two random variables (discrete or continuous),
Spring 7 Geog C: Phaedon C. Kyriakidis Bivariate Distributions Definition: class of multivariate probability distributions describing joint variation of outcomes of two random variables (discrete or continuous),
Review of Probability Theory
 Review of Probability Theory Arian Maleki and Tom Do Stanford University Probability theory is the study of uncertainty Through this class, we will be relying on concepts from probability theory for deriving
Review of Probability Theory Arian Maleki and Tom Do Stanford University Probability theory is the study of uncertainty Through this class, we will be relying on concepts from probability theory for deriving
14.30 Introduction to Statistical Methods in Economics Spring 2009
 MIT OpenCourseWare http://ocw.mit.edu 14.30 Introduction to Statistical Methods in Economics Spring 2009 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms.
MIT OpenCourseWare http://ocw.mit.edu 14.30 Introduction to Statistical Methods in Economics Spring 2009 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms.
Random Variables. Cumulative Distribution Function (CDF) Amappingthattransformstheeventstotherealline.
 Random Variables Amappingthattransformstheeventstotherealline. Example 1. Toss a fair coin. Define a random variable X where X is 1 if head appears and X is if tail appears. P (X =)=1/2 P (X =1)=1/2 Example
Random Variables Amappingthattransformstheeventstotherealline. Example 1. Toss a fair coin. Define a random variable X where X is 1 if head appears and X is if tail appears. P (X =)=1/2 P (X =1)=1/2 Example
Class 8 Review Problems solutions, 18.05, Spring 2014
 Class 8 Review Problems solutions, 8.5, Spring 4 Counting and Probability. (a) Create an arrangement in stages and count the number of possibilities at each stage: ( ) Stage : Choose three of the slots
Class 8 Review Problems solutions, 8.5, Spring 4 Counting and Probability. (a) Create an arrangement in stages and count the number of possibilities at each stage: ( ) Stage : Choose three of the slots
Lecture 2: Repetition of probability theory and statistics
 Algorithms for Uncertainty Quantification SS8, IN2345 Tobias Neckel Scientific Computing in Computer Science TUM Lecture 2: Repetition of probability theory and statistics Concept of Building Block: Prerequisites:
Algorithms for Uncertainty Quantification SS8, IN2345 Tobias Neckel Scientific Computing in Computer Science TUM Lecture 2: Repetition of probability theory and statistics Concept of Building Block: Prerequisites:
Bivariate distributions
 Bivariate distributions 3 th October 017 lecture based on Hogg Tanis Zimmerman: Probability and Statistical Inference (9th ed.) Bivariate Distributions of the Discrete Type The Correlation Coefficient
Bivariate distributions 3 th October 017 lecture based on Hogg Tanis Zimmerman: Probability and Statistical Inference (9th ed.) Bivariate Distributions of the Discrete Type The Correlation Coefficient
This exam is closed book and closed notes. (You will have access to a copy of the Table of Common Distributions given in the back of the text.
 TEST #3 STA 536 December, 00 Name: Please read the following directions. DO NOT TURN THE PAGE UNTIL INSTRUCTED TO DO SO Directions This exam is closed book and closed notes. You will have access to a copy
TEST #3 STA 536 December, 00 Name: Please read the following directions. DO NOT TURN THE PAGE UNTIL INSTRUCTED TO DO SO Directions This exam is closed book and closed notes. You will have access to a copy
Exam P Review Sheet. for a > 0. ln(a) i=0 ari = a. (1 r) 2. (Note that the A i s form a partition)
 Exam P Review Sheet log b (b x ) = x log b (y k ) = k log b (y) log b (y) = ln(y) ln(b) log b (yz) = log b (y) + log b (z) log b (y/z) = log b (y) log b (z) ln(e x ) = x e ln(y) = y for y > 0. d dx ax
Exam P Review Sheet log b (b x ) = x log b (y k ) = k log b (y) log b (y) = ln(y) ln(b) log b (yz) = log b (y) + log b (z) log b (y/z) = log b (y) log b (z) ln(e x ) = x e ln(y) = y for y > 0. d dx ax
The Multivariate Normal Distribution. In this case according to our theorem
 The Multivariate Normal Distribution Defn: Z R 1 N(0, 1) iff f Z (z) = 1 2π e z2 /2. Defn: Z R p MV N p (0, I) if and only if Z = (Z 1,..., Z p ) T with the Z i independent and each Z i N(0, 1). In this
The Multivariate Normal Distribution Defn: Z R 1 N(0, 1) iff f Z (z) = 1 2π e z2 /2. Defn: Z R p MV N p (0, I) if and only if Z = (Z 1,..., Z p ) T with the Z i independent and each Z i N(0, 1). In this
Lecture 2: Review of Probability
 Lecture 2: Review of Probability Zheng Tian Contents 1 Random Variables and Probability Distributions 2 1.1 Defining probabilities and random variables..................... 2 1.2 Probability distributions................................
Lecture 2: Review of Probability Zheng Tian Contents 1 Random Variables and Probability Distributions 2 1.1 Defining probabilities and random variables..................... 2 1.2 Probability distributions................................
Recitation 2: Probability
 Recitation 2: Probability Colin White, Kenny Marino January 23, 2018 Outline Facts about sets Definitions and facts about probability Random Variables and Joint Distributions Characteristics of distributions
Recitation 2: Probability Colin White, Kenny Marino January 23, 2018 Outline Facts about sets Definitions and facts about probability Random Variables and Joint Distributions Characteristics of distributions
Introduction to Normal Distribution
 Introduction to Normal Distribution Nathaniel E. Helwig Assistant Professor of Psychology and Statistics University of Minnesota (Twin Cities) Updated 17-Jan-2017 Nathaniel E. Helwig (U of Minnesota) Introduction
Introduction to Normal Distribution Nathaniel E. Helwig Assistant Professor of Psychology and Statistics University of Minnesota (Twin Cities) Updated 17-Jan-2017 Nathaniel E. Helwig (U of Minnesota) Introduction
Course: ESO-209 Home Work: 1 Instructor: Debasis Kundu
 Home Work: 1 1. Describe the sample space when a coin is tossed (a) once, (b) three times, (c) n times, (d) an infinite number of times. 2. A coin is tossed until for the first time the same result appear
Home Work: 1 1. Describe the sample space when a coin is tossed (a) once, (b) three times, (c) n times, (d) an infinite number of times. 2. A coin is tossed until for the first time the same result appear
Lecture 14: Multivariate mgf s and chf s
 Lecture 14: Multivariate mgf s and chf s Multivariate mgf and chf For an n-dimensional random vector X, its mgf is defined as M X (t) = E(e t X ), t R n and its chf is defined as φ X (t) = E(e ıt X ),
Lecture 14: Multivariate mgf s and chf s Multivariate mgf and chf For an n-dimensional random vector X, its mgf is defined as M X (t) = E(e t X ), t R n and its chf is defined as φ X (t) = E(e ıt X ),
2 (Statistics) Random variables
 2 (Statistics) Random variables References: DeGroot and Schervish, chapters 3, 4 and 5; Stirzaker, chapters 4, 5 and 6 We will now study the main tools use for modeling experiments with unknown outcomes
2 (Statistics) Random variables References: DeGroot and Schervish, chapters 3, 4 and 5; Stirzaker, chapters 4, 5 and 6 We will now study the main tools use for modeling experiments with unknown outcomes
Bivariate Distributions
 STAT/MATH 395 A - PROBABILITY II UW Winter Quarter 17 Néhémy Lim Bivariate Distributions 1 Distributions of Two Random Variables Definition 1.1. Let X and Y be two rrvs on probability space (Ω, A, P).
STAT/MATH 395 A - PROBABILITY II UW Winter Quarter 17 Néhémy Lim Bivariate Distributions 1 Distributions of Two Random Variables Definition 1.1. Let X and Y be two rrvs on probability space (Ω, A, P).
Homework 5 Solutions
 126/DCP126 Probability, Fall 214 Instructor: Prof. Wen-Guey Tzeng Homework 5 Solutions 5-Jan-215 1. Let the joint probability mass function of discrete random variables X and Y be given by { c(x + y) ifx
126/DCP126 Probability, Fall 214 Instructor: Prof. Wen-Guey Tzeng Homework 5 Solutions 5-Jan-215 1. Let the joint probability mass function of discrete random variables X and Y be given by { c(x + y) ifx
STAT215: Solutions for Homework 2
 STAT25: Solutions for Homework 2 Due: Wednesday, Feb 4. (0 pt) Suppose we take one observation, X, from the discrete distribution, x 2 0 2 Pr(X x θ) ( θ)/4 θ/2 /2 (3 θ)/2 θ/4, 0 θ Find an unbiased estimator
STAT25: Solutions for Homework 2 Due: Wednesday, Feb 4. (0 pt) Suppose we take one observation, X, from the discrete distribution, x 2 0 2 Pr(X x θ) ( θ)/4 θ/2 /2 (3 θ)/2 θ/4, 0 θ Find an unbiased estimator
Statistics STAT:5100 (22S:193), Fall Sample Final Exam B
 Statistics STAT:5 (22S:93), Fall 25 Sample Final Exam B Please write your answers in the exam books provided.. Let X, Y, and Y 2 be independent random variables with X N(µ X, σ 2 X ) and Y i N(µ Y, σ 2
Statistics STAT:5 (22S:93), Fall 25 Sample Final Exam B Please write your answers in the exam books provided.. Let X, Y, and Y 2 be independent random variables with X N(µ X, σ 2 X ) and Y i N(µ Y, σ 2
01 Probability Theory and Statistics Review
 NAVARCH/EECS 568, ROB 530 - Winter 2018 01 Probability Theory and Statistics Review Maani Ghaffari January 08, 2018 Last Time: Bayes Filters Given: Stream of observations z 1:t and action data u 1:t Sensor/measurement
NAVARCH/EECS 568, ROB 530 - Winter 2018 01 Probability Theory and Statistics Review Maani Ghaffari January 08, 2018 Last Time: Bayes Filters Given: Stream of observations z 1:t and action data u 1:t Sensor/measurement
Formulas for probability theory and linear models SF2941
 Formulas for probability theory and linear models SF2941 These pages + Appendix 2 of Gut) are permitted as assistance at the exam. 11 maj 2008 Selected formulae of probability Bivariate probability Transforms
Formulas for probability theory and linear models SF2941 These pages + Appendix 2 of Gut) are permitted as assistance at the exam. 11 maj 2008 Selected formulae of probability Bivariate probability Transforms
Problem Set #5. Econ 103. Solution: By the complement rule p(0) = 1 p q. q, 1 x 0 < 0 1 p, 0 x 0 < 1. Solution: E[X] = 1 q + 0 (1 p q) + p 1 = p q
![Problem Set #5. Econ 103. Solution: By the complement rule p(0) = 1 p q. q, 1 x 0 < 0 1 p, 0 x 0 < 1. Solution: E[X] = 1 q + 0 (1 p q) + p 1 = p q Problem Set #5. Econ 103. Solution: By the complement rule p(0) = 1 p q. q, 1 x 0 < 0 1 p, 0 x 0 < 1. Solution: E[X] = 1 q + 0 (1 p q) + p 1 = p q](/thumbs/76/73773120.jpg) Problem Set #5 Econ 103 Part I Problems from the Textbook Chapter 4: 1, 3, 5, 7, 9, 11, 13, 15, 25, 27, 29 Chapter 5: 1, 3, 5, 9, 11, 13, 17 Part II Additional Problems 1. Suppose X is a random variable
Problem Set #5 Econ 103 Part I Problems from the Textbook Chapter 4: 1, 3, 5, 7, 9, 11, 13, 15, 25, 27, 29 Chapter 5: 1, 3, 5, 9, 11, 13, 17 Part II Additional Problems 1. Suppose X is a random variable
Chp 4. Expectation and Variance
 Chp 4. Expectation and Variance 1 Expectation In this chapter, we will introduce two objectives to directly reflect the properties of a random variable or vector, which are the Expectation and Variance.
Chp 4. Expectation and Variance 1 Expectation In this chapter, we will introduce two objectives to directly reflect the properties of a random variable or vector, which are the Expectation and Variance.
4. Distributions of Functions of Random Variables
 4. Distributions of Functions of Random Variables Setup: Consider as given the joint distribution of X 1,..., X n (i.e. consider as given f X1,...,X n and F X1,...,X n ) Consider k functions g 1 : R n
4. Distributions of Functions of Random Variables Setup: Consider as given the joint distribution of X 1,..., X n (i.e. consider as given f X1,...,X n and F X1,...,X n ) Consider k functions g 1 : R n
Actuarial Science Exam 1/P
 Actuarial Science Exam /P Ville A. Satopää December 5, 2009 Contents Review of Algebra and Calculus 2 2 Basic Probability Concepts 3 3 Conditional Probability and Independence 4 4 Combinatorial Principles,
Actuarial Science Exam /P Ville A. Satopää December 5, 2009 Contents Review of Algebra and Calculus 2 2 Basic Probability Concepts 3 3 Conditional Probability and Independence 4 4 Combinatorial Principles,
CHAPTER 4 MATHEMATICAL EXPECTATION. 4.1 Mean of a Random Variable
 CHAPTER 4 MATHEMATICAL EXPECTATION 4.1 Mean of a Random Variable The expected value, or mathematical expectation E(X) of a random variable X is the long-run average value of X that would emerge after a
CHAPTER 4 MATHEMATICAL EXPECTATION 4.1 Mean of a Random Variable The expected value, or mathematical expectation E(X) of a random variable X is the long-run average value of X that would emerge after a
ECSE B Solutions to Assignment 8 Fall 2008
 ECSE 34-35B Solutions to Assignment 8 Fall 28 Problem 8.1 A manufacturing system is governed by a Poisson counting process {N t ; t < } with rate parameter λ >. If a counting event occurs at an instant
ECSE 34-35B Solutions to Assignment 8 Fall 28 Problem 8.1 A manufacturing system is governed by a Poisson counting process {N t ; t < } with rate parameter λ >. If a counting event occurs at an instant
System Identification, Lecture 4
 System Identification, Lecture 4 Kristiaan Pelckmans (IT/UU, 2338) Course code: 1RT880, Report code: 61800 - Spring 2016 F, FRI Uppsala University, Information Technology 13 April 2016 SI-2016 K. Pelckmans
System Identification, Lecture 4 Kristiaan Pelckmans (IT/UU, 2338) Course code: 1RT880, Report code: 61800 - Spring 2016 F, FRI Uppsala University, Information Technology 13 April 2016 SI-2016 K. Pelckmans
1 Probability theory. 2 Random variables and probability theory.
 Probability theory Here we summarize some of the probability theory we need. If this is totally unfamiliar to you, you should look at one of the sources given in the readings. In essence, for the major
Probability theory Here we summarize some of the probability theory we need. If this is totally unfamiliar to you, you should look at one of the sources given in the readings. In essence, for the major
Lecture 2: Probability
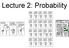 Lecture 2: Probability Statistical Paradigms Statistical Estimator Method of Estimation Output Data Complexity Prior Info Classical Cost Function Analytical Solution Point Estimate Simple No Maximum Likelihood
Lecture 2: Probability Statistical Paradigms Statistical Estimator Method of Estimation Output Data Complexity Prior Info Classical Cost Function Analytical Solution Point Estimate Simple No Maximum Likelihood
Preliminary Statistics. Lecture 3: Probability Models and Distributions
 Preliminary Statistics Lecture 3: Probability Models and Distributions Rory Macqueen (rm43@soas.ac.uk), September 2015 Outline Revision of Lecture 2 Probability Density Functions Cumulative Distribution
Preliminary Statistics Lecture 3: Probability Models and Distributions Rory Macqueen (rm43@soas.ac.uk), September 2015 Outline Revision of Lecture 2 Probability Density Functions Cumulative Distribution
MAS223 Statistical Modelling and Inference Examples
 Chapter MAS3 Statistical Modelling and Inference Examples Example : Sample spaces and random variables. Let S be the sample space for the experiment of tossing two coins; i.e. Define the random variables
Chapter MAS3 Statistical Modelling and Inference Examples Example : Sample spaces and random variables. Let S be the sample space for the experiment of tossing two coins; i.e. Define the random variables
Lecture 1: Bayesian Framework Basics
 Lecture 1: Bayesian Framework Basics Melih Kandemir melih.kandemir@iwr.uni-heidelberg.de April 21, 2014 What is this course about? Building Bayesian machine learning models Performing the inference of
Lecture 1: Bayesian Framework Basics Melih Kandemir melih.kandemir@iwr.uni-heidelberg.de April 21, 2014 What is this course about? Building Bayesian machine learning models Performing the inference of
UC Berkeley Department of Electrical Engineering and Computer Sciences. EECS 126: Probability and Random Processes
 UC Berkeley Department of Electrical Engineering and Computer Sciences EECS 6: Probability and Random Processes Problem Set 3 Spring 9 Self-Graded Scores Due: February 8, 9 Submit your self-graded scores
UC Berkeley Department of Electrical Engineering and Computer Sciences EECS 6: Probability and Random Processes Problem Set 3 Spring 9 Self-Graded Scores Due: February 8, 9 Submit your self-graded scores
Mathematics 426 Robert Gross Homework 9 Answers
 Mathematics 4 Robert Gross Homework 9 Answers. Suppose that X is a normal random variable with mean µ and standard deviation σ. Suppose that PX > 9 PX
Mathematics 4 Robert Gross Homework 9 Answers. Suppose that X is a normal random variable with mean µ and standard deviation σ. Suppose that PX > 9 PX
Machine learning - HT Maximum Likelihood
 Machine learning - HT 2016 3. Maximum Likelihood Varun Kanade University of Oxford January 27, 2016 Outline Probabilistic Framework Formulate linear regression in the language of probability Introduce
Machine learning - HT 2016 3. Maximum Likelihood Varun Kanade University of Oxford January 27, 2016 Outline Probabilistic Framework Formulate linear regression in the language of probability Introduce
Notes on Random Vectors and Multivariate Normal
 MATH 590 Spring 06 Notes on Random Vectors and Multivariate Normal Properties of Random Vectors If X,, X n are random variables, then X = X,, X n ) is a random vector, with the cumulative distribution
MATH 590 Spring 06 Notes on Random Vectors and Multivariate Normal Properties of Random Vectors If X,, X n are random variables, then X = X,, X n ) is a random vector, with the cumulative distribution
18 Bivariate normal distribution I
 8 Bivariate normal distribution I 8 Example Imagine firing arrows at a target Hopefully they will fall close to the target centre As we fire more arrows we find a high density near the centre and fewer
8 Bivariate normal distribution I 8 Example Imagine firing arrows at a target Hopefully they will fall close to the target centre As we fire more arrows we find a high density near the centre and fewer
Probability and Distributions
 Probability and Distributions What is a statistical model? A statistical model is a set of assumptions by which the hypothetical population distribution of data is inferred. It is typically postulated
Probability and Distributions What is a statistical model? A statistical model is a set of assumptions by which the hypothetical population distribution of data is inferred. It is typically postulated
Jointly Distributed Random Variables
 Jointly Distributed Random Variables CE 311S What if there is more than one random variable we are interested in? How should you invest the extra money from your summer internship? To simplify matters,
Jointly Distributed Random Variables CE 311S What if there is more than one random variable we are interested in? How should you invest the extra money from your summer internship? To simplify matters,
Joint Distributions. (a) Scalar multiplication: k = c d. (b) Product of two matrices: c d. (c) The transpose of a matrix:
 Joint Distributions Joint Distributions A bivariate normal distribution generalizes the concept of normal distribution to bivariate random variables It requires a matrix formulation of quadratic forms,
Joint Distributions Joint Distributions A bivariate normal distribution generalizes the concept of normal distribution to bivariate random variables It requires a matrix formulation of quadratic forms,
Mathematical statistics: Estimation theory
 Mathematical statistics: Estimation theory EE 30: Networked estimation and control Prof. Khan I. BASIC STATISTICS The sample space Ω is the set of all possible outcomes of a random eriment. A sample point
Mathematical statistics: Estimation theory EE 30: Networked estimation and control Prof. Khan I. BASIC STATISTICS The sample space Ω is the set of all possible outcomes of a random eriment. A sample point
4. CONTINUOUS RANDOM VARIABLES
 IA Probability Lent Term 4 CONTINUOUS RANDOM VARIABLES 4 Introduction Up to now we have restricted consideration to sample spaces Ω which are finite, or countable; we will now relax that assumption We
IA Probability Lent Term 4 CONTINUOUS RANDOM VARIABLES 4 Introduction Up to now we have restricted consideration to sample spaces Ω which are finite, or countable; we will now relax that assumption We
Quick Tour of Basic Probability Theory and Linear Algebra
 Quick Tour of and Linear Algebra Quick Tour of and Linear Algebra CS224w: Social and Information Network Analysis Fall 2011 Quick Tour of and Linear Algebra Quick Tour of and Linear Algebra Outline Definitions
Quick Tour of and Linear Algebra Quick Tour of and Linear Algebra CS224w: Social and Information Network Analysis Fall 2011 Quick Tour of and Linear Algebra Quick Tour of and Linear Algebra Outline Definitions
MULTIVARIATE PROBABILITY DISTRIBUTIONS
 MULTIVARIATE PROBABILITY DISTRIBUTIONS. PRELIMINARIES.. Example. Consider an experiment that consists of tossing a die and a coin at the same time. We can consider a number of random variables defined
MULTIVARIATE PROBABILITY DISTRIBUTIONS. PRELIMINARIES.. Example. Consider an experiment that consists of tossing a die and a coin at the same time. We can consider a number of random variables defined
MATH 38061/MATH48061/MATH68061: MULTIVARIATE STATISTICS Solutions to Problems on Random Vectors and Random Sampling. 1+ x2 +y 2 ) (n+2)/2
 MATH 3806/MATH4806/MATH6806: MULTIVARIATE STATISTICS Solutions to Problems on Rom Vectors Rom Sampling Let X Y have the joint pdf: fx,y) + x +y ) n+)/ π n for < x < < y < this is particular case of the
MATH 3806/MATH4806/MATH6806: MULTIVARIATE STATISTICS Solutions to Problems on Rom Vectors Rom Sampling Let X Y have the joint pdf: fx,y) + x +y ) n+)/ π n for < x < < y < this is particular case of the
System Identification, Lecture 4
 System Identification, Lecture 4 Kristiaan Pelckmans (IT/UU, 2338) Course code: 1RT880, Report code: 61800 - Spring 2012 F, FRI Uppsala University, Information Technology 30 Januari 2012 SI-2012 K. Pelckmans
System Identification, Lecture 4 Kristiaan Pelckmans (IT/UU, 2338) Course code: 1RT880, Report code: 61800 - Spring 2012 F, FRI Uppsala University, Information Technology 30 Januari 2012 SI-2012 K. Pelckmans
Joint Probability Distributions and Random Samples (Devore Chapter Five)
 Joint Probability Distributions and Random Samples (Devore Chapter Five) 1016-345-01: Probability and Statistics for Engineers Spring 2013 Contents 1 Joint Probability Distributions 2 1.1 Two Discrete
Joint Probability Distributions and Random Samples (Devore Chapter Five) 1016-345-01: Probability and Statistics for Engineers Spring 2013 Contents 1 Joint Probability Distributions 2 1.1 Two Discrete
Statistics GIDP Ph.D. Qualifying Exam Theory Jan 11, 2016, 9:00am-1:00pm
 Statistics GIDP Ph.D. Qualifying Exam Theory Jan, 06, 9:00am-:00pm Instructions: Provide answers on the supplied pads of paper; write on only one side of each sheet. Complete exactly 5 of the 6 problems.
Statistics GIDP Ph.D. Qualifying Exam Theory Jan, 06, 9:00am-:00pm Instructions: Provide answers on the supplied pads of paper; write on only one side of each sheet. Complete exactly 5 of the 6 problems.
Chapter 4 continued. Chapter 4 sections
 Chapter 4 sections Chapter 4 continued 4.1 Expectation 4.2 Properties of Expectations 4.3 Variance 4.4 Moments 4.5 The Mean and the Median 4.6 Covariance and Correlation 4.7 Conditional Expectation SKIP:
Chapter 4 sections Chapter 4 continued 4.1 Expectation 4.2 Properties of Expectations 4.3 Variance 4.4 Moments 4.5 The Mean and the Median 4.6 Covariance and Correlation 4.7 Conditional Expectation SKIP:
3. Probability and Statistics
 FE661 - Statistical Methods for Financial Engineering 3. Probability and Statistics Jitkomut Songsiri definitions, probability measures conditional expectations correlation and covariance some important
FE661 - Statistical Methods for Financial Engineering 3. Probability and Statistics Jitkomut Songsiri definitions, probability measures conditional expectations correlation and covariance some important
Random Variables. P(x) = P[X(e)] = P(e). (1)
![Random Variables. P(x) = P[X(e)] = P(e). (1) Random Variables. P(x) = P[X(e)] = P(e). (1)](/thumbs/86/94250597.jpg) Random Variables Random variable (discrete or continuous) is used to derive the output statistical properties of a system whose input is a random variable or random in nature. Definition Consider an experiment
Random Variables Random variable (discrete or continuous) is used to derive the output statistical properties of a system whose input is a random variable or random in nature. Definition Consider an experiment
STAT Chapter 5 Continuous Distributions
 STAT 270 - Chapter 5 Continuous Distributions June 27, 2012 Shirin Golchi () STAT270 June 27, 2012 1 / 59 Continuous rv s Definition: X is a continuous rv if it takes values in an interval, i.e., range
STAT 270 - Chapter 5 Continuous Distributions June 27, 2012 Shirin Golchi () STAT270 June 27, 2012 1 / 59 Continuous rv s Definition: X is a continuous rv if it takes values in an interval, i.e., range
E X A M. Probability Theory and Stochastic Processes Date: December 13, 2016 Duration: 4 hours. Number of pages incl.
 E X A M Course code: Course name: Number of pages incl. front page: 6 MA430-G Probability Theory and Stochastic Processes Date: December 13, 2016 Duration: 4 hours Resources allowed: Notes: Pocket calculator,
E X A M Course code: Course name: Number of pages incl. front page: 6 MA430-G Probability Theory and Stochastic Processes Date: December 13, 2016 Duration: 4 hours Resources allowed: Notes: Pocket calculator,
Probability. Paul Schrimpf. January 23, UBC Economics 326. Probability. Paul Schrimpf. Definitions. Properties. Random variables.
 Probability UBC Economics 326 January 23, 2018 1 2 3 Wooldridge (2013) appendix B Stock and Watson (2009) chapter 2 Linton (2017) chapters 1-5 Abbring (2001) sections 2.1-2.3 Diez, Barr, and Cetinkaya-Rundel
Probability UBC Economics 326 January 23, 2018 1 2 3 Wooldridge (2013) appendix B Stock and Watson (2009) chapter 2 Linton (2017) chapters 1-5 Abbring (2001) sections 2.1-2.3 Diez, Barr, and Cetinkaya-Rundel
1. Fisher Information
 1. Fisher Information Let f(x θ) be a density function with the property that log f(x θ) is differentiable in θ throughout the open p-dimensional parameter set Θ R p ; then the score statistic (or score
1. Fisher Information Let f(x θ) be a density function with the property that log f(x θ) is differentiable in θ throughout the open p-dimensional parameter set Θ R p ; then the score statistic (or score
Introduction to Machine Learning
 What does this mean? Outline Contents Introduction to Machine Learning Introduction to Probabilistic Methods Varun Chandola December 26, 2017 1 Introduction to Probability 1 2 Random Variables 3 3 Bayes
What does this mean? Outline Contents Introduction to Machine Learning Introduction to Probabilistic Methods Varun Chandola December 26, 2017 1 Introduction to Probability 1 2 Random Variables 3 3 Bayes
