AND THE REST CATEGORICAL. by M. D. Moustafa
|
|
|
- Rodger Walters
- 5 years ago
- Views:
Transcription
1 TESTING OF HYPOTHESES ON A MULTIVARIATE POPULATION SOME OF THE VARIATES BEING CONTINUOUS AND THE REST CATEGORICAL by M. D. Mustafa This eseach was suppted by the United States Ai Fce '~hugh the Ai Fce Office f Scientific Reseach f the Ai Reseach and Develpment Cmmand unde Cntact N. AF 18(600) Repductin in whle in pat is pemitted f any pupse Qf the United States Gvenment. Institute f Statistics Mimegaph Seies N. 179 July ;.
2 3. AFOSR-TN ASTIA-AD UNCLASSIFIED SECURITY INFORJvIATION BIBLIOGRAPHICAL CON/fROL SHEET / 1. Univesity f Nth Calina Chapel Rill N. O. 2. Mathematics Divisin Ai Fce Office f Sientific Reseah 5. TESTING OF HYPOTHESES ON A MULTIVARIATE POPULATION SOME OF THE VARIATES BEING CONTINUOUS AND THE REST CATEGORICAL 6. M. D. Mustafa 7. July AF 18(600) File 3.3
3 TESTING OF HYPOTHESES ON A i1ultivariate POPULATION; SOME OF THE VARIATES BEING CONTINUOUS AND THE REST CATEGORICAL * by f'lj. D. Mustafa Summay: We cnside a (k+:).)-vaiate distibutin in which k vaiates ae cntinuus and i vaiates ae categical. The k vaiates ae assumed t have a cnditinal multivaiate nmal distibutin with espect t the i categical vaiates which ae assumed t have a multinmial distibutin. Apppiate hyptheses ae famed in this situatin analgus t the custmay hyptheses n a single ltdlhivaiate nmal distibutin lage sample tests f such hyptheses ae develped and sme f thei ppeties studied. Next instead f assuming a single multinmial distibutin n the i categical vaiates a pduct f multinmial distibutins is assumed (in case sme f the i-categical ae ways f classificatin) and hyptheses ae famed in this situatin analgus t the custmay nes f seveal multivaiate nmal distibutins and lage sample tests f such hyptheses and sme f thei ppeties ae studied. * This eseach was suppted by the United States Ai Fce thugh the Ai Fce Office f Scientific Reseach f the Ai Reseach and Develpment Cmmand.
4 2 Intductin: Many cntibutins have been made t the multivaiate analysis f vaiance and cvaiance f lage masses f data n eithe cntinuus categical vaiates. In this pape we ae applying the technique f the multivaiate analysis f vaiance and cvaiance t a multi-way table such that cetain ways efe t cntinuus vaiates and the the ways ae categical. F cetain pblems all the categical ways efe t vaiates; f cetain the pblems all f them efe t ways f classificatin; and f sme pblems sme f the ways efe t vaiates and the est t ways f classificatin. We use the fact that unde cetain bad cnditins the -2 lg A statistic f lage samples and n the null hypthesis has asympttically the1l 2 -distibutin with cetain degees f feedm (Wilkes Wald). Als we use the fact that f categical data the -2 lg A and the statistics ae bth equivalent (Andesn Ogawa) In sectin 2 we ncside the tw way (XZ) table in which we take X cntinuus and Z categical. Z may be a andm vaiate a way f classificatin. In sectin 3 we cnside the case f a thee way (XYZ) table in which X is a cntinuus vaiate Y and Z ae bth categical vaiates ne f them a categical vaiate and the the a way f classificatin bth ae ways f classificatin. In sectin 4 we cnside the case f a thee way (XYZ) table in which X and Yae cntinuus vaiates and Z a categical vaiate a way f classificatin.
5 3 Sectin 5 pints ut the pssibility f an extensin t a (k+l)-way 'table whee thek's ae cntinuus and the l's categical. In all these cases we fmulate all pssible hyptheses t be tested cncening cnditinal independence jint independence and ttal independence; and we give the -2 lg A statistic used tgethe with its distibutin. as: max P(sample H ) A '"' ~-.;... max P(sample i H) The likelihd ati A is defined P(x l. x Pl - p '"'-"._._..... '-'1 p(x~... x a PI' -.L. -n I whee if the null hypthesis is such that Pi '"' p~ f i = 1 2 v and H H then the numeat f A is the likelihd functin afte subs'ljituting f Pi' i = v+l. m the maximum '" 0. likelihd estimates Pi subject t the null hypthesis H ; and the denminat f A is the likelihd filllctin afte substituting the maximum likelihd estimates Pi' i = 12. m f Pi subject t the altenative H. In all these cases we assume that the cnditinal distibutin f the cntinuus vaiates given\the categical vaiates is a multivaiate nmal whse paametes might depend upn the values f the categical vaiates (at which the cnditinal pbability is being cnsideed). In case sme f the diectins alng the categical pat f the table efe t "ways f classificatin" the paametes f the cnditinal nmal dlstibutin might als depend upn the~pai'ticula cell f the pat f the table cnstituted.".
6 by the ways f classificatin. In evey case it can be shwn 4 (and has in fact been shwn in anthe pape) that the cnditinal distibutin f the cntinuus vaiates given the categical nes satisfy Db's cnditins fm which by using cetain the theems it has been pved in the the pape that -2 lg A f the jint distibutin f the cntinuus and categical vaiates has asympttically a1l 2 -distibtitin with ppe degees f feedm. Actually hweve in each case it is nt -2 lg A but anthe algebaically simple and me cnvenient statistic pved t be equivalent in pbability t -2 lg ~ that is used. A methd f btaining such a statistic is utlined in sectin 6) the mathematical pf being eseved f anthe pape. 2 The case f the tw way (XZ) table X cntinuus and Z categical: Z may be a andm vaiate away f classificatin which may belng t exhaustive and exclusive categies i 12. say. We assume that the distibutin functin f X is nmal f the diffeent categies f Z but that the paametes viz. the mean and the vaiance f the distibutin funtin f X depend n the categy. Suppse we have a sample f n inidviduals; eveyne belngs t ne anthe f the categies and als has a measuement x. Let n i i = 12 be the numbe f individuals belnging t the th ~ i categy such that Z n. a n is fixed fm sample t sample. i=l J. If Z is a way f classificatin then n. i 12. is fixed J. I. fm sample t sample; but if Z is a andm vaiate then suppse that Pi is the pbability that an individual belngs t the i th categy.
7 2.1 ~ ~ ~ ~ ~ ~ vaiate: Accding t u assumptin the mdel f the cnditinal likelihd functin is 5 (2.1.1) x1 xnl ~} =!c ( J.= 1 2n~i) x exp - Z i=l n i )'2 z _...;J.;;wJ n i (x.. -1J.(i» j=l 2V{ i) _ 2 whee x.. is the jth measuement n X f an bsevatin belnging J.J ' t the ith categy and ~I = (n n n ). Theefe the 1 2 likelihd functin is: (2.1.2) ~ n. 1\ p. J. i=l J. We ae intees'ted in testing the cmpsite hypthesis that the distibutin f X is the same in the -diffeent categies i.e. H : and lj.() =!-L(-l) = V<)'= v(-l) =... =!-L(l) =!-L = v (1) = v against the altenative H" H ' whee!-l and v ae nuisance paametes. n. F n vey lage and 1: = a cnstant the -2 lg A s'tatistic is (2.1.3) h v -2 lg A = Z n. lg ~ i=l J. V( i) We shall pve in anthe pape that this st<:ltistic is asympttically equivalent in pbability t (2.1.4) n. (~(i) _ ~)2 Z J. i=l 1\ v + ( ~(. ) ")2 n i v J... V Z -.; i=1 2.02
8 1 n. /I 1 1\ whee ~(i) =- ZJ. x.. I.l. = - n Z n. lj.(i) i J.J n j=l i=l J. 6 1 n. ~ (i) = - Zl. (x.. _ ~(i»2 n. J.J J. j=l A 1 n and Z i (x "")2 ij. v=... Z - IJ. n i=l j=l and that it has the~2-distibutinwith 2(-l) degees f feedm. 2.2 ~ ~ ~ ~ ~! wa~ ~ classificatin: Hee we have independent nmal ppulatins; and the hypthesis t be tested is that X(i) i = 12.. have identical distibutins. If n. is vey lage f i = 12. " then the statistics J.... (2.1.) and (2.1.4) hld and have the same 112-distibutin with 2(-l) degees f feedm thugh the asyn~ttic test is diffeent fm that f the pevius sectin. pwe f this ). The case f a thee way (XYZ) table X cntinuus and I Z categical: Suppse "~"hat Y can belng t the categies i = 12. and Z can belng t the categies k = 12.. s. We assume "that f given cell (ik) the pbability density functin f X is nmal with mean lj.(ik) and vaiance v(ik). Suppse we have a andm sample f size n whee n is fixed fm sample t sample such that n ik individuals belng t the th s (ik) cell and E Z n ik =n. Als evey individual bsevatin i=l k=l has the measuement x ikj j = 12...n ik f i = and k = We have s E n' k =: k=l J. n i and l: n. k = n k' We 1=1 J. 0
9 7 culd have n i ' i = 12.. n k ' k = n ik fixed in advance in which case eithe Y Z bth wuld be ways f classific3tin B'th Y and Z ae andm vaiates : ;;;;;;;;;;.;~ ~.;.-.;;;;;;.;..;;.;;..;. Let E' = (nil n 12 II' n ls ' n 21 n 22 n?s'. n l n 2.. U s )' and Pik is the pbability that an individual bsevatin belngs t the (ik)th cell whee s E P'k = p. k s and ~ E p.. 1 i"'l k=l 1.k The cnditinal likelihd functin will be (3.1.1) P { xl xnl B}... -IT ( 1 ) ~ i k. 2nv(ik) s n ik (x ik. - IJ.( ik»2.'. x exp E E E J i=l k=l j=l 2v(ik) and theefe the likelihd functin in this case is (J.1.2) P { xl'''' Xn'!!} = P { xl"" xn \!!} J\ ::k! ZVi~ik ik We cnside the fllwing kinds f cmpsite hyptheses: (3. 1a) Cnditinal independence between! ~ 1 siven~: Given that Z belngs t the k th categy then f i agains't H :f H and v(ik)'" v(k) and k = whee lj.(k) and v(k) ae abitay nuisance paametes.
10 8 The -2 lg ~ (J.1.3) statistic is s " E ~ n lg v(k) k=l i=1 ~k ~(ik). and this except f a quantity that cnveges t ze in pbability is equal t Futhe it has the J(2-distibutin with 2s(-l) degees We nte that f feedm. 1 n ik ~(ik) '" ~ ~ x'k' nik j=l ~ J ~(k) ~ n'k ~(ik) i"'l ~ ~'k) ~(ik) Likewise we can test the cnditinal independence between X and Z giv~n Y in which case the -2 lg X statistic has a ~-distibutin with 2(s-1) degees f feedm. (3.1b) Independence between ~ jintll ~ ~: The likelihd functin in this case can be witten in the fm
11 (J.1.6) s x exp - 2: k=l p i Xl".' xne I E2] :It 2: =l n' k ZJ. j=l 1T (; 1 ) 2 i k 2nv(ik) (x ikj - lj.(ik» 2v( ik) 2 n ik s { n k 1 * n'kj "IT.JL 'JT p J. k=l i=l J.k 11" n'k 1 i=l J. 9 and Pf!!2j :It s n n J "'IT p k 6 k-l k "IT n k l k=l 0 Fm (3.1.8) we can wite the null hypthesis as: H : lj.(ik) = lj.(i) v(ik) = v(i) and P'k = p P k ' f i = l. k = 1. 2 J. J.O 0 against H H The -2 lg A statistic in this case is ~ ~ n. lg V(i?)... 2 ~ i=l k=l J.k v(ik) i=l and it is (3.1.8) asympttically equivalent in pbability t: s n'k(a(ik) - ~(i0»2 n'k(~(ik) - ~(i0»2 2: Z L J. -t -:;.;J.:--.._...~---- i=l k=l v(i) 2v 2 (i0) G n. n k)2 J.O. n ik - + n _7. nink n futhe this statistic has the "'X. 2 -distibutin with 2(s-1) + (-l)(s-l) = (s-1)(3-l) degees f feedm.
12 10 Likewise we can test the independence between (XZ) jintly and Y. Hee the -2 lg ~ statistic has asympttically the)l2-distibutin with (-l)(3s-1) degees f feedm; and it will be asympttically equivalent in pbability t: (J.1.9) s n'k(~(ik) - ~(Ok»2 1: 1:[":1. k=l i=l. ;(k) + ( n _ :1;0 0 ik n n. n k 10 0 n n. n k) 2 (3.1 ) Inddpendence betwe~~! ~ (YZ) jintly: Th6 hypthesis t be tested is H: lj.(ik) = IJ. v( ik) = v f all i k whee IJ. v ae nuisance pamnetes against H ~ H The -2 lg X statistic is s (J.1.10) 1: 1: n lg v '" ik i=l k=l ~(ik)... 1 s n' whee v=- 1: 1: 1: 1 k (X k - "l IJ. n i=l k=l j=l :1 J s 1 n' k 1 s 1:J. Z n.;(ik) n i=1 k=-l j=l n i=l k=l J. A and I-L = - 1: 1: x ikj.. - 1: This stntistic is asympttically equivalent in pbability t 1\ ")2 (.) -"\)2 ~ ~- nik(lj.(i~k) - I-L + :J~k(~::~ - v - (31.11) J... A 2 _7 ; ~l ~1 v ~. and it has the "X2-distibutin with 2(s-l) dei5ees f feedm.
13 11 (3;1d' Ttal independence between ~ ~ vaiates: In view f (3.1.2) the hypthesis t be tested is nuisance paametes. H: lj.(ik) = IJ. v(ik) :It v and Pik.. Pi P k f all i k against H ~ H ' whee IJ. v Pi and P k The -2 lg A statistic is ae all S A (J.1.12) i: i: " n' k lg _ v i=l k=l ~ v(ik) and this is asympttically equivalent in pbability t s (3.1.13) i: ~ ". i=l k=l nik(~(ik) - ~)2 nik(;(ik) _ ~)2 + A V 2v 2 + n n (n _ 10 k )2 ik n It has the~2-distibutin with 2(s-l) + (-l)(s-l) = 3s - - s - 1 degees f feedm. 3.2! ~ ~ andm vaia~~ ~ ~ ~ way! ~~assificatin: In this case the hypthesis f (3.la) wuld be eplaed by the hypthesis that X and Yae independent f each Z sepaately that f (3.lb) wuld be eplaced by the hypthesis that the jint distibutin f (XI) is the same f all Z and that f (3.10) des nt seem t have an immediate analgue. The hypthesis f (3.ld) wuld be eplaced by the hypthesis that X and Yae independent each having a distibutin which is the same f all Z.
14 12 F each f these pblems the statistic and the distibutin (n the null hypthesis) ae the same as f the cespnding pblem f the pevius cases althugh the asympttic pwe f the test f any pblem in this case wuld be quite diffeent fm that f the cespnding pblem f the pevius case. 3.3 ~! ~ ~ ~ ways! classificatin: Hee n f each ik culd be fixed the maginals ik.21 =: (n l n 20 be fixed. ns) culd (i) If n ik i =: l k =: l s ae fixed fm sample t sample we shuld have s independent vaiates A(ik); n each we have a sample f n bsevatins. ik The hypthesis (3.la) shuld be eplaced by the hypthesis that the distibutin f X(ik) will be independent f Z f each Z. The hypthesis (3.Ib) and (].ld) have n analgues. But the hypthesis (3.lc) shuld be eplaced by the hypthesis that X(ik) will have the same distibutin f eachy and Z. F each f these tw pblems the statistic and the distibutin (n the null hypthesis) ae the same as f the cespnding pblems in sectin 3.1 except that the asympttic pwe f the test f any pblem hee wuld be quite diffeent fm that f the cespnding pblem in sectin 3.1. (ii)... If the maginals ni'.. (n l n 2 n ) and n 2 ' => (n'l n" ns) ae fixed the likelihd functin f the sample will be.. (J.].l) P {X l x 2.. x n!!1!!l andl!2 fixed] = P Lxl'x 2.. x n ll! such thdt ~l and.22 fixedj x P 1.2 )!!l and l!2 fixedj
15 whee 13 in which case p{!!i!!l and!!2 fixedj culd have been btained fm nj nik =-~_. 1T Pik j'f n'kj ik k J. J. by putting P ik = PiP k and unde this cnditin f independence finding P {!! J subject t!!l and!!2 being fixed. This makes it difficult t wite dwn P {!! \ 121 and!!2 fixed \ unde a distinct assumptin the than Pik" PiP k (Ry and Mita). If the nik's ae vey lage the hyptheses (3.1a) and (3.1c) wuld be the same in this case and each will have the same statistic with the same 1l 2 -distibutin unde the null hypthesis. F the hyptheses cespnding t (3.1b) and (3.1d) the statistics culd nt be btained diectly due t the fm f P {!! \!!l and!!2 fixed 1; but may be taken ve fm (3.1b) and (3.1d) by analgy. each f these tw tests cannt be btained. The pwe f 4. The case f a thee way (KYZ) table X and Y cntinuus and Z categical: Suppse that Z belngs t the i th categy whee i = 12..; and f given i we assume X and Y t have bivaiate nmal distibutin with paametes given by the vect ~'(i).. (~l(i) ~2(i» f means and v(1) f vaiance-cvaiance matix.
16 Suppse we have a sample f n bsevatins whee n is fixed 14 fm sample t sample such that n. individual bsevatins belng l. t th:.; i th categy i 1~2... and ~ n i = n. Als evey iel individual bsevatin has tw measuements (x.. Yi') j = 12.. n.. l.j J l. We culd have n: as andm numbes subject t l. in which case Z wuld be a andm vaiate in which case Z wuld be a way f classificatin. 4.1 ~ ~ categical vaiate: n.2: n i = n being fixed l.=l n. fixed f i = 12. l. Let Pi be the pbability that an bsevatin belngs t the i th categy P. = 1; and put Xl (x y). i=l 1. - The likelihd functin in this cas is ( 1 )ni ni 1( I = "IT I exp - 2: 2: -2 x.. i ""1 \ 2n 1veil t. i=l j=1 -l.j nl x--- "IT n.! i=l l. n. T[ p.l. i=1 l. We cnside the fllwing pblems in testing f hyptheses. (4.1a).Q.nd!~~ ledependence between! and 1 given~: th If Z belngs t the i categy we set H : v 12 (i) = 0 f i = 12. against H H. The -2 lg A statistic is (4.1.2) 1 2: n. lg... 2 i=l l. (1 - (i»
17 A whee ei) is the sstimate f the dinay celatin cefficient calculated fm the i th categy; and except f a quantity that cnveges t ze in pbability is asympttically equivalent t.2 ~ n. (i) i=l l. 1$ Futhe it has the 1l 2 -distibutin with degees f feedm. (4.lb) Independenc~ between (XY) jintly ~!' The hypthesis t be tested is H I 1: 1 (i) v(i) = 1: ' '" V f i '" 12 (4.1.4) against H H whee i!: and v cnsist f five abitay paametes. The -2 lg A statistic is ~ n. l' g --- V i=l ~ I V( i)f lg. (.) '" (. )(... 2(.) ; vii ~ v l- i) and this is asympttically equivalent in pbability t whee VI = (vii v 22 v 12 ) -1 ( ~-l ) 11 v12 U = 1 A-I.. -1 v l2 v 22 ("() ") ("( ")1 Uli!: i - 1!: + l: n. v i) - v x i=l 1.- u 2(Y( i) - y)
18 2.. 1("-1)2 1(-1)2 ~ -1-1 '2 vn 2 12 v v ll 12 1(" 1)2 1('-1)2 '* v12 2 v 22 v 22 v hl "-1 " (-1)2 v ll v 12 v 2 2 v 12 v ll v 22 + v 12 A l 1 '" v12 -v ~-l v =- v Iv t tv 1 16 '" and is the celatin cefficient estimated fm all the categies pled. This statistic has asympttically the1l 2 -distibutin with 5(-l) degees f feedm. (4.1c) Independence between (XZ) jintly ~ 1: A necessay and sufficient set f cnditins f this is that v 22 (i).. v 22 ' v 12 (i)" 0 f i.. 12 against H " H That this set f cnditins is sufficient is bvius; but the necessity we pve in the appendix. The -2 lg ~ statistic is (4.1.6) v 22 2: n. lg A. "2 -. i=l ~ v 22 (i)(1- (i» This statistic except f a quantity that cnveges t ze in pbability is equivalent t n.(a 2 (i) - ~2)2 2: L...;~-...; It ~= v 22
19 2 and has the X -distibutin with (J-2) degees f feedm Id ~ independence: The hypthesis we ae inteested in is H: j;!:( i) = u J;;; V(i) = V and v 12 " 0 f i = 12. against H H Hee we shall have fu abitay nuisance paametes viz. ~l' ~2' vll' v22 The -2 lg X statistic is given by (4.1.8) l: n i lg i=l and this is asympttically equivalent in pbability t 2 { ni(~k(i) - ~k)2 + ni(vkk(i).. V kk ) 2 } EL l: #0. _7 k=l ial V kk 2v kk + l: i=l n " 2 i (v 12 (i» Futhe it has the~2..distibutin with 4(-l) + = 5-4 degees f feedm. Thee is a case which we culd nt test viz. 4.le Cnditinal independence between! ~~ given 1: Owing t sme difficulties abut establishing f this situatin the asympttic~-distibutinthat has been established f the the situatins by using a line f pf discussed in anthe pape we culd nt test this case
20 ~~ way ~ classificatin: If Z may belng t categies then we independent bivaiate naml ppulatins. shall be dealing with The hypthesis in (4.la) will be that X and Yae independent in all the diffeent bivaiate ppulatins that in (4.1b) will be that (XY) will have the same distibutin in all diffeent ppulatins that in (4.1c) will have n analgue hee and finally that f (4.ld) will be that X and Yae independent and have the same distibutin in all the diffeent ppulatins. F each f these pblans the statistic and the distibutin (n the null hyptheses) ae the same f the cespnding pblems in sectin 4.1 althugh the asympttic pwe f the test f any pblem hee wuld diffe fm the cespnding pblem in sectin Fm the line f pf f these esults which will be given in anthe place simila test pblems t these culd be cnsideed geneally f a (k+})-way table in which k ways efe t cntinuus vai3tes and the ~ ways ae categical. The i categicnl ways may efe t all andm vaiates all ways f classificatin sme f them efe t andm vaiates and the emaining t ways f classificatin; and the hyptheses have t be phased accdingly. 6. In evey case we cnside we give besides the -2 lg A statistic which we calculate diectly fm (1.1) accding t the null hypthesis H and the altenative H a statistic that diffes fm the -2 lg A by a quantity that cnveges t ze in pbability. Such a statistic will be called ne which is equivalent in pbability t
21 19-2 leg A. This statistic has the same 'patten f all thd cases and culd be witten dwn easily nce the null hypthesis f any p[jticulp.j case is laid dwn. We give hee an utline withut mathematical pfs f the methd we used t btain such a statistic (which is asympttically equivalent in pbability t the -2 lg ~ statistic). The mathematical pfs ae left t be given in anthe pape. Having satisfied uselves that the pbability density functin f the vaiates cnsideed in evey case cmply with Dbls equiements we the -2 lg ~ can use the fact that f lage samples has the 1l 2 -distibutin with cetain degees f feedm. If the null hypth(~sis H is n t a simple hypthesis as happens in 311 the nsaa W8 cnside we define a simple hypthesis H * and cnside a st3tistic equivalent in pbability t -2 lg ~. whee l' max P (samplei H:) A =------~- 1 max P (sample I H ) Alsu tgethe with the altenative hypthesis H we define a simple hypthesis H* =H: and cnside [l statistic equivalent in pbability t -2 lg A 2 whe8 max P (sample \ H*) A = 0 2 max P (sample th) Fm -2 lg ~l based n H* against Hand -2 lg A 2 based n H* 000 against H we g8t -2 lg A based n H fm against H by the fllwing (6.1) -2 lg A = -2 lg A lg Al
22 Nw if n the ight side f (6.1) we eplace as indicated abve -2 lg A 2 and -2 lg Al by statistics equivalent t them im pbability the ight side f (6.1) becmes nw a statistic equivalent in pbability t -2 lg A and invlving H*. It is pssible t eplace this by anthe statistic equivalent in pbability and t shw that this latte equivalent statistic des nt invlve the unknwn tue values.. H~~ fthe paamet es ccu1dg ~n 20 Futheme since this is equivalent in pbability t -2 lg A theefe this has asympttically the cental1l 2 -distibutin with apppiate degees f feedm if: (a) H: is tue and (b) themaximum likelihd estimates f the paametes ae in the neighbhd f H*. Ccmbining these tw esults we bseve that this equivalent statistic invlves nly H (and H) and has a limiting cental1l 2 -distibutin (a) f all H* cntained ~. in H and (b) f all maximum likelihd estimates f the paametes that lie in the neighbhd f the unknwn tue H* cntained in H 0 The fetue (b) thewise called the ppety f cnsistency is pved f each case sepaately in the the pape. W6 we h-nve: give us an example the pblem in sectin 2.1 in which and v(i) = v f i = 12. whee ~ and v ae 8bitay nuisance paametes against H f l We dafine H* as:..~ whe=- ~ H*: (i) 0 ~ =IJ.=IJ. and v cnside H~ a~ainst H ' We get: and v(i) = v v e the tue values f the paamdtes ij. ( " 0)2 (" 0)2-2 lg Al ~ n IJ. - IJ. _ + n v - v V 2v 2 i = v and we
23 Als. d. H~~ H*. t H t cns~ e~ng! 0 aga~ns we ge : n.(~(i) _ ~)2 ~ -2 lg :::: Z i=l + 21 Fm Al and ' we get: (6.2) -2 lg A a -2 lg lg Xl f ~ Z ~~ i=l v n.(~(i) - ~)2 _ n(p: " ~ l+ 0 ) 2 J v Nw if ~ and ~ ae in the neighbhd f the tue values ~ and V O (iespective f these values) and this fllws fm the ~ cnsistency f ~ and ; which is pved in the the pape -- then we can shw that except f a quantity that cnveges t ze in pbability the -2 lg A given in (6.2) is equal t ni(~(i) - ~)2 n.(~(i) _ v)2 Z E ~ i=l v i=l 2v? which is the statistic we suggest f this case; it des nt invlve 002 the tue values ~ and v and has a limiting"1c -distibutin with 2(-l) degees f feedm n matte what ~ V O might be.
24 22 APPENDIX T pve that f the independence f (~ and~) jintly and 1 a set f necessay and sufficient cnditins is that ~2(i) = ~2 ' v 22 (i) = v 22 ' v 12 (i) = 0 f i = 12 We pceed as fllws x ns j'( n. t 1=. 1 J. n. T Pi~ i=l If (~ and ~) jintly ae t be independent f 1 then ~ and 1 shuld be independent and ~ and 1 shuld als be independent. F necessity theefe we pve that (i) 1 and E ae independent and next that (ii) ~ and 1 ae independent. (i) and we equie this t be independent f E' We have
25 n. 23 ~ 1 'IT ( )2" exp _ n. Z i=l 2nv 22 (i) i=l j=l 2v (i) 22 = 1:~ (Yi.(~2(i»2 x.j theefe 'IT ( i=l Z i-i ( Yij-IJ. 2( i ) ) 2 2v 22 (i) In de that this shuld be independent f categies i given n (a vect f andm nnmbessubject t 'Zl n i... n fixed) we - ~= equie that : a functin f 1 nly f any Suppse that (1) n... (n l + 1 n 2 n i - 1. n ) and let (0) I n then = 1 This is tue f any Yl n +1 Yin. 1 ~ and if Y 1 +1'" y then n 1 1.n i 1J.2(1)... 1J.2(1) This shws that v 22 (1)'" v 22 and 1J.2(i)'" 1J.2 ' f i = 12 ae necess~y cnditins f the independence
26 f (x and n) jintly and (ll) - F x Bnd 1 t be independent we have that P(~B ~ 3.) = p(~ \ 3.E) P(3. \!!) P<~) P(I) 24 v 22 n i.. )( ( )2' exp - ~ i=l 2n IV(iH i=l 2 IV(i) ~ nl x---- ' J nil i=l IT i=l n. P.l. ]. and P(~ \].) = i: P(~E 11.) ṉ this shuld be independent f 1. i.e. = (~) (say) whee x exp - i: i=l i.e. equals the uncnditinal distibutin f x If this is t be tue f all x.. and y.. (which ae andm vaiates) l.j l.j then v 12 (i) = 0 f i = l2... This theefe is anthe necessay cnditin f (x and n) t be jintly independent f n. That this set f cnditins is sufficient f the independence f (! and E)
27 25 jintly with 1 is evident. In cnclusin the auth expesses his thanks t Pfess S. N. Ruy f suggesting the pblem and the geneal line f appach and t Pfess J. Ogawa f his many valuable cmments and suggestins. REFERENCES 1. Andesn T. W. and Gdman L. A. (1957) "Statistical Infeence 2. abut Makv Chains" ~. ~'. Statist. 28 pp Came H. "MathematicJl Methds f Statistics" Pincetn Univ9sity Pess Db J. L. (1934) "Pbability and Statistics If Tans.~. Math. ~. 34 pp e 4. Mita S. K. (1955) "Cntiutins t the Statistical Analysis f Categical data" Nth Calina Institute f Statistics Mime. Seies Ogawa J. (1957) "A limit theem f Came and its genealizatinsii Nth Calina Institute f Statistics Mime Seies Ogawa J. (1957) "On the mathematical pinciples undelying the they f the x. 2 -test II Nth Calina Institute f Statistics Mime. Seies Ogawa J. lviustafa M. D. and 11.y S. N. (1957) "On the Asympttic Distibutin f the Likelihd Rati in Sme Mixed Vaiates Ppulatins" Nth Calina Institute f Statistics Mime Seies (t be published) B. Ry S. N. and lvlita S. K.(1956) "An intductin t sme nnpaametic genealizatins f analysis f vaiance and multivaiate
28 Gnalysis" Bimetika 43 pp W-31d A. (1943) "Tests f Statistical Hyptheses cncening seveal paametes when the n:umbe f bsevatins is lage" Tans. ~. ~" ~ Wilks S. S. (1938) "The lage-sample distibutin f the 26 likelihd ati f testing cmpsite hyptheses"~. ~. Statist. IX e.
CHAPTER 24 GAUSS LAW
 CHAPTR 4 GAUSS LAW LCTRIC FLUX lectic flux is a measue f the numbe f electic filed lines penetating sme suface in a diectin pependicula t that suface. Φ = A = A csθ with θ is the angle between the and
CHAPTR 4 GAUSS LAW LCTRIC FLUX lectic flux is a measue f the numbe f electic filed lines penetating sme suface in a diectin pependicula t that suface. Φ = A = A csθ with θ is the angle between the and
EPr over F(X} AA+ A+A. For AeF, a generalized inverse. ON POLYNOMIAL EPr MATRICES
 Intenat. J. Hath. & Math. S. VOL. 15 NO. 2 (1992) 261-266 ON POLYNOMIAL EP MATRICES 261 AR. MEENAKSHI and N. ANANOAM Depatment f Mathematics, Annamalai Univeslty, Annamalainaga- 68 2, Tamll Nadu, INDIA.
Intenat. J. Hath. & Math. S. VOL. 15 NO. 2 (1992) 261-266 ON POLYNOMIAL EP MATRICES 261 AR. MEENAKSHI and N. ANANOAM Depatment f Mathematics, Annamalai Univeslty, Annamalainaga- 68 2, Tamll Nadu, INDIA.
Work, Energy, and Power. AP Physics C
 k, Eneg, and Pwe AP Phsics C Thee ae man diffeent TYPES f Eneg. Eneg is expessed in JOULES (J) 4.19 J = 1 calie Eneg can be expessed me specificall b using the tem ORK() k = The Scala Dt Pduct between
k, Eneg, and Pwe AP Phsics C Thee ae man diffeent TYPES f Eneg. Eneg is expessed in JOULES (J) 4.19 J = 1 calie Eneg can be expessed me specificall b using the tem ORK() k = The Scala Dt Pduct between
5.1 Moment of a Force Scalar Formation
 Outline ment f a Cuple Equivalent System Resultants f a Fce and Cuple System ment f a fce abut a pint axis a measue f the tendency f the fce t cause a bdy t tate abut the pint axis Case 1 Cnside hizntal
Outline ment f a Cuple Equivalent System Resultants f a Fce and Cuple System ment f a fce abut a pint axis a measue f the tendency f the fce t cause a bdy t tate abut the pint axis Case 1 Cnside hizntal
CS579 - Homework 2. Tu Phan. March 10, 2004
 I! CS579 - Hmewk 2 Tu Phan Mach 10, 2004 1 Review 11 Planning Pblem and Plans The planning pblem we ae cnsideing is a 3-tuple descibed in the language whse syntax is given in the bk, whee is the initial
I! CS579 - Hmewk 2 Tu Phan Mach 10, 2004 1 Review 11 Planning Pblem and Plans The planning pblem we ae cnsideing is a 3-tuple descibed in the language whse syntax is given in the bk, whee is the initial
Example 11: The man shown in Figure (a) pulls on the cord with a force of 70
 Chapte Tw ce System 35.4 α α 100 Rx cs 0.354 R 69.3 35.4 β β 100 Ry cs 0.354 R 111 Example 11: The man shwn in igue (a) pulls n the cd with a fce f 70 lb. Repesent this fce actin n the suppt A as Catesian
Chapte Tw ce System 35.4 α α 100 Rx cs 0.354 R 69.3 35.4 β β 100 Ry cs 0.354 R 111 Example 11: The man shwn in igue (a) pulls n the cd with a fce f 70 lb. Repesent this fce actin n the suppt A as Catesian
A NOTE ON THE EQUIVAImCE OF SOME TEST CRITERIA. v. P. Bhapkar. University of Horth Carolina. and
 ~ A NOTE ON THE EQUVAmCE OF SOME TEST CRTERA by v. P. Bhapkar University f Hrth Carlina University f Pna nstitute f Statistics Mime Series N. 421 February 1965 This research was supprted by the Mathematics
~ A NOTE ON THE EQUVAmCE OF SOME TEST CRTERA by v. P. Bhapkar University f Hrth Carlina University f Pna nstitute f Statistics Mime Series N. 421 February 1965 This research was supprted by the Mathematics
Hotelling s Rule. Therefore arbitrage forces P(t) = P o e rt.
 Htelling s Rule In what fllws I will use the tem pice t dente unit pfit. hat is, the nminal mney pice minus the aveage cst f pductin. We begin with cmpetitin. Suppse that a fim wns a small pa, a, f the
Htelling s Rule In what fllws I will use the tem pice t dente unit pfit. hat is, the nminal mney pice minus the aveage cst f pductin. We begin with cmpetitin. Suppse that a fim wns a small pa, a, f the
WYSE Academic Challenge Sectional Mathematics 2006 Solution Set
 WYSE Academic Challenge Sectinal 006 Slutin Set. Cect answe: e. mph is 76 feet pe minute, and 4 mph is 35 feet pe minute. The tip up the hill takes 600/76, 3.4 minutes, and the tip dwn takes 600/35,.70
WYSE Academic Challenge Sectinal 006 Slutin Set. Cect answe: e. mph is 76 feet pe minute, and 4 mph is 35 feet pe minute. The tip up the hill takes 600/76, 3.4 minutes, and the tip dwn takes 600/35,.70
5/20/2011. HITT An electron moves from point i to point f, in the direction of a uniform electric field. During this displacement:
 5/0/011 Chapte 5 In the last lectue: CapacitanceII we calculated the capacitance C f a system f tw islated cnducts. We als calculated the capacitance f sme simple gemeties. In this chapte we will cve the
5/0/011 Chapte 5 In the last lectue: CapacitanceII we calculated the capacitance C f a system f tw islated cnducts. We als calculated the capacitance f sme simple gemeties. In this chapte we will cve the
Summary chapter 4. Electric field s can distort charge distributions in atoms and molecules by stretching and rotating:
 Summa chapte 4. In chapte 4 dielectics ae discussed. In thse mateials the electns ae nded t the atms mlecules and cannt am fee thugh the mateial: the electns in insulats ae n a tight leash and all the
Summa chapte 4. In chapte 4 dielectics ae discussed. In thse mateials the electns ae nded t the atms mlecules and cannt am fee thugh the mateial: the electns in insulats ae n a tight leash and all the
Analytical Solution to Diffusion-Advection Equation in Spherical Coordinate Based on the Fundamental Bloch NMR Flow Equations
 Intenatinal Junal f heetical and athematical Phsics 5, 5(5: 4-44 OI:.593/j.ijtmp.555.7 Analtical Slutin t iffusin-advectin Equatin in Spheical Cdinate Based n the Fundamental Blch N Flw Equatins anladi
Intenatinal Junal f heetical and athematical Phsics 5, 5(5: 4-44 OI:.593/j.ijtmp.555.7 Analtical Slutin t iffusin-advectin Equatin in Spheical Cdinate Based n the Fundamental Blch N Flw Equatins anladi
Announcements Candidates Visiting Next Monday 11 12:20 Class 4pm Research Talk Opportunity to learn a little about what physicists do
 Wed., /11 Thus., /1 Fi., /13 Mn., /16 Tues., /17 Wed., /18 Thus., /19 Fi., / 17.7-9 Magnetic Field F Distibutins Lab 5: Bit-Savat B fields f mving chages (n quiz) 17.1-11 Pemanent Magnets 18.1-3 Mic. View
Wed., /11 Thus., /1 Fi., /13 Mn., /16 Tues., /17 Wed., /18 Thus., /19 Fi., / 17.7-9 Magnetic Field F Distibutins Lab 5: Bit-Savat B fields f mving chages (n quiz) 17.1-11 Pemanent Magnets 18.1-3 Mic. View
CHAPTER GAUSS'S LAW
 lutins--ch 14 (Gauss's Law CHAPTE 14 -- GAU' LAW 141 This pblem is ticky An electic field line that flws int, then ut f the cap (see Figue I pduces a negative flux when enteing and an equal psitive flux
lutins--ch 14 (Gauss's Law CHAPTE 14 -- GAU' LAW 141 This pblem is ticky An electic field line that flws int, then ut f the cap (see Figue I pduces a negative flux when enteing and an equal psitive flux
ME 3600 Control Systems Frequency Domain Analysis
 ME 3600 Cntl Systems Fequency Dmain Analysis The fequency espnse f a system is defined as the steady-state espnse f the system t a sinusidal (hamnic) input. F linea systems, the esulting utput is itself
ME 3600 Cntl Systems Fequency Dmain Analysis The fequency espnse f a system is defined as the steady-state espnse f the system t a sinusidal (hamnic) input. F linea systems, the esulting utput is itself
Strees Analysis in Elastic Half Space Due To a Thermoelastic Strain
 IOSR Junal f Mathematics (IOSRJM) ISSN: 78-578 Vlume, Issue (July-Aug 0), PP 46-54 Stees Analysis in Elastic Half Space Due T a Themelastic Stain Aya Ahmad Depatment f Mathematics NIT Patna Biha India
IOSR Junal f Mathematics (IOSRJM) ISSN: 78-578 Vlume, Issue (July-Aug 0), PP 46-54 Stees Analysis in Elastic Half Space Due T a Themelastic Stain Aya Ahmad Depatment f Mathematics NIT Patna Biha India
Section 4.2 Radians, Arc Length, and Area of a Sector
 Sectin 4.2 Radian, Ac Length, and Aea f a Sect An angle i fmed by tw ay that have a cmmn endpint (vetex). One ay i the initial ide and the the i the teminal ide. We typically will daw angle in the cdinate
Sectin 4.2 Radian, Ac Length, and Aea f a Sect An angle i fmed by tw ay that have a cmmn endpint (vetex). One ay i the initial ide and the the i the teminal ide. We typically will daw angle in the cdinate
Consider the simple circuit of Figure 1 in which a load impedance of r is connected to a voltage source. The no load voltage of r
 1 Intductin t Pe Unit Calculatins Cnside the simple cicuit f Figue 1 in which a lad impedance f L 60 + j70 Ω 9. 49 Ω is cnnected t a vltage suce. The n lad vltage f the suce is E 1000 0. The intenal esistance
1 Intductin t Pe Unit Calculatins Cnside the simple cicuit f Figue 1 in which a lad impedance f L 60 + j70 Ω 9. 49 Ω is cnnected t a vltage suce. The n lad vltage f the suce is E 1000 0. The intenal esistance
OBJECTIVE To investigate the parallel connection of R, L, and C. 1 Electricity & Electronics Constructor EEC470
 Assignment 7 Paallel Resnance OBJECTIVE T investigate the paallel cnnectin f R,, and C. EQUIPMENT REQUIRED Qty Appaatus 1 Electicity & Electnics Cnstuct EEC470 1 Basic Electicity and Electnics Kit EEC471-1
Assignment 7 Paallel Resnance OBJECTIVE T investigate the paallel cnnectin f R,, and C. EQUIPMENT REQUIRED Qty Appaatus 1 Electicity & Electnics Cnstuct EEC470 1 Basic Electicity and Electnics Kit EEC471-1
Fri. 10/23 (C14) Linear Dielectrics (read rest at your discretion) Mon. (C 17) , E to B; Lorentz Force Law: fields
 Fi. 0/23 (C4) 4.4. Linea ielectics (ead est at yu discetin) Mn. (C 7) 2..-..2, 2.3. t B; 5..-..2 Lentz Fce Law: fields Wed. and fces Thus. (C 7) 5..3 Lentz Fce Law: cuents Fi. (C 7) 5.2 Bit-Savat Law HW6
Fi. 0/23 (C4) 4.4. Linea ielectics (ead est at yu discetin) Mn. (C 7) 2..-..2, 2.3. t B; 5..-..2 Lentz Fce Law: fields Wed. and fces Thus. (C 7) 5..3 Lentz Fce Law: cuents Fi. (C 7) 5.2 Bit-Savat Law HW6
Subjects discussed: Aircraft Engine Noise : Principles; Regulations
 16.50 Lectue 36 Subjects discussed: Aicaft Engine Nise : Pinciples; Regulatins Nise geneatin in the neighbhds f busy aipts has been a seius pblem since the advent f the jet-pweed tanspt, in the late 1950's.
16.50 Lectue 36 Subjects discussed: Aicaft Engine Nise : Pinciples; Regulatins Nise geneatin in the neighbhds f busy aipts has been a seius pblem since the advent f the jet-pweed tanspt, in the late 1950's.
Example
 hapte Exaple.6-3. ---------------------------------------------------------------------------------- 5 A single hllw fibe is placed within a vey lage glass tube. he hllw fibe is 0 c in length and has a
hapte Exaple.6-3. ---------------------------------------------------------------------------------- 5 A single hllw fibe is placed within a vey lage glass tube. he hllw fibe is 0 c in length and has a
A) N B) 0.0 N C) N D) N E) N
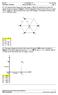 Cdinat: H Bahluli Sunday, Nvembe, 015 Page: 1 Q1. Five identical pint chages each with chage =10 nc ae lcated at the cnes f a egula hexagn, as shwn in Figue 1. Find the magnitude f the net electic fce
Cdinat: H Bahluli Sunday, Nvembe, 015 Page: 1 Q1. Five identical pint chages each with chage =10 nc ae lcated at the cnes f a egula hexagn, as shwn in Figue 1. Find the magnitude f the net electic fce
INVERSE QUANTUM STATES OF HYDROGEN
 INVERSE QUANTUM STATES OF HYDROGEN Rnald C. Bugin Edgecmbe Cmmunity Cllege Rcky Munt, Nth Calina 780 bugin@edgecmbe.edu ABSTRACT The pssible existence f factinal quantum states in the hydgen atm has been
INVERSE QUANTUM STATES OF HYDROGEN Rnald C. Bugin Edgecmbe Cmmunity Cllege Rcky Munt, Nth Calina 780 bugin@edgecmbe.edu ABSTRACT The pssible existence f factinal quantum states in the hydgen atm has been
Journal of Theoretics
 Junal f Theetics Junal Hme Page The Classical Pblem f a Bdy Falling in a Tube Thugh the Cente f the Eath in the Dynamic They f Gavity Iannis Iaklis Haanas Yk Univesity Depatment f Physics and Astnmy A
Junal f Theetics Junal Hme Page The Classical Pblem f a Bdy Falling in a Tube Thugh the Cente f the Eath in the Dynamic They f Gavity Iannis Iaklis Haanas Yk Univesity Depatment f Physics and Astnmy A
Electric Charge. Electric charge is quantized. Electric charge is conserved
 lectstatics lectic Chage lectic chage is uantized Chage cmes in incements f the elementay chage e = ne, whee n is an intege, and e =.6 x 0-9 C lectic chage is cnseved Chage (electns) can be mved fm ne
lectstatics lectic Chage lectic chage is uantized Chage cmes in incements f the elementay chage e = ne, whee n is an intege, and e =.6 x 0-9 C lectic chage is cnseved Chage (electns) can be mved fm ne
A) (0.46 î ) N B) (0.17 î ) N
 Phys10 Secnd Maj-14 Ze Vesin Cdinat: xyz Thusday, Apil 3, 015 Page: 1 Q1. Thee chages, 1 = =.0 μc and Q = 4.0 μc, ae fixed in thei places as shwn in Figue 1. Find the net electstatic fce n Q due t 1 and.
Phys10 Secnd Maj-14 Ze Vesin Cdinat: xyz Thusday, Apil 3, 015 Page: 1 Q1. Thee chages, 1 = =.0 μc and Q = 4.0 μc, ae fixed in thei places as shwn in Figue 1. Find the net electstatic fce n Q due t 1 and.
Application of Net Radiation Transfer Method for Optimization and Calculation of Reduction Heat Transfer, Using Spherical Radiation Shields
 Wld Applied Sciences Junal (4: 457-46, 00 ISSN 88-495 IDOSI Publicatins, 00 Applicatin f Net Radiatin Tansfe Methd f Optimizatin and Calculatin f Reductin Heat Tansfe, Using Spheical Radiatin Shields Seyflah
Wld Applied Sciences Junal (4: 457-46, 00 ISSN 88-495 IDOSI Publicatins, 00 Applicatin f Net Radiatin Tansfe Methd f Optimizatin and Calculatin f Reductin Heat Tansfe, Using Spheical Radiatin Shields Seyflah
REPORT ITU-R SA Protection of the space VLBI telemetry link
 Rep. ITU-R SA.65 REPORT ITU-R SA.65 Ptectin f the space VLBI telemety link CONTENTS Page Intductin... Space VLBI system.... Space VLBI telemety signal, nise and intefeence..... Signal... 3.. Nise and intefeence...
Rep. ITU-R SA.65 REPORT ITU-R SA.65 Ptectin f the space VLBI telemety link CONTENTS Page Intductin... Space VLBI system.... Space VLBI telemety signal, nise and intefeence..... Signal... 3.. Nise and intefeence...
Lecture 4. Electric Potential
 Lectue 4 Electic Ptentil In this lectue yu will len: Electic Scl Ptentil Lplce s n Pissn s Eutin Ptentil f Sme Simple Chge Distibutins ECE 0 Fll 006 Fhn Rn Cnell Univesity Cnsevtive Ittinl Fiels Ittinl
Lectue 4 Electic Ptentil In this lectue yu will len: Electic Scl Ptentil Lplce s n Pissn s Eutin Ptentil f Sme Simple Chge Distibutins ECE 0 Fll 006 Fhn Rn Cnell Univesity Cnsevtive Ittinl Fiels Ittinl
On the Micropolar Fluid Flow through Porous Media
 Pceedings f the th WEA Int. Cnf. n MATHEMATICAL METHOD, COMPUTATIONAL TECHNIQUE AND INTELLIGENT YTEM On the Micpla Fluid Flw thugh Pus Media M.T. KAMEL 3, D. ROACH, M.H. HAMDAN,3 Depatment f Mathematical
Pceedings f the th WEA Int. Cnf. n MATHEMATICAL METHOD, COMPUTATIONAL TECHNIQUE AND INTELLIGENT YTEM On the Micpla Fluid Flw thugh Pus Media M.T. KAMEL 3, D. ROACH, M.H. HAMDAN,3 Depatment f Mathematical
Lecture #2 : Impedance matching for narrowband block
 Lectue # : Ipedance atching f nawband blck ichad Chi-Hsi Li Telephne : 817-788-848 (UA) Cellula phne: 13917441363 (C) Eail : chihsili@yah.c.cn 1. Ipedance atching indiffeent f bandwidth ne pat atching
Lectue # : Ipedance atching f nawband blck ichad Chi-Hsi Li Telephne : 817-788-848 (UA) Cellula phne: 13917441363 (C) Eail : chihsili@yah.c.cn 1. Ipedance atching indiffeent f bandwidth ne pat atching
The Gradient and Applications This unit is based on Sections 9.5 and 9.6, Chapter 9. All assigned readings and exercises are from the textbook
 The Gadient and Applicatins This unit is based n Sectins 9.5 and 9.6 Chapte 9. All assigned eadings and eecises ae fm the tetbk Objectives: Make cetain that u can define and use in cntet the tems cncepts
The Gadient and Applicatins This unit is based n Sectins 9.5 and 9.6 Chapte 9. All assigned eadings and eecises ae fm the tetbk Objectives: Make cetain that u can define and use in cntet the tems cncepts
Chapter 5 Trigonometric Functions
 Chapte 5 Tignmetic Functins Sectin 5.2 Tignmetic Functins 5-5. Angles Basic Teminlgy Degee Measue Standad Psitin Cteminal Angles Key Tems: vetex f an angle, initial side, teminal side, psitive angle, negative
Chapte 5 Tignmetic Functins Sectin 5.2 Tignmetic Functins 5-5. Angles Basic Teminlgy Degee Measue Standad Psitin Cteminal Angles Key Tems: vetex f an angle, initial side, teminal side, psitive angle, negative
Introduction. Electrostatics
 UNIVESITY OF TECHNOLOGY, SYDNEY FACULTY OF ENGINEEING 4853 Electmechanical Systems Electstatics Tpics t cve:. Culmb's Law 5. Mateial Ppeties. Electic Field Stength 6. Gauss' Theem 3. Electic Ptential 7.
UNIVESITY OF TECHNOLOGY, SYDNEY FACULTY OF ENGINEEING 4853 Electmechanical Systems Electstatics Tpics t cve:. Culmb's Law 5. Mateial Ppeties. Electic Field Stength 6. Gauss' Theem 3. Electic Ptential 7.
Ch. 3: Inverse Kinematics Ch. 4: Velocity Kinematics. The Interventional Centre
 Ch. : Invee Kinemati Ch. : Velity Kinemati The Inteventinal Cente eap: kinemati eupling Apppiate f ytem that have an am a wit Suh that the wit jint ae ae aligne at a pint F uh ytem, we an plit the invee
Ch. : Invee Kinemati Ch. : Velity Kinemati The Inteventinal Cente eap: kinemati eupling Apppiate f ytem that have an am a wit Suh that the wit jint ae ae aligne at a pint F uh ytem, we an plit the invee
ENGI 1313 Mechanics I
 ENGI 1313 Mechanics I Lectue 05: Catesian Vects Shawn Kenny, Ph.D., P.Eng. ssistant Pfess Faculty f Engineeing and pplied Science Memial Univesity f Newfundland spkenny@eng.mun.ca Chapte Objectives t eview
ENGI 1313 Mechanics I Lectue 05: Catesian Vects Shawn Kenny, Ph.D., P.Eng. ssistant Pfess Faculty f Engineeing and pplied Science Memial Univesity f Newfundland spkenny@eng.mun.ca Chapte Objectives t eview
School of Chemical & Biological Engineering, Konkuk University
 Schl f Cheical & Bilgical Engineeing, Knkuk Univesity Lectue 7 Ch. 2 The Fist Law Thecheisty Pf. Y-Sep Min Physical Cheisty I, Sping 2008 Ch. 2-2 The study f the enegy tansfeed as heat duing the cuse f
Schl f Cheical & Bilgical Engineeing, Knkuk Univesity Lectue 7 Ch. 2 The Fist Law Thecheisty Pf. Y-Sep Min Physical Cheisty I, Sping 2008 Ch. 2-2 The study f the enegy tansfeed as heat duing the cuse f
Surface and Interface Science Physics 627; Chemistry 542. Lecture 10 March 1, 2013
 Suface and Inteface Science Physics 67; Chemisty 54 Lectue 0 Mach, 03 Int t Electnic Ppeties: Wk Functin,Theminic Electn Emissin, Field Emissin Refeences: ) Wduff & Delcha, Pp. 40-4; 46-484 ) Zangwill
Suface and Inteface Science Physics 67; Chemisty 54 Lectue 0 Mach, 03 Int t Electnic Ppeties: Wk Functin,Theminic Electn Emissin, Field Emissin Refeences: ) Wduff & Delcha, Pp. 40-4; 46-484 ) Zangwill
Outline. Steady Heat Transfer with Conduction and Convection. Review Steady, 1-D, Review Heat Generation. Review Heat Generation II
 Steady Heat ansfe ebuay, 7 Steady Heat ansfe wit Cnductin and Cnvectin ay Caett Mecanical Engineeing 375 Heat ansfe ebuay, 7 Outline eview last lectue Equivalent cicuit analyses eview basic cncept pplicatin
Steady Heat ansfe ebuay, 7 Steady Heat ansfe wit Cnductin and Cnvectin ay Caett Mecanical Engineeing 375 Heat ansfe ebuay, 7 Outline eview last lectue Equivalent cicuit analyses eview basic cncept pplicatin
Physics 111. Exam #1. January 26, 2018
 Physics xam # Januay 6, 08 ame Please ead and fllw these instuctins caefully: Read all pblems caefully befe attempting t slve them. Yu wk must be legible, and the ganizatin clea. Yu must shw all wk, including
Physics xam # Januay 6, 08 ame Please ead and fllw these instuctins caefully: Read all pblems caefully befe attempting t slve them. Yu wk must be legible, and the ganizatin clea. Yu must shw all wk, including
Lyapunov Stability Stability of Equilibrium Points
 Lyapunv Stability Stability f Equilibrium Pints 1. Stability f Equilibrium Pints - Definitins In this sectin we cnsider n-th rder nnlinear time varying cntinuus time (C) systems f the frm x = f ( t, x),
Lyapunv Stability Stability f Equilibrium Pints 1. Stability f Equilibrium Pints - Definitins In this sectin we cnsider n-th rder nnlinear time varying cntinuus time (C) systems f the frm x = f ( t, x),
UNIV1"'RSITY OF NORTH CAROLINA Department of Statistics Chapel Hill, N. C. CUMULATIVE SUM CONTROL CHARTS FOR THE FOLDED NORMAL DISTRIBUTION
 UNIV1"'RSITY OF NORTH CAROLINA Department f Statistics Chapel Hill, N. C. CUMULATIVE SUM CONTROL CHARTS FOR THE FOLDED NORMAL DISTRIBUTION by N. L. Jlmsn December 1962 Grant N. AFOSR -62..148 Methds f
UNIV1"'RSITY OF NORTH CAROLINA Department f Statistics Chapel Hill, N. C. CUMULATIVE SUM CONTROL CHARTS FOR THE FOLDED NORMAL DISTRIBUTION by N. L. Jlmsn December 1962 Grant N. AFOSR -62..148 Methds f
Bootstrap Method > # Purpose: understand how bootstrap method works > obs=c(11.96, 5.03, 67.40, 16.07, 31.50, 7.73, 11.10, 22.38) > n=length(obs) >
 Btstrap Methd > # Purpse: understand hw btstrap methd wrks > bs=c(11.96, 5.03, 67.40, 16.07, 31.50, 7.73, 11.10, 22.38) > n=length(bs) > mean(bs) [1] 21.64625 > # estimate f lambda > lambda = 1/mean(bs);
Btstrap Methd > # Purpse: understand hw btstrap methd wrks > bs=c(11.96, 5.03, 67.40, 16.07, 31.50, 7.73, 11.10, 22.38) > n=length(bs) > mean(bs) [1] 21.64625 > # estimate f lambda > lambda = 1/mean(bs);
Department of Economics, University of California, Davis Ecn 200C Micro Theory Professor Giacomo Bonanno. Insurance Markets
 Department f Ecnmics, University f alifrnia, Davis Ecn 200 Micr Thery Prfessr Giacm Bnann Insurance Markets nsider an individual wh has an initial wealth f. ith sme prbability p he faces a lss f x (0
Department f Ecnmics, University f alifrnia, Davis Ecn 200 Micr Thery Prfessr Giacm Bnann Insurance Markets nsider an individual wh has an initial wealth f. ith sme prbability p he faces a lss f x (0
Magnetism. Chapter 21
 1.1 Magnetic Fields Chapte 1 Magnetism The needle f a cmpass is pemanent magnet that has a nth magnetic ple (N) at ne end and a suth magnetic ple (S) at the the. 1.1 Magnetic Fields 1.1 Magnetic Fields
1.1 Magnetic Fields Chapte 1 Magnetism The needle f a cmpass is pemanent magnet that has a nth magnetic ple (N) at ne end and a suth magnetic ple (S) at the the. 1.1 Magnetic Fields 1.1 Magnetic Fields
A Matrix Representation of Panel Data
 web Extensin 6 Appendix 6.A A Matrix Representatin f Panel Data Panel data mdels cme in tw brad varieties, distinct intercept DGPs and errr cmpnent DGPs. his appendix presents matrix algebra representatins
web Extensin 6 Appendix 6.A A Matrix Representatin f Panel Data Panel data mdels cme in tw brad varieties, distinct intercept DGPs and errr cmpnent DGPs. his appendix presents matrix algebra representatins
NOTE ON THE ANALYSIS OF A RANDOMIZED BLOCK DESIGN. Junjiro Ogawa University of North Carolina
 NOTE ON THE ANALYSIS OF A RANDOMIZED BLOCK DESIGN by Junjir Ogawa University f Nrth Carlina This research was supprted by the Office f Naval Research under Cntract N. Nnr-855(06) fr research in prbability
NOTE ON THE ANALYSIS OF A RANDOMIZED BLOCK DESIGN by Junjir Ogawa University f Nrth Carlina This research was supprted by the Office f Naval Research under Cntract N. Nnr-855(06) fr research in prbability
Exercises for Differential Amplifiers. ECE 102, Fall 2012, F. Najmabadi
 Execises f iffeential mplifies ECE 0, Fall 0, F. Najmabai Execise : Cmpute,, an G if m, 00 Ω, O, an ientical Q &Q with µ n C x 8 m, t, λ 0. F G 0 an B F G. epeat the execise f λ 0. -. This execise shws
Execises f iffeential mplifies ECE 0, Fall 0, F. Najmabai Execise : Cmpute,, an G if m, 00 Ω, O, an ientical Q &Q with µ n C x 8 m, t, λ 0. F G 0 an B F G. epeat the execise f λ 0. -. This execise shws
Chapter 15. ELECTRIC POTENTIALS and ENERGY CONSIDERATIONS
 Ch. 15--Elect. Pt. and Enegy Cns. Chapte 15 ELECTRIC POTENTIALS and ENERGY CONSIDERATIONS A.) Enegy Cnsideatins and the Abslute Electical Ptential: 1.) Cnside the fllwing scenai: A single, fixed, pint
Ch. 15--Elect. Pt. and Enegy Cns. Chapte 15 ELECTRIC POTENTIALS and ENERGY CONSIDERATIONS A.) Enegy Cnsideatins and the Abslute Electical Ptential: 1.) Cnside the fllwing scenai: A single, fixed, pint
ELECTROMAGNETIC INDUCTION PREVIOUS EAMCET BITS
 P P Methd EECTOMAGNETIC INDUCTION PEVIOUS EAMCET BITS [ENGINEEING PAPE]. A cnduct d f length tates with angula speed ω in a unifm magnetic field f inductin B which is pependicula t its mtin. The induced
P P Methd EECTOMAGNETIC INDUCTION PEVIOUS EAMCET BITS [ENGINEEING PAPE]. A cnduct d f length tates with angula speed ω in a unifm magnetic field f inductin B which is pependicula t its mtin. The induced
Journal of Solid Mechanics and Materials Engineering
 Junal f Slid Mechanics and Mateials Engineeing Vl. 4, N. 8, 21 Themal Stess and Heat Tansfe Cefficient f Ceamics Stalk Having Ptubeance Dipping int Mlten Metal* Na-ki NOD**, Henda**, Wenbin LI**, Yasushi
Junal f Slid Mechanics and Mateials Engineeing Vl. 4, N. 8, 21 Themal Stess and Heat Tansfe Cefficient f Ceamics Stalk Having Ptubeance Dipping int Mlten Metal* Na-ki NOD**, Henda**, Wenbin LI**, Yasushi
1. Show that if the angular momentum of a boby is determined with respect to an arbitrary point A, then. r r r. H r A can be expressed by H r r r r
 1. Shw that if the angula entu f a bb is deteined with espect t an abita pint, then H can be epessed b H = ρ / v + H. This equies substituting ρ = ρ + ρ / int H = ρ d v + ρ ( ω ρ ) d and epanding, nte
1. Shw that if the angula entu f a bb is deteined with espect t an abita pint, then H can be epessed b H = ρ / v + H. This equies substituting ρ = ρ + ρ / int H = ρ d v + ρ ( ω ρ ) d and epanding, nte
Chapter 4 Motion in Two and Three Dimensions
 Chapte 4 Mtin in Tw and Thee Dimensins In this chapte we will cntinue t stud the mtin f bjects withut the estictin we put in chapte t me aln a staiht line. Instead we will cnside mtin in a plane (tw dimensinal
Chapte 4 Mtin in Tw and Thee Dimensins In this chapte we will cntinue t stud the mtin f bjects withut the estictin we put in chapte t me aln a staiht line. Instead we will cnside mtin in a plane (tw dimensinal
On the Quasi-inverse of a Non-square Matrix: An Infinite Solution
 Applied Mathematical Sciences, Vol 11, 2017, no 27, 1337-1351 HIKARI Ltd, wwwm-hikaicom https://doiog/1012988/ams20177273 On the Quasi-invese of a Non-squae Matix: An Infinite Solution Ruben D Codeo J
Applied Mathematical Sciences, Vol 11, 2017, no 27, 1337-1351 HIKARI Ltd, wwwm-hikaicom https://doiog/1012988/ams20177273 On the Quasi-invese of a Non-squae Matix: An Infinite Solution Ruben D Codeo J
Appendix A. Appendices. A.1 ɛ ijk and cross products. Vector Operations: δ ij and ɛ ijk
 Appendix A Appendices A1 ɛ and coss poducts A11 Vecto Opeations: δ ij and ɛ These ae some notes on the use of the antisymmetic symbol ɛ fo expessing coss poducts This is an extemely poweful tool fo manipulating
Appendix A Appendices A1 ɛ and coss poducts A11 Vecto Opeations: δ ij and ɛ These ae some notes on the use of the antisymmetic symbol ɛ fo expessing coss poducts This is an extemely poweful tool fo manipulating
A) 100 K B) 150 K C) 200 K D) 250 K E) 350 K
 Phys10 Secnd Maj-09 Ze Vesin Cdinat: k Wednesday, May 05, 010 Page: 1 Q1. A ht bject and a cld bject ae placed in themal cntact and the cmbinatin is islated. They tansfe enegy until they each a final equilibium
Phys10 Secnd Maj-09 Ze Vesin Cdinat: k Wednesday, May 05, 010 Page: 1 Q1. A ht bject and a cld bject ae placed in themal cntact and the cmbinatin is islated. They tansfe enegy until they each a final equilibium
MEM202 Engineering Mechanics Statics Course Web site:
 0 Engineeing Mechanics - Statics 0 Engineeing Mechanics Statics Cuse Web site: www.pages.dexel.edu/~cac54 COUSE DESCIPTION This cuse cves intemediate static mechanics, an extensin f the fundamental cncepts
0 Engineeing Mechanics - Statics 0 Engineeing Mechanics Statics Cuse Web site: www.pages.dexel.edu/~cac54 COUSE DESCIPTION This cuse cves intemediate static mechanics, an extensin f the fundamental cncepts
CHE CHAPTER 11 Spring 2005 GENERAL 2ND ORDER REACTION IN TURBULENT TUBULAR REACTORS
 CHE 52 - CHPTE Sping 2005 GENEL 2ND ODE ECTION IN TUULENT TUUL ECTOS Vassilats & T, IChEJ. (4), 666 (965) Cnside the fllwing stichiety: a + b = P The ass cnsevatin law f species i yields Ci + vci =. Di
CHE 52 - CHPTE Sping 2005 GENEL 2ND ODE ECTION IN TUULENT TUUL ECTOS Vassilats & T, IChEJ. (4), 666 (965) Cnside the fllwing stichiety: a + b = P The ass cnsevatin law f species i yields Ci + vci =. Di
Solutions: Solution. d = 3.0g/cm we can calculate the number of Xe atoms per unit volume, Given m and the given values from Table 7.
 Tutial-09 Tutial - 09 Sectin6: Dielectic Mateials ECE:09 (Electnic and Electical Ppeties f Mateials) Electical and Cmpute Engineeing Depatment Univesity f Watel Tut: Hamid Slutins: 7.3 Electnic plaizatin
Tutial-09 Tutial - 09 Sectin6: Dielectic Mateials ECE:09 (Electnic and Electical Ppeties f Mateials) Electical and Cmpute Engineeing Depatment Univesity f Watel Tut: Hamid Slutins: 7.3 Electnic plaizatin
Electric Fields and Electric Forces
 Cpyight, iley 006 (Cutnell & Jhnsn 9. Ptential Enegy Chapte 9 mgh mgh GPE GPE Electic Fields and Electic Fces 9. Ptential Enegy 9. Ptential Enegy 9. The Electic Ptential Diffeence 9. The Electic Ptential
Cpyight, iley 006 (Cutnell & Jhnsn 9. Ptential Enegy Chapte 9 mgh mgh GPE GPE Electic Fields and Electic Fces 9. Ptential Enegy 9. Ptential Enegy 9. The Electic Ptential Diffeence 9. The Electic Ptential
A Maximum Likelihood Method to Improve Faint-Source Flux and Color Estimates
 Publicatins f the Astnmical Sciety f the Pacific, 110:77 731, 1998 June 1998. The Astnmical Sciety f the Pacific. All ights eseved. Pinted in U.S.A. A Maximum Likelihd Methd t Impve Faint-Suce Flux and
Publicatins f the Astnmical Sciety f the Pacific, 110:77 731, 1998 June 1998. The Astnmical Sciety f the Pacific. All ights eseved. Pinted in U.S.A. A Maximum Likelihd Methd t Impve Faint-Suce Flux and
NOTE. Some New Bounds for Cover-Free Families
 Jounal of Combinatoial Theoy, Seies A 90, 224234 (2000) doi:10.1006jcta.1999.3036, available online at http:.idealibay.com on NOTE Some Ne Bounds fo Cove-Fee Families D. R. Stinson 1 and R. Wei Depatment
Jounal of Combinatoial Theoy, Seies A 90, 224234 (2000) doi:10.1006jcta.1999.3036, available online at http:.idealibay.com on NOTE Some Ne Bounds fo Cove-Fee Families D. R. Stinson 1 and R. Wei Depatment
COMP 551 Applied Machine Learning Lecture 5: Generative models for linear classification
 COMP 551 Applied Machine Learning Lecture 5: Generative mdels fr linear classificatin Instructr: Herke van Hf (herke.vanhf@mail.mcgill.ca) Slides mstly by: Jelle Pineau Class web page: www.cs.mcgill.ca/~hvanh2/cmp551
COMP 551 Applied Machine Learning Lecture 5: Generative mdels fr linear classificatin Instructr: Herke van Hf (herke.vanhf@mail.mcgill.ca) Slides mstly by: Jelle Pineau Class web page: www.cs.mcgill.ca/~hvanh2/cmp551
Journal of Inequalities in Pure and Applied Mathematics
 Jounal of Inequalities in Pue and Applied Mathematics COEFFICIENT INEQUALITY FOR A FUNCTION WHOSE DERIVATIVE HAS A POSITIVE REAL PART S. ABRAMOVICH, M. KLARIČIĆ BAKULA AND S. BANIĆ Depatment of Mathematics
Jounal of Inequalities in Pue and Applied Mathematics COEFFICIENT INEQUALITY FOR A FUNCTION WHOSE DERIVATIVE HAS A POSITIVE REAL PART S. ABRAMOVICH, M. KLARIČIĆ BAKULA AND S. BANIĆ Depatment of Mathematics
THE COUPLING SPECTRUM: A NEW METHOD FOR DETECTING TEMPORAL NONLINEAR CAUSALITY IN FINANCIAL TIME SERIES
 The 7 th Intenatinal Days f Statisti and Ecnmi, Pague, Septembe 9-2, 23 THE COUPLING SPECTRUM: A NEW METHOD FOR DETECTING TEMPORAL NONLINEAR CAUSALIT IN FINANCIAL TIME SERIES Ami Reza Alizad-Rahva Masud
The 7 th Intenatinal Days f Statisti and Ecnmi, Pague, Septembe 9-2, 23 THE COUPLING SPECTRUM: A NEW METHOD FOR DETECTING TEMPORAL NONLINEAR CAUSALIT IN FINANCIAL TIME SERIES Ami Reza Alizad-Rahva Masud
Sensors and Actuators Introduction to sensors
 Senss and Actuats Intductin t senss Sande Stuij (s.stuij@tue.nl) Depatment f Electical Engineeing Electnic Systems AMPLIFIES (Chapte 5.) Infmatin pcessing system nncntact sens cntact sens abslute sens
Senss and Actuats Intductin t senss Sande Stuij (s.stuij@tue.nl) Depatment f Electical Engineeing Electnic Systems AMPLIFIES (Chapte 5.) Infmatin pcessing system nncntact sens cntact sens abslute sens
This section is primarily focused on tools to aid us in finding roots/zeros/ -intercepts of polynomials. Essentially, our focus turns to solving.
 Sectin 3.2: Many f yu WILL need t watch the crrespnding vides fr this sectin n MyOpenMath! This sectin is primarily fcused n tls t aid us in finding rts/zers/ -intercepts f plynmials. Essentially, ur fcus
Sectin 3.2: Many f yu WILL need t watch the crrespnding vides fr this sectin n MyOpenMath! This sectin is primarily fcused n tls t aid us in finding rts/zers/ -intercepts f plynmials. Essentially, ur fcus
Distance oracles in edge-labeled graphs
 Distance acles in edge-labeled gaphs Fancesc Bnchi Aistides Ginis Fancesc Gull Antti Ukknen Yah Labs Bacelna, Spain {bnchi,gull}@yah-inc.cm Helsinki Institute f Infmatin Technlgy HIIT Aalt Univesity {aistides.ginis,antti.ukknen}@aalt.fi
Distance acles in edge-labeled gaphs Fancesc Bnchi Aistides Ginis Fancesc Gull Antti Ukknen Yah Labs Bacelna, Spain {bnchi,gull}@yah-inc.cm Helsinki Institute f Infmatin Technlgy HIIT Aalt Univesity {aistides.ginis,antti.ukknen}@aalt.fi
SUPPLEMENTARY MATERIAL GaGa: a simple and flexible hierarchical model for microarray data analysis
 SUPPLEMENTARY MATERIAL GaGa: a simple and flexible hierarchical mdel fr micrarray data analysis David Rssell Department f Bistatistics M.D. Andersn Cancer Center, Hustn, TX 77030, USA rsselldavid@gmail.cm
SUPPLEMENTARY MATERIAL GaGa: a simple and flexible hierarchical mdel fr micrarray data analysis David Rssell Department f Bistatistics M.D. Andersn Cancer Center, Hustn, TX 77030, USA rsselldavid@gmail.cm
Combustion Chamber. (0.1 MPa)
 ME 354 Tutial #10 Winte 001 Reacting Mixtues Pblem 1: Detemine the mle actins the pducts cmbustin when ctane, C 8 18, is buned with 00% theetical ai. Als, detemine the dew-pint tempeatue the pducts i the
ME 354 Tutial #10 Winte 001 Reacting Mixtues Pblem 1: Detemine the mle actins the pducts cmbustin when ctane, C 8 18, is buned with 00% theetical ai. Als, detemine the dew-pint tempeatue the pducts i the
Direct Torque Control of 5-Phase 10/8 Switched Reluctance Motors
 Dwnladed fm ijeee.iust.ac.i at 18:19 IRST n Fiday Septembe 8th 18 Diect Tque Cntl f -Phase 1/8 Switched Reluctance Mts M. R. Feyzi* and Y. Ebahimi* Abstact: A switched Reluctance mt (SRM) has seveal desiable
Dwnladed fm ijeee.iust.ac.i at 18:19 IRST n Fiday Septembe 8th 18 Diect Tque Cntl f -Phase 1/8 Switched Reluctance Mts M. R. Feyzi* and Y. Ebahimi* Abstact: A switched Reluctance mt (SRM) has seveal desiable
Optimal Design of Transonic Fan Blade Leading Edge Shape Using CFD and Simultaneous Perturbation Stochastic Approximation Method
 1 Optimal Design f Tansnic Fan Blade Leading Edge Shape Using CFD and Simultaneus Petubatin Stchastic Appximatin Methd X.Q.Xing and M.Damdaan Abstact Simultaneus Petubatin Stchastic Appximatin methd has
1 Optimal Design f Tansnic Fan Blade Leading Edge Shape Using CFD and Simultaneus Petubatin Stchastic Appximatin Methd X.Q.Xing and M.Damdaan Abstact Simultaneus Petubatin Stchastic Appximatin methd has
On a quantity that is analogous to potential and a theorem that relates to it
 Su une quantité analogue au potential et su un théoème y elatif C R Acad Sci 7 (87) 34-39 On a quantity that is analogous to potential and a theoem that elates to it By R CLAUSIUS Tanslated by D H Delphenich
Su une quantité analogue au potential et su un théoème y elatif C R Acad Sci 7 (87) 34-39 On a quantity that is analogous to potential and a theoem that elates to it By R CLAUSIUS Tanslated by D H Delphenich
AIR FORCE RESEARCH LABORATORY
 AIR FORC RSARCH LABORATORY The xtinctin Theem as an xample f Reseach Vistas in Mathematical Optics Mach Richad A. Albanese Infmatin Opeatins and Applied Mathematics Human ffectiveness Diectate Bks City-Base
AIR FORC RSARCH LABORATORY The xtinctin Theem as an xample f Reseach Vistas in Mathematical Optics Mach Richad A. Albanese Infmatin Opeatins and Applied Mathematics Human ffectiveness Diectate Bks City-Base
Lecture 17: Free Energy of Multi-phase Solutions at Equilibrium
 Lecture 17: 11.07.05 Free Energy f Multi-phase Slutins at Equilibrium Tday: LAST TIME...2 FREE ENERGY DIAGRAMS OF MULTI-PHASE SOLUTIONS 1...3 The cmmn tangent cnstructin and the lever rule...3 Practical
Lecture 17: 11.07.05 Free Energy f Multi-phase Slutins at Equilibrium Tday: LAST TIME...2 FREE ENERGY DIAGRAMS OF MULTI-PHASE SOLUTIONS 1...3 The cmmn tangent cnstructin and the lever rule...3 Practical
CHAPTER 24: INFERENCE IN REGRESSION. Chapter 24: Make inferences about the population from which the sample data came.
 MATH 1342 Ch. 24 April 25 and 27, 2013 Page 1 f 5 CHAPTER 24: INFERENCE IN REGRESSION Chapters 4 and 5: Relatinships between tw quantitative variables. Be able t Make a graph (scatterplt) Summarize the
MATH 1342 Ch. 24 April 25 and 27, 2013 Page 1 f 5 CHAPTER 24: INFERENCE IN REGRESSION Chapters 4 and 5: Relatinships between tw quantitative variables. Be able t Make a graph (scatterplt) Summarize the
Phys 332 Electricity & Magnetism Day 3. Note: I should have recommended reading section 1.5 (delta function) as well. rˆ rˆ
 Phs 33 lecticit & Magnetism Da 3 Mn. 9/9 Wed. 9/ Thus 9/ Fi. 9/3 (C.-.5,.8). &.5;..-.. Gauss & Div, T Numeical Quadatue (C.-.5,.8)..3 Using Gauss (C.-.5,.8)..3-.. Using Gauss HW quipment Bing in ppt s
Phs 33 lecticit & Magnetism Da 3 Mn. 9/9 Wed. 9/ Thus 9/ Fi. 9/3 (C.-.5,.8). &.5;..-.. Gauss & Div, T Numeical Quadatue (C.-.5,.8)..3 Using Gauss (C.-.5,.8)..3-.. Using Gauss HW quipment Bing in ppt s
Relevance feedback and query expansion. Goal: To refine the answer set by involving the user in the retrieval process (feedback/interaction)
 Relevance feedback and quey epansin Gal: T efine the answe set by invlving the use in the etieval pcess (feedback/inteactin) Lcal Methds (adust the use queies) Relevance feedback Pseud ( Blind) Relevance
Relevance feedback and quey epansin Gal: T efine the answe set by invlving the use in the etieval pcess (feedback/inteactin) Lcal Methds (adust the use queies) Relevance feedback Pseud ( Blind) Relevance
Inference in the Multiple-Regression
 Sectin 5 Mdel Inference in the Multiple-Regressin Kinds f hypthesis tests in a multiple regressin There are several distinct kinds f hypthesis tests we can run in a multiple regressin. Suppse that amng
Sectin 5 Mdel Inference in the Multiple-Regressin Kinds f hypthesis tests in a multiple regressin There are several distinct kinds f hypthesis tests we can run in a multiple regressin. Suppse that amng
Introduction to Mathematical Statistics Robert V. Hogg Joeseph McKean Allen T. Craig Seventh Edition
 Intoduction to Mathematical Statistics Robet V. Hogg Joeseph McKean Allen T. Caig Seventh Edition Peason Education Limited Edinbugh Gate Halow Essex CM2 2JE England and Associated Companies thoughout the
Intoduction to Mathematical Statistics Robet V. Hogg Joeseph McKean Allen T. Caig Seventh Edition Peason Education Limited Edinbugh Gate Halow Essex CM2 2JE England and Associated Companies thoughout the
Hypothesis Tests for One Population Mean
 Hypthesis Tests fr One Ppulatin Mean Chapter 9 Ala Abdelbaki Objective Objective: T estimate the value f ne ppulatin mean Inferential statistics using statistics in rder t estimate parameters We will be
Hypthesis Tests fr One Ppulatin Mean Chapter 9 Ala Abdelbaki Objective Objective: T estimate the value f ne ppulatin mean Inferential statistics using statistics in rder t estimate parameters We will be
4th Indian Institute of Astrophysics - PennState Astrostatistics School July, 2013 Vainu Bappu Observatory, Kavalur. Correlation and Regression
 4th Indian Institute f Astrphysics - PennState Astrstatistics Schl July, 2013 Vainu Bappu Observatry, Kavalur Crrelatin and Regressin Rahul Ry Indian Statistical Institute, Delhi. Crrelatin Cnsider a tw
4th Indian Institute f Astrphysics - PennState Astrstatistics Schl July, 2013 Vainu Bappu Observatry, Kavalur Crrelatin and Regressin Rahul Ry Indian Statistical Institute, Delhi. Crrelatin Cnsider a tw
which represents a straight line whose slope is C 1.
 hapte, Slutin 5. Ye, thi claim i eanable ince in the abence any heat eatin the ate heat tane thugh a plain wall in teady peatin mut be cntant. But the value thi cntant mut be ze ince ne ide the wall i
hapte, Slutin 5. Ye, thi claim i eanable ince in the abence any heat eatin the ate heat tane thugh a plain wall in teady peatin mut be cntant. But the value thi cntant mut be ze ince ne ide the wall i
Dead-beat controller design
 J. Hetthéssy, A. Barta, R. Bars: Dead beat cntrller design Nvember, 4 Dead-beat cntrller design In sampled data cntrl systems the cntrller is realised by an intelligent device, typically by a PLC (Prgrammable
J. Hetthéssy, A. Barta, R. Bars: Dead beat cntrller design Nvember, 4 Dead-beat cntrller design In sampled data cntrl systems the cntrller is realised by an intelligent device, typically by a PLC (Prgrammable
University of Pisa. N. Zaccari, D. Aquaro. Pebble Beds. - ITALY - Department of Mechanical, Nuclear and Production Engineering
 Univesity f Pisa - ITALY - Depatment f Mechanical, Nuclea and Pductin Engineeing Them-Mechanical Behaviu f Li 4 SO 4 and Li TiO 3 N. Zaccai, D. Aqua Cntents f Pesentatin This pesentatin descibes the them-mechanical
Univesity f Pisa - ITALY - Depatment f Mechanical, Nuclea and Pductin Engineeing Them-Mechanical Behaviu f Li 4 SO 4 and Li TiO 3 N. Zaccai, D. Aqua Cntents f Pesentatin This pesentatin descibes the them-mechanical
A proposition is a statement that can be either true (T) or false (F), (but not both).
 400 lecture nte #1 [Ch 2, 3] Lgic and Prfs 1.1 Prpsitins (Prpsitinal Lgic) A prpsitin is a statement that can be either true (T) r false (F), (but nt bth). "The earth is flat." -- F "March has 31 days."
400 lecture nte #1 [Ch 2, 3] Lgic and Prfs 1.1 Prpsitins (Prpsitinal Lgic) A prpsitin is a statement that can be either true (T) r false (F), (but nt bth). "The earth is flat." -- F "March has 31 days."
On the structure of MHD shock waves in a viscous gas
 On the stuctue f MHD shck waves in a viscus gas On the stuctue f MHD shck waves in a viscus gas R. K. Anand and Haish C. Yadav Depatment f Physics, Univesity f Allahabad, Allahabad-, India e-mail: anand.ajkuma@ediffmail.cm
On the stuctue f MHD shck waves in a viscus gas On the stuctue f MHD shck waves in a viscus gas R. K. Anand and Haish C. Yadav Depatment f Physics, Univesity f Allahabad, Allahabad-, India e-mail: anand.ajkuma@ediffmail.cm
Computational modeling techniques
 Cmputatinal mdeling techniques Lecture 4: Mdel checing fr ODE mdels In Petre Department f IT, Åb Aademi http://www.users.ab.fi/ipetre/cmpmd/ Cntent Stichimetric matrix Calculating the mass cnservatin relatins
Cmputatinal mdeling techniques Lecture 4: Mdel checing fr ODE mdels In Petre Department f IT, Åb Aademi http://www.users.ab.fi/ipetre/cmpmd/ Cntent Stichimetric matrix Calculating the mass cnservatin relatins
Electromagnetic Waves
 Chapte 3 lectmagnetic Waves 3.1 Maxwell s quatins and ectmagnetic Waves A. Gauss s Law: # clsed suface aea " da Q enc lectic fields may be geneated by electic chages. lectic field lines stat at psitive
Chapte 3 lectmagnetic Waves 3.1 Maxwell s quatins and ectmagnetic Waves A. Gauss s Law: # clsed suface aea " da Q enc lectic fields may be geneated by electic chages. lectic field lines stat at psitive
MATH 220: SECOND ORDER CONSTANT COEFFICIENT PDE. We consider second order constant coefficient scalar linear PDEs on R n. These have the form
 MATH 220: SECOND ORDER CONSTANT COEFFICIENT PDE ANDRAS VASY We conside second ode constant coefficient scala linea PDEs on R n. These have the fom Lu = f L = a ij xi xj + b i xi + c i whee a ij b i and
MATH 220: SECOND ORDER CONSTANT COEFFICIENT PDE ANDRAS VASY We conside second ode constant coefficient scala linea PDEs on R n. These have the fom Lu = f L = a ij xi xj + b i xi + c i whee a ij b i and
Study Group Report: Plate-fin Heat Exchangers: AEA Technology
 Study Grup Reprt: Plate-fin Heat Exchangers: AEA Technlgy The prblem under study cncerned the apparent discrepancy between a series f experiments using a plate fin heat exchanger and the classical thery
Study Grup Reprt: Plate-fin Heat Exchangers: AEA Technlgy The prblem under study cncerned the apparent discrepancy between a series f experiments using a plate fin heat exchanger and the classical thery
AT622 Section 15 Radiative Transfer Revisited: Two-Stream Models
 AT6 Sectin 5 Radiative Tansfe Revisited: Tw-Steam Mdels The gal f this sectin is t intduce sme elementay cncepts f adiative tansfe that accunts f scatteing, absptin and emissin and intduce simple ways
AT6 Sectin 5 Radiative Tansfe Revisited: Tw-Steam Mdels The gal f this sectin is t intduce sme elementay cncepts f adiative tansfe that accunts f scatteing, absptin and emissin and intduce simple ways
Simple Linear Regression (single variable)
 Simple Linear Regressin (single variable) Intrductin t Machine Learning Marek Petrik January 31, 2017 Sme f the figures in this presentatin are taken frm An Intrductin t Statistical Learning, with applicatins
Simple Linear Regressin (single variable) Intrductin t Machine Learning Marek Petrik January 31, 2017 Sme f the figures in this presentatin are taken frm An Intrductin t Statistical Learning, with applicatins
CHAPTER Read Chapter 17, sections 1,2,3. End of Chapter problems: 25
 CHAPTER 17 1. Read Chapter 17, sectins 1,2,3. End f Chapter prblems: 25 2. Suppse yu are playing a game that uses tw dice. If yu cunt the dts n the dice, yu culd have anywhere frm 2 t 12. The ways f prducing
CHAPTER 17 1. Read Chapter 17, sectins 1,2,3. End f Chapter prblems: 25 2. Suppse yu are playing a game that uses tw dice. If yu cunt the dts n the dice, yu culd have anywhere frm 2 t 12. The ways f prducing
MIL-HDBK OCTOBER 1984 MAINTAINABILITY ANALYSIS
 5 CTBER 984 TABLE 5.3..-: VALUES F R z (t'i_ a ) MST CMMNLY USED IN MAINTAINABILITY ANALYSIS l-
5 CTBER 984 TABLE 5.3..-: VALUES F R z (t'i_ a ) MST CMMNLY USED IN MAINTAINABILITY ANALYSIS l-
Entire Solution of a Singular Semilinear Elliptic Problem
 JOURNAL OF MATEMATICAL ANALYSIS AND APPLICATIONS 200, 498505 1996 ARTICLE NO 0218 Etie Sluti f a Sigula Semiliea Elliptic Pblem Ala V Lai ad Aihua W Shae Depatmet f Mathematics ad Statistics, Ai Fce Istitute
JOURNAL OF MATEMATICAL ANALYSIS AND APPLICATIONS 200, 498505 1996 ARTICLE NO 0218 Etie Sluti f a Sigula Semiliea Elliptic Pblem Ala V Lai ad Aihua W Shae Depatmet f Mathematics ad Statistics, Ai Fce Istitute
CHEMISTRY 383 LECTURE NOTES
 CHEMISRY 383 LECURE NOES Chate III R. H. Schwendeman Deatment f Chemisty Michigan State Univesity East Lansing, MI 4884 Cyight 996 by R. H. Schwendeman All ights eseved. N at f this text may be educed,
CHEMISRY 383 LECURE NOES Chate III R. H. Schwendeman Deatment f Chemisty Michigan State Univesity East Lansing, MI 4884 Cyight 996 by R. H. Schwendeman All ights eseved. N at f this text may be educed,
March 15. Induction and Inductance Chapter 31
 Mach 15 Inductin and Inductance Chapte 31 > Fces due t B fields Lentz fce τ On a mving chage F B On a cuent F il B Cuent caying cil feels a tque = µ B Review > Cuents geneate B field Bit-Savat law = qv
Mach 15 Inductin and Inductance Chapte 31 > Fces due t B fields Lentz fce τ On a mving chage F B On a cuent F il B Cuent caying cil feels a tque = µ B Review > Cuents geneate B field Bit-Savat law = qv
Department of Electrical Engineering, University of Waterloo. Introduction
 Sectin 4: Sequential Circuits Majr Tpics Types f sequential circuits Flip-flps Analysis f clcked sequential circuits Mre and Mealy machines Design f clcked sequential circuits State transitin design methd
Sectin 4: Sequential Circuits Majr Tpics Types f sequential circuits Flip-flps Analysis f clcked sequential circuits Mre and Mealy machines Design f clcked sequential circuits State transitin design methd
