LUSOL: A basis package for constrained optimization
|
|
|
- Maude Cross
- 5 years ago
- Views:
Transcription
1 LUSOL: A basis package for constrained optimization IFORS Triennial Conference on OR/MS Honolulu, HI, July 11 15, 2005 Michael O Sullivan and Michael Saunders Dept of Engineering Science Dept of Management Sci & Eng University of Auckland Stanford University Auckland, New Zealand Stanford, CA michael.osullivan@auckland.ac.nz saunders@stanford.edu LUSOL p.1/34
2 Abstract LUSOL is currently the BFP (basis factorization package) for several optimization packages, including MINOS, SQOPT, SNOPT, ZIP, PATH, and lp solve. Threshold Rook Pivoting is an important feature for basis repair (recovery from unexpected singularity). We review the open source Fortran and C implementations of LUSOL. LUSOL p.2/34
3 LUSOL Maintains LU factors of a general sparse matrix A Gill, Murray, Saunders, and Wright (1987) Code contributors F77 MATLAB Cmex C (for lp solve) Saunders (1986 present) following Duff, Reid, Zlatev, Suhl and Suhl Michael O Sullivan (1999 present) Kjell Eikland (2004 present) Features Square or rectangular A Rank-revealing LU for basis repair Stable updates Bartels-Golub style LUSOL p.3/34
4 LUSOL A = or or = LU FACTOR [L,U,p,q] = lusol(a) SOLVE Lx = y, L T x = y, Ux = y, U T x = y, Ax = y, A T x = y UPDATE Add, replace, delete a column Add, replace, delete a row Add a rank-one matrix MULTIPLY x = Ly, x = L T y, x = Uy, x = U T y, x = Ay, x = A T y LUSOL p.4/34
5 RANK-REVEALING LU LUSOL p.5/34
6 FACTOR [L,U,p,q] = lusol(a) L(p,p) = U(p,q) = Well defined for any square or rectangular A Permutations p, q balance stability and sparsity Markowitz strategy for suggesting sparse pivots Stability options: TPP Threshold Partial Pivoting TRP Threshold Rook Pivoting TCP Threshold Complete Pivoting LUSOL p.6/34
7 Partial Pivoting LUSOL p.7/34
8 Rook Pivoting LUSOL p.8/34
9 Complete Pivoting LUSOL p.9/34
10 TPP: Threshold Partial Pivoting LUSOL p.10/34
11 TRP: Threshold Rook Pivoting LUSOL p.11/34
12 TCP: Threshold Complete Pivoting LUSOL p.12/34
13 Rank-Revealing Factors A = XDY T = X, Y well conditioned, D diagonal cond(a) cond(d) SVD QR with column interchanges LU with Rook Pivoting LU with Complete Pivoting UDV T QDR LDU LDU LUSOL p.13/34
14 L = ( ) cond(l) = 100? LUSOL p.14/34
15 L = ( ) cond(l) = LUSOL p.15/34
16 Stability tolerance τ P AQ = LDU Threshold pivoting bounds elements of L and/or U: TPP TRP TCP } } L ij τ 100 or 10 or 5 L ij, U ij τ 3 or 2 or 1.1 TRP, TCP are more Rank-Revealing with low τ: cond(l), cond(u) < (1 + τ) n cond(d) cond(a) LUSOL p.16/34
17 The need for rank-revealing LU A = δ δ 1 1 δ 1 = LDU δ δ small TPP would give L = I, D = δi, rank(a) = 4 or 0 (!) TRP or TCP would give δ δ 1 1 δ 1 L δ δ 1 1 δ 2 1 δ 3 δ 4 rank(a) 3 LUSOL p.17/34
18 Implementing TRP At each stage of Gaussian elimination: A A lu T α j = biggest element in col j β i = biggest element in row i LUSOL p.18/34
19 Implementing TCP At each stage of Gaussian elimination: A A lu T α j = biggest element in col j Amax = biggest element in A (= max α j = max β i ) LUSOL p.19/34
20 TCP: Store α j in a Heap Thanks to John Gilbert Amax Ha(k) α j Hj(k) j Hk(j) k (location of j in heap) LUSOL p.20/34
21 RESULTS LUSOL p.21/34
22 Problem memplus from Harwell-Boeing collection A = , nonzeros, Scaled τ nnz(l+u) Time TRP RR RR RR RR RR TCP RR RR RR PP (SuperLU, colamd) LUSOL p.22/34
23 TRP Profile CUTE Problem BRATU2D A = , nonzeros TRP, τ = 1.26, LU = nonzeros Update β i for modified rows 57.7% Markowitz Find stable pivot 31.4% Elimination The algebra 4.0% Dense CP % Update α j for modified cols 1.6% LUSOL p.23/34
24 TCP Profile Harwell-Boeing Problem memplus A = , nonzeros TCP, τ = 10.0, LU = nonzeros Markowitz Find stable pivot 65.0% Dense CP % Elimination The algebra 7.4% Update α j for modified cols 4.7% Update heap 0.1% (!) LUSOL p.24/34
25 SOLVE LUSOL p.25/34
26 SOLVE Dense rhs Currently, Lx = y, L T x = y,... assume rhs y is dense Sparse rhs (future) Gilbert and Peierls (1988), CPLEX 7.1 (2001) Lx = y requires L column-wise L T x = y needs second copy of L (row-wise) Similarly for U, U T (not good when updates modify U) Product-form update would be ok: B k = L 0 U 0 E 1 E 2... E k Points to Schur-complement updates LUSOL p.26/34
27 APPLICATIONS LUSOL p.27/34
28 LUSOL in MINOS and SQOPT BR factorization rank detection for square B B = = LU, P LP T = L 1, P UQ = L 2 L 3 U 1 U 2... TRP or TCP, τ 2.5, discard factors BS factorization basis detection for rectangular W = (B S) W T = = LU, P LP T = L 1 L 2 TPP, TRP, or TCP τ 2.5, discard factors, P UQ = U 1 I 0 New B = first m columns of W P T LUSOL p.28/34
29 Ping-Qi Pan: Deficient-basis simplex methods A revised dual projective pivot algorithm for linear programming, SIOPT, to appear 2005 A revised primal deficient-basis simplex algorithm for linear programming, SIOPT, submitted June 2005 Take advantage of degeneracy: A = B N, Bx B = b Thm: cond(b) cond(b a) Apply LUSOL to rectangular B LUSOL p.29/34
30 lp solve An open source Mixed Integer Programming solver solve/ GNU LGPL, implemented in C, runs on most platforms Repository for a C implementation of LUSOL created by Kjell Eikland (F77 Pascal C) Main LU includes dynamic reallocation of storage solve/files/lusol/ Choice of BFPs LUSOL is now the default LUSOL p.30/34
31 SUMMARY LUSOL p.31/34
32 LUSOL Features Square or rectangular A Rank-revealing LU for basis repair Stable updates Bartels-Golub style LUSOL p.32/34
33 Future Tasks FACTOR SOLVE UPDATE Language Improve β i = max element in each row Special handling of dense columns Sparse rhs s Schur-complement (F90, Hanh Huynh s thesis) F77 C always possible via f2c F77 Pascal C done for lp solve F90 C? (NAG F95 compiler?) COIN-OR project LUSOL p.33/34
34 Future Tasks FACTOR SOLVE UPDATE Language Improve β i = max element in each row Special handling of dense columns Sparse rhs s Schur-complement (F90, Hanh Huynh s thesis) F77 C always possible via f2c F77 Pascal C done for lp solve F90 C? (NAG F95 compiler?) COIN-OR project Documentation LUSOL p.34/34
Sparse Rank-Revealing LU Factorization
 Sparse Rank-Revealing LU Factorization Householder Symposium XV on Numerical Linear Algebra Peebles, Scotland, June 2002 Michael O Sullivan and Michael Saunders Dept of Engineering Science Dept of Management
Sparse Rank-Revealing LU Factorization Householder Symposium XV on Numerical Linear Algebra Peebles, Scotland, June 2002 Michael O Sullivan and Michael Saunders Dept of Engineering Science Dept of Management
Sparse Rank-Revealing LU Factorization
 Sparse Rank-Revealing LU Factorization SIAM Conference on Optimization Toronto, May 2002 Michael O Sullivan and Michael Saunders Dept of Engineering Science Dept of Management Sci & Eng University of Auckland
Sparse Rank-Revealing LU Factorization SIAM Conference on Optimization Toronto, May 2002 Michael O Sullivan and Michael Saunders Dept of Engineering Science Dept of Management Sci & Eng University of Auckland
A convex QP solver based on block-lu updates
 Block-LU updates p. 1/24 A convex QP solver based on block-lu updates PP06 SIAM Conference on Parallel Processing for Scientific Computing San Francisco, CA, Feb 22 24, 2006 Hanh Huynh and Michael Saunders
Block-LU updates p. 1/24 A convex QP solver based on block-lu updates PP06 SIAM Conference on Parallel Processing for Scientific Computing San Francisco, CA, Feb 22 24, 2006 Hanh Huynh and Michael Saunders
Implementation of a KKT-based active-set QP solver
 Block-LU updates p. 1/27 Implementation of a KKT-based active-set QP solver ISMP 2006 19th International Symposium on Mathematical Programming Rio de Janeiro, Brazil, July 30 August 4, 2006 Hanh Huynh
Block-LU updates p. 1/27 Implementation of a KKT-based active-set QP solver ISMP 2006 19th International Symposium on Mathematical Programming Rio de Janeiro, Brazil, July 30 August 4, 2006 Hanh Huynh
MS&E 318 (CME 338) Large-Scale Numerical Optimization
 Stanford University, Management Science & Engineering (and ICME MS&E 318 (CME 338 Large-Scale Numerical Optimization 1 Origins Instructor: Michael Saunders Spring 2018 Notes 7: LUSOL: a Basis Factorization
Stanford University, Management Science & Engineering (and ICME MS&E 318 (CME 338 Large-Scale Numerical Optimization 1 Origins Instructor: Michael Saunders Spring 2018 Notes 7: LUSOL: a Basis Factorization
A review of sparsity vs stability in LU updates
 A review of sparsity vs stability in LU updates Michael Saunders Dept of Management Science and Engineering (MS&E) Systems Optimization Laboratory (SOL) Institute for Computational Mathematics and Engineering
A review of sparsity vs stability in LU updates Michael Saunders Dept of Management Science and Engineering (MS&E) Systems Optimization Laboratory (SOL) Institute for Computational Mathematics and Engineering
MS&E 318 (CME 338) Large-Scale Numerical Optimization
 Stanford University, Management Science & Engineering (and ICME MS&E 38 (CME 338 Large-Scale Numerical Optimization Course description Instructor: Michael Saunders Spring 28 Notes : Review The course teaches
Stanford University, Management Science & Engineering (and ICME MS&E 38 (CME 338 Large-Scale Numerical Optimization Course description Instructor: Michael Saunders Spring 28 Notes : Review The course teaches
Satisfying Flux Balance and Mass-Action Kinetics in a Network of Biochemical Reactions
 Satisfying Flux Balance and Mass-Action Kinetics in a Network of Biochemical Reactions Speakers Senior Personnel Collaborators Michael Saunders and Ines Thiele Ronan Fleming, Bernhard Palsson, Yinyu Ye
Satisfying Flux Balance and Mass-Action Kinetics in a Network of Biochemical Reactions Speakers Senior Personnel Collaborators Michael Saunders and Ines Thiele Ronan Fleming, Bernhard Palsson, Yinyu Ye
MS&E 318 (CME 338) Large-Scale Numerical Optimization
 Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization Instructor: Michael Saunders Spring 2015 Notes 11: NPSOL and SNOPT SQP Methods 1 Overview
Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization Instructor: Michael Saunders Spring 2015 Notes 11: NPSOL and SNOPT SQP Methods 1 Overview
MS&E 318 (CME 338) Large-Scale Numerical Optimization
 Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization Instructor: Michael Saunders Spring 2015 Notes 4: The Primal Simplex Method 1 Linear
Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization Instructor: Michael Saunders Spring 2015 Notes 4: The Primal Simplex Method 1 Linear
Revised Simplex Method
 DM545 Linear and Integer Programming Lecture 7 Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. 2. 2 Motivation Complexity of single pivot operation
DM545 Linear and Integer Programming Lecture 7 Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. 2. 2 Motivation Complexity of single pivot operation
Ax=b. Zack 10/4/2013
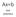 Ax=b Zack 10/4/2013 Iteration method Ax=b v 1, v 2 x k = V k y k Given (A, b) standard orthonormal base v 1, v 2 x k = V k y k For symmetric A, the method to generate V k is called Lanczos Method Lanczos
Ax=b Zack 10/4/2013 Iteration method Ax=b v 1, v 2 x k = V k y k Given (A, b) standard orthonormal base v 1, v 2 x k = V k y k For symmetric A, the method to generate V k is called Lanczos Method Lanczos
STAT 309: MATHEMATICAL COMPUTATIONS I FALL 2018 LECTURE 13
 STAT 309: MATHEMATICAL COMPUTATIONS I FALL 208 LECTURE 3 need for pivoting we saw that under proper circumstances, we can write A LU where 0 0 0 u u 2 u n l 2 0 0 0 u 22 u 2n L l 3 l 32, U 0 0 0 l n l
STAT 309: MATHEMATICAL COMPUTATIONS I FALL 208 LECTURE 3 need for pivoting we saw that under proper circumstances, we can write A LU where 0 0 0 u u 2 u n l 2 0 0 0 u 22 u 2n L l 3 l 32, U 0 0 0 l n l
CME 302: NUMERICAL LINEAR ALGEBRA FALL 2005/06 LECTURE 6
 CME 302: NUMERICAL LINEAR ALGEBRA FALL 2005/06 LECTURE 6 GENE H GOLUB Issues with Floating-point Arithmetic We conclude our discussion of floating-point arithmetic by highlighting two issues that frequently
CME 302: NUMERICAL LINEAR ALGEBRA FALL 2005/06 LECTURE 6 GENE H GOLUB Issues with Floating-point Arithmetic We conclude our discussion of floating-point arithmetic by highlighting two issues that frequently
Bindel, Fall 2016 Matrix Computations (CS 6210) Notes for
 1 Logistics Notes for 2016-09-14 1. There was a goof in HW 2, problem 1 (now fixed) please re-download if you have already started looking at it. 2. CS colloquium (4:15 in Gates G01) this Thurs is Margaret
1 Logistics Notes for 2016-09-14 1. There was a goof in HW 2, problem 1 (now fixed) please re-download if you have already started looking at it. 2. CS colloquium (4:15 in Gates G01) this Thurs is Margaret
DM545 Linear and Integer Programming. Lecture 7 Revised Simplex Method. Marco Chiarandini
 DM545 Linear and Integer Programming Lecture 7 Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. 2. 2 Motivation Complexity of single pivot operation
DM545 Linear and Integer Programming Lecture 7 Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. 2. 2 Motivation Complexity of single pivot operation
Sparse least squares and Q-less QR
 Notes for 2016-02-29 Sparse least squares and Q-less QR Suppose we want to solve a full-rank least squares problem in which A is large and sparse. In principle, we could solve the problem via the normal
Notes for 2016-02-29 Sparse least squares and Q-less QR Suppose we want to solve a full-rank least squares problem in which A is large and sparse. In principle, we could solve the problem via the normal
A Column Pre-ordering Strategy for the Unsymmetric-Pattern Multifrontal Method
 A Column Pre-ordering Strategy for the Unsymmetric-Pattern Multifrontal Method TIMOTHY A. DAVIS University of Florida A new method for sparse LU factorization is presented that combines a column pre-ordering
A Column Pre-ordering Strategy for the Unsymmetric-Pattern Multifrontal Method TIMOTHY A. DAVIS University of Florida A new method for sparse LU factorization is presented that combines a column pre-ordering
1. Introduction. We are concerned with the linear programming (LP) problem in the standard form. minimize subject to Ax = b, x 0,
 A GENERALIZATION OF THE REVISED SIMPLEX ALGORITHM FOR LINEAR PROGRAMMING PING-QI PAN Abstract. Recently the concept of basis, which plays a fundamental role in the simplex methodology, were generalized
A GENERALIZATION OF THE REVISED SIMPLEX ALGORITHM FOR LINEAR PROGRAMMING PING-QI PAN Abstract. Recently the concept of basis, which plays a fundamental role in the simplex methodology, were generalized
Linear Algebra Section 2.6 : LU Decomposition Section 2.7 : Permutations and transposes Wednesday, February 13th Math 301 Week #4
 Linear Algebra Section. : LU Decomposition Section. : Permutations and transposes Wednesday, February 1th Math 01 Week # 1 The LU Decomposition We learned last time that we can factor a invertible matrix
Linear Algebra Section. : LU Decomposition Section. : Permutations and transposes Wednesday, February 1th Math 01 Week # 1 The LU Decomposition We learned last time that we can factor a invertible matrix
Pivoting. Reading: GV96 Section 3.4, Stew98 Chapter 3: 1.3
 Pivoting Reading: GV96 Section 3.4, Stew98 Chapter 3: 1.3 In the previous discussions we have assumed that the LU factorization of A existed and the various versions could compute it in a stable manner.
Pivoting Reading: GV96 Section 3.4, Stew98 Chapter 3: 1.3 In the previous discussions we have assumed that the LU factorization of A existed and the various versions could compute it in a stable manner.
Scientific Computing
 Scientific Computing Direct solution methods Martin van Gijzen Delft University of Technology October 3, 2018 1 Program October 3 Matrix norms LU decomposition Basic algorithm Cost Stability Pivoting Pivoting
Scientific Computing Direct solution methods Martin van Gijzen Delft University of Technology October 3, 2018 1 Program October 3 Matrix norms LU decomposition Basic algorithm Cost Stability Pivoting Pivoting
Matrix decompositions
 Matrix decompositions Zdeněk Dvořák May 19, 2015 Lemma 1 (Schur decomposition). If A is a symmetric real matrix, then there exists an orthogonal matrix Q and a diagonal matrix D such that A = QDQ T. The
Matrix decompositions Zdeněk Dvořák May 19, 2015 Lemma 1 (Schur decomposition). If A is a symmetric real matrix, then there exists an orthogonal matrix Q and a diagonal matrix D such that A = QDQ T. The
The practical revised simplex method (Part 2)
 The practical revised simplex method (Part 2) Julian Hall School of Mathematics University of Edinburgh January 25th 2007 The practical revised simplex method Overview (Part 2) Practical implementation
The practical revised simplex method (Part 2) Julian Hall School of Mathematics University of Edinburgh January 25th 2007 The practical revised simplex method Overview (Part 2) Practical implementation
Scientific Computing: An Introductory Survey
 Scientific Computing: An Introductory Survey Chapter 2 Systems of Linear Equations Prof. Michael T. Heath Department of Computer Science University of Illinois at Urbana-Champaign Copyright c 2002. Reproduction
Scientific Computing: An Introductory Survey Chapter 2 Systems of Linear Equations Prof. Michael T. Heath Department of Computer Science University of Illinois at Urbana-Champaign Copyright c 2002. Reproduction
Scaling and Pivoting in an Out-of-Core Sparse Direct Solver
 Scaling and Pivoting in an Out-of-Core Sparse Direct Solver JENNIFER A. SCOTT Rutherford Appleton Laboratory Out-of-core sparse direct solvers reduce the amount of main memory needed to factorize and solve
Scaling and Pivoting in an Out-of-Core Sparse Direct Solver JENNIFER A. SCOTT Rutherford Appleton Laboratory Out-of-core sparse direct solvers reduce the amount of main memory needed to factorize and solve
Review Questions REVIEW QUESTIONS 71
 REVIEW QUESTIONS 71 MATLAB, is [42]. For a comprehensive treatment of error analysis and perturbation theory for linear systems and many other problems in linear algebra, see [126, 241]. An overview of
REVIEW QUESTIONS 71 MATLAB, is [42]. For a comprehensive treatment of error analysis and perturbation theory for linear systems and many other problems in linear algebra, see [126, 241]. An overview of
What s New in Active-Set Methods for Nonlinear Optimization?
 What s New in Active-Set Methods for Nonlinear Optimization? Philip E. Gill Advances in Numerical Computation, Manchester University, July 5, 2011 A Workshop in Honor of Sven Hammarling UCSD Center for
What s New in Active-Set Methods for Nonlinear Optimization? Philip E. Gill Advances in Numerical Computation, Manchester University, July 5, 2011 A Workshop in Honor of Sven Hammarling UCSD Center for
Lecture Notes to Accompany. Scientific Computing An Introductory Survey. by Michael T. Heath. Chapter 2. Systems of Linear Equations
 Lecture Notes to Accompany Scientific Computing An Introductory Survey Second Edition by Michael T. Heath Chapter 2 Systems of Linear Equations Copyright c 2001. Reproduction permitted only for noncommercial,
Lecture Notes to Accompany Scientific Computing An Introductory Survey Second Edition by Michael T. Heath Chapter 2 Systems of Linear Equations Copyright c 2001. Reproduction permitted only for noncommercial,
Section 3.5 LU Decomposition (Factorization) Key terms. Matrix factorization Forward and back substitution LU-decomposition Storage economization
 Section 3.5 LU Decomposition (Factorization) Key terms Matrix factorization Forward and back substitution LU-decomposition Storage economization In matrix analysis as implemented in modern software the
Section 3.5 LU Decomposition (Factorization) Key terms Matrix factorization Forward and back substitution LU-decomposition Storage economization In matrix analysis as implemented in modern software the
Chapter 8 Cholesky-based Methods for Sparse Least Squares: The Benefits of Regularization
 In L. Adams and J. L. Nazareth eds., Linear and Nonlinear Conjugate Gradient-Related Methods, SIAM, Philadelphia, 92 100 1996. Chapter 8 Cholesky-based Methods for Sparse Least Squares: The Benefits of
In L. Adams and J. L. Nazareth eds., Linear and Nonlinear Conjugate Gradient-Related Methods, SIAM, Philadelphia, 92 100 1996. Chapter 8 Cholesky-based Methods for Sparse Least Squares: The Benefits of
Numerical Linear Algebra
 Numerical Linear Algebra Direct Methods Philippe B. Laval KSU Fall 2017 Philippe B. Laval (KSU) Linear Systems: Direct Solution Methods Fall 2017 1 / 14 Introduction The solution of linear systems is one
Numerical Linear Algebra Direct Methods Philippe B. Laval KSU Fall 2017 Philippe B. Laval (KSU) Linear Systems: Direct Solution Methods Fall 2017 1 / 14 Introduction The solution of linear systems is one
7. LU factorization. factor-solve method. LU factorization. solving Ax = b with A nonsingular. the inverse of a nonsingular matrix
 EE507 - Computational Techniques for EE 7. LU factorization Jitkomut Songsiri factor-solve method LU factorization solving Ax = b with A nonsingular the inverse of a nonsingular matrix LU factorization
EE507 - Computational Techniques for EE 7. LU factorization Jitkomut Songsiri factor-solve method LU factorization solving Ax = b with A nonsingular the inverse of a nonsingular matrix LU factorization
Exploiting hyper-sparsity when computing preconditioners for conjugate gradients in interior point methods
 Exploiting hyper-sparsity when computing preconditioners for conjugate gradients in interior point methods Julian Hall, Ghussoun Al-Jeiroudi and Jacek Gondzio School of Mathematics University of Edinburgh
Exploiting hyper-sparsity when computing preconditioners for conjugate gradients in interior point methods Julian Hall, Ghussoun Al-Jeiroudi and Jacek Gondzio School of Mathematics University of Edinburgh
MS&E 318 (CME 338) Large-Scale Numerical Optimization
 Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization Instructor: Michael Saunders Spring 2017 Notes 10: MINOS Part 1: the Reduced-Gradient
Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization Instructor: Michael Saunders Spring 2017 Notes 10: MINOS Part 1: the Reduced-Gradient
A REGULARIZED ACTIVE-SET METHOD FOR SPARSE CONVEX QUADRATIC PROGRAMMING
 A REGULARIZED ACTIVE-SET METHOD FOR SPARSE CONVEX QUADRATIC PROGRAMMING A DISSERTATION SUBMITTED TO THE INSTITUTE FOR COMPUTATIONAL AND MATHEMATICAL ENGINEERING AND THE COMMITTEE ON GRADUATE STUDIES OF
A REGULARIZED ACTIVE-SET METHOD FOR SPARSE CONVEX QUADRATIC PROGRAMMING A DISSERTATION SUBMITTED TO THE INSTITUTE FOR COMPUTATIONAL AND MATHEMATICAL ENGINEERING AND THE COMMITTEE ON GRADUATE STUDIES OF
CME 302: NUMERICAL LINEAR ALGEBRA FALL 2005/06 LECTURE 0
 CME 302: NUMERICAL LINEAR ALGEBRA FALL 2005/06 LECTURE 0 GENE H GOLUB 1 What is Numerical Analysis? In the 1973 edition of the Webster s New Collegiate Dictionary, numerical analysis is defined to be the
CME 302: NUMERICAL LINEAR ALGEBRA FALL 2005/06 LECTURE 0 GENE H GOLUB 1 What is Numerical Analysis? In the 1973 edition of the Webster s New Collegiate Dictionary, numerical analysis is defined to be the
AMS526: Numerical Analysis I (Numerical Linear Algebra)
 AMS526: Numerical Analysis I (Numerical Linear Algebra) Lecture 12: Gaussian Elimination and LU Factorization Xiangmin Jiao SUNY Stony Brook Xiangmin Jiao Numerical Analysis I 1 / 10 Gaussian Elimination
AMS526: Numerical Analysis I (Numerical Linear Algebra) Lecture 12: Gaussian Elimination and LU Factorization Xiangmin Jiao SUNY Stony Brook Xiangmin Jiao Numerical Analysis I 1 / 10 Gaussian Elimination
Solution of Linear Equations
 Solution of Linear Equations (Com S 477/577 Notes) Yan-Bin Jia Sep 7, 07 We have discussed general methods for solving arbitrary equations, and looked at the special class of polynomial equations A subclass
Solution of Linear Equations (Com S 477/577 Notes) Yan-Bin Jia Sep 7, 07 We have discussed general methods for solving arbitrary equations, and looked at the special class of polynomial equations A subclass
LINEAR PROGRAMMING ALGORITHMS USING LEAST-SQUARES METHOD
 LINEAR PROGRAMMING ALGORITHMS USING LEAST-SQUARES METHOD A Thesis Presented to The Academic Faculty by Seunghyun Kong In Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the
LINEAR PROGRAMMING ALGORITHMS USING LEAST-SQUARES METHOD A Thesis Presented to The Academic Faculty by Seunghyun Kong In Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the
MS&E 318 (CME 338) Large-Scale Numerical Optimization
 Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization 1 Origins Instructor: Michael Saunders Spring 2015 Notes 9: Augmented Lagrangian Methods
Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization 1 Origins Instructor: Michael Saunders Spring 2015 Notes 9: Augmented Lagrangian Methods
14.2 QR Factorization with Column Pivoting
 page 531 Chapter 14 Special Topics Background Material Needed Vector and Matrix Norms (Section 25) Rounding Errors in Basic Floating Point Operations (Section 33 37) Forward Elimination and Back Substitution
page 531 Chapter 14 Special Topics Background Material Needed Vector and Matrix Norms (Section 25) Rounding Errors in Basic Floating Point Operations (Section 33 37) Forward Elimination and Back Substitution
Updating and downdating an upper trapezoidal sparse orthogonal factorization
 IMA Journal of Numerical Analysis (2006) 26, 1 10 doi:10.1093/imanum/dri027 Advance Access publication on July 20, 2005 Updating and downdating an upper trapezoidal sparse orthogonal factorization ÁNGEL
IMA Journal of Numerical Analysis (2006) 26, 1 10 doi:10.1093/imanum/dri027 Advance Access publication on July 20, 2005 Updating and downdating an upper trapezoidal sparse orthogonal factorization ÁNGEL
AMS526: Numerical Analysis I (Numerical Linear Algebra for Computational and Data Sciences)
 AMS526: Numerical Analysis I (Numerical Linear Algebra for Computational and Data Sciences) Lecture 19: Computing the SVD; Sparse Linear Systems Xiangmin Jiao Stony Brook University Xiangmin Jiao Numerical
AMS526: Numerical Analysis I (Numerical Linear Algebra for Computational and Data Sciences) Lecture 19: Computing the SVD; Sparse Linear Systems Xiangmin Jiao Stony Brook University Xiangmin Jiao Numerical
Linear Programming: Simplex
 Linear Programming: Simplex Stephen J. Wright 1 2 Computer Sciences Department, University of Wisconsin-Madison. IMA, August 2016 Stephen Wright (UW-Madison) Linear Programming: Simplex IMA, August 2016
Linear Programming: Simplex Stephen J. Wright 1 2 Computer Sciences Department, University of Wisconsin-Madison. IMA, August 2016 Stephen Wright (UW-Madison) Linear Programming: Simplex IMA, August 2016
Numerical Linear Algebra
 Numerical Linear Algebra Decompositions, numerical aspects Gerard Sleijpen and Martin van Gijzen September 27, 2017 1 Delft University of Technology Program Lecture 2 LU-decomposition Basic algorithm Cost
Numerical Linear Algebra Decompositions, numerical aspects Gerard Sleijpen and Martin van Gijzen September 27, 2017 1 Delft University of Technology Program Lecture 2 LU-decomposition Basic algorithm Cost
Program Lecture 2. Numerical Linear Algebra. Gaussian elimination (2) Gaussian elimination. Decompositions, numerical aspects
 Numerical Linear Algebra Decompositions, numerical aspects Program Lecture 2 LU-decomposition Basic algorithm Cost Stability Pivoting Cholesky decomposition Sparse matrices and reorderings Gerard Sleijpen
Numerical Linear Algebra Decompositions, numerical aspects Program Lecture 2 LU-decomposition Basic algorithm Cost Stability Pivoting Cholesky decomposition Sparse matrices and reorderings Gerard Sleijpen
MATH 3511 Lecture 1. Solving Linear Systems 1
 MATH 3511 Lecture 1 Solving Linear Systems 1 Dmitriy Leykekhman Spring 2012 Goals Review of basic linear algebra Solution of simple linear systems Gaussian elimination D Leykekhman - MATH 3511 Introduction
MATH 3511 Lecture 1 Solving Linear Systems 1 Dmitriy Leykekhman Spring 2012 Goals Review of basic linear algebra Solution of simple linear systems Gaussian elimination D Leykekhman - MATH 3511 Introduction
Preliminary/Qualifying Exam in Numerical Analysis (Math 502a) Spring 2012
 Instructions Preliminary/Qualifying Exam in Numerical Analysis (Math 502a) Spring 2012 The exam consists of four problems, each having multiple parts. You should attempt to solve all four problems. 1.
Instructions Preliminary/Qualifying Exam in Numerical Analysis (Math 502a) Spring 2012 The exam consists of four problems, each having multiple parts. You should attempt to solve all four problems. 1.
B553 Lecture 5: Matrix Algebra Review
 B553 Lecture 5: Matrix Algebra Review Kris Hauser January 19, 2012 We have seen in prior lectures how vectors represent points in R n and gradients of functions. Matrices represent linear transformations
B553 Lecture 5: Matrix Algebra Review Kris Hauser January 19, 2012 We have seen in prior lectures how vectors represent points in R n and gradients of functions. Matrices represent linear transformations
Scientific Computing: Dense Linear Systems
 Scientific Computing: Dense Linear Systems Aleksandar Donev Courant Institute, NYU 1 donev@courant.nyu.edu 1 Course MATH-GA.2043 or CSCI-GA.2112, Spring 2012 February 9th, 2012 A. Donev (Courant Institute)
Scientific Computing: Dense Linear Systems Aleksandar Donev Courant Institute, NYU 1 donev@courant.nyu.edu 1 Course MATH-GA.2043 or CSCI-GA.2112, Spring 2012 February 9th, 2012 A. Donev (Courant Institute)
Novel update techniques for the revised simplex method (and their application)
 Novel update techniques for the revised simplex method (and their application) Qi Huangfu 1 Julian Hall 2 Others 1 FICO 2 School of Mathematics, University of Edinburgh ERGO 30 November 2016 Overview Background
Novel update techniques for the revised simplex method (and their application) Qi Huangfu 1 Julian Hall 2 Others 1 FICO 2 School of Mathematics, University of Edinburgh ERGO 30 November 2016 Overview Background
Experiments with iterative computation of search directions within interior methods for constrained optimization
 Experiments with iterative computation of search directions within interior methods for constrained optimization Santiago Akle and Michael Saunders Institute for Computational Mathematics and Engineering
Experiments with iterative computation of search directions within interior methods for constrained optimization Santiago Akle and Michael Saunders Institute for Computational Mathematics and Engineering
Linear Least squares
 Linear Least squares Method of least squares Measurement errors are inevitable in observational and experimental sciences Errors can be smoothed out by averaging over more measurements than necessary to
Linear Least squares Method of least squares Measurement errors are inevitable in observational and experimental sciences Errors can be smoothed out by averaging over more measurements than necessary to
Linear Systems of n equations for n unknowns
 Linear Systems of n equations for n unknowns In many application problems we want to find n unknowns, and we have n linear equations Example: Find x,x,x such that the following three equations hold: x
Linear Systems of n equations for n unknowns In many application problems we want to find n unknowns, and we have n linear equations Example: Find x,x,x such that the following three equations hold: x
Rank Revealing QR factorization. F. Guyomarc h, D. Mezher and B. Philippe
 Rank Revealing QR factorization F. Guyomarc h, D. Mezher and B. Philippe 1 Outline Introduction Classical Algorithms Full matrices Sparse matrices Rank-Revealing QR Conclusion CSDA 2005, Cyprus 2 Situation
Rank Revealing QR factorization F. Guyomarc h, D. Mezher and B. Philippe 1 Outline Introduction Classical Algorithms Full matrices Sparse matrices Rank-Revealing QR Conclusion CSDA 2005, Cyprus 2 Situation
Key words. numerical linear algebra, direct methods, Cholesky factorization, sparse matrices, mathematical software, matrix updates.
 ROW MODIFICATIONS OF A SPARSE CHOLESKY FACTORIZATION TIMOTHY A. DAVIS AND WILLIAM W. HAGER Abstract. Given a sparse, symmetric positive definite matrix C and an associated sparse Cholesky factorization
ROW MODIFICATIONS OF A SPARSE CHOLESKY FACTORIZATION TIMOTHY A. DAVIS AND WILLIAM W. HAGER Abstract. Given a sparse, symmetric positive definite matrix C and an associated sparse Cholesky factorization
Ax = b. Systems of Linear Equations. Lecture Notes to Accompany. Given m n matrix A and m-vector b, find unknown n-vector x satisfying
 Lecture Notes to Accompany Scientific Computing An Introductory Survey Second Edition by Michael T Heath Chapter Systems of Linear Equations Systems of Linear Equations Given m n matrix A and m-vector
Lecture Notes to Accompany Scientific Computing An Introductory Survey Second Edition by Michael T Heath Chapter Systems of Linear Equations Systems of Linear Equations Given m n matrix A and m-vector
Homework 2 Foundations of Computational Math 2 Spring 2019
 Homework 2 Foundations of Computational Math 2 Spring 2019 Problem 2.1 (2.1.a) Suppose (v 1,λ 1 )and(v 2,λ 2 ) are eigenpairs for a matrix A C n n. Show that if λ 1 λ 2 then v 1 and v 2 are linearly independent.
Homework 2 Foundations of Computational Math 2 Spring 2019 Problem 2.1 (2.1.a) Suppose (v 1,λ 1 )and(v 2,λ 2 ) are eigenpairs for a matrix A C n n. Show that if λ 1 λ 2 then v 1 and v 2 are linearly independent.
A NEW FACE METHOD FOR LINEAR PROGRAMMING. 1. Introduction We are concerned with the standard linear programming (LP) problem
 A NEW FACE METHOD FOR LINEAR PROGRAMMING PING-QI PAN Abstract. An attractive feature of the face method [9 for solving LP problems is that it uses the orthogonal projection of the negative objective gradient
A NEW FACE METHOD FOR LINEAR PROGRAMMING PING-QI PAN Abstract. An attractive feature of the face method [9 for solving LP problems is that it uses the orthogonal projection of the negative objective gradient
TRANSPORTATION PROBLEMS
 Chapter 6 TRANSPORTATION PROBLEMS 61 Transportation Model Transportation models deal with the determination of a minimum-cost plan for transporting a commodity from a number of sources to a number of destinations
Chapter 6 TRANSPORTATION PROBLEMS 61 Transportation Model Transportation models deal with the determination of a minimum-cost plan for transporting a commodity from a number of sources to a number of destinations
BlockMatrixComputations and the Singular Value Decomposition. ATaleofTwoIdeas
 BlockMatrixComputations and the Singular Value Decomposition ATaleofTwoIdeas Charles F. Van Loan Department of Computer Science Cornell University Supported in part by the NSF contract CCR-9901988. Block
BlockMatrixComputations and the Singular Value Decomposition ATaleofTwoIdeas Charles F. Van Loan Department of Computer Science Cornell University Supported in part by the NSF contract CCR-9901988. Block
forms Christopher Engström November 14, 2014 MAA704: Matrix factorization and canonical forms Matrix properties Matrix factorization Canonical forms
 Christopher Engström November 14, 2014 Hermitian LU QR echelon Contents of todays lecture Some interesting / useful / important of matrices Hermitian LU QR echelon Rewriting a as a product of several matrices.
Christopher Engström November 14, 2014 Hermitian LU QR echelon Contents of todays lecture Some interesting / useful / important of matrices Hermitian LU QR echelon Rewriting a as a product of several matrices.
I-v k e k. (I-e k h kt ) = Stability of Gauss-Huard Elimination for Solving Linear Systems. 1 x 1 x x x x
 Technical Report CS-93-08 Department of Computer Systems Faculty of Mathematics and Computer Science University of Amsterdam Stability of Gauss-Huard Elimination for Solving Linear Systems T. J. Dekker
Technical Report CS-93-08 Department of Computer Systems Faculty of Mathematics and Computer Science University of Amsterdam Stability of Gauss-Huard Elimination for Solving Linear Systems T. J. Dekker
LU Preconditioning for Overdetermined Sparse Least Squares Problems
 LU Preconditioning for Overdetermined Sparse Least Squares Problems Gary W. Howell 1 and Marc Baboulin 2 1 North Carolina State University, USA gwhowell@ncsu.edu 2 Université Paris-Sud and Inria, France
LU Preconditioning for Overdetermined Sparse Least Squares Problems Gary W. Howell 1 and Marc Baboulin 2 1 North Carolina State University, USA gwhowell@ncsu.edu 2 Université Paris-Sud and Inria, France
Fundamentals Algorithms for Linear Equation Solution. Gaussian Elimination LU Factorization
 Fundamentals Algorithms for Linear Equation Solution Gaussian Elimination LU Factorization J. Roychowdhury, University of alifornia at erkeley Slide Dense vs Sparse Matrices ircuit Jacobians: typically
Fundamentals Algorithms for Linear Equation Solution Gaussian Elimination LU Factorization J. Roychowdhury, University of alifornia at erkeley Slide Dense vs Sparse Matrices ircuit Jacobians: typically
AN EFFICIENT APPROACH TO UPDATING SIMPLEX MULTIPLIERS IN THE SIMPLEX ALGORITHM
 AN EFFICIENT APPROACH TO UPDATING SIMPLEX MULTIPLIERS IN THE SIMPLEX ALGORITHM JIAN-FENG HU AND PING-QI PAN Abstract. The simplex algorithm computes the simplex multipliers by solving a system (or two
AN EFFICIENT APPROACH TO UPDATING SIMPLEX MULTIPLIERS IN THE SIMPLEX ALGORITHM JIAN-FENG HU AND PING-QI PAN Abstract. The simplex algorithm computes the simplex multipliers by solving a system (or two
AM 205: lecture 8. Last time: Cholesky factorization, QR factorization Today: how to compute the QR factorization, the Singular Value Decomposition
 AM 205: lecture 8 Last time: Cholesky factorization, QR factorization Today: how to compute the QR factorization, the Singular Value Decomposition QR Factorization A matrix A R m n, m n, can be factorized
AM 205: lecture 8 Last time: Cholesky factorization, QR factorization Today: how to compute the QR factorization, the Singular Value Decomposition QR Factorization A matrix A R m n, m n, can be factorized
Direct Methods for Solving Linear Systems. Matrix Factorization
 Direct Methods for Solving Linear Systems Matrix Factorization Numerical Analysis (9th Edition) R L Burden & J D Faires Beamer Presentation Slides prepared by John Carroll Dublin City University c 2011
Direct Methods for Solving Linear Systems Matrix Factorization Numerical Analysis (9th Edition) R L Burden & J D Faires Beamer Presentation Slides prepared by John Carroll Dublin City University c 2011
CS412: Lecture #17. Mridul Aanjaneya. March 19, 2015
 CS: Lecture #7 Mridul Aanjaneya March 9, 5 Solving linear systems of equations Consider a lower triangular matrix L: l l l L = l 3 l 3 l 33 l n l nn A procedure similar to that for upper triangular systems
CS: Lecture #7 Mridul Aanjaneya March 9, 5 Solving linear systems of equations Consider a lower triangular matrix L: l l l L = l 3 l 3 l 33 l n l nn A procedure similar to that for upper triangular systems
GAMS/MINOS MINOS 1 GAMS/MINOS. Table of Contents:
 GAMS/MINOS MINOS 1 GAMS/MINOS Table of Contents:... 1. INTRODUCTION... 2 2. HOW TO RUN A MODEL WITH GAMS/MINOS... 2 3. OVERVIEW OF GAMS/MINOS... 2 3.1. Linear programming... 3 3.2. Problems with a Nonlinear
GAMS/MINOS MINOS 1 GAMS/MINOS Table of Contents:... 1. INTRODUCTION... 2 2. HOW TO RUN A MODEL WITH GAMS/MINOS... 2 3. OVERVIEW OF GAMS/MINOS... 2 3.1. Linear programming... 3 3.2. Problems with a Nonlinear
Numerical Linear Algebra Primer. Ryan Tibshirani Convex Optimization /36-725
 Numerical Linear Algebra Primer Ryan Tibshirani Convex Optimization 10-725/36-725 Last time: proximal gradient descent Consider the problem min g(x) + h(x) with g, h convex, g differentiable, and h simple
Numerical Linear Algebra Primer Ryan Tibshirani Convex Optimization 10-725/36-725 Last time: proximal gradient descent Consider the problem min g(x) + h(x) with g, h convex, g differentiable, and h simple
Bindel, Fall 2009 Matrix Computations (CS 6210) Week 8: Friday, Oct 17
 Logistics Week 8: Friday, Oct 17 1. HW 3 errata: in Problem 1, I meant to say p i < i, not that p i is strictly ascending my apologies. You would want p i > i if you were simply forming the matrices and
Logistics Week 8: Friday, Oct 17 1. HW 3 errata: in Problem 1, I meant to say p i < i, not that p i is strictly ascending my apologies. You would want p i > i if you were simply forming the matrices and
Numerical Methods. Elena loli Piccolomini. Civil Engeneering. piccolom. Metodi Numerici M p. 1/??
 Metodi Numerici M p. 1/?? Numerical Methods Elena loli Piccolomini Civil Engeneering http://www.dm.unibo.it/ piccolom elena.loli@unibo.it Metodi Numerici M p. 2/?? Least Squares Data Fitting Measurement
Metodi Numerici M p. 1/?? Numerical Methods Elena loli Piccolomini Civil Engeneering http://www.dm.unibo.it/ piccolom elena.loli@unibo.it Metodi Numerici M p. 2/?? Least Squares Data Fitting Measurement
The following steps will help you to record your work and save and submit it successfully.
 MATH 22AL Lab # 4 1 Objectives In this LAB you will explore the following topics using MATLAB. Properties of invertible matrices. Inverse of a Matrix Explore LU Factorization 2 Recording and submitting
MATH 22AL Lab # 4 1 Objectives In this LAB you will explore the following topics using MATLAB. Properties of invertible matrices. Inverse of a Matrix Explore LU Factorization 2 Recording and submitting
Downloaded 08/28/12 to Redistribution subject to SIAM license or copyright; see
 SIAMJ.MATRIX ANAL. APPL. c 1997 Society for Industrial and Applied Mathematics Vol. 18, No. 1, pp. 140 158, January 1997 012 AN UNSYMMETRIC-PATTERN MULTIFRONTAL METHOD FOR SPARSE LU FACTORIZATION TIMOTHY
SIAMJ.MATRIX ANAL. APPL. c 1997 Society for Industrial and Applied Mathematics Vol. 18, No. 1, pp. 140 158, January 1997 012 AN UNSYMMETRIC-PATTERN MULTIFRONTAL METHOD FOR SPARSE LU FACTORIZATION TIMOTHY
Lecture 9: Numerical Linear Algebra Primer (February 11st)
 10-725/36-725: Convex Optimization Spring 2015 Lecture 9: Numerical Linear Algebra Primer (February 11st) Lecturer: Ryan Tibshirani Scribes: Avinash Siravuru, Guofan Wu, Maosheng Liu Note: LaTeX template
10-725/36-725: Convex Optimization Spring 2015 Lecture 9: Numerical Linear Algebra Primer (February 11st) Lecturer: Ryan Tibshirani Scribes: Avinash Siravuru, Guofan Wu, Maosheng Liu Note: LaTeX template
Matrix decompositions
 Matrix decompositions How can we solve Ax = b? 1 Linear algebra Typical linear system of equations : x 1 x +x = x 1 +x +9x = 0 x 1 +x x = The variables x 1, x, and x only appear as linear terms (no powers
Matrix decompositions How can we solve Ax = b? 1 Linear algebra Typical linear system of equations : x 1 x +x = x 1 +x +9x = 0 x 1 +x x = The variables x 1, x, and x only appear as linear terms (no powers
Math 102, Winter Final Exam Review. Chapter 1. Matrices and Gaussian Elimination
 Math 0, Winter 07 Final Exam Review Chapter. Matrices and Gaussian Elimination { x + x =,. Different forms of a system of linear equations. Example: The x + 4x = 4. [ ] [ ] [ ] vector form (or the column
Math 0, Winter 07 Final Exam Review Chapter. Matrices and Gaussian Elimination { x + x =,. Different forms of a system of linear equations. Example: The x + 4x = 4. [ ] [ ] [ ] vector form (or the column
CHAPTER 11. A Revision. 1. The Computers and Numbers therein
 CHAPTER A Revision. The Computers and Numbers therein Traditional computer science begins with a finite alphabet. By stringing elements of the alphabet one after another, one obtains strings. A set of
CHAPTER A Revision. The Computers and Numbers therein Traditional computer science begins with a finite alphabet. By stringing elements of the alphabet one after another, one obtains strings. A set of
CS227-Scientific Computing. Lecture 4: A Crash Course in Linear Algebra
 CS227-Scientific Computing Lecture 4: A Crash Course in Linear Algebra Linear Transformation of Variables A common phenomenon: Two sets of quantities linearly related: y = 3x + x 2 4x 3 y 2 = 2.7x 2 x
CS227-Scientific Computing Lecture 4: A Crash Course in Linear Algebra Linear Transformation of Variables A common phenomenon: Two sets of quantities linearly related: y = 3x + x 2 4x 3 y 2 = 2.7x 2 x
Introduction to Mathematical Programming
 Introduction to Mathematical Programming Ming Zhong Lecture 6 September 12, 2018 Ming Zhong (JHU) AMS Fall 2018 1 / 20 Table of Contents 1 Ming Zhong (JHU) AMS Fall 2018 2 / 20 Solving Linear Systems A
Introduction to Mathematical Programming Ming Zhong Lecture 6 September 12, 2018 Ming Zhong (JHU) AMS Fall 2018 1 / 20 Table of Contents 1 Ming Zhong (JHU) AMS Fall 2018 2 / 20 Solving Linear Systems A
Dense LU factorization and its error analysis
 Dense LU factorization and its error analysis Laura Grigori INRIA and LJLL, UPMC February 2016 Plan Basis of floating point arithmetic and stability analysis Notation, results, proofs taken from [N.J.Higham,
Dense LU factorization and its error analysis Laura Grigori INRIA and LJLL, UPMC February 2016 Plan Basis of floating point arithmetic and stability analysis Notation, results, proofs taken from [N.J.Higham,
MATRICES. a m,1 a m,n A =
 MATRICES Matrices are rectangular arrays of real or complex numbers With them, we define arithmetic operations that are generalizations of those for real and complex numbers The general form a matrix of
MATRICES Matrices are rectangular arrays of real or complex numbers With them, we define arithmetic operations that are generalizations of those for real and complex numbers The general form a matrix of
MTH 464: Computational Linear Algebra
 MTH 464: Computational Linear Algebra Lecture Outlines Exam 2 Material Prof. M. Beauregard Department of Mathematics & Statistics Stephen F. Austin State University February 6, 2018 Linear Algebra (MTH
MTH 464: Computational Linear Algebra Lecture Outlines Exam 2 Material Prof. M. Beauregard Department of Mathematics & Statistics Stephen F. Austin State University February 6, 2018 Linear Algebra (MTH
MODULE 7. where A is an m n real (or complex) matrix. 2) Let K(t, s) be a function of two variables which is continuous on the square [0, 1] [0, 1].
![MODULE 7. where A is an m n real (or complex) matrix. 2) Let K(t, s) be a function of two variables which is continuous on the square [0, 1] [0, 1]. MODULE 7. where A is an m n real (or complex) matrix. 2) Let K(t, s) be a function of two variables which is continuous on the square [0, 1] [0, 1].](/thumbs/95/122529712.jpg) Topics: Linear operators MODULE 7 We are going to discuss functions = mappings = transformations = operators from one vector space V 1 into another vector space V 2. However, we shall restrict our sights
Topics: Linear operators MODULE 7 We are going to discuss functions = mappings = transformations = operators from one vector space V 1 into another vector space V 2. However, we shall restrict our sights
Matrix Assembly in FEA
 Matrix Assembly in FEA 1 In Chapter 2, we spoke about how the global matrix equations are assembled in the finite element method. We now want to revisit that discussion and add some details. For example,
Matrix Assembly in FEA 1 In Chapter 2, we spoke about how the global matrix equations are assembled in the finite element method. We now want to revisit that discussion and add some details. For example,
Applied Linear Algebra in Geoscience Using MATLAB
 Applied Linear Algebra in Geoscience Using MATLAB Contents Getting Started Creating Arrays Mathematical Operations with Arrays Using Script Files and Managing Data Two-Dimensional Plots Programming in
Applied Linear Algebra in Geoscience Using MATLAB Contents Getting Started Creating Arrays Mathematical Operations with Arrays Using Script Files and Managing Data Two-Dimensional Plots Programming in
CSE 160 Lecture 13. Numerical Linear Algebra
 CSE 16 Lecture 13 Numerical Linear Algebra Announcements Section will be held on Friday as announced on Moodle Midterm Return 213 Scott B Baden / CSE 16 / Fall 213 2 Today s lecture Gaussian Elimination
CSE 16 Lecture 13 Numerical Linear Algebra Announcements Section will be held on Friday as announced on Moodle Midterm Return 213 Scott B Baden / CSE 16 / Fall 213 2 Today s lecture Gaussian Elimination
9. Numerical linear algebra background
 Convex Optimization Boyd & Vandenberghe 9. Numerical linear algebra background matrix structure and algorithm complexity solving linear equations with factored matrices LU, Cholesky, LDL T factorization
Convex Optimization Boyd & Vandenberghe 9. Numerical linear algebra background matrix structure and algorithm complexity solving linear equations with factored matrices LU, Cholesky, LDL T factorization
Iterative Solution of Sparse Linear Least Squares using LU Factorization
 Iterative Solution of Sparse Linear Least Squares using LU Factorization Gary W. Howell Marc Baboulin Abstract In this paper, we are interested in computing the solution of an overdetermined sparse linear
Iterative Solution of Sparse Linear Least Squares using LU Factorization Gary W. Howell Marc Baboulin Abstract In this paper, we are interested in computing the solution of an overdetermined sparse linear
Main matrix factorizations
 Main matrix factorizations A P L U P permutation matrix, L lower triangular, U upper triangular Key use: Solve square linear system Ax b. A Q R Q unitary, R upper triangular Key use: Solve square or overdetrmined
Main matrix factorizations A P L U P permutation matrix, L lower triangular, U upper triangular Key use: Solve square linear system Ax b. A Q R Q unitary, R upper triangular Key use: Solve square or overdetrmined
Numerical Linear Algebra
 Chapter 3 Numerical Linear Algebra We review some techniques used to solve Ax = b where A is an n n matrix, and x and b are n 1 vectors (column vectors). We then review eigenvalues and eigenvectors and
Chapter 3 Numerical Linear Algebra We review some techniques used to solve Ax = b where A is an n n matrix, and x and b are n 1 vectors (column vectors). We then review eigenvalues and eigenvectors and
Notes on Eigenvalues, Singular Values and QR
 Notes on Eigenvalues, Singular Values and QR Michael Overton, Numerical Computing, Spring 2017 March 30, 2017 1 Eigenvalues Everyone who has studied linear algebra knows the definition: given a square
Notes on Eigenvalues, Singular Values and QR Michael Overton, Numerical Computing, Spring 2017 March 30, 2017 1 Eigenvalues Everyone who has studied linear algebra knows the definition: given a square
9. Numerical linear algebra background
 Convex Optimization Boyd & Vandenberghe 9. Numerical linear algebra background matrix structure and algorithm complexity solving linear equations with factored matrices LU, Cholesky, LDL T factorization
Convex Optimization Boyd & Vandenberghe 9. Numerical linear algebra background matrix structure and algorithm complexity solving linear equations with factored matrices LU, Cholesky, LDL T factorization
Linear Algebra. Solving Linear Systems. Copyright 2005, W.R. Winfrey
 Copyright 2005, W.R. Winfrey Topics Preliminaries Echelon Form of a Matrix Elementary Matrices; Finding A -1 Equivalent Matrices LU-Factorization Topics Preliminaries Echelon Form of a Matrix Elementary
Copyright 2005, W.R. Winfrey Topics Preliminaries Echelon Form of a Matrix Elementary Matrices; Finding A -1 Equivalent Matrices LU-Factorization Topics Preliminaries Echelon Form of a Matrix Elementary
Numerical Methods I Solving Square Linear Systems: GEM and LU factorization
 Numerical Methods I Solving Square Linear Systems: GEM and LU factorization Aleksandar Donev Courant Institute, NYU 1 donev@courant.nyu.edu 1 MATH-GA 2011.003 / CSCI-GA 2945.003, Fall 2014 September 18th,
Numerical Methods I Solving Square Linear Systems: GEM and LU factorization Aleksandar Donev Courant Institute, NYU 1 donev@courant.nyu.edu 1 MATH-GA 2011.003 / CSCI-GA 2945.003, Fall 2014 September 18th,
Sparse BLAS-3 Reduction
 Sparse BLAS-3 Reduction to Banded Upper Triangular (Spar3Bnd) Gary Howell, HPC/OIT NC State University gary howell@ncsu.edu Sparse BLAS-3 Reduction p.1/27 Acknowledgements James Demmel, Gene Golub, Franc
Sparse BLAS-3 Reduction to Banded Upper Triangular (Spar3Bnd) Gary Howell, HPC/OIT NC State University gary howell@ncsu.edu Sparse BLAS-3 Reduction p.1/27 Acknowledgements James Demmel, Gene Golub, Franc
Linear Programming The Simplex Algorithm: Part II Chapter 5
 1 Linear Programming The Simplex Algorithm: Part II Chapter 5 University of Chicago Booth School of Business Kipp Martin October 17, 2017 Outline List of Files Key Concepts Revised Simplex Revised Simplex
1 Linear Programming The Simplex Algorithm: Part II Chapter 5 University of Chicago Booth School of Business Kipp Martin October 17, 2017 Outline List of Files Key Concepts Revised Simplex Revised Simplex
3. Vector spaces 3.1 Linear dependence and independence 3.2 Basis and dimension. 5. Extreme points and basic feasible solutions
 A. LINEAR ALGEBRA. CONVEX SETS 1. Matrices and vectors 1.1 Matrix operations 1.2 The rank of a matrix 2. Systems of linear equations 2.1 Basic solutions 3. Vector spaces 3.1 Linear dependence and independence
A. LINEAR ALGEBRA. CONVEX SETS 1. Matrices and vectors 1.1 Matrix operations 1.2 The rank of a matrix 2. Systems of linear equations 2.1 Basic solutions 3. Vector spaces 3.1 Linear dependence and independence
