MS&E 318 (CME 338) Large-Scale Numerical Optimization
|
|
|
- Barrie Waters
- 5 years ago
- Views:
Transcription
1 Stanford University, Management Science & Engineering (and ICME MS&E 318 (CME 338 Large-Scale Numerical Optimization 1 Origins Instructor: Michael Saunders Spring 2018 Notes 7: LUSOL: a Basis Factorization Package LUSOL is a set of procedures for computing and updating LU factors of a general sparse matrix A. The design aims follow: Allow A to be square or rectangular with arbitrary rank. Factorize A = LU directly, finding suitable row and column orderings. Replace a column or row of A. Add or delete a column or a row (thus altering the size of A. Perform a general rank-one update A A + vw T for sparse v and w. Balance stability and sparsity throughout, keeping L well-conditioned. The primary application of LUSOL has been for square basis factorizations B = LU (and column replacement as part of the optimization packages MINOS [14, 15, 16], SQOPT and SNOPT [7, 9], and the nonlinear complementarity packages MILES [20], PATH [3, 5], and PATHNLP [17]. In the optimization packages it is also applied to rectangular matrices ( B S (transposed to find a column ordering that makes B better conditioned [7]. The original LUSOL procedures are described by Gill, Murray, Saunders and Wright [8]. The main factorization uses a traditional Markowitz strategy with Threshold Partial Pivoting similar to other early sparse LU packages notably Y12M [24], LA05 [18], LA15 [19], MA28 [4] and MOPS [22]. The Bartels-Golub update for column-replacement follows the sparse implementation of Reid [18]. This involves a forward sweep of eliminations. The other updates are implemented similarly (some of them requiring a backward sweep. LUSOL has continued to evolve with the addition of rank-revealing LU factorizations for sparse matrices, using either Threshold Rook Pivoting or Threshold Complete Pivoting. A further option is intended for symmetric quasi-definite matrices [23]. The online source code [21] contains two versions (f77 and f90. The Fortran 77 version is suitable for f77, f90, and later compilers and convertible to C by the f2c translator. A Matlab interface is provided [13]. In 2004, a Fortran 77 Pascal C translation was created by Kjell Eikland for use within the open source LP/MILP system lp solve [12]. Since 2005 it has been lp solve s default basis factorization package (BFP. Since 2012, an f90 version of LUSOL has been running within a new f90 version of SQOPT, and it has a new Matlab interface [10]. In both f77 and f90 versions, the efficiency of rook pivoting was significantly improved in Purpose LUSOL maintains a sparse factorization A = LU and permutations P, Q such that P UQ is a sparse upper triangular (or upper trapezoidal matrix, stored explicitly as a set of sparse rows. Depending on input parameters, L tends to be well-conditioned, while the condition and rank of U reflect the condition and rank of A. The main functions of LUSOL follow: Factor Determine L, U, P, Q directly from A. The initial L = L 0 is such that P L 0 P T is a sparse lower triangular matrix with unit diagonals and bounded off-diagonals, stored explicitly as a set of sparse columns. The initial U 0 is stored explicitly as a set of sparse rows. 47
2 48 MS&E 318 (CME 338 Large-Scale Numerical Optimization Solve Given a dense vector y, use the current factors to solve one of the following systems: Lx = y, L T x = y, Ux = y, U T x = y, Ax = y, A T x = y. Multiply Given a dense vector y, use the factors to form one of the following products: x = Ly, x = L T y, x = Uy, x = U T y, x = Ay, x = A T y. Update Modify L, U, P, Q to reflect one of the following changes to A: Add a column, Replace a column, Delete a column, Add a row, Replace a row, Delete a row, Add a rank-one matrix σvw T. The initial L 0 is not altered but updates are accumulated in a product form L = L 0 M 1 M 2... M l for a sequence of stabilized elementary matrices M j. Updated U factors are maintained explicitly as sparse rows. 3 Factor The factorization procedure lu1fac receives A as a list of triples (i, j, A ij, where each A ij is typically nonzero. (Any zero or tiny elements are deleted. The nonzeros are sorted into a column list containing pointers to the start of each column and the corresponding column lengths (the number of entries. Contiguous storage is used for the entries in any given column, but if new entries arise during factorization, the whole column may be moved to another part of storage. A similar row list is constructed to store the sparsity structure of A by rows. To save storage the row list does not contain the numerical values themselves (although they would improve the efficiency of Threshold Rook Pivoting as mentioned below. Additional data structures are used to sort the columns and rows in order of increasing length. Each stage of the LU factorization computes l and u, the next column of L and the next row of U, using a nonzero A ij as pivot element : l = A.j /A ij, u T = A i., L [ L l ] [ ] U, U u T, A A lu T. Note that the ith row and jth column of A lu T are empty (zero. The data structure holding A has a decreasing number of rows and columns, but a certain amount of fill (new nonzeros may be generated by the rank-one term lu T. 3.1 Data structures The main LU factorization routine looks like this in Fortran 90: subroutine lu1fac( m, n, nelem, lena, luparm, parmlu, & a, indc, indr, p, q, & lenc, lenr, locc, locr, & iploc, iqloc, ipinv, iqinv, w, inform integer(ip, intent(in :: m, n, nelem, lena integer(ip, intent(inout :: luparm(30 integer(ip, intent(out :: inform real(rp, intent(inout :: parmlu(30, a(lena, w(n integer(ip, intent(inout :: indc(lena, indr(lena, & p(m, q(n, & lenc(n, lenr(m, & iploc(n, iqloc(m, & ipinv(m, iqinv(n, & locc(n, locr(m
3 Spring 2018, Notes 7 LUSOL 49 The nonzeros of A are input via parallel arrays a, indc, indr containing nelem triples (aij, i, j in any order. luparm and parmlu contain integer and double precision input parameters, and receive certain output values. During the LU factorization, the sparsity pattern of the remaining (modified A is stored twice, in a column list and a row list. The column list is (a, indc, locc, lenc, where a(* holds the nonzeros, indc(* holds the indices for the column list, locc(j points to the start of column j in a(* and indc(*, lenc(j is the number of nonzeros in column j. The row list is (indr, locr, lenr, where indr(* holds the indices for the row list, locr(i points to the start of row i in indr(*, lenr(i is the number of nonzeros in row i. At all stages, p and q contain complete row and column permutations P, Q. At the start of stage k, p(1,..., p(k-1 are the first k-1 rows of the final P. The remaining rows are stored in an ordered list (p, iploc, ipinv, where iploc(nz points to the start in p(* of the set of rows that currently contain nz nonzeros, ipinv(i points to the position of row i in p(*. iploc(1 = k (and this is where rows of length 1 begin, iploc(2 = k+r if there are r rows of length 1 (and this is where rows of length 2 begin, and so on up to iploc(n. There is a similar ordered list (q, iqloc, iqinv for the column permutation Q. At the end, the final factors are repacked so that L is stored columnwise counting backward from the end of (a, indc, indr, and U is stored rowwise counting forward from the beginning of (a, indc, indr. The array w has w(j 0 if column j seems to be dependent on the other columns. This is how we report singularity. 3.2 Pivot strategies To preserve sparsity, a Markowitz strategy is used to select potential pivots A ij. Pivots should have a low Markowitz merit function M ij (r i 1(c j 1, where r i and c j are the lengths of row i and column j of the current A, because M ij bounds the fill that could be created by lu T. The sparsest columns and rows are searched in turn (columns of length 1, rows of length 1, then columns of length 2, rows of length 2, and so on. The lowest M ij is recorded for pivots that satisfy a specified stability test. Typically only 5 or 10 of the shortest columns and rows are searched, but some of the stability tests may require more extensive searching. To preserve stability, one of the following threshold pivoting strategies is used. Let Ltol be a given number, typically 10 or 5 or perhaps nearer 1. (It controls the size of the offdiagonals of L and possibly those of U. Further, let A max be the largest remaining nonzero and D max the largest remaining diagonal (both absolute values. Strategy Name Stability Test Threshold Partial Pivoting TPP l Ltol Threshold Rook Pivoting TRP l and u/a ij Ltol Threshold Complete Pivoting TCP A max Ltol A ij Threshold Symmetric Pivoting TSP TRP for symmetric A Threshold Diagonal Pivoting TDP D max Ltol A ii
4 50 MS&E 318 (CME 338 Large-Scale Numerical Optimization In practice, TPP is used most often. It preserves sparsity well and is usually sufficiently stable with Ltol = 100 or 10. Smaller values are needed if A is singular or ill-conditioned and rank-revealing properties are desired. Ideally, any rank-deficiency should be identified by the correct number of small diagonals in U, but this is not guaranteed by TPP. The other options are needed for greater reliability in determining rank for example, in the Simplex Method when the first rather arbitrary B is factorized. TPP requires A ij to be sufficiently large compared to other elements in its own column. It can be implemented efficiently, and every column contains at least one entry that satisfies the test, so relatively few columns need be searched. It is convenient to store the largest element in each column in a known place (as the first entry in the column. TRP is symmetric in that A ij must be sufficiently large compared to other elements in its own column and its own row. It costs more than TPP (may require more searching and produce less sparse factors, but it has more definite rank-revealing properties and seems acceptably efficient with Ltol as low as 2 or even 1.1. TCP needs us to keep track of A max, the largest element in the current A. A heap structure is used to store the largest element in each column, and then A max is always at the top of the heap. TCP satisfies the TRP test but in a more restrictive way. If Ltol is too close to 1, the TCP factors are likely to be unacceptably dense. (Note that pathological examples are known for which TRP or even TCP fail to reveal rank correctly. TSP and TDP are intended for symmetric matrices that are either definite or quasidefinite. (In exact arithmetic, symmetric factorizations P AP T = LDL T exist for such matrices for any permutation P. TSP is implemented by pivoting on diagonals only and requiring l Ltol as for TPP. TDP needs D max, the largest remaining diagonal. It has not been implemented yet (and may not be needed. Another heap structure would be needed to store the diagonals A ii, so that D max is available at the top of the heap. The main benefit of TCP and TDP is that they concentrate singularities at the end of P and Q, so that P UQ will be upper trapezoidal. The other strategies may give small diagonals in any part of U (if A is singular. This often indicates singularity correctly, but the following matrix illustrates that TPP may be misleading: A = δ δ 1 1 δ 1, δ δ = 10 4 or 10 11, say. TPP would accept all diagonals and return L = I, U = A. LUSOL s singularity check would then report that all diagonals of U are big enough compared to other entries in their own column (rank(a = 4, or that all are too small (rank(a = 0!. In contrast, the rook pivoting strategy would reject all δ entries because they are too small compared to the other elements in their own column and row. Instead, TRP is likely to choose pivots from the first superdiagonal (effectively permuting the first column to the end. The result for both values of δ is P UQ δ 1 1 δ 2 1 δ 3, rank(a 3. δ Backward and forward triangles The strategy of searching columns of length 1 and then rows of length 1 automatically reveals the following structure in a typical sparse A. For some preliminary permutations P 1 and Q 1, the permuted matrix P 1 AQ 1 appears as in Figure 1, where ˆU 1 V is called the
5 Spring 2018, Notes 7 LUSOL 51 U 1 V P 1 AQ 1 = L 1 M B Figure 1: The backward and forward triangles in a typical sparse matrix» L1 backward triangle (the top rows of U and M is the forward triangle (the first columns of L. No elimination has occurred yet. It remains to compute LU factors of block B. 3.4 Sparse elimination A typical step in the LU factorization of block B is illustrated here. The Markowitz strategy has selected a pivot 1 in a reasonably sparse column and row, and this is regarded as large enough under the TPP stability test when Ltol 2.0. The merit function M 11 predicts that at most 2 3 = 6 new entries will be created in rows 2 3 and columns 2 4 (an over-estimate because 16, 1 and 5 are already nonzero. Note that all other rows and columns will be unaltered. TPP can pivot on 1 TRP can pivot on 4 TCP can pivot on Most of the complexity of lu1fac arises from updating the lists that hold the nonzeros. Recall that they are implemented as arrays (a, locc, lenc, indc for the column list and (locr, lenr, indr for the row list (sparsity structure only. When the pivot row is deleted from the column list (to become the first row of U, there is room in the modified columns for one new entry. In this example, one is sufficient and columns 2 4 can be updated in place. Similarly, when the pivot column is deleted from the row list, row 3 can be updated in place. However, row 2 has two new entries. All of row 2 must be moved to the beginning of the row list s free storage, and its previous space marked as unused. Thus, columns and rows can migrate around memory within their own lists, leaving gaps that are periodically compressed ( garbage collection. After most of the LU factors have been computed, the remaining rows and columns of the updated A will be sufficiently dense (say 50% to warrant a switch to dense processing.
6 52 MS&E 318 (CME 338 Large-Scale Numerical Optimization 4 Solve The current LUSOL procedures for solving Lx = y, Ux = y,... treat y as a dense vector. Solves with L 0 and L T 0 are the most efficient because the columns are processed in natural order (forwards or backwards and never altered. The product-form updates to L are handled reasonably efficiently (but each involves two arbitrary indices. Ideally, new options should be implemented in LUSOL to take advantage of sparse righthand sides y. For example, each iteration of Primal Simplex requires solution of Bv = a s, where a s is a column of A (with an average of only 5 or 10 entries regardless of the size of A. A significant cost in some simplex implementations lies in the most trivial operation: setting a dense vector to zero before unpacking a s. This is true even for m = 10, 000, and certainly for m = 1 million. Gilbert and Peierls [6] show how to solve a triangular system Lx = y in O(p operations, where p is the number of nonzero multiplications needed to form the product Lx. When y is sparse, p may be very small regardless of problem size. The true benefits of this technique have been realized in CPLEX; see Bixby [1]. The GP algorithm requires L to be stored by columns. In LUSOL, this means L 0 x = y, U0 T x = y and updated U T x = y could be solved efficiently. LA05 and LA15 maintain both the row and the column structure of U (and probably of L 0 also. They do take advantage of sparse y. 5 Multiply The Multiply procedures may be needed to recover parts of A from L and U if the original data has been over-written. Less trivially, products with L and L T are needed if an iterative solver (such as LSQR or LSMR is applied to a least-squares problem in the following way. Suppose A is rectangular (m > n with rank(a = n. A sparse factorization A = LU is typically cheaper than a QR factorization. To solve min Ax b 2 we may solve the equivalent problem min Ly b 2, Ux = y using the same iterative solver. Although L is typically less sparse than A, the pivoting strategies keep it well-conditioned even if A is not. Hence the solver may converge sufficiently quickly. Note that U is being used as a right-preconditioner, and we assumed A = LU accurately. If U is exact or just approximate, it may be more efficient to apply the iterative solver to the equivalent problem min AU 1 y b, Ux = y. 6 Update The main work for all updates comes from a forward or backward sweep of stabilized eliminations to triangularize a modified U. Forward sweeps tend to alter only a few rows of U. The most common update (Bartels- Golub-Reid column replacement requires a sparse column to be inserted into U (possibly altering several rows and then a forward sweep to eliminate the sparse row spike that appears, as mentioned in Notes 5. A multiple of one row of U can eliminate the first nonzero in the row spike. A test first determines whether the row of U should be swapped with the row spike (to become the new row spike. This is the stability/sparsity row interchange associated with Bartels, Golub, and Reid. Backward sweeps may alter many rows of U. They eliminate a column spike and generate a row spike that grows in length and must be added to several subsequent rows, with occasional row interchanges. The final row spike must be eliminated by a forward sweep. The more general updates are needed for symmetric matrices (such as KKT systems in active-set methods. They have not received much use, as block-lu updates have prevailed.
7 Spring 2018, Notes 7 LUSOL 53 7 Basis repair A vital use of LUSOL within MINOS, SQOPT, and SNOPT is to ensure that the current basis B is not too ill-conditioned. If necessary, certain columns of B can be replaced by unit vectors (associated with slack variables. The row and column permutations P and Q define which unit vectors should be introduced and which columns they should replace. BR factorization refers to the use of TRP (or TCP when the current B appears to be ill-conditioned (e.g., unexpected growth of x B or y has occurred or when it is important to ensure that B is reasonably well-conditioned (e.g., for the very first basis factorization, or at the start of each major iteration on problems with nonlinear constraints. The name BR indicates the Rank-Revealing requirement. The stability tolerance Ltol needs to be somewhat strict (say 2.5 and may need to be reduced in stages toward 1.0 if singularity persists. BS factorization is sometimes invoked to select a better B from the current basic and superbasic columns ( B S. Since the condition of L is always controlled, the factors ( B T = LU, P LP T = S T ( L1 L 2 I, P UQ = ( U1 0 are relevant. The first m rows of P point to the rows of (1, i.e., the columns of ( B S, that define a possibly better-conditioned basis B, to the extent that one exists: ( B S = ( B S P T. (1 On some regularly-structured problems, TPP with Ltol 2.0 is not reliable. We therefore apply BS factorization with TPP and Ltol = 1.9. Since ( B S may be significantly bigger than B, we use LUSOL s option to compute the permutations P and Q without storing L and U. Thus after BS factorization points to a suitable B, a normal factorization of B must be computed. If necessary, BR factorization is used to repair B. 8 A well-conditioned nullspace operator Z Given a rectangular matrix A (say m n with m < n and rank(a = m, we may need to find a matrix operator Z that spans the nullspace of A (thus AZ = 0, is reasonably wellconditioned, and permits efficient computation of p = Zv or q = Z T w from given vectors v and w. As with BS factorization in (1, we use TPP or TRP to factorize A T with Ltol < 2.0 to keep L well-conditioned: We see that A T = LU, P LP T = ( L1 L 1 A T = U P L 1 A T = P U = L 2 I, P UQ = ( U1. 0 ( U1 Q T ( 0 I P L 1 A T = 0. 0 ( ( 0 0 Hence AZ = 0 with Z L T P T I. Solving L T w = P T v gives us w = Zv, and solving Lw = t and setting s = ( 0 I P w gives us s = Z T t. This Z should be well-conditioned because L and hence L T are, and because Z is just some of the columns of L T. The lusolz package [11] provides Matlab software for computing the nullspace Z of the transpose of a sparse matrix S (so that S T Z = 0. It uses sparse QR or LU factors of either S or S T computed by SuiteSparseQR [2] or LUSOL [10]. Matlab routines are provided to compute products of the form w = Zv and s = Z T t for given vectors v and t.
8 54 MS&E 318 (CME 338 Large-Scale Numerical Optimization References [1] R. E. Bixby. Solving real-world linear programs: a decade and more of progress. Operations Research, 50(1:3 15, [2] T. A. Davis. Algorithm 915, SuiteSparseQR: Multifrontal multithreaded rank-revealing sparse QR factorization. ACM Trans. Math. Software, 38(1:8:1 22, [3] S. Dirkse, M. C. Ferris, and T. S. Munson. PATH nonlinear complementarity solver. cs.wisc.edu/ ferris/path.html, accessed May [4] I. S. Duff. MA28: A set of Fortran subroutines for sparse unsymmetric linear equations. Report R8730, AERE Harwell, Oxfordshire, England, [5] M. C. Ferris and T. S. Munson. PATH nonlinear complementarity solver. latest/docs/solvers/path/, accessed May [6] J. R. Gilbert and T. Peierls. Sparse partial pivoting in time proportional to arithmetic operations. SIAM J. Sci. and Statist. Comput., 9(5: , [7] P. E. Gill, W. Murray, and M. A. Saunders. SNOPT: An SQP algorithm for large-scale constrained optimization. SIAM Review, 47(1:99 131, SIGEST article. [8] P. E. Gill, W. Murray, M. A. Saunders, and M. H. Wright. Maintaining LU factors of a general sparse matrix. Linear Algebra and its Applications, 88/89: , [9] Philip E. Gill, Walter Murray, Michael A. Saunders, and Elizabeth Wong. User s Guide for SNOPT 7.7: Software for Large-Scale Nonlinear Programming. Center for Computational Mathematics Report CCoM 18-1, Department of Mathematics, University of California, San Diego, La Jolla, CA, [10] N. W. Henderson. Matlab interface to LUSOL [11] N. W. Henderson, S. Kim, D. Ma, M. A. Saunders, Y. Sun, R. M. T. Fleming, and I. Thiele. lusolz: Nullspace of sparse matrix via SPQR or LUSOL. [12] lp solve open source LP and MILP solver. solve/. [13] LUSOL mex interface (Nick Henderson, ICME, Stanford University. mex, [14] B. A. Murtagh and M. A. Saunders. Large-scale linearly constrained optimization. Math. Program., 14:41 72, [15] B. A. Murtagh and M. A. Saunders. A projected Lagrangian algorithm and its implementation for sparse nonlinear constraints. Math. Program. Study, 16:84 117, [16] B. A. Murtagh and M. A. Saunders. MINOS nonlinear optimization solver. latest/docs/solvers/minos/, accessed May [17] PATH nonlinear complementarity solver. accessed May [18] J. K. Reid. A sparsity-exploiting variant of the Bartels-Golub decomposition for linear programming bases. Math. Program., 24:55 69, [19] J. K. Reid. LA15 basis factorization package (thread-safe version of LA05. HSL Catalogue, (original version 2001; version dated 9 April [20] T. F. Rutherford. MILES nonlinear complementarity solver. miles/, accessed May [21] SOL downloadable software. [22] U. Suhl and L. Suhl. Computing sparse LU-factorizations for large-scale linear programming bases. ORSA J. of Computing, 2: , [23] R. J. Vanderbei. Symmetric quasi-definite matrices. SIAM J. Optim., 5: , [24] Z. Zlatev, J. Wasniewski, and K. Schaumburg. Y12M: Solution of Large and Sparse Systems of Linear Algebraic Equations. Lecture Notes in Computer Science 121. Springer Verlag, Berlin, Heidelberg, New York, 1981.
LUSOL: A basis package for constrained optimization
 LUSOL: A basis package for constrained optimization IFORS Triennial Conference on OR/MS Honolulu, HI, July 11 15, 2005 Michael O Sullivan and Michael Saunders Dept of Engineering Science Dept of Management
LUSOL: A basis package for constrained optimization IFORS Triennial Conference on OR/MS Honolulu, HI, July 11 15, 2005 Michael O Sullivan and Michael Saunders Dept of Engineering Science Dept of Management
A review of sparsity vs stability in LU updates
 A review of sparsity vs stability in LU updates Michael Saunders Dept of Management Science and Engineering (MS&E) Systems Optimization Laboratory (SOL) Institute for Computational Mathematics and Engineering
A review of sparsity vs stability in LU updates Michael Saunders Dept of Management Science and Engineering (MS&E) Systems Optimization Laboratory (SOL) Institute for Computational Mathematics and Engineering
Sparse Rank-Revealing LU Factorization
 Sparse Rank-Revealing LU Factorization Householder Symposium XV on Numerical Linear Algebra Peebles, Scotland, June 2002 Michael O Sullivan and Michael Saunders Dept of Engineering Science Dept of Management
Sparse Rank-Revealing LU Factorization Householder Symposium XV on Numerical Linear Algebra Peebles, Scotland, June 2002 Michael O Sullivan and Michael Saunders Dept of Engineering Science Dept of Management
Sparse Rank-Revealing LU Factorization
 Sparse Rank-Revealing LU Factorization SIAM Conference on Optimization Toronto, May 2002 Michael O Sullivan and Michael Saunders Dept of Engineering Science Dept of Management Sci & Eng University of Auckland
Sparse Rank-Revealing LU Factorization SIAM Conference on Optimization Toronto, May 2002 Michael O Sullivan and Michael Saunders Dept of Engineering Science Dept of Management Sci & Eng University of Auckland
A convex QP solver based on block-lu updates
 Block-LU updates p. 1/24 A convex QP solver based on block-lu updates PP06 SIAM Conference on Parallel Processing for Scientific Computing San Francisco, CA, Feb 22 24, 2006 Hanh Huynh and Michael Saunders
Block-LU updates p. 1/24 A convex QP solver based on block-lu updates PP06 SIAM Conference on Parallel Processing for Scientific Computing San Francisco, CA, Feb 22 24, 2006 Hanh Huynh and Michael Saunders
MS&E 318 (CME 338) Large-Scale Numerical Optimization
 Stanford University, Management Science & Engineering (and ICME MS&E 38 (CME 338 Large-Scale Numerical Optimization Course description Instructor: Michael Saunders Spring 28 Notes : Review The course teaches
Stanford University, Management Science & Engineering (and ICME MS&E 38 (CME 338 Large-Scale Numerical Optimization Course description Instructor: Michael Saunders Spring 28 Notes : Review The course teaches
Satisfying Flux Balance and Mass-Action Kinetics in a Network of Biochemical Reactions
 Satisfying Flux Balance and Mass-Action Kinetics in a Network of Biochemical Reactions Speakers Senior Personnel Collaborators Michael Saunders and Ines Thiele Ronan Fleming, Bernhard Palsson, Yinyu Ye
Satisfying Flux Balance and Mass-Action Kinetics in a Network of Biochemical Reactions Speakers Senior Personnel Collaborators Michael Saunders and Ines Thiele Ronan Fleming, Bernhard Palsson, Yinyu Ye
Implementation of a KKT-based active-set QP solver
 Block-LU updates p. 1/27 Implementation of a KKT-based active-set QP solver ISMP 2006 19th International Symposium on Mathematical Programming Rio de Janeiro, Brazil, July 30 August 4, 2006 Hanh Huynh
Block-LU updates p. 1/27 Implementation of a KKT-based active-set QP solver ISMP 2006 19th International Symposium on Mathematical Programming Rio de Janeiro, Brazil, July 30 August 4, 2006 Hanh Huynh
MS&E 318 (CME 338) Large-Scale Numerical Optimization
 Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization Instructor: Michael Saunders Spring 2015 Notes 11: NPSOL and SNOPT SQP Methods 1 Overview
Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization Instructor: Michael Saunders Spring 2015 Notes 11: NPSOL and SNOPT SQP Methods 1 Overview
MS&E 318 (CME 338) Large-Scale Numerical Optimization
 Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization 1 Origins Instructor: Michael Saunders Spring 2015 Notes 9: Augmented Lagrangian Methods
Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization 1 Origins Instructor: Michael Saunders Spring 2015 Notes 9: Augmented Lagrangian Methods
MS&E 318 (CME 338) Large-Scale Numerical Optimization
 Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization Instructor: Michael Saunders Spring 2015 Notes 4: The Primal Simplex Method 1 Linear
Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization Instructor: Michael Saunders Spring 2015 Notes 4: The Primal Simplex Method 1 Linear
Ax=b. Zack 10/4/2013
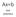 Ax=b Zack 10/4/2013 Iteration method Ax=b v 1, v 2 x k = V k y k Given (A, b) standard orthonormal base v 1, v 2 x k = V k y k For symmetric A, the method to generate V k is called Lanczos Method Lanczos
Ax=b Zack 10/4/2013 Iteration method Ax=b v 1, v 2 x k = V k y k Given (A, b) standard orthonormal base v 1, v 2 x k = V k y k For symmetric A, the method to generate V k is called Lanczos Method Lanczos
Key words. numerical linear algebra, direct methods, Cholesky factorization, sparse matrices, mathematical software, matrix updates.
 ROW MODIFICATIONS OF A SPARSE CHOLESKY FACTORIZATION TIMOTHY A. DAVIS AND WILLIAM W. HAGER Abstract. Given a sparse, symmetric positive definite matrix C and an associated sparse Cholesky factorization
ROW MODIFICATIONS OF A SPARSE CHOLESKY FACTORIZATION TIMOTHY A. DAVIS AND WILLIAM W. HAGER Abstract. Given a sparse, symmetric positive definite matrix C and an associated sparse Cholesky factorization
MS&E 318 (CME 338) Large-Scale Numerical Optimization
 Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization Instructor: Michael Saunders Spring 2017 Notes 10: MINOS Part 1: the Reduced-Gradient
Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization Instructor: Michael Saunders Spring 2017 Notes 10: MINOS Part 1: the Reduced-Gradient
Revised Simplex Method
 DM545 Linear and Integer Programming Lecture 7 Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. 2. 2 Motivation Complexity of single pivot operation
DM545 Linear and Integer Programming Lecture 7 Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. 2. 2 Motivation Complexity of single pivot operation
Scientific Computing
 Scientific Computing Direct solution methods Martin van Gijzen Delft University of Technology October 3, 2018 1 Program October 3 Matrix norms LU decomposition Basic algorithm Cost Stability Pivoting Pivoting
Scientific Computing Direct solution methods Martin van Gijzen Delft University of Technology October 3, 2018 1 Program October 3 Matrix norms LU decomposition Basic algorithm Cost Stability Pivoting Pivoting
Linear Algebra Section 2.6 : LU Decomposition Section 2.7 : Permutations and transposes Wednesday, February 13th Math 301 Week #4
 Linear Algebra Section. : LU Decomposition Section. : Permutations and transposes Wednesday, February 1th Math 01 Week # 1 The LU Decomposition We learned last time that we can factor a invertible matrix
Linear Algebra Section. : LU Decomposition Section. : Permutations and transposes Wednesday, February 1th Math 01 Week # 1 The LU Decomposition We learned last time that we can factor a invertible matrix
Review Questions REVIEW QUESTIONS 71
 REVIEW QUESTIONS 71 MATLAB, is [42]. For a comprehensive treatment of error analysis and perturbation theory for linear systems and many other problems in linear algebra, see [126, 241]. An overview of
REVIEW QUESTIONS 71 MATLAB, is [42]. For a comprehensive treatment of error analysis and perturbation theory for linear systems and many other problems in linear algebra, see [126, 241]. An overview of
CME 302: NUMERICAL LINEAR ALGEBRA FALL 2005/06 LECTURE 6
 CME 302: NUMERICAL LINEAR ALGEBRA FALL 2005/06 LECTURE 6 GENE H GOLUB Issues with Floating-point Arithmetic We conclude our discussion of floating-point arithmetic by highlighting two issues that frequently
CME 302: NUMERICAL LINEAR ALGEBRA FALL 2005/06 LECTURE 6 GENE H GOLUB Issues with Floating-point Arithmetic We conclude our discussion of floating-point arithmetic by highlighting two issues that frequently
Pivoting. Reading: GV96 Section 3.4, Stew98 Chapter 3: 1.3
 Pivoting Reading: GV96 Section 3.4, Stew98 Chapter 3: 1.3 In the previous discussions we have assumed that the LU factorization of A existed and the various versions could compute it in a stable manner.
Pivoting Reading: GV96 Section 3.4, Stew98 Chapter 3: 1.3 In the previous discussions we have assumed that the LU factorization of A existed and the various versions could compute it in a stable manner.
(17) (18)
 Module 4 : Solving Linear Algebraic Equations Section 3 : Direct Solution Techniques 3 Direct Solution Techniques Methods for solving linear algebraic equations can be categorized as direct and iterative
Module 4 : Solving Linear Algebraic Equations Section 3 : Direct Solution Techniques 3 Direct Solution Techniques Methods for solving linear algebraic equations can be categorized as direct and iterative
SMO vs PDCO for SVM: Sequential Minimal Optimization vs Primal-Dual interior method for Convex Objectives for Support Vector Machines
 vs for SVM: Sequential Minimal Optimization vs Primal-Dual interior method for Convex Objectives for Support Vector Machines Ding Ma Michael Saunders Working paper, January 5 Introduction In machine learning,
vs for SVM: Sequential Minimal Optimization vs Primal-Dual interior method for Convex Objectives for Support Vector Machines Ding Ma Michael Saunders Working paper, January 5 Introduction In machine learning,
Bindel, Fall 2016 Matrix Computations (CS 6210) Notes for
 1 Logistics Notes for 2016-09-14 1. There was a goof in HW 2, problem 1 (now fixed) please re-download if you have already started looking at it. 2. CS colloquium (4:15 in Gates G01) this Thurs is Margaret
1 Logistics Notes for 2016-09-14 1. There was a goof in HW 2, problem 1 (now fixed) please re-download if you have already started looking at it. 2. CS colloquium (4:15 in Gates G01) this Thurs is Margaret
Linear Equations in Linear Algebra
 1 Linear Equations in Linear Algebra 1.1 SYSTEMS OF LINEAR EQUATIONS LINEAR EQUATION x 1,, x n A linear equation in the variables equation that can be written in the form a 1 x 1 + a 2 x 2 + + a n x n
1 Linear Equations in Linear Algebra 1.1 SYSTEMS OF LINEAR EQUATIONS LINEAR EQUATION x 1,, x n A linear equation in the variables equation that can be written in the form a 1 x 1 + a 2 x 2 + + a n x n
Downloaded 08/28/12 to Redistribution subject to SIAM license or copyright; see
 SIAM J. MATRIX ANAL. APPL. Vol. 26, No. 3, pp. 621 639 c 2005 Society for Industrial and Applied Mathematics ROW MODIFICATIONS OF A SPARSE CHOLESKY FACTORIZATION TIMOTHY A. DAVIS AND WILLIAM W. HAGER Abstract.
SIAM J. MATRIX ANAL. APPL. Vol. 26, No. 3, pp. 621 639 c 2005 Society for Industrial and Applied Mathematics ROW MODIFICATIONS OF A SPARSE CHOLESKY FACTORIZATION TIMOTHY A. DAVIS AND WILLIAM W. HAGER Abstract.
Chapter 8 Cholesky-based Methods for Sparse Least Squares: The Benefits of Regularization
 In L. Adams and J. L. Nazareth eds., Linear and Nonlinear Conjugate Gradient-Related Methods, SIAM, Philadelphia, 92 100 1996. Chapter 8 Cholesky-based Methods for Sparse Least Squares: The Benefits of
In L. Adams and J. L. Nazareth eds., Linear and Nonlinear Conjugate Gradient-Related Methods, SIAM, Philadelphia, 92 100 1996. Chapter 8 Cholesky-based Methods for Sparse Least Squares: The Benefits of
Matrix decompositions
 Matrix decompositions How can we solve Ax = b? 1 Linear algebra Typical linear system of equations : x 1 x +x = x 1 +x +9x = 0 x 1 +x x = The variables x 1, x, and x only appear as linear terms (no powers
Matrix decompositions How can we solve Ax = b? 1 Linear algebra Typical linear system of equations : x 1 x +x = x 1 +x +9x = 0 x 1 +x x = The variables x 1, x, and x only appear as linear terms (no powers
Numerical Linear Algebra
 Numerical Linear Algebra Decompositions, numerical aspects Gerard Sleijpen and Martin van Gijzen September 27, 2017 1 Delft University of Technology Program Lecture 2 LU-decomposition Basic algorithm Cost
Numerical Linear Algebra Decompositions, numerical aspects Gerard Sleijpen and Martin van Gijzen September 27, 2017 1 Delft University of Technology Program Lecture 2 LU-decomposition Basic algorithm Cost
Program Lecture 2. Numerical Linear Algebra. Gaussian elimination (2) Gaussian elimination. Decompositions, numerical aspects
 Numerical Linear Algebra Decompositions, numerical aspects Program Lecture 2 LU-decomposition Basic algorithm Cost Stability Pivoting Cholesky decomposition Sparse matrices and reorderings Gerard Sleijpen
Numerical Linear Algebra Decompositions, numerical aspects Program Lecture 2 LU-decomposition Basic algorithm Cost Stability Pivoting Cholesky decomposition Sparse matrices and reorderings Gerard Sleijpen
What s New in Active-Set Methods for Nonlinear Optimization?
 What s New in Active-Set Methods for Nonlinear Optimization? Philip E. Gill Advances in Numerical Computation, Manchester University, July 5, 2011 A Workshop in Honor of Sven Hammarling UCSD Center for
What s New in Active-Set Methods for Nonlinear Optimization? Philip E. Gill Advances in Numerical Computation, Manchester University, July 5, 2011 A Workshop in Honor of Sven Hammarling UCSD Center for
CS227-Scientific Computing. Lecture 4: A Crash Course in Linear Algebra
 CS227-Scientific Computing Lecture 4: A Crash Course in Linear Algebra Linear Transformation of Variables A common phenomenon: Two sets of quantities linearly related: y = 3x + x 2 4x 3 y 2 = 2.7x 2 x
CS227-Scientific Computing Lecture 4: A Crash Course in Linear Algebra Linear Transformation of Variables A common phenomenon: Two sets of quantities linearly related: y = 3x + x 2 4x 3 y 2 = 2.7x 2 x
Linear Algebra Linear Algebra : Matrix decompositions Monday, February 11th Math 365 Week #4
 Linear Algebra Linear Algebra : Matrix decompositions Monday, February 11th Math Week # 1 Saturday, February 1, 1 Linear algebra Typical linear system of equations : x 1 x +x = x 1 +x +9x = 0 x 1 +x x
Linear Algebra Linear Algebra : Matrix decompositions Monday, February 11th Math Week # 1 Saturday, February 1, 1 Linear algebra Typical linear system of equations : x 1 x +x = x 1 +x +9x = 0 x 1 +x x
Matrix decompositions
 Matrix decompositions How can we solve Ax = b? 1 Linear algebra Typical linear system of equations : x 1 x +x = x 1 +x +9x = 0 x 1 +x x = The variables x 1, x, and x only appear as linear terms (no powers
Matrix decompositions How can we solve Ax = b? 1 Linear algebra Typical linear system of equations : x 1 x +x = x 1 +x +9x = 0 x 1 +x x = The variables x 1, x, and x only appear as linear terms (no powers
Linear Programming: Simplex
 Linear Programming: Simplex Stephen J. Wright 1 2 Computer Sciences Department, University of Wisconsin-Madison. IMA, August 2016 Stephen Wright (UW-Madison) Linear Programming: Simplex IMA, August 2016
Linear Programming: Simplex Stephen J. Wright 1 2 Computer Sciences Department, University of Wisconsin-Madison. IMA, August 2016 Stephen Wright (UW-Madison) Linear Programming: Simplex IMA, August 2016
Linear Programming The Simplex Algorithm: Part II Chapter 5
 1 Linear Programming The Simplex Algorithm: Part II Chapter 5 University of Chicago Booth School of Business Kipp Martin October 17, 2017 Outline List of Files Key Concepts Revised Simplex Revised Simplex
1 Linear Programming The Simplex Algorithm: Part II Chapter 5 University of Chicago Booth School of Business Kipp Martin October 17, 2017 Outline List of Files Key Concepts Revised Simplex Revised Simplex
MATH 3511 Lecture 1. Solving Linear Systems 1
 MATH 3511 Lecture 1 Solving Linear Systems 1 Dmitriy Leykekhman Spring 2012 Goals Review of basic linear algebra Solution of simple linear systems Gaussian elimination D Leykekhman - MATH 3511 Introduction
MATH 3511 Lecture 1 Solving Linear Systems 1 Dmitriy Leykekhman Spring 2012 Goals Review of basic linear algebra Solution of simple linear systems Gaussian elimination D Leykekhman - MATH 3511 Introduction
Numerical Linear Algebra
 Numerical Linear Algebra Direct Methods Philippe B. Laval KSU Fall 2017 Philippe B. Laval (KSU) Linear Systems: Direct Solution Methods Fall 2017 1 / 14 Introduction The solution of linear systems is one
Numerical Linear Algebra Direct Methods Philippe B. Laval KSU Fall 2017 Philippe B. Laval (KSU) Linear Systems: Direct Solution Methods Fall 2017 1 / 14 Introduction The solution of linear systems is one
Matrix Assembly in FEA
 Matrix Assembly in FEA 1 In Chapter 2, we spoke about how the global matrix equations are assembled in the finite element method. We now want to revisit that discussion and add some details. For example,
Matrix Assembly in FEA 1 In Chapter 2, we spoke about how the global matrix equations are assembled in the finite element method. We now want to revisit that discussion and add some details. For example,
Section 3.5 LU Decomposition (Factorization) Key terms. Matrix factorization Forward and back substitution LU-decomposition Storage economization
 Section 3.5 LU Decomposition (Factorization) Key terms Matrix factorization Forward and back substitution LU-decomposition Storage economization In matrix analysis as implemented in modern software the
Section 3.5 LU Decomposition (Factorization) Key terms Matrix factorization Forward and back substitution LU-decomposition Storage economization In matrix analysis as implemented in modern software the
MTH 464: Computational Linear Algebra
 MTH 464: Computational Linear Algebra Lecture Outlines Exam 2 Material Prof. M. Beauregard Department of Mathematics & Statistics Stephen F. Austin State University February 6, 2018 Linear Algebra (MTH
MTH 464: Computational Linear Algebra Lecture Outlines Exam 2 Material Prof. M. Beauregard Department of Mathematics & Statistics Stephen F. Austin State University February 6, 2018 Linear Algebra (MTH
B553 Lecture 5: Matrix Algebra Review
 B553 Lecture 5: Matrix Algebra Review Kris Hauser January 19, 2012 We have seen in prior lectures how vectors represent points in R n and gradients of functions. Matrices represent linear transformations
B553 Lecture 5: Matrix Algebra Review Kris Hauser January 19, 2012 We have seen in prior lectures how vectors represent points in R n and gradients of functions. Matrices represent linear transformations
STAT 309: MATHEMATICAL COMPUTATIONS I FALL 2018 LECTURE 13
 STAT 309: MATHEMATICAL COMPUTATIONS I FALL 208 LECTURE 3 need for pivoting we saw that under proper circumstances, we can write A LU where 0 0 0 u u 2 u n l 2 0 0 0 u 22 u 2n L l 3 l 32, U 0 0 0 l n l
STAT 309: MATHEMATICAL COMPUTATIONS I FALL 208 LECTURE 3 need for pivoting we saw that under proper circumstances, we can write A LU where 0 0 0 u u 2 u n l 2 0 0 0 u 22 u 2n L l 3 l 32, U 0 0 0 l n l
Scientific Computing: An Introductory Survey
 Scientific Computing: An Introductory Survey Chapter 2 Systems of Linear Equations Prof. Michael T. Heath Department of Computer Science University of Illinois at Urbana-Champaign Copyright c 2002. Reproduction
Scientific Computing: An Introductory Survey Chapter 2 Systems of Linear Equations Prof. Michael T. Heath Department of Computer Science University of Illinois at Urbana-Champaign Copyright c 2002. Reproduction
Gaussian Elimination and Back Substitution
 Jim Lambers MAT 610 Summer Session 2009-10 Lecture 4 Notes These notes correspond to Sections 31 and 32 in the text Gaussian Elimination and Back Substitution The basic idea behind methods for solving
Jim Lambers MAT 610 Summer Session 2009-10 Lecture 4 Notes These notes correspond to Sections 31 and 32 in the text Gaussian Elimination and Back Substitution The basic idea behind methods for solving
DM545 Linear and Integer Programming. Lecture 7 Revised Simplex Method. Marco Chiarandini
 DM545 Linear and Integer Programming Lecture 7 Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. 2. 2 Motivation Complexity of single pivot operation
DM545 Linear and Integer Programming Lecture 7 Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. 2. 2 Motivation Complexity of single pivot operation
Solution of Linear Equations
 Solution of Linear Equations (Com S 477/577 Notes) Yan-Bin Jia Sep 7, 07 We have discussed general methods for solving arbitrary equations, and looked at the special class of polynomial equations A subclass
Solution of Linear Equations (Com S 477/577 Notes) Yan-Bin Jia Sep 7, 07 We have discussed general methods for solving arbitrary equations, and looked at the special class of polynomial equations A subclass
Introduction to Mathematical Programming
 Introduction to Mathematical Programming Ming Zhong Lecture 6 September 12, 2018 Ming Zhong (JHU) AMS Fall 2018 1 / 20 Table of Contents 1 Ming Zhong (JHU) AMS Fall 2018 2 / 20 Solving Linear Systems A
Introduction to Mathematical Programming Ming Zhong Lecture 6 September 12, 2018 Ming Zhong (JHU) AMS Fall 2018 1 / 20 Table of Contents 1 Ming Zhong (JHU) AMS Fall 2018 2 / 20 Solving Linear Systems A
LU Factorization. LU factorization is the most common way of solving linear systems! Ax = b LUx = b
 AM 205: lecture 7 Last time: LU factorization Today s lecture: Cholesky factorization, timing, QR factorization Reminder: assignment 1 due at 5 PM on Friday September 22 LU Factorization LU factorization
AM 205: lecture 7 Last time: LU factorization Today s lecture: Cholesky factorization, timing, QR factorization Reminder: assignment 1 due at 5 PM on Friday September 22 LU Factorization LU factorization
The antitriangular factorisation of saddle point matrices
 The antitriangular factorisation of saddle point matrices J. Pestana and A. J. Wathen August 29, 2013 Abstract Mastronardi and Van Dooren [this journal, 34 (2013) pp. 173 196] recently introduced the block
The antitriangular factorisation of saddle point matrices J. Pestana and A. J. Wathen August 29, 2013 Abstract Mastronardi and Van Dooren [this journal, 34 (2013) pp. 173 196] recently introduced the block
Algebraic Equations. 2.0 Introduction. Nonsingular versus Singular Sets of Equations. A set of linear algebraic equations looks like this:
 Chapter 2. 2.0 Introduction Solution of Linear Algebraic Equations A set of linear algebraic equations looks like this: a 11 x 1 + a 12 x 2 + a 13 x 3 + +a 1N x N =b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 +
Chapter 2. 2.0 Introduction Solution of Linear Algebraic Equations A set of linear algebraic equations looks like this: a 11 x 1 + a 12 x 2 + a 13 x 3 + +a 1N x N =b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 +
9. Numerical linear algebra background
 Convex Optimization Boyd & Vandenberghe 9. Numerical linear algebra background matrix structure and algorithm complexity solving linear equations with factored matrices LU, Cholesky, LDL T factorization
Convex Optimization Boyd & Vandenberghe 9. Numerical linear algebra background matrix structure and algorithm complexity solving linear equations with factored matrices LU, Cholesky, LDL T factorization
CS412: Lecture #17. Mridul Aanjaneya. March 19, 2015
 CS: Lecture #7 Mridul Aanjaneya March 9, 5 Solving linear systems of equations Consider a lower triangular matrix L: l l l L = l 3 l 3 l 33 l n l nn A procedure similar to that for upper triangular systems
CS: Lecture #7 Mridul Aanjaneya March 9, 5 Solving linear systems of equations Consider a lower triangular matrix L: l l l L = l 3 l 3 l 33 l n l nn A procedure similar to that for upper triangular systems
Lecture Notes to Accompany. Scientific Computing An Introductory Survey. by Michael T. Heath. Chapter 2. Systems of Linear Equations
 Lecture Notes to Accompany Scientific Computing An Introductory Survey Second Edition by Michael T. Heath Chapter 2 Systems of Linear Equations Copyright c 2001. Reproduction permitted only for noncommercial,
Lecture Notes to Accompany Scientific Computing An Introductory Survey Second Edition by Michael T. Heath Chapter 2 Systems of Linear Equations Copyright c 2001. Reproduction permitted only for noncommercial,
1.Chapter Objectives
 LU Factorization INDEX 1.Chapter objectives 2.Overview of LU factorization 2.1GAUSS ELIMINATION AS LU FACTORIZATION 2.2LU Factorization with Pivoting 2.3 MATLAB Function: lu 3. CHOLESKY FACTORIZATION 3.1
LU Factorization INDEX 1.Chapter objectives 2.Overview of LU factorization 2.1GAUSS ELIMINATION AS LU FACTORIZATION 2.2LU Factorization with Pivoting 2.3 MATLAB Function: lu 3. CHOLESKY FACTORIZATION 3.1
5.1 Banded Storage. u = temperature. The five-point difference operator. uh (x, y + h) 2u h (x, y)+u h (x, y h) uh (x + h, y) 2u h (x, y)+u h (x h, y)
 5.1 Banded Storage u = temperature u= u h temperature at gridpoints u h = 1 u= Laplace s equation u= h u = u h = grid size u=1 The five-point difference operator 1 u h =1 uh (x + h, y) 2u h (x, y)+u h
5.1 Banded Storage u = temperature u= u h temperature at gridpoints u h = 1 u= Laplace s equation u= h u = u h = grid size u=1 The five-point difference operator 1 u h =1 uh (x + h, y) 2u h (x, y)+u h
Reduced-Hessian Methods for Constrained Optimization
 Reduced-Hessian Methods for Constrained Optimization Philip E. Gill University of California, San Diego Joint work with: Michael Ferry & Elizabeth Wong 11th US & Mexico Workshop on Optimization and its
Reduced-Hessian Methods for Constrained Optimization Philip E. Gill University of California, San Diego Joint work with: Michael Ferry & Elizabeth Wong 11th US & Mexico Workshop on Optimization and its
Numerical Linear Algebra
 Chapter 3 Numerical Linear Algebra We review some techniques used to solve Ax = b where A is an n n matrix, and x and b are n 1 vectors (column vectors). We then review eigenvalues and eigenvectors and
Chapter 3 Numerical Linear Algebra We review some techniques used to solve Ax = b where A is an n n matrix, and x and b are n 1 vectors (column vectors). We then review eigenvalues and eigenvectors and
Lecture 12 (Tue, Mar 5) Gaussian elimination and LU factorization (II)
 Math 59 Lecture 2 (Tue Mar 5) Gaussian elimination and LU factorization (II) 2 Gaussian elimination - LU factorization For a general n n matrix A the Gaussian elimination produces an LU factorization if
Math 59 Lecture 2 (Tue Mar 5) Gaussian elimination and LU factorization (II) 2 Gaussian elimination - LU factorization For a general n n matrix A the Gaussian elimination produces an LU factorization if
Practical Linear Algebra: A Geometry Toolbox
 Practical Linear Algebra: A Geometry Toolbox Third edition Chapter 12: Gauss for Linear Systems Gerald Farin & Dianne Hansford CRC Press, Taylor & Francis Group, An A K Peters Book www.farinhansford.com/books/pla
Practical Linear Algebra: A Geometry Toolbox Third edition Chapter 12: Gauss for Linear Systems Gerald Farin & Dianne Hansford CRC Press, Taylor & Francis Group, An A K Peters Book www.farinhansford.com/books/pla
Computational Methods. Systems of Linear Equations
 Computational Methods Systems of Linear Equations Manfred Huber 2010 1 Systems of Equations Often a system model contains multiple variables (parameters) and contains multiple equations Multiple equations
Computational Methods Systems of Linear Equations Manfred Huber 2010 1 Systems of Equations Often a system model contains multiple variables (parameters) and contains multiple equations Multiple equations
This can be accomplished by left matrix multiplication as follows: I
 1 Numerical Linear Algebra 11 The LU Factorization Recall from linear algebra that Gaussian elimination is a method for solving linear systems of the form Ax = b, where A R m n and bran(a) In this method
1 Numerical Linear Algebra 11 The LU Factorization Recall from linear algebra that Gaussian elimination is a method for solving linear systems of the form Ax = b, where A R m n and bran(a) In this method
Linear Systems of n equations for n unknowns
 Linear Systems of n equations for n unknowns In many application problems we want to find n unknowns, and we have n linear equations Example: Find x,x,x such that the following three equations hold: x
Linear Systems of n equations for n unknowns In many application problems we want to find n unknowns, and we have n linear equations Example: Find x,x,x such that the following three equations hold: x
LAPACK-Style Codes for Pivoted Cholesky and QR Updating. Hammarling, Sven and Higham, Nicholas J. and Lucas, Craig. MIMS EPrint: 2006.
 LAPACK-Style Codes for Pivoted Cholesky and QR Updating Hammarling, Sven and Higham, Nicholas J. and Lucas, Craig 2007 MIMS EPrint: 2006.385 Manchester Institute for Mathematical Sciences School of Mathematics
LAPACK-Style Codes for Pivoted Cholesky and QR Updating Hammarling, Sven and Higham, Nicholas J. and Lucas, Craig 2007 MIMS EPrint: 2006.385 Manchester Institute for Mathematical Sciences School of Mathematics
1 Multiply Eq. E i by λ 0: (λe i ) (E i ) 2 Multiply Eq. E j by λ and add to Eq. E i : (E i + λe j ) (E i )
 Direct Methods for Linear Systems Chapter Direct Methods for Solving Linear Systems Per-Olof Persson persson@berkeleyedu Department of Mathematics University of California, Berkeley Math 18A Numerical
Direct Methods for Linear Systems Chapter Direct Methods for Solving Linear Systems Per-Olof Persson persson@berkeleyedu Department of Mathematics University of California, Berkeley Math 18A Numerical
9. Numerical linear algebra background
 Convex Optimization Boyd & Vandenberghe 9. Numerical linear algebra background matrix structure and algorithm complexity solving linear equations with factored matrices LU, Cholesky, LDL T factorization
Convex Optimization Boyd & Vandenberghe 9. Numerical linear algebra background matrix structure and algorithm complexity solving linear equations with factored matrices LU, Cholesky, LDL T factorization
Numerical Methods I: Numerical linear algebra
 1/3 Numerical Methods I: Numerical linear algebra Georg Stadler Courant Institute, NYU stadler@cimsnyuedu September 1, 017 /3 We study the solution of linear systems of the form Ax = b with A R n n, x,
1/3 Numerical Methods I: Numerical linear algebra Georg Stadler Courant Institute, NYU stadler@cimsnyuedu September 1, 017 /3 We study the solution of linear systems of the form Ax = b with A R n n, x,
Sparse BLAS-3 Reduction
 Sparse BLAS-3 Reduction to Banded Upper Triangular (Spar3Bnd) Gary Howell, HPC/OIT NC State University gary howell@ncsu.edu Sparse BLAS-3 Reduction p.1/27 Acknowledgements James Demmel, Gene Golub, Franc
Sparse BLAS-3 Reduction to Banded Upper Triangular (Spar3Bnd) Gary Howell, HPC/OIT NC State University gary howell@ncsu.edu Sparse BLAS-3 Reduction p.1/27 Acknowledgements James Demmel, Gene Golub, Franc
Applied Linear Algebra in Geoscience Using MATLAB
 Applied Linear Algebra in Geoscience Using MATLAB Contents Getting Started Creating Arrays Mathematical Operations with Arrays Using Script Files and Managing Data Two-Dimensional Plots Programming in
Applied Linear Algebra in Geoscience Using MATLAB Contents Getting Started Creating Arrays Mathematical Operations with Arrays Using Script Files and Managing Data Two-Dimensional Plots Programming in
Lecture 9: Numerical Linear Algebra Primer (February 11st)
 10-725/36-725: Convex Optimization Spring 2015 Lecture 9: Numerical Linear Algebra Primer (February 11st) Lecturer: Ryan Tibshirani Scribes: Avinash Siravuru, Guofan Wu, Maosheng Liu Note: LaTeX template
10-725/36-725: Convex Optimization Spring 2015 Lecture 9: Numerical Linear Algebra Primer (February 11st) Lecturer: Ryan Tibshirani Scribes: Avinash Siravuru, Guofan Wu, Maosheng Liu Note: LaTeX template
Scaling and Pivoting in an Out-of-Core Sparse Direct Solver
 Scaling and Pivoting in an Out-of-Core Sparse Direct Solver JENNIFER A. SCOTT Rutherford Appleton Laboratory Out-of-core sparse direct solvers reduce the amount of main memory needed to factorize and solve
Scaling and Pivoting in an Out-of-Core Sparse Direct Solver JENNIFER A. SCOTT Rutherford Appleton Laboratory Out-of-core sparse direct solvers reduce the amount of main memory needed to factorize and solve
Direct Methods for Solving Linear Systems. Simon Fraser University Surrey Campus MACM 316 Spring 2005 Instructor: Ha Le
 Direct Methods for Solving Linear Systems Simon Fraser University Surrey Campus MACM 316 Spring 2005 Instructor: Ha Le 1 Overview General Linear Systems Gaussian Elimination Triangular Systems The LU Factorization
Direct Methods for Solving Linear Systems Simon Fraser University Surrey Campus MACM 316 Spring 2005 Instructor: Ha Le 1 Overview General Linear Systems Gaussian Elimination Triangular Systems The LU Factorization
Block Bidiagonal Decomposition and Least Squares Problems
 Block Bidiagonal Decomposition and Least Squares Problems Åke Björck Department of Mathematics Linköping University Perspectives in Numerical Analysis, Helsinki, May 27 29, 2008 Outline Bidiagonal Decomposition
Block Bidiagonal Decomposition and Least Squares Problems Åke Björck Department of Mathematics Linköping University Perspectives in Numerical Analysis, Helsinki, May 27 29, 2008 Outline Bidiagonal Decomposition
Matrix Multiplication Chapter IV Special Linear Systems
 Matrix Multiplication Chapter IV Special Linear Systems By Gokturk Poyrazoglu The State University of New York at Buffalo BEST Group Winter Lecture Series Outline 1. Diagonal Dominance and Symmetry a.
Matrix Multiplication Chapter IV Special Linear Systems By Gokturk Poyrazoglu The State University of New York at Buffalo BEST Group Winter Lecture Series Outline 1. Diagonal Dominance and Symmetry a.
AMS 209, Fall 2015 Final Project Type A Numerical Linear Algebra: Gaussian Elimination with Pivoting for Solving Linear Systems
 AMS 209, Fall 205 Final Project Type A Numerical Linear Algebra: Gaussian Elimination with Pivoting for Solving Linear Systems. Overview We are interested in solving a well-defined linear system given
AMS 209, Fall 205 Final Project Type A Numerical Linear Algebra: Gaussian Elimination with Pivoting for Solving Linear Systems. Overview We are interested in solving a well-defined linear system given
Solving linear systems (6 lectures)
 Chapter 2 Solving linear systems (6 lectures) 2.1 Solving linear systems: LU factorization (1 lectures) Reference: [Trefethen, Bau III] Lecture 20, 21 How do you solve Ax = b? (2.1.1) In numerical linear
Chapter 2 Solving linear systems (6 lectures) 2.1 Solving linear systems: LU factorization (1 lectures) Reference: [Trefethen, Bau III] Lecture 20, 21 How do you solve Ax = b? (2.1.1) In numerical linear
14.2 QR Factorization with Column Pivoting
 page 531 Chapter 14 Special Topics Background Material Needed Vector and Matrix Norms (Section 25) Rounding Errors in Basic Floating Point Operations (Section 33 37) Forward Elimination and Back Substitution
page 531 Chapter 14 Special Topics Background Material Needed Vector and Matrix Norms (Section 25) Rounding Errors in Basic Floating Point Operations (Section 33 37) Forward Elimination and Back Substitution
Sparse Linear Systems. Iterative Methods for Sparse Linear Systems. Motivation for Studying Sparse Linear Systems. Partial Differential Equations
 Sparse Linear Systems Iterative Methods for Sparse Linear Systems Matrix Computations and Applications, Lecture C11 Fredrik Bengzon, Robert Söderlund We consider the problem of solving the linear system
Sparse Linear Systems Iterative Methods for Sparse Linear Systems Matrix Computations and Applications, Lecture C11 Fredrik Bengzon, Robert Söderlund We consider the problem of solving the linear system
MH1200 Final 2014/2015
 MH200 Final 204/205 November 22, 204 QUESTION. (20 marks) Let where a R. A = 2 3 4, B = 2 3 4, 3 6 a 3 6 0. For what values of a is A singular? 2. What is the minimum value of the rank of A over all a
MH200 Final 204/205 November 22, 204 QUESTION. (20 marks) Let where a R. A = 2 3 4, B = 2 3 4, 3 6 a 3 6 0. For what values of a is A singular? 2. What is the minimum value of the rank of A over all a
Direct Methods for Solving Linear Systems. Matrix Factorization
 Direct Methods for Solving Linear Systems Matrix Factorization Numerical Analysis (9th Edition) R L Burden & J D Faires Beamer Presentation Slides prepared by John Carroll Dublin City University c 2011
Direct Methods for Solving Linear Systems Matrix Factorization Numerical Analysis (9th Edition) R L Burden & J D Faires Beamer Presentation Slides prepared by John Carroll Dublin City University c 2011
LAPACK-Style Codes for Pivoted Cholesky and QR Updating
 LAPACK-Style Codes for Pivoted Cholesky and QR Updating Sven Hammarling 1, Nicholas J. Higham 2, and Craig Lucas 3 1 NAG Ltd.,Wilkinson House, Jordan Hill Road, Oxford, OX2 8DR, England, sven@nag.co.uk,
LAPACK-Style Codes for Pivoted Cholesky and QR Updating Sven Hammarling 1, Nicholas J. Higham 2, and Craig Lucas 3 1 NAG Ltd.,Wilkinson House, Jordan Hill Road, Oxford, OX2 8DR, England, sven@nag.co.uk,
LU Factorization. Marco Chiarandini. DM559 Linear and Integer Programming. Department of Mathematics & Computer Science University of Southern Denmark
 DM559 Linear and Integer Programming LU Factorization Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark [Based on slides by Lieven Vandenberghe, UCLA] Outline
DM559 Linear and Integer Programming LU Factorization Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark [Based on slides by Lieven Vandenberghe, UCLA] Outline
Exploiting hyper-sparsity when computing preconditioners for conjugate gradients in interior point methods
 Exploiting hyper-sparsity when computing preconditioners for conjugate gradients in interior point methods Julian Hall, Ghussoun Al-Jeiroudi and Jacek Gondzio School of Mathematics University of Edinburgh
Exploiting hyper-sparsity when computing preconditioners for conjugate gradients in interior point methods Julian Hall, Ghussoun Al-Jeiroudi and Jacek Gondzio School of Mathematics University of Edinburgh
A Column Pre-ordering Strategy for the Unsymmetric-Pattern Multifrontal Method
 A Column Pre-ordering Strategy for the Unsymmetric-Pattern Multifrontal Method TIMOTHY A. DAVIS University of Florida A new method for sparse LU factorization is presented that combines a column pre-ordering
A Column Pre-ordering Strategy for the Unsymmetric-Pattern Multifrontal Method TIMOTHY A. DAVIS University of Florida A new method for sparse LU factorization is presented that combines a column pre-ordering
CPE 310: Numerical Analysis for Engineers
 CPE 310: Numerical Analysis for Engineers Chapter 2: Solving Sets of Equations Ahmed Tamrawi Copyright notice: care has been taken to use only those web images deemed by the instructor to be in the public
CPE 310: Numerical Analysis for Engineers Chapter 2: Solving Sets of Equations Ahmed Tamrawi Copyright notice: care has been taken to use only those web images deemed by the instructor to be in the public
CS 542G: Conditioning, BLAS, LU Factorization
 CS 542G: Conditioning, BLAS, LU Factorization Robert Bridson September 22, 2008 1 Why some RBF Kernel Functions Fail We derived some sensible RBF kernel functions, like φ(r) = r 2 log r, from basic principles
CS 542G: Conditioning, BLAS, LU Factorization Robert Bridson September 22, 2008 1 Why some RBF Kernel Functions Fail We derived some sensible RBF kernel functions, like φ(r) = r 2 log r, from basic principles
Linear Algebra, Summer 2011, pt. 2
 Linear Algebra, Summer 2, pt. 2 June 8, 2 Contents Inverses. 2 Vector Spaces. 3 2. Examples of vector spaces..................... 3 2.2 The column space......................... 6 2.3 The null space...........................
Linear Algebra, Summer 2, pt. 2 June 8, 2 Contents Inverses. 2 Vector Spaces. 3 2. Examples of vector spaces..................... 3 2.2 The column space......................... 6 2.3 The null space...........................
ANONSINGULAR tridiagonal linear system of the form
 Generalized Diagonal Pivoting Methods for Tridiagonal Systems without Interchanges Jennifer B. Erway, Roummel F. Marcia, and Joseph A. Tyson Abstract It has been shown that a nonsingular symmetric tridiagonal
Generalized Diagonal Pivoting Methods for Tridiagonal Systems without Interchanges Jennifer B. Erway, Roummel F. Marcia, and Joseph A. Tyson Abstract It has been shown that a nonsingular symmetric tridiagonal
AMS526: Numerical Analysis I (Numerical Linear Algebra for Computational and Data Sciences)
 AMS526: Numerical Analysis I (Numerical Linear Algebra for Computational and Data Sciences) Lecture 19: Computing the SVD; Sparse Linear Systems Xiangmin Jiao Stony Brook University Xiangmin Jiao Numerical
AMS526: Numerical Analysis I (Numerical Linear Algebra for Computational and Data Sciences) Lecture 19: Computing the SVD; Sparse Linear Systems Xiangmin Jiao Stony Brook University Xiangmin Jiao Numerical
Numerical Methods I Non-Square and Sparse Linear Systems
 Numerical Methods I Non-Square and Sparse Linear Systems Aleksandar Donev Courant Institute, NYU 1 donev@courant.nyu.edu 1 MATH-GA 2011.003 / CSCI-GA 2945.003, Fall 2014 September 25th, 2014 A. Donev (Courant
Numerical Methods I Non-Square and Sparse Linear Systems Aleksandar Donev Courant Institute, NYU 1 donev@courant.nyu.edu 1 MATH-GA 2011.003 / CSCI-GA 2945.003, Fall 2014 September 25th, 2014 A. Donev (Courant
IMPROVING THE PERFORMANCE OF SPARSE LU MATRIX FACTORIZATION USING A SUPERNODAL ALGORITHM
 IMPROVING THE PERFORMANCE OF SPARSE LU MATRIX FACTORIZATION USING A SUPERNODAL ALGORITHM Bogdan OANCEA PhD, Associate Professor, Artife University, Bucharest, Romania E-mail: oanceab@ie.ase.ro Abstract:
IMPROVING THE PERFORMANCE OF SPARSE LU MATRIX FACTORIZATION USING A SUPERNODAL ALGORITHM Bogdan OANCEA PhD, Associate Professor, Artife University, Bucharest, Romania E-mail: oanceab@ie.ase.ro Abstract:
2.1 Gaussian Elimination
 2. Gaussian Elimination A common problem encountered in numerical models is the one in which there are n equations and n unknowns. The following is a description of the Gaussian elimination method for
2. Gaussian Elimination A common problem encountered in numerical models is the one in which there are n equations and n unknowns. The following is a description of the Gaussian elimination method for
Fundamentals of Linear Algebra. Marcel B. Finan Arkansas Tech University c All Rights Reserved
 Fundamentals of Linear Algebra Marcel B. Finan Arkansas Tech University c All Rights Reserved 2 PREFACE Linear algebra has evolved as a branch of mathematics with wide range of applications to the natural
Fundamentals of Linear Algebra Marcel B. Finan Arkansas Tech University c All Rights Reserved 2 PREFACE Linear algebra has evolved as a branch of mathematics with wide range of applications to the natural
Fundamentals of Engineering Analysis (650163)
 Philadelphia University Faculty of Engineering Communications and Electronics Engineering Fundamentals of Engineering Analysis (6563) Part Dr. Omar R Daoud Matrices: Introduction DEFINITION A matrix is
Philadelphia University Faculty of Engineering Communications and Electronics Engineering Fundamentals of Engineering Analysis (6563) Part Dr. Omar R Daoud Matrices: Introduction DEFINITION A matrix is
Example: 2x y + 3z = 1 5y 6z = 0 x + 4z = 7. Definition: Elementary Row Operations. Example: Type I swap rows 1 and 3
 Linear Algebra Row Reduced Echelon Form Techniques for solving systems of linear equations lie at the heart of linear algebra. In high school we learn to solve systems with or variables using elimination
Linear Algebra Row Reduced Echelon Form Techniques for solving systems of linear equations lie at the heart of linear algebra. In high school we learn to solve systems with or variables using elimination
CSE 160 Lecture 13. Numerical Linear Algebra
 CSE 16 Lecture 13 Numerical Linear Algebra Announcements Section will be held on Friday as announced on Moodle Midterm Return 213 Scott B Baden / CSE 16 / Fall 213 2 Today s lecture Gaussian Elimination
CSE 16 Lecture 13 Numerical Linear Algebra Announcements Section will be held on Friday as announced on Moodle Midterm Return 213 Scott B Baden / CSE 16 / Fall 213 2 Today s lecture Gaussian Elimination
Krylov Subspaces. Lab 1. The Arnoldi Iteration
 Lab 1 Krylov Subspaces Lab Objective: Discuss simple Krylov Subspace Methods for finding eigenvalues and show some interesting applications. One of the biggest difficulties in computational linear algebra
Lab 1 Krylov Subspaces Lab Objective: Discuss simple Krylov Subspace Methods for finding eigenvalues and show some interesting applications. One of the biggest difficulties in computational linear algebra
Numerical Linear Algebra
 Numerical Linear Algebra The two principal problems in linear algebra are: Linear system Given an n n matrix A and an n-vector b, determine x IR n such that A x = b Eigenvalue problem Given an n n matrix
Numerical Linear Algebra The two principal problems in linear algebra are: Linear system Given an n n matrix A and an n-vector b, determine x IR n such that A x = b Eigenvalue problem Given an n n matrix
Ax = b. Systems of Linear Equations. Lecture Notes to Accompany. Given m n matrix A and m-vector b, find unknown n-vector x satisfying
 Lecture Notes to Accompany Scientific Computing An Introductory Survey Second Edition by Michael T Heath Chapter Systems of Linear Equations Systems of Linear Equations Given m n matrix A and m-vector
Lecture Notes to Accompany Scientific Computing An Introductory Survey Second Edition by Michael T Heath Chapter Systems of Linear Equations Systems of Linear Equations Given m n matrix A and m-vector
Numerical Linear Algebra Primer. Ryan Tibshirani Convex Optimization /36-725
 Numerical Linear Algebra Primer Ryan Tibshirani Convex Optimization 10-725/36-725 Last time: proximal gradient descent Consider the problem min g(x) + h(x) with g, h convex, g differentiable, and h simple
Numerical Linear Algebra Primer Ryan Tibshirani Convex Optimization 10-725/36-725 Last time: proximal gradient descent Consider the problem min g(x) + h(x) with g, h convex, g differentiable, and h simple
Scientific Computing: Dense Linear Systems
 Scientific Computing: Dense Linear Systems Aleksandar Donev Courant Institute, NYU 1 donev@courant.nyu.edu 1 Course MATH-GA.2043 or CSCI-GA.2112, Spring 2012 February 9th, 2012 A. Donev (Courant Institute)
Scientific Computing: Dense Linear Systems Aleksandar Donev Courant Institute, NYU 1 donev@courant.nyu.edu 1 Course MATH-GA.2043 or CSCI-GA.2112, Spring 2012 February 9th, 2012 A. Donev (Courant Institute)
