Sparse Rank-Revealing LU Factorization
|
|
|
- Nigel Cox
- 5 years ago
- Views:
Transcription
1 Sparse Rank-Revealing LU Factorization SIAM Conference on Optimization Toronto, May 2002 Michael O Sullivan and Michael Saunders Dept of Engineering Science Dept of Management Sci & Eng University of Auckland Stanford University Auckland, New Zealand Stanford, CA michael.osullivan@auckland.ac.nz saunders@stanford.edu Sparse Rank-Revealing LU Factorization p.1/26
2 GOALS Sparse Rank-Revealing LU Factorization p.2/26
3 Goals Given a sparse matrix A (m n, usually m n), Determine if A is ill-conditioned? Determine which columns to delete? (or replace) Maintain sparsity P 1 AP 2 = LU, U = Sparse Rank-Revealing LU Factorization p.3/26
4 Motivation Dynamic Programming (Mike O Sullivan s thesis) P substochastic A = P I, at most one singularity Optimization (MINOS and SNOPT) Basis Repair I A = B, square basis, perhaps ill-conditioned Basis Repair II A = (B S) T, look for better B Sparse Rank-Revealing LU Factorization p.4/26
5 RANK-REVEALING FACTORS Sparse Rank-Revealing LU Factorization p.5/26
6 Rank-Revealing Factors A = XDY T = Demmel et al. (1999) X, Y full column rank, well conditioned D diagonal SVD QR with column interchanges LU with Rook Pivoting (Foster 1997) LU with Complete Pivoting Sparse Rank-Revealing LU Factorization p.6/26
7 Sparse Rank-Revealing Factors QR multifrontal Pierce and Lewis (1997) TPP (Threshold Partial Pivoting) TRP (Threshold Rook Pivoting) TCP (Threshold Complete Pivoting) Not RR Perhaps effective? This talk Sparse Rank-Revealing LU Factorization p.7/26
8 PIVOTING NEEDS Amax j = biggest element in col j Amax = biggest element in A Sparse Rank-Revealing LU Factorization p.8/26
9 Partial Pivoting vs. Complete Pivoting Dense Computing L and U O(n 3 ) PP Finding Amax 1 O(n) CP Finding Amax O(n 3 ) Not so bad! Sparse Computing L and U O(nnz(L + U)) TPP Finding Amax j O(nnz(L + U)) TCP Finding Amax O(n 2 )? Too much Sparse Rank-Revealing LU Factorization p.9/26
10 LUSOL Sparse Rank-Revealing LU Factorization p.10/26
11 LUSOL A = LU + updates, L well-conditioned Gill, Murray, Saunders and Wright (1987) Revised , Markowitz strategy for sparse pivots (cf. MA28, Y12M, LA05, MOPS, MA48) TPP (Threshold Partial Pivoting) Search only a few sparse cols and rows Zlatev 1981 Store Amax j at top of col j Suhl & Suhl 1990 TCP (Threshold Complete Pivoting) New Sparse Rank-Revealing LU Factorization p.11/26
12 Stability Tolerance Lmax P 1 AP 2 = LDU, unit diags on L, U Threshold pivoting bounds the off-diags of L and perhaps U: TPP TRP TCP } } L ij Lmax 10.0 L ij, U ij Lmax 5.0 TRP, TCP are more Rank-Revealing with low Lmax: cond(l), cond(u) < (1 + Lmax) n Sparse Rank-Revealing LU Factorization p.12/26
13 Elimination Step Allowable pivots with Lmax = 3 TPP 1 TRP 4 TCP (Markowitz) Just a few columns and rows change Sparse Rank-Revealing LU Factorization p.13/26
14 Finding Amax from Amax j Naive Method Amax j = biggest element in column j Amax = biggest element in A jmax = column containing Amax Find Amax by searching all Amax j O(n 2 ) Theorem Need to search all Amax j only if Amax decreases Sparse Rank-Revealing LU Factorization p.14/26
15 Maintaining Amax j Amax j New Amax j??? Easy to update modified Amax j Sparse Rank-Revealing LU Factorization p.15/26
16 Maintaining Amax Amax is in column jmax, which may be modified: Amax j Amax Amax j Must search Amax + 5 +? for Amax If col jmax is not modified: Amax j Amax Amax j Amax = Sparse Rank-Revealing LU Factorization p.16/26
17 HEAPS Sparse Rank-Revealing LU Factorization p.17/26
18 Storing Amax j in a Heap Thanks to John Gilbert Amax Ha(k) Amax j Hj(k) j Hk(j) location of j in heap Sparse Rank-Revealing LU Factorization p.18/26
19 Calls to Heap Functions build heap from all Amax j for k = 1 : min(m, n) Choose pivot, do elimination Find Amax j for modified cols delete entry for pivot column for l = 2 : lenpivrow change entry for each modified column end end Remarkably little work Sparse Rank-Revealing LU Factorization p.19/26
20 NUMERICAL RESULTS Sparse Rank-Revealing LU Factorization p.20/26
21 Cost of RR Feature Problem memplus from Harwell-Boeing collection A = , nonzeros Lmax nnz(l+u) Time (secs, 350MHz P3) LUSOL (TCP) RR RR RR RR SuperLU (colamd PP) Sparse Rank-Revealing LU Factorization p.21/26
22 Markowitz CP, then Dense CP Modified Zlatev strategy Markowitz1 until 30% dense: Search at least 5 cols, 4 rows 2 Markowitz2 until 50% dense: Search at least 5 cols, 0 rows 3 Dense Complete Pivoting Sparse Rank-Revealing LU Factorization p.22/26
23 Profile Problem memplus A = , nonzeros TCP, Lmax= 10.0, LU = nonzeros Markowitz Find stable pivot 65.0% Dense CP % Elimination The algebra 7.4% Amax j For modified cols 4.7% change Heap update 0.1% (!) Sparse Rank-Revealing LU Factorization p.23/26
24 CONCLUSIONS Sparse Rank-Revealing LU Factorization p.24/26
25 Conclusions Threshold Complete Pivoting is usually Rank-Revealing with Lmax 4.0 (but sometimes needs 2.5) Heap structure allows Amax to be maintained cheaply RRLUs can be rather dense TPP: Work-horse, usually reliable TCP: Markowitz search dominates cost TRP: Worth investigating Sparse Rank-Revealing LU Factorization p.25/26
26 HEAPS of THANKS John Gilbert Philip Gill The CUTE and Harwell-Boeing Teams Maureen Doyle R. Sedgewick Cormen, Leiserson and Rivest Michael Friedlander Sparse Rank-Revealing LU Factorization p.26/26
Sparse Rank-Revealing LU Factorization
 Sparse Rank-Revealing LU Factorization Householder Symposium XV on Numerical Linear Algebra Peebles, Scotland, June 2002 Michael O Sullivan and Michael Saunders Dept of Engineering Science Dept of Management
Sparse Rank-Revealing LU Factorization Householder Symposium XV on Numerical Linear Algebra Peebles, Scotland, June 2002 Michael O Sullivan and Michael Saunders Dept of Engineering Science Dept of Management
LUSOL: A basis package for constrained optimization
 LUSOL: A basis package for constrained optimization IFORS Triennial Conference on OR/MS Honolulu, HI, July 11 15, 2005 Michael O Sullivan and Michael Saunders Dept of Engineering Science Dept of Management
LUSOL: A basis package for constrained optimization IFORS Triennial Conference on OR/MS Honolulu, HI, July 11 15, 2005 Michael O Sullivan and Michael Saunders Dept of Engineering Science Dept of Management
A convex QP solver based on block-lu updates
 Block-LU updates p. 1/24 A convex QP solver based on block-lu updates PP06 SIAM Conference on Parallel Processing for Scientific Computing San Francisco, CA, Feb 22 24, 2006 Hanh Huynh and Michael Saunders
Block-LU updates p. 1/24 A convex QP solver based on block-lu updates PP06 SIAM Conference on Parallel Processing for Scientific Computing San Francisco, CA, Feb 22 24, 2006 Hanh Huynh and Michael Saunders
Implementation of a KKT-based active-set QP solver
 Block-LU updates p. 1/27 Implementation of a KKT-based active-set QP solver ISMP 2006 19th International Symposium on Mathematical Programming Rio de Janeiro, Brazil, July 30 August 4, 2006 Hanh Huynh
Block-LU updates p. 1/27 Implementation of a KKT-based active-set QP solver ISMP 2006 19th International Symposium on Mathematical Programming Rio de Janeiro, Brazil, July 30 August 4, 2006 Hanh Huynh
A review of sparsity vs stability in LU updates
 A review of sparsity vs stability in LU updates Michael Saunders Dept of Management Science and Engineering (MS&E) Systems Optimization Laboratory (SOL) Institute for Computational Mathematics and Engineering
A review of sparsity vs stability in LU updates Michael Saunders Dept of Management Science and Engineering (MS&E) Systems Optimization Laboratory (SOL) Institute for Computational Mathematics and Engineering
MS&E 318 (CME 338) Large-Scale Numerical Optimization
 Stanford University, Management Science & Engineering (and ICME MS&E 318 (CME 338 Large-Scale Numerical Optimization 1 Origins Instructor: Michael Saunders Spring 2018 Notes 7: LUSOL: a Basis Factorization
Stanford University, Management Science & Engineering (and ICME MS&E 318 (CME 338 Large-Scale Numerical Optimization 1 Origins Instructor: Michael Saunders Spring 2018 Notes 7: LUSOL: a Basis Factorization
Ax=b. Zack 10/4/2013
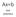 Ax=b Zack 10/4/2013 Iteration method Ax=b v 1, v 2 x k = V k y k Given (A, b) standard orthonormal base v 1, v 2 x k = V k y k For symmetric A, the method to generate V k is called Lanczos Method Lanczos
Ax=b Zack 10/4/2013 Iteration method Ax=b v 1, v 2 x k = V k y k Given (A, b) standard orthonormal base v 1, v 2 x k = V k y k For symmetric A, the method to generate V k is called Lanczos Method Lanczos
STAT 309: MATHEMATICAL COMPUTATIONS I FALL 2018 LECTURE 13
 STAT 309: MATHEMATICAL COMPUTATIONS I FALL 208 LECTURE 3 need for pivoting we saw that under proper circumstances, we can write A LU where 0 0 0 u u 2 u n l 2 0 0 0 u 22 u 2n L l 3 l 32, U 0 0 0 l n l
STAT 309: MATHEMATICAL COMPUTATIONS I FALL 208 LECTURE 3 need for pivoting we saw that under proper circumstances, we can write A LU where 0 0 0 u u 2 u n l 2 0 0 0 u 22 u 2n L l 3 l 32, U 0 0 0 l n l
MS&E 318 (CME 338) Large-Scale Numerical Optimization
 Stanford University, Management Science & Engineering (and ICME MS&E 38 (CME 338 Large-Scale Numerical Optimization Course description Instructor: Michael Saunders Spring 28 Notes : Review The course teaches
Stanford University, Management Science & Engineering (and ICME MS&E 38 (CME 338 Large-Scale Numerical Optimization Course description Instructor: Michael Saunders Spring 28 Notes : Review The course teaches
Revised Simplex Method
 DM545 Linear and Integer Programming Lecture 7 Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. 2. 2 Motivation Complexity of single pivot operation
DM545 Linear and Integer Programming Lecture 7 Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. 2. 2 Motivation Complexity of single pivot operation
Satisfying Flux Balance and Mass-Action Kinetics in a Network of Biochemical Reactions
 Satisfying Flux Balance and Mass-Action Kinetics in a Network of Biochemical Reactions Speakers Senior Personnel Collaborators Michael Saunders and Ines Thiele Ronan Fleming, Bernhard Palsson, Yinyu Ye
Satisfying Flux Balance and Mass-Action Kinetics in a Network of Biochemical Reactions Speakers Senior Personnel Collaborators Michael Saunders and Ines Thiele Ronan Fleming, Bernhard Palsson, Yinyu Ye
Bindel, Fall 2016 Matrix Computations (CS 6210) Notes for
 1 Logistics Notes for 2016-09-14 1. There was a goof in HW 2, problem 1 (now fixed) please re-download if you have already started looking at it. 2. CS colloquium (4:15 in Gates G01) this Thurs is Margaret
1 Logistics Notes for 2016-09-14 1. There was a goof in HW 2, problem 1 (now fixed) please re-download if you have already started looking at it. 2. CS colloquium (4:15 in Gates G01) this Thurs is Margaret
CME 302: NUMERICAL LINEAR ALGEBRA FALL 2005/06 LECTURE 6
 CME 302: NUMERICAL LINEAR ALGEBRA FALL 2005/06 LECTURE 6 GENE H GOLUB Issues with Floating-point Arithmetic We conclude our discussion of floating-point arithmetic by highlighting two issues that frequently
CME 302: NUMERICAL LINEAR ALGEBRA FALL 2005/06 LECTURE 6 GENE H GOLUB Issues with Floating-point Arithmetic We conclude our discussion of floating-point arithmetic by highlighting two issues that frequently
DM545 Linear and Integer Programming. Lecture 7 Revised Simplex Method. Marco Chiarandini
 DM545 Linear and Integer Programming Lecture 7 Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. 2. 2 Motivation Complexity of single pivot operation
DM545 Linear and Integer Programming Lecture 7 Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. 2. 2 Motivation Complexity of single pivot operation
LU factorization with Panel Rank Revealing Pivoting and its Communication Avoiding version
 1 LU factorization with Panel Rank Revealing Pivoting and its Communication Avoiding version Amal Khabou Advisor: Laura Grigori Université Paris Sud 11, INRIA Saclay France SIAMPP12 February 17, 2012 2
1 LU factorization with Panel Rank Revealing Pivoting and its Communication Avoiding version Amal Khabou Advisor: Laura Grigori Université Paris Sud 11, INRIA Saclay France SIAMPP12 February 17, 2012 2
A Column Pre-ordering Strategy for the Unsymmetric-Pattern Multifrontal Method
 A Column Pre-ordering Strategy for the Unsymmetric-Pattern Multifrontal Method TIMOTHY A. DAVIS University of Florida A new method for sparse LU factorization is presented that combines a column pre-ordering
A Column Pre-ordering Strategy for the Unsymmetric-Pattern Multifrontal Method TIMOTHY A. DAVIS University of Florida A new method for sparse LU factorization is presented that combines a column pre-ordering
Scientific Computing
 Scientific Computing Direct solution methods Martin van Gijzen Delft University of Technology October 3, 2018 1 Program October 3 Matrix norms LU decomposition Basic algorithm Cost Stability Pivoting Pivoting
Scientific Computing Direct solution methods Martin van Gijzen Delft University of Technology October 3, 2018 1 Program October 3 Matrix norms LU decomposition Basic algorithm Cost Stability Pivoting Pivoting
Numerical Linear Algebra
 Numerical Linear Algebra Decompositions, numerical aspects Gerard Sleijpen and Martin van Gijzen September 27, 2017 1 Delft University of Technology Program Lecture 2 LU-decomposition Basic algorithm Cost
Numerical Linear Algebra Decompositions, numerical aspects Gerard Sleijpen and Martin van Gijzen September 27, 2017 1 Delft University of Technology Program Lecture 2 LU-decomposition Basic algorithm Cost
Program Lecture 2. Numerical Linear Algebra. Gaussian elimination (2) Gaussian elimination. Decompositions, numerical aspects
 Numerical Linear Algebra Decompositions, numerical aspects Program Lecture 2 LU-decomposition Basic algorithm Cost Stability Pivoting Cholesky decomposition Sparse matrices and reorderings Gerard Sleijpen
Numerical Linear Algebra Decompositions, numerical aspects Program Lecture 2 LU-decomposition Basic algorithm Cost Stability Pivoting Cholesky decomposition Sparse matrices and reorderings Gerard Sleijpen
MS&E 318 (CME 338) Large-Scale Numerical Optimization
 Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization Instructor: Michael Saunders Spring 2015 Notes 11: NPSOL and SNOPT SQP Methods 1 Overview
Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization Instructor: Michael Saunders Spring 2015 Notes 11: NPSOL and SNOPT SQP Methods 1 Overview
V C V L T I 0 C V B 1 V T 0 I. l nk
 Multifrontal Method Kailai Xu September 16, 2017 Main observation. Consider the LDL T decomposition of a SPD matrix [ ] [ ] [ ] [ ] B V T L 0 I 0 L T L A = = 1 V T V C V L T I 0 C V B 1 V T, 0 I where
Multifrontal Method Kailai Xu September 16, 2017 Main observation. Consider the LDL T decomposition of a SPD matrix [ ] [ ] [ ] [ ] B V T L 0 I 0 L T L A = = 1 V T V C V L T I 0 C V B 1 V T, 0 I where
MS&E 318 (CME 338) Large-Scale Numerical Optimization
 Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization Instructor: Michael Saunders Spring 2015 Notes 4: The Primal Simplex Method 1 Linear
Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization Instructor: Michael Saunders Spring 2015 Notes 4: The Primal Simplex Method 1 Linear
Linear Algebra (Review) Volker Tresp 2017
 Linear Algebra (Review) Volker Tresp 2017 1 Vectors k is a scalar (a number) c is a column vector. Thus in two dimensions, c = ( c1 c 2 ) (Advanced: More precisely, a vector is defined in a vector space.
Linear Algebra (Review) Volker Tresp 2017 1 Vectors k is a scalar (a number) c is a column vector. Thus in two dimensions, c = ( c1 c 2 ) (Advanced: More precisely, a vector is defined in a vector space.
Section 5.6. LU and LDU Factorizations
 5.6. LU and LDU Factorizations Section 5.6. LU and LDU Factorizations Note. We largely follow Fraleigh and Beauregard s approach to this topic from Linear Algebra, 3rd Edition, Addison-Wesley (995). See
5.6. LU and LDU Factorizations Section 5.6. LU and LDU Factorizations Note. We largely follow Fraleigh and Beauregard s approach to this topic from Linear Algebra, 3rd Edition, Addison-Wesley (995). See
A Method for Constructing Diagonally Dominant Preconditioners based on Jacobi Rotations
 A Method for Constructing Diagonally Dominant Preconditioners based on Jacobi Rotations Jin Yun Yuan Plamen Y. Yalamov Abstract A method is presented to make a given matrix strictly diagonally dominant
A Method for Constructing Diagonally Dominant Preconditioners based on Jacobi Rotations Jin Yun Yuan Plamen Y. Yalamov Abstract A method is presented to make a given matrix strictly diagonally dominant
AMS526: Numerical Analysis I (Numerical Linear Algebra for Computational and Data Sciences)
 AMS526: Numerical Analysis I (Numerical Linear Algebra for Computational and Data Sciences) Lecture 19: Computing the SVD; Sparse Linear Systems Xiangmin Jiao Stony Brook University Xiangmin Jiao Numerical
AMS526: Numerical Analysis I (Numerical Linear Algebra for Computational and Data Sciences) Lecture 19: Computing the SVD; Sparse Linear Systems Xiangmin Jiao Stony Brook University Xiangmin Jiao Numerical
Bindel, Fall 2016 Matrix Computations (CS 6210) Notes for
 1 A cautionary tale Notes for 2016-10-05 You have been dropped on a desert island with a laptop with a magic battery of infinite life, a MATLAB license, and a complete lack of knowledge of basic geometry.
1 A cautionary tale Notes for 2016-10-05 You have been dropped on a desert island with a laptop with a magic battery of infinite life, a MATLAB license, and a complete lack of knowledge of basic geometry.
Linear Algebra (Review) Volker Tresp 2018
 Linear Algebra (Review) Volker Tresp 2018 1 Vectors k, M, N are scalars A one-dimensional array c is a column vector. Thus in two dimensions, ( ) c1 c = c 2 c i is the i-th component of c c T = (c 1, c
Linear Algebra (Review) Volker Tresp 2018 1 Vectors k, M, N are scalars A one-dimensional array c is a column vector. Thus in two dimensions, ( ) c1 c = c 2 c i is the i-th component of c c T = (c 1, c
Pivoting. Reading: GV96 Section 3.4, Stew98 Chapter 3: 1.3
 Pivoting Reading: GV96 Section 3.4, Stew98 Chapter 3: 1.3 In the previous discussions we have assumed that the LU factorization of A existed and the various versions could compute it in a stable manner.
Pivoting Reading: GV96 Section 3.4, Stew98 Chapter 3: 1.3 In the previous discussions we have assumed that the LU factorization of A existed and the various versions could compute it in a stable manner.
Scaling and Pivoting in an Out-of-Core Sparse Direct Solver
 Scaling and Pivoting in an Out-of-Core Sparse Direct Solver JENNIFER A. SCOTT Rutherford Appleton Laboratory Out-of-core sparse direct solvers reduce the amount of main memory needed to factorize and solve
Scaling and Pivoting in an Out-of-Core Sparse Direct Solver JENNIFER A. SCOTT Rutherford Appleton Laboratory Out-of-core sparse direct solvers reduce the amount of main memory needed to factorize and solve
Review Questions REVIEW QUESTIONS 71
 REVIEW QUESTIONS 71 MATLAB, is [42]. For a comprehensive treatment of error analysis and perturbation theory for linear systems and many other problems in linear algebra, see [126, 241]. An overview of
REVIEW QUESTIONS 71 MATLAB, is [42]. For a comprehensive treatment of error analysis and perturbation theory for linear systems and many other problems in linear algebra, see [126, 241]. An overview of
Rank revealing factorizations, and low rank approximations
 Rank revealing factorizations, and low rank approximations L. Grigori Inria Paris, UPMC January 2018 Plan Low rank matrix approximation Rank revealing QR factorization LU CRTP: Truncated LU factorization
Rank revealing factorizations, and low rank approximations L. Grigori Inria Paris, UPMC January 2018 Plan Low rank matrix approximation Rank revealing QR factorization LU CRTP: Truncated LU factorization
Sparsity-Preserving Difference of Positive Semidefinite Matrix Representation of Indefinite Matrices
 Sparsity-Preserving Difference of Positive Semidefinite Matrix Representation of Indefinite Matrices Jaehyun Park June 1 2016 Abstract We consider the problem of writing an arbitrary symmetric matrix as
Sparsity-Preserving Difference of Positive Semidefinite Matrix Representation of Indefinite Matrices Jaehyun Park June 1 2016 Abstract We consider the problem of writing an arbitrary symmetric matrix as
Main matrix factorizations
 Main matrix factorizations A P L U P permutation matrix, L lower triangular, U upper triangular Key use: Solve square linear system Ax b. A Q R Q unitary, R upper triangular Key use: Solve square or overdetrmined
Main matrix factorizations A P L U P permutation matrix, L lower triangular, U upper triangular Key use: Solve square linear system Ax b. A Q R Q unitary, R upper triangular Key use: Solve square or overdetrmined
LU Factorization. Marco Chiarandini. DM559 Linear and Integer Programming. Department of Mathematics & Computer Science University of Southern Denmark
 DM559 Linear and Integer Programming LU Factorization Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark [Based on slides by Lieven Vandenberghe, UCLA] Outline
DM559 Linear and Integer Programming LU Factorization Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark [Based on slides by Lieven Vandenberghe, UCLA] Outline
Lecture 12 (Tue, Mar 5) Gaussian elimination and LU factorization (II)
 Math 59 Lecture 2 (Tue Mar 5) Gaussian elimination and LU factorization (II) 2 Gaussian elimination - LU factorization For a general n n matrix A the Gaussian elimination produces an LU factorization if
Math 59 Lecture 2 (Tue Mar 5) Gaussian elimination and LU factorization (II) 2 Gaussian elimination - LU factorization For a general n n matrix A the Gaussian elimination produces an LU factorization if
Matrix decompositions
 Matrix decompositions Zdeněk Dvořák May 19, 2015 Lemma 1 (Schur decomposition). If A is a symmetric real matrix, then there exists an orthogonal matrix Q and a diagonal matrix D such that A = QDQ T. The
Matrix decompositions Zdeněk Dvořák May 19, 2015 Lemma 1 (Schur decomposition). If A is a symmetric real matrix, then there exists an orthogonal matrix Q and a diagonal matrix D such that A = QDQ T. The
Linear Algebra Section 2.6 : LU Decomposition Section 2.7 : Permutations and transposes Wednesday, February 13th Math 301 Week #4
 Linear Algebra Section. : LU Decomposition Section. : Permutations and transposes Wednesday, February 1th Math 01 Week # 1 The LU Decomposition We learned last time that we can factor a invertible matrix
Linear Algebra Section. : LU Decomposition Section. : Permutations and transposes Wednesday, February 1th Math 01 Week # 1 The LU Decomposition We learned last time that we can factor a invertible matrix
ANSWERS. E k E 2 E 1 A = B
 MATH 7- Final Exam Spring ANSWERS Essay Questions points Define an Elementary Matrix Display the fundamental matrix multiply equation which summarizes a sequence of swap, combination and multiply operations,
MATH 7- Final Exam Spring ANSWERS Essay Questions points Define an Elementary Matrix Display the fundamental matrix multiply equation which summarizes a sequence of swap, combination and multiply operations,
Bindel, Fall 2016 Matrix Computations (CS 6210) Notes for
 1 Logistics Notes for 2016-08-26 1. Our enrollment is at 50, and there are still a few students who want to get in. We only have 50 seats in the room, and I cannot increase the cap further. So if you are
1 Logistics Notes for 2016-08-26 1. Our enrollment is at 50, and there are still a few students who want to get in. We only have 50 seats in the room, and I cannot increase the cap further. So if you are
On the Skeel condition number, growth factor and pivoting strategies for Gaussian elimination
 On the Skeel condition number, growth factor and pivoting strategies for Gaussian elimination J.M. Peña 1 Introduction Gaussian elimination (GE) with a given pivoting strategy, for nonsingular matrices
On the Skeel condition number, growth factor and pivoting strategies for Gaussian elimination J.M. Peña 1 Introduction Gaussian elimination (GE) with a given pivoting strategy, for nonsingular matrices
IMPROVING THE PERFORMANCE OF SPARSE LU MATRIX FACTORIZATION USING A SUPERNODAL ALGORITHM
 IMPROVING THE PERFORMANCE OF SPARSE LU MATRIX FACTORIZATION USING A SUPERNODAL ALGORITHM Bogdan OANCEA PhD, Associate Professor, Artife University, Bucharest, Romania E-mail: oanceab@ie.ase.ro Abstract:
IMPROVING THE PERFORMANCE OF SPARSE LU MATRIX FACTORIZATION USING A SUPERNODAL ALGORITHM Bogdan OANCEA PhD, Associate Professor, Artife University, Bucharest, Romania E-mail: oanceab@ie.ase.ro Abstract:
LU Factorization with Panel Rank Revealing Pivoting and Its Communication Avoiding Version
 LU Factorization with Panel Rank Revealing Pivoting and Its Communication Avoiding Version Amal Khabou James Demmel Laura Grigori Ming Gu Electrical Engineering and Computer Sciences University of California
LU Factorization with Panel Rank Revealing Pivoting and Its Communication Avoiding Version Amal Khabou James Demmel Laura Grigori Ming Gu Electrical Engineering and Computer Sciences University of California
14.2 QR Factorization with Column Pivoting
 page 531 Chapter 14 Special Topics Background Material Needed Vector and Matrix Norms (Section 25) Rounding Errors in Basic Floating Point Operations (Section 33 37) Forward Elimination and Back Substitution
page 531 Chapter 14 Special Topics Background Material Needed Vector and Matrix Norms (Section 25) Rounding Errors in Basic Floating Point Operations (Section 33 37) Forward Elimination and Back Substitution
This can be accomplished by left matrix multiplication as follows: I
 1 Numerical Linear Algebra 11 The LU Factorization Recall from linear algebra that Gaussian elimination is a method for solving linear systems of the form Ax = b, where A R m n and bran(a) In this method
1 Numerical Linear Algebra 11 The LU Factorization Recall from linear algebra that Gaussian elimination is a method for solving linear systems of the form Ax = b, where A R m n and bran(a) In this method
Rank Revealing QR factorization. F. Guyomarc h, D. Mezher and B. Philippe
 Rank Revealing QR factorization F. Guyomarc h, D. Mezher and B. Philippe 1 Outline Introduction Classical Algorithms Full matrices Sparse matrices Rank-Revealing QR Conclusion CSDA 2005, Cyprus 2 Situation
Rank Revealing QR factorization F. Guyomarc h, D. Mezher and B. Philippe 1 Outline Introduction Classical Algorithms Full matrices Sparse matrices Rank-Revealing QR Conclusion CSDA 2005, Cyprus 2 Situation
Spectrum-Revealing Matrix Factorizations Theory and Algorithms
 Spectrum-Revealing Matrix Factorizations Theory and Algorithms Ming Gu Department of Mathematics University of California, Berkeley April 5, 2016 Joint work with D. Anderson, J. Deursch, C. Melgaard, J.
Spectrum-Revealing Matrix Factorizations Theory and Algorithms Ming Gu Department of Mathematics University of California, Berkeley April 5, 2016 Joint work with D. Anderson, J. Deursch, C. Melgaard, J.
Verified Solutions of Sparse Linear Systems by LU factorization
 Verified Solutions of Sparse Linear Systems by LU factorization TAKESHI OGITA CREST, Japan Science and Technology Agency JST), and Faculty of Science and Engineering, Waseda University, Robert J. Shillman
Verified Solutions of Sparse Linear Systems by LU factorization TAKESHI OGITA CREST, Japan Science and Technology Agency JST), and Faculty of Science and Engineering, Waseda University, Robert J. Shillman
AMS526: Numerical Analysis I (Numerical Linear Algebra)
 AMS526: Numerical Analysis I (Numerical Linear Algebra) Lecture 12: Gaussian Elimination and LU Factorization Xiangmin Jiao SUNY Stony Brook Xiangmin Jiao Numerical Analysis I 1 / 10 Gaussian Elimination
AMS526: Numerical Analysis I (Numerical Linear Algebra) Lecture 12: Gaussian Elimination and LU Factorization Xiangmin Jiao SUNY Stony Brook Xiangmin Jiao Numerical Analysis I 1 / 10 Gaussian Elimination
MATH 3511 Lecture 1. Solving Linear Systems 1
 MATH 3511 Lecture 1 Solving Linear Systems 1 Dmitriy Leykekhman Spring 2012 Goals Review of basic linear algebra Solution of simple linear systems Gaussian elimination D Leykekhman - MATH 3511 Introduction
MATH 3511 Lecture 1 Solving Linear Systems 1 Dmitriy Leykekhman Spring 2012 Goals Review of basic linear algebra Solution of simple linear systems Gaussian elimination D Leykekhman - MATH 3511 Introduction
Solving Linear Systems Using Gaussian Elimination
 Solving Linear Systems Using Gaussian Elimination DEFINITION: A linear equation in the variables x 1,..., x n is an equation that can be written in the form a 1 x 1 +...+a n x n = b, where a 1,...,a n
Solving Linear Systems Using Gaussian Elimination DEFINITION: A linear equation in the variables x 1,..., x n is an equation that can be written in the form a 1 x 1 +...+a n x n = b, where a 1,...,a n
A Block Compression Algorithm for Computing Preconditioners
 A Block Compression Algorithm for Computing Preconditioners J Cerdán, J Marín, and J Mas Abstract To implement efficiently algorithms for the solution of large systems of linear equations in modern computer
A Block Compression Algorithm for Computing Preconditioners J Cerdán, J Marín, and J Mas Abstract To implement efficiently algorithms for the solution of large systems of linear equations in modern computer
Incomplete Cholesky preconditioners that exploit the low-rank property
 anapov@ulb.ac.be ; http://homepages.ulb.ac.be/ anapov/ 1 / 35 Incomplete Cholesky preconditioners that exploit the low-rank property (theory and practice) Artem Napov Service de Métrologie Nucléaire, Université
anapov@ulb.ac.be ; http://homepages.ulb.ac.be/ anapov/ 1 / 35 Incomplete Cholesky preconditioners that exploit the low-rank property (theory and practice) Artem Napov Service de Métrologie Nucléaire, Université
A Sparse QS-Decomposition for Large Sparse Linear System of Equations
 A Sparse QS-Decomposition for Large Sparse Linear System of Equations Wujian Peng 1 and Biswa N. Datta 2 1 Department of Math, Zhaoqing University, Zhaoqing, China, douglas peng@yahoo.com 2 Department
A Sparse QS-Decomposition for Large Sparse Linear System of Equations Wujian Peng 1 and Biswa N. Datta 2 1 Department of Math, Zhaoqing University, Zhaoqing, China, douglas peng@yahoo.com 2 Department
What s New in Active-Set Methods for Nonlinear Optimization?
 What s New in Active-Set Methods for Nonlinear Optimization? Philip E. Gill Advances in Numerical Computation, Manchester University, July 5, 2011 A Workshop in Honor of Sven Hammarling UCSD Center for
What s New in Active-Set Methods for Nonlinear Optimization? Philip E. Gill Advances in Numerical Computation, Manchester University, July 5, 2011 A Workshop in Honor of Sven Hammarling UCSD Center for
Numerical Linear Algebra Primer. Ryan Tibshirani Convex Optimization /36-725
 Numerical Linear Algebra Primer Ryan Tibshirani Convex Optimization 10-725/36-725 Last time: proximal gradient descent Consider the problem min g(x) + h(x) with g, h convex, g differentiable, and h simple
Numerical Linear Algebra Primer Ryan Tibshirani Convex Optimization 10-725/36-725 Last time: proximal gradient descent Consider the problem min g(x) + h(x) with g, h convex, g differentiable, and h simple
Linear Algebraic Equations
 Linear Algebraic Equations 1 Fundamentals Consider the set of linear algebraic equations n a ij x i b i represented by Ax b j with [A b ] [A b] and (1a) r(a) rank of A (1b) Then Axb has a solution iff
Linear Algebraic Equations 1 Fundamentals Consider the set of linear algebraic equations n a ij x i b i represented by Ax b j with [A b ] [A b] and (1a) r(a) rank of A (1b) Then Axb has a solution iff
Enhancing Scalability of Sparse Direct Methods
 Journal of Physics: Conference Series 78 (007) 0 doi:0.088/7-6596/78//0 Enhancing Scalability of Sparse Direct Methods X.S. Li, J. Demmel, L. Grigori, M. Gu, J. Xia 5, S. Jardin 6, C. Sovinec 7, L.-Q.
Journal of Physics: Conference Series 78 (007) 0 doi:0.088/7-6596/78//0 Enhancing Scalability of Sparse Direct Methods X.S. Li, J. Demmel, L. Grigori, M. Gu, J. Xia 5, S. Jardin 6, C. Sovinec 7, L.-Q.
Matrix Multiplication Chapter IV Special Linear Systems
 Matrix Multiplication Chapter IV Special Linear Systems By Gokturk Poyrazoglu The State University of New York at Buffalo BEST Group Winter Lecture Series Outline 1. Diagonal Dominance and Symmetry a.
Matrix Multiplication Chapter IV Special Linear Systems By Gokturk Poyrazoglu The State University of New York at Buffalo BEST Group Winter Lecture Series Outline 1. Diagonal Dominance and Symmetry a.
The design and use of a sparse direct solver for skew symmetric matrices
 The design and use of a sparse direct solver for skew symmetric matrices Iain S. Duff May 6, 2008 RAL-TR-2006-027 c Science and Technology Facilities Council Enquires about copyright, reproduction and
The design and use of a sparse direct solver for skew symmetric matrices Iain S. Duff May 6, 2008 RAL-TR-2006-027 c Science and Technology Facilities Council Enquires about copyright, reproduction and
BlockMatrixComputations and the Singular Value Decomposition. ATaleofTwoIdeas
 BlockMatrixComputations and the Singular Value Decomposition ATaleofTwoIdeas Charles F. Van Loan Department of Computer Science Cornell University Supported in part by the NSF contract CCR-9901988. Block
BlockMatrixComputations and the Singular Value Decomposition ATaleofTwoIdeas Charles F. Van Loan Department of Computer Science Cornell University Supported in part by the NSF contract CCR-9901988. Block
MTH 2530: Linear Algebra. Sec Systems of Linear Equations
 MTH 0 Linear Algebra Professor Chao Huang Department of Mathematics and Statistics Wright State University Week # Section.,. Sec... Systems of Linear Equations... D examples Example Consider a system of
MTH 0 Linear Algebra Professor Chao Huang Department of Mathematics and Statistics Wright State University Week # Section.,. Sec... Systems of Linear Equations... D examples Example Consider a system of
MS&E 318 (CME 338) Large-Scale Numerical Optimization
 Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization Instructor: Michael Saunders Spring 2017 Notes 10: MINOS Part 1: the Reduced-Gradient
Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization Instructor: Michael Saunders Spring 2017 Notes 10: MINOS Part 1: the Reduced-Gradient
Sparse linear solvers
 Sparse linear solvers Laura Grigori ALPINES INRIA and LJLL, UPMC On sabbatical at UC Berkeley March 2015 Plan Sparse linear solvers Sparse matrices and graphs Classes of linear solvers Sparse Cholesky
Sparse linear solvers Laura Grigori ALPINES INRIA and LJLL, UPMC On sabbatical at UC Berkeley March 2015 Plan Sparse linear solvers Sparse matrices and graphs Classes of linear solvers Sparse Cholesky
Using Postordering and Static Symbolic Factorization for Parallel Sparse LU
 Using Postordering and Static Symbolic Factorization for Parallel Sparse LU Michel Cosnard LORIA - INRIA Lorraine Nancy, France Michel.Cosnard@loria.fr Laura Grigori LORIA - Univ. Henri Poincaré Nancy,
Using Postordering and Static Symbolic Factorization for Parallel Sparse LU Michel Cosnard LORIA - INRIA Lorraine Nancy, France Michel.Cosnard@loria.fr Laura Grigori LORIA - Univ. Henri Poincaré Nancy,
Linear Algebra. Solving Linear Systems. Copyright 2005, W.R. Winfrey
 Copyright 2005, W.R. Winfrey Topics Preliminaries Echelon Form of a Matrix Elementary Matrices; Finding A -1 Equivalent Matrices LU-Factorization Topics Preliminaries Echelon Form of a Matrix Elementary
Copyright 2005, W.R. Winfrey Topics Preliminaries Echelon Form of a Matrix Elementary Matrices; Finding A -1 Equivalent Matrices LU-Factorization Topics Preliminaries Echelon Form of a Matrix Elementary
Downloaded 08/28/12 to Redistribution subject to SIAM license or copyright; see
 SIAM J. MATRIX ANAL. APPL. Vol. 22, No. 4, pp. 997 1013 c 2001 Society for Industrial and Applied Mathematics MULTIPLE-RANK MODIFICATIONS OF A SPARSE CHOLESKY FACTORIZATION TIMOTHY A. DAVIS AND WILLIAM
SIAM J. MATRIX ANAL. APPL. Vol. 22, No. 4, pp. 997 1013 c 2001 Society for Industrial and Applied Mathematics MULTIPLE-RANK MODIFICATIONS OF A SPARSE CHOLESKY FACTORIZATION TIMOTHY A. DAVIS AND WILLIAM
ETNA Kent State University
 C 8 Electronic Transactions on Numerical Analysis. Volume 17, pp. 76-2, 2004. Copyright 2004,. ISSN 1068-613. etnamcs.kent.edu STRONG RANK REVEALING CHOLESKY FACTORIZATION M. GU AND L. MIRANIAN Abstract.
C 8 Electronic Transactions on Numerical Analysis. Volume 17, pp. 76-2, 2004. Copyright 2004,. ISSN 1068-613. etnamcs.kent.edu STRONG RANK REVEALING CHOLESKY FACTORIZATION M. GU AND L. MIRANIAN Abstract.
Downloaded 08/28/12 to Redistribution subject to SIAM license or copyright; see
 SIAMJ.MATRIX ANAL. APPL. c 1997 Society for Industrial and Applied Mathematics Vol. 18, No. 1, pp. 140 158, January 1997 012 AN UNSYMMETRIC-PATTERN MULTIFRONTAL METHOD FOR SPARSE LU FACTORIZATION TIMOTHY
SIAMJ.MATRIX ANAL. APPL. c 1997 Society for Industrial and Applied Mathematics Vol. 18, No. 1, pp. 140 158, January 1997 012 AN UNSYMMETRIC-PATTERN MULTIFRONTAL METHOD FOR SPARSE LU FACTORIZATION TIMOTHY
Linear Algebra I Lecture 10
 Linear Algebra I Lecture 10 Xi Chen 1 1 University of Alberta January 30, 2019 Outline 1 Gauss-Jordan Algorithm ] Let A = [a ij m n be an m n matrix. To reduce A to a reduced row echelon form using elementary
Linear Algebra I Lecture 10 Xi Chen 1 1 University of Alberta January 30, 2019 Outline 1 Gauss-Jordan Algorithm ] Let A = [a ij m n be an m n matrix. To reduce A to a reduced row echelon form using elementary
POLI270 - Linear Algebra
 POLI7 - Linear Algebra Septemer 8th Basics a x + a x +... + a n x n b () is the linear form where a, b are parameters and x n are variables. For a given equation such as x +x you only need a variable and
POLI7 - Linear Algebra Septemer 8th Basics a x + a x +... + a n x n b () is the linear form where a, b are parameters and x n are variables. For a given equation such as x +x you only need a variable and
Homework Set #8 Solutions
 Exercises.2 (p. 19) Homework Set #8 Solutions Assignment: Do #6, 8, 12, 14, 2, 24, 26, 29, 0, 2, 4, 5, 6, 9, 40, 42 6. Reducing the matrix to echelon form: 1 5 2 1 R2 R2 R1 1 5 0 18 12 2 1 R R 2R1 1 5
Exercises.2 (p. 19) Homework Set #8 Solutions Assignment: Do #6, 8, 12, 14, 2, 24, 26, 29, 0, 2, 4, 5, 6, 9, 40, 42 6. Reducing the matrix to echelon form: 1 5 2 1 R2 R2 R1 1 5 0 18 12 2 1 R R 2R1 1 5
Using SVD to Recommend Movies
 Michael Percy University of California, Santa Cruz Last update: December 12, 2009 Last update: December 12, 2009 1 / Outline 1 Introduction 2 Singular Value Decomposition 3 Experiments 4 Conclusion Last
Michael Percy University of California, Santa Cruz Last update: December 12, 2009 Last update: December 12, 2009 1 / Outline 1 Introduction 2 Singular Value Decomposition 3 Experiments 4 Conclusion Last
Numerical Linear Algebra
 Numerical Linear Algebra The two principal problems in linear algebra are: Linear system Given an n n matrix A and an n-vector b, determine x IR n such that A x = b Eigenvalue problem Given an n n matrix
Numerical Linear Algebra The two principal problems in linear algebra are: Linear system Given an n n matrix A and an n-vector b, determine x IR n such that A x = b Eigenvalue problem Given an n n matrix
Scientific Computing with Case Studies SIAM Press, Lecture Notes for Unit VII Sparse Matrix
 Scientific Computing with Case Studies SIAM Press, 2009 http://www.cs.umd.edu/users/oleary/sccswebpage Lecture Notes for Unit VII Sparse Matrix Computations Part 1: Direct Methods Dianne P. O Leary c 2008
Scientific Computing with Case Studies SIAM Press, 2009 http://www.cs.umd.edu/users/oleary/sccswebpage Lecture Notes for Unit VII Sparse Matrix Computations Part 1: Direct Methods Dianne P. O Leary c 2008
Eigenvalues and Eigenvectors
 5 Eigenvalues and Eigenvectors 5.2 THE CHARACTERISTIC EQUATION DETERMINANATS n n Let A be an matrix, let U be any echelon form obtained from A by row replacements and row interchanges (without scaling),
5 Eigenvalues and Eigenvectors 5.2 THE CHARACTERISTIC EQUATION DETERMINANATS n n Let A be an matrix, let U be any echelon form obtained from A by row replacements and row interchanges (without scaling),
Communication Avoiding LU Factorization using Complete Pivoting
 Communication Avoiding LU Factorization using Complete Pivoting Implementation and Analysis Avinash Bhardwaj Department of Industrial Engineering and Operations Research University of California, Berkeley
Communication Avoiding LU Factorization using Complete Pivoting Implementation and Analysis Avinash Bhardwaj Department of Industrial Engineering and Operations Research University of California, Berkeley
Chapter 4. Determinants
 4.2 The Determinant of a Square Matrix 1 Chapter 4. Determinants 4.2 The Determinant of a Square Matrix Note. In this section we define the determinant of an n n matrix. We will do so recursively by defining
4.2 The Determinant of a Square Matrix 1 Chapter 4. Determinants 4.2 The Determinant of a Square Matrix Note. In this section we define the determinant of an n n matrix. We will do so recursively by defining
Matrix Factorization and Analysis
 Chapter 7 Matrix Factorization and Analysis Matrix factorizations are an important part of the practice and analysis of signal processing. They are at the heart of many signal-processing algorithms. Their
Chapter 7 Matrix Factorization and Analysis Matrix factorizations are an important part of the practice and analysis of signal processing. They are at the heart of many signal-processing algorithms. Their
MTH 464: Computational Linear Algebra
 MTH 464: Computational Linear Algebra Lecture Outlines Exam 2 Material Prof. M. Beauregard Department of Mathematics & Statistics Stephen F. Austin State University March 2, 2018 Linear Algebra (MTH 464)
MTH 464: Computational Linear Algebra Lecture Outlines Exam 2 Material Prof. M. Beauregard Department of Mathematics & Statistics Stephen F. Austin State University March 2, 2018 Linear Algebra (MTH 464)
Block Bidiagonal Decomposition and Least Squares Problems
 Block Bidiagonal Decomposition and Least Squares Problems Åke Björck Department of Mathematics Linköping University Perspectives in Numerical Analysis, Helsinki, May 27 29, 2008 Outline Bidiagonal Decomposition
Block Bidiagonal Decomposition and Least Squares Problems Åke Björck Department of Mathematics Linköping University Perspectives in Numerical Analysis, Helsinki, May 27 29, 2008 Outline Bidiagonal Decomposition
ANONSINGULAR tridiagonal linear system of the form
 Generalized Diagonal Pivoting Methods for Tridiagonal Systems without Interchanges Jennifer B. Erway, Roummel F. Marcia, and Joseph A. Tyson Abstract It has been shown that a nonsingular symmetric tridiagonal
Generalized Diagonal Pivoting Methods for Tridiagonal Systems without Interchanges Jennifer B. Erway, Roummel F. Marcia, and Joseph A. Tyson Abstract It has been shown that a nonsingular symmetric tridiagonal
Numerical Linear Algebra
 Numerical Linear Algebra Direct Methods Philippe B. Laval KSU Fall 2017 Philippe B. Laval (KSU) Linear Systems: Direct Solution Methods Fall 2017 1 / 14 Introduction The solution of linear systems is one
Numerical Linear Algebra Direct Methods Philippe B. Laval KSU Fall 2017 Philippe B. Laval (KSU) Linear Systems: Direct Solution Methods Fall 2017 1 / 14 Introduction The solution of linear systems is one
9. Numerical linear algebra background
 Convex Optimization Boyd & Vandenberghe 9. Numerical linear algebra background matrix structure and algorithm complexity solving linear equations with factored matrices LU, Cholesky, LDL T factorization
Convex Optimization Boyd & Vandenberghe 9. Numerical linear algebra background matrix structure and algorithm complexity solving linear equations with factored matrices LU, Cholesky, LDL T factorization
LINEAR PROGRAMMING ALGORITHMS USING LEAST-SQUARES METHOD
 LINEAR PROGRAMMING ALGORITHMS USING LEAST-SQUARES METHOD A Thesis Presented to The Academic Faculty by Seunghyun Kong In Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the
LINEAR PROGRAMMING ALGORITHMS USING LEAST-SQUARES METHOD A Thesis Presented to The Academic Faculty by Seunghyun Kong In Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the
Exploiting Fill-in and Fill-out in Gaussian-like Elimination Procedures on the Extended Jacobian Matrix
 2nd European Workshop on AD 1 Exploiting Fill-in and Fill-out in Gaussian-like Elimination Procedures on the Extended Jacobian Matrix Andrew Lyons (Vanderbilt U.) / Uwe Naumann (RWTH Aachen) 2nd European
2nd European Workshop on AD 1 Exploiting Fill-in and Fill-out in Gaussian-like Elimination Procedures on the Extended Jacobian Matrix Andrew Lyons (Vanderbilt U.) / Uwe Naumann (RWTH Aachen) 2nd European
CS227-Scientific Computing. Lecture 4: A Crash Course in Linear Algebra
 CS227-Scientific Computing Lecture 4: A Crash Course in Linear Algebra Linear Transformation of Variables A common phenomenon: Two sets of quantities linearly related: y = 3x + x 2 4x 3 y 2 = 2.7x 2 x
CS227-Scientific Computing Lecture 4: A Crash Course in Linear Algebra Linear Transformation of Variables A common phenomenon: Two sets of quantities linearly related: y = 3x + x 2 4x 3 y 2 = 2.7x 2 x
LU Factorization. LU factorization is the most common way of solving linear systems! Ax = b LUx = b
 AM 205: lecture 7 Last time: LU factorization Today s lecture: Cholesky factorization, timing, QR factorization Reminder: assignment 1 due at 5 PM on Friday September 22 LU Factorization LU factorization
AM 205: lecture 7 Last time: LU factorization Today s lecture: Cholesky factorization, timing, QR factorization Reminder: assignment 1 due at 5 PM on Friday September 22 LU Factorization LU factorization
1. Introduction. We are concerned with the linear programming (LP) problem in the standard form. minimize subject to Ax = b, x 0,
 A GENERALIZATION OF THE REVISED SIMPLEX ALGORITHM FOR LINEAR PROGRAMMING PING-QI PAN Abstract. Recently the concept of basis, which plays a fundamental role in the simplex methodology, were generalized
A GENERALIZATION OF THE REVISED SIMPLEX ALGORITHM FOR LINEAR PROGRAMMING PING-QI PAN Abstract. Recently the concept of basis, which plays a fundamental role in the simplex methodology, were generalized
Sparse least squares and Q-less QR
 Notes for 2016-02-29 Sparse least squares and Q-less QR Suppose we want to solve a full-rank least squares problem in which A is large and sparse. In principle, we could solve the problem via the normal
Notes for 2016-02-29 Sparse least squares and Q-less QR Suppose we want to solve a full-rank least squares problem in which A is large and sparse. In principle, we could solve the problem via the normal
MS&E 318 (CME 338) Large-Scale Numerical Optimization
 Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization 1 Origins Instructor: Michael Saunders Spring 2015 Notes 9: Augmented Lagrangian Methods
Stanford University, Management Science & Engineering (and ICME) MS&E 318 (CME 338) Large-Scale Numerical Optimization 1 Origins Instructor: Michael Saunders Spring 2015 Notes 9: Augmented Lagrangian Methods
22A-2 SUMMER 2014 LECTURE 5
 A- SUMMER 0 LECTURE 5 NATHANIEL GALLUP Agenda Elimination to the identity matrix Inverse matrices LU factorization Elimination to the identity matrix Previously, we have used elimination to get a system
A- SUMMER 0 LECTURE 5 NATHANIEL GALLUP Agenda Elimination to the identity matrix Inverse matrices LU factorization Elimination to the identity matrix Previously, we have used elimination to get a system
Applied Numerical Linear Algebra. Lecture 8
 Applied Numerical Linear Algebra. Lecture 8 1/ 45 Perturbation Theory for the Least Squares Problem When A is not square, we define its condition number with respect to the 2-norm to be k 2 (A) σ max (A)/σ
Applied Numerical Linear Algebra. Lecture 8 1/ 45 Perturbation Theory for the Least Squares Problem When A is not square, we define its condition number with respect to the 2-norm to be k 2 (A) σ max (A)/σ
Section 3.5 LU Decomposition (Factorization) Key terms. Matrix factorization Forward and back substitution LU-decomposition Storage economization
 Section 3.5 LU Decomposition (Factorization) Key terms Matrix factorization Forward and back substitution LU-decomposition Storage economization In matrix analysis as implemented in modern software the
Section 3.5 LU Decomposition (Factorization) Key terms Matrix factorization Forward and back substitution LU-decomposition Storage economization In matrix analysis as implemented in modern software the
Key words. numerical linear algebra, direct methods, Cholesky factorization, sparse matrices, mathematical software, matrix updates.
 ROW MODIFICATIONS OF A SPARSE CHOLESKY FACTORIZATION TIMOTHY A. DAVIS AND WILLIAM W. HAGER Abstract. Given a sparse, symmetric positive definite matrix C and an associated sparse Cholesky factorization
ROW MODIFICATIONS OF A SPARSE CHOLESKY FACTORIZATION TIMOTHY A. DAVIS AND WILLIAM W. HAGER Abstract. Given a sparse, symmetric positive definite matrix C and an associated sparse Cholesky factorization
Some Notes on Least Squares, QR-factorization, SVD and Fitting
 Department of Engineering Sciences and Mathematics January 3, 013 Ove Edlund C000M - Numerical Analysis Some Notes on Least Squares, QR-factorization, SVD and Fitting Contents 1 Introduction 1 The Least
Department of Engineering Sciences and Mathematics January 3, 013 Ove Edlund C000M - Numerical Analysis Some Notes on Least Squares, QR-factorization, SVD and Fitting Contents 1 Introduction 1 The Least
Using Random Butterfly Transformations to Avoid Pivoting in Sparse Direct Methods
 Using Random Butterfly Transformations to Avoid Pivoting in Sparse Direct Methods Marc Baboulin 1, Xiaoye S. Li 2 and François-Henry Rouet 2 1 University of Paris-Sud, Inria Saclay, France 2 Lawrence Berkeley
Using Random Butterfly Transformations to Avoid Pivoting in Sparse Direct Methods Marc Baboulin 1, Xiaoye S. Li 2 and François-Henry Rouet 2 1 University of Paris-Sud, Inria Saclay, France 2 Lawrence Berkeley
I-v k e k. (I-e k h kt ) = Stability of Gauss-Huard Elimination for Solving Linear Systems. 1 x 1 x x x x
 Technical Report CS-93-08 Department of Computer Systems Faculty of Mathematics and Computer Science University of Amsterdam Stability of Gauss-Huard Elimination for Solving Linear Systems T. J. Dekker
Technical Report CS-93-08 Department of Computer Systems Faculty of Mathematics and Computer Science University of Amsterdam Stability of Gauss-Huard Elimination for Solving Linear Systems T. J. Dekker
Numerical Methods I Non-Square and Sparse Linear Systems
 Numerical Methods I Non-Square and Sparse Linear Systems Aleksandar Donev Courant Institute, NYU 1 donev@courant.nyu.edu 1 MATH-GA 2011.003 / CSCI-GA 2945.003, Fall 2014 September 25th, 2014 A. Donev (Courant
Numerical Methods I Non-Square and Sparse Linear Systems Aleksandar Donev Courant Institute, NYU 1 donev@courant.nyu.edu 1 MATH-GA 2011.003 / CSCI-GA 2945.003, Fall 2014 September 25th, 2014 A. Donev (Courant
MATH 2331 Linear Algebra. Section 2.1 Matrix Operations. Definition: A : m n, B : n p. Example: Compute AB, if possible.
 MATH 2331 Linear Algebra Section 2.1 Matrix Operations Definition: A : m n, B : n p ( 1 2 p ) ( 1 2 p ) AB = A b b b = Ab Ab Ab Example: Compute AB, if possible. 1 Row-column rule: i-j-th entry of AB:
MATH 2331 Linear Algebra Section 2.1 Matrix Operations Definition: A : m n, B : n p ( 1 2 p ) ( 1 2 p ) AB = A b b b = Ab Ab Ab Example: Compute AB, if possible. 1 Row-column rule: i-j-th entry of AB:
