CE 530 Molecular Simulation
|
|
|
- Marybeth Nancy Rogers
- 5 years ago
- Views:
Transcription
1 CE 530 Molecular Simulation Lecture Molecular Dynamics Simulation David A. Kofke Department of Chemical Engineering SUNY Buffalo
2 MD of hard disks intuitive Review and Preview collision detection and impulsive dynamics Monte Carlo convenient sampling of ensembles no dynamics biasing possible to improve performance Molecular dynamics equations of motion integration schemes evaluation of dynamical properties extensions to other ensembles focus on atomic systems for now
3 3 Classical Equations of Motion Several formulations are in use Newtonian Lagrangian Hamiltonian Advantages of non-newtonian formulations more general, no need for fictitious forces better suited for multiparticle systems better handling of constraints can be formulated from more basic postulates Assume conservative forces! F =! U Gradient of a scalar potential energy
4 4 Newtonian Formulation Cartesian spatial coordinates r i = (x i,y i,z i ) are primary variables for N atoms, system of N nd-order differential equations m d r i dt m!!r i = F i Sample application: D motion in central force field m!!x = F ê x = f (r)ˆr ê x = xf x + y m!!y = F ê y = f (r)ˆr ê y = yf x + y Polar coordinates are more natural and convenient r F = f (r)ˆr mr! θ = l constant angular momentum m!! r = f (r) + l mr 3 fictitious (centrifugal) force
5 5 Generalized Coordinates Any convenient coordinates for description of particular system use q i as symbol for general coordinate examples diatomic {q,,q 6 } = {x com, y com, z com, r, θ, φ} -D motion in central field {q, q } = {r, θ} Kinetic energy general quadratic form K = M 0 (q) + examples rotating diatomic -D central motion M j (q)!q j + usually vanish M jk (q)!q j!q k ( ) + 8 m!r + r! K = m!q +!q +!q 3 K = m (!r + r θ! ) θ r φ θ + (r sinθ)!φ
6 6 Lagrangian Formulation Independent of coordinate system Define the Lagrangian L(q,!q) K(q,!q) U (q) Equations of motion d dt L!q L = 0 j q j j = N N second-order differential equations Central-force example ( ) U (r) L = m!r + r θ! d dt L!r = L r m!! r = mr θ! f (r)! F r =! r U = f (r) d dt L θ! = L θ d dt ( mr θ! ) = 0
7 7 Hamiltonian Formulation. Motivation Appropriate for application to statistical mechanics and quantum mechanics Newtonian and Lagrangian viewpoints take the q i as the fundamental variables N-variable configuration space!q i appears only as a convenient shorthand for dq/dt working formulas are nd-order differential equations Hamiltonian formulation seeks to work with st-order differential equations N variables treat the coordinate and its time derivative as independent variables appropriate quantum-mechanically
8 Hamiltonian Formulation. Preparation 8 Mathematically, Lagrangian treats q and!q as distinct L(q j,!q j,t) identify the generalized momentum as p j = L!q j e.g. if L = K U = m!q U (q); p = L /!q = m!q Lagrangian equations of motion We would like a formulation in which p is an independent variable p i is the derivative of the Lagrangian with respect to!q i, and we re looking to replace!q i with p i we need? dp dt j L = q j
9 9 Hamiltonian Formulation 3. Defintion a Legendre transform! Define the Hamiltonian, H H(q,p) = L(q,!q) p j!q j = K(q,!q) +U (q) + = a j!q j +U (q) + = + a j!q j +U (q) = K +U K!q!q j j (a j!q j )!q j H equals the total energy (kinetic plus potential)
10 0 Hamiltonian Formulation 4. Dynamics Hamilton s equations of motion From Lagrangian equations, written in terms of momentum Differential change in L dl = L L dq + q!q d!q =!pdq + pd!q Legendre transform H = (L p!q) dh = (!pdq!qdp) dh =!pdq +!qdp!q = + H p!p = H q dp dt =!p = L q p = L!q Lagrange s equation of motion Definition of momentum Hamilton s equations of motion Conservation of energy dh dt =!p dq dt +!q dp dt =!p!q +!q!p = 0
11 Hamiltonian Formulation 5. Example Particle motion in central force field H = K + U r pθ p = + + Ur () m mr r dr p () r dθ p () θ!q = + H = = dt m dt p mr dp (3) r pθ dp = f() r (4) θ!p = H Lagrange s equations = 0 dt 3 q mr dt m!! r = mr θ! f (r)! F r =! r U = f (r) Equations no simpler, but theoretical basis is better d dt ( mr θ! ) = 0
12 Phase Space (again) Return to the complete picture of phase space full specification of microstate of the system is given by the values of all positions and all momenta of all atoms Γ = (p N,r N ) view positions and momenta as completely independent coordinates connection between them comes only through equation of motion Motion through phase space helpful to think of dynamics as simple movement through the highdimensional phase space facilitate connection to quantum mechanics basis for theoretical treatments of dynamics understanding of integrators Γ
13 3 Integration Algorithms Equations of motion in cartesian coordinates dr j dt dp dt j = p j m = F j r = ( r, r ) p = ( p, p ) i= i j F Desirable features of an integrator minimal need to compute forces (a very expensive calculation) good stability for large time steps good accuracy conserves energy and momentum time-reversible area-preserving (symplectic) x x N y y -dimensional space (for example) Fj = Fij pairwise additive forces More on these later
14 Verlet Algorithm. Equations 4 Very simple, very good, very popular algorithm Consider expansion of coordinate forward and backward in time r(t + δt) = r(t) + m p(t)δt + m F(t)δt + 3!!!! r(t)δt3 + O(δt 4 ) r(t δt) = r(t) m p(t)δt + m F(t)δt 3!!!! r(t)δt3 + O(δt 4 ) Add these together Rearrange 4 r( t+ δt) + r( t δt) = r( t) + F( t) δt + O( δt ) update without ever consulting velocities! m m 4 r( t+ δt) = r( t) r( t δt) + F( t) δt + O( δt )
15 Verlet Algorithm. Flow diagram 5 One force evaluation per time step One MD Cycle Configuration r(t) Previous configuration r(t-dt) Compute forces F(t) on all atoms using r(t) Advance all positions according to r(t+δt) = r(t)-r(t-δt)+f(t)/m dt Add to block sum Entire Simulation Initialization Reset block sums New configuration move per cycle Add to block sum cycles per block Compute block average blocks per simulation Compute final results No End of block? Yes Block averages
16 6 Verlet Algorithm. Flow Diagram r v F t-δt t t+δt Given current position and position at end of previous time step Schematic from Allen & Tildesley, Computer Simulation of Liquids
17 7 Verlet Algorithm. Flow Diagram r v F t-δt t t+δt Compute the force at the current position Schematic from Allen & Tildesley, Computer Simulation of Liquids
18 8 Verlet Algorithm. Flow Diagram r v F t-δt t t+δt Compute new position from present and previous positions, and present force Schematic from Allen & Tildesley, Computer Simulation of Liquids
19 9 Verlet Algorithm. Flow Diagram r v F t-δt t-δt t t+δt Advance to next time step, repeat Schematic from Allen & Tildesley, Computer Simulation of Liquids
20 Forces. Formalism 3 Force is the gradient of the potential F Force on, due to = ur ( ) ur ( ) ur ( ) = e x e x y du( r) r r = x dr e + e x y f( r) = x x + y y r e e y y 4 y x r r x x y y = ( ) + ( ) Energy Force / F = F Separation, r/σ.5
21 Forces. LJ Model 4 Force is the gradient of the potential f( r ) F e ey = x x y r + e.g., Lennard-Jones model σ σ ur () = 4ε r r du f() r = dr 6 48ε σ σ =+ σ r r ε σ σ F = x x y σ r + r e e 4 0 y - y x r r x x y y = ( ) + ( ) Energy Force / Separation, r/σ.5
22 7 Verlet Algorithm. 4. Loose Ends Initialization how to get position at previous time step when starting out? simple approximation r( t δt) = r( t ) v( t ) δt Obtaining the velocities not evaluated during normal course of algorithm needed to compute some properties, e.g. temperature diffusion constant finite difference v() t = [ r( t+ δt) r( t δt) ] + O( δt ) δ t
23 Verlet Algorithm 5. Performance Issues 8 Time reversible forward time step replace δt with -δt r( t δt) = r( t) r( t + δt) + F() t δt m same algorithm, with same positions and forces, moves system backward in time Numerical imprecision of adding large/small numbers m r( t+ δt) = r( t) r( t δt) + F( t) δt r( t+ ( δt) ) = r( t) r( t ( δt) ) + F( t) ( δ t) O(δt ) O(δt ) m r( t+ δt) r( t) = r( t) r( t δt) + F( t) δt m O(δt 0 ) O(δt 0 ) O(δt )
24 Initial Velocities (from Lecture 3) Random direction randomize each component independently randomize direction by choosing point on spherical surface Magnitude consistent with desired temperature. Choices: Maxwell-Boltzmann: Uniform over (-/,+/), then scale so that Constant at vx =± kt/ m Same for y, z components ( x ) prob( v ) exp mv / kt Be sure to shift so center-of-mass momentum is zero P x N p i, x p p P ix, ix, x x N v ix, = / kt m 9
25 30 Leapfrog Algorithm Eliminates addition of small numbers O(δt ) to differences in large ones O(δt 0 ) Algorithm δ m r( t+ t) = r( t) + v( t+ δt) δt v( t+ δt) = v( t δt) + F( t) δt
26 3 Leapfrog Algorithm Eliminates addition of small numbers O(δt ) to differences in large ones O(δt 0 ) Algorithm δ m r( t+ t) = r( t) + v( t+ δt) δt v( t+ δt) = v( t δt) + F( t) δt Mathematically equivalent to Verlet algorithm r( t+ δt) = r( t) + ( t t) v δ + F( t) δt δt m
27 3 Leapfrog Algorithm Eliminates addition of small numbers O(δt ) to differences in large ones O(δt 0 ) Algorithm δ m r( t+ t) = r( t) + v( t+ δt) δt v( t+ δt) = v( t δt) + F( t) δt Mathematically equivalent to Verlet algorithm r( t+ δt) = r( t) + ( t t) v δ + F( t) δt δt m r(t) as evaluated from previous time step r() t = r( t δt) + v( t δt) δt
28 33 Leapfrog Algorithm Eliminates addition of small numbers O(δt ) to differences in large ones O(δt 0 ) Algorithm δ m r( t+ t) = r( t) + v( t+ δt) δt v( t+ δt) = v( t δt) + F( t) δt Mathematically equivalent to Verlet algorithm r( t+ δt) = r( t) + ( t t) v δ + F( t) δt δt m r(t) as evaluated from previous time step r() t = r( t δt) + v( t δt) δt ( ) r( t+ δt) = r( t) + r( t) r( t δt) + F( t) δt m
29 34 Leapfrog Algorithm Eliminates addition of small numbers O(δt ) to differences in large ones O(δt 0 ) Algorithm δ m r( t+ t) = r( t) + v( t+ δt) δt v( t+ δt) = v( t δt) + F( t) δt Mathematically equivalent to Verlet algorithm r( t+ δt) = r( t) + ( t t) v δ + F( t) δt δt m r(t) as evaluated from previous time step r() t = r( t δt) + v( t δt) δt ( ) r( t+ δt) = r( t) + r( t) r( t δt) + F( t) δt m r( t+ δt) = r( t) r( t δt) + F( t) δt original algorithm m
30 35 Leapfrog Algorithm. Flow Diagram r v F t-δt t t+δt Given current position, and velocity at last half-step Schematic from Allen & Tildesley, Computer Simulation of Liquids
31 36 Leapfrog Algorithm. Flow Diagram r v F t-δt t t+δt Compute current force Schematic from Allen & Tildesley, Computer Simulation of Liquids
32 37 Leapfrog Algorithm. Flow Diagram r v F t-δt t t+δt Compute velocity at next half-step Schematic from Allen & Tildesley, Computer Simulation of Liquids
33 38 Leapfrog Algorithm. Flow Diagram r v F t-δt t t+δt Compute next position Schematic from Allen & Tildesley, Computer Simulation of Liquids
34 39 Leapfrog Algorithm. Flow Diagram r v F t-δt t-δt t t+δt Advance to next time step, repeat Schematic from Allen & Tildesley, Computer Simulation of Liquids
35 40 Leapfrog Algorithm. 3. Loose Ends Initialization how to get velocity at previous time step when starting out? simple approximation 0 δ = 0 m 0 v( t t) v( t ) F( t ) δt Obtaining the velocities interpolate v() t = ( t δt) ( t δt) v + + v
36 4 Velocity Verlet Algorithm Roundoff advantage of leapfrog, but better treatment of velocities Algorithm v( + ) = v( ) + [ F( ) + F( + ) m ] Implemented in stages given current force compute r at new time add current-force term to velocity (gives v at half-time step) compute new force add new-force term to velocity Also mathematically equivalent to Verlet algorithm (in giving values of r) m r( t + δt) = r( t) + v( t) δt + F( t) δt t δt t t t δt δt
37 4 Velocity Verlet Algorithm. Flow Diagram t-δt t t+δt r v Given current position, velocity, and force F Schematic from Allen & Tildesley, Computer Simulation of Liquids
38 43 Velocity Verlet Algorithm. Flow Diagram t-δt t t+δt r v Compute new position F Schematic from Allen & Tildesley, Computer Simulation of Liquids
39 44 Velocity Verlet Algorithm. Flow Diagram t-δt t t+δt r v Compute velocity at half step F Schematic from Allen & Tildesley, Computer Simulation of Liquids
40 45 Velocity Verlet Algorithm. Flow Diagram t-δt t t+δt r v Compute force at new position F Schematic from Allen & Tildesley, Computer Simulation of Liquids
41 46 Velocity Verlet Algorithm. Flow Diagram t-δt t t+δt r v Compute velocity at full step F Schematic from Allen & Tildesley, Computer Simulation of Liquids
42 47 Velocity Verlet Algorithm. Flow Diagram t-δt t-δt t t+δt r v Advance to next time step, repeat F Schematic from Allen & Tildesley, Computer Simulation of Liquids
43 48 Other Algorithms Predictor-Corrector not time reversible easier to apply in some instances constraints rigid rotations Beeman better treatment of velocities Velocity-corrected Verlet
44 49 Summary Several formulations of mechanics Hamiltonian preferred independence of choice of coordinates emphasis on phase space Integration algorithms Calculation of forces Simple Verlet algorithms Verlet Leapfrog Velocity Verlet Next up: Calculation of dynamical properties
Classical Equations of Motion
 3 Classical Equations of Motion Several formulations are in use Newtonian Lagrangian Hamiltonian Advantages of non-newtonian formulations more general, no need for fictitious forces better suited for multiparticle
3 Classical Equations of Motion Several formulations are in use Newtonian Lagrangian Hamiltonian Advantages of non-newtonian formulations more general, no need for fictitious forces better suited for multiparticle
Introduction to molecular dynamics
 1 Introduction to molecular dynamics Yves Lansac Université François Rabelais, Tours, France Visiting MSE, GIST for the summer Molecular Simulation 2 Molecular simulation is a computational experiment.
1 Introduction to molecular dynamics Yves Lansac Université François Rabelais, Tours, France Visiting MSE, GIST for the summer Molecular Simulation 2 Molecular simulation is a computational experiment.
Introduction to Simulation - Lectures 17, 18. Molecular Dynamics. Nicolas Hadjiconstantinou
 Introduction to Simulation - Lectures 17, 18 Molecular Dynamics Nicolas Hadjiconstantinou Molecular Dynamics Molecular dynamics is a technique for computing the equilibrium and non-equilibrium properties
Introduction to Simulation - Lectures 17, 18 Molecular Dynamics Nicolas Hadjiconstantinou Molecular Dynamics Molecular dynamics is a technique for computing the equilibrium and non-equilibrium properties
CE 530 Molecular Simulation
 1 CE 530 Molecular Simulation Lecture 14 Molecular Models David A. Kofke Department of Chemical Engineering SUNY Buffalo kofke@eng.buffalo.edu 2 Review Monte Carlo ensemble averaging, no dynamics easy
1 CE 530 Molecular Simulation Lecture 14 Molecular Models David A. Kofke Department of Chemical Engineering SUNY Buffalo kofke@eng.buffalo.edu 2 Review Monte Carlo ensemble averaging, no dynamics easy
Curves in the configuration space Q or in the velocity phase space Ω satisfying the Euler-Lagrange (EL) equations,
 Physics 6010, Fall 2010 Hamiltonian Formalism: Hamilton s equations. Conservation laws. Reduction. Poisson Brackets. Relevant Sections in Text: 8.1 8.3, 9.5 The Hamiltonian Formalism We now return to formal
Physics 6010, Fall 2010 Hamiltonian Formalism: Hamilton s equations. Conservation laws. Reduction. Poisson Brackets. Relevant Sections in Text: 8.1 8.3, 9.5 The Hamiltonian Formalism We now return to formal
HAMILTON S PRINCIPLE
 HAMILTON S PRINCIPLE In our previous derivation of Lagrange s equations we started from the Newtonian vector equations of motion and via D Alembert s Principle changed coordinates to generalised coordinates
HAMILTON S PRINCIPLE In our previous derivation of Lagrange s equations we started from the Newtonian vector equations of motion and via D Alembert s Principle changed coordinates to generalised coordinates
Lecture IV: Time Discretization
 Lecture IV: Time Discretization Motivation Kinematics: continuous motion in continuous time Computer simulation: Discrete time steps t Discrete Space (mesh particles) Updating Position Force induces acceleration.
Lecture IV: Time Discretization Motivation Kinematics: continuous motion in continuous time Computer simulation: Discrete time steps t Discrete Space (mesh particles) Updating Position Force induces acceleration.
CE 530 Molecular Simulation
 CE 530 Molecular Simulation Lecture 7 Beyond Atoms: Simulating Molecules David A. Kofke Department of Chemical Engineering SUNY Buffalo kofke@eng.buffalo.edu Review Fundamentals units, properties, statistical
CE 530 Molecular Simulation Lecture 7 Beyond Atoms: Simulating Molecules David A. Kofke Department of Chemical Engineering SUNY Buffalo kofke@eng.buffalo.edu Review Fundamentals units, properties, statistical
From quantum to classical statistical mechanics. Polyatomic ideal gas.
 From quantum to classical statistical mechanics. Polyatomic ideal gas. Peter Košovan peter.kosovan@natur.cuni.cz Dept. of Physical and Macromolecular Chemistry Lecture 5, Statistical Thermodynamics, MC260P105,
From quantum to classical statistical mechanics. Polyatomic ideal gas. Peter Košovan peter.kosovan@natur.cuni.cz Dept. of Physical and Macromolecular Chemistry Lecture 5, Statistical Thermodynamics, MC260P105,
Physics 5153 Classical Mechanics. Canonical Transformations-1
 1 Introduction Physics 5153 Classical Mechanics Canonical Transformations The choice of generalized coordinates used to describe a physical system is completely arbitrary, but the Lagrangian is invariant
1 Introduction Physics 5153 Classical Mechanics Canonical Transformations The choice of generalized coordinates used to describe a physical system is completely arbitrary, but the Lagrangian is invariant
Physics 235 Chapter 7. Chapter 7 Hamilton's Principle - Lagrangian and Hamiltonian Dynamics
 Chapter 7 Hamilton's Principle - Lagrangian and Hamiltonian Dynamics Many interesting physics systems describe systems of particles on which many forces are acting. Some of these forces are immediately
Chapter 7 Hamilton's Principle - Lagrangian and Hamiltonian Dynamics Many interesting physics systems describe systems of particles on which many forces are acting. Some of these forces are immediately
G : Statistical Mechanics
 G25.2651: Statistical Mechanics Notes for Lecture 1 Defining statistical mechanics: Statistical Mechanics provies the connection between microscopic motion of individual atoms of matter and macroscopically
G25.2651: Statistical Mechanics Notes for Lecture 1 Defining statistical mechanics: Statistical Mechanics provies the connection between microscopic motion of individual atoms of matter and macroscopically
Lecture 5. Alexey Boyarsky. October 21, Legendre transformation and the Hamilton equations of motion
 Lecture 5 Alexey Boyarsky October 1, 015 1 The Hamilton equations of motion 1.1 Legendre transformation and the Hamilton equations of motion First-order equations of motion. In the Lagrangian formulation,
Lecture 5 Alexey Boyarsky October 1, 015 1 The Hamilton equations of motion 1.1 Legendre transformation and the Hamilton equations of motion First-order equations of motion. In the Lagrangian formulation,
PHYS 705: Classical Mechanics. Hamiltonian Formulation & Canonical Transformation
 1 PHYS 705: Classical Mechanics Hamiltonian Formulation & Canonical Transformation Legendre Transform Let consider the simple case with ust a real value function: F x F x expresses a relationship between
1 PHYS 705: Classical Mechanics Hamiltonian Formulation & Canonical Transformation Legendre Transform Let consider the simple case with ust a real value function: F x F x expresses a relationship between
Time-Dependent Statistical Mechanics 5. The classical atomic fluid, classical mechanics, and classical equilibrium statistical mechanics
 Time-Dependent Statistical Mechanics 5. The classical atomic fluid, classical mechanics, and classical equilibrium statistical mechanics c Hans C. Andersen October 1, 2009 While we know that in principle
Time-Dependent Statistical Mechanics 5. The classical atomic fluid, classical mechanics, and classical equilibrium statistical mechanics c Hans C. Andersen October 1, 2009 While we know that in principle
2 Canonical quantization
 Phys540.nb 7 Canonical quantization.1. Lagrangian mechanics and canonical quantization Q: How do we quantize a general system?.1.1.lagrangian Lagrangian mechanics is a reformulation of classical mechanics.
Phys540.nb 7 Canonical quantization.1. Lagrangian mechanics and canonical quantization Q: How do we quantize a general system?.1.1.lagrangian Lagrangian mechanics is a reformulation of classical mechanics.
Solution Set Two. 1 Problem #1: Projectile Motion Cartesian Coordinates Polar Coordinates... 3
 : Solution Set Two Northwestern University, Classical Mechanics Classical Mechanics, Third Ed.- Goldstein October 7, 2015 Contents 1 Problem #1: Projectile Motion. 2 1.1 Cartesian Coordinates....................................
: Solution Set Two Northwestern University, Classical Mechanics Classical Mechanics, Third Ed.- Goldstein October 7, 2015 Contents 1 Problem #1: Projectile Motion. 2 1.1 Cartesian Coordinates....................................
Legendre Transforms, Calculus of Varations, and Mechanics Principles
 page 437 Appendix C Legendre Transforms, Calculus of Varations, and Mechanics Principles C.1 Legendre Transforms Legendre transforms map functions in a vector space to functions in the dual space. From
page 437 Appendix C Legendre Transforms, Calculus of Varations, and Mechanics Principles C.1 Legendre Transforms Legendre transforms map functions in a vector space to functions in the dual space. From
Lecture V: The game-engine loop & Time Integration
 Lecture V: The game-engine loop & Time Integration The Basic Game-Engine Loop Previous state: " #, %(#) ( #, )(#) Forces -(#) Integrate velocities and positions Resolve Interpenetrations Per-body change
Lecture V: The game-engine loop & Time Integration The Basic Game-Engine Loop Previous state: " #, %(#) ( #, )(#) Forces -(#) Integrate velocities and positions Resolve Interpenetrations Per-body change
15. Hamiltonian Mechanics
 University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 2015 15. Hamiltonian Mechanics Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License
University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 2015 15. Hamiltonian Mechanics Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License
Under evolution for a small time δt the area A(t) = q p evolves into an area
 Physics 106a, Caltech 6 November, 2018 Lecture 11: Hamiltonian Mechanics II Towards statistical mechanics Phase space volumes are conserved by Hamiltonian dynamics We can use many nearby initial conditions
Physics 106a, Caltech 6 November, 2018 Lecture 11: Hamiltonian Mechanics II Towards statistical mechanics Phase space volumes are conserved by Hamiltonian dynamics We can use many nearby initial conditions
[ ] ( ) L = L = r p. We can deal with this more conveniently by writing: so that L becomes: α α α. α α N N N N
![[ ] ( ) L = L = r p. We can deal with this more conveniently by writing: so that L becomes: α α α. α α N N N N [ ] ( ) L = L = r p. We can deal with this more conveniently by writing: so that L becomes: α α α. α α N N N N](/thumbs/83/87060633.jpg) Lecture 5: Angular Momentum and Energy of a System The total angular momentum is given by the sum of the angular momenta of all particles in the system: We can deal with this more conveniently by writing:
Lecture 5: Angular Momentum and Energy of a System The total angular momentum is given by the sum of the angular momenta of all particles in the system: We can deal with this more conveniently by writing:
Second quantization: where quantization and particles come from?
 110 Phys460.nb 7 Second quantization: where quantization and particles come from? 7.1. Lagrangian mechanics and canonical quantization Q: How do we quantize a general system? 7.1.1.Lagrangian Lagrangian
110 Phys460.nb 7 Second quantization: where quantization and particles come from? 7.1. Lagrangian mechanics and canonical quantization Q: How do we quantize a general system? 7.1.1.Lagrangian Lagrangian
Chapter 1. Principles of Motion in Invariantive Mechanics
 Chapter 1 Principles of Motion in Invariantive Mechanics 1.1. The Euler-Lagrange and Hamilton s equations obtained by means of exterior forms Let L = L(q 1,q 2,...,q n, q 1, q 2,..., q n,t) L(q, q,t) (1.1)
Chapter 1 Principles of Motion in Invariantive Mechanics 1.1. The Euler-Lagrange and Hamilton s equations obtained by means of exterior forms Let L = L(q 1,q 2,...,q n, q 1, q 2,..., q n,t) L(q, q,t) (1.1)
Hamilton s principle and Symmetries
 Hamilton s principle and Symmetries Sourendu Gupta TIFR, Mumbai, India Classical Mechanics 2011 August 18, 2011 The Hamiltonian The change in the Lagrangian due to a virtual change of coordinates is dl
Hamilton s principle and Symmetries Sourendu Gupta TIFR, Mumbai, India Classical Mechanics 2011 August 18, 2011 The Hamiltonian The change in the Lagrangian due to a virtual change of coordinates is dl
Concepts in Theoretical Physics
 Concepts in Theoretical Physics Lecture 1: The Principle of Least Action David Tong Newtonian Mechanics You've all done a course on Newtonian mechanics so you know how to calculate the way things move.
Concepts in Theoretical Physics Lecture 1: The Principle of Least Action David Tong Newtonian Mechanics You've all done a course on Newtonian mechanics so you know how to calculate the way things move.
4.1 Important Notes on Notation
 Chapter 4. Lagrangian Dynamics (Most of the material presented in this chapter is taken from Thornton and Marion, Chap. 7) 4.1 Important Notes on Notation In this chapter, unless otherwise stated, the
Chapter 4. Lagrangian Dynamics (Most of the material presented in this chapter is taken from Thornton and Marion, Chap. 7) 4.1 Important Notes on Notation In this chapter, unless otherwise stated, the
NONLINEAR MECHANICAL SYSTEMS LAGRANGIAN AND HAMILTONIAN FORMULATIONS. Lagrangian formulation. Ek * (f,q) = 1 2 f t I(q) f
 NONLINEAR MECHANICAL SYSTEMS LAGRANGIAN AND HAMILTONIAN FORMULATIONS q f Lagrangian formulation Ek * (f,q) = 1 2 f t I(q) f generalized coordinates (displacement) generalized velocity (flow) Ek * (f,q)
NONLINEAR MECHANICAL SYSTEMS LAGRANGIAN AND HAMILTONIAN FORMULATIONS q f Lagrangian formulation Ek * (f,q) = 1 2 f t I(q) f generalized coordinates (displacement) generalized velocity (flow) Ek * (f,q)
Physical Dynamics (SPA5304) Lecture Plan 2018
 Physical Dynamics (SPA5304) Lecture Plan 2018 The numbers on the left margin are approximate lecture numbers. Items in gray are not covered this year 1 Advanced Review of Newtonian Mechanics 1.1 One Particle
Physical Dynamics (SPA5304) Lecture Plan 2018 The numbers on the left margin are approximate lecture numbers. Items in gray are not covered this year 1 Advanced Review of Newtonian Mechanics 1.1 One Particle
The Particle-Field Hamiltonian
 The Particle-Field Hamiltonian For a fundamental understanding of the interaction of a particle with the electromagnetic field we need to know the total energy of the system consisting of particle and
The Particle-Field Hamiltonian For a fundamental understanding of the interaction of a particle with the electromagnetic field we need to know the total energy of the system consisting of particle and
Review for Final. elementary mechanics. Lagrangian and Hamiltonian Dynamics. oscillations
 Review for Final elementary mechanics Newtonian mechanics gravitation dynamics of systems of particles Lagrangian and Hamiltonian Dynamics Lagrangian mechanics Variational dynamics Hamiltonian dynamics
Review for Final elementary mechanics Newtonian mechanics gravitation dynamics of systems of particles Lagrangian and Hamiltonian Dynamics Lagrangian mechanics Variational dynamics Hamiltonian dynamics
06. Lagrangian Mechanics II
 University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 2015 06. Lagrangian Mechanics II Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License
University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 2015 06. Lagrangian Mechanics II Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License
Sketchy Notes on Lagrangian and Hamiltonian Mechanics
 Sketchy Notes on Lagrangian and Hamiltonian Mechanics Robert Jones Generalized Coordinates Suppose we have some physical system, like a free particle, a pendulum suspended from another pendulum, or a field
Sketchy Notes on Lagrangian and Hamiltonian Mechanics Robert Jones Generalized Coordinates Suppose we have some physical system, like a free particle, a pendulum suspended from another pendulum, or a field
What is Classical Molecular Dynamics?
 What is Classical Molecular Dynamics? Simulation of explicit particles (atoms, ions,... ) Particles interact via relatively simple analytical potential functions Newton s equations of motion are integrated
What is Classical Molecular Dynamics? Simulation of explicit particles (atoms, ions,... ) Particles interact via relatively simple analytical potential functions Newton s equations of motion are integrated
(Most of the material presented in this chapter is taken from Thornton and Marion, Chap. 7) p j . (5.1) !q j. " d dt = 0 (5.2) !p j . (5.
 Chapter 5. Hamiltonian Dynamics (Most of the material presented in this chapter is taken from Thornton and Marion, Chap. 7) 5.1 The Canonical Equations of Motion As we saw in section 4.7.4, the generalized
Chapter 5. Hamiltonian Dynamics (Most of the material presented in this chapter is taken from Thornton and Marion, Chap. 7) 5.1 The Canonical Equations of Motion As we saw in section 4.7.4, the generalized
Lagrangian Dynamics: Derivations of Lagrange s Equations
 Constraints and Degrees of Freedom 1.003J/1.053J Dynamics and Control I, Spring 007 Professor Thomas Peacock 4/9/007 Lecture 15 Lagrangian Dynamics: Derivations of Lagrange s Equations Constraints and
Constraints and Degrees of Freedom 1.003J/1.053J Dynamics and Control I, Spring 007 Professor Thomas Peacock 4/9/007 Lecture 15 Lagrangian Dynamics: Derivations of Lagrange s Equations Constraints and
Lecture 41: Highlights
 Lecture 41: Highlights The goal of this lecture is to remind you of some of the key points that we ve covered this semester Note that this is not the complete set of topics that may appear on the final
Lecture 41: Highlights The goal of this lecture is to remind you of some of the key points that we ve covered this semester Note that this is not the complete set of topics that may appear on the final
Maxima/minima with constraints
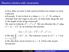 Maxima/minima with constraints Very often we want to find maxima/minima but subject to some constraint Example: A wire is bent to a shape y = 1 x 2. If a string is stretched from the origin to the wire,
Maxima/minima with constraints Very often we want to find maxima/minima but subject to some constraint Example: A wire is bent to a shape y = 1 x 2. If a string is stretched from the origin to the wire,
CP1 REVISION LECTURE 3 INTRODUCTION TO CLASSICAL MECHANICS. Prof. N. Harnew University of Oxford TT 2017
 CP1 REVISION LECTURE 3 INTRODUCTION TO CLASSICAL MECHANICS Prof. N. Harnew University of Oxford TT 2017 1 OUTLINE : CP1 REVISION LECTURE 3 : INTRODUCTION TO CLASSICAL MECHANICS 1. Angular velocity and
CP1 REVISION LECTURE 3 INTRODUCTION TO CLASSICAL MECHANICS Prof. N. Harnew University of Oxford TT 2017 1 OUTLINE : CP1 REVISION LECTURE 3 : INTRODUCTION TO CLASSICAL MECHANICS 1. Angular velocity and
G : Statistical Mechanics
 G25.2651: Statistical Mechanics Notes for Lecture 15 Consider Hamilton s equations in the form I. CLASSICAL LINEAR RESPONSE THEORY q i = H p i ṗ i = H q i We noted early in the course that an ensemble
G25.2651: Statistical Mechanics Notes for Lecture 15 Consider Hamilton s equations in the form I. CLASSICAL LINEAR RESPONSE THEORY q i = H p i ṗ i = H q i We noted early in the course that an ensemble
Central Forces. c 2007 Corinne Manogue. March 1999, last revised February 2009
 Central Forces Corinne A. Manogue with Tevian Dray, Kenneth S. Krane, Jason Janesky Department of Physics Oregon State University Corvallis, OR 97331, USA corinne@physics.oregonstate.edu c 2007 Corinne
Central Forces Corinne A. Manogue with Tevian Dray, Kenneth S. Krane, Jason Janesky Department of Physics Oregon State University Corvallis, OR 97331, USA corinne@physics.oregonstate.edu c 2007 Corinne
Physical Dynamics (PHY-304)
 Physical Dynamics (PHY-304) Gabriele Travaglini March 31, 2012 1 Review of Newtonian Mechanics 1.1 One particle Lectures 1-2. Frame, velocity, acceleration, number of degrees of freedom, generalised coordinates.
Physical Dynamics (PHY-304) Gabriele Travaglini March 31, 2012 1 Review of Newtonian Mechanics 1.1 One particle Lectures 1-2. Frame, velocity, acceleration, number of degrees of freedom, generalised coordinates.
Forces of Constraint & Lagrange Multipliers
 Lectures 30 April 21, 2006 Written or last updated: April 21, 2006 P442 Analytical Mechanics - II Forces of Constraint & Lagrange Multipliers c Alex R. Dzierba Generalized Coordinates Revisited Consider
Lectures 30 April 21, 2006 Written or last updated: April 21, 2006 P442 Analytical Mechanics - II Forces of Constraint & Lagrange Multipliers c Alex R. Dzierba Generalized Coordinates Revisited Consider
Thermodynamics of Three-phase Equilibrium in Lennard Jones System with a Simplified Equation of State
 23 Bulletin of Research Center for Computing and Multimedia Studies, Hosei University, 28 (2014) Thermodynamics of Three-phase Equilibrium in Lennard Jones System with a Simplified Equation of State Yosuke
23 Bulletin of Research Center for Computing and Multimedia Studies, Hosei University, 28 (2014) Thermodynamics of Three-phase Equilibrium in Lennard Jones System with a Simplified Equation of State Yosuke
Electric and Magnetic Forces in Lagrangian and Hamiltonian Formalism
 Electric and Magnetic Forces in Lagrangian and Hamiltonian Formalism Benjamin Hornberger 1/26/1 Phy 55, Classical Electrodynamics, Prof. Goldhaber Lecture notes from Oct. 26, 21 Lecture held by Prof. Weisberger
Electric and Magnetic Forces in Lagrangian and Hamiltonian Formalism Benjamin Hornberger 1/26/1 Phy 55, Classical Electrodynamics, Prof. Goldhaber Lecture notes from Oct. 26, 21 Lecture held by Prof. Weisberger
Lecture Note 12: Dynamics of Open Chains: Lagrangian Formulation
 ECE5463: Introduction to Robotics Lecture Note 12: Dynamics of Open Chains: Lagrangian Formulation Prof. Wei Zhang Department of Electrical and Computer Engineering Ohio State University Columbus, Ohio,
ECE5463: Introduction to Robotics Lecture Note 12: Dynamics of Open Chains: Lagrangian Formulation Prof. Wei Zhang Department of Electrical and Computer Engineering Ohio State University Columbus, Ohio,
Physics 115/242 The leapfrog method and other symplectic algorithms for integrating Newton s laws of motion
 Physics 115/242 The leapfrog method and other symplectic algorithms for integrating Newton s laws of motion Peter Young (Dated: April 14, 2009) I. INTRODUCTION One frequently obtains detailed dynamical
Physics 115/242 The leapfrog method and other symplectic algorithms for integrating Newton s laws of motion Peter Young (Dated: April 14, 2009) I. INTRODUCTION One frequently obtains detailed dynamical
Brief Review of Statistical Mechanics
 Brief Review of Statistical Mechanics Introduction Statistical mechanics: a branch of physics which studies macroscopic systems from a microscopic or molecular point of view (McQuarrie,1976) Also see (Hill,1986;
Brief Review of Statistical Mechanics Introduction Statistical mechanics: a branch of physics which studies macroscopic systems from a microscopic or molecular point of view (McQuarrie,1976) Also see (Hill,1986;
Classical Mechanics and Electrodynamics
 Classical Mechanics and Electrodynamics Lecture notes FYS 3120 Jon Magne Leinaas Department of Physics, University of Oslo December 2009 2 Preface These notes are prepared for the physics course FYS 3120,
Classical Mechanics and Electrodynamics Lecture notes FYS 3120 Jon Magne Leinaas Department of Physics, University of Oslo December 2009 2 Preface These notes are prepared for the physics course FYS 3120,
Marion and Thornton. Tyler Shendruk October 1, Hamilton s Principle - Lagrangian and Hamiltonian dynamics.
 Marion and Thornton Tyler Shendruk October 1, 2010 1 Marion and Thornton Chapter 7 Hamilton s Principle - Lagrangian and Hamiltonian dynamics. 1.1 Problem 6.4 s r z θ Figure 1: Geodesic on circular cylinder
Marion and Thornton Tyler Shendruk October 1, 2010 1 Marion and Thornton Chapter 7 Hamilton s Principle - Lagrangian and Hamiltonian dynamics. 1.1 Problem 6.4 s r z θ Figure 1: Geodesic on circular cylinder
The first order formalism and the transition to the
 Problem 1. Hamiltonian The first order formalism and the transition to the This problem uses the notion of Lagrange multipliers and Legendre transforms to understand the action in the Hamiltonian formalism.
Problem 1. Hamiltonian The first order formalism and the transition to the This problem uses the notion of Lagrange multipliers and Legendre transforms to understand the action in the Hamiltonian formalism.
MATHEMATICAL PHYSICS
 MATHEMATICAL PHYSICS Third Year SEMESTER 1 015 016 Classical Mechanics MP350 Prof. S. J. Hands, Prof. D. M. Heffernan, Dr. J.-I. Skullerud and Dr. M. Fremling Time allowed: 1 1 hours Answer two questions
MATHEMATICAL PHYSICS Third Year SEMESTER 1 015 016 Classical Mechanics MP350 Prof. S. J. Hands, Prof. D. M. Heffernan, Dr. J.-I. Skullerud and Dr. M. Fremling Time allowed: 1 1 hours Answer two questions
Noether s Theorem. 4.1 Ignorable Coordinates
 4 Noether s Theorem 4.1 Ignorable Coordinates A central recurring theme in mathematical physics is the connection between symmetries and conservation laws, in particular the connection between the symmetries
4 Noether s Theorem 4.1 Ignorable Coordinates A central recurring theme in mathematical physics is the connection between symmetries and conservation laws, in particular the connection between the symmetries
The Equipartition Theorem
 Chapter 8 The Equipartition Theorem Topics Equipartition and kinetic energy. The one-dimensional harmonic oscillator. Degrees of freedom and the equipartition theorem. Rotating particles in thermal equilibrium.
Chapter 8 The Equipartition Theorem Topics Equipartition and kinetic energy. The one-dimensional harmonic oscillator. Degrees of freedom and the equipartition theorem. Rotating particles in thermal equilibrium.
CE 530 Molecular Simulation
 1 CE 530 Molecular Simulation Lecture 1 David A. Kofke Department of Chemical Engineering SUNY Buffalo kofke@eng.buffalo.edu 2 Time/s Multi-Scale Modeling Based on SDSC Blue Horizon (SP3) 1.728 Tflops
1 CE 530 Molecular Simulation Lecture 1 David A. Kofke Department of Chemical Engineering SUNY Buffalo kofke@eng.buffalo.edu 2 Time/s Multi-Scale Modeling Based on SDSC Blue Horizon (SP3) 1.728 Tflops
Molecular Dynamics 9/6/16
 Molecular Dynamics What to choose in an integrator The Verlet algorithm Boundary Conditions in Space and time Reading Assignment: Lesar Chpt 6, F&S Chpt 4 1 The Molecular Dynamics (MD) method for classical
Molecular Dynamics What to choose in an integrator The Verlet algorithm Boundary Conditions in Space and time Reading Assignment: Lesar Chpt 6, F&S Chpt 4 1 The Molecular Dynamics (MD) method for classical
The Geometry of Euler s equation. Introduction
 The Geometry of Euler s equation Introduction Part 1 Mechanical systems with constraints, symmetries flexible joint fixed length In principle can be dealt with by applying F=ma, but this can become complicated
The Geometry of Euler s equation Introduction Part 1 Mechanical systems with constraints, symmetries flexible joint fixed length In principle can be dealt with by applying F=ma, but this can become complicated
CHAPTER 9 Statistical Physics
 CHAPTER 9 Statistical Physics 9.1 9.2 9.3 9.4 9.5 9.6 9.7 Historical Overview Maxwell Velocity Distribution Equipartition Theorem Maxwell Speed Distribution Classical and Quantum Statistics Fermi-Dirac
CHAPTER 9 Statistical Physics 9.1 9.2 9.3 9.4 9.5 9.6 9.7 Historical Overview Maxwell Velocity Distribution Equipartition Theorem Maxwell Speed Distribution Classical and Quantum Statistics Fermi-Dirac
Homework 3. 1 Goldstein Part (a) Theoretical Dynamics September 24, The Hamiltonian is given by
 Theoretical Dynamics September 4, 010 Instructor: Dr. Thomas Cohen Homework 3 Submitted by: Vivek Saxena 1 Goldstein 8.1 1.1 Part (a) The Hamiltonian is given by H(q i, p i, t) = p i q i L(q i, q i, t)
Theoretical Dynamics September 4, 010 Instructor: Dr. Thomas Cohen Homework 3 Submitted by: Vivek Saxena 1 Goldstein 8.1 1.1 Part (a) The Hamiltonian is given by H(q i, p i, t) = p i q i L(q i, q i, t)
Ideal Gas Behavior. NC State University
 Chemistry 331 Lecture 6 Ideal Gas Behavior NC State University Macroscopic variables P, T Pressure is a force per unit area (P= F/A) The force arises from the change in momentum as particles hit an object
Chemistry 331 Lecture 6 Ideal Gas Behavior NC State University Macroscopic variables P, T Pressure is a force per unit area (P= F/A) The force arises from the change in momentum as particles hit an object
Lagrangian and Hamiltonian Mechanics (Symon Chapter Nine)
 Lagrangian and Hamiltonian Mechanics (Symon Chapter Nine Physics A301 Spring 2005 Contents 1 Lagrangian Mechanics 3 1.1 Derivation of the Lagrange Equations...................... 3 1.1.1 Newton s Second
Lagrangian and Hamiltonian Mechanics (Symon Chapter Nine Physics A301 Spring 2005 Contents 1 Lagrangian Mechanics 3 1.1 Derivation of the Lagrange Equations...................... 3 1.1.1 Newton s Second
df(x) = h(x) dx Chemistry 4531 Mathematical Preliminaries Spring 2009 I. A Primer on Differential Equations Order of differential equation
 Chemistry 4531 Mathematical Preliminaries Spring 009 I. A Primer on Differential Equations Order of differential equation Linearity of differential equation Partial vs. Ordinary Differential Equations
Chemistry 4531 Mathematical Preliminaries Spring 009 I. A Primer on Differential Equations Order of differential equation Linearity of differential equation Partial vs. Ordinary Differential Equations
Ab initio molecular dynamics and nuclear quantum effects
 Ab initio molecular dynamics and nuclear quantum effects Luca M. Ghiringhelli Fritz Haber Institute Hands on workshop density functional theory and beyond: First principles simulations of molecules and
Ab initio molecular dynamics and nuclear quantum effects Luca M. Ghiringhelli Fritz Haber Institute Hands on workshop density functional theory and beyond: First principles simulations of molecules and
Geometric methods for orbit integration. PiTP 2009 Scott Tremaine
 Geometric methods for orbit integration PiTP 2009 Scott Tremaine spacecraft trajectories Cassini-Huygens trajectory around Saturn, 2004-2008 Planetary orbits lines = current orbits of the four inner planets
Geometric methods for orbit integration PiTP 2009 Scott Tremaine spacecraft trajectories Cassini-Huygens trajectory around Saturn, 2004-2008 Planetary orbits lines = current orbits of the four inner planets
Boltzmann-Gibbs Preserving Langevin Integrators
 Boltzmann-Gibbs Preserving Langevin Integrators Nawaf Bou-Rabee Applied and Comp. Math., Caltech INI Workshop on Markov-Chain Monte-Carlo Methods March 28, 2008 4000 atom cluster simulation Governing Equations
Boltzmann-Gibbs Preserving Langevin Integrators Nawaf Bou-Rabee Applied and Comp. Math., Caltech INI Workshop on Markov-Chain Monte-Carlo Methods March 28, 2008 4000 atom cluster simulation Governing Equations
Multibody simulation
 Multibody simulation Dynamics of a multibody system (Euler-Lagrange formulation) Dimitar Dimitrov Örebro University June 16, 2012 Main points covered Euler-Lagrange formulation manipulator inertia matrix
Multibody simulation Dynamics of a multibody system (Euler-Lagrange formulation) Dimitar Dimitrov Örebro University June 16, 2012 Main points covered Euler-Lagrange formulation manipulator inertia matrix
We start with some important background material in classical and quantum mechanics.
 Chapter Basics We start with some important background material in classical and quantum mechanics.. Classical mechanics Lagrangian mechanics Compared to Newtonian mechanics, Lagrangian mechanics has the
Chapter Basics We start with some important background material in classical and quantum mechanics.. Classical mechanics Lagrangian mechanics Compared to Newtonian mechanics, Lagrangian mechanics has the
Housekeeping. No announcement HW #7: 3.19
 1 Housekeeping No announcement HW #7: 3.19 2 Configuration Space vs. Phase Space 1 A given point in configuration space q q prescribes fully the 1,, n configuration of the system at a given time t. The
1 Housekeeping No announcement HW #7: 3.19 2 Configuration Space vs. Phase Space 1 A given point in configuration space q q prescribes fully the 1,, n configuration of the system at a given time t. The
PLANAR KINETIC EQUATIONS OF MOTION (Section 17.2)
 PLANAR KINETIC EQUATIONS OF MOTION (Section 17.2) We will limit our study of planar kinetics to rigid bodies that are symmetric with respect to a fixed reference plane. As discussed in Chapter 16, when
PLANAR KINETIC EQUATIONS OF MOTION (Section 17.2) We will limit our study of planar kinetics to rigid bodies that are symmetric with respect to a fixed reference plane. As discussed in Chapter 16, when
Classical Mechanics and Electrodynamics
 Classical Mechanics and Electrodynamics Lecture notes FYS 3120 Jon Magne Leinaas Department of Physics, University of Oslo 2 Preface FYS 3120 is a course in classical theoretical physics, which covers
Classical Mechanics and Electrodynamics Lecture notes FYS 3120 Jon Magne Leinaas Department of Physics, University of Oslo 2 Preface FYS 3120 is a course in classical theoretical physics, which covers
Homework 4. Goldstein 9.7. Part (a) Theoretical Dynamics October 01, 2010 (1) P i = F 1. Q i. p i = F 1 (3) q i (5) P i (6)
 Theoretical Dynamics October 01, 2010 Instructor: Dr. Thomas Cohen Homework 4 Submitted by: Vivek Saxena Goldstein 9.7 Part (a) F 1 (q, Q, t) F 2 (q, P, t) P i F 1 Q i (1) F 2 (q, P, t) F 1 (q, Q, t) +
Theoretical Dynamics October 01, 2010 Instructor: Dr. Thomas Cohen Homework 4 Submitted by: Vivek Saxena Goldstein 9.7 Part (a) F 1 (q, Q, t) F 2 (q, P, t) P i F 1 Q i (1) F 2 (q, P, t) F 1 (q, Q, t) +
REVIEW. Hamilton s principle. based on FW-18. Variational statement of mechanics: (for conservative forces) action Equivalent to Newton s laws!
 Hamilton s principle Variational statement of mechanics: (for conservative forces) action Equivalent to Newton s laws! based on FW-18 REVIEW the particle takes the path that minimizes the integrated difference
Hamilton s principle Variational statement of mechanics: (for conservative forces) action Equivalent to Newton s laws! based on FW-18 REVIEW the particle takes the path that minimizes the integrated difference
d 3 r d 3 vf( r, v) = N (2) = CV C = n where n N/V is the total number of molecules per unit volume. Hence e βmv2 /2 d 3 rd 3 v (5)
 LECTURE 12 Maxwell Velocity Distribution Suppose we have a dilute gas of molecules, each with mass m. If the gas is dilute enough, we can ignore the interactions between the molecules and the energy will
LECTURE 12 Maxwell Velocity Distribution Suppose we have a dilute gas of molecules, each with mass m. If the gas is dilute enough, we can ignore the interactions between the molecules and the energy will
Physics 6010, Fall Relevant Sections in Text: Introduction
 Physics 6010, Fall 2016 Introduction. Configuration space. Equations of Motion. Velocity Phase Space. Relevant Sections in Text: 1.1 1.4 Introduction This course principally deals with the variational
Physics 6010, Fall 2016 Introduction. Configuration space. Equations of Motion. Velocity Phase Space. Relevant Sections in Text: 1.1 1.4 Introduction This course principally deals with the variational
Estimating Accuracy in Classical Molecular Simulation
 Estimating Accuracy in Classical Molecular Simulation University of Illinois Urbana-Champaign Department of Computer Science Institute for Mathematics and its Applications July 2007 Acknowledgements Ben
Estimating Accuracy in Classical Molecular Simulation University of Illinois Urbana-Champaign Department of Computer Science Institute for Mathematics and its Applications July 2007 Acknowledgements Ben
CE 530 Molecular Simulation
 CE 530 Molecular Simulation Lecture 20 Phase Equilibria David A. Kofke Department of Chemical Engineering SUNY Buffalo kofke@eng.buffalo.edu 2 Thermodynamic Phase Equilibria Certain thermodynamic states
CE 530 Molecular Simulation Lecture 20 Phase Equilibria David A. Kofke Department of Chemical Engineering SUNY Buffalo kofke@eng.buffalo.edu 2 Thermodynamic Phase Equilibria Certain thermodynamic states
Nonlinear Single-Particle Dynamics in High Energy Accelerators
 Nonlinear Single-Particle Dynamics in High Energy Accelerators Part 2: Basic tools and concepts Nonlinear Single-Particle Dynamics in High Energy Accelerators This course consists of eight lectures: 1.
Nonlinear Single-Particle Dynamics in High Energy Accelerators Part 2: Basic tools and concepts Nonlinear Single-Particle Dynamics in High Energy Accelerators This course consists of eight lectures: 1.
Physics 342 Lecture 26. Angular Momentum. Lecture 26. Physics 342 Quantum Mechanics I
 Physics 342 Lecture 26 Angular Momentum Lecture 26 Physics 342 Quantum Mechanics I Friday, April 2nd, 2010 We know how to obtain the energy of Hydrogen using the Hamiltonian operator but given a particular
Physics 342 Lecture 26 Angular Momentum Lecture 26 Physics 342 Quantum Mechanics I Friday, April 2nd, 2010 We know how to obtain the energy of Hydrogen using the Hamiltonian operator but given a particular
The Accelerator Hamiltonian in a Straight Coordinate System
 Hamiltoninan Dynamics for Particle Accelerators, Lecture 2 The Accelerator Hamiltonian in a Straight Coordinate System Andy Wolski University of Liverpool, and the Cockcroft Institute, Daresbury, UK. Given
Hamiltoninan Dynamics for Particle Accelerators, Lecture 2 The Accelerator Hamiltonian in a Straight Coordinate System Andy Wolski University of Liverpool, and the Cockcroft Institute, Daresbury, UK. Given
Physics 115/242 The leapfrog method and other symplectic algorithms for integrating Newton s laws of motion
 Physics 115/242 The leapfrog method and other symplectic algorithms for integrating Newton s laws of motion Peter Young (Dated: April 17, 23) I. INTRODUCTION One frequently obtains detailed dynamical information
Physics 115/242 The leapfrog method and other symplectic algorithms for integrating Newton s laws of motion Peter Young (Dated: April 17, 23) I. INTRODUCTION One frequently obtains detailed dynamical information
Energy and Equations of Motion
 Energy and Equations of Motion V. Tanrıverdi tanriverdivedat@googlemail.com Physics Department, Middle East Technical University, Ankara / TURKEY Abstract. From the total time derivative of energy an equation
Energy and Equations of Motion V. Tanrıverdi tanriverdivedat@googlemail.com Physics Department, Middle East Technical University, Ankara / TURKEY Abstract. From the total time derivative of energy an equation
Introduction to Hamiltonian Monte Carlo Method
 Introduction to Hamiltonian Monte Carlo Method Mingwei Tang Department of Statistics University of Washington mingwt@uw.edu November 14, 2017 1 Hamiltonian System Notation: q R d : position vector, p R
Introduction to Hamiltonian Monte Carlo Method Mingwei Tang Department of Statistics University of Washington mingwt@uw.edu November 14, 2017 1 Hamiltonian System Notation: q R d : position vector, p R
Langevin Methods. Burkhard Dünweg Max Planck Institute for Polymer Research Ackermannweg 10 D Mainz Germany
 Langevin Methods Burkhard Dünweg Max Planck Institute for Polymer Research Ackermannweg 1 D 55128 Mainz Germany Motivation Original idea: Fast and slow degrees of freedom Example: Brownian motion Replace
Langevin Methods Burkhard Dünweg Max Planck Institute for Polymer Research Ackermannweg 1 D 55128 Mainz Germany Motivation Original idea: Fast and slow degrees of freedom Example: Brownian motion Replace
The Klein-Gordon equation
 Lecture 8 The Klein-Gordon equation WS2010/11: Introduction to Nuclear and Particle Physics The bosons in field theory Bosons with spin 0 scalar (or pseudo-scalar) meson fields canonical field quantization
Lecture 8 The Klein-Gordon equation WS2010/11: Introduction to Nuclear and Particle Physics The bosons in field theory Bosons with spin 0 scalar (or pseudo-scalar) meson fields canonical field quantization
CE 530 Molecular Simulation
 1 CE 530 Molecular Simulation Lecture 16 Dielectrics and Reaction Field Method David A. Kofke Department of Chemical Engineering SUNY Buffalo kofke@eng.buffalo.edu 2 Review Molecular models intramolecular
1 CE 530 Molecular Simulation Lecture 16 Dielectrics and Reaction Field Method David A. Kofke Department of Chemical Engineering SUNY Buffalo kofke@eng.buffalo.edu 2 Review Molecular models intramolecular
G : Statistical Mechanics
 G5.651: Statistical Mechanics Notes for Lecture 1 I. DERIVATION OF THE DISCRETIZED PATH INTEGRAL We begin our discussion of the Feynman path integral with the canonical ensemble. The epressions for the
G5.651: Statistical Mechanics Notes for Lecture 1 I. DERIVATION OF THE DISCRETIZED PATH INTEGRAL We begin our discussion of the Feynman path integral with the canonical ensemble. The epressions for the
Motion under the Influence of a Central Force
 Copyright 004 5 Motion under the Influence of a Central Force The fundamental forces of nature depend only on the distance from the source. All the complex interactions that occur in the real world arise
Copyright 004 5 Motion under the Influence of a Central Force The fundamental forces of nature depend only on the distance from the source. All the complex interactions that occur in the real world arise
Analytical Mechanics for Relativity and Quantum Mechanics
 Analytical Mechanics for Relativity and Quantum Mechanics Oliver Davis Johns San Francisco State University OXPORD UNIVERSITY PRESS CONTENTS Dedication Preface Acknowledgments v vii ix PART I INTRODUCTION:
Analytical Mechanics for Relativity and Quantum Mechanics Oliver Davis Johns San Francisco State University OXPORD UNIVERSITY PRESS CONTENTS Dedication Preface Acknowledgments v vii ix PART I INTRODUCTION:
Hamiltonian Field Theory
 Hamiltonian Field Theory August 31, 016 1 Introduction So far we have treated classical field theory using Lagrangian and an action principle for Lagrangian. This approach is called Lagrangian field theory
Hamiltonian Field Theory August 31, 016 1 Introduction So far we have treated classical field theory using Lagrangian and an action principle for Lagrangian. This approach is called Lagrangian field theory
Physics 106a, Caltech 13 November, Lecture 13: Action, Hamilton-Jacobi Theory. Action-Angle Variables
 Physics 06a, Caltech 3 November, 08 Lecture 3: Action, Hamilton-Jacobi Theory Starred sections are advanced topics for interest and future reference. The unstarred material will not be tested on the final
Physics 06a, Caltech 3 November, 08 Lecture 3: Action, Hamilton-Jacobi Theory Starred sections are advanced topics for interest and future reference. The unstarred material will not be tested on the final
Turning up the heat: thermal expansion
 Lecture 3 Turning up the heat: Kinetic molecular theory & thermal expansion Gas in an oven: at the hot of materials science Here, the size of helium atoms relative to their spacing is shown to scale under
Lecture 3 Turning up the heat: Kinetic molecular theory & thermal expansion Gas in an oven: at the hot of materials science Here, the size of helium atoms relative to their spacing is shown to scale under
Quantum Continuum Mechanics for Many-Body Systems
 Workshop on High Performance and Parallel Computing Methods and Algorithms for Materials Defects, 9-13 February 2015 Quantum Continuum Mechanics for Many-Body Systems J. Tao 1,2, X. Gao 1,3, G. Vignale
Workshop on High Performance and Parallel Computing Methods and Algorithms for Materials Defects, 9-13 February 2015 Quantum Continuum Mechanics for Many-Body Systems J. Tao 1,2, X. Gao 1,3, G. Vignale
Chemistry 532 Practice Final Exam Fall 2012 Solutions
 Chemistry 53 Practice Final Exam Fall Solutions x e ax dx π a 3/ ; π sin 3 xdx 4 3 π cos nx dx π; sin θ cos θ + K x n e ax dx n! a n+ ; r r r r ˆL h r ˆL z h i φ ˆL x i hsin φ + cot θ cos φ θ φ ) ˆLy i
Chemistry 53 Practice Final Exam Fall Solutions x e ax dx π a 3/ ; π sin 3 xdx 4 3 π cos nx dx π; sin θ cos θ + K x n e ax dx n! a n+ ; r r r r ˆL h r ˆL z h i φ ˆL x i hsin φ + cot θ cos φ θ φ ) ˆLy i
Statistical Thermodynamics and Monte-Carlo Evgenii B. Rudnyi and Jan G. Korvink IMTEK Albert Ludwig University Freiburg, Germany
 Statistical Thermodynamics and Monte-Carlo Evgenii B. Rudnyi and Jan G. Korvink IMTEK Albert Ludwig University Freiburg, Germany Preliminaries Learning Goals From Micro to Macro Statistical Mechanics (Statistical
Statistical Thermodynamics and Monte-Carlo Evgenii B. Rudnyi and Jan G. Korvink IMTEK Albert Ludwig University Freiburg, Germany Preliminaries Learning Goals From Micro to Macro Statistical Mechanics (Statistical
Enabling constant pressure hybrid Monte Carlo simulations using the GROMACS molecular simulation package
 Enabling constant pressure hybrid Monte Carlo simulations using the GROMACS molecular simulation package Mario Fernández Pendás MSBMS Group Supervised by Bruno Escribano and Elena Akhmatskaya BCAM 18 October
Enabling constant pressure hybrid Monte Carlo simulations using the GROMACS molecular simulation package Mario Fernández Pendás MSBMS Group Supervised by Bruno Escribano and Elena Akhmatskaya BCAM 18 October
Canonical transformations (Lecture 4)
 Canonical transformations (Lecture 4) January 26, 2016 61/441 Lecture outline We will introduce and discuss canonical transformations that conserve the Hamiltonian structure of equations of motion. Poisson
Canonical transformations (Lecture 4) January 26, 2016 61/441 Lecture outline We will introduce and discuss canonical transformations that conserve the Hamiltonian structure of equations of motion. Poisson
Lecture Note 12: Dynamics of Open Chains: Lagrangian Formulation
 ECE5463: Introduction to Robotics Lecture Note 12: Dynamics of Open Chains: Lagrangian Formulation Prof. Wei Zhang Department of Electrical and Computer Engineering Ohio State University Columbus, Ohio,
ECE5463: Introduction to Robotics Lecture Note 12: Dynamics of Open Chains: Lagrangian Formulation Prof. Wei Zhang Department of Electrical and Computer Engineering Ohio State University Columbus, Ohio,
The Principle of Least Action
 The Principle of Least Action In their never-ending search for general principles, from which various laws of Physics could be derived, physicists, and most notably theoretical physicists, have often made
The Principle of Least Action In their never-ending search for general principles, from which various laws of Physics could be derived, physicists, and most notably theoretical physicists, have often made
THE LAGRANGIAN AND HAMILTONIAN MECHANICAL SYSTEMS
 THE LAGRANGIAN AND HAMILTONIAN MECHANICAL SYSTEMS ALEXANDER TOLISH Abstract. Newton s Laws of Motion, which equate forces with the timerates of change of momenta, are a convenient way to describe mechanical
THE LAGRANGIAN AND HAMILTONIAN MECHANICAL SYSTEMS ALEXANDER TOLISH Abstract. Newton s Laws of Motion, which equate forces with the timerates of change of momenta, are a convenient way to describe mechanical
8. INTRODUCTION TO STATISTICAL THERMODYNAMICS
 n * D n d Fluid z z z FIGURE 8-1. A SYSTEM IS IN EQUILIBRIUM EVEN IF THERE ARE VARIATIONS IN THE NUMBER OF MOLECULES IN A SMALL VOLUME, SO LONG AS THE PROPERTIES ARE UNIFORM ON A MACROSCOPIC SCALE 8. INTRODUCTION
n * D n d Fluid z z z FIGURE 8-1. A SYSTEM IS IN EQUILIBRIUM EVEN IF THERE ARE VARIATIONS IN THE NUMBER OF MOLECULES IN A SMALL VOLUME, SO LONG AS THE PROPERTIES ARE UNIFORM ON A MACROSCOPIC SCALE 8. INTRODUCTION
