Bethe Ansatz solution of the open XX spin chain with nondiagonal boundary terms
|
|
|
- Eustace Greene
- 5 years ago
- Views:
Transcription
1 UMTG 231 Bethe Ansatz solution of the open XX spin chain with nondiagonal boundary terms arxiv:hep-th/ v1 9 Oct 2001 Rafael I. Nepomechie Physics Department, P.O. Box , University of Miami Coral Gables, FL USA Abstract We consider the integrable open XX quantum spin chain with nondiagonal boundary terms. We derive an exact inversion identity, using which we obtain the eigenvalues of the transfer matrix and the Bethe Ansatz equations. For generic values of the boundary parameters, the Bethe Ansatz solution is formulated in terms of Jacobian elliptic functions.
2 1 Introduction We consider in this article the open XX quantum spin chain with nondiagonal boundary terms, defined by the Hamiltonian H = 1 2 { N 1 n=1 ( σ x n σ x n+1 +σy n σy n+1) + icothξ σ1 z + 2iκ σ1 x sinhξ icothξ +σn z + 2iκ } + σn x, (1.1) sinhξ + where σ x,σ y,σ z are the standard Pauli matrices, and ξ ±,κ ± are arbitrary boundary parameters. This model is known to be integrable [1, 2, 3]. It has been investigated [4, 5] using a fermionization technique [6, 7], suitably adapted to accommodate boundary terms [8, 9]. However, this model has until now resisted a direct Bethe Ansatz solution due to the absence of a simple reference (pseudovacuum) state. 1 Such a solution is desirable for a number of reasons. First, the open XX chain is a special case of integrable open XXZ and open XYZ chains, which should also admit Bethe Ansatz solutions but which cannot be solved by fermionization. Second, Bethe Ansatz solutions are particularly well-suited for investigating physical properties, such as ground state, low-lying excitations, scattering matrices, etc. In particular, the Bethe Ansatz approach avoids the projection mechanism [5] which can be implemented only in special cases. (See [4, 5] and references therein for discussions of interesting physical applications of the open XX spin chain.) Finally, the Sklyanin transfer matrix for the open XX spin chain is closely related to the Yang matrix [11, 12, 13] for a large class of integrable N = 2 supersymmetric quantum field theories with boundary [14, 15]. Diagonalization of this matrix is a key step in formulating the thermodynamic Bethe Ansatz equations for these N = 2 supersymmetric models. In this paper we derive an exact inversion identity for the model (1.1), using which we obtain the eigenvalues of the transfer matrix and the Bethe Ansatz equations. (This approach does not completely circumvent the problem of not having a reference state, since the eigenvectors are not determined.) We obtain the inversion identity using the open-chain fusion formula [16] together with the remarkable fact that, for the open XX spin chain/ 6- vertex free-fermion model, the fused transfer matrix is proportional to the identity matrix. A similar strategy has recently been used [13] to solve the open 8-vertex free-fermion [17] model, which corresponds to the case of N = 1 supersymmetry. These techniques are generalizations of those which have been developed for closed spin chains [18, 19, 20, 21]. Even though the transfer matrix is constructed entirely from hyperbolic functions, we find 1 For the special case of diagonal boundary terms (i.e., κ ± = 0), a simple pseudovacuum state does exist, and a Bethe Ansatz solution is known [10, 1]. 1
3 that the Bethe Ansatz solution is formulated in terms of Jacobian elliptic functions for generic values of the boundary parameters. (In contrast, for the XYZ chain [18], such functions appear already in the transfer matrix.) For special values of the boundary parameters, the elliptic functions degenerate into ordinary hyperbolic or trigonometric functions. The outline of this paper is as follows. In Section 2, we review the construction of the Sklyanin transfer matrix for the open XX chain, and derive some of its important properties. We derive in Section 3 the inversion identity, which we then use in Section 4 to determine the Bethe Ansatz solution. In Section 5, we investigate some special cases in which the solution can be expressed in terms of ordinary hyperbolic functions. In particular, we verify that our solution is similar to the known one [10, 1] for the case of diagonal boundary terms. In Section 6, we conclude with a brief discussion of some possible directions for future work. 2 Transfer matrix The object of central importance in the construction of integrable quantum spin chains is the one-parameter family of commuting matrices called the transfer matrix. The transfer matrix for an open chain is made from two basic building blocks, called R (bulk) and K (boundary) matrices. An R matrix is a solution of the Yang-Baxter equation R 12 (u v) R 13 (u) R 23 (v) = R 23 (v) R 13 (u) R 12 (u v). (2.1) (See, e.g., [21, 22, 23].) The XX spin chain is a special case of the XXZ spin chain, corresponding (in the notation of [1]) to the anisotropy value η = iπ. The R matrix is therefore 2 the 4 4 matrix a b c 0 R(u) = 0 c b 0, (2.2) a with matrix elements a = sinh(u+ iπ 2 ), b = sinhu, c = sinh iπ 2, (2.3) which satisfy the free-fermion condition a 2 +b 2 = c 2. (2.4) 2
4 This R matrix has the symmetry properties R 12 (u) = P 12 R 12 (u)p 12 = R 12 (u) t 1t 2, (2.5) where P 12 is the permutation matrix and t denotes transpose. Moreover, it satisfies the unitarity relation R 12 (u) R 12 ( u) = ζ(u)i, ζ(u) = cosh 2 u, (2.6) and the crossing relation R 12 (u) = V 1 R 12 ( u ρ) t 2 V 1, (2.7) with ρ = iπ 2, V = σx. (2.8) Finally, it has the periodicity property R 12 (u+iπ) = σ2 z R 12(u)σ2 z = σz 1 R 12(u)σ1 z. (2.9) The matrix K (u) is a solution of the boundary Yang-Baxter equation [24] R 12 (u v) K 1 (u) R 21(u+v) K 2 (v) = K 2 (v) R 12(u+v) K 1 (u) R 21(u v). (2.10) We consider here the following 2 2 matrix [2, 3] ( K sinh(ξ +u) κ sinh2u (u) = κ sinh2u sinh(ξ u) ), (2.11) which evidently depends on two boundary parameters ξ,κ. We set the matrix K + (u) to be K ( u ρ) with (ξ,κ ) replaced by (ξ +,κ + ); i.e., ( ) K + icosh(ξ + u) κ + sinh2u (u) =, (2.12) κ + sinh2u icosh(ξ + +u) We shall often use an alternative [3] set of boundary parameters (η,ϑ ) which is related to the set (ξ,κ ) by cosη coshϑ = i sinhξ, cos 2 η +cosh 2 ϑ = (2.13) 2κ 4κ 2 The K matrices have the periodicity property K (u+iπ) = σ z K (u)σ z. (2.14) 3
5 The transfer matrix t(u) for an open chain of N spins is given by [1] t(u) = tr 0 K 0 + (u) T 0 (u) K0 (u) ˆT 0 (u), (2.15) where tr 0 denotes trace over the auxiliary space 0, and T 0 (u), ˆT0 (λ) are so-called monodromy matrices 2 T 0 (u) = R 0N (u) R 01 (u), ˆT0 (u) = R 10 (u) R N0 (u). (2.16) Indeed, Sklyanin has shown that t(u) constitutes a one-parameter commutative family of matrices [t(u),t(v)] = 0. (2.17) Typically, the Hamiltonian is proportional to the first derivative of the transfer matrix t (0) [1]. However, this quantity is trivial for the XX model, due to the fact trk + (0) = 0. In order to obtain the Hamiltonian, we must go to the second derivative [25]. We find H = = t (0) 4( 1) N+1 isinhξ trk + (0) N 1 n=1 H n,n+1 + i K1 2sinhξ (0)+ tr 0K 0 + (0) H N0 itr 0 K 0 + (0) HN0 2, (2.18) trk + (0) where H n,n+1 = P n,n+1 R n,n+1(0), and we have made use of the facts K (0) = sinhξ I and tr 0 K + 0 (0) H N0 = trk + (0) = 0. By explicitly evaluating (2.18), we obtain the Hamiltonian (1.1). Notice that the Hamiltonian is Hermitian if ξ ± are imaginary and κ ± are real. The corresponding energy eigenvalues E are given by E = where Λ(u) are eigenvalues of the transfer matrix. The transfer matrix has the periodicity property Λ (0) 8( 1) N+1 sinhξ sinhξ +, (2.19) t(u+iπ) = t(u), (2.20) as follows from (2.9), (2.14). Moreover, the transfer matrix has crossing symmetry t( u iπ ) = t(u), (2.21) 2 which can be proved using a generalization of the methods developed in the appendices of [26]. Finally, we note that the transfer matrix has the asymptotic behavior (for κ ± 0) t(u) κ κ + i Neu(4+2N) I+... for u. (2.22) 21+2N 2 As is customary, we usually suppress the quantum-space subscripts 1,...,N. 4
6 3 Inversion identity Our main objective is to determine the eigenvalues Λ(u) of the open-chain transfer matrix (2.15), from which the energy eigenvalues (2.19) immediately follow. We shall accomplish this using an exact inversion identity, which we first derive. A similar approach was used in [18, 19] for closed chains. This approach is based on the concept of fusion [20, 21]. The derivation of the inversion identity for the open XX spin chain/ 6-vertex free-fermion model closely parallels the one for the 8-vertex free-fermion model considered in [13]. For brevity, weshalloftenrefertothesetwomodelsasthen = 2andN = 1models, respectively. The principal tool which we use to derive the inversion identity is the open-chain fusion formula obtained in [16]. We shall henceforth refer to this reference as I. The matrix R 12 (u) at u = ρ = iπ is proportional to the one-dimensional projector 2 P P12 = , (P 12) 2 = P12. (3.1) As explained in I, from the corresponding degeneration of the (boundary) Yang-Baxter equation, one can derive identities which allow one to prove that fused(boundary) matrices satisfy generalized (boundary) Yang-Baxter equations. The fused R matrix is given by (I 2.13) R <12>3 (u) = P + 12 R 13 (u) R 23 (u+ρ) P + 12, (3.2) where P + 12 = I P 12. An important observation is that the fused R matrix can be brought to the following upper triangular form by a similarity transformation si X 12 R <12>3 (u) X tσ z 2tσ z 0 = 0 0 tσ z 0, (3.3) where s = cosh 2 u, t = icoshusinhu, (3.4) and the 4 4 matrix X is given by X = (3.5)
7 It follows that the fused monodromy matrices (I 4.7), (I 5.4), (I 5.5) T <12> (u) = R <12>N (u) R <12>1 (u), ˆT <12> (u+ρ) = R <12>1 (u) R <12>N (u), (3.6) also become triangular by the same transformation, s N I X 12 T <12> (u) X t N F (( 1) N 1)t N F 0 = 0 0 ( t) N F where F = N i=1 σz i. = X 12 T <12> (u+ρ) X 1 12, (3.7) The corresponding fused K matrices are given by (I 3.5), (I 3.9) since M = V t V = I. K <12> (u) = P+ 12 K 1 (u) R 12(2u+ρ) K 2 (u+ρ) P+ 12, K + <12> (u) = {P+ 12 K+ 1 (u)t 1 R 12 ( 2u 3ρ) K + 2 (u+ρ)t 2 P + 12 }t 12, (3.8) Unlike the N = 1 case [13], the similarity transformation does not bring also the fused K matrices to upper triangular form. 3 Nevertheless, the transformed fused K matrices are almost triangular m 1 X 12 K<12>(u) X m 2 m 5 0 = 0 m 4 m 3 0, (3.9) where m 1 = ± 1 2 sinh2u[ cosh2u cosh2ξ +2κ 2 sinh2 2u ], m 2 = i 2 sinh2u[ sinh2(u±ξ ) 8κ 2 coshusinh 3 u ], m 3 = i 2 sinh2u[ sinh2(u ξ )+8κ 2 cosh3 usinhu ], m 4 = iκ 2 cosh2usinh2 2u, m 5 = ± i 2 sinh4usinh2ξ. (3.10) 3 It is not possible to simultaneously triangularize both R <12>3 (u) and K<12> (u), since their commutator is not nilpotent; i.e., [ R <12>3 (u),k<12> (u)] n 0. A monograph on the general problem of simultaneous triangularization has recently been published [27]. 6
8 The fused transfer matrix t(u) is given by (I 4.5), (I 4.6) t(u) = tr 12 K + <12> (u) T <12>(u) K <12> (u) ˆT <12> (u+ρ). (3.11) With the help of the results (3.7), (3.9),(3.10), we now obtain the remarkable result that the fused transfer matrix is proportional to the identity matrix, where t(u) = Λ(u)I, (3.12) Λ(u) = s 2N m + 1 m 1 +t2n [m + 2 m 2 +m+ 3 m 3 +( 1)N (m + 4 m 5 +m 4 m+ 5 ) + (1 ( 1) N )(m + 3 m 4 +m 3 m+ 4 m+ 2 m 4 m 2 m+ 4 +2m 4 m+ 4 ) ]. (3.13) A similar result also holds for the N = 1 case [13]. The fusion formula is given by (I 4.17), (I 5.1) t(u) t(u+ρ) = 1 [ t(u)+ { K + (u) } { K (u) } }] δ{t(u)}δ{ˆt(u), (3.14) ζ(2u+2ρ) where the transfer matrix t(u) is given by (2.15) (see also (I 4.1), (I 4.2)), and the quantum determinants [28, 21] are given by (I 4.15), (I 5.3), (I 5.7) } δ{t(u)} = δ {ˆT(u) = ζ(u+ρ) N, { K (u) } = tr 12 { P 12 K 1 (u) R 12(2u+ρ) K 2 (u+ρ) V 1 V 2 }, { K + (u) } = tr 12 { P 12 V 1 V 2 K + 2 (u+ρ) R 12 ( 2u 3ρ) K + 1 (u) }. (3.15) It follows from (3.12)-(3.15) that the transfer matrix obeys an exact inversion identity t(u) t(u iπ ) = f(u)i. (3.16) 2 where the function f(u) is given by f(u) = tanh 2 2u [ g 1 (u)cosh 4N u+g 2 (u)sinh 4N u+g 3 (u)sinh 2N ucosh 2N u ], (3.17) with g 1 (u) = 1 4 (cosh2u cosh2ξ +2κ 2 sinh2 2u)(cosh2u cosh2ξ + +2κ 2 + sinh2 2u) = 16κ 2 + κ2 cosh(u+iη )cosh(u iη )cosh(u+iη + )cosh(u iη + ) cosh(u+ϑ )cosh(u ϑ )cosh(u+ϑ + )cosh(u ϑ + ), 7
9 g 2 (u) = g 1 (u+ iπ 2 ), g 3 (u) = 2κ 2 + κ2 [ 1+( 1) N +sinh 2 2u ] sinh 2 2u+( 1) N [ (κ 2 + cosh2ξ +κ 2 cosh2ξ +)sinh 2 2u + 1 ] 2 (cosh2ξ cosh2ξ + sinh 2 2u sinh2ξ sinh2ξ + cosh 2 2u) ( = 2κ 2 +κ 2 [sinh 2 2ucosh 2 2u+( 1) N sin2η sinh2ϑ sin2η + sinh2ϑ + cosh 2 2u )] +cos2η cosh2ϑ cos2η + cosh2ϑ + sinh 2 2u. (3.18) The inversion identity (3.16)-(3.18) is the first main result of our paper. We have checked it numerically up to N = 3. 4 Eigenvalues and Bethe Ansatz Equations Having obtained the inversion identity, we now use it to determine the eigenvalues of the transfer matrix. The commutativity relation (2.17) implies that the transfer matrix has eigenstates Λ which are independent of u, t(u) Λ = Λ(u) Λ, (4.1) where Λ(u) are the corresponding eigenvalues. Acting on Λ with the inversion identity, we obtain the corresponding identity for the eigenvalues Λ(u) Λ(u iπ ) = f(u). (4.2) 2 Similarly, it follows from (2.20) and (2.21) that the eigenvalues have the periodicity and crossing properties Λ(u+iπ) = Λ(u), Λ( u iπ ) = Λ(u). (4.3) 2 Finally, (2.22) implies the asymptotic behavior Λ(u) κ κ + i Neu(4+2N) +... for u. (4.4) 21+2N We shall assume that the eigenvalues have the form Λ(u) = ρsinh2u N sinh(u u j )cosh(u+u j ), (4.5) j=0 8
10 where u j and ρ are (u-independent) parameters which are to be determined. Indeed, this expression satisfies the periodicity and crossing properties(4.3), and it has the correct asymptotic behavior (4.4) provided that we set ρ = i N 4κ κ +. (4.6) We now substitute the Ansatz (4.5) into the inversion identity (4.2), and obtain ( 1) N ρ 2 sinh 2 2u N j=0 1 4 sinh2(u u j)sinh2(u+u j ) = f(u). (4.7) Recalling the explicit expression (3.17),(3.18) for f(u), we verify that both sides of the equation have the same asymptotic behavior e u(8+4n) for u. Since the LHS has zeros ±u j, these must be zeros of f(u). That is, 4 g 1 (u j )cosh 4N u j +g 2 (u j )sinh 4N u j +g 3 (u j )sinh 2N u j cosh 2N u j = 0. (4.8) Dividing by cosh 4N u j, we obtain g 2 (u j )tanh 4N u j +g 3 (u j )tanh 2N u j +g 1 (u j ) = 0. (4.9) Regarding (4.9) as the quadratic equation g 2 x 2 +g 3 x+g 1 = 0 (4.10) in the variable x = tanh 2N u j, we conclude that the parameters u j satisfy the Bethe Ansatz equations where the function h(u) is defined by tanh 2N u j = h(u j) g 2 (u j ), (4.11) h(u) = g 3(u)± g 3 (u) 2 4g 1 (u) g 2 (u) 2. (4.12) The square root in(4.12) can be eliminated by making an appropriate change of variables. Indeed, with the help of (3.18), one can show that h(u) = κ 2 + κ2 { sinh 2 2ucosh 2 2u ( 1) ( N γ 1 cosh 2 2u+γ 2 sinh 2 2u ) } ±sinh2ucosh2u αsinh 2 2u+β, (4.13) u j. 4 The three functions g i (u),i = 1,2,3, are even functions of u. Hence, if u j is a root of f(u), then so is 9
11 where α = 1 2 (cos4η +cos4η + +cosh4ϑ +cosh4ϑ + )+( 1) N [cos2(η +η + )cosh2(ϑ ϑ + ) +cos2(η η + )cosh2(ϑ +ϑ + )], β = [ sin2η sinh2ϑ +( 1) N sin2η + sinh2ϑ + ] [sin2(η +η + )sinh2(ϑ ϑ + ) +sin2(η η + )sinh2(ϑ +ϑ + )] 2, γ 1 = sin2η sinh2ϑ sin2η + sinh2ϑ +, γ 2 = cos2η cosh2ϑ cos2η + cosh2ϑ +. (4.14) Let us change from the spectral parameter u to the new spectral parameter v defined by sinh2u = isn2v, cosh2u = cn2v, (4.15) where the modulus k of the Jacobian elliptic functions is given by With the help of the identities (see, e.g., [29]) k 2 = α β. (4.16) cn 2 z +sn 2 z = 1, dn 2 z +k 2 sn 2 z = 1, (4.17) one can see that the function h(u) can be reexpressed as { h(u) = κ 2 +κ 2 sn 2 2vcn 2 2v ( 1) ( N γ 1 cn 2 2v γ 2 sn 2 2v ) ±isn2vcn2vdn2v } β.(4.18) Hence, the Bethe Ansatz solution (4.5), (4.6), (4.11) can be reformulated as where the parameters v j satisfy Λ(u) = ( 1 2 )N 1 κ + κ sn2v N (sn2v sn2v j ), (4.19) ( ) N cn2vj 1 = sn2 2v j cn 2 2v j ( 1) N (γ 1 cn 2 2v j γ 2 sn 2 2v j )±isn2v j cn2v j dn2v j β. cn2v j +1 (cn2v j cn2iη )(cn2v j cn2ϑ )(cn2v j cn2iη + )(cn2v j cn2ϑ + ) This Bethe Ansatz solution is the second main result of our paper. This result passes several tests. Indeed, for N = 0, 1, the eigenvalues agree with those obtained by direct diagonalization of the transfer matrix. Moreover, as discussed in the following section, our solution is similar to the known one [10, 1] for the case of diagonal boundary terms. 10 j=0 (4.20)
12 5 Special cases For generic values of the boundary parameters, the Bethe Ansatz solution presented in the previous section is formulated in terms of Jacobian elliptic functions. However, for modulus k = 0 or k = 1, these elliptic functions degenerate into ordinary trigonometric or hyperbolic functions. Equivalently, the argument of the square root in (4.13) then becomes a perfect square, and so the square root effectively disappears. We now briefly consider some of these special cases. 5.1 Diagonal case In the limit κ ± 0, the K matrices (2.11), (2.12) become diagonal, and therefore so do the boundary terms in the Hamiltonian (1.1). The transfer matrix t(u) now commutes with the operator F = N i=1 σz i, and hence, both operators can be simultaneously diagonalized. Denoting the corresponding eigenstates by Λ (±), we have t(u) Λ (±) = Λ (±) (u) Λ (±), The transfer matrix now has the asymptotic behavior F Λ (±) = ± Λ (±). (5.1) where t(u) ρ eu(2+2n) F +... for u, (5.2) 21+2N ρ = { icosh(ξ + ξ ) for N= even isinh(ξ + ξ ) for N= odd. (5.3) The eigenvalues are given by Λ (±) (u) = ±ρsinh2u N sinh(u u j )cosh(u+u j ), (5.4) j=1 which is similar to (4.5) except with one less root. In terms of the boundary parameters η ±,ϑ ± (2.13), the limit κ ± 0 corresponds to η ± = iξ ± π 2, e ϑ ± = 1 κ ±. (5.5) In this limit the function h(u) becomes equal (for N = even) to h(u) = sinh(u ξ )cosh(u ξ )sinh(u±ξ + )cosh(u±ξ + ). (5.6) 11
13 Moreover, the Bethe Ansatz equations (4.11) become tanh 2N u j = sinh(u j ξ )sinh(u j ±ξ + ) cosh(u j ±ξ )cosh(u j ξ + ). (5.7) These results are similar to those obtained previously [10, 1] for the XXZ chain. The two choices of signs correspond to the two possible pseudovacua either all spins up or all spins down. 5.2 Nondiagonal cases Within the space of boundary parameters, there are various submanifolds, such as η η + ±i(ϑ ϑ + ) = π 1+( 1) N, (5.8) 2 2 for which α = k = 0. As a simple example, let us consider the particular case N = odd, η = η + η, ϑ = ϑ + ϑ, for which also β = 0. The function h(u) becomes equal to h(u) = κ 2 + κ2 sinh2(u iη)sinh2(u+iη)sinh2(u ϑ)sinh2(u+ϑ). (5.9) We then obtain the Bethe Ansatz equations tanh 2N u j = coth(u j +iη)coth(u j iη)coth(u j +ϑ)coth(u j ϑ). (5.10) 6 Discussion This work raises a number of interesting questions, some of which we list below: We have seen that the doubly-periodic functions in the Bethe Ansatz solution degenerate into singly-periodic functions for special values of the boundary parameters. In[5], important simplifications are also found to occur for special values of the boundary parameters. It is likely that these two observations are related. As we have emphasized, an exact inversion identity for the XX (or N = 2) case is made possible by the key fact that the fused transfer matrix is proportional to the identity matrix. A similar result also holds for the N = 1 case [13]. It would be interesting to better understand the relation of this phenomenon to the free-fermion condition. The model (1.1) is not the most general integrable open XX chain. Indeed, the most general solution [2, 3] of the XXZ boundary Yang-Baxter equation has the off-diagonal terms 12
14 κ (1) ± sinh2uandκ (2) ± sinh2u, whilehere we have restricted tothespecial case κ (1) ± = κ (2) ± κ ±. (See Eqs. (2.11), (2.12).) However, we do not expect that the more general case will lead to new significant complications. In particular, we expect that the same approach can be used to derive an exact inversion identity and to obtain the corresponding Bethe Ansatz solution. Since the model (1.1) has various boundary parameters, its phase diagram is likely to have a rich structure. Our exact Bethe Ansatz solution should provide a means of exploring these phases. Moreover, as mentioned in the Introduction, this solution opens the way to formulating the thermodynamic Bethe Ansatz equations for integrable N = 2 supersymmetric quantum field theories with boundary [14, 15], as was done for the case of N = 1 supersymmetry in [13]. Finally, with the insight gained from the XX chain, it might now be possible to finally solve the open XXZ chain with nondiagonal boundary terms. We hope to report on some of these problems in future publications. Acknowledgments I thank O. Alvarez for helpful discussions. This work was supported in part by the National Science Foundation under Grants PHY and PHY References [1] E.K. Sklyanin, J. Phys. A21 (1988) [2] H.J. de Vega and A. González-Ruiz, J. Phys. A26 (1993) L519. [3] S. Ghoshal and A.B. Zamolodchikov, Int. J. Mod. Phys. A9 (1994) [4] F. Guinea, Phys. Rev. B32 (1985) 7518; F. Guinea, V. Hakim and A. Muramatsu, Phys. Rev. Lett. 54 (1985) 263. [5] U. Bilstein and B. Wehefritz, J. Phys. A32 (1999) 191; U. Bilstein, J. Phys. A33 (2000) 4437; A33 (2000) [6] P. Jordan and E. Wigner, Z. Phys. 47 (1928) 631. [7] E. Lieb, T. Schultz and D. Mattis, Ann. Phys. 16 (1961) 407. [8] J.A. Tjon, Phys. Rev. B2 (1970)
15 [9] R.Z. Bariev and I. Peschel, Phys. Lett. A153 (1991) 166; H. Hinrichsen, K. Krebs and I. Peschel, Z. Phys. B100 (1996) 105. [10] F.C. Alcaraz, M.N. Barber, M.T. Batchelor, R.J. Baxter and G.R.W. Quispel, J. Phys. A20 (1987) [11] C.N. Yang, Phys. Rev. Lett. 19 (1967) [12] P. Fendley and H. Saleur, Nucl. Phys. B428 (1994) 681. [13] C. Ahn and R.I. Nepomechie, Nucl. Phys. B586 (2000) 611. [14] P. Fendley and K. Intriligator, Nucl. Phys. B372 (1992) 533; B380 (1992) 265. [15] R.I. Nepomechie, Phys. Lett. B516 (2001) 161. [16] L. Mezincescu and R.I. Nepomechie, J. Phys. A25 (1992) [17] C. Fan and F.Y. Wu, Phys. Rev. B2 (1970) 723. [18] R.J. Baxter, Exactly Solved Models in Statistical Mechanics (Academic Press, 1982). [19] B.U. Felderhof, Physica 65 (1973) 421; 66 (1973) 279, 509; C. Ahn, Nucl. Phys. B422 (1994) 449. [20] M. Karowski, Nucl. Phys. B153 (1979) 244; P.P. Kulish, N.Yu. Reshetikhin and E.K. Sklyanin, Lett. Math. Phys. 5 (1981) 393. [21] P.P. Kulish and E.K. Sklyanin, Lecture Notes in Physics, Vol. 151, (Springer, 1982), 61. [22] V.E. Korepin, N.M. Bogoliubov, and A.G. Izergin, Quantum Inverse Scattering Method, Correlation Functions and Algebraic Bethe Ansatz (Cambridge University Press, 1993). [23] R.I. Nepomechie, Int. J. Mod. Phys. B13 (1999) [24] I.V. Cherednik, Theor. Math. Phys. 61 (1984) 977. [25] R. Cuerno and A. González-Ruiz, J. Phys. A A26 (1993) L605. [26] L. Mezincescu and R.I. Nepomechie, Nucl. Phys. B372 (1992) 597. [27] H. Radjavi and P. Rosenthal, Simultaneous Triangularization (Springer, 2000). [28] A.G. Izergin and V.E. Korepin, Sov. Phys. Doklady 26 (1981) 653; Nucl. Phys. B205 (1982) 401. [29] E.T. Whittaker and G.N. Watson, A Course of Modern Analysis (Cambridge University Press, 1988) 14
Trigonometric SOS model with DWBC and spin chains with non-diagonal boundaries
 Trigonometric SOS model with DWBC and spin chains with non-diagonal boundaries N. Kitanine IMB, Université de Bourgogne. In collaboration with: G. Filali RAQIS 21, Annecy June 15 - June 19, 21 Typeset
Trigonometric SOS model with DWBC and spin chains with non-diagonal boundaries N. Kitanine IMB, Université de Bourgogne. In collaboration with: G. Filali RAQIS 21, Annecy June 15 - June 19, 21 Typeset
Takeo INAMI and Hitoshi KONNO. Yukawa Institute for Theoretical Physics, Kyoto University, Kyoto , Japan. ABSTRACT
 SLAC{PUB{YITP/K-1084 August 1994 Integrable XYZ Spin Chain with Boundaries Takeo INAMI and Hitoshi KONNO Yukawa Institute for Theoretical Physics, Kyoto University, Kyoto 606-01, Japan. ABSTRACT HEP-TH-9409138
SLAC{PUB{YITP/K-1084 August 1994 Integrable XYZ Spin Chain with Boundaries Takeo INAMI and Hitoshi KONNO Yukawa Institute for Theoretical Physics, Kyoto University, Kyoto 606-01, Japan. ABSTRACT HEP-TH-9409138
Clifford algebras, Fermions and Spin chains
 Clifford algebras, Fermions and Spin chains 1 Birgit Wehefritz-Kaufmann Physics Department, University of Connecticut, U-3046, 15 Hillside Road, Storrs, CT 0669-3046 Abstract. We show how using Clifford
Clifford algebras, Fermions and Spin chains 1 Birgit Wehefritz-Kaufmann Physics Department, University of Connecticut, U-3046, 15 Hillside Road, Storrs, CT 0669-3046 Abstract. We show how using Clifford
Free Fermionic Elliptic Reflection Matrices and Quantum Group Invariance
 IMAFF 93/11 LPTHE PAR 93/1 April 1993 Free Fermionic Elliptic Reflection Matrices and Quantum Group Invariance arxiv:hep-th/930411v1 3 Apr 1993 R. Cuerno Instituto de Matemáticas y Física Fundamental,
IMAFF 93/11 LPTHE PAR 93/1 April 1993 Free Fermionic Elliptic Reflection Matrices and Quantum Group Invariance arxiv:hep-th/930411v1 3 Apr 1993 R. Cuerno Instituto de Matemáticas y Física Fundamental,
The boundary supersymmetric sine-gordon model revisited
 UMTG 7 The boundary supersymmetric sine-gordon model revisited arxiv:hep-th/010309v 7 Mar 001 Rafael I. Nepomechie Physics Department, P.O. Box 48046, University of Miami Coral Gables, FL 3314 USA Abstract
UMTG 7 The boundary supersymmetric sine-gordon model revisited arxiv:hep-th/010309v 7 Mar 001 Rafael I. Nepomechie Physics Department, P.O. Box 48046, University of Miami Coral Gables, FL 3314 USA Abstract
Properties of the Bethe Ansatz equations for Richardson-Gaudin models
 Properties of the Bethe Ansatz equations for Richardson-Gaudin models Inna Luyaneno, Phillip Isaac, Jon Lins Centre for Mathematical Physics, School of Mathematics and Physics, The University of Queensland
Properties of the Bethe Ansatz equations for Richardson-Gaudin models Inna Luyaneno, Phillip Isaac, Jon Lins Centre for Mathematical Physics, School of Mathematics and Physics, The University of Queensland
Systematic construction of (boundary) Lax pairs
 Thessaloniki, October 2010 Motivation Integrable b.c. interesting for integrable systems per ce, new info on boundary phenomena + learn more on bulk behavior. Examples of integrable b.c. that modify the
Thessaloniki, October 2010 Motivation Integrable b.c. interesting for integrable systems per ce, new info on boundary phenomena + learn more on bulk behavior. Examples of integrable b.c. that modify the
Fractional-Spin Integrals of Motion for the Boundary Sine-Gordon Model at the Free Fermion Point
 UMTG 200 Fractional-Spin Integrals of Motion for the Boundary Sine-Gordon Model at the Free Fermion Point Luca Mezincescu and Rafael I. Nepomechie Physics Department, P.O. Box 248046, University of Miami
UMTG 200 Fractional-Spin Integrals of Motion for the Boundary Sine-Gordon Model at the Free Fermion Point Luca Mezincescu and Rafael I. Nepomechie Physics Department, P.O. Box 248046, University of Miami
Difference Equations and Highest Weight Modules of U q [sl(n)]
![Difference Equations and Highest Weight Modules of U q [sl(n)] Difference Equations and Highest Weight Modules of U q [sl(n)]](/thumbs/75/72831271.jpg) arxiv:math/9805089v1 [math.qa] 20 May 1998 Difference Equations and Highest Weight Modules of U q [sl(n)] A. Zapletal 1,2 Institut für Theoretische Physik Freie Universität Berlin, Arnimallee 14, 14195
arxiv:math/9805089v1 [math.qa] 20 May 1998 Difference Equations and Highest Weight Modules of U q [sl(n)] A. Zapletal 1,2 Institut für Theoretische Physik Freie Universität Berlin, Arnimallee 14, 14195
Since the discovery of high T c superconductivity there has been a great interest in the area of integrable highly correlated electron systems. Notabl
 CERN-TH/97-72 Anisotropic Correlated Electron Model Associated With the Temperley-Lieb Algebra Angela Foerster (;y;a), Jon Links (2;b) and Itzhak Roditi (3;z;c) () Institut fur Theoretische Physik, Freie
CERN-TH/97-72 Anisotropic Correlated Electron Model Associated With the Temperley-Lieb Algebra Angela Foerster (;y;a), Jon Links (2;b) and Itzhak Roditi (3;z;c) () Institut fur Theoretische Physik, Freie
THE SPECTRUM OF BOUNDARY SINE- GORDON THEORY
 THE SPECTRUM OF BOUNDARY SINE- GORDON THEORY Z. Bajnok, L. Palla and G. Takács Institute for Theoretical Physics, Eötvös University, Budapest, Hungary Abstract We review our recent results on the on-shell
THE SPECTRUM OF BOUNDARY SINE- GORDON THEORY Z. Bajnok, L. Palla and G. Takács Institute for Theoretical Physics, Eötvös University, Budapest, Hungary Abstract We review our recent results on the on-shell
A tale of two Bethe ansätze
 UMTG 93 A tale of two Bethe ansätze arxiv:171.06475v [math-ph] 6 Apr 018 Antonio Lima-Santos 1, Rafael I. Nepomechie Rodrigo A. Pimenta 3 Abstract We revisit the construction of the eigenvectors of the
UMTG 93 A tale of two Bethe ansätze arxiv:171.06475v [math-ph] 6 Apr 018 Antonio Lima-Santos 1, Rafael I. Nepomechie Rodrigo A. Pimenta 3 Abstract We revisit the construction of the eigenvectors of the
Duality and quantum-algebra symmetry of the A (1) open spin chain with diagonal boundary fields
 UMTG 207 Duality and quantum-algebra symmetry of the A 1) 1 open spin chain with diagonal boundary fields Anastasia Doikou and Rafael I. epomechie Physics Department, P.O. Box 248046, University of Miami
UMTG 207 Duality and quantum-algebra symmetry of the A 1) 1 open spin chain with diagonal boundary fields Anastasia Doikou and Rafael I. epomechie Physics Department, P.O. Box 248046, University of Miami
arxiv: v1 [math-ph] 24 Dec 2013
![arxiv: v1 [math-ph] 24 Dec 2013 arxiv: v1 [math-ph] 24 Dec 2013](/thumbs/95/124403329.jpg) ITP-UU-13/32 SPIN-13/24 Twisted Heisenberg chain and the six-vertex model with DWBC arxiv:1312.6817v1 [math-ph] 24 Dec 2013 W. Galleas Institute for Theoretical Physics and Spinoza Institute, Utrecht University,
ITP-UU-13/32 SPIN-13/24 Twisted Heisenberg chain and the six-vertex model with DWBC arxiv:1312.6817v1 [math-ph] 24 Dec 2013 W. Galleas Institute for Theoretical Physics and Spinoza Institute, Utrecht University,
arxiv: v1 [math-ph] 22 Dec 2014
![arxiv: v1 [math-ph] 22 Dec 2014 arxiv: v1 [math-ph] 22 Dec 2014](/thumbs/75/72506079.jpg) arxiv:1412.6905v1 [math-ph] 22 Dec 2014 Bethe states of the XXZ spin- 1 chain with arbitrary 2 boundary fields Xin Zhang a, Yuan-Yuan Li a, Junpeng Cao a,b, Wen-Li Yang c,d1, Kangjie Shi c and Yupeng Wang
arxiv:1412.6905v1 [math-ph] 22 Dec 2014 Bethe states of the XXZ spin- 1 chain with arbitrary 2 boundary fields Xin Zhang a, Yuan-Yuan Li a, Junpeng Cao a,b, Wen-Li Yang c,d1, Kangjie Shi c and Yupeng Wang
The XYZ spin chain/8-vertex model with quasi-periodic boundary conditions Exact solution by Separation of Variables
 The XYZ spin chain/8-vertex model with quasi-periodic boundary conditions Exact solution by Separation of Variables Véronique TERRAS CNRS & Université Paris Sud, France Workshop: Beyond integrability.
The XYZ spin chain/8-vertex model with quasi-periodic boundary conditions Exact solution by Separation of Variables Véronique TERRAS CNRS & Université Paris Sud, France Workshop: Beyond integrability.
Bethe ansatz solution of a closed spin 1 XXZ Heisenberg chain with quantum algebra symmetry
 Bethe ansatz solution of a closed spin 1 XXZ Heisenberg chain with quantum algebra symmetry Jon Links, Angela Foerster and Michael Karowski arxiv:solv-int/9809001v1 8 Aug 1998 Department of Mathematics,
Bethe ansatz solution of a closed spin 1 XXZ Heisenberg chain with quantum algebra symmetry Jon Links, Angela Foerster and Michael Karowski arxiv:solv-int/9809001v1 8 Aug 1998 Department of Mathematics,
On the algebraic Bethe ansatz approach to correlation functions: the Heisenberg spin chain
 On the algebraic Bethe ansatz approach to correlation functions: the Heisenberg spin chain V. Terras CNRS & ENS Lyon, France People involved: N. Kitanine, J.M. Maillet, N. Slavnov and more recently: J.
On the algebraic Bethe ansatz approach to correlation functions: the Heisenberg spin chain V. Terras CNRS & ENS Lyon, France People involved: N. Kitanine, J.M. Maillet, N. Slavnov and more recently: J.
The continuum limit of the integrable open XYZ spin-1/2 chain
 arxiv:hep-th/9809028v2 8 Sep 1998 The continuum limit of the integrable open XYZ spin-1/2 chain Hiroshi Tsukahara and Takeo Inami Department of Physics, Chuo University, Kasuga, Bunkyo-ku, Tokyo 112-8551
arxiv:hep-th/9809028v2 8 Sep 1998 The continuum limit of the integrable open XYZ spin-1/2 chain Hiroshi Tsukahara and Takeo Inami Department of Physics, Chuo University, Kasuga, Bunkyo-ku, Tokyo 112-8551
arxiv:cond-mat/ v1 [cond-mat.str-el] 9 May 2001
![arxiv:cond-mat/ v1 [cond-mat.str-el] 9 May 2001 arxiv:cond-mat/ v1 [cond-mat.str-el] 9 May 2001](/thumbs/73/69542217.jpg) arxiv:cond-mat/005203v [cond-mat.str-el] 9 May 200 Integrable open boundary conditions for the Bariev model of three coupled XY spin chains A. Foerster a M. D. Gould b X.-W. Guan a I. Roditi cd H.-Q Zhou
arxiv:cond-mat/005203v [cond-mat.str-el] 9 May 200 Integrable open boundary conditions for the Bariev model of three coupled XY spin chains A. Foerster a M. D. Gould b X.-W. Guan a I. Roditi cd H.-Q Zhou
Surface excitations and surface energy of the antiferromagnetic XXZ chain by the Bethe ansatz approach
 J. Phys. A: Math. Gen. 9 (1996) 169 1638. Printed in the UK Surface excitations and surface energy of the antiferromagnetic XXZ chain by the Bethe ansatz approach A Kapustin and S Skorik Physics Department,
J. Phys. A: Math. Gen. 9 (1996) 169 1638. Printed in the UK Surface excitations and surface energy of the antiferromagnetic XXZ chain by the Bethe ansatz approach A Kapustin and S Skorik Physics Department,
arxiv: v2 [math-ph] 14 Jul 2014
![arxiv: v2 [math-ph] 14 Jul 2014 arxiv: v2 [math-ph] 14 Jul 2014](/thumbs/87/96898919.jpg) ITP-UU-14/14 SPIN-14/12 Reflection algebra and functional equations arxiv:1405.4281v2 [math-ph] 14 Jul 2014 W. Galleas and J. Lamers Institute for Theoretical Physics and Spinoza Institute, Utrecht University,
ITP-UU-14/14 SPIN-14/12 Reflection algebra and functional equations arxiv:1405.4281v2 [math-ph] 14 Jul 2014 W. Galleas and J. Lamers Institute for Theoretical Physics and Spinoza Institute, Utrecht University,
arxiv:nlin/ v1 [nlin.si] 24 Jul 2003
![arxiv:nlin/ v1 [nlin.si] 24 Jul 2003 arxiv:nlin/ v1 [nlin.si] 24 Jul 2003](/thumbs/85/92054724.jpg) C (1) n, D (1) n and A (2) 2n 1 reflection K-matrices A. Lima-Santos 1 and R. Malara 2 arxiv:nlin/0307046v1 [nlin.si] 24 Jul 2003 Universidade Federal de São Carlos, Departamento de Física Caixa Postal
C (1) n, D (1) n and A (2) 2n 1 reflection K-matrices A. Lima-Santos 1 and R. Malara 2 arxiv:nlin/0307046v1 [nlin.si] 24 Jul 2003 Universidade Federal de São Carlos, Departamento de Física Caixa Postal
Baxter Q-operators and tau-function for quantum integrable spin chains
 Baxter Q-operators and tau-function for quantum integrable spin chains Zengo Tsuboi Institut für Mathematik und Institut für Physik, Humboldt-Universität zu Berlin This is based on the following papers.
Baxter Q-operators and tau-function for quantum integrable spin chains Zengo Tsuboi Institut für Mathematik und Institut für Physik, Humboldt-Universität zu Berlin This is based on the following papers.
Random Fermionic Systems
 Random Fermionic Systems Fabio Cunden Anna Maltsev Francesco Mezzadri University of Bristol December 9, 2016 Maltsev (University of Bristol) Random Fermionic Systems December 9, 2016 1 / 27 Background
Random Fermionic Systems Fabio Cunden Anna Maltsev Francesco Mezzadri University of Bristol December 9, 2016 Maltsev (University of Bristol) Random Fermionic Systems December 9, 2016 1 / 27 Background
Temperature Correlation Functions in the XXO Heisenberg Chain
 CONGRESSO NAZIONALE DI FISICA DELLA MATERIA Brescia, 13-16 June, 1994 Temperature Correlation Functions in the XXO Heisenberg Chain F. Colomo 1, A.G. Izergin 2,3, V.E. Korepin 4, V. Tognetti 1,5 1 I.N.F.N.,
CONGRESSO NAZIONALE DI FISICA DELLA MATERIA Brescia, 13-16 June, 1994 Temperature Correlation Functions in the XXO Heisenberg Chain F. Colomo 1, A.G. Izergin 2,3, V.E. Korepin 4, V. Tognetti 1,5 1 I.N.F.N.,
An ingenious mapping between integrable supersymmetric chains
 An ingenious mapping between integrable supersymmetric chains Jan de Gier University of Melbourne Bernard Nienhuis 65th birthday, Amsterdam 2017 György Fehér Sasha Garbaly Kareljan Schoutens Jan de Gier
An ingenious mapping between integrable supersymmetric chains Jan de Gier University of Melbourne Bernard Nienhuis 65th birthday, Amsterdam 2017 György Fehér Sasha Garbaly Kareljan Schoutens Jan de Gier
arxiv:nlin/ v1 [nlin.si] 18 Mar 2003
![arxiv:nlin/ v1 [nlin.si] 18 Mar 2003 arxiv:nlin/ v1 [nlin.si] 18 Mar 2003](/thumbs/95/125832175.jpg) UFSCAR-TH-02 Yang-Baxter equation for the asymmetric eight-vertex model. arxiv:nlin/0303036v1 [nlin.si] 18 Mar 2003 W. Galleas and M.J. Martins Departamento de Física, Universidade Federal de São Carlos
UFSCAR-TH-02 Yang-Baxter equation for the asymmetric eight-vertex model. arxiv:nlin/0303036v1 [nlin.si] 18 Mar 2003 W. Galleas and M.J. Martins Departamento de Física, Universidade Federal de São Carlos
Deformed Richardson-Gaudin model
 Deformed Richardson-Gaudin model P Kulish 1, A Stolin and L H Johannesson 1 St. Petersburg Department of Stelov Mathematical Institute, Russian Academy of Sciences Fontana 7, 19103 St. Petersburg, Russia
Deformed Richardson-Gaudin model P Kulish 1, A Stolin and L H Johannesson 1 St. Petersburg Department of Stelov Mathematical Institute, Russian Academy of Sciences Fontana 7, 19103 St. Petersburg, Russia
Exact solution for the Bariev model with boundary fields arxiv:cond-mat/ v1 [cond-mat.str-el] 4 Sep 2000
![Exact solution for the Bariev model with boundary fields arxiv:cond-mat/ v1 [cond-mat.str-el] 4 Sep 2000 Exact solution for the Bariev model with boundary fields arxiv:cond-mat/ v1 [cond-mat.str-el] 4 Sep 2000](/thumbs/73/69542276.jpg) Exact solution for the Bariev model with boundary fields arxiv:cond-mat/0009045v1 [cond-mat.str-el] 4 Sep 000 A. Foerster a, X.-W. Guan a, J. Links c, I. Roditi b, H.-Q Zhou c, Abstract a Instituto de
Exact solution for the Bariev model with boundary fields arxiv:cond-mat/0009045v1 [cond-mat.str-el] 4 Sep 000 A. Foerster a, X.-W. Guan a, J. Links c, I. Roditi b, H.-Q Zhou c, Abstract a Instituto de
Izergin-Korepin determinant reloaded
 Izergin-Korepin determinant reloaded arxiv:math-ph/0409072v1 27 Sep 2004 Yu. G. Stroganov Institute for High Energy Physics 142284 Protvino, Moscow region, Russia Abstract We consider the Izergin-Korepin
Izergin-Korepin determinant reloaded arxiv:math-ph/0409072v1 27 Sep 2004 Yu. G. Stroganov Institute for High Energy Physics 142284 Protvino, Moscow region, Russia Abstract We consider the Izergin-Korepin
Condensation properties of Bethe roots in the XXZ chain
 Condensation properties of Bethe roots in the XXZ chain K K Kozlowski CNRS, aboratoire de Physique, ENS de yon 25 th of August 206 K K Kozlowski "On condensation properties of Bethe roots associated with
Condensation properties of Bethe roots in the XXZ chain K K Kozlowski CNRS, aboratoire de Physique, ENS de yon 25 th of August 206 K K Kozlowski "On condensation properties of Bethe roots associated with
Gaudin Hypothesis for the XYZ Spin Chain
 Gaudin Hypothesis for the XYZ Spin Chain arxiv:cond-mat/9908326v3 2 Nov 1999 Yasuhiro Fujii and Miki Wadati Department of Physics, Graduate School of Science, University of Tokyo, Hongo 7 3 1, Bunkyo-ku,
Gaudin Hypothesis for the XYZ Spin Chain arxiv:cond-mat/9908326v3 2 Nov 1999 Yasuhiro Fujii and Miki Wadati Department of Physics, Graduate School of Science, University of Tokyo, Hongo 7 3 1, Bunkyo-ku,
arxiv:hep-th/ v1 24 Sep 1998
 ICTP/IR/98/19 SISSA/EP/98/101 Quantum Integrability of Certain Boundary Conditions 1 arxiv:hep-th/9809178v1 24 Sep 1998 M. Moriconi 2 The Abdus Salam International Centre for Theoretical Physics Strada
ICTP/IR/98/19 SISSA/EP/98/101 Quantum Integrability of Certain Boundary Conditions 1 arxiv:hep-th/9809178v1 24 Sep 1998 M. Moriconi 2 The Abdus Salam International Centre for Theoretical Physics Strada
Rational Form Solitary Wave Solutions and Doubly Periodic Wave Solutions to (1+1)-Dimensional Dispersive Long Wave Equation
 Commun. Theor. Phys. (Beijing, China) 43 (005) pp. 975 98 c International Academic Publishers Vol. 43, No. 6, June 15, 005 Rational Form Solitary Wave Solutions and Doubly Periodic Wave Solutions to (1+1)-Dimensional
Commun. Theor. Phys. (Beijing, China) 43 (005) pp. 975 98 c International Academic Publishers Vol. 43, No. 6, June 15, 005 Rational Form Solitary Wave Solutions and Doubly Periodic Wave Solutions to (1+1)-Dimensional
Finite temperature form factors in the free Majorana theory
 Finite temperature form factors in the free Majorana theory Benjamin Doyon Rudolf Peierls Centre for Theoretical Physics, Oxford University, UK supported by EPSRC postdoctoral fellowship hep-th/0506105
Finite temperature form factors in the free Majorana theory Benjamin Doyon Rudolf Peierls Centre for Theoretical Physics, Oxford University, UK supported by EPSRC postdoctoral fellowship hep-th/0506105
Introduction to Integrability in AdS/CFT: Lecture 4
 Introduction to Integrability in AdS/CFT: Lecture 4 Rafael Nepomechie University of Miami Introduction Recall: 1-loop dilatation operator for all single-trace operators in N=4 SYM is integrable 1-loop
Introduction to Integrability in AdS/CFT: Lecture 4 Rafael Nepomechie University of Miami Introduction Recall: 1-loop dilatation operator for all single-trace operators in N=4 SYM is integrable 1-loop
arxiv:hep-th/ v2 1 Aug 2001
 Universal amplitude ratios in the two-dimensional Ising model 1 arxiv:hep-th/9710019v2 1 Aug 2001 Gesualdo Delfino Laboratoire de Physique Théorique, Université de Montpellier II Pl. E. Bataillon, 34095
Universal amplitude ratios in the two-dimensional Ising model 1 arxiv:hep-th/9710019v2 1 Aug 2001 Gesualdo Delfino Laboratoire de Physique Théorique, Université de Montpellier II Pl. E. Bataillon, 34095
Introduction to the Mathematics of the XY -Spin Chain
 Introduction to the Mathematics of the XY -Spin Chain Günter Stolz June 9, 2014 Abstract In the following we present an introduction to the mathematical theory of the XY spin chain. The importance of this
Introduction to the Mathematics of the XY -Spin Chain Günter Stolz June 9, 2014 Abstract In the following we present an introduction to the mathematical theory of the XY spin chain. The importance of this
Lecture notes: Quantum gates in matrix and ladder operator forms
 Phys 7 Topics in Particles & Fields Spring 3 Lecture v.. Lecture notes: Quantum gates in matrix and ladder operator forms Jeffrey Yepez Department of Physics and Astronomy University of Hawai i at Manoa
Phys 7 Topics in Particles & Fields Spring 3 Lecture v.. Lecture notes: Quantum gates in matrix and ladder operator forms Jeffrey Yepez Department of Physics and Astronomy University of Hawai i at Manoa
arxiv:hep-th/ v1 20 Oct 1993
 ISAS/EP/93/167 Two-point Correlation Function in Integrable QFT with Anti-Crossing Symmetry arxiv:hep-th/9310130v1 0 Oct 1993 G. Delfino and G. Mussardo International School for Advanced Studies, and Istituto
ISAS/EP/93/167 Two-point Correlation Function in Integrable QFT with Anti-Crossing Symmetry arxiv:hep-th/9310130v1 0 Oct 1993 G. Delfino and G. Mussardo International School for Advanced Studies, and Istituto
Supersymmetry, lattice fermions, independence complexes and cohomology theory
 c 2010 International Press Adv. Theor. Math. Phys. 14 (2010) 643 694 Supersymmetry, lattice fermions, independence complexes and cohomology theory Liza Huijse 1,2 and Kareljan Schoutens 1 1 Institute for
c 2010 International Press Adv. Theor. Math. Phys. 14 (2010) 643 694 Supersymmetry, lattice fermions, independence complexes and cohomology theory Liza Huijse 1,2 and Kareljan Schoutens 1 1 Institute for
Angular Momentum set II
 Angular Momentum set II PH - QM II Sem, 7-8 Problem : Using the commutation relations for the angular momentum operators, prove the Jacobi identity Problem : [ˆL x, [ˆL y, ˆL z ]] + [ˆL y, [ˆL z, ˆL x
Angular Momentum set II PH - QM II Sem, 7-8 Problem : Using the commutation relations for the angular momentum operators, prove the Jacobi identity Problem : [ˆL x, [ˆL y, ˆL z ]] + [ˆL y, [ˆL z, ˆL x
The form factor program a review and new results
 The form factor program a review and new results the nested SU(N)-off-shell Bethe ansatz H. Babujian, A. Foerster, and M. Karowski FU-Berlin Budapest, June 2006 Babujian, Foerster, Karowski (FU-Berlin)
The form factor program a review and new results the nested SU(N)-off-shell Bethe ansatz H. Babujian, A. Foerster, and M. Karowski FU-Berlin Budapest, June 2006 Babujian, Foerster, Karowski (FU-Berlin)
An Improved F-Expansion Method and Its Application to Coupled Drinfel d Sokolov Wilson Equation
 Commun. Theor. Phys. (Beijing, China) 50 (008) pp. 309 314 c Chinese Physical Society Vol. 50, No., August 15, 008 An Improved F-Expansion Method and Its Application to Coupled Drinfel d Sokolov Wilson
Commun. Theor. Phys. (Beijing, China) 50 (008) pp. 309 314 c Chinese Physical Society Vol. 50, No., August 15, 008 An Improved F-Expansion Method and Its Application to Coupled Drinfel d Sokolov Wilson
On the Random XY Spin Chain
 1 CBMS: B ham, AL June 17, 2014 On the Random XY Spin Chain Robert Sims University of Arizona 2 The Isotropic XY-Spin Chain Fix a real-valued sequence {ν j } j 1 and for each integer n 1, set acting on
1 CBMS: B ham, AL June 17, 2014 On the Random XY Spin Chain Robert Sims University of Arizona 2 The Isotropic XY-Spin Chain Fix a real-valued sequence {ν j } j 1 and for each integer n 1, set acting on
ADVANCED TOPICS IN STATISTICAL PHYSICS
 ADVANCED TOPICS IN STATISTICAL PHYSICS Spring term 2013 EXERCISES Note : All undefined notation is the same as employed in class. Exercise 1301. Quantum spin chains a. Show that the 1D Heisenberg and XY
ADVANCED TOPICS IN STATISTICAL PHYSICS Spring term 2013 EXERCISES Note : All undefined notation is the same as employed in class. Exercise 1301. Quantum spin chains a. Show that the 1D Heisenberg and XY
arxiv:solv-int/ v1 5 Jan 1999
 UFSCARF-TH-98-33 Unified algebraic Bethe ansatz for two-dimensional lattice models arxiv:solv-int/9901002v1 5 Jan 1999 M.J. Martins Universidade Federal de São Carlos Departamento de Física C.P. 676, 13565-905,
UFSCARF-TH-98-33 Unified algebraic Bethe ansatz for two-dimensional lattice models arxiv:solv-int/9901002v1 5 Jan 1999 M.J. Martins Universidade Federal de São Carlos Departamento de Física C.P. 676, 13565-905,
G : Quantum Mechanics II
 G5.666: Quantum Mechanics II Notes for Lecture 5 I. REPRESENTING STATES IN THE FULL HILBERT SPACE Given a representation of the states that span the spin Hilbert space, we now need to consider the problem
G5.666: Quantum Mechanics II Notes for Lecture 5 I. REPRESENTING STATES IN THE FULL HILBERT SPACE Given a representation of the states that span the spin Hilbert space, we now need to consider the problem
Space from Superstring Bits 1. Charles Thorn
 Space from Superstring Bits 1 Charles Thorn University of Florida Miami 2014 1 Much of this work in collaboration with Songge Sun A single superstring bit: quantum system with finite # of states Superstring
Space from Superstring Bits 1 Charles Thorn University of Florida Miami 2014 1 Much of this work in collaboration with Songge Sun A single superstring bit: quantum system with finite # of states Superstring
Deformed Richardson-Gaudin model
 Home Search Collections Journals About Contact us My IOPscience Deformed Richardson-Gaudin model This content has been downloaded from IOPscience. Please scroll down to see the full text. View the table
Home Search Collections Journals About Contact us My IOPscience Deformed Richardson-Gaudin model This content has been downloaded from IOPscience. Please scroll down to see the full text. View the table
The six vertex model is an example of a lattice model in statistical mechanics. The data are
 The six vertex model, R-matrices, and quantum groups Jethro van Ekeren. 1 The six vertex model The six vertex model is an example of a lattice model in statistical mechanics. The data are A finite rectangular
The six vertex model, R-matrices, and quantum groups Jethro van Ekeren. 1 The six vertex model The six vertex model is an example of a lattice model in statistical mechanics. The data are A finite rectangular
Department of Applied Mathematics, Dalian University of Technology, Dalian , China
 Commun Theor Phys (Being, China 45 (006 pp 199 06 c International Academic Publishers Vol 45, No, February 15, 006 Further Extended Jacobi Elliptic Function Rational Expansion Method and New Families of
Commun Theor Phys (Being, China 45 (006 pp 199 06 c International Academic Publishers Vol 45, No, February 15, 006 Further Extended Jacobi Elliptic Function Rational Expansion Method and New Families of
arxiv:quant-ph/ v1 15 Dec 2004
 Entanglement in the XX Spin Chain with Energy Current V. Eisler, and Z. Zimborás 2, Institute for Theoretical Physics, Eötvös University, 7 Budapest, Pázmány sétány /a, Hungary 2 Research Institute for
Entanglement in the XX Spin Chain with Energy Current V. Eisler, and Z. Zimborás 2, Institute for Theoretical Physics, Eötvös University, 7 Budapest, Pázmány sétány /a, Hungary 2 Research Institute for
arxiv:quant-ph/ v2 24 Dec 2003
 Quantum Entanglement in Heisenberg Antiferromagnets V. Subrahmanyam Department of Physics, Indian Institute of Technology, Kanpur, India. arxiv:quant-ph/0309004 v2 24 Dec 2003 Entanglement sharing among
Quantum Entanglement in Heisenberg Antiferromagnets V. Subrahmanyam Department of Physics, Indian Institute of Technology, Kanpur, India. arxiv:quant-ph/0309004 v2 24 Dec 2003 Entanglement sharing among
Indecomposability parameters in LCFT
 Indecomposability parameters in LCFT Romain Vasseur Joint work with J.L. Jacobsen and H. Saleur at IPhT CEA Saclay and LPTENS (Nucl. Phys. B 851, 314-345 (2011), arxiv :1103.3134) ACFTA (Institut Henri
Indecomposability parameters in LCFT Romain Vasseur Joint work with J.L. Jacobsen and H. Saleur at IPhT CEA Saclay and LPTENS (Nucl. Phys. B 851, 314-345 (2011), arxiv :1103.3134) ACFTA (Institut Henri
The sl(2) loop algebra symmetry of the XXZ spin chain at roots of unity and applications to the superintegrable chiral Potts model 1
 The sl(2) loop algebra symmetry of the XXZ spin chain at roots of unity and applications to the superintegrable chiral Potts model 1 Tetsuo Deguchi Department of Physics, Ochanomizu Univ. In collaboration
The sl(2) loop algebra symmetry of the XXZ spin chain at roots of unity and applications to the superintegrable chiral Potts model 1 Tetsuo Deguchi Department of Physics, Ochanomizu Univ. In collaboration
Topological Phases in One Dimension
 Topological Phases in One Dimension Lukasz Fidkowski and Alexei Kitaev arxiv:1008.4138 Topological phases in 2 dimensions: - Integer quantum Hall effect - quantized σ xy - robust chiral edge modes - Fractional
Topological Phases in One Dimension Lukasz Fidkowski and Alexei Kitaev arxiv:1008.4138 Topological phases in 2 dimensions: - Integer quantum Hall effect - quantized σ xy - robust chiral edge modes - Fractional
Symmetries for fun and profit
 Symmetries for fun and profit Sourendu Gupta TIFR Graduate School Quantum Mechanics 1 August 28, 2008 Sourendu Gupta (TIFR Graduate School) Symmetries for fun and profit QM I 1 / 20 Outline 1 The isotropic
Symmetries for fun and profit Sourendu Gupta TIFR Graduate School Quantum Mechanics 1 August 28, 2008 Sourendu Gupta (TIFR Graduate School) Symmetries for fun and profit QM I 1 / 20 Outline 1 The isotropic
2. As we shall see, we choose to write in terms of σ x because ( X ) 2 = σ 2 x.
 Section 5.1 Simple One-Dimensional Problems: The Free Particle Page 9 The Free Particle Gaussian Wave Packets The Gaussian wave packet initial state is one of the few states for which both the { x } and
Section 5.1 Simple One-Dimensional Problems: The Free Particle Page 9 The Free Particle Gaussian Wave Packets The Gaussian wave packet initial state is one of the few states for which both the { x } and
Lecture 45: The Eigenvalue Problem of L z and L 2 in Three Dimensions, ct d: Operator Method Date Revised: 2009/02/17 Date Given: 2009/02/11
 Page 757 Lecture 45: The Eigenvalue Problem of L z and L 2 in Three Dimensions, ct d: Operator Method Date Revised: 2009/02/17 Date Given: 2009/02/11 The Eigenvector-Eigenvalue Problem of L z and L 2 Section
Page 757 Lecture 45: The Eigenvalue Problem of L z and L 2 in Three Dimensions, ct d: Operator Method Date Revised: 2009/02/17 Date Given: 2009/02/11 The Eigenvector-Eigenvalue Problem of L z and L 2 Section
LECTURE III Asymmetric Simple Exclusion Process: Bethe Ansatz Approach to the Kolmogorov Equations. Craig A. Tracy UC Davis
 LECTURE III Asymmetric Simple Exclusion Process: Bethe Ansatz Approach to the Kolmogorov Equations Craig A. Tracy UC Davis Bielefeld, August 2013 ASEP on Integer Lattice q p suppressed both suppressed
LECTURE III Asymmetric Simple Exclusion Process: Bethe Ansatz Approach to the Kolmogorov Equations Craig A. Tracy UC Davis Bielefeld, August 2013 ASEP on Integer Lattice q p suppressed both suppressed
Ground state and low excitations of an integrable. Institut fur Physik, Humboldt-Universitat, Theorie der Elementarteilchen
 Ground state and low excitations of an integrable chain with alternating spins St Meinerz and B - D Dorfelx Institut fur Physik, Humboldt-Universitat, Theorie der Elementarteilchen Invalidenstrae 110,
Ground state and low excitations of an integrable chain with alternating spins St Meinerz and B - D Dorfelx Institut fur Physik, Humboldt-Universitat, Theorie der Elementarteilchen Invalidenstrae 110,
arxiv:math-ph/ v2 17 Aug 2004
 EMPG-04-07 Auxiliary matrices on both sides of the equator arxiv:math-ph/0408023v2 17 Aug 2004 Christian Korff School of Mathematics, University of Edinburgh Mayfield Road, Edinburgh EH9 3JZ, UK Abstract
EMPG-04-07 Auxiliary matrices on both sides of the equator arxiv:math-ph/0408023v2 17 Aug 2004 Christian Korff School of Mathematics, University of Edinburgh Mayfield Road, Edinburgh EH9 3JZ, UK Abstract
Bethe states and separation of variables for SU(N) Heisenberg spin chain
 Bethe states and separation of variables for SU(N) Heisenberg spin chain Nikolay Gromov King s College London & PNPI based on 1610.08032 [NG, F. Levkovich-Maslyuk, G. Sizov] Below: FLM = F. Levkovich-Maslyuk
Bethe states and separation of variables for SU(N) Heisenberg spin chain Nikolay Gromov King s College London & PNPI based on 1610.08032 [NG, F. Levkovich-Maslyuk, G. Sizov] Below: FLM = F. Levkovich-Maslyuk
Bethe Ansatz Solutions and Excitation Gap of the Attractive Bose-Hubbard Model
 Journal of the Korean Physical Society, Vol. 39, No., August 001, pp. 03 08 Bethe Ansatz Solutions and Excitation Gap of the Attractive Bose-Hubbard Model Deok-Sun Lee and Doochul Kim School of Physics,
Journal of the Korean Physical Society, Vol. 39, No., August 001, pp. 03 08 Bethe Ansatz Solutions and Excitation Gap of the Attractive Bose-Hubbard Model Deok-Sun Lee and Doochul Kim School of Physics,
arxiv: v2 [quant-ph] 12 Aug 2008
![arxiv: v2 [quant-ph] 12 Aug 2008 arxiv: v2 [quant-ph] 12 Aug 2008](/thumbs/72/66366028.jpg) Complexity of thermal states in quantum spin chains arxiv:85.449v [quant-ph] Aug 8 Marko Žnidarič, Tomaž Prosen and Iztok Pižorn Department of physics, FMF, University of Ljubljana, Jadranska 9, SI- Ljubljana,
Complexity of thermal states in quantum spin chains arxiv:85.449v [quant-ph] Aug 8 Marko Žnidarič, Tomaž Prosen and Iztok Pižorn Department of physics, FMF, University of Ljubljana, Jadranska 9, SI- Ljubljana,
arxiv:math-ph/ v1 29 Dec 1999
 On the classical R-matrix of the degenerate Calogero-Moser models L. Fehér and B.G. Pusztai arxiv:math-ph/9912021v1 29 Dec 1999 Department of Theoretical Physics, József Attila University Tisza Lajos krt
On the classical R-matrix of the degenerate Calogero-Moser models L. Fehér and B.G. Pusztai arxiv:math-ph/9912021v1 29 Dec 1999 Department of Theoretical Physics, József Attila University Tisza Lajos krt
SUPERSYMMETRIC HADRONIC MECHANICAL HARMONIC OSCILLATOR
 SUPERSYMMETRIC HADRONIC MECHANICAL HARMONIC OSCILLATOR A.K.Aringazin Department of Theoretical Physics Karaganda State University Karaganda 470074, USSR 1990 Abstract Lie-isotopic lifting of the commutation
SUPERSYMMETRIC HADRONIC MECHANICAL HARMONIC OSCILLATOR A.K.Aringazin Department of Theoretical Physics Karaganda State University Karaganda 470074, USSR 1990 Abstract Lie-isotopic lifting of the commutation
arxiv:cond-mat/ v1 8 Jun 1993
 arxiv:cond-mat/9306018v1 8 Jun 1993 Excitation spectrum and critical exponents of a one-dimensional integrable model of fermions with correlated hopping* R. Z. Bariev, A. Klümper, A. Schadschneider, and
arxiv:cond-mat/9306018v1 8 Jun 1993 Excitation spectrum and critical exponents of a one-dimensional integrable model of fermions with correlated hopping* R. Z. Bariev, A. Klümper, A. Schadschneider, and
Generalization of the matrix product ansatz for integrable chains
 arxiv:cond-mat/0608177v1 [cond-mat.str-el] 7 Aug 006 Generalization of the matrix product ansatz for integrable chains F. C. Alcaraz, M. J. Lazo Instituto de Física de São Carlos, Universidade de São Paulo,
arxiv:cond-mat/0608177v1 [cond-mat.str-el] 7 Aug 006 Generalization of the matrix product ansatz for integrable chains F. C. Alcaraz, M. J. Lazo Instituto de Física de São Carlos, Universidade de São Paulo,
On elliptic quantum integrability
 On elliptic quantum integrability vertex models, solid-on-solid models and spin chains 1405.4281 with Galleas 1505.06870 with Galleas thesis Ch I and II 1510.00342 thesis Ch I and III in progress with
On elliptic quantum integrability vertex models, solid-on-solid models and spin chains 1405.4281 with Galleas 1505.06870 with Galleas thesis Ch I and II 1510.00342 thesis Ch I and III in progress with
arxiv:solv-int/ v1 19 Dec 1997 M.J.Martins 1,2 and P.B.Ramos 2
 IFTA-97-35/UFSCARTH-97-19 The Quantum Inverse Scattering Method for Hubbard-like Models arxiv:solv-int/9712014v1 19 Dec 1997 M.J.Martins 1,2 and P.B.Ramos 2 1. Instituut voor Theoretische Fysica, Universiteit
IFTA-97-35/UFSCARTH-97-19 The Quantum Inverse Scattering Method for Hubbard-like Models arxiv:solv-int/9712014v1 19 Dec 1997 M.J.Martins 1,2 and P.B.Ramos 2 1. Instituut voor Theoretische Fysica, Universiteit
Matrix Product Operators: Algebras and Applications
 Matrix Product Operators: Algebras and Applications Frank Verstraete Ghent University and University of Vienna Nick Bultinck, Jutho Haegeman, Michael Marien Burak Sahinoglu, Dominic Williamson Ignacio
Matrix Product Operators: Algebras and Applications Frank Verstraete Ghent University and University of Vienna Nick Bultinck, Jutho Haegeman, Michael Marien Burak Sahinoglu, Dominic Williamson Ignacio
Lecture 10. The Dirac equation. WS2010/11: Introduction to Nuclear and Particle Physics
 Lecture 10 The Dirac equation WS2010/11: Introduction to Nuclear and Particle Physics The Dirac equation The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist
Lecture 10 The Dirac equation WS2010/11: Introduction to Nuclear and Particle Physics The Dirac equation The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist
arxiv: v1 [math-ph] 30 Jul 2018
![arxiv: v1 [math-ph] 30 Jul 2018 arxiv: v1 [math-ph] 30 Jul 2018](/thumbs/84/89086852.jpg) LPENSL-TH-08-18 On quantum separation of variables arxiv:1807.11572v1 [math-ph] 30 Jul 2018 J. M. Maillet 1 and G. Niccoli 2 Dedicated to the memory of L. D. Faddeev Abstract. We present a new approach
LPENSL-TH-08-18 On quantum separation of variables arxiv:1807.11572v1 [math-ph] 30 Jul 2018 J. M. Maillet 1 and G. Niccoli 2 Dedicated to the memory of L. D. Faddeev Abstract. We present a new approach
Classical Geometry of Quantum Integrability and Gauge Theory. Nikita Nekrasov IHES
 Classical Geometry of Quantum Integrability and Gauge Theory Nikita Nekrasov IHES This is a work on experimental theoretical physics In collaboration with Alexei Rosly (ITEP) and Samson Shatashvili (HMI
Classical Geometry of Quantum Integrability and Gauge Theory Nikita Nekrasov IHES This is a work on experimental theoretical physics In collaboration with Alexei Rosly (ITEP) and Samson Shatashvili (HMI
arxiv:cond-mat/ Jun 2001
 A supersymmetric U q [osp(2 2)]-extended Hubbard model with boundary fields X.-W. Guan a,b, A. Foerster b, U. Grimm c, R.A. Römer a, M. Schreiber a a Institut für Physik, Technische Universität, 09107
A supersymmetric U q [osp(2 2)]-extended Hubbard model with boundary fields X.-W. Guan a,b, A. Foerster b, U. Grimm c, R.A. Römer a, M. Schreiber a a Institut für Physik, Technische Universität, 09107
The XXZ chain and the six-vertex model
 Chapter 5 The XXZ chain and the six-vertex model The purpose of this chapter is to focus on two models fundamental to the study of both 1d quantum systems and 2d classical systems. They are the XXZ chain
Chapter 5 The XXZ chain and the six-vertex model The purpose of this chapter is to focus on two models fundamental to the study of both 1d quantum systems and 2d classical systems. They are the XXZ chain
On complexified quantum mechanics and space-time
 On complexified quantum mechanics and space-time Dorje C. Brody Mathematical Sciences Brunel University, Uxbridge UB8 3PH dorje.brody@brunel.ac.uk Quantum Physics with Non-Hermitian Operators Dresden:
On complexified quantum mechanics and space-time Dorje C. Brody Mathematical Sciences Brunel University, Uxbridge UB8 3PH dorje.brody@brunel.ac.uk Quantum Physics with Non-Hermitian Operators Dresden:
Travelling wave solutions for a CBS equation in dimensions
 AMERICAN CONFERENCE ON APPLIED MATHEMATICS (MATH '8), Harvard, Massachusetts, USA, March -6, 8 Travelling wave solutions for a CBS equation in + dimensions MARIA LUZ GANDARIAS University of Cádiz Department
AMERICAN CONFERENCE ON APPLIED MATHEMATICS (MATH '8), Harvard, Massachusetts, USA, March -6, 8 Travelling wave solutions for a CBS equation in + dimensions MARIA LUZ GANDARIAS University of Cádiz Department
Bethe vectors for XXX-spin chain
 Journal of Physics: Conference Series OPEN ACCESS Bethe vectors for XXX-spin chain To cite this article: estmír Burdík et al 204 J. Phys.: Conf. Ser. 563 020 View the article online for updates and enhancements.
Journal of Physics: Conference Series OPEN ACCESS Bethe vectors for XXX-spin chain To cite this article: estmír Burdík et al 204 J. Phys.: Conf. Ser. 563 020 View the article online for updates and enhancements.
City Research Online. Permanent City Research Online URL:
 Castro-Alvaredo, O., Fring, A. & Göhmann, F. 2002. On the absence of simultaneous reflection and transmission in integrable impurity systems. Physics Letters, City Research Online Original citation: Castro-Alvaredo,
Castro-Alvaredo, O., Fring, A. & Göhmann, F. 2002. On the absence of simultaneous reflection and transmission in integrable impurity systems. Physics Letters, City Research Online Original citation: Castro-Alvaredo,
arxiv:hep-th/ v1 13 May 1994
 Hirota equation as an example of integrable symplectic map L. Faddeev 1, and A. Yu. Volkov, arxiv:hep-th/9405087v1 13 May 1994 1 Saint Petersburg Branch of the Steklov Mathematical Institute Fontanka 7,
Hirota equation as an example of integrable symplectic map L. Faddeev 1, and A. Yu. Volkov, arxiv:hep-th/9405087v1 13 May 1994 1 Saint Petersburg Branch of the Steklov Mathematical Institute Fontanka 7,
Application of Mean-Field Jordan Wigner Transformation to Antiferromagnet System
 Commun. Theor. Phys. Beijing, China 50 008 pp. 43 47 c Chinese Physical Society Vol. 50, o. 1, July 15, 008 Application of Mean-Field Jordan Wigner Transformation to Antiferromagnet System LI Jia-Liang,
Commun. Theor. Phys. Beijing, China 50 008 pp. 43 47 c Chinese Physical Society Vol. 50, o. 1, July 15, 008 Application of Mean-Field Jordan Wigner Transformation to Antiferromagnet System LI Jia-Liang,
arxiv: v1 [nlin.si] 24 May 2017
![arxiv: v1 [nlin.si] 24 May 2017 arxiv: v1 [nlin.si] 24 May 2017](/thumbs/93/113600722.jpg) Boundary Algebraic Bethe Ansatz for a nineteen vertex model with U q osp ) ) ] symmetry arxiv:1705.08953v1 nlin.si] 4 May 017 R. S. Vieira E-mail: rsvieira@df.ufscar.br Universidade Federal de São Carlos,
Boundary Algebraic Bethe Ansatz for a nineteen vertex model with U q osp ) ) ] symmetry arxiv:1705.08953v1 nlin.si] 4 May 017 R. S. Vieira E-mail: rsvieira@df.ufscar.br Universidade Federal de São Carlos,
3 Symmetry Protected Topological Phase
 Physics 3b Lecture 16 Caltech, 05/30/18 3 Symmetry Protected Topological Phase 3.1 Breakdown of noninteracting SPT phases with interaction Building on our previous discussion of the Majorana chain and
Physics 3b Lecture 16 Caltech, 05/30/18 3 Symmetry Protected Topological Phase 3.1 Breakdown of noninteracting SPT phases with interaction Building on our previous discussion of the Majorana chain and
The Dirac Equation. Topic 3 Spinors, Fermion Fields, Dirac Fields Lecture 13
 The Dirac Equation Dirac s discovery of a relativistic wave equation for the electron was published in 1928 soon after the concept of intrisic spin angular momentum was proposed by Goudsmit and Uhlenbeck
The Dirac Equation Dirac s discovery of a relativistic wave equation for the electron was published in 1928 soon after the concept of intrisic spin angular momentum was proposed by Goudsmit and Uhlenbeck
The Quantum Heisenberg Ferromagnet
 The Quantum Heisenberg Ferromagnet Soon after Schrödinger discovered the wave equation of quantum mechanics, Heisenberg and Dirac developed the first successful quantum theory of ferromagnetism W. Heisenberg,
The Quantum Heisenberg Ferromagnet Soon after Schrödinger discovered the wave equation of quantum mechanics, Heisenberg and Dirac developed the first successful quantum theory of ferromagnetism W. Heisenberg,
arxiv:quant-ph/ v1 29 Mar 2003
 Finite-Dimensional PT -Symmetric Hamiltonians arxiv:quant-ph/0303174v1 29 Mar 2003 Carl M. Bender, Peter N. Meisinger, and Qinghai Wang Department of Physics, Washington University, St. Louis, MO 63130,
Finite-Dimensional PT -Symmetric Hamiltonians arxiv:quant-ph/0303174v1 29 Mar 2003 Carl M. Bender, Peter N. Meisinger, and Qinghai Wang Department of Physics, Washington University, St. Louis, MO 63130,
Correspondence should be addressed to B. Abdesselam,
 Advances in Mathematical Physics Volume 01, Article ID 193190, 1 pages doi:10.1155/01/193190 Research Article Multiparameter Statistical Models from N N Braid Matrices: Explicit Eigenvalues of Transfer
Advances in Mathematical Physics Volume 01, Article ID 193190, 1 pages doi:10.1155/01/193190 Research Article Multiparameter Statistical Models from N N Braid Matrices: Explicit Eigenvalues of Transfer
( 2) ( ) Hyperbolic Functions 6E. cosh d (cosh sech ) d sinh tanh. cosh. x x x x x x C. x 1 x. 2 a. x x x = + = + cosh dx sinh C 3sinh C.
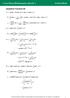 Hyperolic Functions 6E a (sinh+ cosh ) cosh+ sinh+ + cosh cosh (cosh sech ) sinh tanh sinh sinh sechtanh sech+ cosh cosh cosh c a a sinh cosh+ cosh sinh sinh + + ( ) + + ( ) ( ) ( ) ( ) arcosh + ( ) +
Hyperolic Functions 6E a (sinh+ cosh ) cosh+ sinh+ + cosh cosh (cosh sech ) sinh tanh sinh sinh sechtanh sech+ cosh cosh cosh c a a sinh cosh+ cosh sinh sinh + + ( ) + + ( ) ( ) ( ) ( ) arcosh + ( ) +
arxiv:cond-mat/ v2 [cond-mat.stat-mech] 11 Sep 1997
![arxiv:cond-mat/ v2 [cond-mat.stat-mech] 11 Sep 1997 arxiv:cond-mat/ v2 [cond-mat.stat-mech] 11 Sep 1997](/thumbs/86/93807033.jpg) Z. Phys. B 92 (1993) 307 LPSN-93-LT2 arxiv:cond-mat/9306013v2 [cond-mat.stat-mech] 11 Sep 1997 Surface magnetization of aperiodic Ising quantum chains 1. Introduction L Turban and B Berche Laboratoire
Z. Phys. B 92 (1993) 307 LPSN-93-LT2 arxiv:cond-mat/9306013v2 [cond-mat.stat-mech] 11 Sep 1997 Surface magnetization of aperiodic Ising quantum chains 1. Introduction L Turban and B Berche Laboratoire
Incompatibility Paradoxes
 Chapter 22 Incompatibility Paradoxes 22.1 Simultaneous Values There is never any difficulty in supposing that a classical mechanical system possesses, at a particular instant of time, precise values of
Chapter 22 Incompatibility Paradoxes 22.1 Simultaneous Values There is never any difficulty in supposing that a classical mechanical system possesses, at a particular instant of time, precise values of
arxiv: v1 [cond-mat.stat-mech] 24 May 2007
![arxiv: v1 [cond-mat.stat-mech] 24 May 2007 arxiv: v1 [cond-mat.stat-mech] 24 May 2007](/thumbs/79/78843760.jpg) arxiv:0705.3569v1 [cond-mat.stat-mech 4 May 007 A note on the spin- 1 XXZ chain concerning its relation to the Bose gas Alexander Seel 1, Tanaya Bhattacharyya, Frank Göhmann 3 and Andreas Klümper 4 1 Institut
arxiv:0705.3569v1 [cond-mat.stat-mech 4 May 007 A note on the spin- 1 XXZ chain concerning its relation to the Bose gas Alexander Seel 1, Tanaya Bhattacharyya, Frank Göhmann 3 and Andreas Klümper 4 1 Institut
The 1+1-dimensional Ising model
 Chapter 4 The 1+1-dimensional Ising model The 1+1-dimensional Ising model is one of the most important models in statistical mechanics. It is an interacting system, and behaves accordingly. Yet for a variety
Chapter 4 The 1+1-dimensional Ising model The 1+1-dimensional Ising model is one of the most important models in statistical mechanics. It is an interacting system, and behaves accordingly. Yet for a variety
A Quantum Group in the Yang-Baxter Algebra
 Quantum Group in the Yang-Baxter lgebra lexandros erakis December 8, 2013 bstract In these notes we mainly present theory on abstract algebra and how it emerges in the Yang-Baxter equation. First we review
Quantum Group in the Yang-Baxter lgebra lexandros erakis December 8, 2013 bstract In these notes we mainly present theory on abstract algebra and how it emerges in the Yang-Baxter equation. First we review
Lie algebraic aspects of quantum control in interacting spin-1/2 (qubit) chains
 .. Lie algebraic aspects of quantum control in interacting spin-1/2 (qubit) chains Vladimir M. Stojanović Condensed Matter Theory Group HARVARD UNIVERSITY September 16, 2014 V. M. Stojanović (Harvard)
.. Lie algebraic aspects of quantum control in interacting spin-1/2 (qubit) chains Vladimir M. Stojanović Condensed Matter Theory Group HARVARD UNIVERSITY September 16, 2014 V. M. Stojanović (Harvard)
arxiv:quant-ph/ v1 19 Oct 1995
 Generalized Kochen-Specker Theorem arxiv:quant-ph/9510018v1 19 Oct 1995 Asher Peres Department of Physics, Technion Israel Institute of Technology, 32 000 Haifa, Israel Abstract A generalized Kochen-Specker
Generalized Kochen-Specker Theorem arxiv:quant-ph/9510018v1 19 Oct 1995 Asher Peres Department of Physics, Technion Israel Institute of Technology, 32 000 Haifa, Israel Abstract A generalized Kochen-Specker
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Chemistry 5.76 Revised February, 1982 NOTES ON MATRIX METHODS
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Chemistry 5.76 Revised February, 198 NOTES ON MATRIX METHODS 1. Matrix Algebra Margenau and Murphy, The Mathematics of Physics and Chemistry, Chapter 10, give almost
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Chemistry 5.76 Revised February, 198 NOTES ON MATRIX METHODS 1. Matrix Algebra Margenau and Murphy, The Mathematics of Physics and Chemistry, Chapter 10, give almost
