6.854 Advanced Algorithms
|
|
|
- Stephanie Day
- 5 years ago
- Views:
Transcription
1 6.854 Advanced Algorithms Homework Solutions Hashing Bashing. Solution:. O(log U ) for the first level and for each of the O(n) second level functions, giving a total of O(n log U ) 2. Suppose we are using two arrays of size cn.5. Consider the (k+) st item inserted. Since only k buckets (at worst) are occupied, the probability that both candidate locations are occupied is only (k/(cn.5 )) 2. Thus, the expected number of times an item is actually inserted into an already-occupied bucket is at most n (k/(cn.5 )) 2 k0 (n )n(2n ) 6c 2 n 3 O() Another approach. Now let s consider pairwise collisions. Item k collides with item j < k only if (i) one of the candidate locations of item k is the location of item j (this has probability at most 2/(cn.5 )) and (ii) the other candidate location for item k contains at least one element (probability at most k/(cn.5 )). Thus, the probability k collides with j is at most 2k/(c 2 n 3 ). Summing over the k possible values of j < k, we find the expected number of collisions for item k is at most 2k 2 /(c 2 n 3 ). Summing over all k, we get the same result as above: O() expected collisions. 3. Start with a 2-universal family of hash functions mapping n items to 2n.5 locations. Consider any particular set of n items. Consider choosing a random function from the hash family. The probability that item k collides with item j is /2n.5 by pairwise independence, implying by the union bound that the probability k collides with any item is at most /2 n. Now suppose that we allocate two arrays of size 2n.5 and choose a random 2-universal hash function from the family independently for each array. If an item does not have a collision in both arrays, then it will be placed in an empty bucket by the bash function.
2 We need merely analyze the probability that this happens for every item (this would make the bash function perfect). The probability that item k has a collision in both arrays is at most (/2 n) 2 /4n. It follows that the expected number of items colliding with some other item is at most /4. This implies in turn that with probability 3/4, every item is placed in an empty bucket by the (perfect) bash function. This in turn implies that some pair of 2-universal hash functions defines a perfect bash for our set of n items. Since every set of items gets a perfect bash from this scheme, it follows that the family of pairs of 2-universal functions above is a perfect bash family. Since the 2-universal family has size polynomial in the universe, so does the family of pairs of 2-universal functions. Accordingly, the hash function can be described using O(log U ) bits. 4. When we sample a hash function from the above 2-universal family, we get a 3/4 probability of having no collisions. It follows that if we make 2 or more attempts, we can expect to find a collision-free hash function. 5. If we map our n items to k candidate locations in an array of size n +/k, our collision odds work out as above and we get a constant number of collisions. Similarly, k random 2-universal hash families, each mapping to a set of size n +/k, has a constant probability of being perfect for any particular set of items, so the set of all such functions provides a perfect family (of polynomial size for any constant k). This gives a tradeoff of k probes for perfect hashing in space O(n +/k ). Note that while we can achieve perfect hashing to O(n) space, the resulting family does not have polynomial size (since a different, subsidiary hash function must be chosen for each sub-hash-table). 2
3 2 Sampling with Few Bits 2. Solution. Let 0.b b 2... be the binary fraction representation of p. We can treat the random bit stream r, r 2,... also as a binary fraction and return the first item if r 0.r r 2... < p and the second item otherwise. Since the random bit stream is unbiased, we will return the first item with probability p. We will make the comparison of the two binary fractions by comparing b i and r i starting from i. If the two bits differ (with probability 0.5), we can immediately conclude if r < p and return the appropriate item from S. If they are the same (with probability 0.5), we need to compare additional bits to determine the direction of the inequality. Thus, for any arbitrary p, the probability that it will take exactly n comparisons to choose one of the two items is ( n. 2) Thus, the expected number of bits to examine is B ( n n 2) n ( n n 2) + ( n n2 2) + + ( ) n ni O(). 2 2 i 2. When there are more than 2 items in S, we associate S with the root node of a binary tree that at each node divides the associated set into 2 roughly even partitions. For each node i, we can compute the probability p i of drawing an element from the left subtree by summing up the probabilities associated with the elements associated with the subtrees and normalize such that probability of descending into the two subtrees sum up to. To draw a sample from the set, we recursively compare the current random bit stream against p i at the node starting at the root, and descend down the appropriate subtree based on the result of the comparison. The recursion ends when we reach a subtree with only a single element and return that element. Since the height of the tree is O(log n) and each comparison uses O() random bits in expectation, the overall algorithm uses O(log n) random bits in expectation per sample. 3. Assume that m unbiased random bits suffice for the uniform distribution on {, 2, 3}. This means that at the highest resolution, we are able to divide the [0,] interval into 2 m equally sized subintervals. But we need to apportion intervals so that equal numbers of intervals are assigned to elements, 2, and 3. This is impossible since 3 does not divide 2 m. More generally, we have 2 m equi-probable states, which must be evenly divided among three elements. Therefore, finite bits will not suffice in the worst case. By computing cumulative probabilities c i p + +p i and reusing the random bit stream when performing binary comparison over c i, we can further reduce the constant factor of the O(log n) algorithm. 3
4 3 Lower bound for Balls in Bins 3. Solution. We computed the following probability in the class, P[k balls in bin ] ( n k ) ( n ) k ( n) n k. Then by using the mentioned inequality, ( ) ( ) k ( n P[k balls in bin ] ) n k k n n ( n ) ( k k ( k n) ) n k n ( ) k ( ) n k k n ( ) k ( ) k n, for n 2 k e ( ) k. () 2e k Now, we just set k c lg n/ lg lg n, giving us P[c lg n/ lg lg n balls in bin ] ( ) c lg n/ lg lg n 2e c lg n/ lg lg n ( ) c lg n/ lg lg n lg lg n 2e c lg n ( ) c lg n/ lg lg n, for large enough values of n c lg n ( ) c lg n/ lg lg n c2lg lg n c2lg lg n (c lg n/ lg lg n) c2 c lg n cn c Ω(n c ). (2) Setting c /2, we get P[lg n/2 lg lg n balls in bin ] Ω(/ n). 4
5 2. Let B i be the event that bin i has at least k balls. We first show that conditioning on B,, B i only increases the probability that the next bin i does have k balls. We use induction on the number of bins we are conditioning on. The base case is as follows, for i > : P[B i ] P[B i B ] P[B ] + P[B i B ] P[ B ] P[B i B ] P[B ] + P[B i B ] P[ B ] (3) P[B i B ](P[B ] + P[ B ]) P[B i B ]. (4) In line 3, we notice that B i is more likely if the first bin does not have k balls comparing to the case in which the first bin has at least k balls, because then there are more balls that can be in bin i. Next we assume that P[B i ] P[B i B... B j ] (for i > j + ). Then by the same argument we made for line 3, we have: P[B i ] P[B i B... B j ] P[B i B... B j B j+ ] P[B j+ ] + P[B i B... B j B j+ ] P[ B j+ ] P[B i B... B j B j+ ] (5) Thus, we have concluded that conditioning on bins not having k balls increases the chances that the next bin does. Specifically, the induction ends at proving P[B i ] P[B i B... B i ]. Conversely, we have P[ B i ] P[ B i B... B i ], because this is exactly P[B i ]. So now let s solve the real problem, with k lg n/2 lg lg n. From part (a), we have Thus, we have P[B i ] P[Bin i has at least lg n/2 lg lg n balls] 2 n. P[ B i ] P[Bin i has at most lg n/2 lg lg n balls] 2 n. 5
6 So now we just solve for all bins having at most this many balls: P[all bins have lg n/2 lg lg n balls] P[ B ] P[ B 2 B ] P[ B n B... B n ] P[ B ] P[ B 2 ] P[ B n ] ( ) n 2 n e ( 2 n ) n e n/2. (6) So the probability is exponentially small that all bins have have fewer than lg n/2 lg lg n balls. Therefore, we conclude that with high probability, some bin has Ω(lg n/ lg lg n) balls. 6
7 4 Balls and Bins with replacement 4. Solution Here we assume that the number of processors is 0n.. We consider ordering the jobs arbitrarily and processing the jobs in that order. Only the first job that assigns to a processor get executed in that round. Let X i be indicator random variables as follows: { : if job i assigns to a previously occupied processor X i 0 : otherwise The X X i is the number of unprocessed job in a round. In the worst case, when we re considering job i, all previous jobs have been placed in different processors. Thus, there are at most i occupied processors. Therefore, we have P[X i ] i 0n. At this point we may be tempted to apply a Chernoff bound, but X i s are not independent, so we define a new set of random variables Y i such that Y i with probability i 0n. Thus, X is stochastically dominated by Y Y i. Accordingly, to upper bound P[X α 2 n], it suffices to upper bound P[Y α 2 n]. Now: So, P[Y ( α 2 )2 n] P[Y 5E[Y ]]. E[Y ] E[ Y i ] E[Y i ] αn i αn i P[Y i ] i 0n (αn)(αn ) 20n α(αn ) 20 α2 n 20. (7) Applying Chernoff, we conclude that, P[Y 5E[Y ]] e O(α2 n) which is /2n 2 as long as α 2 n c log n for a sufficiently large constant c. We conclude that P[X ( α 2 )2 n] /2n 2. 7
8 2. We call an unlucky round one which has too many unprocessed balls at the end (i.e., more than α 2 n). Since the probability of getting unlucky rounds is /n 2, we can just use union bound to argue that if we run for n rounds (we can t possibly run for more), it s high probability that none of those rounds will be unlucky. Thus, with probability ( /2n), all rounds are lucky. So how many rounds do we need with T (αn) T (( α 2 )2 n) +? Well, that s just O(lg lg n). So what happens when we get down to something like lg n jobs? Well, then we can just look at the probability that two particular jobs colliding is /n. Thus, the probability of any pair of jobs colliding is at most lg 2 n/n. Thus, running for a constant c number of rounds, we can get a probability that is at most (lg 2 n/n) c, which is O(n (c ) ). So once we have few enough jobs left, we re likely to finish in a constant number of rounds, and we re done after a union bound with the probability that all rounds are lucky. 8
9 5 Consistent Hashing with Inconsistent Views 5. Solution Let there be m machines and n clients interested in a specific data item. Using the consistent hashing scheme, each machine and data item is mapped to the cyclical interval [0, ]. For convenience, label the machines,..., m in order of appearance after the position of the data item. Thus, machine owns the data item. However, if a particular client believes that machines,..., k are down, it will query machine k + for the data. Let z j i if client j believes machine i is up and 0 otherwise. Thus, for k < m, the 2 probability that a client j queries machine k + is bounded by: P[client j queries machine k + ] P[z j z j 2 z j k 0] < 2 k Choosing k c log n and applying the union bound, the probability that any of the n clients query machine k + is bounded by n2 k n (c ). Thus, with high probability, no client will query machine O(log n). Alternatively, at most O(log n) machines will be queried with high probability. 9
Problem 1: (Chernoff Bounds via Negative Dependence - from MU Ex 5.15)
 Problem 1: Chernoff Bounds via Negative Dependence - from MU Ex 5.15) While deriving lower bounds on the load of the maximum loaded bin when n balls are thrown in n bins, we saw the use of negative dependence.
Problem 1: Chernoff Bounds via Negative Dependence - from MU Ex 5.15) While deriving lower bounds on the load of the maximum loaded bin when n balls are thrown in n bins, we saw the use of negative dependence.
Design and Analysis of Algorithms
 Design and Analysis of Algorithms 6.046J/18.401J LECTURE 7 Skip Lists Data structure Randomized insertion With high probability (w.h.p.) bound 7/10/15 Copyright 2001-8 by Leiserson et al L9.1 Skip lists
Design and Analysis of Algorithms 6.046J/18.401J LECTURE 7 Skip Lists Data structure Randomized insertion With high probability (w.h.p.) bound 7/10/15 Copyright 2001-8 by Leiserson et al L9.1 Skip lists
Randomized Load Balancing:The Power of 2 Choices
 Randomized Load Balancing: The Power of 2 Choices June 3, 2010 Balls and Bins Problem We have m balls that are thrown into n bins, the location of each ball chosen independently and uniformly at random
Randomized Load Balancing: The Power of 2 Choices June 3, 2010 Balls and Bins Problem We have m balls that are thrown into n bins, the location of each ball chosen independently and uniformly at random
1 Probability Review. CS 124 Section #8 Hashing, Skip Lists 3/20/17. Expectation (weighted average): the expectation of a random quantity X is:
 CS 24 Section #8 Hashing, Skip Lists 3/20/7 Probability Review Expectation (weighted average): the expectation of a random quantity X is: x= x P (X = x) For each value x that X can take on, we look at
CS 24 Section #8 Hashing, Skip Lists 3/20/7 Probability Review Expectation (weighted average): the expectation of a random quantity X is: x= x P (X = x) For each value x that X can take on, we look at
compare to comparison and pointer based sorting, binary trees
 Admin Hashing Dictionaries Model Operations. makeset, insert, delete, find keys are integers in M = {1,..., m} (so assume machine word size, or unit time, is log m) can store in array of size M using power:
Admin Hashing Dictionaries Model Operations. makeset, insert, delete, find keys are integers in M = {1,..., m} (so assume machine word size, or unit time, is log m) can store in array of size M using power:
CS361 Homework #3 Solutions
 CS6 Homework # Solutions. Suppose I have a hash table with 5 locations. I would like to know how many items I can store in it before it becomes fairly likely that I have a collision, i.e., that two items
CS6 Homework # Solutions. Suppose I have a hash table with 5 locations. I would like to know how many items I can store in it before it becomes fairly likely that I have a collision, i.e., that two items
Data Structures and Algorithms
 Data Structures and Algorithms Spring 2017-2018 Outline 1 Sorting Algorithms (contd.) Outline Sorting Algorithms (contd.) 1 Sorting Algorithms (contd.) Analysis of Quicksort Time to sort array of length
Data Structures and Algorithms Spring 2017-2018 Outline 1 Sorting Algorithms (contd.) Outline Sorting Algorithms (contd.) 1 Sorting Algorithms (contd.) Analysis of Quicksort Time to sort array of length
Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort
 Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort Xi Chen Columbia University We continue with two more asymptotic notation: o( ) and ω( ). Let f (n) and g(n) are functions that map
Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort Xi Chen Columbia University We continue with two more asymptotic notation: o( ) and ω( ). Let f (n) and g(n) are functions that map
Data Structures and Algorithms Running time and growth functions January 18, 2018
 Data Structures and Algorithms Running time and growth functions January 18, 2018 Measuring Running Time of Algorithms One way to measure the running time of an algorithm is to implement it and then study
Data Structures and Algorithms Running time and growth functions January 18, 2018 Measuring Running Time of Algorithms One way to measure the running time of an algorithm is to implement it and then study
Introduction to Hash Tables
 Introduction to Hash Tables Hash Functions A hash table represents a simple but efficient way of storing, finding, and removing elements. In general, a hash table is represented by an array of cells. In
Introduction to Hash Tables Hash Functions A hash table represents a simple but efficient way of storing, finding, and removing elements. In general, a hash table is represented by an array of cells. In
Algorithms and Data Structures 2014 Exercises week 5
 Algorithms and Data Structures 014 Exercises week 5 October, 014 Exercises marked by ( ) are hard, but they might show up on the exam. Exercises marked by ( ) are even harder, but they will not be on the
Algorithms and Data Structures 014 Exercises week 5 October, 014 Exercises marked by ( ) are hard, but they might show up on the exam. Exercises marked by ( ) are even harder, but they will not be on the
12 Hash Tables Introduction Chaining. Lecture 12: Hash Tables [Fa 10]
![12 Hash Tables Introduction Chaining. Lecture 12: Hash Tables [Fa 10] 12 Hash Tables Introduction Chaining. Lecture 12: Hash Tables [Fa 10]](/thumbs/82/85322860.jpg) Calvin: There! I finished our secret code! Hobbes: Let s see. Calvin: I assigned each letter a totally random number, so the code will be hard to crack. For letter A, you write 3,004,572,688. B is 28,731,569½.
Calvin: There! I finished our secret code! Hobbes: Let s see. Calvin: I assigned each letter a totally random number, so the code will be hard to crack. For letter A, you write 3,004,572,688. B is 28,731,569½.
CS Data Structures and Algorithm Analysis
 CS 483 - Data Structures and Algorithm Analysis Lecture VII: Chapter 6, part 2 R. Paul Wiegand George Mason University, Department of Computer Science March 22, 2006 Outline 1 Balanced Trees 2 Heaps &
CS 483 - Data Structures and Algorithm Analysis Lecture VII: Chapter 6, part 2 R. Paul Wiegand George Mason University, Department of Computer Science March 22, 2006 Outline 1 Balanced Trees 2 Heaps &
Exercise Sheet #1 Solutions, Computer Science, A M. Hallett, K. Smith a k n b k = n b + k. a k n b k c 1 n b k. a k n b.
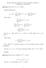 Exercise Sheet #1 Solutions, Computer Science, 308-251A M. Hallett, K. Smith 2002 Question 1.1: Prove (n + a) b = Θ(n b ). Binomial Expansion: Show O(n b ): (n + a) b = For any c 1 > b = O(n b ). Show
Exercise Sheet #1 Solutions, Computer Science, 308-251A M. Hallett, K. Smith 2002 Question 1.1: Prove (n + a) b = Θ(n b ). Binomial Expansion: Show O(n b ): (n + a) b = For any c 1 > b = O(n b ). Show
Topic 17. Analysis of Algorithms
 Topic 17 Analysis of Algorithms Analysis of Algorithms- Review Efficiency of an algorithm can be measured in terms of : Time complexity: a measure of the amount of time required to execute an algorithm
Topic 17 Analysis of Algorithms Analysis of Algorithms- Review Efficiency of an algorithm can be measured in terms of : Time complexity: a measure of the amount of time required to execute an algorithm
Solutions to Problem Set 4
 UC Berkeley, CS 174: Combinatorics and Discrete Probability (Fall 010 Solutions to Problem Set 4 1. (MU 5.4 In a lecture hall containing 100 people, you consider whether or not there are three people in
UC Berkeley, CS 174: Combinatorics and Discrete Probability (Fall 010 Solutions to Problem Set 4 1. (MU 5.4 In a lecture hall containing 100 people, you consider whether or not there are three people in
Lecture: Analysis of Algorithms (CS )
 Lecture: Analysis of Algorithms (CS483-001) Amarda Shehu Spring 2017 1 Outline of Today s Class 2 Choosing Hash Functions Universal Universality Theorem Constructing a Set of Universal Hash Functions Perfect
Lecture: Analysis of Algorithms (CS483-001) Amarda Shehu Spring 2017 1 Outline of Today s Class 2 Choosing Hash Functions Universal Universality Theorem Constructing a Set of Universal Hash Functions Perfect
Assignment 5: Solutions
 Comp 21: Algorithms and Data Structures Assignment : Solutions 1. Heaps. (a) First we remove the minimum key 1 (which we know is located at the root of the heap). We then replace it by the key in the position
Comp 21: Algorithms and Data Structures Assignment : Solutions 1. Heaps. (a) First we remove the minimum key 1 (which we know is located at the root of the heap). We then replace it by the key in the position
Topic 4 Randomized algorithms
 CSE 103: Probability and statistics Winter 010 Topic 4 Randomized algorithms 4.1 Finding percentiles 4.1.1 The mean as a summary statistic Suppose UCSD tracks this year s graduating class in computer science
CSE 103: Probability and statistics Winter 010 Topic 4 Randomized algorithms 4.1 Finding percentiles 4.1.1 The mean as a summary statistic Suppose UCSD tracks this year s graduating class in computer science
Review Of Topics. Review: Induction
 Review Of Topics Asymptotic notation Solving recurrences Sorting algorithms Insertion sort Merge sort Heap sort Quick sort Counting sort Radix sort Medians/order statistics Randomized algorithm Worst-case
Review Of Topics Asymptotic notation Solving recurrences Sorting algorithms Insertion sort Merge sort Heap sort Quick sort Counting sort Radix sort Medians/order statistics Randomized algorithm Worst-case
Lecture 1: Asymptotics, Recurrences, Elementary Sorting
 Lecture 1: Asymptotics, Recurrences, Elementary Sorting Instructor: Outline 1 Introduction to Asymptotic Analysis Rate of growth of functions Comparing and bounding functions: O, Θ, Ω Specifying running
Lecture 1: Asymptotics, Recurrences, Elementary Sorting Instructor: Outline 1 Introduction to Asymptotic Analysis Rate of growth of functions Comparing and bounding functions: O, Θ, Ω Specifying running
Lecture Lecture 3 Tuesday Sep 09, 2014
 CS 4: Advanced Algorithms Fall 04 Lecture Lecture 3 Tuesday Sep 09, 04 Prof. Jelani Nelson Scribe: Thibaut Horel Overview In the previous lecture we finished covering data structures for the predecessor
CS 4: Advanced Algorithms Fall 04 Lecture Lecture 3 Tuesday Sep 09, 04 Prof. Jelani Nelson Scribe: Thibaut Horel Overview In the previous lecture we finished covering data structures for the predecessor
Randomized Algorithms Week 2: Tail Inequalities
 Randomized Algorithms Week 2: Tail Inequalities Rao Kosaraju In this section, we study three ways to estimate the tail probabilities of random variables. Please note that the more information we know about
Randomized Algorithms Week 2: Tail Inequalities Rao Kosaraju In this section, we study three ways to estimate the tail probabilities of random variables. Please note that the more information we know about
Algorithms and Data Structures 2016 Week 5 solutions (Tues 9th - Fri 12th February)
 Algorithms and Data Structures 016 Week 5 solutions (Tues 9th - Fri 1th February) 1. Draw the decision tree (under the assumption of all-distinct inputs) Quicksort for n = 3. answer: (of course you should
Algorithms and Data Structures 016 Week 5 solutions (Tues 9th - Fri 1th February) 1. Draw the decision tree (under the assumption of all-distinct inputs) Quicksort for n = 3. answer: (of course you should
Lower Bounds for Dynamic Connectivity (2004; Pǎtraşcu, Demaine)
 Lower Bounds for Dynamic Connectivity (2004; Pǎtraşcu, Demaine) Mihai Pǎtraşcu, MIT, web.mit.edu/ mip/www/ Index terms: partial-sums problem, prefix sums, dynamic lower bounds Synonyms: dynamic trees 1
Lower Bounds for Dynamic Connectivity (2004; Pǎtraşcu, Demaine) Mihai Pǎtraşcu, MIT, web.mit.edu/ mip/www/ Index terms: partial-sums problem, prefix sums, dynamic lower bounds Synonyms: dynamic trees 1
Selection and Adversary Arguments. COMP 215 Lecture 19
 Selection and Adversary Arguments COMP 215 Lecture 19 Selection Problems We want to find the k'th largest entry in an unsorted array. Could be the largest, smallest, median, etc. Ideas for an n lg n algorithm?
Selection and Adversary Arguments COMP 215 Lecture 19 Selection Problems We want to find the k'th largest entry in an unsorted array. Could be the largest, smallest, median, etc. Ideas for an n lg n algorithm?
Divide and Conquer Algorithms. CSE 101: Design and Analysis of Algorithms Lecture 14
 Divide and Conquer Algorithms CSE 101: Design and Analysis of Algorithms Lecture 14 CSE 101: Design and analysis of algorithms Divide and conquer algorithms Reading: Sections 2.3 and 2.4 Homework 6 will
Divide and Conquer Algorithms CSE 101: Design and Analysis of Algorithms Lecture 14 CSE 101: Design and analysis of algorithms Divide and conquer algorithms Reading: Sections 2.3 and 2.4 Homework 6 will
Discrete Mathematics, Spring 2004 Homework 4 Sample Solutions
 Discrete Mathematics, Spring 2004 Homework 4 Sample Solutions 4.2 #77. Let s n,k denote the number of ways to seat n persons at k round tables, with at least one person at each table. (The numbers s n,k
Discrete Mathematics, Spring 2004 Homework 4 Sample Solutions 4.2 #77. Let s n,k denote the number of ways to seat n persons at k round tables, with at least one person at each table. (The numbers s n,k
6.1 Occupancy Problem
 15-859(M): Randomized Algorithms Lecturer: Anupam Gupta Topic: Occupancy Problems and Hashing Date: Sep 9 Scribe: Runting Shi 6.1 Occupancy Problem Bins and Balls Throw n balls into n bins at random. 1.
15-859(M): Randomized Algorithms Lecturer: Anupam Gupta Topic: Occupancy Problems and Hashing Date: Sep 9 Scribe: Runting Shi 6.1 Occupancy Problem Bins and Balls Throw n balls into n bins at random. 1.
Computer Science 385 Analysis of Algorithms Siena College Spring Topic Notes: Limitations of Algorithms
 Computer Science 385 Analysis of Algorithms Siena College Spring 2011 Topic Notes: Limitations of Algorithms We conclude with a discussion of the limitations of the power of algorithms. That is, what kinds
Computer Science 385 Analysis of Algorithms Siena College Spring 2011 Topic Notes: Limitations of Algorithms We conclude with a discussion of the limitations of the power of algorithms. That is, what kinds
Lecture 4: Hashing and Streaming Algorithms
 CSE 521: Design and Analysis of Algorithms I Winter 2017 Lecture 4: Hashing and Streaming Algorithms Lecturer: Shayan Oveis Gharan 01/18/2017 Scribe: Yuqing Ai Disclaimer: These notes have not been subjected
CSE 521: Design and Analysis of Algorithms I Winter 2017 Lecture 4: Hashing and Streaming Algorithms Lecturer: Shayan Oveis Gharan 01/18/2017 Scribe: Yuqing Ai Disclaimer: These notes have not been subjected
CS 161 Summer 2009 Homework #2 Sample Solutions
 CS 161 Summer 2009 Homework #2 Sample Solutions Regrade Policy: If you believe an error has been made in the grading of your homework, you may resubmit it for a regrade. If the error consists of more than
CS 161 Summer 2009 Homework #2 Sample Solutions Regrade Policy: If you believe an error has been made in the grading of your homework, you may resubmit it for a regrade. If the error consists of more than
Lecture 5: Hashing. David Woodruff Carnegie Mellon University
 Lecture 5: Hashing David Woodruff Carnegie Mellon University Hashing Universal hashing Perfect hashing Maintaining a Dictionary Let U be a universe of keys U could be all strings of ASCII characters of
Lecture 5: Hashing David Woodruff Carnegie Mellon University Hashing Universal hashing Perfect hashing Maintaining a Dictionary Let U be a universe of keys U could be all strings of ASCII characters of
Advanced Implementations of Tables: Balanced Search Trees and Hashing
 Advanced Implementations of Tables: Balanced Search Trees and Hashing Balanced Search Trees Binary search tree operations such as insert, delete, retrieve, etc. depend on the length of the path to the
Advanced Implementations of Tables: Balanced Search Trees and Hashing Balanced Search Trees Binary search tree operations such as insert, delete, retrieve, etc. depend on the length of the path to the
MATH 556: PROBABILITY PRIMER
 MATH 6: PROBABILITY PRIMER 1 DEFINITIONS, TERMINOLOGY, NOTATION 1.1 EVENTS AND THE SAMPLE SPACE Definition 1.1 An experiment is a one-off or repeatable process or procedure for which (a there is a well-defined
MATH 6: PROBABILITY PRIMER 1 DEFINITIONS, TERMINOLOGY, NOTATION 1.1 EVENTS AND THE SAMPLE SPACE Definition 1.1 An experiment is a one-off or repeatable process or procedure for which (a there is a well-defined
Lecture 17: Trees and Merge Sort 10:00 AM, Oct 15, 2018
 CS17 Integrated Introduction to Computer Science Klein Contents Lecture 17: Trees and Merge Sort 10:00 AM, Oct 15, 2018 1 Tree definitions 1 2 Analysis of mergesort using a binary tree 1 3 Analysis of
CS17 Integrated Introduction to Computer Science Klein Contents Lecture 17: Trees and Merge Sort 10:00 AM, Oct 15, 2018 1 Tree definitions 1 2 Analysis of mergesort using a binary tree 1 3 Analysis of
Hon.Algorithms (CSCI-GA 3520), Professor Yap Fall 2012 MIDTERM EXAM. Oct 11, 2012 SOLUTION
 Hon.Algorithms (CSCI-GA 352), Professor Yap Fall 22 MIDTERM EXAM Oct, 22 SOLUTIONS Problem. ( Points) Consider the recurrence T(n) = 4T(n/2)+ n2 lgn. Reduce this to standard form and solve it to Θ-order.
Hon.Algorithms (CSCI-GA 352), Professor Yap Fall 22 MIDTERM EXAM Oct, 22 SOLUTIONS Problem. ( Points) Consider the recurrence T(n) = 4T(n/2)+ n2 lgn. Reduce this to standard form and solve it to Θ-order.
Cache-Oblivious Hashing
 Cache-Oblivious Hashing Zhewei Wei Hong Kong University of Science & Technology Joint work with Rasmus Pagh, Ke Yi and Qin Zhang Dictionary Problem Store a subset S of the Universe U. Lookup: Does x belong
Cache-Oblivious Hashing Zhewei Wei Hong Kong University of Science & Technology Joint work with Rasmus Pagh, Ke Yi and Qin Zhang Dictionary Problem Store a subset S of the Universe U. Lookup: Does x belong
CS 4407 Algorithms Lecture 2: Iterative and Divide and Conquer Algorithms
 CS 4407 Algorithms Lecture 2: Iterative and Divide and Conquer Algorithms Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline CS 4407, Algorithms Growth Functions
CS 4407 Algorithms Lecture 2: Iterative and Divide and Conquer Algorithms Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline CS 4407, Algorithms Growth Functions
Fundamental Algorithms
 Fundamental Algorithms Chapter 5: Searching Michael Bader Winter 2014/15 Chapter 5: Searching, Winter 2014/15 1 Searching Definition (Search Problem) Input: a sequence or set A of n elements (objects)
Fundamental Algorithms Chapter 5: Searching Michael Bader Winter 2014/15 Chapter 5: Searching, Winter 2014/15 1 Searching Definition (Search Problem) Input: a sequence or set A of n elements (objects)
Fast Sorting and Selection. A Lower Bound for Worst Case
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 0 Fast Sorting and Selection USGS NEIC. Public domain government image. A Lower Bound
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 0 Fast Sorting and Selection USGS NEIC. Public domain government image. A Lower Bound
Big O 2/14/13. Administrative. Does it terminate? David Kauchak cs302 Spring 2013
 /4/3 Administrative Big O David Kauchak cs3 Spring 3 l Assignment : how d it go? l Assignment : out soon l CLRS code? l Videos Insertion-sort Insertion-sort Does it terminate? /4/3 Insertion-sort Loop
/4/3 Administrative Big O David Kauchak cs3 Spring 3 l Assignment : how d it go? l Assignment : out soon l CLRS code? l Videos Insertion-sort Insertion-sort Does it terminate? /4/3 Insertion-sort Loop
Balls and Bins: Smaller Hash Families and Faster Evaluation
 Balls and Bins: Smaller Hash Families and Faster Evaluation L. Elisa Celis Omer Reingold Gil Segev Udi Wieder April 22, 2011 Abstract A fundamental fact in the analysis of randomized algorithm is that
Balls and Bins: Smaller Hash Families and Faster Evaluation L. Elisa Celis Omer Reingold Gil Segev Udi Wieder April 22, 2011 Abstract A fundamental fact in the analysis of randomized algorithm is that
Introduction. An Introduction to Algorithms and Data Structures
 Introduction An Introduction to Algorithms and Data Structures Overview Aims This course is an introduction to the design, analysis and wide variety of algorithms (a topic often called Algorithmics ).
Introduction An Introduction to Algorithms and Data Structures Overview Aims This course is an introduction to the design, analysis and wide variety of algorithms (a topic often called Algorithmics ).
CSCI 3110 Assignment 6 Solutions
 CSCI 3110 Assignment 6 Solutions December 5, 2012 2.4 (4 pts) Suppose you are choosing between the following three algorithms: 1. Algorithm A solves problems by dividing them into five subproblems of half
CSCI 3110 Assignment 6 Solutions December 5, 2012 2.4 (4 pts) Suppose you are choosing between the following three algorithms: 1. Algorithm A solves problems by dividing them into five subproblems of half
1 Maintaining a Dictionary
 15-451/651: Design & Analysis of Algorithms February 1, 2016 Lecture #7: Hashing last changed: January 29, 2016 Hashing is a great practical tool, with an interesting and subtle theory too. In addition
15-451/651: Design & Analysis of Algorithms February 1, 2016 Lecture #7: Hashing last changed: January 29, 2016 Hashing is a great practical tool, with an interesting and subtle theory too. In addition
CS 350 Algorithms and Complexity
 CS 350 Algorithms and Complexity Winter 2019 Lecture 15: Limitations of Algorithmic Power Introduction to complexity theory Andrew P. Black Department of Computer Science Portland State University Lower
CS 350 Algorithms and Complexity Winter 2019 Lecture 15: Limitations of Algorithmic Power Introduction to complexity theory Andrew P. Black Department of Computer Science Portland State University Lower
20.1 2SAT. CS125 Lecture 20 Fall 2016
 CS125 Lecture 20 Fall 2016 20.1 2SAT We show yet another possible way to solve the 2SAT problem. Recall that the input to 2SAT is a logical expression that is the conunction (AND) of a set of clauses,
CS125 Lecture 20 Fall 2016 20.1 2SAT We show yet another possible way to solve the 2SAT problem. Recall that the input to 2SAT is a logical expression that is the conunction (AND) of a set of clauses,
Taking Stock. IE170: Algorithms in Systems Engineering: Lecture 3. Θ Notation. Comparing Algorithms
 Taking Stock IE170: Algorithms in Systems Engineering: Lecture 3 Jeff Linderoth Department of Industrial and Systems Engineering Lehigh University January 19, 2007 Last Time Lots of funky math Playing
Taking Stock IE170: Algorithms in Systems Engineering: Lecture 3 Jeff Linderoth Department of Industrial and Systems Engineering Lehigh University January 19, 2007 Last Time Lots of funky math Playing
Asymptotic Analysis. Thomas A. Anastasio. January 7, 2004
 Asymptotic Analysis Thomas A. Anastasio January 7, 004 1 Introduction As a programmer, you often have a choice of data structures and algorithms. Choosing the best one for a particular job involves, among
Asymptotic Analysis Thomas A. Anastasio January 7, 004 1 Introduction As a programmer, you often have a choice of data structures and algorithms. Choosing the best one for a particular job involves, among
Motivation. Dictionaries. Direct Addressing. CSE 680 Prof. Roger Crawfis
 Motivation Introduction to Algorithms Hash Tables CSE 680 Prof. Roger Crawfis Arrays provide an indirect way to access a set. Many times we need an association between two sets, or a set of keys and associated
Motivation Introduction to Algorithms Hash Tables CSE 680 Prof. Roger Crawfis Arrays provide an indirect way to access a set. Many times we need an association between two sets, or a set of keys and associated
CS 4407 Algorithms Lecture 2: Growth Functions
 CS 4407 Algorithms Lecture 2: Growth Functions Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline Growth Functions Mathematical specification of growth functions
CS 4407 Algorithms Lecture 2: Growth Functions Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline Growth Functions Mathematical specification of growth functions
Application: Bucket Sort
 5.2.2. Application: Bucket Sort Bucket sort breaks the log) lower bound for standard comparison-based sorting, under certain assumptions on the input We want to sort a set of =2 integers chosen I+U@R from
5.2.2. Application: Bucket Sort Bucket sort breaks the log) lower bound for standard comparison-based sorting, under certain assumptions on the input We want to sort a set of =2 integers chosen I+U@R from
COS597D: Information Theory in Computer Science October 5, Lecture 6
 COS597D: Information Theory in Computer Science October 5, 2011 Lecture 6 Lecturer: Mark Braverman Scribe: Yonatan Naamad 1 A lower bound for perfect hash families. In the previous lecture, we saw that
COS597D: Information Theory in Computer Science October 5, 2011 Lecture 6 Lecturer: Mark Braverman Scribe: Yonatan Naamad 1 A lower bound for perfect hash families. In the previous lecture, we saw that
Data selection. Lower complexity bound for sorting
 Data selection. Lower complexity bound for sorting Lecturer: Georgy Gimel farb COMPSCI 220 Algorithms and Data Structures 1 / 12 1 Data selection: Quickselect 2 Lower complexity bound for sorting 3 The
Data selection. Lower complexity bound for sorting Lecturer: Georgy Gimel farb COMPSCI 220 Algorithms and Data Structures 1 / 12 1 Data selection: Quickselect 2 Lower complexity bound for sorting 3 The
Lecture 1: Introduction to Sublinear Algorithms
 CSE 522: Sublinear (and Streaming) Algorithms Spring 2014 Lecture 1: Introduction to Sublinear Algorithms March 31, 2014 Lecturer: Paul Beame Scribe: Paul Beame Too much data, too little time, space for
CSE 522: Sublinear (and Streaming) Algorithms Spring 2014 Lecture 1: Introduction to Sublinear Algorithms March 31, 2014 Lecturer: Paul Beame Scribe: Paul Beame Too much data, too little time, space for
CS Communication Complexity: Applications and New Directions
 CS 2429 - Communication Complexity: Applications and New Directions Lecturer: Toniann Pitassi 1 Introduction In this course we will define the basic two-party model of communication, as introduced in the
CS 2429 - Communication Complexity: Applications and New Directions Lecturer: Toniann Pitassi 1 Introduction In this course we will define the basic two-party model of communication, as introduced in the
CSC236 Week 3. Larry Zhang
 CSC236 Week 3 Larry Zhang 1 Announcements Problem Set 1 due this Friday Make sure to read Submission Instructions on the course web page. Search for Teammates on Piazza Educational memes: http://www.cs.toronto.edu/~ylzhang/csc236/memes.html
CSC236 Week 3 Larry Zhang 1 Announcements Problem Set 1 due this Friday Make sure to read Submission Instructions on the course web page. Search for Teammates on Piazza Educational memes: http://www.cs.toronto.edu/~ylzhang/csc236/memes.html
Lecture 7: Passive Learning
 CS 880: Advanced Complexity Theory 2/8/2008 Lecture 7: Passive Learning Instructor: Dieter van Melkebeek Scribe: Tom Watson In the previous lectures, we studied harmonic analysis as a tool for analyzing
CS 880: Advanced Complexity Theory 2/8/2008 Lecture 7: Passive Learning Instructor: Dieter van Melkebeek Scribe: Tom Watson In the previous lectures, we studied harmonic analysis as a tool for analyzing
Analysis of Algorithms CMPSC 565
 Analysis of Algorithms CMPSC 565 LECTURES 38-39 Randomized Algorithms II Quickselect Quicksort Running time Adam Smith L1.1 Types of randomized analysis Average-case analysis : Assume data is distributed
Analysis of Algorithms CMPSC 565 LECTURES 38-39 Randomized Algorithms II Quickselect Quicksort Running time Adam Smith L1.1 Types of randomized analysis Average-case analysis : Assume data is distributed
Asymptotic Analysis. Slides by Carl Kingsford. Jan. 27, AD Chapter 2
 Asymptotic Analysis Slides by Carl Kingsford Jan. 27, 2014 AD Chapter 2 Independent Set Definition (Independent Set). Given a graph G = (V, E) an independent set is a set S V if no two nodes in S are joined
Asymptotic Analysis Slides by Carl Kingsford Jan. 27, 2014 AD Chapter 2 Independent Set Definition (Independent Set). Given a graph G = (V, E) an independent set is a set S V if no two nodes in S are joined
Lecture 4 Thursday Sep 11, 2014
 CS 224: Advanced Algorithms Fall 2014 Lecture 4 Thursday Sep 11, 2014 Prof. Jelani Nelson Scribe: Marco Gentili 1 Overview Today we re going to talk about: 1. linear probing (show with 5-wise independence)
CS 224: Advanced Algorithms Fall 2014 Lecture 4 Thursday Sep 11, 2014 Prof. Jelani Nelson Scribe: Marco Gentili 1 Overview Today we re going to talk about: 1. linear probing (show with 5-wise independence)
Divide-and-Conquer Algorithms Part Two
 Divide-and-Conquer Algorithms Part Two Recap from Last Time Divide-and-Conquer Algorithms A divide-and-conquer algorithm is one that works as follows: (Divide) Split the input apart into multiple smaller
Divide-and-Conquer Algorithms Part Two Recap from Last Time Divide-and-Conquer Algorithms A divide-and-conquer algorithm is one that works as follows: (Divide) Split the input apart into multiple smaller
Higher Cell Probe Lower Bounds for Evaluating Polynomials
 Higher Cell Probe Lower Bounds for Evaluating Polynomials Kasper Green Larsen MADALGO, Department of Computer Science Aarhus University Aarhus, Denmark Email: larsen@cs.au.dk Abstract In this paper, we
Higher Cell Probe Lower Bounds for Evaluating Polynomials Kasper Green Larsen MADALGO, Department of Computer Science Aarhus University Aarhus, Denmark Email: larsen@cs.au.dk Abstract In this paper, we
Average Case Analysis of QuickSort and Insertion Tree Height using Incompressibility
 Average Case Analysis of QuickSort and Insertion Tree Height using Incompressibility Tao Jiang, Ming Li, Brendan Lucier September 26, 2005 Abstract In this paper we study the Kolmogorov Complexity of a
Average Case Analysis of QuickSort and Insertion Tree Height using Incompressibility Tao Jiang, Ming Li, Brendan Lucier September 26, 2005 Abstract In this paper we study the Kolmogorov Complexity of a
1 Terminology and setup
 15-451/651: Design & Analysis of Algorithms August 31, 2017 Lecture #2 last changed: August 29, 2017 In this lecture, we will examine some simple, concrete models of computation, each with a precise definition
15-451/651: Design & Analysis of Algorithms August 31, 2017 Lecture #2 last changed: August 29, 2017 In this lecture, we will examine some simple, concrete models of computation, each with a precise definition
14.1 Finding frequent elements in stream
 Chapter 14 Streaming Data Model 14.1 Finding frequent elements in stream A very useful statistics for many applications is to keep track of elements that occur more frequently. It can come in many flavours
Chapter 14 Streaming Data Model 14.1 Finding frequent elements in stream A very useful statistics for many applications is to keep track of elements that occur more frequently. It can come in many flavours
CS 350 Algorithms and Complexity
 1 CS 350 Algorithms and Complexity Fall 2015 Lecture 15: Limitations of Algorithmic Power Introduction to complexity theory Andrew P. Black Department of Computer Science Portland State University Lower
1 CS 350 Algorithms and Complexity Fall 2015 Lecture 15: Limitations of Algorithmic Power Introduction to complexity theory Andrew P. Black Department of Computer Science Portland State University Lower
Hashing. Data organization in main memory or disk
 Hashing Data organization in main memory or disk sequential, binary trees, The location of a key depends on other keys => unnecessary key comparisons to find a key Question: find key with a single comparison
Hashing Data organization in main memory or disk sequential, binary trees, The location of a key depends on other keys => unnecessary key comparisons to find a key Question: find key with a single comparison
Lecture 4 February 2nd, 2017
 CS 224: Advanced Algorithms Spring 2017 Prof. Jelani Nelson Lecture 4 February 2nd, 2017 Scribe: Rohil Prasad 1 Overview In the last lecture we covered topics in hashing, including load balancing, k-wise
CS 224: Advanced Algorithms Spring 2017 Prof. Jelani Nelson Lecture 4 February 2nd, 2017 Scribe: Rohil Prasad 1 Overview In the last lecture we covered topics in hashing, including load balancing, k-wise
Quiz 1 Solutions. Problem 2. Asymptotics & Recurrences [20 points] (3 parts)
![Quiz 1 Solutions. Problem 2. Asymptotics & Recurrences [20 points] (3 parts) Quiz 1 Solutions. Problem 2. Asymptotics & Recurrences [20 points] (3 parts)](/thumbs/87/95581149.jpg) Introduction to Algorithms October 13, 2010 Massachusetts Institute of Technology 6.006 Fall 2010 Professors Konstantinos Daskalakis and Patrick Jaillet Quiz 1 Solutions Quiz 1 Solutions Problem 1. We
Introduction to Algorithms October 13, 2010 Massachusetts Institute of Technology 6.006 Fall 2010 Professors Konstantinos Daskalakis and Patrick Jaillet Quiz 1 Solutions Quiz 1 Solutions Problem 1. We
Homework 6: Solutions Sid Banerjee Problem 1: (The Flajolet-Martin Counter) ORIE 4520: Stochastics at Scale Fall 2015
 Problem 1: (The Flajolet-Martin Counter) In class (and in the prelim!), we looked at an idealized algorithm for finding the number of distinct elements in a stream, where we sampled uniform random variables
Problem 1: (The Flajolet-Martin Counter) In class (and in the prelim!), we looked at an idealized algorithm for finding the number of distinct elements in a stream, where we sampled uniform random variables
Testing Problems with Sub-Learning Sample Complexity
 Testing Problems with Sub-Learning Sample Complexity Michael Kearns AT&T Labs Research 180 Park Avenue Florham Park, NJ, 07932 mkearns@researchattcom Dana Ron Laboratory for Computer Science, MIT 545 Technology
Testing Problems with Sub-Learning Sample Complexity Michael Kearns AT&T Labs Research 180 Park Avenue Florham Park, NJ, 07932 mkearns@researchattcom Dana Ron Laboratory for Computer Science, MIT 545 Technology
CSCB63 Winter Week10 - Lecture 2 - Hashing. Anna Bretscher. March 21, / 30
 CSCB63 Winter 2019 Week10 - Lecture 2 - Hashing Anna Bretscher March 21, 2019 1 / 30 Today Hashing Open Addressing Hash functions Universal Hashing 2 / 30 Open Addressing Open Addressing. Each entry in
CSCB63 Winter 2019 Week10 - Lecture 2 - Hashing Anna Bretscher March 21, 2019 1 / 30 Today Hashing Open Addressing Hash functions Universal Hashing 2 / 30 Open Addressing Open Addressing. Each entry in
Dominating Set. Chapter 7
 Chapter 7 Dominating Set In this chapter we present another randomized algorithm that demonstrates the power of randomization to break symmetries. We study the problem of finding a small dominating set
Chapter 7 Dominating Set In this chapter we present another randomized algorithm that demonstrates the power of randomization to break symmetries. We study the problem of finding a small dominating set
Chapter 5 Divide and Conquer
 CMPT 705: Design and Analysis of Algorithms Spring 008 Chapter 5 Divide and Conquer Lecturer: Binay Bhattacharya Scribe: Chris Nell 5.1 Introduction Given a problem P with input size n, P (n), we define
CMPT 705: Design and Analysis of Algorithms Spring 008 Chapter 5 Divide and Conquer Lecturer: Binay Bhattacharya Scribe: Chris Nell 5.1 Introduction Given a problem P with input size n, P (n), we define
Module 1: Analyzing the Efficiency of Algorithms
 Module 1: Analyzing the Efficiency of Algorithms Dr. Natarajan Meghanathan Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu What is an Algorithm?
Module 1: Analyzing the Efficiency of Algorithms Dr. Natarajan Meghanathan Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu What is an Algorithm?
Boolean circuits. Lecture Definitions
 Lecture 20 Boolean circuits In this lecture we will discuss the Boolean circuit model of computation and its connection to the Turing machine model. Although the Boolean circuit model is fundamentally
Lecture 20 Boolean circuits In this lecture we will discuss the Boolean circuit model of computation and its connection to the Turing machine model. Although the Boolean circuit model is fundamentally
Tutorial 4. Dynamic Set: Amortized Analysis
 Tutorial 4 Dynamic Set: Amortized Analysis Review Binary tree Complete binary tree Full binary tree 2-tree P115 Unlike common binary tree, the base case is not an empty tree, but a external node Heap Binary
Tutorial 4 Dynamic Set: Amortized Analysis Review Binary tree Complete binary tree Full binary tree 2-tree P115 Unlike common binary tree, the base case is not an empty tree, but a external node Heap Binary
CS261: A Second Course in Algorithms Lecture #18: Five Essential Tools for the Analysis of Randomized Algorithms
 CS261: A Second Course in Algorithms Lecture #18: Five Essential Tools for the Analysis of Randomized Algorithms Tim Roughgarden March 3, 2016 1 Preamble In CS109 and CS161, you learned some tricks of
CS261: A Second Course in Algorithms Lecture #18: Five Essential Tools for the Analysis of Randomized Algorithms Tim Roughgarden March 3, 2016 1 Preamble In CS109 and CS161, you learned some tricks of
Randomized Sorting Algorithms Quick sort can be converted to a randomized algorithm by picking the pivot element randomly. In this case we can show th
 CSE 3500 Algorithms and Complexity Fall 2016 Lecture 10: September 29, 2016 Quick sort: Average Run Time In the last lecture we started analyzing the expected run time of quick sort. Let X = k 1, k 2,...,
CSE 3500 Algorithms and Complexity Fall 2016 Lecture 10: September 29, 2016 Quick sort: Average Run Time In the last lecture we started analyzing the expected run time of quick sort. Let X = k 1, k 2,...,
Theory of Computation
 Theory of Computation Dr. Sarmad Abbasi Dr. Sarmad Abbasi () Theory of Computation 1 / 33 Lecture 20: Overview Incompressible strings Minimal Length Descriptions Descriptive Complexity Dr. Sarmad Abbasi
Theory of Computation Dr. Sarmad Abbasi Dr. Sarmad Abbasi () Theory of Computation 1 / 33 Lecture 20: Overview Incompressible strings Minimal Length Descriptions Descriptive Complexity Dr. Sarmad Abbasi
Balls and Bins: Smaller Hash Families and Faster Evaluation
 Balls and Bins: Smaller Hash Families and Faster Evaluation L. Elisa Celis Omer Reingold Gil Segev Udi Wieder May 1, 2013 Abstract A fundamental fact in the analysis of randomized algorithms is that when
Balls and Bins: Smaller Hash Families and Faster Evaluation L. Elisa Celis Omer Reingold Gil Segev Udi Wieder May 1, 2013 Abstract A fundamental fact in the analysis of randomized algorithms is that when
Baltic Way 2003 Riga, November 2, 2003
 altic Way 2003 Riga, November 2, 2003 Problems and solutions. Let Q + be the set of positive rational numbers. Find all functions f : Q + Q + which for all x Q + fulfil () f ( x ) = f (x) (2) ( + x ) f
altic Way 2003 Riga, November 2, 2003 Problems and solutions. Let Q + be the set of positive rational numbers. Find all functions f : Q + Q + which for all x Q + fulfil () f ( x ) = f (x) (2) ( + x ) f
CS1802 Week 11: Algorithms, Sums, Series, Induction
 CS180 Discrete Structures Recitation Fall 017 Nov 11 - November 17, 017 CS180 Week 11: Algorithms, Sums, Series, Induction 1 Markov chain i. Boston has days which are either sunny or rainy and can be modeled
CS180 Discrete Structures Recitation Fall 017 Nov 11 - November 17, 017 CS180 Week 11: Algorithms, Sums, Series, Induction 1 Markov chain i. Boston has days which are either sunny or rainy and can be modeled
This means that we can assume each list ) is
 This means that we can assume each list ) is of the form ),, ( )with < and Since the sizes of the items are integers, there are at most +1pairs in each list Furthermore, if we let = be the maximum possible
This means that we can assume each list ) is of the form ),, ( )with < and Since the sizes of the items are integers, there are at most +1pairs in each list Furthermore, if we let = be the maximum possible
CS 395T Computational Learning Theory. Scribe: Mike Halcrow. x 4. x 2. x 6
 CS 395T Computational Learning Theory Lecture 3: September 0, 2007 Lecturer: Adam Klivans Scribe: Mike Halcrow 3. Decision List Recap In the last class, we determined that, when learning a t-decision list,
CS 395T Computational Learning Theory Lecture 3: September 0, 2007 Lecturer: Adam Klivans Scribe: Mike Halcrow 3. Decision List Recap In the last class, we determined that, when learning a t-decision list,
CS/COE
 CS/COE 1501 www.cs.pitt.edu/~nlf4/cs1501/ P vs NP But first, something completely different... Some computational problems are unsolvable No algorithm can be written that will always produce the correct
CS/COE 1501 www.cs.pitt.edu/~nlf4/cs1501/ P vs NP But first, something completely different... Some computational problems are unsolvable No algorithm can be written that will always produce the correct
N/4 + N/2 + N = 2N 2.
 CS61B Summer 2006 Instructor: Erin Korber Lecture 24, 7 Aug. 1 Amortized Analysis For some of the data structures we ve discussed (namely hash tables and splay trees), it was claimed that the average time
CS61B Summer 2006 Instructor: Erin Korber Lecture 24, 7 Aug. 1 Amortized Analysis For some of the data structures we ve discussed (namely hash tables and splay trees), it was claimed that the average time
Lecture 6 September 21, 2016
 ICS 643: Advanced Parallel Algorithms Fall 2016 Lecture 6 September 21, 2016 Prof. Nodari Sitchinava Scribe: Tiffany Eulalio 1 Overview In the last lecture, we wrote a non-recursive summation program and
ICS 643: Advanced Parallel Algorithms Fall 2016 Lecture 6 September 21, 2016 Prof. Nodari Sitchinava Scribe: Tiffany Eulalio 1 Overview In the last lecture, we wrote a non-recursive summation program and
Outline. Computer Science 331. Cost of Binary Search Tree Operations. Bounds on Height: Worst- and Average-Case
 Outline Computer Science Average Case Analysis: Binary Search Trees Mike Jacobson Department of Computer Science University of Calgary Lecture #7 Motivation and Objective Definition 4 Mike Jacobson (University
Outline Computer Science Average Case Analysis: Binary Search Trees Mike Jacobson Department of Computer Science University of Calgary Lecture #7 Motivation and Objective Definition 4 Mike Jacobson (University
1 AC 0 and Håstad Switching Lemma
 princeton university cos 522: computational complexity Lecture 19: Circuit complexity Lecturer: Sanjeev Arora Scribe:Tony Wirth Complexity theory s Waterloo As we saw in an earlier lecture, if PH Σ P 2
princeton university cos 522: computational complexity Lecture 19: Circuit complexity Lecturer: Sanjeev Arora Scribe:Tony Wirth Complexity theory s Waterloo As we saw in an earlier lecture, if PH Σ P 2
Data structures Exercise 1 solution. Question 1. Let s start by writing all the functions in big O notation:
 Data structures Exercise 1 solution Question 1 Let s start by writing all the functions in big O notation: f 1 (n) = 2017 = O(1), f 2 (n) = 2 log 2 n = O(n 2 ), f 3 (n) = 2 n = O(2 n ), f 4 (n) = 1 = O
Data structures Exercise 1 solution Question 1 Let s start by writing all the functions in big O notation: f 1 (n) = 2017 = O(1), f 2 (n) = 2 log 2 n = O(n 2 ), f 3 (n) = 2 n = O(2 n ), f 4 (n) = 1 = O
STAT 111 Recitation 1
 STAT 111 Recitation 1 Linjun Zhang January 20, 2017 What s in the recitation This class, and the exam of this class, is a mix of statistical concepts and calculations. We are going to do a little bit of
STAT 111 Recitation 1 Linjun Zhang January 20, 2017 What s in the recitation This class, and the exam of this class, is a mix of statistical concepts and calculations. We are going to do a little bit of
Biased Quantiles. Flip Korn Graham Cormode S. Muthukrishnan
 Biased Quantiles Graham Cormode cormode@bell-labs.com S. Muthukrishnan muthu@cs.rutgers.edu Flip Korn flip@research.att.com Divesh Srivastava divesh@research.att.com Quantiles Quantiles summarize data
Biased Quantiles Graham Cormode cormode@bell-labs.com S. Muthukrishnan muthu@cs.rutgers.edu Flip Korn flip@research.att.com Divesh Srivastava divesh@research.att.com Quantiles Quantiles summarize data
THE KENNESAW STATE UNIVERSITY HIGH SCHOOL MATHEMATICS COMPETITION PART II Calculators are NOT permitted Time allowed: 2 hours
 THE 018-019 KENNESAW STATE UNIVERSITY HIGH SCHOOL MATHEMATICS COMPETITION PART II Calculators are NOT permitted Time allowed: hours 1 Let m be a three-digit integer with distinct digits Find all such integers
THE 018-019 KENNESAW STATE UNIVERSITY HIGH SCHOOL MATHEMATICS COMPETITION PART II Calculators are NOT permitted Time allowed: hours 1 Let m be a three-digit integer with distinct digits Find all such integers
Analysis of Algorithms - Midterm (Solutions)
 Analysis of Algorithms - Midterm (Solutions) K Subramani LCSEE, West Virginia University, Morgantown, WV {ksmani@cseewvuedu} 1 Problems 1 Recurrences: Solve the following recurrences exactly or asymototically
Analysis of Algorithms - Midterm (Solutions) K Subramani LCSEE, West Virginia University, Morgantown, WV {ksmani@cseewvuedu} 1 Problems 1 Recurrences: Solve the following recurrences exactly or asymototically
Fundamental Algorithms
 Chapter 5: Hash Tables, Winter 2018/19 1 Fundamental Algorithms Chapter 5: Hash Tables Jan Křetínský Winter 2018/19 Chapter 5: Hash Tables, Winter 2018/19 2 Generalised Search Problem Definition (Search
Chapter 5: Hash Tables, Winter 2018/19 1 Fundamental Algorithms Chapter 5: Hash Tables Jan Křetínský Winter 2018/19 Chapter 5: Hash Tables, Winter 2018/19 2 Generalised Search Problem Definition (Search
1. [10 marks] Consider the following two algorithms that find the two largest elements in an array A[1..n], where n >= 2.
![1. [10 marks] Consider the following two algorithms that find the two largest elements in an array A[1..n], where n >= 2. 1. [10 marks] Consider the following two algorithms that find the two largest elements in an array A[1..n], where n >= 2.](/thumbs/73/68822500.jpg) CSC 6 H5S Homework Assignment # 1 Spring 010 Worth: 11% Due: Monday February 1 (at class) For each question, please write up detailed answers carefully. Make sure that you use notation and terminology
CSC 6 H5S Homework Assignment # 1 Spring 010 Worth: 11% Due: Monday February 1 (at class) For each question, please write up detailed answers carefully. Make sure that you use notation and terminology
Math 391: Midterm 1.0 Spring 2016
 Math 391: Midterm 1.0 Spring 2016 James Skon skonjp@kenyon.edu Test date: October 5 Submission Instructions: Give all your assumptions. Show all your work. Be as complete as possible. Grading Problem 1
Math 391: Midterm 1.0 Spring 2016 James Skon skonjp@kenyon.edu Test date: October 5 Submission Instructions: Give all your assumptions. Show all your work. Be as complete as possible. Grading Problem 1
