Data structures Exercise 1 solution. Question 1. Let s start by writing all the functions in big O notation:
|
|
|
- Angela Wilkerson
- 5 years ago
- Views:
Transcription
1 Data structures Exercise 1 solution Question 1 Let s start by writing all the functions in big O notation: f 1 (n) = 2017 = O(1), f 2 (n) = 2 log 2 n = O(n 2 ), f 3 (n) = 2 n = O(2 n ), f 4 (n) = 1 = O n (1), f n 5(n) = 3 n = O(3 n ), f 6 (n) = 2 3n = O(2 3n ), f 7 (n) = n n = O(n n ), f 8 (n) = 3 2n = O(3 2n ), f 9 (n) = log( n) = log n 0.5 = 0.5 log n = O(log n), f 10 (n) = log(2 n n 2 ) f 10 (n) = log(2 n n 2 ) = log(2 n ) + log(n 2 ) = n log(2) + 2 log(n) = O(n + log(n)) = O(n), f 11 (n) = log(n 10 ) = 10 log n = O(log n), f 12 (n) = n 2 + log(n) + n = O(n 2 ) Now we can sort these functions from smallest to largest: f 4 f 1 f 9, f 11 f 10 f 2, f 12 f 3 f 5 f 7 f 8 Notable Proofs: f 4 < f 1 : lim f 6 1 n 2017 = 0
2 f 1 < f 9 : lim 2017 O(log( n)) = 0 f 10 < f 2 : log(2n n 2 ) 2 log 2 n = 0 2 log 2 n = (2 2 log 2 n = 2 log n2 = n 2 = O(n 2 ) f 8 < f 6 : 32n 2 3n = 0 The denominator function grows a lot faster than the numerator function. Another way to compare f 8 (n) = 3 2n and f 6 (n) = 2 3n is to take log on both sides. We will get log(3 2n ) = 2 n log3 = O(2 n ), log(2 3n ) = 3 n log2 = 3 n = O(3 n ) Since 2 n log3 < 3 n for large n, we can conclude that 3 2n = O(2 3n ) Question 2 a. Correct: Assuming function f(n) = n n. Then, lim (n k)n k n n Let s take log lim log(n k)n k log n n = lim (n k) log(n k) n log n = lim n(log(n k) log(n)) k log(n k) = lim n(log(n k) log(n)) k log(n k) = b. False. Let s assume by contradiction that there exist n 0, c 0 such that n > n 0, (f(n)) 2 c f(n). Then n > n 0, f(n) c, in contradiction to the fact that f(n) = Ω(log n). c. Correct: Question 3 f(n) + g(n) = O(f(n) + g(n)) = O(max(f(n), g(n)) and assuming both functions are bigger or equal 1 we get O(max(f(n), g(n)) = O(f(n)g(n)). a. T(n) = T( n) + 1 1) By iteration:
3 T(n) = T (n 1 2) + 1 = [T (n 1 4) + 1] + 1 = T (n 1 4) = [T (n 1 8) + 1] = T (n 1 1 8) = = T (n2 i ) + 1 i For a constant c = 2. 1 n2 i = i log n = 1 log n = 2i i = log( log n) 1 T(n) = T (n2 log (log n) ) + 1 log(log n) = T(2) + 1 log(log n) 2) By master method: = Θ(1) + Θ(log(log n)) = Θ(log(log n)) m = log n n = 2 m n = 2 m 2 T(2 m ) = T (2 m 2 ) + 1 S(m) = S ( m 2 ) + 1 a=1, b=2, f(n) = 1 = Θ(1) = Θ(n 0 ) = Θ(n log 1 ) This is case 2 of master method, therefore: S(m) = Θ(log m) T(n) = T(2 m ) = S(m) = Θ(log m) = Θ(log (log n)) b. T(n) = 5T ( n 2 ) + n3 log n 1) By iteration: T(n) = 5T ( n 2 ) + n3 log n = 5 (5T ( n 4 ) + (n 2 ) 3 log ( n 2 )) + n3 log n = 5 (5 (5T ( n 3 8 ) + (n 4 ) log ( n 3 4 )) + (n 2 ) log ( n 2 )) + n3 log n = i 1 5 i T ( n 2 i) + n 3 5j (2 j ) 3 log ( n 2 j) = j=0 Let s find i: n = 1 i = log n. 2i log n 1 5 log n + n 3 log n ( 5 j 8 ) log(2 j ) = j=0 log n 1 5 log n + n 3 log n ( 5 j 8 ) j 5 log n + cn 3 log n = j=0 O(5 log n + n 3 log n) = O(n 3 log n). Obviously T(n) = (n 3 log n) and therefore T(n) = (n 3 log n)
4 2) By master method: a = 5, b=2, f(n) = n 3 log n n log 5 n 2.32 for ε = 0.5 n 3 log n = (n ) a f ( n ) c f(n) b 5 n3 2 3 log n 2 c n3 log n 5 8 log n c log n 2 5 log n 2 log n c 5 log n 2 log n c c = 5 8 This is case 3 of master method, therefore: T(n) = (n 3 log n) c. T(n) = T(cn) + T((1 c)n) + 1, 0 < c < 1 By substitution method (induction) Without loss of generality, let c 1 c, so that 0 < 1 c 1/2 and 1/2 c < 1. We can start be drawing a recursion tree
5 The recursion tree is full for log1/(1 c) n levels, contributing together log 1/(1 c) n, so we guess T(n) = (n) The tree has total log1/c n levels, contributing together log 1/c n, so we guess O(n ). Lower bound: Guess: T(n) dn for all n n 0 Induction base: T(1) = 1 d 1 for d = 1 Induction step: Assume T(m) dm for all 1 m < n Proof: T(n) = T(cn) + T((1 c)n) + 1 dcn + dn(1 c) + 1 = dn + 1 dn T(n) = (n) Upper bound: revise the guess by subtracting a lower-order term Guess: T(n) dn b for all n n 0, b> 0 is a constant Induction base: T(1) = 1 d 1 -b. Clearly it holds for proper choice of d and b. Induction step: Assume T(m) dm b for all 1 m < n Proof: T(n) = T(cn) + T((1 c)n) + 1 dcn b + dn(1 c) b + 1 = dn 2b + 1 dn for b 1/2 T(n) = O(n) d. T(n) = T ( 3n 5 ) + 2T (n 5 ) + n Again, we can start by recursion tree to make a quess T(n) =O(nlogn) and T(n) = (nlogn) and prove both bounds by induction. Upper bound: Guess: T(n) cn log n for n 2
6 Induction base: T(2) = const c for proper choice of c.induction step: Assume T(m) cm log m for all 2 m < n T(n) = T ( 3n 5 ) + 2T (n 5 ) + n c 3n 5 log 3n 5 + 2c n 5 log n 5 + n = c 3n 5 log 3 + c 3n 5 log n c 3n 5 log 5 + 2c n 5 log n 2c n log 5 + n = 5 c 3n log 3 + cn log n cn log 5 + n cn log n if c 3n cn + n 0 n(1 1.37c) 0 c 0.8 Therefore, T(n) = O(n log n) log 3 cn log 5 + n 0 Lower bound: Guess: T(n) dn log n for all n Induction base: T(1) = 1 d 1 log 1 = 0 Induction step: Assume T(m) dm log m for all 1 m < n T(n) = T ( 3n 5 ) + 2T (n 5 ) + n d 3n 5 log 3n 5 + 2d n 5 log n 5 + n = d 3n 5 log 3 + d 3n 5 log n d 3n 5 log 5 + 2d n 5 log n 2d n log 5 + n = 5 d 3n log 3 + dn log n dn log 5 + n dn log n if d 3n dn + n 0 n(1 1.37d) 0 d 0.7 Therefore, T(n) = (n log n). log 3 dn log 5 + n 0 We conclude that T(n) = (n log n). e. T(n) = 2T(n 1) + 1 Use the iteration method: T(n) = 2T(n 1) + 1 = 2[2T(n 2) + 1] + 1 = 4T(n 2) = 4[2T(n 3) + 1] = 8T(n 3) = = 2 i T(n i) + ( n 1 ) After i = n 1 iterations we have reached T(1). T(n) = 2 n 1 T(1) + (2 n 1 1) = (2 n ). Question 4 a. i is looping from 1 to n 1, while j is looping from n down to i + 1. Inside the loop we are doing operations in Θ(1).
7 So this gives: n 1 i+1 T(n) = 1 = n i = n 2 (i) = n 2 i=1 j=n n 1 i=1 = n 2 n2 2 + n 2 = n2 2 + n 2 And in big Θ notation: T(n) = Θ(n 2 ) b. We can define a recursive formula to define this method: When n is 0 or 1: T(1) = 1. Else: T(n) = T(n 1) + c, where c is a constant. Or: 1 n = 0 or 1 T(n) = { T(n 1) + c otherwise n 1 T(n) = T(n 1) + c = T(n 2) + c + c = = T(n k) + k c n k = 1 => k = n 1 => T(n) = T(1) + (n 1) c = Θ(n) i=1 n(n 1) 2 c. In the same way, when n is 0 or 1: T(1) = 1. Else if n is even: T(n) = T(n/2) + c. Else (That is n is odd): T(n) = T((n 1)/2) + c. Again, in the same way as before: 1 n = 0 or 1 T(p) = { T(n/2) + c n is even T((n 1)/2) + c otherwise When n is large, there is almost no difference between n/2 and (n-1)/2 : both cut n nearly evenly in half. Consequently, we make the guess that T(n)= Θ( lg n) and prove it by induction. Question 5 a. Assuming we have two inputs: a sorted array A and integer x, we want to be able to return the index of x or -1 if x doesn t include in the array. Let s define the following function: 1) For an array A we will try the elements in jumps of 2 i, i=0,1,2, until we get to the first element that is bigger or equal to x. That is we will try the elements A[1], A[2], A[4],. Let A[2 j ] be the first element that is bigger than x. Clearly, A[2 j-1 ] < x <= A[2 j ].
8 We will need at most log d + 1 steps to get to A[2 j ], therefore this part takes O(log d). 2) Let A[2 j ] be the first element that is bigger than x. The size of the interval [2 j j ] is at most d therefore a binary search in A[2 j j ] will take O(log d) Let s analyze the complexity: O(log d) + O(log d) = O(log d) b. The idea: At each step we compare the medians of the current arrays A and B. Denote m1 to be the median of A and m2 to be the median of B. 1. If m1=m2 then we are done, m1 (=m2) is the median 2. If m1 > m2, the all the elements A[ n n] cannot be a median, because they 2 are greater that more the half of lements in array A and half of elements in array B (the left halves of A and B respectively). Similarly, elements B[1.. m ] cannot B 2 a median, since each of them less than half of elements in array B and half of elements in array A. 3. The case m2>m1 is similar to (2) Denote the size of A be n and size of B be m. 1. Let m1 and m2 be the medians of A and B respectively 2. If m1 = m2 then we are done. Return m1 3. else if m1 > m2, ignore the right half of A[ n n] and left part of B[1.. m 2 ] 4. else if m2 > m1, ignore the right half of B[ m n] and left part of A B[1.. n 2 ] 5. Repeat the process until one of the base cases 1. A is empty. Return the median of B 2. A has one element. Use binary search on B to find the location of the only element of A in B, then return the median of B assuming the only elements of A has been inserted to B. 3. and 4. similar to 1 and 2 Run time: at each step either size A or B is divided by 2. So we get O(logn + logm)
Data Structures and Algorithms Chapter 3
 Data Structures and Algorithms Chapter 3 1. Divide and conquer 2. Merge sort, repeated substitutions 3. Tiling 4. Recurrences Recurrences Running times of algorithms with recursive calls can be described
Data Structures and Algorithms Chapter 3 1. Divide and conquer 2. Merge sort, repeated substitutions 3. Tiling 4. Recurrences Recurrences Running times of algorithms with recursive calls can be described
Chapter 2. Recurrence Relations. Divide and Conquer. Divide and Conquer Strategy. Another Example: Merge Sort. Merge Sort Example. Merge Sort Example
 Recurrence Relations Chapter 2 Divide and Conquer Equation or an inequality that describes a function by its values on smaller inputs. Recurrence relations arise when we analyze the running time of iterative
Recurrence Relations Chapter 2 Divide and Conquer Equation or an inequality that describes a function by its values on smaller inputs. Recurrence relations arise when we analyze the running time of iterative
Algorithm efficiency analysis
 Algorithm efficiency analysis Mădălina Răschip, Cristian Gaţu Faculty of Computer Science Alexandru Ioan Cuza University of Iaşi, Romania DS 2017/2018 Content Algorithm efficiency analysis Recursive function
Algorithm efficiency analysis Mădălina Răschip, Cristian Gaţu Faculty of Computer Science Alexandru Ioan Cuza University of Iaşi, Romania DS 2017/2018 Content Algorithm efficiency analysis Recursive function
In-Class Soln 1. CS 361, Lecture 4. Today s Outline. In-Class Soln 2
 In-Class Soln 1 Let f(n) be an always positive function and let g(n) = f(n) log n. Show that f(n) = o(g(n)) CS 361, Lecture 4 Jared Saia University of New Mexico For any positive constant c, we want to
In-Class Soln 1 Let f(n) be an always positive function and let g(n) = f(n) log n. Show that f(n) = o(g(n)) CS 361, Lecture 4 Jared Saia University of New Mexico For any positive constant c, we want to
The maximum-subarray problem. Given an array of integers, find a contiguous subarray with the maximum sum. Very naïve algorithm:
 The maximum-subarray problem Given an array of integers, find a contiguous subarray with the maximum sum. Very naïve algorithm: Brute force algorithm: At best, θ(n 2 ) time complexity 129 Can we do divide
The maximum-subarray problem Given an array of integers, find a contiguous subarray with the maximum sum. Very naïve algorithm: Brute force algorithm: At best, θ(n 2 ) time complexity 129 Can we do divide
CS 161 Summer 2009 Homework #2 Sample Solutions
 CS 161 Summer 2009 Homework #2 Sample Solutions Regrade Policy: If you believe an error has been made in the grading of your homework, you may resubmit it for a regrade. If the error consists of more than
CS 161 Summer 2009 Homework #2 Sample Solutions Regrade Policy: If you believe an error has been made in the grading of your homework, you may resubmit it for a regrade. If the error consists of more than
CS 4407 Algorithms Lecture 2: Iterative and Divide and Conquer Algorithms
 CS 4407 Algorithms Lecture 2: Iterative and Divide and Conquer Algorithms Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline CS 4407, Algorithms Growth Functions
CS 4407 Algorithms Lecture 2: Iterative and Divide and Conquer Algorithms Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline CS 4407, Algorithms Growth Functions
1 Substitution method
 Recurrence Relations we have discussed asymptotic analysis of algorithms and various properties associated with asymptotic notation. As many algorithms are recursive in nature, it is natural to analyze
Recurrence Relations we have discussed asymptotic analysis of algorithms and various properties associated with asymptotic notation. As many algorithms are recursive in nature, it is natural to analyze
Divide and Conquer. Arash Rafiey. 27 October, 2016
 27 October, 2016 Divide the problem into a number of subproblems Divide the problem into a number of subproblems Conquer the subproblems by solving them recursively or if they are small, there must be
27 October, 2016 Divide the problem into a number of subproblems Divide the problem into a number of subproblems Conquer the subproblems by solving them recursively or if they are small, there must be
When we use asymptotic notation within an expression, the asymptotic notation is shorthand for an unspecified function satisfying the relation:
 CS 124 Section #1 Big-Oh, the Master Theorem, and MergeSort 1/29/2018 1 Big-Oh Notation 1.1 Definition Big-Oh notation is a way to describe the rate of growth of functions. In CS, we use it to describe
CS 124 Section #1 Big-Oh, the Master Theorem, and MergeSort 1/29/2018 1 Big-Oh Notation 1.1 Definition Big-Oh notation is a way to describe the rate of growth of functions. In CS, we use it to describe
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 4 - Jan. 10, 2018 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. 1 /
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 4 - Jan. 10, 2018 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. 1 /
Data Structures and Algorithms Chapter 3
 1 Data Structures and Algorithms Chapter 3 Werner Nutt 2 Acknowledgments The course follows the book Introduction to Algorithms, by Cormen, Leiserson, Rivest and Stein, MIT Press [CLRST]. Many examples
1 Data Structures and Algorithms Chapter 3 Werner Nutt 2 Acknowledgments The course follows the book Introduction to Algorithms, by Cormen, Leiserson, Rivest and Stein, MIT Press [CLRST]. Many examples
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 4 - Jan. 14, 2019 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. COMP
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 4 - Jan. 14, 2019 CLRS 1.1, 1.2, 2.2, 3.1, 4.3, 4.5 University of Manitoba Picture is from the cover of the textbook CLRS. COMP
Analysis of Algorithms Review
 COMP171 Fall 2005 Analysis of Algorithms Review Adapted from Notes of S. Sarkar of UPenn, Skiena of Stony Brook, etc. Introduction to Analysis of Algorithms / Slide 2 Outline Why Does Growth Rate Matter?
COMP171 Fall 2005 Analysis of Algorithms Review Adapted from Notes of S. Sarkar of UPenn, Skiena of Stony Brook, etc. Introduction to Analysis of Algorithms / Slide 2 Outline Why Does Growth Rate Matter?
CS 5321: Advanced Algorithms - Recurrence. Acknowledgement. Outline. Ali Ebnenasir Department of Computer Science Michigan Technological University
 CS 5321: Advanced Algorithms - Recurrence Ali Ebnenasir Department of Computer Science Michigan Technological University Acknowledgement Eric Torng Moon Jung Chung Charles Ofria Outline Motivating example:
CS 5321: Advanced Algorithms - Recurrence Ali Ebnenasir Department of Computer Science Michigan Technological University Acknowledgement Eric Torng Moon Jung Chung Charles Ofria Outline Motivating example:
Lecture 3. Big-O notation, more recurrences!!
 Lecture 3 Big-O notation, more recurrences!! Announcements! HW1 is posted! (Due Friday) See Piazza for a list of HW clarifications First recitation section was this morning, there s another tomorrow (same
Lecture 3 Big-O notation, more recurrences!! Announcements! HW1 is posted! (Due Friday) See Piazza for a list of HW clarifications First recitation section was this morning, there s another tomorrow (same
CS 5321: Advanced Algorithms Analysis Using Recurrence. Acknowledgement. Outline
 CS 5321: Advanced Algorithms Analysis Using Recurrence Ali Ebnenasir Department of Computer Science Michigan Technological University Acknowledgement Eric Torng Moon Jung Chung Charles Ofria Outline Motivating
CS 5321: Advanced Algorithms Analysis Using Recurrence Ali Ebnenasir Department of Computer Science Michigan Technological University Acknowledgement Eric Torng Moon Jung Chung Charles Ofria Outline Motivating
CSCI Honor seminar in algorithms Homework 2 Solution
 CSCI 493.55 Honor seminar in algorithms Homework 2 Solution Saad Mneimneh Visiting Professor Hunter College of CUNY Problem 1: Rabin-Karp string matching Consider a binary string s of length n and another
CSCI 493.55 Honor seminar in algorithms Homework 2 Solution Saad Mneimneh Visiting Professor Hunter College of CUNY Problem 1: Rabin-Karp string matching Consider a binary string s of length n and another
Practical Session #3 - Recursions
 Practical Session #3 - Recursions Substitution method Guess the form of the solution and prove it by induction Iteration Method Convert the recurrence into a summation and solve it Tightly bound a recurrence
Practical Session #3 - Recursions Substitution method Guess the form of the solution and prove it by induction Iteration Method Convert the recurrence into a summation and solve it Tightly bound a recurrence
CIS 121. Analysis of Algorithms & Computational Complexity. Slides based on materials provided by Mary Wootters (Stanford University)
 CIS 121 Analysis of Algorithms & Computational Complexity Slides based on materials provided by Mary Wootters (Stanford University) Today Sorting: InsertionSort vs MergeSort Analyzing the correctness of
CIS 121 Analysis of Algorithms & Computational Complexity Slides based on materials provided by Mary Wootters (Stanford University) Today Sorting: InsertionSort vs MergeSort Analyzing the correctness of
Lecture 1: Asymptotics, Recurrences, Elementary Sorting
 Lecture 1: Asymptotics, Recurrences, Elementary Sorting Instructor: Outline 1 Introduction to Asymptotic Analysis Rate of growth of functions Comparing and bounding functions: O, Θ, Ω Specifying running
Lecture 1: Asymptotics, Recurrences, Elementary Sorting Instructor: Outline 1 Introduction to Asymptotic Analysis Rate of growth of functions Comparing and bounding functions: O, Θ, Ω Specifying running
CSCI 3110 Assignment 6 Solutions
 CSCI 3110 Assignment 6 Solutions December 5, 2012 2.4 (4 pts) Suppose you are choosing between the following three algorithms: 1. Algorithm A solves problems by dividing them into five subproblems of half
CSCI 3110 Assignment 6 Solutions December 5, 2012 2.4 (4 pts) Suppose you are choosing between the following three algorithms: 1. Algorithm A solves problems by dividing them into five subproblems of half
More Asymptotic Analysis Spring 2018 Discussion 8: March 6, 2018
 CS 61B More Asymptotic Analysis Spring 2018 Discussion 8: March 6, 2018 Here is a review of some formulas that you will find useful when doing asymptotic analysis. ˆ N i=1 i = 1 + 2 + 3 + 4 + + N = N(N+1)
CS 61B More Asymptotic Analysis Spring 2018 Discussion 8: March 6, 2018 Here is a review of some formulas that you will find useful when doing asymptotic analysis. ˆ N i=1 i = 1 + 2 + 3 + 4 + + N = N(N+1)
CS 310 Advanced Data Structures and Algorithms
 CS 310 Advanced Data Structures and Algorithms Runtime Analysis May 31, 2017 Tong Wang UMass Boston CS 310 May 31, 2017 1 / 37 Topics Weiss chapter 5 What is algorithm analysis Big O, big, big notations
CS 310 Advanced Data Structures and Algorithms Runtime Analysis May 31, 2017 Tong Wang UMass Boston CS 310 May 31, 2017 1 / 37 Topics Weiss chapter 5 What is algorithm analysis Big O, big, big notations
Chapter 4. Recurrences
 Chapter 4. Recurrences Outline Offers three methods for solving recurrences, that is for obtaining asymptotic bounds on the solution In the substitution method, we guess a bound and then use mathematical
Chapter 4. Recurrences Outline Offers three methods for solving recurrences, that is for obtaining asymptotic bounds on the solution In the substitution method, we guess a bound and then use mathematical
b + O(n d ) where a 1, b > 1, then O(n d log n) if a = b d d ) if a < b d O(n log b a ) if a > b d
 CS161, Lecture 4 Median, Selection, and the Substitution Method Scribe: Albert Chen and Juliana Cook (2015), Sam Kim (2016), Gregory Valiant (2017) Date: January 23, 2017 1 Introduction Last lecture, we
CS161, Lecture 4 Median, Selection, and the Substitution Method Scribe: Albert Chen and Juliana Cook (2015), Sam Kim (2016), Gregory Valiant (2017) Date: January 23, 2017 1 Introduction Last lecture, we
Solving recurrences. Frequently showing up when analysing divide&conquer algorithms or, more generally, recursive algorithms.
 Solving recurrences Frequently showing up when analysing divide&conquer algorithms or, more generally, recursive algorithms Example: Merge-Sort(A, p, r) 1: if p < r then 2: q (p + r)/2 3: Merge-Sort(A,
Solving recurrences Frequently showing up when analysing divide&conquer algorithms or, more generally, recursive algorithms Example: Merge-Sort(A, p, r) 1: if p < r then 2: q (p + r)/2 3: Merge-Sort(A,
Objective. - mathematical induction, recursive definitions - arithmetic manipulations, series, products
 Recurrences Objective running time as recursive function solve recurrence for order of growth method: substitution method: iteration/recursion tree method: MASTER method prerequisite: - mathematical induction,
Recurrences Objective running time as recursive function solve recurrence for order of growth method: substitution method: iteration/recursion tree method: MASTER method prerequisite: - mathematical induction,
i=1 i B[i] B[i] + A[i, j]; c n for j n downto i + 1 do c n i=1 (n i) C[i] C[i] + A[i, j]; c n
![i=1 i B[i] B[i] + A[i, j]; c n for j n downto i + 1 do c n i=1 (n i) C[i] C[i] + A[i, j]; c n i=1 i B[i] B[i] + A[i, j]; c n for j n downto i + 1 do c n i=1 (n i) C[i] C[i] + A[i, j]; c n](/thumbs/76/73723628.jpg) Fundamental Algorithms Homework #1 Set on June 25, 2009 Due on July 2, 2009 Problem 1. [15 pts] Analyze the worst-case time complexity of the following algorithms,and give tight bounds using the Theta
Fundamental Algorithms Homework #1 Set on June 25, 2009 Due on July 2, 2009 Problem 1. [15 pts] Analyze the worst-case time complexity of the following algorithms,and give tight bounds using the Theta
A design paradigm. Divide and conquer: (When) does decomposing a problem into smaller parts help? 09/09/ EECS 3101
 A design paradigm Divide and conquer: (When) does decomposing a problem into smaller parts help? 09/09/17 112 Multiplying complex numbers (from Jeff Edmonds slides) INPUT: Two pairs of integers, (a,b),
A design paradigm Divide and conquer: (When) does decomposing a problem into smaller parts help? 09/09/17 112 Multiplying complex numbers (from Jeff Edmonds slides) INPUT: Two pairs of integers, (a,b),
What we have learned What is algorithm Why study algorithm The time and space efficiency of algorithm The analysis framework of time efficiency Asympt
 Lecture 3 The Analysis of Recursive Algorithm Efficiency What we have learned What is algorithm Why study algorithm The time and space efficiency of algorithm The analysis framework of time efficiency
Lecture 3 The Analysis of Recursive Algorithm Efficiency What we have learned What is algorithm Why study algorithm The time and space efficiency of algorithm The analysis framework of time efficiency
An analogy from Calculus: limits
 COMP 250 Fall 2018 35 - big O Nov. 30, 2018 We have seen several algorithms in the course, and we have loosely characterized their runtimes in terms of the size n of the input. We say that the algorithm
COMP 250 Fall 2018 35 - big O Nov. 30, 2018 We have seen several algorithms in the course, and we have loosely characterized their runtimes in terms of the size n of the input. We say that the algorithm
Asymptotic Analysis and Recurrences
 Appendix A Asymptotic Analysis and Recurrences A.1 Overview We discuss the notion of asymptotic analysis and introduce O, Ω, Θ, and o notation. We then turn to the topic of recurrences, discussing several
Appendix A Asymptotic Analysis and Recurrences A.1 Overview We discuss the notion of asymptotic analysis and introduce O, Ω, Θ, and o notation. We then turn to the topic of recurrences, discussing several
Computational Complexity - Pseudocode and Recursions
 Computational Complexity - Pseudocode and Recursions Nicholas Mainardi 1 Dipartimento di Elettronica e Informazione Politecnico di Milano nicholas.mainardi@polimi.it June 6, 2018 1 Partly Based on Alessandro
Computational Complexity - Pseudocode and Recursions Nicholas Mainardi 1 Dipartimento di Elettronica e Informazione Politecnico di Milano nicholas.mainardi@polimi.it June 6, 2018 1 Partly Based on Alessandro
Algorithms, Design and Analysis. Order of growth. Table 2.1. Big-oh. Asymptotic growth rate. Types of formulas for basic operation count
 Types of formulas for basic operation count Exact formula e.g., C(n) = n(n-1)/2 Algorithms, Design and Analysis Big-Oh analysis, Brute Force, Divide and conquer intro Formula indicating order of growth
Types of formulas for basic operation count Exact formula e.g., C(n) = n(n-1)/2 Algorithms, Design and Analysis Big-Oh analysis, Brute Force, Divide and conquer intro Formula indicating order of growth
CSE332: Data Structures & Parallelism Lecture 2: Algorithm Analysis. Ruth Anderson Winter 2019
 CSE332: Data Structures & Parallelism Lecture 2: Algorithm Analysis Ruth Anderson Winter 2019 Today Algorithm Analysis What do we care about? How to compare two algorithms Analyzing Code Asymptotic Analysis
CSE332: Data Structures & Parallelism Lecture 2: Algorithm Analysis Ruth Anderson Winter 2019 Today Algorithm Analysis What do we care about? How to compare two algorithms Analyzing Code Asymptotic Analysis
CS 4104 Data and Algorithm Analysis. Recurrence Relations. Modeling Recursive Function Cost. Solving Recurrences. Clifford A. Shaffer.
 Department of Computer Science Virginia Tech Blacksburg, Virginia Copyright c 2010,2017 by Clifford A. Shaffer Data and Algorithm Analysis Title page Data and Algorithm Analysis Clifford A. Shaffer Spring
Department of Computer Science Virginia Tech Blacksburg, Virginia Copyright c 2010,2017 by Clifford A. Shaffer Data and Algorithm Analysis Title page Data and Algorithm Analysis Clifford A. Shaffer Spring
Data Structures and Algorithms CSE 465
 Data Structures and Algorithms CSE 465 LECTURE 3 Asymptotic Notation O-, Ω-, Θ-, o-, ω-notation Divide and Conquer Merge Sort Binary Search Sofya Raskhodnikova and Adam Smith /5/0 Review Questions If input
Data Structures and Algorithms CSE 465 LECTURE 3 Asymptotic Notation O-, Ω-, Θ-, o-, ω-notation Divide and Conquer Merge Sort Binary Search Sofya Raskhodnikova and Adam Smith /5/0 Review Questions If input
CS2223 Algorithms D Term 2009 Exam 3 Solutions
 CS2223 Algorithms D Term 2009 Exam 3 Solutions May 4, 2009 By Prof. Carolina Ruiz Dept. of Computer Science WPI PROBLEM 1: Asymptoptic Growth Rates (10 points) Let A and B be two algorithms with runtimes
CS2223 Algorithms D Term 2009 Exam 3 Solutions May 4, 2009 By Prof. Carolina Ruiz Dept. of Computer Science WPI PROBLEM 1: Asymptoptic Growth Rates (10 points) Let A and B be two algorithms with runtimes
EECS 477: Introduction to algorithms. Lecture 5
 EECS 477: Introduction to algorithms. Lecture 5 Prof. Igor Guskov guskov@eecs.umich.edu September 19, 2002 1 Lecture outline Asymptotic notation: applies to worst, best, average case performance, amortized
EECS 477: Introduction to algorithms. Lecture 5 Prof. Igor Guskov guskov@eecs.umich.edu September 19, 2002 1 Lecture outline Asymptotic notation: applies to worst, best, average case performance, amortized
Algorithm Analysis Recurrence Relation. Chung-Ang University, Jaesung Lee
 Algorithm Analysis Recurrence Relation Chung-Ang University, Jaesung Lee Recursion 2 Recursion 3 Recursion in Real-world Fibonacci sequence = + Initial conditions: = 0 and = 1. = + = + = + 0, 1, 1, 2,
Algorithm Analysis Recurrence Relation Chung-Ang University, Jaesung Lee Recursion 2 Recursion 3 Recursion in Real-world Fibonacci sequence = + Initial conditions: = 0 and = 1. = + = + = + 0, 1, 1, 2,
Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort
 Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort Xi Chen Columbia University We continue with two more asymptotic notation: o( ) and ω( ). Let f (n) and g(n) are functions that map
Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort Xi Chen Columbia University We continue with two more asymptotic notation: o( ) and ω( ). Let f (n) and g(n) are functions that map
Methods for solving recurrences
 Methods for solving recurrences Analyzing the complexity of mergesort The merge function Consider the following implementation: 1 int merge ( int v1, int n1, int v, int n ) { 3 int r = malloc ( ( n1+n
Methods for solving recurrences Analyzing the complexity of mergesort The merge function Consider the following implementation: 1 int merge ( int v1, int n1, int v, int n ) { 3 int r = malloc ( ( n1+n
CSE 373: Data Structures and Algorithms Pep Talk; Algorithm Analysis. Riley Porter Winter 2017
 CSE 373: Data Structures and Algorithms Pep Talk; Algorithm Analysis Riley Porter Announcements Op4onal Java Review Sec4on: PAA A102 Tuesday, January 10 th, 3:30-4:30pm. Any materials covered will be posted
CSE 373: Data Structures and Algorithms Pep Talk; Algorithm Analysis Riley Porter Announcements Op4onal Java Review Sec4on: PAA A102 Tuesday, January 10 th, 3:30-4:30pm. Any materials covered will be posted
CSE332: Data Structures & Parallelism Lecture 2: Algorithm Analysis. Ruth Anderson Winter 2018
 CSE332: Data Structures & Parallelism Lecture 2: Algorithm Analysis Ruth Anderson Winter 2018 Today Algorithm Analysis What do we care about? How to compare two algorithms Analyzing Code Asymptotic Analysis
CSE332: Data Structures & Parallelism Lecture 2: Algorithm Analysis Ruth Anderson Winter 2018 Today Algorithm Analysis What do we care about? How to compare two algorithms Analyzing Code Asymptotic Analysis
Divide and Conquer Algorithms. CSE 101: Design and Analysis of Algorithms Lecture 14
 Divide and Conquer Algorithms CSE 101: Design and Analysis of Algorithms Lecture 14 CSE 101: Design and analysis of algorithms Divide and conquer algorithms Reading: Sections 2.3 and 2.4 Homework 6 will
Divide and Conquer Algorithms CSE 101: Design and Analysis of Algorithms Lecture 14 CSE 101: Design and analysis of algorithms Divide and conquer algorithms Reading: Sections 2.3 and 2.4 Homework 6 will
Math 391: Midterm 1.0 Spring 2016
 Math 391: Midterm 1.0 Spring 2016 James Skon skonjp@kenyon.edu Test date: October 5 Submission Instructions: Give all your assumptions. Show all your work. Be as complete as possible. Grading Problem 1
Math 391: Midterm 1.0 Spring 2016 James Skon skonjp@kenyon.edu Test date: October 5 Submission Instructions: Give all your assumptions. Show all your work. Be as complete as possible. Grading Problem 1
Lecture 3: Big-O and Big-Θ
 Lecture 3: Big-O and Big-Θ COSC4: Algorithms and Data Structures Brendan McCane Department of Computer Science, University of Otago Landmark functions We saw that the amount of work done by Insertion Sort,
Lecture 3: Big-O and Big-Θ COSC4: Algorithms and Data Structures Brendan McCane Department of Computer Science, University of Otago Landmark functions We saw that the amount of work done by Insertion Sort,
CS/SE 2C03. Sample solutions to the assignment 1.
 CS/SE 2C03. Sample solutions to the assignment 1. Total of this assignment is 131pts, but 100% = 111pts. There are 21 bonus points. Each assignment is worth 7%. If you think your solution has been marked
CS/SE 2C03. Sample solutions to the assignment 1. Total of this assignment is 131pts, but 100% = 111pts. There are 21 bonus points. Each assignment is worth 7%. If you think your solution has been marked
data structures and algorithms lecture 2
 data structures and algorithms 2018 09 06 lecture 2 recall: insertion sort Algorithm insertionsort(a, n): for j := 2 to n do key := A[j] i := j 1 while i 1 and A[i] > key do A[i + 1] := A[i] i := i 1 A[i
data structures and algorithms 2018 09 06 lecture 2 recall: insertion sort Algorithm insertionsort(a, n): for j := 2 to n do key := A[j] i := j 1 while i 1 and A[i] > key do A[i + 1] := A[i] i := i 1 A[i
CSE332: Data Structures & Parallelism Lecture 2: Algorithm Analysis. Ruth Anderson Winter 2018
 CSE332: Data Structures & Parallelism Lecture 2: Algorithm Analysis Ruth Anderson Winter 2018 Today Algorithm Analysis What do we care about? How to compare two algorithms Analyzing Code Asymptotic Analysis
CSE332: Data Structures & Parallelism Lecture 2: Algorithm Analysis Ruth Anderson Winter 2018 Today Algorithm Analysis What do we care about? How to compare two algorithms Analyzing Code Asymptotic Analysis
MIDTERM I CMPS Winter 2013 Warmuth
 test I 1 MIDTERM I CMPS 101 - Winter 2013 Warmuth With Solutions NAME: Student ID: This exam is closed book, notes, computer and cell phone. Show partial solutions to get partial credit. Make sure you
test I 1 MIDTERM I CMPS 101 - Winter 2013 Warmuth With Solutions NAME: Student ID: This exam is closed book, notes, computer and cell phone. Show partial solutions to get partial credit. Make sure you
Recommended readings: Description of Quicksort in my notes, Ch7 of your CLRS text.
 Chapter 1 Quicksort 1.1 Prerequisites You need to be familiar with the divide-and-conquer paradigm, standard notations for expressing the time-complexity of an algorithm, like the big-oh, big-omega notations.
Chapter 1 Quicksort 1.1 Prerequisites You need to be familiar with the divide-and-conquer paradigm, standard notations for expressing the time-complexity of an algorithm, like the big-oh, big-omega notations.
Asymptotic Analysis. Thomas A. Anastasio. January 7, 2004
 Asymptotic Analysis Thomas A. Anastasio January 7, 004 1 Introduction As a programmer, you often have a choice of data structures and algorithms. Choosing the best one for a particular job involves, among
Asymptotic Analysis Thomas A. Anastasio January 7, 004 1 Introduction As a programmer, you often have a choice of data structures and algorithms. Choosing the best one for a particular job involves, among
CS 344 Design and Analysis of Algorithms. Tarek El-Gaaly Course website:
 CS 344 Design and Analysis of Algorithms Tarek El-Gaaly tgaaly@cs.rutgers.edu Course website: www.cs.rutgers.edu/~tgaaly/cs344.html Course Outline Textbook: Algorithms by S. Dasgupta, C.H. Papadimitriou,
CS 344 Design and Analysis of Algorithms Tarek El-Gaaly tgaaly@cs.rutgers.edu Course website: www.cs.rutgers.edu/~tgaaly/cs344.html Course Outline Textbook: Algorithms by S. Dasgupta, C.H. Papadimitriou,
When we use asymptotic notation within an expression, the asymptotic notation is shorthand for an unspecified function satisfying the relation:
 CS 124 Section #1 Big-Oh, the Master Theorem, and MergeSort 1/29/2018 1 Big-Oh Notation 1.1 Definition Big-Oh notation is a way to describe the rate of growth of functions. In CS, we use it to describe
CS 124 Section #1 Big-Oh, the Master Theorem, and MergeSort 1/29/2018 1 Big-Oh Notation 1.1 Definition Big-Oh notation is a way to describe the rate of growth of functions. In CS, we use it to describe
Analysis of Algorithms - Using Asymptotic Bounds -
 Analysis of Algorithms - Using Asymptotic Bounds - Andreas Ermedahl MRTC (Mälardalens Real-Time Research Center) andreas.ermedahl@mdh.se Autumn 004 Rehersal: Asymptotic bounds Gives running time bounds
Analysis of Algorithms - Using Asymptotic Bounds - Andreas Ermedahl MRTC (Mälardalens Real-Time Research Center) andreas.ermedahl@mdh.se Autumn 004 Rehersal: Asymptotic bounds Gives running time bounds
CS 577 Introduction to Algorithms: Strassen s Algorithm and the Master Theorem
 CS 577 Introduction to Algorithms: Jin-Yi Cai University of Wisconsin Madison In the last class, we described InsertionSort and showed that its worst-case running time is Θ(n 2 ). Check Figure 2.2 for
CS 577 Introduction to Algorithms: Jin-Yi Cai University of Wisconsin Madison In the last class, we described InsertionSort and showed that its worst-case running time is Θ(n 2 ). Check Figure 2.2 for
Recurrence Relations
 Recurrence Relations Analysis Tools S.V. N. (vishy) Vishwanathan University of California, Santa Cruz vishy@ucsc.edu January 15, 2016 S.V. N. Vishwanathan (UCSC) CMPS101 1 / 29 Recurrences Outline 1 Recurrences
Recurrence Relations Analysis Tools S.V. N. (vishy) Vishwanathan University of California, Santa Cruz vishy@ucsc.edu January 15, 2016 S.V. N. Vishwanathan (UCSC) CMPS101 1 / 29 Recurrences Outline 1 Recurrences
Asymptotic Algorithm Analysis & Sorting
 Asymptotic Algorithm Analysis & Sorting (Version of 5th March 2010) (Based on original slides by John Hamer and Yves Deville) We can analyse an algorithm without needing to run it, and in so doing we can
Asymptotic Algorithm Analysis & Sorting (Version of 5th March 2010) (Based on original slides by John Hamer and Yves Deville) We can analyse an algorithm without needing to run it, and in so doing we can
Data Structures and Algorithms. Asymptotic notation
 Data Structures and Algorithms Asymptotic notation Estimating Running Time Algorithm arraymax executes 7n 1 primitive operations in the worst case. Define: a = Time taken by the fastest primitive operation
Data Structures and Algorithms Asymptotic notation Estimating Running Time Algorithm arraymax executes 7n 1 primitive operations in the worst case. Define: a = Time taken by the fastest primitive operation
Data Structures and Algorithms CMPSC 465
 Data Structures and Algorithms CMPSC 465 LECTURE 9 Solving recurrences Substitution method Adam Smith S. Raskhodnikova and A. Smith; based on slides by E. Demaine and C. Leiserson Review question Draw
Data Structures and Algorithms CMPSC 465 LECTURE 9 Solving recurrences Substitution method Adam Smith S. Raskhodnikova and A. Smith; based on slides by E. Demaine and C. Leiserson Review question Draw
Algorithms Chapter 4 Recurrences
 Algorithms Chapter 4 Recurrences Instructor: Ching Chi Lin 林清池助理教授 chingchi.lin@gmail.com Department of Computer Science and Engineering National Taiwan Ocean University Outline The substitution method
Algorithms Chapter 4 Recurrences Instructor: Ching Chi Lin 林清池助理教授 chingchi.lin@gmail.com Department of Computer Science and Engineering National Taiwan Ocean University Outline The substitution method
Divide and Conquer. CSE21 Winter 2017, Day 9 (B00), Day 6 (A00) January 30,
 Divide and Conquer CSE21 Winter 2017, Day 9 (B00), Day 6 (A00) January 30, 2017 http://vlsicad.ucsd.edu/courses/cse21-w17 Merging sorted lists: WHAT Given two sorted lists a 1 a 2 a 3 a k b 1 b 2 b 3 b
Divide and Conquer CSE21 Winter 2017, Day 9 (B00), Day 6 (A00) January 30, 2017 http://vlsicad.ucsd.edu/courses/cse21-w17 Merging sorted lists: WHAT Given two sorted lists a 1 a 2 a 3 a k b 1 b 2 b 3 b
Analysis of Algorithms
 September 29, 2017 Analysis of Algorithms CS 141, Fall 2017 1 Analysis of Algorithms: Issues Correctness/Optimality Running time ( time complexity ) Memory requirements ( space complexity ) Power I/O utilization
September 29, 2017 Analysis of Algorithms CS 141, Fall 2017 1 Analysis of Algorithms: Issues Correctness/Optimality Running time ( time complexity ) Memory requirements ( space complexity ) Power I/O utilization
Homework 1 Submission
 Homework Submission Sample Solution; Due Date: Thursday, May 4, :59 pm Directions: Your solutions should be typed and submitted as a single pdf on Gradescope by the due date. L A TEX is preferred but not
Homework Submission Sample Solution; Due Date: Thursday, May 4, :59 pm Directions: Your solutions should be typed and submitted as a single pdf on Gradescope by the due date. L A TEX is preferred but not
Exercise Sheet #1 Solutions, Computer Science, A M. Hallett, K. Smith a k n b k = n b + k. a k n b k c 1 n b k. a k n b.
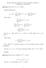 Exercise Sheet #1 Solutions, Computer Science, 308-251A M. Hallett, K. Smith 2002 Question 1.1: Prove (n + a) b = Θ(n b ). Binomial Expansion: Show O(n b ): (n + a) b = For any c 1 > b = O(n b ). Show
Exercise Sheet #1 Solutions, Computer Science, 308-251A M. Hallett, K. Smith 2002 Question 1.1: Prove (n + a) b = Θ(n b ). Binomial Expansion: Show O(n b ): (n + a) b = For any c 1 > b = O(n b ). Show
Taking Stock. IE170: Algorithms in Systems Engineering: Lecture 3. Θ Notation. Comparing Algorithms
 Taking Stock IE170: Algorithms in Systems Engineering: Lecture 3 Jeff Linderoth Department of Industrial and Systems Engineering Lehigh University January 19, 2007 Last Time Lots of funky math Playing
Taking Stock IE170: Algorithms in Systems Engineering: Lecture 3 Jeff Linderoth Department of Industrial and Systems Engineering Lehigh University January 19, 2007 Last Time Lots of funky math Playing
Chapter 4 Divide-and-Conquer
 Chapter 4 Divide-and-Conquer 1 About this lecture (1) Recall the divide-and-conquer paradigm, which we used for merge sort: Divide the problem into a number of subproblems that are smaller instances of
Chapter 4 Divide-and-Conquer 1 About this lecture (1) Recall the divide-and-conquer paradigm, which we used for merge sort: Divide the problem into a number of subproblems that are smaller instances of
CSE 421 Algorithms: Divide and Conquer
 CSE 42 Algorithms: Divide and Conquer Larry Ruzzo Thanks to Richard Anderson, Paul Beame, Kevin Wayne for some slides Outline: General Idea algorithm design paradigms: divide and conquer Review of Merge
CSE 42 Algorithms: Divide and Conquer Larry Ruzzo Thanks to Richard Anderson, Paul Beame, Kevin Wayne for some slides Outline: General Idea algorithm design paradigms: divide and conquer Review of Merge
Data Structures and Algorithms
 Data Structures and Algorithms Spring 2017-2018 Outline 1 Sorting Algorithms (contd.) Outline Sorting Algorithms (contd.) 1 Sorting Algorithms (contd.) Analysis of Quicksort Time to sort array of length
Data Structures and Algorithms Spring 2017-2018 Outline 1 Sorting Algorithms (contd.) Outline Sorting Algorithms (contd.) 1 Sorting Algorithms (contd.) Analysis of Quicksort Time to sort array of length
Algorithms. Adnan YAZICI Dept. of Computer Engineering Middle East Technical Univ. Ankara - TURKEY. Algorihms, A.Yazici, Fall 2007 CEng 315
 Algorithms Adnan YAZICI Dept. of Computer Engineering Middle East Technical Univ. Ankara - TURKEY Algorihms, A.Yazici, Fall 2007 CEng 315 1 Design and Analysis of Algorithms Aspects of studying algorithms:
Algorithms Adnan YAZICI Dept. of Computer Engineering Middle East Technical Univ. Ankara - TURKEY Algorihms, A.Yazici, Fall 2007 CEng 315 1 Design and Analysis of Algorithms Aspects of studying algorithms:
Design Patterns for Data Structures. Chapter 3. Recursive Algorithms
 Chapter 3 Recursive Algorithms Writing recurrences + Writing recurrences To determine the statement execution count is a two-step problem. Write down the recurrence from the recursive code for the algorithm.
Chapter 3 Recursive Algorithms Writing recurrences + Writing recurrences To determine the statement execution count is a two-step problem. Write down the recurrence from the recursive code for the algorithm.
CS 470/570 Divide-and-Conquer. Format of Divide-and-Conquer algorithms: Master Recurrence Theorem (simpler version)
 CS 470/570 Divide-and-Conquer Format of Divide-and-Conquer algorithms: Divide: Split the array or list into smaller pieces Conquer: Solve the same problem recursively on smaller pieces Combine: Build the
CS 470/570 Divide-and-Conquer Format of Divide-and-Conquer algorithms: Divide: Split the array or list into smaller pieces Conquer: Solve the same problem recursively on smaller pieces Combine: Build the
Divide-and-Conquer. a technique for designing algorithms
 Divide-and-Conquer a technique for designing algorithms decomposing instance to be solved into subinstances of the same problem solving each subinstance combining subsolutions to obtain the solution to
Divide-and-Conquer a technique for designing algorithms decomposing instance to be solved into subinstances of the same problem solving each subinstance combining subsolutions to obtain the solution to
CMPT 307 : Divide-and-Conqer (Study Guide) Should be read in conjunction with the text June 2, 2015
 CMPT 307 : Divide-and-Conqer (Study Guide) Should be read in conjunction with the text June 2, 2015 1 Introduction The divide-and-conquer strategy is a general paradigm for algorithm design. This strategy
CMPT 307 : Divide-and-Conqer (Study Guide) Should be read in conjunction with the text June 2, 2015 1 Introduction The divide-and-conquer strategy is a general paradigm for algorithm design. This strategy
Divide and Conquer. Andreas Klappenecker. [based on slides by Prof. Welch]
![Divide and Conquer. Andreas Klappenecker. [based on slides by Prof. Welch] Divide and Conquer. Andreas Klappenecker. [based on slides by Prof. Welch]](/thumbs/84/89083836.jpg) Divide and Conquer Andreas Klappenecker [based on slides by Prof. Welch] Divide and Conquer Paradigm An important general technique for designing algorithms: divide problem into subproblems recursively
Divide and Conquer Andreas Klappenecker [based on slides by Prof. Welch] Divide and Conquer Paradigm An important general technique for designing algorithms: divide problem into subproblems recursively
CS325: Analysis of Algorithms, Fall Midterm
 CS325: Analysis of Algorithms, Fall 2017 Midterm I don t know policy: you may write I don t know and nothing else to answer a question and receive 25 percent of the total points for that problem whereas
CS325: Analysis of Algorithms, Fall 2017 Midterm I don t know policy: you may write I don t know and nothing else to answer a question and receive 25 percent of the total points for that problem whereas
LECTURE NOTES ON DESIGN AND ANALYSIS OF ALGORITHMS
 G.PULLAIAH COLLEGE OF ENGINEERING AND TECHNOLOGY LECTURE NOTES ON DESIGN AND ANALYSIS OF ALGORITHMS Department of Computer Science and Engineering 1 UNIT 1 Basic Concepts Algorithm An Algorithm is a finite
G.PULLAIAH COLLEGE OF ENGINEERING AND TECHNOLOGY LECTURE NOTES ON DESIGN AND ANALYSIS OF ALGORITHMS Department of Computer Science and Engineering 1 UNIT 1 Basic Concepts Algorithm An Algorithm is a finite
MA008/MIIZ01 Design and Analysis of Algorithms Lecture Notes 3
 MA008 p.1/37 MA008/MIIZ01 Design and Analysis of Algorithms Lecture Notes 3 Dr. Markus Hagenbuchner markus@uow.edu.au. MA008 p.2/37 Exercise 1 (from LN 2) Asymptotic Notation When constants appear in exponents
MA008 p.1/37 MA008/MIIZ01 Design and Analysis of Algorithms Lecture Notes 3 Dr. Markus Hagenbuchner markus@uow.edu.au. MA008 p.2/37 Exercise 1 (from LN 2) Asymptotic Notation When constants appear in exponents
Asymptotic Running Time of Algorithms
 Asymptotic Complexity: leading term analysis Asymptotic Running Time of Algorithms Comparing searching and sorting algorithms so far: Count worst-case of comparisons as function of array size. Drop lower-order
Asymptotic Complexity: leading term analysis Asymptotic Running Time of Algorithms Comparing searching and sorting algorithms so far: Count worst-case of comparisons as function of array size. Drop lower-order
Introduction to Divide and Conquer
 Introduction to Divide and Conquer Sorting with O(n log n) comparisons and integer multiplication faster than O(n 2 ) Periklis A. Papakonstantinou York University Consider a problem that admits a straightforward
Introduction to Divide and Conquer Sorting with O(n log n) comparisons and integer multiplication faster than O(n 2 ) Periklis A. Papakonstantinou York University Consider a problem that admits a straightforward
Section 1.8 The Growth of Functions. We quantify the concept that g grows at least as fast as f.
 Section 1.8 The Growth of Functions We quantify the concept that g grows at least as fast as f. What really matters in comparing the complexity of algorithms? We only care about the behavior for large
Section 1.8 The Growth of Functions We quantify the concept that g grows at least as fast as f. What really matters in comparing the complexity of algorithms? We only care about the behavior for large
Divide & Conquer. CS 320, Fall Dr. Geri Georg, Instructor CS320 Div&Conq 1
 Divide & Conquer CS 320, Fall 2017 Dr. Geri Georg, Instructor georg@colostate.edu CS320 Div&Conq 1 Strategy 1. Divide the problem up into equal sized sub problems 2. Solve the sub problems recursively
Divide & Conquer CS 320, Fall 2017 Dr. Geri Georg, Instructor georg@colostate.edu CS320 Div&Conq 1 Strategy 1. Divide the problem up into equal sized sub problems 2. Solve the sub problems recursively
Big O 2/14/13. Administrative. Does it terminate? David Kauchak cs302 Spring 2013
 /4/3 Administrative Big O David Kauchak cs3 Spring 3 l Assignment : how d it go? l Assignment : out soon l CLRS code? l Videos Insertion-sort Insertion-sort Does it terminate? /4/3 Insertion-sort Loop
/4/3 Administrative Big O David Kauchak cs3 Spring 3 l Assignment : how d it go? l Assignment : out soon l CLRS code? l Videos Insertion-sort Insertion-sort Does it terminate? /4/3 Insertion-sort Loop
CPS 616 DIVIDE-AND-CONQUER 6-1
 CPS 616 DIVIDE-AND-CONQUER 6-1 DIVIDE-AND-CONQUER Approach 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances recursively 3. Obtain solution to original (larger)
CPS 616 DIVIDE-AND-CONQUER 6-1 DIVIDE-AND-CONQUER Approach 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances recursively 3. Obtain solution to original (larger)
Divide and Conquer. Andreas Klappenecker
 Divide and Conquer Andreas Klappenecker The Divide and Conquer Paradigm The divide and conquer paradigm is important general technique for designing algorithms. In general, it follows the steps: - divide
Divide and Conquer Andreas Klappenecker The Divide and Conquer Paradigm The divide and conquer paradigm is important general technique for designing algorithms. In general, it follows the steps: - divide
Divide and Conquer. Recurrence Relations
 Divide and Conquer Recurrence Relations Divide-and-Conquer Strategy: Break up problem into parts. Solve each part recursively. Combine solutions to sub-problems into overall solution. 2 MergeSort Mergesort.
Divide and Conquer Recurrence Relations Divide-and-Conquer Strategy: Break up problem into parts. Solve each part recursively. Combine solutions to sub-problems into overall solution. 2 MergeSort Mergesort.
Mathematical Background. Unsigned binary numbers. Powers of 2. Logs and exponents. Mathematical Background. Today, we will review:
 Mathematical Background Mathematical Background CSE 373 Data Structures Today, we will review: Logs and eponents Series Recursion Motivation for Algorithm Analysis 5 January 007 CSE 373 - Math Background
Mathematical Background Mathematical Background CSE 373 Data Structures Today, we will review: Logs and eponents Series Recursion Motivation for Algorithm Analysis 5 January 007 CSE 373 - Math Background
Analysis of Multithreaded Algorithms
 Analysis of Multithreaded Algorithms Marc Moreno Maza University of Western Ontario, London, Ontario (Canada) CS 4435 - CS 9624 (Moreno Maza) Analysis of Multithreaded Algorithms CS 4435 - CS 9624 1 /
Analysis of Multithreaded Algorithms Marc Moreno Maza University of Western Ontario, London, Ontario (Canada) CS 4435 - CS 9624 (Moreno Maza) Analysis of Multithreaded Algorithms CS 4435 - CS 9624 1 /
Divide-and-Conquer. Reading: CLRS Sections 2.3, 4.1, 4.2, 4.3, 28.2, CSE 6331 Algorithms Steve Lai
 Divide-and-Conquer Reading: CLRS Sections 2.3, 4.1, 4.2, 4.3, 28.2, 33.4. CSE 6331 Algorithms Steve Lai Divide and Conquer Given an instance x of a prolem, the method works as follows: divide-and-conquer
Divide-and-Conquer Reading: CLRS Sections 2.3, 4.1, 4.2, 4.3, 28.2, 33.4. CSE 6331 Algorithms Steve Lai Divide and Conquer Given an instance x of a prolem, the method works as follows: divide-and-conquer
Review Of Topics. Review: Induction
 Review Of Topics Asymptotic notation Solving recurrences Sorting algorithms Insertion sort Merge sort Heap sort Quick sort Counting sort Radix sort Medians/order statistics Randomized algorithm Worst-case
Review Of Topics Asymptotic notation Solving recurrences Sorting algorithms Insertion sort Merge sort Heap sort Quick sort Counting sort Radix sort Medians/order statistics Randomized algorithm Worst-case
Section 3.2 The Growth of Functions. We quantify the concept that g grows at least as fast as f.
 Section 3.2 The Growth of Functions We quantify the concept that g grows at least as fast as f. What really matters in comparing the complexity of algorithms? We only care about the behavior for large
Section 3.2 The Growth of Functions We quantify the concept that g grows at least as fast as f. What really matters in comparing the complexity of algorithms? We only care about the behavior for large
Midterm Exam. CS 3110: Design and Analysis of Algorithms. June 20, Group 1 Group 2 Group 3
 Banner ID: Name: Midterm Exam CS 3110: Design and Analysis of Algorithms June 20, 2006 Group 1 Group 2 Group 3 Question 1.1 Question 2.1 Question 3.1 Question 1.2 Question 2.2 Question 3.2 Question 3.3
Banner ID: Name: Midterm Exam CS 3110: Design and Analysis of Algorithms June 20, 2006 Group 1 Group 2 Group 3 Question 1.1 Question 2.1 Question 3.1 Question 1.2 Question 2.2 Question 3.2 Question 3.3
Chapter 5. Divide and Conquer CLRS 4.3. Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved.
 Chapter 5 Divide and Conquer CLRS 4.3 Slides by Kevin Wayne. Copyright 25 Pearson-Addison Wesley. All rights reserved. Divide-and-Conquer Divide-and-conquer. Break up problem into several parts. Solve
Chapter 5 Divide and Conquer CLRS 4.3 Slides by Kevin Wayne. Copyright 25 Pearson-Addison Wesley. All rights reserved. Divide-and-Conquer Divide-and-conquer. Break up problem into several parts. Solve
CSC236H Lecture 2. Ilir Dema. September 19, 2018
 CSC236H Lecture 2 Ilir Dema September 19, 2018 Simple Induction Useful to prove statements depending on natural numbers Define a predicate P(n) Prove the base case P(b) Prove that for all n b, P(n) P(n
CSC236H Lecture 2 Ilir Dema September 19, 2018 Simple Induction Useful to prove statements depending on natural numbers Define a predicate P(n) Prove the base case P(b) Prove that for all n b, P(n) P(n
Search Algorithms. Analysis of Algorithms. John Reif, Ph.D. Prepared by
 Search Algorithms Analysis of Algorithms Prepared by John Reif, Ph.D. Search Algorithms a) Binary Search: average case b) Interpolation Search c) Unbounded Search (Advanced material) Readings Reading Selection:
Search Algorithms Analysis of Algorithms Prepared by John Reif, Ph.D. Search Algorithms a) Binary Search: average case b) Interpolation Search c) Unbounded Search (Advanced material) Readings Reading Selection:
Problem Set 1 Solutions
 Introduction to Algorithms September 24, 2004 Massachusetts Institute of Technology 6.046J/18.410J Professors Piotr Indyk and Charles E. Leiserson Handout 7 Problem Set 1 Solutions Exercise 1-1. Do Exercise
Introduction to Algorithms September 24, 2004 Massachusetts Institute of Technology 6.046J/18.410J Professors Piotr Indyk and Charles E. Leiserson Handout 7 Problem Set 1 Solutions Exercise 1-1. Do Exercise
CS Non-recursive and Recursive Algorithm Analysis
 CS483-04 Non-recursive and Recursive Algorithm Analysis Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 4:30pm - 5:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/
CS483-04 Non-recursive and Recursive Algorithm Analysis Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 4:30pm - 5:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/
Space Complexity of Algorithms
 Space Complexity of Algorithms So far we have considered only the time necessary for a computation Sometimes the size of the memory necessary for the computation is more critical. The amount of memory
Space Complexity of Algorithms So far we have considered only the time necessary for a computation Sometimes the size of the memory necessary for the computation is more critical. The amount of memory
