Baltic Way 2003 Riga, November 2, 2003
|
|
|
- Aubrey Fox
- 6 years ago
- Views:
Transcription
1 altic Way 2003 Riga, November 2, 2003 Problems and solutions. Let Q + be the set of positive rational numbers. Find all functions f : Q + Q + which for all x Q + fulfil () f ( x ) = f (x) (2) ( + x ) f (x) = f (x + ) Solution: Set g(x) = f (x). Function g fulfils (), (2) and g() =. First we prove that if f () g exists then it is unique. We prove that g is uniquely defined on x = p q by induction on max(p, q). If max(p, q) = then x = and g() =. If p = q then x = and g(x) is unique. If p = q then we can assume (according to ()) that p > q. From (2) we get g( p q ) = ( + q p q now give that g( p q )g( p q q ). The induction assumption and max(p, q) > max(p q, q) ) is unique. Define the function g by g( p q ) = pq where p and q are chosen such that gcd(p, q) =. It is easily seen that g fulfils (), (2) and g() =. All functions fulfilling () and (2) are therefore f ( p q ) = apq, where gcd(p, q) = and a Q Prove that any real solution of x 3 + px + q = 0 satisfies the inequality 4qx p 2. Solution: Let x 0 be a root of the qubic, then x 3 + px + q = (x x 0 )(x 2 + ax + b) = x 3 + (a x 0 )x 2 + (b ax 0 )x bx 0. So a = x 0, p = b ax 0 = b x 2 0, q = bx 0. Hence p 2 = b 2 2bx x4 0. Also 4x 0q = 4x 2 0 b. So p2 4x 0 q = b 2 + 2bx x4 0 = (b + x2 0 )2 0. Solution 2: As the equation x 0 x 2 + px + q = 0 has a root (x = x 0 ), we must have D 0 p 2 4qx 0 0. (Also the equation x 2 + px + qx 0 = 0 having the root x = x 2 0 can be considered.) 3. Let x, y and z be positive real numbers such that xyz =. Prove that ( + x)( + y)( + z) 2 ( + 3 y x + 3 z y + 3 x z ). Solution: Put a = bx, b = cy and c = az. The given inequality then takes the form ( + a )( + b )( + c ) b 2 c 2 ( + 3 b c a ac + 2 a 3 ab + 2 ) 3 bc ( = 2 + a + b + c ) 3 3. abc y the AM-GM inequality we have ( + a )( + b )( + c ) b c a = a + b + c + a + b + c a b ( a + b + c ) 3 3 abc + a + b + c c 2 a + b + c 3 abc + 3 = 2 ( + a + b + c 3 abc ).
2 Solution 2: Expanding the left side we obtain x + y + z + x + y + z 2 ( 3 y As 3 y x 3( y + x + ) etc., it suffices to prove that which follows from a + a 2. x + 3 z y + 3 x + y + z + x + y + z 2 3( x + y + z + x + y + z ) + 2, 4. Let a, b, c be positive real numbers. Prove that 2a a 2 + bc + Solution: First we prove that 2b b 2 + ca + x z ). 2c c 2 + ab a bc + b ca + c ab. 2a a 2 + bc 2( b + ), c which is equivalent to 0 b(a c) 2 + c(a b) 2, and therefore holds true. Now we turn to the inequality b + c ( 2a 2 bc + b ca + c ), ab which by multiplying by 2abc is seen to be equivalent to 0 (a b) 2 + (a c) 2. Hence we have proved that Analogously we have 2a a 2 + bc ( 2a 4 bc + b ca + c ). ab 2b b 2 + ca ( 2b 4 ca + c ab + a ), bc 2c c 2 + ab ( 2c 4 ab + a bc + b ) ca and it suffices to sum the above three inequalities. Solution 2: As a 2 + bc 2a bc etc., it is sufficient to prove that + + a bc ac ab bc + b ca + c ab, which can be obtained by inserting a + b + c between the left side and the right side. 5. A sequence (a n ) is defined as follows: a = 2, a 2 = 2, and a n+ = a n a 2 n for n 2. Prove that for every n we have ( + a )( + a 2 ) ( + a n ) < (2 + 2)a a 2 a n. Solution: First we prove inductively that for n, a n = 2 2n 2. We have a = 2 2, a 2 = 2 20 and a n+ = 2 2n 2 (2 2n 3 ) 2 = 2 2n 2 2 2n 2 = 2 2n. 2
3 Since + a = + 2, we must prove, that The right-hand side is equal to ( + a 2 )( + a 3 ) ( + a n ) < 2a 2 a 3 a n. and the left-hand side The proof is complete n 2 = 2 2n ( )( ) ( + 2 2n 2 ) = n 2 = n = 2 2n. 6. Let n 2 and d be integers with d n, and let x, x 2,..., x n be real numbers such that x + x x n = 0. Prove that there are at least ( n d ) choices of d indices i < i 2 < < i d n such that x i + x i2 + + x id 0. Solution: Put m = n/d and [n] = {, 2,..., n}, and consider all partitions [n] = A A 2 A m of [n] into d-element subsets A i, i =, 2,..., m. The number of such partitions is denoted by t. Clearly, there are exactly ( n d ) d-element subsets of [n] each of which occurs in the same number of partitions. Hence, every A [n] with A = d occurs in exactly s := tm/( n d ) partitions. On the other hand, every partition contains at least one d-element set A such that i A x i 0. Consequently, the total number of sets with this property is at least t/s = ( n d )/m = d n (n d ) = (n d ). 7. Let X be a subset of {, 2, 3,..., 0000} with the following property: If a, b X, a = b, then a b / X. What is the maximal number of elements in X? Answer: 990. Solution: If X = {00, 0, 02,..., 9999, 0000}, then for any two selected a and b, a = b, a b 00 0 > 0000, so a b X. So X may have 990 elements. Suppose that x < x 2 < < x k are all elements of X that are less than 00. If there are none of them, no more than 990 numbers can be in the set X. Otherwise, if x = no other number can be in the set X, so suppose x > and consider the pairs 200 x, (200 x ) x 200 x 2, (200 x 2 ) x x k, (200 x k ) x k Clearly x < x 2 < < x k < 00 < 200 x k < 200 x k < < 200 x 2 < 200 x < 200 < (200 x ) x < (200 x 2 ) x 2 < < (200 x k ) x k. So all numbers in these pairs are different and greater than 00. So at most one from each pair is in the set X. Therefore, there are at least k numbers greater than 00 and 99 k numbers less than 00 that are not in the set X, together at least 99 numbers out of 0000 not being in the set X. 3
4 8. There are 2003 pieces of candy on a table. Two players alternately make moves. A move consists of eating one candy or half of the candies on the table (the lesser half if there is an odd number of candies); at least one candy must be eaten at each move. The loser is the one who eats the last candy. Which player the first or the second has a winning strategy? Answer: The second. Solution: Let us prove inductively that for 2n pieces of candy the first player has a winning strategy. For n = it is obvious. Suppose it is true for 2n pieces, and let s consider 2n + 2 pieces. If for 2n + pieces the second is the winner, then the first eats piece and becomes the second in the game starting with 2n + pieces. So suppose that for 2n + pieces the first is the winner. His winning move for 2n + is not eating piece (according to the inductive assumption). So his winning move is to eat n pieces, leaving the second with n + pieces, when the second must lose. ut the first can leave the second with n + pieces from the starting position with 2n + 2 pieces, eating n + pieces; so 2n + 2 is a winning position for the first. Now if there are 2003 pieces of candy on the table, the first must eat either or 00 candies, leaving an even number of candies on the table. So the second player will be the first player in a game with even number of candies and therefore has a winning strategy. In general, if there is an odd number N of candies, write N = 2 m r +, where r is odd. Then the first player wins if m is even, and the second player wins if m is odd: At each move, the player must avoid leaving the other with an even number of candies, so he must eat half of the candies. ut this means that the number of candies descend as 2 m r +, 2 m r +,..., 2r +, r +, and eventually there is an even number of candies. 9. It is known that n is a positive integer, n 44. Ten questions of type Is n smaller than a? are allowed. Answers are given with a delay: The answer to the i th question is given only after the (i + ) st question is asked, i =, 2,..., 9. The answer to the tenth question is given immediately after it is asked. Find a strategy for identifying n. Solution: Let the Fibonacci numbers be denoted F 0 =, F = 2, F 2 = 3 etc. Then F 0 = 44. We will prove by induction on k that using k questions subject to the conditions of the problem, it is possible to determine any positive integer n F k. First, for k = 0 it is trivial, since without asking we know that n =. For k =, we simply ask if n is smaller than 2. For k = 2, we ask if n is smaller than 3 and if n is smaller than 2; from the two answers we can determine n. Now, in general, our first two questions will always be Is n smaller than F k +? and Is n smaller than F k 2 +. We then receive the answer to the first question. As long as we receive affirmative answers to the i st question, the i + st question will be Is n smaller than F k (i+) +?. If at any point, say after asking the j th question, we receive a negative answer to the j st question, we then know that F k (j ) + n F k (j 2), so n is one of F k (j 2) F k (j ) = F k j consecutive integers, and by induction we may determine n using the remaining k j questions. Otherwise, we receive affirmative answers to all the questions, the last being Is n smaller than F k k + = 2? ; so n = in that case. 0. A lattice point in the plane is a point whose coordinates are both integral. The centroid of four points (x i, y i ), i =, 2, 3, 4, is the point ( x +x 2 +x 3 +x 4 4, y +y 2 +y 3 +y 4 4 ). Let n be the largest natural number with the following property: There are n distinct lattice points in the plane such that the centroid of any four of them is not a lattice point. Prove that n = 2. Solution: To prove n 2, we have to show that there are 2 lattice points (x i, y i ), i =, 2,..., 2, such that no four determine a lattice point centroid. This is guaranteed if we just choose the points such that x i 0 (mod 4) for i =,..., 6, x i (mod 4) for 4
5 i = 7,..., 2, y i 0 (mod 4) for i =, 2, 3, 0,, 2, y i (mod 4) for i = 4,..., 9. Now let P i, i =, 2,..., 3, be lattice points. We have to show that some four of them determine a lattice point centroid. First observe that, by the Pigeonhole Principle, among any five of the points we find two such that their x-coordinates as well as their y-coordinates have the same parity. Consequently, among any five of the points there are two whose midpoint is a lattice point. Iterated application of this observation implies that among the 3 points in question we find five disjoint pairs of points whose midpoint is a lattice point. Among these five midpoints we again find two, say M and M, such that their midpoint C is a lattice point. Finally, if M and M are the midpoints of P i P j and P k P l, respectively, {i, j, k, l} {, 2,..., 3}, then C is the centroid of P i, P j, P k, P l.. Is it possible to select 000 points in a plane so that at least 6000 distances between two of them are equal? Answer: Yes. Solution: Let s start with configuration of 4 points and 5 distances equal to d, like in this figure: (α) Now take (α) and two copies of it obtainable by parallel shifts along vectors a and b, a = b = d and ( a, b) = 60. Vectors a and b should be chosen so that no two vertices of (α) and of the two copies coincide. We get 3 4 = 2 points and = 27 distances. Proceeding in the same way, we get gradually 3 2 = 36 points and = 7 distances; 3 36 = 08 points and = 459 distances; 3 08 = 324 points and = 70 distances; = 972 points and = 6075 distances. 2. Let ACD be a square. Let M be an inner point on side C and N be an inner point on side CD with MAN = 45. Prove that the circumcentre of AMN lies on AC. Solution: Draw a circle ω through M, C, N; let it intersect AC at O. We claim that O is the circumcentre of AMN. Clearly MON = 80 MCN = 90. If the radius of ω is R, then OM = 2R sin 45 = R 2; similarly ON = R 2. Hence we get that OM = ON. Then the circle with centre O and radius R 2 will pass through A, since MAN = 2 MON. M d C ω O N A D 3. Let ACD be a rectangle and C = 2 A. Let E be the midpoint of C and P an arbitrary inner point of AD. Let F and G be the feet of perpendiculars drawn correspondingly from A to P and from D to CP. Prove that the points E, F, P, G are concyclic. Solution: From rectangular triangle AP we have P F = A 2 = E 2. Therefore the circumference through F and P touching the line C between and C touches it at E. 5
6 Analogously, the circumference through P and G touching the line C between and C touches it at E. ut there is only one circumference touching C at E and passing through P. E C F G A P D 4. Let AC be an arbitrary triangle and AM, NC, CKA regular triangles outward of AC. Through the midpoint of MN a perpendicular to AC is constructed; similarly through the midpoints of NK resp. KM perpendiculars to A resp. C are constructed. Prove that these three perpendiculars intersect at the same point. Solution: Let O be the midpoint of MN, and let E and F be the midpoints of A and C, respectively. As triangle MC transforms into triangle AN when rotated 60 around we get MC = AN (it is also a well-known fact). Considering now the quadrangles AMN and CMN we get OE = OF (from Eiler s formula a 2 + b 2 + c 2 + d 2 = e 2 + f PQ 2 or otherwise). As EF AC we get from this that the perpendicular to AC through O passes through the circumcentre of EFG, as it is the perpendicular bisector of EF. The same holds for the other two perpendiculars. N M E O F N A G C K First solution Second solution Solution 2: Let us denote the midpoints of the segments MN, NK, KM by, C, A, respectively. It is easy to see that triangle A C is homothetic to triangle NKM via the homothety centered at the intersection of the medians of triangle N MK and dilation 2. The perpendiculars through M, N, K to A, C, CA, respectively, are also the perpendicular bisectors of these sides, so they intersect in the circumcentre of triangle AC. The desired result follows now from the homothety, and we find that that the common point of intersection is the circumcentre of the image of triangle AC under the homothety; that is, the circumcentre of the triangle with vertices the midpoints of the sides A, C, CA. 5. Let P be the intersection point of the diagonals AC and D in a cyclic quadrilateral. A circle through P touches the side CD in the midpoint M of this side and intersects the segments D and AC in the points Q and R, respectively. Let S be a point on the segment D such that S = DQ. The parallel to A through S intersects AC at T. Prove that AT = RC. Solution: With reference to the figure below we have CR CP = DQ DP = CM 2 = DM 2, which is equivalent to RC = DQ DP AT CP. We also have S = AP P = AT AP DQ DQ, so AT = P. Since ACD is cyclic the result now comes from the fact that DP P = AP CP (due to a well-known theorem). M 6 A A C C
7 A D T S P Q R M C 6. Find all pairs of positive integers (a, b) such that a b is a prime and ab is a perfect square. Answer: Pairs (a, b) = (( p+ 2 )2, ( p 2 )2 ), where p is a prime greater than 2. Solution: Let p be a prime such that a b = p and let ab = k 2. Insert a = b + p in the equation ab = k 2. Then which is equivalent to k 2 = (b + p)b = (b + p 2 )2 p2 4 p 2 = (2b + p) 2 4k 2 = (2b + p + 2k)(2b + p 2k). Since 2b + p + 2k > 2b + p 2k and p is a prime, we conclude 2b + p + 2k = p 2 and 2b + p 2k =. y adding these equations we get 2b + p = p2 + 2 and then b = ( p 2 )2, so a = b + p = ( p+ 2 )2. y checking we conclude that all the solutions are (a, b) = (( p+ 2 )2, ( p 2 )2 ) with p a prime greater than 2. Solution 2: Let p be a prime such that a b = p and let ab = k 2. We have (b + p)b = k 2, so gcd(b, b + p) = gcd(b, p) is equal either to or p. If gcd(b, b + p) = p, let b = b p. Then p 2 b (b + ) = k 2, b (b + ) = m 2, but this equation has no solutions. Hence gcd(b, b + p) =, and b = u 2 b + p = v 2 so that p = v 2 u 2 = (v + u)(v u). This in turn implies that v u = and v + u = p, from which we finally obtain a = ( p+) 2, ( 2 b = p ) 2, 2 where p must be an odd prime. 7. All the positive divisors of a positive integer n are stored into an array in increasing order. Mary has to write a program which decides for an arbitrarily chosen divisor d > whether it is a prime. Let n have k divisors not greater than d. Mary claims that it suffices to check divisibility of d by the first k/2 divisors of n: If a divisor of d greater than is found among them, then d is composite, otherwise d is prime. Is Mary right? Answer: Yes, Mary is right. Solution: Let d > be a divisor of n. Suppose Mary s program outputs composite for d. That means it has found a divisor of d greater than. Since d >, the array contains at least 2 divisors of d, namely and d. Thus Mary s program does not check divisibility of d by d (the first half gets complete before reaching d) which means that the divisor found lays strictly between and d. Hence d is composite indeed. Suppose now d being composite. Let p be its smallest prime divisor; then d p p or, equivalently, d p 2. As p is a divisor of n, it occurs in the array. Let a,..., a k all divisors of n smaller than p. Then pa,..., pa k are less than p 2 and hence less than d. 7
8 As a,..., a k are all relatively prime with p, all the numbers pa,..., pa k divide n. The numbers a,..., a k, pa,..., pa k are pairwise different by construction. Thus there are at least 2k + divisors of n not greater than d. So Mary s program checks divisibility of d by at least k + smallest divisors of n, among which it finds p, and outputs composite. 8. Every integer is coloured with exactly one of the colours blue, green, red, yellow. Can this be done in such a way that if a, b, c, d are not all 0 and have the same colour, then 3a 2b = 2c 3d? Answer: Yes. Solution: A colouring with the required property can be defined as follows. For a non-zero integer k let k be the integer uniquely defined by k = 5 m k, where m is a nonnegative integer and 5 k. We also define 0 = 0. Two non-zero integers k, k 2 receive the same colour if and only if k k 2 (mod 5); we assign 0 any colour. Assume a, b, c, d has the same colour and that 3a 2b = 2c 3d, which we rewrite as 3a 2b 2c + 3d = 0. Dividing both sides by the largest power of 5 which simultaneously divides a, b, c, d (this makes sense since not all of a, b, c, d are 0), we obtain 3 5 A a 2 5 b 2 5 C c D d = 0, where A,, C, D are nonnegative integers at least one of which is equal to 0. The above equality implies 3(5 A a + 5 b + 5 C c + 5 D d ) 0 (mod 5). Assume a, b, c, d are all non-zero. Then a b c d 0 (mod 5). This implies 5 A C + 5 D 0 (mod 5) () which is impossible since at least one of the numbers A,, C, D is equal to 0. If one or more of a, b, c, d are 0, we simply omit the corresponding terms from (), and the same conclusion holds. 9. Let a and b be positive integers. Prove that if a 3 + b 3 is the square of an integer, then a + b is not a product of two different prime numbers. Solution: Suppose a + b = pq, where p = q are two prime numbers. We may assume that p = 3. Since a 3 + b 3 = (a + b)(a 2 ab + b 2 ) is a square, the number a 2 ab + b 2 = (a + b) 2 3ab must be divisible by p and q, whence 3ab must be divisible by p and q. ut p = 3, so p a or p b; but p a + b, so p a and p b. Write a = pk, b = pl for some integers k, l. Notice that q = 3, since otherwise, repeating the above argument, we would have q a, q b and a + b > pq). So we have 3p = a + b = p(k + l) and we conclude that a = p, b = 2p or a = 2p, b = p. Then a 3 + b 3 = 9p 3 is obviously not a square, a contradiction. 20. Let n be a positive integer such that the sum of all the positive divisors of n (except n) plus the number of these divisors is equal to n. Prove that n = 2m 2 for some integer m. Solution: Let t < t 2 < < t s be all positive odd divisors of n, and let 2 k be the maximal power of 2 that divides n. Then the full list of divisors of n is the following: t,..., t s, 2t,..., 2t s,..., 2 k t,..., 2 k t s. 8
9 Hence, 2n = (2 k+ )(t + t t s ) + (k + )s. The right-hand side can be even only if both k and s are odd. In this case the number n/2 k has an odd number of divisors and therefore it is equal to a perfect square r 2. Writing k = 2a +, we have n = 2 k r 2 = 2(2 a r) 2. 9
Baltic Way 2008 Gdańsk, November 8, 2008
 Baltic Way 008 Gdańsk, November 8, 008 Problems and solutions Problem 1. Determine all polynomials p(x) with real coefficients such that p((x + 1) ) = (p(x) + 1) and p(0) = 0. Answer: p(x) = x. Solution:
Baltic Way 008 Gdańsk, November 8, 008 Problems and solutions Problem 1. Determine all polynomials p(x) with real coefficients such that p((x + 1) ) = (p(x) + 1) and p(0) = 0. Answer: p(x) = x. Solution:
1. Suppose that a, b, c and d are four different integers. Explain why. (a b)(a c)(a d)(b c)(b d)(c d) a 2 + ab b = 2018.
 New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
The sum x 1 + x 2 + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E): None of the above. How many pairs of positive integers (x, y) are there, those satisfy
 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice questions, stick only the letters (A, B, C, D or E) of your choice. No calculator is allowed.
Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice questions, stick only the letters (A, B, C, D or E) of your choice. No calculator is allowed.
41st International Mathematical Olympiad
 41st International Mathematical Olympiad Taejon, Korea, July 2000 1 Two circles Γ 1 and Γ 2 intersect at M and N Let l be the common tangent to Γ 1 and Γ 2 so that M is closer to l than N is Let l touch
41st International Mathematical Olympiad Taejon, Korea, July 2000 1 Two circles Γ 1 and Γ 2 intersect at M and N Let l be the common tangent to Γ 1 and Γ 2 so that M is closer to l than N is Let l touch
EGMO 2016, Day 1 Solutions. Problem 1. Let n be an odd positive integer, and let x1, x2,..., xn be non-negative real numbers.
 EGMO 2016, Day 1 Solutions Problem 1. Let n be an odd positive integer, and let x1, x2,..., xn be non-negative real numbers. Show that min (x2i + x2i+1 ) max (2xj xj+1 ), j=1,...,n i=1,...,n where xn+1
EGMO 2016, Day 1 Solutions Problem 1. Let n be an odd positive integer, and let x1, x2,..., xn be non-negative real numbers. Show that min (x2i + x2i+1 ) max (2xj xj+1 ), j=1,...,n i=1,...,n where xn+1
Organization Team Team ID#
 1. [4] A random number generator will always output 7. Sam uses this random number generator once. What is the expected value of the output? 2. [4] Let A, B, C, D, E, F be 6 points on a circle in that
1. [4] A random number generator will always output 7. Sam uses this random number generator once. What is the expected value of the output? 2. [4] Let A, B, C, D, E, F be 6 points on a circle in that
1 Hanoi Open Mathematical Competition 2017
 1 Hanoi Open Mathematical Competition 017 1.1 Junior Section Question 1. Suppose x 1, x, x 3 are the roots of polynomial P (x) = x 3 6x + 5x + 1. The sum x 1 + x + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E):
1 Hanoi Open Mathematical Competition 017 1.1 Junior Section Question 1. Suppose x 1, x, x 3 are the roots of polynomial P (x) = x 3 6x + 5x + 1. The sum x 1 + x + x 3 is (A): 4 (B): 6 (C): 8 (D): 14 (E):
(q 1)p q. = 1 (p 1)(q 1).
 altic Way 001 Hamburg, November 4, 001 Problems 1. set of 8 problems was prepared for an examination. Each student was given 3 of them. No two students received more than one common problem. What is the
altic Way 001 Hamburg, November 4, 001 Problems 1. set of 8 problems was prepared for an examination. Each student was given 3 of them. No two students received more than one common problem. What is the
IMO Training Camp Mock Olympiad #2 Solutions
 IMO Training Camp Mock Olympiad #2 Solutions July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the
IMO Training Camp Mock Olympiad #2 Solutions July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the
Olimpiada Matemática de Centroamérica y el Caribe
 Olimpiada Matemática de Centroamérica y el Caribe 1st Centromerican 1999 Problem A1 A, B, C, D, E each has a unique piece of news. They make a series of phone calls to each other. In each call, the caller
Olimpiada Matemática de Centroamérica y el Caribe 1st Centromerican 1999 Problem A1 A, B, C, D, E each has a unique piece of news. They make a series of phone calls to each other. In each call, the caller
XX Asian Pacific Mathematics Olympiad
 XX Asian Pacific Mathematics Olympiad March, 008 Problem 1. Let ABC be a triangle with A < 60. Let X and Y be the points on the sides AB and AC, respectively, such that CA + AX = CB + BX and BA + AY =
XX Asian Pacific Mathematics Olympiad March, 008 Problem 1. Let ABC be a triangle with A < 60. Let X and Y be the points on the sides AB and AC, respectively, such that CA + AX = CB + BX and BA + AY =
2010 Shortlist JBMO - Problems
 Chapter 1 2010 Shortlist JBMO - Problems 1.1 Algebra A1 The real numbers a, b, c, d satisfy simultaneously the equations abc d = 1, bcd a = 2, cda b = 3, dab c = 6. Prove that a + b + c + d 0. A2 Determine
Chapter 1 2010 Shortlist JBMO - Problems 1.1 Algebra A1 The real numbers a, b, c, d satisfy simultaneously the equations abc d = 1, bcd a = 2, cda b = 3, dab c = 6. Prove that a + b + c + d 0. A2 Determine
HANOI OPEN MATHEMATICS COMPETITON PROBLEMS
 HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICS COMPETITON PROBLEMS 2006-2013 HANOI - 2013 Contents 1 Hanoi Open Mathematics Competition 3 1.1 Hanoi Open Mathematics Competition 2006...
HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICS COMPETITON PROBLEMS 2006-2013 HANOI - 2013 Contents 1 Hanoi Open Mathematics Competition 3 1.1 Hanoi Open Mathematics Competition 2006...
CHMMC 2015 Individual Round Problems
 CHMMC 05 Individual Round Problems November, 05 Problem 0.. The following number is the product of the divisors of n. What is n? 6 3 3 Solution.. In general, the product of the divisors of n is n # of
CHMMC 05 Individual Round Problems November, 05 Problem 0.. The following number is the product of the divisors of n. What is n? 6 3 3 Solution.. In general, the product of the divisors of n is n # of
(D) (A) Q.3 To which of the following circles, the line y x + 3 = 0 is normal at the point ? 2 (A) 2
 CIRCLE [STRAIGHT OBJECTIVE TYPE] Q. The line x y + = 0 is tangent to the circle at the point (, 5) and the centre of the circles lies on x y = 4. The radius of the circle is (A) 3 5 (B) 5 3 (C) 5 (D) 5
CIRCLE [STRAIGHT OBJECTIVE TYPE] Q. The line x y + = 0 is tangent to the circle at the point (, 5) and the centre of the circles lies on x y = 4. The radius of the circle is (A) 3 5 (B) 5 3 (C) 5 (D) 5
First selection test. a n = 3n + n 2 1. b n = 2( n 2 + n + n 2 n),
 First selection test Problem. Find the positive real numbers a, b, c which satisfy the inequalities 4(ab + bc + ca) a 2 + b 2 + c 2 3(a 3 + b 3 + c 3 ). Laurenţiu Panaitopol Problem 2. Consider the numbers
First selection test Problem. Find the positive real numbers a, b, c which satisfy the inequalities 4(ab + bc + ca) a 2 + b 2 + c 2 3(a 3 + b 3 + c 3 ). Laurenţiu Panaitopol Problem 2. Consider the numbers
2011 Olympiad Solutions
 011 Olympiad Problem 1 Let A 0, A 1, A,..., A n be nonnegative numbers such that Prove that A 0 A 1 A A n. A i 1 n A n. Note: x means the greatest integer that is less than or equal to x.) Solution: We
011 Olympiad Problem 1 Let A 0, A 1, A,..., A n be nonnegative numbers such that Prove that A 0 A 1 A A n. A i 1 n A n. Note: x means the greatest integer that is less than or equal to x.) Solution: We
CANADIAN MATHEMATICAL OLYMPIAD 2010 PROBLEMS AND SOLUTIONS
 CANADIAN MATHEMATICAL OLYMPIAD 2010 PROBLEMS AND SOLUTIONS (1) For a positive integer n, an n-staircase is a figure consisting of unit squares, with one square in the first row, two squares in the second
CANADIAN MATHEMATICAL OLYMPIAD 2010 PROBLEMS AND SOLUTIONS (1) For a positive integer n, an n-staircase is a figure consisting of unit squares, with one square in the first row, two squares in the second
11 th Philippine Mathematical Olympiad Questions, Answers, and Hints
 view.php3 (JPEG Image, 840x888 pixels) - Scaled (71%) https://mail.ateneo.net/horde/imp/view.php3?mailbox=inbox&inde... 1 of 1 11/5/2008 5:02 PM 11 th Philippine Mathematical Olympiad Questions, Answers,
view.php3 (JPEG Image, 840x888 pixels) - Scaled (71%) https://mail.ateneo.net/horde/imp/view.php3?mailbox=inbox&inde... 1 of 1 11/5/2008 5:02 PM 11 th Philippine Mathematical Olympiad Questions, Answers,
NEW YORK CITY INTERSCHOLASTIC MATHEMATICS LEAGUE Senior A Division CONTEST NUMBER 1
 Senior A Division CONTEST NUMBER 1 PART I FALL 2011 CONTEST 1 TIME: 10 MINUTES F11A1 Larry selects a 13-digit number while David selects a 10-digit number. Let be the number of digits in the product of
Senior A Division CONTEST NUMBER 1 PART I FALL 2011 CONTEST 1 TIME: 10 MINUTES F11A1 Larry selects a 13-digit number while David selects a 10-digit number. Let be the number of digits in the product of
HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS
 HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS HANOI - 2013 Contents 1 Hanoi Open Mathematical Competition 3 1.1 Hanoi Open Mathematical Competition 2006... 3 1.1.1
HANOI MATHEMATICAL SOCIETY NGUYEN VAN MAU HANOI OPEN MATHEMATICAL COMPETITON PROBLEMS HANOI - 2013 Contents 1 Hanoi Open Mathematical Competition 3 1.1 Hanoi Open Mathematical Competition 2006... 3 1.1.1
So, eqn. to the bisector containing (-1, 4) is = x + 27y = 0
 Q.No. The bisector of the acute angle between the lines x - 4y + 7 = 0 and x + 5y - = 0, is: Option x + y - 9 = 0 Option x + 77y - 0 = 0 Option x - y + 9 = 0 Correct Answer L : x - 4y + 7 = 0 L :-x- 5y
Q.No. The bisector of the acute angle between the lines x - 4y + 7 = 0 and x + 5y - = 0, is: Option x + y - 9 = 0 Option x + 77y - 0 = 0 Option x - y + 9 = 0 Correct Answer L : x - 4y + 7 = 0 L :-x- 5y
2007 Shortlist JBMO - Problems
 Chapter 1 007 Shortlist JBMO - Problems 1.1 Algebra A1 Let a be a real positive number such that a 3 = 6(a + 1). Prove that the equation x + ax + a 6 = 0 has no solution in the set of the real number.
Chapter 1 007 Shortlist JBMO - Problems 1.1 Algebra A1 Let a be a real positive number such that a 3 = 6(a + 1). Prove that the equation x + ax + a 6 = 0 has no solution in the set of the real number.
Hanoi Open Mathematical Competition 2017
 Hanoi Open Mathematical Competition 2017 Junior Section Saturday, 4 March 2017 08h30-11h30 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice
Hanoi Open Mathematical Competition 2017 Junior Section Saturday, 4 March 2017 08h30-11h30 Important: Answer to all 15 questions. Write your answers on the answer sheets provided. For the multiple choice
Solutions of APMO 2017
 Solutions of APMO 2017 Problem 1. We call a 5-tuple of integers arrangeable if its elements can be labeled a, b, c, d, e in some order so that a b + c d + e = 29. Determine all 2017-tuples of integers
Solutions of APMO 2017 Problem 1. We call a 5-tuple of integers arrangeable if its elements can be labeled a, b, c, d, e in some order so that a b + c d + e = 29. Determine all 2017-tuples of integers
UNC Charlotte 2005 Comprehensive March 7, 2005
 March 7, 2005 1. The numbers x and y satisfy 2 x = 15 and 15 y = 32. What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D Solution: C. Note that (2 x ) y = 15 y = 32 so 2 xy = 2 5 and
March 7, 2005 1. The numbers x and y satisfy 2 x = 15 and 15 y = 32. What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D Solution: C. Note that (2 x ) y = 15 y = 32 so 2 xy = 2 5 and
First selection test
 First selection test Problem 1. Let ABC be a triangle right at C and consider points D, E on the sides BC, CA, respectively such that BD = AE = k. Lines BE and AC CD AD intersect at point O. Show that
First selection test Problem 1. Let ABC be a triangle right at C and consider points D, E on the sides BC, CA, respectively such that BD = AE = k. Lines BE and AC CD AD intersect at point O. Show that
Hanoi Open Mathematical Olympiad
 HEXAGON inspiring minds always Let x = 6+2 + Hanoi Mathematical Olympiad 202 6 2 Senior Section 20 Find the value of + x x 7 202 2 Arrange the numbers p = 2 2, q =, t = 2 + 2 in increasing order Let ABCD
HEXAGON inspiring minds always Let x = 6+2 + Hanoi Mathematical Olympiad 202 6 2 Senior Section 20 Find the value of + x x 7 202 2 Arrange the numbers p = 2 2, q =, t = 2 + 2 in increasing order Let ABCD
International Mathematical Olympiad. Preliminary Selection Contest 2011 Hong Kong. Outline of Solutions
 International Mathematical Olympiad Preliminary Selection Contest Hong Kong Outline of Solutions Answers:.. 76... 6. 7.. 6.. 6. 6.... 6. 7.. 76. 6. 7 Solutions:. Such fractions include. They can be grouped
International Mathematical Olympiad Preliminary Selection Contest Hong Kong Outline of Solutions Answers:.. 76... 6. 7.. 6.. 6. 6.... 6. 7.. 76. 6. 7 Solutions:. Such fractions include. They can be grouped
2013 IMO Shortlist. a b c d 1
 IMO Shortlist 2013 Algebra A1 A2 Letnbeapositiveintegerandleta 1,...,a n 1 bearbitraryrealnumbers. Define the sequences u 0,...,u n and v 0,...,v n inductively by u 0 = u 1 = v 0 = v 1 = 1, and u k+1 =
IMO Shortlist 2013 Algebra A1 A2 Letnbeapositiveintegerandleta 1,...,a n 1 bearbitraryrealnumbers. Define the sequences u 0,...,u n and v 0,...,v n inductively by u 0 = u 1 = v 0 = v 1 = 1, and u k+1 =
37th United States of America Mathematical Olympiad
 37th United States of America Mathematical Olympiad 1. Prove that for each positive integer n, there are pairwise relatively prime integers k 0, k 1,..., k n, all strictly greater than 1, such that k 0
37th United States of America Mathematical Olympiad 1. Prove that for each positive integer n, there are pairwise relatively prime integers k 0, k 1,..., k n, all strictly greater than 1, such that k 0
15th Bay Area Mathematical Olympiad. BAMO Exam. February 26, Solutions to BAMO-8 and BAMO-12 Problems
 15th Bay Area Mathematical Olympiad BAMO Exam February 26, 2013 Solutions to BAMO-8 and BAMO-12 Problems 1 How many different sets of three points in this equilateral triangular grid are the vertices of
15th Bay Area Mathematical Olympiad BAMO Exam February 26, 2013 Solutions to BAMO-8 and BAMO-12 Problems 1 How many different sets of three points in this equilateral triangular grid are the vertices of
45-th Moldova Mathematical Olympiad 2001
 45-th Moldova Mathematical Olympiad 200 Final Round Chişinǎu, March 2 Grade 7. Prove that y 3 2x+ x 3 2y x 2 + y 2 for any numbers x,y [, 2 3 ]. When does equality occur? 2. Let S(n) denote the sum of
45-th Moldova Mathematical Olympiad 200 Final Round Chişinǎu, March 2 Grade 7. Prove that y 3 2x+ x 3 2y x 2 + y 2 for any numbers x,y [, 2 3 ]. When does equality occur? 2. Let S(n) denote the sum of
2017 Harvard-MIT Mathematics Tournament
 Team Round 1 Let P(x), Q(x) be nonconstant polynomials with real number coefficients. Prove that if P(y) = Q(y) for all real numbers y, then P(x) = Q(x) for all real numbers x. 2 Does there exist a two-variable
Team Round 1 Let P(x), Q(x) be nonconstant polynomials with real number coefficients. Prove that if P(y) = Q(y) for all real numbers y, then P(x) = Q(x) for all real numbers x. 2 Does there exist a two-variable
Singapore International Mathematical Olympiad 2008 Senior Team Training. Take Home Test Solutions. 15x 2 7y 2 = 9 y 2 0 (mod 3) x 0 (mod 3).
 Singapore International Mathematical Olympiad 2008 Senior Team Training Take Home Test Solutions. Show that the equation 5x 2 7y 2 = 9 has no solution in integers. If the equation has a solution in integer,
Singapore International Mathematical Olympiad 2008 Senior Team Training Take Home Test Solutions. Show that the equation 5x 2 7y 2 = 9 has no solution in integers. If the equation has a solution in integer,
1. Let g(x) and h(x) be polynomials with real coefficients such that
 1. Let g(x) and h(x) be polynomials with real coefficients such that g(x)(x 2 3x + 2) = h(x)(x 2 + 3x + 2) and f(x) = g(x)h(x) + (x 4 5x 2 + 4). Prove that f(x) has at least four real roots. 2. Let M be
1. Let g(x) and h(x) be polynomials with real coefficients such that g(x)(x 2 3x + 2) = h(x)(x 2 + 3x + 2) and f(x) = g(x)h(x) + (x 4 5x 2 + 4). Prove that f(x) has at least four real roots. 2. Let M be
Winter Mathematical Competition Varna, February, 9-11, 2007
 Winter Mathematical Competition Varna, February, 9-11, 007 Problem 91 (Peter Boyvalenkov) Find all values of the real parameter p such that the equation x + (p + 1)x + p = has two real distinct roots x
Winter Mathematical Competition Varna, February, 9-11, 007 Problem 91 (Peter Boyvalenkov) Find all values of the real parameter p such that the equation x + (p + 1)x + p = has two real distinct roots x
Solutions and Marking Schemes
 THIRTY FIRST IRISH MATHEMATICAL OLYMPIAD 1. Proposed by Bernd Kreussler. Saturday, 1 May 018 First Paper Solutions and Marking Schemes Mary and Pat play the following number game. Mary picks an initial
THIRTY FIRST IRISH MATHEMATICAL OLYMPIAD 1. Proposed by Bernd Kreussler. Saturday, 1 May 018 First Paper Solutions and Marking Schemes Mary and Pat play the following number game. Mary picks an initial
Solutions. cos ax + cos bx = 0. a sin ax + b sin bx = 0.
 Solutions 85. Find all pairs (a, b) of positive integers with a b for which the system cos ax + cos bx = 0 a sin ax + b sin bx = 0. Solution 1. Suppose that the system is solvable; note that x = 0 is not
Solutions 85. Find all pairs (a, b) of positive integers with a b for which the system cos ax + cos bx = 0 a sin ax + b sin bx = 0. Solution 1. Suppose that the system is solvable; note that x = 0 is not
HMMT November 2012 Saturday 10 November 2012
 HMMT November 01 Saturday 10 November 01 1. [5] 10 total. The prime numbers under 0 are:,, 5, 7, 11, 1, 17, 19,, 9. There are 10 in. [5] 180 Albert s choice of burgers, sides, and drinks are independent
HMMT November 01 Saturday 10 November 01 1. [5] 10 total. The prime numbers under 0 are:,, 5, 7, 11, 1, 17, 19,, 9. There are 10 in. [5] 180 Albert s choice of burgers, sides, and drinks are independent
Problems and Solutions
 46 th Canadian Mathematical Olympiad Wednesday, April 2, 204 Problems and Solutions. Let a, a 2,..., a n be positive real numbers whose product is. Show that the sum a a 2 + + a ( + a )( + a 2 ) + a 3
46 th Canadian Mathematical Olympiad Wednesday, April 2, 204 Problems and Solutions. Let a, a 2,..., a n be positive real numbers whose product is. Show that the sum a a 2 + + a ( + a )( + a 2 ) + a 3
PUTNAM TRAINING EASY PUTNAM PROBLEMS
 PUTNAM TRAINING EASY PUTNAM PROBLEMS (Last updated: September 24, 2018) Remark. This is a list of exercises on Easy Putnam Problems Miguel A. Lerma Exercises 1. 2017-A1. Let S be the smallest set of positive
PUTNAM TRAINING EASY PUTNAM PROBLEMS (Last updated: September 24, 2018) Remark. This is a list of exercises on Easy Putnam Problems Miguel A. Lerma Exercises 1. 2017-A1. Let S be the smallest set of positive
1. Matrices and Determinants
 Important Questions 1. Matrices and Determinants Ex.1.1 (2) x 3x y Find the values of x, y, z if 2x + z 3y w = 0 7 3 2a Ex 1.1 (3) 2x 3x y If 2x + z 3y w = 3 2 find x, y, z, w 4 7 Ex 1.1 (13) 3 7 3 2 Find
Important Questions 1. Matrices and Determinants Ex.1.1 (2) x 3x y Find the values of x, y, z if 2x + z 3y w = 0 7 3 2a Ex 1.1 (3) 2x 3x y If 2x + z 3y w = 3 2 find x, y, z, w 4 7 Ex 1.1 (13) 3 7 3 2 Find
The 3rd Olympiad of Metropolises
 The 3rd Olympiad of Metropolises Day 1. Solutions Problem 1. Solve the system of equations in real numbers: (x 1)(y 1)(z 1) xyz 1, Answer: x 1, y 1, z 1. (x )(y )(z ) xyz. (Vladimir Bragin) Solution 1.
The 3rd Olympiad of Metropolises Day 1. Solutions Problem 1. Solve the system of equations in real numbers: (x 1)(y 1)(z 1) xyz 1, Answer: x 1, y 1, z 1. (x )(y )(z ) xyz. (Vladimir Bragin) Solution 1.
1998 IMO Shortlist BM BN BA BC AB BC CD DE EF BC CA AE EF FD
 IMO Shortlist 1998 Geometry 1 A convex quadrilateral ABCD has perpendicular diagonals. The perpendicular bisectors of the sides AB and CD meet at a unique point P inside ABCD. the quadrilateral ABCD is
IMO Shortlist 1998 Geometry 1 A convex quadrilateral ABCD has perpendicular diagonals. The perpendicular bisectors of the sides AB and CD meet at a unique point P inside ABCD. the quadrilateral ABCD is
2018 LEHIGH UNIVERSITY HIGH SCHOOL MATH CONTEST
 08 LEHIGH UNIVERSITY HIGH SCHOOL MATH CONTEST. A right triangle has hypotenuse 9 and one leg. What is the length of the other leg?. Don is /3 of the way through his run. After running another / mile, he
08 LEHIGH UNIVERSITY HIGH SCHOOL MATH CONTEST. A right triangle has hypotenuse 9 and one leg. What is the length of the other leg?. Don is /3 of the way through his run. After running another / mile, he
1. If two angles of a triangle measure 40 and 80, what is the measure of the other angle of the triangle?
 1 For all problems, NOTA stands for None of the Above. 1. If two angles of a triangle measure 40 and 80, what is the measure of the other angle of the triangle? (A) 40 (B) 60 (C) 80 (D) Cannot be determined
1 For all problems, NOTA stands for None of the Above. 1. If two angles of a triangle measure 40 and 80, what is the measure of the other angle of the triangle? (A) 40 (B) 60 (C) 80 (D) Cannot be determined
Syllabus. + + x + n 1 n. + x + 2
 1. Special Functions This class will cover problems involving algebraic functions other than polynomials, such as square roots, the floor function, and logarithms. Example Problem: Let n be a positive
1. Special Functions This class will cover problems involving algebraic functions other than polynomials, such as square roots, the floor function, and logarithms. Example Problem: Let n be a positive
International Mathematical Olympiad. Preliminary Selection Contest 2017 Hong Kong. Outline of Solutions 5. 3*
 International Mathematical Olympiad Preliminary Selection Contest Hong Kong Outline of Solutions Answers: 06 0000 * 6 97 7 6 8 7007 9 6 0 6 8 77 66 7 7 0 6 7 7 6 8 9 8 0 0 8 *See the remar after the solution
International Mathematical Olympiad Preliminary Selection Contest Hong Kong Outline of Solutions Answers: 06 0000 * 6 97 7 6 8 7007 9 6 0 6 8 77 66 7 7 0 6 7 7 6 8 9 8 0 0 8 *See the remar after the solution
THE UNIVERSITY OF TORONTO UNDERGRADUATE MATHEMATICS COMPETITION. Sunday, March 14, 2004 Time: hours No aids or calculators permitted.
 THE UNIVERSITY OF TORONTO UNDERGRADUATE MATHEMATICS COMPETITION Sunday, March 1, Time: 3 1 hours No aids or calculators permitted. 1. Prove that, for any complex numbers z and w, ( z + w z z + w w z +
THE UNIVERSITY OF TORONTO UNDERGRADUATE MATHEMATICS COMPETITION Sunday, March 1, Time: 3 1 hours No aids or calculators permitted. 1. Prove that, for any complex numbers z and w, ( z + w z z + w w z +
Unofficial Solutions
 Canadian Open Mathematics Challenge 2016 Unofficial Solutions COMC exams from other years, with or without the solutions included, are free to download online. Please visit http://comc.math.ca/2016/practice.html
Canadian Open Mathematics Challenge 2016 Unofficial Solutions COMC exams from other years, with or without the solutions included, are free to download online. Please visit http://comc.math.ca/2016/practice.html
2013 Sharygin Geometry Olympiad
 Sharygin Geometry Olympiad 2013 First Round 1 Let ABC be an isosceles triangle with AB = BC. Point E lies on the side AB, and ED is the perpendicular from E to BC. It is known that AE = DE. Find DAC. 2
Sharygin Geometry Olympiad 2013 First Round 1 Let ABC be an isosceles triangle with AB = BC. Point E lies on the side AB, and ED is the perpendicular from E to BC. It is known that AE = DE. Find DAC. 2
36th United States of America Mathematical Olympiad
 36th United States of America Mathematical Olympiad 1. Let n be a positive integer. Define a sequence by setting a 1 = n and, for each k > 1, letting a k be the unique integer in the range 0 a k k 1 for
36th United States of America Mathematical Olympiad 1. Let n be a positive integer. Define a sequence by setting a 1 = n and, for each k > 1, letting a k be the unique integer in the range 0 a k k 1 for
1 2n. i=1. 2m+1 i = m, while. 2m + 1 = 1. is the best possible for any odd n.
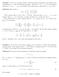 Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
Solutions to CRMO-2003
 Solutions to CRMO-003 1. Let ABC be a triangle in which AB AC and CAB 90. Suppose M and N are points on the hypotenuse BC such that BM + CN MN. Prove that MAN 45. Solution: Draw CP perpendicular to CB
Solutions to CRMO-003 1. Let ABC be a triangle in which AB AC and CAB 90. Suppose M and N are points on the hypotenuse BC such that BM + CN MN. Prove that MAN 45. Solution: Draw CP perpendicular to CB
BRITISH COLUMBIA SECONDARY SCHOOL MATHEMATICS CONTEST,
 BRITISH COLUMBIA SECONDARY SCHOOL MATHEMATICS CONTEST, 014 Solutions Junior Preliminary 1. Rearrange the sum as (014 + 01 + 010 + + ) (013 + 011 + 009 + + 1) = (014 013) + (01 011) + + ( 1) = 1 + 1 + +
BRITISH COLUMBIA SECONDARY SCHOOL MATHEMATICS CONTEST, 014 Solutions Junior Preliminary 1. Rearrange the sum as (014 + 01 + 010 + + ) (013 + 011 + 009 + + 1) = (014 013) + (01 011) + + ( 1) = 1 + 1 + +
= 10 such triples. If it is 5, there is = 1 such triple. Therefore, there are a total of = 46 such triples.
 . Two externally tangent unit circles are constructed inside square ABCD, one tangent to AB and AD, the other to BC and CD. Compute the length of AB. Answer: + Solution: Observe that the diagonal of the
. Two externally tangent unit circles are constructed inside square ABCD, one tangent to AB and AD, the other to BC and CD. Compute the length of AB. Answer: + Solution: Observe that the diagonal of the
HMMT February 2018 February 10, 2018
 HMMT February 018 February 10, 018 Algebra and Number Theory 1. For some real number c, the graphs of the equation y = x 0 + x + 18 and the line y = x + c intersect at exactly one point. What is c? 18
HMMT February 018 February 10, 018 Algebra and Number Theory 1. For some real number c, the graphs of the equation y = x 0 + x + 18 and the line y = x + c intersect at exactly one point. What is c? 18
TARGET : JEE 2013 SCORE. JEE (Advanced) Home Assignment # 03. Kota Chandigarh Ahmedabad
 TARGT : J 01 SCOR J (Advanced) Home Assignment # 0 Kota Chandigarh Ahmedabad J-Mathematics HOM ASSIGNMNT # 0 STRAIGHT OBJCTIV TYP 1. If x + y = 0 is a tangent at the vertex of a parabola and x + y 7 =
TARGT : J 01 SCOR J (Advanced) Home Assignment # 0 Kota Chandigarh Ahmedabad J-Mathematics HOM ASSIGNMNT # 0 STRAIGHT OBJCTIV TYP 1. If x + y = 0 is a tangent at the vertex of a parabola and x + y 7 =
International Mathematics TOURNAMENT OF THE TOWNS
 International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Fall 2011 1 Pete has marked at least 3 points in the plane such that all distances between them are different A pair of marked points
International Mathematics TOURNAMENT OF THE TOWNS Senior A-Level Paper Fall 2011 1 Pete has marked at least 3 points in the plane such that all distances between them are different A pair of marked points
PUTNAM TRAINING NUMBER THEORY. Exercises 1. Show that the sum of two consecutive primes is never twice a prime.
 PUTNAM TRAINING NUMBER THEORY (Last updated: December 11, 2017) Remark. This is a list of exercises on Number Theory. Miguel A. Lerma Exercises 1. Show that the sum of two consecutive primes is never twice
PUTNAM TRAINING NUMBER THEORY (Last updated: December 11, 2017) Remark. This is a list of exercises on Number Theory. Miguel A. Lerma Exercises 1. Show that the sum of two consecutive primes is never twice
Math Day at the Beach 2017 Solutions
 Math Day at the Beach 07 Solutions Mike Bao, Brendan Brzycki, Benjamin Chen, Samuel Cui, Michael Diao, Ayush Kamat, Emma Qin, Jack Sun, Jason Ye, Xuyang Yu, Beckman Math Club Individual Round Problem.
Math Day at the Beach 07 Solutions Mike Bao, Brendan Brzycki, Benjamin Chen, Samuel Cui, Michael Diao, Ayush Kamat, Emma Qin, Jack Sun, Jason Ye, Xuyang Yu, Beckman Math Club Individual Round Problem.
14 th Annual Harvard-MIT Mathematics Tournament Saturday 12 February 2011
 14 th Annual Harvard-MIT Mathematics Tournament Saturday 1 February 011 1. Let a, b, and c be positive real numbers. etermine the largest total number of real roots that the following three polynomials
14 th Annual Harvard-MIT Mathematics Tournament Saturday 1 February 011 1. Let a, b, and c be positive real numbers. etermine the largest total number of real roots that the following three polynomials
International Mathematics TOURNAMENT OF THE TOWNS: SOLUTIONS
 International Mathematics TOURNAMENT OF THE TOWNS: SOLUTIONS Juniors (Grades up to 10) A-Level Paper Spring 2003. 1 Answer: Yes. Example. Consider quadratic equation x 2 + 5x + 6 = 0. It could be transformed
International Mathematics TOURNAMENT OF THE TOWNS: SOLUTIONS Juniors (Grades up to 10) A-Level Paper Spring 2003. 1 Answer: Yes. Example. Consider quadratic equation x 2 + 5x + 6 = 0. It could be transformed
13 th Annual Harvard-MIT Mathematics Tournament Saturday 20 February 2010
 13 th Annual Harvard-MIT Mathematics Tournament Saturday 0 February 010 1. [3] Suppose that x and y are positive reals such that Find x. x y = 3, x + y = 13. 3+ Answer: 17 Squaring both sides of x y =
13 th Annual Harvard-MIT Mathematics Tournament Saturday 0 February 010 1. [3] Suppose that x and y are positive reals such that Find x. x y = 3, x + y = 13. 3+ Answer: 17 Squaring both sides of x y =
Baltic Way 2016 Solutions
 Baltic Way 2016 Solutions 1. Find all pairs of primes (p, q) such that p 3 q 5 =(p + q) 2. Solution. Assume first that neither of the numbers equals 3. Then, if p q mod 3, the left hand side is divisible
Baltic Way 2016 Solutions 1. Find all pairs of primes (p, q) such that p 3 q 5 =(p + q) 2. Solution. Assume first that neither of the numbers equals 3. Then, if p q mod 3, the left hand side is divisible
1. Prove that for every positive integer n there exists an n-digit number divisible by 5 n all of whose digits are odd.
 32 nd United States of America Mathematical Olympiad Proposed Solutions May, 23 Remark: The general philosophy of this marking scheme follows that of IMO 22. This scheme encourages complete solutions.
32 nd United States of America Mathematical Olympiad Proposed Solutions May, 23 Remark: The general philosophy of this marking scheme follows that of IMO 22. This scheme encourages complete solutions.
USA Mathematical Talent Search Round 4 Solutions Year 20 Academic Year
 1/4/20. Consider a sequence {a n } with a 1 = 2 and a n = a2 n 1 a n 2 for all n 3. If we know that a 2 and a 5 are positive integers and a 5 2009, then what are the possible values of a 5? Since a 1 and
1/4/20. Consider a sequence {a n } with a 1 = 2 and a n = a2 n 1 a n 2 for all n 3. If we know that a 2 and a 5 are positive integers and a 5 2009, then what are the possible values of a 5? Since a 1 and
QUESTION BANK ON STRAIGHT LINE AND CIRCLE
 QUESTION BANK ON STRAIGHT LINE AND CIRCLE Select the correct alternative : (Only one is correct) Q. If the lines x + y + = 0 ; 4x + y + 4 = 0 and x + αy + β = 0, where α + β =, are concurrent then α =,
QUESTION BANK ON STRAIGHT LINE AND CIRCLE Select the correct alternative : (Only one is correct) Q. If the lines x + y + = 0 ; 4x + y + 4 = 0 and x + αy + β = 0, where α + β =, are concurrent then α =,
Canadian Open Mathematics Challenge
 The Canadian Mathematical Society in collaboration with The CENTRE for EDUCATION in MATHEMATICS and COMPUTING presents the Canadian Open Mathematics Challenge Wednesday, November, 006 Supported by: Solutions
The Canadian Mathematical Society in collaboration with The CENTRE for EDUCATION in MATHEMATICS and COMPUTING presents the Canadian Open Mathematics Challenge Wednesday, November, 006 Supported by: Solutions
Introduction to Number Theory
 Introduction to Number Theory Paul Yiu Department of Mathematics Florida Atlantic University Spring 017 March 7, 017 Contents 10 Pythagorean and Heron triangles 57 10.1 Construction of Pythagorean triangles....................
Introduction to Number Theory Paul Yiu Department of Mathematics Florida Atlantic University Spring 017 March 7, 017 Contents 10 Pythagorean and Heron triangles 57 10.1 Construction of Pythagorean triangles....................
This class will demonstrate the use of bijections to solve certain combinatorial problems simply and effectively.
 . Induction This class will demonstrate the fundamental problem solving technique of mathematical induction. Example Problem: Prove that for every positive integer n there exists an n-digit number divisible
. Induction This class will demonstrate the fundamental problem solving technique of mathematical induction. Example Problem: Prove that for every positive integer n there exists an n-digit number divisible
USA Mathematical Talent Search Round 3 Solutions Year 20 Academic Year
 1/3/20. Let S be the set of all 10-digit numbers (which by definition may not begin with 0) in which each digit 0 through 9 appears exactly once. For example, the number 3,820,956,714 is in S. A number
1/3/20. Let S be the set of all 10-digit numbers (which by definition may not begin with 0) in which each digit 0 through 9 appears exactly once. For example, the number 3,820,956,714 is in S. A number
Putnam Pigeonhole Principle October 25, 2005
 Putnam Pigeonhole Principle October 5, 005 Introduction 1. If n > m pigeons are placed into m boxes, then there exists (at least) one box with at least two pigeons.. If n > m, then any function f : [n]
Putnam Pigeonhole Principle October 5, 005 Introduction 1. If n > m pigeons are placed into m boxes, then there exists (at least) one box with at least two pigeons.. If n > m, then any function f : [n]
Q.1 If a, b, c are distinct positive real in H.P., then the value of the expression, (A) 1 (B) 2 (C) 3 (D) 4. (A) 2 (B) 5/2 (C) 3 (D) none of these
 Q. If a, b, c are distinct positive real in H.P., then the value of the expression, b a b c + is equal to b a b c () (C) (D) 4 Q. In a triangle BC, (b + c) = a bc where is the circumradius of the triangle.
Q. If a, b, c are distinct positive real in H.P., then the value of the expression, b a b c + is equal to b a b c () (C) (D) 4 Q. In a triangle BC, (b + c) = a bc where is the circumradius of the triangle.
34 th United States of America Mathematical Olympiad
 34 th United States of America Mathematical Olympiad 1. Determine all composite positive integers n for which it is possible to arrange all divisors of n that are greater than 1 in a circle so that no
34 th United States of America Mathematical Olympiad 1. Determine all composite positive integers n for which it is possible to arrange all divisors of n that are greater than 1 in a circle so that no
OLYMON. Produced by the Canadian Mathematical Society and the Department of Mathematics of the University of Toronto. Issue 9:4.
 OLYMON Produced by the Canadian Mathematical Society and the Department of Mathematics of the University of Toronto. Please send your solution to Ms. Valeria Pandelieva 64 Kirkwood Avenue Ottawa, ON KZ
OLYMON Produced by the Canadian Mathematical Society and the Department of Mathematics of the University of Toronto. Please send your solution to Ms. Valeria Pandelieva 64 Kirkwood Avenue Ottawa, ON KZ
Chapter (Circle) * Circle - circle is locus of such points which are at equidistant from a fixed point in
 Chapter - 10 (Circle) Key Concept * Circle - circle is locus of such points which are at equidistant from a fixed point in a plane. * Concentric circle - Circle having same centre called concentric circle.
Chapter - 10 (Circle) Key Concept * Circle - circle is locus of such points which are at equidistant from a fixed point in a plane. * Concentric circle - Circle having same centre called concentric circle.
32 nd United States of America Mathematical Olympiad Recommended Marking Scheme May 1, 2003
 32 nd United States of America Mathematical Olympiad Recommended Marking Scheme May 1, 23 Remark: The general philosophy of this marking scheme follows that of IMO 22. This scheme encourages complete solutions.
32 nd United States of America Mathematical Olympiad Recommended Marking Scheme May 1, 23 Remark: The general philosophy of this marking scheme follows that of IMO 22. This scheme encourages complete solutions.
41st International Mathematical Olympiad
 41st International Mathematical Olympiad Taejon, Korea July 13 25, 2001 Problems Problem 1 A B is tangent to the circles C A M N and N M B D. M lies between C and D on the line C D, and C D is parallel
41st International Mathematical Olympiad Taejon, Korea July 13 25, 2001 Problems Problem 1 A B is tangent to the circles C A M N and N M B D. M lies between C and D on the line C D, and C D is parallel
INTERNATIONAL MATHEMATICAL OLYMPIADS. Hojoo Lee, Version 1.0. Contents 1. Problems 1 2. Answers and Hints References
 INTERNATIONAL MATHEMATICAL OLYMPIADS 1990 2002 Hojoo Lee, Version 1.0 Contents 1. Problems 1 2. Answers and Hints 15 3. References 16 1. Problems 021 Let n be a positive integer. Let T be the set of points
INTERNATIONAL MATHEMATICAL OLYMPIADS 1990 2002 Hojoo Lee, Version 1.0 Contents 1. Problems 1 2. Answers and Hints 15 3. References 16 1. Problems 021 Let n be a positive integer. Let T be the set of points
USA Mathematical Talent Search Round 2 Solutions Year 20 Academic Year
 //0. Sarah and Joe play a standard 3-by-3 game of tic-tac-toe. Sarah goes first and plays X, and Joe goes second and plays O. They alternate turns placing their letter in an empty space, and the first
//0. Sarah and Joe play a standard 3-by-3 game of tic-tac-toe. Sarah goes first and plays X, and Joe goes second and plays O. They alternate turns placing their letter in an empty space, and the first
1983 FG8.1, 1991 HG9, 1996 HG9
 nswers: (1- HKMO Heat Events) reated by: Mr. Francis Hung Last updated: 6 February 017 - Individual 1 11 70 6 1160 7 11 8 80 1 10 1 km 6 11-1 Group 6 7 7 6 8 70 10 Individual Events I1 X is a point on
nswers: (1- HKMO Heat Events) reated by: Mr. Francis Hung Last updated: 6 February 017 - Individual 1 11 70 6 1160 7 11 8 80 1 10 1 km 6 11-1 Group 6 7 7 6 8 70 10 Individual Events I1 X is a point on
Sun Life Financial Canadian Open Mathematics Challenge Section A 4 marks each. Official Solutions
 Sun Life Financial Canadian Open Mathematics Challenge 2015 Official Solutions COMC exams from other years, with or without the solutions included, are free to download online. Please visit http://comc.math.ca/2015/practice.html
Sun Life Financial Canadian Open Mathematics Challenge 2015 Official Solutions COMC exams from other years, with or without the solutions included, are free to download online. Please visit http://comc.math.ca/2015/practice.html
b UVW is a right-angled triangle, therefore VW is the diameter of the circle. Centre of circle = Midpoint of VW = (8 2) + ( 2 6) = 100
 Circles 6F a U(, 8), V(7, 7) and W(, ) UV = ( x x ) ( y y ) = (7 ) (7 8) = 8 VW = ( 7) ( 7) = 64 UW = ( ) ( 8) = 8 Use Pythagoras' theorem to show UV UW = VW 8 8 = 64 = VW Therefore, UVW is a right-angled
Circles 6F a U(, 8), V(7, 7) and W(, ) UV = ( x x ) ( y y ) = (7 ) (7 8) = 8 VW = ( 7) ( 7) = 64 UW = ( ) ( 8) = 8 Use Pythagoras' theorem to show UV UW = VW 8 8 = 64 = VW Therefore, UVW is a right-angled
2016 Canadian Senior Mathematics Contest
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 2016 Canadian Senior Mathematics Contest Wednesday, November 23, 2016 (in North America and South America) Thursday, November 24,
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 2016 Canadian Senior Mathematics Contest Wednesday, November 23, 2016 (in North America and South America) Thursday, November 24,
Logic. Facts (with proofs) CHAPTER 1. Definitions
 CHAPTER 1 Logic Definitions D1. Statements (propositions), compound statements. D2. Truth values for compound statements p q, p q, p q, p q. Truth tables. D3. Converse and contrapositive. D4. Tautologies
CHAPTER 1 Logic Definitions D1. Statements (propositions), compound statements. D2. Truth values for compound statements p q, p q, p q, p q. Truth tables. D3. Converse and contrapositive. D4. Tautologies
27th Russian Mathematics Olympiad
 27th Russian Mathematics Olympiad 10 April 2001 (Communicated by Fedor Petrov) 9 FORM 1. The integers from 1 to 999999 are partioned into two groups: those integers for which the nearest perfect square
27th Russian Mathematics Olympiad 10 April 2001 (Communicated by Fedor Petrov) 9 FORM 1. The integers from 1 to 999999 are partioned into two groups: those integers for which the nearest perfect square
UNC Charlotte 2005 Comprehensive March 7, 2005
 March 7, 2005 1 The numbers x and y satisfy 2 x = 15 and 15 y = 32 What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D 2 Suppose x, y, z, and w are real numbers satisfying x/y = 4/7,
March 7, 2005 1 The numbers x and y satisfy 2 x = 15 and 15 y = 32 What is the value xy? (A) 3 (B) 4 (C) 5 (D) 6 (E) none of A, B, C or D 2 Suppose x, y, z, and w are real numbers satisfying x/y = 4/7,
NMTC IX,X-2018 Bhaskara contest -Junior Level
 NMTC IX,X-2018 Bhaskara contest -Junior Level November 5, 2018 1. ABC is a right triangle with BC hypotenuse. The medians drawn to BC and AC are perpendicular to each other. If AB has length 1 cm, find
NMTC IX,X-2018 Bhaskara contest -Junior Level November 5, 2018 1. ABC is a right triangle with BC hypotenuse. The medians drawn to BC and AC are perpendicular to each other. If AB has length 1 cm, find
Recreational Mathematics
 Recreational Mathematics Paul Yiu Department of Mathematics Florida Atlantic University Summer 2003 Chapters 5 8 Version 030630 Chapter 5 Greatest common divisor 1 gcd(a, b) as an integer combination of
Recreational Mathematics Paul Yiu Department of Mathematics Florida Atlantic University Summer 2003 Chapters 5 8 Version 030630 Chapter 5 Greatest common divisor 1 gcd(a, b) as an integer combination of
NUMBER SYSTEM NATURAL NUMBERS
 NUMBER SYSTEM In Hindu Arabic System, we use ten symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 called digits to represent any number. This is the decimal system where we use the numbers 0 to 9. 0 is called insignificant
NUMBER SYSTEM In Hindu Arabic System, we use ten symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 called digits to represent any number. This is the decimal system where we use the numbers 0 to 9. 0 is called insignificant
2007 Mathematical Olympiad Summer Program Tests
 2007 Mathematical Olympiad Summer Program Tests Edited by Zuming Feng Mathematics Olympiad Summer Program 2007 Tests 1 Practice Test 1 1.1. In triangle ABC three distinct triangles are inscribed, similar
2007 Mathematical Olympiad Summer Program Tests Edited by Zuming Feng Mathematics Olympiad Summer Program 2007 Tests 1 Practice Test 1 1.1. In triangle ABC three distinct triangles are inscribed, similar
VKR Classes TIME BOUND TESTS 1-7 Target JEE ADVANCED For Class XI VKR Classes, C , Indra Vihar, Kota. Mob. No
 VKR Classes TIME BOUND TESTS -7 Target JEE ADVANCED For Class XI VKR Classes, C-9-0, Indra Vihar, Kota. Mob. No. 9890605 Single Choice Question : PRACTICE TEST-. The smallest integer greater than log +
VKR Classes TIME BOUND TESTS -7 Target JEE ADVANCED For Class XI VKR Classes, C-9-0, Indra Vihar, Kota. Mob. No. 9890605 Single Choice Question : PRACTICE TEST-. The smallest integer greater than log +
( 1 ) Show that P ( a, b + c ), Q ( b, c + a ) and R ( c, a + b ) are collinear.
 Problems 01 - POINT Page 1 ( 1 ) Show that P ( a, b + c ), Q ( b, c + a ) and R ( c, a + b ) are collinear. ( ) Prove that the two lines joining the mid-points of the pairs of opposite sides and the line
Problems 01 - POINT Page 1 ( 1 ) Show that P ( a, b + c ), Q ( b, c + a ) and R ( c, a + b ) are collinear. ( ) Prove that the two lines joining the mid-points of the pairs of opposite sides and the line
= 126 possible 5-tuples.
 19th Philippine Mathematical Olympiad 1 January, 017 JUDGES COPY EASY 15 seconds, points 1. If g (x) = x x 5 Answer: 14 Solution: Note that x x and f ( g ( x)) = x, find f (). x 6 = = x = 1. Hence f ()
19th Philippine Mathematical Olympiad 1 January, 017 JUDGES COPY EASY 15 seconds, points 1. If g (x) = x x 5 Answer: 14 Solution: Note that x x and f ( g ( x)) = x, find f (). x 6 = = x = 1. Hence f ()
Individual Round CHMMC November 20, 2016
 Individual Round CHMMC 20 November 20, 20 Problem. We say that d k d k d d 0 represents the number n in base 2 if each d i is either 0 or, and n d k ( 2) k + d k ( 2) k + + d ( 2) + d 0. For example, 0
Individual Round CHMMC 20 November 20, 20 Problem. We say that d k d k d d 0 represents the number n in base 2 if each d i is either 0 or, and n d k ( 2) k + d k ( 2) k + + d ( 2) + d 0. For example, 0
IMO Training Camp Mock Olympiad #2
 IMO Training Camp Mock Olympiad #2 July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the circumcircle
IMO Training Camp Mock Olympiad #2 July 3, 2008 1. Given an isosceles triangle ABC with AB = AC. The midpoint of side BC is denoted by M. Let X be a variable point on the shorter arc MA of the circumcircle
MADHAVA MATHEMATICS COMPETITION, December 2015 Solutions and Scheme of Marking
 MADHAVA MATHEMATICS COMPETITION, December 05 Solutions and Scheme of Marking NB: Part I carries 0 marks, Part II carries 30 marks and Part III carries 50 marks Part I NB Each question in Part I carries
MADHAVA MATHEMATICS COMPETITION, December 05 Solutions and Scheme of Marking NB: Part I carries 0 marks, Part II carries 30 marks and Part III carries 50 marks Part I NB Each question in Part I carries
Official Solutions 2014 Sun Life Financial CMO Qualifying Rêpechage 1
 Official s 2014 Sun Life Financial CMO Qualifying Rêpechage 1 1. Let f : Z Z + be a function, and define h : Z Z Z + by h(x, y) = gcd(f(x), f(y)). If h(x, y) is a two-variable polynomial in x and y, prove
Official s 2014 Sun Life Financial CMO Qualifying Rêpechage 1 1. Let f : Z Z + be a function, and define h : Z Z Z + by h(x, y) = gcd(f(x), f(y)). If h(x, y) is a two-variable polynomial in x and y, prove
