Appendix. A. Simulation study on the effect of aggregate data
|
|
|
- Linette Henry
- 5 years ago
- Views:
Transcription
1 36 Article submitted to Operations Research; manuscript no. Appendix A. Simulation study on the effect of aggregate data One of the main limitations of our data are that they are aggregate at the annual level, which introduces certain difficulties in our analysis and in interpreting our results. For example, we may be underestimating the importance of temporal undercapacity or overcapacity. In order to understand the impact of data aggregation, we conducted a simulation study. In this study we chose a sample of 30 random hospitals from our data set. For each of these hospitals, we had the arrival rate, the number of beds, and the diversion probability, which allowed us to find, the service rate that resulted in the reported diversion probability (using a simple line search). Based on this data, we simulated 12 months of data for this random cohort of 30 EDs. We then estimated an OLS model on the cross-sectional data that represented the monthly average of each hospital. Then, we also estimated a fixed effects model on the panel data (12 observations of 30 hospitals) that accounted for hospital and time fixed effects. The results of this analysis are shown in Table 9. Note that it is not possible to estimate the effect of ED size (REL ED SIZE) in the panel data because the number of ED beds does not vary over time in our simulation and hence is subsumed within the hospital fixed-effect. We find that the interaction effect is significant in panel estimation even though it is not so in the cross-sectional estimation. The coefficient of normalized ICU capacity is higher in absolute magnitude in the cross-sectional estimation but note that it is only at the average value of the relative ED size. In conclusion, based on this simulation study, we believe that our empirical findings will be stronger if a panel dataset is used instead of the cross-sectional dataset. B. Simulation In this section, we simulate the diffusion model described in section 4 to assess the accuracy of the simplifications and approximations made during our analysis in section 5.1. The performance measure of primary interest is the fraction of time on diversion but we also assess the accuracy of the delay probability estimation. We compute the fraction of time on diversion using the two approximations and a discrete-event simulation tool where we vary the size of the hospital and fix the other parameters. We choose our parameter values to roughly match with the median values in our data set. In the validated setting, we assume that K = 7, and N 1 = 15, the arrival rates are λ a = 6, λ w = 12, and λ n = 5, the service times are m 1 = 0.75, and m 2 = 2. We also assume that the likelihood that patients arriving to the emergency department continue to an inpatient department are p a = 0.6 and p w = Table 10 shows the estimates of fraction of time on diversion using both diffusion approximation and simulation, and the difference between along with the estimated traffic intensity level of the inpatient department. First, observe that the accuracy of the approximation is extremely high as long as the traffic intensity of the hospital is high enough. Second, as we fix the arrival rates and the size of the ED, the fraction of time on
2 Article submitted to Operations Research; manuscript no. 37 Table 9 Results of estimating fixed-effect and OLS models on panel and cross-sectional simulated data respectively Panel estimation Cross-sectional estimation INTERCEPT (0.09) (0.12) REL ED SIZE CTR 0.12 (0.04) NORM ICU CAP CTR (0.04) (0.09) REL ED SIZE CTR*NORM ICU CAP CTR 0.11 (0.03) (0.02) CS (0.1) CS (0.11) CS (0.22) CS (0.11) CS (0.11) CS6 0.1 (0.11) CS (0.11) CS (0.12) CS (0.13) CS (0.11) CS (0.11) CS (0.11) CS (0.12) CS (0.13) CS15 0 (0.16) CS (0.14) CS (0.1) CS (0.11) CS (0.14) CS (0.12) CS (0.18) CS (0.1) CS (0.28) CS (0.16) CS (0.16) CS (0.12) CS (0.23) CS (0.14) CS (0.12) TS (0.07) TS (0.07) TS (0.07) TS (0.07) TS (0.07) TS6-0.5 (0.07) TS7-0.4 (0.07) TS (0.07) TS (0.07) TS (0.07) TS (0.07) Notes: Standard Errors are shown in parentheses. Log Likelihood for the LIML estimation method is corresponding to the Probit model for the selection equation. p < 0.01; p < 0.05; p < 0.10 diversion decreases with increasing number of inpatient beds, as estimated by the simulation and computed by the approximation.
3 38 Article submitted to Operations Research; manuscript no. Table 10 Estimation of fraction of time on diversion: approximation vs simulation N ρ 2 Approximation Simulation Difference % % % % % % % Table 11 Estimation delay probability: approximation vs simulation N 1 ρ 1 Approximation Simulation Difference % % % % % % % Next, we validate the accuracy of the delay probability estimates via the diffusion approximation relative to a simulation-based estimation. We fix the parameter as described above. In addition, we fix the number of inpatient beds to N = 18. Table 11 reports, for different sizes of the ED, the delay probability as computed by the diffusion approximation and a discrete-event simulation, as well as the difference between the two estimates. The table also reports the traffic intensity of the emergency department. Again, observe that the accuracy of the delay probability estimate increases as the traffic intensity of the emergency department increases. These results suggest that the series of approximations introduced in Section 4 and the diffusion approximation provide a very good description of the actual dynamics of the original network. We also conducted a numerical study to validate the accuracy of the approximation when varying the threshold level at which the hospital begin diverting ambulances. We fix the parameters described above as well as the ICU size at 18 beds and the ED size at 15 beds. We vary the threshold and compute the delay probability and the diversion probability. Table 12 reports these probabilities as well as the accuracy of the diversion probability approximation. Consistent with our explanation above, as the hospital increases the threshold, the diversion probability decreases, yet the probability of being delayed increases. Lastly, we conducted a numerical study that aimed at testing the sensitivity of the approximation to violation of the condition λ a (1 δ)p a >> λ w p w. We fixed the parameters discussed above as well as the size of the hospital to 30 beds and computed the diversion probability for different values of p w. As we
4 Article submitted to Operations Research; manuscript no. 39 Table 12 Estimation diversion probability, approximation vs simulation, as a function of the boarding-beds-threshold K Delay probability Diversion Approximation Diversion Simulation Difference % % % % % % % Table 13 Estimation diversion probability, approximation vs simulation, as a function of the probability of admitting a walk-in patient p w ρ 2 Approximation Simulation Difference % % % % % % increase the probability above 0.2 the condition is violated. Table 13 reports the comparison between the approximation and the simulation and shows that even when the condition is violated the approximation is still fairly accurate. The main conclusion from this table is that while the assumption is required for the purpose of analytical tractability, even if the condition is not satisfied, the accuracy of the model is quite high. C. Background of heavy traffic theory To illustrate the approach, consider an M/M/s system with arrival rate λ and service rate µ for each server. To derive the heavy traffic limit, we consider a sequence of M/M/n systems, each with service rate µ and indexed by n = 1, 2,.., that satisfies the following conditions: (A1) For the n th system, the number of servers is n and the arrival rate is λ n, where the superscript n denotes the n th system (A2) λ s = λ, i.e., the s th system in the sequence is the original system, and (A3) n(1 ρ n ) β for some constant β as n, where ρ n = λ n /(nµ) is the traffic intensity of the n th system. Condition (A3) is critical and needs more explanation. It states that for large systems, the excess capacity (1 ρ) should be approximately inversely proportional to the square-root of the number of servers. It is not
5 40 Article submitted to Operations Research; manuscript no. only consistent with the common wisdom that the appropriate level of server utilization in service systems should increase with the size of the system but also further specifies that this increases at a rate proportional to the square root of the system size. This condition is also the theoretical underpinning for the famous square-root staffing rule that is used in call center management. Halfin and Whitt (1981) provide theoretical justification for (A3) by showing that the probability of delay is approximately equal for each of the systems in the sequence if and only if this condition is satisfied. If the fraction of excess capacity goes down at a rate faster than 1/ n, then an arriving customer has to wait almost surely. On the other hand, if the fraction of excess capacity goes down at a rate slower than 1/ n, an arriving customer almost never waits. Halfin and Whitt (1981) further show that under condition (A3), in steady state, the normalized queue length Q n ( ) = ( Q n ( ) n ) / n converges to a diffusion process Q( ) in distribution. Therefore, we can approximate Q n ( ) by n Q( ) + n, a property that will be used extensively to characterize the performance measures for the system of our interest. Similar approach can be adopted for an M/M/s/K system (Whitt 2004) by considering the limit of a sequence of systems, each with service rate µ and indexed by n such that: (B1) The n th system is an M/M/n/K n system with arrival rate λ n (B2) λ s = λ and K s = K, i.e., the s th system in the sequence is the original system, and (B3) n(1 ρ n ) β and K n / n κ for some constants β and κ as n. D. Estimation on Delay Probability P d In this section, we derive the function P d (N 1, N 2, β 2, κ) that we use to approximate the delay probability P d. Let ρ 1 denote the traffic intensity of station 1 (the ED). It is clear that ρ 1 = (λ w + (1 δ)λ a )m 1 /(N 1 B). (5) [ Using Proposition ] 1 of Halfin and Whitt (1981), we can approximate the delay probability in the ED by β 1Φ(β 1 ) φ(β 1, where ) β 1 = N 1 B(1 ρ 1 ). (6) Therefore, to obtain an estimate of P d, we need estimates of B, the average number of boarding patients, and ρ 1, the traffic intensity of the ED. We first approximate B using the steady state distribution of Q 2 given in Whitt (2004), B(N 2, β 2, κ) = N 2 1 e κβ 2(1 + κ) β 2 (1 e κβ 2 + β φ(β 2 ) Φ(β 2 ) ) (7)
6 Article submitted to Operations Research; manuscript no. 41 Next, from (5), we can approximate ρ 1 as ρ 1 (N 1, N 2, β 2, κ) = λ a(1 δ(n 2, β 2, κ)) + λ w N 1 B(N m 1, (8) 2, β 2, κ) where δ and B are given in (1) and (7) respectively. [ We can then substitute ] (8) and (7) in (6) to obtain 1 β 1 (N 1, N 2, β 2, κ). And P d (N 1, N 2, β 2, κ) = 1 + β 1 (N 1,N 2,β 2,κ)Φ( β 1 (N 1,N 2,β 2,κ)) φ( β. 1 (N 1,N 2,β 2,κ)) E. Proofs Proof of Proposition 1 To prove result (i), let g 1 (β 2 ) = ( N 2 β 2 )e κβ 2/2 and g 2 (β 2 ) = eκβ 2 /2 e κβ 2 /2. We know that β 2 +e κβ 2 /2 Φ(β 2 ) φ(β 2 ) δ(n 2, β 2, κ) = [g 1 (β 2 )g 2 (β 2 )] 1. Hence, it is sufficient to show that g 1 is nondecreasing and g 2 is increasing in β 2. To show g 1 is nondecreasing, we look at the first order derivative: g 1(β 2 ) =e κβ 2/2 [κ( N 2 β 2 )/2 1] (9) =e κβ 2/2 (Kρ 2 /2 1) 0. (10) For g 2, it is easy to see that e κβ 2/2 Φ(β 2 )/φ(β 2 ) is increasing in β 2. Therefore, it remains to show that g 3 (β 2 ) = (e κβ 2/2 e κβ 2/2 )/β 2 is nondecreasing in β 2. Again, we take the first order derivative: g 3(β 2 ) = [(κβ 2 /2)(e κβ 2/2 + e κβ 2/2 ) e κβ 2/2 + e κβ 2/2 ]/β 2 2 = f(κβ 2 /2)/β 2 2, where f(x) = x(e x + e x ) e x + e x. Obviously f(0) = 0. Moreover f(x) is nondecreasing in x because f (x) = x(e x e x ) 0. Therefore, f(x) 0 for x 0, proving g 3(β 2 ) 0. To prove result (ii), we can rewrite (1) as δ(n 2, β 2, κ) = The result then follows because the function Proof of Proposition 2 We can rewrite equation (7) as B(N 2, β 2, κ) = N 2 ( 1 β 2 κe κβ 2 β 2 ( ( ). N 2 β 2 ) e κβ e κβ 2β2 Φ(β 2 ) φ(β 2 ) ( ) e κβ e κβ Φ(β 2β 2 ) 2 φ(β 2 is increasing in κ. ) (1 e κβ 2 ) ) ( ) β 2 Φ(β 2 ) / 1 +. φ(β 2 )(1 e κβ 2 ) It is easy to see that B is increasing in κ because κe κβ 2 = 1 e κβ 2 κ/(eκβ 2 1) is decreasing in κ. Since δ is decreasing in κ, β 1 is decreasing in κ. Therefore, P d is increasing in κ. Proof of Proposition 3 It is equivalent to show that κ is increasing in N 1. It is easy to see that P d is decreasing in N 1 because, clearly, β 1 is increasing in N 1. Now for any N 1,1 < N 1,2, let κ 1 = κ (N 1,1, N 2, β 2, P d ) and κ 2 = κ (N 1,2, N 2, β 2, P d ). It suffices to show κ 1 < κ 2. Suppose κ 1 κ 2. Because N 1,1 < N 1,2, we have P d (N 1,1, N 2, β 2, P d ) > P d (N 1,2, N 2, β 2, P d ), which contradicts with the fact that P d (N 1,1, N 2, β 2, P d ) = P d (N 1,2, N 2, β 2, P d ) = P d.
7 42 Article submitted to Operations Research; manuscript no. F. Details of the fluid approximation F.1. Diversion Probability Let Q 2 (t) denote the number of patients that have completed service in the ED but are yet to complete service in the inpatient department including the boarding patients (Figure 4(c)). K 0 (< N 2 ) denotes the number of patients in the inpatient department at time 0 and let τ represent the first time that diversion starts, i.e., τ = min{t : Q 2 (t) = N 2 + K}. From t = 0 to t = τ, i.e., when not on diversion, the nominal arrival rate to the inpatient department can be approximated by λ h ap a + λ h wp w since ambulance arrivals receive priority over walk-in arrivals and we assume that λ h ap a >> λ h wp w and N 1 /m 1 > λ h ap a + λ h wp w > N 2 /m 2. Thus, from t = 0 to t = τ, the number of patients in the inpatient department including the boarding patients increase at a rate of r 1 = λ h ap a + λ h wp w N 2 /m 2. Thus, N 2 + K = K 0 + r 1 τ. (11) Next, consider the diversion period, i.e., from t = τ to t = τ. Since the fluid model does not capture individual patient level dynamics, we model diversion as a fraction of ambulances that are not accepted by the ED, using a parameter 0 < δ < 1. Thus, the nominal arrival rate to the inpatient department during diversion is λ h ap a (1 δ ) + λ h wp w. Since Q 2 (t) is equal to N 2 + K at all times during the diversion, the flows in and out of the ED must be balanced. Hence, λ h ap a (1 δ ) + λ h wp w = N 2 /m 2. (12) At time τ, when the peak period ends and arrival rates jump from high to low, the number of patients Q 2 (t) depletes at a rate of r 2 = N 2 /m 2 λ l ap a λ l wp w and drops below N 2 + K thereby ending diversion. Since time T is also time 0 of next decision cycle, Q 2 (T ) = Q 2 (0) = K 0. Note that balancing the flow between times t = τ and t = T, we obtain N 2 + K K 0 = r 2 (T τ). (13) Now, we can approximate the diversion probability as δ = δ (τ τ )/T since the ED diverts a fraction δ of the ambulances during the time between τ and τ. Thus, combining (12), (11) and (13) we have δ = λh ap a + λ h wp w N 2 /m ( 2 λ h ap a 1 (N 2 + K K 0 )(r 1 + r 2 ) r 1 r 2 T While the above is a closed-form expression for the diversion probability δ, it contains several parameters that are not observable in the data. Hence, we use the fact that the utilization of the inpatient department is given by ρ 2 = 1 ( ) (N 2 K 0 ) 2 2r + (N 2 K 0 )2 1 2r 2 T N 2. In addition, we restrict ourselves to analyzing the diversion probability δ for a sequence of hospitals where the arrival rate scales linearly with the size of the inpatient department, i.e., λ j i = β j i N 2, i {a, w}, j {h, l}. ).
8 Article submitted to Operations Research; manuscript no. 43 Making these two substitutions, we obtain: δ = βh a p a + βwp h w 1/m ( 2 2(1 ρ2 ) 1 βa h p a T K ) N 2 T It is clear from the above expression that δ is decreasing in θ 2 = 1 ρ 2 and decreasing in κ = K N 2 where we use κ to distinguish it from κ used in the previous section. Note that if the arrival rate increases less than linearly with the size of the hospital, the diversion probability will tend to zero for very large hospitals. On the other hand, if the arrival rate increases more than linearly with the size of the hospital, the diversion probability will converge to one for very large hospitals. Since we do not observe both of these scenarios in our data, we believe that choosing a linear scaling provides the best explanatory power to the model based on fluid approximation. F.2. Delay Probability Figure 4(d) depicts the build-up and draw-down of the number of patients that have not completed their service in the ED, Q 1 (t). We assume that the day begins with an empty ED, i.e., Q 1 (0) = 0. Before the diversion begins, i.e., from t = 0 to t = τ, the number of patients in the ED builds up since λ h a + λ h w > N 1 /m 1. During diversion, i.e., from t = τ to t = τ, rate of build up (or draw down) changes to λ h w (N 1 K)/m 1 due to simultaneous changes in arrival rate (due to ambulance diversion) and service rate (due to blocking). After diversion, i.e., from t = τ to t = T, the number of patients draws down at the rate of N 1 /m 1 λ a l λ w l until all patients are discharged. Note that in this model, the ED operates under two extreme regimes: arrivals to the ED either surely wait for a bed when Q 1 (t) < N 1 or surely do not wait for the bed when Q 1 (t) > N 1. We define the fraction of time spent in the latter regime as the delay probability for this model. In order to show that an optimal threshold K is increasing in N 1, we make two observations. First, for fixed N 1, an increase in K leads to an increase in the slope of Q 1 (t) during periods of diversion, i.e., from t = τ t = τ thereby increasing Q 1 (t) t > τ and hence increasing the probability of delay. Second, for fixed K, an increase in N 1 leads to a reduction in slope of Q 1 (t) from t = 0 to t = τ and an increase in the slope for t > τ thereby reducing Q 1 (t) t and hence decreasing the probability of delay. Combining the above two arguments, we can see that for a fixed delay probability, the threshold K is increasing in N 1. G. Estimates for alternative specifications This section contains the estimation results for alternate specifications B and C for all three families of models - diffusion, fluid, and basic. These are shown in Tables H. FIML estimates for all models and specifications This section contains the estimation results of various specifications using the Full Information Maximum Likelihood (FIML) method. These are shown in Tables 19 to 21. Here, the likelihood function corresponding to the bivariate normal distribution is constructed and maximized using standard methods to obtain ML estimates. (14)
9 44 Article submitted to Operations Research; manuscript no. Table 14 Estimates for alternate specifications based on diffusion approximation. Standard Errors are shown in parentheses. p < 0.01; p < 0.05; p < Specification B Specification C LEVEL EQUATION INTERCEPT 6.34 (0.83) 6.69 (0.3) REL ED SIZE HT CTR (0.09) (0.06) NORM ICU CAP CTR (0.11) (0.08) (REL ED SIZE HT CTR)*(NORM ICU CAP CTR) (0.04) (0.04) RURAL (1.55) INVESTOR 0.17 (0.76) GOVERNMENT (0.53) INVERSE MILLS RATIO (1.63) (0.54) R F-value CHOICE EQUATION INTERCEPT 0.46 (0.11) 0.47 (0.11) REL ED SIZE HT CTR 0.13 (0.04) NORM ICU CAP CTR (0.06) (REL ED SIZE HT CTR)*(NORM ICU CAP CTR) 0.02 (0.03) RURAL (0.27) (0.26) INVESTOR 0.68 (0.22) 0.5 (0.21) GOVERNMENT (0.3) (0.29) TRAUMA 0.38 (0.23) 0.36 (0.22) Log Likelihood Table 15 Simple slopes for Relative ED size for different values of normalized ICU spare capacity. σ N is the standard deviation of the normalized ICU spare capacity in the sample. Standard Errors are shown in parentheses. p < 0.01; p < 0.05; p < 0.10 Specification B Specification C NORM ICU CAP CTR = -2*σ N 0.13 (0.13) 0.15 (0.12) NORM ICU CAP CTR = (0.11) (0.06) NORM ICU CAP CTR = 2*σ N (0.19) (0.14) I. Results of nonlinear specifications of the basic model This section contains the results for two nonlinear specifications of the basic model shown in Table 22.
10 Article submitted to Operations Research; manuscript no. 45 Table 16 Simple slope for Normalized ICU spare capacity for different values of relative ED size. σ R is the standard deviation of the relative ED size in the sample. Standard Errors are shown in parentheses. p < 0.01; p < 0.05; p < 0.10 Specification B Specification C REL ED SIZE HT CTR = -2*σ R 0.21 (0.21) 0.16 (0.19) REL ED SIZE HT CTR = (0.09) (0.08) REL ED SIZE HT CTR = 2*σ R (0.20) (0.2) Table 17 Estimates for alternate specifications based on fluid approximation. Standard Errors are shown in parentheses. p < 0.01; p < 0.05; p < 0.10 Specification B Specification C LEVEL EQUATION INTERCEPT 6.80 (0.37) 7.32 (0.4) SQRT ICU CAP 0.07 (1.24) (0.41) REL ED SIZE FL (5.05) (2.42) RURAL (1.64) INVESTOR (0.52) GOVERNMENT 0.38 (0.98) INVERSE MILLS RATIO -0.7 (2.23) (0.55) R F-value CHOICE EQUATION INTERCEPT 1.45 (0.24) 0.48 (0.11) SQRT ICU CAP (0.29) REL ED SIZE FL (1.37) RURAL (0.28) (0.26) INVESTOR 0.51 (0.21) 0.45 (0.2) GOVERNMENT -0.6 (0.3) (0.29) TRAUMA 0.20 (0.22) 0.26 (0.21) Log Likelihood
11 46 Article submitted to Operations Research; manuscript no. Table 18 Estimates for alternate specifications based on basic model. Standard Errors are shown in parentheses. p < 0.01; p < 0.05; p < 0.10 Specification B Specification C LEVEL EQUATION INTERCEPT 2.82 (2.00) 5.82 (0.45) ICU CAP 0.79 (0.47) (0.31) ICU SIZE 0.03 (0.01) 0.01 (0.01) ED SIZE 0.04 (0.03) 0.01 (0.01) RURAL (1.5) INVESTOR 0.93 (0.71) GOVERNMENT (0.79) INVERSE MILLS RATIO 2.93 (2.05) (0.53) R F-value CHOICE EQUATION INTERCEPT (0.28) (0.27) ICU CAP 0.49 (0.22) ICU SIZE 0.01 (0.01) ED SIZE 0.03 (0.01) RURAL (0.29) (0.26) INVESTOR 0.75 (0.22) 0.81 (0.22) GOVERNMENT (0.29) (0.30) TRAUMA (0.24) 0.36 (0.22) Log Likelihood
12 Article submitted to Operations Research; manuscript no. 47 Table 19 LEVEL EQUATION INTERCEPT REL ED SIZE HT CTR Estimation results for selection models based on diffusion approximation. Spec A Spec B Spec C 7.33 (0.16) (0.07) NORM ICU CAP CTR 0.01 (0.10) (REL ED SIZE HT CTR)*(NORM ICU CAP CTR) (0.04) 7.40 (0.19) (0.07) (0.10) (0.05) RURAL 1.11 (0.56) INVESTOR (0.35) GOVERNMENT 0.69 (0.59) CHOICE EQUATION INTERCEPT 0.55 (0.08) REL ED SIZE HT CTR 0.08 (0.13) NORM ICU CAP CTR (0.04) (REL ED SIZE HT CTR)*(NORM ICU CAP CTR) 0.03 (0.02) RURAL (0.04) INVESTOR GOVERNMENT (0.04) (0.03) TRAUMA 0.11 (0.08) 0.51 (0.10) 0.08 (0.04) (0.05) 0.03 (0.03) (0.24) 0.23 (0.16) (0.26) 0.08 (0.15) 7.35 (0.15) (0.05) (0.03) (0.02) 0.47 (0.09) (0.04) (0.03) (0.02) 0.15 (0.18) Log Likelihood Notes: Standard Errors are shown in parentheses. Log Likelihood for the LIML estimation method is corresponding to the Probit model for the selection equation. p < 0.01; p < 0.05; p < 0.10
13 48 Article submitted to Operations Research; manuscript no. Table 20 LEVEL EQUATION Estimation results for selection models based on fluid approximation. Specification A Specification B Specification C INTERCEPT 6.3 (0.37) 6.5 (0.38) 7.73 (0.31) SQRT ICU CAP 1.55 (0.47) 1.37 (0.47) 0.04 (0.13) REL ED SIZE FL 4.04 (2.61) 2.85 (2.54) (0.06) RURAL 1.08 (0.57) INVESTOR (0.33) GOVERNMENT 0.69 (0.58) CHOICE EQUATION INTERCEPT 1.08 (0.17) 1.07 (0.18) 0.44 (0.09) SQRT ICU CAP (0.2) (0.22) REL ED SIZE FL (1.3) (1.15) RURAL -0.2 (0.17) (0.25) (0.06) INVESTOR (0.05) 0.21 (0.15) (0.06) GOVERNMENT (0.06) (0.26) 0.31 (0.16) TRAUMA 0.23 (0.12) 0.2 (0.07) (0.03) Log Likelihood Notes: Standard Errors are shown in parentheses. Log Likelihood for the LIML estimation method is corresponding to the Probit model for the selection equation. p < 0.01; p < 0.05; p < 0.10
14 Article submitted to Operations Research; manuscript no. 49 Table 21 LEVEL EQUATION Estimation results for selection models based on the basic model. Specification A Specification B Specification C INTERCEPT 7.44 (0.5) 5.21 (0.64) 7.19 (0.17) ICU CAP -0.1 (0.37) 0.46 (0.31) (0.08) ICU SIZE 0.01 (0.01) 0.02 (0.01) 0.00 (0.01) ED SIZE (0.02) 0.01 (0.02) 0.00 (0.01) RURAL (0.76) (0.24) INVESTOR 0.13 (0.34) GOVERNMENT 0.2 (0.61) CHOICE EQUATION INTERCEPT (0.24) (0.28) (0.24) ICU CAP 0.32 (0.19) (0.29) ICU SIZE 0 (0.01) 0.05 (0.25) ED SIZE 0.02 (0.01) 0.79 (0.22) RURAL -0.6 (0.23) (0.29) (0.04) INVESTOR 0.17 (0.19) 0.45 (0.22) 0.18 (0.19) GOVERNMENT (0.19) 0.01 (0.01) (0.19) TRAUMA (0.17) 0.03 (0.01) 0.01 (0.06) Log Likelihood Notes: Standard Errors are shown in parentheses. Log Likelihood for the LIML estimation method is corresponding to the Probit model for the selection equation. p < 0.01; p < 0.05; p < 0.10
15 50 Article submitted to Operations Research; manuscript no. Table 22 Two non-linear specifications of the basic model LEVEL EQUATION INTERCEPT 5.48 (0.72) 6.02 (0.64) ICU CAP 0.42 (0.35) 0.15 (0.47) ED SIZE (0.01) (0.01) ICU SIZE (0.02) ICU SIZE*ICU CAP 0.02 (0.03) SQRT ICU SIZE 0.16 (0.1) LAMBDA (0.57) (0.54) CHOICE EQUATION INTERCEPT (0.36) (0.3) ICU CAP 0.61 (0.23) 0.08 (0.3) ED SIZE 0.03 (0.01) 0.03 (0.01) ICU SIZE (0.01) ICU SIZE*ICU CAP 0.06 (0.02) SQRT ICU SIZE 0.11 (0.08) TRAUMA 0.06 (0.25) (0.26) INVESTOR 0.82 (0.22) 0.87 (0.23) GOVERNMENT (0.3) (0.3) RURAL (0.29) (0.29)
Dynamic Control of Parallel-Server Systems
 Dynamic Control of Parallel-Server Systems Jim Dai Georgia Institute of Technology Tolga Tezcan University of Illinois at Urbana-Champaign May 13, 2009 Jim Dai (Georgia Tech) Many-Server Asymptotic Optimality
Dynamic Control of Parallel-Server Systems Jim Dai Georgia Institute of Technology Tolga Tezcan University of Illinois at Urbana-Champaign May 13, 2009 Jim Dai (Georgia Tech) Many-Server Asymptotic Optimality
Economy of Scale in Multiserver Service Systems: A Retrospective. Ward Whitt. IEOR Department. Columbia University
 Economy of Scale in Multiserver Service Systems: A Retrospective Ward Whitt IEOR Department Columbia University Ancient Relics A. K. Erlang (1924) On the rational determination of the number of circuits.
Economy of Scale in Multiserver Service Systems: A Retrospective Ward Whitt IEOR Department Columbia University Ancient Relics A. K. Erlang (1924) On the rational determination of the number of circuits.
A Fluid Approximation for Service Systems Responding to Unexpected Overloads
 Submitted to Operations Research manuscript 28-9-55.R2, Longer Online Version 6/28/1 A Fluid Approximation for Service Systems Responding to Unexpected Overloads Ohad Perry Centrum Wiskunde & Informatica
Submitted to Operations Research manuscript 28-9-55.R2, Longer Online Version 6/28/1 A Fluid Approximation for Service Systems Responding to Unexpected Overloads Ohad Perry Centrum Wiskunde & Informatica
Routing and Staffing in Large-Scale Service Systems: The Case of Homogeneous Impatient Customers and Heterogeneous Servers 1
 Routing and Staffing in Large-Scale Service Systems: The Case of Homogeneous Impatient Customers and Heterogeneous Servers 1 Mor Armony 2 Avishai Mandelbaum 3 June 25, 2008 Abstract Motivated by call centers,
Routing and Staffing in Large-Scale Service Systems: The Case of Homogeneous Impatient Customers and Heterogeneous Servers 1 Mor Armony 2 Avishai Mandelbaum 3 June 25, 2008 Abstract Motivated by call centers,
Lecture 9: Deterministic Fluid Models and Many-Server Heavy-Traffic Limits. IEOR 4615: Service Engineering Professor Whitt February 19, 2015
 Lecture 9: Deterministic Fluid Models and Many-Server Heavy-Traffic Limits IEOR 4615: Service Engineering Professor Whitt February 19, 2015 Outline Deterministic Fluid Models Directly From Data: Cumulative
Lecture 9: Deterministic Fluid Models and Many-Server Heavy-Traffic Limits IEOR 4615: Service Engineering Professor Whitt February 19, 2015 Outline Deterministic Fluid Models Directly From Data: Cumulative
Class 11 Non-Parametric Models of a Service System; GI/GI/1, GI/GI/n: Exact & Approximate Analysis.
 Service Engineering Class 11 Non-Parametric Models of a Service System; GI/GI/1, GI/GI/n: Exact & Approximate Analysis. G/G/1 Queue: Virtual Waiting Time (Unfinished Work). GI/GI/1: Lindley s Equations
Service Engineering Class 11 Non-Parametric Models of a Service System; GI/GI/1, GI/GI/n: Exact & Approximate Analysis. G/G/1 Queue: Virtual Waiting Time (Unfinished Work). GI/GI/1: Lindley s Equations
State Space Collapse in Many-Server Diffusion Limits of Parallel Server Systems. J. G. Dai. Tolga Tezcan
 State Space Collapse in Many-Server Diffusion imits of Parallel Server Systems J. G. Dai H. Milton Stewart School of Industrial and Systems Engineering, Georgia Institute of Technology, Atlanta, Georgia
State Space Collapse in Many-Server Diffusion imits of Parallel Server Systems J. G. Dai H. Milton Stewart School of Industrial and Systems Engineering, Georgia Institute of Technology, Atlanta, Georgia
Overflow Networks: Approximations and Implications to Call-Center Outsourcing
 Overflow Networks: Approximations and Implications to Call-Center Outsourcing Itai Gurvich (Northwestern University) Joint work with Ohad Perry (CWI) Call Centers with Overflow λ 1 λ 2 Source of complexity:
Overflow Networks: Approximations and Implications to Call-Center Outsourcing Itai Gurvich (Northwestern University) Joint work with Ohad Perry (CWI) Call Centers with Overflow λ 1 λ 2 Source of complexity:
Electronic Companion Fluid Models for Overloaded Multi-Class Many-Server Queueing Systems with FCFS Routing
 Submitted to Management Science manuscript MS-251-27 Electronic Companion Fluid Models for Overloaded Multi-Class Many-Server Queueing Systems with FCFS Routing Rishi Talreja, Ward Whitt Department of
Submitted to Management Science manuscript MS-251-27 Electronic Companion Fluid Models for Overloaded Multi-Class Many-Server Queueing Systems with FCFS Routing Rishi Talreja, Ward Whitt Department of
Online Supplement to Delay-Based Service Differentiation with Many Servers and Time-Varying Arrival Rates
 Online Supplement to Delay-Based Service Differentiation with Many Servers and Time-Varying Arrival Rates Xu Sun and Ward Whitt Department of Industrial Engineering and Operations Research, Columbia University
Online Supplement to Delay-Based Service Differentiation with Many Servers and Time-Varying Arrival Rates Xu Sun and Ward Whitt Department of Industrial Engineering and Operations Research, Columbia University
Erlang-C = M/M/N. agents. queue ACD. arrivals. busy ACD. queue. abandonment BACK FRONT. lost calls. arrivals. lost calls
 Erlang-C = M/M/N agents arrivals ACD queue Erlang-A lost calls FRONT BACK arrivals busy ACD queue abandonment lost calls Erlang-C = M/M/N agents arrivals ACD queue Rough Performance Analysis
Erlang-C = M/M/N agents arrivals ACD queue Erlang-A lost calls FRONT BACK arrivals busy ACD queue abandonment lost calls Erlang-C = M/M/N agents arrivals ACD queue Rough Performance Analysis
Online Supplement to Creating Work Breaks From Available Idleness
 Online Supplement to Creating Work Breaks From Available Idleness Xu Sun and Ward Whitt Department of Industrial Engineering and Operations Research, Columbia University New York, NY, 127 June 3, 217 1
Online Supplement to Creating Work Breaks From Available Idleness Xu Sun and Ward Whitt Department of Industrial Engineering and Operations Research, Columbia University New York, NY, 127 June 3, 217 1
Online Supplement to Creating Work Breaks From Available Idleness
 Online Supplement to Creating Work Breaks From Available Idleness Xu Sun and Ward Whitt Department of Industrial Engineering and Operations Research, Columbia University New York, NY, 127 September 7,
Online Supplement to Creating Work Breaks From Available Idleness Xu Sun and Ward Whitt Department of Industrial Engineering and Operations Research, Columbia University New York, NY, 127 September 7,
Service-Level Differentiation in Many-Server Service Systems Via Queue-Ratio Routing
 Submitted to Operations Research manuscript (Please, provide the mansucript number!) Service-Level Differentiation in Many-Server Service Systems Via Queue-Ratio Routing Itay Gurvich Kellogg School of
Submitted to Operations Research manuscript (Please, provide the mansucript number!) Service-Level Differentiation in Many-Server Service Systems Via Queue-Ratio Routing Itay Gurvich Kellogg School of
Dynamic Call Center Routing Policies Using Call Waiting and Agent Idle Times Online Supplement
 Submitted to imanufacturing & Service Operations Management manuscript MSOM-11-370.R3 Dynamic Call Center Routing Policies Using Call Waiting and Agent Idle Times Online Supplement (Authors names blinded
Submitted to imanufacturing & Service Operations Management manuscript MSOM-11-370.R3 Dynamic Call Center Routing Policies Using Call Waiting and Agent Idle Times Online Supplement (Authors names blinded
Queueing Theory I Summary! Little s Law! Queueing System Notation! Stationary Analysis of Elementary Queueing Systems " M/M/1 " M/M/m " M/M/1/K "
 Queueing Theory I Summary Little s Law Queueing System Notation Stationary Analysis of Elementary Queueing Systems " M/M/1 " M/M/m " M/M/1/K " Little s Law a(t): the process that counts the number of arrivals
Queueing Theory I Summary Little s Law Queueing System Notation Stationary Analysis of Elementary Queueing Systems " M/M/1 " M/M/m " M/M/1/K " Little s Law a(t): the process that counts the number of arrivals
Online Supplement: Managing Hospital Inpatient Bed Capacity through Partitioning Care into Focused Wings
 Online Supplement: Managing Hospital Inpatient Bed Capacity through Partitioning Care into Focused Wings Thomas J. Best, Burhaneddin Sandıkçı, Donald D. Eisenstein University of Chicago Booth School of
Online Supplement: Managing Hospital Inpatient Bed Capacity through Partitioning Care into Focused Wings Thomas J. Best, Burhaneddin Sandıkçı, Donald D. Eisenstein University of Chicago Booth School of
Design, staffing and control of large service systems: The case of a single customer class and multiple server types. April 2, 2004 DRAFT.
 Design, staffing and control of large service systems: The case of a single customer class and multiple server types. Mor Armony 1 Avishai Mandelbaum 2 April 2, 2004 DRAFT Abstract Motivated by modern
Design, staffing and control of large service systems: The case of a single customer class and multiple server types. Mor Armony 1 Avishai Mandelbaum 2 April 2, 2004 DRAFT Abstract Motivated by modern
Stein s Method for Steady-State Approximations: Error Bounds and Engineering Solutions
 Stein s Method for Steady-State Approximations: Error Bounds and Engineering Solutions Jim Dai Joint work with Anton Braverman and Jiekun Feng Cornell University Workshop on Congestion Games Institute
Stein s Method for Steady-State Approximations: Error Bounds and Engineering Solutions Jim Dai Joint work with Anton Braverman and Jiekun Feng Cornell University Workshop on Congestion Games Institute
We consider how two networked large-scale service systems that normally operate separately, such as call
 MANAGEMENT SCIENCE Vol. 55, No. 8, August 2009, pp. 1353 1367 issn 0025-1909 eissn 1526-5501 09 5508 1353 informs doi 10.1287/mnsc.1090.1025 2009 INFORMS Responding to Unexpected Overloads in Large-Scale
MANAGEMENT SCIENCE Vol. 55, No. 8, August 2009, pp. 1353 1367 issn 0025-1909 eissn 1526-5501 09 5508 1353 informs doi 10.1287/mnsc.1090.1025 2009 INFORMS Responding to Unexpected Overloads in Large-Scale
A Fluid Approximation for Service Systems Responding to Unexpected Overloads
 OPERATIONS RESEARCH Vol. 59, No. 5, September October 2011, pp. 1159 1170 issn 0030-364X eissn 1526-5463 11 5905 1159 http://dx.doi.org/10.1287/opre.1110.0985 2011 INFORMS A Fluid Approximation for Service
OPERATIONS RESEARCH Vol. 59, No. 5, September October 2011, pp. 1159 1170 issn 0030-364X eissn 1526-5463 11 5905 1159 http://dx.doi.org/10.1287/opre.1110.0985 2011 INFORMS A Fluid Approximation for Service
Dynamic Control of a Tandem Queueing System with Abandonments
 Dynamic Control of a Tandem Queueing System with Abandonments Gabriel Zayas-Cabán 1 Jungui Xie 2 Linda V. Green 3 Mark E. Lewis 1 1 Cornell University Ithaca, NY 2 University of Science and Technology
Dynamic Control of a Tandem Queueing System with Abandonments Gabriel Zayas-Cabán 1 Jungui Xie 2 Linda V. Green 3 Mark E. Lewis 1 1 Cornell University Ithaca, NY 2 University of Science and Technology
Other properties of M M 1
 Other properties of M M 1 Přemysl Bejda premyslbejda@gmail.com 2012 Contents 1 Reflected Lévy Process 2 Time dependent properties of M M 1 3 Waiting times and queue disciplines in M M 1 Contents 1 Reflected
Other properties of M M 1 Přemysl Bejda premyslbejda@gmail.com 2012 Contents 1 Reflected Lévy Process 2 Time dependent properties of M M 1 3 Waiting times and queue disciplines in M M 1 Contents 1 Reflected
BRAVO for QED Queues
 1 BRAVO for QED Queues Yoni Nazarathy, The University of Queensland Joint work with Daryl J. Daley, The University of Melbourne, Johan van Leeuwaarden, EURANDOM, Eindhoven University of Technology. Applied
1 BRAVO for QED Queues Yoni Nazarathy, The University of Queensland Joint work with Daryl J. Daley, The University of Melbourne, Johan van Leeuwaarden, EURANDOM, Eindhoven University of Technology. Applied
IOE 202: lectures 11 and 12 outline
 IOE 202: lectures 11 and 12 outline Announcements Last time... Queueing models intro Performance characteristics of a queueing system Steady state analysis of an M/M/1 queueing system Other queueing systems,
IOE 202: lectures 11 and 12 outline Announcements Last time... Queueing models intro Performance characteristics of a queueing system Steady state analysis of an M/M/1 queueing system Other queueing systems,
Data analytics in the practice of Emergency Medicine
 Data analytics in the practice of Emergency Medicine Devashish Das Industrial and Management Systems Engineering University of South Florida November 16, 2018 Outline Healthcare systems engineering in
Data analytics in the practice of Emergency Medicine Devashish Das Industrial and Management Systems Engineering University of South Florida November 16, 2018 Outline Healthcare systems engineering in
Managing Service Systems with an Offline Waiting Option and Customer Abandonment: Companion Note
 Managing Service Systems with an Offline Waiting Option and Customer Abandonment: Companion Note Vasiliki Kostami Amy R. Ward September 25, 28 The Amusement Park Ride Setting An amusement park ride departs
Managing Service Systems with an Offline Waiting Option and Customer Abandonment: Companion Note Vasiliki Kostami Amy R. Ward September 25, 28 The Amusement Park Ride Setting An amusement park ride departs
Proactive Care with Degrading Class Types
 Proactive Care with Degrading Class Types Yue Hu (DRO, Columbia Business School) Joint work with Prof. Carri Chan (DRO, Columbia Business School) and Prof. Jing Dong (DRO, Columbia Business School) Motivation
Proactive Care with Degrading Class Types Yue Hu (DRO, Columbia Business School) Joint work with Prof. Carri Chan (DRO, Columbia Business School) and Prof. Jing Dong (DRO, Columbia Business School) Motivation
This paper investigates the impact of dependence among successive service times on the transient and
 MANUFACTURING & SERVICE OPERATIONS MANAGEMENT Vol. 14, No. 2, Spring 212, pp. 262 278 ISSN 1523-4614 (print) ISSN 1526-5498 (online) http://dx.doi.org/1.1287/msom.111.363 212 INFORMS The Impact of Dependent
MANUFACTURING & SERVICE OPERATIONS MANAGEMENT Vol. 14, No. 2, Spring 212, pp. 262 278 ISSN 1523-4614 (print) ISSN 1526-5498 (online) http://dx.doi.org/1.1287/msom.111.363 212 INFORMS The Impact of Dependent
Load Balancing in Distributed Service System: A Survey
 Load Balancing in Distributed Service System: A Survey Xingyu Zhou The Ohio State University zhou.2055@osu.edu November 21, 2016 Xingyu Zhou (OSU) Load Balancing November 21, 2016 1 / 29 Introduction and
Load Balancing in Distributed Service System: A Survey Xingyu Zhou The Ohio State University zhou.2055@osu.edu November 21, 2016 Xingyu Zhou (OSU) Load Balancing November 21, 2016 1 / 29 Introduction and
Stochastic-Process Limits
 Ward Whitt Stochastic-Process Limits An Introduction to Stochastic-Process Limits and Their Application to Queues With 68 Illustrations Springer Contents Preface vii 1 Experiencing Statistical Regularity
Ward Whitt Stochastic-Process Limits An Introduction to Stochastic-Process Limits and Their Application to Queues With 68 Illustrations Springer Contents Preface vii 1 Experiencing Statistical Regularity
1.225 Transportation Flow Systems Quiz (December 17, 2001; Duration: 3 hours)
 1.225 Transportation Flow Systems Quiz (December 17, 2001; Duration: 3 hours) Student Name: Alias: Instructions: 1. This exam is open-book 2. No cooperation is permitted 3. Please write down your name
1.225 Transportation Flow Systems Quiz (December 17, 2001; Duration: 3 hours) Student Name: Alias: Instructions: 1. This exam is open-book 2. No cooperation is permitted 3. Please write down your name
Routing and Staffing in Large-Scale Service Systems: The Case of Homogeneous Impatient Customers and Heterogeneous Servers
 OPERATIONS RESEARCH Vol. 59, No. 1, January February 2011, pp. 50 65 issn 0030-364X eissn 1526-5463 11 5901 0050 informs doi 10.1287/opre.1100.0878 2011 INFORMS Routing and Staffing in Large-Scale Service
OPERATIONS RESEARCH Vol. 59, No. 1, January February 2011, pp. 50 65 issn 0030-364X eissn 1526-5463 11 5901 0050 informs doi 10.1287/opre.1100.0878 2011 INFORMS Routing and Staffing in Large-Scale Service
The Performance Impact of Delay Announcements
 The Performance Impact of Delay Announcements Taking Account of Customer Response IEOR 4615, Service Engineering, Professor Whitt Supplement to Lecture 21, April 21, 2015 Review: The Purpose of Delay Announcements
The Performance Impact of Delay Announcements Taking Account of Customer Response IEOR 4615, Service Engineering, Professor Whitt Supplement to Lecture 21, April 21, 2015 Review: The Purpose of Delay Announcements
Introduction to queuing theory
 Introduction to queuing theory Claude Rigault ENST claude.rigault@enst.fr Introduction to Queuing theory 1 Outline The problem The number of clients in a system The client process Delay processes Loss
Introduction to queuing theory Claude Rigault ENST claude.rigault@enst.fr Introduction to Queuing theory 1 Outline The problem The number of clients in a system The client process Delay processes Loss
Simulating a Medical Observation Unit for a Pediatric Emergency Department. Mark Grum July 29 th, 2015
 Simulating a Medical Observation Unit for a Pediatric Emergency Department Mark Grum July 29 th, 2015 Acknowledgements Amy Cohn, Ph.D Gabriel Zayas-Caban, Ph.D Michelle Macy, MD Allison Cator, MD Hassan
Simulating a Medical Observation Unit for a Pediatric Emergency Department Mark Grum July 29 th, 2015 Acknowledgements Amy Cohn, Ph.D Gabriel Zayas-Caban, Ph.D Michelle Macy, MD Allison Cator, MD Hassan
Chapter 4 Describing the Relation between Two Variables
 Chapter 4 Describing the Relation between Two Variables 4.1 Scatter Diagrams and Correlation The is the variable whose value can be explained by the value of the or. A is a graph that shows the relationship
Chapter 4 Describing the Relation between Two Variables 4.1 Scatter Diagrams and Correlation The is the variable whose value can be explained by the value of the or. A is a graph that shows the relationship
BIRTH DEATH PROCESSES AND QUEUEING SYSTEMS
 BIRTH DEATH PROCESSES AND QUEUEING SYSTEMS Andrea Bobbio Anno Accademico 999-2000 Queueing Systems 2 Notation for Queueing Systems /λ mean time between arrivals S = /µ ρ = λ/µ N mean service time traffic
BIRTH DEATH PROCESSES AND QUEUEING SYSTEMS Andrea Bobbio Anno Accademico 999-2000 Queueing Systems 2 Notation for Queueing Systems /λ mean time between arrivals S = /µ ρ = λ/µ N mean service time traffic
On the Resource/Performance Tradeoff in Large Scale Queueing Systems
 On the Resource/Performance Tradeoff in Large Scale Queueing Systems David Gamarnik MIT Joint work with Patrick Eschenfeldt, John Tsitsiklis and Martin Zubeldia (MIT) High level comments High level comments
On the Resource/Performance Tradeoff in Large Scale Queueing Systems David Gamarnik MIT Joint work with Patrick Eschenfeldt, John Tsitsiklis and Martin Zubeldia (MIT) High level comments High level comments
Blind Fair Routing in Large-Scale Service Systems with Heterogeneous Customers and Servers
 OPERATIONS RESEARCH Vol. 6, No., January February 23, pp. 228 243 ISSN 3-364X (print) ISSN 526-5463 (online) http://dx.doi.org/.287/opre.2.29 23 INFORMS Blind Fair Routing in Large-Scale Service Systems
OPERATIONS RESEARCH Vol. 6, No., January February 23, pp. 228 243 ISSN 3-364X (print) ISSN 526-5463 (online) http://dx.doi.org/.287/opre.2.29 23 INFORMS Blind Fair Routing in Large-Scale Service Systems
The Offered-Load Process: Modeling, Inference and Applications. Research Thesis
 The Offered-Load Process: Modeling, Inference and Applications Research Thesis Submitted in Partial Fulfillment of the Requirements for the Degree of Master of Science in Statistics Michael Reich Submitted
The Offered-Load Process: Modeling, Inference and Applications Research Thesis Submitted in Partial Fulfillment of the Requirements for the Degree of Master of Science in Statistics Michael Reich Submitted
L = λ W time average number in Line or system arrival rate W average Waiting time per customer
 IEOR 4615, Lecture 3, January 27, 2015 L λ Little s Law* L = λ W time average number in Line or system arrival rate W average Waiting time per customer *J. D. C. Little, A proof of the queueing formula:
IEOR 4615, Lecture 3, January 27, 2015 L λ Little s Law* L = λ W time average number in Line or system arrival rate W average Waiting time per customer *J. D. C. Little, A proof of the queueing formula:
The Institute for Integrating Statistics in Decision Sciences
 The Institute for Integrating Statistics in Decision Sciences Technical Report TR-- December, Predicting Gridlocks in Emergency Departments: A Bayesian Discrete Time Queueing Theoretic Approach Toros Caglar
The Institute for Integrating Statistics in Decision Sciences Technical Report TR-- December, Predicting Gridlocks in Emergency Departments: A Bayesian Discrete Time Queueing Theoretic Approach Toros Caglar
IEEE TRANSACTIONS ON AUTOMATIC CONTROL, VOL. 43, NO. 3, MARCH
 IEEE TRANSACTIONS ON AUTOMATIC CONTROL, VOL. 43, NO. 3, MARCH 1998 315 Asymptotic Buffer Overflow Probabilities in Multiclass Multiplexers: An Optimal Control Approach Dimitris Bertsimas, Ioannis Ch. Paschalidis,
IEEE TRANSACTIONS ON AUTOMATIC CONTROL, VOL. 43, NO. 3, MARCH 1998 315 Asymptotic Buffer Overflow Probabilities in Multiclass Multiplexers: An Optimal Control Approach Dimitris Bertsimas, Ioannis Ch. Paschalidis,
THE HEAVY-TRAFFIC BOTTLENECK PHENOMENON IN OPEN QUEUEING NETWORKS. S. Suresh and W. Whitt AT&T Bell Laboratories Murray Hill, New Jersey 07974
 THE HEAVY-TRAFFIC BOTTLENECK PHENOMENON IN OPEN QUEUEING NETWORKS by S. Suresh and W. Whitt AT&T Bell Laboratories Murray Hill, New Jersey 07974 ABSTRACT This note describes a simulation experiment involving
THE HEAVY-TRAFFIC BOTTLENECK PHENOMENON IN OPEN QUEUEING NETWORKS by S. Suresh and W. Whitt AT&T Bell Laboratories Murray Hill, New Jersey 07974 ABSTRACT This note describes a simulation experiment involving
IEOR 6711: Stochastic Models I, Fall 2003, Professor Whitt. Solutions to Final Exam: Thursday, December 18.
 IEOR 6711: Stochastic Models I, Fall 23, Professor Whitt Solutions to Final Exam: Thursday, December 18. Below are six questions with several parts. Do as much as you can. Show your work. 1. Two-Pump Gas
IEOR 6711: Stochastic Models I, Fall 23, Professor Whitt Solutions to Final Exam: Thursday, December 18. Below are six questions with several parts. Do as much as you can. Show your work. 1. Two-Pump Gas
Queuing Networks: Burke s Theorem, Kleinrock s Approximation, and Jackson s Theorem. Wade Trappe
 Queuing Networks: Burke s Theorem, Kleinrock s Approximation, and Jackson s Theorem Wade Trappe Lecture Overview Network of Queues Introduction Queues in Tandem roduct Form Solutions Burke s Theorem What
Queuing Networks: Burke s Theorem, Kleinrock s Approximation, and Jackson s Theorem Wade Trappe Lecture Overview Network of Queues Introduction Queues in Tandem roduct Form Solutions Burke s Theorem What
Homework 1 - SOLUTION
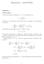 Homework - SOLUTION Problem M/M/ Queue ) Use the fact above to express π k, k > 0, as a function of π 0. π k = ( ) k λ π 0 µ 2) Using λ < µ and the fact that all π k s sum to, compute π 0 (as a function
Homework - SOLUTION Problem M/M/ Queue ) Use the fact above to express π k, k > 0, as a function of π 0. π k = ( ) k λ π 0 µ 2) Using λ < µ and the fact that all π k s sum to, compute π 0 (as a function
Control of Fork-Join Networks in Heavy-Traffic
 in Heavy-Traffic Asaf Zviran Based on MSc work under the guidance of Rami Atar (Technion) and Avishai Mandelbaum (Technion) Industrial Engineering and Management Technion June 2010 Introduction Network
in Heavy-Traffic Asaf Zviran Based on MSc work under the guidance of Rami Atar (Technion) and Avishai Mandelbaum (Technion) Industrial Engineering and Management Technion June 2010 Introduction Network
Queues in Hospitals: Queueing Networks with ReEntering Customers in the QED Regime
 Queues in Hospitals: Queueing Networks with ReEntering Customers in the QED Regime QED = Quality- and Efficiency-Driven Galit Bracha Yom-Tov Queues in Hospitals: Stochastic Networks with ReEntering Customers
Queues in Hospitals: Queueing Networks with ReEntering Customers in the QED Regime QED = Quality- and Efficiency-Driven Galit Bracha Yom-Tov Queues in Hospitals: Stochastic Networks with ReEntering Customers
Queueing Systems: Lecture 3. Amedeo R. Odoni October 18, Announcements
 Queueing Systems: Lecture 3 Amedeo R. Odoni October 18, 006 Announcements PS #3 due tomorrow by 3 PM Office hours Odoni: Wed, 10/18, :30-4:30; next week: Tue, 10/4 Quiz #1: October 5, open book, in class;
Queueing Systems: Lecture 3 Amedeo R. Odoni October 18, 006 Announcements PS #3 due tomorrow by 3 PM Office hours Odoni: Wed, 10/18, :30-4:30; next week: Tue, 10/4 Quiz #1: October 5, open book, in class;
Managing Call Centers with Many Strategic Agents
 Managing Call Centers with Many Strategic Agents Rouba Ibrahim, Kenan Arifoglu Management Science and Innovation, UCL YEQT Workshop - Eindhoven November 2014 Work Schedule Flexibility 86SwofwthewqBestwCompanieswtowWorkwForqwofferw
Managing Call Centers with Many Strategic Agents Rouba Ibrahim, Kenan Arifoglu Management Science and Innovation, UCL YEQT Workshop - Eindhoven November 2014 Work Schedule Flexibility 86SwofwthewqBestwCompanieswtowWorkwForqwofferw
Classical Queueing Models.
 Sergey Zeltyn January 2005 STAT 99. Service Engineering. The Wharton School. University of Pennsylvania. Based on: Classical Queueing Models. Mandelbaum A. Service Engineering course, Technion. http://iew3.technion.ac.il/serveng2005w
Sergey Zeltyn January 2005 STAT 99. Service Engineering. The Wharton School. University of Pennsylvania. Based on: Classical Queueing Models. Mandelbaum A. Service Engineering course, Technion. http://iew3.technion.ac.il/serveng2005w
Technical Appendix for: When Promotions Meet Operations: Cross-Selling and Its Effect on Call-Center Performance
 Technical Appendix for: When Promotions Meet Operations: Cross-Selling and Its Effect on Call-Center Performance In this technical appendix we provide proofs for the various results stated in the manuscript
Technical Appendix for: When Promotions Meet Operations: Cross-Selling and Its Effect on Call-Center Performance In this technical appendix we provide proofs for the various results stated in the manuscript
A STAFFING ALGORITHM FOR CALL CENTERS WITH SKILL-BASED ROUTING: SUPPLEMENTARY MATERIAL
 A STAFFING ALGORITHM FOR CALL CENTERS WITH SKILL-BASED ROUTING: SUPPLEMENTARY MATERIAL by Rodney B. Wallace IBM and The George Washington University rodney.wallace@us.ibm.com Ward Whitt Columbia University
A STAFFING ALGORITHM FOR CALL CENTERS WITH SKILL-BASED ROUTING: SUPPLEMENTARY MATERIAL by Rodney B. Wallace IBM and The George Washington University rodney.wallace@us.ibm.com Ward Whitt Columbia University
Centralized vs. Decentralized Ambulance Diversion: A Network Perspective
 Centralized vs. Decentralized Ambulance Diversion: A Network Perspective Sarang Deo Itai Gurvich Abstract In recent years, growth in the demand for emergency medical services along with decline in the
Centralized vs. Decentralized Ambulance Diversion: A Network Perspective Sarang Deo Itai Gurvich Abstract In recent years, growth in the demand for emergency medical services along with decline in the
SENSITIVITY OF PERFORMANCE IN THE ERLANG-A QUEUEING MODEL TO CHANGES IN THE MODEL PARAMETERS
 SENSITIVITY OF PERFORMANCE IN THE ERLANG-A QUEUEING MODEL TO CHANGES IN THE MODEL PARAMETERS by Ward Whitt Department of Industrial Engineering and Operations Research Columbia University, New York, NY
SENSITIVITY OF PERFORMANCE IN THE ERLANG-A QUEUEING MODEL TO CHANGES IN THE MODEL PARAMETERS by Ward Whitt Department of Industrial Engineering and Operations Research Columbia University, New York, NY
Stabilizing Customer Abandonment in Many-Server Queues with Time-Varying Arrivals
 OPERATIONS RESEARCH Vol. 6, No. 6, November December 212, pp. 1551 1564 ISSN 3-364X (print) ISSN 1526-5463 (online) http://dx.doi.org/1.1287/opre.112.114 212 INFORMS Stabilizing Customer Abandonment in
OPERATIONS RESEARCH Vol. 6, No. 6, November December 212, pp. 1551 1564 ISSN 3-364X (print) ISSN 1526-5463 (online) http://dx.doi.org/1.1287/opre.112.114 212 INFORMS Stabilizing Customer Abandonment in
6 Solving Queueing Models
 6 Solving Queueing Models 6.1 Introduction In this note we look at the solution of systems of queues, starting with simple isolated queues. The benefits of using predefined, easily classified queues will
6 Solving Queueing Models 6.1 Introduction In this note we look at the solution of systems of queues, starting with simple isolated queues. The benefits of using predefined, easily classified queues will
Technical Appendix for: When Promotions Meet Operations: Cross-Selling and Its Effect on Call-Center Performance
 Technical Appendix for: When Promotions Meet Operations: Cross-Selling and Its Effect on Call-Center Performance In this technical appendix we provide proofs for the various results stated in the manuscript
Technical Appendix for: When Promotions Meet Operations: Cross-Selling and Its Effect on Call-Center Performance In this technical appendix we provide proofs for the various results stated in the manuscript
A DIFFUSION APPROXIMATION FOR THE G/GI/n/m QUEUE
 A DIFFUSION APPROXIMATION FOR THE G/GI/n/m QUEUE by Ward Whitt Department of Industrial Engineering and Operations Research Columbia University, New York, NY 10027 July 5, 2002 Revision: June 27, 2003
A DIFFUSION APPROXIMATION FOR THE G/GI/n/m QUEUE by Ward Whitt Department of Industrial Engineering and Operations Research Columbia University, New York, NY 10027 July 5, 2002 Revision: June 27, 2003
Dynamic Call Center Routing Policies Using Call Waiting and Agent Idle Times Online Supplement
 Dynamic Call Center Routing Policies Using Call Waiting and Agent Idle Times Online Supplement Wyean Chan DIRO, Université de Montréal, C.P. 6128, Succ. Centre-Ville, Montréal (Québec), H3C 3J7, CANADA,
Dynamic Call Center Routing Policies Using Call Waiting and Agent Idle Times Online Supplement Wyean Chan DIRO, Université de Montréal, C.P. 6128, Succ. Centre-Ville, Montréal (Québec), H3C 3J7, CANADA,
Contact Centers with a Call-Back Option and Real-Time Delay Information
 OPERATIOS RESEARCH Vol. 52, o. 4, July August 2004, pp. 527 545 issn 0030-364X eissn 526-5463 04 5204 0527 informs doi 0.287/opre.040.023 2004 IFORMS Contact Centers with a Call-Back Option and Real-Time
OPERATIOS RESEARCH Vol. 52, o. 4, July August 2004, pp. 527 545 issn 0030-364X eissn 526-5463 04 5204 0527 informs doi 0.287/opre.040.023 2004 IFORMS Contact Centers with a Call-Back Option and Real-Time
Markov Processes Cont d. Kolmogorov Differential Equations
 Markov Processes Cont d Kolmogorov Differential Equations The Kolmogorov Differential Equations characterize the transition functions {P ij (t)} of a Markov process. The time-dependent behavior of the
Markov Processes Cont d Kolmogorov Differential Equations The Kolmogorov Differential Equations characterize the transition functions {P ij (t)} of a Markov process. The time-dependent behavior of the
Designing a Telephone Call Center with Impatient Customers
 Designing a Telephone Call Center with Impatient Customers with Ofer Garnett Marty Reiman Sergey Zeltyn Appendix: Strong Approximations of M/M/ + Source: ErlangA QEDandSTROG FIAL.tex M/M/ + M System Poisson
Designing a Telephone Call Center with Impatient Customers with Ofer Garnett Marty Reiman Sergey Zeltyn Appendix: Strong Approximations of M/M/ + Source: ErlangA QEDandSTROG FIAL.tex M/M/ + M System Poisson
IEOR 8100: Topics in OR: Asymptotic Methods in Queueing Theory. Fall 2009, Professor Whitt. Class Lecture Notes: Wednesday, September 9.
 IEOR 8100: Topics in OR: Asymptotic Methods in Queueing Theory Fall 2009, Professor Whitt Class Lecture Notes: Wednesday, September 9. Heavy-Traffic Limits for the GI/G/1 Queue 1. The GI/G/1 Queue We will
IEOR 8100: Topics in OR: Asymptotic Methods in Queueing Theory Fall 2009, Professor Whitt Class Lecture Notes: Wednesday, September 9. Heavy-Traffic Limits for the GI/G/1 Queue 1. The GI/G/1 Queue We will
Erlang-R: A Time-Varying Queue with Reentrant Customers, in Support of Healthcare Staffing
 Submitted to Manufacturing & Service Operations Management manuscript (Please, provide the mansucript number! Authors are encouraged to submit new papers to INFORMS journals by means of a style file template,
Submitted to Manufacturing & Service Operations Management manuscript (Please, provide the mansucript number! Authors are encouraged to submit new papers to INFORMS journals by means of a style file template,
Introduction to Queueing Theory with Applications to Air Transportation Systems
 Introduction to Queueing Theory with Applications to Air Transportation Systems John Shortle George Mason University February 28, 2018 Outline Why stochastic models matter M/M/1 queue Little s law Priority
Introduction to Queueing Theory with Applications to Air Transportation Systems John Shortle George Mason University February 28, 2018 Outline Why stochastic models matter M/M/1 queue Little s law Priority
ESTIMATING WAITING TIMES WITH THE TIME-VARYING LITTLE S LAW
 ESTIMATING WAITING TIMES WITH THE TIME-VARYING LITTLE S LAW Song-Hee Kim and Ward Whitt Industrial Engineering and Operations Research Columbia University New York, NY, 10027 {sk3116, ww2040}@columbia.edu
ESTIMATING WAITING TIMES WITH THE TIME-VARYING LITTLE S LAW Song-Hee Kim and Ward Whitt Industrial Engineering and Operations Research Columbia University New York, NY, 10027 {sk3116, ww2040}@columbia.edu
Solutions to COMP9334 Week 8 Sample Problems
 Solutions to COMP9334 Week 8 Sample Problems Problem 1: Customers arrive at a grocery store s checkout counter according to a Poisson process with rate 1 per minute. Each customer carries a number of items
Solutions to COMP9334 Week 8 Sample Problems Problem 1: Customers arrive at a grocery store s checkout counter according to a Poisson process with rate 1 per minute. Each customer carries a number of items
Advanced Computer Networks Lecture 3. Models of Queuing
 Advanced Computer Networks Lecture 3. Models of Queuing Husheng Li Min Kao Department of Electrical Engineering and Computer Science University of Tennessee, Knoxville Spring, 2016 1/13 Terminology of
Advanced Computer Networks Lecture 3. Models of Queuing Husheng Li Min Kao Department of Electrical Engineering and Computer Science University of Tennessee, Knoxville Spring, 2016 1/13 Terminology of
Markov Processes and Queues
 MIT 2.853/2.854 Introduction to Manufacturing Systems Markov Processes and Queues Stanley B. Gershwin Laboratory for Manufacturing and Productivity Massachusetts Institute of Technology Markov Processes
MIT 2.853/2.854 Introduction to Manufacturing Systems Markov Processes and Queues Stanley B. Gershwin Laboratory for Manufacturing and Productivity Massachusetts Institute of Technology Markov Processes
A QUEUE-LENGTH CUTOFF MODEL FOR A PREEMPTIVE TWO-PRIORITY M/M/1 SYSTEM
 A QUEUE-LENGTH CUTOFF MODEL FOR A PREEMPTIVE TWO-PRIORITY M/M/1 SYSTEM QIANG GONG AND RAJAN BATTA Abstract We consider a two-priority preemptive single-server queueing model Each customer is classified
A QUEUE-LENGTH CUTOFF MODEL FOR A PREEMPTIVE TWO-PRIORITY M/M/1 SYSTEM QIANG GONG AND RAJAN BATTA Abstract We consider a two-priority preemptive single-server queueing model Each customer is classified
I, A BRIEF REVIEW ON INFINITE QUEUE MODEL M.
 A BRIEF REVIEW ON INFINITE QUEUE MODEL M. Vasuki*, A. Dinesh Kumar** & G. Vijayaprabha** * Assistant Professor, Department of Mathematics, Srinivasan College of Arts and Science, Perambalur, Tamilnadu
A BRIEF REVIEW ON INFINITE QUEUE MODEL M. Vasuki*, A. Dinesh Kumar** & G. Vijayaprabha** * Assistant Professor, Department of Mathematics, Srinivasan College of Arts and Science, Perambalur, Tamilnadu
Beyond the Target Customer: Social Effects of CRM Campaigns
 Beyond the Target Customer: Social Effects of CRM Campaigns Eva Ascarza, Peter Ebbes, Oded Netzer, Matthew Danielson Link to article: http://journals.ama.org/doi/abs/10.1509/jmr.15.0442 WEB APPENDICES
Beyond the Target Customer: Social Effects of CRM Campaigns Eva Ascarza, Peter Ebbes, Oded Netzer, Matthew Danielson Link to article: http://journals.ama.org/doi/abs/10.1509/jmr.15.0442 WEB APPENDICES
Asymptotics for Polling Models with Limited Service Policies
 Asymptotics for Polling Models with Limited Service Policies Woojin Chang School of Industrial and Systems Engineering Georgia Institute of Technology Atlanta, GA 30332-0205 USA Douglas G. Down Department
Asymptotics for Polling Models with Limited Service Policies Woojin Chang School of Industrial and Systems Engineering Georgia Institute of Technology Atlanta, GA 30332-0205 USA Douglas G. Down Department
The Offered-Load Process: Modeling, Inference and Applications. Research Thesis
 The Offered-Load Process: Modeling, Inference and Applications Research Thesis Submitted in Partial Fulfillment of the Requirements for the Degree of Master of Science in Statistics Michael Reich Submitted
The Offered-Load Process: Modeling, Inference and Applications Research Thesis Submitted in Partial Fulfillment of the Requirements for the Degree of Master of Science in Statistics Michael Reich Submitted
Using Future Information to Reduce Waiting Times in the Emergency Department via Diversion
 Using Future Information to Reduce Waiting Times in the Emergency Department via Diversion Kuang Xu* Microsoft Research - Inria Joint Centre kuang.xu@inria.fr Carri W. Chan Decision, Risk, and Operations,
Using Future Information to Reduce Waiting Times in the Emergency Department via Diversion Kuang Xu* Microsoft Research - Inria Joint Centre kuang.xu@inria.fr Carri W. Chan Decision, Risk, and Operations,
Little s result. T = average sojourn time (time spent) in the system N = average number of customers in the system. Little s result says that
 J. Virtamo 38.143 Queueing Theory / Little s result 1 Little s result The result Little s result or Little s theorem is a very simple (but fundamental) relation between the arrival rate of customers, average
J. Virtamo 38.143 Queueing Theory / Little s result 1 Little s result The result Little s result or Little s theorem is a very simple (but fundamental) relation between the arrival rate of customers, average
Session-Based Queueing Systems
 Session-Based Queueing Systems Modelling, Simulation, and Approximation Jeroen Horters Supervisor VU: Sandjai Bhulai Executive Summary Companies often offer services that require multiple steps on the
Session-Based Queueing Systems Modelling, Simulation, and Approximation Jeroen Horters Supervisor VU: Sandjai Bhulai Executive Summary Companies often offer services that require multiple steps on the
T. Liggett Mathematics 171 Final Exam June 8, 2011
 T. Liggett Mathematics 171 Final Exam June 8, 2011 1. The continuous time renewal chain X t has state space S = {0, 1, 2,...} and transition rates (i.e., Q matrix) given by q(n, n 1) = δ n and q(0, n)
T. Liggett Mathematics 171 Final Exam June 8, 2011 1. The continuous time renewal chain X t has state space S = {0, 1, 2,...} and transition rates (i.e., Q matrix) given by q(n, n 1) = δ n and q(0, n)
Blind Fair Routing in Large-Scale Service Systems with Heterogeneous Customers and Servers
 Blind Fair Routing in Large-Scale Service Systems with Heterogeneous Customers and Servers Mor Armony Amy R. Ward 2 October 6, 2 Abstract In a call center, arriving customers must be routed to available
Blind Fair Routing in Large-Scale Service Systems with Heterogeneous Customers and Servers Mor Armony Amy R. Ward 2 October 6, 2 Abstract In a call center, arriving customers must be routed to available
Fluid Limit of A Many-Server Queueing Network with Abandonment
 Fluid Limit of A Many-Server Queueing Networ with Abandonment Weining Kang Guodong Pang October 22, 213 Abstract This paper studies a non-marovian many-server queueing networ with abandonment, where externally
Fluid Limit of A Many-Server Queueing Networ with Abandonment Weining Kang Guodong Pang October 22, 213 Abstract This paper studies a non-marovian many-server queueing networ with abandonment, where externally
REAL-TIME DELAY ESTIMATION BASED ON DELAY HISTORY IN MANY-SERVER SERVICE SYSTEMS WITH TIME-VARYING ARRIVALS
 REAL-TIME DELAY ESTIMATION BASED ON DELAY HISTORY IN MANY-SERVER SERVICE SYSTEMS WITH TIME-VARYING ARRIVALS by Rouba Ibrahim and Ward Whitt IEOR Department Columbia University 500 West 120th Street 313
REAL-TIME DELAY ESTIMATION BASED ON DELAY HISTORY IN MANY-SERVER SERVICE SYSTEMS WITH TIME-VARYING ARRIVALS by Rouba Ibrahim and Ward Whitt IEOR Department Columbia University 500 West 120th Street 313
ENGINEERING SOLUTION OF A BASIC CALL-CENTER MODEL
 ENGINEERING SOLUTION OF A BASIC CALL-CENTER MODEL by Ward Whitt Department of Industrial Engineering and Operations Research Columbia University, New York, NY 10027 Abstract An algorithm is developed to
ENGINEERING SOLUTION OF A BASIC CALL-CENTER MODEL by Ward Whitt Department of Industrial Engineering and Operations Research Columbia University, New York, NY 10027 Abstract An algorithm is developed to
Queueing Theory (Part 4)
 Queueing Theory (Part 4) Nonexponential Queueing Systems and Economic Analysis Queueing Theory-1 Queueing Models with Nonexponential Distributions M/G/1 Model Poisson input process, general service time
Queueing Theory (Part 4) Nonexponential Queueing Systems and Economic Analysis Queueing Theory-1 Queueing Models with Nonexponential Distributions M/G/1 Model Poisson input process, general service time
Simulation. Where real stuff starts
 1 Simulation Where real stuff starts ToC 1. What is a simulation? 2. Accuracy of output 3. Random Number Generators 4. How to sample 5. Monte Carlo 6. Bootstrap 2 1. What is a simulation? 3 What is a simulation?
1 Simulation Where real stuff starts ToC 1. What is a simulation? 2. Accuracy of output 3. Random Number Generators 4. How to sample 5. Monte Carlo 6. Bootstrap 2 1. What is a simulation? 3 What is a simulation?
A Study on Performance Analysis of Queuing System with Multiple Heterogeneous Servers
 UNIVERSITY OF OKLAHOMA GENERAL EXAM REPORT A Study on Performance Analysis of Queuing System with Multiple Heterogeneous Servers Prepared by HUSNU SANER NARMAN husnu@ou.edu based on the papers 1) F. S.
UNIVERSITY OF OKLAHOMA GENERAL EXAM REPORT A Study on Performance Analysis of Queuing System with Multiple Heterogeneous Servers Prepared by HUSNU SANER NARMAN husnu@ou.edu based on the papers 1) F. S.
Figure 10.1: Recording when the event E occurs
 10 Poisson Processes Let T R be an interval. A family of random variables {X(t) ; t T} is called a continuous time stochastic process. We often consider T = [0, 1] and T = [0, ). As X(t) is a random variable
10 Poisson Processes Let T R be an interval. A family of random variables {X(t) ; t T} is called a continuous time stochastic process. We often consider T = [0, 1] and T = [0, ). As X(t) is a random variable
LIMITS FOR QUEUES AS THE WAITING ROOM GROWS. Bell Communications Research AT&T Bell Laboratories Red Bank, NJ Murray Hill, NJ 07974
 LIMITS FOR QUEUES AS THE WAITING ROOM GROWS by Daniel P. Heyman Ward Whitt Bell Communications Research AT&T Bell Laboratories Red Bank, NJ 07701 Murray Hill, NJ 07974 May 11, 1988 ABSTRACT We study the
LIMITS FOR QUEUES AS THE WAITING ROOM GROWS by Daniel P. Heyman Ward Whitt Bell Communications Research AT&T Bell Laboratories Red Bank, NJ 07701 Murray Hill, NJ 07974 May 11, 1988 ABSTRACT We study the
AAMC s Approach to Managing Patient Throughput. Barbara S Jacobs, MSN, RN-BC, NEA-BC, CCRN-K, Chief Nursing Officer
 AAMC s Approach to Managing Patient Throughput Barbara S Jacobs, MSN, RN-BC, NEA-BC, CCRN-K, Chief Nursing Officer Our Original State June 2016 375 Licensed beds 97,000 Emergency Department visits per
AAMC s Approach to Managing Patient Throughput Barbara S Jacobs, MSN, RN-BC, NEA-BC, CCRN-K, Chief Nursing Officer Our Original State June 2016 375 Licensed beds 97,000 Emergency Department visits per
Erlang loss bounds for OT ICU systems
 Queueing Syst (2009) 63: 253 280 DOI 10.1007/s11134-009-9149-2 Erlang loss bounds for OT ICU systems N.M. van Dijk N. Kortbeek Received: 22 December 2008 / Revised: 30 October 2009 / Published online:
Queueing Syst (2009) 63: 253 280 DOI 10.1007/s11134-009-9149-2 Erlang loss bounds for OT ICU systems N.M. van Dijk N. Kortbeek Received: 22 December 2008 / Revised: 30 October 2009 / Published online:
A Constrained Optimization Problem for a Two-Class Queueing Model
 A Constrained Optimization Problem for a Two-Class Queueing Model Cory Girard 1, Linda V. Green 2, Mark E. Lewis 3, and Jingui Xie 4 1 School of Operations Research and Information Engineering Cornell
A Constrained Optimization Problem for a Two-Class Queueing Model Cory Girard 1, Linda V. Green 2, Mark E. Lewis 3, and Jingui Xie 4 1 School of Operations Research and Information Engineering Cornell
Delay Announcements. Predicting Queueing Delays for Delay Announcements. IEOR 4615, Service Engineering, Professor Whitt. Lecture 21, April 21, 2015
 Delay Announcements Predicting Queueing Delays for Delay Announcements IEOR 4615, Service Engineering, Professor Whitt Lecture 21, April 21, 2015 OUTLINE Delay Announcements: Why, What and When? [Slide
Delay Announcements Predicting Queueing Delays for Delay Announcements IEOR 4615, Service Engineering, Professor Whitt Lecture 21, April 21, 2015 OUTLINE Delay Announcements: Why, What and When? [Slide
PROOFS FOR MANAGING PRODUCT ROLLOVERS BY
 APPENDIX A: PROOFS FOR MANAGING PRODUCT ROLLOVERS BY KOCA, SOUZA AND DRUEHL Derivation of h(γ) Let R it denote the reservation price for product i at time t, a random variable. We write R t = u(ω)ε t,
APPENDIX A: PROOFS FOR MANAGING PRODUCT ROLLOVERS BY KOCA, SOUZA AND DRUEHL Derivation of h(γ) Let R it denote the reservation price for product i at time t, a random variable. We write R t = u(ω)ε t,
MAT SYS 5120 (Winter 2012) Assignment 5 (not to be submitted) There are 4 questions.
 MAT 4371 - SYS 5120 (Winter 2012) Assignment 5 (not to be submitted) There are 4 questions. Question 1: Consider the following generator for a continuous time Markov chain. 4 1 3 Q = 2 5 3 5 2 7 (a) Give
MAT 4371 - SYS 5120 (Winter 2012) Assignment 5 (not to be submitted) There are 4 questions. Question 1: Consider the following generator for a continuous time Markov chain. 4 1 3 Q = 2 5 3 5 2 7 (a) Give
MODELING WEBCHAT SERVICE CENTER WITH MANY LPS SERVERS
 MODELING WEBCHAT SERVICE CENTER WITH MANY LPS SERVERS Jiheng Zhang Oct 26, 211 Model and Motivation Server Pool with multiple LPS servers LPS Server K Arrival Buffer. Model and Motivation Server Pool with
MODELING WEBCHAT SERVICE CENTER WITH MANY LPS SERVERS Jiheng Zhang Oct 26, 211 Model and Motivation Server Pool with multiple LPS servers LPS Server K Arrival Buffer. Model and Motivation Server Pool with
Introduction to Markov Chains, Queuing Theory, and Network Performance
 Introduction to Markov Chains, Queuing Theory, and Network Performance Marceau Coupechoux Telecom ParisTech, departement Informatique et Réseaux marceau.coupechoux@telecom-paristech.fr IT.2403 Modélisation
Introduction to Markov Chains, Queuing Theory, and Network Performance Marceau Coupechoux Telecom ParisTech, departement Informatique et Réseaux marceau.coupechoux@telecom-paristech.fr IT.2403 Modélisation
REAL-TIME DELAY ESTIMATION BASED ON DELAY HISTORY SUPPLEMENTARY MATERIAL
 REAL-TIME DELAY ESTIMATION BASED ON DELAY HISTORY SUPPLEMENTARY MATERIAL by Rouba Ibrahim and Ward Whitt IEOR Department Columbia University {rei2101, ww2040}@columbia.edu Abstract Motivated by interest
REAL-TIME DELAY ESTIMATION BASED ON DELAY HISTORY SUPPLEMENTARY MATERIAL by Rouba Ibrahim and Ward Whitt IEOR Department Columbia University {rei2101, ww2040}@columbia.edu Abstract Motivated by interest
Multi-class, multi-server queues with non-preemptive priorities
 Multi-class, multi-server queues with non-preemptive priorities Andrei Sleptcheno. EURANDOM, Eindhoven University of Technology, P.O. Box 53, 5600MB Eindhoven, The Netherlands. e-mail:sleptcheno@eurandom.tue.nl
Multi-class, multi-server queues with non-preemptive priorities Andrei Sleptcheno. EURANDOM, Eindhoven University of Technology, P.O. Box 53, 5600MB Eindhoven, The Netherlands. e-mail:sleptcheno@eurandom.tue.nl
