Tuesday, September 29, Page 453. Problem 5
|
|
|
- Brittney Peters
- 5 years ago
- Views:
Transcription
1 Tuesday, September 9, 15 Page 5 Problem 5 Problem. Set up and evaluate the integral that gives the volume of the solid formed by revolving the region bounded by y = x, y = x 5 about the x-axis. Solution. The inner radius is R 1 x) = x 5 and the outer radius is R x) = x. The extremities are x = and x = 1. So the volume is Problem 6 π x ) x 5 ) ) dx x x 1) dx 1 5 x x ) 11 = 6π 55. Problem. Set up and evaluate the integral that gives the volume of the solid formed by revolving the region bounded by y =, ] 1 y = x about the x-axis. Solution. The inner radius is R 1 x) = and the outer radius is R x) = x. The 1
2 extremities are x = and x =. So the volume is ) ) V x dx ) ) 16 x + x dx 16 ) 1 x + x dx 16 1x x x5 ] ) 5 ) Problem 11b) ) 8 = 168π x ) + 18 )] )5 )] about the y-axis. y = x, y =, x = Solution. Because we are revolving about the y-axis, we should write our functions as functions of y. So we have x = y. Now, the inner radius is R 1 y) = y and the
3 outer radius is R y) =. The extremities are y = and y =. So the volume is Problem 11d) π y ) ) dy 9 y ) dy 9y 15 ] y5 9 1 ) 5 9 = 6π 5. about the line x = 6. y = x, y =, x = Solution. The inner radius is from x = 6 to x =, so R 1 y) = 6 = and the outer radius is R y) = 6 y. The extremities are y = and y =. The volume is π 6 y ) ) dy 7 1y + y ) dy 7y y + 15 ] y5 7 ) + 15 ) ) 5 = 8π 5.
4 Problem 15 about the line y =. y = x, y =, x = Solution. We are revolving about a horizontal line, so we must integrate in the x direction and make vertical slices. The inner radius goes from y = to y =, so R 1 = 1. The outer radius goes from y = to y = x, so R = x. The extremities are from x = to x =. The volume is π x) 1 ) dx 15 8x + x ) dx 15x x + 1 x ] ) = 18π. Problem y = x, y =, y =, x = about the line x = 5.
5 Solution. We are revolving about a vertical line, so we must integrate in the y direction and make horizontal slices. The inner radius goes from x = 5 to x = y, so R 1 = 5 y) = y +. The outer radius goes from x = 5 to x =, so R = 5. The extremities are from y = to y =. The volume is Problem 1 π 5 y + ) ) dy 1 y y ) dy 1y y 1 ] y 8 8 ) = 9π. about the line x = 5. x = y, x = Solution. We are revolving about a vertical line, so we must integrate in the y direction and make horizontal slices. The inner radius goes from x = 5 to x =, so R 1 = 1. The outer radius goes from x = 5 to x = y, so R = 5 y. The extremities are from y = to y = =. The 5
6 volume is π 5 y ) 1 ) dy 1y + y ) dy y 1 y y ) 5 = 8π 15. ] Problem 9 y = x + 1, y = x + x + 5, x =, x = about the x-axis Solution. The graph is We are revolving about a horizontal line, so we must integrate in the x direction and make vertical slices. Furthermore, we see from the graph that the upper and lower function switch at x =, so we must set up two integrals. 6
7 In the first integral, the inner radius goes from y = to y = x +1, so R 1 = x +1. The outer radius goes from y = to y = x + x + 5, so R = x + x + 5. The extremities are from x = to x =. The first volume is V 1 = π x + x + 5) x + 1) ) dx x 8x + x + ) dx x 8 ] x + 1x + x 16 6 ) = 15π. In the second integral, the inner radius goes from y = to y = x + x + 5, so R 1 = x + x + 5. The outer radius goes from y = to y = x + 1, so R = x + 1. The extremities are from x = to x =. The second volume is V = Thus, the combined volume is π x + 1) x + x + 5) ) dx x + 8x x ) dx ] x + 8 x 1x x ) ) = 15π. )) 8 V 1 + V = 15π = 77π. + 15π 7
8 Problem y = x, y = 1 x +, x =, x = 8 about the x-axis Solution. The graph is We are revolving about a horizontal line, so we must integrate in the x direction and make vertical slices. Furthermore, we see from the graph that the upper and lower function switch at x =, so we must set up two integrals. In the first integral, the inner radius goes from y = to y = x, so R 1 = x. The outer radius goes from y = to y = 1x +, so R = 1 x +. The extremities 8
9 are from x = to x =. The first volume is V 1 1 x + ) ) x) dx ) 1 x 5x + 16 dx 1 1 x 5 ] x + 16x ) = 88π In the second integral, the inner radius goes from y = to y = x + x + 5, so R 1 = x + x + 5. The outer radius goes from y = to y = x + 1, so R = x + 1. The extremities are from x = to x = 8. The second volume is 8 V x) 1 ) x + ) dx 8 1 ) x + 5x 16 dx Thus, the combined volume is 1 1 x + 5 ] 8 x 16x 18 ) ) = 56π. 16 )) + 6 V 1 + V = 88π + 56π = 1π = 8π. 9
10 Problem 1 Problem. Find the volume of the solid generated by rotating region R 1 see diagram) about the line x =. Solution. The inner radius is R 1 = 1 x and the outer radius is R = 1. The extremities are x = and x = 1. The volume is π 1 1 x) ) dx ) x x dx x 1 ] 1 x 1 1 ) = π. Problem 5 Problem. Find the volume of the solid generated by rotating region R see diagram) about the line x =. Solution. The inner radius is R 1 = and the outer radius is R = x. The extremities are x = and x = 1. Because R 1 =, this is the disk method. The volume is 5. π x ) ) dx 1 5 x5 x dx ] 1 Problem 7 Problem. Find the volume of the solid generated by rotating region R see diagram) about the line x =. 1
11 Solution. Having worked problems 1 and 5, a quick way to get this volume is to subtract the other two volumes from the volume of all three regions rotated about the x-axis. That solid is a cylinder of radius 1 and height 1, so its volume is π. Then the volume of region R rotated must be V π π 5 = π 15. Let s use the washer method and see whether we get the same answer. The inner radius is R 1 = x and the outer radius is R = x. The extremities are x = and x = 1. The volume is Yep. = π 15. π x x ) ) dx x x ) dx 1 x 1 5 x5 ] 1 11
LESSON 14: VOLUME OF SOLIDS OF REVOLUTION SEPTEMBER 27, 2017
 LESSON 4: VOLUME OF SOLIDS OF REVOLUTION SEPTEMBER 27, 27 We continue to expand our understanding of solids of revolution. The key takeaway from today s lesson is that finding the volume of a solid of
LESSON 4: VOLUME OF SOLIDS OF REVOLUTION SEPTEMBER 27, 27 We continue to expand our understanding of solids of revolution. The key takeaway from today s lesson is that finding the volume of a solid of
Volumes of Solids of Revolution. We revolve this curve about the x-axis and create a solid of revolution.
 Volumes of Solids of Revolution Consider the function ( ) from a = to b = 9. 5 6 7 8 9 We revolve this curve about the x-axis and create a solid of revolution. - 5 6 7 8 9 - - - We want to find the volume
Volumes of Solids of Revolution Consider the function ( ) from a = to b = 9. 5 6 7 8 9 We revolve this curve about the x-axis and create a solid of revolution. - 5 6 7 8 9 - - - We want to find the volume
Volume: The Disk Method. Using the integral to find volume.
 Volume: The Disk Method Using the integral to find volume. If a region in a plane is revolved about a line, the resulting solid is a solid of revolution and the line is called the axis of revolution. y
Volume: The Disk Method Using the integral to find volume. If a region in a plane is revolved about a line, the resulting solid is a solid of revolution and the line is called the axis of revolution. y
Technique 1: Volumes by Slicing
 Finding Volumes of Solids We have used integrals to find the areas of regions under curves; it may not seem obvious at first, but we can actually use similar methods to find volumes of certain types of
Finding Volumes of Solids We have used integrals to find the areas of regions under curves; it may not seem obvious at first, but we can actually use similar methods to find volumes of certain types of
Review: Exam Material to be covered: 6.1, 6.2, 6.3, 6.5 plus review of u, du substitution.
 Review: Exam. Goals for this portion of the course: Be able to compute the area between curves, the volume of solids of revolution, and understand the mean value of a function. We had three basic volumes:
Review: Exam. Goals for this portion of the course: Be able to compute the area between curves, the volume of solids of revolution, and understand the mean value of a function. We had three basic volumes:
Volume of Solid of Known Cross-Sections
 Volume of Solid of Known Cross-Sections Problem: To find the volume of a given solid S. What do we know about the solid? Suppose we are told what the cross-sections perpendicular to some axis are. Figure:
Volume of Solid of Known Cross-Sections Problem: To find the volume of a given solid S. What do we know about the solid? Suppose we are told what the cross-sections perpendicular to some axis are. Figure:
Integrals. D. DeTurck. January 1, University of Pennsylvania. D. DeTurck Math A: Integrals 1 / 61
 Integrals D. DeTurck University of Pennsylvania January 1, 2018 D. DeTurck Math 104 002 2018A: Integrals 1 / 61 Integrals Start with dx this means a little bit of x or a little change in x If we add up
Integrals D. DeTurck University of Pennsylvania January 1, 2018 D. DeTurck Math 104 002 2018A: Integrals 1 / 61 Integrals Start with dx this means a little bit of x or a little change in x If we add up
Intermediate Algebra Section 9.1 Composite Functions and Inverse Functions
 Intermediate Algebra Section 9. Composite Functions and Inverse Functions We have added, subtracted, multiplied, and divided functions in previous chapters. Another way to combine functions is called composite
Intermediate Algebra Section 9. Composite Functions and Inverse Functions We have added, subtracted, multiplied, and divided functions in previous chapters. Another way to combine functions is called composite
Chapter 6 Some Applications of the Integral
 Chapter 6 Some Applications of the Integral Section 6.1 More on Area a. Representative Rectangle b. Vertical Separation c. Example d. Integration with Respect to y e. Example Section 6.2 Volume by Parallel
Chapter 6 Some Applications of the Integral Section 6.1 More on Area a. Representative Rectangle b. Vertical Separation c. Example d. Integration with Respect to y e. Example Section 6.2 Volume by Parallel
8 + 6) x 2 ) y = h(x)
 . a. Horizontal shift 6 left and vertical shift up. Notice B' is ( 6, ) and B is (0, 0). b. h(x) = 0.5(x + 6) + (Enter in a grapher to check.) c. Use the graph. Notice A' to see h(x) crosses the x-axis
. a. Horizontal shift 6 left and vertical shift up. Notice B' is ( 6, ) and B is (0, 0). b. h(x) = 0.5(x + 6) + (Enter in a grapher to check.) c. Use the graph. Notice A' to see h(x) crosses the x-axis
f x and the x axis on an interval from x a and
 Unit 6: Chapter 8 Areas and Volumes & Density Functions Part 1: Areas To find the area bounded by a function bwe use the integral: f d b a b 0 f d f d. a b a f and the ais on an interval from a and. This
Unit 6: Chapter 8 Areas and Volumes & Density Functions Part 1: Areas To find the area bounded by a function bwe use the integral: f d b a b 0 f d f d. a b a f and the ais on an interval from a and. This
14.1. Multiple Integration. Iterated Integrals and Area in the Plane. Iterated Integrals. Iterated Integrals. MAC2313 Calculus III - Chapter 14
 14 Multiple Integration 14.1 Iterated Integrals and Area in the Plane Objectives Evaluate an iterated integral. Use an iterated integral to find the area of a plane region. Copyright Cengage Learning.
14 Multiple Integration 14.1 Iterated Integrals and Area in the Plane Objectives Evaluate an iterated integral. Use an iterated integral to find the area of a plane region. Copyright Cengage Learning.
Math 75B Practice Midterm III Solutions Chapter 6 (Stewart) Multiple Choice. Circle the letter of the best answer.
 Math 75B Practice Midterm III Solutions Chapter 6 Stewart) English system formulas: Metric system formulas: ft. = in. F = m a 58 ft. = mi. g = 9.8 m/s 6 oz. = lb. cm = m Weight of water: ω = 6.5 lb./ft.
Math 75B Practice Midterm III Solutions Chapter 6 Stewart) English system formulas: Metric system formulas: ft. = in. F = m a 58 ft. = mi. g = 9.8 m/s 6 oz. = lb. cm = m Weight of water: ω = 6.5 lb./ft.
5.5 Volumes: Tubes. The Tube Method. = (2π [radius]) (height) ( x k ) = (2πc k ) f (c k ) x k. 5.5 volumes: tubes 435
![5.5 Volumes: Tubes. The Tube Method. = (2π [radius]) (height) ( x k ) = (2πc k ) f (c k ) x k. 5.5 volumes: tubes 435 5.5 Volumes: Tubes. The Tube Method. = (2π [radius]) (height) ( x k ) = (2πc k ) f (c k ) x k. 5.5 volumes: tubes 435](/thumbs/78/77255700.jpg) 5.5 volumes: tubes 45 5.5 Volumes: Tubes In Section 5., we devised the disk method to find the volume swept out when a region is revolved about a line. To find the volume swept out when revolving a region
5.5 volumes: tubes 45 5.5 Volumes: Tubes In Section 5., we devised the disk method to find the volume swept out when a region is revolved about a line. To find the volume swept out when revolving a region
Lecture 21. Section 6.1 More on Area Section 6.2 Volume by Parallel Cross Section. Jiwen He. Department of Mathematics, University of Houston
 Section 6.1 Section 6.2 Lecture 21 Section 6.1 More on Area Section 6.2 Volume by Parallel Cross Section Jiwen He Department of Mathematics, University of Houston jiwenhe@math.uh.edu math.uh.edu/ jiwenhe/math1431
Section 6.1 Section 6.2 Lecture 21 Section 6.1 More on Area Section 6.2 Volume by Parallel Cross Section Jiwen He Department of Mathematics, University of Houston jiwenhe@math.uh.edu math.uh.edu/ jiwenhe/math1431
Math 132 Information for Test 2
 Math 13 Information for Test Test will cover material from Sections 5.6, 5.7, 5.8, 6.1, 6., 6.3, 7.1, 7., and 7.3. The use of graphing calculators will not be allowed on the test. Some practice questions
Math 13 Information for Test Test will cover material from Sections 5.6, 5.7, 5.8, 6.1, 6., 6.3, 7.1, 7., and 7.3. The use of graphing calculators will not be allowed on the test. Some practice questions
HOMEWORK SOLUTIONS MATH 1910 Sections 6.1, 6.2, 6.3 Fall 2016
 HOMEWORK SOLUTIONS MATH 191 Sections.1,.,. Fall 1 Problem.1.19 Find the area of the shaded region. SOLUTION. The equation of the line passing through ( π, is given by y 1() = π, and the equation of the
HOMEWORK SOLUTIONS MATH 191 Sections.1,.,. Fall 1 Problem.1.19 Find the area of the shaded region. SOLUTION. The equation of the line passing through ( π, is given by y 1() = π, and the equation of the
AP Calculus AB. Review for Test: Applications of Integration
 Name Review for Test: Applications of Integration AP Calculus AB Test Topics: Mean Value Theorem for Integrals (section 4.4) Average Value of a Function (manipulation of MVT for Integrals) (section 4.4)
Name Review for Test: Applications of Integration AP Calculus AB Test Topics: Mean Value Theorem for Integrals (section 4.4) Average Value of a Function (manipulation of MVT for Integrals) (section 4.4)
New York City College of Technology, CUNY Mathematics Department. MAT 1575 Final Exam Review Problems. 3x (a) x 2 (x 3 +1) 3 dx (b) dx.
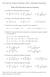 New York City College of Technology, CUNY Mathematics Department MAT 575 Final Exam eview Problems. Evaluate the following definite integrals: x x (a) x (x +) dx (b) dx 0 0 x + 9 (c) 0 x + dx. Evaluate
New York City College of Technology, CUNY Mathematics Department MAT 575 Final Exam eview Problems. Evaluate the following definite integrals: x x (a) x (x +) dx (b) dx 0 0 x + 9 (c) 0 x + dx. Evaluate
MEMORIAL UNIVERSITY OF NEWFOUNDLAND
 MEMORIAL UNIVERSITY OF NEWFOUNDLAND DEPARTMENT OF MATHEMATICS AND STATISTICS Volumes Math 11 Winter 17 SOLUTIONS 1. (a) i. The axis of smmetr is a horizontal line, so we integrate with respect to x. The
MEMORIAL UNIVERSITY OF NEWFOUNDLAND DEPARTMENT OF MATHEMATICS AND STATISTICS Volumes Math 11 Winter 17 SOLUTIONS 1. (a) i. The axis of smmetr is a horizontal line, so we integrate with respect to x. The
Exam 3. MA 114 Exam 3 Fall Multiple Choice Questions. 1. Find the average value of the function f (x) = 2 sin x sin 2x on 0 x π. C. 0 D. 4 E.
 Exam 3 Multiple Choice Questions 1. Find the average value of the function f (x) = sin x sin x on x π. A. π 5 π C. E. 5. Find the volume of the solid S whose base is the disk bounded by the circle x +
Exam 3 Multiple Choice Questions 1. Find the average value of the function f (x) = sin x sin x on x π. A. π 5 π C. E. 5. Find the volume of the solid S whose base is the disk bounded by the circle x +
t 2 + 2t dt = (t + 1) dt + 1 = arctan t x + 6 x(x 3)(x + 2) = A x +
 MATH 06 0 Practice Exam #. (0 points) Evaluate the following integrals: (a) (0 points). t +t+7 This is an irreducible quadratic; its denominator can thus be rephrased via completion of the square as a
MATH 06 0 Practice Exam #. (0 points) Evaluate the following integrals: (a) (0 points). t +t+7 This is an irreducible quadratic; its denominator can thus be rephrased via completion of the square as a
Math 10C - Fall Final Exam
 Math 1C - Fall 217 - Final Exam Problem 1. Consider the function f(x, y) = 1 x 2 (y 1) 2. (i) Draw the level curve through the point P (1, 2). Find the gradient of f at the point P and draw the gradient
Math 1C - Fall 217 - Final Exam Problem 1. Consider the function f(x, y) = 1 x 2 (y 1) 2. (i) Draw the level curve through the point P (1, 2). Find the gradient of f at the point P and draw the gradient
1985 AP Calculus AB: Section I
 985 AP Calculus AB: Section I 9 Minutes No Calculator Notes: () In this eamination, ln denotes the natural logarithm of (that is, logarithm to the base e). () Unless otherwise specified, the domain of
985 AP Calculus AB: Section I 9 Minutes No Calculator Notes: () In this eamination, ln denotes the natural logarithm of (that is, logarithm to the base e). () Unless otherwise specified, the domain of
MATH 18.01, FALL PROBLEM SET # 6 SOLUTIONS
 MATH 181, FALL 17 - PROBLEM SET # 6 SOLUTIONS Part II (5 points) 1 (Thurs, Oct 6; Second Fundamental Theorem; + + + + + = 16 points) Let sinc(x) denote the sinc function { 1 if x =, sinc(x) = sin x if
MATH 181, FALL 17 - PROBLEM SET # 6 SOLUTIONS Part II (5 points) 1 (Thurs, Oct 6; Second Fundamental Theorem; + + + + + = 16 points) Let sinc(x) denote the sinc function { 1 if x =, sinc(x) = sin x if
Chapter 21: Gauss law Tuesday September 13 th. Gauss law and conductors Electrostatic potential energy (more likely on Thu.)
 Chapter 21: Gauss law Tuesday September 13 th LABS START THIS WEEK Quick review of Gauss law The flux of a vector field The shell theorem Gauss law for other symmetries A uniformly charged sheet A uniformly
Chapter 21: Gauss law Tuesday September 13 th LABS START THIS WEEK Quick review of Gauss law The flux of a vector field The shell theorem Gauss law for other symmetries A uniformly charged sheet A uniformly
Integration to Compute Volumes, Work. Goals: Volumes by Slicing Volumes by Cylindrical Shells Work
 Week #8: Integration to Compute Volumes, Work Goals: Volumes by Slicing Volumes by Cylindrical Shells Work 1 Volumes by Slicing - 1 Volumes by Slicing In the integration problems considered in this section
Week #8: Integration to Compute Volumes, Work Goals: Volumes by Slicing Volumes by Cylindrical Shells Work 1 Volumes by Slicing - 1 Volumes by Slicing In the integration problems considered in this section
Double integrals using polar coordinates Let s look at a motivating example:
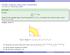 Double integrals using polar coordinates Let s look at a motivating example: Example Evaluate e x +y da where is the bounded region in the first quadrant (x 0, y 0) between the circles of radius 1 and
Double integrals using polar coordinates Let s look at a motivating example: Example Evaluate e x +y da where is the bounded region in the first quadrant (x 0, y 0) between the circles of radius 1 and
Green s Theorem. MATH 311, Calculus III. J. Robert Buchanan. Fall Department of Mathematics. J. Robert Buchanan Green s Theorem
 Green s Theorem MATH 311, alculus III J. obert Buchanan Department of Mathematics Fall 2011 Main Idea Main idea: the line integral around a positively oriented, simple closed curve is related to a double
Green s Theorem MATH 311, alculus III J. obert Buchanan Department of Mathematics Fall 2011 Main Idea Main idea: the line integral around a positively oriented, simple closed curve is related to a double
Prelim 1 Solutions V2 Math 1120
 Feb., Prelim Solutions V Math Please show your reasoning and all your work. This is a 9 minute exam. Calculators are not needed or permitted. Good luck! Problem ) ( Points) Calculate the following: x a)
Feb., Prelim Solutions V Math Please show your reasoning and all your work. This is a 9 minute exam. Calculators are not needed or permitted. Good luck! Problem ) ( Points) Calculate the following: x a)
6.1 Area Between Curves. Example 1: Calculate the area of the region between the parabola y = 1 x 2 and the line y = 1 x
 AP Calculus 6.1 Area Between Curves Name: Goal: Calculate the Area between curves Keys to Success: Top Curve Bottom Curve (integrate w/respect to x or dx) Right Curve Left Curve (integrate w/respect to
AP Calculus 6.1 Area Between Curves Name: Goal: Calculate the Area between curves Keys to Success: Top Curve Bottom Curve (integrate w/respect to x or dx) Right Curve Left Curve (integrate w/respect to
Level 3 Calculus, 2014
 91578 915780 3SUPERVISOR S Level 3 Calculus, 2014 91578 Apply differentiation methods in solving problems 9.30 am Tuesday 18 November 2014 Credits: Six Achievement Achievement with Merit Achievement with
91578 915780 3SUPERVISOR S Level 3 Calculus, 2014 91578 Apply differentiation methods in solving problems 9.30 am Tuesday 18 November 2014 Credits: Six Achievement Achievement with Merit Achievement with
f(p i )Area(T i ) F ( r(u, w) ) (r u r w ) da
 MAH 55 Flux integrals Fall 16 1. Review 1.1. Surface integrals. Let be a surface in R. Let f : R be a function defined on. efine f ds = f(p i Area( i lim mesh(p as a limit of Riemann sums over sampled-partitions.
MAH 55 Flux integrals Fall 16 1. Review 1.1. Surface integrals. Let be a surface in R. Let f : R be a function defined on. efine f ds = f(p i Area( i lim mesh(p as a limit of Riemann sums over sampled-partitions.
Solutions to Homework 1
 Solutions to Homework 1 1. Let f(x) = x 2, a = 1, b = 2, and let x = a = 1, x 1 = 1.1, x 2 = 1.2, x 3 = 1.4, x 4 = b = 2. Let P = (x,..., x 4 ), so that P is a partition of the interval [1, 2]. List the
Solutions to Homework 1 1. Let f(x) = x 2, a = 1, b = 2, and let x = a = 1, x 1 = 1.1, x 2 = 1.2, x 3 = 1.4, x 4 = b = 2. Let P = (x,..., x 4 ), so that P is a partition of the interval [1, 2]. List the
Problem Solving 3: Calculating the Electric Field of Highly Symmetric Distributions of Charge Using Gauss s Law
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics Problem Solving 3: Calculating the Electric Field of Highly Symmetric Distributions of Charge Using Gauss s Law REFERENCE: Section 4.2, 8.02
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics Problem Solving 3: Calculating the Electric Field of Highly Symmetric Distributions of Charge Using Gauss s Law REFERENCE: Section 4.2, 8.02
Chapter 7: Applications of Integration
 Chapter 7: Applications of Integration Fall 214 Department of Mathematics Hong Kong Baptist University 1 / 21 7.1 Volumes by Slicing Solids of Revolution In this section, we show how volumes of certain
Chapter 7: Applications of Integration Fall 214 Department of Mathematics Hong Kong Baptist University 1 / 21 7.1 Volumes by Slicing Solids of Revolution In this section, we show how volumes of certain
MAT 132 Midterm 1 Spring 2017
 MAT Midterm Spring 7 Name: ID: Problem 5 6 7 8 Total ( pts) ( pts) ( pts) ( pts) ( pts) ( pts) (5 pts) (5 pts) ( pts) Score Instructions: () Fill in your name and Stony Brook ID number at the top of this
MAT Midterm Spring 7 Name: ID: Problem 5 6 7 8 Total ( pts) ( pts) ( pts) ( pts) ( pts) ( pts) (5 pts) (5 pts) ( pts) Score Instructions: () Fill in your name and Stony Brook ID number at the top of this
8.2 APPLICATIONS TO GEOMETRY
 8.2 APPLICATIONS TO GEOMETRY In Section 8.1, we calculated volumes using slicing and definite integrals. In this section, we use the same method to calculate the volumes of more complicated regions as
8.2 APPLICATIONS TO GEOMETRY In Section 8.1, we calculated volumes using slicing and definite integrals. In this section, we use the same method to calculate the volumes of more complicated regions as
Math 76 Practice Problems for Midterm II Solutions
 Math 76 Practice Problems for Midterm II Solutions 6.4-8. DISCLAIMER. This collection of practice problems is not guaranteed to be identical, in length or content, to the actual exam. You may expect to
Math 76 Practice Problems for Midterm II Solutions 6.4-8. DISCLAIMER. This collection of practice problems is not guaranteed to be identical, in length or content, to the actual exam. You may expect to
Arnie Pizer Rochester Problem Library Fall 2005 WeBWorK assignment VMultIntegrals1Double due 04/03/2008 at 02:00am EST.
 WeBWorK assignment VMultIntegralsouble due 04/03/2008 at 02:00am ST.. ( pt) rochesterlibrary/setvmultintegralsouble/ur vc 8.pg Consider the solid that lies above the square = [0,2] [0,2] and below the
WeBWorK assignment VMultIntegralsouble due 04/03/2008 at 02:00am ST.. ( pt) rochesterlibrary/setvmultintegralsouble/ur vc 8.pg Consider the solid that lies above the square = [0,2] [0,2] and below the
Answers for Ch. 6 Review: Applications of the Integral
 Answers for Ch. 6 Review: Applications of the Integral. The formula for the average value of a function, which you must have stored in your magical mathematical brain, is b b a f d. a d / / 8 6 6 ( 8 )
Answers for Ch. 6 Review: Applications of the Integral. The formula for the average value of a function, which you must have stored in your magical mathematical brain, is b b a f d. a d / / 8 6 6 ( 8 )
Rectangular box of sizes (dimensions) w,l,h wlh Right cylinder of radius r and height h r 2 h
 Volumes: Slicing Method, Method of Disks and Washers -.,.. Volumes of Some Regular Solids: Solid Volume Rectangular bo of sizes (dimensions) w,l,h wlh Right clinder of radius r and height h r h Right cone
Volumes: Slicing Method, Method of Disks and Washers -.,.. Volumes of Some Regular Solids: Solid Volume Rectangular bo of sizes (dimensions) w,l,h wlh Right clinder of radius r and height h r h Right cone
Sample Final Questions: Solutions Math 21B, Winter y ( y 1)(1 + y)) = A y + B
 Sample Final Questions: Solutions Math 2B, Winter 23. Evaluate the following integrals: tan a) y y dy; b) x dx; c) 3 x 2 + x dx. a) We use partial fractions: y y 3 = y y ) + y)) = A y + B y + C y +. Putting
Sample Final Questions: Solutions Math 2B, Winter 23. Evaluate the following integrals: tan a) y y dy; b) x dx; c) 3 x 2 + x dx. a) We use partial fractions: y y 3 = y y ) + y)) = A y + B y + C y +. Putting
Problem. Set up the definite integral that gives the area of the region. y 1 = x 2 6x, y 2 = 0. dx = ( 2x 2 + 6x) dx.
 Wednesday, September 3, 5 Page Problem Problem. Set up the definite integral that gives the area of the region y x 6x, y Solution. The graphs intersect at x and x 6 and y is the uppermost function. So
Wednesday, September 3, 5 Page Problem Problem. Set up the definite integral that gives the area of the region y x 6x, y Solution. The graphs intersect at x and x 6 and y is the uppermost function. So
Chapter 10 Conics, Parametric Equations, and Polar Coordinates Conics and Calculus
 Chapter 10 Conics, Parametric Equations, and Polar Coordinates 10.1 Conics and Calculus 1. Parabola A parabola is the set of all points x, y ( ) that are equidistant from a fixed line and a fixed point
Chapter 10 Conics, Parametric Equations, and Polar Coordinates 10.1 Conics and Calculus 1. Parabola A parabola is the set of all points x, y ( ) that are equidistant from a fixed line and a fixed point
Calculus II (Fall 2015) Practice Problems for Exam 1
 Calculus II (Fall 15) Practice Problems for Exam 1 Note: Section divisions and instructions below are the same as they will be on the exam, so you will have a better idea of what to expect, though I will
Calculus II (Fall 15) Practice Problems for Exam 1 Note: Section divisions and instructions below are the same as they will be on the exam, so you will have a better idea of what to expect, though I will
D. Correct! This is the correct answer. It is found by dy/dx = (dy/dt)/(dx/dt).
 Calculus II - Problem Solving Drill 4: Calculus for Parametric Equations Question No. of 0 Instructions: () Read the problem and answer choices carefully () Work the problems on paper as. Find dy/dx where
Calculus II - Problem Solving Drill 4: Calculus for Parametric Equations Question No. of 0 Instructions: () Read the problem and answer choices carefully () Work the problems on paper as. Find dy/dx where
Math 20C Homework 2 Partial Solutions
 Math 2C Homework 2 Partial Solutions Problem 1 (12.4.14). Calculate (j k) (j + k). Solution. The basic properties of the cross product are found in Theorem 2 of Section 12.4. From these properties, we
Math 2C Homework 2 Partial Solutions Problem 1 (12.4.14). Calculate (j k) (j + k). Solution. The basic properties of the cross product are found in Theorem 2 of Section 12.4. From these properties, we
HOMEWORK SOLUTIONS MATH 1910 Sections 6.4, 6.5, 7.1 Fall 2016
 HOMEWORK SOLUTIONS MATH 9 Sections 6.4, 6.5, 7. Fall 6 Problem 6.4. Sketch the region enclosed by x = 4 y +, x = 4y, and y =. Use the Shell Method to calculate the volume of rotation about the x-axis SOLUTION.
HOMEWORK SOLUTIONS MATH 9 Sections 6.4, 6.5, 7. Fall 6 Problem 6.4. Sketch the region enclosed by x = 4 y +, x = 4y, and y =. Use the Shell Method to calculate the volume of rotation about the x-axis SOLUTION.
Math 140 Final Sample A Solutions. Tyrone Crisp
 Math 4 Final Sample A Solutions Tyrone Crisp (B) Direct substitution gives, so the limit is infinite. When is close to, but greater than,, the numerator is negative while the denominator is positive. So
Math 4 Final Sample A Solutions Tyrone Crisp (B) Direct substitution gives, so the limit is infinite. When is close to, but greater than,, the numerator is negative while the denominator is positive. So
Math Boot Camp: Integration
 Math Boot Camp: Integration You can skip this boot camp if you can answer the following questions: What is the line integral of 1 r 2 r along a radial path starting from r = and ending at r = R? Prove
Math Boot Camp: Integration You can skip this boot camp if you can answer the following questions: What is the line integral of 1 r 2 r along a radial path starting from r = and ending at r = R? Prove
8.1 Integral as Net Change
 8.1 Integral as Net Change Key Concepts/Skill Objectives Chapter 8 Review Guide 1) Solve problems in which a rate is integrated to find the net change over time in a variety of Terms: applications Linear
8.1 Integral as Net Change Key Concepts/Skill Objectives Chapter 8 Review Guide 1) Solve problems in which a rate is integrated to find the net change over time in a variety of Terms: applications Linear
Vertex Form of a Parabola
 Verte Form of a Parabola In this investigation ou will graph different parabolas and compare them to what is known as the Basic Parabola. THE BASIC PARABOLA Equation = 2-3 -2-1 0 1 2 3 verte? What s the
Verte Form of a Parabola In this investigation ou will graph different parabolas and compare them to what is known as the Basic Parabola. THE BASIC PARABOLA Equation = 2-3 -2-1 0 1 2 3 verte? What s the
Problem Set x Classical Mechanics, Fall 2016 Massachusetts Institute of Technology. 1. Moment of Inertia: Disc and Washer
 8.01x Classical Mechanics, Fall 2016 Massachusetts Institute of Technology Problem Set 10 1. Moment of Inertia: Disc and Washer (a) A thin uniform disc of mass M and radius R is mounted on an axis passing
8.01x Classical Mechanics, Fall 2016 Massachusetts Institute of Technology Problem Set 10 1. Moment of Inertia: Disc and Washer (a) A thin uniform disc of mass M and radius R is mounted on an axis passing
Midterm Exam #1. (y 2, y) (y + 2, y) (1, 1)
 Math 5B Integral Calculus March 7, 7 Midterm Eam # Name: Answer Key David Arnold Instructions. points) This eam is open notes, open book. This includes any supplementary tets or online documents. You are
Math 5B Integral Calculus March 7, 7 Midterm Eam # Name: Answer Key David Arnold Instructions. points) This eam is open notes, open book. This includes any supplementary tets or online documents. You are
Math 113 (Calculus II) Final Exam KEY
 Math (Calculus II) Final Exam KEY Short Answer. Fill in the blank with the appropriate answer.. (0 points) a. Let y = f (x) for x [a, b]. Give the formula for the length of the curve formed by the b graph
Math (Calculus II) Final Exam KEY Short Answer. Fill in the blank with the appropriate answer.. (0 points) a. Let y = f (x) for x [a, b]. Give the formula for the length of the curve formed by the b graph
The Volume of a Hypersphere
 The hypersphere has the equation The Volume of a Hypersphere x 2 y 2 x 2 w 2 = 2 if centered at the origin (,,,) and has a radius of in four dimensional space. We approach the project of determining its
The hypersphere has the equation The Volume of a Hypersphere x 2 y 2 x 2 w 2 = 2 if centered at the origin (,,,) and has a radius of in four dimensional space. We approach the project of determining its
Unit #13 - Integration to Find Areas and Volumes, Volumes of Revolution
 Unit #1 - Integration to Find Areas and Volumes, Volumes of Revolution Some problems and solutions selected or adapted from Hughes-Hallett Calculus. Areas In Questions #1-8, find the area of one strip
Unit #1 - Integration to Find Areas and Volumes, Volumes of Revolution Some problems and solutions selected or adapted from Hughes-Hallett Calculus. Areas In Questions #1-8, find the area of one strip
For the intersections: cos x = 0 or sin x = 1 2
 Chapter 6 Set-up examples The purpose of this document is to demonstrate the work that will be required if you are asked to set-up integrals on an exam and/or quiz.. Areas () Set up, do not evaluate, any
Chapter 6 Set-up examples The purpose of this document is to demonstrate the work that will be required if you are asked to set-up integrals on an exam and/or quiz.. Areas () Set up, do not evaluate, any
Sample Questions to the Final Exam in Math 1111 Chapter 2 Section 2.1: Basics of Functions and Their Graphs
 Sample Questions to the Final Eam in Math 1111 Chapter Section.1: Basics of Functions and Their Graphs 1. Find the range of the function: y 16. a.[-4,4] b.(, 4],[4, ) c.[0, ) d.(, ) e.. Find the domain
Sample Questions to the Final Eam in Math 1111 Chapter Section.1: Basics of Functions and Their Graphs 1. Find the range of the function: y 16. a.[-4,4] b.(, 4],[4, ) c.[0, ) d.(, ) e.. Find the domain
Chapter 6: Applications of Integration
 Chapter 6: Applications of Integration Section 6.3 Volumes by Cylindrical Shells Sec. 6.3: Volumes: Cylindrical Shell Method Cylindrical Shell Method dv = 2πrh thickness V = න a b 2πrh thickness Thickness
Chapter 6: Applications of Integration Section 6.3 Volumes by Cylindrical Shells Sec. 6.3: Volumes: Cylindrical Shell Method Cylindrical Shell Method dv = 2πrh thickness V = න a b 2πrh thickness Thickness
36. Double Integration over Non-Rectangular Regions of Type II
 36. Double Integration over Non-Rectangular Regions of Type II When establishing the bounds of a double integral, visualize an arrow initially in the positive x direction or the positive y direction. A
36. Double Integration over Non-Rectangular Regions of Type II When establishing the bounds of a double integral, visualize an arrow initially in the positive x direction or the positive y direction. A
Electric Field Mapping
 Name: Date: PC1143 Physics III Electric Field Mapping 5 Laboratory Worksheet Part A: Parallel Electrodes Distance between parallel electrodes: d = Attach your plots of equipotential lines and electric
Name: Date: PC1143 Physics III Electric Field Mapping 5 Laboratory Worksheet Part A: Parallel Electrodes Distance between parallel electrodes: d = Attach your plots of equipotential lines and electric
The base of each cylinder is called a cross-section.
 6. Volume y Slicing Gol: To find the volume of olid uing econd emeter clculu Volume y Cro-Section Volume y Dik Volume y Wher Volume y Slicing Volume y Shell 6. Volume y Slicing 6. Volume y Slicing Gol:
6. Volume y Slicing Gol: To find the volume of olid uing econd emeter clculu Volume y Cro-Section Volume y Dik Volume y Wher Volume y Slicing Volume y Shell 6. Volume y Slicing 6. Volume y Slicing Gol:
d` = 1+( dy , which is part of the cone.
 7.5 Surface area When we did areas, the basic slices were rectangles, with A = h x or h y. When we did volumes of revolution, the basic slices came from revolving rectangles around an axis. Depending on
7.5 Surface area When we did areas, the basic slices were rectangles, with A = h x or h y. When we did volumes of revolution, the basic slices came from revolving rectangles around an axis. Depending on
Math 221 Exam III (50 minutes) Friday April 19, 2002 Answers
 Math Exam III (5 minutes) Friday April 9, Answers I. ( points.) Fill in the boxes as to complete the following statement: A definite integral can be approximated by a Riemann sum. More precisely, if a
Math Exam III (5 minutes) Friday April 9, Answers I. ( points.) Fill in the boxes as to complete the following statement: A definite integral can be approximated by a Riemann sum. More precisely, if a
8.4 Density and 8.5 Work Group Work Target Practice
 8.4 Density and 8.5 Work Group Work Target Practice 1. The density of oil in a circular oil slick on the surface of the ocean at a distance meters from the center of the slick is given by δ(r) = 5 1+r
8.4 Density and 8.5 Work Group Work Target Practice 1. The density of oil in a circular oil slick on the surface of the ocean at a distance meters from the center of the slick is given by δ(r) = 5 1+r
APM1612. Tutorial letter 203/1/2018. Mechanics 2. Semester 1. Department of Mathematical Sciences APM1612/203/1/2018
 APM6/03//08 Tutorial letter 03//08 Mechanics APM6 Semester Department of Mathematical Sciences IMPORTANT INFORMATION: This tutorial letter contains solutions to assignment 3, Sem. BARCODE Define tomorrow.
APM6/03//08 Tutorial letter 03//08 Mechanics APM6 Semester Department of Mathematical Sciences IMPORTANT INFORMATION: This tutorial letter contains solutions to assignment 3, Sem. BARCODE Define tomorrow.
MATH 263 ASSIGNMENT 9 SOLUTIONS. F dv =
 MAH AIGNMEN 9 OLUION ) Let F = (x yz)î + (y + xz)ĵ + (z + xy)ˆk and let be the portion of the cylinder x + y = that lies inside the sphere x + y + z = 4 be the portion of the sphere x + y + z = 4 that
MAH AIGNMEN 9 OLUION ) Let F = (x yz)î + (y + xz)ĵ + (z + xy)ˆk and let be the portion of the cylinder x + y = that lies inside the sphere x + y + z = 4 be the portion of the sphere x + y + z = 4 that
Volumes of Solids of Revolution Lecture #6 a
 Volumes of Solids of Revolution Lecture #6 a Sphereoid Parabaloid Hyperboloid Whateveroid Volumes Calculating 3-D Space an Object Occupies Take a cross-sectional slice. Compute the area of the slice. Multiply
Volumes of Solids of Revolution Lecture #6 a Sphereoid Parabaloid Hyperboloid Whateveroid Volumes Calculating 3-D Space an Object Occupies Take a cross-sectional slice. Compute the area of the slice. Multiply
MITOCW ocw-18_02-f07-lec17_220k
 MITOCW ocw-18_02-f07-lec17_220k The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free.
MITOCW ocw-18_02-f07-lec17_220k The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free.
AB 1: Find lim. x a.
 AB 1: Find lim x a f ( x) AB 1 Answer: Step 1: Find f ( a). If you get a zero in the denominator, Step 2: Factor numerator and denominator of f ( x). Do any cancellations and go back to Step 1. If you
AB 1: Find lim x a f ( x) AB 1 Answer: Step 1: Find f ( a). If you get a zero in the denominator, Step 2: Factor numerator and denominator of f ( x). Do any cancellations and go back to Step 1. If you
MATH 1371 Fall 2010 Sec 043, 045 Jered Bright (Hard) Mock Test for Midterm 2
 1. A container in the shape of a paraboloid (a parabola revolved around an axis going through the vertex of the parabola and the directrix, so every horizontal slice, or cross section, is a circle.) is
1. A container in the shape of a paraboloid (a parabola revolved around an axis going through the vertex of the parabola and the directrix, so every horizontal slice, or cross section, is a circle.) is
Implicit Differentiation
 Implicit Differentiation Much of our algebraic study of mathematics has dealt with functions. In pre-calculus, we talked about two different types of equations that relate x and y explicit and implicit.
Implicit Differentiation Much of our algebraic study of mathematics has dealt with functions. In pre-calculus, we talked about two different types of equations that relate x and y explicit and implicit.
Calculus II Practice Test 1 Problems: , 6.5, Page 1 of 10
 Calculus II Practice Test Problems: 6.-6.3, 6.5, 7.-7.3 Page of This is in no way an inclusive set of problems there can be other types of problems on the actual test. To prepare for the test: review homework,
Calculus II Practice Test Problems: 6.-6.3, 6.5, 7.-7.3 Page of This is in no way an inclusive set of problems there can be other types of problems on the actual test. To prepare for the test: review homework,
Calculus II. Philippe Rukimbira. Department of Mathematics Florida International University PR (FIU) MAC / 1
 Calculus II Philippe Rukimbira Department of Mathematics Florida International University PR (FIU) MAC 2312 1 / 1 5.4. Sigma notation; The definition of area as limit Assignment: page 350, #11-15, 27,
Calculus II Philippe Rukimbira Department of Mathematics Florida International University PR (FIU) MAC 2312 1 / 1 5.4. Sigma notation; The definition of area as limit Assignment: page 350, #11-15, 27,
A = (cosh x sinh x) dx = (sinh x cosh x) = sinh1 cosh1 sinh 0 + cosh 0 =
 Calculus 7 Review Consider the region between curves y= cosh, y= sinh, =, =.. Find the area of the region. e + e e e Solution. Recall that cosh = and sinh =, whence sinh cosh. Therefore the area is given
Calculus 7 Review Consider the region between curves y= cosh, y= sinh, =, =.. Find the area of the region. e + e e e Solution. Recall that cosh = and sinh =, whence sinh cosh. Therefore the area is given
Math 131. The Derivative and the Tangent Line Problem Larson Section 2.1
 Math 131. The Derivative and the Tangent Line Problem Larson Section.1 From precalculus, the secant line through the two points (c, f(c)) and (c +, f(c + )) is given by m sec = rise f(c + ) f(c) f(c +
Math 131. The Derivative and the Tangent Line Problem Larson Section.1 From precalculus, the secant line through the two points (c, f(c)) and (c +, f(c + )) is given by m sec = rise f(c + ) f(c) f(c +
14.7 Triple Integrals In Cylindrical and Spherical Coordinates Contemporary Calculus TRIPLE INTEGRALS IN CYLINDRICAL AND SPHERICAL COORDINATES
 14.7 Triple Integrals In Cylindrical and Spherical Coordinates Contemporary Calculus 1 14.7 TIPLE INTEGALS IN CYLINDICAL AND SPHEICAL COODINATES In physics everything is straight, flat or round. Statement
14.7 Triple Integrals In Cylindrical and Spherical Coordinates Contemporary Calculus 1 14.7 TIPLE INTEGALS IN CYLINDICAL AND SPHEICAL COODINATES In physics everything is straight, flat or round. Statement
AP Calculus BC Fall Final Part IIa
 AP Calculus BC 18-19 Fall Final Part IIa Calculator Required Name: 1. At time t = 0, there are 120 gallons of oil in a tank. During the time interval 0 t 10 hours, oil flows into the tank at a rate of
AP Calculus BC 18-19 Fall Final Part IIa Calculator Required Name: 1. At time t = 0, there are 120 gallons of oil in a tank. During the time interval 0 t 10 hours, oil flows into the tank at a rate of
Name: Answer Key David Arnold. Math 50B Integral Calculus May 13, Final Exam
 Math 5B Integral Calculus May 3, 7 Final Exam Name: Answer Key David Arnold Instructions. (9 points) Follow the directions exactly! Whatever you are asked to do, you must do to receive full credit for
Math 5B Integral Calculus May 3, 7 Final Exam Name: Answer Key David Arnold Instructions. (9 points) Follow the directions exactly! Whatever you are asked to do, you must do to receive full credit for
Examples from Section 6.3: Volume by Cylindrical Shells Page 1
 Examples from Section 6.3: Volume by Cylindrical Shells Page 1 Questions Example Find the volume of the region which is created when we rotate the region below y = x x 3 and above < x < about the y-axis.
Examples from Section 6.3: Volume by Cylindrical Shells Page 1 Questions Example Find the volume of the region which is created when we rotate the region below y = x x 3 and above < x < about the y-axis.
AP CALCULUS AB 2003 SCORING GUIDELINES
 CORING GUIDELINE Question Let R be the shaded region bounded by the graphs of y the vertical line =, as shown in the figure above. = and y = e and (b) Find the volume of the solid generated when R is revolved
CORING GUIDELINE Question Let R be the shaded region bounded by the graphs of y the vertical line =, as shown in the figure above. = and y = e and (b) Find the volume of the solid generated when R is revolved
Answer Key. ( 1) n (2x+3) n. n n=1. (2x+3) n. = lim. < 1 or 2x+3 < 4. ( 1) ( 1) 2n n
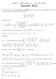 Math Midterm Eam #3 December, 3 Answer Key. [5 Points] Find the Interval and Radius of Convergence for the following power series. Analyze carefully and with full justification. Use Ratio Test. L lim a
Math Midterm Eam #3 December, 3 Answer Key. [5 Points] Find the Interval and Radius of Convergence for the following power series. Analyze carefully and with full justification. Use Ratio Test. L lim a
Applied Calculus I. Lecture 36
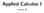 Applied Calculus I Lecture 36 Computing the volume Consider a continuous function over an interval [a, b]. y a b x Computing the volume Consider a continuous function over an interval [a, b]. y y a b x
Applied Calculus I Lecture 36 Computing the volume Consider a continuous function over an interval [a, b]. y a b x Computing the volume Consider a continuous function over an interval [a, b]. y y a b x
Concentric Circles Puzzle
 In the image above, the inner circle has a circumference of 10 and the distance between the inner and outer circles is 3. If the circumference of the inner circle is increased to 11, and the distance between
In the image above, the inner circle has a circumference of 10 and the distance between the inner and outer circles is 3. If the circumference of the inner circle is increased to 11, and the distance between
(a) Use washer cross sections: a washer has
 Section 8 V / (sec tan ) / / / / [ tan sec tan ] / / (sec sec tan + tan ) + tan sec / + A( ) s w (sec tan ), and / V (sec tan ), which b / same method as in part (a) equals A cross section has width w
Section 8 V / (sec tan ) / / / / [ tan sec tan ] / / (sec sec tan + tan ) + tan sec / + A( ) s w (sec tan ), and / V (sec tan ), which b / same method as in part (a) equals A cross section has width w
Two Dimensional Rotational Kinematics Challenge Problem Solutions
 Two Dimensional Rotational Kinematics Challenge Problem Solutions Problem 1: Moment of Inertia: Uniform Disc A thin uniform disc of mass M and radius R is mounted on an axis passing through the center
Two Dimensional Rotational Kinematics Challenge Problem Solutions Problem 1: Moment of Inertia: Uniform Disc A thin uniform disc of mass M and radius R is mounted on an axis passing through the center
Linear Equations. Find the domain and the range of the following set. {(4,5), (7,8), (-1,3), (3,3), (2,-3)}
 Linear Equations Domain and Range Domain refers to the set of possible values of the x-component of a point in the form (x,y). Range refers to the set of possible values of the y-component of a point in
Linear Equations Domain and Range Domain refers to the set of possible values of the x-component of a point in the form (x,y). Range refers to the set of possible values of the y-component of a point in
Math 142, Final Exam. 12/7/10.
 Math 4, Final Exam. /7/0. No notes, calculator, or text. There are 00 points total. Partial credit may be given. Write your full name in the upper right corner of page. Number the pages in the upper right
Math 4, Final Exam. /7/0. No notes, calculator, or text. There are 00 points total. Partial credit may be given. Write your full name in the upper right corner of page. Number the pages in the upper right
and y c from x 0 to x 1
 Math 44 Activity 9 (Due by end of class August 6). Find the value of c, c, that minimizes the volume of the solid generated by revolving the region between the graphs of y 4 and y c from to about the line
Math 44 Activity 9 (Due by end of class August 6). Find the value of c, c, that minimizes the volume of the solid generated by revolving the region between the graphs of y 4 and y c from to about the line
MATH 162. Midterm 2 ANSWERS November 18, 2005
 MATH 62 Midterm 2 ANSWERS November 8, 2005. (0 points) Does the following integral converge or diverge? To get full credit, you must justify your answer. 3x 2 x 3 + 4x 2 + 2x + 4 dx You may not be able
MATH 62 Midterm 2 ANSWERS November 8, 2005. (0 points) Does the following integral converge or diverge? To get full credit, you must justify your answer. 3x 2 x 3 + 4x 2 + 2x + 4 dx You may not be able
( afa, ( )) [ 12, ]. Math 226 Notes Section 7.4 ARC LENGTH AND SURFACES OF REVOLUTION
![( afa, ( )) [ 12, ]. Math 226 Notes Section 7.4 ARC LENGTH AND SURFACES OF REVOLUTION ( afa, ( )) [ 12, ]. Math 226 Notes Section 7.4 ARC LENGTH AND SURFACES OF REVOLUTION](/thumbs/86/93981005.jpg) Math 6 Notes Section 7.4 ARC LENGTH AND SURFACES OF REVOLUTION A curve is rectifiable if it has a finite arc length. It is sufficient that f be continuous on [ab, ] in order for f to be rectifiable between
Math 6 Notes Section 7.4 ARC LENGTH AND SURFACES OF REVOLUTION A curve is rectifiable if it has a finite arc length. It is sufficient that f be continuous on [ab, ] in order for f to be rectifiable between
Westside. Algebra 2 PreAP
 Westside Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for
Westside Algebra 2 PreAP Name Period IMPORTANT INSTRUCTIONS FOR STUDENTS!!! We understand that students come to Algebra II with different strengths and needs. For this reason, students have options for
= first derivative evaluated at that point: ( )
 Calculus 130, section 5.1-5. Functions: Increasing, Decreasing, Extrema notes by Tim Pilachowski Reminder: You will not be able to use a graphing calculator on tests! First, a quick scan of what we know
Calculus 130, section 5.1-5. Functions: Increasing, Decreasing, Extrema notes by Tim Pilachowski Reminder: You will not be able to use a graphing calculator on tests! First, a quick scan of what we know
9.1 Circles and Parabolas. Copyright Cengage Learning. All rights reserved.
 9.1 Circles and Parabolas Copyright Cengage Learning. All rights reserved. What You Should Learn Recognize a conic as the intersection of a plane and a double-napped cone. Write equations of circles in
9.1 Circles and Parabolas Copyright Cengage Learning. All rights reserved. What You Should Learn Recognize a conic as the intersection of a plane and a double-napped cone. Write equations of circles in
1 Wyner PreCalculus Fall 2013
 1 Wyner PreCalculus Fall 2013 CHAPTER ONE: FUNCTIONS AND THEIR GRAPHS Summary, Terms, and Objectives Most of calculus and precalculus is based on functions. A function is a process that takes one or more
1 Wyner PreCalculus Fall 2013 CHAPTER ONE: FUNCTIONS AND THEIR GRAPHS Summary, Terms, and Objectives Most of calculus and precalculus is based on functions. A function is a process that takes one or more
Problem 2: Experiment 09 Physical Pendulum. Part One: Ruler Pendulum
 Problem : Experiment 9 Physical Pendulum Part One: Ruler Pendulum The ruler has a mass m r =.159 k, a width a =.8 m, a lenth b = 1. m, and the distance from the pivot point to the center of mass is l =.479
Problem : Experiment 9 Physical Pendulum Part One: Ruler Pendulum The ruler has a mass m r =.159 k, a width a =.8 m, a lenth b = 1. m, and the distance from the pivot point to the center of mass is l =.479
AP Physics C. Gauss s Law. Free Response Problems
 AP Physics Gauss s Law Free Response Problems 1. A flat sheet of glass of area 0.4 m 2 is placed in a uniform electric field E = 500 N/. The normal line to the sheet makes an angle θ = 60 ẘith the electric
AP Physics Gauss s Law Free Response Problems 1. A flat sheet of glass of area 0.4 m 2 is placed in a uniform electric field E = 500 N/. The normal line to the sheet makes an angle θ = 60 ẘith the electric
E. not enough information given to decide
 Q22.1 A spherical Gaussian surface (#1) encloses and is centered on a point charge +q. A second spherical Gaussian surface (#2) of the same size also encloses the charge but is not centered on it. Compared
Q22.1 A spherical Gaussian surface (#1) encloses and is centered on a point charge +q. A second spherical Gaussian surface (#2) of the same size also encloses the charge but is not centered on it. Compared
