Problem 2: Experiment 09 Physical Pendulum. Part One: Ruler Pendulum
|
|
|
- Candice Hart
- 5 years ago
- Views:
Transcription
1 Problem : Experiment 9 Physical Pendulum Part One: Ruler Pendulum The ruler has a mass m r =.159 k, a width a =.8 m, a lenth b = 1. m, and the distance from the pivot point to the center of mass is l =.479 m. Enter your measured period into the T meas column of the table below and calculate the other entries usin the formulas and with = 9.85 ms -. T = π l theory / T ideal = π l / I θ 1+ ml 16 θ T meas T theory T ideal.1.5 Part Two: Added Mass Consider the effect of a brass weiht clipped to the ruler. The weiht is shaped like a washer with an outer radius r o =.16 m and an inner radius r i =. m; it has a mass m w =.5 k. It is clipped to the ruler so that the inner hole is over the.5 m mark on the ruler, or l =.479 m from the pivot point. The clip has a mass m c =.86 k and you may assume its center of mass is also over the.5 m mark on the ruler. If you treat the washer and clip as point masses, 3
2 then, as was discussed in the notes for Experiment 8, the combined unit (ruler, weiht and clip) has a moment of inertia about the pivot point I P = m ( a + b ) + m 1 r r c w l + (m + m )d where d = l for this situation. The restorin torque that tries to return the pendulum to a vertical position will be τ = (m l + m d + m ) d sin θ (m l + m d + m ) d θ r c w r c w 1. Use these two expressions to derive an equation of motion for the pendulum and calculate its period T in the small amplitude (sinθ θ ) approximation. Express your answer alebraically in terms of the variables a, b, d, l, m r, m w, m c, and.. Evaluate your result numerically and compare with the value you measured in your experiment. 3. If you treat the brass object washer as a point mass, its moment of inertia about the pivot point P is I w,p = m w l. If the brass object is a washer with an inner radius r i and outer radius r, then moment of inertia about its center of mass iven by I = 1 m r + r o w ( w o i ). If the washer is a solid disc with radius r, the moment of inertia about its center of mass iven by I = 1 w mr w.when this is taken into account, what is the new (and more accurate) expression for I w,p? How many percent does this differ from the simpler expression I w,p = m w l? 4
3 Problem : Experiment 9 Physical Pendulum Part One: Ruler Pendulum The ruler has a mass m r =.159 k, a width a =.8 m, a lenth b = 1. m, and the distance from the pivot point to the center of mass is l =.479 m. Enter your measured period into the T meas column of the table below and calculate the other entries usin the formulas and T = π l theory / T ideal = π l / I θ 1+ ml 16 with = 9.85 ms -. Solution: The first part of the analysis of the experiment is to calculate the moment of inertia about an axis passin throuh the center of mass, perpendicular to the plane formed by the sides of the ruler. In particular, choose Cartesian coordinates with the oriin at the center of mass, and the x-axis alon the lenth, and y-axis alon the width. The mass per unit area σ = mass m 1 =. Area ab The mass element is rotatin about the z-axis in a circular orbit with radius r = ( x + y ) 1, so the moment of inertia about the center of mass of the ruler is 3
4 x = b y = a I cm = (r ) dm = σ,cm ( x + y ) dy body x= b y= a dx We first do the interal in the y-direction, 3 I = m x= b 1 x y + y x = b 3 y a dx = m = 1 a cm y= a x a + dx ab x= b 3 ab x= b 1 We now do the interal in the x-direction = = a + x = m b 1 a + b = m 1 ( b + a x= b ) m I 1 x a x b a S ab 3 1 ab = (.159k ) ((1. m) + (.8m) ) = k m 1 Now use the parallel axis theorem to calculate the moment of inertia about the pivot point, = m 1 ( b + a ) + ml 1 1 cm Usin the data for the ruler, the moment about the pivot point is = k m + (.159 k )(.479 m ) = k m. θ T meas T theory T ideal Part Two: Added Mass Consider the effect of a brass weiht clipped to the ruler. The weiht is shaped like a washer with an outer radius r o =.16 m and an inner radius r i =. m; it has a mass m w =.5 k. It is clipped to the ruler so that the inner hole is over the.5 m mark on the ruler, or l =.479 m from the pivot point. The clip has a mass m c =.86 k and you may assume its center of mass is also over the.5 m mark on the ruler. If you treat the washer and clip as point masses, 4
5 then, as was discussed in the notes for Experiment 8, the combined unit (ruler, weiht and clip) has a moment of inertia about the pivot point I P = m ( a + b ) + m l 1 r + (m + m ) d r c w where d = l for this situation. The restorin torque that tries to return the pendulum to a vertical position will be τ = (m l + md + m d) sin θ (m l + md + m d) θ r c w r c w 1. Use these two expressions to derive an equation of motion for the pendulum and calculate its period T in the small amplitude (sinθ θ ) approximation. Express your answer alebraically in terms of the variables a, b, d, l, m r, m w, m c, and. Answer:. Evaluate your result numerically and compare with the value you measured in your experiment. Solution The moment of inertia of the washer and binder clip treated as point masses about the pivot point is cw = ( m + m,, c w ) l cm ( =.586 k.479 m ) = k m 5
6 Thus the total moment of inertia is total = m (b + a ) + ml + (m c + m ) l 1 cm w cm total = k m k m = k m. So the new period is π T = π ω p cm total 1 k m l m total = π 6.3 (.479 m )(.18 k )(9.85 m s - ) = 1.56 s So the approximation ives ood areement with the data. Displacement [ m ] Measured Period [ s ] Calculated Period T [ s ] If you treat the brass object washer as a point mass, its moment of inertia about the pivot point P is I w,p = m w l. If the brass object is a washer with an inner radius r i and outer radius r, then moment of inertia about its center of mass iven by I = 1 m r + r o w ( w o i ). If the washer is a solid disc with radius r, the moment of inertia about its center of mass iven by I = 1 w mr w. When this is taken into account, what is the new (and more accurate) expression for I w,p? How many percent does this differ from the simpler expression I w,p = m w l? Solution: In Problem 1, you showed that the moment of inertia of a washer about the center of mass is iven by the result, I = 1 m r + r ) cm w ( i, so the total moment of inertia is now total = m (b + a ) + ml + ( m + m ) l + 1 m w (r + r ) cm c w cm i 1 6
7 The moment of inertia of the washer about the center of mass is I cm, w 1 = m r + r ) i = 1 (.5k)((.16m) + (.m) ) = k m. w ( 6 This is neliible compared to the overall moment of inertia. The ratio of the moment of the washer about its center of mass compared to the moment of the washer treated as a point mass about the pivot point is I cm, w k m = wcm k m ml =
In-Class Problems 30-32: Moment of Inertia, Torque, and Pendulum: Solutions
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics Physics 8.01 TEAL Fall Term 004 In-Class Problems 30-3: Moment of Inertia, Torque, and Pendulum: Solutions Problem 30 Moment of Inertia of a
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics Physics 8.01 TEAL Fall Term 004 In-Class Problems 30-3: Moment of Inertia, Torque, and Pendulum: Solutions Problem 30 Moment of Inertia of a
Handout 6: Rotational motion and moment of inertia. Angular velocity and angular acceleration
 1 Handout 6: Rotational motion and moment of inertia Angular velocity and angular acceleration In Figure 1, a particle b is rotating about an axis along a circular path with radius r. The radius sweeps
1 Handout 6: Rotational motion and moment of inertia Angular velocity and angular acceleration In Figure 1, a particle b is rotating about an axis along a circular path with radius r. The radius sweeps
OSCILLATIONS
 OSCIAIONS Important Points:. Simple Harmonic Motion: a) he acceleration is directly proportional to the displacement of the body from the fixed point and it is always directed towards the fixed point in
OSCIAIONS Important Points:. Simple Harmonic Motion: a) he acceleration is directly proportional to the displacement of the body from the fixed point and it is always directed towards the fixed point in
APM1612. Tutorial letter 203/1/2018. Mechanics 2. Semester 1. Department of Mathematical Sciences APM1612/203/1/2018
 APM6/03//08 Tutorial letter 03//08 Mechanics APM6 Semester Department of Mathematical Sciences IMPORTANT INFORMATION: This tutorial letter contains solutions to assignment 3, Sem. BARCODE Define tomorrow.
APM6/03//08 Tutorial letter 03//08 Mechanics APM6 Semester Department of Mathematical Sciences IMPORTANT INFORMATION: This tutorial letter contains solutions to assignment 3, Sem. BARCODE Define tomorrow.
For a rigid body that is constrained to rotate about a fixed axis, the gravitational torque about the axis is
 Experiment 14 The Physical Pendulum The period of oscillation of a physical pendulum is found to a high degree of accuracy by two methods: theory and experiment. The values are then compared. Theory For
Experiment 14 The Physical Pendulum The period of oscillation of a physical pendulum is found to a high degree of accuracy by two methods: theory and experiment. The values are then compared. Theory For
Parametric Equations
 Parametric Equations Suppose a cricket jumps off of the round with an initial velocity v 0 at an anle θ. If we take his initial position as the oriin, his horizontal and vertical positions follow the equations:
Parametric Equations Suppose a cricket jumps off of the round with an initial velocity v 0 at an anle θ. If we take his initial position as the oriin, his horizontal and vertical positions follow the equations:
Experiment 08: Physical Pendulum. 8.01t Nov 10, 2004
 Experiment 08: Physical Pendulum 8.01t Nov 10, 2004 Goals Investigate the oscillation of a real (physical) pendulum and compare to an ideal (point mass) pendulum. Angular frequency calculation: Practice
Experiment 08: Physical Pendulum 8.01t Nov 10, 2004 Goals Investigate the oscillation of a real (physical) pendulum and compare to an ideal (point mass) pendulum. Angular frequency calculation: Practice
Chapter 12. Recall that when a spring is stretched a distance x, it will pull back with a force given by: F = -kx
 Chapter 1 Lecture Notes Chapter 1 Oscillatory Motion Recall that when a spring is stretched a distance x, it will pull back with a force given by: F = -kx When the mass is released, the spring will pull
Chapter 1 Lecture Notes Chapter 1 Oscillatory Motion Recall that when a spring is stretched a distance x, it will pull back with a force given by: F = -kx When the mass is released, the spring will pull
Two Dimensional Rotational Kinematics Challenge Problem Solutions
 Two Dimensional Rotational Kinematics Challenge Problem Solutions Problem 1: Moment of Inertia: Uniform Disc A thin uniform disc of mass M and radius R is mounted on an axis passing through the center
Two Dimensional Rotational Kinematics Challenge Problem Solutions Problem 1: Moment of Inertia: Uniform Disc A thin uniform disc of mass M and radius R is mounted on an axis passing through the center
Experiment 3 The Simple Pendulum
 PHY191 Fall003 Experiment 3: The Simple Pendulum 10/7/004 Pae 1 Suested Readin for this lab Experiment 3 The Simple Pendulum Read Taylor chapter 5. (You can skip section 5.6.IV if you aren't comfortable
PHY191 Fall003 Experiment 3: The Simple Pendulum 10/7/004 Pae 1 Suested Readin for this lab Experiment 3 The Simple Pendulum Read Taylor chapter 5. (You can skip section 5.6.IV if you aren't comfortable
Chapter K. Oscillatory Motion. Blinn College - Physics Terry Honan. Interactive Figure
 K. - Simple Harmonic Motion Chapter K Oscillatory Motion Blinn Collee - Physics 2425 - Terry Honan The Mass-Sprin System Interactive Fiure Consider a mass slidin without friction on a horizontal surface.
K. - Simple Harmonic Motion Chapter K Oscillatory Motion Blinn Collee - Physics 2425 - Terry Honan The Mass-Sprin System Interactive Fiure Consider a mass slidin without friction on a horizontal surface.
Rotational Motion, Torque, Angular Acceleration, and Moment of Inertia. 8.01t Nov 3, 2004
 Rotational Motion, Torque, Angular Acceleration, and Moment of Inertia 8.01t Nov 3, 2004 Rotation and Translation of Rigid Body Motion of a thrown object Translational Motion of the Center of Mass Total
Rotational Motion, Torque, Angular Acceleration, and Moment of Inertia 8.01t Nov 3, 2004 Rotation and Translation of Rigid Body Motion of a thrown object Translational Motion of the Center of Mass Total
Mechanics Cycle 3 Chapter 12++ Chapter 12++ Revisit Circular Motion
 Chapter 12++ Revisit Circular Motion Revisit: Anular variables Second laws for radial and tanential acceleration Circular motion CM 2 nd aw with F net To-Do: Vertical circular motion in ravity Complete
Chapter 12++ Revisit Circular Motion Revisit: Anular variables Second laws for radial and tanential acceleration Circular motion CM 2 nd aw with F net To-Do: Vertical circular motion in ravity Complete
PHYS 211 Lecture 21 - Moments of inertia 21-1
 PHYS 211 Lecture 21 - Moments of inertia 21-1 Lecture 21 - Moments of inertia Text: similar to Fowles and Cassiday, Chap. 8 As discussed previously, the moment of inertia I f a single mass m executing
PHYS 211 Lecture 21 - Moments of inertia 21-1 Lecture 21 - Moments of inertia Text: similar to Fowles and Cassiday, Chap. 8 As discussed previously, the moment of inertia I f a single mass m executing
Rotation. I. Kinematics - Angular analogs
 Rotation I. Kinematics - Angular analogs II. III. IV. Dynamics - Torque and Rotational Inertia Work and Energy Angular Momentum - Bodies and particles V. Elliptical Orbits The student will be able to:
Rotation I. Kinematics - Angular analogs II. III. IV. Dynamics - Torque and Rotational Inertia Work and Energy Angular Momentum - Bodies and particles V. Elliptical Orbits The student will be able to:
Rotational Kinetic Energy
 Lecture 17, Chapter 10: Rotational Energy and Angular Momentum 1 Rotational Kinetic Energy Consider a rigid body rotating with an angular velocity ω about an axis. Clearly every point in the rigid body
Lecture 17, Chapter 10: Rotational Energy and Angular Momentum 1 Rotational Kinetic Energy Consider a rigid body rotating with an angular velocity ω about an axis. Clearly every point in the rigid body
Moment of Inertia & Newton s Laws for Translation & Rotation
 Moment of Inertia & Newton s Laws for Translation & Rotation In this training set, you will apply Newton s 2 nd Law for rotational motion: Στ = Σr i F i = Iα I is the moment of inertia of an object: I
Moment of Inertia & Newton s Laws for Translation & Rotation In this training set, you will apply Newton s 2 nd Law for rotational motion: Στ = Σr i F i = Iα I is the moment of inertia of an object: I
f 1. (8.1.1) This means that SI unit for frequency is going to be s 1 also known as Hertz d1hz
 ecture 8-1 Oscillations 1. Oscillations Simple Harmonic Motion So far we have considered two basic types of motion: translational motion and rotational motion. But these are not the only types of motion
ecture 8-1 Oscillations 1. Oscillations Simple Harmonic Motion So far we have considered two basic types of motion: translational motion and rotational motion. But these are not the only types of motion
Rotational Motion and Torque
 Rotational Motion and Torque Introduction to Angular Quantities Sections 8- to 8-2 Introduction Rotational motion deals with spinning objects, or objects rotating around some point. Rotational motion is
Rotational Motion and Torque Introduction to Angular Quantities Sections 8- to 8-2 Introduction Rotational motion deals with spinning objects, or objects rotating around some point. Rotational motion is
CP1 REVISION LECTURE 3 INTRODUCTION TO CLASSICAL MECHANICS. Prof. N. Harnew University of Oxford TT 2017
 CP1 REVISION LECTURE 3 INTRODUCTION TO CLASSICAL MECHANICS Prof. N. Harnew University of Oxford TT 2017 1 OUTLINE : CP1 REVISION LECTURE 3 : INTRODUCTION TO CLASSICAL MECHANICS 1. Angular velocity and
CP1 REVISION LECTURE 3 INTRODUCTION TO CLASSICAL MECHANICS Prof. N. Harnew University of Oxford TT 2017 1 OUTLINE : CP1 REVISION LECTURE 3 : INTRODUCTION TO CLASSICAL MECHANICS 1. Angular velocity and
University of Alabama Department of Physics and Astronomy. PH 125 / LeClair Fall Exam III Solution
 University of Alabama Department of Physics and Astronomy PH 5 / LeClair Fall 07 Exam III Solution. A child throws a ball with an initial speed of 8.00 m/s at an anle of 40.0 above the horizontal. The
University of Alabama Department of Physics and Astronomy PH 5 / LeClair Fall 07 Exam III Solution. A child throws a ball with an initial speed of 8.00 m/s at an anle of 40.0 above the horizontal. The
Prof. Rupak Mahapatra. Physics 218, Chapter 15 & 16
 Physics 218 Chap 14 & 15 Prof. Rupak Mahapatra Physics 218, Chapter 15 & 16 1 Angular Quantities Position Angle θ Velocity Angular Velocity ω Acceleration Angular Acceleration α Moving forward: Force Mass
Physics 218 Chap 14 & 15 Prof. Rupak Mahapatra Physics 218, Chapter 15 & 16 1 Angular Quantities Position Angle θ Velocity Angular Velocity ω Acceleration Angular Acceleration α Moving forward: Force Mass
Announcements. Last year s final exam has been posted. Final exam is worth 200 points and is 2 hours: Quiz #9 this Wednesday:
 Announceents sartphysics hoework deadlines have been reset to :0 PM on eceber 15 (beinnin of final exa). You can et 100% credit if you o back and correct ANY proble on the HW fro the beinnin of the seester!
Announceents sartphysics hoework deadlines have been reset to :0 PM on eceber 15 (beinnin of final exa). You can et 100% credit if you o back and correct ANY proble on the HW fro the beinnin of the seester!
Name Date: Course number: MAKE SURE TA & TI STAMPS EVERY PAGE BEFORE YOU START. Grade: EXPERIMENT 4
 Laboratory Section: Last Revised on June 18, 2018 Partners Names: Grade: EXPERIMENT 4 Moment of Inertia & Oscillations 0 Pre-Laboratory Work [20 pts] 1 a) In Section 31, describe briefly the steps you
Laboratory Section: Last Revised on June 18, 2018 Partners Names: Grade: EXPERIMENT 4 Moment of Inertia & Oscillations 0 Pre-Laboratory Work [20 pts] 1 a) In Section 31, describe briefly the steps you
Two-Dimensional Rotational Dynamics
 Two-Dimensional Rotational Dynamics 8.01 W09D2 W09D2 Reading Assignment: MIT 8.01 Course Notes: Chapter 17 Two Dimensional Rotational Dynamics Sections 17.1-17.5 Chapter 18 Static Equilibrium Sections
Two-Dimensional Rotational Dynamics 8.01 W09D2 W09D2 Reading Assignment: MIT 8.01 Course Notes: Chapter 17 Two Dimensional Rotational Dynamics Sections 17.1-17.5 Chapter 18 Static Equilibrium Sections
Static Equilibrium, Gravitation, Periodic Motion
 This test covers static equilibrium, universal gravitation, and simple harmonic motion, with some problems requiring a knowledge of basic calculus. Part I. Multiple Choice 1. 60 A B 10 kg A mass of 10
This test covers static equilibrium, universal gravitation, and simple harmonic motion, with some problems requiring a knowledge of basic calculus. Part I. Multiple Choice 1. 60 A B 10 kg A mass of 10
PHYSICS 220. Lecture 15. Textbook Sections Lecture 15 Purdue University, Physics 220 1
 PHYSICS 220 Lecture 15 Angular Momentum Textbook Sections 9.3 9.6 Lecture 15 Purdue University, Physics 220 1 Last Lecture Overview Torque = Force that causes rotation τ = F r sin θ Work done by torque
PHYSICS 220 Lecture 15 Angular Momentum Textbook Sections 9.3 9.6 Lecture 15 Purdue University, Physics 220 1 Last Lecture Overview Torque = Force that causes rotation τ = F r sin θ Work done by torque
Classical Mechanics Lecture 15
 Classical Mechanics Lecture 5 Today s Concepts: a) Parallel Axis Theorem b) Torque & Angular Acceleration Mechanics Lecture 5, Slide Unit 4 Main Points Mechanics Lecture 4, Slide Unit 4 Main Points Mechanics
Classical Mechanics Lecture 5 Today s Concepts: a) Parallel Axis Theorem b) Torque & Angular Acceleration Mechanics Lecture 5, Slide Unit 4 Main Points Mechanics Lecture 4, Slide Unit 4 Main Points Mechanics
Two-Dimensional Rotational Kinematics
 Two-Dimensional Rotational Kinematics Rigid Bodies A rigid body is an extended object in which the distance between any two points in the object is constant in time. Springs or human bodies are non-rigid
Two-Dimensional Rotational Kinematics Rigid Bodies A rigid body is an extended object in which the distance between any two points in the object is constant in time. Springs or human bodies are non-rigid
Simple and Physical Pendulums Challenge Problem Solutions
 Simple and Physical Pendulums Challenge Problem Solutions Problem 1 Solutions: For this problem, the answers to parts a) through d) will rely on an analysis of the pendulum motion. There are two conventional
Simple and Physical Pendulums Challenge Problem Solutions Problem 1 Solutions: For this problem, the answers to parts a) through d) will rely on an analysis of the pendulum motion. There are two conventional
Notes on Torque. We ve seen that if we define torque as rfsinθ, and the N 2. i i
 Notes on Torque We ve seen that if we define torque as rfsinθ, and the moment of inertia as N, we end up with an equation mr i= 1 that looks just like Newton s Second Law There is a crucial difference,
Notes on Torque We ve seen that if we define torque as rfsinθ, and the moment of inertia as N, we end up with an equation mr i= 1 that looks just like Newton s Second Law There is a crucial difference,
= 2 5 MR2. I sphere = MR 2. I hoop = 1 2 MR2. I disk
 A sphere (green), a disk (blue), and a hoop (red0, each with mass M and radius R, all start from rest at the top of an inclined plane and roll to the bottom. Which object reaches the bottom first? (Use
A sphere (green), a disk (blue), and a hoop (red0, each with mass M and radius R, all start from rest at the top of an inclined plane and roll to the bottom. Which object reaches the bottom first? (Use
Problem Solving Session 10 Simple Harmonic Oscillator Solutions
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics 8.01 Problem Solving Session 10 Simple Harmonic Oscillator Solutions W13D3-0 Group Problem Gravitational Simple Harmonic Oscillator Two identical
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Physics 8.01 Problem Solving Session 10 Simple Harmonic Oscillator Solutions W13D3-0 Group Problem Gravitational Simple Harmonic Oscillator Two identical
!T = 2# T = 2! " The velocity and acceleration of the object are found by taking the first and second derivative of the position:
 A pendulum swinging back and forth or a mass oscillating on a spring are two examples of (SHM.) SHM occurs any time the position of an object as a function of time can be represented by a sine wave. We
A pendulum swinging back and forth or a mass oscillating on a spring are two examples of (SHM.) SHM occurs any time the position of an object as a function of time can be represented by a sine wave. We
ONLINE: MATHEMATICS EXTENSION 2 Topic 6 MECHANICS 6.3 HARMONIC MOTION
 ONINE: MATHEMATICS EXTENSION Topic 6 MECHANICS 6.3 HARMONIC MOTION Vibrations or oscillations are motions that repeated more or less reularly in time. The topic is very broad and diverse and covers phenomena
ONINE: MATHEMATICS EXTENSION Topic 6 MECHANICS 6.3 HARMONIC MOTION Vibrations or oscillations are motions that repeated more or less reularly in time. The topic is very broad and diverse and covers phenomena
Experiment 1: Simple Pendulum
 COMSATS Institute of Information Technoloy, Islamabad Campus PHY-108 : Physics Lab 1 (Mechanics of Particles) Experiment 1: Simple Pendulum A simple pendulum consists of a small object (known as the bob)
COMSATS Institute of Information Technoloy, Islamabad Campus PHY-108 : Physics Lab 1 (Mechanics of Particles) Experiment 1: Simple Pendulum A simple pendulum consists of a small object (known as the bob)
11 Free vibrations: one degree of freedom
 11 Free vibrations: one deree of freedom 11.1 A uniform riid disk of radius r and mass m rolls without slippin inside a circular track of radius R, as shown in the fiure. The centroidal moment of inertia
11 Free vibrations: one deree of freedom 11.1 A uniform riid disk of radius r and mass m rolls without slippin inside a circular track of radius R, as shown in the fiure. The centroidal moment of inertia
Physics Mechanics. Lecture 32 Oscillations II
 Physics 170 - Mechanics Lecture 32 Oscillations II Gravitational Potential Energy A plot of the gravitational potential energy U g looks like this: Energy Conservation Total mechanical energy of an object
Physics 170 - Mechanics Lecture 32 Oscillations II Gravitational Potential Energy A plot of the gravitational potential energy U g looks like this: Energy Conservation Total mechanical energy of an object
Rotation. Kinematics Rigid Bodies Kinetic Energy. Torque Rolling. featuring moments of Inertia
 Rotation Kinematics Rigid Bodies Kinetic Energy featuring moments of Inertia Torque Rolling Angular Motion We think about rotation in the same basic way we do about linear motion How far does it go? How
Rotation Kinematics Rigid Bodies Kinetic Energy featuring moments of Inertia Torque Rolling Angular Motion We think about rotation in the same basic way we do about linear motion How far does it go? How
SECTION A Torque and Statics
 AP Physics C Multiple Choice Practice Rotation SECTON A Torque and Statics 1. A square piece o plywood on a horizontal tabletop is subjected to the two horizontal orces shown above. Where should a third
AP Physics C Multiple Choice Practice Rotation SECTON A Torque and Statics 1. A square piece o plywood on a horizontal tabletop is subjected to the two horizontal orces shown above. Where should a third
Oscillations. Oscillations and Simple Harmonic Motion
 Oscillations AP Physics C Oscillations and Simple Harmonic Motion 1 Equilibrium and Oscillations A marble that is free to roll inside a spherical bowl has an equilibrium position at the bottom of the bowl
Oscillations AP Physics C Oscillations and Simple Harmonic Motion 1 Equilibrium and Oscillations A marble that is free to roll inside a spherical bowl has an equilibrium position at the bottom of the bowl
Chapter 15 Oscillations
 Chapter 5 Oscillations Any motion or event that repeats itself at reular intervals is said to be periodic. Oscillation: n eneral, an oscillation is a periodic fluctuation in the value of a physical quantity
Chapter 5 Oscillations Any motion or event that repeats itself at reular intervals is said to be periodic. Oscillation: n eneral, an oscillation is a periodic fluctuation in the value of a physical quantity
Oscillatory Motion. Solutions of Selected Problems
 Chapter 15 Oscillatory Motion. Solutions of Selected Problems 15.1 Problem 15.18 (In the text book) A block-spring system oscillates with an amplitude of 3.50 cm. If the spring constant is 250 N/m and
Chapter 15 Oscillatory Motion. Solutions of Selected Problems 15.1 Problem 15.18 (In the text book) A block-spring system oscillates with an amplitude of 3.50 cm. If the spring constant is 250 N/m and
Torque and Simple Harmonic Motion
 Torque and Simple Harmonic Motion Recall: Fixed Axis Rotation Angle variable Angular velocity Angular acceleration Mass element Radius of orbit Kinematics!! " d# / dt! " d 2 # / dt 2!m i Moment of inertia
Torque and Simple Harmonic Motion Recall: Fixed Axis Rotation Angle variable Angular velocity Angular acceleration Mass element Radius of orbit Kinematics!! " d# / dt! " d 2 # / dt 2!m i Moment of inertia
DP Physics Torque Simulation
 DP Physics Torque Simulation Name Go to Phet Simulation: ( http://phet.colorado.edu/simulations/sims.php?sim=torque ) Part I: Torque 1. Click the tab at the top that says torque 2. Set the force equal
DP Physics Torque Simulation Name Go to Phet Simulation: ( http://phet.colorado.edu/simulations/sims.php?sim=torque ) Part I: Torque 1. Click the tab at the top that says torque 2. Set the force equal
Chapter 10. Rotation of a Rigid Object about a Fixed Axis
 Chapter 10 Rotation of a Rigid Object about a Fixed Axis Angular Position Axis of rotation is the center of the disc Choose a fixed reference line. Point P is at a fixed distance r from the origin. A small
Chapter 10 Rotation of a Rigid Object about a Fixed Axis Angular Position Axis of rotation is the center of the disc Choose a fixed reference line. Point P is at a fixed distance r from the origin. A small
Angular Motion, General Notes
 Angular Motion, General Notes! When a rigid object rotates about a fixed axis in a given time interval, every portion on the object rotates through the same angle in a given time interval and has the same
Angular Motion, General Notes! When a rigid object rotates about a fixed axis in a given time interval, every portion on the object rotates through the same angle in a given time interval and has the same
Rotational N.2 nd Law
 Lecture 0 Chapter 1 Physics I Rotational N. nd Law Torque Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi IN THIS CHAPTER, you will continue discussing rotational dynamics Today
Lecture 0 Chapter 1 Physics I Rotational N. nd Law Torque Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi IN THIS CHAPTER, you will continue discussing rotational dynamics Today
Physical Pendulum. 1. Rotary Motion Sensor w/pulley 2. Thin Rod. 3. Brass Mass 4. Protractor/ Ruler
 Physical Pendulum 3 4. Rotary Motion Sensor w/pulley. Thin Rod 3. Brass Mass 4. Protractor/ Ruler The Rotary Motion Sensor is a high precision measuring device and is very delicate. Please handle with
Physical Pendulum 3 4. Rotary Motion Sensor w/pulley. Thin Rod 3. Brass Mass 4. Protractor/ Ruler The Rotary Motion Sensor is a high precision measuring device and is very delicate. Please handle with
Tuesday, September 29, Page 453. Problem 5
 Tuesday, September 9, 15 Page 5 Problem 5 Problem. Set up and evaluate the integral that gives the volume of the solid formed by revolving the region bounded by y = x, y = x 5 about the x-axis. Solution.
Tuesday, September 9, 15 Page 5 Problem 5 Problem. Set up and evaluate the integral that gives the volume of the solid formed by revolving the region bounded by y = x, y = x 5 about the x-axis. Solution.
θ + mgl θ = 0 or θ + ω 2 θ = 0 (2) ω 2 = I θ = mgl sinθ (1) + Ml 2 I = I CM mgl Kater s Pendulum The Compound Pendulum
 Kater s Pendulum The Compound Pendulum A compound pendulum is the term that generally refers to an arbitrary lamina that is allowed to oscillate about a point located some distance from the lamina s center
Kater s Pendulum The Compound Pendulum A compound pendulum is the term that generally refers to an arbitrary lamina that is allowed to oscillate about a point located some distance from the lamina s center
ENGI Multiple Integration Page 8-01
 ENGI 345 8. Multiple Integration Page 8-01 8. Multiple Integration This chapter provides only a very brief introduction to the major topic of multiple integration. Uses of multiple integration include
ENGI 345 8. Multiple Integration Page 8-01 8. Multiple Integration This chapter provides only a very brief introduction to the major topic of multiple integration. Uses of multiple integration include
LAST TIME: Simple Pendulum:
 LAST TIME: Simple Pendulum: The displacement from equilibrium, x is the arclength s = L. s / L x / L Accelerating & Restoring Force in the tangential direction, taking cw as positive initial displacement
LAST TIME: Simple Pendulum: The displacement from equilibrium, x is the arclength s = L. s / L x / L Accelerating & Restoring Force in the tangential direction, taking cw as positive initial displacement
Two small balls, each of mass m, with perpendicular bisector of the line joining the two balls as the axis of rotation:
 PHYSCS LOCUS 17 summation in mi ri becomes an integration. We imagine the body to be subdivided into infinitesimal elements, each of mass dm, as shown in figure 7.17. Let r be the distance from such an
PHYSCS LOCUS 17 summation in mi ri becomes an integration. We imagine the body to be subdivided into infinitesimal elements, each of mass dm, as shown in figure 7.17. Let r be the distance from such an
AP Physics. Harmonic Motion. Multiple Choice. Test E
 AP Physics Harmonic Motion Multiple Choice Test E A 0.10-Kg block is attached to a spring, initially unstretched, of force constant k = 40 N m as shown below. The block is released from rest at t = 0 sec.
AP Physics Harmonic Motion Multiple Choice Test E A 0.10-Kg block is attached to a spring, initially unstretched, of force constant k = 40 N m as shown below. The block is released from rest at t = 0 sec.
Homework # 2. SOLUTION - We start writing Newton s second law for x and y components: F x = 0, (1) F y = mg (2) x (t) = 0 v x (t) = v 0x (3)
 Physics 411 Homework # Due:..18 Mechanics I 1. A projectile is fired from the oriin of a coordinate system, in the x-y plane (x is the horizontal displacement; y, the vertical with initial velocity v =
Physics 411 Homework # Due:..18 Mechanics I 1. A projectile is fired from the oriin of a coordinate system, in the x-y plane (x is the horizontal displacement; y, the vertical with initial velocity v =
Moments of Inertia (7 pages; 23/3/18)
 Moments of Inertia (7 pages; 3/3/8) () Suppose that an object rotates about a fixed axis AB with angular velocity θ. Considering the object to be made up of particles, suppose that particle i (with mass
Moments of Inertia (7 pages; 3/3/8) () Suppose that an object rotates about a fixed axis AB with angular velocity θ. Considering the object to be made up of particles, suppose that particle i (with mass
14. Rotational Kinematics and Moment of Inertia
 14. Rotational Kinematics and Moment of nertia A) Overview n this unit we will introduce rotational motion. n particular, we will introduce the angular kinematic variables that are used to describe the
14. Rotational Kinematics and Moment of nertia A) Overview n this unit we will introduce rotational motion. n particular, we will introduce the angular kinematic variables that are used to describe the
Lecture 10 - Moment of Inertia
 Lecture 10 - oment of Inertia A Puzzle... Question For any object, there are typically many ways to calculate the moment of inertia I = r 2 dm, usually by doing the integration by considering different
Lecture 10 - oment of Inertia A Puzzle... Question For any object, there are typically many ways to calculate the moment of inertia I = r 2 dm, usually by doing the integration by considering different
Chapter 10. Rotation
 Chapter 10 Rotation Rotation Rotational Kinematics: Angular velocity and Angular Acceleration Rotational Kinetic Energy Moment of Inertia Newton s nd Law for Rotation Applications MFMcGraw-PHY 45 Chap_10Ha-Rotation-Revised
Chapter 10 Rotation Rotation Rotational Kinematics: Angular velocity and Angular Acceleration Rotational Kinetic Energy Moment of Inertia Newton s nd Law for Rotation Applications MFMcGraw-PHY 45 Chap_10Ha-Rotation-Revised
JUST THE MATHS UNIT NUMBER INTEGRATION APPLICATIONS 13 (Second moments of a volume (A)) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 13.13 INTEGRATION APPLICATIONS 13 (Second moments of a volume (A)) by A.J.Hobson 13.13.1 Introduction 13.13. The second moment of a volume of revolution about the y-axis 13.13.3
JUST THE MATHS UNIT NUMBER 13.13 INTEGRATION APPLICATIONS 13 (Second moments of a volume (A)) by A.J.Hobson 13.13.1 Introduction 13.13. The second moment of a volume of revolution about the y-axis 13.13.3
1.1. Rotational Kinematics Description Of Motion Of A Rotating Body
 PHY 19- PHYSICS III 1. Moment Of Inertia 1.1. Rotational Kinematics Description Of Motion Of A Rotating Body 1.1.1. Linear Kinematics Consider the case of linear kinematics; it concerns the description
PHY 19- PHYSICS III 1. Moment Of Inertia 1.1. Rotational Kinematics Description Of Motion Of A Rotating Body 1.1.1. Linear Kinematics Consider the case of linear kinematics; it concerns the description
SOLUTION di x = y2 dm. rdv. m = a 2 bdx. = 2 3 rpab2. I x = 1 2 rp L0. b 4 a1 - x2 a 2 b. = 4 15 rpab4. Thus, I x = 2 5 mb2. Ans.
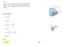 17 4. Determine the moment of inertia of the semiellipsoid with respect to the x axis and express the result in terms of the mass m of the semiellipsoid. The material has a constant density r. y x y a
17 4. Determine the moment of inertia of the semiellipsoid with respect to the x axis and express the result in terms of the mass m of the semiellipsoid. The material has a constant density r. y x y a
CHAPTER 12 OSCILLATORY MOTION
 CHAPTER 1 OSCILLATORY MOTION Before starting the discussion of the chapter s concepts it is worth to define some terms we will use frequently in this chapter: 1. The period of the motion, T, is the time
CHAPTER 1 OSCILLATORY MOTION Before starting the discussion of the chapter s concepts it is worth to define some terms we will use frequently in this chapter: 1. The period of the motion, T, is the time
Rotational Kinematics
 Rotational Kinematics Rotational Coordinates Ridged objects require six numbers to describe their position and orientation: 3 coordinates 3 axes of rotation Rotational Coordinates Use an angle θ to describe
Rotational Kinematics Rotational Coordinates Ridged objects require six numbers to describe their position and orientation: 3 coordinates 3 axes of rotation Rotational Coordinates Use an angle θ to describe
Problem Set x Classical Mechanics, Fall 2016 Massachusetts Institute of Technology. 1. Moment of Inertia: Disc and Washer
 8.01x Classical Mechanics, Fall 2016 Massachusetts Institute of Technology Problem Set 10 1. Moment of Inertia: Disc and Washer (a) A thin uniform disc of mass M and radius R is mounted on an axis passing
8.01x Classical Mechanics, Fall 2016 Massachusetts Institute of Technology Problem Set 10 1. Moment of Inertia: Disc and Washer (a) A thin uniform disc of mass M and radius R is mounted on an axis passing
Chapter 10: Rotation
 Chapter 10: Rotation Review of translational motion (motion along a straight line) Position x Displacement x Velocity v = dx/dt Acceleration a = dv/dt Mass m Newton s second law F = ma Work W = Fdcosφ
Chapter 10: Rotation Review of translational motion (motion along a straight line) Position x Displacement x Velocity v = dx/dt Acceleration a = dv/dt Mass m Newton s second law F = ma Work W = Fdcosφ
Midterm Feb. 17, 2009 Physics 110B Secret No.=
 Midterm Feb. 17, 29 Physics 11B Secret No.= PROBLEM (1) (4 points) The radient operator = x i ê i transforms like a vector. Use ɛ ijk to prove that if B( r) = A( r), then B( r) =. B i = x i x i = x j =
Midterm Feb. 17, 29 Physics 11B Secret No.= PROBLEM (1) (4 points) The radient operator = x i ê i transforms like a vector. Use ɛ ijk to prove that if B( r) = A( r), then B( r) =. B i = x i x i = x j =
Winter Midterm Review Questions
 Winter Midterm Review Questions PHYS106 February 24, 2008 PHYS106 () Winter Midterm Review Questions February 24, 2008 1 / 12 MassCenter003 Calculate the position of the mass center of the rigid system
Winter Midterm Review Questions PHYS106 February 24, 2008 PHYS106 () Winter Midterm Review Questions February 24, 2008 1 / 12 MassCenter003 Calculate the position of the mass center of the rigid system
Physics 201. Professor P. Q. Hung. 311B, Physics Building. Physics 201 p. 1/1
 Physics 201 p. 1/1 Physics 201 Professor P. Q. Hung 311B, Physics Building Physics 201 p. 2/1 Rotational Kinematics and Energy Rotational Kinetic Energy, Moment of Inertia All elements inside the rigid
Physics 201 p. 1/1 Physics 201 Professor P. Q. Hung 311B, Physics Building Physics 201 p. 2/1 Rotational Kinematics and Energy Rotational Kinetic Energy, Moment of Inertia All elements inside the rigid
ENGI 4430 Multiple Integration Cartesian Double Integrals Page 3-01
 ENGI 4430 Multiple Integration Cartesian Double Integrals Page 3-01 3. Multiple Integration This chapter provides only a very brief introduction to the major topic of multiple integration. Uses of multiple
ENGI 4430 Multiple Integration Cartesian Double Integrals Page 3-01 3. Multiple Integration This chapter provides only a very brief introduction to the major topic of multiple integration. Uses of multiple
MULTIVARIABLE INTEGRATION
 MULTIVARIABLE INTEGRATION (SPHERICAL POLAR COORDINATES) Question 1 a) Determine with the aid of a diagram an expression for the volume element in r, θ, ϕ. spherical polar coordinates, ( ) [You may not
MULTIVARIABLE INTEGRATION (SPHERICAL POLAR COORDINATES) Question 1 a) Determine with the aid of a diagram an expression for the volume element in r, θ, ϕ. spherical polar coordinates, ( ) [You may not
MCE 366 System Dynamics, Spring Problem Set 2. Solutions to Set 2
 MCE 366 System Dynamics, Spring 2012 Problem Set 2 Reading: Chapter 2, Sections 2.3 and 2.4, Chapter 3, Sections 3.1 and 3.2 Problems: 2.22, 2.24, 2.26, 2.31, 3.4(a, b, d), 3.5 Solutions to Set 2 2.22
MCE 366 System Dynamics, Spring 2012 Problem Set 2 Reading: Chapter 2, Sections 2.3 and 2.4, Chapter 3, Sections 3.1 and 3.2 Problems: 2.22, 2.24, 2.26, 2.31, 3.4(a, b, d), 3.5 Solutions to Set 2 2.22
Lecture II: Rigid-Body Physics
 Rigid-Body Motion Previously: Point dimensionless objects moving through a trajectory. Today: Objects with dimensions, moving as one piece. 2 Rigid-Body Kinematics Objects as sets of points. Relative distances
Rigid-Body Motion Previously: Point dimensionless objects moving through a trajectory. Today: Objects with dimensions, moving as one piece. 2 Rigid-Body Kinematics Objects as sets of points. Relative distances
Rotational & Rigid-Body Mechanics. Lectures 3+4
 Rotational & Rigid-Body Mechanics Lectures 3+4 Rotational Motion So far: point objects moving through a trajectory. Next: moving actual dimensional objects and rotating them. 2 Circular Motion - Definitions
Rotational & Rigid-Body Mechanics Lectures 3+4 Rotational Motion So far: point objects moving through a trajectory. Next: moving actual dimensional objects and rotating them. 2 Circular Motion - Definitions
Rotational Kinematics and Dynamics. UCVTS AIT Physics
 Rotational Kinematics and Dynamics UCVTS AIT Physics Angular Position Axis of rotation is the center of the disc Choose a fixed reference line Point P is at a fixed distance r from the origin Angular Position,
Rotational Kinematics and Dynamics UCVTS AIT Physics Angular Position Axis of rotation is the center of the disc Choose a fixed reference line Point P is at a fixed distance r from the origin Angular Position,
Solution Derivations for Capa #12
 Solution Derivations for Capa #12 1) A hoop of radius 0.200 m and mass 0.460 kg, is suspended by a point on it s perimeter as shown in the figure. If the hoop is allowed to oscillate side to side as a
Solution Derivations for Capa #12 1) A hoop of radius 0.200 m and mass 0.460 kg, is suspended by a point on it s perimeter as shown in the figure. If the hoop is allowed to oscillate side to side as a
Physics 201 Lab 9: Torque and the Center of Mass Dr. Timothy C. Black
 Theoretical Discussion Physics 201 Lab 9: Torque and the Center of Mass Dr. Timothy C. Black For each of the linear kinematic variables; displacement r, velocity v and acceleration a; there is a corresponding
Theoretical Discussion Physics 201 Lab 9: Torque and the Center of Mass Dr. Timothy C. Black For each of the linear kinematic variables; displacement r, velocity v and acceleration a; there is a corresponding
PhysicsAndMathsTutor.com
 1. A uniform lamina ABC of mass m is in the shape of an isosceles triangle with AB = AC = 5a and BC = 8a. (a) Show, using integration, that the moment of inertia of the lamina about an axis through A,
1. A uniform lamina ABC of mass m is in the shape of an isosceles triangle with AB = AC = 5a and BC = 8a. (a) Show, using integration, that the moment of inertia of the lamina about an axis through A,
Chapter 12: Rotation of Rigid Bodies. Center of Mass Moment of Inertia Torque Angular Momentum Rolling Statics
 Chapter 1: Rotation of Rigid Bodies Center of Mass Moment of Inertia Torque Angular Momentum Rolling Statics Translational vs Rotational / / 1/ m x v dx dt a dv dt F ma p mv KE mv Work Fd P Fv / / 1/ I
Chapter 1: Rotation of Rigid Bodies Center of Mass Moment of Inertia Torque Angular Momentum Rolling Statics Translational vs Rotational / / 1/ m x v dx dt a dv dt F ma p mv KE mv Work Fd P Fv / / 1/ I
Chapter 13: Oscillatory Motions
 Chapter 13: Oscillatory Motions Simple harmonic motion Spring and Hooe s law When a mass hanging from a spring and in equilibrium, the Newton s nd law says: Fy ma Fs Fg 0 Fs Fg This means the force due
Chapter 13: Oscillatory Motions Simple harmonic motion Spring and Hooe s law When a mass hanging from a spring and in equilibrium, the Newton s nd law says: Fy ma Fs Fg 0 Fs Fg This means the force due
PLANAR KINETIC EQUATIONS OF MOTION (Section 17.2)
 PLANAR KINETIC EQUATIONS OF MOTION (Section 17.2) We will limit our study of planar kinetics to rigid bodies that are symmetric with respect to a fixed reference plane. As discussed in Chapter 16, when
PLANAR KINETIC EQUATIONS OF MOTION (Section 17.2) We will limit our study of planar kinetics to rigid bodies that are symmetric with respect to a fixed reference plane. As discussed in Chapter 16, when
Physics 5A Final Review Solutions
 Physics A Final Review Solutions Eric Reichwein Department of Physics University of California, Santa Cruz November 6, 0. A stone is dropped into the water from a tower 44.m above the ground. Another stone
Physics A Final Review Solutions Eric Reichwein Department of Physics University of California, Santa Cruz November 6, 0. A stone is dropped into the water from a tower 44.m above the ground. Another stone
NONLINEAR MECHANICAL SYSTEMS (MECHANISMS)
 NONLINEAR MECHANICAL SYSTEMS (MECHANISMS) The analogy between dynamic behavior in different energy domains can be useful. Closer inspection reveals that the analogy is not complete. One key distinction
NONLINEAR MECHANICAL SYSTEMS (MECHANISMS) The analogy between dynamic behavior in different energy domains can be useful. Closer inspection reveals that the analogy is not complete. One key distinction
Physics 1A Lecture 10B
 Physics 1A Lecture 10B "Sometimes the world puts a spin on life. When our equilibrium returns to us, we understand more because we've seen the whole picture. --Davis Barton Cross Products Another way to
Physics 1A Lecture 10B "Sometimes the world puts a spin on life. When our equilibrium returns to us, we understand more because we've seen the whole picture. --Davis Barton Cross Products Another way to
Harmonic Oscillator - Model Systems
 3_Model Systems HarmonicOscillators.nb Chapter 3 Harmonic Oscillator - Model Systems 3.1 Mass on a spring in a gravitation field a 0.5 3.1.1 Force Method The two forces on the mass are due to the spring,
3_Model Systems HarmonicOscillators.nb Chapter 3 Harmonic Oscillator - Model Systems 3.1 Mass on a spring in a gravitation field a 0.5 3.1.1 Force Method The two forces on the mass are due to the spring,
CIRCULAR MOTION AND ROTATION
 1. UNIFORM CIRCULAR MOTION So far we have learned a great deal about linear motion. This section addresses rotational motion. The simplest kind of rotational motion is an object moving in a perfect circle
1. UNIFORM CIRCULAR MOTION So far we have learned a great deal about linear motion. This section addresses rotational motion. The simplest kind of rotational motion is an object moving in a perfect circle
Chapter 10: Rotation. Chapter 10: Rotation
 Chapter 10: Rotation Change in Syllabus: Only Chapter 10 problems (CH10: 04, 27, 67) are due on Thursday, Oct. 14. The Chapter 11 problems (Ch11: 06, 37, 50) will be due on Thursday, Oct. 21 in addition
Chapter 10: Rotation Change in Syllabus: Only Chapter 10 problems (CH10: 04, 27, 67) are due on Thursday, Oct. 14. The Chapter 11 problems (Ch11: 06, 37, 50) will be due on Thursday, Oct. 21 in addition
Simple Harmonic Motion
 Pendula Simple Harmonic Motion diff. eq. d 2 y dt 2 =!Ky 1. Know frequency (& period) immediately from diff. eq.! = K 2. Initial conditions: they will be of 2 kinds A. at rest initially y(0) = y o v y
Pendula Simple Harmonic Motion diff. eq. d 2 y dt 2 =!Ky 1. Know frequency (& period) immediately from diff. eq.! = K 2. Initial conditions: they will be of 2 kinds A. at rest initially y(0) = y o v y
Motion Of An Extended Object. Physics 201, Lecture 17. Translational Motion And Rotational Motion. Motion of Rigid Object: Translation + Rotation
 Physics 01, Lecture 17 Today s Topics q Rotation of Rigid Object About A Fixed Axis (Chap. 10.1-10.4) n Motion of Extend Object n Rotational Kinematics: n Angular Velocity n Angular Acceleration q Kinetic
Physics 01, Lecture 17 Today s Topics q Rotation of Rigid Object About A Fixed Axis (Chap. 10.1-10.4) n Motion of Extend Object n Rotational Kinematics: n Angular Velocity n Angular Acceleration q Kinetic
Cross Product Angular Momentum
 Lecture 21 Chapter 12 Physics I Cross Product Angular Momentum Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi IN THIS CHAPTER, you will continue discussing rotational dynamics
Lecture 21 Chapter 12 Physics I Cross Product Angular Momentum Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi IN THIS CHAPTER, you will continue discussing rotational dynamics
Circular motion. Aug. 22, 2017
 Circular motion Aug. 22, 2017 Until now, we have been observers to Newtonian physics through inertial reference frames. From our discussion of Newton s laws, these are frames which obey Newton s first
Circular motion Aug. 22, 2017 Until now, we have been observers to Newtonian physics through inertial reference frames. From our discussion of Newton s laws, these are frames which obey Newton s first
Problem 1. Mathematics of rotations
 Problem 1. Mathematics of rotations (a) Show by algebraic means (i.e. no pictures) that the relationship between ω and is: φ, ψ, θ Feel free to use computer algebra. ω X = φ sin θ sin ψ + θ cos ψ (1) ω
Problem 1. Mathematics of rotations (a) Show by algebraic means (i.e. no pictures) that the relationship between ω and is: φ, ψ, θ Feel free to use computer algebra. ω X = φ sin θ sin ψ + θ cos ψ (1) ω
Earth s Magnetic Field Adapted by MMWaite from Measurement of Earth's Magnetic Field [Horizontal Component] by Dr. Harold Skelton
![Earth s Magnetic Field Adapted by MMWaite from Measurement of Earth's Magnetic Field [Horizontal Component] by Dr. Harold Skelton Earth s Magnetic Field Adapted by MMWaite from Measurement of Earth's Magnetic Field [Horizontal Component] by Dr. Harold Skelton](/thumbs/79/78981217.jpg) Adapted by MMWaite from Measurement of Earth's Magnetic Field [Horizontal Component] by Dr. Harold Skelton Object: The purpose of this lab is to determine the horizontal component of the Earth s Magnetic
Adapted by MMWaite from Measurement of Earth's Magnetic Field [Horizontal Component] by Dr. Harold Skelton Object: The purpose of this lab is to determine the horizontal component of the Earth s Magnetic
Parameterization and Vector Fields
 Parameterization and Vector Fields 17.1 Parameterized Curves Curves in 2 and 3-space can be represented by parametric equations. Parametric equations have the form x x(t), y y(t) in the plane and x x(t),
Parameterization and Vector Fields 17.1 Parameterized Curves Curves in 2 and 3-space can be represented by parametric equations. Parametric equations have the form x x(t), y y(t) in the plane and x x(t),
Physics 2001/2051 The Compound Pendulum Experiment 4 and Helical Springs
 PY001/051 Compound Pendulum and Helical Springs Experiment 4 Physics 001/051 The Compound Pendulum Experiment 4 and Helical Springs Prelab 1 Read the following background/setup and ensure you are familiar
PY001/051 Compound Pendulum and Helical Springs Experiment 4 Physics 001/051 The Compound Pendulum Experiment 4 and Helical Springs Prelab 1 Read the following background/setup and ensure you are familiar
Classical Mechanics Comprehensive Exam Solution
 Classical Mechanics Comprehensive Exam Solution January 31, 011, 1:00 pm 5:pm Solve the following six problems. In the following problems, e x, e y, and e z are unit vectors in the x, y, and z directions,
Classical Mechanics Comprehensive Exam Solution January 31, 011, 1:00 pm 5:pm Solve the following six problems. In the following problems, e x, e y, and e z are unit vectors in the x, y, and z directions,
Qualifying Exam. Aug Part II. Please use blank paper for your work do not write on problems sheets!
 Qualifying Exam Aug. 2015 Part II Please use blank paper for your work do not write on problems sheets! Solve only one problem from each of the four sections Mechanics, Quantum Mechanics, Statistical Physics
Qualifying Exam Aug. 2015 Part II Please use blank paper for your work do not write on problems sheets! Solve only one problem from each of the four sections Mechanics, Quantum Mechanics, Statistical Physics
E = K + U. p mv. p i = p f. F dt = p. J t 1. a r = v2. F c = m v2. s = rθ. a t = rα. r 2 dm i. m i r 2 i. I ring = MR 2.
 v = v i + at x = x i + v i t + 1 2 at2 E = K + U p mv p i = p f L r p = Iω τ r F = rf sin θ v 2 = v 2 i + 2a x F = ma = dp dt = U v dx dt a dv dt = d2 x dt 2 A circle = πr 2 A sphere = 4πr 2 V sphere =
v = v i + at x = x i + v i t + 1 2 at2 E = K + U p mv p i = p f L r p = Iω τ r F = rf sin θ v 2 = v 2 i + 2a x F = ma = dp dt = U v dx dt a dv dt = d2 x dt 2 A circle = πr 2 A sphere = 4πr 2 V sphere =
ET-105(A) : PHYSICS. Show that only an infinitesimal rotation can be regarded as a vector.
 No. of Printed Pages : 7 ET-105(A) B.Tech. Civil (Construction Management) / B.Tech. Civil (Water Resources Engineering) / BTCLEVI / BTMEVI / BTELVI / BTECVI / BTCSVI Term-End Examination June, 2017 ET-105(A)
No. of Printed Pages : 7 ET-105(A) B.Tech. Civil (Construction Management) / B.Tech. Civil (Water Resources Engineering) / BTCLEVI / BTMEVI / BTELVI / BTECVI / BTCSVI Term-End Examination June, 2017 ET-105(A)
