STATISTICS DEPARTMENT. Technical Report
|
|
|
- Alice Parks
- 5 years ago
- Views:
Transcription
1 STATISTICS DEPARTMENT Technicl Report RT-MAE Miniml repir ge replcement in heterogeneous popultion: n optiml stopping problem by Vnderlei d Cost Bueno Institute of Mthemtics nd Sttistics University of São Pulo São Pulo - Brzil
2 This pper is of exclusive responsibility of the uthors. Reproduction of this text nd the dt it contins is llowed s long s the source is cited. Reproductions for commercil purposes re prohibited. 2
3 Miniml repir ge replcement in heterogeneous popultion: n optiml stopping problem Vnderlei d Cost Bueno Abstrct In this note we nlyse miniml repir ge replcement policy s solution of n optiml stopping problem under point process mrtingle theory. Keywords: Semi-mrtingle, optiml stopping rule, miniml repir, ge replcement policy. 1 Introduction The most common, populr nd importnt replcement policy might be the ge dependent preventive mintennce policy. Under this policy, unit is lwys replced t its ge T or its filure, whichever occurs first nd T is constnt. Lter, s the concepts of miniml repirs becme more nd more stblish, lrge vriety of extensions nd modifictions of the ge-replcement policy were proposed. An overview on the mintennce theory from theoreticl point of view cn be found in Ncgw (25). More sophisticted models hve lso been developed in Mi, J.(1994), Ch, J.H. (21), Ch, J.H. (23), Ebrhimi, N. (1997), Aven nd Jensen (2) nd Bdi, F.G. et l. ( 21). Most of the previous reserch on mintennce models hs been focused on those for items from homogeneous popultion, however popultion heterogeneity hs been widely recognized in relibility re nd lot of studies on the stochstic properties of heterogeneous popultions hve been recently performed in relibility context, s in Bdi, F.G. et l. ( 23), Ch nd Finkelstein (211) nd Finkelstein nd Ch (213). In this pper we consider mixed popultion which is composed of ordered subpopultions through its intensities. An item is selected of n unknown subpopultion nd during its opertion is minimlly repired on ech filure nd it is replced t fixed ge. As the subpopultion re stochsticlly ordered, the ge t which the corresponding item is replced should be different depending on the subpopultion from which the item in opertion is selected. When the opertionl history of the item, which my contin some importnt informtion bout the corresponding subpopultion, cn be obtined during the field opertion, it is resonble to employ it in determining the replcement policy of the item. To be more specific, the items from stronger subpopultions nd those from weker subpopultions would exhibit different filure ptterns during field opertions. Thus, news replcement policies cn be nlysed, the ge t which the corresponding item will be replced is not determined before the opertion of the item, but it will be determined bsed on the filure/repir history of the observed item during its initil opertion, which is n stopping time problem. This problem ws studied in Ch, J. H. (215) considering 1
4 week nd strong sub-popultions in stochstic process frmework. However, the nturl pproch to consider effectively the informtion of pssed events in time is the point process mrtingle theory which consider the incresing informtion in time through incresing fmilies of σ-lgebrs. In this context, in this pper, we resumes to solve nd generlizes the bsic miniml repir ge replcement optiml stopping problem using n infinitesiml-look-hed stopping rule. In Section 2 we describe the miniml repir process in n heterogeneous popultions nd in Section 3 we nlyse miniml repir ge replcement optiml stopping problem in heterogenious popultions. 2 Miniml repir processes in heterogeneous popultions In this section we describe the heterogeneous popultion nd the corresponding miniml repir process s in Ch nd Finkelstein (211). Let filures of repirble items be repired instntneously. Then the process of repirs cn be described by stochstic point process or, equivlently, by its stochstic intensity λ t, t, (see Aven nd Jensen (1991) nd Bremud (1981)). The stochstic intensity of point process (N t ) t is defined s P (N t,t+ t = 1 I t ) λ t = lim t t = lim t E[N t,t+ t I t ]. t where N t,t+ t = N t+ t N t nd I t = σ{s i, 1 i N t }. A clssicl exmple is the deterministic intensity λ t = λ(t) which defines the nonhomogeneous Poisson process (NHPP) of repirs with intensity λ(t). It is well known tht the NHPP cn be interpreted s the miniml repir process. To describe n heterogeneous popultion we let S be n item lifetime com cumultive distribution function F (t) nd ssume tht it is indexed by rndom vrible Z, i.e. F (t, z) = P (S t Z = z) = P (S t z) nd tht the probbility density function f(t, z) exists. Then the corresponding filure rte λ(t, z) is f(t,z). F (t,z) Let Z be non negtive rndom vrible with support in [, b], < b, nd probbility density function π(z). The setting leds nturlly to considering mixtures of distribution functions which re useful to describing heterogeneity: F m (t) = F (t, z)π(z)dz. In ccordnce with this definition, the mixture filure rte is λ m (t) = f(t, z)π(z)dz = F (t, z)π(z)dz 2 λ(t, z)π(z t)dz,
5 where F (t, z) π(z t) = π(z T > t) = π(z). F (t, z)π(z)dz is the conditionl probbility function on {S > t}. Let return to the stochstic intensity nd modify it with respect to the heterogeneous cse, when the orderly point process is indexed (conditioned) by the rndom vrible Z: P (N t,t+ t = 1 I t, σ(z)) λ t = lim t t = lim E[P (N t,t+ t = 1 I t, σ(z)) ] = E[λ t,z ]. t t where the expecttion is with respect to the conditionl distribution (Z I t ). We, now, consider the miniml repir process of n item selected, t time t =, from our heterogeneous popultion. At ech filure, perform miniml repir. In this cse if Z = z t time t =, the corresponding intensity reliztion is deterministic, λ t,z = λ(t, Z), t, in view tht t t =, the informtion is the degenerted σ- field, σ{ω, } nd the distribution π(z). So, if t 1 is the reliztion of the first filure T 1 in the intervl [, t 1 ), λ(t, Z) = λ m (t) = λ 1 m(t) is just the mixture of the filure rte. The corresponding stochstic intensity λ t is the expecttion of λ(t, Z) with respect to the distribution (Z I t ). This opertions mens tht lthough the vlue of Z is chosen t t = nd is fixed, its distribution is updted with time s informtion bout the filures emerges. In the next intervl [t 1, t 2 ), where t 2 is the reliztion of T 2, given the dditionl informtion tht n item hs filed t t = t 1, the probbility density function of Z is ctulized s π 2 (z) = λ(t 1, z) exp{ t 1 λ(s, z)ds}π(z) λ(t 1, z) exp{ t 1. λ(s, z)ds}π(z)dz The conditionl distribution of (Z I t ) is λ(t 1, z) exp{ t λ(s, z)ds}π(z) λ(t 1, z) exp{ t λ(s, z)ds}π(z)dz nd the corresponding stochstic intensity is λ 2 m(t) = λ(t, z) λ(t 1, z) exp{ t λ(s, z)ds}π(z) λ(t 1, z) exp{ t λ(s, z)ds}π(z)dz in [t 1, t 2 ). More generlly, for t [t n 1, t n ), the conditionl distribution (Z I t ) is defined by π n (z t 1,..., t n 1 ) = λ(t 1, z)...λ(t n 1, z) exp{ t λ(s, z)ds}π(z) λ(t 1, z)...λ(t n 1, z) exp{. t λ(s, z)ds}π(z)dz 3
6 Therefore in [t n 1, t n ) nd λ n m(t) = λ(t, z)π n (z t 1,..., t n 1 )dz λ t = λ n m(t)1 {Tn 1 t<t n}, T =. n=1 3 Miniml repir ge replcement optiml stopping problem in heterogeneous popultion. An item is rndomly selected of unknown subpopultion nd during its opertion is minimlly repired in ech filure nd replced t fixed ge T. We suppose cost c m for ech miniml repir nd cost c r for replcement. If N t is the number of miniml repirs in (, t], the totl cost up to time t, for the item, is c m N t + c r. The totl cost for unit time is C(t) = cmnt+cr. The gol is to find the replcement ge tht minimizes the long run t verge cost per unit time C(T ) = c me[n T ] + c r. E[T ] The replcement policies cn be strongly connected to the following stopping problem: Minimize C τ = E[Z τ] E[X τ ], in suitble clss of stopping time relted to filtrtion (I t ) t which represents our observtions, in the probbility spce (Ω, I, P ), ssumed to fulfill the usul conditions of right continuity nd completeness. The stochstic processes Z t nd X t re observble in (I t ) t, tht is, Z t nd X t re I t -mesurble. As before, T represents the ge replcement nd S the item lifetime. We let (Z t ) t, with Z t = c m N t + c r nd (X t ) t, with X t = t be rel right continuous stochstic processes dpted to I t nd such tht E[Z S ] > nd E[ X S ] <. We intend to minimize the rte C τ = E[Z τ] E[X τ ] over the clss of I t -stopping time C It S = {τ : τ is n I t stopping time, τ S, E[Z τ ] >, E[ X τ ] < }, tht is, to find stopping time σ C It S, with C = C σ = inf{c τ : τ C It S }. 4
7 It is well known tht smooth semi-mrtingle (see ppendix 2.1) representtions for the processes (Z t ) t nd (X t ) t, is n excellent tool to crry out the stopping problem. Under Section 2, the semi-mrtingle representtion for Z t is : = c m n=1 t Z t = c m N t + c r = c m { t λ n m(s)ds + M t } + c r n=1 1 {tn 1 t<t n}λ(t, z)π n (z t 1,..., t n 1 )dzds + M t } + cr, where M t is n uniformly integrl zero men I t -mrtingle. Also X t = t = t ds = t 1 {tn 1 t<t n}π n (z t 1,..., t n 1 )dzds. n=1 To solve the bove stopping problem is equivlent to solve the following mximiztion problem. Observe tht the inequlity C τ = E[Zτ ] E[X τ ] C is equivlent to C E[X τ ] E[Z τ ] for ll τ C It S, where the equlity holds for n optiml stopping time. We hve the mximiztion problem: Find σ C It S, with E[Y σ ] = sup{e[y τ ] : τ C It S } =, where Y t = C X t Z t nd C = inf{c τ : τ C It S }. A smooth semi-mrtingle representtion for Y t for the miniml repir ge replcement policy is where λ s = Therefore n=1 1 {tn 1 t<t n} Y t = c r + t (C c m λ s )ds + M t λ(t, z)π n (z t 1,..., t n 1 )dz. E[Y t ] = E[C X t Z t ] = c + E[ t (C c m λ s )ds] To find n explicit solution of the stopping problem we dopt condition clled the monotone cse: Definition 3.1 (MON) Let Y = (f, M) be n SSM. Then the following condition {f t } {f t+h }, t, h R +, {f t } = Ω t R + 5
8 is sid to be the monotone cse nd the stopping time σ = inf{t R + : f t } is clled the ILA-stopping rule ( infinitesiml-look-hed). Obviously in the monotone cse the process f driving the smooth semi-mrtingle Y t remins non-positive if once crosses zero from bove nd the ILA-stopping rule σ is cndidte to solve the mximiztion problem. Aven nd Jensen (1991), proves tht Theorem 3.2 Let Y = (f, M) be n SSM nd σ the ILA-stopping rule. Then, in the monotone cse, E[Y σ ] = sup{e[y τ ] : τ C It }, where C It = {τ : τ is n I t stopping time, τ <, E[Y τ ] > }. Clerly, the monotone cse holds when λ s is incresing,.s., λ < C c m nd lim s λ s > C c m. However it is seem too restrictive to demnd tht λ s is incresing.s.. We would like the monotone cse to cover cses s the bth-tub-shped functions, which decrese first up to sme vlue, nd increse fter tht vlue. The definition of (, b)-incresing function llows such cses, see ppendix A.2.2. The min ide to solve the stopping problem, for the bsic replcement policy, using the monotonicity condition is, insted to considering ll stopping time in C It T we my restrict the serch for n optiml stopping time to the clss of index stopping times ρ x = inf{s R + : x c m λ s } T, inf =, x R. The optiml stopping level cn be determined from E[Y τ ] = nd coincides with C s in the following Theorem from Aven nd Jensen (1991). Theorem 3.3 If the process (Y t ) t in its SSM representtion hs n intensity with (, b) incresing pths on (, T ], then σ = ρ x, with x = inf{x R : xe[ρ x ] E[Z ρx ] } is n optiml stopping time with x = C. 6
9 nd, In our context λ s = t n=1 λ(t, z)π n (z t 1,..., t n 1 )dz. t = c r + E{ n=1 E[Y t ] = c r + E[ t (C c m λ s )ds] 1 {tn 1 s<t n}π n (z t 1,..., t n 1 )[C c m λ(s, z)]dzds. ρ x = inf{s R + : x c m λ(s, z) } T, inf =, x R considering vlues of x in [ cr + qλ E[T ], cme[ T λ(s,z)ds]+cr ] obtined from Lemm A.2.3. E[T ] This mens: Replce the items the first time the sum of the intensities reches level x. This level hs to be determined s x = inf{x R : xe[ρ x ] E[c m N(ρ x ) + c r ] }. The cse of deterministic intensities is of specil interest nd is stted s corollry under the ssumption of the lst theorem. Lemm 3.4 If λ(t, z) is deterministic with inverse λ 1 = inf{t R : λ(t, z) x}, x R nd X =, then σ = t T is optiml with t = λ 1 (C ) R + { } nd C = inf{x R : where S is the item lifetime. λ 1 (x) [x c m λ(s, z)]p (S > s)ds c r }, We observe tht the bove result is lso pplied for doubly stochstic Poisson process, lso clled Cox process, when the intensity is rndom vrible which is known t the time origin, tht is, λ is I mesurble. We cn tke I = σ{λ s,z, (s, z) R 2 +} nd I t = I σ{n s, s t}. Consider subpopultions of items with Weibull distribution F (t, ) = 1 exp[ ( t η ) β ], η < t <, < < 1, β >. The index is rndom with probbility density π() = (β 1) β, < < 1, An item of n unknown subpopultion is selected nd during its opertion is minimlly repired 7
10 following ordered Weibull process, forming Cox Process. In prcticl we consider the ordered lifetimes with conditionl survivl function given by F (t i t 1, t 2,..., t i 1 ) = exp[ ( t i η i ) β + ( t i η i 1 ) β ] for η i t i 1 < t i where t i re the ordered observtions. The density function is f(t 1, t 2,..., t n ) = π n i=1f(t i t 1, t 2,..., t i 1 ) = Follows tht ( β )(t 1 η 1 ) β 1 exp[( t 1 η 1 exp[ ( t i η i ) β ]πi=2( n β )(t i η i ) β 1 ) β + ( t i η i 1 ) β ]. λ(t i, t 1, t 2,..., t i 1 ) = f(t 1, t 2,..., t n ) F (t i t 1, t 2,..., t i 1 ) = (β )(t η i ) β 1, t i 1 t < t i, t = is deterministic nd λ 1 (t) = inf{s R + : c m λ(s, z) x c r } T, inf =, x R We ssumes β > 1, which mke λ(t, ) incresing in t, nd λ 1 (t) = ( (t c r) β 1 ) 1 β 1 + ηi. c m β As, in this cse, the intensity is deterministic, we cn pply Corollry 3.4 nd get the ge replcement T, indexed by. 4 Appendix. 4.1 A.1 An extended nd positive rndom vrible τ is n I t -stopping time if, nd only if, {τ t} I t, for ll t ; n I t -stopping time τ is clled predictble if n incresing sequence (τ n ) n of I t -stopping time, τ n < τ, exists such tht lim n τ n = τ; n I t -stopping time τ is totlly inccessible if P (τ = σ < ) = for ll predictble I t -stopping time σ. For bsis of stochstic processes see the book of Bremud [2]. 8
11 4.2 A.2 The stopping problem. Definition A.2.1 A stochstic process Z = (Z t ) t is clled smooth semimrtingle representtion (SSM) if it hs decomposition of the form Z t = Z + t f s ds + M t, where (f t ) t, is progressively mesurble process with E[ t f s ds < for ll t R, E[ Z ] < nd (M t ) t n zero men uniformly integrble I t mrtingle. We denote SSM by Z = (f, M). Definition A.2.2 Let, b R {, }, b. Then function f : R + R is clled (, b)-incresing if for ll t, h R +, f(t), implies f(t + h) min{f(t), b}. Roughly spoken, n (, b)-incresing function f(t) psses with incresing t the levels, b from bellow nd never flls bck bellow such level. The first step to detect the prmeters nd b is to estblish bounds for C : Lemm A.2.3 Let X = (g, L) nd Z = (f, M) be smooth semimrtingles under the bove ssumptions nd Then q = inf{ f t(w) g t (w) holds true, where the bounds re given by : t < S(w), w Ω} >. b l C b u b u = E[Z S] E[X S ], b l = E[Z qx E[X S ] + q, if E[Z qx ] > ;E[Z ] E[X ],otherwise. 9
12 5 Conclusions News replcement policies cn be nlysed, the ge t which the corresponding item will be replced is not determined before the opertion of the item, but it will be determined bsed on the filure/repir history of the observed item during its initil opertion, view s n stopping time problem. We conjecture the vlidtion of such model for more sophisticted policies. 6 Acknowledgements This work ws prtilly supported by FAPESP, Proc No. 215/ nd by the University of São Pulo. 7 References [1] Aven, T. nd Jensen, U. Stochstic Models in Relibility. Springer Verlg, New York, [2] Aven, T. nd Jensen, U. A generl miniml repir model, J. Appl. Probbility, 37,, , 2. [3] Bdi, F. G., Berrde, M.D. nd Cmpos, C.A. Optimiztion of inspection intervls bsed on cost, J. Appl. Probbility, 38, , 21. [4] Bdi, F. G., Berrde, M.D. nd Cmpos, C.A. Why does the filure rte decrese?, in Proc. VIIth Zrgoz-Pu Conf. Appl. Mth. Sttistics, 97-14, 23. [5] Brlow nd Proschn,F. Sttisticl Theory of Relibility nd Life Testing: Probbility models. Hold, Reinhrt nd Wiston, Inc. Silver Spring, MD [5] Bremud, P. Point Processes nd Queues: Mrtingles Dynmics. Springer Verlg, New York, [6] Ch, J. H. nd Finkelstein, M. Stochstic intensity for miniml repirs in heterogeneous popultions. J. Al. Prob., 48, , 211. [7] Ch, J. H. Burn-in procedures for generlized model, J. Appl. Probbility, 38, , 21. [8] Ch, J. H. A further extension of generlized burn-in model, J. Appl. Probbility, 4, , 23. 1
13 [9] Ch, J. H. Optiml replcement of heterogeneous items with minimlrepirs, IEEE Trnsctions on Relibility, 1-11, 215. [1] Ebrhimi, N. Multivrite ge replecement, J. Appl. Probbility, 34, , [11]Finkelstein, M. nd Ch, J.H. Stochstic modelling for relibility (Shocks, Burn-in nd Heterogeneous popultions) Springer, LOndon, Uk, 213. [12] Mi, J. Burn-in nd mintennce policies. Adv. Appl. Probbility, 26, , [13] Nkgw, T. Mintennce theory of relibility. Springer, London, Uk,
Continuous Random Variables
 STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 217 Néhémy Lim Continuous Rndom Vribles Nottion. The indictor function of set S is rel-vlued function defined by : { 1 if x S 1 S (x) if x S Suppose tht
STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 217 Néhémy Lim Continuous Rndom Vribles Nottion. The indictor function of set S is rel-vlued function defined by : { 1 if x S 1 S (x) if x S Suppose tht
Chapter 5 : Continuous Random Variables
 STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 216 Néhémy Lim Chpter 5 : Continuous Rndom Vribles Nottions. N {, 1, 2,...}, set of nturl numbers (i.e. ll nonnegtive integers); N {1, 2,...}, set of ll
STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 216 Néhémy Lim Chpter 5 : Continuous Rndom Vribles Nottions. N {, 1, 2,...}, set of nturl numbers (i.e. ll nonnegtive integers); N {1, 2,...}, set of ll
Advanced Calculus: MATH 410 Notes on Integrals and Integrability Professor David Levermore 17 October 2004
 Advnced Clculus: MATH 410 Notes on Integrls nd Integrbility Professor Dvid Levermore 17 October 2004 1. Definite Integrls In this section we revisit the definite integrl tht you were introduced to when
Advnced Clculus: MATH 410 Notes on Integrls nd Integrbility Professor Dvid Levermore 17 October 2004 1. Definite Integrls In this section we revisit the definite integrl tht you were introduced to when
On the Generalized Weighted Quasi-Arithmetic Integral Mean 1
 Int. Journl of Mth. Anlysis, Vol. 7, 2013, no. 41, 2039-2048 HIKARI Ltd, www.m-hikri.com http://dx.doi.org/10.12988/ijm.2013.3499 On the Generlized Weighted Qusi-Arithmetic Integrl Men 1 Hui Sun School
Int. Journl of Mth. Anlysis, Vol. 7, 2013, no. 41, 2039-2048 HIKARI Ltd, www.m-hikri.com http://dx.doi.org/10.12988/ijm.2013.3499 On the Generlized Weighted Qusi-Arithmetic Integrl Men 1 Hui Sun School
Reversals of Signal-Posterior Monotonicity for Any Bounded Prior
 Reversls of Signl-Posterior Monotonicity for Any Bounded Prior Christopher P. Chmbers Pul J. Hely Abstrct Pul Milgrom (The Bell Journl of Economics, 12(2): 380 391) showed tht if the strict monotone likelihood
Reversls of Signl-Posterior Monotonicity for Any Bounded Prior Christopher P. Chmbers Pul J. Hely Abstrct Pul Milgrom (The Bell Journl of Economics, 12(2): 380 391) showed tht if the strict monotone likelihood
Imperfect repair and lifesaving in heterogeneous populations
 ARTICLE IN PRESS Relibility Engineering nd System Sfety 92 (27) 1671 1676 www.elsevier.com/locte/ress Imperfect repir nd lifesving in heterogeneous popultions Mxim Finkelstein,b, Deprtment of Mthemticl
ARTICLE IN PRESS Relibility Engineering nd System Sfety 92 (27) 1671 1676 www.elsevier.com/locte/ress Imperfect repir nd lifesving in heterogeneous popultions Mxim Finkelstein,b, Deprtment of Mthemticl
Lecture 3 ( ) (translated and slightly adapted from lecture notes by Martin Klazar)
 Lecture 3 (5.3.2018) (trnslted nd slightly dpted from lecture notes by Mrtin Klzr) Riemnn integrl Now we define precisely the concept of the re, in prticulr, the re of figure U(, b, f) under the grph of
Lecture 3 (5.3.2018) (trnslted nd slightly dpted from lecture notes by Mrtin Klzr) Riemnn integrl Now we define precisely the concept of the re, in prticulr, the re of figure U(, b, f) under the grph of
UNIFORM CONVERGENCE. Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3
 UNIFORM CONVERGENCE Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3 Suppose f n : Ω R or f n : Ω C is sequence of rel or complex functions, nd f n f s n in some sense. Furthermore,
UNIFORM CONVERGENCE Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3 Suppose f n : Ω R or f n : Ω C is sequence of rel or complex functions, nd f n f s n in some sense. Furthermore,
The Regulated and Riemann Integrals
 Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Math 8 Winter 2015 Applications of Integration
 Mth 8 Winter 205 Applictions of Integrtion Here re few importnt pplictions of integrtion. The pplictions you my see on n exm in this course include only the Net Chnge Theorem (which is relly just the Fundmentl
Mth 8 Winter 205 Applictions of Integrtion Here re few importnt pplictions of integrtion. The pplictions you my see on n exm in this course include only the Net Chnge Theorem (which is relly just the Fundmentl
arxiv:math/ v2 [math.ho] 16 Dec 2003
![arxiv:math/ v2 [math.ho] 16 Dec 2003 arxiv:math/ v2 [math.ho] 16 Dec 2003](/thumbs/92/109668180.jpg) rxiv:mth/0312293v2 [mth.ho] 16 Dec 2003 Clssicl Lebesgue Integrtion Theorems for the Riemnn Integrl Josh Isrlowitz 244 Ridge Rd. Rutherford, NJ 07070 jbi2@njit.edu Februry 1, 2008 Abstrct In this pper,
rxiv:mth/0312293v2 [mth.ho] 16 Dec 2003 Clssicl Lebesgue Integrtion Theorems for the Riemnn Integrl Josh Isrlowitz 244 Ridge Rd. Rutherford, NJ 07070 jbi2@njit.edu Februry 1, 2008 Abstrct In this pper,
Review of Calculus, cont d
 Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
ODE: Existence and Uniqueness of a Solution
 Mth 22 Fll 213 Jerry Kzdn ODE: Existence nd Uniqueness of Solution The Fundmentl Theorem of Clculus tells us how to solve the ordinry differentil eqution (ODE) du = f(t) dt with initil condition u() =
Mth 22 Fll 213 Jerry Kzdn ODE: Existence nd Uniqueness of Solution The Fundmentl Theorem of Clculus tells us how to solve the ordinry differentil eqution (ODE) du = f(t) dt with initil condition u() =
Hybrid Group Acceptance Sampling Plan Based on Size Biased Lomax Model
 Mthemtics nd Sttistics 2(3): 137-141, 2014 DOI: 10.13189/ms.2014.020305 http://www.hrpub.org Hybrid Group Acceptnce Smpling Pln Bsed on Size Bised Lomx Model R. Subb Ro 1,*, A. Ng Durgmmb 2, R.R.L. Kntm
Mthemtics nd Sttistics 2(3): 137-141, 2014 DOI: 10.13189/ms.2014.020305 http://www.hrpub.org Hybrid Group Acceptnce Smpling Pln Bsed on Size Bised Lomx Model R. Subb Ro 1,*, A. Ng Durgmmb 2, R.R.L. Kntm
A product convergence theorem for Henstock Kurzweil integrals
 A product convergence theorem for Henstock Kurzweil integrls Prsr Mohnty Erik Tlvil 1 Deprtment of Mthemticl nd Sttisticl Sciences University of Albert Edmonton AB Cnd T6G 2G1 pmohnty@mth.ulbert.c etlvil@mth.ulbert.c
A product convergence theorem for Henstock Kurzweil integrls Prsr Mohnty Erik Tlvil 1 Deprtment of Mthemticl nd Sttisticl Sciences University of Albert Edmonton AB Cnd T6G 2G1 pmohnty@mth.ulbert.c etlvil@mth.ulbert.c
Math 554 Integration
 Mth 554 Integrtion Hndout #9 4/12/96 Defn. A collection of n + 1 distinct points of the intervl [, b] P := {x 0 = < x 1 < < x i 1 < x i < < b =: x n } is clled prtition of the intervl. In this cse, we
Mth 554 Integrtion Hndout #9 4/12/96 Defn. A collection of n + 1 distinct points of the intervl [, b] P := {x 0 = < x 1 < < x i 1 < x i < < b =: x n } is clled prtition of the intervl. In this cse, we
The First Fundamental Theorem of Calculus. If f(x) is continuous on [a, b] and F (x) is any antiderivative. f(x) dx = F (b) F (a).
![The First Fundamental Theorem of Calculus. If f(x) is continuous on [a, b] and F (x) is any antiderivative. f(x) dx = F (b) F (a). The First Fundamental Theorem of Calculus. If f(x) is continuous on [a, b] and F (x) is any antiderivative. f(x) dx = F (b) F (a).](/thumbs/78/77467690.jpg) The Fundmentl Theorems of Clculus Mth 4, Section 0, Spring 009 We now know enough bout definite integrls to give precise formultions of the Fundmentl Theorems of Clculus. We will lso look t some bsic emples
The Fundmentl Theorems of Clculus Mth 4, Section 0, Spring 009 We now know enough bout definite integrls to give precise formultions of the Fundmentl Theorems of Clculus. We will lso look t some bsic emples
Entropy and Ergodic Theory Notes 10: Large Deviations I
 Entropy nd Ergodic Theory Notes 10: Lrge Devitions I 1 A chnge of convention This is our first lecture on pplictions of entropy in probbility theory. In probbility theory, the convention is tht ll logrithms
Entropy nd Ergodic Theory Notes 10: Lrge Devitions I 1 A chnge of convention This is our first lecture on pplictions of entropy in probbility theory. In probbility theory, the convention is tht ll logrithms
Properties of Integrals, Indefinite Integrals. Goals: Definition of the Definite Integral Integral Calculations using Antiderivatives
 Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b.
![We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b. We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b.](/thumbs/93/114277851.jpg) Mth 255 - Vector lculus II Notes 4.2 Pth nd Line Integrls We begin with discussion of pth integrls (the book clls them sclr line integrls). We will do this for function of two vribles, but these ides cn
Mth 255 - Vector lculus II Notes 4.2 Pth nd Line Integrls We begin with discussion of pth integrls (the book clls them sclr line integrls). We will do this for function of two vribles, but these ides cn
W. We shall do so one by one, starting with I 1, and we shall do it greedily, trying
 Vitli covers 1 Definition. A Vitli cover of set E R is set V of closed intervls with positive length so tht, for every δ > 0 nd every x E, there is some I V with λ(i ) < δ nd x I. 2 Lemm (Vitli covering)
Vitli covers 1 Definition. A Vitli cover of set E R is set V of closed intervls with positive length so tht, for every δ > 0 nd every x E, there is some I V with λ(i ) < δ nd x I. 2 Lemm (Vitli covering)
Math 426: Probability Final Exam Practice
 Mth 46: Probbility Finl Exm Prctice. Computtionl problems 4. Let T k (n) denote the number of prtitions of the set {,..., n} into k nonempty subsets, where k n. Argue tht T k (n) kt k (n ) + T k (n ) by
Mth 46: Probbility Finl Exm Prctice. Computtionl problems 4. Let T k (n) denote the number of prtitions of the set {,..., n} into k nonempty subsets, where k n. Argue tht T k (n) kt k (n ) + T k (n ) by
Some estimates on the Hermite-Hadamard inequality through quasi-convex functions
 Annls of University of Criov, Mth. Comp. Sci. Ser. Volume 3, 7, Pges 8 87 ISSN: 13-693 Some estimtes on the Hermite-Hdmrd inequlity through qusi-convex functions Dniel Alexndru Ion Abstrct. In this pper
Annls of University of Criov, Mth. Comp. Sci. Ser. Volume 3, 7, Pges 8 87 ISSN: 13-693 Some estimtes on the Hermite-Hdmrd inequlity through qusi-convex functions Dniel Alexndru Ion Abstrct. In this pper
A PROOF OF THE FUNDAMENTAL THEOREM OF CALCULUS USING HAUSDORFF MEASURES
 INROADS Rel Anlysis Exchnge Vol. 26(1), 2000/2001, pp. 381 390 Constntin Volintiru, Deprtment of Mthemtics, University of Buchrest, Buchrest, Romni. e-mil: cosv@mt.cs.unibuc.ro A PROOF OF THE FUNDAMENTAL
INROADS Rel Anlysis Exchnge Vol. 26(1), 2000/2001, pp. 381 390 Constntin Volintiru, Deprtment of Mthemtics, University of Buchrest, Buchrest, Romni. e-mil: cosv@mt.cs.unibuc.ro A PROOF OF THE FUNDAMENTAL
New Integral Inequalities for n-time Differentiable Functions with Applications for pdfs
 Applied Mthemticl Sciences, Vol. 2, 2008, no. 8, 353-362 New Integrl Inequlities for n-time Differentible Functions with Applictions for pdfs Aristides I. Kechriniotis Technologicl Eductionl Institute
Applied Mthemticl Sciences, Vol. 2, 2008, no. 8, 353-362 New Integrl Inequlities for n-time Differentible Functions with Applictions for pdfs Aristides I. Kechriniotis Technologicl Eductionl Institute
f(x)dx . Show that there 1, 0 < x 1 does not exist a differentiable function g : [ 1, 1] R such that g (x) = f(x) for all
![f(x)dx . Show that there 1, 0 < x 1 does not exist a differentiable function g : [ 1, 1] R such that g (x) = f(x) for all f(x)dx . Show that there 1, 0 < x 1 does not exist a differentiable function g : [ 1, 1] R such that g (x) = f(x) for all](/thumbs/94/119531908.jpg) 3 Definite Integrl 3.1 Introduction In school one comes cross the definition of the integrl of rel vlued function defined on closed nd bounded intervl [, b] between the limits nd b, i.e., f(x)dx s the
3 Definite Integrl 3.1 Introduction In school one comes cross the definition of the integrl of rel vlued function defined on closed nd bounded intervl [, b] between the limits nd b, i.e., f(x)dx s the
Czechoslovak Mathematical Journal, 55 (130) (2005), , Abbotsford. 1. Introduction
 Czechoslovk Mthemticl Journl, 55 (130) (2005), 933 940 ESTIMATES OF THE REMAINDER IN TAYLOR S THEOREM USING THE HENSTOCK-KURZWEIL INTEGRAL, Abbotsford (Received Jnury 22, 2003) Abstrct. When rel-vlued
Czechoslovk Mthemticl Journl, 55 (130) (2005), 933 940 ESTIMATES OF THE REMAINDER IN TAYLOR S THEOREM USING THE HENSTOCK-KURZWEIL INTEGRAL, Abbotsford (Received Jnury 22, 2003) Abstrct. When rel-vlued
Numerical Analysis: Trapezoidal and Simpson s Rule
 nd Simpson s Mthemticl question we re interested in numericlly nswering How to we evlute I = f (x) dx? Clculus tells us tht if F(x) is the ntiderivtive of function f (x) on the intervl [, b], then I =
nd Simpson s Mthemticl question we re interested in numericlly nswering How to we evlute I = f (x) dx? Clculus tells us tht if F(x) is the ntiderivtive of function f (x) on the intervl [, b], then I =
Tests for the Ratio of Two Poisson Rates
 Chpter 437 Tests for the Rtio of Two Poisson Rtes Introduction The Poisson probbility lw gives the probbility distribution of the number of events occurring in specified intervl of time or spce. The Poisson
Chpter 437 Tests for the Rtio of Two Poisson Rtes Introduction The Poisson probbility lw gives the probbility distribution of the number of events occurring in specified intervl of time or spce. The Poisson
Math 1B, lecture 4: Error bounds for numerical methods
 Mth B, lecture 4: Error bounds for numericl methods Nthn Pflueger 4 September 0 Introduction The five numericl methods descried in the previous lecture ll operte by the sme principle: they pproximte the
Mth B, lecture 4: Error bounds for numericl methods Nthn Pflueger 4 September 0 Introduction The five numericl methods descried in the previous lecture ll operte by the sme principle: they pproximte the
Research Article Moment Inequalities and Complete Moment Convergence
 Hindwi Publishing Corportion Journl of Inequlities nd Applictions Volume 2009, Article ID 271265, 14 pges doi:10.1155/2009/271265 Reserch Article Moment Inequlities nd Complete Moment Convergence Soo Hk
Hindwi Publishing Corportion Journl of Inequlities nd Applictions Volume 2009, Article ID 271265, 14 pges doi:10.1155/2009/271265 Reserch Article Moment Inequlities nd Complete Moment Convergence Soo Hk
New Expansion and Infinite Series
 Interntionl Mthemticl Forum, Vol. 9, 204, no. 22, 06-073 HIKARI Ltd, www.m-hikri.com http://dx.doi.org/0.2988/imf.204.4502 New Expnsion nd Infinite Series Diyun Zhng College of Computer Nnjing University
Interntionl Mthemticl Forum, Vol. 9, 204, no. 22, 06-073 HIKARI Ltd, www.m-hikri.com http://dx.doi.org/0.2988/imf.204.4502 New Expnsion nd Infinite Series Diyun Zhng College of Computer Nnjing University
5.7 Improper Integrals
 458 pplictions of definite integrls 5.7 Improper Integrls In Section 5.4, we computed the work required to lift pylod of mss m from the surfce of moon of mss nd rdius R to height H bove the surfce of the
458 pplictions of definite integrls 5.7 Improper Integrls In Section 5.4, we computed the work required to lift pylod of mss m from the surfce of moon of mss nd rdius R to height H bove the surfce of the
Lecture 1. Functional series. Pointwise and uniform convergence.
 1 Introduction. Lecture 1. Functionl series. Pointwise nd uniform convergence. In this course we study mongst other things Fourier series. The Fourier series for periodic function f(x) with period 2π is
1 Introduction. Lecture 1. Functionl series. Pointwise nd uniform convergence. In this course we study mongst other things Fourier series. The Fourier series for periodic function f(x) with period 2π is
Travelling Profile Solutions For Nonlinear Degenerate Parabolic Equation And Contour Enhancement In Image Processing
 Applied Mthemtics E-Notes 8(8) - c IN 67-5 Avilble free t mirror sites of http://www.mth.nthu.edu.tw/ men/ Trvelling Profile olutions For Nonliner Degenerte Prbolic Eqution And Contour Enhncement In Imge
Applied Mthemtics E-Notes 8(8) - c IN 67-5 Avilble free t mirror sites of http://www.mth.nthu.edu.tw/ men/ Trvelling Profile olutions For Nonliner Degenerte Prbolic Eqution And Contour Enhncement In Imge
8 Laplace s Method and Local Limit Theorems
 8 Lplce s Method nd Locl Limit Theorems 8. Fourier Anlysis in Higher DImensions Most of the theorems of Fourier nlysis tht we hve proved hve nturl generliztions to higher dimensions, nd these cn be proved
8 Lplce s Method nd Locl Limit Theorems 8. Fourier Anlysis in Higher DImensions Most of the theorems of Fourier nlysis tht we hve proved hve nturl generliztions to higher dimensions, nd these cn be proved
Solution to Fredholm Fuzzy Integral Equations with Degenerate Kernel
 Int. J. Contemp. Mth. Sciences, Vol. 6, 2011, no. 11, 535-543 Solution to Fredholm Fuzzy Integrl Equtions with Degenerte Kernel M. M. Shmivnd, A. Shhsvrn nd S. M. Tri Fculty of Science, Islmic Azd University
Int. J. Contemp. Mth. Sciences, Vol. 6, 2011, no. 11, 535-543 Solution to Fredholm Fuzzy Integrl Equtions with Degenerte Kernel M. M. Shmivnd, A. Shhsvrn nd S. M. Tri Fculty of Science, Islmic Azd University
Administrivia CSE 190: Reinforcement Learning: An Introduction
 Administrivi CSE 190: Reinforcement Lerning: An Introduction Any emil sent to me bout the course should hve CSE 190 in the subject line! Chpter 4: Dynmic Progrmming Acknowledgment: A good number of these
Administrivi CSE 190: Reinforcement Lerning: An Introduction Any emil sent to me bout the course should hve CSE 190 in the subject line! Chpter 4: Dynmic Progrmming Acknowledgment: A good number of these
UNIFORM CONVERGENCE MA 403: REAL ANALYSIS, INSTRUCTOR: B. V. LIMAYE
 UNIFORM CONVERGENCE MA 403: REAL ANALYSIS, INSTRUCTOR: B. V. LIMAYE 1. Pointwise Convergence of Sequence Let E be set nd Y be metric spce. Consider functions f n : E Y for n = 1, 2,.... We sy tht the sequence
UNIFORM CONVERGENCE MA 403: REAL ANALYSIS, INSTRUCTOR: B. V. LIMAYE 1. Pointwise Convergence of Sequence Let E be set nd Y be metric spce. Consider functions f n : E Y for n = 1, 2,.... We sy tht the sequence
ON THE C-INTEGRAL BENEDETTO BONGIORNO
 ON THE C-INTEGRAL BENEDETTO BONGIORNO Let F : [, b] R be differentible function nd let f be its derivtive. The problem of recovering F from f is clled problem of primitives. In 1912, the problem of primitives
ON THE C-INTEGRAL BENEDETTO BONGIORNO Let F : [, b] R be differentible function nd let f be its derivtive. The problem of recovering F from f is clled problem of primitives. In 1912, the problem of primitives
FUNDAMENTALS OF REAL ANALYSIS by. III.1. Measurable functions. f 1 (
 FUNDAMNTALS OF RAL ANALYSIS by Doğn Çömez III. MASURABL FUNCTIONS AND LBSGU INTGRAL III.. Mesurble functions Hving the Lebesgue mesure define, in this chpter, we will identify the collection of functions
FUNDAMNTALS OF RAL ANALYSIS by Doğn Çömez III. MASURABL FUNCTIONS AND LBSGU INTGRAL III.. Mesurble functions Hving the Lebesgue mesure define, in this chpter, we will identify the collection of functions
Journal of Inequalities in Pure and Applied Mathematics
 Journl of Inequlities in Pure nd Applied Mthemtics GENERALIZATIONS OF THE TRAPEZOID INEQUALITIES BASED ON A NEW MEAN VALUE THEOREM FOR THE REMAINDER IN TAYLOR S FORMULA volume 7, issue 3, rticle 90, 006.
Journl of Inequlities in Pure nd Applied Mthemtics GENERALIZATIONS OF THE TRAPEZOID INEQUALITIES BASED ON A NEW MEAN VALUE THEOREM FOR THE REMAINDER IN TAYLOR S FORMULA volume 7, issue 3, rticle 90, 006.
Mapping the delta function and other Radon measures
 Mpping the delt function nd other Rdon mesures Notes for Mth583A, Fll 2008 November 25, 2008 Rdon mesures Consider continuous function f on the rel line with sclr vlues. It is sid to hve bounded support
Mpping the delt function nd other Rdon mesures Notes for Mth583A, Fll 2008 November 25, 2008 Rdon mesures Consider continuous function f on the rel line with sclr vlues. It is sid to hve bounded support
Chapter 0. What is the Lebesgue integral about?
 Chpter 0. Wht is the Lebesgue integrl bout? The pln is to hve tutoril sheet ech week, most often on Fridy, (to be done during the clss) where you will try to get used to the ides introduced in the previous
Chpter 0. Wht is the Lebesgue integrl bout? The pln is to hve tutoril sheet ech week, most often on Fridy, (to be done during the clss) where you will try to get used to the ides introduced in the previous
S. S. Dragomir. 2, we have the inequality. b a
 Bull Koren Mth Soc 005 No pp 3 30 SOME COMPANIONS OF OSTROWSKI S INEQUALITY FOR ABSOLUTELY CONTINUOUS FUNCTIONS AND APPLICATIONS S S Drgomir Abstrct Compnions of Ostrowski s integrl ineulity for bsolutely
Bull Koren Mth Soc 005 No pp 3 30 SOME COMPANIONS OF OSTROWSKI S INEQUALITY FOR ABSOLUTELY CONTINUOUS FUNCTIONS AND APPLICATIONS S S Drgomir Abstrct Compnions of Ostrowski s integrl ineulity for bsolutely
Solution for Assignment 1 : Intro to Probability and Statistics, PAC learning
 Solution for Assignment 1 : Intro to Probbility nd Sttistics, PAC lerning 10-701/15-781: Mchine Lerning (Fll 004) Due: Sept. 30th 004, Thursdy, Strt of clss Question 1. Bsic Probbility ( 18 pts) 1.1 (
Solution for Assignment 1 : Intro to Probbility nd Sttistics, PAC lerning 10-701/15-781: Mchine Lerning (Fll 004) Due: Sept. 30th 004, Thursdy, Strt of clss Question 1. Bsic Probbility ( 18 pts) 1.1 (
Calculus of Variations
 Clculus of Vritions Com S 477/577 Notes) Yn-Bin Ji Dec 4, 2017 1 Introduction A functionl ssigns rel number to ech function or curve) in some clss. One might sy tht functionl is function of nother function
Clculus of Vritions Com S 477/577 Notes) Yn-Bin Ji Dec 4, 2017 1 Introduction A functionl ssigns rel number to ech function or curve) in some clss. One might sy tht functionl is function of nother function
THIELE CENTRE. Linear stochastic differential equations with anticipating initial conditions
 THIELE CENTRE for pplied mthemtics in nturl science Liner stochstic differentil equtions with nticipting initil conditions Nrjess Khlif, Hui-Hsiung Kuo, Hbib Ouerdine nd Benedykt Szozd Reserch Report No.
THIELE CENTRE for pplied mthemtics in nturl science Liner stochstic differentil equtions with nticipting initil conditions Nrjess Khlif, Hui-Hsiung Kuo, Hbib Ouerdine nd Benedykt Szozd Reserch Report No.
A SHORT NOTE ON THE MONOTONICITY OF THE ERLANG C FORMULA IN THE HALFIN-WHITT REGIME. Bernardo D Auria 1
 Working Pper 11-42 (31) Sttistics nd Econometrics Series December, 2011 Deprtmento de Estdístic Universidd Crlos III de Mdrid Clle Mdrid, 126 28903 Getfe (Spin) Fx (34) 91 624-98-49 A SHORT NOTE ON THE
Working Pper 11-42 (31) Sttistics nd Econometrics Series December, 2011 Deprtmento de Estdístic Universidd Crlos III de Mdrid Clle Mdrid, 126 28903 Getfe (Spin) Fx (34) 91 624-98-49 A SHORT NOTE ON THE
Review of basic calculus
 Review of bsic clculus This brief review reclls some of the most importnt concepts, definitions, nd theorems from bsic clculus. It is not intended to tech bsic clculus from scrtch. If ny of the items below
Review of bsic clculus This brief review reclls some of the most importnt concepts, definitions, nd theorems from bsic clculus. It is not intended to tech bsic clculus from scrtch. If ny of the items below
Appendix to Notes 8 (a)
 Appendix to Notes 8 () 13 Comprison of the Riemnn nd Lebesgue integrls. Recll Let f : [, b] R be bounded. Let D be prtition of [, b] such tht Let D = { = x 0 < x 1
Appendix to Notes 8 () 13 Comprison of the Riemnn nd Lebesgue integrls. Recll Let f : [, b] R be bounded. Let D be prtition of [, b] such tht Let D = { = x 0 < x 1
New data structures to reduce data size and search time
 New dt structures to reduce dt size nd serch time Tsuneo Kuwbr Deprtment of Informtion Sciences, Fculty of Science, Kngw University, Hirtsuk-shi, Jpn FIT2018 1D-1, No2, pp1-4 Copyright (c)2018 by The Institute
New dt structures to reduce dt size nd serch time Tsuneo Kuwbr Deprtment of Informtion Sciences, Fculty of Science, Kngw University, Hirtsuk-shi, Jpn FIT2018 1D-1, No2, pp1-4 Copyright (c)2018 by The Institute
Expected Value of Function of Uncertain Variables
 Journl of Uncertin Systems Vol.4, No.3, pp.8-86, 2 Online t: www.jus.org.uk Expected Vlue of Function of Uncertin Vribles Yuhn Liu, Minghu H College of Mthemtics nd Computer Sciences, Hebei University,
Journl of Uncertin Systems Vol.4, No.3, pp.8-86, 2 Online t: www.jus.org.uk Expected Vlue of Function of Uncertin Vribles Yuhn Liu, Minghu H College of Mthemtics nd Computer Sciences, Hebei University,
1 Probability Density Functions
 Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
Reinforcement learning II
 CS 1675 Introduction to Mchine Lerning Lecture 26 Reinforcement lerning II Milos Huskrecht milos@cs.pitt.edu 5329 Sennott Squre Reinforcement lerning Bsics: Input x Lerner Output Reinforcement r Critic
CS 1675 Introduction to Mchine Lerning Lecture 26 Reinforcement lerning II Milos Huskrecht milos@cs.pitt.edu 5329 Sennott Squre Reinforcement lerning Bsics: Input x Lerner Output Reinforcement r Critic
THE EXISTENCE-UNIQUENESS THEOREM FOR FIRST-ORDER DIFFERENTIAL EQUATIONS.
 THE EXISTENCE-UNIQUENESS THEOREM FOR FIRST-ORDER DIFFERENTIAL EQUATIONS RADON ROSBOROUGH https://intuitiveexplntionscom/picrd-lindelof-theorem/ This document is proof of the existence-uniqueness theorem
THE EXISTENCE-UNIQUENESS THEOREM FOR FIRST-ORDER DIFFERENTIAL EQUATIONS RADON ROSBOROUGH https://intuitiveexplntionscom/picrd-lindelof-theorem/ This document is proof of the existence-uniqueness theorem
Research Article Harmonic Deformation of Planar Curves
 Interntionl Journl of Mthemtics nd Mthemticl Sciences Volume, Article ID 9, pges doi:.55//9 Reserch Article Hrmonic Deformtion of Plnr Curves Eleutherius Symeonidis Mthemtisch-Geogrphische Fkultät, Ktholische
Interntionl Journl of Mthemtics nd Mthemticl Sciences Volume, Article ID 9, pges doi:.55//9 Reserch Article Hrmonic Deformtion of Plnr Curves Eleutherius Symeonidis Mthemtisch-Geogrphische Fkultät, Ktholische
A basic logarithmic inequality, and the logarithmic mean
 Notes on Number Theory nd Discrete Mthemtics ISSN 30 532 Vol. 2, 205, No., 3 35 A bsic logrithmic inequlity, nd the logrithmic men József Sándor Deprtment of Mthemtics, Bbeş-Bolyi University Str. Koglnicenu
Notes on Number Theory nd Discrete Mthemtics ISSN 30 532 Vol. 2, 205, No., 3 35 A bsic logrithmic inequlity, nd the logrithmic men József Sándor Deprtment of Mthemtics, Bbeş-Bolyi University Str. Koglnicenu
AMATH 731: Applied Functional Analysis Fall Some basics of integral equations
 AMATH 731: Applied Functionl Anlysis Fll 2009 1 Introduction Some bsics of integrl equtions An integrl eqution is n eqution in which the unknown function u(t) ppers under n integrl sign, e.g., K(t, s)u(s)
AMATH 731: Applied Functionl Anlysis Fll 2009 1 Introduction Some bsics of integrl equtions An integrl eqution is n eqution in which the unknown function u(t) ppers under n integrl sign, e.g., K(t, s)u(s)
Convex Sets and Functions
 B Convex Sets nd Functions Definition B1 Let L, +, ) be rel liner spce nd let C be subset of L The set C is convex if, for ll x,y C nd ll [, 1], we hve 1 )x+y C In other words, every point on the line
B Convex Sets nd Functions Definition B1 Let L, +, ) be rel liner spce nd let C be subset of L The set C is convex if, for ll x,y C nd ll [, 1], we hve 1 )x+y C In other words, every point on the line
Math 31S. Rumbos Fall Solutions to Assignment #16
 Mth 31S. Rumbos Fll 2016 1 Solutions to Assignment #16 1. Logistic Growth 1. Suppose tht the growth of certin niml popultion is governed by the differentil eqution 1000 dn N dt = 100 N, (1) where N(t)
Mth 31S. Rumbos Fll 2016 1 Solutions to Assignment #16 1. Logistic Growth 1. Suppose tht the growth of certin niml popultion is governed by the differentil eqution 1000 dn N dt = 100 N, (1) where N(t)
Properties of the Riemann Integral
 Properties of the Riemnn Integrl Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University Februry 15, 2018 Outline 1 Some Infimum nd Supremum Properties 2
Properties of the Riemnn Integrl Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University Februry 15, 2018 Outline 1 Some Infimum nd Supremum Properties 2
The steps of the hypothesis test
 ttisticl Methods I (EXT 7005) Pge 78 Mosquito species Time of dy A B C Mid morning 0.0088 5.4900 5.5000 Mid Afternoon.3400 0.0300 0.8700 Dusk 0.600 5.400 3.000 The Chi squre test sttistic is the sum of
ttisticl Methods I (EXT 7005) Pge 78 Mosquito species Time of dy A B C Mid morning 0.0088 5.4900 5.5000 Mid Afternoon.3400 0.0300 0.8700 Dusk 0.600 5.400 3.000 The Chi squre test sttistic is the sum of
p-adic Egyptian Fractions
 p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
Positive Solutions of Operator Equations on Half-Line
 Int. Journl of Mth. Anlysis, Vol. 3, 29, no. 5, 211-22 Positive Solutions of Opertor Equtions on Hlf-Line Bohe Wng 1 School of Mthemtics Shndong Administrtion Institute Jinn, 2514, P.R. Chin sdusuh@163.com
Int. Journl of Mth. Anlysis, Vol. 3, 29, no. 5, 211-22 Positive Solutions of Opertor Equtions on Hlf-Line Bohe Wng 1 School of Mthemtics Shndong Administrtion Institute Jinn, 2514, P.R. Chin sdusuh@163.com
WHEN IS A FUNCTION NOT FLAT? 1. Introduction. {e 1 0, x = 0. f(x) =
 WHEN IS A FUNCTION NOT FLAT? YIFEI PAN AND MEI WANG Abstrct. In this pper we prove unique continution property for vector vlued functions of one vrible stisfying certin differentil inequlity. Key words:
WHEN IS A FUNCTION NOT FLAT? YIFEI PAN AND MEI WANG Abstrct. In this pper we prove unique continution property for vector vlued functions of one vrible stisfying certin differentil inequlity. Key words:
A HELLY THEOREM FOR FUNCTIONS WITH VALUES IN METRIC SPACES. 1. Introduction
 Ttr Mt. Mth. Publ. 44 (29), 159 168 DOI: 1.2478/v1127-9-56-z t m Mthemticl Publictions A HELLY THEOREM FOR FUNCTIONS WITH VALUES IN METRIC SPACES Miloslv Duchoň Peter Mličký ABSTRACT. We present Helly
Ttr Mt. Mth. Publ. 44 (29), 159 168 DOI: 1.2478/v1127-9-56-z t m Mthemticl Publictions A HELLY THEOREM FOR FUNCTIONS WITH VALUES IN METRIC SPACES Miloslv Duchoň Peter Mličký ABSTRACT. We present Helly
A NOTE ON ESTIMATION OF THE GLOBAL INTENSITY OF A CYCLIC POISSON PROCESS IN THE PRESENCE OF LINEAR TREND
 A NOTE ON ESTIMATION OF THE GLOBAL INTENSITY OF A CYCLIC POISSON PROCESS IN THE PRESENCE OF LINEAR TREND I WAYAN MANGKU Deprtment of Mthemtics, Fculty of Mthemtics nd Nturl Sciences, Bogor Agriculturl
A NOTE ON ESTIMATION OF THE GLOBAL INTENSITY OF A CYCLIC POISSON PROCESS IN THE PRESENCE OF LINEAR TREND I WAYAN MANGKU Deprtment of Mthemtics, Fculty of Mthemtics nd Nturl Sciences, Bogor Agriculturl
Riemann is the Mann! (But Lebesgue may besgue to differ.)
 Riemnn is the Mnn! (But Lebesgue my besgue to differ.) Leo Livshits My 2, 2008 1 For finite intervls in R We hve seen in clss tht every continuous function f : [, b] R hs the property tht for every ɛ >
Riemnn is the Mnn! (But Lebesgue my besgue to differ.) Leo Livshits My 2, 2008 1 For finite intervls in R We hve seen in clss tht every continuous function f : [, b] R hs the property tht for every ɛ >
1 1D heat and wave equations on a finite interval
 1 1D het nd wve equtions on finite intervl In this section we consider generl method of seprtion of vribles nd its pplictions to solving het eqution nd wve eqution on finite intervl ( 1, 2. Since by trnsltion
1 1D het nd wve equtions on finite intervl In this section we consider generl method of seprtion of vribles nd its pplictions to solving het eqution nd wve eqution on finite intervl ( 1, 2. Since by trnsltion
MAC-solutions of the nonexistent solutions of mathematical physics
 Proceedings of the 4th WSEAS Interntionl Conference on Finite Differences - Finite Elements - Finite Volumes - Boundry Elements MAC-solutions of the nonexistent solutions of mthemticl physics IGO NEYGEBAUE
Proceedings of the 4th WSEAS Interntionl Conference on Finite Differences - Finite Elements - Finite Volumes - Boundry Elements MAC-solutions of the nonexistent solutions of mthemticl physics IGO NEYGEBAUE
1 Online Learning and Regret Minimization
 2.997 Decision-Mking in Lrge-Scle Systems My 10 MIT, Spring 2004 Hndout #29 Lecture Note 24 1 Online Lerning nd Regret Minimiztion In this lecture, we consider the problem of sequentil decision mking in
2.997 Decision-Mking in Lrge-Scle Systems My 10 MIT, Spring 2004 Hndout #29 Lecture Note 24 1 Online Lerning nd Regret Minimiztion In this lecture, we consider the problem of sequentil decision mking in
Introduction to Some Convergence theorems
 Lecture Introduction to Some Convergence theorems Fridy 4, 005 Lecturer: Nti Linil Notes: Mukund Nrsimhn nd Chris Ré. Recp Recll tht for f : T C, we hd defined ˆf(r) = π T f(t)e irt dt nd we were trying
Lecture Introduction to Some Convergence theorems Fridy 4, 005 Lecturer: Nti Linil Notes: Mukund Nrsimhn nd Chris Ré. Recp Recll tht for f : T C, we hd defined ˆf(r) = π T f(t)e irt dt nd we were trying
Handout: Natural deduction for first order logic
 MATH 457 Introduction to Mthemticl Logic Spring 2016 Dr Json Rute Hndout: Nturl deduction for first order logic We will extend our nturl deduction rules for sententil logic to first order logic These notes
MATH 457 Introduction to Mthemticl Logic Spring 2016 Dr Json Rute Hndout: Nturl deduction for first order logic We will extend our nturl deduction rules for sententil logic to first order logic These notes
For the percentage of full time students at RCC the symbols would be:
 Mth 17/171 Chpter 7- ypothesis Testing with One Smple This chpter is s simple s the previous one, except it is more interesting In this chpter we will test clims concerning the sme prmeters tht we worked
Mth 17/171 Chpter 7- ypothesis Testing with One Smple This chpter is s simple s the previous one, except it is more interesting In this chpter we will test clims concerning the sme prmeters tht we worked
The use of a so called graphing calculator or programmable calculator is not permitted. Simple scientific calculators are allowed.
 ERASMUS UNIVERSITY ROTTERDAM Informtion concerning the Entrnce exmintion Mthemtics level 1 for Interntionl Bchelor in Communiction nd Medi Generl informtion Avilble time: 2 hours 30 minutes. The exmintion
ERASMUS UNIVERSITY ROTTERDAM Informtion concerning the Entrnce exmintion Mthemtics level 1 for Interntionl Bchelor in Communiction nd Medi Generl informtion Avilble time: 2 hours 30 minutes. The exmintion
Theoretical foundations of Gaussian quadrature
 Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
GENERALIZED ABSTRACTED MEAN VALUES
 GENERALIZED ABSTRACTED MEAN VALUES FENG QI Abstrct. In this rticle, the uthor introduces the generlized bstrcted men vlues which etend the concepts of most mens with two vribles, nd reserches their bsic
GENERALIZED ABSTRACTED MEAN VALUES FENG QI Abstrct. In this rticle, the uthor introduces the generlized bstrcted men vlues which etend the concepts of most mens with two vribles, nd reserches their bsic
Section 14.3 Arc Length and Curvature
 Section 4.3 Arc Length nd Curvture Clculus on Curves in Spce In this section, we ly the foundtions for describing the movement of n object in spce.. Vector Function Bsics In Clc, formul for rc length in
Section 4.3 Arc Length nd Curvture Clculus on Curves in Spce In this section, we ly the foundtions for describing the movement of n object in spce.. Vector Function Bsics In Clc, formul for rc length in
Duality # Second iteration for HW problem. Recall our LP example problem we have been working on, in equality form, is given below.
 Dulity #. Second itertion for HW problem Recll our LP emple problem we hve been working on, in equlity form, is given below.,,,, 8 m F which, when written in slightly different form, is 8 F Recll tht we
Dulity #. Second itertion for HW problem Recll our LP emple problem we hve been working on, in equlity form, is given below.,,,, 8 m F which, when written in slightly different form, is 8 F Recll tht we
19 Optimal behavior: Game theory
 Intro. to Artificil Intelligence: Dle Schuurmns, Relu Ptrscu 1 19 Optiml behvior: Gme theory Adversril stte dynmics hve to ccount for worst cse Compute policy π : S A tht mximizes minimum rewrd Let S (,
Intro. to Artificil Intelligence: Dle Schuurmns, Relu Ptrscu 1 19 Optiml behvior: Gme theory Adversril stte dynmics hve to ccount for worst cse Compute policy π : S A tht mximizes minimum rewrd Let S (,
Thinning Algorithms for Simulating Point Processes
 Thinning Algorithms for Simulting Point Processes Yund Chen September, 2016 Abstrct In this tlk we will discuss the lgorithms for simulting point processes. The simplest point process is the (homogeneous)
Thinning Algorithms for Simulting Point Processes Yund Chen September, 2016 Abstrct In this tlk we will discuss the lgorithms for simulting point processes. The simplest point process is the (homogeneous)
Credibility Hypothesis Testing of Fuzzy Triangular Distributions
 666663 Journl of Uncertin Systems Vol.9, No., pp.6-74, 5 Online t: www.jus.org.uk Credibility Hypothesis Testing of Fuzzy Tringulr Distributions S. Smpth, B. Rmy Received April 3; Revised 4 April 4 Abstrct
666663 Journl of Uncertin Systems Vol.9, No., pp.6-74, 5 Online t: www.jus.org.uk Credibility Hypothesis Testing of Fuzzy Tringulr Distributions S. Smpth, B. Rmy Received April 3; Revised 4 April 4 Abstrct
Kinematics equations, some numbers
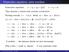 Kinemtics equtions, some numbers Kinemtics equtions: x = x 0 + v 0 t + 1 2 t2, v = v 0 + t. They describe motion with constnt ccelertion. Brking exmple, = 1m/s. Initil: x 0 = 10m, v 0 = 10m/s. x(t=1s)
Kinemtics equtions, some numbers Kinemtics equtions: x = x 0 + v 0 t + 1 2 t2, v = v 0 + t. They describe motion with constnt ccelertion. Brking exmple, = 1m/s. Initil: x 0 = 10m, v 0 = 10m/s. x(t=1s)
LECTURE NOTE #12 PROF. ALAN YUILLE
 LECTURE NOTE #12 PROF. ALAN YUILLE 1. Clustering, K-mens, nd EM Tsk: set of unlbeled dt D = {x 1,..., x n } Decompose into clsses w 1,..., w M where M is unknown. Lern clss models p(x w)) Discovery of
LECTURE NOTE #12 PROF. ALAN YUILLE 1. Clustering, K-mens, nd EM Tsk: set of unlbeled dt D = {x 1,..., x n } Decompose into clsses w 1,..., w M where M is unknown. Lern clss models p(x w)) Discovery of
Euler, Ioachimescu and the trapezium rule. G.J.O. Jameson (Math. Gazette 96 (2012), )
 Euler, Iochimescu nd the trpezium rule G.J.O. Jmeson (Mth. Gzette 96 (0), 36 4) The following results were estblished in recent Gzette rticle [, Theorems, 3, 4]. Given > 0 nd 0 < s
Euler, Iochimescu nd the trpezium rule G.J.O. Jmeson (Mth. Gzette 96 (0), 36 4) The following results were estblished in recent Gzette rticle [, Theorems, 3, 4]. Given > 0 nd 0 < s
THE INTERVAL LATTICE BOLTZMANN METHOD FOR TRANSIENT HEAT TRANSFER IN A SILICON THIN FILM
 ROMAI J., v.9, no.2(2013), 173 179 THE INTERVAL LATTICE BOLTZMANN METHOD FOR TRANSIENT HEAT TRANSFER IN A SILICON THIN FILM Alicj Piseck-Belkhyt, Ann Korczk Institute of Computtionl Mechnics nd Engineering,
ROMAI J., v.9, no.2(2013), 173 179 THE INTERVAL LATTICE BOLTZMANN METHOD FOR TRANSIENT HEAT TRANSFER IN A SILICON THIN FILM Alicj Piseck-Belkhyt, Ann Korczk Institute of Computtionl Mechnics nd Engineering,
Spanning tree congestion of some product graphs
 Spnning tree congestion of some product grphs Hiu-Fi Lw Mthemticl Institute Oxford University 4-9 St Giles Oxford, OX1 3LB, United Kingdom e-mil: lwh@mths.ox.c.uk nd Mikhil I. Ostrovskii Deprtment of Mthemtics
Spnning tree congestion of some product grphs Hiu-Fi Lw Mthemticl Institute Oxford University 4-9 St Giles Oxford, OX1 3LB, United Kingdom e-mil: lwh@mths.ox.c.uk nd Mikhil I. Ostrovskii Deprtment of Mthemtics
(4.1) D r v(t) ω(t, v(t))
 1.4. Differentil inequlities. Let D r denote the right hnd derivtive of function. If ω(t, u) is sclr function of the sclrs t, u in some open connected set Ω, we sy tht function v(t), t < b, is solution
1.4. Differentil inequlities. Let D r denote the right hnd derivtive of function. If ω(t, u) is sclr function of the sclrs t, u in some open connected set Ω, we sy tht function v(t), t < b, is solution
Definition of Continuity: The function f(x) is continuous at x = a if f(a) exists and lim
 Mth 9 Course Summry/Study Guide Fll, 2005 [1] Limits Definition of Limit: We sy tht L is the limit of f(x) s x pproches if f(x) gets closer nd closer to L s x gets closer nd closer to. We write lim f(x)
Mth 9 Course Summry/Study Guide Fll, 2005 [1] Limits Definition of Limit: We sy tht L is the limit of f(x) s x pproches if f(x) gets closer nd closer to L s x gets closer nd closer to. We write lim f(x)
Online Supplements to Performance-Based Contracts for Outpatient Medical Services
 Jing, Png nd Svin: Performnce-bsed Contrcts Article submitted to Mnufcturing & Service Opertions Mngement; mnuscript no. MSOM-11-270.R2 1 Online Supplements to Performnce-Bsed Contrcts for Outptient Medicl
Jing, Png nd Svin: Performnce-bsed Contrcts Article submitted to Mnufcturing & Service Opertions Mngement; mnuscript no. MSOM-11-270.R2 1 Online Supplements to Performnce-Bsed Contrcts for Outptient Medicl
Normal Distribution. Lecture 6: More Binomial Distribution. Properties of the Unit Normal Distribution. Unit Normal Distribution
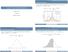 Norml Distribution Lecture 6: More Binomil Distribution If X is rndom vrible with norml distribution with men µ nd vrince σ 2, X N (µ, σ 2, then P(X = x = f (x = 1 e 1 (x µ 2 2 σ 2 σ Sttistics 104 Colin
Norml Distribution Lecture 6: More Binomil Distribution If X is rndom vrible with norml distribution with men µ nd vrince σ 2, X N (µ, σ 2, then P(X = x = f (x = 1 e 1 (x µ 2 2 σ 2 σ Sttistics 104 Colin
Acceptance Sampling by Attributes
 Introduction Acceptnce Smpling by Attributes Acceptnce smpling is concerned with inspection nd decision mking regrding products. Three spects of smpling re importnt: o Involves rndom smpling of n entire
Introduction Acceptnce Smpling by Attributes Acceptnce smpling is concerned with inspection nd decision mking regrding products. Three spects of smpling re importnt: o Involves rndom smpling of n entire
7.2 The Definite Integral
 7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H. Thomas Shores Department of Mathematics University of Nebraska Spring 2007
 A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
Math Calculus with Analytic Geometry II
 orem of definite Mth 5.0 with Anlytic Geometry II Jnury 4, 0 orem of definite If < b then b f (x) dx = ( under f bove x-xis) ( bove f under x-xis) Exmple 8 0 3 9 x dx = π 3 4 = 9π 4 orem of definite Problem
orem of definite Mth 5.0 with Anlytic Geometry II Jnury 4, 0 orem of definite If < b then b f (x) dx = ( under f bove x-xis) ( bove f under x-xis) Exmple 8 0 3 9 x dx = π 3 4 = 9π 4 orem of definite Problem
UniversitaireWiskundeCompetitie. Problem 2005/4-A We have k=1. Show that for every q Q satisfying 0 < q < 1, there exists a finite subset K N so that
 Problemen/UWC NAW 5/7 nr juni 006 47 Problemen/UWC UniversitireWiskundeCompetitie Edition 005/4 For Session 005/4 we received submissions from Peter Vndendriessche, Vldislv Frnk, Arne Smeets, Jn vn de
Problemen/UWC NAW 5/7 nr juni 006 47 Problemen/UWC UniversitireWiskundeCompetitie Edition 005/4 For Session 005/4 we received submissions from Peter Vndendriessche, Vldislv Frnk, Arne Smeets, Jn vn de
1. On some properties of definite integrals. We prove
 This short collection of notes is intended to complement the textbook Anlisi Mtemtic 2 by Crl Mdern, published by Città Studi Editore, [M]. We refer to [M] for nottion nd the logicl stremline of the rguments.
This short collection of notes is intended to complement the textbook Anlisi Mtemtic 2 by Crl Mdern, published by Città Studi Editore, [M]. We refer to [M] for nottion nd the logicl stremline of the rguments.
Conservation Law. Chapter Goal. 5.2 Theory
 Chpter 5 Conservtion Lw 5.1 Gol Our long term gol is to understnd how mny mthemticl models re derived. We study how certin quntity chnges with time in given region (sptil domin). We first derive the very
Chpter 5 Conservtion Lw 5.1 Gol Our long term gol is to understnd how mny mthemticl models re derived. We study how certin quntity chnges with time in given region (sptil domin). We first derive the very
Lecture 3 Gaussian Probability Distribution
 Introduction Lecture 3 Gussin Probbility Distribution Gussin probbility distribution is perhps the most used distribution in ll of science. lso clled bell shped curve or norml distribution Unlike the binomil
Introduction Lecture 3 Gussin Probbility Distribution Gussin probbility distribution is perhps the most used distribution in ll of science. lso clled bell shped curve or norml distribution Unlike the binomil
