Substituting this into the differential equation and solving for u, we have. + u2. du = 3x + c. ( )
|
|
|
- Chastity Barber
- 5 years ago
- Views:
Transcription
1 Worked Solutions 27 Chapter 6: Simplifying Through Substitution 6 a Let u = 3 + 3y + 2 Solving for y computing y we then see that 3y = u 3 2 y = u = d [ u = 3 Substituting this into the differential equation solving for u we have = 3 + 3y = 3 = + = + u2 + = 3 + = = + u2 3 = 3 + c ) + u2 Computing the last integral ignoring the arbitrary constant): + u + = 2 + [ = = u arctanu) + So equation ) becomes u arctanu) = 3 + c which cannot be solved for u So we now replace each u with its formula in terms of y from the original substitution u = 3 + 3y + 2 ) simplify the resulting equation as much as practical: 3 + 3y + 2 arctan3 + 3y + 2) = 3 + c arctan3 + 3y + 2) = 3y c = 3y + C 3 + 3y + 2 = tan3y + C) 6 c Using the substitution u = 4y we have y = 4 [u = u = cos4y 8 + 3) = cos4y 8 + 3) [ cosu) = cosu)
2 28 Simplifying Through Substitution cosu) cosu) = cosu) cosu) = 8 cosu) = 8 sinu) = 8 + c u = arcsin8 + c) Plugging the last formula for u into the formula for y based on the original substitution yields the final answer y = [u = 4 [arcsin8 + c) = 4 arcsin8 + c) a Rewriting the differential equation: 2 y = y2 = y y + Since the equation is homogeneous our substitution is based on u = y from which we derive y = u = d Using this with our differential equation: [u = u + = u + = y y + u + = u + u2 Obviously u = 0 is the only constant solution which in turn also yields = u2 y = u = 0 = 0 as a constant solution to the original equation For the other solutions: = u2 u 2 = u 2 = u = ln + c u = ln + c This along with our formula for y in terms of u yields [ y = u = = ln + c ln + c which along with y = 0 describes all the solutions 63 c The substitution: u = y y = u = d [u = u +
3 Worked Solutions 29 So y )[ cos [ cosu) y u + ) u y ) = + sin = + sinu) cosu) = + sinu) The constant solutions of this are given by those values of u where + sinu) = 0 ; that is u = arcsin ) = 2nπ π for n = 0 ± ±2 2 For the nonconstant solutions: = + sinu) cosu) cosu) + sinu) = cosu) + sinu) = ln + sinu) = ln + c + sinu) = ±e ln +c = A u = arcsina ) Note that the last formula for u also yields the constant solutions So all the solutions to our original differential equation are given by y = u = arcsina ) 65 a First observe that y = 0 is clearly a constant solution Here n = 3 from the 3y 3 term) So the substitution is based on u = y 3 = y 2 Hence we also have y = ±u / 2 Using this substitution: = d [±u / 2 [ = ± 2 u 3 / 2 + 3y = 3y3 ) 2 u 3 / u / 2 = 3 u / 2 2u 3 )[ / 2 2 u 3 / 2 + 3u / 2 = 3u 3 / 2 6u = 6 The integrating factor for the last differential equation is µ) = e 6) = e 6 Using this with the last differential equation above: [ e 6 6u = 6 e 6 6e 6 u = 6e 6 d [ e 6 u = 6e 6 e 6 u = 6e 6 = e 6 + c u = + ce 6
4 30 Simplifying Through Substitution This with the original substitution then gives y = ±u / 2 = ± + ce 6) / 2 So any solution to the original differential equation is given by the above formula for y or y = 0 65 c Again we note that y = 0 is a solution The substitution: u = y 2 / 3 = y / 3 y = u 3 Using the substitution to find the linear equation for u : + 3 cot)y = 6 cos)y2 / cot)u3 = 6 cos) u 3)2 / 3 + cot)u = 2 cos) = 3u2 The integrating factor is given by ) µ) = cot) cos) e = ep sin) = epln sin) ) = sin) As noted in chapter 5 we can simply use µ = sin) Doing so: [ sin) + cot)u = 2 cos) d [sin)u = 2 sin) cos) sin)u = 2 sin) cos) = sin 2 ) + c u = sin) + c sin) y = u 3 = sin) + c ) 3 sin) The last equation along with y = 0 describes all solutions to our original differential equation 67 a This is obviously in the form = formula of y So it is a homogeneous equation we use the corresponding substitution u = y y = u = d [u = u +
5 Worked Solutions 3 Doing so: = y + u + y = u + u 2 = = 3 u3 = ln + c u = 3 ln + 3c) / 3 y = u = 3 ln + C) / 3 67 c Since the equation is + 2 y = 4y / 2 it is a Bernoulli equation with n = / 2 One solution is y = 0 The others are obtained using the substitution Hence u = y / 2 = y / 2 y = = 2u + 2 y = 4y / 2 2u + 2 u2 = 4 ) / 2 + u = 2 The integrating factor is µ) = e / = = So + u = 2 [ + u = 2 d [u = 2 u = + c u = y = = 2 = 2 + c + c 67 e The y factor suggests using the linear substitution u = y Then Using this y = u + = d y ) = u [ + u = u [u + = + = u u Note that the derivative of u is zero if only if u = So u = is the only constant solution to this last equation The corresponding solution to the original equation is then y = u + = + =
6 32 Simplifying Through Substitution For the other solutions we ll need u u u = u [ = u Back to the last differential equation above: u u = = u u = u ln u + C u u = u ln u = + c y ) ln y ) = + c ln y + = c y y + = ±e c y = Ae y y = + Ae y This last equation describes all solutions since it does rece to the solution y) = + when A = 0 67 g = 2 + 2y + 2y 2 2y = 2y + 2 2) = 2 + 2y + 2y 2 [ y y ) [ 2 2 y = y y y + 2 So the equation is homogeneous we use the substitution u = y Hence y = u = d [u = u + = + 2 y y y u u2 = ) = u = + u2 + u2 = 2u2 + 2u = ) = + 2u = ln + c + 2u ln + c) = 0
7 Worked Solutions 33 u = 2 ± 2 2 4[ ln + c) = ± ln + C 2 [ y = u = ± ln + C = ± ln + C 67 i Clearly the substitution u = 2 + y 3 is in order With this y = u = d [u = 2 = y = 2 u 2 = 2 u Note that this last equation has one constant solution u = 0 Corresponding to this is the solution to the original equation y = u = = 3 2 For the other solutions we continue the above computations: = u u / 2 = 2 2u / 2 = 2 + C u = + c y = u = + c So each solution is given by either the last formula or by y = k y = y + 2 = y + y + 2 = y + y + )/ 2 So the equation is homogeneous we use the substitution u = y Hence y = u = d [u = u + = y + y + )/ 2 u + = u + u + ) / 2 = u + ) / 2 ) Note that the derivative of u is zero if u = So u = is a constant solution the corresponding solution to our original equation is y = u = ) =
8 34 Simplifying Through Substitution For the rest of the solutions we divide equation ) by u + ) / 2 continue the process: u + ) / 2 = u + ) / 2 = 2u + ) / 2 = ln + C u = y = u = [ 2 ln + c = 2 ln + c 2 ln + c So every solution is given by either the last formula for y or by y = 67 m Clearly the linear substitution u = y + 3 is appropriate Using this y = u + 3 = d [ u + 3 = = y + 3)2 = u2 = u2 Here the derivative of u is zero if u = ± So this differential equation has two constant solutions u = u = Since y = u + 3 the corresponding solutions to the original equation are y = + 3 = + 2 y = ) + 3 = + 4 To find the other solutions we divide the last differential equation above by proceed as usual using partial fractions to rewrite ) in more convenient form for integration: = = + u) u) = + c [ 2 + u + = + c u [ln + u ln u = + c 2 ln + u = 2 + 2c u + u u = ±e2s+2c = Ae 2 + u = Ae 2 u Ae 2 u = Ae2 Ae 2 + y) = u + 3 = Ae2 Ae 2 +
9 Worked Solutions 35 Note that the last formula for y reces to the constant solution y = + 2 if A = 0 but does not rece to the constant solution y = + 4 for any value of A So to describe all solutions we need both y = Ae2 Ae 2 + y = o We need a formula of y maybe f y) such that the differential equation reces to a simple differential equation for u when we let u = f y) Because the given equation involves both siny) cosy) two possible choices for the substitution are obviously Differentiating these yield respectively u = cosy) u = siny) = siny) = cosy) the second of which matches eactly the left side of the given differential equation So let s use the second choice u = siny) as our substitution Doing so we get with = cosy) cosy) = e siny) = e u + u = e This is a simple linear equation with integrating factor µ) = e = e Multiplying our differential equation for u by this integrating factor continuing: e u = [ e + u = e d [ e u = = + c u = + c)e siny) = + c)e y = arcsin + c)e )
4181H Problem Set 10 Selected Solutions. Chapter 15. = lim. (by L Hôpital s Rule) (0) = lim. x 2, = lim x 3 ( sin x)x + cos x cos x = lim
 48H Problem Set 0 Selected Solutions Chapter 5 # 3(a From the definition of the derivative we have sin f f( f(0 (0 sin 0 0 0 0 = cos (by L Hôpital s Rule = sin (by L Hôpital s Rule = 0 (b From the definition
48H Problem Set 0 Selected Solutions Chapter 5 # 3(a From the definition of the derivative we have sin f f( f(0 (0 sin 0 0 0 0 = cos (by L Hôpital s Rule = sin (by L Hôpital s Rule = 0 (b From the definition
Math RE - Calculus I Trigonometry Limits & Derivatives Page 1 of 8. x = 1 cos x. cos x 1 = lim
 Math 0-0-RE - Calculus I Trigonometry Limits & Derivatives Page of 8 Trigonometric Limits It has been shown in class that: lim 0 sin lim 0 sin lim 0 cos cos 0 lim 0 cos lim 0 + cos + To evaluate trigonometric
Math 0-0-RE - Calculus I Trigonometry Limits & Derivatives Page of 8 Trigonometric Limits It has been shown in class that: lim 0 sin lim 0 sin lim 0 cos cos 0 lim 0 cos lim 0 + cos + To evaluate trigonometric
Math Midterm Solutions
 Math 50 - Midterm Solutions November 4, 009. a) If f ) > 0 for all in a, b), then the graph of f is concave upward on a, b). If f ) < 0 for all in a, b), then the graph of f is downward on a, b). This
Math 50 - Midterm Solutions November 4, 009. a) If f ) > 0 for all in a, b), then the graph of f is concave upward on a, b). If f ) < 0 for all in a, b), then the graph of f is downward on a, b). This
Review for Ma 221 Final Exam
 Review for Ma 22 Final Exam The Ma 22 Final Exam from December 995.a) Solve the initial value problem 2xcosy 3x2 y dx x 3 x 2 sin y y dy 0 y 0 2 The equation is first order, for which we have techniques
Review for Ma 22 Final Exam The Ma 22 Final Exam from December 995.a) Solve the initial value problem 2xcosy 3x2 y dx x 3 x 2 sin y y dy 0 y 0 2 The equation is first order, for which we have techniques
The Explicit Form of a Function
 Section 3 5 Implicit Differentiation The Eplicit Form of a Function The normal way we see function notation has f () on one sie of an equation an an epression in terms of on the other sie. We know the
Section 3 5 Implicit Differentiation The Eplicit Form of a Function The normal way we see function notation has f () on one sie of an equation an an epression in terms of on the other sie. We know the
2.2 Separable Equations
 82 2.2 Separable Equations An equation y = f(x, y) is called separable provided algebraic operations, usually multiplication, division and factorization, allow it to be written in a separable form y =
82 2.2 Separable Equations An equation y = f(x, y) is called separable provided algebraic operations, usually multiplication, division and factorization, allow it to be written in a separable form y =
3 Algebraic Methods. we can differentiate both sides implicitly to obtain a differential equation involving x and y:
 3 Algebraic Methods b The first appearance of the equation E Mc 2 in Einstein s handwritten notes. So far, the only general class of differential equations that we know how to solve are directly integrable
3 Algebraic Methods b The first appearance of the equation E Mc 2 in Einstein s handwritten notes. So far, the only general class of differential equations that we know how to solve are directly integrable
Solutions of Math 53 Midterm Exam I
 Solutions of Math 53 Midterm Exam I Problem 1: (1) [8 points] Draw a direction field for the given differential equation y 0 = t + y. (2) [8 points] Based on the direction field, determine the behavior
Solutions of Math 53 Midterm Exam I Problem 1: (1) [8 points] Draw a direction field for the given differential equation y 0 = t + y. (2) [8 points] Based on the direction field, determine the behavior
2 nd ORDER O.D.E.s SUBSTITUTIONS
 nd ORDER O.D.E.s SUBSTITUTIONS Question 1 (***+) d y y 8y + 16y = d d d, y 0, Find the general solution of the above differential equation by using the transformation equation t = y. Give the answer in
nd ORDER O.D.E.s SUBSTITUTIONS Question 1 (***+) d y y 8y + 16y = d d d, y 0, Find the general solution of the above differential equation by using the transformation equation t = y. Give the answer in
Math 121. Exam II. November 28 th, 2018
 Math 121 Exam II November 28 th, 2018 Name: Section: The following rules apply: This is a closed-book exam. You may not use any books or notes on this exam. For free response questions, you must show all
Math 121 Exam II November 28 th, 2018 Name: Section: The following rules apply: This is a closed-book exam. You may not use any books or notes on this exam. For free response questions, you must show all
2 Trigonometric functions
 Theodore Voronov. Mathematics 1G1. Autumn 014 Trigonometric functions Trigonometry provides methods to relate angles and lengths but the functions we define have many other applications in mathematics..1
Theodore Voronov. Mathematics 1G1. Autumn 014 Trigonometric functions Trigonometry provides methods to relate angles and lengths but the functions we define have many other applications in mathematics..1
SET 1. (1) Solve for x: (a) e 2x = 5 3x
 () Solve for x: (a) e x = 5 3x SET We take natural log on both sides: ln(e x ) = ln(5 3x ) x = 3 x ln(5) Now we take log base on both sides: log ( x ) = log (3 x ln 5) x = log (3 x ) + log (ln(5)) x x
() Solve for x: (a) e x = 5 3x SET We take natural log on both sides: ln(e x ) = ln(5 3x ) x = 3 x ln(5) Now we take log base on both sides: log ( x ) = log (3 x ln 5) x = log (3 x ) + log (ln(5)) x x
I.e., the range of f(x) = arctan(x) is all real numbers y such that π 2 < y < π 2
 Inverse Trigonometric Functions: The inverse sine function, denoted by fx = arcsinx or fx = sin 1 x is defined by: y = sin 1 x if and only if siny = x and π y π I.e., the range of fx = arcsinx is all real
Inverse Trigonometric Functions: The inverse sine function, denoted by fx = arcsinx or fx = sin 1 x is defined by: y = sin 1 x if and only if siny = x and π y π I.e., the range of fx = arcsinx is all real
Homework Solutions: , plus Substitutions
 Homework Solutions: 2.-2.2, plus Substitutions Section 2. I have not included any drawings/direction fields. We can see them using Maple or by hand, so we ll be focusing on getting the analytic solutions
Homework Solutions: 2.-2.2, plus Substitutions Section 2. I have not included any drawings/direction fields. We can see them using Maple or by hand, so we ll be focusing on getting the analytic solutions
Chapter 3: Transcendental Functions
 Chapter 3: Transcendental Functions Spring 2018 Department of Mathematics Hong Kong Baptist University 1 / 32 Except for the power functions, the other basic elementary functions are also called the transcendental
Chapter 3: Transcendental Functions Spring 2018 Department of Mathematics Hong Kong Baptist University 1 / 32 Except for the power functions, the other basic elementary functions are also called the transcendental
Chapter 13: General Solutions to Homogeneous Linear Differential Equations
 Worked Solutions 1 Chapter 13: General Solutions to Homogeneous Linear Differential Equations 13.2 a. Verifying that {y 1, y 2 } is a fundamental solution set: We have y 1 (x) = cos(2x) y 1 (x) = 2 sin(2x)
Worked Solutions 1 Chapter 13: General Solutions to Homogeneous Linear Differential Equations 13.2 a. Verifying that {y 1, y 2 } is a fundamental solution set: We have y 1 (x) = cos(2x) y 1 (x) = 2 sin(2x)
4 Exact Equations. F x + F. dy dx = 0
 Chapter 1: First Order Differential Equations 4 Exact Equations Discussion: The general solution to a first order equation has 1 arbitrary constant. If we solve for that constant, we can write the general
Chapter 1: First Order Differential Equations 4 Exact Equations Discussion: The general solution to a first order equation has 1 arbitrary constant. If we solve for that constant, we can write the general
2 Recollection of elementary functions. II
 Recollection of elementary functions. II Last updated: October 5, 08. In this section we continue recollection of elementary functions. In particular, we consider exponential, trigonometric and hyperbolic
Recollection of elementary functions. II Last updated: October 5, 08. In this section we continue recollection of elementary functions. In particular, we consider exponential, trigonometric and hyperbolic
10.7 Trigonometric Equations and Inequalities
 0.7 Trigonometric Equations and Inequalities 857 0.7 Trigonometric Equations and Inequalities In Sections 0. 0. and most recently 0. we solved some basic equations involving the trigonometric functions.
0.7 Trigonometric Equations and Inequalities 857 0.7 Trigonometric Equations and Inequalities In Sections 0. 0. and most recently 0. we solved some basic equations involving the trigonometric functions.
EXACT EQUATIONS AND INTEGRATING FACTORS
 MAP- EXACT EQUATIONS AND INTEGRATING FACTORS First-order Differential Equations for Which We Can Find Eact Solutions Stu the patterns carefully. The first step of any solution is correct identification
MAP- EXACT EQUATIONS AND INTEGRATING FACTORS First-order Differential Equations for Which We Can Find Eact Solutions Stu the patterns carefully. The first step of any solution is correct identification
Variation of Parameters
 Variation of Parameters James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University April 13, 218 Outline Variation of Parameters Example One We eventually
Variation of Parameters James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University April 13, 218 Outline Variation of Parameters Example One We eventually
Math 181, Exam 1, Study Guide 2 Problem 1 Solution. =[17ln 5 +3(5)] [17 ln 1 +3(1)] =17ln = 17ln5+12
![Math 181, Exam 1, Study Guide 2 Problem 1 Solution. =[17ln 5 +3(5)] [17 ln 1 +3(1)] =17ln = 17ln5+12 Math 181, Exam 1, Study Guide 2 Problem 1 Solution. =[17ln 5 +3(5)] [17 ln 1 +3(1)] =17ln = 17ln5+12](/thumbs/83/87603917.jpg) Math 8, Exam, Study Guide Problem Solution. Compute the definite integral: 5 ( ) 7 x +3 dx Solution: UsingtheFundamentalTheoremofCalculusPartI,thevalueof the integral is: 5 ( ) 7 [ ] 5 x +3 dx = 7 ln x
Math 8, Exam, Study Guide Problem Solution. Compute the definite integral: 5 ( ) 7 x +3 dx Solution: UsingtheFundamentalTheoremofCalculusPartI,thevalueof the integral is: 5 ( ) 7 [ ] 5 x +3 dx = 7 ln x
Odd Answers: Chapter Eight Contemporary Calculus 1 { ( 3+2 } = lim { 1. { 2. arctan(a) 2. arctan(3) } = 2( π 2 ) 2. arctan(3)
 Odd Answers: Chapter Eight Contemporary Calculus PROBLEM ANSWERS Chapter Eight Section 8.. lim { A 0 } lim { ( A ) ( 00 ) } lim { 00 A } 00.. lim {. arctan() A } lim {. arctan(a). arctan() } ( π ). arctan()
Odd Answers: Chapter Eight Contemporary Calculus PROBLEM ANSWERS Chapter Eight Section 8.. lim { A 0 } lim { ( A ) ( 00 ) } lim { 00 A } 00.. lim {. arctan() A } lim {. arctan(a). arctan() } ( π ). arctan()
secθ 1 cosθ The pythagorean identities can also be expressed as radicals
 Basic Identities Section Objectives: Students will know how to use fundamental trigonometric identities to evaluate trigonometric functions and simplify trigonometric expressions. We use trig. identities
Basic Identities Section Objectives: Students will know how to use fundamental trigonometric identities to evaluate trigonometric functions and simplify trigonometric expressions. We use trig. identities
Lecture 5: Inverse Trigonometric Functions
 Lecture 5: Inverse Trigonometric Functions 5 The inverse sine function The function f(x = sin(x is not one-to-one on (,, but is on [ π, π Moreover, f still has range [, when restricte to this interval
Lecture 5: Inverse Trigonometric Functions 5 The inverse sine function The function f(x = sin(x is not one-to-one on (,, but is on [ π, π Moreover, f still has range [, when restricte to this interval
Chapter 7, Continued
 Math 150, Fall 008, c Benjamin Aurispa Chapter 7, Continued 7.3 Double-Angle, Half-Angle, and Product-Sum Formulas Double-Angle Formulas Formula for Sine: Formulas for Cosine: Formula for Tangent: sin
Math 150, Fall 008, c Benjamin Aurispa Chapter 7, Continued 7.3 Double-Angle, Half-Angle, and Product-Sum Formulas Double-Angle Formulas Formula for Sine: Formulas for Cosine: Formula for Tangent: sin
ORDINARY DIFFERENTIAL EQUATIONS
 ORDINARY DIFFERENTIAL EQUATIONS Basic concepts: Find y(x) where x is the independent and y the dependent varible, based on an equation involving x, y(x), y 0 (x),...e.g.: y 00 (x) = 1+y(x) y0 (x) 1+x or,
ORDINARY DIFFERENTIAL EQUATIONS Basic concepts: Find y(x) where x is the independent and y the dependent varible, based on an equation involving x, y(x), y 0 (x),...e.g.: y 00 (x) = 1+y(x) y0 (x) 1+x or,
ME 391 Mechanical Engineering Analysis
 Solve the following differential equations. ME 9 Mechanical Engineering Analysis Eam # Practice Problems Solutions. e u 5sin() with u(=)= We may rearrange this equation to e u 5sin() and note that it is
Solve the following differential equations. ME 9 Mechanical Engineering Analysis Eam # Practice Problems Solutions. e u 5sin() with u(=)= We may rearrange this equation to e u 5sin() and note that it is
Analytic Trigonometry
 Chapter 5 Analytic Trigonometry Course Number Section 5.1 Using Fundamental Identities Objective: In this lesson you learned how to use fundamental trigonometric identities to evaluate trigonometric functions
Chapter 5 Analytic Trigonometry Course Number Section 5.1 Using Fundamental Identities Objective: In this lesson you learned how to use fundamental trigonometric identities to evaluate trigonometric functions
MATH 1501G1/G2/G3 Test III Fall 2006
 MATH 5G/G2/G Test III Fall 26 Name: GTid (9: Instructor: Mitchel T. Keller Teaching Assistant and Section: There are 6 questions on this eam on pages (not counting this coverpage. Answer each question
MATH 5G/G2/G Test III Fall 26 Name: GTid (9: Instructor: Mitchel T. Keller Teaching Assistant and Section: There are 6 questions on this eam on pages (not counting this coverpage. Answer each question
10.7 Trigonometric Equations and Inequalities
 0.7 Trigonometric Equations and Inequalities 857 0.7 Trigonometric Equations and Inequalities In Sections 0., 0. and most recently 0., we solved some basic equations involving the trigonometric functions.
0.7 Trigonometric Equations and Inequalities 857 0.7 Trigonometric Equations and Inequalities In Sections 0., 0. and most recently 0., we solved some basic equations involving the trigonometric functions.
Chapter 5 Analytic Trigonometry
 Chapter 5 Analytic Trigonometry Section 1 Section 2 Section 3 Section 4 Section 5 Using Fundamental Identities Verifying Trigonometric Identities Solving Trigonometric Equations Sum and Difference Formulas
Chapter 5 Analytic Trigonometry Section 1 Section 2 Section 3 Section 4 Section 5 Using Fundamental Identities Verifying Trigonometric Identities Solving Trigonometric Equations Sum and Difference Formulas
Inverse Trigonometric Functions. September 5, 2018
 Inverse Trigonometric Functions September 5, 08 / 7 Restricted Sine Function. The trigonometric function sin x is not a one-to-one functions..0 0.5 Π 6, 5Π 6, Π Π Π Π 0.5 We still want an inverse, so what
Inverse Trigonometric Functions September 5, 08 / 7 Restricted Sine Function. The trigonometric function sin x is not a one-to-one functions..0 0.5 Π 6, 5Π 6, Π Π Π Π 0.5 We still want an inverse, so what
MTH 3311 Test #1. order 3, linear. The highest order of derivative of y is 2. Furthermore, y and its derivatives are all raised to the
 MTH 3311 Test #1 F 018 Pat Rossi Name Show CLEARLY how you arrive at your answers. 1. Classify the following according to order and linearity. If an equation is not linear, eplain why. (a) y + y y = 4
MTH 3311 Test #1 F 018 Pat Rossi Name Show CLEARLY how you arrive at your answers. 1. Classify the following according to order and linearity. If an equation is not linear, eplain why. (a) y + y y = 4
f(g(x)) g (x) dx = f(u) du.
 1. Techniques of Integration Section 8-IT 1.1. Basic integration formulas. Integration is more difficult than derivation. The derivative of every rational function or trigonometric function is another
1. Techniques of Integration Section 8-IT 1.1. Basic integration formulas. Integration is more difficult than derivation. The derivative of every rational function or trigonometric function is another
VII. Techniques of Integration
 VII. Techniques of Integration Integration, unlike differentiation, is more of an art-form than a collection of algorithms. Many problems in applied mathematics involve the integration of functions given
VII. Techniques of Integration Integration, unlike differentiation, is more of an art-form than a collection of algorithms. Many problems in applied mathematics involve the integration of functions given
Inverse Trig Functions
 6.6i Inverse Trigonometric Functions Inverse Sine Function Does g(x) = sin(x) have an inverse? What restriction would we need to make so that at least a piece of this function has an inverse? Given f (x)
6.6i Inverse Trigonometric Functions Inverse Sine Function Does g(x) = sin(x) have an inverse? What restriction would we need to make so that at least a piece of this function has an inverse? Given f (x)
Math 201 Solutions to Assignment 1. 2ydy = x 2 dx. y = C 1 3 x3
 Math 201 Solutions to Assignment 1 1. Solve the initial value problem: x 2 dx + 2y = 0, y(0) = 2. x 2 dx + 2y = 0, y(0) = 2 2y = x 2 dx y 2 = 1 3 x3 + C y = C 1 3 x3 Notice that y is not defined for some
Math 201 Solutions to Assignment 1 1. Solve the initial value problem: x 2 dx + 2y = 0, y(0) = 2. x 2 dx + 2y = 0, y(0) = 2 2y = x 2 dx y 2 = 1 3 x3 + C y = C 1 3 x3 Notice that y is not defined for some
Integration Techniques for the AB exam
 For the AB eam, students need to: determine antiderivatives of the basic functions calculate antiderivatives of functions using u-substitution use algebraic manipulation to rewrite the integrand prior
For the AB eam, students need to: determine antiderivatives of the basic functions calculate antiderivatives of functions using u-substitution use algebraic manipulation to rewrite the integrand prior
Problem Set. Assignment #1. Math 3350, Spring Feb. 6, 2004 ANSWERS
 Problem Set Assignment #1 Math 3350, Spring 2004 Feb. 6, 2004 ANSWERS i Problem 1. [Section 1.4, Problem 4] A rocket is shot straight up. During the initial stages of flight is has acceleration 7t m /s
Problem Set Assignment #1 Math 3350, Spring 2004 Feb. 6, 2004 ANSWERS i Problem 1. [Section 1.4, Problem 4] A rocket is shot straight up. During the initial stages of flight is has acceleration 7t m /s
The answers below are not comprehensive and are meant to indicate the correct way to solve the problem. sin
 Math : Practice Final Answer Key Name: The answers below are not comprehensive and are meant to indicate the correct way to solve the problem. Problem : Consider the definite integral I = 5 sin ( ) d.
Math : Practice Final Answer Key Name: The answers below are not comprehensive and are meant to indicate the correct way to solve the problem. Problem : Consider the definite integral I = 5 sin ( ) d.
INVERSE FUNCTIONS DERIVATIVES. terms on one side and everything else on the other. (3) Factor out dy. for the following functions: 1.
 INVERSE FUNCTIONS DERIVATIVES Recall the steps for computing y implicitly: (1) Take of both sies, treating y like a function. (2) Expan, a, subtract to get the y terms on one sie an everything else on
INVERSE FUNCTIONS DERIVATIVES Recall the steps for computing y implicitly: (1) Take of both sies, treating y like a function. (2) Expan, a, subtract to get the y terms on one sie an everything else on
Unit #11 - Integration by Parts, Average of a Function
 Unit # - Integration by Parts, Average of a Function Some problems and solutions selected or adapted from Hughes-Hallett Calculus. Integration by Parts. For each of the following integrals, indicate whether
Unit # - Integration by Parts, Average of a Function Some problems and solutions selected or adapted from Hughes-Hallett Calculus. Integration by Parts. For each of the following integrals, indicate whether
6.6 Inverse Trigonometric Functions
 6.6 6.6 Inverse Trigonometric Functions We recall the following definitions from trigonometry. If we restrict the sine function, say fx) sinx, π x π then we obtain a one-to-one function. π/, /) π/ π/ Since
6.6 6.6 Inverse Trigonometric Functions We recall the following definitions from trigonometry. If we restrict the sine function, say fx) sinx, π x π then we obtain a one-to-one function. π/, /) π/ π/ Since
Section 3.5: Implicit Differentiation
 Section 3.5: Implicit Differentiation In the previous sections, we considered the problem of finding the slopes of the tangent line to a given function y = f(x). The idea of a tangent line however is not
Section 3.5: Implicit Differentiation In the previous sections, we considered the problem of finding the slopes of the tangent line to a given function y = f(x). The idea of a tangent line however is not
Handbook of Ordinary Differential Equations
 Handbook of Ordinary Differential Equations Mark Sullivan July, 28 i Contents Preliminaries. Why bother?...............................2 What s so ordinary about ordinary differential equations?......
Handbook of Ordinary Differential Equations Mark Sullivan July, 28 i Contents Preliminaries. Why bother?...............................2 What s so ordinary about ordinary differential equations?......
16 Inverse Trigonometric Functions
 6 Inverse Trigonometric Functions Concepts: Restricting the Domain of the Trigonometric Functions The Inverse Sine Function The Inverse Cosine Function The Inverse Tangent Function Using the Inverse Trigonometric
6 Inverse Trigonometric Functions Concepts: Restricting the Domain of the Trigonometric Functions The Inverse Sine Function The Inverse Cosine Function The Inverse Tangent Function Using the Inverse Trigonometric
Chapter 13: Integrals
 Chapter : Integrals Chapter Overview: The Integral Calculus is essentially comprised of two operations. Interspersed throughout the chapters of this book has been the first of these operations the derivative.
Chapter : Integrals Chapter Overview: The Integral Calculus is essentially comprised of two operations. Interspersed throughout the chapters of this book has been the first of these operations the derivative.
First Midterm Examination
 Çankaya University Department of Mathematics 016-017 Fall Semester MATH 155 - Calculus for Engineering I First Midterm Eamination 1) Find the domain and range of the following functions. Eplain your solution.
Çankaya University Department of Mathematics 016-017 Fall Semester MATH 155 - Calculus for Engineering I First Midterm Eamination 1) Find the domain and range of the following functions. Eplain your solution.
Convergence of Fourier Series
 MATH 454: Analysis Two James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University April, 8 MATH 454: Analysis Two Outline The Cos Family MATH 454: Analysis
MATH 454: Analysis Two James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University April, 8 MATH 454: Analysis Two Outline The Cos Family MATH 454: Analysis
y = ± x 2 + c. ln y = 2 ln x + 2C sin(x) dx
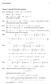 Worked Solutions Chapter 4: Separable First-Order Equations 43 a Factoring out 2, we get 3 sinx)) 2, which is f x)g), ds with f x) 3 sinx) and g) 2 So the equation is separable 43 c x x )2 x )2 f x)g)
Worked Solutions Chapter 4: Separable First-Order Equations 43 a Factoring out 2, we get 3 sinx)) 2, which is f x)g), ds with f x) 3 sinx) and g) 2 So the equation is separable 43 c x x )2 x )2 f x)g)
90 Chapter 5 Logarithmic, Exponential, and Other Transcendental Functions. Name Class. (a) (b) ln x (c) (a) (b) (c) 1 x. y e (a) 0 (b) y.
 90 Chapter 5 Logarithmic, Eponential, and Other Transcendental Functions Test Form A Chapter 5 Name Class Date Section. Find the derivative: f ln. 6. Differentiate: y. ln y y y y. Find dy d if ey y. y
90 Chapter 5 Logarithmic, Eponential, and Other Transcendental Functions Test Form A Chapter 5 Name Class Date Section. Find the derivative: f ln. 6. Differentiate: y. ln y y y y. Find dy d if ey y. y
Calculus IV - HW 1. Section 20. Due 6/16
 Calculus IV - HW Section 0 Due 6/6 Section.. Given both of the equations y = 4 y and y = 3y 3, draw a direction field for the differential equation. Based on the direction field, determine the behavior
Calculus IV - HW Section 0 Due 6/6 Section.. Given both of the equations y = 4 y and y = 3y 3, draw a direction field for the differential equation. Based on the direction field, determine the behavior
MTH ALGEBRA and TRIGONOMETRY SPRING 2011 SCIENCE 318 MTWF 11:30 12:30 CONTENTS:
 MTH-105-0 ALGEBRA and TRIGONOMETRY SPRING 011 SCIENCE 318 MTWF 11:30 1:30 CONTENTS: 1. Syllabus. Reviews for tests 1 7 3. Review for the final eam SYLLABUS Math 105: Algebra and Trigonometry Instructor:
MTH-105-0 ALGEBRA and TRIGONOMETRY SPRING 011 SCIENCE 318 MTWF 11:30 1:30 CONTENTS: 1. Syllabus. Reviews for tests 1 7 3. Review for the final eam SYLLABUS Math 105: Algebra and Trigonometry Instructor:
If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy. du du. If y = f (u) then y = f (u) u
 Section 3 4B The Chain Rule If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy du du dx or If y = f (u) then f (u) u The Chain Rule with the Power
Section 3 4B The Chain Rule If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy du du dx or If y = f (u) then f (u) u The Chain Rule with the Power
2 (x 2 + a 2 ) x 2. is easy. Do this first.
 MAC 3 INTEGRATION BY PARTS General Remark: Unless specified otherwise, you will solve the following problems using integration by parts, combined, if necessary with simple substitutions We will not explicitly
MAC 3 INTEGRATION BY PARTS General Remark: Unless specified otherwise, you will solve the following problems using integration by parts, combined, if necessary with simple substitutions We will not explicitly
Ma 221 Homework Solutions Due Date: January 24, 2012
 Ma Homewk Solutions Due Date: January, 0. pg. 3 #, 3, 6,, 5, 7 9,, 3;.3 p.5-55 #, 3, 5, 7, 0, 7, 9, (Underlined problems are handed in) In problems, and 5, determine whether the given differential equation
Ma Homewk Solutions Due Date: January, 0. pg. 3 #, 3, 6,, 5, 7 9,, 3;.3 p.5-55 #, 3, 5, 7, 0, 7, 9, (Underlined problems are handed in) In problems, and 5, determine whether the given differential equation
 Practice Test 3 A Sections.4 and.5, (11634851) Question 345678910111314151617181903456789303133334353 Description This is practice test A to help prepare for Test 3. It covers sections.4 and.5. Part B
Practice Test 3 A Sections.4 and.5, (11634851) Question 345678910111314151617181903456789303133334353 Description This is practice test A to help prepare for Test 3. It covers sections.4 and.5. Part B
NOTES 10: ANALYTIC TRIGONOMETRY
 NOTES 0: ANALYTIC TRIGONOMETRY Name: Date: Period: Mrs. Nguyen s Initial: LESSON 0. USING FUNDAMENTAL TRIGONOMETRIC IDENTITIES FUNDAMENTAL TRIGONOMETRIC INDENTITIES Reciprocal Identities sin csc cos sec
NOTES 0: ANALYTIC TRIGONOMETRY Name: Date: Period: Mrs. Nguyen s Initial: LESSON 0. USING FUNDAMENTAL TRIGONOMETRIC IDENTITIES FUNDAMENTAL TRIGONOMETRIC INDENTITIES Reciprocal Identities sin csc cos sec
Review For the Final: Problem 1 Find the general solutions of the following DEs. a) x 2 y xy y 2 = 0 solution: = 0 : homogeneous equation.
 Review For the Final: Problem 1 Find the general solutions of the following DEs. a) x 2 y xy y 2 = 0 solution: y y x y2 = 0 : homogeneous equation. x2 v = y dy, y = vx, and x v + x dv dx = v + v2. dx =
Review For the Final: Problem 1 Find the general solutions of the following DEs. a) x 2 y xy y 2 = 0 solution: y y x y2 = 0 : homogeneous equation. x2 v = y dy, y = vx, and x v + x dv dx = v + v2. dx =
If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy. du du. If y = f (u) then y = f (u) u
 Section 3 4B Lecture The Chain Rule If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy du du dx or If y = f (u) then y = f (u) u The Chain Rule
Section 3 4B Lecture The Chain Rule If y = f (u) is a differentiable function of u and u = g(x) is a differentiable function of x then dy dx = dy du du dx or If y = f (u) then y = f (u) u The Chain Rule
June 9 Math 1113 sec 002 Summer 2014
 June 9 Math 1113 sec 002 Summer 2014 Section 6.5: Inverse Trigonometric Functions Definition: (Inverse Sine) For x in the interval [ 1, 1] the inverse sine of x is denoted by either and is defined by the
June 9 Math 1113 sec 002 Summer 2014 Section 6.5: Inverse Trigonometric Functions Definition: (Inverse Sine) For x in the interval [ 1, 1] the inverse sine of x is denoted by either and is defined by the
MAP 2302 Midterm 1 Review Solutions 1
 MAP 2302 Midterm 1 Review Solutions 1 The exam will cover sections 1.2, 1.3, 2.2, 2.3, 2.4, and 2.6. All topics from this review sheet or from the suggested exercises are fair game. 1 Give explicit solutions
MAP 2302 Midterm 1 Review Solutions 1 The exam will cover sections 1.2, 1.3, 2.2, 2.3, 2.4, and 2.6. All topics from this review sheet or from the suggested exercises are fair game. 1 Give explicit solutions
MAT 132 Midterm 1 Spring 2017
 MAT Midterm Spring 7 Name: ID: Problem 5 6 7 8 Total ( pts) ( pts) ( pts) ( pts) ( pts) ( pts) (5 pts) (5 pts) ( pts) Score Instructions: () Fill in your name and Stony Brook ID number at the top of this
MAT Midterm Spring 7 Name: ID: Problem 5 6 7 8 Total ( pts) ( pts) ( pts) ( pts) ( pts) ( pts) (5 pts) (5 pts) ( pts) Score Instructions: () Fill in your name and Stony Brook ID number at the top of this
Formulas to remember
 Complex numbers Let z = x + iy be a complex number The conjugate z = x iy Formulas to remember The real part Re(z) = x = z+z The imaginary part Im(z) = y = z z i The norm z = zz = x + y The reciprocal
Complex numbers Let z = x + iy be a complex number The conjugate z = x iy Formulas to remember The real part Re(z) = x = z+z The imaginary part Im(z) = y = z z i The norm z = zz = x + y The reciprocal
Precalculus Review. Functions to KNOW! 1. Polynomial Functions. Types: General form Generic Graph and unique properties. Constants. Linear.
 Precalculus Review Functions to KNOW! 1. Polynomial Functions Types: General form Generic Graph and unique properties Constants Linear Quadratic Cubic Generalizations for Polynomial Functions - The domain
Precalculus Review Functions to KNOW! 1. Polynomial Functions Types: General form Generic Graph and unique properties Constants Linear Quadratic Cubic Generalizations for Polynomial Functions - The domain
Chapter 6. Techniques of Integration. 6.1 Differential notation
 Chapter 6 Techniques of Integration In this chapter, we expand our repertoire for antiderivatives beyond the elementary functions discussed so far. A review of the table of elementary antiderivatives (found
Chapter 6 Techniques of Integration In this chapter, we expand our repertoire for antiderivatives beyond the elementary functions discussed so far. A review of the table of elementary antiderivatives (found
Inverse Trig Functions
 Inverse Trig Functions -7-08 If you restrict fx) = sinx to the interval π x π, the function increases: y = sin x - / / This implies that the function is one-to-one, an hence it has an inverse. The inverse
Inverse Trig Functions -7-08 If you restrict fx) = sinx to the interval π x π, the function increases: y = sin x - / / This implies that the function is one-to-one, an hence it has an inverse. The inverse
Ordinary Differential Equations (ODEs)
 Chapter 13 Ordinary Differential Equations (ODEs) We briefly review how to solve some of the most standard ODEs. 13.1 First Order Equations 13.1.1 Separable Equations A first-order ordinary differential
Chapter 13 Ordinary Differential Equations (ODEs) We briefly review how to solve some of the most standard ODEs. 13.1 First Order Equations 13.1.1 Separable Equations A first-order ordinary differential
For a semi-circle with radius r, its circumfrence is πr, so the radian measure of a semi-circle (a straight line) is
 Radian Measure Given any circle with radius r, if θ is a central angle of the circle and s is the length of the arc sustained by θ, we define the radian measure of θ by: θ = s r For a semi-circle with
Radian Measure Given any circle with radius r, if θ is a central angle of the circle and s is the length of the arc sustained by θ, we define the radian measure of θ by: θ = s r For a semi-circle with
MATHEMATICS FOR ENGINEERS & SCIENTISTS 23
 MATHEMATICS FOR ENGINEERS & SCIENTISTS 3.5. Second order linear O.D.E.s: non-homogeneous case.. We ll now consider non-homogeneous second order linear O.D.E.s. These are of the form a + by + c rx) for
MATHEMATICS FOR ENGINEERS & SCIENTISTS 3.5. Second order linear O.D.E.s: non-homogeneous case.. We ll now consider non-homogeneous second order linear O.D.E.s. These are of the form a + by + c rx) for
Trigonometry Trigonometry comes from the Greek word meaning measurement of triangles Angles are typically labeled with Greek letters
 Trigonometry Trigonometry comes from the Greek word meaning measurement of triangles Angles are typically labeled with Greek letters α( alpha), β ( beta), θ ( theta) as well as upper case letters A,B,
Trigonometry Trigonometry comes from the Greek word meaning measurement of triangles Angles are typically labeled with Greek letters α( alpha), β ( beta), θ ( theta) as well as upper case letters A,B,
Chapter 6. Techniques of Integration. 6.1 Differential notation
 Chapter 6 Techniques of Integration In this chapter, we expand our repertoire for antiderivatives beyond the elementary functions discussed so far. A review of the table of elementary antiderivatives (found
Chapter 6 Techniques of Integration In this chapter, we expand our repertoire for antiderivatives beyond the elementary functions discussed so far. A review of the table of elementary antiderivatives (found
Solutions. MATH 1060 Exam 3 Fall (10 points) For 2 sin(3x π) + 1 give the. amplitude. period. phase shift. vertical shift.
 MATH 060 Exam Fall 008 Solutions. (0 points) For sin(x π) + give the amplitude period phase shift vertical shift amplitude= period= π phase shift= π vertical shift=. (5 points) Consider a sine curve with
MATH 060 Exam Fall 008 Solutions. (0 points) For sin(x π) + give the amplitude period phase shift vertical shift amplitude= period= π phase shift= π vertical shift=. (5 points) Consider a sine curve with
6.5 Second Trigonometric Rules
 662 CHAPTER 6. BASIC INTEGRATION 6.5 Second Trigonometric Rules We first looked at the simplest trigonometric integration rules those arising from the derivatives of the trignometric functions in Section
662 CHAPTER 6. BASIC INTEGRATION 6.5 Second Trigonometric Rules We first looked at the simplest trigonometric integration rules those arising from the derivatives of the trignometric functions in Section
7.6 Double-angle and Half-angle Formulas
 8 CHAPTER 7 Analytic Trigonometry. Explain why formula (7) cannot be used to show that tana p - ub cot u Establish this identity by using formulas (a) and (b). Are You Prepared? Answers.. -. (a) (b). -
8 CHAPTER 7 Analytic Trigonometry. Explain why formula (7) cannot be used to show that tana p - ub cot u Establish this identity by using formulas (a) and (b). Are You Prepared? Answers.. -. (a) (b). -
µ Differential Equations MAΘ National Convention 2017 For all questions, answer choice E) NOTA means that none of the above answers is correct.
 µ Differential Equations MAΘ National Convention 07 For all questions, answer choice E) NOTA means that none of the above answers is correct.. C) Since f (, ) = +, (0) = and h =. Use Euler s method, we
µ Differential Equations MAΘ National Convention 07 For all questions, answer choice E) NOTA means that none of the above answers is correct.. C) Since f (, ) = +, (0) = and h =. Use Euler s method, we
Lesson 3: Linear differential equations of the first order Solve each of the following differential equations by two methods.
 Lesson 3: Linear differential equations of the first der Solve each of the following differential equations by two methods. Exercise 3.1. Solution. Method 1. It is clear that y + y = 3 e dx = e x is an
Lesson 3: Linear differential equations of the first der Solve each of the following differential equations by two methods. Exercise 3.1. Solution. Method 1. It is clear that y + y = 3 e dx = e x is an
Math 123, Week 9: Separable, First-Order Linear, and Substitution Methods. Section 1: Separable DEs
 Math 123, Week 9: Separable, First-Order Linear, and Substitution Methods Section 1: Separable DEs We are finally to the point in the course where we can consider how to find solutions to differential
Math 123, Week 9: Separable, First-Order Linear, and Substitution Methods Section 1: Separable DEs We are finally to the point in the course where we can consider how to find solutions to differential
MTH 112: Elementary Functions
 1/19 MTH 11: Elementary Functions Section 6.6 6.6:Inverse Trigonometric functions /19 Inverse Trig functions 1 1 functions satisfy the horizontal line test: Any horizontal line crosses the graph of a 1
1/19 MTH 11: Elementary Functions Section 6.6 6.6:Inverse Trigonometric functions /19 Inverse Trig functions 1 1 functions satisfy the horizontal line test: Any horizontal line crosses the graph of a 1
MATH 151, FALL SEMESTER 2011 COMMON EXAMINATION 3 - VERSION B - SOLUTIONS
 Name (print): Signature: MATH 5, FALL SEMESTER 0 COMMON EXAMINATION - VERSION B - SOLUTIONS Instructor s name: Section No: Part Multiple Choice ( questions, points each, No Calculators) Write your name,
Name (print): Signature: MATH 5, FALL SEMESTER 0 COMMON EXAMINATION - VERSION B - SOLUTIONS Instructor s name: Section No: Part Multiple Choice ( questions, points each, No Calculators) Write your name,
8.a: Integrating Factors in Differential Equations. y = 5y + t (2)
 8.a: Integrating Factors in Differential Equations 0.0.1 Basics of Integrating Factors Until now we have dealt with separable differential equations. Net we will focus on a more specific type of differential
8.a: Integrating Factors in Differential Equations 0.0.1 Basics of Integrating Factors Until now we have dealt with separable differential equations. Net we will focus on a more specific type of differential
1969 AP Calculus BC: Section I
 969 AP Calculus BC: Section I 9 Minutes No Calculator Note: In this eamination, ln denotes the natural logarithm of (that is, logarithm to the base e).. t The asymptotes of the graph of the parametric
969 AP Calculus BC: Section I 9 Minutes No Calculator Note: In this eamination, ln denotes the natural logarithm of (that is, logarithm to the base e).. t The asymptotes of the graph of the parametric
Integration Techniques for the AB exam
 For the AB eam, students need to: determine antiderivatives of the basic functions calculate antiderivatives of functions using u-substitution use algebraic manipulation to rewrite the integrand prior
For the AB eam, students need to: determine antiderivatives of the basic functions calculate antiderivatives of functions using u-substitution use algebraic manipulation to rewrite the integrand prior
Subsequences and Limsups. Some sequences of numbers converge to limits, and some do not. For instance,
 Subsequences and Limsups Some sequences of numbers converge to limits, and some do not. For instance,,, 3, 4, 5,,... converges to 0 3, 3., 3.4, 3.4, 3.45, 3.459,... converges to π, 3,, 3.,, 3.4,... does
Subsequences and Limsups Some sequences of numbers converge to limits, and some do not. For instance,,, 3, 4, 5,,... converges to 0 3, 3., 3.4, 3.4, 3.45, 3.459,... converges to π, 3,, 3.,, 3.4,... does
6.6 Substitution with All Basic Forms
 670 CHAPTER 6. BASIC INTEGRATION 6.6 Substitution with All Basic Forms In this section we will add to our forms for substitution and recall some rather general guidelines for substitution. Ecept for our
670 CHAPTER 6. BASIC INTEGRATION 6.6 Substitution with All Basic Forms In this section we will add to our forms for substitution and recall some rather general guidelines for substitution. Ecept for our
Techniques of Integration
 Chapter 8 Techniques of Integration 8. Trigonometric Integrals Summary (a) Integrals of the form sin m x cos n x. () sin k+ x cos n x = ( cos x) k cos n x (sin x ), then apply the substitution u = cos
Chapter 8 Techniques of Integration 8. Trigonometric Integrals Summary (a) Integrals of the form sin m x cos n x. () sin k+ x cos n x = ( cos x) k cos n x (sin x ), then apply the substitution u = cos
MAS113 CALCULUS II SPRING 2008, QUIZ 5 SOLUTIONS. x 2 dx = 3y + y 3 = x 3 + c. It can be easily verified that the differential equation is exact, as
 MAS113 CALCULUS II SPRING 008, QUIZ 5 SOLUTIONS Quiz 5a Solutions (1) Solve the differential equation y = x 1 + y. (1 + y )y = x = (1 + y ) = x = 3y + y 3 = x 3 + c. () Solve the differential equation
MAS113 CALCULUS II SPRING 008, QUIZ 5 SOLUTIONS Quiz 5a Solutions (1) Solve the differential equation y = x 1 + y. (1 + y )y = x = (1 + y ) = x = 3y + y 3 = x 3 + c. () Solve the differential equation
Differential Calculus
 Differential Calculus. Compute the derivatives of the following functions a() = 4 3 7 + 4 + 5 b() = 3 + + c() = 3 + d() = sin cos e() = sin f() = log g() = tan h() = 3 6e 5 4 i() = + tan 3 j() = e k()
Differential Calculus. Compute the derivatives of the following functions a() = 4 3 7 + 4 + 5 b() = 3 + + c() = 3 + d() = sin cos e() = sin f() = log g() = tan h() = 3 6e 5 4 i() = + tan 3 j() = e k()
MATH 2250 Final Exam Solutions
 MATH 225 Final Exam Solutions Tuesday, April 29, 28, 6: 8:PM Write your name and ID number at the top of this page. Show all your work. You may refer to one double-sided sheet of notes during the exam
MATH 225 Final Exam Solutions Tuesday, April 29, 28, 6: 8:PM Write your name and ID number at the top of this page. Show all your work. You may refer to one double-sided sheet of notes during the exam
UNIVERSITY OF SOUTHAMPTON
 UNIVERSITY OF SOUTHAMPTON MATH03W SEMESTER EXAMINATION 0/ MATHEMATICS FOR ELECTRONIC & ELECTRICAL ENGINEERING Duration: 0 min This paper has two parts, part A and part B. Answer all questions from part
UNIVERSITY OF SOUTHAMPTON MATH03W SEMESTER EXAMINATION 0/ MATHEMATICS FOR ELECTRONIC & ELECTRICAL ENGINEERING Duration: 0 min This paper has two parts, part A and part B. Answer all questions from part
( ) 2 + 2x 3! ( x x ) 2
 Review for The Final Math 195 1. Rewrite as a single simplified fraction: 1. Rewrite as a single simplified fraction:. + 1 + + 1! 3. Rewrite as a single simplified fraction:! 4! 4 + 3 3 + + 5! 3 3! 4!
Review for The Final Math 195 1. Rewrite as a single simplified fraction: 1. Rewrite as a single simplified fraction:. + 1 + + 1! 3. Rewrite as a single simplified fraction:! 4! 4 + 3 3 + + 5! 3 3! 4!
MATH 307: Problem Set #3 Solutions
 : Problem Set #3 Solutions Due on: May 3, 2015 Problem 1 Autonomous Equations Recall that an equilibrium solution of an autonomous equation is called stable if solutions lying on both sides of it tend
: Problem Set #3 Solutions Due on: May 3, 2015 Problem 1 Autonomous Equations Recall that an equilibrium solution of an autonomous equation is called stable if solutions lying on both sides of it tend
Name Class. 5. Find the particular solution to given the general solution y C cos x and the. x 2 y
 10 Differential Equations Test Form A 1. Find the general solution to the first order differential equation: y 1 yy 0. 1 (a) (b) ln y 1 y ln y 1 C y y C y 1 C y 1 y C. Find the general solution to the
10 Differential Equations Test Form A 1. Find the general solution to the first order differential equation: y 1 yy 0. 1 (a) (b) ln y 1 y ln y 1 C y y C y 1 C y 1 y C. Find the general solution to the
Definition 1.1 Let a and b be numbers, a smaller than b. Then the set of all numbers between a and b :
 1 Week 1 Definition 1.1 Let a and b be numbers, a smaller than b. Then the set of all numbers between a and b : a and b included is denoted [a, b] a included, b excluded is denoted [a, b) a excluded, b
1 Week 1 Definition 1.1 Let a and b be numbers, a smaller than b. Then the set of all numbers between a and b : a and b included is denoted [a, b] a included, b excluded is denoted [a, b) a excluded, b
Math Reading assignment for Chapter 1: Study Sections 1.1 and 1.2.
 Math 3350 1 Chapter 1 Reading assignment for Chapter 1: Study Sections 1.1 and 1.2. 1.1 Material for Section 1.1 An Ordinary Differential Equation (ODE) is a relation between an independent variable x
Math 3350 1 Chapter 1 Reading assignment for Chapter 1: Study Sections 1.1 and 1.2. 1.1 Material for Section 1.1 An Ordinary Differential Equation (ODE) is a relation between an independent variable x
Math 1060 Midterm 2 Review Dugopolski Trigonometry Edition 3, Chapter 3 and 4
 Math 1060 Midterm Review Dugopolski Trigonometry Edition, Chapter and.1 Use identities to find the exact value of the function for the given value. 1) sin α = and α is in quadrant II; Find tan α. Simplify
Math 1060 Midterm Review Dugopolski Trigonometry Edition, Chapter and.1 Use identities to find the exact value of the function for the given value. 1) sin α = and α is in quadrant II; Find tan α. Simplify
e y [cos(x) + i sin(x)] e y [cos(x) i sin(x)] ] sin(x) + ey e y x = nπ for n = 0, ±1, ±2,... cos(nπ) = ey e y 0 = ey e y sin(z) = 0,
![e y [cos(x) + i sin(x)] e y [cos(x) i sin(x)] ] sin(x) + ey e y x = nπ for n = 0, ±1, ±2,... cos(nπ) = ey e y 0 = ey e y sin(z) = 0, e y [cos(x) + i sin(x)] e y [cos(x) i sin(x)] ] sin(x) + ey e y x = nπ for n = 0, ±1, ±2,... cos(nπ) = ey e y 0 = ey e y sin(z) = 0,](/thumbs/93/111506001.jpg) Worked Solutions 83 Chapter 3: Power Series Solutions II: Generalizations Theory 34 a Suppose that e z = 0 for some z = x + iy Then both the real imaginary parts of e z must be zero, e x cos(y) = 0 e x
Worked Solutions 83 Chapter 3: Power Series Solutions II: Generalizations Theory 34 a Suppose that e z = 0 for some z = x + iy Then both the real imaginary parts of e z must be zero, e x cos(y) = 0 e x
Analytic Trigonometry
 0 Analytic Trigonometry In this chapter, you will study analytic trigonometry. Analytic trigonometry is used to simplify trigonometric epressions and solve trigonometric equations. In this chapter, you
0 Analytic Trigonometry In this chapter, you will study analytic trigonometry. Analytic trigonometry is used to simplify trigonometric epressions and solve trigonometric equations. In this chapter, you
TOTAL NAME DATE PERIOD AP CALCULUS AB UNIT 4 ADVANCED DIFFERENTIATION TECHNIQUES DATE TOPIC ASSIGNMENT /6 10/8 10/9 10/10 X X X X 10/11 10/12
 NAME DATE PERIOD AP CALCULUS AB UNIT ADVANCED DIFFERENTIATION TECHNIQUES DATE TOPIC ASSIGNMENT 0 0 0/6 0/8 0/9 0/0 X X X X 0/ 0/ 0/5 0/6 QUIZ X X X 0/7 0/8 0/9 0/ 0/ 0/ 0/5 UNIT EXAM X X X TOTAL AP Calculus
NAME DATE PERIOD AP CALCULUS AB UNIT ADVANCED DIFFERENTIATION TECHNIQUES DATE TOPIC ASSIGNMENT 0 0 0/6 0/8 0/9 0/0 X X X X 0/ 0/ 0/5 0/6 QUIZ X X X 0/7 0/8 0/9 0/ 0/ 0/ 0/5 UNIT EXAM X X X TOTAL AP Calculus
