Review for Ma 221 Final Exam
|
|
|
- Annabella Sanders
- 6 years ago
- Views:
Transcription
1 Review for Ma 22 Final Exam The Ma 22 Final Exam from December 995.a) Solve the initial value problem 2xcosy 3x2 y dx x 3 x 2 sin y y dy 0 y 0 2 The equation is first order, for which we have techniques for four types, viz. separable, linear, exact and Bernoulli. It is not separable, linear or a Bernoulli d.e., so we will test to see if it s exact. P(x,y)dx Q(x,y)dy is exact if there is a function F x,y such that df P x,y dx Q x,y dy The test is that when this is true, then P y Q x. Here P 2xcosy 3x 2 y and Q x 3 x 2 sin y y. Calculating the partial derivatives, we have P y 2xsin y 3x 2 and Q x 3x 2 2xsiny which are equal. So the equation is exact and we proceed to find F. Then implicit solutions of the d.e. will be given by F x,y c. WemusthavethatF x P and F y Q. So F x P 2xcosy 3x2 y. Hence F x 2 cosy x 3 y g y, where g(y) is any function of y. Now taking the partial derivative of F with respect to y, F y 2xsin y x3 g y Q x 3 x 2 sin y y. Thus, we have that g y y andsuchag y is g y 2 y2, and the solution of the d.e. is given by F x,y x 2 cosy x 3 y 2 y2 c. Finally we will use the initial condition to find c. Substituting into the equation, we have F 0,2 0 cos c. In conclusion, the solution is given implicitly by x 2 cosy x 3 y 2 y2 2..b) Find the general solution to 4xy x 2 y x. There are two apparent ways to solve this problem. It is both separable and linear. Separable Approach: First we write the d.e. in the form x 2 y x 4xy x 4y.
2 Thus 4y dy dx x x 2. ln 4y ln x 2 2 4c. Integration yields 4 ln 4y 2 ln x2 c. I.e., Thence, 4y e ln x2 2 4c e 4c e ln x2 2 4y e 4c x 2 2. e 4c x 2 2. This could be written Finally, we have y 4 k x2 2, sweeping all of the constant fussing into a new arbitrary constant, k, and observing that this also yields a solution when k 0.. Linear Approach: For this the d.e. is put into the form y P x y Q x, and the integrating factor is calculated. The d.e. is y 4x x 2 y x x 2. The integrating factor is e P x dx 4x e x 2 dx e 2ln x2 e ln x2 2 x 2 2. Multiplying the d.e. by the integrating factor produces x 2 2 y 4x x 2 y x x 2. This is equivalent to d dx x2 2 y x 3 x. Integration produces x 2 2 y 4 x4 2 x2 c. Finally, we have y 4 x4 2x 2 x 2 2 c x 2 2. You can put this in the form obtained in the separable approach by setting c k 4 little more. and fussing a.c) Find the general solution of y 3 2x y 2x y. First we observe that this is a Bernoulli d.e. Multiplying both sides by y we get yy 3 2x y2 2x. Let v y 2. Then v 2yy. Substituting into the d.e., we have 2 v 3 v 2x, which is linear. 2x In standard form, this is v 3 x v 4x. The integrating factor is e 3 x dx e 3lnx e lnx 3 x 3. Multiplying by the integrating factor yields x 3 v 3x 4 v 4x 2. This can be rewritten as d dx x 3 v 4x 2. Integrating we obtain x 3 v 4x c. I.e. v cx 3 4x 2. Hence y 2 cx 3 4x 2 or y cx 3 4x 2. 2
3 3
4 2. Find the general solution to the differential equations. a) y y 4x 0sinx. The auxiliary equation is r 2 0. The roots are r i. So a general solution for the homogeneous equation is y h c cosx c 2 sinx. To find a particular solution for y y 4x, wetryy p ax b. Since y p 0, substitution yields ax b 4x, hence a 4andb 0. For y y 0sinx, we observe that the right hand is a solution of the homogeneous equation and thus we must seek a solution in the form y p2 Axcosx Bxsin x. Then, y p2 Acosx Axsin x Bsin x Bxcosx and y p2 2Asin x Axcosx 2Bcosx Bxsin x. Substituting these into the d.e., we obtain 2Asinx Axcosx 2Bcosx Bxsin x Axcosx Bxsinx 0sinx Equating the coefficients of sinx and cosx, we obtain 2A 0 A 5 or 2B 0 B 0 Putting everything, our general solution is y y h y p y p2 c cosx c 2 sin x 4x 5xcosx. b) y 9y 4 csc3x The auxiliary equation is r 2 9 0, whose roots are r 3i. A general solution of the homogeneous equation is y h c cos3x c 2 sin3x. For the non-homogeneous equation, we will use the method of variation of parameters. I.e., we seek a solution of the form y v x cos3x v 2 x sin3x. Then y v cos3x v 2 sin 3x 3v sin 3x 3v 2 cos3x. We will assume that v cos3x v 2 sin 3x 0 4
5 Then y 3v sin 3x 3v 2 cos3x 9v cos3x 9v 2 sin3x.. Substituting into the d.e. produces 3v sin3x 3v 2 cos3x 9v cos3x 9v 2 sin3x 9 v x cos3x v 2 x sin3x 4 csc3x Simplifying and repeating the assumption, we have 2 equations for v and v 2. 3v sin3x 3v 2 cos3x 4 csc3x v cos3x v 2 sin 3x 0 Multiply the first equation by -sin3x, the second equation by 3cos3x and add to obtain 3v sin 2 3x cos 2 3x 4 csc3xsin 3x. I.e. 3v 4. So, v 2 x. Substituting v 2 into the second equation yields 2 cos3x v 2 sin 3x 0. I.e. v 2 cos 3x 2sin3x. So, v 2 cos 3x 2sin3x dx 36 ln sin 3x. At last, we have a general solution in the form y c 2 x cos3x c 2 36 ln sin 3x sin3x. 3.a) Find L 3s s 4 s 2 First, we must find the partial fractions expansion. Then, we can use the table to find the inverse Laplace transform. 3s s 4 s 2 A s 4 B s 2 Cross multiplying to clear the denominators yields 3s A s 2 B s 4. Let s 2. Thus, we have 6 B 2 or B 3. Similarly with s 4, we obtain 2 A 2 or A 6. Now, from the table we obtain the final result that 5
6 L 3s s 4 s 2 3e2t 6e 4t b) Use Laplace Transforms to solve the initial value problem y 2y 8y 0 y 0 3 y 0 6 Taking the Laplace Transform of the d.e., we obtain s 2 ŷ sy 0 y 0 2 sŷ y 0 8 ŷ 0 s 2 2s 8 ŷ 3s s 2 2s 8 ŷ 3s ŷ 3s s 2 2s 8 3s s 4 s 2 A s 4 B s 2 As before, we cross multiply and set to -2 and 4 to obtain the coefficients. 3s A s 2 B s 4 s 2 6 6B,B s 4 2 6A,A 2 Hence, y 2e 4t e 2t. 4.a) Find L s 2 s 2 4s 8 L s 2 s 2 4s 8 L s 2 s 2 4s 4 4 L L s 2 2L 2 s s b) Not applicable for this course. 5.a) Solve dy dx 7x6 y y y 0 The equation is both separable and linear. s 2 L s 2 4 s s e 2t cos2t 2e 2t sin2t 6
7 Let s try separable first. We write the d.e. in the form y dy 7x6 dx Integrating, we have y dy 7x6 dx ln y x 7 x c y e c e x7 x Applying the initial condition, we obtain e c Thus, the solution is y e x7 x Alternatively, we can solve the d.e. as a linear d.e. First we rewrite the equation in the form dy dx 7x6 y 0 So, the integrating factor is IF e 7x6 dx e x 7 x Multiplying through by the integrating factor, gathering terms and integrating, we obtain e x7 x dy dx 7x6 e x7 x y 0 d dx e x7 x y 0 e x7 x y c y ce x7 x Finally, we apply the initial condition to find y 0 c. As before, we have the solution in the form y e x7 x b) Find the general solution to y 3y 2y 4e 3x e 2x. The auxiliary equation is r 2 3r 2 r 2 r 0. So the roots are r,2. Therefore, a general solution to the homogeneous equation is y h c e x c 2 e 2x. 7
8 Since one of the terms on the right hand side, e 2x, is a solution of the homogeneous equation, we seek a particular solution in the form y p Ae 3x Bxe 2x y p 3Ae 3x B 2xe 2x e 2x y p 9Ae 3x B 4xe 2x 2e 2x 2e 2x Substituting into the d.e. and gathering like terms produces 9Ae 3x B 4xe 2x 4e 2x 3 3Ae 3x B 2xe 2x e 2x 2 Ae 3x Bxe 2x 4e 3x e 2x Ae 3x 4x 4 6x 3 2x Be 2x 4e 3x e 2x 2Ae 3x Be 2x 4e 3x e 2x I.e. A 2,B Combining everything, we have y y h y p c e x c 2 e 2x 2e 3x xe 2x. 6. a) Not applicable for Fall 2002 course. b) Solution to be provided by Prof. Levine. 7.a) Solve cosy y 2xsin y 2x The hint is to let z sin y. Then z cosy y. Substituting, we have z 2xz 2x. Once again, we have a first order d.e. which is both separable and linear. The separable approach is as follows: z 2xz 2x 2x z dz 2xdx z dz 2xdx z ln z x 2 c z e c e x2 ke x2, noting that k 0 also gives a solution. 8
9 We will undo the substitution after trying the other (linear) approach. Here, we start with the d.e. in the form z 2xz 2x. The integrating factor is IF e 2xdx e x2 Multiplication by the integrating factor and integrating yields e x2 z 2xe x2 z 2xe x2 d dx e x2 z 2xe x2. d dx e x2 z dx 2xe x2 dx e x2 z e x2 c z ce x2 So we have the same result and conclude with the steps z siny ce x2 y arcsin ce x2 b) Find L s 2 s 2 3 First, we must find the partial fractions decomposition, as follows: s 2 s 2 3 A s B s 2 Cs D s 2 3 As s 2 3 B s 2 3 Cs D s 2 Setting s 0 yields 3B, i.e. B 3. Next, equating the coefficients of the various powers of s gives the following: s 0 3A 9
10 s 2 0 B D s 3 0 A C So, A 0, C A 0, D B 3 s 2 s 2 3 3s 2 3 s 2 3 L s 2 s L s 2 3 L s t 3 sin 3 t 8.a) Find L e 2s s 3 Since 2 t2 L s 3, we have s t2 e st dt 0 2 u2 e su du Then, e 2s s 3 e 2s 0 2 u2 e su du 0 2 u2 e s u 2 du In this integral, let t u 2. Thus, we have e 2s s t 2 2 e st dt So, we can interpret this as the Laplace transform of the function f t 2 t 2 2 if t 2 0 if t 2 y x b) Show that x 2 is an integrating factor for the differential equation 2x2 y dx x 2 y x dy 0 0
11 and solve the differential equation. By an integrating factor, we mean a function such that when we multiply the d.e. by the function, the equation is more easily integrated, i.e. solved. Let s multiply through by the given function. 2 y x 2 dx y x dy 0 This is neither linear nor separable, so we test it for exactness. y 2 y x 2 x 2 x y x. These are equal, so we have an exact d.e. 2 x We seek F(x,y) such that df is the given expression. F x 2 y x 2 yields F 2x y x g y Then F y x g y y x,so g y y and g y 2 y2 Finally, the solution is given implicitly by F x,y 2x y x 2 y2 c. 9.a) Not applicable for our course. b) Find the general solution of x 2 y 3xy 3y 2x 4 e x. First, we observe that the homogeneous equation is an Euler equation. The solution has the form y x r,y rx r,y r r x r 2. Substituting, we have r r 3r 3 x r 0 I.e., r 2 4r 3 r r 3 0. So we have a solutions for r andr 3, and y h c x c 2 x 3. Now, we can attempt to solve the non-homogeneous d.e. by variation of parameters. I.e., we seek a solution in the form y xv x 3 v 2 Then y xv x 3 v 2 v 3x 2 v 2 We simplify by requiring that xv x 3 v 2 0
12 Now y v 3x 2 v 2 6xv 2 Substitution into the d.e. yields x 2 v 3x 2 v 2 6xv 2 3x v 3x 2 v 2 3 xv x 3 v 2 2x 4 e x I.e. x 2 v 3x 2 v 2 2x 4 e x So we have two equations, after clearing common powers of x. v 3x 2 v 2 2x 2 e x v x 2 v 2 0 Subtracting the second from the first, 2x 2 v 2 2x 2 e x or v 2 e x so v 2 e x Then from the second equation, v x 2 v 2 x 2 e x The integral is provided, so we are spared one integration by parts to have v x 2 e x 2xe x 2e x and finally, combine everything to have y c x 2 e x 2xe x 2e x x c 2 e x x 3. 2
Assignment # 8, Math 370, Fall 2018 SOLUTIONS:
 Assignment # 8, Math 370, Fall 018 SOLUTIONS: Problem 1: Solve the equations (a) y y = 3x + x 4, (i) y(0) = 1, y (0) = 1, y (0) = 1. Characteristic equation: α 3 α = 0 so α 1, = 0 and α 3 =. y c = C 1
Assignment # 8, Math 370, Fall 018 SOLUTIONS: Problem 1: Solve the equations (a) y y = 3x + x 4, (i) y(0) = 1, y (0) = 1, y (0) = 1. Characteristic equation: α 3 α = 0 so α 1, = 0 and α 3 =. y c = C 1
Ma 221 Final Exam Solutions 5/14/13
 Ma 221 Final Exam Solutions 5/14/13 1. Solve (a) (8 pts) Solution: The equation is separable. dy dx exy y 1 y0 0 y 1e y dy e x dx y 1e y dy e x dx ye y e y dy e x dx ye y e y e y e x c The last step comes
Ma 221 Final Exam Solutions 5/14/13 1. Solve (a) (8 pts) Solution: The equation is separable. dy dx exy y 1 y0 0 y 1e y dy e x dx y 1e y dy e x dx ye y e y dy e x dx ye y e y e y e x c The last step comes
Homework Solutions: , plus Substitutions
 Homework Solutions: 2.-2.2, plus Substitutions Section 2. I have not included any drawings/direction fields. We can see them using Maple or by hand, so we ll be focusing on getting the analytic solutions
Homework Solutions: 2.-2.2, plus Substitutions Section 2. I have not included any drawings/direction fields. We can see them using Maple or by hand, so we ll be focusing on getting the analytic solutions
Polytechnic Institute of NYU MA 2132 Final Practice Answers Fall 2012
 Polytechnic Institute of NYU MA Final Practice Answers Fall Studying from past or sample exams is NOT recommended. If you do, it should be only AFTER you know how to do all of the homework and worksheet
Polytechnic Institute of NYU MA Final Practice Answers Fall Studying from past or sample exams is NOT recommended. If you do, it should be only AFTER you know how to do all of the homework and worksheet
MATH 307: Problem Set #3 Solutions
 : Problem Set #3 Solutions Due on: May 3, 2015 Problem 1 Autonomous Equations Recall that an equilibrium solution of an autonomous equation is called stable if solutions lying on both sides of it tend
: Problem Set #3 Solutions Due on: May 3, 2015 Problem 1 Autonomous Equations Recall that an equilibrium solution of an autonomous equation is called stable if solutions lying on both sides of it tend
MATH 101: PRACTICE MIDTERM 2
 MATH : PRACTICE MIDTERM INSTRUCTOR: PROF. DRAGOS GHIOCA March 7, Duration of examination: 7 minutes This examination includes pages and 6 questions. You are responsible for ensuring that your copy of the
MATH : PRACTICE MIDTERM INSTRUCTOR: PROF. DRAGOS GHIOCA March 7, Duration of examination: 7 minutes This examination includes pages and 6 questions. You are responsible for ensuring that your copy of the
ORDINARY DIFFERENTIAL EQUATIONS
 ORDINARY DIFFERENTIAL EQUATIONS Basic concepts: Find y(x) where x is the independent and y the dependent varible, based on an equation involving x, y(x), y 0 (x),...e.g.: y 00 (x) = 1+y(x) y0 (x) 1+x or,
ORDINARY DIFFERENTIAL EQUATIONS Basic concepts: Find y(x) where x is the independent and y the dependent varible, based on an equation involving x, y(x), y 0 (x),...e.g.: y 00 (x) = 1+y(x) y0 (x) 1+x or,
Solutions to Exam 1, Math Solution. Because f(x) is one-to-one, we know the inverse function exists. Recall that (f 1 ) (a) =
 Solutions to Exam, Math 56 The function f(x) e x + x 3 + x is one-to-one (there is no need to check this) What is (f ) ( + e )? Solution Because f(x) is one-to-one, we know the inverse function exists
Solutions to Exam, Math 56 The function f(x) e x + x 3 + x is one-to-one (there is no need to check this) What is (f ) ( + e )? Solution Because f(x) is one-to-one, we know the inverse function exists
6 Second Order Linear Differential Equations
 6 Second Order Linear Differential Equations A differential equation for an unknown function y = f(x) that depends on a variable x is any equation that ties together functions of x with y and its derivatives.
6 Second Order Linear Differential Equations A differential equation for an unknown function y = f(x) that depends on a variable x is any equation that ties together functions of x with y and its derivatives.
Ordinary differential equations
 CP3 REVISION LECTURE ON Ordinary differential equations 1 First order linear equations First order nonlinear equations 3 Second order linear equations with constant coefficients 4 Systems of linear ordinary
CP3 REVISION LECTURE ON Ordinary differential equations 1 First order linear equations First order nonlinear equations 3 Second order linear equations with constant coefficients 4 Systems of linear ordinary
MATHEMATICS FOR ENGINEERS & SCIENTISTS 23
 MATHEMATICS FOR ENGINEERS & SCIENTISTS 3.5. Second order linear O.D.E.s: non-homogeneous case.. We ll now consider non-homogeneous second order linear O.D.E.s. These are of the form a + by + c rx) for
MATHEMATICS FOR ENGINEERS & SCIENTISTS 3.5. Second order linear O.D.E.s: non-homogeneous case.. We ll now consider non-homogeneous second order linear O.D.E.s. These are of the form a + by + c rx) for
MAS113 CALCULUS II SPRING 2008, QUIZ 5 SOLUTIONS. x 2 dx = 3y + y 3 = x 3 + c. It can be easily verified that the differential equation is exact, as
 MAS113 CALCULUS II SPRING 008, QUIZ 5 SOLUTIONS Quiz 5a Solutions (1) Solve the differential equation y = x 1 + y. (1 + y )y = x = (1 + y ) = x = 3y + y 3 = x 3 + c. () Solve the differential equation
MAS113 CALCULUS II SPRING 008, QUIZ 5 SOLUTIONS Quiz 5a Solutions (1) Solve the differential equation y = x 1 + y. (1 + y )y = x = (1 + y ) = x = 3y + y 3 = x 3 + c. () Solve the differential equation
UNIVERSITY OF SOUTHAMPTON
 UNIVERSITY OF SOUTHAMPTON MATH03W SEMESTER EXAMINATION 0/ MATHEMATICS FOR ELECTRONIC & ELECTRICAL ENGINEERING Duration: 0 min This paper has two parts, part A and part B. Answer all questions from part
UNIVERSITY OF SOUTHAMPTON MATH03W SEMESTER EXAMINATION 0/ MATHEMATICS FOR ELECTRONIC & ELECTRICAL ENGINEERING Duration: 0 min This paper has two parts, part A and part B. Answer all questions from part
3 Algebraic Methods. we can differentiate both sides implicitly to obtain a differential equation involving x and y:
 3 Algebraic Methods b The first appearance of the equation E Mc 2 in Einstein s handwritten notes. So far, the only general class of differential equations that we know how to solve are directly integrable
3 Algebraic Methods b The first appearance of the equation E Mc 2 in Einstein s handwritten notes. So far, the only general class of differential equations that we know how to solve are directly integrable
Handbook of Ordinary Differential Equations
 Handbook of Ordinary Differential Equations Mark Sullivan July, 28 i Contents Preliminaries. Why bother?...............................2 What s so ordinary about ordinary differential equations?......
Handbook of Ordinary Differential Equations Mark Sullivan July, 28 i Contents Preliminaries. Why bother?...............................2 What s so ordinary about ordinary differential equations?......
Chapter 3: Transcendental Functions
 Chapter 3: Transcendental Functions Spring 2018 Department of Mathematics Hong Kong Baptist University 1 / 32 Except for the power functions, the other basic elementary functions are also called the transcendental
Chapter 3: Transcendental Functions Spring 2018 Department of Mathematics Hong Kong Baptist University 1 / 32 Except for the power functions, the other basic elementary functions are also called the transcendental
Grade: The remainder of this page has been left blank for your workings. VERSION D. Midterm D: Page 1 of 12
 First Name: Student-No: Last Name: Section: Grade: The remainder of this page has been left blank for your workings. Midterm D: Page of 2 Indefinite Integrals. 9 marks Each part is worth marks. Please
First Name: Student-No: Last Name: Section: Grade: The remainder of this page has been left blank for your workings. Midterm D: Page of 2 Indefinite Integrals. 9 marks Each part is worth marks. Please
a x a y = a x+y a x a = y ax y (a x ) r = a rx and log a (xy) = log a (x) + log a (y) log a ( x y ) = log a(x) log a (y) log a (x r ) = r log a (x).
 You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
EXAM. Exam #1. Math 3350 Summer II, July 21, 2000 ANSWERS
 EXAM Exam #1 Math 3350 Summer II, 2000 July 21, 2000 ANSWERS i 100 pts. Problem 1. 1. In each part, find the general solution of the differential equation. dx = x2 e y We use the following sequence of
EXAM Exam #1 Math 3350 Summer II, 2000 July 21, 2000 ANSWERS i 100 pts. Problem 1. 1. In each part, find the general solution of the differential equation. dx = x2 e y We use the following sequence of
M343 Homework 3 Enrique Areyan May 17, 2013
 M343 Homework 3 Enrique Areyan May 17, 013 Section.6 3. Consider the equation: (3x xy + )dx + (6y x + 3)dy = 0. Let M(x, y) = 3x xy + and N(x, y) = 6y x + 3. Since: y = x = N We can conclude that this
M343 Homework 3 Enrique Areyan May 17, 013 Section.6 3. Consider the equation: (3x xy + )dx + (6y x + 3)dy = 0. Let M(x, y) = 3x xy + and N(x, y) = 6y x + 3. Since: y = x = N We can conclude that this
Ma 221 Homework Solutions Due Date: January 24, 2012
 Ma Homewk Solutions Due Date: January, 0. pg. 3 #, 3, 6,, 5, 7 9,, 3;.3 p.5-55 #, 3, 5, 7, 0, 7, 9, (Underlined problems are handed in) In problems, and 5, determine whether the given differential equation
Ma Homewk Solutions Due Date: January, 0. pg. 3 #, 3, 6,, 5, 7 9,, 3;.3 p.5-55 #, 3, 5, 7, 0, 7, 9, (Underlined problems are handed in) In problems, and 5, determine whether the given differential equation
Mathematics 104 Fall Term 2006 Solutions to Final Exam. sin(ln t) dt = e x sin(x) dx.
 Mathematics 14 Fall Term 26 Solutions to Final Exam 1. Evaluate sin(ln t) dt. Solution. We first make the substitution t = e x, for which dt = e x. This gives sin(ln t) dt = e x sin(x). To evaluate the
Mathematics 14 Fall Term 26 Solutions to Final Exam 1. Evaluate sin(ln t) dt. Solution. We first make the substitution t = e x, for which dt = e x. This gives sin(ln t) dt = e x sin(x). To evaluate the
Consider an ideal pendulum as shown below. l θ is the angular acceleration θ is the angular velocity
 1 Second Order Ordinary Differential Equations 1.1 The harmonic oscillator Consider an ideal pendulum as shown below. θ l Fr mg l θ is the angular acceleration θ is the angular velocity A point mass m
1 Second Order Ordinary Differential Equations 1.1 The harmonic oscillator Consider an ideal pendulum as shown below. θ l Fr mg l θ is the angular acceleration θ is the angular velocity A point mass m
MAT 132 Midterm 1 Spring 2017
 MAT Midterm Spring 7 Name: ID: Problem 5 6 7 8 Total ( pts) ( pts) ( pts) ( pts) ( pts) ( pts) (5 pts) (5 pts) ( pts) Score Instructions: () Fill in your name and Stony Brook ID number at the top of this
MAT Midterm Spring 7 Name: ID: Problem 5 6 7 8 Total ( pts) ( pts) ( pts) ( pts) ( pts) ( pts) (5 pts) (5 pts) ( pts) Score Instructions: () Fill in your name and Stony Brook ID number at the top of this
Solutions to Exam 2, Math 10560
 Solutions to Exam, Math 6. Which of the following expressions gives the partial fraction decomposition of the function x + x + f(x = (x (x (x +? Solution: Notice that (x is not an irreducile factor. If
Solutions to Exam, Math 6. Which of the following expressions gives the partial fraction decomposition of the function x + x + f(x = (x (x (x +? Solution: Notice that (x is not an irreducile factor. If
Diff. Eq. App.( ) Midterm 1 Solutions
 Diff. Eq. App.(110.302) Midterm 1 Solutions Johns Hopkins University February 28, 2011 Problem 1.[3 15 = 45 points] Solve the following differential equations. (Hint: Identify the types of the equations
Diff. Eq. App.(110.302) Midterm 1 Solutions Johns Hopkins University February 28, 2011 Problem 1.[3 15 = 45 points] Solve the following differential equations. (Hint: Identify the types of the equations
M GENERAL MATHEMATICS -2- Dr. Tariq A. AlFadhel 1 Solution of the First Mid-Term Exam First semester H
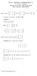 M - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 38-39 H 3 Q. Let A =, B = and C = 3 Compute (if possible) : A+B and BC A+B is impossible. ( ) BC = 3
M - GENERAL MATHEMATICS -- Dr. Tariq A. AlFadhel Solution of the First Mid-Term Exam First semester 38-39 H 3 Q. Let A =, B = and C = 3 Compute (if possible) : A+B and BC A+B is impossible. ( ) BC = 3
Title: Solving Ordinary Differential Equations (ODE s)
 ... Mathematics Support Centre Title: Solving Ordinary Differential Equations (ODE s) Target: On completion of this workbook you should be able to recognise and apply the appropriate method for solving
... Mathematics Support Centre Title: Solving Ordinary Differential Equations (ODE s) Target: On completion of this workbook you should be able to recognise and apply the appropriate method for solving
MAP 2302 Midterm 1 Review Solutions 1
 MAP 2302 Midterm 1 Review Solutions 1 The exam will cover sections 1.2, 1.3, 2.2, 2.3, 2.4, and 2.6. All topics from this review sheet or from the suggested exercises are fair game. 1 Give explicit solutions
MAP 2302 Midterm 1 Review Solutions 1 The exam will cover sections 1.2, 1.3, 2.2, 2.3, 2.4, and 2.6. All topics from this review sheet or from the suggested exercises are fair game. 1 Give explicit solutions
Substituting this into the differential equation and solving for u, we have. + u2. du = 3x + c. ( )
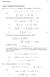 Worked Solutions 27 Chapter 6: Simplifying Through Substitution 6 a Let u = 3 + 3y + 2 Solving for y computing y we then see that 3y = u 3 2 y = u 3 2 3 = d [ u 3 2 3 = 3 Substituting this into the differential
Worked Solutions 27 Chapter 6: Simplifying Through Substitution 6 a Let u = 3 + 3y + 2 Solving for y computing y we then see that 3y = u 3 2 y = u 3 2 3 = d [ u 3 2 3 = 3 Substituting this into the differential
Ma 221. The material below was covered during the lecture given last Wed. (1/29/14). Homogeneous Linear Equations with Constant Coefficients
 Ma 1 The material below was covered during the lecture given last Wed. (1/9/1). Homogeneous Linear Equations with Constant Coefficients We shall now discuss the problem of solving the homogeneous equation
Ma 1 The material below was covered during the lecture given last Wed. (1/9/1). Homogeneous Linear Equations with Constant Coefficients We shall now discuss the problem of solving the homogeneous equation
MATH 151, FALL SEMESTER 2011 COMMON EXAMINATION 3 - VERSION B - SOLUTIONS
 Name (print): Signature: MATH 5, FALL SEMESTER 0 COMMON EXAMINATION - VERSION B - SOLUTIONS Instructor s name: Section No: Part Multiple Choice ( questions, points each, No Calculators) Write your name,
Name (print): Signature: MATH 5, FALL SEMESTER 0 COMMON EXAMINATION - VERSION B - SOLUTIONS Instructor s name: Section No: Part Multiple Choice ( questions, points each, No Calculators) Write your name,
4 Differential Equations
 Advanced Calculus Chapter 4 Differential Equations 65 4 Differential Equations 4.1 Terminology Let U R n, and let y : U R. A differential equation in y is an equation involving y and its (partial) derivatives.
Advanced Calculus Chapter 4 Differential Equations 65 4 Differential Equations 4.1 Terminology Let U R n, and let y : U R. A differential equation in y is an equation involving y and its (partial) derivatives.
Indefinite Integration
 Indefinite Integration 1 An antiderivative of a function y = f(x) defined on some interval (a, b) is called any function F(x) whose derivative at any point of this interval is equal to f(x): F'(x) = f(x)
Indefinite Integration 1 An antiderivative of a function y = f(x) defined on some interval (a, b) is called any function F(x) whose derivative at any point of this interval is equal to f(x): F'(x) = f(x)
THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK. Summer Examination 2009.
 OLLSCOIL NA héireann, CORCAIGH THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK Summer Examination 2009 First Engineering MA008 Calculus and Linear Algebra
OLLSCOIL NA héireann, CORCAIGH THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK Summer Examination 2009 First Engineering MA008 Calculus and Linear Algebra
0.1 Problems to solve
 0.1 Problems to solve Homework Set No. NEEP 547 Due September 0, 013 DLH Nonlinear Eqs. reducible to first order: 1. 5pts) Find the general solution to the differential equation: y = [ 1 + y ) ] 3/. 5pts)
0.1 Problems to solve Homework Set No. NEEP 547 Due September 0, 013 DLH Nonlinear Eqs. reducible to first order: 1. 5pts) Find the general solution to the differential equation: y = [ 1 + y ) ] 3/. 5pts)
Math 250 Skills Assessment Test
 Math 5 Skills Assessment Test Page Math 5 Skills Assessment Test The purpose of this test is purely diagnostic (before beginning your review, it will be helpful to assess both strengths and weaknesses).
Math 5 Skills Assessment Test Page Math 5 Skills Assessment Test The purpose of this test is purely diagnostic (before beginning your review, it will be helpful to assess both strengths and weaknesses).
DIFFERENTIAL EQUATIONS
 DIFFERENTIAL EQUATIONS 1. Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt
DIFFERENTIAL EQUATIONS 1. Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt
UNIVERSITY OF SOUTHAMPTON. A foreign language dictionary (paper version) is permitted provided it contains no notes, additions or annotations.
 UNIVERSITY OF SOUTHAMPTON MATH055W SEMESTER EXAMINATION 03/4 MATHEMATICS FOR ELECTRONIC & ELECTRICAL ENGINEERING Duration: 0 min Solutions Only University approved calculators may be used. A foreign language
UNIVERSITY OF SOUTHAMPTON MATH055W SEMESTER EXAMINATION 03/4 MATHEMATICS FOR ELECTRONIC & ELECTRICAL ENGINEERING Duration: 0 min Solutions Only University approved calculators may be used. A foreign language
APPLIED MATHEMATICS. Part 1: Ordinary Differential Equations. Wu-ting Tsai
 APPLIED MATHEMATICS Part 1: Ordinary Differential Equations Contents 1 First Order Differential Equations 3 1.1 Basic Concepts and Ideas................... 4 1.2 Separable Differential Equations................
APPLIED MATHEMATICS Part 1: Ordinary Differential Equations Contents 1 First Order Differential Equations 3 1.1 Basic Concepts and Ideas................... 4 1.2 Separable Differential Equations................
Math Reading assignment for Chapter 1: Study Sections 1.1 and 1.2.
 Math 3350 1 Chapter 1 Reading assignment for Chapter 1: Study Sections 1.1 and 1.2. 1.1 Material for Section 1.1 An Ordinary Differential Equation (ODE) is a relation between an independent variable x
Math 3350 1 Chapter 1 Reading assignment for Chapter 1: Study Sections 1.1 and 1.2. 1.1 Material for Section 1.1 An Ordinary Differential Equation (ODE) is a relation between an independent variable x
Ma 227 Final Exam Solutions 12/17/07
 Ma 7 Final Exam olutions /7/7 Name: Lecture ection: I pledge my honor that I have abided by the tevens Honor ystem. You may not use a calculator, cell phone, or computer while taking this exam. All work
Ma 7 Final Exam olutions /7/7 Name: Lecture ection: I pledge my honor that I have abided by the tevens Honor ystem. You may not use a calculator, cell phone, or computer while taking this exam. All work
Review For the Final: Problem 1 Find the general solutions of the following DEs. a) x 2 y xy y 2 = 0 solution: = 0 : homogeneous equation.
 Review For the Final: Problem 1 Find the general solutions of the following DEs. a) x 2 y xy y 2 = 0 solution: y y x y2 = 0 : homogeneous equation. x2 v = y dy, y = vx, and x v + x dv dx = v + v2. dx =
Review For the Final: Problem 1 Find the general solutions of the following DEs. a) x 2 y xy y 2 = 0 solution: y y x y2 = 0 : homogeneous equation. x2 v = y dy, y = vx, and x v + x dv dx = v + v2. dx =
6.6 Inverse Trigonometric Functions
 6.6 6.6 Inverse Trigonometric Functions We recall the following definitions from trigonometry. If we restrict the sine function, say fx) sinx, π x π then we obtain a one-to-one function. π/, /) π/ π/ Since
6.6 6.6 Inverse Trigonometric Functions We recall the following definitions from trigonometry. If we restrict the sine function, say fx) sinx, π x π then we obtain a one-to-one function. π/, /) π/ π/ Since
for any C, including C = 0, because y = 0 is also a solution: dy
 Math 3200-001 Fall 2014 Practice exam 1 solutions 2/16/2014 Each problem is worth 0 to 4 points: 4=correct, 3=small error, 2=good progress, 1=some progress 0=nothing relevant. If the result is correct,
Math 3200-001 Fall 2014 Practice exam 1 solutions 2/16/2014 Each problem is worth 0 to 4 points: 4=correct, 3=small error, 2=good progress, 1=some progress 0=nothing relevant. If the result is correct,
Mar 10, Calculus with Algebra and Trigonometry II Lecture 14Undoing the Marproduct 10, 2015 rule: integration 1 / 18
 Calculus with Algebra and Trigonometry II Lecture 14 Undoing the product rule: integration by parts Mar 10, 2015 Calculus with Algebra and Trigonometry II Lecture 14Undoing the Marproduct 10, 2015 rule:
Calculus with Algebra and Trigonometry II Lecture 14 Undoing the product rule: integration by parts Mar 10, 2015 Calculus with Algebra and Trigonometry II Lecture 14Undoing the Marproduct 10, 2015 rule:
Integration by Parts
 Calculus 2 Lia Vas Integration by Parts Using integration by parts one transforms an integral of a product of two functions into a simpler integral. Divide the initial function into two parts called u
Calculus 2 Lia Vas Integration by Parts Using integration by parts one transforms an integral of a product of two functions into a simpler integral. Divide the initial function into two parts called u
Lectures on Differential Equations
 Lectures on Differential Equations Philip Korman Department of Mathematical Sciences University of Cincinnati Cincinnati Ohio 4522-0025 Copyright @ 2008, by Philip L. Korman Contents First Order Equations
Lectures on Differential Equations Philip Korman Department of Mathematical Sciences University of Cincinnati Cincinnati Ohio 4522-0025 Copyright @ 2008, by Philip L. Korman Contents First Order Equations
(1 + 2y)y = x. ( x. The right-hand side is a standard integral, so in the end we have the implicit solution. y(x) + y 2 (x) = x2 2 +C.
 Midterm 1 33B-1 015 October 1 Find the exact solution of the initial value problem. Indicate the interval of existence. y = x, y( 1) = 0. 1 + y Solution. We observe that the equation is separable, and
Midterm 1 33B-1 015 October 1 Find the exact solution of the initial value problem. Indicate the interval of existence. y = x, y( 1) = 0. 1 + y Solution. We observe that the equation is separable, and
DIFFERENTIAL EQUATIONS
 DIFFERENTIAL EQUATIONS Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt =
DIFFERENTIAL EQUATIONS Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt =
Fourier transforms. c n e inπx. f (x) = Write same thing in an equivalent form, using n = 1, f (x) = l π
 Fourier transforms We can imagine our periodic function having periodicity taken to the limits ± In this case, the function f (x) is not necessarily periodic, but we can still use Fourier transforms (related
Fourier transforms We can imagine our periodic function having periodicity taken to the limits ± In this case, the function f (x) is not necessarily periodic, but we can still use Fourier transforms (related
Advanced Eng. Mathematics
 Koya University Faculty of Engineering Petroleum Engineering Department Advanced Eng. Mathematics Lecture 6 Prepared by: Haval Hawez E-mail: haval.hawez@koyauniversity.org 1 Second Order Linear Ordinary
Koya University Faculty of Engineering Petroleum Engineering Department Advanced Eng. Mathematics Lecture 6 Prepared by: Haval Hawez E-mail: haval.hawez@koyauniversity.org 1 Second Order Linear Ordinary
Form A. 1. Which of the following is a second-order, linear, homogenous differential equation? 2
 Form A Math 4 Common Part of Final Exam December 6, 996 INSTRUCTIONS: Please enter your NAME, ID NUMBER, FORM designation, and INDEX NUMBER on your op scan sheet. The index number should be written in
Form A Math 4 Common Part of Final Exam December 6, 996 INSTRUCTIONS: Please enter your NAME, ID NUMBER, FORM designation, and INDEX NUMBER on your op scan sheet. The index number should be written in
First and Second Order ODEs
 Civil Engineering 2 Mathematics Autumn 211 M. Ottobre First and Second Order ODEs Warning: all the handouts that I will provide during the course are in no way exhaustive, they are just short recaps. Notation
Civil Engineering 2 Mathematics Autumn 211 M. Ottobre First and Second Order ODEs Warning: all the handouts that I will provide during the course are in no way exhaustive, they are just short recaps. Notation
Elementary ODE Review
 Elementary ODE Review First Order ODEs First Order Equations Ordinary differential equations of the fm y F(x, y) () are called first der dinary differential equations. There are a variety of techniques
Elementary ODE Review First Order ODEs First Order Equations Ordinary differential equations of the fm y F(x, y) () are called first der dinary differential equations. There are a variety of techniques
Chapter 3. Reading assignment: In this chapter we will cover Sections dx 1 + a 0(x)y(x) = g(x). (1)
 Chapter 3 3 Introduction Reading assignment: In this chapter we will cover Sections 3.1 3.6. 3.1 Theory of Linear Equations Recall that an nth order Linear ODE is an equation that can be written in the
Chapter 3 3 Introduction Reading assignment: In this chapter we will cover Sections 3.1 3.6. 3.1 Theory of Linear Equations Recall that an nth order Linear ODE is an equation that can be written in the
4 Partial Differentiation
 4 Partial Differentiation Many equations in engineering, physics and mathematics tie together more than two variables. For example Ohm s Law (V = IR) and the equation for an ideal gas, PV = nrt, which
4 Partial Differentiation Many equations in engineering, physics and mathematics tie together more than two variables. For example Ohm s Law (V = IR) and the equation for an ideal gas, PV = nrt, which
2.1 The derivative. Rates of change. m sec = y f (a + h) f (a)
 2.1 The derivative Rates of change 1 The slope of a secant line is m sec = y f (b) f (a) = x b a and represents the average rate of change over [a, b]. Letting b = a + h, we can express the slope of the
2.1 The derivative Rates of change 1 The slope of a secant line is m sec = y f (b) f (a) = x b a and represents the average rate of change over [a, b]. Letting b = a + h, we can express the slope of the
MATH 261 MATH 261: Elementary Differential Equations MATH 261 FALL 2005 FINAL EXAM FALL 2005 FINAL EXAM EXAMINATION COVER PAGE Professor Moseley
 MATH 6 MATH 6: Elementary Differential Equations MATH 6 FALL 5 FINAL EXAM FALL 5 FINAL EXAM EXAMINATION COVER PAGE Professor Moseley PRINT NAME ( ) Last Name, First Name MI (What you wish to be called)
MATH 6 MATH 6: Elementary Differential Equations MATH 6 FALL 5 FINAL EXAM FALL 5 FINAL EXAM EXAMINATION COVER PAGE Professor Moseley PRINT NAME ( ) Last Name, First Name MI (What you wish to be called)
2326 Problem Sheet 1. Solutions 1. First Order Differential Equations. Question 1: Solve the following, given an explicit solution if possible:
 2326 Problem Sheet. Solutions First Order Differential Equations Question : Solve the following, given an explicit solution if possible:. 2 x = 4x3, () = 3, ( ) The given equation is a first order linear
2326 Problem Sheet. Solutions First Order Differential Equations Question : Solve the following, given an explicit solution if possible:. 2 x = 4x3, () = 3, ( ) The given equation is a first order linear
25. Chain Rule. Now, f is a function of t only. Expand by multiplication:
 25. Chain Rule The Chain Rule is present in all differentiation. If z = f(x, y) represents a two-variable function, then it is plausible to consider the cases when x and y may be functions of other variable(s).
25. Chain Rule The Chain Rule is present in all differentiation. If z = f(x, y) represents a two-variable function, then it is plausible to consider the cases when x and y may be functions of other variable(s).
Math 4381 / 6378 Symmetry Analysis
 Math 438 / 6378 Smmetr Analsis Elementar ODE Review First Order Equations Ordinar differential equations of the form = F(x, ( are called first order ordinar differential equations. There are a variet of
Math 438 / 6378 Smmetr Analsis Elementar ODE Review First Order Equations Ordinar differential equations of the form = F(x, ( are called first order ordinar differential equations. There are a variet of
More Techniques. for Solving First Order ODE'S. and. a Classification Scheme for Techniques
 A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 1 A COLLECTION OF HANDOUTS ON FIRST ORDER ORDINARY DIFFERENTIAL
A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 1 A COLLECTION OF HANDOUTS ON FIRST ORDER ORDINARY DIFFERENTIAL
Answers and Solutions to Section 13.3 Homework Problems 1-23 (odd) and S. F. Ellermeyer. f dr
 Answers and Solutions to Section 13.3 Homework Problems 1-23 (odd) and 29-33 S. F. Ellermeyer 1. By looking at the picture in the book, we see that f dr 5 1 4. 3. For the vector field Fx,y 6x 5yi 5x 4yj,
Answers and Solutions to Section 13.3 Homework Problems 1-23 (odd) and 29-33 S. F. Ellermeyer 1. By looking at the picture in the book, we see that f dr 5 1 4. 3. For the vector field Fx,y 6x 5yi 5x 4yj,
Spring 2015 Sample Final Exam
 Math 1151 Spring 2015 Sample Final Exam Final Exam on 4/30/14 Name (Print): Time Limit on Final: 105 Minutes Go on carmen.osu.edu to see where your final exam will be. NOTE: This exam is much longer than
Math 1151 Spring 2015 Sample Final Exam Final Exam on 4/30/14 Name (Print): Time Limit on Final: 105 Minutes Go on carmen.osu.edu to see where your final exam will be. NOTE: This exam is much longer than
Analysis III Solutions - Serie 12
 .. Necessary condition Let us consider the following problem for < x, y < π, u =, for < x, y < π, u y (x, π) = x a, for < x < π, u y (x, ) = a x, for < x < π, u x (, y) = u x (π, y) =, for < y < π. Find
.. Necessary condition Let us consider the following problem for < x, y < π, u =, for < x, y < π, u y (x, π) = x a, for < x < π, u y (x, ) = a x, for < x < π, u x (, y) = u x (π, y) =, for < y < π. Find
Math 266, Midterm Exam 1
 Math 266, Midterm Exam 1 February 19th 2016 Name: Ground Rules: 1. Calculator is NOT allowed. 2. Show your work for every problem unless otherwise stated (partial credits are available). 3. You may use
Math 266, Midterm Exam 1 February 19th 2016 Name: Ground Rules: 1. Calculator is NOT allowed. 2. Show your work for every problem unless otherwise stated (partial credits are available). 3. You may use
3. Identify and find the general solution of each of the following first order differential equations.
 Final Exam MATH 33, Sample Questions. Fall 7. y = Cx 3 3 is the general solution of a differential equation. Find the equation. Answer: y = 3y + 9 xy. y = C x + C x is the general solution of a differential
Final Exam MATH 33, Sample Questions. Fall 7. y = Cx 3 3 is the general solution of a differential equation. Find the equation. Answer: y = 3y + 9 xy. y = C x + C x is the general solution of a differential
كلية العلوم قسم الرياضيات المعادالت التفاضلية العادية
 الجامعة اإلسالمية كلية العلوم غزة قسم الرياضيات المعادالت التفاضلية العادية Elementary differential equations and boundary value problems المحاضرون أ.د. رائد صالحة د. فاتن أبو شوقة 1 3 4 5 6 بسم هللا
الجامعة اإلسالمية كلية العلوم غزة قسم الرياضيات المعادالت التفاضلية العادية Elementary differential equations and boundary value problems المحاضرون أ.د. رائد صالحة د. فاتن أبو شوقة 1 3 4 5 6 بسم هللا
Calculus I: Practice Midterm II
 Calculus I: Practice Mierm II April 3, 2015 Name: Write your solutions in the space provided. Continue on the back for more space. Show your work unless asked otherwise. Partial credit will be given for
Calculus I: Practice Mierm II April 3, 2015 Name: Write your solutions in the space provided. Continue on the back for more space. Show your work unless asked otherwise. Partial credit will be given for
Math 201 Solutions to Assignment 1. 2ydy = x 2 dx. y = C 1 3 x3
 Math 201 Solutions to Assignment 1 1. Solve the initial value problem: x 2 dx + 2y = 0, y(0) = 2. x 2 dx + 2y = 0, y(0) = 2 2y = x 2 dx y 2 = 1 3 x3 + C y = C 1 3 x3 Notice that y is not defined for some
Math 201 Solutions to Assignment 1 1. Solve the initial value problem: x 2 dx + 2y = 0, y(0) = 2. x 2 dx + 2y = 0, y(0) = 2 2y = x 2 dx y 2 = 1 3 x3 + C y = C 1 3 x3 Notice that y is not defined for some
Note: Final Exam is at 10:45 on Tuesday, 5/3/11 (This is the Final Exam time reserved for our labs). From Practice Test I
 MA Practice Final Answers in Red 4/8/ and 4/9/ Name Note: Final Exam is at :45 on Tuesday, 5// (This is the Final Exam time reserved for our labs). From Practice Test I Consider the integral 5 x dx. Sketch
MA Practice Final Answers in Red 4/8/ and 4/9/ Name Note: Final Exam is at :45 on Tuesday, 5// (This is the Final Exam time reserved for our labs). From Practice Test I Consider the integral 5 x dx. Sketch
Sample Questions Exam II, FS2009 Paulette Saab Calculators are neither needed nor allowed.
 Sample Questions Exam II, FS2009 Paulette Saab Calculators are neither needed nor allowed. Part A: (SHORT ANSWER QUESTIONS) Do the following problems. Write the answer in the space provided. Only the answers
Sample Questions Exam II, FS2009 Paulette Saab Calculators are neither needed nor allowed. Part A: (SHORT ANSWER QUESTIONS) Do the following problems. Write the answer in the space provided. Only the answers
Practice Problems: Integration by Parts
 Practice Problems: Integration by Parts Answers. (a) Neither term will get simpler through differentiation, so let s try some choice for u and dv, and see how it works out (we can always go back and try
Practice Problems: Integration by Parts Answers. (a) Neither term will get simpler through differentiation, so let s try some choice for u and dv, and see how it works out (we can always go back and try
Differential Equations Class Notes
 Differential Equations Class Notes Dan Wysocki Spring 213 Contents 1 Introduction 2 2 Classification of Differential Equations 6 2.1 Linear vs. Non-Linear.................................. 7 2.2 Seperable
Differential Equations Class Notes Dan Wysocki Spring 213 Contents 1 Introduction 2 2 Classification of Differential Equations 6 2.1 Linear vs. Non-Linear.................................. 7 2.2 Seperable
Section 7.2 Addition and Subtraction Identities. In this section, we begin expanding our repertoire of trigonometric identities.
 Section 7. Addition and Subtraction Identities 47 Section 7. Addition and Subtraction Identities In this section, we begin expanding our repertoire of trigonometric identities. Identities The sum and difference
Section 7. Addition and Subtraction Identities 47 Section 7. Addition and Subtraction Identities In this section, we begin expanding our repertoire of trigonometric identities. Identities The sum and difference
3. Identify and find the general solution of each of the following first order differential equations.
 Final Exam MATH 33, Sample Questions. Fall 6. y = Cx 3 3 is the general solution of a differential equation. Find the equation. Answer: y = 3y + 9 xy. y = C x + C is the general solution of a differential
Final Exam MATH 33, Sample Questions. Fall 6. y = Cx 3 3 is the general solution of a differential equation. Find the equation. Answer: y = 3y + 9 xy. y = C x + C is the general solution of a differential
MATH 307 Introduction to Differential Equations Autumn 2017 Midterm Exam Monday November
 MATH 307 Introduction to Differential Equations Autumn 2017 Midterm Exam Monday November 6 2017 Name: Student ID Number: I understand it is against the rules to cheat or engage in other academic misconduct
MATH 307 Introduction to Differential Equations Autumn 2017 Midterm Exam Monday November 6 2017 Name: Student ID Number: I understand it is against the rules to cheat or engage in other academic misconduct
DIFFERENTIAL EQUATIONS
 DIFFERENTIAL EQUATIONS Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt =
DIFFERENTIAL EQUATIONS Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt =
MATH 2250 Final Exam Solutions
 MATH 225 Final Exam Solutions Tuesday, April 29, 28, 6: 8:PM Write your name and ID number at the top of this page. Show all your work. You may refer to one double-sided sheet of notes during the exam
MATH 225 Final Exam Solutions Tuesday, April 29, 28, 6: 8:PM Write your name and ID number at the top of this page. Show all your work. You may refer to one double-sided sheet of notes during the exam
Ordinary Differential Equations (ODEs)
 Chapter 13 Ordinary Differential Equations (ODEs) We briefly review how to solve some of the most standard ODEs. 13.1 First Order Equations 13.1.1 Separable Equations A first-order ordinary differential
Chapter 13 Ordinary Differential Equations (ODEs) We briefly review how to solve some of the most standard ODEs. 13.1 First Order Equations 13.1.1 Separable Equations A first-order ordinary differential
OCR A2 Level Mathematics Core Mathematics Scheme of Work
 OCR A Level Mathematics Core Mathematics Scheme of Work Examination in June of Year 13 The Solomen press worksheets are an excellent resource and incorporated into the SOW NUMERICAL METHODS (6 ) (Solomen
OCR A Level Mathematics Core Mathematics Scheme of Work Examination in June of Year 13 The Solomen press worksheets are an excellent resource and incorporated into the SOW NUMERICAL METHODS (6 ) (Solomen
Math 180, Exam 2, Practice Fall 2009 Problem 1 Solution. f(x) = arcsin(2x + 1) = sin 1 (3x + 1), lnx
 Math 80, Exam, Practice Fall 009 Problem Solution. Differentiate the functions: (do not simplify) f(x) = x ln(x + ), f(x) = xe x f(x) = arcsin(x + ) = sin (3x + ), f(x) = e3x lnx Solution: For the first
Math 80, Exam, Practice Fall 009 Problem Solution. Differentiate the functions: (do not simplify) f(x) = x ln(x + ), f(x) = xe x f(x) = arcsin(x + ) = sin (3x + ), f(x) = e3x lnx Solution: For the first
Problem Max. Possible Points Total
 MA 262 Exam 1 Fall 2011 Instructor: Raphael Hora Name: Max Possible Student ID#: 1234567890 1. No books or notes are allowed. 2. You CAN NOT USE calculators or any electronic devices. 3. Show all work
MA 262 Exam 1 Fall 2011 Instructor: Raphael Hora Name: Max Possible Student ID#: 1234567890 1. No books or notes are allowed. 2. You CAN NOT USE calculators or any electronic devices. 3. Show all work
Solutions to the Review Questions
 Solutions to the Review Questions Short Answer/True or False. True or False, and explain: (a) If y = y + 2t, then 0 = y + 2t is an equilibrium solution. False: (a) Equilibrium solutions are only defined
Solutions to the Review Questions Short Answer/True or False. True or False, and explain: (a) If y = y + 2t, then 0 = y + 2t is an equilibrium solution. False: (a) Equilibrium solutions are only defined
FLAP M6.1 Introducing differential equations COPYRIGHT 1998 THE OPEN UNIVERSITY S570 V1.1
 F1 (a) This equation is of first order and of first degree. It is a linear equation, since the dependent variable y and its derivative only appear raised to the first power, and there are no products of
F1 (a) This equation is of first order and of first degree. It is a linear equation, since the dependent variable y and its derivative only appear raised to the first power, and there are no products of
SOLUTIONS FOR PRACTICE FINAL EXAM
 SOLUTIONS FOR PRACTICE FINAL EXAM ANDREW J. BLUMBERG. Solutions () Short answer questions: (a) State the mean value theorem. Proof. The mean value theorem says that if f is continuous on (a, b) and differentiable
SOLUTIONS FOR PRACTICE FINAL EXAM ANDREW J. BLUMBERG. Solutions () Short answer questions: (a) State the mean value theorem. Proof. The mean value theorem says that if f is continuous on (a, b) and differentiable
Topics and Concepts. 1. Limits
 Topics and Concepts 1. Limits (a) Evaluating its (Know: it exists if and only if the it from the left is the same as the it from the right) (b) Infinite its (give rise to vertical asymptotes) (c) Limits
Topics and Concepts 1. Limits (a) Evaluating its (Know: it exists if and only if the it from the left is the same as the it from the right) (b) Infinite its (give rise to vertical asymptotes) (c) Limits
APPLIED MATHEMATICS. Introduction to Differential Equations APM2A10. Supplementary Test 1: 23/03/2016
 APPLIED MATHEMATICS Introduction to Differential Equations APMA0 Supplementary Test : 3/03/06 Duration: 70 minutes Marks: 30 Assessor: Mr KD Anderson Moderator: Prof M Khumalo Instructions:. Answer all
APPLIED MATHEMATICS Introduction to Differential Equations APMA0 Supplementary Test : 3/03/06 Duration: 70 minutes Marks: 30 Assessor: Mr KD Anderson Moderator: Prof M Khumalo Instructions:. Answer all
Prelim 2 Math Please show your reasoning and all your work. This is a 90 minute exam. Calculators are not needed or permitted. Good luck!
 April 4, Prelim Math Please show your reasoning and all your work. This is a 9 minute exam. Calculators are not needed or permitted. Good luck! Trigonometric Formulas sin x sin x cos x cos (u + v) cos
April 4, Prelim Math Please show your reasoning and all your work. This is a 9 minute exam. Calculators are not needed or permitted. Good luck! Trigonometric Formulas sin x sin x cos x cos (u + v) cos
Monday, 6 th October 2008
 MA211 Lecture 9: 2nd order differential eqns Monday, 6 th October 2008 MA211 Lecture 9: 2nd order differential eqns 1/19 Class test next week... MA211 Lecture 9: 2nd order differential eqns 2/19 This morning
MA211 Lecture 9: 2nd order differential eqns Monday, 6 th October 2008 MA211 Lecture 9: 2nd order differential eqns 1/19 Class test next week... MA211 Lecture 9: 2nd order differential eqns 2/19 This morning
2t t dt.. So the distance is (t2 +6) 3/2
 Math 8, Solutions to Review for the Final Exam Question : The distance is 5 t t + dt To work that out, integrate by parts with u t +, so that t dt du The integral is t t + dt u du u 3/ (t +) 3/ So the
Math 8, Solutions to Review for the Final Exam Question : The distance is 5 t t + dt To work that out, integrate by parts with u t +, so that t dt du The integral is t t + dt u du u 3/ (t +) 3/ So the
Solutions to the Review Questions
 Solutions to the Review Questions Short Answer/True or False. True or False, and explain: (a) If y = y + 2t, then 0 = y + 2t is an equilibrium solution. False: This is an isocline associated with a slope
Solutions to the Review Questions Short Answer/True or False. True or False, and explain: (a) If y = y + 2t, then 0 = y + 2t is an equilibrium solution. False: This is an isocline associated with a slope
Math 106: Review for Exam II - SOLUTIONS
 Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
Calculus I Announcements
 Slide 1 Calculus I Announcements Read sections 4.2,4.3,4.4,4.1 and 5.3 Do the homework from sections 4.2,4.3,4.4,4.1 and 5.3 Exam 3 is Thursday, November 12th See inside for a possible exam question. Slide
Slide 1 Calculus I Announcements Read sections 4.2,4.3,4.4,4.1 and 5.3 Do the homework from sections 4.2,4.3,4.4,4.1 and 5.3 Exam 3 is Thursday, November 12th See inside for a possible exam question. Slide
Lecture Notes on. Differential Equations. Emre Sermutlu
 Lecture Notes on Differential Equations Emre Sermutlu ISBN: Copyright Notice: To my wife Nurten and my daughters İlayda and Alara Contents Preface ix 1 First Order ODE 1 1.1 Definitions.............................
Lecture Notes on Differential Equations Emre Sermutlu ISBN: Copyright Notice: To my wife Nurten and my daughters İlayda and Alara Contents Preface ix 1 First Order ODE 1 1.1 Definitions.............................
Jim Lambers MAT 280 Summer Semester Practice Final Exam Solution. dy + xz dz = x(t)y(t) dt. t 3 (4t 3 ) + e t2 (2t) + t 7 (3t 2 ) dt
 Jim Lambers MAT 28 ummer emester 212-1 Practice Final Exam olution 1. Evaluate the line integral xy dx + e y dy + xz dz, where is given by r(t) t 4, t 2, t, t 1. olution From r (t) 4t, 2t, t 2, we obtain
Jim Lambers MAT 28 ummer emester 212-1 Practice Final Exam olution 1. Evaluate the line integral xy dx + e y dy + xz dz, where is given by r(t) t 4, t 2, t, t 1. olution From r (t) 4t, 2t, t 2, we obtain
Calculus I Review Solutions
 Calculus I Review Solutions. Compare and contrast the three Value Theorems of the course. When you would typically use each. The three value theorems are the Intermediate, Mean and Extreme value theorems.
Calculus I Review Solutions. Compare and contrast the three Value Theorems of the course. When you would typically use each. The three value theorems are the Intermediate, Mean and Extreme value theorems.
Practice Problems for the Final Exam
 Math 114 Spring 2017 Practice Problems for the Final Exam 1. The planes 3x + 2y + z = 6 and x + y = 2 intersect in a line l. Find the distance from the origin to l. (Answer: 24 3 ) 2. Find the area of
Math 114 Spring 2017 Practice Problems for the Final Exam 1. The planes 3x + 2y + z = 6 and x + y = 2 intersect in a line l. Find the distance from the origin to l. (Answer: 24 3 ) 2. Find the area of
7.2 Parts (Undoing the Product Rule)
 7.2 Parts (Undoing the Product Rule) 7.1 Substitution (Undoing the Chain Rule) Often w inside of some other function, dw up to constant What I want you to show me... w, dw, with respect to w 7.2 Parts
7.2 Parts (Undoing the Product Rule) 7.1 Substitution (Undoing the Chain Rule) Often w inside of some other function, dw up to constant What I want you to show me... w, dw, with respect to w 7.2 Parts
