Odd Answers: Chapter Eight Contemporary Calculus 1 { ( 3+2 } = lim { 1. { 2. arctan(a) 2. arctan(3) } = 2( π 2 ) 2. arctan(3)
|
|
|
- George Stewart
- 5 years ago
- Views:
Transcription
1 Odd Answers: Chapter Eight Contemporary Calculus PROBLEM ANSWERS Chapter Eight Section 8.. lim { A 0 } lim { ( A ) ( 00 ) } lim { 00 A } 00.. lim {. arctan() A } lim {. arctan(a). arctan() } ( π ). arctan() Use u ln(). lim { 5. ln( ln() ) A e } lim { 5. ln( ln(a) ) 5. ln( ln(e) ) } lim { 5. ln( ln(a) ) 0 }. DIVERGES.. lim { ln( ) A } lim { ln(a ) ln( ) } lim { ln(a ) 0 }. DIVERGES. 9. lim { A ( ) } lim { (A ) ( ) } lim { (A ) + }.. lim { + A } lim { A+ + } lim { A+ + 5 } 5.. lim A!0 + { 4 A } lim A!0 + { 4 A } lim { 4 6 /4 } lim A!0 + A { 4 (6) /4 4 A/4 } lim { 4 A/4 }. A!0 + A!0 +. lim A! " { arcsin( ) A 0 } lim A! " { arcsin( A ) arcsin( 0 ) } π 0 π. 9. lim { cos() A } lim { cos(a) cos( ) } lim 0.46 cos(a) DNE. DIVERGES.. lim / { ln cos() A 0 } DIVERGES. lim { ln cos(a) ln cos(0) } lim / 0 ln cos(a) DNE. /
2 Odd Answers: Chapter Eight Contemporary Calculus. (a) A R: R A R: R (b) lim R R P d R P( R ) R P( R R R ) RP. R R P d R P( R ) R P( R R R ) RP. R P # d lim R +A R R P( R+A ) R lim R P( R+A R ) R P( R ) RP. 5. ( + ) d d which converges by the p test. + d < Therefore, ( + ) d converges.. Fof > 0, ln() < so + ln() < and Then d + ln() >. d which diverges by the p test. Therefore, + ln() d diverges. 9. cos() so 0 + cos() and 0 + cos(). Then + cos() d d which converges by the p test. Therefore, + cos() d converges.. V 0 π ( 4 d which converges by the p test. + ) d < π 0 Therefore, V 0 π ( + ) d converges.. (a) A d < A k k (b) A d > A k k Section 8.. u +, du d, du 6 d: u du u + C ( + ) + C.. u, du d, du 6 d: u du. u
3 Odd Answers: Chapter Eight Contemporary Calculus 5. u + : 6 ln( + ) + C.. u + : cos( + ) + C. 9. u e +, du e d: sec ( u ) du tan( u ) tan(e + ) 0 tan(e + ) tan(+).9. u ln(), du d: u du u + C ( ln() ) + C.. u sin(), du cos() d: e u du e u + C e sin() + C. 5. u, du d: u du 5 arctan( u ) 5 arctan( ) 5 arctan(9) 5 arctan(). u, du d: cos(u) du sin(u) sin( ) ( sin( ) ( sin() ) u 5 + sin (), du. sin(). cos() d: u du ln u + C ln 5 + sin () + C.. 5 ln C.. ln 5 + ln 48 ln 8 ln 48 8 ln( 6 ) arctan( + ) 0 arctan( ) arctan(.5 ) u e, du e d: + u du arctan( u ) + C arctan( e ) + C. 9. u + ln(), du d: u du ln u ln + ln() e ln.08. u, du d: u du u/ ( ) / 0 (0) / () /. u + sin(), du cos() d: u du 4 u4 + C 4 ( + sin() ) 4 + C. 5. u ln(), du d: u du u/ ( ln() ) / e ( ln(e) ) / ( ln() ) /.
4 Odd Answers: Chapter Eight Contemporary Calculus 4. u 5 + tan(), du sec () d: u du ln u + C ln 5 + tan() + C. 9. u 5, du d: tan(u) du ln sec(u) + C ln sec( 5) + C. 4. u 5, du 5 d: 5 eu du 5 eu 5 e5 0 5 e5 5 e (+) + d. arctan( + ) + C. 45. (+5) + 4 d. arctan( +5 ) + C. ( ) + 49 d. arctan( ) + C. 49. ln arctan( + ) + C. 5.. ln arctan( ) + C d + ( ) + 9 d. ln arctan( ) + C. Section 8... ln() d u ln(). Then dv d, du d, and v 6. v du ln() d 6 ln() 6 d 6 ln() +C.. 4 ln() d dv 4 d. Then u ln(), du d, and v 5 5. v du ln() d 5 5. ln() 5 4 d 5.. arctan() d dv d. Then u arctan(), du v du arctan().. + d, and v. + d. arctan() 5 5. ln() C. + d. arctan() { arctan() } + C. arctan(). +. arctan() } + C.. 0 e d 0. e d. Put u. Then dv e d, du d, and v e. v du. e e d. e 9 e 0 {. e () 9 e () } { 0. e (0) 9 e (0) } e.
5 Odd Answers: Chapter Eight Contemporary Calculus sec(). tan() d. Put u. Then dv sec(). tan() d, du d, and v sec(). v du. sec() sec() d. sec() ln sec() + tan() + C. π/. π/. cos() d Put u. Then dv cos() d, du d, and v sin(). v du. sin() sin(). d. sin() + 9 cos() π/ {.π. sin(.π ) + 9 cos(.π } {.π. sin(.π ) + 9 cos(.π ) }.88. π/.. cos( ) d. Use u substitution! Put u. Then du 6 d and du d. cos( u ). du. sin( u ) + C. sin( ) + C. 5. ln( + 5) d. Put u ln( + 5). Then dv d, du + 5 d, and v. v du ln( + 5) d. ln( + 5) d. ln( + 5) { 5. ln + 5 } {. ln() + 5. ln } {. ln() + 5. ln }. ln(). ln() 4.8. e. ( ln() ) d. Put u ( ln() ). Then dv d, du. ln(). d, and v. v du ( ln() ).. ln(). d. ( ln() ). ln() d. ( ln() ) {. ln() } e { e( ln(e) ) e. ln(e) + e } { ( ln() ). ln() + } e arcsin() d. Put u arcsin(). Then dv d, du v du arcsin()... arcsin() d, and v. d (use u sub with u ) d. arcsin() u ( ) du. arcsin() + u + C. arcsin() + + C.
6 Odd Answers: Chapter Eight Contemporary Calculus 6.. arctan() d. Put u arctan(). Then dv d, du v du arctan() d, and v. + 9 d. arctan() / + 9 d. arctan() { 9. arctan() } + C. arctan() arctan() } + C.. ln() d. Use u substitution! Put u ln(). Then du d. u du u ( ln() ) ( ln() ) ( ln() ) ( ln() ) (a) sin () d { S. C + S d } { S. C C } + K { sin (). cos(). cos() } + K. (b) sin 4 () d 4 { S. C + S d } 4 { S4. C + [ ( SC + ) ] } + K 4 { S. C SC + } + K 4 { sin (). cos() sin(). cos() + } + K (c) on your own.. (a) sec () d { sec()tan() + sec() d } { sec(). tan() + ln sec() + tan() } + K (b) and (c) on your own. 9. cos ( + ) d. First do a substitution: u +. Then du d and d du. cos ( u ) du { ( C. S + C du ) } 6 { C. S + S } + K 6 { cos (u). sin(u) + sin(u) } + K 6 { cos ( + ). sin( + ) + sin( + ) } + K.. ( + 5) 9 d. (a) By parts: put u. Then dv ( + 5) 9 d, du d, and v 40 ( + 5) 0. v du. 40 ( + 5) ( + 5) ( + 5) + C. 40 ( + 5) 0 d (b) Substitution: put u + 5. Then du d and d du. Also, ( u 5 ). ( u 5 ). u 9 du 4 u 0 5u 9 du 4 { u 5 0 u0 } + C 84 ( + 5) 5 80 ( + 5) 0 + C. The answers (antiderivatives) in parts (a) and (b) look different, but you can check that the derivative of each answer is. ( + 5) 9.
7 Odd Answers: Chapter Eight Contemporary Calculus. (a) Make an informed prediction. (b) 0 sin() d cos() 0 ( cos()) ( cos(0)) cos(0) cos() sin() d. cos() + sin() 0 {. cos() + sin()} { 0. cos(0) + sin(0)} sin() cos() (a) Make an informed prediction. (b) See problem : V ais V y ais. On your own. y0 e π. y. e y dy π π( ln() ) d π(e ).5. y. e y dy (use integration by parts with u y, dv e y dy : see Eample ) y0 π( y. e y e y ) 0 π(. e e ) π(0. e 0 e 0 ) π(0) π( ) π arctan() d. Put u arctan(). Then dv d, du + d, and v. v du arctan() On your own.. arctan() d + + d (dividing by + ). arctan() { ln( + ) } + C. arctan() ln( + ) } + C. Section 8.4. A + B A + + B Divide first: ( + 5) ( + 5) ( + 5)( ) A + B +5 + C A( + 4 5) + B( ) + C( + 5) ( + 5)( ). Solving : A + B + C 6 : 4A B + 5C 9 k: 5A 5 we get A, B, and C 0 so
8 Odd Answers: Chapter Eight Contemporary Calculus ( + 5)( ) ( + ) A + B + C + A( + ) + (B + C) ( + ). Solving : A + B 8 : C k: A we get A, B 5, and C so 8 + ( + ) ( + ) A + B + C + A()( + ) + B( + ) +C( ) ( + ). Solving : A + C : A + B k: B 6 we get A 0, B, and C so ( + ) ( + )( 5) d d ln ln 5 + C d + + d ln + + ln ln + 5 ln( 4 6 ) ln( ) () d. ln + 5. ln + + C () d. ln ln + C d + 5 d + 5. ln + C d d +. ln + ln C.. d. Use u substitution with u. Then du so u du ln u + C ln + C. A partial fraction decomposition also works but takes longer.
9 Odd Answers: Chapter Eight Contemporary Calculus d + 6 d + 6ln + C d d. ln ln + + C d + + d. ln +. arctan( ) + C.. (a) + + d (+) + d arctan( + ) + C. (b) + + d ( + ) d ( + ) + C + + C. (c) d ( + ) d / + / + d ln. Prob. : f() () + 5. ( + ). Then Prob. : g() f '(). () 5. ( + ) and f ''() 4. () + 0. ( + ) ( + ) + 4. ( ). Then ln + + C. g '(). ( + ) 4. ( ) and g ''() 6. ( + ) + 8. ( ) Prob. 5: f() + 5 Prob. 6: On your own. + 5 so f '() 5 and f ''() 0. d. (a) Solve dt (00 ). Separate the variables: (00 ) d dt. Use partial fractions: (00 ) A + B (solving A+B 0 and 00A ) so { } d dt and, integrating, d dt. Then 0.0. ln 0.0. ln 00 t + C so ln Using the initial condition (0) 50: ln 00 00t + K. ( K 00C is a constant ) ln( ) 00. (0) + K so K ln( ). Finally, ln t + ln() so 00 e00t. e ln(). e 00t and 00. e 00t. e 00t. Graph this on your own.
10 Odd Answers: Chapter Eight Contemporary Calculus 0 (b) In this part it is easier to use the form Put 0 and solve Put 0 and solve Put 00. Then e 00t e 00t : 6. e 00t so t e 00t :. e 00t so t ln( ) ln( ) 0.0. is undefined (division by 0) so (t) is never equal to 00. (c) limit (as t becomes arbitrarily large) of 00. e 00t. e 00t is (d) The population (t) is decling to the "carrying capacity" M 00 of the enviroment. 9. (a) Solve d dt ( )(5 ) by separating the variables and using partial fractions to rewrite the fraction. (b) 5 5 ekt and (t). e kt 5. e kt. (As t gets big, approaches 5.) Solve d dt (6 )(6 ) (6 ) by separating the variables: (6 ) d dt and integrating. 6 t + C (C 6 ) so 6t + t + 6 6t + 6 6t +. (As t gets big, approaches 6.) Section sin(θ) (a) 9 9 9sin (θ) 9( sin (θ) ) 9cos (θ) so (b) d cos(θ) dθ 9 cos(θ)... sec(θ) (a) 9 9sec (θ) 9 9( sec (θ) ) 9tan (θ) so (b) d sec(θ)tan(θ) dθ 9 tan(θ). 5. tan(θ) (a) + + tan (θ) ( + tan (θ) ) sec (θ) so (b) d sec (θ) dθ + sec(θ)... sin(θ) (a) θ arcsin( / ) (b) & (c) f(θ) cos(θ). tan(θ) cos( arcsin(/) ). tan( arcsin(/) ) sec(θ) (a) θ arcsec( / ) (b) & (c) f(θ) + sin (θ) + sin ( arcsec(/) ) + ( 9 )
11 Odd Answers: Chapter Eight Contemporary Calculus. 5. tan(θ) (a) θ arctan( /5 ) (b) & (c) f(θ) cos (θ) + cot(θ) ( ) + ( 5 ) Same as Practice. Sorry. 5.. tan(θ). d sec (θ) dθ tan (θ) ( tan (θ) + ) 49 sec (θ) d 49 sec (θ) sec (θ) dθ sec(θ) dθ ln sec(θ) + tan(θ) + C ln sec( arctan(/) ) + tan( arctan(/) ) + C ln C.. 6. sin(θ). d 6 cos(θ) dθ. 6 6 cos (θ). 6 d 6 cos (θ) 6 cos(θ) dθ 6 cos (θ) dθ (use Table #4) 6 { θ + sin(θ). cos(θ) } + C 6 { arcsin( /6 ) + ( 6 ). ( 6 6 ) } + C tan(θ). d 6. sec (θ) dθ sec (θ). 6 + d sec (θ) dθ sec(θ) dθ (use Table #) ln sec(θ) + tan(θ) + C ln C or ln K.. Similar to 9:. tan(θ) d ln C.. 5. sin(θ). 5 cos( arcsin(/5) ) + C C 5 + C. 5.. tan(θ). ln cos( arctan(/) ) + C ln + C (now some algebra) 49 + ln + ln C ln K. (A u substitution with u 49 + is much easier.)
12 Odd Answers: Chapter Eight Contemporary Calculus.. sec(θ). 9 cos(θ) sin (θ) dθ (put u sin(θ) ) 9 sin(θ) + C csc(θ) + C C sec(θ). θ + C arcsec( 5 ) + C.. 5. sin(θ). 5 ln sec(θ) + tan(θ) + C 5 ln C (after lots of algebra) 0 ln C.. Similar to 9. ln a + a + a + C ln a K. 5. a. tan(θ). a a + + C.. + u. Then u. tan(θ). ln sec(θ) + tan(θ) + C ln u u + C ln u +9 + u ln() + C ln u +9 + u + K ln (+) (+) + K. 9. arctan( +5 ) + C 4. ln (+) C. Section 8.6. sin ( ) d sin( 6 ) + C sin( ). cos( ) 6 + C.. Put u sin( e ). sin ( e ) + C. ( If you put w cos( e ) then cos ( e ) + C.) π. 4 4 sin ( ) + C or 4 cos ( ) + C. Put u cos( ). 8 cos4 ( ) + C.
13 Odd Answers: Chapter Eight Contemporary Calculus. sin ( ) cos ( ) d ( cos(6) ) ( + cos(6) ) d 4 cos ( 6 ) d 4 4 cos ( 6 ) d 4 4 { + sin( ) 4 } + C tan ( 5 ) + C.. 9 sec ( ) + C. π 9. m n. 0 sin( m ) sin( n ) d { sin( (m n)π ) m n { sin( (m n) ) m n sin( (m+n)π ) m + n } sin( (m+n) ) m + n } π 0 sin( (m n)0 ) { m n sin( (m+n)0 ) m + n } { 0 0 } { 0 0 } 0. π. 0 π sin( m ) sin( m ) d 0 { π sin ( m ) d sin( mπ ) cos( mπ ) m } { sin( m ) cos( m ) m π 0 sin( 0 ) cos( 0 ) m } π. 0. On your own.
1. Evaluate the integrals. a. (9 pts) x e x/2 dx. Solution: Using integration by parts, let u = x du = dx and dv = e x/2 dx v = 2e x/2.
 MATH 8 Test -SOLUTIONS Spring 4. Evaluate the integrals. a. (9 pts) e / Solution: Using integration y parts, let u = du = and dv = e / v = e /. Then e / = e / e / e / = e / + e / = e / 4e / + c MATH 8
MATH 8 Test -SOLUTIONS Spring 4. Evaluate the integrals. a. (9 pts) e / Solution: Using integration y parts, let u = du = and dv = e / v = e /. Then e / = e / e / e / = e / + e / = e / 4e / + c MATH 8
Math Calculus II Homework # Due Date Solutions
 Math 35 - Calculus II Homework # - 007.08.3 Due Date - 007.09.07 Solutions Part : Problems from sections 7.3 and 7.4. Section 7.3: 9. + d We will use the substitution cot(θ, d csc (θ. This gives + + cot
Math 35 - Calculus II Homework # - 007.08.3 Due Date - 007.09.07 Solutions Part : Problems from sections 7.3 and 7.4. Section 7.3: 9. + d We will use the substitution cot(θ, d csc (θ. This gives + + cot
FUNDAMENTAL TRIGONOMETRIC INDENTITIES 1 = cos. sec θ 1 = sec. = cosθ. Odd Functions sin( t) = sint. csc( t) = csct tan( t) = tant
 NOTES 8: ANALYTIC TRIGONOMETRY Name: Date: Period: Mrs. Nguyen s Initial: LESSON 8.1 TRIGONOMETRIC IDENTITIES FUNDAMENTAL TRIGONOMETRIC INDENTITIES Reciprocal Identities sinθ 1 cscθ cosθ 1 secθ tanθ 1
NOTES 8: ANALYTIC TRIGONOMETRY Name: Date: Period: Mrs. Nguyen s Initial: LESSON 8.1 TRIGONOMETRIC IDENTITIES FUNDAMENTAL TRIGONOMETRIC INDENTITIES Reciprocal Identities sinθ 1 cscθ cosθ 1 secθ tanθ 1
2016 FAMAT Convention Mu Integration 1 = 80 0 = 80. dx 1 + x 2 = arctan x] k2
![2016 FAMAT Convention Mu Integration 1 = 80 0 = 80. dx 1 + x 2 = arctan x] k2 2016 FAMAT Convention Mu Integration 1 = 80 0 = 80. dx 1 + x 2 = arctan x] k2](/thumbs/96/127235785.jpg) 6 FAMAT Convention Mu Integration. A. 3 3 7 6 6 3 ] 3 6 6 3. B. For quadratic functions, Simpson s Rule is eact. Thus, 3. D.. B. lim 5 3 + ) 3 + ] 5 8 8 cot θ) dθ csc θ ) dθ cot θ θ + C n k n + k n lim
6 FAMAT Convention Mu Integration. A. 3 3 7 6 6 3 ] 3 6 6 3. B. For quadratic functions, Simpson s Rule is eact. Thus, 3. D.. B. lim 5 3 + ) 3 + ] 5 8 8 cot θ) dθ csc θ ) dθ cot θ θ + C n k n + k n lim
MATH 1080 Test 2 -Version A-SOLUTIONS Fall a. (8 pts) Find the exact length of the curve on the given interval.
 MATH 8 Test -Version A-SOLUTIONS Fall 4. Consider the curve defined by y = ln( sec x), x. a. (8 pts) Find the exact length of the curve on the given interval. sec x tan x = = tan x sec x L = + tan x =
MATH 8 Test -Version A-SOLUTIONS Fall 4. Consider the curve defined by y = ln( sec x), x. a. (8 pts) Find the exact length of the curve on the given interval. sec x tan x = = tan x sec x L = + tan x =
Math156 Review for Exam 4
 Math56 Review for Eam 4. What will be covered in this eam: Representing functions as power series, Taylor and Maclaurin series, calculus with parametric curves, calculus with polar coordinates.. Eam Rules:
Math56 Review for Eam 4. What will be covered in this eam: Representing functions as power series, Taylor and Maclaurin series, calculus with parametric curves, calculus with polar coordinates.. Eam Rules:
6.6 Inverse Trigonometric Functions
 6.6 6.6 Inverse Trigonometric Functions We recall the following definitions from trigonometry. If we restrict the sine function, say fx) sinx, π x π then we obtain a one-to-one function. π/, /) π/ π/ Since
6.6 6.6 Inverse Trigonometric Functions We recall the following definitions from trigonometry. If we restrict the sine function, say fx) sinx, π x π then we obtain a one-to-one function. π/, /) π/ π/ Since
Analytic Trigonometry
 Chapter 5 Analytic Trigonometry Course Number Section 5.1 Using Fundamental Identities Objective: In this lesson you learned how to use fundamental trigonometric identities to evaluate trigonometric functions
Chapter 5 Analytic Trigonometry Course Number Section 5.1 Using Fundamental Identities Objective: In this lesson you learned how to use fundamental trigonometric identities to evaluate trigonometric functions
Math Analysis Chapter 5 Notes: Analytic Trigonometric
 Math Analysis Chapter 5 Notes: Analytic Trigonometric Day 9: Section 5.1-Verifying Trigonometric Identities Fundamental Trig Identities Reciprocal Identities: 1 1 1 sin u = cos u = tan u = cscu secu cot
Math Analysis Chapter 5 Notes: Analytic Trigonometric Day 9: Section 5.1-Verifying Trigonometric Identities Fundamental Trig Identities Reciprocal Identities: 1 1 1 sin u = cos u = tan u = cscu secu cot
AP Calculus Summer Packet
 AP Calculus Summer Packet Writing The Equation Of A Line Example: Find the equation of a line that passes through ( 1, 2) and (5, 7). ü Things to remember: Slope formula, point-slope form, slopeintercept
AP Calculus Summer Packet Writing The Equation Of A Line Example: Find the equation of a line that passes through ( 1, 2) and (5, 7). ü Things to remember: Slope formula, point-slope form, slopeintercept
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. and θ is in quadrant IV. 1)
 Chapter 5-6 Review Math 116 Name SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Use the fundamental identities to find the value of the trigonometric
Chapter 5-6 Review Math 116 Name SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Use the fundamental identities to find the value of the trigonometric
Chapter 7: Techniques of Integration
 Chapter 7: Techniques of Integration MATH 206-01: Calculus II Department of Mathematics University of Louisville last corrected September 14, 2013 1 / 43 Chapter 7: Techniques of Integration 7.1. Integration
Chapter 7: Techniques of Integration MATH 206-01: Calculus II Department of Mathematics University of Louisville last corrected September 14, 2013 1 / 43 Chapter 7: Techniques of Integration 7.1. Integration
Chapter 2 Overview: Anti-Derivatives. As noted in the introduction, Calculus is essentially comprised of four operations.
 Chapter Overview: Anti-Derivatives As noted in the introduction, Calculus is essentially comprised of four operations. Limits Derivatives Indefinite Integrals (or Anti-Derivatives) Definite Integrals There
Chapter Overview: Anti-Derivatives As noted in the introduction, Calculus is essentially comprised of four operations. Limits Derivatives Indefinite Integrals (or Anti-Derivatives) Definite Integrals There
Math 1B Calculus Test 3 Spring 10 Name Write all responses on separate paper. Show your work for credit.
 ath B Calculus Test Spring Name Write all responses on separate paper. Show our work for credit.. Determine whether each integral is convergent or divergent. Evaluate those that are convergent. a. / 4
ath B Calculus Test Spring Name Write all responses on separate paper. Show our work for credit.. Determine whether each integral is convergent or divergent. Evaluate those that are convergent. a. / 4
7.3 Inverse Trigonometric Functions
 58 transcendental functions 73 Inverse Trigonometric Functions We now turn our attention to the inverse trigonometric functions, their properties and their graphs, focusing on properties and techniques
58 transcendental functions 73 Inverse Trigonometric Functions We now turn our attention to the inverse trigonometric functions, their properties and their graphs, focusing on properties and techniques
The answers below are not comprehensive and are meant to indicate the correct way to solve the problem. sin
 Math : Practice Final Answer Key Name: The answers below are not comprehensive and are meant to indicate the correct way to solve the problem. Problem : Consider the definite integral I = 5 sin ( ) d.
Math : Practice Final Answer Key Name: The answers below are not comprehensive and are meant to indicate the correct way to solve the problem. Problem : Consider the definite integral I = 5 sin ( ) d.
Pre- Calculus Mathematics Trigonometric Identities and Equations
 Pre- Calculus Mathematics 12 6.1 Trigonometric Identities and Equations Goal: 1. Identify the Fundamental Trigonometric Identities 2. Simplify a Trigonometric Expression 3. Determine the restrictions on
Pre- Calculus Mathematics 12 6.1 Trigonometric Identities and Equations Goal: 1. Identify the Fundamental Trigonometric Identities 2. Simplify a Trigonometric Expression 3. Determine the restrictions on
Review (2) Calculus II (201-nyb-05/05,06) Winter 2019
 Review () Calculus II (-nyb-5/5,6) Winter 9 Note. You should also review the integrals eercises on the first review sheet. Eercise. Evaluate each of the following integrals. a. sin 3 ( )cos ( csc 3 (log)cot
Review () Calculus II (-nyb-5/5,6) Winter 9 Note. You should also review the integrals eercises on the first review sheet. Eercise. Evaluate each of the following integrals. a. sin 3 ( )cos ( csc 3 (log)cot
MA40S Pre-calculus UNIT C Trigonometric Identities CLASS NOTES Analyze Trigonometric Identities Graphically and Verify them Algebraically
 1 MA40S Pre-calculus UNIT C Trigonometric Identities CLASS NOTES Analyze Trigonometric Identities Graphically and Verify them Algebraically Definition Trigonometric identity Investigate 1. Using the diagram
1 MA40S Pre-calculus UNIT C Trigonometric Identities CLASS NOTES Analyze Trigonometric Identities Graphically and Verify them Algebraically Definition Trigonometric identity Investigate 1. Using the diagram
2 Trigonometric functions
 Theodore Voronov. Mathematics 1G1. Autumn 014 Trigonometric functions Trigonometry provides methods to relate angles and lengths but the functions we define have many other applications in mathematics..1
Theodore Voronov. Mathematics 1G1. Autumn 014 Trigonometric functions Trigonometry provides methods to relate angles and lengths but the functions we define have many other applications in mathematics..1
Trigonometry Trigonometry comes from the Greek word meaning measurement of triangles Angles are typically labeled with Greek letters
 Trigonometry Trigonometry comes from the Greek word meaning measurement of triangles Angles are typically labeled with Greek letters α( alpha), β ( beta), θ ( theta) as well as upper case letters A,B,
Trigonometry Trigonometry comes from the Greek word meaning measurement of triangles Angles are typically labeled with Greek letters α( alpha), β ( beta), θ ( theta) as well as upper case letters A,B,
First Midterm Examination
 Çankaya University Department of Mathematics 016-017 Fall Semester MATH 155 - Calculus for Engineering I First Midterm Eamination 1) Find the domain and range of the following functions. Eplain your solution.
Çankaya University Department of Mathematics 016-017 Fall Semester MATH 155 - Calculus for Engineering I First Midterm Eamination 1) Find the domain and range of the following functions. Eplain your solution.
1. The following problems are not related: (a) (15 pts, 5 pts ea.) Find the following limits or show that they do not exist: arcsin(x)
 APPM 5 Final Eam (5 pts) Fall. The following problems are not related: (a) (5 pts, 5 pts ea.) Find the following limits or show that they do not eist: (i) lim e (ii) lim arcsin() (b) (5 pts) Find and classify
APPM 5 Final Eam (5 pts) Fall. The following problems are not related: (a) (5 pts, 5 pts ea.) Find the following limits or show that they do not eist: (i) lim e (ii) lim arcsin() (b) (5 pts) Find and classify
EXAM. Practice for Second Exam. Math , Fall Nov 4, 2003 ANSWERS
 EXAM Practice for Second Eam Math 135-006, Fall 003 Nov 4, 003 ANSWERS i Problem 1. In each part, find the integral. A. d (4 ) 3/ Make the substitution sin(θ). d cos(θ) dθ. We also have Then, we have d/dθ
EXAM Practice for Second Eam Math 135-006, Fall 003 Nov 4, 003 ANSWERS i Problem 1. In each part, find the integral. A. d (4 ) 3/ Make the substitution sin(θ). d cos(θ) dθ. We also have Then, we have d/dθ
Sect 7.4 Trigonometric Functions of Any Angles
 Sect 7.4 Trigonometric Functions of Any Angles Objective #: Extending the definition to find the trigonometric function of any angle. Before we can extend the definition our trigonometric functions, we
Sect 7.4 Trigonometric Functions of Any Angles Objective #: Extending the definition to find the trigonometric function of any angle. Before we can extend the definition our trigonometric functions, we
a k 0, then k + 1 = 2 lim 1 + 1
 Math 7 - Midterm - Form A - Page From the desk of C. Davis Buenger. https://people.math.osu.edu/buenger.8/ Problem a) [3 pts] If lim a k = then a k converges. False: The divergence test states that if
Math 7 - Midterm - Form A - Page From the desk of C. Davis Buenger. https://people.math.osu.edu/buenger.8/ Problem a) [3 pts] If lim a k = then a k converges. False: The divergence test states that if
8.3 Partial Fraction Decomposition
 8.3 partial fraction decomposition 575 8.3 Partial Fraction Decomposition Rational functions (polynomials divided by polynomials) and their integrals play important roles in mathematics and applications,
8.3 partial fraction decomposition 575 8.3 Partial Fraction Decomposition Rational functions (polynomials divided by polynomials) and their integrals play important roles in mathematics and applications,
Trigonometric substitutions (8.3).
 Review for Eam 2. 5 or 6 problems. No multiple choice questions. No notes, no books, no calculators. Problems similar to homeworks. Eam covers: 7.4, 7.6, 7.7, 8-IT, 8., 8.2. Solving differential equations
Review for Eam 2. 5 or 6 problems. No multiple choice questions. No notes, no books, no calculators. Problems similar to homeworks. Eam covers: 7.4, 7.6, 7.7, 8-IT, 8., 8.2. Solving differential equations
90 Chapter 5 Logarithmic, Exponential, and Other Transcendental Functions. Name Class. (a) (b) ln x (c) (a) (b) (c) 1 x. y e (a) 0 (b) y.
 90 Chapter 5 Logarithmic, Eponential, and Other Transcendental Functions Test Form A Chapter 5 Name Class Date Section. Find the derivative: f ln. 6. Differentiate: y. ln y y y y. Find dy d if ey y. y
90 Chapter 5 Logarithmic, Eponential, and Other Transcendental Functions Test Form A Chapter 5 Name Class Date Section. Find the derivative: f ln. 6. Differentiate: y. ln y y y y. Find dy d if ey y. y
Integration Techniques for the AB exam
 For the AB eam, students need to: determine antiderivatives of the basic functions calculate antiderivatives of functions using u-substitution use algebraic manipulation to rewrite the integrand prior
For the AB eam, students need to: determine antiderivatives of the basic functions calculate antiderivatives of functions using u-substitution use algebraic manipulation to rewrite the integrand prior
Lesson 33 - Trigonometric Identities. Pre-Calculus
 Lesson 33 - Trigonometric Identities Pre-Calculus 1 (A) Review of Equations An equation is an algebraic statement that is true for only several values of the variable The linear equation 5 = 2x 3 is only
Lesson 33 - Trigonometric Identities Pre-Calculus 1 (A) Review of Equations An equation is an algebraic statement that is true for only several values of the variable The linear equation 5 = 2x 3 is only
1969 AP Calculus BC: Section I
 969 AP Calculus BC: Section I 9 Minutes No Calculator Note: In this eamination, ln denotes the natural logarithm of (that is, logarithm to the base e).. t The asymptotes of the graph of the parametric
969 AP Calculus BC: Section I 9 Minutes No Calculator Note: In this eamination, ln denotes the natural logarithm of (that is, logarithm to the base e).. t The asymptotes of the graph of the parametric
Solutions to Homework Assignment #2
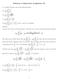 Solutions to Homework Assignment #. [4 marks] Evaluate each of the following limits. n i a lim n. b lim c lim d lim n i. sin πi n. a i n + b, where a and b are constants. n a There are ways to do this
Solutions to Homework Assignment #. [4 marks] Evaluate each of the following limits. n i a lim n. b lim c lim d lim n i. sin πi n. a i n + b, where a and b are constants. n a There are ways to do this
MATH 162. Midterm Exam 1 - Solutions February 22, 2007
 MATH 62 Midterm Exam - Solutions February 22, 27. (8 points) Evaluate the following integrals: (a) x sin(x 4 + 7) dx Solution: Let u = x 4 + 7, then du = 4x dx and x sin(x 4 + 7) dx = 4 sin(u) du = 4 [
MATH 62 Midterm Exam - Solutions February 22, 27. (8 points) Evaluate the following integrals: (a) x sin(x 4 + 7) dx Solution: Let u = x 4 + 7, then du = 4x dx and x sin(x 4 + 7) dx = 4 sin(u) du = 4 [
Math 181, Exam 2, Study Guide 2 Problem 1 Solution. 1 + dx. 1 + (cos x)2 dx. 1 + cos2 xdx. = π ( 1 + cos π 2
 Math 8, Exam, Study Guide Problem Solution. Use the trapezoid rule with n to estimate the arc-length of the curve y sin x between x and x π. Solution: The arclength is: L b a π π + ( ) dy + (cos x) + cos
Math 8, Exam, Study Guide Problem Solution. Use the trapezoid rule with n to estimate the arc-length of the curve y sin x between x and x π. Solution: The arclength is: L b a π π + ( ) dy + (cos x) + cos
SET 1. (1) Solve for x: (a) e 2x = 5 3x
 () Solve for x: (a) e x = 5 3x SET We take natural log on both sides: ln(e x ) = ln(5 3x ) x = 3 x ln(5) Now we take log base on both sides: log ( x ) = log (3 x ln 5) x = log (3 x ) + log (ln(5)) x x
() Solve for x: (a) e x = 5 3x SET We take natural log on both sides: ln(e x ) = ln(5 3x ) x = 3 x ln(5) Now we take log base on both sides: log ( x ) = log (3 x ln 5) x = log (3 x ) + log (ln(5)) x x
Fall 2016, MA 252, Calculus II, Final Exam Preview Solutions
 Fall 6, MA 5, Calculus II, Final Exam Preview Solutions I will put the following formulas on the front of the final exam, to speed up certain problems. You do not need to put them on your index card, and
Fall 6, MA 5, Calculus II, Final Exam Preview Solutions I will put the following formulas on the front of the final exam, to speed up certain problems. You do not need to put them on your index card, and
Math 181, Exam 2, Fall 2014 Problem 1 Solution. sin 3 (x) cos(x) dx.
 Math 8, Eam 2, Fall 24 Problem Solution. Integrals, Part I (Trigonometric integrals: 6 points). Evaluate the integral: sin 3 () cos() d. Solution: We begin by rewriting sin 3 () as Then, after using the
Math 8, Eam 2, Fall 24 Problem Solution. Integrals, Part I (Trigonometric integrals: 6 points). Evaluate the integral: sin 3 () cos() d. Solution: We begin by rewriting sin 3 () as Then, after using the
Precalculus Review. Functions to KNOW! 1. Polynomial Functions. Types: General form Generic Graph and unique properties. Constants. Linear.
 Precalculus Review Functions to KNOW! 1. Polynomial Functions Types: General form Generic Graph and unique properties Constants Linear Quadratic Cubic Generalizations for Polynomial Functions - The domain
Precalculus Review Functions to KNOW! 1. Polynomial Functions Types: General form Generic Graph and unique properties Constants Linear Quadratic Cubic Generalizations for Polynomial Functions - The domain
Department of Mathematical Sciences. Math 226 Calculus Spring 2016 Exam 2V2 DO NOT TURN OVER THIS PAGE UNTIL INSTRUCTED TO DO SO
 Department of Mathematical Sciences Math 6 Calculus Spring 6 Eam V DO NOT TURN OVER THIS PAGE UNTIL INSTRUCTED TO DO SO NAME (Printed): INSTRUCTOR: SECTION NO.: When instructed, turn over this cover page
Department of Mathematical Sciences Math 6 Calculus Spring 6 Eam V DO NOT TURN OVER THIS PAGE UNTIL INSTRUCTED TO DO SO NAME (Printed): INSTRUCTOR: SECTION NO.: When instructed, turn over this cover page
HOMEWORK SOLUTIONS MATH 1910 Sections 8.2, 8.3, 8.5 Fall 2016
 HOMEWORK SOLUTIONS MATH 191 Sections 8., 8., 8.5 Fall 16 Problem 8..19 Evaluate using methods similar to those that apply to integral tan m xsec n x. cot x SOLUTION. Using the reduction formula for cot
HOMEWORK SOLUTIONS MATH 191 Sections 8., 8., 8.5 Fall 16 Problem 8..19 Evaluate using methods similar to those that apply to integral tan m xsec n x. cot x SOLUTION. Using the reduction formula for cot
Calculus II Practice Test Problems for Chapter 7 Page 1 of 6
 Calculus II Practice Test Problems for Chapter 7 Page of 6 This is a set of practice test problems for Chapter 7. This is in no way an inclusive set of problems there can be other types of problems on
Calculus II Practice Test Problems for Chapter 7 Page of 6 This is a set of practice test problems for Chapter 7. This is in no way an inclusive set of problems there can be other types of problems on
Math 226 Calculus Spring 2016 Exam 2V1
 Math 6 Calculus Spring 6 Exam V () (35 Points) Evaluate the following integrals. (a) (7 Points) tan 5 (x) sec 3 (x) dx (b) (8 Points) cos 4 (x) dx Math 6 Calculus Spring 6 Exam V () (Continued) Evaluate
Math 6 Calculus Spring 6 Exam V () (35 Points) Evaluate the following integrals. (a) (7 Points) tan 5 (x) sec 3 (x) dx (b) (8 Points) cos 4 (x) dx Math 6 Calculus Spring 6 Exam V () (Continued) Evaluate
Final Exam Review Quesitons
 Final Exam Review Quesitons. Compute the following integrals. (a) x x 4 (x ) (x + 4) dx. The appropriate partial fraction form is which simplifies to x x 4 (x ) (x + 4) = A x + B (x ) + C x + 4 + Dx x
Final Exam Review Quesitons. Compute the following integrals. (a) x x 4 (x ) (x + 4) dx. The appropriate partial fraction form is which simplifies to x x 4 (x ) (x + 4) = A x + B (x ) + C x + 4 + Dx x
MATH QUIZ 3 1/2. sin 1 xdx. π/2. cos 2 (x)dx. x 3 4x 10 x 2 x 6 dx.
 NAME: I.D.: MATH 56 - QUIZ 3 Instruction: Each problem is worth of point in this take home project. Circle your answers and show all your work CLEARLY. Use additional paper if needed. Solutions with answer
NAME: I.D.: MATH 56 - QUIZ 3 Instruction: Each problem is worth of point in this take home project. Circle your answers and show all your work CLEARLY. Use additional paper if needed. Solutions with answer
Section 7.4 #1, 5, 6, 8, 12, 13, 44, 53; Section 7.5 #7, 10, 11, 20, 22; Section 7.7 #1, 4, 10, 15, 22, 44
 Math B Prof. Audrey Terras HW #4 Solutions Due Tuesday, Oct. 9 Section 7.4 #, 5, 6, 8,, 3, 44, 53; Section 7.5 #7,,,, ; Section 7.7 #, 4,, 5,, 44 7.4. Since 5 = 5 )5 + ), start with So, 5 = A 5 + B 5 +.
Math B Prof. Audrey Terras HW #4 Solutions Due Tuesday, Oct. 9 Section 7.4 #, 5, 6, 8,, 3, 44, 53; Section 7.5 #7,,,, ; Section 7.7 #, 4,, 5,, 44 7.4. Since 5 = 5 )5 + ), start with So, 5 = A 5 + B 5 +.
Methods of Integration
 Methods of Integration Essential Formulas k d = k +C sind = cos +C n d = n+ n + +C cosd = sin +C e d = e +C tand = ln sec +C d = ln +C cotd = ln sin +C + d = tan +C lnd = ln +C secd = ln sec + tan +C cscd
Methods of Integration Essential Formulas k d = k +C sind = cos +C n d = n+ n + +C cosd = sin +C e d = e +C tand = ln sec +C d = ln +C cotd = ln sin +C + d = tan +C lnd = ln +C secd = ln sec + tan +C cscd
x n cos 2x dx. dx = nx n 1 and v = 1 2 sin(2x). Andreas Fring (City University London) AS1051 Lecture Autumn / 36
 We saw in Example 5.4. that we sometimes need to apply integration by parts several times in the course of a single calculation. Example 5.4.4: For n let S n = x n cos x dx. Find an expression for S n
We saw in Example 5.4. that we sometimes need to apply integration by parts several times in the course of a single calculation. Example 5.4.4: For n let S n = x n cos x dx. Find an expression for S n
Chapter 5 Notes. 5.1 Using Fundamental Identities
 Chapter 5 Notes 5.1 Using Fundamental Identities 1. Simplify each expression to its lowest terms. Write the answer to part as the product of factors. (a) sin x csc x cot x ( 1+ sinσ + cosσ ) (c) 1 tanx
Chapter 5 Notes 5.1 Using Fundamental Identities 1. Simplify each expression to its lowest terms. Write the answer to part as the product of factors. (a) sin x csc x cot x ( 1+ sinσ + cosσ ) (c) 1 tanx
1993 AP Calculus AB: Section I
 99 AP Calculus AB: Section I 90 Minutes Scientific Calculator Notes: () The eact numerical value of the correct answer does not always appear among the choices given. When this happens, select from among
99 AP Calculus AB: Section I 90 Minutes Scientific Calculator Notes: () The eact numerical value of the correct answer does not always appear among the choices given. When this happens, select from among
Math 152 Take Home Test 1
 Math 5 Take Home Test Due Monday 5 th October (5 points) The following test will be done at home in order to ensure that it is a fair and representative reflection of your own ability in mathematics I
Math 5 Take Home Test Due Monday 5 th October (5 points) The following test will be done at home in order to ensure that it is a fair and representative reflection of your own ability in mathematics I
Unit 3. Integration. 3A. Differentials, indefinite integration. y x. c) Method 1 (slow way) Substitute: u = 8 + 9x, du = 9dx.
 Unit 3. Integration 3A. Differentials, indefinite integration 3A- a) 7 6 d. (d(sin ) = because sin is a constant.) b) (/) / d c) ( 9 8)d d) (3e 3 sin + e 3 cos)d e) (/ )d + (/ y)dy = implies dy = / d /
Unit 3. Integration 3A. Differentials, indefinite integration 3A- a) 7 6 d. (d(sin ) = because sin is a constant.) b) (/) / d c) ( 9 8)d d) (3e 3 sin + e 3 cos)d e) (/ )d + (/ y)dy = implies dy = / d /
secθ 1 cosθ The pythagorean identities can also be expressed as radicals
 Basic Identities Section Objectives: Students will know how to use fundamental trigonometric identities to evaluate trigonometric functions and simplify trigonometric expressions. We use trig. identities
Basic Identities Section Objectives: Students will know how to use fundamental trigonometric identities to evaluate trigonometric functions and simplify trigonometric expressions. We use trig. identities
Final Exam 2011 Winter Term 2 Solutions
 . (a Find the radius of convergence of the series: ( k k+ x k. Solution: Using the Ratio Test, we get: L = lim a k+ a k = lim ( k+ k+ x k+ ( k k+ x k = lim x = x. Note that the series converges for L
. (a Find the radius of convergence of the series: ( k k+ x k. Solution: Using the Ratio Test, we get: L = lim a k+ a k = lim ( k+ k+ x k+ ( k k+ x k = lim x = x. Note that the series converges for L
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals 8. Basic Integration Rules In this section we will review various integration strategies. Strategies: I. Separate
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals 8. Basic Integration Rules In this section we will review various integration strategies. Strategies: I. Separate
Math Section 4.3 Unit Circle Trigonometry
 Math 10 - Section 4. Unit Circle Trigonometry An angle is in standard position if its vertex is at the origin and its initial side is along the positive x axis. Positive angles are measured counterclockwise
Math 10 - Section 4. Unit Circle Trigonometry An angle is in standard position if its vertex is at the origin and its initial side is along the positive x axis. Positive angles are measured counterclockwise
Lesson 28 Working with Special Triangles
 Lesson 28 Working with Special Triangles Pre-Calculus 3/3/14 Pre-Calculus 1 Review Where We ve Been We have a new understanding of angles as we have now placed angles in a circle on a coordinate plane
Lesson 28 Working with Special Triangles Pre-Calculus 3/3/14 Pre-Calculus 1 Review Where We ve Been We have a new understanding of angles as we have now placed angles in a circle on a coordinate plane
Math 102 Spring 2008: Solutions: HW #3 Instructor: Fei Xu
 Math Spring 8: Solutions: HW #3 Instructor: Fei Xu. section 7., #8 Evaluate + 3 d. + We ll solve using partial fractions. If we assume 3 A + B + C, clearing denominators gives us A A + B B + C +. Then
Math Spring 8: Solutions: HW #3 Instructor: Fei Xu. section 7., #8 Evaluate + 3 d. + We ll solve using partial fractions. If we assume 3 A + B + C, clearing denominators gives us A A + B B + C +. Then
2 Recollection of elementary functions. II
 Recollection of elementary functions. II Last updated: October 5, 08. In this section we continue recollection of elementary functions. In particular, we consider exponential, trigonometric and hyperbolic
Recollection of elementary functions. II Last updated: October 5, 08. In this section we continue recollection of elementary functions. In particular, we consider exponential, trigonometric and hyperbolic
Summer Packet Greetings Future AP Calculus Scholar,
 Summer Packet 2017 Greetings Future AP Calculus Scholar, I am excited about the work that we will do together during the 2016-17 school year. I do not yet know what your math capability is, but I can assure
Summer Packet 2017 Greetings Future AP Calculus Scholar, I am excited about the work that we will do together during the 2016-17 school year. I do not yet know what your math capability is, but I can assure
9. The x axis is a horizontal line so a 1 1 function can touch the x axis in at most one place.
 O Answers: Chapter 7 Contemporary Calculus PROBLEM ANSWERS Chapter Seven Section 7.0. f is one to one ( ), y is, g is not, h is not.. f is not, y is, g is, h is not. 5. I think SS numbers are supposeo
O Answers: Chapter 7 Contemporary Calculus PROBLEM ANSWERS Chapter Seven Section 7.0. f is one to one ( ), y is, g is not, h is not.. f is not, y is, g is, h is not. 5. I think SS numbers are supposeo
THE INVERSE TRIGONOMETRIC FUNCTIONS
 THE INVERSE TRIGONOMETRIC FUNCTIONS Question 1 (**+) Solve the following trigonometric equation ( x ) π + 3arccos + 1 = 0. 1 x = Question (***) It is given that arcsin x = arccos y. Show, by a clear method,
THE INVERSE TRIGONOMETRIC FUNCTIONS Question 1 (**+) Solve the following trigonometric equation ( x ) π + 3arccos + 1 = 0. 1 x = Question (***) It is given that arcsin x = arccos y. Show, by a clear method,
Math 162: Calculus IIA
 Math 62: Calculus IIA Final Exam ANSWERS December 9, 26 Part A. (5 points) Evaluate the integral x 4 x 2 dx Substitute x 2 cos θ: x 8 cos dx θ ( 2 sin θ) dθ 4 x 2 2 sin θ 8 cos θ dθ 8 cos 2 θ cos θ dθ
Math 62: Calculus IIA Final Exam ANSWERS December 9, 26 Part A. (5 points) Evaluate the integral x 4 x 2 dx Substitute x 2 cos θ: x 8 cos dx θ ( 2 sin θ) dθ 4 x 2 2 sin θ 8 cos θ dθ 8 cos 2 θ cos θ dθ
Math 1000 Final Exam Review Solutions. (x + 3)(x 2) = lim. = lim x 2 = 3 2 = 5. (x + 1) 1 x( x ) = lim. = lim. f f(1 + h) f(1) (1) = lim
 Math Final Eam Review Solutions { + 3 if < Consider f() Find the following limits: (a) lim f() + + (b) lim f() + 3 3 (c) lim f() does not eist Find each of the following limits: + 6 (a) lim 3 + 3 (b) lim
Math Final Eam Review Solutions { + 3 if < Consider f() Find the following limits: (a) lim f() + + (b) lim f() + 3 3 (c) lim f() does not eist Find each of the following limits: + 6 (a) lim 3 + 3 (b) lim
Differential Equaitons Equations
 Welcome to Multivariable Calculus / Dierential Equaitons Equations The Attached Packet is or all students who are planning to take Multibariable Multivariable Calculus/ Dierential Equations in the all.
Welcome to Multivariable Calculus / Dierential Equaitons Equations The Attached Packet is or all students who are planning to take Multibariable Multivariable Calculus/ Dierential Equations in the all.
More Final Practice Problems
 8.0 Calculus Jason Starr Final Exam at 9:00am sharp Fall 005 Tuesday, December 0, 005 More 8.0 Final Practice Problems Here are some further practice problems with solutions for the 8.0 Final Exam. Many
8.0 Calculus Jason Starr Final Exam at 9:00am sharp Fall 005 Tuesday, December 0, 005 More 8.0 Final Practice Problems Here are some further practice problems with solutions for the 8.0 Final Exam. Many
APPM 1360 Final Exam Spring 2016
 APPM 36 Final Eam Spring 6. 8 points) State whether each of the following quantities converge or diverge. Eplain your reasoning. a) The sequence a, a, a 3,... where a n ln8n) lnn + ) n!) b) ln d c) arctan
APPM 36 Final Eam Spring 6. 8 points) State whether each of the following quantities converge or diverge. Eplain your reasoning. a) The sequence a, a, a 3,... where a n ln8n) lnn + ) n!) b) ln d c) arctan
MATH 101 Midterm Examination Spring 2009
 MATH Midterm Eamination Spring 9 Date: May 5, 9 Time: 7 minutes Surname: (Please, print!) Given name(s): Signature: Instructions. This is a closed book eam: No books, no notes, no calculators are allowed!.
MATH Midterm Eamination Spring 9 Date: May 5, 9 Time: 7 minutes Surname: (Please, print!) Given name(s): Signature: Instructions. This is a closed book eam: No books, no notes, no calculators are allowed!.
Mathematics 1052, Calculus II Exam 1, April 3rd, 2010
 Mathematics 5, Calculus II Exam, April 3rd,. (8 points) If an unknown function y satisfies the equation y = x 3 x + 4 with the condition that y()=, then what is y? Solution: We must integrate y against
Mathematics 5, Calculus II Exam, April 3rd,. (8 points) If an unknown function y satisfies the equation y = x 3 x + 4 with the condition that y()=, then what is y? Solution: We must integrate y against
MA 114 Worksheet #01: Integration by parts
 Fall 8 MA 4 Worksheet Thursday, 3 August 8 MA 4 Worksheet #: Integration by parts. For each of the following integrals, determine if it is best evaluated by integration by parts or by substitution. If
Fall 8 MA 4 Worksheet Thursday, 3 August 8 MA 4 Worksheet #: Integration by parts. For each of the following integrals, determine if it is best evaluated by integration by parts or by substitution. If
https://sites.google.com/site/dhseisen/
 Name: Calculus AP - Summer Assignment 2017 All questions and concerns related to this assignment should be directed to Ms. Eisen on or before Wednesday, June 21, 2017. If any concerns should arise over
Name: Calculus AP - Summer Assignment 2017 All questions and concerns related to this assignment should be directed to Ms. Eisen on or before Wednesday, June 21, 2017. If any concerns should arise over
Summary: Primer on Integral Calculus:
 Physics 2460 Electricity and Magnetism I, Fall 2006, Primer on Integration: Part I 1 Summary: Primer on Integral Calculus: Part I 1. Integrating over a single variable: Area under a curve Properties of
Physics 2460 Electricity and Magnetism I, Fall 2006, Primer on Integration: Part I 1 Summary: Primer on Integral Calculus: Part I 1. Integrating over a single variable: Area under a curve Properties of
(x/2) 2 +1 Add them together and throw in a constant c.
 Calculus, 5/6, Solutions Solutions Chapter Solutions to Eercises... (a) 6 + + c (b) 5 + c (c) This integral can be evaluated using the substitution u +. Alternatively, we can first use polynomial division
Calculus, 5/6, Solutions Solutions Chapter Solutions to Eercises... (a) 6 + + c (b) 5 + c (c) This integral can be evaluated using the substitution u +. Alternatively, we can first use polynomial division
4.4 Integration by u-sub & pattern recognition
 Calculus Maimus 4.4 Integration by u-sub & pattern recognition Eample 1: d 4 Evaluate tan e = Eample : 4 4 Evaluate 8 e sec e = We can think of composite functions as being a single function that, like
Calculus Maimus 4.4 Integration by u-sub & pattern recognition Eample 1: d 4 Evaluate tan e = Eample : 4 4 Evaluate 8 e sec e = We can think of composite functions as being a single function that, like
Spring 2015, MA 252, Calculus II, Final Exam Preview Solutions
 Spring 5, MA 5, Calculus II, Final Exam Preview Solutions I will put the following formulas on the front of the final exam, to speed up certain problems. You do not need to put them on your index card,
Spring 5, MA 5, Calculus II, Final Exam Preview Solutions I will put the following formulas on the front of the final exam, to speed up certain problems. You do not need to put them on your index card,
AP CALCULUS. DUE THE FIRST DAY OF SCHOOL! This work will count as part of your first quarter grade.
 Celina High School Math Department Summer Review Packet AP CALCULUS DUE THE FIRST DAY OF SCHOOL! This work will count as part of your first quarter grade. The problems in this packet are designed to help
Celina High School Math Department Summer Review Packet AP CALCULUS DUE THE FIRST DAY OF SCHOOL! This work will count as part of your first quarter grade. The problems in this packet are designed to help
Solutions to Test 2 Spring = y+x dy dx +0 = ex+y x+y dy. e x = dy dx (ex+y x) = y e x+y. dx = y ex+y e x+y x
 12pt 1 Consider the equation e +y = y +10 Solutions to Test 2 Spring 2018 (a) Use implicit differentiation to find dy d d d (e+y ) = d ( (y+10) e+y 1+ dy ) d d = y+ dy d +0 = e+y +y dy +e d = y+ dy d +y
12pt 1 Consider the equation e +y = y +10 Solutions to Test 2 Spring 2018 (a) Use implicit differentiation to find dy d d d (e+y ) = d ( (y+10) e+y 1+ dy ) d d = y+ dy d +0 = e+y +y dy +e d = y+ dy d +y
Calculus I Sample Final exam
 Calculus I Sample Final exam Solutions [] Compute the following integrals: a) b) 4 x ln x) Substituting u = ln x, 4 x ln x) = ln 4 ln u du = u ln 4 ln = ln ln 4 Taking common denominator, using properties
Calculus I Sample Final exam Solutions [] Compute the following integrals: a) b) 4 x ln x) Substituting u = ln x, 4 x ln x) = ln 4 ln u du = u ln 4 ln = ln ln 4 Taking common denominator, using properties
Public Assessment of the HKDSE Mathematics Examination
 Public Assessment of the HKDSE Mathematics Examination. Exam Format (a) The examination consists of one paper. (b) All questions are conventional questions. (c) The duration is hours and 30 minutes. Section
Public Assessment of the HKDSE Mathematics Examination. Exam Format (a) The examination consists of one paper. (b) All questions are conventional questions. (c) The duration is hours and 30 minutes. Section
( ) ( ) ( ) ( ) MATHEMATICS Precalculus Martin Huard Fall 2007 Semester Review. 1. Simplify each expression. 4a b c. x y. 18x. x 2x.
 MATHEMATICS 0-009-0 Precalculus Martin Huard Fall 007. Simplif each epression. a) 8 8 g) ( ) ( j) m) a b c a b 8 8 8 n f) t t ) h) + + + + k) + + + n) + + + + + ( ) i) + n 8 + 9 z + l) 8 o) ( + ) ( + )
MATHEMATICS 0-009-0 Precalculus Martin Huard Fall 007. Simplif each epression. a) 8 8 g) ( ) ( j) m) a b c a b 8 8 8 n f) t t ) h) + + + + k) + + + n) + + + + + ( ) i) + n 8 + 9 z + l) 8 o) ( + ) ( + )
PRELIM 2 REVIEW QUESTIONS Math 1910 Section 205/209
 PRELIM 2 REVIEW QUESTIONS Math 9 Section 25/29 () Calculate the following integrals. (a) (b) x 2 dx SOLUTION: This is just the area under a semicircle of radius, so π/2. sin 2 (x) cos (x) dx SOLUTION:
PRELIM 2 REVIEW QUESTIONS Math 9 Section 25/29 () Calculate the following integrals. (a) (b) x 2 dx SOLUTION: This is just the area under a semicircle of radius, so π/2. sin 2 (x) cos (x) dx SOLUTION:
MATH Section 210
 MATH 101 - Section 10 Instructor: Avner Segal (avners@math.ubc.ca) January 31 st 017 Common course page: http://www.math.ubc.ca/~gerg/teaching/101-winter017/ Individual section page: http://www.math.ubc.ca/~avners/courses/math101-017.html
MATH 101 - Section 10 Instructor: Avner Segal (avners@math.ubc.ca) January 31 st 017 Common course page: http://www.math.ubc.ca/~gerg/teaching/101-winter017/ Individual section page: http://www.math.ubc.ca/~avners/courses/math101-017.html
Integration Techniques for the AB exam
 For the AB eam, students need to: determine antiderivatives of the basic functions calculate antiderivatives of functions using u-substitution use algebraic manipulation to rewrite the integrand prior
For the AB eam, students need to: determine antiderivatives of the basic functions calculate antiderivatives of functions using u-substitution use algebraic manipulation to rewrite the integrand prior
MATH section 3.1 Maximum and Minimum Values Page 1 of 7
 MATH section. Maimum and Minimum Values Page of 7 Definition : Let c be a number in the domain D of a function f. Then c ) is the Absolute maimum value of f on D if ) c f() for all in D. Absolute minimum
MATH section. Maimum and Minimum Values Page of 7 Definition : Let c be a number in the domain D of a function f. Then c ) is the Absolute maimum value of f on D if ) c f() for all in D. Absolute minimum
Section 1.2 A Catalog of Essential Functions
 Page 1 of 6 Section 1. A Catalog of Essential Functions Linear Models: All linear equations have the form y = m + b. rise change in horizontal The letter m is the slope of the line, or. It can be positive,
Page 1 of 6 Section 1. A Catalog of Essential Functions Linear Models: All linear equations have the form y = m + b. rise change in horizontal The letter m is the slope of the line, or. It can be positive,
Part I: Multiple Choice Mark the correct answer on the bubble sheet provided. n=1. a) None b) 1 c) 2 d) 3 e) 1, 2 f) 1, 3 g) 2, 3 h) 1, 2, 3
 Math (Calculus II) Final Eam Form A Fall 22 RED KEY Part I: Multiple Choice Mark the correct answer on the bubble sheet provided.. Which of the following series converge absolutely? ) ( ) n 2) n 2 n (
Math (Calculus II) Final Eam Form A Fall 22 RED KEY Part I: Multiple Choice Mark the correct answer on the bubble sheet provided.. Which of the following series converge absolutely? ) ( ) n 2) n 2 n (
Integration Exercises - Part 3 (Sol'ns) (Hyperbolic Functions) (12 pages; 6/2/18) (The constant of integration has been omitted throughout.
 Integration Eercises - Part (Sol'ns) (Hyperbolic Functions) ( pages; 6//8) (The constant of integration has been omitted throughout.) () cosech Given that d tanh = sech, we could investigate d coth = d
Integration Eercises - Part (Sol'ns) (Hyperbolic Functions) ( pages; 6//8) (The constant of integration has been omitted throughout.) () cosech Given that d tanh = sech, we could investigate d coth = d
Monroe Township High School Mathematics Department
 To: AP Calculus AB Re: Summer Project 017 Date: June 017 Monroe Township High School Mathematics Department To help begin your study of Calculus, you will be required to complete a review project this
To: AP Calculus AB Re: Summer Project 017 Date: June 017 Monroe Township High School Mathematics Department To help begin your study of Calculus, you will be required to complete a review project this
MATH 127 SAMPLE FINAL EXAM I II III TOTAL
 MATH 17 SAMPLE FINAL EXAM Name: Section: Do not write on this page below this line Part I II III TOTAL Score Part I. Multiple choice answer exercises with exactly one correct answer. Each correct answer
MATH 17 SAMPLE FINAL EXAM Name: Section: Do not write on this page below this line Part I II III TOTAL Score Part I. Multiple choice answer exercises with exactly one correct answer. Each correct answer
Final Exam SOLUTIONS MAT 131 Fall 2011
 1. Compute the following its. (a) Final Exam SOLUTIONS MAT 131 Fall 11 x + 1 x 1 x 1 The numerator is always positive, whereas the denominator is negative for numbers slightly smaller than 1. Also, as
1. Compute the following its. (a) Final Exam SOLUTIONS MAT 131 Fall 11 x + 1 x 1 x 1 The numerator is always positive, whereas the denominator is negative for numbers slightly smaller than 1. Also, as
b n x n + b n 1 x n b 1 x + b 0
 Math Partial Fractions Stewart 7.4 Integrating basic rational functions. For a function f(x), we have examined several algebraic methods for finding its indefinite integral (antiderivative) F (x) = f(x)
Math Partial Fractions Stewart 7.4 Integrating basic rational functions. For a function f(x), we have examined several algebraic methods for finding its indefinite integral (antiderivative) F (x) = f(x)
WORKSHEET 1 SOLUTION Chapter 2 Differentiation
 United Arab Emirates University College of Sciences Department of Mathematical Sciences WORKSHEET SOLUTION Chapter Differentiation Calculus I for Engineering MATH SECTION CRN : :5 on Sunday & Tuesday Due
United Arab Emirates University College of Sciences Department of Mathematical Sciences WORKSHEET SOLUTION Chapter Differentiation Calculus I for Engineering MATH SECTION CRN : :5 on Sunday & Tuesday Due
Fall 2013 Hour Exam 2 11/08/13 Time Limit: 50 Minutes
 Math 8 Fall Hour Exam /8/ Time Limit: 5 Minutes Name (Print): This exam contains 9 pages (including this cover page) and 7 problems. Check to see if any pages are missing. Enter all requested information
Math 8 Fall Hour Exam /8/ Time Limit: 5 Minutes Name (Print): This exam contains 9 pages (including this cover page) and 7 problems. Check to see if any pages are missing. Enter all requested information
Calculus First Semester Review Name: Section: Evaluate the function: (g o f )( 2) f (x + h) f (x) h. m(x + h) m(x)
 Evaluate the function: c. (g o f )(x + 2) d. ( f ( f (x)) 1. f x = 4x! 2 a. f( 2) b. f(x 1) c. f (x + h) f (x) h 4. g x = 3x! + 1 Find g!! (x) 5. p x = 4x! + 2 Find p!! (x) 2. m x = 3x! + 2x 1 m(x + h)
Evaluate the function: c. (g o f )(x + 2) d. ( f ( f (x)) 1. f x = 4x! 2 a. f( 2) b. f(x 1) c. f (x + h) f (x) h 4. g x = 3x! + 1 Find g!! (x) 5. p x = 4x! + 2 Find p!! (x) 2. m x = 3x! + 2x 1 m(x + h)
Math Final Exam Review
 Math - Final Exam Review. Find dx x + 6x +. Name: Solution: We complete the square to see if this function has a nice form. Note we have: x + 6x + (x + + dx x + 6x + dx (x + + Note that this looks a lot
Math - Final Exam Review. Find dx x + 6x +. Name: Solution: We complete the square to see if this function has a nice form. Note we have: x + 6x + (x + + dx x + 6x + dx (x + + Note that this looks a lot
y = x 3 and y = 2x 2 x. 2x 2 x = x 3 x 3 2x 2 + x = 0 x(x 2 2x + 1) = 0 x(x 1) 2 = 0 x = 0 and x = (x 3 (2x 2 x)) dx
 Millersville University Name Answer Key Mathematics Department MATH 2, Calculus II, Final Examination May 4, 2, 8:AM-:AM Please answer the following questions. Your answers will be evaluated on their correctness,
Millersville University Name Answer Key Mathematics Department MATH 2, Calculus II, Final Examination May 4, 2, 8:AM-:AM Please answer the following questions. Your answers will be evaluated on their correctness,
Integration by Substitution
 Integration by Substitution Dr. Philippe B. Laval Kennesaw State University Abstract This handout contains material on a very important integration method called integration by substitution. Substitution
Integration by Substitution Dr. Philippe B. Laval Kennesaw State University Abstract This handout contains material on a very important integration method called integration by substitution. Substitution
Review for Cumulative Test 2
 Review for Cumulative Test We will have our second course-wide cumulative test on Tuesday February 9 th or Wednesday February 10 th, covering from the beginning of the course up to section 4.3 in our textbook.
Review for Cumulative Test We will have our second course-wide cumulative test on Tuesday February 9 th or Wednesday February 10 th, covering from the beginning of the course up to section 4.3 in our textbook.
Flash Card Construction Instructions
 Flash Car Construction Instructions *** THESE CARDS ARE FOR CALCULUS HONORS, AP CALCULUS AB AND AP CALCULUS BC. AP CALCULUS BC WILL HAVE ADDITIONAL CARDS FOR THE COURSE (IN A SEPARATE FILE). The left column
Flash Car Construction Instructions *** THESE CARDS ARE FOR CALCULUS HONORS, AP CALCULUS AB AND AP CALCULUS BC. AP CALCULUS BC WILL HAVE ADDITIONAL CARDS FOR THE COURSE (IN A SEPARATE FILE). The left column
Math Worksheet 1 SHOW ALL OF YOUR WORK! f(x) = (x a) 2 + b. = x 2 + 6x + ( 6 2 )2 ( 6 2 )2 + 7 = (x 2 + 6x + 9) = (x + 3) 2 2
 Names Date. Consider the function Math 0550 Worksheet SHOW ALL OF YOUR WORK! f() = + 6 + 7 (a) Complete the square and write the function in the form f() = ( a) + b. f() = + 6 + 7 = + 6 + ( 6 ) ( 6 ) +
Names Date. Consider the function Math 0550 Worksheet SHOW ALL OF YOUR WORK! f() = + 6 + 7 (a) Complete the square and write the function in the form f() = ( a) + b. f() = + 6 + 7 = + 6 + ( 6 ) ( 6 ) +
