Chapter (a) ζ. ω. 5 2 (a) Type 0 (b) Type 0 (c) Type 1 (d) Type 2 (e) Type 3 (f) Type 3. (g) type 2 (h) type (a) K G s.
|
|
|
- Veronica Hart
- 6 years ago
- Views:
Transcription
1 Chapter (a) ζ. ω rad / ec (b) 0 ζ ω rad / ec (c) ζ ω 5 rad / ec (d) 0. 5 ζ ω 0. 5 rad / ec 5 (a) Type 0 (b) Type 0 (c) Type 1 (d) Type (e) Type 3 (f) Type 3 (g) type (h) type (a) K G p lim ( ) 1000 K lim G( ) 0 K lim G( ) 0 0 v 0 a 0 (b) K p lim G( ) 0 K v lim G( ) 1 K lim G( ) a 0
2 (c) K p lim G( ) 0 K lim G( ) K v 0 K a lim G( ) 0 0 (d) K p lim G( ) 0 K v lim G( ) 0 K a lim G( ) 1 0 (e) K p lim G( ) 0 K v lim G( ) 1 K lim G( ) 0 0 a 0 (f) K p lim G( ) 0 K v lim G( ) 0 K lim G( ) K a (a) Iput Error Cotat Steady tate Error u t K 1000 p tu t K 0 v t u ()/ t K a 0 (b) Iput Error Cotat Steady tate Error u t K p 0 tu t K 1 v 1 t u ()/ t K a 0 (c) Iput Error Cotat Steady tate Error u () t K 0 p 5
3 tu () t K K 1/ K v t u ()/ t K a 0 The above reult are valid if the value of K correpod to a table cloed loop ytem. (d) The cloed loop ytem i utable. It i meaigle to coduct a teady tate error aalyi. (e) Iput Error Cotat Steady tate Error u t K p 0 tu t K 1 v 1 t u ()/ t K a 0 (f) Iput Error Cotat Steady tate Error u () t K 0 p tu () t K 0 v t u ()/ t K K 1/ K a The cloed loop ytem i table for all poitive value of K. Thu the above reult are valid. 5 5 (a) K H ( 0) 1 M G( ) ( ) H 1 + GH ( ) ( ) a 3, a 3, a, b 1, b Uit tep Iput: e 1 bk 0 H 1 K H a
4 Uit ramp iput: a b K Thu e. 0 0 H Uit parabolic Iput: a b K 0 ad a b K 1 0. Thu e. 0 0 H 1 1 H (b) K H ( 0) 5 H G( ) 1 M( ) a 5, a 5, b 1, b GH ( ) ( ) Uit tep Iput: e 1 bk 1 5 K a 5 5 H 0 0 H Uit ramp Iput: i 0: a b K 0 i 1: a b K H 1 1 H e a b K 1 1 ak 0 H H Uit parabolic Iput: e (c) K H ( 0) 1/ 5 H G( ) M( ) 1 + GH ( ) ( ) + 5 The ytem i table a 1, a 1, a 50, a 15, b 5, b Uit tep Iput: e 1 bk 5/5 K a 1 H 0 0 H Uit ramp Iput: 5 4
5 i 0: a b K 0 i 1: a b K 4/ H 1 1 H e a b K 1 1 ak 0 H H 1 1/ 5 4 1/ 5 Uit parabolic Iput: e (d) K H ( 0) 10 H G( ) 1 M( ) The ytem i table GH ( ) ( ) a 10, a 5, a 1, b 1, b 0, b Uit tep Iput: e 1 bk 1 10 K a H 0 0 H Uit ramp Iput: i 0: a b K 0 i 1: a b K H 1 1 H e a b K 1 1 ak 0 H H Uit parabolic Iput: e 5 6 (a) M ( ) + 4 K 4 3 H 1 The ytem i table Uit tep Iput: a 4, a 4, a 48, a 16, b 4, b 1, b 0, b e 1 bk 4 K a 4 H 0 0 H Uit ramp iput: i 0: a b K 0 i 1: a b K H 1 1 H 5 5
6 e a b K 1 1 ak 0 H H Uit parabolic Iput: e (b) M( ) K( + 3) K 3 H 1 The ytem i table for K > ( K+ ) + 3K a 3K, a K+, a 3, b 3K, b K Uit tep Iput: e 1 bk 3K K a 3K H 0 0 H Uit ramp Iput: i 0: a b K 0 i 1: a b K K + K H 1 1 H e a b K 1 1 ak 0 H H K+ K 3K 3K Uit parabolic Iput: e The above reult are valid for K > 0. (c) M H ( ) H( ) K lim ( ) 4 3 H Uit tep Iput: a 0, a 10, a 50, a 15, b 5, b e 1 a bk H K H a Uit ramp Iput: 5 6
7 Uit parabolic Iput: e e (d) M ( ) K( + 5) K H 1 The ytem i table for 0 < K < K + 5K a 5K, a 5K, a 60, a 17, b 5K, b K Uit tep Iput: e 1 bk 5K K a 5K H 0 0 H Uit ramp Iput: i 0: a b K 0 i 1: a b K 5K K 4K H 1 1 H e Uit parabolic Iput: a b K 1 1 ak 0 H H 5K K 5K e 4 5 The reult are valid for 0 < K <
8 5-7) Type of the ytem i zero Pole: i, i, ad Zero: ) 5( + 1) ( + )( + 3) a) Poitio error: lim G lim b) Velocity error: lim lim c) Acceleratio error: lim lim 0 5-9) a) Steady tate error for uit tep iput: Referrig to the reult of problem 5-8, 0 b) Steady tate error for ramp iput: 5 8
9 Regardig the reult of problem 5-8, c) Steady tate error for parabolic iput: Regardig the reult of problem 5-8, ) 4( + 1) ( + ) a) Step error cotat: lim b) Ramp error cotat: lim c) Parabolic error cotat: lim 5-11) 3 4 where x 1 i a uit tep iput, x i a ramp iput, ad x 3 i a uit parabola iput. Sice the ytem i liear, the the effect of X() i the ummatio of effect of each idividual iput. That i: 3 4 So:
10 5-1) The tep iput repoe of the ytem i: Therefore: The rie time i the time that uit tep repoe value reache from 0.1 to 0.9. The: It i obviou that t r > 0, the: A k < 1, the 0 Therefore.. 0 or.. which yield: ) Y( ) G ( ) E( ) KG ( ) 0 p 100K 1+ KG ( ) 0( K ) t p t Type 1 ytem. 5K Error cotat: K, K, K 0 p v a K t (a) rt () u(): t e (b) r() t tu (): t e (c) rt () tu ()/ t : e 1 K a K p 1 1 K K 5K v t 5 10
11 5 14 G p 100 Y( ) KG ( ) p ( ) G ( ) ( )( ) E( ) 0 1+ K G ( ) 100K G ( ) 0 ( )( ) + 100K t t p 5K Error cotat: K, K, K 0 p v a K t (a) rt () u(): t e (b) r() t tu (): t e (c) rt () tu ()/ t : e 1 K a K p 1 1 K K 5K v t Sice the ytem i of the third order, the value of K ad K t mut be cotraied o that the ytem i table. The characteritic equatio i Routh Tabulatio: ( ) 3 K K t K 1 100K K 100K 1 100K t t Stability Coditio: K > 0 ( K ) K 1 t K > 0 or > t 5K 1 Thu, the miimum teady tate error that ca be obtaied with a uit ramp iput i 1/
12 5 15 (a) From Figure 3P 9, KK KK + KKKK 1 i b 1 i t Θ () R + L ( R + L )( B + J ) o a a a a t t Θ () KK KK + KKKK KKKKN r 1 i b 1 i t 1 i R + L R + L B + J R + L B + J ( )( ) ( )( ) a a a a t t a a t t [ ( R + L)( B + J) + KK ( B + J) + KK + KKKK] a a t t 1 t t i b 1 i t ( ) ( ) Θ ( ) o Θ ( ) L J L B R J K K J R B K K KK K K K K B KK K K N r a t a t a t 1 t a t i b i 1 t 1 t 1 i 1 () (), () lim Θ () 0 e θ r t u t Θ r 0 Provided that all the pole of Θ ( ) are all i the left half plae. e (b) For a uit ramp iput, Θ r ( ) 1/. e lim θ ( t) lim Θ ( ) t e 0 e RB+ KKB+ KK + KKKK a t 1 t i b 1 i t KK K K N 1 i if the limit i valid. 5 1
13 5 16 (a) Forward path trafer fuctio: [(t) 0]: K( ) Y( ) ( + 5) K( ) G () E ( ) KK t 5 KK 1+ ( + 5) ( + + t ) Type 1 ytem. 1 Error Cotat: K, K, K 0 p v a K 1 1 For a uit ramp iput, r() t tu (), t R(), e lim e() t lim E() K t 0 K t v t Routh Tabulatio: 3 1 KK + 0.0K t K ( ) 5K K K t 5 K Stability Coditio: ( ) K > 0 5 K K > 0 or K > 0.0 t t (b) With r(t) 0, t u t N 1 () (), () /. Sytem Trafer Fuctio with N() a Iput: K ( ) ( 5) Y + K N K( ) KK + + K K + + K ( ) 3 ( ) t t Steady State Output due to (t): ( + 5) ( + 5) y lim y( t) lim Y( ) 1 if the limit i valid. t
14 5 17 You may ue MATLAB i all Routh Hurwitz calculatio. 1. Activate MATLAB. Go to the directory cotaiig the ACSYS oftware. 3. Type i Acy 4. The pre the trafer fuctio Symbolic ad eter the Characteritic equatio 5. The pre the Routh Hurwitz butto 6. For example look at below Figure 5 14
15 (a) () t 0, r() t tu (). t Forward path Trafer fuctio: Y() K( + α)( + 3) G () E () 1 0 ( ) Type 1 ytem. Ramp error cotat: K lim G( ) 3Kα v 0 Steady tate error: e 1 1 K 3K v v 3 Characteritic equatio: + K + [ K( 3+ α) 1] + 3α K 0 Routh Tabulatio: 1 3K+ αk 1 K 3αK K( 3K+ αk 1) 3αK K 3αK Stability Coditio: 1 3K 3K+ αk 1 3α > 0 or K > + 3+ α αk > 0 (b) Whe r(t) 0, t u t N 1 () (), () /. Trafer Fuctio betwee (t) ad y(t): K( + 3) Y( ) 1 K( + 3) 3 N( ) K( + α)( + 3) + K + [ K( + α) 1] + 3α K r 0 1+ ( 1) Steady State Output due to (t): y lim y( t) lim Y( ) 0 if the limit i valid. t
16 5 18 Percet maximum overhoot 0.5 e πζ 1 ζ Thu ( ) πζ 1 ζ l π ζ ζ Solvig for ζ from the lat equatio, we have ζ Peak Time t max ω π 1 ζ 001. ec. Thu, ω π ( 0.404) rad / ec Trafer Fuctio of the Secod order Prototype Sytem: Y( ) ω R ( ) + ζω + ω
17 Exteded MATLAB olutio of problem imilar to appear later o e.g Cloed Loop Trafer Fuctio: Characteritic equatio: Y( ) 5K R K K ( ) () t ( ) K K t For a ecod order prototype ytem, whe the maximum overhoot i 4.3%, ζ Rie Time: ω 5K, ζω K K t ζ ζ ec Thu ω 108. rad / ec t r ω ω Thu, K ω ( 10. 8) + K ω Thu K t t With K 4.68 ad K t , the ytem trafer fuctio i Y ( ) 117 R ( ) Uit tep Repoe: y 0.1 at t ec. y 0.9 at t 0.44 ec. t r ec. y max ( 4.3% max. overhoot) 5 17
18 5 0 Cloed loop Trafer Fuctio: Characteritic Equatio: Y( ) 5K R K K ( ) () t ( ) K K t πζ Whe Maximum overhoot 10%, l πζ ( ) ζ Solvig for ζ, we get ζ ζ The Natural udamped frequecy i ω 5K Thu, K ζω 118. ω Rie Time: t ζ. 917ζ. t r. ω ω ec. Thu ω rad / ec ω K Thu K t With K 1.58 ad K t , the ytem trafer fuctio i Y ( ) 313 R ( ) Uit tep Repoe: y 0.1 whe t 0.08 ec. y 0.9 whe t ec. t r ec. y max 11. ( 10% max. overhoot) 5 18
19 5 1 Cloed Loop Trafer Fuctio: Characteritic Equatio: Y ( ) 5K R ( ) + ( K ) + 5K ( ) t t πζ K + 5K 0 Whe Maximum overhoot 0%, l πζ ( ).59 1 ζ Solvig for ζ, we get ζ ζ The Natural udamped frequecy ω 5K K ζω 0. 91ω Rie Time: ζ. 917ζ t r 005. ω ω t ec. Thu, ω ω K K 0. 91ω 584. Thu, K t t 5 With K 3.1 ad K t , the ytem trafer fuctio i Y ( ) R ( ) Uit tep Repoe: y 0.1 whe t ec. y 0.9 whe t 0.07 ec. t r ec. y max 1. ( 0% max. overhoot) 5 19
20 5 Cloed Loop Trafer Fuctio: Characteritic Equatio: Y( ) 5K R K K ( ) () t ( ) K K t Delay time t d ζ ζ ω 01. ec Whe Maximum overhoot 4.3%, ζ t d 01. ω ec. Thu ω 14.3 rad/ec. ω 14.3 K K t ζω 1.414ω Thu K t With K 0.1 ad K t , the ytem trafer fuctio i Uit Step Repoe: Y ( ) 0. 5 R ( ) Whe y 0.5, t ec. Thu, t d ec. y max ( 4.3% max. overhoot) 5 0
21 5 3 Cloed Loop Trafer Fuctio: Characteritic Equatio: Y( ) 5K R K K ( ) () t ( ) K K t Delay time t d ζ ζ ω ω Thu, ω ω 6.74 K K ζω Thu K t t With K 8.6 ad K t , the ytem trafer fuctio i Y ( ) 715 R ( ) Uit Step Repoe: y 0.5 whe t ec. Thu, t d ec. y max ( % max. overhoot) 5 1
22 5 4 Cloed Loop Trafer Fuctio: Characteritic Equatio: Y( ) 5K R K K ( ) () t ( ) K K t For Maximum overhoot 0., ζ Delay time t d ζ ζ ω ω ec Natural Udamped Frequecy ω rad/ec. Thu, 001. ω K ζω Thu, K t K t With K 69.5 ad K t 0.188, the ytem trafer fuctio i Y ( ) R ( ) Uit tep Repoe: y 0.5 whe t ec. Thu, t d ec. y max 1. ( 0% max. overhoot) 5
23 5 5 Cloed Loop Trafer Fuctio: Characteritic Equatio: Y( ) 5K R K K ( ) () t ( ) K K t ζ 0. 6 ζω K 1.ω t Settlig time t 01. ζω 06. ω 3. ec. Thu, ω rad / ec 006. K t 1.ω 5 ω K Sytem Trafer Fuctio: Y ( ) 844 R ( ) Uit tep Repoe: y(t) reache 1.00 ad ever exceed thi value at t ec. Thu, t ec. 5 3
24 5 6 (a) Cloed Loop Trafer Fuctio: Characteritic Equatio: Y( ) 5K R K K ( ) () t ( ) K K t For maximum overhoot 0.1, ζ ζω 0. 59ω 118. ω K t Settlig time: t ζω 059. ω 3. ec. ω K t 118. ω 5 ω 0.46 K Sytem Trafer Fuctio: Y ( ) R ( ) Uit Step Repoe: y(t) reache 1.05 ad ever exceed thi value at t ec. Thu, t ec. (b) For maximum overhoot 0., ζ ζω 0. 91ω K t Settlig time t 001. ec. ω ζω 0.456ω rad / ec K t ω Sytem Trafer Fuctio: Y ( ) Uit Step Repoe: R ( )
25 y(t) reache 1.05 ad ever exceed thi value at t ec. Thu, t ec. Thi i le tha the calculated value of 0.01 ec. 5 5
26 5 7 Cloed Loop Trafer Fuctio: Characteritic Equatio: Y( ) 5K R K K ( ) () t ( ) K K t Dampig ratio ζ Settlig time t Sytem Trafer Fuctio: 4.5ζ ec. Thu, ω rad/ec. ω ω ω K ζω Thu, K K t t ζ Y ( ) 101. R ( ) Uit Step Repoe: The uit tep repoe reache 0.95 at t 0.09 ec. which i the meaured t. 5 6
27 5 8 (a) Whe ζ 05., the rie time i ζ ζ t r ω ω ec. Thu ω 151. rad/ec. The ecod order term of the characteritic equatio i writte + ζω + ω The characteritic equatio of the ytem i + ( a+ 30) + 30a+ K 0 Dividig the characteritic equatio by , we have For zero remaider, 8.48 a Thu, a 16. K a Forward Path Trafer Fuctio: G ( ) ( )( + 30) Uit Step Repoe: y 0.1 whe t ec. y 0.9 whe t 1.43 ec. Rie Time: t r ec. 5 7
28 (b) The ytem i type 1. (i) For a uit tep iput, e 0. (ii) For a uit ramp iput, K G v K lim ( ) 1.45 e a K v 5 9 (a) Characteritic Equatio: ( + K) K 0 Apply the Routh Hurwitz criterio to fid the rage of K for tability. Routh Tabulatio: K K 3 K K Stability Coditio: 1.5 < K < 0 Thi implifie the earch for K for two equal root. Whe K , the characteritic equatio root are: 0.347, 0.347, ad (b) Uit Step Repoe: (K ) 5 8
29 (c) Uit Step Repoe (K 1) The tep repoe i (a) ad (b) all have a egative uderhoot for mall value of t. Thi i due to the zero of G() that lie i the right half plae. 5 9
30 5 30 (a) The tate equatio of the cloed loop ytem are: dx dt 1 dx x + 5x 6x k x k x + r dt The characteritic equatio of the cloed loop ytem i Δ + ( 1+ k ) + ( 30+ 5k + k ) k + k 1 For ω 10 rad / ec, k + k ω 100. Thu 5k + k k (b) For ζ , ζω 1+ k. Thu ω ( 1+ k ) ω k + k Thu k k 1 1 (c) For ω ζ 10 rad / ec ad , 5k + k 100 ad 1 + k ζω Thu k Solvig for k, we have k (d) The cloed loop trafer fuctio i Y( ) 5 5 R k k k ( ) ( ) ( ) For a uit tep iput, lim y( t ) lim Y ( ) 005. t (e) For zero teady tate error due to a uit tep iput, k + k 5 Thu 5k + k
31 Parameter Plae k 1 veru k : 5 31 (a) Cloed Loop Trafer Fuctio (b) Characteritic Equatio: ( K + K ) Y( ) 100 P D R + K+ K ( ) D P + 100K + 100K 0 D P The ytem i table for K P > 0 ad K > 0. D (b) For ζ, ζω ω 1 100K. D 10 K Thu ω 100K 0 K K 0. K P D P D P (c) See parameter plae i part (g). 5 31
32 (d) See parameter plae i part (g). (e) Parabolic error cotat K a 1000 ec ( ) K G K K K K lim ( ) lim Thu 10 a P D P P 0 0 (f) Natural udamped frequecy ω 50 rad/ec. ω K P Thu K P (g) Whe K P 0, K K D G ( ) D (pole zero cacellatio) 5 3
33 5 3 (a) Forward path Trafer Fuctio: Y() KK 10K i G () E ( ) J(1 T) KK K [ + + ] i t ( + + t) K 1 Whe r() t tu (), t K lim G() e v 0 K K t v K t K (b) Whe r(t) 0 Y() 1+ T T ( ) J(1 + T) + K K + KK K + 10K [ ] ( ) d i t i t For T d 1 1 ( ) lim y( t ) lim Y ( ) t 0 10K if the ytem i table. (c) The characteritic equatio of the cloed loop ytem i K 0 The ytem i utable for K > 0.1. So we ca et K to jut le tha 0.1. The, the miimum value of the teady tate value of y(t) i 1 10 K K However, with thi value of K, the ytem repoe will be very ocillatory. The maximum overhoot will be early 100%. (d) For K 0.1, the characteritic equatio i t K or K t 5 33
34 For the two complex root to have real part of /5. we let the characteritic equatio be writte a ( )( ) 3 a b a b ab or + ( + 5) + (5 + ) + 0 The, a a 5 ab 1000 b 00 5a + b 10 K K The three root are: a 5 a 5. 5± j t t 5-33) Rie time: Peak time: Maximum overhoot:. Settlig time:
35 5-34) K ( J + a + KK f ) exp 0. ξ ω
36 5-35) a) Subtitutig ito equatio () give: Sice the ytem i multi iput ad multi output, there are 4 trafer fuctio a:,,, To fid the uit tep repoe of the ytem, let coider By lookig at the Laplace traform fuctio table: where co i 1 b) 5 36
37 Therefore: A a reult: which mea: 1 1 The uit tep repoe i: 1 1 Therefore a a reult: i 1 where ω 1 ad ξ ω 1 / c) 4 Therefore: 1 1 A a reult, the tep repoe of the ytem i: 1 1 By lookig up at the Laplace trafer fuctio table: 5 37
38 5-36) MATLAB CODE (a) where ω 1, ad ξ ω 1 ξ 1 / i 1 where θ co -1 (ξ -1) co -1 (0.5), therefore, clear all Amat[-1-1;6.5 0] Bmat[1 1;1 0] Cmat[1 0;0 1] Dmat[0 0;0 0] dip(' State-Space Model i:') Statemodel(Amat,Bmat,Cmat,Dmat) [ma,a]ize(amat); rakarak(amat); dip(' Characteritic Polyomial:') chareqpoly(amat); 1 3 i 3 % p poly(a) where A i a -by- matrix retur a +1 elemet %row vector whoe elemet are the coefficiet of the characteritic %polyomialdet(i-a). The coefficiet are ordered i decedig power. [mchareq,chareq]ize(chareq); ym ''; polyym(chareq,) dip(' Equivalet Trafer Fuctio Model i:') HmatCmat*iv(*eye()-Amat)*Bmat+Dmat Sice the ytem i multi iput ad multi output, there are 4 trafer fuctio a: To fid the uit tep repoe of the ytem, let coider,,,
39 Let obtai thi term ad fid Y () time repoe for a tep iput. HHmat(,) ilaplace(h/) Pretty(H) Hpolytf([13/],chareq) tep(hpoly) H 13/(*^+*+13) a 1-1/5*exp(-1/*t)*(5*co(5/*t)+i(5/*t)) Trafer fuctio: ^ To fid the tep repoe H11, H1, ad H1 follow the ame procedure. Other part are the ame. 5 39
40 5-37) Impule repoe: a).. b) c) where α co -1 ξ ad 1, therefore, 1 i 1 1 i i ) Ue the approach i 5-36 except: HHmat(,) ilaplace(h) Pretty(H) Hpolytf([13/],chareq) impule(hpoly) H 13/(*^+*+13) a 13/5*exp(-1/*t)*i(5/*t) Trafer fuctio: ^
41 Other part are the ame. 5-39) a) The diplacemet of the bar i: The the equatio of motio i: i 0 A x i a fuctio of θ ad chagig with time, the co If θ i mall eough, the i θ θ ad co θ 1. Therefore, the equatio of motio i rewritte a:
42 (b) To fid the uit tep repoe, you ca ue the ymbolic approach how i Toolbox -1-1: clear all %tf( ); ym B L K ThetaB*//L/(B*+K) ilaplace(theta) Theta B/L/(B*+K) a 1/L*exp(-K*t/B) Alteratively, aig value to B L K ad fid the tep repoe ee olutio to problem (a) K t oz - i / rad The Forward Path Trafer Fuctio: K G () ( ) K ( + 116)( )( j3178.3)( j3178.3) Routh Tabulatio: K K K 9 10 K K K K K 5 4
43 From the 1 row, the coditio of tability i K. 84K > 0 or K K < 0 or ( K )( K ) < 0 Stability Coditio: 0 < K < The critical value of K for tability i With thi value of K, the root of the characteritic equatio are: , j3113.3, j3113.3, j75.68, ad j75.68 (b) K L 1000 oz i/rad. The forward path trafer fuctio i K G () ( ) K ( )( )( j1005)( j1005) (c) Characteritic Equatio of the Cloed Loop Sytem: K 0 Routh Tabulatio: K K K 9 10 K K K K K 5 43
44 4 From the 1 row, the coditio of tability i K. 83K > 0 Or, K K < 0 or ( K 1400)( K ) < 0 Stability Coditio: 0 < K < 1400 The critical value of K for tability i With thi value of K, the characteritic equatio root are: , j676, j676, j748.44, ad j (c) K L. Forward Path Trafer Fuctio: K K K i G () J J + J T m L ( ) L J + R J + R L + R B + K K a T a T m a a m i b K K ( + 116)( ) ( ) Characteritic Equatio of the Cloed Loop Sytem: K 0 Routh Tabulatio: K K K From the 1 row, the coditio of K for tability i K >
45 Stability Coditio: 0 < K < The critical value of K for tability i With K , the characteritic equatio root are 5000, j75.79, ad j Whe the motor haft i flexible, K L i fiite, two of the ope loop pole are complex. A the haft become tiffer, K L icreae, ad the imagiary part of the ope loop pole alo icreae. Whe K L, the haft i rigid, the pole of the forward path trafer fuctio are all real. Similar effect are oberved for the root of the characteritic equatio with repect to the value of K L (a) 100( + ) G ( ) 1 G( ) c 1 K p lim G( ) 00 0 Whe d(t) 0, the teady tate error due to a uit tep iput i e K p (b) + α 100( + )( + α) G ( ) G( ) K e 0 c p ( 1) (c) α 5 maximum overhoot 5.6% α 50 maximum overhoot % α 500 maximum overhoot 54.6% 5 45
46 A the value of α icreae, the maximum overhoot icreae becaue the dampig effect of the zero at α become le effective. Uit Step Repoe: (d) rt () G (). dt () u () t D () 1 0 ad 1 c Sytem Trafer Fuctio: (r 0) Y( ) D ( ) r ( + ) ( α) + 00α Output Due to Uit Step Iput: Y( ) 3 100( + ) ( α) + 00α 00 1 y lim y( t) lim Y( ) t 0 00α α (e) rt () 0, dt () u() t G ( ) c + α 5 46
47 Sytem Trafer Fuctio [r(t) 0] Y( ) D ( ) r ( ( α) + 00α 1 D ( ) y lim y( t) lim Y( ) 0 t 0 (f) Y( ) α 5 D ( ) r 0 Y( ) α 50 D ( ) r 0 Y( ) α 5000 D ( ) r ( + ) ( + ) ( + ) Uit Step Repoe: (g) A the value of α icreae, the output repoe y(t) due to r(t) become more ocillatory, ad the overhoot i larger. A the value of α icreae, the amplitude of the output repoe y(t) due to d(t) become maller ad more ocillatory. 5 47
48 5 4 (a) Forward Path Trafer fuctio: Characteritic Equatio: H( ) 10N N G ( ) E( ) ( + 1)( + 10) ( + 1) + + N 0 N1: Characteritic Equatio: ζ 05. ω 1 rad/ec. Maximum overhoot e πζ 1 ζ (16.3%) Peak time t max ω π 1 ζ ec. N10: Characteritic Equatio: ζ ω 10 rad/ec. πζ 1 ζ Maximum overhoot e (60.5%) Peak time t (b) Uit Step Repoe: N 1 max ω π 1 ζ ec. 5 48
49 Secod order Sytem Third order Sytem Maximum overhoot Peak time 3.68 ec ec. Uit Step Repoe: N 10 Secod order Sytem Third order Sytem Maximum overhoot Peak time ec ec. 5 49
50 5 43 Uit Step Repoe: Whe T z i mall, the effect i lower overhoot due to improved dampig. Whe T z i very large, the overhoot become very large due to the derivative effect. T z improve the rie time, ice 1+ T z derivative cotrol or a high pa filter. i a 5 50
51 5 44 Uit Step Repoe The effect of addig the pole at 1 to G() i to icreae the rie time ad the overhoot. The ytem i T p le table. Whe T p > , the cloed loop ytem i table. 5 51
52 5-45) You may ue the ACSYS oftware developed for thi book. For decriptio refer to Chapter 9. We ue a MATLAB code imilar to toolbox --1 ad thoe i Chapter 5 to olve thi problem. (a) Uig Toolbox clear all um []; de [ ]; Gzpk(um,de,1) t0:0.001:15; tep(g,t); hold o; for Tz[1 5 0]; t0:0.001:15; um [-1/Tz]; de [ ]; Gzpk(um,de,1) tep(g,t); hold o; ed xlabel('time(ec)') ylabel('y(t)') title('uit-tep repoe of the ytem') Zero/pole/gai: (+0.55) (+1.5) Zero/pole/gai: (+1) (+0.55) (+1.5) Zero/pole/gai: (+0.) (+0.55) (+1.5) Zero/pole/gai: (+0.05) (+0.55) (+1.5) 5 5
53 (b) clear all for Tz[ ]; t0:0.001:15; um [Tz 1]; de [1 ]; Gtf(um,de) tep(g,t); hold o; ed xlabel('time(ec)') ylabel('y(t)') title('uit-tep repoe of the ytem') Trafer fuctio: ^ + + Trafer fuctio: ^ + + Trafer fuctio: ^
54 Trafer fuctio: ^ + + Follow the ame procedure for other part. 5-46) Sice the ytem i liear we ue uperpoitio to fid Y, for iput X ad D Firt, coider D 0 k K J + a K f The 1 ; 5 54
55 Kk ( J + a + KK k) f Accordig to above block diagram: Now coider X 0, the: k K J + a K f +1 Accordigly, ad 1 I thi cae, E() D-KY()
56 Now the teady tate error ca be eaily calculated by: 1 1/: lim 1 1 lim lim : lim lim lim (c) The overall repoe i obtaied through uperpoitio Y() Y() + Y() D 0 X 0 yt () yt () + yt () d() t 0 x() t MATLAB clear all ym K k J a Kf X1/; D1/^ YK*k*X/(*(J*+a+K*k*Kf)+K*k)+k*(Kf+)*D/(*(J*+a)+k*(Kf+)*K) ilaplace(y) D 1/^ Y K*k//(*(J*+a+K*k*Kf)+K*k)+k*(Kf+)/^/(*(J*+a)+k*(Kf+)*K) a 1+t/K+1/k/K^/Kf/(a^+*a*K*k+K^*k^- 4*J*K*k*Kf)^(1/)*ih(1/*t/J*(a^+*a*K*k+K^*k^-4*J*K*k*Kf)^(1/))*exp(- 1/*(a+K*k)/J*t)*(a^+a*K*k-*J*K*k*Kf)-coh(1/*t/J*(a^+*a*K*k*Kf+K^*k^*Kf^- 4*J*K*k)^(1/))*exp(-1/*(a+K*k*Kf)/J*t)-(a+K*k*Kf)/(a^+*a*K*k*Kf+K^*k^*Kf^- 4*J*K*k)^(1/)*ih(1/*t/J*(a^+*a*K*k*Kf+K^*k^*Kf^-4*J*K*k)^(1/))*exp(- 1/*(a+K*k*Kf)/J*t)+1/k/K^/Kf*a*(-1+exp(- 1/*(a+K*k)/J*t)*coh(1/*t/J*(a^+*a*K*k+K^*k^-4*J*K*k*Kf)^(1/))) 5 56
57 5-47) (a) Fid the e( t) dt whe e(t) i the error i the uit tep repoe. 0 A the ytem i table the e( t) dt will coverge to a cotat value: 0 0 E( ) e( t) dt lim lim E( ) 0 0 Y ( ) G( ) ( A1 + 1)( A X ( ) 1 + G( ) ( B + 1)( B 1 + 1)...( A + 1)...( B m + 1) + 1) m Try to relate thi to Equatio (5-40). G () 1 E ( ) X() Y() X() X() X() 1 + G ( ) 1 + G ( ) ( A+ 1)( A+ 1)...( A+ 1) ( B+ 1)( B + 1)...( B + 1) ( A+ 1)( A+ 1)...( A+ 1) X X 1 1 m 1 1 ( ) ( ) ( B 1 + 1)( B + 1)...( Bm+ 1) ( B 1 + 1)( B + 1)...( Bm+ 1) 1 ( B 1 + 1)( B + 1)...( Bm+ 1) ( A 1 + 1)( A + 1)...( A + 1) lim E ( ) lim 0 0 ( B 1 + 1)( B+ 1)...( Bm+ 1) B + B + L+ B A + A + L+ A ( ) ( ) 1 m 1 ( B+ 1)( B+ 1)...( B + 1) ( B 1 + 1)( B + 1)...( Bm+ 1) ( A 1 + 1)( A + 1)...( A + 1) 1 m () 1 G ( A 1 + 1)( A + 1)...( A + 1) G () ( B 1 + 1)( B + 1)...( Bm+ 1) ( A 1 + 1)( A + 1)...( A + 1) 1 ( A+ 1)( A+ 1)...( A+ 1) e B B B 1 lim ( 1 + 1)( + 1)...( m + 1) 5 57
58 (b) Calculate Recall 1 K 1 lim G( ) 0 G () 1 E ( ) X() Y() X() X() X() 1 + G ( ) 1 + G ( ) Hece lim E ( ) lim X( ) lim lim G ( ) 0 + G ( ) 0 G ( ) K Ramp Error Cotat v 5 58
59 5-48) Comparig with the ecod order prototype ytem ad matchig deomiator: exp 10.5 Let ξ 0.4 ad ω 80 The , clear all p9; K56.5; um [10 10*K]; de [1 35+p 5*p+10*K]; Gtf(um,de) tep(g); xlabel('time(ec)') ylabel('y(t)') title('uit-tep repoe of the ytem') Trafer fuctio: ^
60 5-49) Accordig to the maximum overhoot: which hould be le tha t, the or 1 jω π / t ω 1 ξ σ π / t ω 1 ξ 5 60
61 5-50) Uig a d order prototype ytem format, from Figure 5-15, ω i the radial ditace from the complex cojugate root to the origi of the -plae, the ω with repect to the origi of the how regio i ω 3.6. Therefore the atural frequecy rage i the regio how i aroud.6 ω 4.6 O the other had, the dampig ratio ζ at the two dahed radial lie i obtaied from: ζ co/ i ζ co/ i The approximatio from the figure give: ζ 0.56 ζ 0.91 Therefore 0.56 ζ 0.91 b) A K p, the: 1 If the root of the characteritic equatio are aumed to be lied i the cetre of the how regio: Comparig with the characteritic equatio: c) The characteritic equatio i a ecod order polyomial with two root. Thee two root ca be determied by two term (p+kk p ) ad KK p K I which iclude four parameter. Regardle of the p ad K p value, we ca alway chooe K ad o that to place the root i a deired locatio. 5 61
62 5-51) a) By ubtitutig the value: b) Speed of the motor i lim (c) d) A a reult: e) A exp 0., the, ξ Accordig to the trafer fuctio, 0.109, the where 0. K< f) A..., the 0.6, a 0., therefore; / 5 6
63 g) MATLAB clear all for K[0.5 1 ]; t0:0.001:15; um [0.*K]; de [ *K]; Gtf(um,de) tep(g,t); hold o; ed xlabel('time(ec)') ylabel('y(t)') title('uit-tep repoe of the ytem') Trafer fuctio: ^ Trafer fuctio: ^ Trafer fuctio: ^
64 Rie time decreae with K icreaig. Overhoot icreae with K. 5 64
65 5-5) exp 0.1, therefore, ξ 0.59 A., the, Therefore: 3 3 If p i a o-domiat pole; therefore comparig both ide of above equatio ad: 3 3 If we coider p 10a (o-domiat pole), ξ 0.6 ad ω 4, the: clear all K160; a8.3; b89.8; p83; um [K K*a]; de [1 3+b 3*b+K K*a]; Gtf(um,de) tep(g); xlabel('time(ec)') ylabel('y(t)') title('uit-tep repoe of the ytem') Trafer fuctio: ^ ^
66 Both Overhoot ad ettlig time value are met. No eed to adjut parameter. 5-53) For the cotroller ad the plat to be i erie ad uig a uity feedback loop we have: MATLAB USE toolbox clear all um[ 1 3]; deom[ 3+qrt(9 40) 3 qrt(9 40) 0.0+qrt( ) 0.0 qrt( ) 10]; Gzpk(um,deom,60) rlocu(g) Zero/pole/gai: 60 (+1) (+) (+3) (+10) (^ ) (^ ) 5 66
67 Note the ytem ha two domiat complex pole cloe to the imagiary axi. Let zoom i the root locu diagram ad ue the curor to fid the parameter value. 5 67
68 A how for K0.933 the domiat cloed loop pole are at 0.46±j 0.66 AND OVERSHOOT IS ALMOST 10%. Icreaig K will puh the pole cloer toward le domiat zero ad pole. A a proce the deig proce become le trivial ad more difficult. To cofirm ue Mfeedback(G*.933,1) %See toolbox 5 4 tep(m) Zero/pole/gai: (+3) (+) (+1) (+7.048) (^ ) (^ ) 5 68
69 To reduce rie time, the pole have to move to left to make the ecodary pole more domiat. A a reult the little bump i the left had ide of the above graph hould rie. Try K3: >> Mfeedback(G*3,1) Zero/pole/gai: 180 (+3) (+) (+1) (+5.01) (^ ) (^ ) >> tep(m) **Try a higher K value, but lookig at the root locu ad the time plot, it appear that the overhoot ad rie time criteria will ever be met imultaeouly. 5 69
70 K5 Mfeedback(G*5,1) %See toolbox 5-4- tep(m) Zero/pole/gai: 300 (+3) (+) (+1) (+4.434) (^ ) (^ ) 5 70
71 5 71
72 5-54) Forward path Trafer Fuctio: M( ) K G ( ) 3 1 M( ) + ( 0 + a) + ( a) + 00a K For type 1 ytem, 00a K 0 Thu K 00a Ramp error cotat: K v K 00a lim G( ) 5 Thu a 10 K a a MATLAB Symbolic tool ca be ued to olve above. We ue it to fid the root for the ext part: >> ym a K >>olve(5*00+5*0*a 00a) a 10 >> D(^+0*+00)*+a)) D (^+0*+00)*(+a) >> expad(d) a ^3+^*a+0*^+0**a+00*+00*a >> olve(a,) a a 10+10*i 10 10*i The forward path trafer fuctio i The cotroller trafer fuctio i 5 7
73 G () 000 ( ) ( + + ) ( + + ) G () G () c G () p MATLAB The maximum overhoot of the uit tep repoe i 0 percet. clear all K000; a10; um []; de [-10+10i i -a]; Gzpk(um,de,K) tep(g); xlabel('time(ec)') ylabel('y(t)') title('uit-tep repoe of the ytem') Zero/pole/gai: (+10) (^ ) Clearly PO
74 5-55) Forward path Trafer Fuctio: M( ) K G ( ) 3 1 M( ) + ( 0 + a) + ( a) + 00a K For type 1 ytem, 00a K 0 Thu K 00a Ramp error cotat: K v K 00a lim G( ) 9 Thu a 90 K a a MATLAB Symbolic tool ca be ued to olve above. We ue it to fid the root for the ext part: >> ym a K olve(9*00+9*0*a 00*a) a 90 >>D(^+0*+00)*+a)) D (^+0*+00)*(+a) >> expad(d) a ^3+^*a+0*^+0**a+00*+00*a >> olve(a,) a a 10+10*i 10 10*i The forward path trafer fuctio i The cotroller trafer fuctio i 5 74
75 G () ( ) ( + + ) ( + + ) G () G () c G ( ) p The maximum overhoot of the uit tep repoe i 4.3 percet. From the expreio for the ramp error cotat, we ee that a a or K goe to ifiity, K v approache 10. Thu the maximum value of K v that ca be realized i 10. The difficultie with very large value of K ad a are that a high gai amplifier i eeded ad urealitic circuit parameter are eeded for the cotroller. clear all K18000; a90; um []; de [-10+10i i -a]; Gzpk(um,de,K) tep(g); xlabel('time(ec)') ylabel('y(t)') title('uit-tep repoe of the ytem') Zero/pole/gai: (+90) (^ ) PO i le tha
76 5-56) (a) Ramp error Cotat: MATLAB clear all ym Kp Kd kv Gum(Kp+Kd*)*1000 Gde (*(+10)) GGum/Gde Kv*G 0 eval(kv) Gum 1000*Kp+1000*Kd* Gde *(+10) G (1000*Kp+1000*Kd*)//(+10) Kv (1000*Kp+1000*Kd*)/(+10) 0 a 100*Kp ( + ) 1000 K K 1000K P D P K lim 100K 1000 v P 0 ( + 10) 10 Thu K P 10 Kp10 clear ym Mum(Kp+Kd*)*1000//(+10) Mde1+(Kp+Kd*)*1000//(+10) 5 76
77 Kp 10 Mum ( *Kd*)//(+10) Mde 1+( *Kd*)//(+10) a (^+10* *Kd*)//(+10) Characteritic Equatio: ( ) Match with a d order prototype ytem K K 0 D P ω 1000K P rad/ec ζω K D olve( *kd 100) a 9/ Thu K D Ue the ame procedure for other part. (b) For K v 1000 ad ζ , ad from part (a), ω 100 rad/ec, ζω K D Thu K D (c) For K v 1000 ad ζ 1.0, ad from part (a), ω 100 rad/ec, 190 ζω K D Thu K D
78 5-57) The ramp error cotat: ( K + K ) 1000 P D K lim 100K 10, 000 Thu K 100 v P P 0 ( + 10) The forward path trafer fuctio i: ( + K ) G () ( + 10) D clear all for KD0.:0.:1.0; um [-100/KD]; de [0-10]; Gzpk(um,de,1000); Mfeedback(G,1) tep(m); hold o; ed xlabel('time(ec)') ylabel('y(t)') title('uit-tep repoe of the ytem') Zero/pole/gai: 1000 (+500) (^ e005) Zero/pole/gai: 1000 (+50) (+434.1) (+575.9) Zero/pole/gai: 1000 (+166.7) (+07.7) (+80.3) 5 78
79 Zero/pole/gai: 1000 (+15) (+144.4) (+865.6) Zero/pole/gai: 1000 (+100) (+111.3) (+898.7) Ue the curor to obtai the PO ad tr value. For part b the maximum value of KD reult i the miimum overhoot. 5 79
80 5-58) (a) Forward path Trafer Fuctio: ( + ) 4500K K K P D G () G() G() c p ( ) 4500KK P Ramp Error Cotat: K lim G( ) 1.458KK v e Thu KK P 80. Let K K P K KK 1 ad 80. v P clear all KP1; K80.; figure(1) um [-KP]; de [0-361.]; Gzpk(um,de,4500*K) Mfeedback(G,1) tep(m) hold o; for KD :0.0005:0.00; um [-KP/KD]; de [0-361.]; Gzpk(um,de,4500*K*KD) Mfeedback(G,1) tep(m) ed xlabel('time(ec)') ylabel('y(t)') title('uit-tep repoe of the ytem') P Zero/pole/gai: (+1) (+361.) Zero/pole/gai: (+1) (+0.999) (+3.613e005) Zero/pole/gai: (+000) (+361.) Zero/pole/gai: (+000) 5 80
81 (^ e005) Zero/pole/gai: (+1000) (+361.) Zero/pole/gai: (+1000) (^ e005) Zero/pole/gai: (+666.7) (+361.) Zero/pole/gai: (+666.7) (^ e005) Zero/pole/gai: 71.8 (+500) (+361.) Zero/pole/gai: 71.8 (+500) (^ e005) 5 81
82 K D t r (ec) t (ec) Max Overhoot (%)
83 5-59) The forward path Trafer Fuctio: N 0 00( K + K ) P D G () ( + 1)( + 10) To tabilize the ytem, we ca reduce the forward path gai. Sice the ytem i type 1, reducig the gai doe ot affect the teady tate liquid level to a tep iput. Let K P 005. ( + K ) D G () ( + 1)( + 10) ALSO try other Kp value ad compare your reult. clear all figure(1) KD0 um []; de [ ]; Gzpk(um,de,00*0.05) Mfeedback(G,1) tep(m) hold o; for KD0.01:0.01:0.1; KD um [-0.05/KD]; Gzpk(um,de,00*KD) Mfeedback(G,1) tep(m) ed xlabel('time(ec)') ylabel('y(t)') title('uit-tep repoe of the ytem') KD 0 Zero/pole/gai: 10 (+1) (+10) Zero/pole/gai: 10 (+10.11) (^ ) KD
84 Zero/pole/gai: (+5) (+1) (+10) Zero/pole/gai: (+5) (+9.889) (^ ) KD Zero/pole/gai: 4 (+.5) (+1) (+10) Zero/pole/gai: 4 (+.5) (+9.658) (^ ) KD Zero/pole/gai: 6 (+1.667) (+1) (+10) Zero/pole/gai: 6 (+1.667) (+9.413) (^ ) KD Zero/pole/gai: 8 (+1.5) (+1) (+10) Zero/pole/gai: 8 (+1.5) (+9.153) (^ ) 5 84
85 KD Zero/pole/gai: 10 (+1) (+1) (+10) Zero/pole/gai: 10 (+1) (+8.873) (+1.17) (+1) KD Zero/pole/gai: 1 ( ) (+1) (+10) Zero/pole/gai: 1 ( ) (+8.569) (+1.773) (+0.658) KD Zero/pole/gai: 14 ( ) (+1) (+10) Zero/pole/gai: 14 ( ) (+8.3) (+.1) (+0.547) KD Zero/pole/gai: 16 (+0.65) (+1) (+10) Zero/pole/gai: 16 (+0.65) (+7.85) (+.673) ( ) 5 85
86 KD Zero/pole/gai: 18 ( ) (+1) (+10) Zero/pole/gai: 18 ( ) (+7.398) (+3.177) (+0.455) KD Zero/pole/gai: 0 (+0.5) (+1) (+10) Zero/pole/gai: 0 (+0.5) ( ) (+3.803) (+6.811) 5 86
87 Uit tep Repoe Attribute: K D t (ec) Max Overhoot (%) Whe K D 005. the rie time i.71 ec, ad the tep repoe ha o overhoot. 5 87
88 5-60) (a) For e 1, ( K + K ) 00 P D K lim G( ) lim 0K 1 v P 0 0 ( + 1)( + 10) Thu K P 005. Forward path Trafer Fuctio: ( + K ) D G () ( + 1)( + 10) Becaue of the choice of Kp thi i the ame a previou part. 5-61) (a) Forward path Trafer Fuctio: K I 100 K + P G ( ) For ( K+ K) 100 P I K 10, K lim G( ) lim K 10 v v I 0 0 ( ) Thu K I 10. G cl ( ) ( ) ( ) P I P 3 3 ( ) ) 100 K + K 100 K K + K (1 + K P I P (b) Let the complex root of the characteritic equatio be writte a σ + j σ j The quadratic portio of the characteritic equatio i σ ( σ ) The characteritic equatio of the ytem i ( ) 15 ad K The quadratic equatio mut atify the characteritic equatio. Uig log diviio ad olve for zero remaider coditio. P 5 88
89 + (10 σ ) ( ) 3 σ σ K P ( σ ) σ ( σ P ) ( ) ( ) (10 σ) + 100K (10 σ) + 0σ 4 σ + (10 σ) + 5 ( KP ) σ 0σ 15 + σ 10σ + 450σ For zero remaider, σ 10σ + 450σ (1) ad 100K P + 3σ 0σ 15 0 () The real olutio of Eq. (1) i σ From Eq. (), 15+ 0σ 3σ K P The characteritic equatio root are: j15, j15, ad 10 + σ 4.89 (c) Root Cotour: 3 Dividig both ide of ( ) K by the term that do ot cotai K p we have: P 100K P G eq 100K 100K P P G () eq ( )( ) Root Cotour: See Chapter 9 toolbox 9 5 for more iformatio clear all Kp.001; um [100*Kp 0]; de [ ]; rlocu(um,de) 5 89
90 5 90
91 5-6) (a) Forward path Trafer Fuctio: K I 100 K + P G ( ) For ( K+ K) 100 P I K 10, K lim G( ) lim K 10 v v I 0 0 ( ) Thu the forward path trafer fuctio become G () ( + K ) ( ) P G cl ( ) ( ) ( ) P I P 3 3 ( ) ) 100 K+ K 100 K K + K (1 + K P I P clear all for Kp.4:0.4:; um [100*Kp 1000]; de [ ]; [umcl,decl]cloop(um,de); GCLtf(umCL,deCL); tep(gcl) hold o; ed 5 91
92 Ue the curer to fid the maximum overhoot ad rie time. For example whe K p, PO43 ad tr100%0.15 ec. Trafer fuctio: ^ ^
93 5-63) (a) Forward path Trafer Fuctio: 100 G () ( K+ K) P ( ) I For K v 100, ( K+ K) 100 P I K lim G( ) lim K 100 v I 0 0 ( ) 3 (b) The characteritic equatio i ( ) Routh Tabulatio: K + 100K 0 P I Thu K I K P K 900 P 10,000 0 For tability, 100K 900 > 0 Thu K > 9 P P 0 10, Activate MATLAB 8. Go to the directory cotaiig the ACSYS oftware. 9. Type i Acy 10. The pre the trafer fuctio Symbolic ad eter the Characteritic equatio 11. The pre the Routh Hurwitz butto 5 93
94 RH [ 1, *kp] [ 10, 10000] [ *kp, 0] [ ( *kp)/( *kp), 0] 5 94
95 Root Cotour: G eq ( ) 100K 100K P P ,000 ( )( j19.4)( j19.4) Root Cotour: See Chapter 9 toolbox 9 5 for more iformatio clear all Kp.001; um [100*Kp 0]; de [ ]; rlocu(um,de) 5 95
96 (c) K I 100 ( K+ ) P G () ( ) The followig maximum overhoot of the ytem are computed for variou value of K P. clear all Kp[ ]; [N,M]ize(Kp); for i1:m um [100*Kp(i) 10000]; de [ ]; [umcl,decl]cloop(um,de); GCLtf(umCL,deCL); figure(i) tep(gcl) ed K P
97 y max Whe K P 5, miimum y max Ue: cloe all to cloe all the figure widow. 5 97
98 5-64) MATLAB olutio i the ame a (a) Forward path Trafer Fuctio: 100 G () ( K+ K) P ( ) I For K v 100K I 10, K 10 I 100 (b) 3 Characteritic Equatio: ( ) Routh Tabulatio: K P K K 1000 P 0 P For tability, K P > 0 Root Cotour: G eq ( ) 3 100K P 5 98
99 (c) The maximum overhoot of the ytem for differet value of K P ragig from 0.5 to 0 are computed ad tabulated below. K P y max Whe K P 1.7, maximum y max ) ( ) + + G ( ) K + K + 1+ K K + c P D D1 P where K K K K K I D P I I K K + K K K K K K K P P D1 I D D1 P I I Forward path Trafer Fuctio: 100 G () G() G() c p ( KD + KP+ KI) ( ) Thu Ad reame the ratio: K / K A, K / K B D P I P K K v I KI lim G( )
100 ForK D beig ufficietly mall: Forward path Trafer Fuctio: ( K+ ) P G () ( ) Characteritic Equatio: ( ) 3 K P , For tability, K p >9. Select K p 10 ad oberve the repoe. clear all Kp10; um [100*Kp 10000]; de [ ]; [umcl,decl]cloop(um,de); GCLtf(umCL,deCL) tep(gcl) Trafer fuctio: ^ ^ Obviouly by icreaig Kp more ocillatio will occur. Add K D to reduce ocillatio. clear all Kp10; Kd; um [100*Kd 100*Kp 10000]; de [ ]; [umcl,decl]cloop(um,de); GCLtf(umCL,deCL) tep(gcl) 5 100
101 Trafer fuctio: 00 ^ ^ ^ Uit tep Repoe The rie time eem reaoable. But we eed to icreae Kp to improve approach to teady tate. Icreae Kp to Kp30. clear all Kp30; Kd1; um [100*Kd 100*Kp 10000]; de [ ]; [umcl,decl]cloop(um,de); GCLtf(umCL,deCL) tep(gcl) Trafer fuctio: 100 ^ ^ ^
102 To obtai a better repoe cotiue adjutig KD ad KP. 5 10
103 5-66) Thi problem ha received exteded treatmet i Chapter 6, Cotrol Lab ee Sectio 6-6. For the ake implicity, thi problem we aume the cotrol force f(t) i applied i parallel to the prig K ad damper B. We will ot cocer the detail of what actuator or eor are ued. Let look at Figure 4-84 ad equatio 4-3 ad m c x c m c k c k m w c x w m x m w k w c w k w c w y k c y (a) (b) (c) Figure 4-84 Quarter car model realizatio: (a) quarter car, (b) degree of freedom, ad (c) 1 degree of freedom model. The equatio of motio of the ytem i defied a follow: mx &&() t + cx& () t + kx() t cy& () t + ky() t (4-3) which ca be implified by ubtitutig the relatio z(t) x(t) y(t) ad o dimeioalizig the coefficiet to the form && zt + zt & + zt && yt (4-33) () ζω () ω () () The Laplace traform of Eq. (4 33) yield the iput output relatiohip 5 103
104 Z() 1 Y&& () + ζω+ ω (4-34) Now let apply cotrol ee ectio 6-6 for more detail. m x k k f(t) c y For implicity ad better preetatio, we have caled the cotrol force a kf(t) we rewrite (4-34) a: mx &&() t + cx& () t + kx() t cy& () t + ky() t + kf () t && zt ζω zt & ω zt && yt ω f t () + () + () () + () + ζω+ ω A( ) + ω F( ) A () Y&& () (4-34) Settig the cotroller tructure uch that the vehicle bouce Z () X() Y() i miimized: KI F () 0 KP + K D + Z () Z () 1 A () K + ζω+ ω 1+ KP + KD+ I Z () A () + ζω + ω 1+ K + K + K (( ) ) 3 P D I See Equatio (6-4). For proportioal cotrol K D K I
105 Pick ς ad ω 1 for implicity. Thi i ow a uderdamped ytem. Ue MATLAB to obtai repoe ow. clear all Kp1; Kd0; Ki0; um [-1 0]; de [1 *0.707+Kd 1+Kp Ki]; Gtf(um,de) tep(g) Trafer fuctio: ^ ^ + Adjut parameter to get the deired repoe if eceary. The proce i the ame for part b, c ad d
106 5-67) Replace F() with KI F () Xref KP + K D + X () B ζω M K ω M X() 1 Xref () KI + ζω+ ω + KP + KD+ Ue MATLAB to obtai repoe ow. clear all Kp1; Kd0; Ki0; B10; K0; M1; omegaqrt(k/m); zeta(b/m)//omega; um [1 0]; de [1 *zeta*omega+kd omega^+kp Ki]; Gtf(um,de) tep(g) rafer fuctio: ^ ^ + 1 T0 achieve the proper repoe, adjut cotroller gai accordigly
107 5-68) From problem 4-3 a) Rotatioal kietic eergy: Tralatioal kietic eergy: Relatio betwee tralatioal diplacemet ad rotatioal diplacemet: 1 Potetial eergy: A we kow, the: By differetiatig, we have: 0 0 Sice caot be zero, the 0 b) 0 c) 5 107
108 1 1 1 where at the maximum eergy. 1 1 The: 1 1 Or: J d) G () ( m + K) % elect value of m, J ad K K100; J5; m5; Gtf([J],[m 0 K]) Pole(G) impule(g,10) xlabel( 'Time(ec)'); ylabel('amplitude'); Trafer fuctio: ^ a i i 5 108
109 Ucotrolled With a proportioal cotroller oe ca adjut the ocillatio amplitude the trafer fuctio i rewritte a: G () cl JK p ( m + K + JK p ) % elect value of m, J ad K Kp0.1 K100; J5; m5; Gtf([J*Kp],[m 0 (K+J*Kp)]) Pole(G) impule(g,10) xlabel( 'Time(ec)'); ylabel('amplitude'); 5 109
110 Kp Trafer fuctio: ^ a i i A PD cotroller mut be ued to damp the ocillatio ad reduce overhoot. Ue Example a a guide
111 5-69) From Problem 4-6 we have: a) y K( y 1 y ) K( y 1 y ) y 1 μmg& y μmg& y 1 b) From Newto Law: c) If y 1 ad y are coidered a a poitio ad v 1 ad v a velocity variable The: The output equatio ca be the velocity of the egie, which mea Obtaiig require olvig above equatio with repect to Y () From the firt equatio: Subtitutig ito the ecod equatio: 5 111
112 By olvig above equatio: 1 Replace Force F with a proportioal cotroller o that FK(Z-Z ref ): K P Z ref _ F Z ) Alo ee derivatio i 4-9. x(t) L M F L θ Here i a alterative repreetatio icludig frictio (dampig) μ. I thi cae the agle θ i meaured differetly. Let fid the dyamic model of the ytem: 5 11
113 1) ) Let. If Φ i mall eough the 1 ad, therefore which give: Φ F Igorig frictio 0. Φ F where ; Igorig actuator dyamic (DC motor equatio), we ca icorporate feedback cotrol uig a erie PD compeator ad uity feedback. Hece, K P +K D R _ F Φ ( ( ) ) ( ) () p D ( ) F K R Φ KR Φ The ytem trafer fuctio i: Φ R ( Cotrol i achieved by eurig tability (K p >B) A ( Kp + KD) D + ( p ) + K A K B 5 113
114 Ue Routh Hurwitz to etablih tability firt. Ue Acy to do that a demotrated i thi chapter problem. Alo Chapter ha may example. Ue MATLAB to imulate repoe: clear all Kp10; Kd5; A10; B8; um [A*Kd A*Kp]; de [1 Kd A*(Kp-B)]; Gtf(um,de) tep(g) Trafer fuctio: ^ Adjut parameter to achieve deired repoe. Ue THE PROCEDURE i Example You may look at the root locu of the forward path trafer fuctio to get a better perpective
115 ( K + K ) AK ( z+ ) Φ A E AB fix z ad vary K. p D D clear all z100; Kd0.01; A10; B8; um [A*Kd A*Kd*z]; de [1 0 -(A*B)]; Gtf(um,de) rlocu(g) Trafer fuctio: ^ 80 D AB For z10, a large K D reult i: 5 115
116 clear all Kd0.805; Kp10*Kd; A10; B8; um [A*Kd A*Kp]; de [1 Kd A*(Kp-B)]; Gtf(um,de) pole(g) zero(g) tep(g) Trafer fuctio: ^ a i i a -10 Lookig at domiat pole we expect to ee a ocillatory repoe with overhoot cloe to deired value. For a better deig, ad to meet rie time criterio, ue Example
ELEC 372 LECTURE NOTES, WEEK 4 Dr. Amir G. Aghdam Concordia University
 ELEC 37 LECTURE NOTES, WEE 4 Dr Amir G Aghdam Cocordia Uiverity Part of thee ote are adapted from the material i the followig referece: Moder Cotrol Sytem by Richard C Dorf ad Robert H Bihop, Pretice Hall
ELEC 37 LECTURE NOTES, WEE 4 Dr Amir G Aghdam Cocordia Uiverity Part of thee ote are adapted from the material i the followig referece: Moder Cotrol Sytem by Richard C Dorf ad Robert H Bihop, Pretice Hall
Introduction to Control Systems
 Itroductio to Cotrol Sytem CLASSIFICATION OF MATHEMATICAL MODELS Icreaig Eae of Aalyi Static Icreaig Realim Dyamic Determiitic Stochatic Lumped Parameter Ditributed Parameter Liear Noliear Cotat Coefficiet
Itroductio to Cotrol Sytem CLASSIFICATION OF MATHEMATICAL MODELS Icreaig Eae of Aalyi Static Icreaig Realim Dyamic Determiitic Stochatic Lumped Parameter Ditributed Parameter Liear Noliear Cotat Coefficiet
CONTROL SYSTEMS. Chapter 7 : Bode Plot. 40dB/dec 1.0. db/dec so resultant slope will be 20 db/dec and this is due to the factor s
 CONTROL SYSTEMS Chapter 7 : Bode Plot GATE Objective & Numerical Type Solutio Quetio 6 [Practice Book] [GATE EE 999 IIT-Bombay : 5 Mark] The aymptotic Bode plot of the miimum phae ope-loop trafer fuctio
CONTROL SYSTEMS Chapter 7 : Bode Plot GATE Objective & Numerical Type Solutio Quetio 6 [Practice Book] [GATE EE 999 IIT-Bombay : 5 Mark] The aymptotic Bode plot of the miimum phae ope-loop trafer fuctio
System Control. Lesson #19a. BME 333 Biomedical Signals and Systems - J.Schesser
 Sytem Cotrol Leo #9a 76 Sytem Cotrol Baic roblem Say you have a ytem which you ca ot alter but it repoe i ot optimal Example Motor cotrol for exokeleto Robotic cotrol roblem that ca occur Utable Traiet
Sytem Cotrol Leo #9a 76 Sytem Cotrol Baic roblem Say you have a ytem which you ca ot alter but it repoe i ot optimal Example Motor cotrol for exokeleto Robotic cotrol roblem that ca occur Utable Traiet
State space systems analysis
 State pace ytem aalyi Repreetatio of a ytem i tate-pace (tate-pace model of a ytem To itroduce the tate pace formalim let u tart with a eample i which the ytem i dicuio i a imple electrical circuit with
State pace ytem aalyi Repreetatio of a ytem i tate-pace (tate-pace model of a ytem To itroduce the tate pace formalim let u tart with a eample i which the ytem i dicuio i a imple electrical circuit with
The Performance of Feedback Control Systems
 The Performace of Feedbac Cotrol Sytem Objective:. Secify the meaure of erformace time-domai the firt te i the deig roce Percet overhoot / Settlig time T / Time to rie / Steady-tate error e. ut igal uch
The Performace of Feedbac Cotrol Sytem Objective:. Secify the meaure of erformace time-domai the firt te i the deig roce Percet overhoot / Settlig time T / Time to rie / Steady-tate error e. ut igal uch
Time Response. First Order Systems. Time Constant, T c We call 1/a the time constant of the response. Chapter 4 Time Response
 Time Repoe Chapter 4 Time Repoe Itroductio The output repoe of a ytem i the um of two repoe: the forced repoe ad the atural repoe. Although may techique, uch a olvig a differetial equatio or takig the
Time Repoe Chapter 4 Time Repoe Itroductio The output repoe of a ytem i the um of two repoe: the forced repoe ad the atural repoe. Although may techique, uch a olvig a differetial equatio or takig the
Automatic Control Systems
 Automatic Cotrol Sytem Lecture-5 Time Domai Aalyi of Orer Sytem Emam Fathy Departmet of Electrical a Cotrol Egieerig email: emfmz@yahoo.com Itrouctio Compare to the implicity of a firt-orer ytem, a eco-orer
Automatic Cotrol Sytem Lecture-5 Time Domai Aalyi of Orer Sytem Emam Fathy Departmet of Electrical a Cotrol Egieerig email: emfmz@yahoo.com Itrouctio Compare to the implicity of a firt-orer ytem, a eco-orer
EECE 301 Signals & Systems Prof. Mark Fowler
 EECE 30 Sigal & Sytem Prof. Mark Fowler Note Set #8 C-T Sytem: Laplace Traform Solvig Differetial Equatio Readig Aigmet: Sectio 6.4 of Kame ad Heck / Coure Flow Diagram The arrow here how coceptual flow
EECE 30 Sigal & Sytem Prof. Mark Fowler Note Set #8 C-T Sytem: Laplace Traform Solvig Differetial Equatio Readig Aigmet: Sectio 6.4 of Kame ad Heck / Coure Flow Diagram The arrow here how coceptual flow
CONTROL ENGINEERING LABORATORY
 Uiverity of Techology Departmet of Electrical Egieerig Cotrol Egieerig Lab. CONTROL ENGINEERING LABORATORY By Dr. Abdul. Rh. Humed M.Sc. Quay Salim Tawfeeq M.Sc. Nihad Mohammed Amee M.Sc. Waleed H. Habeeb
Uiverity of Techology Departmet of Electrical Egieerig Cotrol Egieerig Lab. CONTROL ENGINEERING LABORATORY By Dr. Abdul. Rh. Humed M.Sc. Quay Salim Tawfeeq M.Sc. Nihad Mohammed Amee M.Sc. Waleed H. Habeeb
Lecture 30: Frequency Response of Second-Order Systems
 Lecture 3: Frequecy Repoe of Secod-Order Sytem UHTXHQF\ 5HVSRQVH RI 6HFRQGUGHU 6\VWHPV A geeral ecod-order ytem ha a trafer fuctio of the form b + b + b H (. (9.4 a + a + a It ca be table, utable, caual
Lecture 3: Frequecy Repoe of Secod-Order Sytem UHTXHQF\ 5HVSRQVH RI 6HFRQGUGHU 6\VWHPV A geeral ecod-order ytem ha a trafer fuctio of the form b + b + b H (. (9.4 a + a + a It ca be table, utable, caual
Last time: Ground rules for filtering and control system design
 6.3 Stochatic Etimatio ad Cotrol, Fall 004 Lecture 7 Lat time: Groud rule for filterig ad cotrol ytem deig Gral ytem Sytem parameter are cotaied i w( t ad w ( t. Deired output i grated by takig the igal
6.3 Stochatic Etimatio ad Cotrol, Fall 004 Lecture 7 Lat time: Groud rule for filterig ad cotrol ytem deig Gral ytem Sytem parameter are cotaied i w( t ad w ( t. Deired output i grated by takig the igal
ECEN620: Network Theory Broadband Circuit Design Fall 2014
 ECE60: etwork Theory Broadbad Circuit Deig Fall 04 Lecture 3: PLL Aalyi Sam Palermo Aalog & Mixed-Sigal Ceter Texa A&M Uiverity Ageda & Readig PLL Overview & Applicatio PLL Liear Model Phae & Frequecy
ECE60: etwork Theory Broadbad Circuit Deig Fall 04 Lecture 3: PLL Aalyi Sam Palermo Aalog & Mixed-Sigal Ceter Texa A&M Uiverity Ageda & Readig PLL Overview & Applicatio PLL Liear Model Phae & Frequecy
THE CONCEPT OF THE ROOT LOCUS. H(s) THE CONCEPT OF THE ROOT LOCUS
 So far i the tudie of cotrol yte the role of the characteritic equatio polyoial i deteriig the behavior of the yte ha bee highlighted. The root of that polyoial are the pole of the cotrol yte, ad their
So far i the tudie of cotrol yte the role of the characteritic equatio polyoial i deteriig the behavior of the yte ha bee highlighted. The root of that polyoial are the pole of the cotrol yte, ad their
Last time: Completed solution to the optimum linear filter in real-time operation
 6.3 tochatic Etimatio ad Cotrol, Fall 4 ecture at time: Completed olutio to the oimum liear filter i real-time operatio emi-free cofiguratio: t D( p) F( p) i( p) dte dp e π F( ) F( ) ( ) F( p) ( p) 4444443
6.3 tochatic Etimatio ad Cotrol, Fall 4 ecture at time: Completed olutio to the oimum liear filter i real-time operatio emi-free cofiguratio: t D( p) F( p) i( p) dte dp e π F( ) F( ) ( ) F( p) ( p) 4444443
u t u 0 ( 7) Intuitively, the maximum principles can be explained by the following observation. Recall
 Oct. Heat Equatio M aximum priciple I thi lecture we will dicu the maximum priciple ad uiquee of olutio for the heat equatio.. Maximum priciple. The heat equatio alo ejoy maximum priciple a the Laplace
Oct. Heat Equatio M aximum priciple I thi lecture we will dicu the maximum priciple ad uiquee of olutio for the heat equatio.. Maximum priciple. The heat equatio alo ejoy maximum priciple a the Laplace
Fig. 1: Streamline coordinates
 1 Equatio of Motio i Streamlie Coordiate Ai A. Soi, MIT 2.25 Advaced Fluid Mechaic Euler equatio expree the relatiohip betwee the velocity ad the preure field i ivicid flow. Writte i term of treamlie coordiate,
1 Equatio of Motio i Streamlie Coordiate Ai A. Soi, MIT 2.25 Advaced Fluid Mechaic Euler equatio expree the relatiohip betwee the velocity ad the preure field i ivicid flow. Writte i term of treamlie coordiate,
We will look for series solutions to (1) around (at most) regular singular points, which without
 ENM 511 J. L. Baai April, 1 Frobeiu Solutio to a d order ODE ear a regular igular poit Coider the ODE y 16 + P16 y 16 + Q1616 y (1) We will look for erie olutio to (1) aroud (at mot) regular igular poit,
ENM 511 J. L. Baai April, 1 Frobeiu Solutio to a d order ODE ear a regular igular poit Coider the ODE y 16 + P16 y 16 + Q1616 y (1) We will look for erie olutio to (1) aroud (at mot) regular igular poit,
Lecture 11. Course Review. (The Big Picture) G. Hovland Input-Output Limitations (Skogestad Ch. 3) Discrete. Time Domain
 MER4 Advaced Cotrol Lecture Coure Review (he ig Picture MER4 ADVANCED CONROL EMEER, 4 G. Hovlad 4 Mai heme of MER4 Frequecy Domai Aalyi (Nie Chapter Phae ad Gai Margi Iput-Output Limitatio (kogetad Ch.
MER4 Advaced Cotrol Lecture Coure Review (he ig Picture MER4 ADVANCED CONROL EMEER, 4 G. Hovlad 4 Mai heme of MER4 Frequecy Domai Aalyi (Nie Chapter Phae ad Gai Margi Iput-Output Limitatio (kogetad Ch.
High-Speed Serial Interface Circuits and Systems. Lect. 4 Phase-Locked Loop (PLL) Type 1 (Chap. 8 in Razavi)
 High-Speed Serial Iterface Circuit ad Sytem Lect. 4 Phae-Locked Loop (PLL) Type 1 (Chap. 8 i Razavi) PLL Phae lockig loop A (egative-feedback) cotrol ytem that geerate a output igal whoe phae (ad frequecy)
High-Speed Serial Iterface Circuit ad Sytem Lect. 4 Phae-Locked Loop (PLL) Type 1 (Chap. 8 i Razavi) PLL Phae lockig loop A (egative-feedback) cotrol ytem that geerate a output igal whoe phae (ad frequecy)
Brief Review of Linear System Theory
 Brief Review of Liear Sytem heory he followig iformatio i typically covered i a coure o liear ytem theory. At ISU, EE 577 i oe uch coure ad i highly recommeded for power ytem egieerig tudet. We have developed
Brief Review of Liear Sytem heory he followig iformatio i typically covered i a coure o liear ytem theory. At ISU, EE 577 i oe uch coure ad i highly recommeded for power ytem egieerig tudet. We have developed
Dynamic Response of Linear Systems
 Dyamic Respose of Liear Systems Liear System Respose Superpositio Priciple Resposes to Specific Iputs Dyamic Respose of st Order Systems Characteristic Equatio - Free Respose Stable st Order System Respose
Dyamic Respose of Liear Systems Liear System Respose Superpositio Priciple Resposes to Specific Iputs Dyamic Respose of st Order Systems Characteristic Equatio - Free Respose Stable st Order System Respose
EE Control Systems
 Copyright FL Lewis 7 All rights reserved Updated: Moday, November 1, 7 EE 4314 - Cotrol Systems Bode Plot Performace Specificatios The Bode Plot was developed by Hedrik Wade Bode i 1938 while he worked
Copyright FL Lewis 7 All rights reserved Updated: Moday, November 1, 7 EE 4314 - Cotrol Systems Bode Plot Performace Specificatios The Bode Plot was developed by Hedrik Wade Bode i 1938 while he worked
STABILITY OF THE ACTIVE VIBRATION CONTROL OF CANTILEVER BEAMS
 Iteratioal Coferece o Vibratio Problem September 9-,, Liboa, Portugal STBILITY OF THE CTIVE VIBRTIO COTROL OF CTILEVER BEMS J. Tůma, P. Šuráe, M. Mahdal VSB Techical Uierity of Otraa Czech Republic Outlie.
Iteratioal Coferece o Vibratio Problem September 9-,, Liboa, Portugal STBILITY OF THE CTIVE VIBRTIO COTROL OF CTILEVER BEMS J. Tůma, P. Šuráe, M. Mahdal VSB Techical Uierity of Otraa Czech Republic Outlie.
a 1 = 1 a a a a n n s f() s = Σ log a 1 + a a n log n sup log a n+1 + a n+2 + a n+3 log n sup () s = an /n s s = + t i
 0 Dirichlet Serie & Logarithmic Power Serie. Defiitio & Theorem Defiitio.. (Ordiary Dirichlet Serie) Whe,a,,3, are complex umber, we call the followig Ordiary Dirichlet Serie. f() a a a a 3 3 a 4 4 Note
0 Dirichlet Serie & Logarithmic Power Serie. Defiitio & Theorem Defiitio.. (Ordiary Dirichlet Serie) Whe,a,,3, are complex umber, we call the followig Ordiary Dirichlet Serie. f() a a a a 3 3 a 4 4 Note
ECM Control Engineering Dr Mustafa M Aziz (2013) SYSTEM RESPONSE
 ECM5 - Cotrol Egieerig Dr Mutafa M Aziz (3) SYSTEM RESPONSE. Itroductio. Repoe Aalyi of Firt-Order Sytem 3. Secod-Order Sytem 4. Siuoidal Repoe of the Sytem 5. Bode Diagram 6. Baic Fact About Egieerig
ECM5 - Cotrol Egieerig Dr Mutafa M Aziz (3) SYSTEM RESPONSE. Itroductio. Repoe Aalyi of Firt-Order Sytem 3. Secod-Order Sytem 4. Siuoidal Repoe of the Sytem 5. Bode Diagram 6. Baic Fact About Egieerig
ECE 422 Power System Operations & Planning 6 Small Signal Stability. Spring 2015 Instructor: Kai Sun
 ECE 4 Power Sytem Operatio & Plaig 6 Small Sigal Stability Sprig 15 Itructor: Kai Su 1 Referece Saadat Chapter 11.4 EPRI Tutorial Chapter 8 Power Ocillatio Kudur Chapter 1 Power Ocillatio The power ytem
ECE 4 Power Sytem Operatio & Plaig 6 Small Sigal Stability Sprig 15 Itructor: Kai Su 1 Referece Saadat Chapter 11.4 EPRI Tutorial Chapter 8 Power Ocillatio Kudur Chapter 1 Power Ocillatio The power ytem
Chapter #5 EEE Control Systems
 Sprig EEE Chpter #5 EEE Cotrol Sytem Deig Bed o Root Locu Chpter / Sprig EEE Deig Bed Root Locu Led Cotrol (equivlet to PD cotrol) Ued whe the tedy tte propertie of the ytem re ok but there i poor performce,
Sprig EEE Chpter #5 EEE Cotrol Sytem Deig Bed o Root Locu Chpter / Sprig EEE Deig Bed Root Locu Led Cotrol (equivlet to PD cotrol) Ued whe the tedy tte propertie of the ytem re ok but there i poor performce,
Mechatronics. Time Response & Frequency Response 2 nd -Order Dynamic System 2-Pole, Low-Pass, Active Filter
 Time Respose & Frequecy Respose d -Order Dyamic System -Pole, Low-Pass, Active Filter R 4 R 7 C 5 e i R 1 C R 3 - + R 6 - + e out Assigmet: Perform a Complete Dyamic System Ivestigatio of the Two-Pole,
Time Respose & Frequecy Respose d -Order Dyamic System -Pole, Low-Pass, Active Filter R 4 R 7 C 5 e i R 1 C R 3 - + R 6 - + e out Assigmet: Perform a Complete Dyamic System Ivestigatio of the Two-Pole,
Performance-Based Plastic Design (PBPD) Procedure
 Performace-Baed Platic Deig (PBPD) Procedure 3. Geeral A outlie of the tep-by-tep, Performace-Baed Platic Deig (PBPD) procedure follow, with detail to be dicued i ubequet ectio i thi chapter ad theoretical
Performace-Baed Platic Deig (PBPD) Procedure 3. Geeral A outlie of the tep-by-tep, Performace-Baed Platic Deig (PBPD) procedure follow, with detail to be dicued i ubequet ectio i thi chapter ad theoretical
x z Increasing the size of the sample increases the power (reduces the probability of a Type II error) when the significance level remains fixed.
 ] z-tet for the mea, μ If the P-value i a mall or maller tha a pecified value, the data are tatitically igificat at igificace level. Sigificace tet for the hypothei H 0: = 0 cocerig the ukow mea of a populatio
] z-tet for the mea, μ If the P-value i a mall or maller tha a pecified value, the data are tatitically igificat at igificace level. Sigificace tet for the hypothei H 0: = 0 cocerig the ukow mea of a populatio
Explicit scheme. Fully implicit scheme Notes. Fully implicit scheme Notes. Fully implicit scheme Notes. Notes
 Explicit cheme So far coidered a fully explicit cheme to umerically olve the diffuio equatio: T + = ( )T + (T+ + T ) () with = κ ( x) Oly table for < / Thi cheme i ometime referred to a FTCS (forward time
Explicit cheme So far coidered a fully explicit cheme to umerically olve the diffuio equatio: T + = ( )T + (T+ + T ) () with = κ ( x) Oly table for < / Thi cheme i ometime referred to a FTCS (forward time
Course Outline. Designing Control Systems. Proportional Controller. Amme 3500 : System Dynamics and Control. Root Locus. Dr. Stefan B.
 Amme 3500 : System Dyamics ad Cotrol Root Locus Course Outlie Week Date Cotet Assigmet Notes Mar Itroductio 8 Mar Frequecy Domai Modellig 3 5 Mar Trasiet Performace ad the s-plae 4 Mar Block Diagrams Assig
Amme 3500 : System Dyamics ad Cotrol Root Locus Course Outlie Week Date Cotet Assigmet Notes Mar Itroductio 8 Mar Frequecy Domai Modellig 3 5 Mar Trasiet Performace ad the s-plae 4 Mar Block Diagrams Assig
1 Routh Array: 15 points
 EE C28 / ME34 Problem Set 3 Solution Fall 2 Routh Array: 5 point Conider the ytem below, with D() k(+), w(t), G() +2, and H y() 2 ++2 2(+). Find the cloed loop tranfer function Y () R(), and range of k
EE C28 / ME34 Problem Set 3 Solution Fall 2 Routh Array: 5 point Conider the ytem below, with D() k(+), w(t), G() +2, and H y() 2 ++2 2(+). Find the cloed loop tranfer function Y () R(), and range of k
Delhi Noida Bhopal Hyderabad Jaipur Lucknow Indore Pune Bhubaneswar Kolkata Patna Web: Ph:
 Serial :. PT_EE_A+C_Control Sytem_798 Delhi Noida Bhopal Hyderabad Jaipur Lucknow Indore Pune Bhubanewar olkata Patna Web: E-mail: info@madeeay.in Ph: -4546 CLASS TEST 8-9 ELECTRICAL ENGINEERING Subject
Serial :. PT_EE_A+C_Control Sytem_798 Delhi Noida Bhopal Hyderabad Jaipur Lucknow Indore Pune Bhubanewar olkata Patna Web: E-mail: info@madeeay.in Ph: -4546 CLASS TEST 8-9 ELECTRICAL ENGINEERING Subject
Chapter 2 Feedback Control Theory Continued
 Chapter Feedback Cotrol Theor Cotiued. Itroductio I the previous chapter, the respose characteristic of simple first ad secod order trasfer fuctios were studied. It was show that first order trasfer fuctio,
Chapter Feedback Cotrol Theor Cotiued. Itroductio I the previous chapter, the respose characteristic of simple first ad secod order trasfer fuctios were studied. It was show that first order trasfer fuctio,
MAHALAKSHMI ENGINEERING COLLEGE TIRUCHIRAPALLI
 MAHALASHMI ENGINEERING COLLEGE TIRUCHIRAPALLI-63. QUESTION BAN DEPARTMENT: ECE SUBJECT CODE: EC55 SEMESTER - III SUBJECT NAME: CONTROL SYSTEMS UNIT- SYSTEMS AND THEIR REPRESENTATION. Write Mao gai formula.
MAHALASHMI ENGINEERING COLLEGE TIRUCHIRAPALLI-63. QUESTION BAN DEPARTMENT: ECE SUBJECT CODE: EC55 SEMESTER - III SUBJECT NAME: CONTROL SYSTEMS UNIT- SYSTEMS AND THEIR REPRESENTATION. Write Mao gai formula.
Root Locus Contents. Root locus, sketching algorithm. Root locus, examples. Root locus, proofs. Root locus, control examples
 Root Locu Content Root locu, ketching algorithm Root locu, example Root locu, proof Root locu, control example Root locu, influence of zero and pole Root locu, lead lag controller deign 9 Spring ME45 -
Root Locu Content Root locu, ketching algorithm Root locu, example Root locu, proof Root locu, control example Root locu, influence of zero and pole Root locu, lead lag controller deign 9 Spring ME45 -
1it is said to be overdamped. When 1, the roots of
 Homework 3 AERE573 Fall 8 Due /8(M) SOLUTIO PROBLEM (4pt) Coider a D order uderdamped tem trafer fuctio H( ) ratio The deomiator i the tem characteritic polomial P( ) (a)(5pt) Ue the quadratic formula,
Homework 3 AERE573 Fall 8 Due /8(M) SOLUTIO PROBLEM (4pt) Coider a D order uderdamped tem trafer fuctio H( ) ratio The deomiator i the tem characteritic polomial P( ) (a)(5pt) Ue the quadratic formula,
The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j
![The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j](/thumbs/82/85448534.jpg) The -Trasform 7. Itroductio Geeralie the complex siusoidal represetatio offered by DTFT to a represetatio of complex expoetial sigals. Obtai more geeral characteristics for discrete-time LTI systems. 7.
The -Trasform 7. Itroductio Geeralie the complex siusoidal represetatio offered by DTFT to a represetatio of complex expoetial sigals. Obtai more geeral characteristics for discrete-time LTI systems. 7.
Erick L. Oberstar Fall 2001 Project: Sidelobe Canceller & GSC 1. Advanced Digital Signal Processing Sidelobe Canceller (Beam Former)
 Erick L. Obertar Fall 001 Project: Sidelobe Caceller & GSC 1 Advaced Digital Sigal Proceig Sidelobe Caceller (Beam Former) Erick L. Obertar 001 Erick L. Obertar Fall 001 Project: Sidelobe Caceller & GSC
Erick L. Obertar Fall 001 Project: Sidelobe Caceller & GSC 1 Advaced Digital Sigal Proceig Sidelobe Caceller (Beam Former) Erick L. Obertar 001 Erick L. Obertar Fall 001 Project: Sidelobe Caceller & GSC
3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,
![3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense, 3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,](/thumbs/82/85448051.jpg) 3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
REVIEW OF SIMPLE LINEAR REGRESSION SIMPLE LINEAR REGRESSION
 REVIEW OF SIMPLE LINEAR REGRESSION SIMPLE LINEAR REGRESSION I liear regreio, we coider the frequecy ditributio of oe variable (Y) at each of everal level of a ecod variable (X). Y i kow a the depedet variable.
REVIEW OF SIMPLE LINEAR REGRESSION SIMPLE LINEAR REGRESSION I liear regreio, we coider the frequecy ditributio of oe variable (Y) at each of everal level of a ecod variable (X). Y i kow a the depedet variable.
ELEC 372 LECTURE NOTES, WEEK 1 Dr. Amir G. Aghdam Concordia University
 EEC 37 ECTURE NOTES, WEEK Dr Amir G Aghdam Cocordia Uiverity Part of thee ote are adapted from the material i the followig referece: Moder Cotrol Sytem by Richard C Dorf ad Robert H Bihop, Pretice Hall
EEC 37 ECTURE NOTES, WEEK Dr Amir G Aghdam Cocordia Uiverity Part of thee ote are adapted from the material i the followig referece: Moder Cotrol Sytem by Richard C Dorf ad Robert H Bihop, Pretice Hall
Chapter 7: The z-transform. Chih-Wei Liu
 Chapter 7: The -Trasform Chih-Wei Liu Outlie Itroductio The -Trasform Properties of the Regio of Covergece Properties of the -Trasform Iversio of the -Trasform The Trasfer Fuctio Causality ad Stability
Chapter 7: The -Trasform Chih-Wei Liu Outlie Itroductio The -Trasform Properties of the Regio of Covergece Properties of the -Trasform Iversio of the -Trasform The Trasfer Fuctio Causality ad Stability
Heat Equation: Maximum Principles
 Heat Equatio: Maximum Priciple Nov. 9, 0 I thi lecture we will dicu the maximum priciple ad uiquee of olutio for the heat equatio.. Maximum priciple. The heat equatio alo ejoy maximum priciple a the Laplace
Heat Equatio: Maximum Priciple Nov. 9, 0 I thi lecture we will dicu the maximum priciple ad uiquee of olutio for the heat equatio.. Maximum priciple. The heat equatio alo ejoy maximum priciple a the Laplace
Control Systems Engineering ( Chapter 7. Steady-State Errors ) Prof. Kwang-Chun Ho Tel: Fax:
 Control Sytem Engineering ( Chapter 7. Steady-State Error Prof. Kwang-Chun Ho kwangho@hanung.ac.kr Tel: 0-760-453 Fax:0-760-4435 Introduction In thi leon, you will learn the following : How to find the
Control Sytem Engineering ( Chapter 7. Steady-State Error Prof. Kwang-Chun Ho kwangho@hanung.ac.kr Tel: 0-760-453 Fax:0-760-4435 Introduction In thi leon, you will learn the following : How to find the
Homework 12 Solution - AME30315, Spring 2013
 Homework 2 Solution - AME335, Spring 23 Problem :[2 pt] The Aerotech AGS 5 i a linear motor driven XY poitioning ytem (ee attached product heet). A friend of mine, through careful experimentation, identified
Homework 2 Solution - AME335, Spring 23 Problem :[2 pt] The Aerotech AGS 5 i a linear motor driven XY poitioning ytem (ee attached product heet). A friend of mine, through careful experimentation, identified
EE/ME/AE324: Dynamical Systems. Chapter 8: Transfer Function Analysis
 EE/ME/AE34: Dynamical Sytem Chapter 8: Tranfer Function Analyi The Sytem Tranfer Function Conider the ytem decribed by the nth-order I/O eqn.: ( n) ( n 1) ( m) y + a y + + a y = b u + + bu n 1 0 m 0 Taking
EE/ME/AE34: Dynamical Sytem Chapter 8: Tranfer Function Analyi The Sytem Tranfer Function Conider the ytem decribed by the nth-order I/O eqn.: ( n) ( n 1) ( m) y + a y + + a y = b u + + bu n 1 0 m 0 Taking
Isolated Word Recogniser
 Lecture 5 Iolated Word Recogitio Hidde Markov Model of peech State traitio ad aligmet probabilitie Searchig all poible aligmet Dyamic Programmig Viterbi Aligmet Iolated Word Recogitio 8. Iolated Word Recogier
Lecture 5 Iolated Word Recogitio Hidde Markov Model of peech State traitio ad aligmet probabilitie Searchig all poible aligmet Dyamic Programmig Viterbi Aligmet Iolated Word Recogitio 8. Iolated Word Recogier
ELEC 372 LECTURE NOTES, WEEK 6 Dr. Amir G. Aghdam Concordia University
 ELEC 37 LECTURE NOTES, WEE 6 Dr mir G ghdm Cocordi Uiverity Prt of thee ote re dpted from the mteril i the followig referece: Moder Cotrol Sytem by Richrd C Dorf d Robert H Bihop, Pretice Hll Feedbck Cotrol
ELEC 37 LECTURE NOTES, WEE 6 Dr mir G ghdm Cocordi Uiverity Prt of thee ote re dpted from the mteril i the followig referece: Moder Cotrol Sytem by Richrd C Dorf d Robert H Bihop, Pretice Hll Feedbck Cotrol
Comments on Discussion Sheet 18 and Worksheet 18 ( ) An Introduction to Hypothesis Testing
 Commet o Dicuio Sheet 18 ad Workheet 18 ( 9.5-9.7) A Itroductio to Hypothei Tetig Dicuio Sheet 18 A Itroductio to Hypothei Tetig We have tudied cofidece iterval for a while ow. Thee are method that allow
Commet o Dicuio Sheet 18 ad Workheet 18 ( 9.5-9.7) A Itroductio to Hypothei Tetig Dicuio Sheet 18 A Itroductio to Hypothei Tetig We have tudied cofidece iterval for a while ow. Thee are method that allow
Adaptive control design for a Mimo chemical reactor
 Automatio, Cotrol ad Itelliget Sytem 013; 1(3): 64-70 Publihed olie July 10, 013 (http://www.ciecepublihiggroup.com/j/aci) doi: 10.11648/j.aci.0130103.15 Adaptive cotrol deig for a Mimo chemical reactor
Automatio, Cotrol ad Itelliget Sytem 013; 1(3): 64-70 Publihed olie July 10, 013 (http://www.ciecepublihiggroup.com/j/aci) doi: 10.11648/j.aci.0130103.15 Adaptive cotrol deig for a Mimo chemical reactor
EE 508 Lecture 6. Dead Networks Scaling, Normalization and Transformations
 EE 508 Lecture 6 Dead Network Scalig, Normalizatio ad Traformatio Filter Cocept ad Termiology 2-d order polyomial characterizatio Biquadratic Factorizatio Op Amp Modelig Stability ad Itability Roll-off
EE 508 Lecture 6 Dead Network Scalig, Normalizatio ad Traformatio Filter Cocept ad Termiology 2-d order polyomial characterizatio Biquadratic Factorizatio Op Amp Modelig Stability ad Itability Roll-off
Statistical Inference Procedures
 Statitical Iferece Procedure Cofidece Iterval Hypothei Tet Statitical iferece produce awer to pecific quetio about the populatio of iteret baed o the iformatio i a ample. Iferece procedure mut iclude a
Statitical Iferece Procedure Cofidece Iterval Hypothei Tet Statitical iferece produce awer to pecific quetio about the populatio of iteret baed o the iformatio i a ample. Iferece procedure mut iclude a
Weak formulation and Lagrange equations of motion
 Chapter 4 Weak formulatio ad Lagrage equatio of motio A mot commo approach to tudy tructural dyamic i the ue of the Lagrage equatio of motio. Thee are obtaied i thi chapter tartig from the Cauchy equatio
Chapter 4 Weak formulatio ad Lagrage equatio of motio A mot commo approach to tudy tructural dyamic i the ue of the Lagrage equatio of motio. Thee are obtaied i thi chapter tartig from the Cauchy equatio
Complex Numbers Solutions
 Complex Numbers Solutios Joseph Zoller February 7, 06 Solutios. (009 AIME I Problem ) There is a complex umber with imagiary part 64 ad a positive iteger such that Fid. [Solutio: 697] 4i + + 4i. 4i 4i
Complex Numbers Solutios Joseph Zoller February 7, 06 Solutios. (009 AIME I Problem ) There is a complex umber with imagiary part 64 ad a positive iteger such that Fid. [Solutio: 697] 4i + + 4i. 4i 4i
Class 07 Time domain analysis Part II 2 nd order systems
 Class 07 Time domai aalysis Part II d order systems Time domai aalysis d order systems iput S output Secod order systems of the type α G(s) as + bs + c Time domai aalysis d order systems iput S α as +
Class 07 Time domai aalysis Part II d order systems Time domai aalysis d order systems iput S output Secod order systems of the type α G(s) as + bs + c Time domai aalysis d order systems iput S α as +
Problem 1. Problem Engineering Dynamics Problem Set 9--Solution. Find the equation of motion for the system shown with respect to:
 2.003 Egieerig Dyamics Problem Set 9--Solutio Problem 1 Fid the equatio of motio for the system show with respect to: a) Zero sprig force positio. Draw the appropriate free body diagram. b) Static equilibrium
2.003 Egieerig Dyamics Problem Set 9--Solutio Problem 1 Fid the equatio of motio for the system show with respect to: a) Zero sprig force positio. Draw the appropriate free body diagram. b) Static equilibrium
x c the remainder is Pc ().
 Algebra, Polyomial ad Ratioal Fuctios Page 1 K.Paulk Notes Chapter 3, Sectio 3.1 to 3.4 Summary Sectio Theorem Notes 3.1 Zeros of a Fuctio Set the fuctio to zero ad solve for x. The fuctio is zero at these
Algebra, Polyomial ad Ratioal Fuctios Page 1 K.Paulk Notes Chapter 3, Sectio 3.1 to 3.4 Summary Sectio Theorem Notes 3.1 Zeros of a Fuctio Set the fuctio to zero ad solve for x. The fuctio is zero at these
EE Control Systems LECTURE 14
 Updated: Tueday, March 3, 999 EE 434 - Control Sytem LECTURE 4 Copyright FL Lewi 999 All right reerved ROOT LOCUS DESIGN TECHNIQUE Suppoe the cloed-loop tranfer function depend on a deign parameter k We
Updated: Tueday, March 3, 999 EE 434 - Control Sytem LECTURE 4 Copyright FL Lewi 999 All right reerved ROOT LOCUS DESIGN TECHNIQUE Suppoe the cloed-loop tranfer function depend on a deign parameter k We
Gain-scheduling of Acceleration Estimator for Low-velocity Measurement with Encoders
 Jue -5, INTEX, Gyeoggi-Do, orea Gai-chedulig of Acceleratio Etimator for Low-velocity Meauremet with Ecoder Seug-Woo So, Sag-Hu Lee ad Jog-Sug Hur Electro-Mechaical Reearch Ititute, Hyudai Heavy Idutrie
Jue -5, INTEX, Gyeoggi-Do, orea Gai-chedulig of Acceleratio Etimator for Low-velocity Meauremet with Ecoder Seug-Woo So, Sag-Hu Lee ad Jog-Sug Hur Electro-Mechaical Reearch Ititute, Hyudai Heavy Idutrie
Zeta-reciprocal Extended reciprocal zeta function and an alternate formulation of the Riemann hypothesis By M. Aslam Chaudhry
 Zeta-reciprocal Eteded reciprocal zeta fuctio ad a alterate formulatio of the Riema hypothei By. Alam Chaudhry Departmet of athematical Sciece, Kig Fahd Uiverity of Petroleum ad ieral Dhahra 36, Saudi
Zeta-reciprocal Eteded reciprocal zeta fuctio ad a alterate formulatio of the Riema hypothei By. Alam Chaudhry Departmet of athematical Sciece, Kig Fahd Uiverity of Petroleum ad ieral Dhahra 36, Saudi
Digital Control System
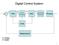 Digital Control Sytem - A D D A Micro ADC DAC Proceor Correction Element Proce Clock Meaurement A: Analog D: Digital Continuou Controller and Digital Control Rt - c Plant yt Continuou Controller Digital
Digital Control Sytem - A D D A Micro ADC DAC Proceor Correction Element Proce Clock Meaurement A: Analog D: Digital Continuou Controller and Digital Control Rt - c Plant yt Continuou Controller Digital
LECTURE 13 SIMULTANEOUS EQUATIONS
 NOVEMBER 5, 26 Demad-upply ytem LETURE 3 SIMULTNEOUS EQUTIONS I thi lecture, we dicu edogeeity problem that arie due to imultaeity, i.e. the left-had ide variable ad ome of the right-had ide variable are
NOVEMBER 5, 26 Demad-upply ytem LETURE 3 SIMULTNEOUS EQUTIONS I thi lecture, we dicu edogeeity problem that arie due to imultaeity, i.e. the left-had ide variable ad ome of the right-had ide variable are
Feedback Control Systems (FCS)
 Feedback Control Sytem (FCS) Lecture19-20 Routh-Herwitz Stability Criterion Dr. Imtiaz Huain email: imtiaz.huain@faculty.muet.edu.pk URL :http://imtiazhuainkalwar.weebly.com/ Stability of Higher Order
Feedback Control Sytem (FCS) Lecture19-20 Routh-Herwitz Stability Criterion Dr. Imtiaz Huain email: imtiaz.huain@faculty.muet.edu.pk URL :http://imtiazhuainkalwar.weebly.com/ Stability of Higher Order
2.004 Dynamics and Control II Spring 2008
 MIT OpeCourseWare http://ocw.mit.edu 2.004 Dyamics ad Cotrol II Sprig 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. Massachusetts Istitute of Techology
MIT OpeCourseWare http://ocw.mit.edu 2.004 Dyamics ad Cotrol II Sprig 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. Massachusetts Istitute of Techology
COMPARISONS INVOLVING TWO SAMPLE MEANS. Two-tail tests have these types of hypotheses: H A : 1 2
 Tetig Hypothee COMPARISONS INVOLVING TWO SAMPLE MEANS Two type of hypothee:. H o : Null Hypothei - hypothei of o differece. or 0. H A : Alterate Hypothei hypothei of differece. or 0 Two-tail v. Oe-tail
Tetig Hypothee COMPARISONS INVOLVING TWO SAMPLE MEANS Two type of hypothee:. H o : Null Hypothei - hypothei of o differece. or 0. H A : Alterate Hypothei hypothei of differece. or 0 Two-tail v. Oe-tail
ME 375 FINAL EXAM Wednesday, May 6, 2009
 ME 375 FINAL EXAM Wedneday, May 6, 9 Diviion Meckl :3 / Adam :3 (circle one) Name_ Intruction () Thi i a cloed book examination, but you are allowed three ingle-ided 8.5 crib heet. A calculator i NOT allowed.
ME 375 FINAL EXAM Wedneday, May 6, 9 Diviion Meckl :3 / Adam :3 (circle one) Name_ Intruction () Thi i a cloed book examination, but you are allowed three ingle-ided 8.5 crib heet. A calculator i NOT allowed.
Massachusetts Institute of Technology Dynamics and Control II
 I E Maachuett Intitute of Technology Department of Mechanical Engineering 2.004 Dynamic and Control II Laboratory Seion 5: Elimination of Steady-State Error Uing Integral Control Action 1 Laboratory Objective:
I E Maachuett Intitute of Technology Department of Mechanical Engineering 2.004 Dynamic and Control II Laboratory Seion 5: Elimination of Steady-State Error Uing Integral Control Action 1 Laboratory Objective:
EE 508 Lecture 6. Scaling, Normalization and Transformation
 EE 508 Lecture 6 Scalig, Normalizatio ad Traformatio Review from Lat Time Dead Network X IN T X OUT T X OUT N T = D D The dead etwork of ay liear circuit i obtaied by ettig ALL idepedet ource to zero.
EE 508 Lecture 6 Scalig, Normalizatio ad Traformatio Review from Lat Time Dead Network X IN T X OUT T X OUT N T = D D The dead etwork of ay liear circuit i obtaied by ettig ALL idepedet ource to zero.
STUDENT S t-distribution AND CONFIDENCE INTERVALS OF THE MEAN ( )
 STUDENT S t-distribution AND CONFIDENCE INTERVALS OF THE MEAN Suppoe that we have a ample of meaured value x1, x, x3,, x of a igle uow quatity. Aumig that the meauremet are draw from a ormal ditributio
STUDENT S t-distribution AND CONFIDENCE INTERVALS OF THE MEAN Suppoe that we have a ample of meaured value x1, x, x3,, x of a igle uow quatity. Aumig that the meauremet are draw from a ormal ditributio
Lecture 8 - SISO Loop Design
 Lecture 8 - SISO Loop Deign Deign approache, given pec Loophaping: in-band and out-of-band pec Fundamental deign limitation for the loop Gorinevky Control Engineering 8-1 Modern Control Theory Appy reult
Lecture 8 - SISO Loop Deign Deign approache, given pec Loophaping: in-band and out-of-band pec Fundamental deign limitation for the loop Gorinevky Control Engineering 8-1 Modern Control Theory Appy reult
FREE VIBRATION RESPONSE OF A SYSTEM WITH COULOMB DAMPING
 Mechaical Vibratios FREE VIBRATION RESPONSE OF A SYSTEM WITH COULOMB DAMPING A commo dampig mechaism occurrig i machies is caused by slidig frictio or dry frictio ad is called Coulomb dampig. Coulomb dampig
Mechaical Vibratios FREE VIBRATION RESPONSE OF A SYSTEM WITH COULOMB DAMPING A commo dampig mechaism occurrig i machies is caused by slidig frictio or dry frictio ad is called Coulomb dampig. Coulomb dampig
ON THE SCALE PARAMETER OF EXPONENTIAL DISTRIBUTION
 Review of the Air Force Academy No. (34)/7 ON THE SCALE PARAMETER OF EXPONENTIAL DISTRIBUTION Aca Ileaa LUPAŞ Military Techical Academy, Bucharet, Romaia (lua_a@yahoo.com) DOI:.96/84-938.7.5..6 Abtract:
Review of the Air Force Academy No. (34)/7 ON THE SCALE PARAMETER OF EXPONENTIAL DISTRIBUTION Aca Ileaa LUPAŞ Military Techical Academy, Bucharet, Romaia (lua_a@yahoo.com) DOI:.96/84-938.7.5..6 Abtract:
ME 410 MECHANICAL ENGINEERING SYSTEMS LABORATORY REGRESSION ANALYSIS
 ME 40 MECHANICAL ENGINEERING REGRESSION ANALYSIS Regreio problem deal with the relatiohip betwee the frequec ditributio of oe (depedet) variable ad aother (idepedet) variable() which i (are) held fied
ME 40 MECHANICAL ENGINEERING REGRESSION ANALYSIS Regreio problem deal with the relatiohip betwee the frequec ditributio of oe (depedet) variable ad aother (idepedet) variable() which i (are) held fied
Definition of z-transform.
 - Trasforms Frequecy domai represetatios of discretetime sigals ad LTI discrete-time systems are made possible with the use of DTFT. However ot all discrete-time sigals e.g. uit step sequece are guarateed
- Trasforms Frequecy domai represetatios of discretetime sigals ad LTI discrete-time systems are made possible with the use of DTFT. However ot all discrete-time sigals e.g. uit step sequece are guarateed
Applied Mathematical Sciences, Vol. 9, 2015, no. 3, HIKARI Ltd,
 Applied Mathematical Sciece Vol 9 5 o 3 7 - HIKARI Ltd wwwm-hiaricom http://dxdoiorg/988/am54884 O Poitive Defiite Solutio of the Noliear Matrix Equatio * A A I Saa'a A Zarea* Mathematical Sciece Departmet
Applied Mathematical Sciece Vol 9 5 o 3 7 - HIKARI Ltd wwwm-hiaricom http://dxdoiorg/988/am54884 O Poitive Defiite Solutio of the Noliear Matrix Equatio * A A I Saa'a A Zarea* Mathematical Sciece Departmet
Homework 7 Solution - AME 30315, Spring s 2 + 2s (s 2 + 2s + 4)(s + 20)
 1 Homework 7 Solution - AME 30315, Spring 2015 Problem 1 [10/10 pt] Ue partial fraction expanion to compute x(t) when X 1 () = 4 2 + 2 + 4 Ue partial fraction expanion to compute x(t) when X 2 () = ( )
1 Homework 7 Solution - AME 30315, Spring 2015 Problem 1 [10/10 pt] Ue partial fraction expanion to compute x(t) when X 1 () = 4 2 + 2 + 4 Ue partial fraction expanion to compute x(t) when X 2 () = ( )
EE 4343 Lab#4 PID Control Design of Rigid Bodies
 EE 44 Lab#4 PID Cotrol Desig of Rigid Bodies Prepared by: Stacy Caso E-mail: scaso@arri.uta.edu Updated: July 9, 1999 This lab demostrates some key cocepts associated with proportioal plus derivative (PD
EE 44 Lab#4 PID Cotrol Desig of Rigid Bodies Prepared by: Stacy Caso E-mail: scaso@arri.uta.edu Updated: July 9, 1999 This lab demostrates some key cocepts associated with proportioal plus derivative (PD
Professor: Mihnea UDREA DIGITAL SIGNAL PROCESSING. Grading: Web: MOODLE. 1. Introduction. General information
 Geeral iformatio DIGITL SIGL PROCESSIG Profeor: ihea UDRE B29 mihea@comm.pub.ro Gradig: Laboratory: 5% Proect: 5% Tet: 2% ial exam : 5% Coure quiz: ±% Web: www.electroica.pub.ro OODLE 2 alog igal proceig
Geeral iformatio DIGITL SIGL PROCESSIG Profeor: ihea UDRE B29 mihea@comm.pub.ro Gradig: Laboratory: 5% Proect: 5% Tet: 2% ial exam : 5% Coure quiz: ±% Web: www.electroica.pub.ro OODLE 2 alog igal proceig
Assignment 1 - Solutions. ECSE 420 Parallel Computing Fall November 2, 2014
 Aigmet - Solutio ECSE 420 Parallel Computig Fall 204 ovember 2, 204. (%) Decribe briefly the followig term, expoe their caue, ad work-aroud the idutry ha udertake to overcome their coequece: (i) Memory
Aigmet - Solutio ECSE 420 Parallel Computig Fall 204 ovember 2, 204. (%) Decribe briefly the followig term, expoe their caue, ad work-aroud the idutry ha udertake to overcome their coequece: (i) Memory
Chapter #2 EEE Subsea Control and Communication Systems
 EEE 87 Chpter # EEE 87 Sube Cotrol d Commuictio Sytem Trfer fuctio Pole loctio d -ple Time domi chrcteritic Extr pole d zero Chpter /8 EEE 87 Trfer fuctio Lplce Trform Ued oly o LTI ytem Differetil expreio
EEE 87 Chpter # EEE 87 Sube Cotrol d Commuictio Sytem Trfer fuctio Pole loctio d -ple Time domi chrcteritic Extr pole d zero Chpter /8 EEE 87 Trfer fuctio Lplce Trform Ued oly o LTI ytem Differetil expreio
Chapter 4 : Laplace Transform
 4. Itroductio Laplace trasform is a alterative to solve the differetial equatio by the complex frequecy domai ( s = σ + jω), istead of the usual time domai. The DE ca be easily trasformed ito a algebraic
4. Itroductio Laplace trasform is a alterative to solve the differetial equatio by the complex frequecy domai ( s = σ + jω), istead of the usual time domai. The DE ca be easily trasformed ito a algebraic
MAT 271 Project: Partial Fractions for certain rational functions
 MAT 7 Project: Partial Fractios for certai ratioal fuctios Prerequisite kowledge: partial fractios from MAT 7, a very good commad of factorig ad complex umbers from Precalculus. To complete this project,
MAT 7 Project: Partial Fractios for certai ratioal fuctios Prerequisite kowledge: partial fractios from MAT 7, a very good commad of factorig ad complex umbers from Precalculus. To complete this project,
Digital Control System
 Digital Control Sytem Summary # he -tranform play an important role in digital control and dicrete ignal proceing. he -tranform i defined a F () f(k) k () A. Example Conider the following equence: f(k)
Digital Control Sytem Summary # he -tranform play an important role in digital control and dicrete ignal proceing. he -tranform i defined a F () f(k) k () A. Example Conider the following equence: f(k)
Reliable Decentralized PID Stabilization of MIMO Systems
 Proceedig of the 6 America Cotrol Coferece Mieapoli, Mieota, USA, Jue 4-6, 6 FrB.5 Reliable Decetralized PID Stabilizatio of MIMO Sytem A. N. Mete, A. N. Güdeş, ad A. N. Palazoğlu Abtract Sytematic method
Proceedig of the 6 America Cotrol Coferece Mieapoli, Mieota, USA, Jue 4-6, 6 FrB.5 Reliable Decetralized PID Stabilizatio of MIMO Sytem A. N. Mete, A. N. Güdeş, ad A. N. Palazoğlu Abtract Sytematic method
732 Appendix E: Previous EEE480 Exams. Rules: One sheet permitted, calculators permitted. GWC 352,
 732 Aedix E: Previous EEE0 Exams EEE0 Exam 2, Srig 2008 A.A. Rodriguez Rules: Oe 8. sheet ermitted, calculators ermitted. GWC 32, 9-372 Problem Aalysis of a Feedback System Cosider the feedback system
732 Aedix E: Previous EEE0 Exams EEE0 Exam 2, Srig 2008 A.A. Rodriguez Rules: Oe 8. sheet ermitted, calculators ermitted. GWC 32, 9-372 Problem Aalysis of a Feedback System Cosider the feedback system
376 CHAPTER 6. THE FREQUENCY-RESPONSE DESIGN METHOD. D(s) = we get the compensated system with :
 376 CHAPTER 6. THE FREQUENCY-RESPONSE DESIGN METHOD Therefore by applying the lead compenator with ome gain adjutment : D() =.12 4.5 +1 9 +1 we get the compenated ytem with : PM =65, ω c = 22 rad/ec, o
376 CHAPTER 6. THE FREQUENCY-RESPONSE DESIGN METHOD Therefore by applying the lead compenator with ome gain adjutment : D() =.12 4.5 +1 9 +1 we get the compenated ytem with : PM =65, ω c = 22 rad/ec, o
Lecture 4. Chapter 11 Nise. Controller Design via Frequency Response. G. Hovland 2004
 METR4200 Advanced Control Lecture 4 Chapter Nie Controller Deign via Frequency Repone G. Hovland 2004 Deign Goal Tranient repone via imple gain adjutment Cacade compenator to improve teady-tate error Cacade
METR4200 Advanced Control Lecture 4 Chapter Nie Controller Deign via Frequency Repone G. Hovland 2004 Deign Goal Tranient repone via imple gain adjutment Cacade compenator to improve teady-tate error Cacade
STRONG DEVIATION THEOREMS FOR THE SEQUENCE OF CONTINUOUS RANDOM VARIABLES AND THE APPROACH OF LAPLACE TRANSFORM
 Joural of Statitic: Advace i Theory ad Applicatio Volume, Number, 9, Page 35-47 STRONG DEVIATION THEORES FOR THE SEQUENCE OF CONTINUOUS RANDO VARIABLES AND THE APPROACH OF LAPLACE TRANSFOR School of athematic
Joural of Statitic: Advace i Theory ad Applicatio Volume, Number, 9, Page 35-47 STRONG DEVIATION THEORES FOR THE SEQUENCE OF CONTINUOUS RANDO VARIABLES AND THE APPROACH OF LAPLACE TRANSFOR School of athematic
The Root Locus Method
 The Root Locu Method MEM 355 Performance Enhancement of Dynamical Sytem Harry G. Kwatny Department of Mechanical Engineering & Mechanic Drexel Univerity Outline The root locu method wa introduced by Evan
The Root Locu Method MEM 355 Performance Enhancement of Dynamical Sytem Harry G. Kwatny Department of Mechanical Engineering & Mechanic Drexel Univerity Outline The root locu method wa introduced by Evan
MODERN CONTROL SYSTEMS
 MODERN CONTROL SYSTEMS Lecture 1 Root Locu Emam Fathy Department of Electrical and Control Engineering email: emfmz@aat.edu http://www.aat.edu/cv.php?dip_unit=346&er=68525 1 Introduction What i root locu?
MODERN CONTROL SYSTEMS Lecture 1 Root Locu Emam Fathy Department of Electrical and Control Engineering email: emfmz@aat.edu http://www.aat.edu/cv.php?dip_unit=346&er=68525 1 Introduction What i root locu?
Dr. Seeler Department of Mechanical Engineering Fall 2009 Lafayette College ME 479: Control Systems and Mechatronics Design and Analysis
 Dr. Seeler Departmet of Mechaical Egieerig Fall 009 Lafayette College ME 479: Cotrol Systems ad Mechatroics Desig ad Aalysis Lab 0: Review of the First ad Secod Order Step Resposes The followig remarks
Dr. Seeler Departmet of Mechaical Egieerig Fall 009 Lafayette College ME 479: Cotrol Systems ad Mechatroics Desig ad Aalysis Lab 0: Review of the First ad Secod Order Step Resposes The followig remarks
Given the following circuit with unknown initial capacitor voltage v(0): X(s) Immediately, we know that the transfer function H(s) is
 EE 4G Note: Chapter 6 Intructor: Cheung More about ZSR and ZIR. Finding unknown initial condition: Given the following circuit with unknown initial capacitor voltage v0: F v0/ / Input xt 0Ω Output yt -
EE 4G Note: Chapter 6 Intructor: Cheung More about ZSR and ZIR. Finding unknown initial condition: Given the following circuit with unknown initial capacitor voltage v0: F v0/ / Input xt 0Ω Output yt -
Root Locus Diagram. Root loci: The portion of root locus when k assume positive values: that is 0
 Objective Root Locu Diagram Upon completion of thi chapter you will be able to: Plot the Root Locu for a given Tranfer Function by varying gain of the ytem, Analye the tability of the ytem from the root
Objective Root Locu Diagram Upon completion of thi chapter you will be able to: Plot the Root Locu for a given Tranfer Function by varying gain of the ytem, Analye the tability of the ytem from the root
MEM 355 Performance Enhancement of Dynamical Systems Root Locus Analysis
 MEM 355 Performance Enhancement of Dynamical Sytem Root Locu Analyi Harry G. Kwatny Department of Mechanical Engineering & Mechanic Drexel Univerity Outline The root locu method wa introduced by Evan in
MEM 355 Performance Enhancement of Dynamical Sytem Root Locu Analyi Harry G. Kwatny Department of Mechanical Engineering & Mechanic Drexel Univerity Outline The root locu method wa introduced by Evan in
TR/46 OCTOBER THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION A. TALBOT
 TR/46 OCTOBER 974 THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION by A. TALBOT .. Itroductio. A problem i approximatio theory o which I have recetly worked [] required for its solutio a proof that the
TR/46 OCTOBER 974 THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION by A. TALBOT .. Itroductio. A problem i approximatio theory o which I have recetly worked [] required for its solutio a proof that the
Chapter 7, Solution 1C.
 hapter 7, Solutio 1. he velocity of the fluid relative to the immered olid body ufficietly far away from a body i called the free-tream velocity,. he uptream or approach velocity i the velocity of the
hapter 7, Solutio 1. he velocity of the fluid relative to the immered olid body ufficietly far away from a body i called the free-tream velocity,. he uptream or approach velocity i the velocity of the
1the 1it is said to be overdamped. When 1, the roots of
 Homework 3 AERE573 Fall 08 Due 0/8(M) ame PROBLEM (40pts) Cosider a D order uderdamped system trasfer fuctio H( s) s ratio 0 The deomiator is the system characteristic polyomial P( s) s s (a)(5pts) Use
Homework 3 AERE573 Fall 08 Due 0/8(M) ame PROBLEM (40pts) Cosider a D order uderdamped system trasfer fuctio H( s) s ratio 0 The deomiator is the system characteristic polyomial P( s) s s (a)(5pts) Use
