On Fractional Operational Calculus pertaining to the product of H- functions
|
|
|
- Eustace Ray
- 6 years ago
- Views:
Transcription
1 nenonl eh ounl of Enneen n ehnolo RE e-ssn: Volume: 2 ue: 3 une-25 wwwene -SSN: On Fonl Oeonl Clulu enn o he ou of - funon D VBL Chu, C A 2 Demen of hem, Unve of Rhn, u-3255, n E-ml : vl@hooom 2 Demen of hem, ov o ue Collee, Neemuh E-ml: of76@mlom *** A- he mn m of h e o on ome eul ln wo fonl nel oeo of Olhm n Sne [6] on he ou -funon of one vle n -funon of evel omlex vle he fonl nel fomule n -funon en hee e n om fom n n nue Some nown n new eul hve een evlue n ffeen vlue of mee Fo e of lluon, we menon hee ome el e of ou mn eul e wo n he: Fonl nel oeo, ulvle -funon, Fox -funon hem Sue Clfon 2 : 26A33, 33C7 NRODUCON We noun en efnon: he ee eeenon of he Fox -funon,n, e E f F,! F Whee f f F F N e N e E E n f F One of he el e of -funon [5,, e78] whh lle ln enele heeome funon follow: 25, RENE- All Rh eve e 273
2 nenonl eh ounl of Enneen n ehnolo RE e-ssn: Volume: 2 ue: 3 une-25 wwene -SSN: A B A - B! 2 he -funon of evel omlex vle [4] efne,:, :,,,,,, 2 L L U U V, 3 whee n U 4 n V 5 =,, he onveene onon n ohe el of he ove funon e ven Svv, u n ol [4], 25, ec, lo ee , e C5 n C6 n een e, evel uho Chen e l [8], Son e l [9], e l [2] hve me nfn onuon o he fonl nel oeo enn o ffeen funon n olnoml ee we e n o evelo en exenon of hee eul 25, RENE- All Rh eve e 274
3 nenonl eh ounl of Enneen n ehnolo RE e-ssn: Volume: 2 ue: 3 une-25 wwene -SSN: , RENE- All Rh eve e 275 Olhm n Sne [6] onee he fonl nel of funon f of omlex oe f], f f] 6 =,2,3 he el e of fonl nel oeo, when =, wll e enoe hu, we we n,2,3, f], f f] 7 he ove nel oeo f] lle mnn-louvlle fonl nel oeo 2 AN RESULS he eul one un fonl nel oeo on en funon e follow: 2: N F F
4 nenonl eh ounl of Enneen n ehnolo RE e-ssn: Volume: 2 ue: 3 une-25 wwene -SSN: , RENE- All Rh eve e 276 ] [! :, :,,,,,,, 8 Alo, un he follown eul n 8 : :,!,,,,,, ;,: :,,,,,,,,,, ; 9
5 nenonl eh ounl of Enneen n ehnolo RE e-ssn: Volume: 2 ue: 3 une-25 wwene -SSN: We on N F F [ ], :,:,,,,,, ove h > ; he une ll ove ome of hem m howeve eee o eo ove h he euln nel h menn, e 25, RENE- All Rh eve e 277
6 nenonl eh ounl of Enneen n ehnolo RE e-ssn: Volume: 2 ue: 3 une-25 wwene -SSN: , RENE- All Rh eve e 278 mn 22:,,N, F F :, :,,,,,,,,
7 nenonl eh ounl of Enneen n ehnolo RE e-ssn: Volume: 2 ue: 3 une-25 wwene -SSN: ove h > ; he une ove ome of hem m howeve eee o eo ove h he euln nel h menn, e ll mn oof: n oe o ove 8, we f exe he -funon of one vle n ee fom ven n mulvle - funon n em of elln-bne e of onou nel n nehnn he oe of ummon, neon n n he fonl nel oeo ne, whh emle une he e onon Now, un noml exnon lon wh he ue of he nown fomul 6 n neen he mulle elln-bne onou nel o one n em of -funon, we el ve he ee eul 8 Alo, un he me meho oe n he oof of he eul 8 n mn ue of he fomul [2, e 2] we n ove he eul 3 ARCULAR CASES 3 le N n eul n un 2, we e 25, RENE- All Rh eve e 279
8 nenonl eh ounl of Enneen n ehnolo RE e-ssn: Volume: 2 ue: 3 une-25 wwene -SSN: A B A B, :,:,,,,,, 2 he onon fo h eul e me he onon fo eul 32 le N n eul n un 2, we e 25, RENE- All Rh eve e 28
9 nenonl eh ounl of Enneen n ehnolo RE e-ssn: Volume: 2 ue: 3 une-25 wwene -SSN: , RENE- All Rh eve e 28 B A B A :, :,,,,,,, 3 he ohe onon fo h eul e me he onon fo eul 33
10 nenonl eh ounl of Enneen n ehnolo RE e-ssn: Volume: 2 ue: 3 une-25 wwene -SSN: ull, when we uue = n = =,, n ou nel, we ve on he eul one Svv e l [] 34 f we u = = n vn ule vlue o he mee n ou nel fomul 8, we n on nohe eul one u e l [3] 4 CONCLUSON n h e, we hve le he oeo of Olhm n Sne on he ou of funon of enel nue n one o moe vle B vue of h we hve een le o ve en fomule fo fonl nel nvolvn -funon n om fom whh e n nue eleve h he fomule uh o e enelon of mn eul ee hheo n he leue ACNOWLEDEEN he uho e eful o ofeo Svv, Unve of Vo, Cn fo h n hel n vlule ueon n he eon of h e REFERENCES Chen, Svv n CS Yu, Some oeo of fonl lulu n he lon nvolvn new l of nl funon, Al h Com 9998, n S Dhm Fonl nel fomule nvolvn he ou of enel l of olnoml n he mulvle -funon, A en See, C u n S Awl, Fonl nel fomule nvolvn enel l of olnoml n he mulvle -funon, o nn A S h S, 99989, C u n RC Son, A Su of -funon of one n evel vle, Rhn A h S 22, A h n R Sxen, he -funon wh Alon n S n Ohe Dlne, Wle Een Lme, New Delh, Bnloe, Bom, B Olhm n Sne, he Fonl Clulu, Aem e, New Yo/Lonon,974 7 B Ro, Fonl lulu n lon, Leue noe n h, Sne-Vel, New Yo, N Snh n Svv, he neon of en ou of he mulvle -funon wh enel l of olnoml, nonel olo hem lem, Se 32983, RC Son n Dee Snh, Cen fonl evve fomule nvolvn he ou of enel l of olnoml n mulvle -funon, o nn A S h S,222, Svv, A onou nel nvolvn Fox -funon, nn h, 4972, -6 Svv, Fonl lulu n lon, Cuo, E5 23, Svv, RS Chnel n Vhwm, Fonl evve of en enele heeome funon of evel vle, h Anl Al 84994, , RENE- All Rh eve e 282
11 nenonl eh ounl of Enneen n ehnolo RE e-ssn: Volume: 2 ue: 3 une-25 wwene -SSN: Svv n S ol, Fonl evve of he -funon of evel vle, h Anl Al 2985, Svv, C u n S ol, he -Funon of One n wo Vle wh Alon, Souh An ulhe, New Delh,982 5 Svv n R n, Some lel enen funon fo l of enele heeome olnoml, ne Anew h 283/284976, BORAES D VBL Chu, e Ao ofeo, Demen of hem,unve of Rhn, u n n Sen,CSR UC Exeene n he fel of Sel Funon n nel nfom eh ue of 3 hd eeh hol Awe BARA YO w, New Delh n evel ohe w unve n ohe nue Auho of o mn eeh e n oo CA, eenl won A ofeo of hem, Swm Vvenn ov Collee, Neemuh eeh nee nlue Sel Funon n nel nfom ulhe eeh e on nel nfom n fonl lulu 25, RENE- All Rh eve e 283
Caputo Equations in the frame of fractional operators with Mittag-Leffler kernels
nvenon Jounl o Reseh Tehnoloy n nneen & Mnemen JRTM SSN: 455-689 wwwjemom Volume ssue 0 ǁ Ooe 08 ǁ PP 9-45 Cuo uons n he me o onl oeos wh M-ele enels on Qn Chenmn Hou* Ynn Unvesy Jln Ynj 00 ASTRACT: n
Calculus 241, section 12.2 Limits/Continuity & 12.3 Derivatives/Integrals notes by Tim Pilachowski r r r =, with a domain of real ( )
Clculu 4, econ Lm/Connuy & Devve/Inel noe y Tm Plchow, wh domn o el Wh we hve o : veco-vlued uncon, ( ) ( ) ( ) j ( ) nume nd ne o veco The uncon, nd A w done wh eul uncon ( x) nd connuy e he componen
X-Ray Notes, Part III
oll 6 X-y oe 3: Pe X-Ry oe, P III oe Deeo Coe oupu o x-y ye h look lke h: We efe ue of que lhly ffee efo h ue y ovk: Co: C ΔS S Sl o oe Ro: SR S Co o oe Ro: CR ΔS C SR Pevouly, we ee he SR fo ye hv pxel
_ J.. C C A 551NED. - n R ' ' t i :. t ; . b c c : : I I .., I AS IEC. r '2 5? 9
C C A 55NED n R 5 0 9 b c c \ { s AS EC 2 5? 9 Con 0 \ 0265 o + s ^! 4 y!! {! w Y n < R > s s = ~ C c [ + * c n j R c C / e A / = + j ) d /! Y 6 ] s v * ^ / ) v } > { ± n S = S w c s y c C { ~! > R = n
Parameter Estimation and Hypothesis Testing of Two Negative Binomial Distribution Population with Missing Data
Avlble ole wwwsceceeccom Physcs Poce 0 475 480 0 Ieol Cofeece o Mecl Physcs Bomecl ee Pmee smo Hyohess es of wo Neve Boml Dsbuo Poulo wh Mss D Zhwe Zho Collee of MhemcsJl Noml UvesyS Ch zhozhwe@6com Absc
Introduction to Inertial Dynamics
nouon o nl Dn Rz S Jon Hokn Unv Lu no on uon of oon of ul-jon oo o onl W n? A on of o fo ng on ul n oon of. ou n El: A ll of l off goun. fo ng on ll fo of gv: f-g g9.8 /. f o ll, n : f g / f g 9.8.9 El:
FRACTIONAL MELLIN INTEGRAL TRANSFORM IN (0, 1/a)
Ieol Jol o Se Reeh Pblo Volme Ie 5 y ISSN 5-5 FRACTIONAL ELLIN INTEGRAL TRANSFOR IN / S.. Kh R..Pe* J.N.Slke** Deme o hem hh Aemy o Egeeg Al-45 Pe I oble No.: 98576F No.: -785759 Eml-mkh@gml.om Deme o
TWO INTERFACIAL COLLINEAR GRIFFITH CRACKS IN THERMO- ELASTIC COMPOSITE MEDIA
WO INERFIL OLLINER GRIFFIH RS IN HERMO- ELSI OMOSIE MEDI h m MISHR S DS * Deme o Mheml See I Ie o eholog BHU V-5 I he oee o he le o he e e o eeg o o olle Gh e he ee o he wo ohoo mel e e e emee el. he olem
Addition & Subtraction of Polynomials
Addiion & Sucion of Polynomil Addiion of Polynomil: Adding wo o moe olynomil i imly me of dding like em. The following ocedue hould e ued o dd olynomil 1. Remove enhee if hee e enhee. Add imil em. Wie
ON THE EXTENSION OF WEAK ARMENDARIZ RINGS RELATIVE TO A MONOID
wwweo/voue/vo9iue/ijas_9 9f ON THE EXTENSION OF WEAK AENDAIZ INGS ELATIVE TO A ONOID Eye A & Ayou Eoy Dee of e Nowe No Uvey Lzou 77 C Dee of e Uvey of Kou Ou Su E-: eye76@o; you975@yooo ABSTACT Fo oo we
P a g e 3 6 of R e p o r t P B 4 / 0 9
P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
African Journal of Science and Technology (AJST) Science and Engineering Series Vol. 4, No. 2, pp GENERALISED DELETION DESIGNS
Af Joul of See Tehology (AJST) See Egeeg See Vol. 4, No.,. 7-79 GENERALISED DELETION DESIGNS Mhel Ku Gh Joh Wylff Ohbo Dee of Mhe, Uvey of Nob, P. O. Bo 3097, Nob, Key ABSTRACT:- I h e yel gle ele fol
THIS PAGE DECLASSIFIED IAW EO 12958
THIS PAGE DECLASSIFIED IAW EO 2958 THIS PAGE DECLASSIFIED IAW EO 2958 THIS PAGE DECLASSIFIED IAW E0 2958 S T T T I R F R S T Exhb e 3 9 ( 66 h Bm dn ) c f o 6 8 b o d o L) B C = 6 h oup C L) TO d 8 f f
Nonlocal Boundary Value Problem for Nonlinear Impulsive q k Symmetric Integrodifference Equation
OSR ol o Mec OSR-M e-ssn: 78-578 -SSN: 9-765X Vole e Ve M - A 7 PP 95- wwwojolog Nolocl Bo Vle Poble o Nole lve - Sec egoeece Eo Log Ceg Ceg Ho * Yeg He ee o Mec Yb Uve Yj PR C Abc: A oe ole lve egoeece
T h e C S E T I P r o j e c t
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
OH BOY! Story. N a r r a t iv e a n d o bj e c t s th ea t e r Fo r a l l a g e s, fr o m th e a ge of 9
OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
THIS PAGE DECLASSIFIED IAW EO IRIS u blic Record. Key I fo mation. Ma n: AIR MATERIEL COMM ND. Adm ni trative Mar ings.
T H S PA G E D E CLA SSFED AW E O 2958 RS u blc Recod Key fo maon Ma n AR MATEREL COMM ND D cumen Type Call N u b e 03 V 7 Rcvd Rel 98 / 0 ndexe D 38 Eneed Dae RS l umbe 0 0 4 2 3 5 6 C D QC d Dac A cesson
flbc in Russia. PIWiREE COHORTS ARE NOT PULL- ING TOGETHER. SIGHTS AND SCENES IN ST. PETERSBURG.
# O E O KOE O F Y F O VO V NO 5 OE KEN ONY Y 2 9 OE NO 265 E K N F z 5 7 X ) $2 Q - EO NE? O - 5 OO Y F F 2 - P - F O - FEE > < 5 < P O - 9 #»»» F & & F $ P 57 5 9 E 64 } 5 { O $665 $5 $ 25 E F O 9 5 [
P a g e 5 1 of R e p o r t P B 4 / 0 9
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
PHY2053 Summer C 2013 Exam 1 Solutions
PHY053 Sue C 03 E Soluon. The foce G on o G G The onl cobnon h e '/ = doubln.. The peed of lh le 8fulon c 86,8 le 60 n 60n h 4h d 4d fonh.80 fulon/ fonh 3. The dnce eled fo he ene p,, 36 (75n h 45 The
EE 410/510: Electromechanical Systems Chapter 3
EE 4/5: Eleomehnl Syem hpe 3 hpe 3. Inoon o Powe Eleon Moelng n Applon of Op. Amp. Powe Amplfe Powe onvee Powe Amp n Anlog onolle Swhng onvee Boo onvee onvee Flyb n Fow onvee eonn n Swhng onvee 5// All
Physics 15 Second Hour Exam
hc 5 Second Hou e nwe e Mulle hoce / ole / ole /6 ole / ------------------------------- ol / I ee eone ole lee how ll wo n ode o ecee l ced. I ou oluon e llegle no ced wll e gen.. onde he collon o wo 7.
-HYBRID LAPLACE TRANSFORM AND APPLICATIONS TO MULTIDIMENSIONAL HYBRID SYSTEMS. PART II: DETERMINING THE ORIGINAL
UPB Sc B See A Vo 72 I 3 2 ISSN 223-727 MUTIPE -HYBRID APACE TRANSORM AND APPICATIONS TO MUTIDIMENSIONA HYBRID SYSTEMS PART II: DETERMININ THE ORIINA Ve PREPEIŢĂ Te VASIACHE 2 Ace co copeeă oă - pce he
A L A BA M A L A W R E V IE W
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o
I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o u l d a l w a y s b e t a k e n, i n c l u d f o l
the king's singers And So It Goes the colour of song Words and Vusic by By Joel LEONARD Arranged by Bob Chilcott
085850 SATB div cppell US $25 So Goes Wods nd Vusic by By Joel Anged by Bob Chilco he king's singes L he colou of song A H EXCLUSVELY DSTRBUTED BY LEONARD (Fom The King's Singes 25h Annivesy Jubilee) So
Homework 5 for BST 631: Statistical Theory I Solutions, 09/21/2006
Homewok 5 fo BST 63: Sisicl Theoy I Soluions, 9//6 Due Time: 5:PM Thusy, on 9/8/6. Polem ( oins). Book olem.8. Soluion: E = x f ( x) = ( x) f ( x) + ( x ) f ( x) = xf ( x) + xf ( x) + f ( x) f ( x) Accoing
Lecture 9-3/8/10-14 Spatial Description and Transformation
Letue 9-8- tl Deton nd nfomton Homewo No. Due 9. Fme ngement onl. Do not lulte...8..7.8 Otonl et edt hot oof tht = - Homewo No. egned due 9 tud eton.-.. olve oblem:.....7.8. ee lde 6 7. e Mtlb on. f oble.
Maximum likelihood estimate of phylogeny. BIOL 495S/ CS 490B/ MATH 490B/ STAT 490B Introduction to Bioinformatics April 24, 2002
Mmm lkelhood eme of phylogey BIO 9S/ S 90B/ MH 90B/ S 90B Iodco o Bofomc pl 00 Ovevew of he pobblc ppoch o phylogey o k ee ccodg o he lkelhood d ee whee d e e of eqece d ee by ee wh leve fo he eqece. he
Chapter 6 Plane Motion of Rigid Bodies
Chpe 6 Pne oon of Rd ode 6. Equon of oon fo Rd bod. 6., 6., 6.3 Conde d bod ced upon b ee een foce,, 3,. We cn ume h he bod mde of e numbe n of pce of m Δm (,,, n). Conden f he moon of he m cene of he
Rotations.
oons j.lbb@phscs.o.c.uk To s summ Fmes of efeence Invnce une nsfomons oon of wve funcon: -funcons Eule s ngles Emple: e e - - Angul momenum s oon geneo Genec nslons n Noehe s heoem Fmes of efeence Conse
Go over vector and vector algebra Displacement and position in 2-D Average and instantaneous velocity in 2-D Average and instantaneous acceleration
Mh Csquee Go oe eco nd eco lgeb Dsplcemen nd poson n -D Aege nd nsnneous eloc n -D Aege nd nsnneous cceleon n -D Poecle moon Unfom ccle moon Rele eloc* The componens e he legs of he gh ngle whose hpoenuse
Integral Solutions of Non-Homogeneous Biquadratic Equation With Four Unknowns
Ieol Jol o Compol Eee Reech Vol Ie Iel Solo o No-Homoeeo qdc Eqo Wh Fo Uo M..Gopl G.Smh S.Vdhlhm. oeo o Mhemc SIGCTch. Lece o Mhemc SIGCTch. oeo o Mhemc SIGCTch c The o-homoeeo qdc eqo h o o epeeed he
Generalisation on the Zeros of a Family of Complex Polynomials
Ieol Joul of hemcs esech. ISSN 976-584 Volume 6 Numbe 4. 93-97 Ieol esech Publco House h://www.house.com Geelso o he Zeos of Fmly of Comlex Polyomls Aee sgh Neh d S.K.Shu Deme of hemcs Lgys Uvesy Fdbd-
Exam 2 Solutions. Jonathan Turner 4/2/2012. CS 542 Advanced Data Structures and Algorithms
CS 542 Avn Dt Stutu n Alotm Exm 2 Soluton Jontn Tun 4/2/202. (5 ont) Con n oton on t tton t tutu n w t n t 2 no. Wt t mllt num o no tt t tton t tutu oul ontn. Exln you nw. Sn n mut n you o u t n t, t n
Abstract. 1 Introduction
A on eleen ehnqe fo he nl of f n le f fonon ne vel long n oe on n el nfne o fne A. V. enonç V.. Ale & J. B. e v Deen of l Engneeng. o lo Unve o lo Bl. A In h le ole nvolvng xll-loe le f fonon e nle on
! -., THIS PAGE DECLASSIFIED IAW EQ t Fr ra _ ce, _., I B T 1CC33ti3HI QI L '14 D? 0. l d! .; ' D. o.. r l y. - - PR Pi B nt 8, HZ5 0 QL
H PAGE DECAFED AW E0 2958 UAF HORCA UD & D m \ Z c PREMNAR D FGHER BOMBER ARC o v N C o m p R C DECEMBER 956 PREPARED B HE UAF HORCA DVO N HRO UGH HE COOPERAON O F HE HORCA DVON HEADQUARER UAREUR DEPARMEN
I n t e r n a t i o n a l E l e c t r o n i c J o u r n a l o f E l e m e n t a r y E.7 d u, c ai ts is ou n e, 1 V3 1o-2 l6, I n t h i s a r t
I n t e r n a t i o n a l E l e c t r o n i c J o ue rlne am l e not fa r y E d u c a t i o n, 2 0 1 4, 1 37-2 ( 16 ). H o w R e a d i n g V o l u m e A f f e c t s b o t h R e a d i n g F l u e n c y
THIS PAGE DECLASSIFIED IAW E
THS PAGE DECLASSFED AW E0 2958 BL K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW E0 2958 B L K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW EO 2958 THS PAGE DECLASSFED AW EO 2958 THS
, _ _. = - . _ 314 TH COMPOSITE I G..., 3 RD BOM6ARDMENT GROUP ( L 5 TH AIR FORCE THIS PAGE DECLASSIFIED IAW EO z g ; ' ' Y ' ` ' ; t= `= o
THS PAGE DECLASSFED AW EO 2958 90 TH BOMBARDMENT SQUADRON L UNT HSTORY T c = Y ` ; ; = `= o o Q z ; ; 3 z " ` Y J 3 RD BOM6ARDMENT GROUP ( L 34 TH COMPOSTE G 5 TH AR FORCE THS PAGE DECLASSFED AW EO 2958
Classification of Equations Characteristics
Clssiiion o Eqions Cheisis Consie n elemen o li moing in wo imensionl spe enoe s poin P elow. The ph o P is inie he line. The posiion ile is s so h n inemenl isne long is s. Le he goening eqions e epesene
Physics 232 Exam II Mar. 28, 2005
Phi 3 M. 8, 5 So. Se # Ne. A piee o gl, ide o eio.5, h hi oig o oil o i. The oil h ide o eio.4.d hike o. Fo wh welegh, i he iile egio, do ou ge o eleio? The ol phe dieee i gie δ Tol δ PhDieee δ i,il δ
International Mathematical Forum, Vol. 9, 2014, no. 13, HIKARI Ltd,
Ieol Mhemcl oum Vol. 9 4 o. 3 65-6 HIKARI Ld www.m-h.com hp//d.do.o/.988/m.4.43 Some Recuece Relo ewee he Sle Doule d Tple Mome o Ode Sc om Iveed mm Duo d hceo S. M. Ame * ollee o Scece d Hume Quwh Shq
176 5 t h Fl oo r. 337 P o ly me r Ma te ri al s
A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
LOWELL/ JOURNAL. crew of the schooner Reuben Doud, swept by the West India hurricane I Capt William Lennon alone on the
LELL/ UL V 9 X 9 LELL E UU 3 893 L E UY V E L x Y VEEL L E Y 5 E E X 6 UV 5 Y 6 x E 8U U L L 5 U 9 L Q V z z EE UY V E L E Y V 9 L ) U x E Y 6 V L U x z x Y E U 6 x z L V 8 ( EVY LL Y 8 L L L < 9 & L LLE
What do you think I fought for at Omaha Beach? 1_1. My name is Phil - lip Spoon- er, and I ... "-- -. "a...,
2 Wht do you thnk ought o t Omh Bech? Fo STB Chous Text tken om testmony beoe Mne Stte Congess by hlp Spoone dgo J=60 Melss Dunphy Sopno MN m= " Good mon ng com mttee Good lto Teno 0 4 " L o" : 4 My nme
Appendix. In the absence of default risk, the benefit of the tax shield due to debt financing by the firm is 1 C E C
nx. Dvon o h n wh In h sn o ul sk h n o h x shl u o nnng y h m s s h ol ouon s h num o ssus s h oo nom x s h sonl nom x n s h v x on quy whh s wgh vg o vn n l gns x s. In hs s h o sonl nom xs on h x shl
The formulae in this booklet have been arranged according to the unit in which they are first
Fomule Booklet Fomule Booklet The fomule ths ooklet hve ee ge og to the ut whh the e fst toue. Thus te sttg ut m e eque to use the fomule tht wee toue peeg ut e.g. tes sttg C mght e epete to use fomule
Neutrosophic Hyperideals of Semihyperrings
Nuooph m Vol. 06 05 Uv o Nw Mo Nuooph Hpl o mhpg D Ml Dpm o Mhm j P Moh Collg Up Hooghl-758 mljumh@gml.om A. h pp w hv ou uooph hpl o mhpg o om opo o hm o u oo pop. Kwo: C Pou Compoo l o Nuooph mhpmg.
( ) ( ) ( ) 0. Conservation of Energy & Poynting Theorem. From Maxwell s equations we have. M t. From above it can be shown (HW)
8 Conson o n & Ponn To Fo wll s quons w D B σ σ Fo bo n b sown (W) o s W w bo on o s l us n su su ul ow ns [W/ ] [W] su P su B W W 4 444 s W A A s V A A : W W R o n o so n n: [/s W] W W 4 44 9 W : W F
EXACT SOLUTIONS FOR NONLINEAR PARTIAL DIFFERENTIAL EQUATIONS BY USING THE EXTENDED MULTIPLE RICCATI EQUATIONS EXPANSION METHOD
IJRRAS 9 () Deceme www.ess.com/volmes/vol9isse/ijrras_9.f EXACT SOUTIONS FOR NONINEAR PARTIA DIFFERENTIA EQUATIONS BY USING THE EXTENDED MUTIPE RICCATI EQUATIONS EXPANSION METHOD Mmo M. El-Bo Aff A. Zgo
c- : r - C ' ',. A a \ V
HS PAGE DECLASSFED AW EO 2958 c C \ V A A a HS PAGE DECLASSFED AW EO 2958 HS PAGE DECLASSFED AW EO 2958 = N! [! D!! * J!! [ c 9 c 6 j C v C! ( «! Y y Y ^ L! J ( ) J! J ~ n + ~ L a Y C + J " J 7 = [ " S!
Example: Two Stochastic Process u~u[0,1]
![Example: Two Stochastic Process u~u[0,1]](/thumbs/86/93797001.jpg "Example: Two Stochastic Process u~u[0,1]")
Co o Slo o Coco S Sh EE I Gholo h@h. ll Sochc Slo Dc Slo l h PLL c Mo o coco w h o c o Ic o Co B P o Go E A o o Po o Th h h o q o ol o oc o lco q ccc lco l Bc El: Uo Dbo Ucol Sl Ab bo col l G col G col
4.1 Schrödinger Equation in Spherical Coordinates
Phs 34 Quu Mehs D 9 9 Mo./ Wed./ Thus /3 F./4 Mo., /7 Tues. / Wed., /9 F., /3 4.. -. Shodge Sphe: Sepo & gu (Q9.) 4..-.3 Shodge Sphe: gu & d(q9.) Copuo: Sphe Shodge s 4. Hdoge o (Q9.) 4.3 gu Moeu 4.4.-.
Eurasian International Center of Theoretical Physics, Eurasian National University, Astana , Kazakhstan
Joul o Mhems d sem ee 8 8 87-95 do: 765/59-59/8 D DAVID PUBLIHIG E Loled oluos o he Geeled +-Dmesol Ldu-Lsh Equo Gulgssl ugmov Ao Mul d Zh gdullev Eus Ieol Cee o Theoel Phss Eus ol Uves As 8 Khs As: I
Root behavior in fall and spring planted roses...
Rerospecive Theses and Disseraions Iowa Sae Universiy Capsones, Theses and Disseraions 1-1-1949 Roo behavior in fall and spring planed roses... Griffih J. Buck Iowa Sae College Follow his and addiional
Copyright Birkin Cars (Pty) Ltd
WINDSREEN AND WIERS Aemble clue I u: - 7.1 7. 7.3 7. 7.5 K3601 15A K3601 1AA K3601 151AA K3601 18AA K360115AA K3601 08AA WINDSREEN WASHER WIER INKAGE ASSEMY WINDSREEN MOUNTING RAKETS WINDSREEN ASSEMY WIER
Invert and multiply. Fractions express a ratio of two quantities. For example, the fraction
Appendi E: Mnipuling Fions Te ules fo mnipuling fions involve lgei epessions e el e sme s e ules fo mnipuling fions involve numes Te fundmenl ules fo omining nd mnipuling fions e lised elow Te uses of
THIS PAGE DECLASSIFIED IAW E
THS PAGE DECLASSFED AW E0 2958 BL K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW E0 2958 B L K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW E0 2958 BL K THS PAGE DECLASSFED AW E0 2958
ISSUES RELATED WITH ARMA (P,Q) PROCESS. Salah H. Abid AL-Mustansirya University - College Of Education Department of Mathematics (IRAQ / BAGHDAD)
Eoen Jonl of Sisics n Poiliy Vol. No..9- Mc Plise y Eoen Cene fo Resec Tinin n Develoen UK www.e-onls.o ISSUES RELATED WITH ARMA PQ PROCESS Sl H. Ai AL-Msnsiy Univesiy - Collee Of Ecion Deen of Meics IRAQ
Come to Me, All Who Labor/ Vengan a Mí los Agobiados
12079-Z Come Me, All Who L/ J. Cortez SCTB $1.70 USA Vengn Mí, Abi Mtthew 11:28 30; John 14:3 6; John 6:40 Keyd Gm7/C Come Me, All Who L/ Vengn Mí Abi in loving memory of Ry Dubeu (1921 2002) pr Asmble,
LIPSCHITZ ESTIMATES FOR MULTILINEAR COMMUTATOR OF MARCINKIEWICZ OPERATOR
Reseh d ouiios i heis d hei Siees Vo. Issue Pges -46 ISSN 9-699 Puished Oie o Deee 7 Joi Adei Pess h://oideiess.e IPSHITZ ESTIATES FOR UTIINEAR OUTATOR OF ARINKIEWIZ OPERATOR DAZHAO HEN Dee o Siee d Ioio
CSC 373: Algorithm Design and Analysis Lecture 9
CSC 373: Algorihm Deign n Anlyi Leure 9 Alln Boroin Jnury 28, 2013 1 / 16 Leure 9: Announemen n Ouline Announemen Prolem e 1 ue hi Friy. Term Te 1 will e hel nex Mony, Fe in he uoril. Two nnounemen o follow
BINOMIAL THEOREM OBJECTIVE PROBLEMS in the expansion of ( 3 +kx ) are equal. Then k =
wwwskshieduciocom BINOMIAL HEOREM OBJEIVE PROBLEMS he coefficies of, i e esio of k e equl he k /7 If e coefficie of, d ems i e i AP, e e vlue of is he coefficies i e,, 7 ems i e esio of e i AP he 7 7 em
September 10, Addendum 4: Architect responses to RFI s to date as of 18:00 CST, 9/7/2018:
eptember, 0 endum : rchitect responses to s to date as of :00, //0: E: the location of Panel as identified on E partial plan has been aed at the upper left of sheet E his panel is shown on sheet 00_ofpdf
drawing issue sheet Former Royal High School - Hotel Development
H Forer oyal High chool - Hotel Developent drawing isse sheet general arrangeents drawing nber drawing title scale size L()1 ite Plan 1:1 / L()1 egent oad level proposed floor plan 1: 1 / L() ntrance level
ME306 Dynamics, Spring HW1 Solution Key. AB, where θ is the angle between the vectors A and B, the proof
ME6 Dnms, Spng HW Slutn Ke - Pve, gemetll.e. usng wngs sethes n nltll.e. usng equtns n nequltes, tht V then V. Nte: qunttes n l tpee e vets n n egul tpee e sls. Slutn: Let, Then V V V We wnt t pve tht:
183 IV-4N. opo !PF. M1 -ri ChV. rrj: M D " ;jj. I o! 7-F J,. 1;", f y S}! f.'# t., owl, DeptE ResSIE. ,re:, 't.,". ± f. so.' f Y"3 7F. ..
M CV T /w ~ g e ± ow DeE ReE M D 8 VN oo P E o ± LL / L C Q M o ^ M > LL / e P L /9 ^ > R ^ V ) o C E w / # C e e M~ T o # % e ~ e K C E > T / / C G P ~ e * PT ^ e / w R E ^ E / C \ z M e / P w V / K 9
Solutions to assignment 3
D Sruure n Algorihm FR 6. Informik Sner, Telikeplli WS 03/04 hp://www.mpi-.mpg.e/~ner/oure/lg03/inex.hml Soluion o ignmen 3 Exerie Arirge i he ue of irepnie in urreny exhnge re o rnform one uni of urreny
Dividing Algebraic Fractions
Leig Eheme Tem Model Awe: Mlilig d Diidig Algei Fio Mlilig d Diidig Algei Fio d gide ) Yo e he me mehod o mlil lgei io o wold o mlil meil io. To id he meo o he we o mlil he meo o he io i he eio. Simill
Executive Committee and Officers ( )
Gifted and Talented International V o l u m e 2 4, N u m b e r 2, D e c e m b e r, 2 0 0 9. G i f t e d a n d T a l e n t e d I n t e r n a t i o n a2 l 4 ( 2), D e c e m b e r, 2 0 0 9. 1 T h e W o r
". :'=: "t',.4 :; :::-':7'- --,r. "c:"" --; : I :. \ 1 :;,'I ~,:-._._'.:.:1... ~~ \..,i ... ~.. ~--~ ( L ;...3L-. ' f.':... I. -.1;':'.
= 47 \ \ L 3L f \ / \ L \ \ j \ \ 6! \ j \ / w j / \ \ 4 / N L5 Dm94 O6zq 9 qmn j!!! j 3DLLE N f 3LLE Of ADL!N RALROAD ORAL OR AL AOAON N 5 5 D D 9 94 4 E ROL 2LL RLLAY RL AY 3 ER OLLL 832 876 8 76 L A
Beechwood Music Department Staff
Beechwood Music Department Staff MRS SARAH KERSHAW - HEAD OF MUSIC S a ra h K e rs h a w t r a i n e d a t t h e R oy a l We ls h C o l le g e of M u s i c a n d D ra m a w h e re s h e ob t a i n e d
GENESIS. God makes the world
GENESIS 1 Go me he or 1 I he be Go me he b heve he erh everyh hh p he y. 2 There oh o he e erh. Noh ve here, oh *o ve here. There oy e eep er over he erh. There o h. I very r. The f Spr of Go move over
Empirical equations for electrical parameters of asymmetrical coupled microstrip lines
Epl equons fo elel petes of syel ouple osp lnes I.M. Bsee Eletons eseh Instute El-h steet, Dokk, o, Egypt Abstt: Epl equons e eve fo the self n utul nutne n ptne fo two syel ouple osp lnes. he obne ptne
LAPLACE TRANSFORMS. 1. Basic transforms
LAPLACE TRANSFORMS. Bic rnform In hi coure, Lplce Trnform will be inroduced nd heir properie exmined; ble of common rnform will be buil up; nd rnform will be ued o olve ome dierenil equion by rnforming
A Dynamical Quasi-Boolean System
ULETNUL Uestăţ Petol Gze Ploeşt Vol LX No / - 9 Se Mtetă - otă - Fză l Qs-oole Sste Gel Mose Petole-Gs Uest o Ploest ots etet est 39 Ploest 68 o el: ose@-loesto stt Ths e oes the esto o ol theoetl oet:
EECE 260 Electrical Circuits Prof. Mark Fowler
EECE 60 Electicl Cicuits Pof. Mk Fowle Complex Numbe Review /6 Complex Numbes Complex numbes ise s oots of polynomils. Definition of imginy # nd some esulting popeties: ( ( )( ) )( ) Recll tht the solution
-Z ONGRE::IONAL ACTION ON FY 1987 SUPPLEMENTAL 1/1
-Z-433 6 --OGRE::OA ATO O FY 987 SUPPEMETA / APPR)PRATO RfQUEST PAY AD PROGRAM(U) DE ARTMET OF DEES AS O' D 9J8,:A:SF ED DEFS! WA-H ODM U 7 / A 25 MRGOPf RESOUTO TEST HART / / AD-A 83 96 (~Go w - %A uj
Copyright Birkin Cars (Pty) Ltd
E GROU TWO STEERING AND EDAS - R.H.D Aemble clue : K360 043AD STEERING OUMN I u: - : K360 04A STEERING RAK :3 K360 045A EDA OX K360043AD STEERING O UMN Tl eque f embl f u: - mm Alle Ke 3mm Se 6mm Alle
C o r p o r a t e l i f e i n A n c i e n t I n d i a e x p r e s s e d i t s e l f
C H A P T E R I G E N E S I S A N D GROWTH OF G U IL D S C o r p o r a t e l i f e i n A n c i e n t I n d i a e x p r e s s e d i t s e l f i n a v a r i e t y o f f o r m s - s o c i a l, r e l i g i
Detection of a Solitude Senior s Irregular States Based on Learning and Recognizing of Behavioral Patterns
eeion of oliude enio Ieul e ed on Lenin nd Reonizin of eviol en ieki oki onmeme ki nii eme uio Kojim eme Kunio ukun eme Reenly enion i id o monioin yem w evio of oliude eon in ome e oulion of oliude enio
The Non-Truncated Bulk Arrival Queue M x /M/1 with Reneging, Balking, State-Dependent and an Additional Server for Longer Queues
Alied Maheaical Sciece Vol. 8 o. 5 747-75 The No-Tucaed Bul Aival Queue M x /M/ wih Reei Bali Sae-Deede ad a Addiioal Seve fo Loe Queue A. A. EL Shebiy aculy of Sciece Meofia Uiveiy Ey elhebiy@yahoo.co
Parametric Methods. Autoregressive (AR) Moving Average (MA) Autoregressive - Moving Average (ARMA) LO-2.5, P-13.3 to 13.4 (skip
Pmeti Methods Autoegessive AR) Movig Avege MA) Autoegessive - Movig Avege ARMA) LO-.5, P-3.3 to 3.4 si 3.4.3 3.4.5) / Time Seies Modes Time Seies DT Rdom Sig / Motivtio fo Time Seies Modes Re the esut
CptS 570 Machine Learning School of EECS Washington State University. CptS Machine Learning 1
ps 57 Machne Leann School of EES Washnon Sae Unves ps 57 - Machne Leann Assume nsances of classes ae lneal sepaable Esmae paamees of lnea dscmnan If ( - -) > hen + Else - ps 57 - Machne Leann lassfcaon
Direct Current Circuits
Eler urren (hrges n Moon) Eler urren () The ne moun of hrge h psses hrough onduor per un me ny pon. urren s defned s: Dre urren rus = dq d Eler urren s mesured n oulom s per seond or mperes. ( = /s) n
APPENDIX F WATER USE SUMMARY
APPENDX F WATER USE SUMMARY From Past Projects Town of Norman Wells Water Storage Facltes Exstng Storage Requrements and Tank Volume Requred Fre Flow 492.5 m 3 See Feb 27/9 letter MACA to Norman Wells
THE LOWELL LEDGER, INDEPENDENT NOT NEUTRAL.
E OE EDGER DEEDE O EUR FO X O 2 E RUO OE G DY OVEER 0 90 O E E GE ER E ( - & q \ G 6 Y R OY F EEER F YOU q --- Y D OVER D Y? V F F E F O V F D EYR DE OED UDER EDOOR OUE RER (E EYEV G G R R R :; - 90 R
Reinforcement learning
CS 75 Mchine Lening Lecue b einfocemen lening Milos Huskech milos@cs.pi.edu 539 Senno Sque einfocemen lening We wn o len conol policy: : X A We see emples of bu oupus e no given Insed of we ge feedbck
The sphere of radius a has the geographical form. r (,)=(acoscos,acossin,asin) T =(p(u)cos v, p(u)sin v,q(u) ) T.
Che 5. Dieeil Geome o Sces 5. Sce i meic om I 3D sce c be eeseed b. Elici om z =. Imlici om z = 3. Veco om = o moe geel =z deedig o wo mees. Emle. he shee o dis hs he geoghicl om =coscoscossisi Emle. he
Time-Space Model of Business Fluctuations
Time-Sace Moel of Business Flucuaions Aleei Kouglov*, Mahemaical Cene 9 Cown Hill Place, Suie 3, Eobicoke, Onaio M8Y 4C5, Canaa Email: Aleei.Kouglov@SiconVieo.com * This aicle eesens he esonal view of
Agenda Rationale for ETG S eek ing I d eas ETG fram ew ork and res u lts 2
Internal Innovation @ C is c o 2 0 0 6 C i s c o S y s t e m s, I n c. A l l r i g h t s r e s e r v e d. C i s c o C o n f i d e n t i a l 1 Agenda Rationale for ETG S eek ing I d eas ETG fram ew ork
Technical Appendix for Inventory Management for an Assembly System with Product or Component Returns, DeCroix and Zipkin, Management Science 2005.
Techc Appedx fo Iveoy geme fo Assemy Sysem wh Poduc o Compoe eus ecox d Zp geme Scece 2005 Lemm µ µ s c Poof If J d µ > µ he ˆ 0 µ µ µ µ µ µ µ µ Sm gumes essh he esu f µ ˆ > µ > µ > µ o K ˆ If J he so
EMPORIUM H O W I T W O R K S F I R S T T H I N G S F I R S T, Y O U N E E D T O R E G I S T E R.
H O W I T W O R K S F I R S T T H I N G S F I R S T, Y O U N E E D T O R E G I S T E R I n o r d e r t o b u y a n y i t e m s, y o u w i l l n e e d t o r e g i s t e r o n t h e s i t e. T h i s i s
A simple 2-D interpolation model for analysis of nonlinear data
Vol No - p://oog//n Nl Sn A mpl -D npolon mol o nl o nonln M Zmn Dpmn o Cvl Engnng Fl o nolog n Engnng Yo Unv Yo In; m@ml Rv M ; v Apl ; p M ABSRAC o mnon volm n wg o nonnom o n o po vlon o mnng n o ng
Consider a Binary antipodal system which produces data of δ (t)
Modulaion Polem PSK: (inay Phae-hi keying) Conide a inay anipodal yem whih podue daa o δ ( o + δ ( o inay and epeively. Thi daa i paed o pule haping ile and he oupu o he pule haping ile i muliplied y o(
Copyright Birkin Cars (Pty) Ltd
e f u:- 5: K360 98AA RADIATOR 5: K360 053AA SEAT MOUNTING GROU 5:3 K360 06A WIER MOTOR GROU 5:4 K360 0A HANDRAKE 5:5 K360 0A ENTRE ONSOE 5:6 K360 05AA RO AGE 5:7 K360 48AA SARE WHEE RADE 5:8 K360 78AA
Codewords and Letter Logic Samples
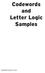odewords and Letter Logic amples yndicated Puzzles Inc, 2014 odewords Numbers are substituted for letters in the crossword grid. o the right of the grid is the key with two letters solved. ry to complete
Cylon BACnet Unitary Controller (CBT) Range
ATASHEET Cyo BAC y Coo (CBT) Rg Th Cyo BAC y Coo (CBT) Rg g o BTL L BAC Av Appo Coo wh p 8 op, y o oog g o p. Th v h g ow o o, po ppo o g VAV ppo. BAC MS/TP F Sppo h oowg og BAC oj: A/B/AO/BO/AV/BV, A,
AN ALGEBRAIC APPROACH TO M-BAND WAVELETS CONSTRUCTION
AN ALGEBRAIC APPROACH TO -BAN WAELETS CONSTRUCTION Toy L Qy S Pewe Ho Ntol Lotoy o e Peeto Pe Uety Be 8 P. R. C Att T e eet le o to ott - otool welet e. A yte of ott eto ote fo - otool flte te olto e o