X-Ray Notes, Part III
|
|
|
- Maryann Collins
- 6 years ago
- Views:
Transcription
1 oll 6 X-y oe 3: Pe X-Ry oe, P III oe Deeo Coe oupu o x-y ye h look lke h: We efe ue of que lhly ffee efo h ue y ovk: Co: C ΔS S Sl o oe Ro: SR S Co o oe Ro: CR ΔS C SR Pevouly, we ee he SR fo ye hv pxel ue o o Poo R.V. If he e vlue of he phoo ou fo pxel, he he l o oe o of fo h pxel wll e: S SR S The poly ey fuo fo he Poo R.V. : e p k k k! k k We wll ow ee he poly uo of eee phoo. Suppoe he e x-y phoo v he eeo e Poo h he eeo h effey, ee pevouly. We vew he eeo y o ye whh he phoo eee wh poly p :
2 oll 6 X-y oe 3: Pe whee Q k P { k phoo e eee} P Bol k k Poo k k k! k e p p k!! k! k k e p p k!! k k e p p e k! p k e p k! Poo p { k phoo e eee k phoo e e} P{ k phoo e e} Thu, he eee phoo e lo Poo ue, u wll hve poly he SR of he eee phoo ow: SR e Coe:. I lo ey o how h he ue of phoo h e o eee lo Poo poe wh pee poly -.. The u of Poo poee lo Poo. 3. Flly, f he e phoo e Poo, he he ue of phoo h eh he eeo wll lo e Poo. Aeuo poee h epeely ffe phoo wok exly ove.
3 oll 6 X-y oe 3: Pe 3 Ce Poo Poee Coe x-y phoo h e wh he eeo eee howe of phoo: We oel he ue of lh phoo,, he ue of o vle: X whee X he ue of lh phoo fo x-y phoo ue he ue of x-y phoo Poo. Fo ow, lo vewe he of lh oveo poe. We ow eee he he of : X X X X j j flly:
4 oll 6 X-y oe 3: Pe X X Th h wo opoe: he f epee he ve he ue of phoo fo ve u leh he eo epee he vo h oe fo he he leh of he u. Th lo e we : we ow we ew expeo fo he SR: SR Th l p of h expeo e houh of he SR eo e. If he vey le, he h poe wll eul eelly o lo of SR. Fo ol e Poo poee, e..: Z W whee Z Poo he: Z W Z Z W follow h: W W he SR e we :
5 oll 6 X-y oe 3: Pe 5 SR Fo ol e poee, h uo oue: SR 3... If y of he e e ll o eve loe o oe he he SR wll e eue. Thu, he e of eeo ye, po h he pou of ll of he kep le. Fo exple, we w >>, >>, 3 >>, xple Coe ll ee h poue 5 lh phoox-y phoo eee h ke ouhly lh phoo o ove lve hle ple o oevle he evelope fl h,. The SR euo fo wll he e: The e, whh le, oe oue o y lo of SR. The e he oue of SR euo. Ovell Sye Repoe SR xple Le oe he follow ye:
6 oll 6 X-y oe 3: Pe 6. The oue fuo e: exp whee h u of phoo.. The o fuo : exp whee exp epee he leo h we e y o ee. The o he o fuo C. 3. We ll ee he eoe epoe fuo he eo of lh pue y he peue of he fe op oupl: exp h.. Le,. 5. z: he oje fo fo he oue fo fo The e 5 lh phooeo,. e pue y he opl oupl, he opol 3 phoophoo he lh plfe,.5 fo he fe loe, opl oupl effee of he CCD. The fuo he ue : **exp exp ** exp ** ** h I Th ovoluo o ely olve he Foue o: exp, 8 exp exp, exp ρ δ ρ ρ δ ρ ρ v u v u I k o he e o: exp 8 I Fo h expeo, le he leo o fe he ye epoe wll e:
7 oll 6 X-y oe 3: Pe C whh eue y ou % fo he pu fuo. The ue of x-y phoo h fll wh pxel he e of he opl oupl : 8 The fl SR wh ou 3 : 8 CR whee he SR euo fo : wh he opol lh plfe, he SR euo fo : whh eoe oo pe of e ye e efe, fo exple efoe he low opoe lu he hu eye.
8 oll 6 X-y oe 3: Pe 8 Copo See X-y Coe he follow oje wh x-y opque oe: he oupu e h look lke h: o whh we efe o C ΔS S o o oe o CR ΔS. ow, oe h he ee phoo hee oe fo of he ee phoo wll e fow wll eee ol phoo he fl e. The uo of he ee phoo wll look oeh lke he oje ovolve wh he fow e uo. The fl e wll e he u of he e phoo he ee phoo. By e S he ee phoo wll eue oh he o he o o oe o. How y phoo e ee? Deve fo ovk, Pole 3. Le look oje of leh l hv euo oeffe. Le e pe
9 oll 6 X-y oe 3: Pe 9 he ue phoo e upo he oje h he ue of phoo h hve o ee eph x x. The ue of ee phoo evl x wll e: x x he ol ue of ee phoo wll e: x l x x l l x x exp x x exp l oe h -exp-l he ol ue of phoo h e wh he oje. Ave oe X-Ry I Thee e wo k of ve oe h we wll oe. The f zeo-e ve oe, fo exple, eleo oe ze e. I h e, he e vlue oe he, u he ve oe. I o e, he ve oe wll e epee of he Poo vo he eeve phoo hu, he ve wll :
10 oll 6 X-y oe 3: Pe whee he ve of he ve oe he Poo ve. Thu, he SR : S SR The ohe k of ve oe h we wll oe e. Se e lo Poo ue, zeo e, we ve ue efoe, oe ffe he o. Coe he e whee we hve e phoo ee phoo l ffeee of Δ. The ol o w: ou eue o : C C Δ Δ We lo kow h he ve of he kou l wll e he u of he ve of he o oue Poo poee: hu, he eue o o oe o wll e: CR Δ C C The e CR euo fo o Ψ, whee e phoo o e phoo. Ψ he o of
11 oll 6 X-y oe 3: Pe SR Reuo To e e of how y phoo e ee ke he eeo, we look exple wh oop oje wh euo oeffe e opoe : F, he ue of ee phoo eee eh eel hke : z z z e z z We ke vey of upo:. Ioe olque. Aue pllel y eoey fo e ey 3. Aue eey epee. ele ulple e 5. Aue oop e Thu, fo he ue of ee phoo, oe fo, Fz, wll e pue: Ω z F z e Lz The ue of ee phoo he eeo wll he e:
12 oll 6 X-y oe 3: Pe G z z e z e e z z z z F L L z z L L L Ω Ω whee G eoe, oje epee fo whh h u of leh. Fo h we oje, G.5L h eul fo Ωz fo lo, l oje G. Theefoe: G Ψ If we ke ypl vlue fo euo oeffe fo we kev,.6, L we wll le G.L, he: Ψ.8 eul euo of SR of:.5 Ψ 5% euo SR. Se Reuo G The o oo wy of eu e houh he ue of e euo : whee he e ou of oe hh el lke P, W h wll lok y phoo h ke. The wok pplly y u ow o he epe le fo ee phoo, Ω:
13 oll 6 X-y oe 3: Pe 3 We efe e euo fo: Ω' z z R Ω z z whee Ω z he epe le of he e euo. I o o eu he e, h lo eul euo of e phoo. We efe effey of he y oe e phoo loke y eue y he flle el: equo, h wll e: The CR wll ow e: exp f h CR C R C RΨ whee R Ψ he ew SR euo fo.
14 oll 6 X-y oe 3: Pe The Relohp of Poo Poe o he xpoel R.V. Le T e expoel R.V. h ee he e ewee eve Poo poe. The evo follow. Rell h he poly h eve ou evl Δ wll e p λδ. Alo, oe h he poly h o eve ou evl Δ wll e q - λδ. ow, uppoe he we w o kow wh he poly h o eve oue ewee. Th he e y h we hve Δ vevl whh o eve ou. If hee evl e epee h y h he phoo o e wh eh ohe o e o oe oup o wheve, he poly h o eve oue ewee wll e q : Δ { o eve ou, } Δ P λ we eee h fuo Δ : P λδ λ λ { o eve ou, } λδ e The poly ey fuo of T, f, ee he poly h eve ou e poly uo fuo of T el of f ee he poly h eve ou y e wll e equl o: l Δ λ e, fo F P{ o eve ou, }, fo < he poly ey fuo he evve of h fuo: λ λe, fo f, fo < The expoel R.V. ouou R.V. of he e ewee eve ee : whh h e ve of: T ~ xpoelλ T λ T λ
15 oll 6 X-y oe 3: Pe 5 eoyle Popey The expoel R.V. eoyle, e h uo ey of eve e he fuue o ffee y p eve, h, y po e, he e ul he ex eve expoel R.V. wh pee λ. Th he e y h ju eue we hve ee eve lo e, we e o oe lkely o hve eve oo. Ju lke he le flly. Speflly, { T > T > } P{ T > } P whh y ve h eve h oue y e, he poly h eve wll o ou y e wll e e he poly h o eve ou,. Poof: P { T > T > } F F exp λ exp λ exp λ F P { T > }
ON THE EXTENSION OF WEAK ARMENDARIZ RINGS RELATIVE TO A MONOID
 wwweo/voue/vo9iue/ijas_9 9f ON THE EXTENSION OF WEAK AENDAIZ INGS ELATIVE TO A ONOID Eye A & Ayou Eoy Dee of e Nowe No Uvey Lzou 77 C Dee of e Uvey of Kou Ou Su E-: eye76@o; you975@yooo ABSTACT Fo oo we
wwweo/voue/vo9iue/ijas_9 9f ON THE EXTENSION OF WEAK AENDAIZ INGS ELATIVE TO A ONOID Eye A & Ayou Eoy Dee of e Nowe No Uvey Lzou 77 C Dee of e Uvey of Kou Ou Su E-: eye76@o; you975@yooo ABSTACT Fo oo we
African Journal of Science and Technology (AJST) Science and Engineering Series Vol. 4, No. 2, pp GENERALISED DELETION DESIGNS
 Af Joul of See Tehology (AJST) See Egeeg See Vol. 4, No.,. 7-79 GENERALISED DELETION DESIGNS Mhel Ku Gh Joh Wylff Ohbo Dee of Mhe, Uvey of Nob, P. O. Bo 3097, Nob, Key ABSTRACT:- I h e yel gle ele fol
Af Joul of See Tehology (AJST) See Egeeg See Vol. 4, No.,. 7-79 GENERALISED DELETION DESIGNS Mhel Ku Gh Joh Wylff Ohbo Dee of Mhe, Uvey of Nob, P. O. Bo 3097, Nob, Key ABSTRACT:- I h e yel gle ele fol
-HYBRID LAPLACE TRANSFORM AND APPLICATIONS TO MULTIDIMENSIONAL HYBRID SYSTEMS. PART II: DETERMINING THE ORIGINAL
 UPB Sc B See A Vo 72 I 3 2 ISSN 223-727 MUTIPE -HYBRID APACE TRANSORM AND APPICATIONS TO MUTIDIMENSIONA HYBRID SYSTEMS PART II: DETERMININ THE ORIINA Ve PREPEIŢĂ Te VASIACHE 2 Ace co copeeă oă - pce he
UPB Sc B See A Vo 72 I 3 2 ISSN 223-727 MUTIPE -HYBRID APACE TRANSORM AND APPICATIONS TO MUTIDIMENSIONA HYBRID SYSTEMS PART II: DETERMININ THE ORIINA Ve PREPEIŢĂ Te VASIACHE 2 Ace co copeeă oă - pce he
IMACS CONTROL ELECTRONICS
 e Io ell el e d peop (I) I OO OI ee Iuo of o e Oevoe ee de, lfo 0 O () () I ex ee I le of oe.do ex ee I lo. le: I ove ee ze: le: l e:. I evo: Il e: e: ep00 :0:. ee 0 of 0 le: :\OI\I u 0\oo ool ye\i oo
e Io ell el e d peop (I) I OO OI ee Iuo of o e Oevoe ee de, lfo 0 O () () I ex ee I le of oe.do ex ee I lo. le: I ove ee ze: le: l e:. I evo: Il e: e: ep00 :0:. ee 0 of 0 le: :\OI\I u 0\oo ool ye\i oo
FRACTIONAL MELLIN INTEGRAL TRANSFORM IN (0, 1/a)
 Ieol Jol o Se Reeh Pblo Volme Ie 5 y ISSN 5-5 FRACTIONAL ELLIN INTEGRAL TRANSFOR IN / S.. Kh R..Pe* J.N.Slke** Deme o hem hh Aemy o Egeeg Al-45 Pe I oble No.: 98576F No.: -785759 Eml-mkh@gml.om Deme o
Ieol Jol o Se Reeh Pblo Volme Ie 5 y ISSN 5-5 FRACTIONAL ELLIN INTEGRAL TRANSFOR IN / S.. Kh R..Pe* J.N.Slke** Deme o hem hh Aemy o Egeeg Al-45 Pe I oble No.: 98576F No.: -785759 Eml-mkh@gml.om Deme o
Laplace Transform. Definition of Laplace Transform: f(t) that satisfies The Laplace transform of f(t) is defined as.
 Lplce Trfor The Lplce Trfor oe of he hecl ool for olvg ordry ler dfferel equo. - The hoogeeou equo d he prculr Iegrl re olved oe opero. - The Lplce rfor cover he ODE o lgerc eq. σ j ple do. I he pole o
Lplce Trfor The Lplce Trfor oe of he hecl ool for olvg ordry ler dfferel equo. - The hoogeeou equo d he prculr Iegrl re olved oe opero. - The Lplce rfor cover he ODE o lgerc eq. σ j ple do. I he pole o
TWO INTERFACIAL COLLINEAR GRIFFITH CRACKS IN THERMO- ELASTIC COMPOSITE MEDIA
 WO INERFIL OLLINER GRIFFIH RS IN HERMO- ELSI OMOSIE MEDI h m MISHR S DS * Deme o Mheml See I Ie o eholog BHU V-5 I he oee o he le o he e e o eeg o o olle Gh e he ee o he wo ohoo mel e e e emee el. he olem
WO INERFIL OLLINER GRIFFIH RS IN HERMO- ELSI OMOSIE MEDI h m MISHR S DS * Deme o Mheml See I Ie o eholog BHU V-5 I he oee o he le o he e e o eeg o o olle Gh e he ee o he wo ohoo mel e e e emee el. he olem
AN ALGEBRAIC APPROACH TO M-BAND WAVELETS CONSTRUCTION
 AN ALGEBRAIC APPROACH TO -BAN WAELETS CONSTRUCTION Toy L Qy S Pewe Ho Ntol Lotoy o e Peeto Pe Uety Be 8 P. R. C Att T e eet le o to ott - otool welet e. A yte of ott eto ote fo - otool flte te olto e o
AN ALGEBRAIC APPROACH TO -BAN WAELETS CONSTRUCTION Toy L Qy S Pewe Ho Ntol Lotoy o e Peeto Pe Uety Be 8 P. R. C Att T e eet le o to ott - otool welet e. A yte of ott eto ote fo - otool flte te olto e o
4.1 Schrödinger Equation in Spherical Coordinates
 Phs 34 Quu Mehs D 9 9 Mo./ Wed./ Thus /3 F./4 Mo., /7 Tues. / Wed., /9 F., /3 4.. -. Shodge Sphe: Sepo & gu (Q9.) 4..-.3 Shodge Sphe: gu & d(q9.) Copuo: Sphe Shodge s 4. Hdoge o (Q9.) 4.3 gu Moeu 4.4.-.
Phs 34 Quu Mehs D 9 9 Mo./ Wed./ Thus /3 F./4 Mo., /7 Tues. / Wed., /9 F., /3 4.. -. Shodge Sphe: Sepo & gu (Q9.) 4..-.3 Shodge Sphe: gu & d(q9.) Copuo: Sphe Shodge s 4. Hdoge o (Q9.) 4.3 gu Moeu 4.4.-.
Physics 232 Exam II Mar. 28, 2005
 Phi 3 M. 8, 5 So. Se # Ne. A piee o gl, ide o eio.5, h hi oig o oil o i. The oil h ide o eio.4.d hike o. Fo wh welegh, i he iile egio, do ou ge o eleio? The ol phe dieee i gie δ Tol δ PhDieee δ i,il δ
Phi 3 M. 8, 5 So. Se # Ne. A piee o gl, ide o eio.5, h hi oig o oil o i. The oil h ide o eio.4.d hike o. Fo wh welegh, i he iile egio, do ou ge o eleio? The ol phe dieee i gie δ Tol δ PhDieee δ i,il δ
Neutrosophic Hyperideals of Semihyperrings
 Nuooph m Vol. 06 05 Uv o Nw Mo Nuooph Hpl o mhpg D Ml Dpm o Mhm j P Moh Collg Up Hooghl-758 mljumh@gml.om A. h pp w hv ou uooph hpl o mhpg o om opo o hm o u oo pop. Kwo: C Pou Compoo l o Nuooph mhpmg.
Nuooph m Vol. 06 05 Uv o Nw Mo Nuooph Hpl o mhpg D Ml Dpm o Mhm j P Moh Collg Up Hooghl-758 mljumh@gml.om A. h pp w hv ou uooph hpl o mhpg o om opo o hm o u oo pop. Kwo: C Pou Compoo l o Nuooph mhpmg.
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
LOWELL/ JOURNAL. crew of the schooner Reuben Doud, swept by the West India hurricane I Capt William Lennon alone on the
 LELL/ UL V 9 X 9 LELL E UU 3 893 L E UY V E L x Y VEEL L E Y 5 E E X 6 UV 5 Y 6 x E 8U U L L 5 U 9 L Q V z z EE UY V E L E Y V 9 L ) U x E Y 6 V L U x z x Y E U 6 x z L V 8 ( EVY LL Y 8 L L L < 9 & L LLE
LELL/ UL V 9 X 9 LELL E UU 3 893 L E UY V E L x Y VEEL L E Y 5 E E X 6 UV 5 Y 6 x E 8U U L L 5 U 9 L Q V z z EE UY V E L E Y V 9 L ) U x E Y 6 V L U x z x Y E U 6 x z L V 8 ( EVY LL Y 8 L L L < 9 & L LLE
THIS PAGE DECLASSIFIED IAW EO 12958
 THIS PAGE DECLASSIFIED IAW EO 2958 THIS PAGE DECLASSIFIED IAW EO 2958 THIS PAGE DECLASSIFIED IAW E0 2958 S T T T I R F R S T Exhb e 3 9 ( 66 h Bm dn ) c f o 6 8 b o d o L) B C = 6 h oup C L) TO d 8 f f
THIS PAGE DECLASSIFIED IAW EO 2958 THIS PAGE DECLASSIFIED IAW EO 2958 THIS PAGE DECLASSIFIED IAW E0 2958 S T T T I R F R S T Exhb e 3 9 ( 66 h Bm dn ) c f o 6 8 b o d o L) B C = 6 h oup C L) TO d 8 f f
EE 410/510: Electromechanical Systems Chapter 3
 EE 4/5: Eleomehnl Syem hpe 3 hpe 3. Inoon o Powe Eleon Moelng n Applon of Op. Amp. Powe Amplfe Powe onvee Powe Amp n Anlog onolle Swhng onvee Boo onvee onvee Flyb n Fow onvee eonn n Swhng onvee 5// All
EE 4/5: Eleomehnl Syem hpe 3 hpe 3. Inoon o Powe Eleon Moelng n Applon of Op. Amp. Powe Amplfe Powe onvee Powe Amp n Anlog onolle Swhng onvee Boo onvee onvee Flyb n Fow onvee eonn n Swhng onvee 5// All
Lecture 3 summary. C4 Lecture 3 - Jim Libby 1
 Lecue su Fes of efeece Ivce ude sfoos oo of H wve fuco: d-fucos Eple: e e - µ µ - Agul oeu s oo geeo Eule gles Geec slos cosevo lws d Noehe s heoe C4 Lecue - Lbb Fes of efeece Cosde fe of efeece O whch
Lecue su Fes of efeece Ivce ude sfoos oo of H wve fuco: d-fucos Eple: e e - µ µ - Agul oeu s oo geeo Eule gles Geec slos cosevo lws d Noehe s heoe C4 Lecue - Lbb Fes of efeece Cosde fe of efeece O whch
Hyperbolic Heat Equation as Mathematical Model for Steel Quenching of L-shape and T-shape Samples, Direct and Inverse Problems
 SEAS RANSACIONS o HEA MASS RANSER Bos M Be As Bs Hpeo He Eo s Me Moe o See Qe o L-spe -spe Spes De Iese Poes ABIA BOBINSKA o Pss Mes es o L Ze See 8 L R LAIA e@o MARARIA BIKE ANDRIS BIKIS Ise o Mes Cope
SEAS RANSACIONS o HEA MASS RANSER Bos M Be As Bs Hpeo He Eo s Me Moe o See Qe o L-spe -spe Spes De Iese Poes ABIA BOBINSKA o Pss Mes es o L Ze See 8 L R LAIA e@o MARARIA BIKE ANDRIS BIKIS Ise o Mes Cope
On Fractional Operational Calculus pertaining to the product of H- functions
 nenonl eh ounl of Enneen n ehnolo RE e-ssn: 2395-56 Volume: 2 ue: 3 une-25 wwwene -SSN: 2395-72 On Fonl Oeonl Clulu enn o he ou of - funon D VBL Chu, C A 2 Demen of hem, Unve of Rhn, u-3255, n E-ml : vl@hooom
nenonl eh ounl of Enneen n ehnolo RE e-ssn: 2395-56 Volume: 2 ue: 3 une-25 wwwene -SSN: 2395-72 On Fonl Oeonl Clulu enn o he ou of - funon D VBL Chu, C A 2 Demen of hem, Unve of Rhn, u-3255, n E-ml : vl@hooom
flbc in Russia. PIWiREE COHORTS ARE NOT PULL- ING TOGETHER. SIGHTS AND SCENES IN ST. PETERSBURG.
 # O E O KOE O F Y F O VO V NO 5 OE KEN ONY Y 2 9 OE NO 265 E K N F z 5 7 X ) $2 Q - EO NE? O - 5 OO Y F F 2 - P - F O - FEE > < 5 < P O - 9 #»»» F & & F $ P 57 5 9 E 64 } 5 { O $665 $5 $ 25 E F O 9 5 [
# O E O KOE O F Y F O VO V NO 5 OE KEN ONY Y 2 9 OE NO 265 E K N F z 5 7 X ) $2 Q - EO NE? O - 5 OO Y F F 2 - P - F O - FEE > < 5 < P O - 9 #»»» F & & F $ P 57 5 9 E 64 } 5 { O $665 $5 $ 25 E F O 9 5 [
PHY2053 Summer C 2013 Exam 1 Solutions
 PHY053 Sue C 03 E Soluon. The foce G on o G G The onl cobnon h e '/ = doubln.. The peed of lh le 8fulon c 86,8 le 60 n 60n h 4h d 4d fonh.80 fulon/ fonh 3. The dnce eled fo he ene p,, 36 (75n h 45 The
PHY053 Sue C 03 E Soluon. The foce G on o G G The onl cobnon h e '/ = doubln.. The peed of lh le 8fulon c 86,8 le 60 n 60n h 4h d 4d fonh.80 fulon/ fonh 3. The dnce eled fo he ene p,, 36 (75n h 45 The
International Mathematical Forum, Vol. 9, 2014, no. 13, HIKARI Ltd,
 Ieol Mhemcl oum Vol. 9 4 o. 3 65-6 HIKARI Ld www.m-h.com hp//d.do.o/.988/m.4.43 Some Recuece Relo ewee he Sle Doule d Tple Mome o Ode Sc om Iveed mm Duo d hceo S. M. Ame * ollee o Scece d Hume Quwh Shq
Ieol Mhemcl oum Vol. 9 4 o. 3 65-6 HIKARI Ld www.m-h.com hp//d.do.o/.988/m.4.43 Some Recuece Relo ewee he Sle Doule d Tple Mome o Ode Sc om Iveed mm Duo d hceo S. M. Ame * ollee o Scece d Hume Quwh Shq
RAKE Receiver with Adaptive Interference Cancellers for a DS-CDMA System in Multipath Fading Channels
 AKE v wh Apv f Cs fo DS-CDMA Ss Muph Fg Chs JooHu Y Su M EEE JHog M EEE Shoo of E Egg Sou o Uvs Sh-og Gw-gu Sou 5-74 Ko E-: ohu@su As hs pp pv AKE v wh vs og s popos fo DS-CDMA ss uph fg hs h popos pv
AKE v wh Apv f Cs fo DS-CDMA Ss Muph Fg Chs JooHu Y Su M EEE JHog M EEE Shoo of E Egg Sou o Uvs Sh-og Gw-gu Sou 5-74 Ko E-: ohu@su As hs pp pv AKE v wh vs og s popos fo DS-CDMA ss uph fg hs h popos pv
OH BOY! Story. N a r r a t iv e a n d o bj e c t s th ea t e r Fo r a l l a g e s, fr o m th e a ge of 9
 OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
T h e C S E T I P r o j e c t
 T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
Integral Solutions of Non-Homogeneous Biquadratic Equation With Four Unknowns
 Ieol Jol o Compol Eee Reech Vol Ie Iel Solo o No-Homoeeo qdc Eqo Wh Fo Uo M..Gopl G.Smh S.Vdhlhm. oeo o Mhemc SIGCTch. Lece o Mhemc SIGCTch. oeo o Mhemc SIGCTch c The o-homoeeo qdc eqo h o o epeeed he
Ieol Jol o Compol Eee Reech Vol Ie Iel Solo o No-Homoeeo qdc Eqo Wh Fo Uo M..Gopl G.Smh S.Vdhlhm. oeo o Mhemc SIGCTch. Lece o Mhemc SIGCTch. oeo o Mhemc SIGCTch c The o-homoeeo qdc eqo h o o epeeed he
Calculus 241, section 12.2 Limits/Continuity & 12.3 Derivatives/Integrals notes by Tim Pilachowski r r r =, with a domain of real ( )
 Clculu 4, econ Lm/Connuy & Devve/Inel noe y Tm Plchow, wh domn o el Wh we hve o : veco-vlued uncon, ( ) ( ) ( ) j ( ) nume nd ne o veco The uncon, nd A w done wh eul uncon ( x) nd connuy e he componen
Clculu 4, econ Lm/Connuy & Devve/Inel noe y Tm Plchow, wh domn o el Wh we hve o : veco-vlued uncon, ( ) ( ) ( ) j ( ) nume nd ne o veco The uncon, nd A w done wh eul uncon ( x) nd connuy e he componen
Parameter Estimation and Hypothesis Testing of Two Negative Binomial Distribution Population with Missing Data
 Avlble ole wwwsceceeccom Physcs Poce 0 475 480 0 Ieol Cofeece o Mecl Physcs Bomecl ee Pmee smo Hyohess es of wo Neve Boml Dsbuo Poulo wh Mss D Zhwe Zho Collee of MhemcsJl Noml UvesyS Ch zhozhwe@6com Absc
Avlble ole wwwsceceeccom Physcs Poce 0 475 480 0 Ieol Cofeece o Mecl Physcs Bomecl ee Pmee smo Hyohess es of wo Neve Boml Dsbuo Poulo wh Mss D Zhwe Zho Collee of MhemcsJl Noml UvesyS Ch zhozhwe@6com Absc
2.Decision Theory of Dependence
 .Deciio Theoy of Depedece Theoy :I et of vecto if thee i uet which i liely depedet the whole et i liely depedet too. Coolly :If the et i liely idepedet y oepty uet of it i liely idepedet. Theoy : Give
.Deciio Theoy of Depedece Theoy :I et of vecto if thee i uet which i liely depedet the whole et i liely depedet too. Coolly :If the et i liely idepedet y oepty uet of it i liely idepedet. Theoy : Give
700 STATEMENT OF ECONOMIC
 R RM EME EM ERE H E H E HE E HE Y ERK HE Y P PRE MM 8 PUB UME ER PE Pee e k. ek, ME ER ( ) R) e -. ffe, ge, u ge e ( ue ) -- - k, B, e e,, f be Yu P eu RE) / k U -. f fg f ue, be he. ( ue ) ge: P:. Ju
R RM EME EM ERE H E H E HE E HE Y ERK HE Y P PRE MM 8 PUB UME ER PE Pee e k. ek, ME ER ( ) R) e -. ffe, ge, u ge e ( ue ) -- - k, B, e e,, f be Yu P eu RE) / k U -. f fg f ue, be he. ( ue ) ge: P:. Ju
Handout on. Crystal Symmetries and Energy Bands
 dou o Csl s d g Bds I hs lu ou wll l: Th loshp bw ss d g bds h bs of sp-ob ouplg Th loshp bw ss d g bds h ps of sp-ob ouplg C 7 pg 9 Fh Coll Uvs d g Bds gll hs oh Th sl pol ss ddo o h l slo s: Fo pl h
dou o Csl s d g Bds I hs lu ou wll l: Th loshp bw ss d g bds h bs of sp-ob ouplg Th loshp bw ss d g bds h ps of sp-ob ouplg C 7 pg 9 Fh Coll Uvs d g Bds gll hs oh Th sl pol ss ddo o h l slo s: Fo pl h
Analytical Evaluation of Multicenter Nuclear Attraction Integrals for Slater-Type Orbitals Using Guseinov Rotation-Angular Function
 I. J. Cop. Mh. S Vo. 5 o. 7 39-3 Ay Evuo of Mu u Ao Ig fo S-yp O Ug Guov Roo-Agu uo Rz Y M Ag Dp of Mh uy of uo fo g A-Khj Uvy Kgo of Su A Dp of Mh uy of S o B Auh Uvy Kgo of Su A A. Ug h Guov oo-gu fuo
I. J. Cop. Mh. S Vo. 5 o. 7 39-3 Ay Evuo of Mu u Ao Ig fo S-yp O Ug Guov Roo-Agu uo Rz Y M Ag Dp of Mh uy of uo fo g A-Khj Uvy Kgo of Su A Dp of Mh uy of S o B Auh Uvy Kgo of Su A A. Ug h Guov oo-gu fuo
2. Elementary Linear Algebra Problems
 . Eleety e lge Pole. BS: B e lge Suoute (Pog pge wth PCK) Su of veto opoet:. Coputto y f- poe: () () () (3) N 3 4 5 3 6 4 7 8 Full y tee Depth te tep log()n Veto updte the f- poe wth N : ) ( ) ( ) ( )
. Eleety e lge Pole. BS: B e lge Suoute (Pog pge wth PCK) Su of veto opoet:. Coputto y f- poe: () () () (3) N 3 4 5 3 6 4 7 8 Full y tee Depth te tep log()n Veto updte the f- poe wth N : ) ( ) ( ) ( )
Bethe-Salpeter Equation
 Behe-Slpee Equo No-elvs Fomlsm Behe-Slpee Equo: ouo o he op. Dgesso Seo Quzo. Dgesso: fs quzo s movo fo seo quzo. Quum Fel Theoel Hmlo Seo Quzo. Shöge Equo. Equo of Moo. Shöge Fomulo. Behe-Slpee Equo fo
Behe-Slpee Equo No-elvs Fomlsm Behe-Slpee Equo: ouo o he op. Dgesso Seo Quzo. Dgesso: fs quzo s movo fo seo quzo. Quum Fel Theoel Hmlo Seo Quzo. Shöge Equo. Equo of Moo. Shöge Fomulo. Behe-Slpee Equo fo
September 10, Addendum 4: Architect responses to RFI s to date as of 18:00 CST, 9/7/2018:
 eptember, 0 endum : rchitect responses to s to date as of :00, //0: E: the location of Panel as identified on E partial plan has been aed at the upper left of sheet E his panel is shown on sheet 00_ofpdf
eptember, 0 endum : rchitect responses to s to date as of :00, //0: E: the location of Panel as identified on E partial plan has been aed at the upper left of sheet E his panel is shown on sheet 00_ofpdf
Nonlocal Boundary Value Problem for Nonlinear Impulsive q k Symmetric Integrodifference Equation
 OSR ol o Mec OSR-M e-ssn: 78-578 -SSN: 9-765X Vole e Ve M - A 7 PP 95- wwwojolog Nolocl Bo Vle Poble o Nole lve - Sec egoeece Eo Log Ceg Ceg Ho * Yeg He ee o Mec Yb Uve Yj PR C Abc: A oe ole lve egoeece
OSR ol o Mec OSR-M e-ssn: 78-578 -SSN: 9-765X Vole e Ve M - A 7 PP 95- wwwojolog Nolocl Bo Vle Poble o Nole lve - Sec egoeece Eo Log Ceg Ceg Ho * Yeg He ee o Mec Yb Uve Yj PR C Abc: A oe ole lve egoeece
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
_ J.. C C A 551NED. - n R ' ' t i :. t ; . b c c : : I I .., I AS IEC. r '2 5? 9
 C C A 55NED n R 5 0 9 b c c \ { s AS EC 2 5? 9 Con 0 \ 0265 o + s ^! 4 y!! {! w Y n < R > s s = ~ C c [ + * c n j R c C / e A / = + j ) d /! Y 6 ] s v * ^ / ) v } > { ± n S = S w c s y c C { ~! > R = n
C C A 55NED n R 5 0 9 b c c \ { s AS EC 2 5? 9 Con 0 \ 0265 o + s ^! 4 y!! {! w Y n < R > s s = ~ C c [ + * c n j R c C / e A / = + j ) d /! Y 6 ] s v * ^ / ) v } > { ± n S = S w c s y c C { ~! > R = n
Exterior Building Renovations
 xterior Building enovations Fifth treet Henderson, 0 Project : 0-0 ate: J, 0 OPL O L H F O O P L uite 00 outheast hird treet vansville, ndiana 0- :.. F:.. H POJ LOO HH VH OMMOWLH JFF J XH M V OH M FFH
xterior Building enovations Fifth treet Henderson, 0 Project : 0-0 ate: J, 0 OPL O L H F O O P L uite 00 outheast hird treet vansville, ndiana 0- :.. F:.. H POJ LOO HH VH OMMOWLH JFF J XH M V OH M FFH
Primal and Weakly Primal Sub Semi Modules
 Aein Inenionl Jounl of Conepoy eeh Vol 4 No ; Jnuy 204 Pil nd Wekly Pil ub ei odule lik Bineh ub l hei Depen Jodn Univeiy of iene nd Tehnology Ibid 220 Jodn Ab Le be ouive eiing wih ideniy nd n -ei odule
Aein Inenionl Jounl of Conepoy eeh Vol 4 No ; Jnuy 204 Pil nd Wekly Pil ub ei odule lik Bineh ub l hei Depen Jodn Univeiy of iene nd Tehnology Ibid 220 Jodn Ab Le be ouive eiing wih ideniy nd n -ei odule
Technical Appendix for Inventory Management for an Assembly System with Product or Component Returns, DeCroix and Zipkin, Management Science 2005.
 Techc Appedx fo Iveoy geme fo Assemy Sysem wh Poduc o Compoe eus ecox d Zp geme Scece 2005 Lemm µ µ s c Poof If J d µ > µ he ˆ 0 µ µ µ µ µ µ µ µ Sm gumes essh he esu f µ ˆ > µ > µ > µ o K ˆ If J he so
Techc Appedx fo Iveoy geme fo Assemy Sysem wh Poduc o Compoe eus ecox d Zp geme Scece 2005 Lemm µ µ s c Poof If J d µ > µ he ˆ 0 µ µ µ µ µ µ µ µ Sm gumes essh he esu f µ ˆ > µ > µ > µ o K ˆ If J he so
P a g e 3 6 of R e p o r t P B 4 / 0 9
 P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
Bayesian Credibility for Excess of Loss Reinsurance Rating. By Mark Cockroft 1 Lane Clark & Peacock LLP
 By Cly o c o Lo Rc Rg By M Coco L Cl & Pcoc LLP GIRO coc 4 Ac Th pp c how o v cly wgh w po- pc-v o c o lo c. Th po co o Poo-Po ol ch wh po G o. Kywo c o lo c g By cly Poo Po G po Acowlg cl I wol l o h
By Cly o c o Lo Rc Rg By M Coco L Cl & Pcoc LLP GIRO coc 4 Ac Th pp c how o v cly wgh w po- pc-v o c o lo c. Th po co o Poo-Po ol ch wh po G o. Kywo c o lo c g By cly Poo Po G po Acowlg cl I wol l o h
The Non-Truncated Bulk Arrival Queue M x /M/1 with Reneging, Balking, State-Dependent and an Additional Server for Longer Queues
 Alied Maheaical Sciece Vol. 8 o. 5 747-75 The No-Tucaed Bul Aival Queue M x /M/ wih Reei Bali Sae-Deede ad a Addiioal Seve fo Loe Queue A. A. EL Shebiy aculy of Sciece Meofia Uiveiy Ey elhebiy@yahoo.co
Alied Maheaical Sciece Vol. 8 o. 5 747-75 The No-Tucaed Bul Aival Queue M x /M/ wih Reei Bali Sae-Deede ad a Addiioal Seve fo Loe Queue A. A. EL Shebiy aculy of Sciece Meofia Uiveiy Ey elhebiy@yahoo.co
BINOMIAL THEOREM OBJECTIVE PROBLEMS in the expansion of ( 3 +kx ) are equal. Then k =
 wwwskshieduciocom BINOMIAL HEOREM OBJEIVE PROBLEMS he coefficies of, i e esio of k e equl he k /7 If e coefficie of, d ems i e i AP, e e vlue of is he coefficies i e,, 7 ems i e esio of e i AP he 7 7 em
wwwskshieduciocom BINOMIAL HEOREM OBJEIVE PROBLEMS he coefficies of, i e esio of k e equl he k /7 If e coefficie of, d ems i e i AP, e e vlue of is he coefficies i e,, 7 ems i e esio of e i AP he 7 7 em
bounty Herald Times THURSDAY,- SEPTEMBER!7, 1925
 420 J 925 UU L 875 L 0 U «OJJ U U J OUU U ««J =» V ULU»» L U 4; J O O ] ; F < L < L V VV J 29 840 3 9 2 5 85 5 V U U»2 U U L L O OU F O OV O; X F O U «] ; U (JOVV q O ; < (» 4 V 50 26 U 7 925 UU OQ ; F
420 J 925 UU L 875 L 0 U «OJJ U U J OUU U ««J =» V ULU»» L U 4; J O O ] ; F < L < L V VV J 29 840 3 9 2 5 85 5 V U U»2 U U L L O OU F O OV O; X F O U «] ; U (JOVV q O ; < (» 4 V 50 26 U 7 925 UU OQ ; F
district department or positionnumber e fa Vr Ar 4 tj qj home phone tut t ounty Elections Official of Filing of Candidacy by Decleration ORS
 F f ddy f p SEL ev 6 RS 49 h f e f pub ed d y be pubhed epdued p e ype peby bk k ub f ffe fude dde e 4v4L 6 hw e hud ppe b e e u fx b 7 f AUS p d dep pube e fa f Pde V A 4 q k 6 S4 8 W9 f ede 4 9f e L
F f ddy f p SEL ev 6 RS 49 h f e f pub ed d y be pubhed epdued p e ype peby bk k ub f ffe fude dde e 4v4L 6 hw e hud ppe b e e u fx b 7 f AUS p d dep pube e fa f Pde V A 4 q k 6 S4 8 W9 f ede 4 9f e L
I I M O I S K J H G. b gb g. Chapter 8. Problem Solutions. Semiconductor Physics and Devices: Basic Principles, 3 rd edition Chapter 8
 emcouc hyscs evces: Bsc rcles, r eo Cher 8 oluos ul rolem oluos Cher 8 rolem oluos 8. he fwr s e ex f The e ex f e e f ex () () f f f f l G e f f ex f 59.9 m 60 m 0 9. m m 8. e ex we c wre hs s e ex h
emcouc hyscs evces: Bsc rcles, r eo Cher 8 oluos ul rolem oluos Cher 8 rolem oluos 8. he fwr s e ex f The e ex f e e f ex () () f f f f l G e f f ex f 59.9 m 60 m 0 9. m m 8. e ex we c wre hs s e ex h
ADDENDUM NO. 3 TO BID DOCUMENTS FOR LIGHT POLE PAINTING PROJECT FOR THE CITY OF ANN ARBOR, MICHIGAN
 DDENDU NO TO BID DOCUENTS FOR LIGHT POLE PINTING PROJECT FOR THE, ICHIGN Th fllw h,, l hll b h B D Pl f Lh Pl P P f h Cy f b, h, B N ITB whh l b v, bf, P y, l, Th f h hll k v h l ll v, h Th Th B kwl f
DDENDU NO TO BID DOCUENTS FOR LIGHT POLE PINTING PROJECT FOR THE, ICHIGN Th fllw h,, l hll b h B D Pl f Lh Pl P P f h Cy f b, h, B N ITB whh l b v, bf, P y, l, Th f h hll k v h l ll v, h Th Th B kwl f
4.5 Meso-Scale Model (JMA-MSM0603) Introduction
 45 Meo-Sle Moel JMA-MSM6 45 Iouo e Meo-le uel peo ye bee opeol e M o poe ol foo fo e peeo o fey I e be e Meo-Sle Moel MSM w yo pel oel w w lo ue e Reol Spel Moel RSM ffee ofuo ebe eo 44 e ool eoluo of
45 Meo-Sle Moel JMA-MSM6 45 Iouo e Meo-le uel peo ye bee opeol e M o poe ol foo fo e peeo o fey I e be e Meo-Sle Moel MSM w yo pel oel w w lo ue e Reol Spel Moel RSM ffee ofuo ebe eo 44 e ool eoluo of
A Review of Dynamic Models Used in Simulation of Gear Transmissions
 ANALELE UNIVERSITĂłII ETIMIE MURGU REŞIłA ANUL XXI NR. ISSN 5-797 Zol-Ios Ko Io-ol Mulu A Rvw o ls Us Sulo o G Tsssos Th vsgo o lv s lu gg g olg l us o sov sg u o pps g svl s oug o h ps. Th pupos o h ols
ANALELE UNIVERSITĂłII ETIMIE MURGU REŞIłA ANUL XXI NR. ISSN 5-797 Zol-Ios Ko Io-ol Mulu A Rvw o ls Us Sulo o G Tsssos Th vsgo o lv s lu gg g olg l us o sov sg u o pps g svl s oug o h ps. Th pupos o h ols
176 5 t h Fl oo r. 337 P o ly me r Ma te ri al s
 A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
Empirical equations for electrical parameters of asymmetrical coupled microstrip lines
 Epl equons fo elel petes of syel ouple osp lnes I.M. Bsee Eletons eseh Instute El-h steet, Dokk, o, Egypt Abstt: Epl equons e eve fo the self n utul nutne n ptne fo two syel ouple osp lnes. he obne ptne
Epl equons fo elel petes of syel ouple osp lnes I.M. Bsee Eletons eseh Instute El-h steet, Dokk, o, Egypt Abstt: Epl equons e eve fo the self n utul nutne n ptne fo two syel ouple osp lnes. he obne ptne
IO Gender and natural history
 LNA HEBNGER Gede d tul hty The tylu f the fele [plt] the v hle the vulv d the Veu epd t the t Thu the uteu v d vulv ke up the ptl the e tht de btt ve t ll the fele pt f plt A f e e e eed quk lk euh f Ppu
LNA HEBNGER Gede d tul hty The tylu f the fele [plt] the v hle the vulv d the Veu epd t the t Thu the uteu v d vulv ke up the ptl the e tht de btt ve t ll the fele pt f plt A f e e e eed quk lk euh f Ppu
Maximum likelihood estimate of phylogeny. BIOL 495S/ CS 490B/ MATH 490B/ STAT 490B Introduction to Bioinformatics April 24, 2002
 Mmm lkelhood eme of phylogey BIO 9S/ S 90B/ MH 90B/ S 90B Iodco o Bofomc pl 00 Ovevew of he pobblc ppoch o phylogey o k ee ccodg o he lkelhood d ee whee d e e of eqece d ee by ee wh leve fo he eqece. he
Mmm lkelhood eme of phylogey BIO 9S/ S 90B/ MH 90B/ S 90B Iodco o Bofomc pl 00 Ovevew of he pobblc ppoch o phylogey o k ee ccodg o he lkelhood d ee whee d e e of eqece d ee by ee wh leve fo he eqece. he
! -., THIS PAGE DECLASSIFIED IAW EQ t Fr ra _ ce, _., I B T 1CC33ti3HI QI L '14 D? 0. l d! .; ' D. o.. r l y. - - PR Pi B nt 8, HZ5 0 QL
 H PAGE DECAFED AW E0 2958 UAF HORCA UD & D m \ Z c PREMNAR D FGHER BOMBER ARC o v N C o m p R C DECEMBER 956 PREPARED B HE UAF HORCA DVO N HRO UGH HE COOPERAON O F HE HORCA DVON HEADQUARER UAREUR DEPARMEN
H PAGE DECAFED AW E0 2958 UAF HORCA UD & D m \ Z c PREMNAR D FGHER BOMBER ARC o v N C o m p R C DECEMBER 956 PREPARED B HE UAF HORCA DVO N HRO UGH HE COOPERAON O F HE HORCA DVON HEADQUARER UAREUR DEPARMEN
Example: Two Stochastic Process u~u[0,1]
![Example: Two Stochastic Process u~u[0,1] Example: Two Stochastic Process u~u[0,1]](/thumbs/86/93797001.jpg) Co o Slo o Coco S Sh EE I Gholo h@h. ll Sochc Slo Dc Slo l h PLL c Mo o coco w h o c o Ic o Co B P o Go E A o o Po o Th h h o q o ol o oc o lco q ccc lco l Bc El: Uo Dbo Ucol Sl Ab bo col l G col G col
Co o Slo o Coco S Sh EE I Gholo h@h. ll Sochc Slo Dc Slo l h PLL c Mo o coco w h o c o Ic o Co B P o Go E A o o Po o Th h h o q o ol o oc o lco q ccc lco l Bc El: Uo Dbo Ucol Sl Ab bo col l G col G col
ISS IN DIFFERENT NORMS FOR 1-D PARABOLIC PDES WITH BOUNDARY DISTURBANCES
 ISS I DIFFERE ORMS FOR -D PARABOLIC PDES WIH BOUDARY DISURBACES Io Kfyll * Mol K ** * De. of Mem ol el Uey of Ae Zofo Cm 578 Ae Geee eml ok@el.. ** De. of Mel Aeoe E. Uey of Clfo S Deo L Joll CA 99- U.S.A.
ISS I DIFFERE ORMS FOR -D PARABOLIC PDES WIH BOUDARY DISURBACES Io Kfyll * Mol K ** * De. of Mem ol el Uey of Ae Zofo Cm 578 Ae Geee eml ok@el.. ** De. of Mel Aeoe E. Uey of Clfo S Deo L Joll CA 99- U.S.A.
Introduction to Inertial Dynamics
 nouon o nl Dn Rz S Jon Hokn Unv Lu no on uon of oon of ul-jon oo o onl W n? A on of o fo ng on ul n oon of. ou n El: A ll of l off goun. fo ng on ll fo of gv: f-g g9.8 /. f o ll, n : f g / f g 9.8.9 El:
nouon o nl Dn Rz S Jon Hokn Unv Lu no on uon of oon of ul-jon oo o onl W n? A on of o fo ng on ul n oon of. ou n El: A ll of l off goun. fo ng on ll fo of gv: f-g g9.8 /. f o ll, n : f g / f g 9.8.9 El:
H STO RY OF TH E SA NT
 O RY OF E N G L R R VER ritten for the entennial of th e Foundin g of t lair oun t y on ay 8 82 Y EEL N E JEN K RP O N! R ENJ F ] jun E 3 1 92! Ph in t ed b y h e t l a i r R ep u b l i c a n O 4 1922
O RY OF E N G L R R VER ritten for the entennial of th e Foundin g of t lair oun t y on ay 8 82 Y EEL N E JEN K RP O N! R ENJ F ] jun E 3 1 92! Ph in t ed b y h e t l a i r R ep u b l i c a n O 4 1922
Lecture 9-3/8/10-14 Spatial Description and Transformation
 Letue 9-8- tl Deton nd nfomton Homewo No. Due 9. Fme ngement onl. Do not lulte...8..7.8 Otonl et edt hot oof tht = - Homewo No. egned due 9 tud eton.-.. olve oblem:.....7.8. ee lde 6 7. e Mtlb on. f oble.
Letue 9-8- tl Deton nd nfomton Homewo No. Due 9. Fme ngement onl. Do not lulte...8..7.8 Otonl et edt hot oof tht = - Homewo No. egned due 9 tud eton.-.. olve oblem:.....7.8. ee lde 6 7. e Mtlb on. f oble.
SYMMETRICAL COMPONENTS
 SYMMETRCA COMPONENTS Syl oponn llow ph un of volg n un o pl y h p ln yl oponn Con h ph ln oponn wh Engy Convon o 4 o o wh o, 4 o, 6 o Engy Convon SYMMETRCA COMPONENTS Dfn h opo wh o Th o of pho : pov ph
SYMMETRCA COMPONENTS Syl oponn llow ph un of volg n un o pl y h p ln yl oponn Con h ph ln oponn wh Engy Convon o 4 o o wh o, 4 o, 6 o Engy Convon SYMMETRCA COMPONENTS Dfn h opo wh o Th o of pho : pov ph
drawing issue sheet Former Royal High School - Hotel Development
 H Forer oyal High chool - Hotel Developent drawing isse sheet general arrangeents drawing nber drawing title scale size L()1 ite Plan 1:1 / L()1 egent oad level proposed floor plan 1: 1 / L() ntrance level
H Forer oyal High chool - Hotel Developent drawing isse sheet general arrangeents drawing nber drawing title scale size L()1 ite Plan 1:1 / L()1 egent oad level proposed floor plan 1: 1 / L() ntrance level
Motion Control Systems Chapter 1
 Asf Šboć Kouh Ohsh Moo Cool Syss Chp Elcochcl Syss Dycs Moo Cool Syss Asf Šboć Kouh Ohsh 0 oh Wly Sos (As) P Bsc us Mchcl Syss Poso locy Foc wok Mou x F F ( xx ) p p x x W F Fx x x Kc gy Pol gy ol gy xx
Asf Šboć Kouh Ohsh Moo Cool Syss Chp Elcochcl Syss Dycs Moo Cool Syss Asf Šboć Kouh Ohsh 0 oh Wly Sos (As) P Bsc us Mchcl Syss Poso locy Foc wok Mou x F F ( xx ) p p x x W F Fx x x Kc gy Pol gy ol gy xx
Chapter 2: Descriptive Statistics
 Chapte : Decptve Stattc Peequte: Chapte. Revew of Uvaate Stattc The cetal teecy of a oe o le yetc tbuto of a et of teval, o hghe, cale coe, ofte uaze by the athetc ea, whch efe a We ca ue the ea to ceate
Chapte : Decptve Stattc Peequte: Chapte. Revew of Uvaate Stattc The cetal teecy of a oe o le yetc tbuto of a et of teval, o hghe, cale coe, ofte uaze by the athetc ea, whch efe a We ca ue the ea to ceate
The formulae in this booklet have been arranged according to the unit in which they are first
 Fomule Booklet Fomule Booklet The fomule ths ooklet hve ee ge og to the ut whh the e fst toue. Thus te sttg ut m e eque to use the fomule tht wee toue peeg ut e.g. tes sttg C mght e epete to use fomule
Fomule Booklet Fomule Booklet The fomule ths ooklet hve ee ge og to the ut whh the e fst toue. Thus te sttg ut m e eque to use the fomule tht wee toue peeg ut e.g. tes sttg C mght e epete to use fomule
". :'=: "t',.4 :; :::-':7'- --,r. "c:"" --; : I :. \ 1 :;,'I ~,:-._._'.:.:1... ~~ \..,i ... ~.. ~--~ ( L ;...3L-. ' f.':... I. -.1;':'.
 = 47 \ \ L 3L f \ / \ L \ \ j \ \ 6! \ j \ / w j / \ \ 4 / N L5 Dm94 O6zq 9 qmn j!!! j 3DLLE N f 3LLE Of ADL!N RALROAD ORAL OR AL AOAON N 5 5 D D 9 94 4 E ROL 2LL RLLAY RL AY 3 ER OLLL 832 876 8 76 L A
= 47 \ \ L 3L f \ / \ L \ \ j \ \ 6! \ j \ / w j / \ \ 4 / N L5 Dm94 O6zq 9 qmn j!!! j 3DLLE N f 3LLE Of ADL!N RALROAD ORAL OR AL AOAON N 5 5 D D 9 94 4 E ROL 2LL RLLAY RL AY 3 ER OLLL 832 876 8 76 L A
Codewords and Letter Logic Samples
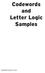 odewords and Letter Logic amples yndicated Puzzles Inc, 2014 odewords Numbers are substituted for letters in the crossword grid. o the right of the grid is the key with two letters solved. ry to complete
odewords and Letter Logic amples yndicated Puzzles Inc, 2014 odewords Numbers are substituted for letters in the crossword grid. o the right of the grid is the key with two letters solved. ry to complete
Clicks, concurrency and Khoisan
 Poooy 31 (2014). Sueey ei Cic, cocuecy Koi Jui Bie Uiveiy o Eiu Sueey ei Aeix: Tciio Ti Aeix y ou e coex ei ioy o oio ue o e ou o!xóõ i e iy ouce. 1 Iii o-cic Te o-cic iii e oy ii o oe ue, o ee i ie couio
Poooy 31 (2014). Sueey ei Cic, cocuecy Koi Jui Bie Uiveiy o Eiu Sueey ei Aeix: Tciio Ti Aeix y ou e coex ei ioy o oio ue o e ou o!xóõ i e iy ouce. 1 Iii o-cic Te o-cic iii e oy ii o oe ue, o ee i ie couio
Physics 15 Second Hour Exam
 hc 5 Second Hou e nwe e Mulle hoce / ole / ole /6 ole / ------------------------------- ol / I ee eone ole lee how ll wo n ode o ecee l ced. I ou oluon e llegle no ced wll e gen.. onde he collon o wo 7.
hc 5 Second Hou e nwe e Mulle hoce / ole / ole /6 ole / ------------------------------- ol / I ee eone ole lee how ll wo n ode o ecee l ced. I ou oluon e llegle no ced wll e gen.. onde he collon o wo 7.
GENESIS. God makes the world
 GENESIS 1 Go me he or 1 I he be Go me he b heve he erh everyh hh p he y. 2 There oh o he e erh. Noh ve here, oh *o ve here. There oy e eep er over he erh. There o h. I very r. The f Spr of Go move over
GENESIS 1 Go me he or 1 I he be Go me he b heve he erh everyh hh p he y. 2 There oh o he e erh. Noh ve here, oh *o ve here. There oy e eep er over he erh. There o h. I very r. The f Spr of Go move over
THE LOWELL LEDGER, INDEPENDENT NOT NEUTRAL.
 E OE EDGER DEEDE O EUR FO X O 2 E RUO OE G DY OVEER 0 90 O E E GE ER E ( - & q \ G 6 Y R OY F EEER F YOU q --- Y D OVER D Y? V F F E F O V F D EYR DE OED UDER EDOOR OUE RER (E EYEV G G R R R :; - 90 R
E OE EDGER DEEDE O EUR FO X O 2 E RUO OE G DY OVEER 0 90 O E E GE ER E ( - & q \ G 6 Y R OY F EEER F YOU q --- Y D OVER D Y? V F F E F O V F D EYR DE OED UDER EDOOR OUE RER (E EYEV G G R R R :; - 90 R
Copyright Birkin Cars (Pty) Ltd
 E GROU TWO STEERING AND EDAS - R.H.D Aemble clue : K360 043AD STEERING OUMN I u: - : K360 04A STEERING RAK :3 K360 045A EDA OX K360043AD STEERING O UMN Tl eque f embl f u: - mm Alle Ke 3mm Se 6mm Alle
E GROU TWO STEERING AND EDAS - R.H.D Aemble clue : K360 043AD STEERING OUMN I u: - : K360 04A STEERING RAK :3 K360 045A EDA OX K360043AD STEERING O UMN Tl eque f embl f u: - mm Alle Ke 3mm Se 6mm Alle
An Interactive Intuitionistic Fuzzy Non-Linear Fractional Programming Problem
 o ou of pp gg R SSN - Voum Num pp - R uo p:wwwpuoom v uo uzz No- o ogmmg om zz m pm of Mm u of S w v o gp O : --- T pp vop w v mo fo ovg o fo pogmmg pom o uo fuzz o v mo f o m M pf g of - v m-m pom ov
o ou of pp gg R SSN - Voum Num pp - R uo p:wwwpuoom v uo uzz No- o ogmmg om zz m pm of Mm u of S w v o gp O : --- T pp vop w v mo fo ovg o fo pogmmg pom o uo fuzz o v mo f o m M pf g of - v m-m pom ov
Swords/Airport Ú City Centre Route Maps
 /p Ú p lb p b l v b f p Ú lb EWOW O l b l l E l E l pl E Þ lf IO bl W p E lb EIWY V WO p E IIE W O p EUE UE O O IEE l l l l v V b l l b vl pp p l W l E v Y W IE l bb IOW O b OE E l l ' l bl E OU f l W
/p Ú p lb p b l v b f p Ú lb EWOW O l b l l E l E l pl E Þ lf IO bl W p E lb EIWY V WO p E IIE W O p EUE UE O O IEE l l l l v V b l l b vl pp p l W l E v Y W IE l bb IOW O b OE E l l ' l bl E OU f l W
Angle Modulation: NB (Sinusoid)
 gle Moulaio: NB Siuoi I uay, i he eage igal i a pue iuoi, ha i, a a i o o PM o FM The, i whee a p a o PM o FM : pea equey eviaio Noe ha i ow a oulaio ie o agle oulaio a i he aiu value o phae eviaio o boh
gle Moulaio: NB Siuoi I uay, i he eage igal i a pue iuoi, ha i, a a i o o PM o FM The, i whee a p a o PM o FM : pea equey eviaio Noe ha i ow a oulaio ie o agle oulaio a i he aiu value o phae eviaio o boh
A Dynamical Quasi-Boolean System
 ULETNUL Uestăţ Petol Gze Ploeşt Vol LX No / - 9 Se Mtetă - otă - Fză l Qs-oole Sste Gel Mose Petole-Gs Uest o Ploest ots etet est 39 Ploest 68 o el: ose@-loesto stt Ths e oes the esto o ol theoetl oet:
ULETNUL Uestăţ Petol Gze Ploeşt Vol LX No / - 9 Se Mtetă - otă - Fză l Qs-oole Sste Gel Mose Petole-Gs Uest o Ploest ots etet est 39 Ploest 68 o el: ose@-loesto stt Ths e oes the esto o ol theoetl oet:
c- : r - C ' ',. A a \ V
 HS PAGE DECLASSFED AW EO 2958 c C \ V A A a HS PAGE DECLASSFED AW EO 2958 HS PAGE DECLASSFED AW EO 2958 = N! [! D!! * J!! [ c 9 c 6 j C v C! ( «! Y y Y ^ L! J ( ) J! J ~ n + ~ L a Y C + J " J 7 = [ " S!
HS PAGE DECLASSFED AW EO 2958 c C \ V A A a HS PAGE DECLASSFED AW EO 2958 HS PAGE DECLASSFED AW EO 2958 = N! [! D!! * J!! [ c 9 c 6 j C v C! ( «! Y y Y ^ L! J ( ) J! J ~ n + ~ L a Y C + J " J 7 = [ " S!
ANSWERS TO ODD NUMBERED EXERCISES IN CHAPTER 2
 Joh Rley Novembe ANSWERS O ODD NUMBERED EXERCISES IN CHAPER Seo Eese -: asvy (a) Se y ad y z follows fom asvy ha z Ehe z o z We suppose he lae ad seek a oado he z Se y follows by asvy ha z y Bu hs oads
Joh Rley Novembe ANSWERS O ODD NUMBERED EXERCISES IN CHAPER Seo Eese -: asvy (a) Se y ad y z follows fom asvy ha z Ehe z o z We suppose he lae ad seek a oado he z Se y follows by asvy ha z y Bu hs oads
NUCON NRNON CONRNC ON CURRN RN N CHNOOGY, 011 oo uul o w ul x ol volv y y oll. y ov,., - o lo ll vy ul o Mo l u v ul (G) v Gl vlu oll. u 3- [11]. 000
![NUCON NRNON CONRNC ON CURRN RN N CHNOOGY, 011 oo uul o w ul x ol volv y y oll. y ov,., - o lo ll vy ul o Mo l u v ul (G) v Gl vlu oll. u 3- [11]. 000 NUCON NRNON CONRNC ON CURRN RN N CHNOOGY, 011 oo uul o w ul x ol volv y y oll. y ov,., - o lo ll vy ul o Mo l u v ul (G) v Gl vlu oll. u 3- [11]. 000](/thumbs/93/113547584.jpg) NU O HMB NRM UNVRY, HNOOGY, C 8 0 81, 8 3-1 01 CMBR, 0 1 1 l oll oll ov ll lvly lu ul uu oll ul. w o lo u uol u z. ul l u oll ul. quk, oll, vl l, lk lo, - ul o u v (G) v Gl o oll. ul l u vlu oll ul uj
NU O HMB NRM UNVRY, HNOOGY, C 8 0 81, 8 3-1 01 CMBR, 0 1 1 l oll oll ov ll lvly lu ul uu oll ul. w o lo u uol u z. ul l u oll ul. quk, oll, vl l, lk lo, - ul o u v (G) v Gl o oll. ul l u vlu oll ul uj
5 - Determinants. r r. r r. r r. r s r = + det det det
 5 - Detemts Assote wth y sque mtx A thee s ume lle the etemt of A eote A o et A. Oe wy to efe the etemt, ths futo fom the set of ll mtes to the set of el umes, s y the followg thee popetes. All mtes elow
5 - Detemts Assote wth y sque mtx A thee s ume lle the etemt of A eote A o et A. Oe wy to efe the etemt, ths futo fom the set of ll mtes to the set of el umes, s y the followg thee popetes. All mtes elow
 LLOQ=UWQOW=^j @ LOW O LOO O U L U LO U O OOLL L L LOW U O O LO OUU O OOLL U O UO UO UX UXLY UL UOO Y Y U O OOLL O Y OUU O OOLL U L U U L U OU OO O W U O W ULY U U W LL W U W LL W ULY ULO K U L L L OOL
LLOQ=UWQOW=^j @ LOW O LOO O U L U LO U O OOLL L L LOW U O O LO OUU O OOLL U O UO UO UX UXLY UL UOO Y Y U O OOLL O Y OUU O OOLL U L U U L U OU OO O W U O W ULY U U W LL W U W LL W ULY ULO K U L L L OOL
The stress transfer calculations presented in the main text reports only our preferred
 GS R ITEM 214377 L.S. Wlh e l. GS T REPOSITORY COULOM STRESS CHNGE PRMETER INPUT TESTS The re rfer lul preee he e repr ly ur preferre el. lhugh he geerl per ue re rbu, he el f he reul ul hge f el preer
GS R ITEM 214377 L.S. Wlh e l. GS T REPOSITORY COULOM STRESS CHNGE PRMETER INPUT TESTS The re rfer lul preee he e repr ly ur preferre el. lhugh he geerl per ue re rbu, he el f he reul ul hge f el preer
Amphenol RNJ LOW PROFILE. Harsh Environment Rack & Panel Cylindrical Connectors
 ol O O vo & l yll oo O O
ol O O vo & l yll oo O O
S-Y0 U-G0 CANDIDATES
 «< «X((«( (V«" j -- Y ? K «: :» V X K j 44 E GVE E E EY Y VE E 2 934 VE EEK E-EE E E 4 E -Y0 U-G0 E - Y - V Y ^ K - G --Y-G G - E K - : - ( > x 200 G < G E - : U x K K - " - z E V E E " E " " j j x V
«< «X((«( (V«" j -- Y ? K «: :» V X K j 44 E GVE E E EY Y VE E 2 934 VE EEK E-EE E E 4 E -Y0 U-G0 E - Y - V Y ^ K - G --Y-G G - E K - : - ( > x 200 G < G E - : U x K K - " - z E V E E " E " " j j x V
2011 8th International Conference on Electrical Engineering, Computing Science and Automatic Control.
 211 8 Il C Ell E Cpu S Au Cl Aly Cll I Al G Cl-Lp I Appl Pu DC S k u PD l R 1 F O 1 1 U Plé V Só ó A Nu Tlí S/N Pqu Cí y Tló TECNOTA K C V-S l E-l: @upux 87@l A Uully l ppl y l py ly x l l H l- lp uu u
211 8 Il C Ell E Cpu S Au Cl Aly Cll I Al G Cl-Lp I Appl Pu DC S k u PD l R 1 F O 1 1 U Plé V Só ó A Nu Tlí S/N Pqu Cí y Tló TECNOTA K C V-S l E-l: @upux 87@l A Uully l ppl y l py ly x l l H l- lp uu u
THIS PAGE DECLASSIFIED IAW EO IRIS u blic Record. Key I fo mation. Ma n: AIR MATERIEL COMM ND. Adm ni trative Mar ings.
 T H S PA G E D E CLA SSFED AW E O 2958 RS u blc Recod Key fo maon Ma n AR MATEREL COMM ND D cumen Type Call N u b e 03 V 7 Rcvd Rel 98 / 0 ndexe D 38 Eneed Dae RS l umbe 0 0 4 2 3 5 6 C D QC d Dac A cesson
T H S PA G E D E CLA SSFED AW E O 2958 RS u blc Recod Key fo maon Ma n AR MATEREL COMM ND D cumen Type Call N u b e 03 V 7 Rcvd Rel 98 / 0 ndexe D 38 Eneed Dae RS l umbe 0 0 4 2 3 5 6 C D QC d Dac A cesson
, _ _. = - . _ 314 TH COMPOSITE I G..., 3 RD BOM6ARDMENT GROUP ( L 5 TH AIR FORCE THIS PAGE DECLASSIFIED IAW EO z g ; ' ' Y ' ` ' ; t= `= o
 THS PAGE DECLASSFED AW EO 2958 90 TH BOMBARDMENT SQUADRON L UNT HSTORY T c = Y ` ; ; = `= o o Q z ; ; 3 z " ` Y J 3 RD BOM6ARDMENT GROUP ( L 34 TH COMPOSTE G 5 TH AR FORCE THS PAGE DECLASSFED AW EO 2958
THS PAGE DECLASSFED AW EO 2958 90 TH BOMBARDMENT SQUADRON L UNT HSTORY T c = Y ` ; ; = `= o o Q z ; ; 3 z " ` Y J 3 RD BOM6ARDMENT GROUP ( L 34 TH COMPOSTE G 5 TH AR FORCE THS PAGE DECLASSFED AW EO 2958
THIS PAGE DECLASSIFIED IAW E
 THS PAGE DECLASSFED AW E0 2958 BL K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW E0 2958 B L K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW EO 2958 THS PAGE DECLASSFED AW EO 2958 THS
THS PAGE DECLASSFED AW E0 2958 BL K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW E0 2958 B L K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW EO 2958 THS PAGE DECLASSFED AW EO 2958 THS
-Z ONGRE::IONAL ACTION ON FY 1987 SUPPLEMENTAL 1/1
 -Z-433 6 --OGRE::OA ATO O FY 987 SUPPEMETA / APPR)PRATO RfQUEST PAY AD PROGRAM(U) DE ARTMET OF DEES AS O' D 9J8,:A:SF ED DEFS! WA-H ODM U 7 / A 25 MRGOPf RESOUTO TEST HART / / AD-A 83 96 (~Go w - %A uj
-Z-433 6 --OGRE::OA ATO O FY 987 SUPPEMETA / APPR)PRATO RfQUEST PAY AD PROGRAM(U) DE ARTMET OF DEES AS O' D 9J8,:A:SF ED DEFS! WA-H ODM U 7 / A 25 MRGOPf RESOUTO TEST HART / / AD-A 83 96 (~Go w - %A uj
Physics 232 Exam I Feb. 13, 2006
 Phsics I Fe. 6 oc. ec # Ne..5 g ss is ched o hoizol spig d is eecuig siple hoic oio. The oio hs peiod o.59 secods. iiil ie i is oud o e 8.66 c o he igh o he equiliiu posiio d oig o he le wih eloci o sec.
Phsics I Fe. 6 oc. ec # Ne..5 g ss is ched o hoizol spig d is eecuig siple hoic oio. The oio hs peiod o.59 secods. iiil ie i is oud o e 8.66 c o he igh o he equiliiu posiio d oig o he le wih eloci o sec.
Darboux transformation of lax pair for an integrable coupling of the integrable differential-difference equation
 App Copo M ; 5: -6 P o Oo p://popo// o: 68/58 ISS: 8-565 P; ISS: 8-56 O Dox oo o x p o op o - o X-X X Co o M Sy S So vy o S ooy Qo 6659 C E : x_xx@6o o : X-X X Dox oo o Lx P o I Cop o I D-D Eo App Copo
App Copo M ; 5: -6 P o Oo p://popo// o: 68/58 ISS: 8-565 P; ISS: 8-56 O Dox oo o x p o op o - o X-X X Co o M Sy S So vy o S ooy Qo 6659 C E : x_xx@6o o : X-X X Dox oo o Lx P o I Cop o I D-D Eo App Copo
Generalisation on the Zeros of a Family of Complex Polynomials
 Ieol Joul of hemcs esech. ISSN 976-584 Volume 6 Numbe 4. 93-97 Ieol esech Publco House h://www.house.com Geelso o he Zeos of Fmly of Comlex Polyomls Aee sgh Neh d S.K.Shu Deme of hemcs Lgys Uvesy Fdbd-
Ieol Joul of hemcs esech. ISSN 976-584 Volume 6 Numbe 4. 93-97 Ieol esech Publco House h://www.house.com Geelso o he Zeos of Fmly of Comlex Polyomls Aee sgh Neh d S.K.Shu Deme of hemcs Lgys Uvesy Fdbd-
Then the number of elements of S of weight n is exactly the number of compositions of n into k parts.
 Geneating Function In a geneal combinatoial poblem, we have a univee S of object, and we want to count the numbe of object with a cetain popety. Fo example, if S i the et of all gaph, we might want to
Geneating Function In a geneal combinatoial poblem, we have a univee S of object, and we want to count the numbe of object with a cetain popety. Fo example, if S i the et of all gaph, we might want to
Cylon BACnet Unitary Controller (CBT) Range
 ATASHEET Cyo BAC y Coo (CBT) Rg Th Cyo BAC y Coo (CBT) Rg g o BTL L BAC Av Appo Coo wh p 8 op, y o oog g o p. Th v h g ow o o, po ppo o g VAV ppo. BAC MS/TP F Sppo h oowg og BAC oj: A/B/AO/BO/AV/BV, A,
ATASHEET Cyo BAC y Coo (CBT) Rg Th Cyo BAC y Coo (CBT) Rg g o BTL L BAC Av Appo Coo wh p 8 op, y o oog g o p. Th v h g ow o o, po ppo o g VAV ppo. BAC MS/TP F Sppo h oowg og BAC oj: A/B/AO/BO/AV/BV, A,
Years. Marketing without a plan is like navigating a maze; the solution is unclear.
 F Q 2018 E Mk l lk z; l l Mk El M C C 1995 O Y O S P R j lk q D C Dl Off P W H S P W Sl M Y Pl Cl El M Cl FIRST QUARTER 2018 E El M & D I C/O Jff P RGD S C D M Sl 57 G S Alx ON K0C 1A0 C Tl: 6134821159
F Q 2018 E Mk l lk z; l l Mk El M C C 1995 O Y O S P R j lk q D C Dl Off P W H S P W Sl M Y Pl Cl El M Cl FIRST QUARTER 2018 E El M & D I C/O Jff P RGD S C D M Sl 57 G S Alx ON K0C 1A0 C Tl: 6134821159
Physics 232 Exam I Feb. 14, 2005
 Phsics I Fe., 5 oc. ec # Ne..5 g ss is ched o hoizol spig d is eecuig siple hoic oio wih gul eloci o dissec. gie is i ie i is oud o e 8 c o he igh o he equiliiu posiio d oig o he le wih eloci o.5 sec..
Phsics I Fe., 5 oc. ec # Ne..5 g ss is ched o hoizol spig d is eecuig siple hoic oio wih gul eloci o dissec. gie is i ie i is oud o e 8 c o he igh o he equiliiu posiio d oig o he le wih eloci o.5 sec..
Executive Committee and Officers ( )
 Gifted and Talented International V o l u m e 2 4, N u m b e r 2, D e c e m b e r, 2 0 0 9. G i f t e d a n d T a l e n t e d I n t e r n a t i o n a2 l 4 ( 2), D e c e m b e r, 2 0 0 9. 1 T h e W o r
Gifted and Talented International V o l u m e 2 4, N u m b e r 2, D e c e m b e r, 2 0 0 9. G i f t e d a n d T a l e n t e d I n t e r n a t i o n a2 l 4 ( 2), D e c e m b e r, 2 0 0 9. 1 T h e W o r
On the hydrogen wave function in Momentum-space, Clifford algebra and the Generating function of Gegenbauer polynomial
 O he hoge we fco Moe-sce ffo geb he eeg fco of egebe oo Meh Hge Hss To ce hs eso: Meh Hge Hss O he hoge we fco Moe-sce ffo geb he eeg fco of egebe oo 8 HL I: h- hs://hches-oeesf/h- Sbe o J 8 HL s
O he hoge we fco Moe-sce ffo geb he eeg fco of egebe oo Meh Hge Hss To ce hs eso: Meh Hge Hss O he hoge we fco Moe-sce ffo geb he eeg fco of egebe oo 8 HL I: h- hs://hches-oeesf/h- Sbe o J 8 HL s
GUELPH HUMANE SOCIETY 190 HANLON CREEK BLVD. GUELPH, ONTARIO ISOMETRIC VIEWS 3D VIEW - SOUTH WEST 3D VIEW - SOUTH EAST 3D VIEW - NORTH WEST
 o. VW - O W VW - O ate F., 0 peedvale venue West Guelph, Ontario el:..000 O V O F O P arch,0-0- O L.. O Y 00 G O FO L P GLP OY 0 LO K LV. GLP, OO O VW VW - O W VW - O rawn y: O ate: -0- OV. 0 0 F G K L
o. VW - O W VW - O ate F., 0 peedvale venue West Guelph, Ontario el:..000 O V O F O P arch,0-0- O L.. O Y 00 G O FO L P GLP OY 0 LO K LV. GLP, OO O VW VW - O W VW - O rawn y: O ate: -0- OV. 0 0 F G K L
Beechwood Music Department Staff
 Beechwood Music Department Staff MRS SARAH KERSHAW - HEAD OF MUSIC S a ra h K e rs h a w t r a i n e d a t t h e R oy a l We ls h C o l le g e of M u s i c a n d D ra m a w h e re s h e ob t a i n e d
Beechwood Music Department Staff MRS SARAH KERSHAW - HEAD OF MUSIC S a ra h K e rs h a w t r a i n e d a t t h e R oy a l We ls h C o l le g e of M u s i c a n d D ra m a w h e re s h e ob t a i n e d
