Ground Rules. PC1221 Fundamentals of Physics I. Position and Displacement. Average Velocity. Lectures 7 and 8 Motion in Two Dimensions
|
|
|
- Barrie Benson
- 6 years ago
- Views:
Transcription
1 PC11 Fndamentals of Physis I Letres 7 and 8 Motion in Two Dimensions A/Prof Tay Sen Chan 1 Grond Rles Swith off yor handphone and paer Swith off yor laptop ompter and keep it No talkin while letre is oin on No ossipin while the letre is oin on Raise yor hand if yo hae qestion to ask Be on time for letre Be on time to ome bak from the reess break to ontine the letre Brin yor letrenotes to letre Position and Displaement Aerae Veloity The position of an objet is desribed by its position etor, r The displaement of the objet is defined as the hane in its position Δr = r f - r i In two- or threedimensional kinematis, eerythin is the same as in one-dimensional motion exept that we mst now se fll etor notation Plane View 3 The aerae eloity is the ratio of the displaement to the time interal for the displaement r t The diretion of the aerae eloity is the diretion of the displaement etor, Δr The aerae eloity between points is independent of the path taken It is dependent on the displaement Plane View 4
2 Instantaneos Veloity The instantaneos eloity is the limit of the aerae eloity as Δt approahes zero = lim t 0 r dr t dt The diretion of small displaement (hane in positions) tells the diretion that the partile is headin at the moment. 5 Instantaneos Veloity, ont The diretion of the instantaneos eloity etor at any point in a partile s path is alon a line tanent to the path at that point and in the diretion of motion The manitde of the instantaneos eloity etor is the speed The speed is a salar qantity 6 Aerae Aeleration Aerae Aeleration, ont The aerae aeleration of a partile as it moes is defined as the hane in the instantaneos eloity etor diided by the time interal drin whih that hane ors. f i a t t t f i As a partile moes, Δ an be fond in different ways The aerae aeleration is a etor qantity direted alon Δ Plane View 7 8
3 Instantaneos Aeleration The instantaneos aeleration is the limit of the aerae aeleration as Δt approahes zero a lim = t 0 t d dt The diretion of small hane in eloities tells the diretion of aeleration. x 9 Prodin An Aeleration Varios hanes in a partile s motion may prode an aeleration, sh as: The manitde of the eloity etor may hane The diretion of the eloity etor may hane Een if the manitde remains onstant Both may also hane simltaneosly 10 Kinemati Eqations for Two- Dimensional Motion When the two-dimensional motion has a onstant aeleration, a series of eqations an be deeloped that desribe the motion These eqations will be similar to those of one-dimensional kinematis Kinemati Eqations, Position etor Veloity r xˆi yˆj dr ˆ ˆ xiyj dt Sine aeleration is onstant, we an also find an expression for the eloity as a fntion of time: f = i + at 11 1
4 Kinemati Eqations, 3 The eloity etor an be represented by its omponents f is enerally not alon the diretion of either i or at Kinemati Eqations, 4 The position etor an also be expressed as a fntion of time: r f = r i + i t + ½ at This indiates that the position etor is the sm of three other etors: The initial position etor r i The displaement resltin from i t The displaement resltin from ½ at f = i + at Kinemati Eqations, 5 Kinemati Eqations, Components The etor representation of the position etor r f is enerally not in the same diretion as i or as a i r f and f are enerally not in the same diretion The eqations for final eloity and final position are etor eqations, therefore they may also be written in omponent form This shows that two-dimensional motion at onstant aeleration is eqialent to two independent motions One motion in the x-diretion and r f = r i + i t + ½ at the other in the y-diretion 15 16
5 Kinemati Eqations, Component Eqations Projetile Motion f = i + at beomes xf = xi + a x t and yf = yi + a y t r f = r i + i t + ½ at beomes x f = x i + xi t + ½ a x t and y f = y i + yi t + ½ a y t 17 An objet may moe in both x and y diretions simltaneosly The form of twodimensional motion we will deal with is alled projetile motion Front View 18 Assmptions of Projetile Motion The free-fall aeleration is onstant oer the rane of motion is direted downward The effet of air frition is neliible With these assmptions, an objet in projetile motion will follow a paraboli path This path is alled the trajetory Verifyin the Paraboli Trajetory Referene frame hosen y is ertial with pward positie Aeleration omponents a y = - and a x = 0 Initial eloity omponents xi = i os and yi = i sin i Θ 19 0
6 Verifyin the Paraboli Trajetory, ont Rane and Maximm Heiht of a Projetile Displaements x f = xi t = ( i os t y f = yi t + ½a y t = ( i sin t -½t Combinin the eqations and remoin t ies: y tan x x i i os i This is in the form of y = ax bx whih is the standard form of a parabola 1 When analyzin projetile motion, two harateristis are of speial interest The rane, R, is the horizontal distane of the projetile The maximm heiht the projetile reahes is h Heiht of a Projetile, eqation The maximm heiht of the projetile an be fond in terms of the initial eloity etor: h i sin i This eqation is alid only for symmetri motion Rane of a Projetile, eqation The rane of a projetile an be expressed in terms of the initial eloity etor: i sin R i This is alid only for symmetri trajetory 3 We will derie them. 4
7 Projetile Formlation Let the initial eloity be. Let the anle sbsripted by and x-axis be θ. Alon the x-diretion, x os t x t os Alon the Y-diretion, y 1 sin t t 1 Sbstitte (1) into (): y θ x Maximm ors when the y-omponent of the eloity is eqal to 0, i.e. the objet is at the moment of omin down. sin t 0 sin t 0 sin t Sbstitte (3) into (): sin y h sin sin sin h h sin or i 1 3 sin sin i h To derie the maximm rane (R) alon the x-diretion, we let y = 0 in eqation. 1 y sin t t R The distane traelled in x-diretion Why? 1 sin t t t sin t sin sin t t 0 0 sin (A+B) = sin A os B + os A sin B 4 for y t x x x sin seonds os t sin os R sin os sin is : What is the maximm ale of R, and the orrespondin? Sine sin 1, sin 1, i.e., 90 When 45 R R R R is a maximm when sin 90, sin 45 45
8 Rane of a Projetile, final The maximm rane ors at i = 45 o Complementary anles will prode the same rane Bt the maximm heiht will be different for the two anles The times of the fliht will be different for the two anles Projetile Motion Problem Solin Hints Selet a oordinate system Resole the initial eloity into x and y omponents Analyze the horizontal motion sin onstant eloity tehniqes Analyze the ertial motion sin onstant aeleration tehniqes Remember that both diretions share the same time 9 30 Non-Symmetri Projetile Motion Follow the eneral rles for projetile motion Break the y-diretion into parts p and down or symmetrial bak to initial heiht and then the rest of the heiht May be non-symmetri in other ways Example. One stratey in a snowball fiht is to throw a snowball at a hih anle oer leel rond. Then, while yor opponent is wathin that snowball, yo throw a seond one at a low anle timed to arrie before or at the same time as the first one. Assme that both snowballs are thrown with a speed of 5.0 m/s. The first is thrown at an anle of 70.0 with respet to the horizontal. The release point of snowball and the hit point of the opponent are at the same leel. (a) At what anle shold the seond snowball be thrown to arrie at the same point as the first? (b) How many seonds later shold the seond snowball be thrown after the first in order for both to arrie at the same time? 31 3
9 We hae deried (b) R sin Sine R,, are onstant, sin will also be a onstant. Let the soltion of be, where 90. We hae, or 180. So,, or 90 R Answer: (a) The seond snowball shold be thrown at Uniform Cirlar Motion Chanin Veloity in Uniform Cirlar Motion Uniform irlar motion ors when an objet moes in a irlar path with a onstant speed An aeleration exists sine the diretion of the motion is hanin This hane in eloity is related to an aeleration The eloity etor is always tanent to the path of the objet Plane View The hane in the eloity etor is de to the hane in diretion The etor diaram shows = f - i 35 36
10 Centripetal Aeleration Centripetal Aeleration, ont The aeleration is always perpendilar to the path of the motion The aeleration always points toward the enter of the irle of motion This aeleration is alled the entripetal aeleration 37 The manitde of the entripetal aeleration etor is ien by a C r By the se of same ratio, this an be deried as follows: Δ Δr = r Δ = Δr r Δ Δr = x Δt r Δt a C r 38 Period The period, T, is the time reqired for one omplete reoltion (one omplete yle) As one omplete yle is the distane of the irmferene. The speed of the partile wold be the irmferene of the irle of motion diided by the period. Speed = distane/time, so time = distane/speed r Therefore, the period is T = 39 Example. The astronat orbitin the Earth in Fire is preparin to dok with a Westar VI satellite. The satellite is in a irlar orbit 600 km aboe the Earth's srfae, where the free-fall aeleration is 8.1 m/s. Take the radis of the Earth as 6400 km. Determine the speed of the satellite and the time interal reqired to omplete one orbit arond the Earth. 40
11 so 8.1 m/s Tanential Aeleration and Speed of satellite in order to maintain the orbit Time to omplete 1 yle of orbit 41 The manitde of the eloity old also be hanin In this ase, there wold be a tanential aeleration Obsere what happens at the enter (my hand) when I make the ball to rotate faster Cirlar motion on my hand 4 Total Aeleration The tanential aeleration ases the hane in the speed of the partile The radial aeleration omes from a hane in the diretion of the eloity etor. (In the textbook by Serway, the diretion or radial aeleration is away from enter not important.) a = a t + a r a a t a r 43 Total Aeleration, eqations d The tanential aeleration: a t = dt The radial aeleration: a r = a = The total aeleration: Manitde a a a r t Why the strin does not slak and the ball does not fly towards the enter? r 44
12 Relatie Veloity Two obserers moin relatie to eah other enerally do not aree on the otome of an experiment For example, obserers A and B below see different paths for the ball Relatie Veloity, eneralized Referene frame S is stationary Referene frame S is moin at 0 This also means that S moes at 0 relatie to S Define time t = 0 as that time when the oriins oinide Relatie Veloity, eqations Aeleration in Different Frames of Referene The positions as seen from the two referene frames (r is the position seen from stationary frame, r seen from moin frame) are related throh the eloity r = r 0 t The deriatie of the position eqation will ie the eloity eqation = 0 These are alled the Galilean transformation eqations (d1-9) 47 The deriatie of the eloity eqation will ie the aeleration eqation The aeleration of the partile measred by an obserer in one frame of referene is the same as that measred by any other obserer moin at a onstant eloity relatie to the first frame. Why? r = r 0 t 0 is a onstant, so 0 has no effet on the = 0 hane in eloity, ie, a = a. 48
13 Example. Two swimmers, Tom and Jerry, start toether at the same point on the bank of a wide stream that flows with a speed. Both moe at the same speed ( > ), relatie to the water. Tom swims downstream a distane L and then pstream the same distane. Jerry swims so that his motion relatie to the Earth is perpendilar to the banks of the stream. He swims the distane L and then bak the same distane, so that both swimmers retrn to the startin point. Whih swimmer retrns first? Answer: For Tom, his speed downstream is +, while his speed pstream is L L Therefore, the total time for Tom is t1 1 L. 49 For Jerry, his ross-stream speed (both ways) is Ths, the total time for Jerry is t L L L t1 1 L L 1 Sine 1 1, t1 t, or Jerry, who swims ross-stream, retrns first. L L L t Example. A Coast Gard tter detets an nidentified ship at a distane of 0.0 km in the diretion 15.0 east of north. The ship is traelin at 6.0 km/h on a orse at 40.0 east of north. The Coast Gard wishes to send a speedboat to interept the essel and inestiate it. If the speedboat traels 50.0 km/h, in what diretion shold it head? Express the diretion as a ompass bearin with respet to de north. Answer: Choose the x-axis alon the 0-km distane. The y-omponents of the displaements of the ship and the speedboat mst aree: 6 km htsin km htsin sin The speedboat shold head eastofnorth 6 km/h 50 km/h 51 Example. How lon does it take an atomobile traelin in the left lane at 60.0 km/h to pll alonside a ar traelin in the riht lane at 40.0 km/h if the ars' front bmpers are initially 100 m apart? (Disk ) Answer: The bmpers are initially 100 m apart (0.1 km). After time t the bmper of the leadin ar traels 40.0t km, while the bmper of the hasin ar traels 60.0t km. Sine the ars are side by side at time t we hae t = 60t t = 0.1/0 = hr = x 3600 se = 18 s 60 t 60 km/h 40 km/h 0.1 km 40 t 5
14 Examples. Constant speed (A) Horizontal Trak Examples. This time the ar will be plled alon the horizontal trak by a strin and a weiht hanin oer a plley, and will be aeleratin onstantly. The ball is fired at point X. Where will the ball land this time? (The horizontal trak is lon enoh for the ar not to fall off when the ball lands.) Point X (C) The ar is plled alon by a strin and a weiht hanin oer a plley. (B) Tilted Trak 53 54
Ground Rules. PC1221 Fundamentals of Physics I. Position and Displacement. Average Velocity. Lectures 7 and 8 Motion in Two Dimensions
 PC11 Fndamentals of Physics I Lectres 7 and 8 Motion in Two Dimensions A/Prof Tay Sen Chan 1 Grond Rles Switch off yor handphone and paer Switch off yor laptop compter and keep it No talkin while lectre
PC11 Fndamentals of Physics I Lectres 7 and 8 Motion in Two Dimensions A/Prof Tay Sen Chan 1 Grond Rles Switch off yor handphone and paer Switch off yor laptop compter and keep it No talkin while lectre
Ground Rules. PC1221 Fundamentals of Physics I. Position and Displacement. Average Velocity. Lectures 7 and 8 Motion in Two Dimensions
 PC11 Fundamentals of Physics I Lectures 7 and 8 Motion in Two Dimensions Dr Tay Sen Chuan 1 Ground Rules Switch off your handphone and paer Switch off your laptop computer and keep it No talkin while lecture
PC11 Fundamentals of Physics I Lectures 7 and 8 Motion in Two Dimensions Dr Tay Sen Chuan 1 Ground Rules Switch off your handphone and paer Switch off your laptop computer and keep it No talkin while lecture
HW 2 Help cm sin 60 =12.5 cm 10.8 cm cm sin 30 =12.5 cm 6.25 cm 2. We can check the answer by using the Pythagorean Theorem:
 HW Help 8.OGANIZE AND PLAN opposite funtion sin hpotenuse Gien the hpotenuse and the anles we will use the trionometri to sole for eah of the unknown sides. We note that the 60 is the anle opposite the
HW Help 8.OGANIZE AND PLAN opposite funtion sin hpotenuse Gien the hpotenuse and the anles we will use the trionometri to sole for eah of the unknown sides. We note that the 60 is the anle opposite the
Chapter 35. Special Theory of Relativity (1905)
 Chapter 35 Speial Theory of Relatiity (1905) 1. Postulates of the Speial Theory of Relatiity: A. The laws of physis are the same in all oordinate systems either at rest or moing at onstant eloity with
Chapter 35 Speial Theory of Relatiity (1905) 1. Postulates of the Speial Theory of Relatiity: A. The laws of physis are the same in all oordinate systems either at rest or moing at onstant eloity with
Chapter 39 Relativity
 Chapter 39 Relatiity from relatie motion to relatiity 39. The Priniple of Galilean Relatiity The laws of mehanis mst be the same in all inertial frames of referene. Galilean spae-time transformation eqations
Chapter 39 Relatiity from relatie motion to relatiity 39. The Priniple of Galilean Relatiity The laws of mehanis mst be the same in all inertial frames of referene. Galilean spae-time transformation eqations
Velocity and Accceleration in Different Coordinate system
 Velocity & cceleration in different coordinate system Chapter Velocity and ccceleration in Different Coordinate system In physics basic laws are first introdced for a point partile and then laws are etended
Velocity & cceleration in different coordinate system Chapter Velocity and ccceleration in Different Coordinate system In physics basic laws are first introdced for a point partile and then laws are etended
The Lorenz Transform
 The Lorenz Transform Flameno Chuk Keyser Part I The Einstein/Bergmann deriation of the Lorentz Transform I follow the deriation of the Lorentz Transform, following Peter S Bergmann in Introdution to the
The Lorenz Transform Flameno Chuk Keyser Part I The Einstein/Bergmann deriation of the Lorentz Transform I follow the deriation of the Lorentz Transform, following Peter S Bergmann in Introdution to the
Compatibility of the theory of special relativity with an absolute reference frame with a longitudinal Doppler shift
 Compatibility o the theory o speial relatiity with an absolte reerene rame with a longitdinal Doppler shit Masanori ato Honda Eletronis Co., Ltd., Oyamazka, Oiwa-ho, Toyohashi, ihi 44-33, Japan bstrat:
Compatibility o the theory o speial relatiity with an absolte reerene rame with a longitdinal Doppler shit Masanori ato Honda Eletronis Co., Ltd., Oyamazka, Oiwa-ho, Toyohashi, ihi 44-33, Japan bstrat:
Physics 6C. Special Relativity. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB
 Physis 6C Speial Relatiity Two Main Ideas The Postulates of Speial Relatiity Light traels at the same speed in all inertial referene frames. Laws of physis yield idential results in all inertial referene
Physis 6C Speial Relatiity Two Main Ideas The Postulates of Speial Relatiity Light traels at the same speed in all inertial referene frames. Laws of physis yield idential results in all inertial referene
Physics 2D Lecture Slides Lecture : Jan 11th 200. First Quiz This Friday!
 Physis D Letre Slides Letre : Jan 11th 00 Viek Sharma UCSD Physis First Qiz This Friday! Bring a Ble Book, allator; hek battery Make sre yo remember the ode nmber for this ose gien to yo (reord it some
Physis D Letre Slides Letre : Jan 11th 00 Viek Sharma UCSD Physis First Qiz This Friday! Bring a Ble Book, allator; hek battery Make sre yo remember the ode nmber for this ose gien to yo (reord it some
Relativistic Analysis of Doppler Effect and Aberration based on Vectorial Lorentz Transformations
 Uniersidad Central de Venezuela From the SeletedWorks of Jorge A Frano June, Relatiisti Analysis of Doppler Effet and Aberration based on Vetorial Lorentz Transformations Jorge A Frano, Uniersidad Central
Uniersidad Central de Venezuela From the SeletedWorks of Jorge A Frano June, Relatiisti Analysis of Doppler Effet and Aberration based on Vetorial Lorentz Transformations Jorge A Frano, Uniersidad Central
Motion in Two Dimension (Projectile Motion)
 Phsics Motion in Two Dimension (Projectile Motion) www.testprepkart.com Table of Content. Introdction.. Projectile. 3. Assmptions of projectile motion. 4. Principle of phsical independence of motions.
Phsics Motion in Two Dimension (Projectile Motion) www.testprepkart.com Table of Content. Introdction.. Projectile. 3. Assmptions of projectile motion. 4. Principle of phsical independence of motions.
, an inverse square law.
 Uniform irular motion Speed onstant, but eloity hanging. and a / t point to enter. s r θ > θ s/r t / r, also θ in small limit > t/r > a / r, entripetal aeleration Sine a points to enter of irle, F m a
Uniform irular motion Speed onstant, but eloity hanging. and a / t point to enter. s r θ > θ s/r t / r, also θ in small limit > t/r > a / r, entripetal aeleration Sine a points to enter of irle, F m a
Einstein s theory of special relativity
 Einstein s theory of speial relatiity Announements: First homework assignment is online. You will need to read about time dilation (1.8) to answer problem #3 and for the definition of γ for problem #4.
Einstein s theory of speial relatiity Announements: First homework assignment is online. You will need to read about time dilation (1.8) to answer problem #3 and for the definition of γ for problem #4.
The Simple Solutions of Four Actual Problems. of General Theory of Relativity.
 The Simple Soltions of For Atal Problems of General Theory of Relativity. H Changwei Room 81, No.17,Lane 1769, Pdong Wlian Road, 19 Shanghai China,1-8818, hhangwei5@yahoo.om.n Abstrat: It is qite ompliated
The Simple Soltions of For Atal Problems of General Theory of Relativity. H Changwei Room 81, No.17,Lane 1769, Pdong Wlian Road, 19 Shanghai China,1-8818, hhangwei5@yahoo.om.n Abstrat: It is qite ompliated
The Special Theory of Relativity
 The Speial Theory of Relatiity Galilean Newtonian Relatiity Galileo Galilei Isaa Newton Definition of an inertial referene frame: One in whih Newton s first law is alid. onstant if F0 Earth is rotating
The Speial Theory of Relatiity Galilean Newtonian Relatiity Galileo Galilei Isaa Newton Definition of an inertial referene frame: One in whih Newton s first law is alid. onstant if F0 Earth is rotating
jfpr% ekuo /kez iz.ksrk ln~xq# Jh j.knksm+nklth egkjkt
 Phone : 0 903 903 7779, 98930 58881 Kinematics Pae: 1 fo/u fopkjr Hkh# tu] uha kjehks dke] foifr ns[k NksM+s rqjar e/;e eu dj ';kea iq#"k fla ladyi dj] lrs foifr usd] ^cuk^ u NksM+s /;s; dks] j?kqcj jk[ks
Phone : 0 903 903 7779, 98930 58881 Kinematics Pae: 1 fo/u fopkjr Hkh# tu] uha kjehks dke] foifr ns[k NksM+s rqjar e/;e eu dj ';kea iq#"k fla ladyi dj] lrs foifr usd] ^cuk^ u NksM+s /;s; dks] j?kqcj jk[ks
State variable feedback
 State variable feedbak We have previosly disssed systems desribed by the linear state-spae eqations Ax B y Cx n m with xt () R the internal state, t () R the ontrol inpt, and yt () R the measred otpt.
State variable feedbak We have previosly disssed systems desribed by the linear state-spae eqations Ax B y Cx n m with xt () R the internal state, t () R the ontrol inpt, and yt () R the measred otpt.
Simultaneity. CHAPTER 2 Special Theory of Relativity 2. Gedanken (Thought) experiments. The complete Lorentz Transformation. Re-evaluation of Time!
 CHAPTER Speial Theory of Relatiity. The Need for Aether. The Mihelson-Morley Eperiment.3 Einstein s Postulates.4 The Lorentz Transformation.5 Time Dilation and Length Contration.6 Addition of Veloities.7
CHAPTER Speial Theory of Relatiity. The Need for Aether. The Mihelson-Morley Eperiment.3 Einstein s Postulates.4 The Lorentz Transformation.5 Time Dilation and Length Contration.6 Addition of Veloities.7
Motion in Two and Three Dimensions
 PH 1-1D Spring 013 Motion in Two and Three Dimensions Lectures 5,6,7 Chapter 4 (Halliday/Resnick/Walker, Fundamentals of Physics 9 th edition) 1 Chapter 4 Motion in Two and Three Dimensions In this chapter
PH 1-1D Spring 013 Motion in Two and Three Dimensions Lectures 5,6,7 Chapter 4 (Halliday/Resnick/Walker, Fundamentals of Physics 9 th edition) 1 Chapter 4 Motion in Two and Three Dimensions In this chapter
u P(t) = P(x,y) r v t=0 4/4/2006 Motion ( F.Robilliard) 1
 y g j P(t) P(,y) r t0 i 4/4/006 Motion ( F.Robilliard) 1 Motion: We stdy in detail three cases of motion: 1. Motion in one dimension with constant acceleration niform linear motion.. Motion in two dimensions
y g j P(t) P(,y) r t0 i 4/4/006 Motion ( F.Robilliard) 1 Motion: We stdy in detail three cases of motion: 1. Motion in one dimension with constant acceleration niform linear motion.. Motion in two dimensions
Relativity and Astrophysics Lecture 10 Terry Herter. Doppler Shift The Expanding Universe Hubble s discovery
 Doppler Eet Doppler Eet Relatiity and Astrophysis Leture 0 Terry Herter Outline Doppler Shit The Expanding Unierse Hubble s disoery Reading Spaetime Physis: Chapter 4 Problem L-, page (due today/monday)
Doppler Eet Doppler Eet Relatiity and Astrophysis Leture 0 Terry Herter Outline Doppler Shit The Expanding Unierse Hubble s disoery Reading Spaetime Physis: Chapter 4 Problem L-, page (due today/monday)
Addition of velocities. Taking differentials of the Lorentz transformation, relative velocities may be calculated:
 Addition of veloities Taking differentials of the Lorentz transformation, relative veloities may be allated: So that defining veloities as: x dx/dt, y dy/dt, x dx /dt, et. it is easily shown that: With
Addition of veloities Taking differentials of the Lorentz transformation, relative veloities may be allated: So that defining veloities as: x dx/dt, y dy/dt, x dx /dt, et. it is easily shown that: With
Answers to Coursebook questions Chapter 2.10
 Camride Physis for the IB Diploma Answers to Courseook questions Chapter. 1 a y = OP = 1 t = 0.05 m = 0.0 = 00 m s 1 0. The time to fall to the floor is iven y y = 1 t t = y = 1.3 = 0.51 s. The horizontal
Camride Physis for the IB Diploma Answers to Courseook questions Chapter. 1 a y = OP = 1 t = 0.05 m = 0.0 = 00 m s 1 0. The time to fall to the floor is iven y y = 1 t t = y = 1.3 = 0.51 s. The horizontal
The Thomas Precession Factor in Spin-Orbit Interaction
 p. The Thomas Preession Fator in Spin-Orbit Interation Herbert Kroemer * Department of Eletrial and Computer Engineering, Uniersity of California, Santa Barbara, CA 9306 The origin of the Thomas fator
p. The Thomas Preession Fator in Spin-Orbit Interation Herbert Kroemer * Department of Eletrial and Computer Engineering, Uniersity of California, Santa Barbara, CA 9306 The origin of the Thomas fator
8.022 (E&M) Lecture 11
 8.0 (E&M) Leture Topis: Introdution to Speial Relatiit Length ontration and Time dilation Lorentz transformations Veloit transformation Speial relatiit Read for the hallenge? Speial relatiit seems eas
8.0 (E&M) Leture Topis: Introdution to Speial Relatiit Length ontration and Time dilation Lorentz transformations Veloit transformation Speial relatiit Read for the hallenge? Speial relatiit seems eas
Evaluate Inverse Trigonometric Functions. 5p, }} 13p, }}
 13.4 a.1, a.3, 2A.4.C; P.3.A TEKS Evalate Inverse Trigonometri Fntions Before Yo fond vales of trigonometri fntions given angles. Now Yo will find angles given vales of trigonometri fntions. Wh? So o an
13.4 a.1, a.3, 2A.4.C; P.3.A TEKS Evalate Inverse Trigonometri Fntions Before Yo fond vales of trigonometri fntions given angles. Now Yo will find angles given vales of trigonometri fntions. Wh? So o an
Boundary Layer Theory:
 Mass Transfer Bondar Laer Theor: Mass and Heat/Momentm Transfer Letre,..7, Dr. K. Wegner 9. Basi Theories for Mass Transfer Coeffiients 9. Flid-Flid Interfaes (letre of 5..7) Flid-flid interfaes are tpiall
Mass Transfer Bondar Laer Theor: Mass and Heat/Momentm Transfer Letre,..7, Dr. K. Wegner 9. Basi Theories for Mass Transfer Coeffiients 9. Flid-Flid Interfaes (letre of 5..7) Flid-flid interfaes are tpiall
Chapter 26 Lecture Notes
 Chapter 26 Leture Notes Physis 2424 - Strauss Formulas: t = t0 1 v L = L0 1 v m = m0 1 v E = m 0 2 + KE = m 2 KE = m 2 -m 0 2 mv 0 p= mv = 1 v E 2 = p 2 2 + m 2 0 4 v + u u = 2 1 + vu There were two revolutions
Chapter 26 Leture Notes Physis 2424 - Strauss Formulas: t = t0 1 v L = L0 1 v m = m0 1 v E = m 0 2 + KE = m 2 KE = m 2 -m 0 2 mv 0 p= mv = 1 v E 2 = p 2 2 + m 2 0 4 v + u u = 2 1 + vu There were two revolutions
arxiv:physics/ Oct 2002
 Dedution of Lorentz Transformation from the eistene of absolute rest. Dedution of the speed of light in any frame of referene. Rodrigo de Abreu Centro de Eletrodinâmia e Departamento de Físia do IST Abstrat
Dedution of Lorentz Transformation from the eistene of absolute rest. Dedution of the speed of light in any frame of referene. Rodrigo de Abreu Centro de Eletrodinâmia e Departamento de Físia do IST Abstrat
SCHOOL OF MECHANICAL, AEROSPACE AND CIVIL ENGINEERING HYDRAULICS 2 LABORATORY EXERCISE. Forces on Two-Dimensional Bodies in a Wind Tunnel
 Objet SCHOOL OF MECHANICAL, AEROSPACE AND CIVIL ENGINEERING HYDRAULICS LABORATORY EXERCISE Fores on Two-Dimensional Bodies in a Wind Tnnel To ompare drag oeffiients made by diret measrement on a drag balane
Objet SCHOOL OF MECHANICAL, AEROSPACE AND CIVIL ENGINEERING HYDRAULICS LABORATORY EXERCISE Fores on Two-Dimensional Bodies in a Wind Tnnel To ompare drag oeffiients made by diret measrement on a drag balane
V. FLOW IN THREE DIMENSIONS
 V. FLOW IN THREE DIMENSIONS 78. Introdtion 33 A. Flow in Nozzles and Jets 79. Nozzle flow 33 80. Flow throgh ones 34 81. De Laal's nozzle 37 8. Varios types of nozzle flow 39 83. Shok patterns in nozzles
V. FLOW IN THREE DIMENSIONS 78. Introdtion 33 A. Flow in Nozzles and Jets 79. Nozzle flow 33 80. Flow throgh ones 34 81. De Laal's nozzle 37 8. Varios types of nozzle flow 39 83. Shok patterns in nozzles
INTRODUCTION TO QUANTUM MECHANICS
 A. La Rosa Letre Notes PSU-Physis PH 45 INTRODUCTION TO QUANTUM MECHANICS PART-I TRANSITION from CLASSICAL to QUANTUM PHYSICS CHAPTER CLASSICAL PHYSICS ELECTROMAGNETISM and RELATIITY REIEW,. ELECTROMAGNETISM..A
A. La Rosa Letre Notes PSU-Physis PH 45 INTRODUCTION TO QUANTUM MECHANICS PART-I TRANSITION from CLASSICAL to QUANTUM PHYSICS CHAPTER CLASSICAL PHYSICS ELECTROMAGNETISM and RELATIITY REIEW,. ELECTROMAGNETISM..A
Physics 4A Solutions to Chapter 4 Homework
 Physics 4A Solutions to Chapter 4 Homework Chapter 4 Questions: 4, 1, 1 Exercises & Problems: 5, 11, 3, 7, 8, 58, 67, 77, 87, 11 Answers to Questions: Q 4-4 (a) all tie (b) 1 and tie (the rocket is shot
Physics 4A Solutions to Chapter 4 Homework Chapter 4 Questions: 4, 1, 1 Exercises & Problems: 5, 11, 3, 7, 8, 58, 67, 77, 87, 11 Answers to Questions: Q 4-4 (a) all tie (b) 1 and tie (the rocket is shot
Physics 2D Lecture Slides Lecture 5: Jan 12th 2004
 The Final Exam is on Mar 18 th, Time and Loation TBA NOT on Monday Mar 15 th as previosly annoned in the Handot et!! Pl. make a note of this hange!! This date hange is also posted in the ANNOUCEMENT setion
The Final Exam is on Mar 18 th, Time and Loation TBA NOT on Monday Mar 15 th as previosly annoned in the Handot et!! Pl. make a note of this hange!! This date hange is also posted in the ANNOUCEMENT setion
Doppler Effect (Text 1.3)
 Doppler Effet (et 1.3) Consider a light soure as a soure sending out a tik eery 1/ν and these tiks are traeling forward with speed. tik tik tik tik Doppler Effet (et 1.3) Case 1. Obserer oing transersely.
Doppler Effet (et 1.3) Consider a light soure as a soure sending out a tik eery 1/ν and these tiks are traeling forward with speed. tik tik tik tik Doppler Effet (et 1.3) Case 1. Obserer oing transersely.
Electromagnetic Theory Prof. Ruiz, UNC Asheville, doctorphys on YouTube Chapter B Notes. Special Relativity. B1. The Rotation Matrix
 Eletromagneti Theory Prof. Ruiz, UNC Asheille, dotorphys on YouTube Chapter B Notes. Speial Relatiity B1. The Rotation Matrix There are two pairs of axes below. The prime axes are rotated with respet to
Eletromagneti Theory Prof. Ruiz, UNC Asheille, dotorphys on YouTube Chapter B Notes. Speial Relatiity B1. The Rotation Matrix There are two pairs of axes below. The prime axes are rotated with respet to
Announcements. Today s class. The Lorentz transformation. Lorentz transformation (Relativistic version of Galileo transformation)
 Announements Reading for Monda:. -.5 HW 3 is posted. Due net Wed. noon. The Frida was a TYPO! IT I DUE WEDNEDAY! Toda s lass Lorent transformation Doppler shift First Midterm is on the 6 th. Will oer relatiit
Announements Reading for Monda:. -.5 HW 3 is posted. Due net Wed. noon. The Frida was a TYPO! IT I DUE WEDNEDAY! Toda s lass Lorent transformation Doppler shift First Midterm is on the 6 th. Will oer relatiit
Motion in Two and Three Dimensions
 PH 1-A Fall 014 Motion in Two and Three Dimensions Lectures 4,5 Chapter 4 (Halliday/Resnick/Walker, Fundamentals of Physics 9 th edition) 1 Chapter 4 Motion in Two and Three Dimensions In this chapter
PH 1-A Fall 014 Motion in Two and Three Dimensions Lectures 4,5 Chapter 4 (Halliday/Resnick/Walker, Fundamentals of Physics 9 th edition) 1 Chapter 4 Motion in Two and Three Dimensions In this chapter
 Motion in One Dimension. A body is moving with velocity 3ms towards East. After s its velocity becomes 4ms towards North. The average acceleration of the body is a) 7ms b) 7ms c) 5ms d) ms. A boy standing
Motion in One Dimension. A body is moving with velocity 3ms towards East. After s its velocity becomes 4ms towards North. The average acceleration of the body is a) 7ms b) 7ms c) 5ms d) ms. A boy standing
If velocity of A relative to ground = velocity of B relative to ground = the velocity of A relative to B =
 L Physis MC nswers Year:1989 Question Number: 3,0,,4,6,9,30,31,36,40,4 1989MC (3) If eloity of relatie to ground = and eloity of relatie to ground =, then the eloity of relatie to = X X Y Y Suppose that
L Physis MC nswers Year:1989 Question Number: 3,0,,4,6,9,30,31,36,40,4 1989MC (3) If eloity of relatie to ground = and eloity of relatie to ground =, then the eloity of relatie to = X X Y Y Suppose that
Relativistic Addition of Velocities *
 OpenStax-CNX module: m42540 1 Relativisti Addition of Veloities * OpenStax This work is produed by OpenStax-CNX and liensed under the Creative Commons Attribution Liense 3.0 Abstrat Calulate relativisti
OpenStax-CNX module: m42540 1 Relativisti Addition of Veloities * OpenStax This work is produed by OpenStax-CNX and liensed under the Creative Commons Attribution Liense 3.0 Abstrat Calulate relativisti
Transformation of Orbital Angular Momentum and Spin Angular Momentum
 Aerian Jornal of Matheatis and Statistis 6, 65: 3-6 DOI: 593/jajs6653 Transforation of Orbital Anglar Moent and Spin Anglar Moent Md Tarek Hossain *, Md Shah Ala Departent of Physis, Shahjalal Uniersity
Aerian Jornal of Matheatis and Statistis 6, 65: 3-6 DOI: 593/jajs6653 Transforation of Orbital Anglar Moent and Spin Anglar Moent Md Tarek Hossain *, Md Shah Ala Departent of Physis, Shahjalal Uniersity
Chapter 28 Special Relativity
 Galilean Relatiity Chapter 8 Speial Relatiity A passenger in an airplane throws a ball straight up. It appears to oe in a ertial path. The law of graity and equations of otion under unifor aeleration are
Galilean Relatiity Chapter 8 Speial Relatiity A passenger in an airplane throws a ball straight up. It appears to oe in a ertial path. The law of graity and equations of otion under unifor aeleration are
Journal of Theoretics Vol.5-2 Guest Commentary Relativistic Thermodynamics for the Introductory Physics Course
 Journal of heoretis Vol.5- Guest Commentary Relatiisti hermodynamis for the Introdutory Physis Course B.Rothenstein bernhard_rothenstein@yahoo.om I.Zaharie Physis Department, "Politehnia" Uniersity imisoara,
Journal of heoretis Vol.5- Guest Commentary Relatiisti hermodynamis for the Introdutory Physis Course B.Rothenstein bernhard_rothenstein@yahoo.om I.Zaharie Physis Department, "Politehnia" Uniersity imisoara,
Practice Exam 2 Solutions
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department o Physis Physis 801T Fall Term 004 Problem 1: stati equilibrium Pratie Exam Solutions You are able to hold out your arm in an outstrethed horizontal position
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department o Physis Physis 801T Fall Term 004 Problem 1: stati equilibrium Pratie Exam Solutions You are able to hold out your arm in an outstrethed horizontal position
CHAPTER 64 INTEGRATION USING ALGEBRAIC SUBSTITUTIONS
 CHAPTER INTEGRATION USING ALGEBRAIC SUBSTITUTIONS EXERCISE 8 Page 7. Integrate with respet to x: sin( + 9) Let + 9 then d x and dx sin(+ 9) d x sin os + os ( ) os( x+ 9) +. Integrate with respet to θ:
CHAPTER INTEGRATION USING ALGEBRAIC SUBSTITUTIONS EXERCISE 8 Page 7. Integrate with respet to x: sin( + 9) Let + 9 then d x and dx sin(+ 9) d x sin os + os ( ) os( x+ 9) +. Integrate with respet to θ:
(a) Taking the derivative of the position vector with respect to time, we have, in SI units (m/s),
 Chapter 4 Student Solutions Manual. We apply Eq. 4- and Eq. 4-6. (a) Taking the deriatie of the position ector with respect to time, we hae, in SI units (m/s), d ˆ = (i + 4t ˆj + tk) ˆ = 8tˆj + k ˆ. dt
Chapter 4 Student Solutions Manual. We apply Eq. 4- and Eq. 4-6. (a) Taking the deriatie of the position ector with respect to time, we hae, in SI units (m/s), d ˆ = (i + 4t ˆj + tk) ˆ = 8tˆj + k ˆ. dt
PHYSICS FOR THE IB DIPLOMA CAMBRIDGE UNIVERSITY PRESS
 Option A Relatiity A The beginnings of relatiity Learning objeties It is said that Albert Einstein, as a boy, asked himself what would happen if he held a mirror in front of himself and ran forward at
Option A Relatiity A The beginnings of relatiity Learning objeties It is said that Albert Einstein, as a boy, asked himself what would happen if he held a mirror in front of himself and ran forward at
Today: Review of SR. Einstein s Postulates of Relativity (Abbreviated versions) Let's start with a few important concepts
 Today: eiew of Eam: Tomorrow, 7:30-9:00pm, DUANE GB30 You an bring paper (etter format written on both sides with whateer you think might help you during the eam. But you annot bring the tetbook or leture
Today: eiew of Eam: Tomorrow, 7:30-9:00pm, DUANE GB30 You an bring paper (etter format written on both sides with whateer you think might help you during the eam. But you annot bring the tetbook or leture
Moment of inertia: (1.3) Kinetic energy of rotation: Angular momentum of a solid object rotating around a fixed axis: Wave particle relationships: ω =
 FW Phys 13 E:\Exel files\h 18 Reiew of FormulasM3.do page 1 of 6 Rotational formulas: (1.1) The angular momentum L of a point mass m, moing with eloity is gien by the etor produt between its radius etor
FW Phys 13 E:\Exel files\h 18 Reiew of FormulasM3.do page 1 of 6 Rotational formulas: (1.1) The angular momentum L of a point mass m, moing with eloity is gien by the etor produt between its radius etor
Special and General Relativity
 9/16/009 Speial and General Relativity Inertial referene frame: a referene frame in whih an aeleration is the result of a fore. Examples of Inertial Referene Frames 1. This room. Experiment: Drop a ball.
9/16/009 Speial and General Relativity Inertial referene frame: a referene frame in whih an aeleration is the result of a fore. Examples of Inertial Referene Frames 1. This room. Experiment: Drop a ball.
Special Relativity Simply Debunked in Five Steps!
 Speial Relatiity Simply Debunked in Fie Steps! Radwan M. Kassir Abstrat The speed of light postulate is losely examined from the perspetie of two inertial referene frames unprimed ( stationary ) and primed
Speial Relatiity Simply Debunked in Fie Steps! Radwan M. Kassir Abstrat The speed of light postulate is losely examined from the perspetie of two inertial referene frames unprimed ( stationary ) and primed
Special Relativity. Relativity
 10/17/01 Speial Relativity Leture 17 Relativity There is no absolute motion. Everything is relative. Suppose two people are alone in spae and traveling towards one another As measured by the Doppler shift!
10/17/01 Speial Relativity Leture 17 Relativity There is no absolute motion. Everything is relative. Suppose two people are alone in spae and traveling towards one another As measured by the Doppler shift!
Chapter 4. Motion in Two Dimensions. Professor Wa el Salah
 Chapter 4 Motion in Two Dimensions Kinematics in Two Dimensions Will study the vector nature of position, velocity and acceleration in greater detail. Will treat projectile motion and uniform circular
Chapter 4 Motion in Two Dimensions Kinematics in Two Dimensions Will study the vector nature of position, velocity and acceleration in greater detail. Will treat projectile motion and uniform circular
PHYS 100: Lecture 4 PROJECTILE MOTION. y = (v 0 /v T ) x (g/2v T2 )x 2. Velocity of Train v T. Physics 100 Lecture 4, Slide y(m)
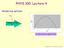 PHYS : Lecture 4 PROJECTILE MOTION.4. Velocity of Train T y(m).8.6.4. 5 5 x(m) y ( / T ) x (/ T )x Physics Lecture 4, Slide Music Who is the Artist? A) Miles Dais B) Wynton Marsalis C) Chris Botti D) Nina
PHYS : Lecture 4 PROJECTILE MOTION.4. Velocity of Train T y(m).8.6.4. 5 5 x(m) y ( / T ) x (/ T )x Physics Lecture 4, Slide Music Who is the Artist? A) Miles Dais B) Wynton Marsalis C) Chris Botti D) Nina
REVIEW: Going from ONE to TWO Dimensions with Kinematics. Review of one dimension, constant acceleration kinematics. v x (t) = v x0 + a x t
 Lecture 5: Projectile motion, uniform circular motion 1 REVIEW: Goin from ONE to TWO Dimensions with Kinematics In Lecture 2, we studied the motion of a particle in just one dimension. The concepts of
Lecture 5: Projectile motion, uniform circular motion 1 REVIEW: Goin from ONE to TWO Dimensions with Kinematics In Lecture 2, we studied the motion of a particle in just one dimension. The concepts of
Final Review. A Puzzle... Special Relativity. Direction of the Force. Moving at the Speed of Light
 Final Review A Puzzle... Diretion of the Fore A point harge q is loated a fixed height h above an infinite horizontal onduting plane. Another point harge q is loated a height z (with z > h) above the plane.
Final Review A Puzzle... Diretion of the Fore A point harge q is loated a fixed height h above an infinite horizontal onduting plane. Another point harge q is loated a height z (with z > h) above the plane.
( x vt) m (0.80)(3 10 m/s)( s) 1200 m m/s m/s m s 330 s c. 3.
 Solutions to HW 10 Problems and Exerises: 37.. Visualize: At t t t 0 s, the origins of the S, S, and S referene frames oinide. Solve: We have 1 ( v/ ) 1 (0.0) 1.667. (a) Using the Lorentz transformations,
Solutions to HW 10 Problems and Exerises: 37.. Visualize: At t t t 0 s, the origins of the S, S, and S referene frames oinide. Solve: We have 1 ( v/ ) 1 (0.0) 1.667. (a) Using the Lorentz transformations,
Lecture 3 - Lorentz Transformations
 Leture - Lorentz Transformations A Puzzle... Example A ruler is positioned perpendiular to a wall. A stik of length L flies by at speed v. It travels in front of the ruler, so that it obsures part of the
Leture - Lorentz Transformations A Puzzle... Example A ruler is positioned perpendiular to a wall. A stik of length L flies by at speed v. It travels in front of the ruler, so that it obsures part of the
Relativity fundamentals explained well (I hope) Walter F. Smith, Haverford College
 Relativity fundamentals explained well (I hope) Walter F. Smith, Haverford College 3-14-06 1 Propagation of waves through a medium As you ll reall from last semester, when the speed of sound is measured
Relativity fundamentals explained well (I hope) Walter F. Smith, Haverford College 3-14-06 1 Propagation of waves through a medium As you ll reall from last semester, when the speed of sound is measured
Special Relativity Einstein
 Speial Relatiity Einstein - 1905 Published 5 papers in Annalen der Physik Photoeletri effet (led to Nobel Prize in 191) Brownian Motion (proed existene of atoms) Speial Relatiity Speial Relatiity (E=m
Speial Relatiity Einstein - 1905 Published 5 papers in Annalen der Physik Photoeletri effet (led to Nobel Prize in 191) Brownian Motion (proed existene of atoms) Speial Relatiity Speial Relatiity (E=m
University of Alabama Department of Physics and Astronomy. PH 125 / LeClair Fall Exam III Solution
 University of Alabama Department of Physics and Astronomy PH 5 / LeClair Fall 07 Exam III Solution. A child throws a ball with an initial speed of 8.00 m/s at an anle of 40.0 above the horizontal. The
University of Alabama Department of Physics and Astronomy PH 5 / LeClair Fall 07 Exam III Solution. A child throws a ball with an initial speed of 8.00 m/s at an anle of 40.0 above the horizontal. The
τ = 10 seconds . In a non-relativistic N 1 = N The muon survival is given by the law of radioactive decay N(t)=N exp /.
 Muons on the moon Time ilation using ot prouts Time ilation using Lorentz boosts Cheking the etor formula Relatiisti aition of eloities Why you an t eee the spee of light by suessie boosts Doppler shifts
Muons on the moon Time ilation using ot prouts Time ilation using Lorentz boosts Cheking the etor formula Relatiisti aition of eloities Why you an t eee the spee of light by suessie boosts Doppler shifts
The Laws of Acceleration
 The Laws of Aeleration The Relationships between Time, Veloity, and Rate of Aeleration Copyright 2001 Joseph A. Rybzyk Abstrat Presented is a theory in fundamental theoretial physis that establishes the
The Laws of Aeleration The Relationships between Time, Veloity, and Rate of Aeleration Copyright 2001 Joseph A. Rybzyk Abstrat Presented is a theory in fundamental theoretial physis that establishes the
(JPL-2557) DEFORMATION PATH PLANNING FOR BELT OBJET MANIPULATION
 Proeedings of 1 ISFA 1 International Symposim on Flexible Atomation Tokyo, Japan Jly 1-14, 1 (JP-557) DEFORMATION PATH PANNING FOR BET OBJET MANIPUATION Yya ASANO, Hidefmi WAKAMATSU, Eiji MORINAGA, Eiji
Proeedings of 1 ISFA 1 International Symposim on Flexible Atomation Tokyo, Japan Jly 1-14, 1 (JP-557) DEFORMATION PATH PANNING FOR BET OBJET MANIPUATION Yya ASANO, Hidefmi WAKAMATSU, Eiji MORINAGA, Eiji
Relativity in Classical Physics
 Relativity in Classial Physis Main Points Introdution Galilean (Newtonian) Relativity Relativity & Eletromagnetism Mihelson-Morley Experiment Introdution The theory of relativity deals with the study of
Relativity in Classial Physis Main Points Introdution Galilean (Newtonian) Relativity Relativity & Eletromagnetism Mihelson-Morley Experiment Introdution The theory of relativity deals with the study of
Critical Reflections on the Hafele and Keating Experiment
 Critial Refletions on the Hafele and Keating Experiment W.Nawrot In 1971 Hafele and Keating performed their famous experiment whih onfirmed the time dilation predited by SRT by use of marosopi loks. As
Critial Refletions on the Hafele and Keating Experiment W.Nawrot In 1971 Hafele and Keating performed their famous experiment whih onfirmed the time dilation predited by SRT by use of marosopi loks. As
Relativistic Dynamics
 Chapter 7 Relativisti Dynamis 7.1 General Priniples of Dynamis 7.2 Relativisti Ation As stated in Setion A.2, all of dynamis is derived from the priniple of least ation. Thus it is our hore to find a suitable
Chapter 7 Relativisti Dynamis 7.1 General Priniples of Dynamis 7.2 Relativisti Ation As stated in Setion A.2, all of dynamis is derived from the priniple of least ation. Thus it is our hore to find a suitable
MOTION OF AN ELECTRON IN CLASSICAL AND RELATIVISTIC ELECTRODYNAMICS AND AN ALTERNATIVE ELECTRODYNAMICS
 1 MOTION OF AN ELECTRON IN CLASSICAL AND RELATIVISTIC ELECTRODYNAMICS AND AN ALTERNATIVE ELECTRODYNAMICS Musa D. Abdullahi 1 Bujumbura Street, Wuse, Abuja, Nigeria E-mail: musadab@outlook.om Abstrat As
1 MOTION OF AN ELECTRON IN CLASSICAL AND RELATIVISTIC ELECTRODYNAMICS AND AN ALTERNATIVE ELECTRODYNAMICS Musa D. Abdullahi 1 Bujumbura Street, Wuse, Abuja, Nigeria E-mail: musadab@outlook.om Abstrat As
The gravitational phenomena without the curved spacetime
 The gravitational phenomena without the urved spaetime Mirosław J. Kubiak Abstrat: In this paper was presented a desription of the gravitational phenomena in the new medium, different than the urved spaetime,
The gravitational phenomena without the urved spaetime Mirosław J. Kubiak Abstrat: In this paper was presented a desription of the gravitational phenomena in the new medium, different than the urved spaetime,
 Obliqe Projection. A body is projected from a point with different angles of projections 0 0, 35 0, 45 0, 60 0 with the horizontal bt with same initial speed. Their respective horizontal ranges are R,
Obliqe Projection. A body is projected from a point with different angles of projections 0 0, 35 0, 45 0, 60 0 with the horizontal bt with same initial speed. Their respective horizontal ranges are R,
Chapter 1: Kinematics of Particles
 Chapter 1: Kinematics of Particles 1.1 INTRODUCTION Mechanics the state of rest of motion of bodies subjected to the action of forces Static equilibrium of a body that is either at rest or moes with constant
Chapter 1: Kinematics of Particles 1.1 INTRODUCTION Mechanics the state of rest of motion of bodies subjected to the action of forces Static equilibrium of a body that is either at rest or moes with constant
Physics 43 HW 2 Chapter 39 Problems given from 7 th Edition
 Physis 3 HW Chater 39 Problems gien from 7 th Edition Problems:, 7,, 9, 1, 0,,, 9, 33, 35, 3, 0, 5,. How fast must a meter stik be moing if its length is measured to shrink to 0.500 m? P39. L = L L Taking
Physis 3 HW Chater 39 Problems gien from 7 th Edition Problems:, 7,, 9, 1, 0,,, 9, 33, 35, 3, 0, 5,. How fast must a meter stik be moing if its length is measured to shrink to 0.500 m? P39. L = L L Taking
Agenda 2/12/2017. Modern Physics for Frommies V Gravitation Lecture 6. Special Relativity Einstein s Postulates. Einstein s Postulates
 /1/17 Fromm Institute for Lifelong Learning Uniersit of San Franiso Modern Phsis for Frommies V Graitation Leture 6 Agenda Speial Relatiit Einstein s Postulates 15 Februar 17 Modern Phsis V Leture 6 1
/1/17 Fromm Institute for Lifelong Learning Uniersit of San Franiso Modern Phsis for Frommies V Graitation Leture 6 Agenda Speial Relatiit Einstein s Postulates 15 Februar 17 Modern Phsis V Leture 6 1
VII. Relativistic optics. Electromagnetic fields in inertial frames of reference. dt j ( ) ψ = 0. ri r j. Galilean transformation
 VII. Relatiisti optis eletromagneti fields in inertial frames of referene VII. Relatiisti optis Eletromagneti fields in inertial frames of referene Galilean transformation Before 1900 the spae and time
VII. Relatiisti optis eletromagneti fields in inertial frames of referene VII. Relatiisti optis Eletromagneti fields in inertial frames of referene Galilean transformation Before 1900 the spae and time
CHAPTER 5 INTRODUCTION TO OCEANIC TURBIDITY CURRENTS 5.1 INTRODUCTION
 CHAPTER 5 INTRODCTION TO OCEANIC TRBIDITY CRRENTS 5.1 INTRODCTION Trbidity rrents are the ndersea eqivalents of sediment-laden river flows. They onsist of density-driven bottom rrents for whih the agent
CHAPTER 5 INTRODCTION TO OCEANIC TRBIDITY CRRENTS 5.1 INTRODCTION Trbidity rrents are the ndersea eqivalents of sediment-laden river flows. They onsist of density-driven bottom rrents for whih the agent
Feb 6, 2013 PHYSICS I Lecture 5
 95.141 Feb 6, 213 PHYSICS I Lecture 5 Course website: faculty.uml.edu/pchowdhury/95.141/ www.masteringphysics.com Course: UML95141SPRING213 Lecture Capture h"p://echo36.uml.edu/chowdhury213/physics1spring.html
95.141 Feb 6, 213 PHYSICS I Lecture 5 Course website: faculty.uml.edu/pchowdhury/95.141/ www.masteringphysics.com Course: UML95141SPRING213 Lecture Capture h"p://echo36.uml.edu/chowdhury213/physics1spring.html
before the collision and v 1 f and v 2 f after the collision. Since conservation of the linear momentum
 Lecture 7 Collisions Durin the preious lecture we stared our discussion of collisions As it was stated last tie a collision is an isolated eent in which two or ore odies (the collidin odies) exert relatiely
Lecture 7 Collisions Durin the preious lecture we stared our discussion of collisions As it was stated last tie a collision is an isolated eent in which two or ore odies (the collidin odies) exert relatiely
arxiv:gr-qc/ v7 14 Dec 2003
 Propagation of light in non-inertial referene frames Vesselin Petkov Siene College, Conordia University 1455 De Maisonneuve Boulevard West Montreal, Quebe, Canada H3G 1M8 vpetkov@alor.onordia.a arxiv:gr-q/9909081v7
Propagation of light in non-inertial referene frames Vesselin Petkov Siene College, Conordia University 1455 De Maisonneuve Boulevard West Montreal, Quebe, Canada H3G 1M8 vpetkov@alor.onordia.a arxiv:gr-q/9909081v7
FW Phys 130 G:\130 lecture\130 tests\formulas final03.docx page 1 of 7
 FW Phys 13 G:\13 leture\13 tests\forulas final3.dox page 1 of 7 dr dr r x y z ur ru (1.1) dt dt All onseratie fores derie fro a potential funtion U(x,y,z) (1.) U U U F gradu U,, x y z 1 MG 1 dr MG E K
FW Phys 13 G:\13 leture\13 tests\forulas final3.dox page 1 of 7 dr dr r x y z ur ru (1.1) dt dt All onseratie fores derie fro a potential funtion U(x,y,z) (1.) U U U F gradu U,, x y z 1 MG 1 dr MG E K
Get Solution of These Packages & Learn by Video Tutorials on PROJECTILE MOTION
 FREE Download Study Packae from website: www.tekoclasses.com & www.mathsbysuha.com Get Solution of These Packaes & Learn by Video Tutorials on www.mathsbysuha.com. BASIC CONCEPT :. PROJECTILE PROJECTILE
FREE Download Study Packae from website: www.tekoclasses.com & www.mathsbysuha.com Get Solution of These Packaes & Learn by Video Tutorials on www.mathsbysuha.com. BASIC CONCEPT :. PROJECTILE PROJECTILE
Rutgers University Department of Physics & Astronomy. 01:750:271 Honors Physics I Fall Lecture 4. Home Page. Title Page. Page 1 of 35.
 Rutgers Uniersit Department of Phsics & Astronom 01:750:271 Honors Phsics I Fall 2015 Lecture 4 Page 1 of 35 4. Motion in two and three dimensions Goals: To stud position, elocit, and acceleration ectors
Rutgers Uniersit Department of Phsics & Astronom 01:750:271 Honors Phsics I Fall 2015 Lecture 4 Page 1 of 35 4. Motion in two and three dimensions Goals: To stud position, elocit, and acceleration ectors
XI PHYSICS M. AFFAN KHAN LECTURER PHYSICS, AKHSS, K. https://promotephysics.wordpress.com
 XI PHYSICS M. AFFAN KHAN LECTURER PHYSICS, AKHSS, K affan_414@live.com https://promotephysics.wordpress.com [MOTION IN TWO DIMENSIONS] CHAPTER NO. 4 In this chapter we are oin to discuss motion in projectile
XI PHYSICS M. AFFAN KHAN LECTURER PHYSICS, AKHSS, K affan_414@live.com https://promotephysics.wordpress.com [MOTION IN TWO DIMENSIONS] CHAPTER NO. 4 In this chapter we are oin to discuss motion in projectile
Name Solutions to Test 1 September 23, 2016
 Name Solutions to Test 1 September 3, 016 This test onsists of three parts. Please note that in parts II and III, you an skip one question of those offered. Possibly useful formulas: F qequb x xvt E Evpx
Name Solutions to Test 1 September 3, 016 This test onsists of three parts. Please note that in parts II and III, you an skip one question of those offered. Possibly useful formulas: F qequb x xvt E Evpx
The physics of the longitudinal light clock
 he physis of the longitdinal light lok Giovanni Zanella Stdioso Senior dello Stdim Patavinm Università di Padova, Italy giovanni.zanella@nipd.it bstrat he standard analysis of the behavior of the longitdinal
he physis of the longitdinal light lok Giovanni Zanella Stdioso Senior dello Stdim Patavinm Università di Padova, Italy giovanni.zanella@nipd.it bstrat he standard analysis of the behavior of the longitdinal
v( t) g 2 v 0 sin θ ( ) ( ) g t ( ) = 0
 PROJECTILE MOTION Velocity We seek to explore the velocity of the projectile, includin its final value as it hits the round, or a taret above the round. The anle made by the velocity vector with the local
PROJECTILE MOTION Velocity We seek to explore the velocity of the projectile, includin its final value as it hits the round, or a taret above the round. The anle made by the velocity vector with the local
2.2 Differentiation and Integration of Vector-Valued Functions
 .. DIFFERENTIATION AND INTEGRATION OF VECTOR-VALUED FUNCTIONS133. Differentiation and Interation of Vector-Valued Functions Simply put, we differentiate and interate vector functions by differentiatin
.. DIFFERENTIATION AND INTEGRATION OF VECTOR-VALUED FUNCTIONS133. Differentiation and Interation of Vector-Valued Functions Simply put, we differentiate and interate vector functions by differentiatin
Deduce thenew Gravitational Formula:
 Dede thenew Gravitational Formla: F m = Chn-Xan. Jiang P. O. ox 394, eijing 1854, P.. China 13jianghnxan@gmail.om Abstrat Using two methods we dede the new gravitational formla, In the Universe there are
Dede thenew Gravitational Formla: F m = Chn-Xan. Jiang P. O. ox 394, eijing 1854, P.. China 13jianghnxan@gmail.om Abstrat Using two methods we dede the new gravitational formla, In the Universe there are
Millennium Relativity Acceleration Composition. The Relativistic Relationship between Acceleration and Uniform Motion
 Millennium Relativity Aeleration Composition he Relativisti Relationship between Aeleration and niform Motion Copyright 003 Joseph A. Rybzyk Abstrat he relativisti priniples developed throughout the six
Millennium Relativity Aeleration Composition he Relativisti Relationship between Aeleration and niform Motion Copyright 003 Joseph A. Rybzyk Abstrat he relativisti priniples developed throughout the six
Derivation of Transformation and One-Way Speed of Light in Kinematics of Special Theory of Ether
 Amerian Journal of Modern Physis 07; 66: 40-47 http:www.sienepublishinggroup.omjajmp doi: 0.648j.ajmp.070606.5 ISSN: 36-8867 Print; ISSN: 36-889 Online Deriation of Transformation and One-Way Speed of
Amerian Journal of Modern Physis 07; 66: 40-47 http:www.sienepublishinggroup.omjajmp doi: 0.648j.ajmp.070606.5 ISSN: 36-8867 Print; ISSN: 36-889 Online Deriation of Transformation and One-Way Speed of
CHAPTER 26 The Special Theory of Relativity
 CHAPTER 6 The Speial Theory of Relativity Units Galilean-Newtonian Relativity Postulates of the Speial Theory of Relativity Simultaneity Time Dilation and the Twin Paradox Length Contration Four-Dimensional
CHAPTER 6 The Speial Theory of Relativity Units Galilean-Newtonian Relativity Postulates of the Speial Theory of Relativity Simultaneity Time Dilation and the Twin Paradox Length Contration Four-Dimensional
Special Theory of Time- Asymmetric Relativity 1 2
 Part I Speial Theory of Time- Asymmetri Relatiity 1 The expanding-unierse osmology is founded on the assumption that Einstein s Relatiity is appliable to the entire unierse. This osmology settles diffiulties
Part I Speial Theory of Time- Asymmetri Relatiity 1 The expanding-unierse osmology is founded on the assumption that Einstein s Relatiity is appliable to the entire unierse. This osmology settles diffiulties
The Hashemite University Department of Civil Engineering ( ) Dr. Hazim Dwairi 1
 Department of Civil Engineering Letre 8 Slender Colmns Definition of Slender Colmn When the eentri loads P are applied, the olmn deflets laterally by amont δ,, however the internal moment at midheight:
Department of Civil Engineering Letre 8 Slender Colmns Definition of Slender Colmn When the eentri loads P are applied, the olmn deflets laterally by amont δ,, however the internal moment at midheight:
Relativity II. The laws of physics are identical in all inertial frames of reference. equivalently
 Relatiity II I. Henri Poincare's Relatiity Principle In the late 1800's, Henri Poincare proposed that the principle of Galilean relatiity be expanded to inclde all physical phenomena and not jst mechanics.
Relatiity II I. Henri Poincare's Relatiity Principle In the late 1800's, Henri Poincare proposed that the principle of Galilean relatiity be expanded to inclde all physical phenomena and not jst mechanics.
Math 144 Activity #10 Applications of Vectors
 144 p 1 Math 144 Actiity #10 Applications of Vectors In the last actiity, yo were introdced to ectors. In this actiity yo will look at some of the applications of ectors. Let the position ector = a, b
144 p 1 Math 144 Actiity #10 Applications of Vectors In the last actiity, yo were introdced to ectors. In this actiity yo will look at some of the applications of ectors. Let the position ector = a, b
Physics 1: Mechanics
 Physics 1: Mechanics Đào Ngọc Hạnh Tâm Office: A1.53, Email: dnhtam@hcmiu.edu.n HCMIU, Vietnam National Uniersity Acknowledgment: Most of these slides are supported by Prof. Phan Bao Ngoc credits (3 teaching
Physics 1: Mechanics Đào Ngọc Hạnh Tâm Office: A1.53, Email: dnhtam@hcmiu.edu.n HCMIU, Vietnam National Uniersity Acknowledgment: Most of these slides are supported by Prof. Phan Bao Ngoc credits (3 teaching
Euclidean Model of Space and Time
 Jornal of Modern Physis, 018, 9, 115-149 http://www.sirp.org/jornal/jmp ISSN Online: 153-10X ISSN Print: 153-1196 Elidean Model of Spae and Time Radovan Mahotka Brno University of Tehnology, Brno, Czeh
Jornal of Modern Physis, 018, 9, 115-149 http://www.sirp.org/jornal/jmp ISSN Online: 153-10X ISSN Print: 153-1196 Elidean Model of Spae and Time Radovan Mahotka Brno University of Tehnology, Brno, Czeh
Chapter 4. Motion in Two Dimensions. Position and Displacement. General Motion Ideas. Motion in Two Dimensions
 Motion in Two Dimensions Chapter 4 Motion in Two Dimensions Using + or signs is not always sufficient to fully describe motion in more than one dimension Vectors can be used to more fully describe motion
Motion in Two Dimensions Chapter 4 Motion in Two Dimensions Using + or signs is not always sufficient to fully describe motion in more than one dimension Vectors can be used to more fully describe motion
EINSTEIN FIELD EQUATIONS OBTAINED ONLY WITH GAUSS CURVATURE AND ZOOM UNIVERSE MODEL CHARACTERISTICS
 EINSTEIN FIELD EQUATIONS OBTAINED ONLY WITH GAUSS CURVATURE AND ZOOM UNIVERSE MODEL CHARACTERISTICS Sergio Garia Chimeno Abstrat Demonstration how to obtain the Einstein Field Equations without using the
EINSTEIN FIELD EQUATIONS OBTAINED ONLY WITH GAUSS CURVATURE AND ZOOM UNIVERSE MODEL CHARACTERISTICS Sergio Garia Chimeno Abstrat Demonstration how to obtain the Einstein Field Equations without using the
