YORK UNIVERSITY. Faculty of Science and Engineering Faculty of Liberal Arts and Professional Studies MATH A Test #2.
|
|
|
- Jason Baldwin
- 6 years ago
- Views:
Transcription
1 YORK UNIVERSITY Faculty of Science and Engineering Faculty of Liberal Arts and Professional Studies MATH A Test #2 June 27, 212 Surname (print): Given Name: Student No: Signature: INSTRUCTIONS: 1. Please write your name, student number and final answers in ink. 2. This is a closed-book test, duration- 75 minutes. 3. No calculator is permitted. 4. There are seven questions on eight pages. Answer all the questions. 5. Show all work necessary to justify each answer you give. Clearly indicate each time you use the back of a page for your work. 6. Remain seated until we collect all the test papers. 7. Do the easiest questions first. GOOD LUCK! Question I Points I Scored I Total: 6
2 Name: Student No: 1. (2 + 2 pts) Choose the one alternative that best completes the statement. (a) When two ratios in a simplex tableau tie for being smallest, i. there is a possibility for multiple optimum degenerate BFS will occur. iii. the problem has an unbounded solution. ANSWER: (t-'c.'), (b) In a simplex tableau that gives an optimum solution, a zero indicator for a nonbasic variable suggests i. the problem has an unbounded solution. ii. a degenerate BFS will is a possibility for multiple optimum solutions. 2. ( pts) Consider the following LP: ANSWER: (Jt-t_') max z = 2XI- X2 + X3, subject to 3XI + X2 + X3 < XI- X2 + 2X3 < XI+ X2- X3 < Xl, X2, X3 > (a) Write the initial simplex tableau for the solution of the problem by the Simplex Algorithm. O.tftf Cc_ VtJ.A/,; " 1 2- CJM.J,& 3. fu rl_ ({ff-/j st- <- +, f:tc_e_ et/tj;fvcm.- > r-eckve-4j, fo (,- fl.. LP tla fo.,vcr IM -z. s.f. o2. X 1 - X z... -t- ")C 3. A::, -t- + )C3 "'\- " -=- " x.\- X2- -t 2 x ' :X. + X - 'X -t- 1 r.l. So? cw:h.: iec;"i' M c z x, x2... JC3..4.!::>:L ":!. RttS' - { _ 1. () - v Continues... 1
3 Name: (b) After one iteration the simplex tableau for this problem is z XI X2 X3 S RHS Student No: Determine basic variables and write the basic feasible solution corresponding to this tableau. Ba._yt...'e.. \fakc: tv.. -\, A 3>., 1ke_ Cc-rre.'(1 OM..J Fe; i<; ANSWER:
4 3. (7 pts) The following LINGO program is given. Write the LP problem, which is solved using this program. MODEL: SETS: DAYS/1.. 5/:X,Y,DEMAND; ENDSETS DAYS( I) I I # GT # 1:X(1)=.9*X(I-1)+ Y(l-1)- DEMAND( 5*Y 2 DEMAND; DATA: DEMAND= 4,6,7,75,5; ENDDATA END L-L "'z_ -=- (3 'l:l\ t- 5' ca- J '"{- (3aJ Xz_ + 15 ) t -\ ( 3oO 'X.s- + 15S') ==- 3 ( ')( + '):2-* ")( -\- "')(tot -t- :X: s-'yt- 5' ( 1 +- '--\- <cj 3 + '"( k 5" ') :J S.t. X" =- Lt, x2.-, "+-(fa- Goo, X -=-. 3 'X.l. + t;f-'-- 'foo J xt -=- o.ca 'X:> +- <i 3-5> -:x: =- o. g ')(_ '< -\- lf - s-oo-> G x,- 6''(1- )- 4 > G Xz.- s-'2-" G x3.- Su_ ::rw <f.) G x4-5u > r:rso <fl.f --- > 1\ G xs- - 5 s- s-oo/ '): x X )( X u u u "., '> 3.., 4> 'S)(J"''o,(f><a4>Cf?::o. Continues... 3
5 Name: Student No: 4. (1 + 4 pts) (a) Suppose that we have five different maximization LP's and assume that, in trying to solve them, after several iterations we have arrived to the following simplex tableaus: LP 1: LP 2: LP 3: LP 4: [ [ X! X2 X3 X4 rhs ] 7/4 1/8 55 z = /2 28 X2 = 28 ' 1 1/4-1/8 9 X!= 9 X! X2 X3 X4 rhs ] -1 3/2 5 z =5 1 1/2 2 X!= 2 ' 1-1 1/2 1 X2 = 1 u X! X2 X3 X4 rhs 2 1 z = 1 1/2 1 1/2 5/2 X2 = 5/2 ' 1/2-1/2 1 3/2 X4 = 3/2 X! X2 X4 X3 a rhs [ LP 5: [ ] z=44m] 1+5M M 2+4M X2 = 2 ' a=4 X! X2 X3 X4 rhs z = bv 17 ] X3 = 8 ' X4 = where a is an artificial variable. Denote by AS = alternative optimal solutions, DEG = degeneracy, INFS = infeasible solution, UBS = unbounded solution, NONE = none of the above. Specify for each problem which one of the possible answers mentioned above is true? LP 1: NONE ; LP 2: f) B s ; LP 3: _._A--'-"S=<----_ LP 4: INJ=$ ; LP 5: Z> EG-- Note: No explanation is required. Evaluation: +2 for each correct answer, for each unanswered part, -1 for each incorrect answer - but zero is the lowest total score for this question. (b) For the unbounded LP from part (a), find a direction of unboundedness. L.P o1. is u"'e.of. LP. FrDiM 1tu_ ) x L e.,.kwi.a--t 1H.W'C:aifL, GM J X -1 =- JJJ C4t :t?.2.-.x 3 -=-1 'X" -=-.:lo $ - ): 2- =-{ + 3. ' Ust..e.-re... )C3 C 2A..<.._ {ku'" UMJ. /) O_ /J i..t.e-b-re.) a.. tft, re.d.c.. ef- 'j J -:::::: [ O 1 1 OJ Continues... 4
6 Name: Student No: 5. (1 + 2 pts) Consider the LP: max z = Xl +xz +2x3 subject to 2x 1 +xz +x3 < 2 3xl +4xz +2x3 > 8 x 1, Xz, x3 > (a) Solve the problem above by the Big-M Method using the largest coefficient rule. If there is a tie in choosing a leaving variable, priority should be given to an artificial variable. '"2.. "= XII ;- ')C 2-. t- c1?<:-.!:. - Mo-) s. f.. a '):-i -r -:x: Jc 3. t- -==-..L X. A + 4 "l:2-2. X 3. - e 2. + C\._ -=:. _& (! ) S<J 'X-1 )')C2.) XJ..) h" ' '- 'a_ 'V.. ) # o+ f!:,\1 s. -::::. ( : Y Ut..r<. ft ::::- 2-) 1 # o-f. /VTJV G-2-= l(j UM.J t-c sv C\W J. CL. lo e.e...\u..c.: ki. f;.:cl'a.k: Va.-Yc.-'.fY 1<'2-' 'M <;jwctd v ';} Q-z_ M a cl- to "2- -==- XA + 'XL cl. ")( 3:. - M c.-_ + 3 t-j\'x" -+ L(f-.1\.x.L * 2.M X> - MeL M a-.8 M \IWVJC-.;_ -=- ( M,f) f'jc ( 4 M -t- -i') -x.l- + ( \'-'1 -\- 2. 'yx: - M e.2.-.& M f{-u.-tu.) ch:a.r <;.:&x { t:s CD A.e.. 2- R+t S V RM-Lo M o -gm z. :::-&M -..t. ot &'\ = T =.t. -1 t1 <;:\A-u... Wwc.. va.v t' xl (JAA. tk.'vt.- & -=-& t-=cl (Q,) VM"f&_ i'<;..) ft. "lreji otaj- -& rl-- () ) u c;:{w<; ( )Ro, ) 1<-z + (4M-;-1) {:2-x.._ CJA<of Continues... A-() Px2.- to ocfcu f:gzcu..r 5
7 ),, t<2 -+G_) Rx 3 : 2--l)l2-:tl; Student No: Name: (p ")(: )C..z...? :!:> -\ e Q_ Rt-ts r3v Ra.b. o..\ _i._ -;z_ -- Lf MT1... ei.. Z-=-2 Lt '-{ s- Qi), t1.-1 ==- t:( y --l.f '1 -L( 'i " -., =- ' k L '):.2._'=c1- c1...:l -r::=4 s- --1 :; L _L Ci<- ) 2._ L M- Z--=-j_, 2- s- J_...L _.L 'X?>=- ":f- J..., ol.l- _1._ t1 -i.l :C.z._-= -.L " L 2-.. S-t."'-c..L -s t's a,u r;p+- ( 1faie_ ') 1- / -xpf--=-1.) xpf-::::- o ) x ;rt--=-o 7_ wa;(-=- L. (b) How many optimal solutions does the above given LP have? Explain. 1L_ LP 6 9uL ot+ - 4-d. af- re.oj fo Jiff-e,r lo._ refah:4 to k'fterej- 'BFS. as o of: ) {(_. l.ni -<.:c. VCVV'. x ) 'X:z._ 1 ") -\ x2. 'x3.l.) -\. x2- ; ) V- 'X:2..' e 2..1 (k_ 'Cal-J. Re.caif tfu..l Je.se...e/e Oceu S eu=- 1L. /Vt 5: f.o CL B V h1j>peua fe f e_ e.-y"o' Continues... o+- c._ CLLJ- CPYY'e..C pow. "'9-6
8 Name: Student No: 6. (7 pts) Consider the LP: max z = 2xl + 3x2 subject to 2x1 + x2 < 1 (') Xl + X2 < 6 (..2.) -xl + X2 < 4 () X1,X2 > (Be very careful with your work because it will Lj <:!. 1 (J l) 1\ h \ 1 PI / 1\ / \ la 1(.1,6 "" VJ rk 5'\ l/t o--,/),_ ;_\ h' Vj c JJ. {L, ) """- lfo tt'\ \ f-';> 7 "\ 8 f IR..1" t i \ '""' (b) Find the allowable range of change for the OFC of x2, for which the current optimal basis remains optimal. Justify your answer. J_ei z -:= ci..x., +X c...t..t r"ej-..st...'s ANSWER: [J. 1 J re.:.;:: -h.: t.<,-.e,ve,.r - 4: > C 'S.'\ 6:; C c2_ 7.v.tltv C. >O.. I Oo \. -- a vam-rc...- fp..r (.. s L..t, J (c) Find the allowable range of change for the RHS f the second constraint, for which the current optimal basis remains optimal. Justify your answer. 1U- -red- "-- {;-t.answer: [lf 1 g J t:.c (Le_ e. u_ :t-1 +- ')C:z._ =-6 H.<. a/ tv c:fr.e-e f. &} rc,k;f C(o 7 4) 9;( 7J()G). Sb/ ('2-) '('<;u:f ZJ R-11 -=-&;. (2-) fo C:. -='> fh1.s: =- L[. f-- Cont'"ues... e.>. /D fl. g1 7 t>..,t. t-s L..,) j.
9 Name: Student No: 7. (6 pts) Consider the LP: max z = 3xl + 4x2 subject to 2xl + x2 < 8 4xl + x2 < 1 X}, X2 2- In optimal tableau of the LP, the basic variables are x 1 and x 2. Use Important Formulas from Section 6.2 to find optimal simplex tableau and optimal solution to the problem. Note: No points will be given to any other answer._ - _ fl.+ (cn -1 N =-1 en'!_) )cno.v-::: e,v f:> ANSWER: l 'k 'I -\- JJ ')<:_N flv -==- B. 1 e... c v -== [ - ) )2.. " 3 Lt ],.g -=- [ " J T ) -=- \_ 4 1\ ) N-=- 1 2 c.nv [o o].., -" -==- r- 2- \ -.,.g -=- --- "z_ l c \ -:::. 1 \_ - J ">..t -A j J (; c r.,v - [-=- c.n.v ( - t;)-=- l L11 ( -=- :J..1-) c_ f!:n f!:,- ' N - c_ N (!, v = c I!> v - 1 -=- [ It J l } _\ J -t-i - J., u.z.. o- t-o...: A- trm ki"& {a._fku --z_ :x:" Jc x 3 x 4 R H s BY Ra.:h.' o t{ 3-5'.i +-- z -==J o -;, CD t "- - G ). )R R -+(s;_)r -xtt. o [). o -L 1. "'Z.'=:s' Jctr xl.- =- JS ( R xtr)
YORK UNIVERSITY. Faculty of Science and Engineering Faculty of Liberal Arts and Professional Studies. MATH B Test #1. September 28, 2012
 YORK UNIVERSITY Faculty of Science and Engineering Faculty of Liberal Arts and Professional Studies MATH 1013 3.00 B Test #1 September 28, 2012 Surname (print):------------ Given Name: Student No: --------------
YORK UNIVERSITY Faculty of Science and Engineering Faculty of Liberal Arts and Professional Studies MATH 1013 3.00 B Test #1 September 28, 2012 Surname (print):------------ Given Name: Student No: --------------
i;\-'i frz q > R>? >tr E*+ [S I z> N g> F 'x sa :r> >,9 T F >= = = I Y E H H>tr iir- g-i I * s I!,i --' - = a trx - H tnz rqx o >.F g< s Ire tr () -s
 5 C /? >9 T > ; '. ; J ' ' J. \ ;\' \.> ). L; c\ u ( (J ) \ 1 ) : C ) (... >\ > 9 e!) T C). '1!\ /_ \ '\ ' > 9 C > 9.' \( T Z > 9 > 5 P + 9 9 ) :> : + (. \ z : ) z cf C : u 9 ( :!z! Z c (! $ f 1 :.1 f.
5 C /? >9 T > ; '. ; J ' ' J. \ ;\' \.> ). L; c\ u ( (J ) \ 1 ) : C ) (... >\ > 9 e!) T C). '1!\ /_ \ '\ ' > 9 C > 9.' \( T Z > 9 > 5 P + 9 9 ) :> : + (. \ z : ) z cf C : u 9 ( :!z! Z c (! $ f 1 :.1 f.
35H MPa Hydraulic Cylinder 3.5 MPa Hydraulic Cylinder 35H-3
 - - - - ff ff - - - - - - B B BB f f f f f f f 6 96 f f f f f f f 6 f LF LZ f 6 MM f 9 P D RR DD M6 M6 M6 M. M. M. M. M. SL. E 6 6 9 ZB Z EE RC/ RC/ RC/ RC/ RC/ ZM 6 F FP 6 K KK M. M. M. M. M M M M f f
- - - - ff ff - - - - - - B B BB f f f f f f f 6 96 f f f f f f f 6 f LF LZ f 6 MM f 9 P D RR DD M6 M6 M6 M. M. M. M. M. SL. E 6 6 9 ZB Z EE RC/ RC/ RC/ RC/ RC/ ZM 6 F FP 6 K KK M. M. M. M. M M M M f f
Standard Form An LP is in standard form when: All variables are non-negativenegative All constraints are equalities Putting an LP formulation into sta
 Chapter 4 Linear Programming: The Simplex Method An Overview of the Simplex Method Standard Form Tableau Form Setting Up the Initial Simplex Tableau Improving the Solution Calculating the Next Tableau
Chapter 4 Linear Programming: The Simplex Method An Overview of the Simplex Method Standard Form Tableau Form Setting Up the Initial Simplex Tableau Improving the Solution Calculating the Next Tableau
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
MATH 445/545 Homework 2: Due March 3rd, 2016
 MATH 445/545 Homework 2: Due March 3rd, 216 Answer the following questions. Please include the question with the solution (write or type them out doing this will help you digest the problem). I do not
MATH 445/545 Homework 2: Due March 3rd, 216 Answer the following questions. Please include the question with the solution (write or type them out doing this will help you digest the problem). I do not
~,. :'lr. H ~ j. l' ", ...,~l. 0 '" ~ bl '!; 1'1. :<! f'~.., I,," r: t,... r':l G. t r,. 1'1 [<, ."" f'" 1n. t.1 ~- n I'>' 1:1 , I. <1 ~'..
 ,, 'l t (.) :;,/.I I n ri' ' r l ' rt ( n :' (I : d! n t, :?rj I),.. fl.),. f!..,,., til, ID f-i... j I. 't' r' t II!:t () (l r El,, (fl lj J4 ([) f., () :. -,,.,.I :i l:'!, :I J.A.. t,.. p, - ' I I I
,, 'l t (.) :;,/.I I n ri' ' r l ' rt ( n :' (I : d! n t, :?rj I),.. fl.),. f!..,,., til, ID f-i... j I. 't' r' t II!:t () (l r El,, (fl lj J4 ([) f., () :. -,,.,.I :i l:'!, :I J.A.. t,.. p, - ' I I I
APPH 4200 Physics of Fluids
 APPH 42 Physics of Fluids Problem Solving and Vorticity (Ch. 5) 1.!! Quick Review 2.! Vorticity 3.! Kelvin s Theorem 4.! Examples 1 How to solve fluid problems? (Like those in textbook) Ç"Tt=l I $T1P#(
APPH 42 Physics of Fluids Problem Solving and Vorticity (Ch. 5) 1.!! Quick Review 2.! Vorticity 3.! Kelvin s Theorem 4.! Examples 1 How to solve fluid problems? (Like those in textbook) Ç"Tt=l I $T1P#(
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
Dr. Maddah ENMG 500 Engineering Management I 10/21/07
 Dr. Maddah ENMG 500 Engineering Management I 10/21/07 Computational Procedure of the Simplex Method The optimal solution of a general LP problem is obtained in the following steps: Step 1. Express the
Dr. Maddah ENMG 500 Engineering Management I 10/21/07 Computational Procedure of the Simplex Method The optimal solution of a general LP problem is obtained in the following steps: Step 1. Express the
IE 400: Principles of Engineering Management. Simplex Method Continued
 IE 400: Principles of Engineering Management Simplex Method Continued 1 Agenda Simplex for min problems Alternative optimal solutions Unboundedness Degeneracy Big M method Two phase method 2 Simplex for
IE 400: Principles of Engineering Management Simplex Method Continued 1 Agenda Simplex for min problems Alternative optimal solutions Unboundedness Degeneracy Big M method Two phase method 2 Simplex for
176 5 t h Fl oo r. 337 P o ly me r Ma te ri al s
 A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
::::l<r/ L- 1-1>(=-ft\ii--r(~1J~:::: Fo. l. AG -=(0,.2,L}> M - &-c ==- < ) I) ~..-.::.1 ( \ I 0. /:rf!:,-t- f1c =- <I _,, -2...
 Math 3298 Exam 1 NAME: SCORE: l. Given three points A(I, l, 1), B(l,;2, 3), C(2, - l, 2). (a) Find vectors AD, AC, nc. (b) Find AB+ DC, AB - AC, and 2AD. -->,,. /:rf!:,-t- f1c =-
Math 3298 Exam 1 NAME: SCORE: l. Given three points A(I, l, 1), B(l,;2, 3), C(2, - l, 2). (a) Find vectors AD, AC, nc. (b) Find AB+ DC, AB - AC, and 2AD. -->,,. /:rf!:,-t- f1c =-
T h e C S E T I P r o j e c t
 T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
AP Calculus AB. Sample Student Responses and Scoring Commentary. Inside: Free Response Question 1. Scoring Guideline.
 218 AP Calculus AB Sample Student Responses and Scoring Commentary Inside: Free Response Question 1 RR Scoring Guideline RR Student Samples RR Scoring Commentary 218 The College Board. College Board, Advanced
218 AP Calculus AB Sample Student Responses and Scoring Commentary Inside: Free Response Question 1 RR Scoring Guideline RR Student Samples RR Scoring Commentary 218 The College Board. College Board, Advanced
Systems Analysis in Construction
 Systems Analysis in Construction CB312 Construction & Building Engineering Department- AASTMT by A h m e d E l h a k e e m & M o h a m e d S a i e d 3. Linear Programming Optimization Simplex Method 135
Systems Analysis in Construction CB312 Construction & Building Engineering Department- AASTMT by A h m e d E l h a k e e m & M o h a m e d S a i e d 3. Linear Programming Optimization Simplex Method 135
February 17, Simplex Method Continued
 15.053 February 17, 2005 Simplex Method Continued 1 Today s Lecture Review of the simplex algorithm. Formalizing the approach Alternative Optimal Solutions Obtaining an initial bfs Is the simplex algorithm
15.053 February 17, 2005 Simplex Method Continued 1 Today s Lecture Review of the simplex algorithm. Formalizing the approach Alternative Optimal Solutions Obtaining an initial bfs Is the simplex algorithm
MATH 445/545 Test 1 Spring 2016
 MATH 445/545 Test Spring 06 Note the problems are separated into two sections a set for all students and an additional set for those taking the course at the 545 level. Please read and follow all of these
MATH 445/545 Test Spring 06 Note the problems are separated into two sections a set for all students and an additional set for those taking the course at the 545 level. Please read and follow all of these
YORK UNIVERSITY. Faculty of Science Department of Mathematics and Statistics. MATH C Test #1. October 23, 2013.
 YORK UNIVERSITY Faculty of Science Department of Mathematics and Statistics MATH 1505 6.00 C Test #1 October 3, 013 Solutions Family Name (print): Student No: Given Name: Signature: INSTRUCTIONS: 1. Please
YORK UNIVERSITY Faculty of Science Department of Mathematics and Statistics MATH 1505 6.00 C Test #1 October 3, 013 Solutions Family Name (print): Student No: Given Name: Signature: INSTRUCTIONS: 1. Please
Summary of the simplex method
 MVE165/MMG631,Linear and integer optimization with applications The simplex method: degeneracy; unbounded solutions; starting solutions; infeasibility; alternative optimal solutions Ann-Brith Strömberg
MVE165/MMG631,Linear and integer optimization with applications The simplex method: degeneracy; unbounded solutions; starting solutions; infeasibility; alternative optimal solutions Ann-Brith Strömberg
Special cases of linear programming
 Special cases of linear programming Infeasible solution Multiple solution (infinitely many solution) Unbounded solution Degenerated solution Notes on the Simplex tableau 1. The intersection of any basic
Special cases of linear programming Infeasible solution Multiple solution (infinitely many solution) Unbounded solution Degenerated solution Notes on the Simplex tableau 1. The intersection of any basic
SOME ALGORITHMS FOR SOLVING EXTREME POINT MATHEMATICAL PROGRAMMING PROBLEMS**
 127 NZOR volume 7 number 2 July 1979 SOME ALGORITHMS FOR SOLVING EXTREME POINT MATHEMATICAL PROGRAMMING PROBLEMS** S. Kumar, R o y a l M e l b o u r n e I n s t i t u t e o f T e c h n o l o g y D. W a
127 NZOR volume 7 number 2 July 1979 SOME ALGORITHMS FOR SOLVING EXTREME POINT MATHEMATICAL PROGRAMMING PROBLEMS** S. Kumar, R o y a l M e l b o u r n e I n s t i t u t e o f T e c h n o l o g y D. W a
Summary of the simplex method
 MVE165/MMG630, The simplex method; degeneracy; unbounded solutions; infeasibility; starting solutions; duality; interpretation Ann-Brith Strömberg 2012 03 16 Summary of the simplex method Optimality condition:
MVE165/MMG630, The simplex method; degeneracy; unbounded solutions; infeasibility; starting solutions; duality; interpretation Ann-Brith Strömberg 2012 03 16 Summary of the simplex method Optimality condition:
l~ 0 0 'JL 1. )t\ 1-, 'x,,; 1-r
 Test 1 Math 2407 Spring 2011 1. (9 points) For each of the following augmented matrices answer the following questions. ~ 1 0 0 5 6] i. [ 0 000 1 X( 1('1 7ty: Number of equations of the corresponding system
Test 1 Math 2407 Spring 2011 1. (9 points) For each of the following augmented matrices answer the following questions. ~ 1 0 0 5 6] i. [ 0 000 1 X( 1('1 7ty: Number of equations of the corresponding system
21. Solve the LP given in Exercise 19 using the big-m method discussed in Exercise 20.
 Extra Problems for Chapter 3. Linear Programming Methods 20. (Big-M Method) An alternative to the two-phase method of finding an initial basic feasible solution by minimizing the sum of the artificial
Extra Problems for Chapter 3. Linear Programming Methods 20. (Big-M Method) An alternative to the two-phase method of finding an initial basic feasible solution by minimizing the sum of the artificial
(tnaiaun uaejna) o il?smitfl?^ni7wwuiinuvitgviisyiititvi2a-a a imaviitjivi5a^ qw^ww^i fiaa!i-j?s'u'uil?g'ijimqwuwiijami.wti. a nmj 1,965,333.
 0 fltu77jjiimviu«7mi^ gi^"ijhm?'ijjw?flfi^ V m 1 /14 il?mitfl?^i7wwuiinuvitgviiyiititvi2- imviitvi^ qw^ww^i fi!i-j?'u'uil?g'iqwuwiijmi.wti twwrlf^ imii2^
0 fltu77jjiimviu«7mi^ gi^"ijhm?'ijjw?flfi^ V m 1 /14 il?mitfl?^i7wwuiinuvitgviiyiititvi2- imviitvi^ qw^ww^i fi!i-j?'u'uil?g'iqwuwiijmi.wti twwrlf^ imii2^
In Chapters 3 and 4 we introduced linear programming
 SUPPLEMENT The Simplex Method CD3 In Chapters 3 and 4 we introduced linear programming and showed how models with two variables can be solved graphically. We relied on computer programs (WINQSB, Excel,
SUPPLEMENT The Simplex Method CD3 In Chapters 3 and 4 we introduced linear programming and showed how models with two variables can be solved graphically. We relied on computer programs (WINQSB, Excel,
THIS PAGE DECLASSIFIED IAW E
 THS PAGE DECLASSFED AW E0 2958 BL K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW E0 2958 B L K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW EO 2958 THS PAGE DECLASSFED AW EO 2958 THS
THS PAGE DECLASSFED AW E0 2958 BL K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW E0 2958 B L K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW EO 2958 THS PAGE DECLASSFED AW EO 2958 THS
 H NT Z N RT L 0 4 n f lt r h v d lt n r n, h p l," "Fl d nd fl d " ( n l d n l tr l t nt r t t n t nt t nt n fr n nl, th t l n r tr t nt. r d n f d rd n t th nd r nt r d t n th t th n r lth h v b n f
H NT Z N RT L 0 4 n f lt r h v d lt n r n, h p l," "Fl d nd fl d " ( n l d n l tr l t nt r t t n t nt t nt n fr n nl, th t l n r tr t nt. r d n f d rd n t th nd r nt r d t n th t th n r lth h v b n f
Exhibit 2-9/30/15 Invoice Filing Page 1841 of Page 3660 Docket No
 xhibit 2-9/3/15 Invie Filing Pge 1841 f Pge 366 Dket. 44498 F u v 7? u ' 1 L ffi s xs L. s 91 S'.e q ; t w W yn S. s t = p '1 F? 5! 4 ` p V -', {} f6 3 j v > ; gl. li -. " F LL tfi = g us J 3 y 4 @" V)
xhibit 2-9/3/15 Invie Filing Pge 1841 f Pge 366 Dket. 44498 F u v 7? u ' 1 L ffi s xs L. s 91 S'.e q ; t w W yn S. s t = p '1 F? 5! 4 ` p V -', {} f6 3 j v > ; gl. li -. " F LL tfi = g us J 3 y 4 @" V)
ECE430 Name 5 () ( '-'1-+/~ Or"- f w.s. Section: (Circle One) 10 MWF 12:30 TuTh (Sauer) (Liu) TOTAL: USEFUL INFORMATION
 " ~~~~~,",,_~"",,"cr,~ - r " ECE430 Name 5 () ( '-'1-+/~ Or"- f ws Exam #2 (print Name) Spring 2005 Section: (Circle One) 10 MWF 12:30 TuTh (Sauer) (Liu) Problem 1 Problem 2 Problem 3 Problem 4 TOTAL:
" ~~~~~,",,_~"",,"cr,~ - r " ECE430 Name 5 () ( '-'1-+/~ Or"- f ws Exam #2 (print Name) Spring 2005 Section: (Circle One) 10 MWF 12:30 TuTh (Sauer) (Liu) Problem 1 Problem 2 Problem 3 Problem 4 TOTAL:
-Z ONGRE::IONAL ACTION ON FY 1987 SUPPLEMENTAL 1/1
 -Z-433 6 --OGRE::OA ATO O FY 987 SUPPEMETA / APPR)PRATO RfQUEST PAY AD PROGRAM(U) DE ARTMET OF DEES AS O' D 9J8,:A:SF ED DEFS! WA-H ODM U 7 / A 25 MRGOPf RESOUTO TEST HART / / AD-A 83 96 (~Go w - %A uj
-Z-433 6 --OGRE::OA ATO O FY 987 SUPPEMETA / APPR)PRATO RfQUEST PAY AD PROGRAM(U) DE ARTMET OF DEES AS O' D 9J8,:A:SF ED DEFS! WA-H ODM U 7 / A 25 MRGOPf RESOUTO TEST HART / / AD-A 83 96 (~Go w - %A uj
MPM 2D Final Exam Prep 2, June b) Y = 2(x + 1)2-18. ~..: 2. (xl- 1:'}")( t J') -' ( B. vi::: 2 ~ 1-'+ 4 1<. -t-:2 -( 6! '.
 MPM 2D Final Exam Prep 2 June 2017 1. Express each equation in standard form and factored form: ~ ~ +et's 'leu t W (.. ".>tak( a) y = (x + 5)2 + 1 on ::t~'t.{1'" ~heeh v 1' K 1 C'. T.) '. (J. lr lov J
MPM 2D Final Exam Prep 2 June 2017 1. Express each equation in standard form and factored form: ~ ~ +et's 'leu t W (.. ".>tak( a) y = (x + 5)2 + 1 on ::t~'t.{1'" ~heeh v 1' K 1 C'. T.) '. (J. lr lov J
SOUTHWESTERN ELECTRIC POWER COMPANY SCHEDULE H-6.1b NUCLEAR UNIT OUTAGE DATA. For the Test Year Ended March 31, 2009
 Schedule H-6.lb SOUTHWSTRN LCTRIC POWR COMPANY SCHDUL H-6.1b NUCLAR UNIT OUTAG DATA For the Test Year nded March 31, 29 This schedule is not applicable to SVvPCO. 5 Schedule H-6.1 c SOUTHWSTRN LCTRIC POWR
Schedule H-6.lb SOUTHWSTRN LCTRIC POWR COMPANY SCHDUL H-6.1b NUCLAR UNIT OUTAG DATA For the Test Year nded March 31, 29 This schedule is not applicable to SVvPCO. 5 Schedule H-6.1 c SOUTHWSTRN LCTRIC POWR
b. e> nsjfitmjs - cne> Nursing Services Center, Faculty of Nursing Chiang Mai University. njauynfaa phuapmiu e'linaula* ftvnflwtivlvm ofooo
 /. > Af Nursing ervices Center, Faculty f Nursing Chiang Mai University. njauynfaa phuapmiu e'linaula* ftvnflwtivlvm f ((&n) sjentpilg:, gtectigf, ctctfaffrfld Ivnem ( cn) babbjqci b. e> nsjfitmjs cne>
/. > Af Nursing ervices Center, Faculty f Nursing Chiang Mai University. njauynfaa phuapmiu e'linaula* ftvnflwtivlvm f ((&n) sjentpilg:, gtectigf, ctctfaffrfld Ivnem ( cn) babbjqci b. e> nsjfitmjs cne>
necessita d'interrogare il cielo
 gigi nei necessia d'inegae i cie cic pe sax span s inuie a dispiegaa fma dea uce < affeandi ves i cen dea uce isnane " sienzi dei padi sie veic dei' anima 5 J i f H 5 f AL J) i ) L '3 J J "' U J J ö'
gigi nei necessia d'inegae i cie cic pe sax span s inuie a dispiegaa fma dea uce < affeandi ves i cen dea uce isnane " sienzi dei padi sie veic dei' anima 5 J i f H 5 f AL J) i ) L '3 J J "' U J J ö'
Simplex Method for LP (II)
 Simplex Method for LP (II) Xiaoxi Li Wuhan University Sept. 27, 2017 (week 4) Operations Research (Li, X.) Simplex Method for LP (II) Sept. 27, 2017 (week 4) 1 / 31 Organization of this lecture Contents:
Simplex Method for LP (II) Xiaoxi Li Wuhan University Sept. 27, 2017 (week 4) Operations Research (Li, X.) Simplex Method for LP (II) Sept. 27, 2017 (week 4) 1 / 31 Organization of this lecture Contents:
I n t e r n a t i o n a l E l e c t r o n i c J o u r n a l o f E l e m e n t a r y E.7 d u, c ai ts is ou n e, 1 V3 1o-2 l6, I n t h i s a r t
 I n t e r n a t i o n a l E l e c t r o n i c J o ue rlne am l e not fa r y E d u c a t i o n, 2 0 1 4, 1 37-2 ( 16 ). H o w R e a d i n g V o l u m e A f f e c t s b o t h R e a d i n g F l u e n c y
I n t e r n a t i o n a l E l e c t r o n i c J o ue rlne am l e not fa r y E d u c a t i o n, 2 0 1 4, 1 37-2 ( 16 ). H o w R e a d i n g V o l u m e A f f e c t s b o t h R e a d i n g F l u e n c y
2.' -4-5 I fo. - /30 + ;3, x + G: ~ / ~ ) ~ ov. Fd'r evt.'i') cutckf' ()y\e.._o OYLt dtt:vl. t'"'i ~ _) y =.5_21/2-+. 8"'- 2.
 Statistics 100 Sample FINAL Instructions: I. WORK ALL PROBLEMS. Please, give details and explanations and SHOW ALL YOUR WORK so that partial credits can be given. 2. You may use four pages of notes, tables
Statistics 100 Sample FINAL Instructions: I. WORK ALL PROBLEMS. Please, give details and explanations and SHOW ALL YOUR WORK so that partial credits can be given. 2. You may use four pages of notes, tables
Answer the following questions: Q1: Choose the correct answer ( 20 Points ):
 Benha University Final Exam. (ختلفات) Class: 2 rd Year Students Subject: Operations Research Faculty of Computers & Informatics Date: - / 5 / 2017 Time: 3 hours Examiner: Dr. El-Sayed Badr Answer the following
Benha University Final Exam. (ختلفات) Class: 2 rd Year Students Subject: Operations Research Faculty of Computers & Informatics Date: - / 5 / 2017 Time: 3 hours Examiner: Dr. El-Sayed Badr Answer the following
Keep this exam closed until you are told to begin.
 Name: (please print) Signature: ECE 2300 -- Exam #1 October 11, 2014 Keep this exam closed until you are told to begin. 1. This exam is closed book, closed notes. You may use one 8.5 x 11 crib sheet, or
Name: (please print) Signature: ECE 2300 -- Exam #1 October 11, 2014 Keep this exam closed until you are told to begin. 1. This exam is closed book, closed notes. You may use one 8.5 x 11 crib sheet, or
< < or a. * or c w u. "* \, w * r? ««m * * Z * < -4 * if # * « * W * <r? # *» */>* - 2r 2 * j j. # w O <» x <» V X * M <2 * * * *
 - W # a a 2T. mj 5 a a s " V l UJ a > M tf U > n &. at M- ~ a f ^ 3 T N - H f Ml fn -> M - M. a w ma a Z a ~ - «2-5 - J «a -J -J Uk. D tm -5. U U # f # -J «vfl \ \ Q f\ \ y; - z «w W ^ z ~ ~ / 5 - - ^
- W # a a 2T. mj 5 a a s " V l UJ a > M tf U > n &. at M- ~ a f ^ 3 T N - H f Ml fn -> M - M. a w ma a Z a ~ - «2-5 - J «a -J -J Uk. D tm -5. U U # f # -J «vfl \ \ Q f\ \ y; - z «w W ^ z ~ ~ / 5 - - ^
,. *â â > V>V. â ND * 828.
 BL D,. *â â > V>V Z V L. XX. J N R â J N, 828. LL BL D, D NB R H â ND T. D LL, TR ND, L ND N. * 828. n r t d n 20 2 2 0 : 0 T http: hdl.h ndl.n t 202 dp. 0 02802 68 Th N : l nd r.. N > R, L X. Fn r f,
BL D,. *â â > V>V Z V L. XX. J N R â J N, 828. LL BL D, D NB R H â ND T. D LL, TR ND, L ND N. * 828. n r t d n 20 2 2 0 : 0 T http: hdl.h ndl.n t 202 dp. 0 02802 68 Th N : l nd r.. N > R, L X. Fn r f,
PHYS 232 QUIZ minutes.
 / PHYS 232 QUIZ 1 02-18-2005 50 minutes. This quiz has 3 questions. Please show all your work. If your final answer is not correct, you will get partial credit based on your work shown. You are allowed
/ PHYS 232 QUIZ 1 02-18-2005 50 minutes. This quiz has 3 questions. Please show all your work. If your final answer is not correct, you will get partial credit based on your work shown. You are allowed
Th n nt T p n n th V ll f x Th r h l l r r h nd xpl r t n rr d nt ff t b Pr f r ll N v n d r n th r 8 l t p t, n z n l n n th n rth t rn p rt n f th v
 Th n nt T p n n th V ll f x Th r h l l r r h nd xpl r t n rr d nt ff t b Pr f r ll N v n d r n th r 8 l t p t, n z n l n n th n rth t rn p rt n f th v ll f x, h v nd d pr v n t fr tf l t th f nt r n r
Th n nt T p n n th V ll f x Th r h l l r r h nd xpl r t n rr d nt ff t b Pr f r ll N v n d r n th r 8 l t p t, n z n l n n th n rth t rn p rt n f th v ll f x, h v nd d pr v n t fr tf l t th f nt r n r
2. Write your full name and section on the space provided at the top of each odd numbered page.
 I NAME: E - SECTION: Page 1 MATH 152 - COMMON FINAL Spring 2005 General Instructions: 1. The exam consists of 10 pages, including this cover; the test is printed on both sides of the page, and contains
I NAME: E - SECTION: Page 1 MATH 152 - COMMON FINAL Spring 2005 General Instructions: 1. The exam consists of 10 pages, including this cover; the test is printed on both sides of the page, and contains
Future Self-Guides. E,.?, :0-..-.,0 Q., 5...q ',D5', 4,] 1-}., d-'.4.., _. ZoltAn Dbrnyei Introduction. u u rt 5,4) ,-,4, a. a aci,, u 4.
![Future Self-Guides. E,.?, :0-..-.,0 Q., 5...q ',D5', 4,] 1-}., d-'.4.., _. ZoltAn Dbrnyei Introduction. u u rt 5,4) ,-,4, a. a aci,, u 4. Future Self-Guides. E,.?, :0-..-.,0 Q., 5...q ',D5', 4,] 1-}., d-'.4.., _. ZoltAn Dbrnyei Introduction. u u rt 5,4) ,-,4, a. a aci,, u 4.](/thumbs/92/109036622.jpg) te SelfGi ZltAn Dbnyei Intdtin ; ) Q) 4 t? ) t _ 4 73 y S _ E _ p p 4 t t 4) 1_ ::_ J 1 `i () L VI O I4 " " 1 D 4 L e Q) 1 k) QJ 7 j ZS _Le t 1 ej!2 i1 L 77 7 G (4) 4 6 t (1 ;7 bb F) t f; n (i M Q) 7S
te SelfGi ZltAn Dbnyei Intdtin ; ) Q) 4 t? ) t _ 4 73 y S _ E _ p p 4 t t 4) 1_ ::_ J 1 `i () L VI O I4 " " 1 D 4 L e Q) 1 k) QJ 7 j ZS _Le t 1 ej!2 i1 L 77 7 G (4) 4 6 t (1 ;7 bb F) t f; n (i M Q) 7S
ORF307 Optimization Practice Midterm 1
 Princeton University Department of Operations Research and inaocial Engineering OR307 Optimization Practice Midterm 1 Closed book. No computers. Calculators allowed (but not needed). You are permined to
Princeton University Department of Operations Research and inaocial Engineering OR307 Optimization Practice Midterm 1 Closed book. No computers. Calculators allowed (but not needed). You are permined to
Kr7. wd /J-t- To pick up your graded exam from a box outside 5100A Pacific Hall sign here:
 wd /J-t- To pick up your graded exam from a box outside 5100A Pacific Hall sign here: Kr7 chemtsrry 140A FTNAL EXAM 1v & s 6" Eo1 DEC 8,2011 NAME (please print) SIGNATURE FIBST LAST ID NUMBER LAST NAME
wd /J-t- To pick up your graded exam from a box outside 5100A Pacific Hall sign here: Kr7 chemtsrry 140A FTNAL EXAM 1v & s 6" Eo1 DEC 8,2011 NAME (please print) SIGNATURE FIBST LAST ID NUMBER LAST NAME
SOLUTION SET. Chapter 9 REQUIREMENTS FOR OBTAINING POPULATION INVERSIONS "LASER FUNDAMENTALS" Second Edition. By William T.
 SOLUTION SET Chapter 9 REQUIREMENTS FOR OBTAINING POPULATION INVERSIONS "LASER FUNDAMENTALS" Second Edition By William T. Silfvast C.11 q 1. Using the equations (9.8), (9.9), and (9.10) that were developed
SOLUTION SET Chapter 9 REQUIREMENTS FOR OBTAINING POPULATION INVERSIONS "LASER FUNDAMENTALS" Second Edition By William T. Silfvast C.11 q 1. Using the equations (9.8), (9.9), and (9.10) that were developed
Review Solutions, Exam 2, Operations Research
 Review Solutions, Exam 2, Operations Research 1. Prove the weak duality theorem: For any x feasible for the primal and y feasible for the dual, then... HINT: Consider the quantity y T Ax. SOLUTION: To
Review Solutions, Exam 2, Operations Research 1. Prove the weak duality theorem: For any x feasible for the primal and y feasible for the dual, then... HINT: Consider the quantity y T Ax. SOLUTION: To
The Simplex Method. Standard form (max) z c T x = 0 such that Ax = b.
 The Simplex Method Standard form (max) z c T x = 0 such that Ax = b. The Simplex Method Standard form (max) z c T x = 0 such that Ax = b. Build initial tableau. z c T 0 0 A b The Simplex Method Standard
The Simplex Method Standard form (max) z c T x = 0 such that Ax = b. The Simplex Method Standard form (max) z c T x = 0 such that Ax = b. Build initial tableau. z c T 0 0 A b The Simplex Method Standard
P a g e 3 6 of R e p o r t P B 4 / 0 9
 P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
Last 4 Digits of USC ID:
 Chemistry 05 B Practice Exam Dr. Jessica Parr First Letter of last Name PLEASE PRINT YOUR NAME IN BLOCK LETTERS Name: Last 4 Digits of USC ID: Lab TA s Name: Question Points Score Grader 8 2 4 3 9 4 0
Chemistry 05 B Practice Exam Dr. Jessica Parr First Letter of last Name PLEASE PRINT YOUR NAME IN BLOCK LETTERS Name: Last 4 Digits of USC ID: Lab TA s Name: Question Points Score Grader 8 2 4 3 9 4 0
Contents. 4.5 The(Primal)SimplexMethod NumericalExamplesoftheSimplexMethod
 Contents 4 The Simplex Method for Solving LPs 149 4.1 Transformations to be Carried Out On an LP Model Before Applying the Simplex Method On It... 151 4.2 Definitions of Various Types of Basic Vectors
Contents 4 The Simplex Method for Solving LPs 149 4.1 Transformations to be Carried Out On an LP Model Before Applying the Simplex Method On It... 151 4.2 Definitions of Various Types of Basic Vectors
Slack Variable. Max Z= 3x 1 + 4x 2 + 5X 3. Subject to: X 1 + X 2 + X x 1 + 4x 2 + X X 1 + X 2 + 4X 3 10 X 1 0, X 2 0, X 3 0
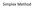 Simplex Method Slack Variable Max Z= 3x 1 + 4x 2 + 5X 3 Subject to: X 1 + X 2 + X 3 20 3x 1 + 4x 2 + X 3 15 2X 1 + X 2 + 4X 3 10 X 1 0, X 2 0, X 3 0 Standard Form Max Z= 3x 1 +4x 2 +5X 3 + 0S 1 + 0S 2
Simplex Method Slack Variable Max Z= 3x 1 + 4x 2 + 5X 3 Subject to: X 1 + X 2 + X 3 20 3x 1 + 4x 2 + X 3 15 2X 1 + X 2 + 4X 3 10 X 1 0, X 2 0, X 3 0 Standard Form Max Z= 3x 1 +4x 2 +5X 3 + 0S 1 + 0S 2
AM 121: Intro to Optimization
 AM 121: Intro to Optimization Models and Methods Lecture 6: Phase I, degeneracy, smallest subscript rule. Yiling Chen SEAS Lesson Plan Phase 1 (initialization) Degeneracy and cycling Smallest subscript
AM 121: Intro to Optimization Models and Methods Lecture 6: Phase I, degeneracy, smallest subscript rule. Yiling Chen SEAS Lesson Plan Phase 1 (initialization) Degeneracy and cycling Smallest subscript
5 s. 00 S aaaog. 3s a o. gg pq ficfi^pq. So c o. H «o3 g gpq ^fi^ s 03 co -*«10 eo 5^ - 3 d s3.s. as fe«jo. Table of General Ordinances.
 5 s Tble f Generl rinnes. q=! j-j 3 -ri j -s 3s m s3 0,0 0) fife s fert " 7- CN i-l r-l - p D fife s- 3 Ph' h ^q 3 3 (j; fe QtL. S &&X* «««i s PI 0) g #r
5 s Tble f Generl rinnes. q=! j-j 3 -ri j -s 3s m s3 0,0 0) fife s fert " 7- CN i-l r-l - p D fife s- 3 Ph' h ^q 3 3 (j; fe QtL. S &&X* «««i s PI 0) g #r
Parts Manual. EPIC II Critical Care Bed REF 2031
 EPIC II Critical Care Bed REF 2031 Parts Manual For parts or technical assistance call: USA: 1-800-327-0770 2013/05 B.0 2031-109-006 REV B www.stryker.com Table of Contents English Product Labels... 4
EPIC II Critical Care Bed REF 2031 Parts Manual For parts or technical assistance call: USA: 1-800-327-0770 2013/05 B.0 2031-109-006 REV B www.stryker.com Table of Contents English Product Labels... 4
Tausend Und Eine Nacht
 Connecticut College Digital Commons @ Connecticut College Historic Sheet Music Collection Greer Music Library 87 Tausend Und Eine Nacht Johann Strauss Follow this and additional works at: https:digitalcommonsconncolledusheetmusic
Connecticut College Digital Commons @ Connecticut College Historic Sheet Music Collection Greer Music Library 87 Tausend Und Eine Nacht Johann Strauss Follow this and additional works at: https:digitalcommonsconncolledusheetmusic
PR D NT N n TR T F R 6 pr l 8 Th Pr d nt Th h t H h n t n, D D r r. Pr d nt: n J n r f th r d t r v th tr t d rn z t n pr r f th n t d t t. n
 R P RT F TH PR D NT N N TR T F R N V R T F NN T V D 0 0 : R PR P R JT..P.. D 2 PR L 8 8 J PR D NT N n TR T F R 6 pr l 8 Th Pr d nt Th h t H h n t n, D.. 20 00 D r r. Pr d nt: n J n r f th r d t r v th
R P RT F TH PR D NT N N TR T F R N V R T F NN T V D 0 0 : R PR P R JT..P.. D 2 PR L 8 8 J PR D NT N n TR T F R 6 pr l 8 Th Pr d nt Th h t H h n t n, D.. 20 00 D r r. Pr d nt: n J n r f th r d t r v th
Planning for Reactive Behaviors in Hide and Seek
 University of Pennsylvania ScholarlyCommons Center for Human Modeling and Simulation Department of Computer & Information Science May 1995 Planning for Reactive Behaviors in Hide and Seek Michael B. Moore
University of Pennsylvania ScholarlyCommons Center for Human Modeling and Simulation Department of Computer & Information Science May 1995 Planning for Reactive Behaviors in Hide and Seek Michael B. Moore
Chemistry 3411 MWF 9:00AM Spring Physical Chemistry I - Exam #2, Version A (Dated: February 27, 2009)
 Chemistry 3411 MWF 9:00AM Spring 2009 Physical Chemistry I - Exam #2, Version A (Dated: February 27, 2009) 1 Name: GT-ID: NOTE: Partial Credit will be awarded! However, full credit will be awarded only
Chemistry 3411 MWF 9:00AM Spring 2009 Physical Chemistry I - Exam #2, Version A (Dated: February 27, 2009) 1 Name: GT-ID: NOTE: Partial Credit will be awarded! However, full credit will be awarded only
The Simplex Method. Lecture 5 Standard and Canonical Forms and Setting up the Tableau. Lecture 5 Slide 1. FOMGT 353 Introduction to Management Science
 The Simplex Method Lecture 5 Standard and Canonical Forms and Setting up the Tableau Lecture 5 Slide 1 The Simplex Method Formulate Constrained Maximization or Minimization Problem Convert to Standard
The Simplex Method Lecture 5 Standard and Canonical Forms and Setting up the Tableau Lecture 5 Slide 1 The Simplex Method Formulate Constrained Maximization or Minimization Problem Convert to Standard
Name,~l&,) class. .f~c ~l y = 2 D 6x + 5y = 2 -~-.-$" ,U~:---=~~~tc: {', \~(~)+ 11(-la~::t\'C
 Name,l&,) class II!IIIIiIIIIiiIiI: 1 i:1pqr isa right triangle with mlp = 900 It point P,hascoordinates (1-5) and point Q has coordinates (-2, O),what is the slope of line PR? 4 Which graph shows a line!!ar
Name,l&,) class II!IIIIiIIIIiiIiI: 1 i:1pqr isa right triangle with mlp = 900 It point P,hascoordinates (1-5) and point Q has coordinates (-2, O),what is the slope of line PR? 4 Which graph shows a line!!ar
Using the Rational Root Theorem to Find Real and Imaginary Roots Real roots can be one of two types: ra...-\; 0 or - l (- - ONLl --
 Using the Rational Root Theorem to Find Real and Imaginary Roots Real roots can be one of two types: ra...-\; 0 or - l (- - ONLl -- Consider the function h(x) =IJ\ 4-8x 3-12x 2 + 24x {?\whose graph is
Using the Rational Root Theorem to Find Real and Imaginary Roots Real roots can be one of two types: ra...-\; 0 or - l (- - ONLl -- Consider the function h(x) =IJ\ 4-8x 3-12x 2 + 24x {?\whose graph is
Signature: Name (PRINT CLEARLY) and ID number:
 AMS 540 / MBA 540 (Fall, 2008) Estie Arkin Linear Programming - Midterm Do all problems. Write your answers on the exam. You are permitted to use the text, your notes and any material handed out in class.
AMS 540 / MBA 540 (Fall, 2008) Estie Arkin Linear Programming - Midterm Do all problems. Write your answers on the exam. You are permitted to use the text, your notes and any material handed out in class.
ECE 4213/5213 Test 1. SHOW ALL OF YOUR WORK for maximum partial credit! GOOD LUCK!
 ECE 4213/5213 Test 1 Fall 2018 Dr. Havlicek Monday, October 15, 2018 4:30 PM - 5:45 PM Name: S_O_L_U_'T_I Q_t\l Student Num: Directions: This test is open book. You may also use a calculator, a clean copy
ECE 4213/5213 Test 1 Fall 2018 Dr. Havlicek Monday, October 15, 2018 4:30 PM - 5:45 PM Name: S_O_L_U_'T_I Q_t\l Student Num: Directions: This test is open book. You may also use a calculator, a clean copy
THE USE OF A CALCULATOR, CELL PHONE, OR ANY OTHER ELEC- TRONIC DEVICE IS NOT PERMITTED DURING THIS EXAMINATION.
 MATH 220 NAME So\,t\\OV\ '. FINAL EXAM 18, 2007\ FORMA STUDENT NUMBER INSTRUCTOR SECTION NUMBER This examination will be machine processed by the University Testing Service. Use only a number 2 pencil
MATH 220 NAME So\,t\\OV\ '. FINAL EXAM 18, 2007\ FORMA STUDENT NUMBER INSTRUCTOR SECTION NUMBER This examination will be machine processed by the University Testing Service. Use only a number 2 pencil
 Th pr nt n f r n th f ft nth nt r b R b rt Pr t r. Pr t r, R b rt, b. 868. xf rd : Pr nt d f r th B bl r ph l t t th xf rd n v r t Pr, 00. http://hdl.handle.net/2027/nyp.33433006349173 P bl D n n th n
Th pr nt n f r n th f ft nth nt r b R b rt Pr t r. Pr t r, R b rt, b. 868. xf rd : Pr nt d f r th B bl r ph l t t th xf rd n v r t Pr, 00. http://hdl.handle.net/2027/nyp.33433006349173 P bl D n n th n
The Simplex Algorithm
 The Simplex Algorithm How to Convert an LP to Standard Form Before the simplex algorithm can be used to solve an LP, the LP must be converted into a problem where all the constraints are equations and
The Simplex Algorithm How to Convert an LP to Standard Form Before the simplex algorithm can be used to solve an LP, the LP must be converted into a problem where all the constraints are equations and
SOLUTION SET. Chapter 8 LASER OSCILLATION ABOVE THRESHOLD "LASER FUNDAMENTALS" Second Edition
 SOLUTION SET Chapter 8 LASER OSCILLATION ABOVE THRESHOLD "LASER FUNDAMENTALS" Second Edition By William T. Silfvast - 1. An argon ion laser (as shown in Figure 10-S(b)) operating at 488.0 nm with a gainregion
SOLUTION SET Chapter 8 LASER OSCILLATION ABOVE THRESHOLD "LASER FUNDAMENTALS" Second Edition By William T. Silfvast - 1. An argon ion laser (as shown in Figure 10-S(b)) operating at 488.0 nm with a gainregion
. ~ ~~::::~m Review Sheet #1
 . ~ ~~::::~m Review Sheet #1 Math lla 1. 2. Which ofthe following represents a function(s)? (1) Y... v \ J 1\ -.. - -\ V i e5 3. The solution set for 2-7 + 12 = 0 is :---:---:- --:...:-._",,, :- --;- --:---;-..!,..;-,...
. ~ ~~::::~m Review Sheet #1 Math lla 1. 2. Which ofthe following represents a function(s)? (1) Y... v \ J 1\ -.. - -\ V i e5 3. The solution set for 2-7 + 12 = 0 is :---:---:- --:...:-._",,, :- --;- --:---;-..!,..;-,...
106 70/140H-8 70/140H-8
 7/H- 6 H 7/H- 7 H ffffff ff ff ff ff ff ff ff ff f f f f f f f f f f f ff f f f H 7/H- 7/H- H φφ φφ φφ φφ! H 1 7/H- 7/H- H 1 f f f f f f f f f f f f f f f f f f f f f f f f f f f f f ff ff ff ff φ φ φ
7/H- 6 H 7/H- 7 H ffffff ff ff ff ff ff ff ff ff f f f f f f f f f f f ff f f f H 7/H- 7/H- H φφ φφ φφ φφ! H 1 7/H- 7/H- H 1 f f f f f f f f f f f f f f f f f f f f f f f f f f f f f ff ff ff ff φ φ φ
1 Review Session. 1.1 Lecture 2
 1 Review Session Note: The following lists give an overview of the material that was covered in the lectures and sections. Your TF will go through these lists. If anything is unclear or you have questions
1 Review Session Note: The following lists give an overview of the material that was covered in the lectures and sections. Your TF will go through these lists. If anything is unclear or you have questions
Robado del Archivo del Dr. Antonio Rafael de la Cova
 Robado del Archvo del Dr. Antono Raael de la Cova http:www.latnamercanstudes.org/ Muster Roll: 655-858. Under ea.ch COlnl?ny are recorded the nams o the man wth nom.:lton show ng ran.'l< when hare and
Robado del Archvo del Dr. Antono Raael de la Cova http:www.latnamercanstudes.org/ Muster Roll: 655-858. Under ea.ch COlnl?ny are recorded the nams o the man wth nom.:lton show ng ran.'l< when hare and
 D t r l f r th n t d t t pr p r d b th t ff f th l t tt n N tr t n nd H n N d, n t d t t n t. n t d t t. h n t n :.. vt. Pr nt. ff.,. http://hdl.handle.net/2027/uiug.30112023368936 P bl D n, l d t z d
D t r l f r th n t d t t pr p r d b th t ff f th l t tt n N tr t n nd H n N d, n t d t t n t. n t d t t. h n t n :.. vt. Pr nt. ff.,. http://hdl.handle.net/2027/uiug.30112023368936 P bl D n, l d t z d
CO350 Linear Programming Chapter 8: Degeneracy and Finite Termination
 CO350 Linear Programming Chapter 8: Degeneracy and Finite Termination 27th June 2005 Chapter 8: Finite Termination 1 The perturbation method Recap max c T x (P ) s.t. Ax = b x 0 Assumption: B is a feasible
CO350 Linear Programming Chapter 8: Degeneracy and Finite Termination 27th June 2005 Chapter 8: Finite Termination 1 The perturbation method Recap max c T x (P ) s.t. Ax = b x 0 Assumption: B is a feasible
min 4x 1 5x 2 + 3x 3 s.t. x 1 + 2x 2 + x 3 = 10 x 1 x 2 6 x 1 + 3x 2 + x 3 14
 The exam is three hours long and consists of 4 exercises. The exam is graded on a scale 0-25 points, and the points assigned to each question are indicated in parenthesis within the text. If necessary,
The exam is three hours long and consists of 4 exercises. The exam is graded on a scale 0-25 points, and the points assigned to each question are indicated in parenthesis within the text. If necessary,
OH BOY! Story. N a r r a t iv e a n d o bj e c t s th ea t e r Fo r a l l a g e s, fr o m th e a ge of 9
 OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
,y. ~ (Lo )-Y2 ') '---~ F( '...J ( '1, 4. \fer-\{:k. ('X -5)'1.-+ :tl\ ~\:,) ~::; fi(~ S:;')'"'--t L. X-lOX t ~5 = IJ~-~+~5.
 Name. Date 18. Write the equation of this conic: No,y. ~ '---~ F( '...J ( '1, 4 2A. Write the equation of this conic: \fer-\{:k. (lo) -3~2 ') (Lo )-Y2 ') 28. Write the equation of this conic: - - - -...
Name. Date 18. Write the equation of this conic: No,y. ~ '---~ F( '...J ( '1, 4 2A. Write the equation of this conic: \fer-\{:k. (lo) -3~2 ') (Lo )-Y2 ') 28. Write the equation of this conic: - - - -...
2014/2015 SEMESTER 1 MID-TERM TEST. September/October :30pm to 9:30pm PLEASE READ THE FOLLOWING INSTRUCTIONS CAREFULLY:
 2014/2015 SEMESTER 1 MID-TERM TEST MA1505 MATHEMATICS I September/October 2014 8:30pm to 9:30pm PLEASE READ THE FOLLOWING INSTRUCTIONS CAREFULLY: 1. This test paper consists of TEN (10) multiple choice
2014/2015 SEMESTER 1 MID-TERM TEST MA1505 MATHEMATICS I September/October 2014 8:30pm to 9:30pm PLEASE READ THE FOLLOWING INSTRUCTIONS CAREFULLY: 1. This test paper consists of TEN (10) multiple choice
V o. 'f o. 'NJ. 'Ni c.. l ~ u u. YI \lv\ ~ ~ f fov c.tr '+- Cu w11.t r M o'n ~\'1
 la~t ~'fr\l. 1.. i~: ~ =-M:X tb Cirili. lx-~~t ly-~)\ fi. Tu~ll~: ~ Hli'JJ'"~ \WWI 1 we' II 'vj YH'\~ i\i\ M1t. t 0 V o. 'f o. 'NJ. 'Ni c.. l ~ u u. YI \lv\ ~ ~ f fov c.tr '+- Cu w11.t r M o'n ~\'1 ~I
la~t ~'fr\l. 1.. i~: ~ =-M:X tb Cirili. lx-~~t ly-~)\ fi. Tu~ll~: ~ Hli'JJ'"~ \WWI 1 we' II 'vj YH'\~ i\i\ M1t. t 0 V o. 'f o. 'NJ. 'Ni c.. l ~ u u. YI \lv\ ~ ~ f fov c.tr '+- Cu w11.t r M o'n ~\'1 ~I
ON THE NUMBER OF POSITIVE SUMS OF INDEPENDENT RANDOM VARIABLES
 ON THE NUMBER OF POSITIVE SUMS OF INDEPENDENT RANDOM VARIABLES P. ERDÖS AND M. KAC 1 1. Introduction. In a recent paper 2 the authors have introduced a method for proving certain limit theorems of the
ON THE NUMBER OF POSITIVE SUMS OF INDEPENDENT RANDOM VARIABLES P. ERDÖS AND M. KAC 1 1. Introduction. In a recent paper 2 the authors have introduced a method for proving certain limit theorems of the
828.^ 2 F r, Br n, nd t h. n, v n lth h th n l nd h d n r d t n v l l n th f v r x t p th l ft. n ll n n n f lt ll th t p n nt r f d pp nt nt nd, th t
 2Â F b. Th h ph rd l nd r. l X. TH H PH RD L ND R. L X. F r, Br n, nd t h. B th ttr h ph rd. n th l f p t r l l nd, t t d t, n n t n, nt r rl r th n th n r l t f th f th th r l, nd d r b t t f nn r r pr
2Â F b. Th h ph rd l nd r. l X. TH H PH RD L ND R. L X. F r, Br n, nd t h. B th ttr h ph rd. n th l f p t r l l nd, t t d t, n n t n, nt r rl r th n th n r l t f th f th th r l, nd d r b t t f nn r r pr
Lesson 27 Linear Programming; The Simplex Method
 Lesson Linear Programming; The Simplex Method Math 0 April 9, 006 Setup A standard linear programming problem is to maximize the quantity c x + c x +... c n x n = c T x subject to constraints a x + a x
Lesson Linear Programming; The Simplex Method Math 0 April 9, 006 Setup A standard linear programming problem is to maximize the quantity c x + c x +... c n x n = c T x subject to constraints a x + a x
ORF 522. Linear Programming and Convex Analysis
 ORF 5 Linear Programming and Convex Analysis Initial solution and particular cases Marco Cuturi Princeton ORF-5 Reminder: Tableaux At each iteration, a tableau for an LP in standard form keeps track of....................
ORF 5 Linear Programming and Convex Analysis Initial solution and particular cases Marco Cuturi Princeton ORF-5 Reminder: Tableaux At each iteration, a tableau for an LP in standard form keeps track of....................
4 8 N v btr 20, 20 th r l f ff nt f l t. r t pl n f r th n tr t n f h h v lr d b n r d t, rd n t h h th t b t f l rd n t f th rld ll b n tr t d n R th
 n r t d n 20 2 :24 T P bl D n, l d t z d http:.h th tr t. r pd l 4 8 N v btr 20, 20 th r l f ff nt f l t. r t pl n f r th n tr t n f h h v lr d b n r d t, rd n t h h th t b t f l rd n t f th rld ll b n
n r t d n 20 2 :24 T P bl D n, l d t z d http:.h th tr t. r pd l 4 8 N v btr 20, 20 th r l f ff nt f l t. r t pl n f r th n tr t n f h h v lr d b n r d t, rd n t h h th t b t f l rd n t f th rld ll b n
q-..1 c.. 6' .-t i.] ]J rl trn (dl q-..1 Orr --l o(n ._t lr< +J(n tj o CB OQ ._t --l (-) lre "_1 otr o Ctq c,) ..1 .lj '--1 .IJ C] O.u tr_..
![q-..1 c.. 6' .-t i.] ]J rl trn (dl q-..1 Orr --l o(n ._t lr< +J(n tj o CB OQ ._t --l (-) lre _1 otr o Ctq c,) ..1 .lj '--1 .IJ C] O.u tr_.. q-..1 c.. 6' .-t i.] ]J rl trn (dl q-..1 Orr --l o(n ._t lr< +J(n tj o CB OQ ._t --l (-) lre _1 otr o Ctq c,) ..1 .lj '--1 .IJ C] O.u tr_..](/thumbs/85/92086558.jpg) l_-- 5. r.{ q-{.r{ ul 1 rl l P -r ' v -r1-1.r ( q-r ( @- ql N -.r.p.p 0.) (^5] @ Z l l i Z r,l -; ^ CJ (\, -l ọ..,] q r 1] ( -. r._1 p q-r ) (\. _l (._1 \C ' q-l.. q) i.] r - 0r) >.4.-.rr J p r q-r r 0
l_-- 5. r.{ q-{.r{ ul 1 rl l P -r ' v -r1-1.r ( q-r ( @- ql N -.r.p.p 0.) (^5] @ Z l l i Z r,l -; ^ CJ (\, -l ọ..,] q r 1] ( -. r._1 p q-r ) (\. _l (._1 \C ' q-l.. q) i.] r - 0r) >.4.-.rr J p r q-r r 0
Years. Marketing without a plan is like navigating a maze; the solution is unclear.
 F Q 2018 E Mk l lk z; l l Mk El M C C 1995 O Y O S P R j lk q D C Dl Off P W H S P W Sl M Y Pl Cl El M Cl FIRST QUARTER 2018 E El M & D I C/O Jff P RGD S C D M Sl 57 G S Alx ON K0C 1A0 C Tl: 6134821159
F Q 2018 E Mk l lk z; l l Mk El M C C 1995 O Y O S P R j lk q D C Dl Off P W H S P W Sl M Y Pl Cl El M Cl FIRST QUARTER 2018 E El M & D I C/O Jff P RGD S C D M Sl 57 G S Alx ON K0C 1A0 C Tl: 6134821159
a a T = «*5S?; i; S 25* a o - 5 n s o s*- o c S «c o * * * 3 : -2 W r-< r-j r^ x w to i_q pq J ^ i_5 ft "ag i-s Coo S S o f-trj. rh.,-j,»<l,3<l) 5 s?
 Tble f Generl rdnnce CP CB >J >> c; 5 fc5 5 S hh CD d; CC02 5^ CD Cb
Tble f Generl rdnnce CP CB >J >> c; 5 fc5 5 S hh CD d; CC02 5^ CD Cb
> DC < D CO LU > Z> CJ LU
 C C FNS TCNCAL NFRMATN CNTR [itpfttiiknirike?fi-'.;t C'JM.V TC hs determined n \ _\}. L\\ tht this Technicl cment hs the istribtin Sttement checked belw. The crnt distribtin fr this dcment cn be telind
C C FNS TCNCAL NFRMATN CNTR [itpfttiiknirike?fi-'.;t C'JM.V TC hs determined n \ _\}. L\\ tht this Technicl cment hs the istribtin Sttement checked belw. The crnt distribtin fr this dcment cn be telind
4 4 N v b r t, 20 xpr n f th ll f th p p l t n p pr d. H ndr d nd th nd f t v L th n n f th pr v n f V ln, r dn nd l r thr n nt pr n, h r th ff r d nd
 n r t d n 20 20 0 : 0 T P bl D n, l d t z d http:.h th tr t. r pd l 4 4 N v b r t, 20 xpr n f th ll f th p p l t n p pr d. H ndr d nd th nd f t v L th n n f th pr v n f V ln, r dn nd l r thr n nt pr n,
n r t d n 20 20 0 : 0 T P bl D n, l d t z d http:.h th tr t. r pd l 4 4 N v b r t, 20 xpr n f th ll f th p p l t n p pr d. H ndr d nd th nd f t v L th n n f th pr v n f V ln, r dn nd l r thr n nt pr n,
n
 p l p bl t n t t f Fl r d, D p rt nt f N t r l R r, D v n f nt r r R r, B r f l. n.24 80 T ll h, Fl. : Fl r d D p rt nt f N t r l R r, B r f l, 86. http://hdl.handle.net/2027/mdp.39015007497111 r t v n
p l p bl t n t t f Fl r d, D p rt nt f N t r l R r, D v n f nt r r R r, B r f l. n.24 80 T ll h, Fl. : Fl r d D p rt nt f N t r l R r, B r f l, 86. http://hdl.handle.net/2027/mdp.39015007497111 r t v n
rhtre PAID U.S. POSTAGE Can't attend? Pass this on to a friend. Cleveland, Ohio Permit No. 799 First Class
 rhtr irt Cl.S. POSTAG PAD Cllnd, Ohi Prmit. 799 Cn't ttnd? P thi n t frind. \ ; n l *di: >.8 >,5 G *' >(n n c. if9$9$.jj V G. r.t 0 H: u ) ' r x * H > x > i M
rhtr irt Cl.S. POSTAG PAD Cllnd, Ohi Prmit. 799 Cn't ttnd? P thi n t frind. \ ; n l *di: >.8 >,5 G *' >(n n c. if9$9$.jj V G. r.t 0 H: u ) ' r x * H > x > i M
(308 ) EXAMPLES. 1. FIND the quotient and remainder when. II. 1. Find a root of the equation x* = +J Find a root of the equation x 6 = ^ - 1.
 (308 ) EXAMPLES. N 1. FIND the quotient and remainder when is divided by x 4. I. x 5 + 7x* + 3a; 3 + 17a 2 + 10* - 14 2. Expand (a + bx) n in powers of x, and then obtain the first derived function of
(308 ) EXAMPLES. N 1. FIND the quotient and remainder when is divided by x 4. I. x 5 + 7x* + 3a; 3 + 17a 2 + 10* - 14 2. Expand (a + bx) n in powers of x, and then obtain the first derived function of
Prelude to the Simplex Algorithm. The Algebraic Approach The search for extreme point solutions.
 Prelude to the Simplex Algorithm The Algebraic Approach The search for extreme point solutions. 1 Linear Programming-1 x 2 12 8 (4,8) Max z = 6x 1 + 4x 2 Subj. to: x 1 + x 2
Prelude to the Simplex Algorithm The Algebraic Approach The search for extreme point solutions. 1 Linear Programming-1 x 2 12 8 (4,8) Max z = 6x 1 + 4x 2 Subj. to: x 1 + x 2
The Simplex Algorithm and Goal Programming
 The Simplex Algorithm and Goal Programming In Chapter 3, we saw how to solve two-variable linear programming problems graphically. Unfortunately, most real-life LPs have many variables, so a method is
The Simplex Algorithm and Goal Programming In Chapter 3, we saw how to solve two-variable linear programming problems graphically. Unfortunately, most real-life LPs have many variables, so a method is
Simplex Algorithm Using Canonical Tableaus
 41 Simplex Algorithm Using Canonical Tableaus Consider LP in standard form: Min z = cx + α subject to Ax = b where A m n has rank m and α is a constant In tableau form we record it as below Original Tableau
41 Simplex Algorithm Using Canonical Tableaus Consider LP in standard form: Min z = cx + α subject to Ax = b where A m n has rank m and α is a constant In tableau form we record it as below Original Tableau
wo(..lr.i L"'J b]. tr+ +&..) i'> 't\uow).,...,. (o.. J \,} --ti \(' m'\...\,,.q.)).
![wo(..lr.i L'J b]. tr+ +&..) i'> 't\uow).,...,. (o.. J \,} --ti \(' m'\...\,,.q.)). wo(..lr.i L'J b]. tr+ +&..) i'> 't\uow).,...,. (o.. J \,} --ti \(' m'\...\,,.q.)).](/thumbs/94/120320379.jpg) Applying Theorems in Calculus 11ter111ediate Value Theorem, Ettreme Value Theorem, Rolle 's Theorem, and l\ea11 Value Theorem Before we begin. let's remember what each of these theorems says about a function.
Applying Theorems in Calculus 11ter111ediate Value Theorem, Ettreme Value Theorem, Rolle 's Theorem, and l\ea11 Value Theorem Before we begin. let's remember what each of these theorems says about a function.
