Linear Algebra and Dirac Notation, Pt. 2

Transcription

1 Linear Algebra and Dirac Notation, Pt. 2 PHYS Southern Illinois University February 1, 2017 PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

2 The Identity The identity operator I is the unique operator that satisfies I ψ = ψ for all ψ H. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

3 The Identity The identity operator I is the unique operator that satisfies I ψ = ψ for all ψ H. Proposition (A very useful one!) For any orthonormal basis { b i } d i=1, the identity can be written as I = b i b i. i=1 PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

4 The Identity The identity operator I is the unique operator that satisfies I ψ = ψ for all ψ H. Proposition (A very useful one!) For any orthonormal basis { b i } d i=1, the identity can be written as I = b i b i. i=1 Proof PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

5 Trace of an Operator Definition For a linear operator T acting on H, its trace is defined by Tr[T ] := b i T b i = i=1 [[T b ]] i,i, i=1 where { b i } d i=1 is an arbitrary orthonormal basis for H. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

6 Trace of an Operator Definition For a linear operator T acting on H, its trace is defined by Tr[T ] := b i T b i = i=1 [[T b ]] i,i, i=1 where { b i } d i=1 is an arbitrary orthonormal basis for H. The value of Tr[T ] = d i=1 b i T b i is the same for every orthonormal basis { b i } d i=1. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

7 Trace of an Operator Definition For a linear operator T acting on H, its trace is defined by Tr[T ] := b i T b i = i=1 [[T b ]] i,i, i=1 where { b i } d i=1 is an arbitrary orthonormal basis for H. The value of Tr[T ] = d i=1 b i T b i is the same for every orthonormal basis { b i } d i=1. Notice that Tr[T ] = b i T b i = b i T b i = Tr[T ]. PHYS Southern Illinois Universityi=1 Linear Algebra and Dirac i=1 Notation, Pt. 2 February 1, / 14

8 Determinants, Eigenspaces and Eigenvalues Definition The determinant of an operator T, denoted by det(t ), is the matrix determinant of its matrix representation T b (for any basis { b i } i ). PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

9 Determinants, Eigenspaces and Eigenvalues Definition The determinant of an operator T, denoted by det(t ), is the matrix determinant of its matrix representation T b (for any basis { b i } i ). Definition An eigenspace of an operator T acting on H is a subspace S λ H such that T ψ = λ ψ for ψ S λ and λ C. The number λ is called the eigenvalue associated with the subspace S λ. The dimension of S λ, denoted by dim(s λ ), is called the multiplicity of λ. The rank of T, denoted rk(t ), is the number of nonzero eigenvalues (including multiplicity). Equivalently, rk(t ) = dim(h) dim(ker(t )), where ker(t ) = { ψ : T ψ = 0} is the kernel of T. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

10 Determinants, Eigenspaces and Eigenvalues Definition The determinant of an operator T, denoted by det(t ), is the matrix determinant of its matrix representation T b (for any basis { b i } i ). Definition An eigenspace of an operator T acting on H is a subspace S λ H such that T ψ = λ ψ for ψ S λ and λ C. The number λ is called the eigenvalue associated with the subspace S λ. The dimension of S λ, denoted by dim(s λ ), is called the multiplicity of λ. The rank of T, denoted rk(t ), is the number of nonzero eigenvalues (including multiplicity). Equivalently, rk(t ) = dim(h) dim(ker(t )), where ker(t ) = { ψ : T ψ = 0} is the kernel of T. A number λ is an eigenvalue of T if and only if det(t λi) = 0. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

11 Normal Operators Definition An operator T on H is called normal if T T = TT. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

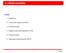
12 Normal Operators Definition An operator T on H is called normal if T T = TT. Normal, Unitary, Hermitian, Positive, and Projection Operators Diagram: PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

13 Unitary Operators Definition (Unitary Operators) An operator U is called unitary if U U = UU = I. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

14 Unitary Operators Definition (Unitary Operators) An operator U is called unitary if U U = UU = I. Example For arbitrary α, β, γ R the operator U(α, β, γ) on C 2 given by is unitary. U(α, β, γ). = ( e i(α+γ)/2 cos β/2 e i(α γ)/2 ) sin β/2 e i( α+γ)/2 sin β/2 e i(α+γ)/2 cos β/2 PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

15 Hermitian, Positive, and Projection Operators Definition (Hermitian Operators) An operator H is called hermitian (or self-adjoint) if H = H. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

16 Hermitian, Positive, and Projection Operators Definition (Hermitian Operators) An operator H is called hermitian (or self-adjoint) if H = H. Definition (Positive Operators) A positive operator is any hermitian operator P satisfying ψ P ψ 0 for all ψ H. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

17 Hermitian, Positive, and Projection Operators Definition (Hermitian Operators) An operator H is called hermitian (or self-adjoint) if H = H. Definition (Positive Operators) A positive operator is any hermitian operator P satisfying ψ P ψ 0 for all ψ H. Definition (Orthogonal Projectors) An orthogonal projector is any hermitian operator P satisfying P 2 = P. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

18 Hermitian, Positive, and Projection Operators Definition (Hermitian Operators) An operator H is called hermitian (or self-adjoint) if H = H. Definition (Positive Operators) A positive operator is any hermitian operator P satisfying ψ P ψ 0 for all ψ H. Definition (Orthogonal Projectors) An orthogonal projector is any hermitian operator P satisfying P 2 = P. Example For any normalized vector ψ, the operator ψ ψ is a projector. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

19 Projectors Proposition Every orthogonal projector is a positive operator. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

20 Projectors Proposition Every orthogonal projector is a positive operator. Proof PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

21 Projectors If P is a projector, then its only possible eigenvalues are 0 and 1: P ψ = λ ψ P 2 ψ = λ 2 ψ = P ψ (since P 2 = P) = λ ψ. Therefore λ(λ 1) ψ = 0 which is only possible if λ = 0, 1. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

22 Projectors If P is a projector, then its only possible eigenvalues are 0 and 1: P ψ = λ ψ P 2 ψ = λ 2 ψ = P ψ (since P 2 = P) = λ ψ. Therefore λ(λ 1) ψ = 0 which is only possible if λ = 0, 1. Every projector is uniquely associated with a subspace S such that P ψ = ψ for all ψ S and P ψ = 0 for all ψ S, the orthogonal complement of S. P is called the subspace projector for S. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

23 Projectors If P is a projector, then its only possible eigenvalues are 0 and 1: P ψ = λ ψ P 2 ψ = λ 2 ψ = P ψ (since P 2 = P) = λ ψ. Therefore λ(λ 1) ψ = 0 which is only possible if λ = 0, 1. Every projector is uniquely associated with a subspace S such that P ψ = ψ for all ψ S and P ψ = 0 for all ψ S, the orthogonal complement of S. P is called the subspace projector for S. If S is a subspace of H with orthonormal basis { b i } dim(s) i=1, its subspace projector is P S = dim(s) i=1 b i b i. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

24 Spectral Decomposition of Normal Operators Theorem (Spectral Decomposition Theorem) For every normal operator N, there exists a unique set of orthogonal projectors {P i } r i=1 such that (i) N = r i=1 λ ip i for λ i C; (ii) P i P j = δ ij P i (orthogonality of eigenspaces); (iii) r i=1 P i = I (completeness of eigenspaces). PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

25 Spectral Decomposition of Normal Operators Theorem (Spectral Decomposition Theorem) For every normal operator N, there exists a unique set of orthogonal projectors {P i } r i=1 such that (i) N = r i=1 λ ip i for λ i C; (ii) P i P j = δ ij P i (orthogonality of eigenspaces); (iii) r i=1 P i = I (completeness of eigenspaces). If N is hermitian then its eigenvalues are real; λ i R. If N is positive then its eigenvalues are nonnegative; λ i 0. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

26 Spectral Decomposition of Normal Operators Theorem (Spectral Decomposition Theorem) For every normal operator N, there exists a unique set of orthogonal projectors {P i } r i=1 such that (i) N = r i=1 λ ip i for λ i C; (ii) P i P j = δ ij P i (orthogonality of eigenspaces); (iii) r i=1 P i = I (completeness of eigenspaces). If N is hermitian then its eigenvalues are real; λ i R. If N is positive then its eigenvalues are nonnegative; λ i 0. Each P i is a subspace projector for some subspace S i. For each normal operator N, there exists a unique decomposition of the Hilbert space: H = S 1 S 2 S r. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

27 Spectral Decomposition of Normal Operators Recall the orthogonal direct sum decomposition of a vector space H = S 1 S 2 S r means that every ψ H can be uniquely written as ψ = r α i ϕ i i=1 with ϕ i S i and ϕ i ϕ j = δ ij. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

28 Spectral Decomposition of Normal Operators Recall the orthogonal direct sum decomposition of a vector space H = S 1 S 2 S r means that every ψ H can be uniquely written as ψ = r α i ϕ i i=1 with ϕ i S i and ϕ i ϕ j = δ ij. Then N = r i=1 λ ip i implies N ψ = r α i λ i ϕ i. i=1 PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

29 Spectral Decomposition of Normal Operators For a normal operator N = r i=1 λ ip i with P i being a subspace S i, we can further decompose d i P i = b ij b ij, j=1 where { b ij } d i j=1 is a orthonormal basis for S i. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

30 Spectral Decomposition of Normal Operators For a normal operator N = r i=1 λ ip i with P i being a subspace S i, we can further decompose d i P i = b ij b ij, j=1 where { b ij } d i j=1 is a orthonormal basis for S i. Then r r d i N = λ i P i = λ i b ij b ij = λ µ b µ b µ, i=1 i=1 j=1 µ=1 where { b µ } d µ=1 is an orthonormal basis for H. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

31 Spectral Decomposition of Normal Operators It is typical to express the spectral decomposition in this way, as a linear combination of orthogonal rank-one projectors: N = λ µ b µ b µ. µ=1 PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

32 Spectral Decomposition of Normal Operators It is typical to express the spectral decomposition in this way, as a linear combination of orthogonal rank-one projectors: N = λ µ b µ b µ. µ=1 If { 0, 1, d 1 } is the computational basis, then we can always write N = UΛU, where Λ =. ( λ1 0 ) 0 λ 2 0 is diagonal in the computational basis, and 0 0 λ d U = d i=1 b i i 1 is orthogonal. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

33 Functions of Normal Operators The spectral decomposition allows us to define functions of operators. Notice that N = λ µ b µ b µ N m = µ=1 λ m µ b µ b µ for all m = 1,. µ=1 PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

34 Functions of Normal Operators The spectral decomposition allows us to define functions of operators. Notice that N = λ µ b µ b µ N m = µ=1 λ m µ b µ b µ for all m = 1,. µ=1 Then for any complex function f (z) with Taylor expansion f (z) = k=0 α kz k, we define the operator function ˆf (N) := k=0 α kn k. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14

35 Functions of Normal Operators The spectral decomposition allows us to define functions of operators. Notice that N = λ µ b µ b µ N m = µ=1 λ m µ b µ b µ for all m = 1,. µ=1 Then for any complex function f (z) with Taylor expansion f (z) = k=0 α kz k, we define the operator function ˆf (N) := k=0 α kn k. An important example is the exponential function: e N = k=0 1 k! Nk. PHYS Southern Illinois University Linear Algebra and Dirac Notation, Pt. 2 February 1, / 14