10 3. Determine the moment of inertia of the area about the x axis.
|
|
|
- Bertram Eaton
- 6 years ago
- Views:
Transcription
1 10 3. Determine the moment of inertia of the area about the ais. m m
2 10 4. Determine the moment of inertia of the area about the ais. m m
3 10 3. Determine the moment of inertia of the shaded area about the ais. SOLUTION Differential Element: The area of the differential element shown shaded in Fig. a is da = (rdu) dr. Moment of Inertia: Appling Eq. 10 1, we have I = LA da = L a> = L a> - a> L0 = L a> - a> = L a> - a> r 0 - a> L0 r4 4 ` r 0 sin udu 0 r sin udu r 0 r 3 sin udrdu r sin u(rdu)dr a a r 0 r 0 However, sin u = 1 (1 - cos u). Thus, I = L a> - a> r 0 4 (1 - cos u)du 8 = r Bu - 1 sin ur ` a> - a> = r 0 4 (a - sin a) 8
4 10 4. Determine the moment of inertia of the shaded area about the ais. a r 0 SOLUTION Differential Element: The area of the differential element shown shaded in Fig. a is da = (rdu)dr. Moment of Inertia: Appling Eq. 10 1, we have I = LA da = L a> = L a> - a> L0 = L a> - a> = L a> - a> r 0 r4 4 ` r 0 cos udu 0 r a> L0 r 3 cos udrdu 4 cos udu r 0 r cos u(rdu)dr a r 0 However, cos u = 1 ( cos u + 1). Thus, a> 4 r 0 I = ( cos u + 1)du L 8 - a> = r B 1 sin u + ur ` a> - a> = r 0 4 ( sin a + a) 8
5 Determine the distance to the centroid of the beam s cross-sectional area; then determine the moment of inertia about the ais. _ 5 mm 50 mm 75 mm 75 mm 50 mm C 5 mm 5 mm SOLUTION Centroid: The area of each segment and its respective centroid are tabulated below. 5 mm Segment A (mm ) (mm) A(mm 3 ) 1 50(100) (10 3 ) 35(5) l.565(10 3 ) 3 5(100) 50 15(10 3 ) 15.65(10 3 ) (10 3 ) Thus, = A A = (103 ) 15.65(10 3 =.5 mm ) Moment of Inertia: The moment of inertia about the ais for each segment can be determined using the parallel-ais theorem I + I + Ad. Segment A Ad AI AAd B AI B i (mm 4 i (mm 4 B i (mm 4 i (mm ) B i (mm) ) ) ) Thus, (100) (50) (1003 ) (10 6 ) (10 6 ) 35(5) (35) (53 ) 0.815(10 6 ) 1.36(10 6 ) 3 5(100) (5) (1003 ) (10 6 ) 15.4(10 6 ) I = (I ) i = 34.41A10 6 B mm 4 = 34.4A10 6 B mm 4
6 Determine the moment of inertia of the beam s crosssectional area about the ais. 5 mm 5 mm _ 50 mm 75 mm 75 mm 50 mm C 5 mm SOLUTION 5 mm Moment of Inertia: The moment of inertia about the ais for each segment can be determined using the parallel-ais theorem I = I + Ad. Segment 1 A i (mm ) [100(5)] Ad B i (mm) 100 AI B i (mm 4 ) C 1 1 (100) (53 )D AAd B i (mm 4 ) 50.0(10 6 ) AI B i (mm 4 ) 50.60(10 6 ) Thus, 1 5(35) 0 1 (5) (353 ) (10 6 ) 3 100(5) (100) (53 ) (10 6 ) I = (I ) i = 11.91A10 6 B mm 4 = 1A10 6 B mm 4
7 Determine the moments of inertia I u and I v of the shaded area. v 0 mm u SOLUTION 00 mm 45 0 mm 0 mm Moment and Product of Inertia about and Aes: Since the shaded area is smmetrical about the ais, I = 0. I = = mm 4 I = = mm 4 40 mm 00 mm Moment of Inertia about the Inclined u and u = 45, we have v Aes: Appling Eq with I u = I + I + I - I cos u - I sin u = a + cos 90-01sin 90 b110 6 = mm 4 I v = I + I - I - I cos u + I sin u = a - cos 90-01sin 90 b110 6 = mm 4
8 Determine the moments of inertia and the product of inertia of the beam s cross sectional area with respect to the u and v aes. v u SOLUTION Moments and product of Inertia with Respect to the and Aes: The perpendicular distances measured from the centroid of the triangular segment to the ais are indicated in Fig. a. C mm 150 mm I = 1 36 (400)(4503 ) = 101.5(10 6 ) mm 4 00 mm 00 mm I = B 1 36 (450)(003 ) + 1 (450)(00)(66.67 )R = 600(10 6 ) mm 4 Since the cross-sectional area is smmetrical about the ais, I = 0. Moment and product of Inertia with Respect to the u and v Aes: Appling Eq with u = 30, we have I u = I + I + I - I cos u - I sin u = B + cos 60-0 sin 60 R(10 6 ) = (10 6 ) mm 4 = 909(10 6 ) mm 4 I v = I + I - I - I cos u + I sin u = B - cos sin 60R(10 6 ) = (10 6 ) mm 4 = 703(10 6 ) mm 4 I uv = I - I = B sin u + I cos u sin cos 60 R(10 6 ) = 178.6(10 6 ) mm 4 = 179(10 6 ) mm 4
9 Solve Prob using Mohr s circle. Hint: Once the circle is established, rotate u = 60 counterclockwise from the reference OA, then find the coordinates of the points that define the diameter of the circle. v u 300 mm SOLUTION Moments and product of Inertia with Respect to the and Aes: The perpendicular distances measured from the centroid of the triangular segment to the ais are indicated in Fig. a. C mm I = 1 36 (400)(4503 ) = 101.5(10 6 ) mm 4 00 mm 00 mm I = B 1 36 (450)(003 ) + 1 (450)(00)(66.67 )R = 600(10 6 ) mm 4 Since the cross-sectional area is smmetrical about the ais, I = 0. Construction of Mohr s Circle: The center of C of the circle lies along the I ais at a distance I avg = I + I = a b(10 6 )mm 4 = 806.5(10 6 ) mm 4 The coordinates of the reference point A are [101.5, 0](10 6 ) mm 4. The circle can be constructed as shown in Fig. b. The radius of the circle is R = CA = ( )(10 6 ) = 06.5(10 6 ) mm 4 Moment and Product of Inertia with Respect to the u and v Aes: B referring to the geometr of the circle, we obtain I u = ( cos 60 )(10 6 ) = 909(10 6 ) mm 4 I v = ( cos 60 )(10 6 ) = 703(10 6 ) mm 4 I uv = 06.5 sin 60 = 179(10 6 ) mm 4
10 10 7. Locate the centroid of the beam s cross-sectional area and then determine the moments of inertia and the product of inertia ofthis area with respect to the and aes. 50 mm 450 mm 450 mm u 50 mm 400 mm C mm 800 mm Centroid: The perpendicular distances measured from the centroid of each subdivided segment to the bottom of the beam s cross sectional area are indicated in Fig. a. Thus, = Σ A ΣA C = 15(1000)(50) + [1000(400)(50)] + 600(100)(100) 1000(50) + (400)(50) + 100(100) = 85 mm Moment and Product of Inertia with Respect to the and Aes: The perpendicular distances measured from the centroid of each segment to the and aes are indicated in Fig. b. Using the parallel ais theorem, 1 3 I = (1000)(50 ) (50)(400) (50)(400 ) + 50(400)(175) + (100)(100 ) + 100(100)(5) = (10 8 ) mm 4 1 I = 1 (50)(10003 ) (400)(50 ) + 400(50)(75) + 1 = 45 (10 8 ) mm 4 Since the cross sectional area is smmetrical about the ais, I = (100)(1003 ) Moment and Product of Inertia with Respect to the u and v Aes: With = 60, I u = I + I + I I cos I sin = cos 10 0 sin 10 (10 8 ) = (10 8 ) mm 4 = 109 (10 8 ) mm 4 I v = I + I I I cos + I sin = cos sin 10 (10 8 ) = (10 8 ) mm 4 = 38 (10 8 ) mm 4
11 I uv = I I sin + I cos = sin cos 10 (10 8 ) = (10 8 ) mm 4 = 111 (10 8 ) mm 4 50 mm 500 mm 500 mm 75 mm 75 mm 400 mm 50 mm 1000 mm 600 mm 1000 mm 15 mm 4000 mm = 85 mm 175 mm 5 mm
12 Solve Prob using Mohr s circle. Centroid: The perpendicular distances measured from the centroid of each subdivided segment to the bottom of the beam s cross sectional area are indicated in Fig. a. Thus, = Σ A ΣA = 15(1000)(50) + [1000(400)(50)] + 600(100)(100) 1000(50) + (400)(50) + 100(100) = 85 mm Moment and Product of Inertia with Respect to the and Aes: The perpendicular distances measured from the centroid of each segment to the and aes are indicated in Fig. b. Using the parallel ais theorem, 1 3 I = (1000)(50 ) (50)(400) (50)(400 ) + 50(400)(175) (100)(100 ) + 100(100)(5) = (10 8 ) mm 4 1 I = 1 (50)(10003 ) (400)(50 ) + 400(50)(75) + 1 = 45 (10 8 ) mm 4 I = 60(5)( 14.35)(13.15) + 55(15)(15.65)( 14.35) = (10 4 ) mm 4 Since the cross sectional area is smmetrical about the ais, I = (100)(1003 ) Construction of Mohr s Circle: The center C of the circle lies along the u ais at a distance I avg = I + I = (108 ) = (10 8 ) mm 4 The coordinates of the reference point A are (30.44, 0) (10 8 ) mm 4. The circle can be constructed as shown in Fig. c. The radius of the circle is R = CA = ( ) (10 8 ) = 18.7 (10 8 ) mm 4 Moment and Product of Inertia with Respect to the u and v Aes: B referring to the geometr of the circle, I u = ( cos 60 ) (10 8 ) = 109 (10 8 ) mm 4 I v = ( cos 60 ) (10 8 ) = 38 (10 8 ) mm 4 I uv = (18.7 sin 60 ) (10 8 ) = 111 (10 8 ) mm 4 (10 8 mm 4 ) 50 mm 500 mm 500 mm 75 mm 75 mm 400 mm 50 mm 600 mm 1000 mm 15 mm 400 mm = 85 mm 175 mm 5 mm (10 8 mm 4 )
13 Locate the centroid of the beam s cross-sectional area and then determine the moments of inertia of this area and the product of inertia with respect to the u and v aes. The aes have their origin at the centroid C. 5 mm 5 mm v 00 mm C 60 5 mm 75 mm 75 mm u
14
15 Solve Prob using Mohr s circle.
16 Locate the centroid of the beam s cross-sectional area and then determine the moments of inertia and the product of inertia of this area with respect to the u and v aes. The aes have their origin at the centroid C. 0 mm v 00 mm 00 mm 0 mm C 60 0 mm 175 mm u
17 Solve Prob using Mohr s circle.
18 Determine the principal moments of inertia for the angle s cross-sectional area with respect to a set of principal aes that have their origin located at the centroid C. Use the equation developed in Section For the calculation, assume all corners to be square. 0 mm 3. mm C 3. mm SOLUTION 0 mm I = c 1 1 (0)(100) (0)(50-3.) d + c 1 1 (80)(0)3 + 80(0)( ) d = 3.14(10 6 )mm 4 I = c 1 1 (100)(0) (0)( ) d + c 1 1 (0)(80)3 + 80(0)(60-3.) d = 3.14(10 6 )mm 4 I = A = -( )(50-3.)(100)(0) - (60-3.)(3.- 10)(80)(0) = (10 6 )mm 4 I ma/min = I + I ; a I - I b + I C = 3.14(10 6 ) ; 0 + {( )(10 6 )} I ma = 4.9(10 6 )mm 4 I min = 1.36(10 6 )mm 4
19 Solve Prob using Mohr s circle. 0 mm 3. mm SOLUTION Solve Prob I = 3.14(10 6 )mm 4 I = 3.14(10 6 )mm 4 C 3. mm 0 mm I = 1.778(10 6 )mm 4 Center of circle: I + I = 3.14(10 6 )mm 4 R = ( ) + (-1.778) (10 6 ) = 1.778(10 6 )mm 4 I ma = 3.14(10 6 ) (10 6 ) = 4.9(10 6 )mm 4 I min = 3.14(10 6 ) (10 6 ) = 1.36(10 6 )mm 4
20 Determine the orientation of the principal aes, which have their origin at centroid C of the beam s crosssectional area. Also, find the principal moments of inertia. 0 mm 0 mm 150 mm C 150 mm 0 mm
21
22 Solve Prob using Mohr s circle.
23 10 8. Locate the centroid of the beam s cross-sectional area and then determine the moments of inertia of this area and the product of inertia with respect to the u and v aes. The aes have their origin at the centroid C. 0 mm 0 mm v 00 mm C 60 0 mm 80 mm 80mm u [100(00)(0)] + 10(0)(10) = = 79.3 mm (00)(0) + 0(10) I I = (0)(00 ) + 0(00)(0.77) + (10)(0 ) + 10(0)(69.3) = 41.70(10 ) mm = (00)(0 ) + 00(0)(70) + (0)(10 ) = 4.35(10 ) mm I u I + I I I = + cos θ Isin θ + = cos( 10 ) 0sin( 10 ) (10 6 ) 6 4 = 4.(10 ) mm I v I + I I I = + cos θ + Isin θ + = cos( 10 ) 0sin( 10 ) (10 6 ) 6 4 = 41.9(10 ) mm
24 I uv I I = sin θ + I cosθ sin( 10 ) 0cos( 10 = + ) 6 4 = 0.8(10 ) mm mm 70 mm 0.77 mm mm 69.3 mm 60 60
25 Solve Prob using Mohr s circle. [100(00)(0)] + 10(0)(10) = = 79.3 mm (00)(0) + 0(10) (0)(00 ) 0(00)(0.77) (10)(0 3 ) 10(0)(69.3) I = = 41.70(10 6 ) mm I (00)(0 ) 00(0)(70) (0)(10 3 = + ) = 4.5(10 6 ) mm 4 I + I I (10 6 )mm (10 6 )mm 4 avg = = = R = CA = ( )(10 6 ) = 0.75(10 6 ) mm 4 I ( cos60 )(10 6 ) 41.86(10 6 )mm 4 v = = I ( cos60 )(10 6 ) 4.19(10 6 )mm 4 u = = I 0.35sin60 0.8(10 6 )mm 4 uv = = I u 70 mm 70 mm 0.77 mm mm 69.3 mm R = I v 4.5
26 Determine the mass moment of inertia I of the solid formed b revolving the shaded area around the ais. The total mass of the solid is 1500 kg. z 4m z m O SOLUTION Differential Element: The mass of the disk element shown shaded in Fig. a is dm = rdv = rpr. Here,.Thus, dm = rpa > b d d r = z = 1 = rp 16 3 d 4 3> The mass moment of inertia of this element about the ais is di = 1. dmr = 1 Arpr dbr = rp r4 d = rp a 1 4 3> b 4d = rp 51 6 d Mass: The mass of the solid can be determined b integrating dm. Thus, 4m rp m = dm = L L 16 3 d = rp ` 4 m 0 0 = 4pr The mass of the solid is m = 1500 kg. Thus, 1500 = 4pr r = 375 p Mass Moment of Inertia: Integrating di, 4m rp I = di = L L Substituting r = 375 into I, p kg>m3 0 kg>m d = rp ` 4m 0 = 3p 7 r I = 3p 7 a 375 p b = 1.71(103 )kg# m
27 Determine the mass moment of inertia of the assembl about the z ais. The densit of the material is 7.85 Mg> m 3. z SOLUTION Composite Parts: The assembl can be subdivided into two circular cone segments (1) and (3) and a hemispherical segment () as shown in Fig. a. Since segment (3) is a hole, it should be considered as a negative part. From the similar triangles, we obtain z z = Mass: The mass of each segment is calculated as z = 0.5m 300 mm 450 mm 300 mm m 1 = rv 1 = ra 1 3 pr hb = 7.85(10 3 )c 1 3 p(0.3 )(0.675) d = p kg m = rv = ra 3 pr3 b = 7.85(10 3 )c 3 p(0.33 ) d = 141.3p kg m 3 = rv 3 = ra 1 3 pr hb = 7.85(10 3 )c 1 3 p(0.1 )(0.5) d = p kg Mass Moment of Inertia: Since the z ais is parallel to the ais of the cone and the hemisphere and passes through their center of mass, the mass moment of inertia can be 3 computed from (I and. Thus, 10 m 3r3 z ) 1 = 3 10 m 1r1, (I z ) = 5 m r, I z = (I z ) i = 3 10 ( p)(0.3 ) + 5 (141.3p)(0.3 ) (5.8875p)(0.1 ) = 9.4 kg # m
28 The thin plate has a mass per unit area of 10 kg>m. Determine its mass moment of inertia about the ais. z 00 mm 00 mm SOLUTION Composite Parts: The thin plate can be subdivided into segments as shown in Fig. a. Since the segments labeled () are both holes, the should be considered as negative parts. Mass moment of Inertia: The mass of segments (1) and () are m and m = p(0.1 1 = 0.4(0.4)(10) = 1.6 kg )(10) = 0.1p kg. The perpendicular distances measured from the centroid of each segment to the ais are indicated in Fig. a. The mass moment of inertia of each segment about the ais can be determined using the parallel-ais theorem. I = AI B G + md = c 1 1 (1.6)(0.4 ) + 1.6(0. ) d - c 1 4 (0.1p)(0.1 ) + 0.1p(0. ) d 00 mm 00 mm 00 mm 00 mm 00 mm 00 mm = kg # m
29 The thin plate has a mass per unit area of 10 kg>m. Determine its mass moment of inertia about the z ais. z 00 mm 00 mm SOLUTION Composite Parts: The thin plate can be subdivided into four segments as shown in Fig. a. Since segments (3) and (4) are both holes, the should be considered as negative parts. Mass moment of Inertia: Here, the mass for segments (1), (), (3), and (4) are m and m 3 = m 4 = p(0.1 1 = m = 0.4(0.4)(10) = 1.6 kg )(10) = 0.1p kg. The mass moment of inertia of each segment about the z ais can be determined using the parallel-ais theorem. I z = AI z B G + md 00 mm 00 mm 00 mm 00 mm 00 mm 00 mm = 1 1 (1.6)(0.4 ) + c 1 1 (1.6)( ) + 1.6(0. ) d (0.1p)(0.1 ) - c 1 (0.1p)(0.1 ) + 0.1p(0. ) d = kg # m
30 Determine the mass moment of inertia of the overhung crank about the ais. The material is steel having a densit of r = 7.85 Mg>m 3. 0 mm 90 mm 30 mm 50 mm 180 mm 0 mm 30 mm 0 mm 50 mm 30 mm = kg m = 3.5 g m.
31 Determine the mass moment of inertia of the overhung crank about the ais. The material is steel having a densit of r = 7.85 Mg>m 3. 0 mm 90 mm 30 mm 50 mm 180 mm 0 mm 30 mm 0 mm 50 mm 30 mm kg m
SOLUTION Determine the moment of inertia for the shaded area about the x axis. I x = y 2 da = 2 y 2 (xdy) = 2 y y dy
 5. Determine the moment of inertia for the shaded area about the ais. 4 4m 4 4 I = da = (d) 4 = 4 - d I = B (5 + (4)() + 8(4) ) (4 - ) 3-5 4 R m m I = 39. m 4 6. Determine the moment of inertia for the
5. Determine the moment of inertia for the shaded area about the ais. 4 4m 4 4 I = da = (d) 4 = 4 - d I = B (5 + (4)() + 8(4) ) (4 - ) 3-5 4 R m m I = 39. m 4 6. Determine the moment of inertia for the
ME 101: Engineering Mechanics
 ME 0: Engineering Mechanics Rajib Kumar Bhattacharja Department of Civil Engineering ndian nstitute of Technolog Guwahati M Block : Room No 005 : Tel: 8 www.iitg.ernet.in/rkbc Area Moments of nertia Parallel
ME 0: Engineering Mechanics Rajib Kumar Bhattacharja Department of Civil Engineering ndian nstitute of Technolog Guwahati M Block : Room No 005 : Tel: 8 www.iitg.ernet.in/rkbc Area Moments of nertia Parallel
Distributed Forces: Moments of Inertia
 Distributed Forces: Moments of nertia Contents ntroduction Moments of nertia of an Area Moments of nertia of an Area b ntegration Polar Moments of nertia Radius of Gration of an Area Sample Problems Parallel
Distributed Forces: Moments of nertia Contents ntroduction Moments of nertia of an Area Moments of nertia of an Area b ntegration Polar Moments of nertia Radius of Gration of an Area Sample Problems Parallel
ME 141. Lecture 8: Moment of Inertia
 ME 4 Engineering Mechanics Lecture 8: Moment of nertia Ahmad Shahedi Shakil Lecturer, Dept. of Mechanical Engg, BUET E-mail: sshakil@me.buet.ac.bd, shakil679@gmail.com Website: teacher.buet.ac.bd/sshakil
ME 4 Engineering Mechanics Lecture 8: Moment of nertia Ahmad Shahedi Shakil Lecturer, Dept. of Mechanical Engg, BUET E-mail: sshakil@me.buet.ac.bd, shakil679@gmail.com Website: teacher.buet.ac.bd/sshakil
SOLUTION y ' A = 7.5(15) (150) + 90(150) (15) + 215(p)(50) 2. = mm 2. A = 15(150) + 150(15) + p(50) 2. =
 9 58. Determine the location of the centroidal ais - of the beam s cross-sectional area. Neglect the size of the corner welds at A and B for the calculation. 15 mm 15 mm B 15 mm 15 mm A = 7.5(15) (15)
9 58. Determine the location of the centroidal ais - of the beam s cross-sectional area. Neglect the size of the corner welds at A and B for the calculation. 15 mm 15 mm B 15 mm 15 mm A = 7.5(15) (15)
STATICS. Moments of Inertia VECTOR MECHANICS FOR ENGINEERS: Ninth Edition CHAPTER. Ferdinand P. Beer E. Russell Johnston, Jr.
 N E 9 Distributed CHAPTER VECTOR MECHANCS FOR ENGNEERS: STATCS Ferdinand P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Walt Oler Teas Tech Universit Forces: Moments of nertia Contents ntroduction
N E 9 Distributed CHAPTER VECTOR MECHANCS FOR ENGNEERS: STATCS Ferdinand P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Walt Oler Teas Tech Universit Forces: Moments of nertia Contents ntroduction
STATICS. Moments of Inertia VECTOR MECHANICS FOR ENGINEERS: Seventh Edition CHAPTER. Ferdinand P. Beer
 00 The McGraw-Hill Companies, nc. All rights reserved. Seventh E CHAPTER VECTOR MECHANCS FOR ENGNEERS: 9 STATCS Ferdinand P. Beer E. Russell Johnston, Jr. Distributed Forces: Lecture Notes: J. Walt Oler
00 The McGraw-Hill Companies, nc. All rights reserved. Seventh E CHAPTER VECTOR MECHANCS FOR ENGNEERS: 9 STATCS Ferdinand P. Beer E. Russell Johnston, Jr. Distributed Forces: Lecture Notes: J. Walt Oler
Second Moments or Moments of Inertia
 Second Moments or Moments of Inertia The second moment of inertia of an element of area such as da in Figure 1 with respect to any axis is defined as the product of the area of the element and the square
Second Moments or Moments of Inertia The second moment of inertia of an element of area such as da in Figure 1 with respect to any axis is defined as the product of the area of the element and the square
I xx + I yy + I zz = (y 2 + z 2 )dm + (x 2 + y 2 )dm. (x 2 + z 2 )dm + (x 2 + y 2 + z 2 )dm = 2
 9196_1_s1_p095-0987 6/8/09 1:09 PM Page 95 010 Pearson Education, Inc., Upper Saddle River, NJ. ll rights reserved. This material is protected under all copright laws as the currentl 1 1. Show that the
9196_1_s1_p095-0987 6/8/09 1:09 PM Page 95 010 Pearson Education, Inc., Upper Saddle River, NJ. ll rights reserved. This material is protected under all copright laws as the currentl 1 1. Show that the
SOLUTION di x = y2 dm. rdv. m = a 2 bdx. = 2 3 rpab2. I x = 1 2 rp L0. b 4 a1 - x2 a 2 b. = 4 15 rpab4. Thus, I x = 2 5 mb2. Ans.
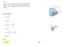 17 4. Determine the moment of inertia of the semiellipsoid with respect to the x axis and express the result in terms of the mass m of the semiellipsoid. The material has a constant density r. y x y a
17 4. Determine the moment of inertia of the semiellipsoid with respect to the x axis and express the result in terms of the mass m of the semiellipsoid. The material has a constant density r. y x y a
MOI (SEM. II) EXAMINATION.
 Problems Based On Centroid And MOI (SEM. II) EXAMINATION. 2006-07 1- Find the centroid of a uniform wire bent in form of a quadrant of the arc of a circle of radius R. 2- State the parallel axis theorem.
Problems Based On Centroid And MOI (SEM. II) EXAMINATION. 2006-07 1- Find the centroid of a uniform wire bent in form of a quadrant of the arc of a circle of radius R. 2- State the parallel axis theorem.
3/31/ Product of Inertia. Sample Problem Sample Problem 10.6 (continue)
 /1/01 10.6 Product of Inertia Product of Inertia: I xy = xy da When the x axis, the y axis, or both are an axis of symmetry, the product of inertia is zero. Parallel axis theorem for products of inertia:
/1/01 10.6 Product of Inertia Product of Inertia: I xy = xy da When the x axis, the y axis, or both are an axis of symmetry, the product of inertia is zero. Parallel axis theorem for products of inertia:
MOMENT OF INERTIA. Applications. Parallel-Axis Theorem
 MOMENT OF INERTIA Today s Objectives: Students will be able to: 1. Determine the mass moment of inertia of a rigid body or a system of rigid bodies. In-Class Activities: Applications Mass Moment of Inertia
MOMENT OF INERTIA Today s Objectives: Students will be able to: 1. Determine the mass moment of inertia of a rigid body or a system of rigid bodies. In-Class Activities: Applications Mass Moment of Inertia
ENGI 4430 Multiple Integration Cartesian Double Integrals Page 3-01
 ENGI 4430 Multiple Integration Cartesian Double Integrals Page 3-01 3. Multiple Integration This chapter provides only a very brief introduction to the major topic of multiple integration. Uses of multiple
ENGI 4430 Multiple Integration Cartesian Double Integrals Page 3-01 3. Multiple Integration This chapter provides only a very brief introduction to the major topic of multiple integration. Uses of multiple
Statics: Lecture Notes for Sections 10.1,10.2,10.3 1
 Chapter 10 MOMENTS of INERTIA for AREAS, RADIUS OF GYRATION Today s Objectives: Students will be able to: a) Define the moments of inertia (MoI) for an area. b) Determine the MoI for an area by integration.
Chapter 10 MOMENTS of INERTIA for AREAS, RADIUS OF GYRATION Today s Objectives: Students will be able to: a) Define the moments of inertia (MoI) for an area. b) Determine the MoI for an area by integration.
ENGR-1100 Introduction to Engineering Analysis. Lecture 17
 ENGR-1100 Introduction to Engineering Analysis Lecture 17 CENTROID OF COMPOSITE AREAS Today s Objective : Students will: a) Understand the concept of centroid. b) Be able to determine the location of the
ENGR-1100 Introduction to Engineering Analysis Lecture 17 CENTROID OF COMPOSITE AREAS Today s Objective : Students will: a) Understand the concept of centroid. b) Be able to determine the location of the
EXERCISES Chapter 15: Multiple Integrals. Evaluating Integrals in Cylindrical Coordinates
 08 Chapter 5: Multiple Integrals EXERCISES 5.6 Evaluating Integrals in Clindrical Evaluate the clindrical coordinate integrals in Eercises 6... 3. 4. 5. 6. Changing Order of Integration in Clindrical The
08 Chapter 5: Multiple Integrals EXERCISES 5.6 Evaluating Integrals in Clindrical Evaluate the clindrical coordinate integrals in Eercises 6... 3. 4. 5. 6. Changing Order of Integration in Clindrical The
ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 3 Solutions [Multiple Integration; Lines of Force]
![ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 3 Solutions [Multiple Integration; Lines of Force] ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 3 Solutions [Multiple Integration; Lines of Force]](/thumbs/84/89723886.jpg) ENGI 44 Advanced Calculus for Engineering Facult of Engineering and Applied Science Problem Set Solutions [Multiple Integration; Lines of Force]. Evaluate D da over the triangular region D that is bounded
ENGI 44 Advanced Calculus for Engineering Facult of Engineering and Applied Science Problem Set Solutions [Multiple Integration; Lines of Force]. Evaluate D da over the triangular region D that is bounded
MAHALAKSHMI ENGINEERING COLLEGE TIRUCHIRAPPALLI Distinguish between centroid and centre of gravity. (AU DEC 09,DEC 12)
 MAHALAKSHMI ENGINEERING COLLEGE TIRUCHIRAPPALLI 621213 Sub Code: GE 6253 Semester: II Subject: ENGINEERING MECHANICS Unit III: PROPERTIES OF SURFACES AND SOLIDS PART A 1. Distinguish between centroid and
MAHALAKSHMI ENGINEERING COLLEGE TIRUCHIRAPPALLI 621213 Sub Code: GE 6253 Semester: II Subject: ENGINEERING MECHANICS Unit III: PROPERTIES OF SURFACES AND SOLIDS PART A 1. Distinguish between centroid and
Chapter 5 Equilibrium of a Rigid Body Objectives
 Chapter 5 Equilibrium of a Rigid Bod Objectives Develop the equations of equilibrium for a rigid bod Concept of the free-bod diagram for a rigid bod Solve rigid-bod equilibrium problems using the equations
Chapter 5 Equilibrium of a Rigid Bod Objectives Develop the equations of equilibrium for a rigid bod Concept of the free-bod diagram for a rigid bod Solve rigid-bod equilibrium problems using the equations
h p://edugen.wileyplus.com/edugen/courses/crs1404/pc/b03/c2hlch...
 n this appendix we discuss... 1 of 4 16-Sep-12 19:35 APPENDIX C In this appendix we discuss how to calculate the moment of inertia of an area. 1 The moment of inertia of an area was first introduced in
n this appendix we discuss... 1 of 4 16-Sep-12 19:35 APPENDIX C In this appendix we discuss how to calculate the moment of inertia of an area. 1 The moment of inertia of an area was first introduced in
PROBLEM Area of Problem I = 471,040 mm xy 2(471,040) 252,757 1,752,789 = or θ m = and = (1,002,773 ± 885,665) mm
 PROBLEM 9.88 F the area indicated, determine the ientation of the principal aes at the igin the cresponding values of the moments of inertia. Area of Problem 9.75. From Problem 9.8: Problem 9.75: = 5,757
PROBLEM 9.88 F the area indicated, determine the ientation of the principal aes at the igin the cresponding values of the moments of inertia. Area of Problem 9.75. From Problem 9.8: Problem 9.75: = 5,757
DEFINITION OF MOMENTS OF INERTIA FOR AREAS, RADIUS OF GYRATION OF AN AREA
 DEFINITION OF MOMENTS OF INERTIA FOR AREAS, RADIUS OF GYRATION OF AN AREA Today s Objectives: Students will be able to: a) Define the moments of inertia (MoI) for an area. b) Determine the moment of inertia
DEFINITION OF MOMENTS OF INERTIA FOR AREAS, RADIUS OF GYRATION OF AN AREA Today s Objectives: Students will be able to: a) Define the moments of inertia (MoI) for an area. b) Determine the moment of inertia
The University of Melbourne Engineering Mechanics
 The University of Melbourne 436-291 Engineering Mechanics Tutorial Eleven Instantaneous Centre and General Motion Part A (Introductory) 1. (Problem 5/93 from Meriam and Kraige - Dynamics) For the instant
The University of Melbourne 436-291 Engineering Mechanics Tutorial Eleven Instantaneous Centre and General Motion Part A (Introductory) 1. (Problem 5/93 from Meriam and Kraige - Dynamics) For the instant
Chapter 9 Moment of Inertia
 Chapter 9 Moment of Inertia Dr. Khairul Salleh Basaruddin Applied Mechanics Division School of Mechatronic Engineering Universiti Malaysia Perlis (UniMAP) khsalleh@unimap.edu.my PARALLEL-AXIS THEOREM,
Chapter 9 Moment of Inertia Dr. Khairul Salleh Basaruddin Applied Mechanics Division School of Mechatronic Engineering Universiti Malaysia Perlis (UniMAP) khsalleh@unimap.edu.my PARALLEL-AXIS THEOREM,
STATICS. Distributed Forces: Moments of Inertia VECTOR MECHANICS FOR ENGINEERS: Eighth Edition CHAPTER. Ferdinand P. Beer E. Russell Johnston, Jr.
 007 The McGraw-Hill Companies, nc. All rights reserved. Eighth E CHAPTER 9 VECTOR MECHANCS FOR ENGNEERS: STATCS Ferdinand P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Walt Oler Texas Tech University
007 The McGraw-Hill Companies, nc. All rights reserved. Eighth E CHAPTER 9 VECTOR MECHANCS FOR ENGNEERS: STATCS Ferdinand P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Walt Oler Texas Tech University
Bending Stress. Sign convention. Centroid of an area
 Bending Stress Sign convention The positive shear force and bending moments are as shown in the figure. Centroid of an area Figure 40: Sign convention followed. If the area can be divided into n parts
Bending Stress Sign convention The positive shear force and bending moments are as shown in the figure. Centroid of an area Figure 40: Sign convention followed. If the area can be divided into n parts
ENGI Multiple Integration Page 8-01
 ENGI 345 8. Multiple Integration Page 8-01 8. Multiple Integration This chapter provides only a very brief introduction to the major topic of multiple integration. Uses of multiple integration include
ENGI 345 8. Multiple Integration Page 8-01 8. Multiple Integration This chapter provides only a very brief introduction to the major topic of multiple integration. Uses of multiple integration include
Chapter 5. Distributed Forces: Centroids and Centers of Gravity
 Chapter 5 Distributed Forces: Centroids and Centers of Gravity Application There are many examples in engineering analysis of distributed loads. It is convenient in some cases to represent such loads as
Chapter 5 Distributed Forces: Centroids and Centers of Gravity Application There are many examples in engineering analysis of distributed loads. It is convenient in some cases to represent such loads as
Handout 6: Rotational motion and moment of inertia. Angular velocity and angular acceleration
 1 Handout 6: Rotational motion and moment of inertia Angular velocity and angular acceleration In Figure 1, a particle b is rotating about an axis along a circular path with radius r. The radius sweeps
1 Handout 6: Rotational motion and moment of inertia Angular velocity and angular acceleration In Figure 1, a particle b is rotating about an axis along a circular path with radius r. The radius sweeps
AREAS, RADIUS OF GYRATION
 Chapter 10 MOMENTS of INERTIA for AREAS, RADIUS OF GYRATION Today s Objectives: Students will be able to: a) Define the moments of inertia (MoI) for an area. b) Determine the MoI for an area by integration.
Chapter 10 MOMENTS of INERTIA for AREAS, RADIUS OF GYRATION Today s Objectives: Students will be able to: a) Define the moments of inertia (MoI) for an area. b) Determine the MoI for an area by integration.
SOLUTION (y 2 + z 2 )dm + (x 2 + y 2 )dm. (x 2 + z 2 )dm + I xx + I yy + I zz = = 2. (x 2 + y 2 + z 2 )dm
 1 1. Show that the sum of the moments of inertia of a bod, I + I + I, is independent of the orientation of the,, aes and thus depends onl on the location of its origin. I + I + I = Lm ( + )dm + Lm ( +
1 1. Show that the sum of the moments of inertia of a bod, I + I + I, is independent of the orientation of the,, aes and thus depends onl on the location of its origin. I + I + I = Lm ( + )dm + Lm ( +
2 4πε ( ) ( r θ. , symmetric about the x-axis, as shown in Figure What is the electric field E at the origin O?
 p E( r, θ) = cosθ 3 ( sinθ ˆi + cosθ ˆj ) + sinθ cosθ ˆi + ( cos θ 1) ˆj r ( ) ( p = cosθ sinθ ˆi + cosθ ˆj + sinθ cosθ ˆi sinθ ˆj 3 r where the trigonometric identit ( θ ) vectors ˆr and cos 1 = sin θ
p E( r, θ) = cosθ 3 ( sinθ ˆi + cosθ ˆj ) + sinθ cosθ ˆi + ( cos θ 1) ˆj r ( ) ( p = cosθ sinθ ˆi + cosθ ˆj + sinθ cosθ ˆi sinθ ˆj 3 r where the trigonometric identit ( θ ) vectors ˆr and cos 1 = sin θ
Chapter 10: Moments of Inertia
 Chapter 10: Moments of Inertia Chapter Objectives To develop a method for determining the moment of inertia and product of inertia for an area with respect to given x- and y-axes. To develop a method for
Chapter 10: Moments of Inertia Chapter Objectives To develop a method for determining the moment of inertia and product of inertia for an area with respect to given x- and y-axes. To develop a method for
Statics Chapter II Fall 2018 Exercises Corresponding to Sections 2.1, 2.2, and 2.3
 Statics Chapter II Fall 2018 Exercises Corresponding to Sections 2.1, 2.2, and 2.3 2 3 Determine the magnitude of the resultant force FR = F1 + F2 and its direction, measured counterclockwise from the
Statics Chapter II Fall 2018 Exercises Corresponding to Sections 2.1, 2.2, and 2.3 2 3 Determine the magnitude of the resultant force FR = F1 + F2 and its direction, measured counterclockwise from the
Determine the moment of inertia of the area about the x axis Determine the moment of inertia of the area about the y axis.
 10 Solutions 44918 1/28/09 4:21 PM Page 941 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copright laws as the currentl eist. No portion
10 Solutions 44918 1/28/09 4:21 PM Page 941 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copright laws as the currentl eist. No portion
Chapter 6: Cross-Sectional Properties of Structural Members
 Chapter 6: Cross-Sectional Properties of Structural Members Introduction Beam design requires the knowledge of the following. Material strengths (allowable stresses) Critical shear and moment values Cross
Chapter 6: Cross-Sectional Properties of Structural Members Introduction Beam design requires the knowledge of the following. Material strengths (allowable stresses) Critical shear and moment values Cross
Moments of Inertia (7 pages; 23/3/18)
 Moments of Inertia (7 pages; 3/3/8) () Suppose that an object rotates about a fixed axis AB with angular velocity θ. Considering the object to be made up of particles, suppose that particle i (with mass
Moments of Inertia (7 pages; 3/3/8) () Suppose that an object rotates about a fixed axis AB with angular velocity θ. Considering the object to be made up of particles, suppose that particle i (with mass
Moment of Inertia and Centroid
 Chapter- Moment of nertia and Centroid Page- 1. Moment of nertia and Centroid Theory at a Glance (for ES, GATE, PSU).1 Centre of gravity: The centre of gravity of a body defined as the point through which
Chapter- Moment of nertia and Centroid Page- 1. Moment of nertia and Centroid Theory at a Glance (for ES, GATE, PSU).1 Centre of gravity: The centre of gravity of a body defined as the point through which
University of Pretoria Department of Mechanical & Aeronautical Engineering MOW 227, 2 nd Semester 2014
 Universit of Pretoria Department of Mechanical & Aeronautical Engineering MOW 7, nd Semester 04 Semester Test Date: August, 04 Total: 00 Internal eaminer: Duration: hours Mr. Riaan Meeser Instructions:
Universit of Pretoria Department of Mechanical & Aeronautical Engineering MOW 7, nd Semester 04 Semester Test Date: August, 04 Total: 00 Internal eaminer: Duration: hours Mr. Riaan Meeser Instructions:
Properties of surfaces II: Second moment of area
 Properties of surfaces II: Second moment of area Just as we have discussing first moment of an area and its relation with problems in mechanics, we will now describe second moment and product of area of
Properties of surfaces II: Second moment of area Just as we have discussing first moment of an area and its relation with problems in mechanics, we will now describe second moment and product of area of
Moments of Inertia. Notation:
 RCH 1 Note Set 9. S015abn Moments of nertia Notation: b d d d h c Jo O = name for area = name for a (base) width = calculus smbol for differentiation = name for a difference = name for a depth = difference
RCH 1 Note Set 9. S015abn Moments of nertia Notation: b d d d h c Jo O = name for area = name for a (base) width = calculus smbol for differentiation = name for a difference = name for a depth = difference
h p://edugen.wileyplus.com/edugen/courses/crs1404/pc/c08/c2hlch...
 Digital Vision/PictureQuestW... 1 of 2 30-Sep-12 18:41 CHAPTER 8 DISTRIBUTED FORCE Digital Vision/PictureQuest We have looked at a variety of systems and defined the conditions under which they are in
Digital Vision/PictureQuestW... 1 of 2 30-Sep-12 18:41 CHAPTER 8 DISTRIBUTED FORCE Digital Vision/PictureQuest We have looked at a variety of systems and defined the conditions under which they are in
Hong Kong Institute of Vocational Education (Tsing Yi) Higher Diploma in Civil Engineering Structural Mechanics. Chapter 2 SECTION PROPERTIES
 Section Properties Centroid The centroid of an area is the point about which the area could be balanced if it was supported from that point. The word is derived from the word center, and it can be though
Section Properties Centroid The centroid of an area is the point about which the area could be balanced if it was supported from that point. The word is derived from the word center, and it can be though
Statics: Lecture Notes for Sections
 0.5 MOMENT OF INERTIA FOR A COMPOSITE AREA A composite area is made by adding or subtracting a series of simple shaped areas like rectangles, triangles, and circles. For example, the area on the left can
0.5 MOMENT OF INERTIA FOR A COMPOSITE AREA A composite area is made by adding or subtracting a series of simple shaped areas like rectangles, triangles, and circles. For example, the area on the left can
and F NAME: ME rd Sample Final Exam PROBLEM 1 (25 points) Prob. 1 questions are all or nothing. PROBLEM 1A. (5 points)
 ME 270 3 rd Sample inal Exam PROBLEM 1 (25 points) Prob. 1 questions are all or nothing. PROBLEM 1A. (5 points) IND: In your own words, please state Newton s Laws: 1 st Law = 2 nd Law = 3 rd Law = PROBLEM
ME 270 3 rd Sample inal Exam PROBLEM 1 (25 points) Prob. 1 questions are all or nothing. PROBLEM 1A. (5 points) IND: In your own words, please state Newton s Laws: 1 st Law = 2 nd Law = 3 rd Law = PROBLEM
10.5 MOMENT OF INERTIA FOR A COMPOSITE AREA
 10.5 MOMENT OF NERTA FOR A COMPOSTE AREA A composite area is made by adding or subtracting a series of simple shaped areas like rectangles, triangles, and circles. For example, the area on the left can
10.5 MOMENT OF NERTA FOR A COMPOSTE AREA A composite area is made by adding or subtracting a series of simple shaped areas like rectangles, triangles, and circles. For example, the area on the left can
CHAPTER 4 Stress Transformation
 CHAPTER 4 Stress Transformation ANALYSIS OF STRESS For this topic, the stresses to be considered are not on the perpendicular and parallel planes only but also on other inclined planes. A P a a b b P z
CHAPTER 4 Stress Transformation ANALYSIS OF STRESS For this topic, the stresses to be considered are not on the perpendicular and parallel planes only but also on other inclined planes. A P a a b b P z
MTE 119 STATICS LECTURE MATERIALS FINAL REVIEW PAGE NAME & ID DATE. Example Problem F.1: (Beer & Johnston Example 9-11)
 Eample Problem F.: (Beer & Johnston Eample 9-) Determine the mass moment of inertia with respect to: (a) its longitudinal ais (-ais) (b) the y-ais SOLUTION: a) Mass moment of inertia about the -ais: Step
Eample Problem F.: (Beer & Johnston Eample 9-) Determine the mass moment of inertia with respect to: (a) its longitudinal ais (-ais) (b) the y-ais SOLUTION: a) Mass moment of inertia about the -ais: Step
Solution ME 323 EXAM #2 FALL SEMESTER :00 PM 9:30 PM Nov. 2, 2010
 Solution ME 33 EXAM # FALL SEMESTER 1 8: PM 9:3 PM Nov., 1 Instructions 1. Begin each problem in the space provided on the eamination sheets. If additional space is required, use the paper provided. Work
Solution ME 33 EXAM # FALL SEMESTER 1 8: PM 9:3 PM Nov., 1 Instructions 1. Begin each problem in the space provided on the eamination sheets. If additional space is required, use the paper provided. Work
MATH 52 FINAL EXAM SOLUTIONS
 MAH 5 FINAL EXAM OLUION. (a) ketch the region R of integration in the following double integral. x xe y5 dy dx R = {(x, y) x, x y }. (b) Express the region R as an x-simple region. R = {(x, y) y, x y }
MAH 5 FINAL EXAM OLUION. (a) ketch the region R of integration in the following double integral. x xe y5 dy dx R = {(x, y) x, x y }. (b) Express the region R as an x-simple region. R = {(x, y) y, x y }
Stress and Strain ( , 3.14) MAE 316 Strength of Mechanical Components NC State University Department of Mechanical & Aerospace Engineering
 (3.8-3.1, 3.14) MAE 316 Strength of Mechanical Components NC State Universit Department of Mechanical & Aerospace Engineering 1 Introduction MAE 316 is a continuation of MAE 314 (solid mechanics) Review
(3.8-3.1, 3.14) MAE 316 Strength of Mechanical Components NC State Universit Department of Mechanical & Aerospace Engineering 1 Introduction MAE 316 is a continuation of MAE 314 (solid mechanics) Review
Two small balls, each of mass m, with perpendicular bisector of the line joining the two balls as the axis of rotation:
 PHYSCS LOCUS 17 summation in mi ri becomes an integration. We imagine the body to be subdivided into infinitesimal elements, each of mass dm, as shown in figure 7.17. Let r be the distance from such an
PHYSCS LOCUS 17 summation in mi ri becomes an integration. We imagine the body to be subdivided into infinitesimal elements, each of mass dm, as shown in figure 7.17. Let r be the distance from such an
Chapter 6 Planar Kinetics of a Rigid Body: Force and Acceleration
 Chapter 6 Planar Kinetics of a Rigid Body: Force and Acceleration Dr. Khairul Salleh Basaruddin Applied Mechanics Division School of Mechatronic Engineering Universiti Malaysia Perlis (UniMAP) khsalleh@unimap.edu.my
Chapter 6 Planar Kinetics of a Rigid Body: Force and Acceleration Dr. Khairul Salleh Basaruddin Applied Mechanics Division School of Mechatronic Engineering Universiti Malaysia Perlis (UniMAP) khsalleh@unimap.edu.my
Problem 4. = 1 1 = 1. = m 4. = m 4
 Problem. (a) Calculate the stress in the bolt that connects steel plates and the wooden block as shown if the section is subjected to V kn. ssume the elastic moduli of steel as GPa and of wood as 1.5 GPa.
Problem. (a) Calculate the stress in the bolt that connects steel plates and the wooden block as shown if the section is subjected to V kn. ssume the elastic moduli of steel as GPa and of wood as 1.5 GPa.
Moment of Inertia & Newton s Laws for Translation & Rotation
 Moment of Inertia & Newton s Laws for Translation & Rotation In this training set, you will apply Newton s 2 nd Law for rotational motion: Στ = Σr i F i = Iα I is the moment of inertia of an object: I
Moment of Inertia & Newton s Laws for Translation & Rotation In this training set, you will apply Newton s 2 nd Law for rotational motion: Στ = Σr i F i = Iα I is the moment of inertia of an object: I
PHY 5246: Theoretical Dynamics, Fall Assignment # 9, Solutions. y CM (θ = 0) = 2 ρ m
 PHY 546: Theoretical Dnamics, Fall 5 Assignment # 9, Solutions Graded Problems Problem (.a) l l/ l/ CM θ x In order to find the equation of motion of the triangle, we need to write the Lagrangian, with
PHY 546: Theoretical Dnamics, Fall 5 Assignment # 9, Solutions Graded Problems Problem (.a) l l/ l/ CM θ x In order to find the equation of motion of the triangle, we need to write the Lagrangian, with
Determine the resultant internal loadings acting on the cross section at C of the beam shown in Fig. 1 4a.
 E X M P L E 1.1 Determine the resultant internal loadings acting on the cross section at of the beam shown in Fig. 1 a. 70 N/m m 6 m Fig. 1 Support Reactions. This problem can be solved in the most direct
E X M P L E 1.1 Determine the resultant internal loadings acting on the cross section at of the beam shown in Fig. 1 a. 70 N/m m 6 m Fig. 1 Support Reactions. This problem can be solved in the most direct
ME 201 Engineering Mechanics: Statics
 ME 0 Engineering Mechanics: Statics Unit 9. Moments of nertia Definition of Moments of nertia for Areas Parallel-Axis Theorem for an Area Radius of Gyration of an Area Moments of nertia for Composite Areas
ME 0 Engineering Mechanics: Statics Unit 9. Moments of nertia Definition of Moments of nertia for Areas Parallel-Axis Theorem for an Area Radius of Gyration of an Area Moments of nertia for Composite Areas
Stress Transformation Equations: u = +135 (Fig. a) s x = 80 MPa s y = 0 t xy = 45 MPa. we obtain, cos u + t xy sin 2u. s x = s x + s y.
 014 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently 9 7. Determine the normal stress and shear stress acting
014 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently 9 7. Determine the normal stress and shear stress acting
y=1/4 x x=4y y=x 3 x=y 1/3 Example: 3.1 (1/2, 1/8) (1/2, 1/8) Find the area in the positive quadrant bounded by y = 1 x and y = x3
 Eample: 3.1 Find the area in the positive quadrant bounded b 1 and 3 4 First find the points of intersection of the two curves: clearl the curves intersect at (, ) and at 1 4 3 1, 1 8 Select a strip at
Eample: 3.1 Find the area in the positive quadrant bounded b 1 and 3 4 First find the points of intersection of the two curves: clearl the curves intersect at (, ) and at 1 4 3 1, 1 8 Select a strip at
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 --review Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the area of the shaded region. ) f() = + - ) 0 0 (, 8) 0 (0, 0) - - - - - - -0
--review Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the area of the shaded region. ) f() = + - ) 0 0 (, 8) 0 (0, 0) - - - - - - -0
5. Triple Integrals. 5A. Triple integrals in rectangular and cylindrical coordinates. 2 + y + z x=0. y Outer: 1
 5. Triple Integrals 5A. Triple integrals in rectangular and clindrical coordinates ] 5A- a) (x + + )dxdd Inner: x + x( + ) + + x ] ] Middle: + + + ( ) + Outer: + 6 x ] x b) x ddxd Inner: x x 3 4 ] ] +
5. Triple Integrals 5A. Triple integrals in rectangular and clindrical coordinates ] 5A- a) (x + + )dxdd Inner: x + x( + ) + + x ] ] Middle: + + + ( ) + Outer: + 6 x ] x b) x ddxd Inner: x x 3 4 ] ] +
Math 323 Exam 2 - Practice Problem Solutions. 2. Given the vectors a = 1,2,0, b = 1,0,2, and c = 0,1,1, compute the following:
 Math 323 Eam 2 - Practice Problem Solutions 1. Given the vectors a = 2,, 1, b = 3, 2,4, and c = 1, 4,, compute the following: (a) A unit vector in the direction of c. u = c c = 1, 4, 1 4 =,, 1+16+ 17 17
Math 323 Eam 2 - Practice Problem Solutions 1. Given the vectors a = 2,, 1, b = 3, 2,4, and c = 1, 4,, compute the following: (a) A unit vector in the direction of c. u = c c = 1, 4, 1 4 =,, 1+16+ 17 17
PROBLEM 16.4 SOLUTION
 PROBLEM 16.4 The motion of the.5-kg rod AB is guided b two small wheels which roll freel in horizontal slots. If a force P of magnitude 8 N is applied at B, determine (a) the acceleration of the rod, (b)
PROBLEM 16.4 The motion of the.5-kg rod AB is guided b two small wheels which roll freel in horizontal slots. If a force P of magnitude 8 N is applied at B, determine (a) the acceleration of the rod, (b)
Exercises. . Evaluate f (, ) xydawhere. 2, 1 x< 3, 0 y< (Answer: 14) 3, 3 x 4, 0 y 2. (Answer: 12) ) f x. ln 2 1 ( ) = (Answer: 1)
 Eercises Eercises. Let = {(, : 4, }. Evaluate f (,,
Eercises Eercises. Let = {(, : 4, }. Evaluate f (,,
ME 323 Examination #2
 ME 33 Eamination # SOUTION Novemer 14, 17 ROEM NO. 1 3 points ma. The cantilever eam D of the ending stiffness is sujected to a concentrated moment M at C. The eam is also supported y a roller at. Using
ME 33 Eamination # SOUTION Novemer 14, 17 ROEM NO. 1 3 points ma. The cantilever eam D of the ending stiffness is sujected to a concentrated moment M at C. The eam is also supported y a roller at. Using
Mechanical Design in Optical Engineering
 Torsion Torsion: Torsion refers to the twisting of a structural member that is loaded by couples (torque) that produce rotation about the member s longitudinal axis. In other words, the member is loaded
Torsion Torsion: Torsion refers to the twisting of a structural member that is loaded by couples (torque) that produce rotation about the member s longitudinal axis. In other words, the member is loaded
Moments and Product of Inertia
 Moments and Product of nertia Contents ntroduction( 绪论 ) Moments of nertia of an Area( 平面图形的惯性矩 ) Moments of nertia of an Area b ntegration( 积分法求惯性矩 ) Polar Moments of nertia( 极惯性矩 ) Radius of Gration
Moments and Product of nertia Contents ntroduction( 绪论 ) Moments of nertia of an Area( 平面图形的惯性矩 ) Moments of nertia of an Area b ntegration( 积分法求惯性矩 ) Polar Moments of nertia( 极惯性矩 ) Radius of Gration
Ch. 5: Distributed Forces
 234 5.0 Outline 234 Introduction 235 Center of Mass 236 Centroids (Line, Area, Volume) 241 Composite Bodies and Figures 257 Theorem of Pappus 265 Fluid Statics 272 5.0 Outline 5.0 Introduction Ch. 5: Distributed
234 5.0 Outline 234 Introduction 235 Center of Mass 236 Centroids (Line, Area, Volume) 241 Composite Bodies and Figures 257 Theorem of Pappus 265 Fluid Statics 272 5.0 Outline 5.0 Introduction Ch. 5: Distributed
APM1612. Tutorial letter 203/1/2018. Mechanics 2. Semester 1. Department of Mathematical Sciences APM1612/203/1/2018
 APM6/03//08 Tutorial letter 03//08 Mechanics APM6 Semester Department of Mathematical Sciences IMPORTANT INFORMATION: This tutorial letter contains solutions to assignment 3, Sem. BARCODE Define tomorrow.
APM6/03//08 Tutorial letter 03//08 Mechanics APM6 Semester Department of Mathematical Sciences IMPORTANT INFORMATION: This tutorial letter contains solutions to assignment 3, Sem. BARCODE Define tomorrow.
if the initial displacement and velocities are zero each. [ ] PART-B
![if the initial displacement and velocities are zero each. [ ] PART-B if the initial displacement and velocities are zero each. [ ] PART-B](/thumbs/86/94772448.jpg) Set No - 1 I. Tech II Semester Regular Examinations ugust - 2014 ENGINEERING MECHNICS (Common to ECE, EEE, EIE, io-tech, E Com.E, gri. E) Time: 3 hours Max. Marks: 70 Question Paper Consists of Part- and
Set No - 1 I. Tech II Semester Regular Examinations ugust - 2014 ENGINEERING MECHNICS (Common to ECE, EEE, EIE, io-tech, E Com.E, gri. E) Time: 3 hours Max. Marks: 70 Question Paper Consists of Part- and
MECHANICS OF MATERIALS
 CHAPTER MECHANICS OF MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Lecture Notes: J. Walt Oler Teas Tech Universit Transformations of Stress and Strain 006 The McGraw-Hill Companies,
CHAPTER MECHANICS OF MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Lecture Notes: J. Walt Oler Teas Tech Universit Transformations of Stress and Strain 006 The McGraw-Hill Companies,
Math 52 First Midterm January 29, 2009
 Math 5 First Midterm Januar 9, 9 Name : KEY Section Leader: Josh Lan Xiannan (Circle one) Genauer Huang Li Section Time: : : :5 :5 (Circle one) This is a closed-book, closed-notes eam. No calculators or
Math 5 First Midterm Januar 9, 9 Name : KEY Section Leader: Josh Lan Xiannan (Circle one) Genauer Huang Li Section Time: : : :5 :5 (Circle one) This is a closed-book, closed-notes eam. No calculators or
Exam 05: Chapters 10 and 11
 Name: Exam 05: Chapters 10 and 11 Select and solve five of the following problems to the best of your ability. You must choose two problem from each column, and a final problem at your own discretion.
Name: Exam 05: Chapters 10 and 11 Select and solve five of the following problems to the best of your ability. You must choose two problem from each column, and a final problem at your own discretion.
Add Math (4047) Paper 2
 1. Solve the simultaneous equations 5 and 1. [5]. (i) Sketch the graph of, showing the coordinates of the points where our graph meets the coordinate aes. [] Solve the equation 10, giving our answer correct
1. Solve the simultaneous equations 5 and 1. [5]. (i) Sketch the graph of, showing the coordinates of the points where our graph meets the coordinate aes. [] Solve the equation 10, giving our answer correct
STRESS. Bar. ! Stress. ! Average Normal Stress in an Axially Loaded. ! Average Shear Stress. ! Allowable Stress. ! Design of Simple Connections
 STRESS! Stress Evisdom! verage Normal Stress in an xially Loaded ar! verage Shear Stress! llowable Stress! Design of Simple onnections 1 Equilibrium of a Deformable ody ody Force w F R x w(s). D s y Support
STRESS! Stress Evisdom! verage Normal Stress in an xially Loaded ar! verage Shear Stress! llowable Stress! Design of Simple onnections 1 Equilibrium of a Deformable ody ody Force w F R x w(s). D s y Support
The region enclosed by the curve of f and the x-axis is rotated 360 about the x-axis. Find the volume of the solid formed.
 Section A ln. Let g() =, for > 0. ln Use the quotient rule to show that g ( ). 3 (b) The graph of g has a maimum point at A. Find the -coordinate of A. (Total 7 marks) 6. Let h() =. Find h (0). cos 3.
Section A ln. Let g() =, for > 0. ln Use the quotient rule to show that g ( ). 3 (b) The graph of g has a maimum point at A. Find the -coordinate of A. (Total 7 marks) 6. Let h() =. Find h (0). cos 3.
Properties of plane surfaces I: First moment and centroid of area
 Properties of plane surfaces I: First moment and centroid of area Having deal with trusses and frictional forces, we now change gears and go on to discuss some properties of surfaces mathematically. Of
Properties of plane surfaces I: First moment and centroid of area Having deal with trusses and frictional forces, we now change gears and go on to discuss some properties of surfaces mathematically. Of
(Please write your Roll No. immediately) Mid Term Examination. Regular (Feb 2017)
 (Please write your Roll No. immediately) Roll No... Mid Term Examination Regular (Feb 2017) B.Tech-II sem Sub-Engineering Mechanics Paper code- ETME-110 Time-1.5 hours Max Marks-30 Note: 1. Q.No. 1 is
(Please write your Roll No. immediately) Roll No... Mid Term Examination Regular (Feb 2017) B.Tech-II sem Sub-Engineering Mechanics Paper code- ETME-110 Time-1.5 hours Max Marks-30 Note: 1. Q.No. 1 is
Afternoon Section. Physics 1210 Exam 2 November 8, ! v = d! r dt. a avg. = v2. ) T 2! w = m g! f s. = v at v 2 1.
 Name Physics 1210 Exam 2 November 8, 2012 Afternoon Section Please write directly on the exam and attach other sheets of work if necessary. Calculators are allowed. No notes or books may be used. Multiple-choice
Name Physics 1210 Exam 2 November 8, 2012 Afternoon Section Please write directly on the exam and attach other sheets of work if necessary. Calculators are allowed. No notes or books may be used. Multiple-choice
Consider a cross section with a general shape such as shown in Figure B.2.1 with the x axis normal to the cross section. Figure B.2.1.
 ppendix B rea Properties of Cross Sections B.1 Introduction The area, the centroid of area, and the area moments of inertia of the cross sections are needed in slender bar calculations for stress and deflection.
ppendix B rea Properties of Cross Sections B.1 Introduction The area, the centroid of area, and the area moments of inertia of the cross sections are needed in slender bar calculations for stress and deflection.
SOLUTIONS TO THE FINAL EXAM. December 14, 2010, 9:00am-12:00 (3 hours)
 SOLUTIONS TO THE 18.02 FINAL EXAM BJORN POONEN December 14, 2010, 9:00am-12:00 (3 hours) 1) For each of (a)-(e) below: If the statement is true, write TRUE. If the statement is false, write FALSE. (Please
SOLUTIONS TO THE 18.02 FINAL EXAM BJORN POONEN December 14, 2010, 9:00am-12:00 (3 hours) 1) For each of (a)-(e) below: If the statement is true, write TRUE. If the statement is false, write FALSE. (Please
MECHANICS OF MATERIALS
 00 The McGraw-Hill Companies, Inc. All rights reserved. T Edition CHAPTER MECHANICS OF MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Lecture Notes: J. Walt Oler Teas Tech Universit
00 The McGraw-Hill Companies, Inc. All rights reserved. T Edition CHAPTER MECHANICS OF MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Lecture Notes: J. Walt Oler Teas Tech Universit
2015 ENGINEERING MECHANICS
 Set No - 1 I B.Tech I Semester Regular/Supple. Examinations Nov./Dec. 2015 ENGINEERING MECHANICS (Common to CE, ME, CSE, PCE, IT, Chem. E, Aero E, AME, Min E, PE, Metal E, Textile Engg.) Time: 3 hours
Set No - 1 I B.Tech I Semester Regular/Supple. Examinations Nov./Dec. 2015 ENGINEERING MECHANICS (Common to CE, ME, CSE, PCE, IT, Chem. E, Aero E, AME, Min E, PE, Metal E, Textile Engg.) Time: 3 hours
Math 175 Common Exam 2A Spring 2018
 Math 175 Common Exam 2A Spring 2018 Part I: Short Form The first seven (7) pages are short answer. You don t need to show work. Partial credit will be rare and small. 1. (8 points) Suppose f(x) is a function
Math 175 Common Exam 2A Spring 2018 Part I: Short Form The first seven (7) pages are short answer. You don t need to show work. Partial credit will be rare and small. 1. (8 points) Suppose f(x) is a function
2. a) Explain the equilibrium of i) Concurrent force system, and ii) General force system.
 Code No: R21031 R10 SET - 1 II B. Tech I Semester Supplementary Examinations Dec 2013 ENGINEERING MECHANICS (Com to ME, AE, AME, MM) Time: 3 hours Max. Marks: 75 Answer any FIVE Questions All Questions
Code No: R21031 R10 SET - 1 II B. Tech I Semester Supplementary Examinations Dec 2013 ENGINEERING MECHANICS (Com to ME, AE, AME, MM) Time: 3 hours Max. Marks: 75 Answer any FIVE Questions All Questions
ME 243. Lecture 10: Combined stresses
 ME 243 Mechanics of Solids Lecture 10: Combined stresses Ahmad Shahedi Shakil Lecturer, Dept. of Mechanical Engg, BUET E-mail: sshakil@me.buet.ac.bd, shakil6791@gmail.com Website: teacher.buet.ac.bd/sshakil
ME 243 Mechanics of Solids Lecture 10: Combined stresses Ahmad Shahedi Shakil Lecturer, Dept. of Mechanical Engg, BUET E-mail: sshakil@me.buet.ac.bd, shakil6791@gmail.com Website: teacher.buet.ac.bd/sshakil
MECHANICS OF MATERIALS REVIEW
 MCHANICS OF MATRIALS RVIW Notation: - normal stress (psi or Pa) - shear stress (psi or Pa) - normal strain (in/in or m/m) - shearing strain (in/in or m/m) I - area moment of inertia (in 4 or m 4 ) J -
MCHANICS OF MATRIALS RVIW Notation: - normal stress (psi or Pa) - shear stress (psi or Pa) - normal strain (in/in or m/m) - shearing strain (in/in or m/m) I - area moment of inertia (in 4 or m 4 ) J -
MATH 52 MIDTERM 1. April 23, 2004
 MATH 5 MIDTERM April 3, Student ID: Signature: Instructions: Print your name and student ID number and write your signature to indicate that you accept the honor code. During the test, you may not use
MATH 5 MIDTERM April 3, Student ID: Signature: Instructions: Print your name and student ID number and write your signature to indicate that you accept the honor code. During the test, you may not use
Identifying second degree equations
 Chapter 7 Identifing second degree equations 71 The eigenvalue method In this section we appl eigenvalue methods to determine the geometrical nature of the second degree equation a 2 + 2h + b 2 + 2g +
Chapter 7 Identifing second degree equations 71 The eigenvalue method In this section we appl eigenvalue methods to determine the geometrical nature of the second degree equation a 2 + 2h + b 2 + 2g +
Exam 05: Chapters 10 and 11
 Name: Exam 05: Chapters 10 and 11 Select and solve four of the following problems to the best of your ability. You must choose two problem from each column. Please notice that it is possible to select
Name: Exam 05: Chapters 10 and 11 Select and solve four of the following problems to the best of your ability. You must choose two problem from each column. Please notice that it is possible to select
Rotation. EMU Physics Department. Ali ÖVGÜN.
 Rotation Ali ÖVGÜN EMU Physics Department www.aovgun.com Rotational Motion Angular Position and Radians Angular Velocity Angular Acceleration Rigid Object under Constant Angular Acceleration Angular and
Rotation Ali ÖVGÜN EMU Physics Department www.aovgun.com Rotational Motion Angular Position and Radians Angular Velocity Angular Acceleration Rigid Object under Constant Angular Acceleration Angular and
[4] Properties of Geometry
![[4] Properties of Geometry [4] Properties of Geometry](/thumbs/91/107196493.jpg) [4] Properties of Geometr Page 1 of 6 [4] Properties of Geometr [4.1] Center of Gravit and Centroid [4.] Composite Bodies [4.3] Moments of Inertia [4.4] Composite reas and Products of Inertia [4] Properties
[4] Properties of Geometr Page 1 of 6 [4] Properties of Geometr [4.1] Center of Gravit and Centroid [4.] Composite Bodies [4.3] Moments of Inertia [4.4] Composite reas and Products of Inertia [4] Properties
(a) We split the square up into four pieces, parametrizing and integrating one a time. Right side: C 1 is parametrized by r 1 (t) = (1, t), 0 t 1.
 Thursda, November 5 Green s Theorem Green s Theorem is a 2-dimensional version of the Fundamental Theorem of alculus: it relates the (integral of) a vector field F on the boundar of a region to the integral
Thursda, November 5 Green s Theorem Green s Theorem is a 2-dimensional version of the Fundamental Theorem of alculus: it relates the (integral of) a vector field F on the boundar of a region to the integral
EMA 3702 Mechanics & Materials Science (Mechanics of Materials) Chapter 4 Pure Bending
 EA 3702 echanics & aterials Science (echanics of aterials) Chapter 4 Pure Bending Pure Bending Ch 2 Aial Loading & Parallel Loading: uniform normal stress and shearing stress distribution Ch 3 Torsion:
EA 3702 echanics & aterials Science (echanics of aterials) Chapter 4 Pure Bending Pure Bending Ch 2 Aial Loading & Parallel Loading: uniform normal stress and shearing stress distribution Ch 3 Torsion:
Tuesday, February 11, Chapter 3. Load and Stress Analysis. Dr. Mohammad Suliman Abuhaiba, PE
 1 Chapter 3 Load and Stress Analysis 2 Chapter Outline Equilibrium & Free-Body Diagrams Shear Force and Bending Moments in Beams Singularity Functions Stress Cartesian Stress Components Mohr s Circle for
1 Chapter 3 Load and Stress Analysis 2 Chapter Outline Equilibrium & Free-Body Diagrams Shear Force and Bending Moments in Beams Singularity Functions Stress Cartesian Stress Components Mohr s Circle for
MATH141: Calculus II Exam #1 review 6/8/2017 Page 1
 MATH: Calculus II Eam # review /8/7 Page No review sheet can cover everything that is potentially fair game for an eam, but I tried to hit on all of the topics with these questions, as well as show you
MATH: Calculus II Eam # review /8/7 Page No review sheet can cover everything that is potentially fair game for an eam, but I tried to hit on all of the topics with these questions, as well as show you
PHYS 211 Lecture 21 - Moments of inertia 21-1
 PHYS 211 Lecture 21 - Moments of inertia 21-1 Lecture 21 - Moments of inertia Text: similar to Fowles and Cassiday, Chap. 8 As discussed previously, the moment of inertia I f a single mass m executing
PHYS 211 Lecture 21 - Moments of inertia 21-1 Lecture 21 - Moments of inertia Text: similar to Fowles and Cassiday, Chap. 8 As discussed previously, the moment of inertia I f a single mass m executing
MATRIX TRANSFORMATIONS
 CHAPTER 5. MATRIX TRANSFORMATIONS INSTITIÚID TEICNEOLAÍOCHTA CHEATHARLACH INSTITUTE OF TECHNOLOGY CARLOW MATRIX TRANSFORMATIONS Matri Transformations Definition Let A and B be sets. A function f : A B
CHAPTER 5. MATRIX TRANSFORMATIONS INSTITIÚID TEICNEOLAÍOCHTA CHEATHARLACH INSTITUTE OF TECHNOLOGY CARLOW MATRIX TRANSFORMATIONS Matri Transformations Definition Let A and B be sets. A function f : A B
