SOLUTION Determine the moment of inertia for the shaded area about the x axis. I x = y 2 da = 2 y 2 (xdy) = 2 y y dy
|
|
|
- Millicent Shaw
- 5 years ago
- Views:
Transcription
1 5. Determine the moment of inertia for the shaded area about the ais. 4 4m 4 4 I = da = (d) 4 = 4 - d I = B (5 + (4)() + 8(4) ) (4 - ) R m m I = 39. m 4
2 6. Determine the moment of inertia for the shaded area about the ais. 4 4m I = da = (4 - ) d A m m = B R I = 8.53 m 4
3 7. Determine the moment of inertia for the shaded area about the ais. m m.5 m di = d ()3 I = di = 3 ( -.5 )3> d = 3 B 5(-.5) ( -.5)5> R =.533 m 4 Also, da = d = ( - ) d I = da = ( - ) d - = B R - =.533 m 4
4 * 8. Determine the moment of inertia for the shaded area about the ais. m m.5 m da = d I = da = ( -.5) / d = B (8 - (-.5) + 5(-.5) )( -.5) 3 5(-.5) 3 R =.4 4 Also, I = di = 3 3 d 8 = 3 ( - ) 3 d = a 8 3 b B R =.4 4
5 9. Determine the moment of inertia of the shaded area about the ais. Here, the area must be divided into two segments as shown in Fig. a. The moment of inertia of segment () about the ais can be determined using (I ) = while the moment of inertia of segment () about the ais bh3 + A h, can be determined b appling Eq.. The area of the rectangular differential element in Fig. a is da = ( - )d. Here, = 4. Thus, da = 4. - d m 4 m Appling Eq. to segment () about the ais (I ) = da = 4 A m - d = m a4 - bd = ` m = 9 m 4 The moment of inertia of segment () about the ais is (I ) = (3)(3 ) + (3)()(.5 ) = m 4 Thus, I = (I ) + (I ) = 9 + = m 4 The area of the rectangular differential element in Fig. b is da = d. The moment inertia of this element about the ais is di = di + da '. Here,. Thus, di = = = 4 d = 64 d3 + d = 3 3 d 3 3d Performing the integration, we have 64 3 I = dl = d = 3 - m 3 3 ` m = m 4
6 *. Determine the moment of inertia of the shaded area about the ais. The area of the rectangular differential element in Fig. a is da = d. Here, = 4. 4 Thus, da = 4. d Appling Eq., I = da = a 4 A m bd = 4 d = a b ` = 3 m 4 m m Here, the area must be divided into two segments as shown in Fig. b. The moment of inertia of segment () about the ais can be determined using (I ) =, while the moment of inertia of segment () about the bh3 + A h ais can be determined b computing the moment of inertia of the element parallel to the ais shown in Fig. b. The area of this element is da = ( - ) d and its moment of inertia about the ais is m m di = di + da ' = (d)( - )3 + ( - )db ( + )R = a d Here, = 4. Thus, dl = B Rd = d Performing the integration, the moment of inertia of segment () about the ais is (I ) = di = m d = ` = 9 m 4 m The moment of inertia of segment () about the ais is Thus, (I ) = ()(33 ) + ()(3)(.5 ) = m 4 I = (I ) + (I ) = 9 + = 3 m 4
7 46. Determine the distance to the centroid of the beam s cross-sectional area; then determine the moment of inertia about the ais. _ 5 mm 5 mm 75 mm 75 mm 5 mm mm C 5 mm mm 5 mm Centroid: The area of each segment and its respective centroid are tabulated below. 5 mm Segment A (mm ) (mm) A(mm 3 ) 5() ( 3 ) 35(5).5 l.565( 3 ) 3 5() 5 5( 3 ) 5.65( 3 ) ( 3 ) Thus, = A A = (3 ) 5.65( 3 =.5 mm ) Moment of Inertia: The moment of inertia about the ais for each segment can be determined using the parallel-ais theorem I + I + Ad. Segment A Ad AI AAd B AI B i (mm 4 i (mm 4 B i (mm 4 i (mm ) B i (mm) ) ) ) Thus, 5() 5.5 (5) (3 ) 3.78( 6 ) 7.948( 6 ) 35(5) (35) (53 ).85( 6 ).36( 6 ) 3 5() 7.5 (5) (3 ) 3.4( 6 ) 5.4( 6 ) I = (I ) i = 34.4A 6 B mm 4 = 34.4A 6 B mm 4
8 47. Determine the moment of inertia of the beam s crosssectional area about the ais. 5 mm 5 mm _ 5 mm 75 mm 75 mm 5 mm mm C mm 5 mm 5 mm Moment of Inertia: The moment of inertia about the ais for each segment can be determined using the parallel-ais theorem I = I + Ad. Segment A i (mm ) [(5)] Ad B i (mm) AI B i (mm 4 ) C () (53 )D AAd B i (mm 4 ) 5.( 6 ) AI B i (mm 4 ) 5.6( 6 ) Thus, 5(35) (5) (353 ) 7.57( 6 ) 3 (5) () (53 ).3( 6 ) I = (I ) i =.9A 6 B mm 4 = A 6 B mm 4
9 63. Determine the product of inertia for the beam s crosssectional area with respect to the u and v aes. 5 mm v 5 mm u Moments of inertia I and I I = (3)(4)3 - (8)(36)3 = 5.36() 6 mm 4 mm C mm mm I = c ()(3)3 d + (36)()3 = 9.4() 6 mm 4 The section is smmetric about both and aes; therefore I =. I uv = I - I sin u + I cos u = a sin 4 + cos 4 b 6 = 35() 6 mm 4
10 * 64. Determine the moments of inertia for the shaded area with respect to the u and v aes. v.5 in. u Moment and Product of Inertia about and Aes: Since the shaded area is smmetrical about the ais, I =. 5in. 3.5 in..5 in. I = ()(53 ) + (4)(3 ) =.75 in 4 I = ()(43 )+(4)(.5) + (5)(3 ) = 3.75 in 4 Moment of Inertia about the Inclined u and v Aes: Appling Eq. -9 with u = 3, we have in. 4in. I u = I + I + I - I cos u - I sin u = cos 6 - (sin 6 ) = 5.75 in 4 I v = I + I - I - I cos u + I sin u = cos 6 + (sin 6 ) = 5.75 in 4
11 74. Determine the principal moments of inertia for the beam s cross-sectional area about the principal aes that have their origin located at the centroid C. Use the equations developed in Section.7. For the calculation, assume all corners to be square. 3 8 in. 4in. 3 8 in. C 4in. I = c (4)a 3 8 b 3 + 4a 3 8 ba4-3 6 b d + a 3 8 ba8-6 8 b 3 4in. = in 4 I = c a 3 8 ba4-3 8 b 3 + (8)a 3 8 b a4-3 8 bea4-3 8 b f d 4in. = 3.89 in 4 I = A = -[( )(3.83)(3.65)(.375)] + = -.73 in 4 I ma>min = I + I ; a I - I b + I C = ; C a b + (-.73) I ma = 64. in 4 I min = 5.33 in 4
12 75. Solve Prob. 74 using Mohr s circle. 4in. 3 8 in. 3 8 in. C 4 in. I = c (4)a 3 8 b 3 + 4a 3 8 ba4-3 6 b d + a 3 8 ba8-6 8 b 3 = in 4 4 in. I = c a 3 8 ba4-3 8 b a4-3 8 bea4-3 8 b f d 4in. + (8)a 3 8 b 3 = 3.89 in 4 I = A = -[( )(3.83)(3.65)(.375)] + = -.73 in 4 Center of circle: I + I = 34.7 in 4 R = ( ) + (-.73) = 9.39 in 4 I ma = = 64. in 4 I min = = 5.33 in 4
13 6. The thin plate has a mass per unit area of kg>m. Determine its mass moment of inertia about the ais. z mm mm mm Composite Parts: The thin plate can be subdivided into segments as shown in Fig. a. Since the segments labeled () are both holes, the should be considered as negative parts. Mass moment of Inertia: The mass of segments () and () are m and m = p(. =.4(.4)() =.6 kg )() =.p kg. The perpendicular distances measured from the centroid of each segment to the ais are indicated in Fig. a. The mass moment of inertia of each segment about the ais can be determined using the parallel-ais theorem. I = AI B G + md = c (.6)(.4 ) +.6(. ) d - c 4 (.p)(. ) +.p(. ) d mm mm mm mm mm mm mm =.44 kg # m
14 7. The thin plate has a mass per unit area of kg>m. Determine its mass moment of inertia about the z ais. z mm mm mm Composite Parts: The thin plate can be subdivided into four segments as shown in Fig. a. Since segments (3) and (4) are both holes, the should be considered as negative parts. Mass moment of Inertia: Here, the mass for segments (), (), (3), and (4) are m and m 3 = m 4 = p(. = m =.4(.4)() =.6 kg )() =.p kg. The mass moment of inertia of each segment about the z ais can be determined using the parallel-ais theorem. I z = AI z B G + md mm mm mm mm mm mm mm = (.6)(.4 ) + c (.6)( ) +.6(. ) d - 4 (.p)(. ) - c (.p)(. ) +.p(. ) d =.3 kg # m
10 3. Determine the moment of inertia of the area about the x axis.
 10 3. Determine the moment of inertia of the area about the ais. m m 10 4. Determine the moment of inertia of the area about the ais. m m 10 3. Determine the moment of inertia of the shaded area about
10 3. Determine the moment of inertia of the area about the ais. m m 10 4. Determine the moment of inertia of the area about the ais. m m 10 3. Determine the moment of inertia of the shaded area about
ME 141. Lecture 8: Moment of Inertia
 ME 4 Engineering Mechanics Lecture 8: Moment of nertia Ahmad Shahedi Shakil Lecturer, Dept. of Mechanical Engg, BUET E-mail: sshakil@me.buet.ac.bd, shakil679@gmail.com Website: teacher.buet.ac.bd/sshakil
ME 4 Engineering Mechanics Lecture 8: Moment of nertia Ahmad Shahedi Shakil Lecturer, Dept. of Mechanical Engg, BUET E-mail: sshakil@me.buet.ac.bd, shakil679@gmail.com Website: teacher.buet.ac.bd/sshakil
ME 101: Engineering Mechanics
 ME 0: Engineering Mechanics Rajib Kumar Bhattacharja Department of Civil Engineering ndian nstitute of Technolog Guwahati M Block : Room No 005 : Tel: 8 www.iitg.ernet.in/rkbc Area Moments of nertia Parallel
ME 0: Engineering Mechanics Rajib Kumar Bhattacharja Department of Civil Engineering ndian nstitute of Technolog Guwahati M Block : Room No 005 : Tel: 8 www.iitg.ernet.in/rkbc Area Moments of nertia Parallel
Distributed Forces: Moments of Inertia
 Distributed Forces: Moments of nertia Contents ntroduction Moments of nertia of an Area Moments of nertia of an Area b ntegration Polar Moments of nertia Radius of Gration of an Area Sample Problems Parallel
Distributed Forces: Moments of nertia Contents ntroduction Moments of nertia of an Area Moments of nertia of an Area b ntegration Polar Moments of nertia Radius of Gration of an Area Sample Problems Parallel
STATICS. Moments of Inertia VECTOR MECHANICS FOR ENGINEERS: Ninth Edition CHAPTER. Ferdinand P. Beer E. Russell Johnston, Jr.
 N E 9 Distributed CHAPTER VECTOR MECHANCS FOR ENGNEERS: STATCS Ferdinand P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Walt Oler Teas Tech Universit Forces: Moments of nertia Contents ntroduction
N E 9 Distributed CHAPTER VECTOR MECHANCS FOR ENGNEERS: STATCS Ferdinand P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Walt Oler Teas Tech Universit Forces: Moments of nertia Contents ntroduction
STATICS. Moments of Inertia VECTOR MECHANICS FOR ENGINEERS: Seventh Edition CHAPTER. Ferdinand P. Beer
 00 The McGraw-Hill Companies, nc. All rights reserved. Seventh E CHAPTER VECTOR MECHANCS FOR ENGNEERS: 9 STATCS Ferdinand P. Beer E. Russell Johnston, Jr. Distributed Forces: Lecture Notes: J. Walt Oler
00 The McGraw-Hill Companies, nc. All rights reserved. Seventh E CHAPTER VECTOR MECHANCS FOR ENGNEERS: 9 STATCS Ferdinand P. Beer E. Russell Johnston, Jr. Distributed Forces: Lecture Notes: J. Walt Oler
SOLUTION y ' A = 7.5(15) (150) + 90(150) (15) + 215(p)(50) 2. = mm 2. A = 15(150) + 150(15) + p(50) 2. =
 9 58. Determine the location of the centroidal ais - of the beam s cross-sectional area. Neglect the size of the corner welds at A and B for the calculation. 15 mm 15 mm B 15 mm 15 mm A = 7.5(15) (15)
9 58. Determine the location of the centroidal ais - of the beam s cross-sectional area. Neglect the size of the corner welds at A and B for the calculation. 15 mm 15 mm B 15 mm 15 mm A = 7.5(15) (15)
Second Moments or Moments of Inertia
 Second Moments or Moments of Inertia The second moment of inertia of an element of area such as da in Figure 1 with respect to any axis is defined as the product of the area of the element and the square
Second Moments or Moments of Inertia The second moment of inertia of an element of area such as da in Figure 1 with respect to any axis is defined as the product of the area of the element and the square
Determine the moment of inertia of the area about the x axis Determine the moment of inertia of the area about the y axis.
 10 Solutions 44918 1/28/09 4:21 PM Page 941 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copright laws as the currentl eist. No portion
10 Solutions 44918 1/28/09 4:21 PM Page 941 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copright laws as the currentl eist. No portion
Chapter 5 Equilibrium of a Rigid Body Objectives
 Chapter 5 Equilibrium of a Rigid Bod Objectives Develop the equations of equilibrium for a rigid bod Concept of the free-bod diagram for a rigid bod Solve rigid-bod equilibrium problems using the equations
Chapter 5 Equilibrium of a Rigid Bod Objectives Develop the equations of equilibrium for a rigid bod Concept of the free-bod diagram for a rigid bod Solve rigid-bod equilibrium problems using the equations
Statics: Lecture Notes for Sections 10.1,10.2,10.3 1
 Chapter 10 MOMENTS of INERTIA for AREAS, RADIUS OF GYRATION Today s Objectives: Students will be able to: a) Define the moments of inertia (MoI) for an area. b) Determine the MoI for an area by integration.
Chapter 10 MOMENTS of INERTIA for AREAS, RADIUS OF GYRATION Today s Objectives: Students will be able to: a) Define the moments of inertia (MoI) for an area. b) Determine the MoI for an area by integration.
3/31/ Product of Inertia. Sample Problem Sample Problem 10.6 (continue)
 /1/01 10.6 Product of Inertia Product of Inertia: I xy = xy da When the x axis, the y axis, or both are an axis of symmetry, the product of inertia is zero. Parallel axis theorem for products of inertia:
/1/01 10.6 Product of Inertia Product of Inertia: I xy = xy da When the x axis, the y axis, or both are an axis of symmetry, the product of inertia is zero. Parallel axis theorem for products of inertia:
h p://edugen.wileyplus.com/edugen/courses/crs1404/pc/b03/c2hlch...
 n this appendix we discuss... 1 of 4 16-Sep-12 19:35 APPENDIX C In this appendix we discuss how to calculate the moment of inertia of an area. 1 The moment of inertia of an area was first introduced in
n this appendix we discuss... 1 of 4 16-Sep-12 19:35 APPENDIX C In this appendix we discuss how to calculate the moment of inertia of an area. 1 The moment of inertia of an area was first introduced in
PROBLEM Area of Problem I = 471,040 mm xy 2(471,040) 252,757 1,752,789 = or θ m = and = (1,002,773 ± 885,665) mm
 PROBLEM 9.88 F the area indicated, determine the ientation of the principal aes at the igin the cresponding values of the moments of inertia. Area of Problem 9.75. From Problem 9.8: Problem 9.75: = 5,757
PROBLEM 9.88 F the area indicated, determine the ientation of the principal aes at the igin the cresponding values of the moments of inertia. Area of Problem 9.75. From Problem 9.8: Problem 9.75: = 5,757
ENGI 4430 Multiple Integration Cartesian Double Integrals Page 3-01
 ENGI 4430 Multiple Integration Cartesian Double Integrals Page 3-01 3. Multiple Integration This chapter provides only a very brief introduction to the major topic of multiple integration. Uses of multiple
ENGI 4430 Multiple Integration Cartesian Double Integrals Page 3-01 3. Multiple Integration This chapter provides only a very brief introduction to the major topic of multiple integration. Uses of multiple
Chapter 10: Moments of Inertia
 Chapter 10: Moments of Inertia Chapter Objectives To develop a method for determining the moment of inertia and product of inertia for an area with respect to given x- and y-axes. To develop a method for
Chapter 10: Moments of Inertia Chapter Objectives To develop a method for determining the moment of inertia and product of inertia for an area with respect to given x- and y-axes. To develop a method for
SOLUTION di x = y2 dm. rdv. m = a 2 bdx. = 2 3 rpab2. I x = 1 2 rp L0. b 4 a1 - x2 a 2 b. = 4 15 rpab4. Thus, I x = 2 5 mb2. Ans.
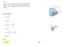 17 4. Determine the moment of inertia of the semiellipsoid with respect to the x axis and express the result in terms of the mass m of the semiellipsoid. The material has a constant density r. y x y a
17 4. Determine the moment of inertia of the semiellipsoid with respect to the x axis and express the result in terms of the mass m of the semiellipsoid. The material has a constant density r. y x y a
Bending Stress. Sign convention. Centroid of an area
 Bending Stress Sign convention The positive shear force and bending moments are as shown in the figure. Centroid of an area Figure 40: Sign convention followed. If the area can be divided into n parts
Bending Stress Sign convention The positive shear force and bending moments are as shown in the figure. Centroid of an area Figure 40: Sign convention followed. If the area can be divided into n parts
MAHALAKSHMI ENGINEERING COLLEGE TIRUCHIRAPPALLI Distinguish between centroid and centre of gravity. (AU DEC 09,DEC 12)
 MAHALAKSHMI ENGINEERING COLLEGE TIRUCHIRAPPALLI 621213 Sub Code: GE 6253 Semester: II Subject: ENGINEERING MECHANICS Unit III: PROPERTIES OF SURFACES AND SOLIDS PART A 1. Distinguish between centroid and
MAHALAKSHMI ENGINEERING COLLEGE TIRUCHIRAPPALLI 621213 Sub Code: GE 6253 Semester: II Subject: ENGINEERING MECHANICS Unit III: PROPERTIES OF SURFACES AND SOLIDS PART A 1. Distinguish between centroid and
AREAS, RADIUS OF GYRATION
 Chapter 10 MOMENTS of INERTIA for AREAS, RADIUS OF GYRATION Today s Objectives: Students will be able to: a) Define the moments of inertia (MoI) for an area. b) Determine the MoI for an area by integration.
Chapter 10 MOMENTS of INERTIA for AREAS, RADIUS OF GYRATION Today s Objectives: Students will be able to: a) Define the moments of inertia (MoI) for an area. b) Determine the MoI for an area by integration.
Moments of Inertia. Notation:
 RCH 1 Note Set 9. S015abn Moments of nertia Notation: b d d d h c Jo O = name for area = name for a (base) width = calculus smbol for differentiation = name for a difference = name for a depth = difference
RCH 1 Note Set 9. S015abn Moments of nertia Notation: b d d d h c Jo O = name for area = name for a (base) width = calculus smbol for differentiation = name for a difference = name for a depth = difference
Consider a cross section with a general shape such as shown in Figure B.2.1 with the x axis normal to the cross section. Figure B.2.1.
 ppendix B rea Properties of Cross Sections B.1 Introduction The area, the centroid of area, and the area moments of inertia of the cross sections are needed in slender bar calculations for stress and deflection.
ppendix B rea Properties of Cross Sections B.1 Introduction The area, the centroid of area, and the area moments of inertia of the cross sections are needed in slender bar calculations for stress and deflection.
Hong Kong Institute of Vocational Education (Tsing Yi) Higher Diploma in Civil Engineering Structural Mechanics. Chapter 2 SECTION PROPERTIES
 Section Properties Centroid The centroid of an area is the point about which the area could be balanced if it was supported from that point. The word is derived from the word center, and it can be though
Section Properties Centroid The centroid of an area is the point about which the area could be balanced if it was supported from that point. The word is derived from the word center, and it can be though
Properties of surfaces II: Second moment of area
 Properties of surfaces II: Second moment of area Just as we have discussing first moment of an area and its relation with problems in mechanics, we will now describe second moment and product of area of
Properties of surfaces II: Second moment of area Just as we have discussing first moment of an area and its relation with problems in mechanics, we will now describe second moment and product of area of
ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 3 Solutions [Multiple Integration; Lines of Force]
![ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 3 Solutions [Multiple Integration; Lines of Force] ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 3 Solutions [Multiple Integration; Lines of Force]](/thumbs/84/89723886.jpg) ENGI 44 Advanced Calculus for Engineering Facult of Engineering and Applied Science Problem Set Solutions [Multiple Integration; Lines of Force]. Evaluate D da over the triangular region D that is bounded
ENGI 44 Advanced Calculus for Engineering Facult of Engineering and Applied Science Problem Set Solutions [Multiple Integration; Lines of Force]. Evaluate D da over the triangular region D that is bounded
Statics: Lecture Notes for Sections
 0.5 MOMENT OF INERTIA FOR A COMPOSITE AREA A composite area is made by adding or subtracting a series of simple shaped areas like rectangles, triangles, and circles. For example, the area on the left can
0.5 MOMENT OF INERTIA FOR A COMPOSITE AREA A composite area is made by adding or subtracting a series of simple shaped areas like rectangles, triangles, and circles. For example, the area on the left can
Chapter 9 Moment of Inertia
 Chapter 9 Moment of Inertia Dr. Khairul Salleh Basaruddin Applied Mechanics Division School of Mechatronic Engineering Universiti Malaysia Perlis (UniMAP) khsalleh@unimap.edu.my PARALLEL-AXIS THEOREM,
Chapter 9 Moment of Inertia Dr. Khairul Salleh Basaruddin Applied Mechanics Division School of Mechatronic Engineering Universiti Malaysia Perlis (UniMAP) khsalleh@unimap.edu.my PARALLEL-AXIS THEOREM,
STATICS. Distributed Forces: Moments of Inertia VECTOR MECHANICS FOR ENGINEERS: Eighth Edition CHAPTER. Ferdinand P. Beer E. Russell Johnston, Jr.
 007 The McGraw-Hill Companies, nc. All rights reserved. Eighth E CHAPTER 9 VECTOR MECHANCS FOR ENGNEERS: STATCS Ferdinand P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Walt Oler Texas Tech University
007 The McGraw-Hill Companies, nc. All rights reserved. Eighth E CHAPTER 9 VECTOR MECHANCS FOR ENGNEERS: STATCS Ferdinand P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Walt Oler Texas Tech University
10.5 MOMENT OF INERTIA FOR A COMPOSITE AREA
 10.5 MOMENT OF NERTA FOR A COMPOSTE AREA A composite area is made by adding or subtracting a series of simple shaped areas like rectangles, triangles, and circles. For example, the area on the left can
10.5 MOMENT OF NERTA FOR A COMPOSTE AREA A composite area is made by adding or subtracting a series of simple shaped areas like rectangles, triangles, and circles. For example, the area on the left can
Chapter 5. Distributed Forces: Centroids and Centers of Gravity
 Chapter 5 Distributed Forces: Centroids and Centers of Gravity Application There are many examples in engineering analysis of distributed loads. It is convenient in some cases to represent such loads as
Chapter 5 Distributed Forces: Centroids and Centers of Gravity Application There are many examples in engineering analysis of distributed loads. It is convenient in some cases to represent such loads as
MOI (SEM. II) EXAMINATION.
 Problems Based On Centroid And MOI (SEM. II) EXAMINATION. 2006-07 1- Find the centroid of a uniform wire bent in form of a quadrant of the arc of a circle of radius R. 2- State the parallel axis theorem.
Problems Based On Centroid And MOI (SEM. II) EXAMINATION. 2006-07 1- Find the centroid of a uniform wire bent in form of a quadrant of the arc of a circle of radius R. 2- State the parallel axis theorem.
I xx + I yy + I zz = (y 2 + z 2 )dm + (x 2 + y 2 )dm. (x 2 + z 2 )dm + (x 2 + y 2 + z 2 )dm = 2
 9196_1_s1_p095-0987 6/8/09 1:09 PM Page 95 010 Pearson Education, Inc., Upper Saddle River, NJ. ll rights reserved. This material is protected under all copright laws as the currentl 1 1. Show that the
9196_1_s1_p095-0987 6/8/09 1:09 PM Page 95 010 Pearson Education, Inc., Upper Saddle River, NJ. ll rights reserved. This material is protected under all copright laws as the currentl 1 1. Show that the
and F NAME: ME rd Sample Final Exam PROBLEM 1 (25 points) Prob. 1 questions are all or nothing. PROBLEM 1A. (5 points)
 ME 270 3 rd Sample inal Exam PROBLEM 1 (25 points) Prob. 1 questions are all or nothing. PROBLEM 1A. (5 points) IND: In your own words, please state Newton s Laws: 1 st Law = 2 nd Law = 3 rd Law = PROBLEM
ME 270 3 rd Sample inal Exam PROBLEM 1 (25 points) Prob. 1 questions are all or nothing. PROBLEM 1A. (5 points) IND: In your own words, please state Newton s Laws: 1 st Law = 2 nd Law = 3 rd Law = PROBLEM
2. Supports which resist forces in two directions. Fig Hinge. Rough Surface. Fig Rocker. Roller. Frictionless Surface
 4. Structural Equilibrium 4.1 ntroduction n statics, it becomes convenient to ignore the small deformation and displacement. We pretend that the materials used are rigid, having the propert or infinite
4. Structural Equilibrium 4.1 ntroduction n statics, it becomes convenient to ignore the small deformation and displacement. We pretend that the materials used are rigid, having the propert or infinite
DEFINITION OF MOMENTS OF INERTIA FOR AREAS, RADIUS OF GYRATION OF AN AREA
 DEFINITION OF MOMENTS OF INERTIA FOR AREAS, RADIUS OF GYRATION OF AN AREA Today s Objectives: Students will be able to: a) Define the moments of inertia (MoI) for an area. b) Determine the moment of inertia
DEFINITION OF MOMENTS OF INERTIA FOR AREAS, RADIUS OF GYRATION OF AN AREA Today s Objectives: Students will be able to: a) Define the moments of inertia (MoI) for an area. b) Determine the moment of inertia
Chapter Objectives. Copyright 2011 Pearson Education South Asia Pte Ltd
 Chapter Objectives To generalize the procedure by formulating equations that can be plotted so that they describe the internal shear and moment throughout a member. To use the relations between distributed
Chapter Objectives To generalize the procedure by formulating equations that can be plotted so that they describe the internal shear and moment throughout a member. To use the relations between distributed
ENGR-1100 Introduction to Engineering Analysis. Lecture 17
 ENGR-1100 Introduction to Engineering Analysis Lecture 17 CENTROID OF COMPOSITE AREAS Today s Objective : Students will: a) Understand the concept of centroid. b) Be able to determine the location of the
ENGR-1100 Introduction to Engineering Analysis Lecture 17 CENTROID OF COMPOSITE AREAS Today s Objective : Students will: a) Understand the concept of centroid. b) Be able to determine the location of the
Moment of Inertia and Centroid
 Chapter- Moment of nertia and Centroid Page- 1. Moment of nertia and Centroid Theory at a Glance (for ES, GATE, PSU).1 Centre of gravity: The centre of gravity of a body defined as the point through which
Chapter- Moment of nertia and Centroid Page- 1. Moment of nertia and Centroid Theory at a Glance (for ES, GATE, PSU).1 Centre of gravity: The centre of gravity of a body defined as the point through which
ME 201 Engineering Mechanics: Statics
 ME 0 Engineering Mechanics: Statics Unit 9. Moments of nertia Definition of Moments of nertia for Areas Parallel-Axis Theorem for an Area Radius of Gyration of an Area Moments of nertia for Composite Areas
ME 0 Engineering Mechanics: Statics Unit 9. Moments of nertia Definition of Moments of nertia for Areas Parallel-Axis Theorem for an Area Radius of Gyration of an Area Moments of nertia for Composite Areas
University of Pretoria Department of Mechanical & Aeronautical Engineering MOW 227, 2 nd Semester 2014
 Universit of Pretoria Department of Mechanical & Aeronautical Engineering MOW 7, nd Semester 04 Semester Test Date: August, 04 Total: 00 Internal eaminer: Duration: hours Mr. Riaan Meeser Instructions:
Universit of Pretoria Department of Mechanical & Aeronautical Engineering MOW 7, nd Semester 04 Semester Test Date: August, 04 Total: 00 Internal eaminer: Duration: hours Mr. Riaan Meeser Instructions:
Lecture 6: Distributed Forces Part 2 Second Moment of Area
 Lecture 6: Distributed Forces Part Second Moment of rea The second moment of area is also sometimes called the. This quantit takes the form of The phsical representation of the above integral can be described
Lecture 6: Distributed Forces Part Second Moment of rea The second moment of area is also sometimes called the. This quantit takes the form of The phsical representation of the above integral can be described
Mechanics of Solids notes
 Mechanics of Solids notes 1 UNIT II Pure Bending Loading restrictions: As we are aware of the fact internal reactions developed on any cross-section of a beam may consists of a resultant normal force,
Mechanics of Solids notes 1 UNIT II Pure Bending Loading restrictions: As we are aware of the fact internal reactions developed on any cross-section of a beam may consists of a resultant normal force,
Moments and Product of Inertia
 Moments and Product of nertia Contents ntroduction( 绪论 ) Moments of nertia of an Area( 平面图形的惯性矩 ) Moments of nertia of an Area b ntegration( 积分法求惯性矩 ) Polar Moments of nertia( 极惯性矩 ) Radius of Gration
Moments and Product of nertia Contents ntroduction( 绪论 ) Moments of nertia of an Area( 平面图形的惯性矩 ) Moments of nertia of an Area b ntegration( 积分法求惯性矩 ) Polar Moments of nertia( 极惯性矩 ) Radius of Gration
EMA 3702 Mechanics & Materials Science (Mechanics of Materials) Chapter 4 Pure Bending
 EA 3702 echanics & aterials Science (echanics of aterials) Chapter 4 Pure Bending Pure Bending Ch 2 Aial Loading & Parallel Loading: uniform normal stress and shearing stress distribution Ch 3 Torsion:
EA 3702 echanics & aterials Science (echanics of aterials) Chapter 4 Pure Bending Pure Bending Ch 2 Aial Loading & Parallel Loading: uniform normal stress and shearing stress distribution Ch 3 Torsion:
Stress and Strain ( , 3.14) MAE 316 Strength of Mechanical Components NC State University Department of Mechanical & Aerospace Engineering
 (3.8-3.1, 3.14) MAE 316 Strength of Mechanical Components NC State Universit Department of Mechanical & Aerospace Engineering 1 Introduction MAE 316 is a continuation of MAE 314 (solid mechanics) Review
(3.8-3.1, 3.14) MAE 316 Strength of Mechanical Components NC State Universit Department of Mechanical & Aerospace Engineering 1 Introduction MAE 316 is a continuation of MAE 314 (solid mechanics) Review
Vectors. Paper 1 Section A. Each correct answer in this section is worth two marks. 4. The point B has coordinates
 PSf Vectors Paper Section A Each correct answer in this section is worth two marks.. A vector v is given b 2. 6 What is the length, in units, of v? A. 7 B. 5. 2 D. 49 4. The point B has coordinates (,
PSf Vectors Paper Section A Each correct answer in this section is worth two marks.. A vector v is given b 2. 6 What is the length, in units, of v? A. 7 B. 5. 2 D. 49 4. The point B has coordinates (,
- Beams are structural member supporting lateral loadings, i.e., these applied perpendicular to the axes.
 4. Shear and Moment functions - Beams are structural member supporting lateral loadings, i.e., these applied perpendicular to the aes. - The design of such members requires a detailed knowledge of the
4. Shear and Moment functions - Beams are structural member supporting lateral loadings, i.e., these applied perpendicular to the aes. - The design of such members requires a detailed knowledge of the
ENGI Multiple Integration Page 8-01
 ENGI 345 8. Multiple Integration Page 8-01 8. Multiple Integration This chapter provides only a very brief introduction to the major topic of multiple integration. Uses of multiple integration include
ENGI 345 8. Multiple Integration Page 8-01 8. Multiple Integration This chapter provides only a very brief introduction to the major topic of multiple integration. Uses of multiple integration include
Chapter 6: Cross-Sectional Properties of Structural Members
 Chapter 6: Cross-Sectional Properties of Structural Members Introduction Beam design requires the knowledge of the following. Material strengths (allowable stresses) Critical shear and moment values Cross
Chapter 6: Cross-Sectional Properties of Structural Members Introduction Beam design requires the knowledge of the following. Material strengths (allowable stresses) Critical shear and moment values Cross
Questions from all units
 Questions from all units S.NO 1. 1 UNT NO QUESTON Explain the concept of force and its characteristics. BLOOMS LEVEL LEVEL 2. 2 Explain different types of force systems with examples. Determine the magnitude
Questions from all units S.NO 1. 1 UNT NO QUESTON Explain the concept of force and its characteristics. BLOOMS LEVEL LEVEL 2. 2 Explain different types of force systems with examples. Determine the magnitude
[4] Properties of Geometry
![[4] Properties of Geometry [4] Properties of Geometry](/thumbs/91/107196493.jpg) [4] Properties of Geometr Page 1 of 6 [4] Properties of Geometr [4.1] Center of Gravit and Centroid [4.] Composite Bodies [4.3] Moments of Inertia [4.4] Composite reas and Products of Inertia [4] Properties
[4] Properties of Geometr Page 1 of 6 [4] Properties of Geometr [4.1] Center of Gravit and Centroid [4.] Composite Bodies [4.3] Moments of Inertia [4.4] Composite reas and Products of Inertia [4] Properties
Chapter 8 BIAXIAL BENDING
 Chapter 8 BAXAL BENDN 8.1 DEFNTON A cross section is subjected to biaial (oblique) bending if the normal (direct) stresses from section are reduced to two bending moments and. enerall oblique bending is
Chapter 8 BAXAL BENDN 8.1 DEFNTON A cross section is subjected to biaial (oblique) bending if the normal (direct) stresses from section are reduced to two bending moments and. enerall oblique bending is
Problem 4. = 1 1 = 1. = m 4. = m 4
 Problem. (a) Calculate the stress in the bolt that connects steel plates and the wooden block as shown if the section is subjected to V kn. ssume the elastic moduli of steel as GPa and of wood as 1.5 GPa.
Problem. (a) Calculate the stress in the bolt that connects steel plates and the wooden block as shown if the section is subjected to V kn. ssume the elastic moduli of steel as GPa and of wood as 1.5 GPa.
Add Math (4047) Paper 2
 1. Solve the simultaneous equations 5 and 1. [5]. (i) Sketch the graph of, showing the coordinates of the points where our graph meets the coordinate aes. [] Solve the equation 10, giving our answer correct
1. Solve the simultaneous equations 5 and 1. [5]. (i) Sketch the graph of, showing the coordinates of the points where our graph meets the coordinate aes. [] Solve the equation 10, giving our answer correct
I B.TECH EXAMINATIONS, JUNE ENGINEERING MECHANICS (COMMON TO CE, ME, CHEM, MCT, MMT, AE, AME, MIE, MIM)
 Code.No: 09A1BS05 R09 SET-1 I B.TECH EXAMINATIONS, JUNE - 2011 ENGINEERING MECHANICS (COMMON TO CE, ME, CHEM, MCT, MMT, AE, AME, MIE, MIM) Time: 3 hours Max. Marks: 75 Answer any FIVE questions All questions
Code.No: 09A1BS05 R09 SET-1 I B.TECH EXAMINATIONS, JUNE - 2011 ENGINEERING MECHANICS (COMMON TO CE, ME, CHEM, MCT, MMT, AE, AME, MIE, MIM) Time: 3 hours Max. Marks: 75 Answer any FIVE questions All questions
MOMENTS OF INERTIA FOR AREAS, RADIUS OF GYRATION OF AN AREA, & MOMENTS OF INTERTIA BY INTEGRATION
 MOMENTS OF INERTIA FOR AREAS, RADIUS OF GYRATION OF AN AREA, & MOMENTS OF INTERTIA BY INTEGRATION Today s Objectives: Students will be able to: a) Define the moments of inertia (MoI) for an area. b) Determine
MOMENTS OF INERTIA FOR AREAS, RADIUS OF GYRATION OF AN AREA, & MOMENTS OF INTERTIA BY INTEGRATION Today s Objectives: Students will be able to: a) Define the moments of inertia (MoI) for an area. b) Determine
Moment of Inertia & Newton s Laws for Translation & Rotation
 Moment of Inertia & Newton s Laws for Translation & Rotation In this training set, you will apply Newton s 2 nd Law for rotational motion: Στ = Σr i F i = Iα I is the moment of inertia of an object: I
Moment of Inertia & Newton s Laws for Translation & Rotation In this training set, you will apply Newton s 2 nd Law for rotational motion: Στ = Σr i F i = Iα I is the moment of inertia of an object: I
Determine the resultant internal loadings acting on the cross section at C of the beam shown in Fig. 1 4a.
 E X M P L E 1.1 Determine the resultant internal loadings acting on the cross section at of the beam shown in Fig. 1 a. 70 N/m m 6 m Fig. 1 Support Reactions. This problem can be solved in the most direct
E X M P L E 1.1 Determine the resultant internal loadings acting on the cross section at of the beam shown in Fig. 1 a. 70 N/m m 6 m Fig. 1 Support Reactions. This problem can be solved in the most direct
2.8 Hydrostatic Force on a Plane Surface
 CEE 3310 Hydrostatics, Sept. 7, 2018 35 2.7 Review Pressure is a scalar - independent of direction. Hydrostatics: P = γ k. pressure, vertical motion: z P, z P. Horizontal motion in the same fluid - no
CEE 3310 Hydrostatics, Sept. 7, 2018 35 2.7 Review Pressure is a scalar - independent of direction. Hydrostatics: P = γ k. pressure, vertical motion: z P, z P. Horizontal motion in the same fluid - no
[8] Bending and Shear Loading of Beams
![[8] Bending and Shear Loading of Beams [8] Bending and Shear Loading of Beams](/thumbs/92/110949676.jpg) [8] Bending and Shear Loading of Beams Page 1 of 28 [8] Bending and Shear Loading of Beams [8.1] Bending of Beams (will not be covered in class) [8.2] Bending Strain and Stress [8.3] Shear in Straight
[8] Bending and Shear Loading of Beams Page 1 of 28 [8] Bending and Shear Loading of Beams [8.1] Bending of Beams (will not be covered in class) [8.2] Bending Strain and Stress [8.3] Shear in Straight
Angular Momentum. Objectives CONSERVATION OF ANGULAR MOMENTUM
 Angular Momentum CONSERVATION OF ANGULAR MOMENTUM Objectives Calculate the angular momentum vector for a moving particle Calculate the angular momentum vector for a rotating rigid object where angular
Angular Momentum CONSERVATION OF ANGULAR MOMENTUM Objectives Calculate the angular momentum vector for a moving particle Calculate the angular momentum vector for a rotating rigid object where angular
Stress Transformation Equations: u = +135 (Fig. a) s x = 80 MPa s y = 0 t xy = 45 MPa. we obtain, cos u + t xy sin 2u. s x = s x + s y.
 014 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently 9 7. Determine the normal stress and shear stress acting
014 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently 9 7. Determine the normal stress and shear stress acting
6. Bending CHAPTER OBJECTIVES
 CHAPTER OBJECTIVES Determine stress in members caused by bending Discuss how to establish shear and moment diagrams for a beam or shaft Determine largest shear and moment in a member, and specify where
CHAPTER OBJECTIVES Determine stress in members caused by bending Discuss how to establish shear and moment diagrams for a beam or shaft Determine largest shear and moment in a member, and specify where
5 Equilibrium of a Rigid Body Chapter Objectives
 5 Equilibrium of a Rigid Body Chapter Objectives Develop the equations of equilibrium for a rigid body Concept of the free-body diagram for a rigid body Solve rigid-body equilibrium problems using the
5 Equilibrium of a Rigid Body Chapter Objectives Develop the equations of equilibrium for a rigid body Concept of the free-body diagram for a rigid body Solve rigid-body equilibrium problems using the
Sub:Strength of Material (22306)
 Sub:Strength of Material (22306) UNIT 1. Moment of Inertia 1.1 Concept of Moment of Inertia (Ml). Effect of MI in case of beam and column. 1.2 MI about axes passing through centroid. Parallel and Perpendicular
Sub:Strength of Material (22306) UNIT 1. Moment of Inertia 1.1 Concept of Moment of Inertia (Ml). Effect of MI in case of beam and column. 1.2 MI about axes passing through centroid. Parallel and Perpendicular
STATICS VECTOR MECHANICS FOR ENGINEERS: Distributed Forces: Centroids and Centers of Gravity. Tenth Edition CHAPTER
 Tenth E CHAPTER 5 VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. David F. Mazurek Lecture Notes: John Chen California Polytechnic State University Distributed Forces:
Tenth E CHAPTER 5 VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. David F. Mazurek Lecture Notes: John Chen California Polytechnic State University Distributed Forces:
Statics Chapter II Fall 2018 Exercises Corresponding to Sections 2.1, 2.2, and 2.3
 Statics Chapter II Fall 2018 Exercises Corresponding to Sections 2.1, 2.2, and 2.3 2 3 Determine the magnitude of the resultant force FR = F1 + F2 and its direction, measured counterclockwise from the
Statics Chapter II Fall 2018 Exercises Corresponding to Sections 2.1, 2.2, and 2.3 2 3 Determine the magnitude of the resultant force FR = F1 + F2 and its direction, measured counterclockwise from the
(Please write your Roll No. immediately) Mid Term Examination. Regular (Feb 2017)
 (Please write your Roll No. immediately) Roll No... Mid Term Examination Regular (Feb 2017) B.Tech-II sem Sub-Engineering Mechanics Paper code- ETME-110 Time-1.5 hours Max Marks-30 Note: 1. Q.No. 1 is
(Please write your Roll No. immediately) Roll No... Mid Term Examination Regular (Feb 2017) B.Tech-II sem Sub-Engineering Mechanics Paper code- ETME-110 Time-1.5 hours Max Marks-30 Note: 1. Q.No. 1 is
Two small balls, each of mass m, with perpendicular bisector of the line joining the two balls as the axis of rotation:
 PHYSCS LOCUS 17 summation in mi ri becomes an integration. We imagine the body to be subdivided into infinitesimal elements, each of mass dm, as shown in figure 7.17. Let r be the distance from such an
PHYSCS LOCUS 17 summation in mi ri becomes an integration. We imagine the body to be subdivided into infinitesimal elements, each of mass dm, as shown in figure 7.17. Let r be the distance from such an
MTE 119 STATICS LECTURE MATERIALS FINAL REVIEW PAGE NAME & ID DATE. Example Problem F.1: (Beer & Johnston Example 9-11)
 Eample Problem F.: (Beer & Johnston Eample 9-) Determine the mass moment of inertia with respect to: (a) its longitudinal ais (-ais) (b) the y-ais SOLUTION: a) Mass moment of inertia about the -ais: Step
Eample Problem F.: (Beer & Johnston Eample 9-) Determine the mass moment of inertia with respect to: (a) its longitudinal ais (-ais) (b) the y-ais SOLUTION: a) Mass moment of inertia about the -ais: Step
Stopper rod tilt and effect on nozzle flow. Rajneesh Chaudhary (Graduate Student) & Brian G. Thomas. Department of Mechanical Science and Engineering
 Stopper rod tilt and effect on nozzle flow Rajneesh Chaudhary (Graduate Student) & Brian G. Thomas Department of Mechanical Science and Engineering University of Illinois at Urbana-Champaign, IL Project
Stopper rod tilt and effect on nozzle flow Rajneesh Chaudhary (Graduate Student) & Brian G. Thomas Department of Mechanical Science and Engineering University of Illinois at Urbana-Champaign, IL Project
Exam 05: Chapters 10 and 11
 Name: Exam 05: Chapters 10 and 11 Select and solve four of the following problems to the best of your ability. You must choose two problem from each column. Please notice that it is possible to select
Name: Exam 05: Chapters 10 and 11 Select and solve four of the following problems to the best of your ability. You must choose two problem from each column. Please notice that it is possible to select
Stress Analysis Lecture 4 ME 276 Spring Dr./ Ahmed Mohamed Nagib Elmekawy
 Stress Analysis Lecture 4 ME 76 Spring 017-018 Dr./ Ahmed Mohamed Nagib Elmekawy Shear and Moment Diagrams Beam Sign Convention The positive directions are as follows: The internal shear force causes a
Stress Analysis Lecture 4 ME 76 Spring 017-018 Dr./ Ahmed Mohamed Nagib Elmekawy Shear and Moment Diagrams Beam Sign Convention The positive directions are as follows: The internal shear force causes a
storage tank, or the hull of a ship at rest, is subjected to fluid pressure distributed over its surface.
 Hydrostatic Forces on Submerged Plane Surfaces Hydrostatic forces mean forces exerted by fluid at rest. - A plate exposed to a liquid, such as a gate valve in a dam, the wall of a liquid storage tank,
Hydrostatic Forces on Submerged Plane Surfaces Hydrostatic forces mean forces exerted by fluid at rest. - A plate exposed to a liquid, such as a gate valve in a dam, the wall of a liquid storage tank,
Stress transformation and Mohr s circle for stresses
 Stress transformation and Mohr s circle for stresses 1.1 General State of stress Consider a certain body, subjected to external force. The force F is acting on the surface over an area da of the surface.
Stress transformation and Mohr s circle for stresses 1.1 General State of stress Consider a certain body, subjected to external force. The force F is acting on the surface over an area da of the surface.
EXERCISES Chapter 15: Multiple Integrals. Evaluating Integrals in Cylindrical Coordinates
 08 Chapter 5: Multiple Integrals EXERCISES 5.6 Evaluating Integrals in Clindrical Evaluate the clindrical coordinate integrals in Eercises 6... 3. 4. 5. 6. Changing Order of Integration in Clindrical The
08 Chapter 5: Multiple Integrals EXERCISES 5.6 Evaluating Integrals in Clindrical Evaluate the clindrical coordinate integrals in Eercises 6... 3. 4. 5. 6. Changing Order of Integration in Clindrical The
Engineering Tripos Part IIA Supervisor Version. Module 3D4 Structural Analysis and Stability Handout 1
 Engineering Tripos Part A Supervisor Version Module 3D4 Structural Analysis and Stability Handout 1 Elastic Analysis (8 Lectures) Fehmi Cirak (fc86@) Stability (8 Lectures) Allan McRobie (fam @eng) January
Engineering Tripos Part A Supervisor Version Module 3D4 Structural Analysis and Stability Handout 1 Elastic Analysis (8 Lectures) Fehmi Cirak (fc86@) Stability (8 Lectures) Allan McRobie (fam @eng) January
MECHANICS LAB AM 317 EXP 3 BENDING STRESS IN A BEAM
 MECHANICS LAB AM 37 EXP 3 BENDING STRESS IN A BEAM I. OBJECTIVES I. To compare the experimentally determined stresses in a beam with those predicted from the simple beam theory (a.k.a. Euler-Bernoull beam
MECHANICS LAB AM 37 EXP 3 BENDING STRESS IN A BEAM I. OBJECTIVES I. To compare the experimentally determined stresses in a beam with those predicted from the simple beam theory (a.k.a. Euler-Bernoull beam
Chapter 9 BIAXIAL SHEARING
 9. DEFNTON Chapter 9 BAXAL SHEARNG As we have seen in the previous chapter, biaial (oblique) shearing produced b the shear forces and, appears in a bar onl accompanied b biaial bending (we ma discuss about
9. DEFNTON Chapter 9 BAXAL SHEARNG As we have seen in the previous chapter, biaial (oblique) shearing produced b the shear forces and, appears in a bar onl accompanied b biaial bending (we ma discuss about
7 TRANSVERSE SHEAR transverse shear stress longitudinal shear stresses
 7 TRANSVERSE SHEAR Before we develop a relationship that describes the shear-stress distribution over the cross section of a beam, we will make some preliminary remarks regarding the way shear acts within
7 TRANSVERSE SHEAR Before we develop a relationship that describes the shear-stress distribution over the cross section of a beam, we will make some preliminary remarks regarding the way shear acts within
(Refer Slide Time: 2:08 min)
 Applied Mechanics Prof. R. K. Mittal Department of Applied Mechanics Indian Institute of Technology, Delhi Lecture No. 11 Properties of Surfaces (Contd.) Today we will take up lecture eleven which is a
Applied Mechanics Prof. R. K. Mittal Department of Applied Mechanics Indian Institute of Technology, Delhi Lecture No. 11 Properties of Surfaces (Contd.) Today we will take up lecture eleven which is a
MECE 3321 MECHANICS OF SOLIDS CHAPTER 1
 MECE 3321 MECHANICS O SOLIDS CHAPTER 1 Samantha Ramirez, MSE WHAT IS MECHANICS O MATERIALS? Rigid Bodies Statics Dynamics Mechanics Deformable Bodies Solids/Mech. Of Materials luids 1 WHAT IS MECHANICS
MECE 3321 MECHANICS O SOLIDS CHAPTER 1 Samantha Ramirez, MSE WHAT IS MECHANICS O MATERIALS? Rigid Bodies Statics Dynamics Mechanics Deformable Bodies Solids/Mech. Of Materials luids 1 WHAT IS MECHANICS
EMA 3702 Mechanics & Materials Science (Mechanics of Materials) Chapter 6 Shearing Stress in Beams & Thin-Walled Members
 EMA 3702 Mechanics & Materials Science (Mechanics of Materials) Chapter 6 Shearing Stress in Beams & Thin-Walled Members Beams Bending & Shearing EMA 3702 Mechanics & Materials Science Zhe Cheng (2018)
EMA 3702 Mechanics & Materials Science (Mechanics of Materials) Chapter 6 Shearing Stress in Beams & Thin-Walled Members Beams Bending & Shearing EMA 3702 Mechanics & Materials Science Zhe Cheng (2018)
CHAPTER 2. Copyright McGraw-Hill Education. Permission required for reproduction or display.
 CHAPTER 2 PROBLEM 2.1 Two forces are applied as shown to a hook. Determinee graphicall the magnitude and direction of their resultant using (a) the parallelogram law, (b) the triangle rule. (a) Parallelogram
CHAPTER 2 PROBLEM 2.1 Two forces are applied as shown to a hook. Determinee graphicall the magnitude and direction of their resultant using (a) the parallelogram law, (b) the triangle rule. (a) Parallelogram
Now we are going to use our free body analysis to look at Beam Bending (W3L1) Problems 17, F2002Q1, F2003Q1c
 Now we are going to use our free body analysis to look at Beam Bending (WL1) Problems 17, F00Q1, F00Q1c One of the most useful applications of the free body analysis method is to be able to derive equations
Now we are going to use our free body analysis to look at Beam Bending (WL1) Problems 17, F00Q1, F00Q1c One of the most useful applications of the free body analysis method is to be able to derive equations
KINEMATIC RELATIONS IN DEFORMATION OF SOLIDS
 Chapter 8 KINEMATIC RELATIONS IN DEFORMATION OF SOLIDS Figure 8.1: 195 196 CHAPTER 8. KINEMATIC RELATIONS IN DEFORMATION OF SOLIDS 8.1 Motivation In Chapter 3, the conservation of linear momentum for a
Chapter 8 KINEMATIC RELATIONS IN DEFORMATION OF SOLIDS Figure 8.1: 195 196 CHAPTER 8. KINEMATIC RELATIONS IN DEFORMATION OF SOLIDS 8.1 Motivation In Chapter 3, the conservation of linear momentum for a
Tuesday, February 11, Chapter 3. Load and Stress Analysis. Dr. Mohammad Suliman Abuhaiba, PE
 1 Chapter 3 Load and Stress Analysis 2 Chapter Outline Equilibrium & Free-Body Diagrams Shear Force and Bending Moments in Beams Singularity Functions Stress Cartesian Stress Components Mohr s Circle for
1 Chapter 3 Load and Stress Analysis 2 Chapter Outline Equilibrium & Free-Body Diagrams Shear Force and Bending Moments in Beams Singularity Functions Stress Cartesian Stress Components Mohr s Circle for
Section I 10 marks (pages 2 5) Attempt Questions 1 10 Allow about 15 minutes for this section
 017 HIGHER SCHOOL CERTIFICATE EXAMINATION Mathematics General Instructions Reading time 5 minutes Working time hours Write using black pen NESA approved calculators may be used A reference sheet is provided
017 HIGHER SCHOOL CERTIFICATE EXAMINATION Mathematics General Instructions Reading time 5 minutes Working time hours Write using black pen NESA approved calculators may be used A reference sheet is provided
MECH 401 Mechanical Design Applications
 MECH 401 Mechanical Design Applications Dr. M. O Malley Master Notes Spring 008 Dr. D. M. McStravick Rice University Updates HW 1 due Thursday (1-17-08) Last time Introduction Units Reliability engineering
MECH 401 Mechanical Design Applications Dr. M. O Malley Master Notes Spring 008 Dr. D. M. McStravick Rice University Updates HW 1 due Thursday (1-17-08) Last time Introduction Units Reliability engineering
Mechanics of Materials
 Mechanics of Materials 2. Introduction Dr. Rami Zakaria References: 1. Engineering Mechanics: Statics, R.C. Hibbeler, 12 th ed, Pearson 2. Mechanics of Materials: R.C. Hibbeler, 9 th ed, Pearson 3. Mechanics
Mechanics of Materials 2. Introduction Dr. Rami Zakaria References: 1. Engineering Mechanics: Statics, R.C. Hibbeler, 12 th ed, Pearson 2. Mechanics of Materials: R.C. Hibbeler, 9 th ed, Pearson 3. Mechanics
7.6 Stress in symmetrical elastic beam transmitting both shear force and bending moment
 7.6 Stress in symmetrical elastic beam transmitting both shear force and bending moment à It is more difficult to obtain an exact solution to this problem since the presence of the shear force means that
7.6 Stress in symmetrical elastic beam transmitting both shear force and bending moment à It is more difficult to obtain an exact solution to this problem since the presence of the shear force means that
ME 323 Examination #2 April 11, 2018
 ME 2 Eamination #2 April, 2 PROBLEM NO. 25 points ma. A thin-walled pressure vessel is fabricated b welding together two, open-ended stainless-steel vessels along a 6 weld line. The welded vessel has an
ME 2 Eamination #2 April, 2 PROBLEM NO. 25 points ma. A thin-walled pressure vessel is fabricated b welding together two, open-ended stainless-steel vessels along a 6 weld line. The welded vessel has an
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 Please review the followg statement: I certify that I have not given unauthorized aid nor have I received aid the completion of this eam. Signature: INSTRUCTIONS Beg each problem the space provided on
Please review the followg statement: I certify that I have not given unauthorized aid nor have I received aid the completion of this eam. Signature: INSTRUCTIONS Beg each problem the space provided on
20 Torque & Circular Motion
 Chapter 0 Torque & Circular Motion 0 Torque & Circular Motion The mistake that crops up in the application of Newton s nd Law for Rotational Motion involves the replacement of the sum of the torques about
Chapter 0 Torque & Circular Motion 0 Torque & Circular Motion The mistake that crops up in the application of Newton s nd Law for Rotational Motion involves the replacement of the sum of the torques about
Errata Sheet for S. D. Rajan, Introduction to Structural Analysis & Design (1 st Edition) John Wiley & Sons Publication
 S D Rajan, Introduction to Structural Analsis & Design ( st Edition) Errata Sheet for S D Rajan, Introduction to Structural Analsis & Design ( st Edition) John Wile & Sons Publication Chapter Page Correction
S D Rajan, Introduction to Structural Analsis & Design ( st Edition) Errata Sheet for S D Rajan, Introduction to Structural Analsis & Design ( st Edition) John Wile & Sons Publication Chapter Page Correction
2001 Higher Maths Non-Calculator PAPER 1 ( Non-Calc. )
 001 PAPER 1 ( Non-Calc. ) 1 1) Find the equation of the straight line which is parallel to the line with equation x + 3y = 5 and which passes through the point (, 1). Parallel lines have the same gradient.
001 PAPER 1 ( Non-Calc. ) 1 1) Find the equation of the straight line which is parallel to the line with equation x + 3y = 5 and which passes through the point (, 1). Parallel lines have the same gradient.
ME 243. Lecture 10: Combined stresses
 ME 243 Mechanics of Solids Lecture 10: Combined stresses Ahmad Shahedi Shakil Lecturer, Dept. of Mechanical Engg, BUET E-mail: sshakil@me.buet.ac.bd, shakil6791@gmail.com Website: teacher.buet.ac.bd/sshakil
ME 243 Mechanics of Solids Lecture 10: Combined stresses Ahmad Shahedi Shakil Lecturer, Dept. of Mechanical Engg, BUET E-mail: sshakil@me.buet.ac.bd, shakil6791@gmail.com Website: teacher.buet.ac.bd/sshakil
PESIT- Bangalore South Campus Dept of science & Humanities Sub: Elements Of Civil Engineering & Engineering Mechanics 1 st module QB
 PESIT- Bangalore South Campus Dept of science & Humanities Sub: Elements Of Civil Engineering & Engineering Mechanics 1 st module QB Sub Code: 15CIV13/23 1. Briefly give the scope of different fields in
PESIT- Bangalore South Campus Dept of science & Humanities Sub: Elements Of Civil Engineering & Engineering Mechanics 1 st module QB Sub Code: 15CIV13/23 1. Briefly give the scope of different fields in
BOOK OF COURSE WORKS ON STRENGTH OF MATERIALS FOR THE 2 ND YEAR STUDENTS OF THE UACEG
 BOOK OF COURSE WORKS ON STRENGTH OF MATERIALS FOR THE ND YEAR STUDENTS OF THE UACEG Assoc.Prof. Dr. Svetlana Lilkova-Markova, Chief. Assist. Prof. Dimitar Lolov Sofia, 011 STRENGTH OF MATERIALS GENERAL
BOOK OF COURSE WORKS ON STRENGTH OF MATERIALS FOR THE ND YEAR STUDENTS OF THE UACEG Assoc.Prof. Dr. Svetlana Lilkova-Markova, Chief. Assist. Prof. Dimitar Lolov Sofia, 011 STRENGTH OF MATERIALS GENERAL
Properties of plane surfaces I: First moment and centroid of area
 Properties of plane surfaces I: First moment and centroid of area Having deal with trusses and frictional forces, we now change gears and go on to discuss some properties of surfaces mathematically. Of
Properties of plane surfaces I: First moment and centroid of area Having deal with trusses and frictional forces, we now change gears and go on to discuss some properties of surfaces mathematically. Of
