Saint-Venant's problem for a second-order piezoelectric prismatic bar

Transcription

1 International Journal of Engineering Science 38 (2000) 21±45 Saint-Venant's problem for a second-order piezoelectric prismatic bar S. Vidoli a, R.C. Batra b,*, F. dell'isola a a Dipartimento di Ingegneria Strutturale e Geotecnica, Universita di Roma `La Sapienza', Roma, Italy b Department of Engineering Science and Mechanics, Virginia Polytechnic Institute and State University, MC 0219, Blacksburg, V 24061, US Received 27 October 1998; received in revised form 6 January 1999; accepted 6 January 1999 bstract For a homogeneous, transversely isotropic, second-order piezoelectric and in nitesimally prebent, prepolarized and prestretched prismatic bar, we nd second-order Saint-Venant solutions. It is found that the electric eld alone does not introduce any bending in the second-order piezoelectric bar. However, the electric eld induced by the bending of the bar can be used to ascertain the magnitude and direction of the bending vector. The curvature of the centroidal axis of the bar can be changed by the simultaneous application of the electric eld and the bending moment. Ó 1999 Elsevier Science Ltd. ll rights reserved. Keywords: Signorini's expansion; Saint-Venant's solutions; Semi-inverse method 1. Introduction Saint-Venant [1,2] studied the extension, bending, torsion and exure of a homogeneous prismatic body made of an isotropic linear elastic material. Iesan [3±6] has analysed the Saint- Venant problem for inhomogeneous and anisotropic linear elastic bodies, elastic dielectrics and microstretch elastic solids. Dell'Isola and Rosa [7,8] and Davi [9] have investigated the problem for linear piezoelectric materials and dell'isola and Batra [10] for linear elastic isotropic porous solids. Batra and Yang [11] have proved Toupin's version [12] of the Saint-Venant principle for a linear piezoelectric bar. Rivlin [13] has used the second-order elasticity theory to explain the Poynting e ect [14], i.e., the axial elongation of an elastic bar subjected to torques only at the end faces is proportional to the * Corresponding author. Tel.: ; fax: address: rbatra@vt.edu (R.C. Batra) /00/$ ± see front matter Ó 1999 Elsevier Science Ltd. ll rights reserved. PII: S (99)

2 22 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 square of the angular twist. Rivlin showed that the elongation was proportional to the secondorder elasticities. Signorini [15] proposed a perturbation method to reduce the solution of a nonlinear elastic problem to that of a series of nonhomogeneous linear elastic traction boundary value problems in which the loads for the nth problem depend upon the solution of the previous (n 1) problems. These loads must satisfy compatibility conditions for the nth-order problem to have a solution. Truesdell and Noll [16] have reviewed the pertinent literature on the Poynting e ect and the Signorini method. Green and dkins [17] pointed out that when the displacements and in nitesimal rotations of the centroid of one end face vanish, then the compatibility conditions for the loads in the nth order Signorini problem are automatically satis ed. Green and dkins [17] and Green and Shield [18] have studied the Poynting e ect in nonlinear elastic prismatic bodies. Recently, dell'isola et al. [19,20] used the Signorini expansion method to nd a solution of the Saint-Venant problem for a prismatic bar made of a second-order elastic material with the rst-order solution corresponding to either an in nitesimal twist or small bending and stretching. Batra et al. [21] used the Signorini expansion method to analyze electromechanical deformations of a transversely isotropic circular cylindrical bar made of a second-order piezoelectric material for which constitutive relations had been derived by Yang and Batra [22]. The rst-order deformations were assumed to be an in nitesimal twist and small electric eld. Here Batra et al.'s [21] work is extended to a prismatic body of a general cross-section which is initially twisted, stretched and electrically polarized by a small amount. For a bar subjected to bending moments only at the end faces, it is found that there is a second-order Poisson's e ect proportional to the square of the magnitude of the bending vector and a torsional e ect proportional to the square of the axial distance from the `clamped' end. Other second-order e ects are stated in the paper. 2. Formulation of the problem We consider a transversely isotropic and homogeneous prismatic body of cross-section and length ` occupying the domain X ˆ 0; `Š in the stress and polarization free con guration with its axis along the unit vector e that is also the direction of transverse isotropy. In the referential description of deformation, the balance of linear momentum, the balance of moment of momentum, the Maxwell law for the electric displacement with the free body charge density set equal to zero and the boundary conditions are Div T T E ˆ 0 in X; T T E F T ˆ F T T E T in X; DivD ˆ 0 in X; T T E N ˆ 0; D N ˆ 0 0; `Š; T T E e ˆ f; D e ˆ q on 0 and `; u ˆ 0; H H T ˆ 0; and w ˆ 0 at point C:

3 Here T is the rst Piola±Kirchho stress tensor, T E the rst Piola±Kirchho ±Maxwell stress tensor, D the referential electric displacement, Div the divergence operator in the reference con guration, F the deformation gradient, N a unit outward normal to the mantle in the reference con guration, f the surface traction per unit undeformed area, q the charge density, u ˆ x X the displacement of a material point that occupied place X in the reference con guration and is at place x in the present con guration, H ˆ Grad u the displacement gradient, Grad the gradient operator with respect to coordinates in the reference con guration, w the electric potential and point C is the centroid of the cross-section 0 f0g. The clamping condition (6) eliminates trivial solutions of the problem. For the problem to have a solution, f and q must satisfy f d f d ˆ 0; qd qd ˆ 0; 0 ` 0 ` 7 x ^ f d x ^ f d ˆ 0; 0 where S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 23 ` a ^ b ˆ a b b a; a b c ˆ b c a; for arbitrary vectors a, b and c. Eqs. (4), (5) and (7) imply that 0 0 T T ed E ˆ 0; D ed ˆ 0; 0 x ^ T T E ed xj 0 rˆ0 ^ T T E ed ˆ 0; 8 9 where we have taken the origin of our coordinate system at the centroid of the cross-section 0 and set X ˆ r ze: 10 In Eq. (9) a prime indicates di erentiation with respect to the axial coordinate, z. Recall that T ˆ JrF 1T ; T E ˆ Jr E F 1T ; D ˆ JF 1 D; 11 where J ˆ det F, r is the Cauchy stress tensor, r E the Cauchy±Maxwell stress tensor and D the electric displacement in the present con guration. For a piezoelectric material, we introduce, in the present con guration, electric eld ^E and electric polarization P through D ˆ P ^E: 12 Quantities P and ^E are related to their counterparts P and W in the reference con guration by P ˆ JF 1 P; W ˆ F T ^E ˆ Gradw: 13

4 24 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 The existence of w is guaranteed by I ^E dx ˆ 0; 14 where the integration is on any closed curve in X. In order to complete the formulation of the problem we need to give the constitutive relations. We choose r and r E to be symmetric tensors so that the balance of moment of momentum (2) is identically satis ed. Following braham et al. (see [23], Eqn.3.6,22,23) we take r E ˆ P ^E s ^E ^E 1 2 ^E 2 1; 15 where a b s ˆ a b b a =2; 16 ^E is the magnitude of ^E and 1 is the identity tensor. We assume that the prismatic body is made of a transversely isotropic second-order piezoelectric material. For such a material, Yang and Batra [22] have derived constitutive relations for the second Piola-Kirchho stress tensor S and the referential polarization P. We use those to obtain expressions for T and D and retain terms upto second-order in H and W. These rather long expressions are omitted. However, the expressions used herein to obtain a solution of the problem by the method of Signorini's series expansion are given in ppendix. 3. Signorini's expansion We write the displacement eld u and the electric eld W as u ˆ we v; W ˆ w 0 e gradw : 17 That is, w and v are the axial and in-plane components of the displacement u of a point and w 0 and gradw equal the axial and in-plane components of W. The operators grad and div signify, respectively, the two-dimensional gradient and divergence operators with respect to referential coordinates in the cross-section. The displacement u, the electric potential w, surface tractions f and surface charge q are assumed to have a series expansion u ˆ g_u g 2 u ; w ˆ g w _ g 2 w ; f ˆ g f _ g 2 f ; q ˆ g _q g 2 q ; 18 where g is a small, yet to be identi ed, parameter in the problem. Substitutions for u and w in the expressions for the constitutive relations for T and D give T ˆ g _ T g 2 T ; D ˆ g _D g 2 D ; T E ˆ g 2 T E 19

5 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 25 Expressions for T; _ E T; T ; _D and D are given in the ppendix. Substituting from Eqs. (18) and (19) into the balance laws (1)±(3), the boundary conditions (4)±(6) and integrability conditions (9) and equating like powers of g on both sides of these equations, we arrive at the following equations for the rst and second-order problems: Div T _ ˆ 0; Div _D ˆ 0 in X; _TN ˆ 0; _D N ˆ 0 0; `Š; _Te ˆ _f; _D e ˆ _q on 0 and `; 0 0 _Ted ˆ 0; _D ed ˆ 0; 0 X ^ _Ted Xj 0 rˆ0 ^ _Ted ˆ 0; 20 Div T T E ˆ 0; Div D J _ W _ 2 H _ s _W ˆ 0 in X; T T E N ˆ 0; D J _ W _ 2 H _ s _W N ˆ 0 0; `Š; T T E e ˆ f; D J _ W _ 2 H _ s _W e ˆ q on 0 and `; 0 0 T T ed E ˆ 0; D J _ W _ 2 H _ s _W ed ˆ 0; _TeŠd 0 X ^ T T E e _u ^ e ^ T T E ed _uj 0 rˆ0 ^ We decompose T and D as _Ted ˆ 0: 21 T ˆ T T s ; D ˆ D D s ; where T and D are related to u and w in the same way as _ T and _D to _u and _ w. Expressions for T and D in terms of u and w are 22 2 T ˆ ~l gradv s c 3 k w 0 0 kdivv e 2w Š^I n ~l v 0 grad w e 3 gradwš o e 2 c 1 k=2 c 3 c 4 l w 0 c 3 k divv e 1 e 2 2e 3 w 0 Še e; D ˆ gradw e 3 v 0 grad w s w 0 e 1 e 2 2e 3 w 0 e 2 divvše: Here ^I is the two-dimensional identity tensor and c 1 ; c 3 ; c 4 ; e 1 ; e 2 ; e 3 ; 1 and 2 are material parameters and ~l ˆ c 4 2l =2 is the shear modulus in the direction of transverse isotropy. Eq. (23) with two superimposed dots replaced by a superimposed dot are constitutive relations for a linear transversely isotropic piezoelectric material. We assume that k; l; c 1 ; c 3 ;

6 26 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 c 4 ; e 1 ; e 2 ; e 3 ; 1 and 2 are such that the strain energy density is positive de nite so that the solution of a traction boundary value problem for a linear piezoelectric body is unique to within a trivial solution. Substituting from Eq. (12) into Eq. (21) and rewriting equations in the same form as Eq. (20), we obtain Div T ˆ b s ; Div D ˆ c s in X; TN ˆ f ms ; D N ˆ q ms 0; `Š; Ted ˆ f d R fs ; D ed ˆ qd R qs ; X ^ Te d ˆ X ^ f d R ms ; T 0 ed ˆ h s ; D 0 ed ˆ i s ; X ^ Te 0 d e ^ Ted ˆ g s ; 24 where b s ˆ DivT se ; c s ˆ Div D sp ; f ms ˆ T se N; q ms ˆ D sp N; R fs ˆ T se ed; R ms ˆ X ^ T se e d; R qs ˆ D sp ed; h s ˆ T se 0 ed; g s ˆ i s ˆ T se ˆ T s T E ; X ^ T se e _u ^ _Te 0 d e ^ D sp 0 ed; D sp ˆ D s _ J _ W 2 _ H s _W: T se ed _uj 0 rˆ0 ^ _Te d; 25 We assume that the rst-order deformation corresponds to the in nitesimal bending, extension and polarization of the bar. That is, where _w ˆ z x b ; _u ˆ ~m r r s b z2 2 b m ax r z ax b r e; 26 a ˆ e 2 =c 3 ; m ˆ k=2 k l ; r ˆ e r; b ˆ c 3 =e 2 ; ~m ˆ c 3 k =2 k l ; 27

7 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 27 ; x and b characterize the in nitesimal extension, polarization and bending of the prismatic body. Note that vector b is in the cross-section. Relations between x; and b in terms of loads and electric charge applied at the end faces are given below as Eqs. (46) and (47). In order for the deformations caused by the bending, extension and the electric eld to be of the same order of magnitude, ax ˆ ˆ jbjr where 2R is the diameter of the cross-section, i.e., the diameter of the smallest circle enclosing the cross-section and jbj is the magnitude of b. The small parameter g in Eq. (18) can be identi ed with ax; or jbjr. The terms on the right-hand sides of Eq. (25) are quadratic forms in x; and b and their expressions given below were obtained by performing the symbolic operations in Mathematica: c s ˆ v 1 b bz; q ms ˆ v 2 x b v 3 b b r v 4 b b r v 5 b Š Nz; b s ˆ v 6 b bze v 7 x b v 8 b b r v 9 b b r v 10 b ; f ms ˆ z v 11 x b v 12 b b r v 13 b b r v 14 b Š Ne z2 2 v 15 b b N v 16 b b NŠ v 17 x v 18 x 2 v 19 2 v 20 x b r v 21 b r v 22 b r b r v 23 b r 2 ŠN; i s ˆ v 25 b b z; h s ˆ v 26 b b v 27 b b Šr v 28 z b b e v 29 b v 30 x b ; g s ˆ z v 31 b b v 32 b b r v 33 v 34 x b Š v 35 b r v 36 v 37 xš b r e; R qs ˆ z2 2 v 38 b b v 39 2 v 40 x 2 v 41 x v 42 J b b v 43 J b b ; R fs ˆ z2 2 v 44 b b v 47 2 v 48 x 2 v 49 x v 50 J b b v 51 J b b e z v 45 v 46 x b ; 28 R ms ˆ z2 2 v 52 v 53 x b v 55 v 56 x J b zv 54 J b b e: Here v 1 ; v 2 ;... ; v 56 are material constants; their expressions in terms of the elastic constants used in the constitutive relation are given in ppendix. equals the area of the cross-section, J ˆ r r d is the inertia tensor, vectors g s and R ms are equivalent to the skew symmetric tensors g s and R ms, respectively.

8 28 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 Substitution for T and D from Eq. (23) into Eq. (24) 1 -Eq. (24) 4 and recalling Eq. (17), we arrive at the following eld equations for the determination of u and w: F v c 3 k ~l grad w 0 e 2 e 3 gradw 0 ~lv 0 ˆ b s in ; D R ~w c 3 k ~l divv 0 2 c 1 k 2 c 3 c 4 l w 00 e 1 e 2 2e 3 w 00 ˆ b se ; in ; D Rw ~ e2 e 3 divv =2 w 00 e 1 e 2 2e 3 w 00 ˆ c s ; in ; 29 G v N c 3 k w 0 0 e 2w ŠN ˆ f ms ; grad ~w N ~lv 0 N ˆ f mse ; grad w ~ N e3 v 0 N ˆ q ms ; where 30 F v ˆ ld R v k l graddivv; G v ˆ 2l gradv s k divv ^I; ~w ˆ ~l w e 3w; w ~ ˆ e3 w w; b s ˆ b s b se e; f ms ˆ f ms f mse e; 31 D R is the Laplacian operator and F ˆ divg is the Navier operator in the cross-section. 4. Saint-Venant/lmansi solution We seek a solution of Eq. (29) of the form w ˆ Xm iˆ0 z i i! w i r ; v ˆ Xm iˆ0 z i i! v X i r ; w m ˆ iˆ0 z i i! w i r : 32 Substituting from Eq. (32) into Eq. (29), recalling Eq. (28) and equating like powers of z i =i! on both sides, we obtain partial di erential equations, boundary conditions and integrability conditions to determine terms in Eq. (32). For i > 3, these boundary value problems have null solutions. Henceforth we denote various constants by a superscript zero. For i ˆ 3, the solution is v 3 ˆ v 0 3 h0 3 r ; w 3 ˆ w 0 3 ; w3 ˆ w 0 3 : 33 The integrability conditions for the torque, axial force and the charge require that

9 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 29 h 0 3 ˆ 0; w0 3 ˆ n 3b b; w 0 3 ˆ n 4b b; 34 where n 3 ; n 4 and other n's introduced below are de ned in terms of other elastic constants in ppendix. With Eqs. (32) and (33), equations for the determination of v 2 ; w 2 and w 2 are F v 2 ˆ 0; D R ~w 2 ˆ 0; D Rw2 ~ ˆ 0; in ; G v 2 ˆ v 15 b b N v 16 e 3 n 4 c 3 k n 3 b b N; 35 grad ~w 2 N ˆ ~lv 0 3 N; grad w2 ~ N ˆ e 3 v 0 3 N; and their solution is v 2 ˆ v 0 2 h0 2 r B vr; w 2 ˆ w 0 2 v0 3 r; w2 ˆ w 0 2 ; 36 where B v ˆ n 5 b b r n 1 b b r n 2 b b r: 37 The integrability conditions for the torque, axial force and the electric charge require that h 0 2 ˆ v 12 v 13 v 35 J b b ~l w 0 2 ˆ 0; w0 2 ˆ 0: r 2 grad/ r d ; 38 Field equations and boundary conditions for the determination of v 1 ; w 1 and w 1 are F v 1 ˆ c 3 k v 0 3 ; D R ~w 1 ˆ n 6 b b; D R ~ w1 ˆ n 7 b b; G v 1 N ˆ c 3 k v 0 3 r N; grad ~w 1 N ˆ ~l v 0 2 N h0 2 r N v 11x v 14 b N ~ln 5 b b r N v 13 ~ln 1 b b r N v 12 ~ln 2 b b r N; 39 gradw 1 N ˆ e 3 v 0 2 N e 3h 0 2 r N v 2x v 5 b N e 3 n 5 b b r N v 4 e 3 n 1 b b r N v 3 e 3 n 2 b b r N: The solution of the boundary-value problem (39) is v 1 ˆ v 0 1 h0 1 r ~m r r s v0 3 ; w 1 ˆ w 0 1 v0 2 r h0 2 / r n 8x n 9 b r B w r r; 40 w 1 ˆ w 0 1 n 13x n 14 b r B w r r;

10 30 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 where B w ˆ n 10 b b n 11 b b n 12 b b ^IŠ; B w ˆ n 15 b b n 16 b b n 17 b b ^IŠ; 41 and ~m ˆ c 3 k =2 k l is the Poisson's ratio in the direction of transverse isotropy. Equations for nding elds v 0 ; w 0 and w 0 can be written as F v 0 ˆ c 3 k v 0 2 h0 2 c 3 k ~l grad/ ~l r Š n 18 x n 19 b Br; D R ~w 0 ˆ n 22 v 0 3 r; D R ~ w0 ˆ n 23 v 0 3 r; G v 0 N ˆ c 3 k v 0 2 r h0 2 / v 17x v 18 x 2 v 19 2 c 3 k w 0 1 e 2w 0 1 n 20 x n 21 b r Br r=2šn v 24 b r b r N ; grad ~w 0 N ˆ ~l v 0 1 h0 1 r ~m r r s v0 3 Š N; 42 grad w0 ~ N ˆ e 3 v 0 1 h0 1 r ~m r r s v0 3 Š N; where B ˆ v 8 b b v 9 b b 2 c 3 k ~l B w 2 e 2 e 3 B w ~lb v : 43 Note that B is a bilinear form in b and its eigenvectors are b and b. The solution of Eq. (42) is v 0 ˆ v 0 0 h0 0 r ~m r r s v0 2 v 17x v 18 x 2 v 19 2 c 3 k w 0 1 e 2w 0 1 r 2 k l n 18x n 19 r r r r b H r ; 4 k l w 0 ˆ w 0 0 v0 1 r h0 1 / r n 26U r n 27 W r ; w 0 ˆ w 0 0 n 27U r n 28 W r ; 44 where functions H; U and W are solutions of F H ˆ h 0 2 c 3 k ~l grad/ ~l r Š Br; G H N ˆ h 0 2 /N 1 Br rn; 2 D R U ˆ n 22 v 0 3 r; gradu N ˆ n 24 r r s v 0 3 ; D R W ˆ n 23 v 0 3 r; gradw N ˆ n 25 r r s v 0 3 : 45 The clamping conditions (6) require that v 0 0 ˆ 0; w0 0 ˆ 0; h0 0 ˆ 0; w0 0 ˆ 0; v0 1 ˆ 0: 46

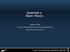
11 The second-order solution is speci ed by seven constants v 0 3 ; v0 2 ; h0 1 ; w0 1 and w0 1 representing second-order exure, bending, torsion, elongation and electric potential, respectively. We now consider the case when the resultant loads are R F ˆ f d ˆ Ne; R Q ˆ qd ˆ Q; R M ˆ x ^ f d ˆ Me ^ k; 47 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 31 where k is a unit vector in the cross-section. For these loads, ˆ n 29 N n 30 Q; x ˆ n 30 N n 31 Q; b ˆ ~EMJ 1 k ; 48 where ~E is the Young's modulus in the direction of transverse isotropy; an expression for ~E in terms of other material constants is given in the ppendix (see the line between expressions for n 31 and n 32 ). For loads given by Eq. (47) v r; z ˆ ~m 1 n 32 n 33 x r r s b m ax n 34 x n 35 2 n 36 x 2 J= n 38 b b n 39 b b r z2 2 1 ~m n 32 n 33 x b n 18x n 19 r r r r b H r z2 4 k l 2 h0 2 r B vr ; w r; z ˆ z ax m n 35 2 n 34 x n 36 x 2 ~m J n 38b b n 39 b b 49 z b r 1 ~mn 32 ~mn 33 x z h 0 2 / r B wr rš z3 6 n 3b b; h w r; z ˆ z x b m b 2 n 35 2 n 34 x n 36 a 2 x 2 ~m bj= n 38 b b i n 39 b b B w r r z3 6 n 4b b: 5. Discussion of results We now observe a few interesting features of the solution. When N ˆ Q ˆ 0 and M 6ˆ 0, i.e., the end faces of the bar are subjected to a pure bending moment, we conclude from Eq. (48) that ˆ x ˆ 0 and from Eq. (49) we get a second-order Poisson's e ect proportional to kbk 2 and a torsional e ect proportional to the square of the axial distance from the end face whose centroid is clamped. The term z 2 =2 B v r implies that a circular cross-section will be deformed into an ellipse and this distortion of the cross-section is proportional to the square of the distance from the `clamped' end face. In addition to the classical axial strain in the linear theory, there is an axial strain which depends quadratically upon b and also on z 2. For an isotropic material n 3 ˆ 1 and our results reduce to those of dell'isola et al. [19]. The term zh 0 2 / r in Eq. (49) 2 is associated with the torsional e ect mentioned above. The potential di erence

12 32 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 between the end faces is proportional to the cube of the length and is quadratic in b. The term multiplying z in Eq. (49) 3 can vanish for some cross-sections but that multiplying z 3 is always non-zero. Even if the magnitude of n 4 is small, one can enhance the potential di erence by increasing the length of the bar. One can determine the direction of bending because of the term zb w r r and the eigenvectors of B w are b and b. For an arbitrary choice of the values of material parameters and a circular cross-section, Fig. 1 depicts the electric potential generated by the term zb w r r for z ˆ 1. When M ˆ 0, b ˆ 0 but x and need not vanish. In this case we get second-order Poisson's e ect, axial strain and potential di erence between the end faces which are the same for every cross-section. Even for a second-order piezoelectric material, the electric eld does not induce any bending of the bar. The loadings M 6ˆ 0 and Q 6ˆ 0 result in interesting coupling e ects between bending and electric polarization. The curvature of the centroidal axis is given by v 00 j rˆ0 ˆ b 1 ~m n 32 n 33 x : 50 Thus the electric eld in uences the curvature of a prebent bar. The Poisson e ect and the axial strain associated with this are represented by the terms ~m r r s n 32 n 33 x b, ~m n 32 n 33 x b r in Eq. (49) 1 and Eq. (49) 2, respectively. Fig. 1. The electric potential generated by b w r r in a circular bar bent about the horizontal axis.

13 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 33 For a prismatic bar of circular cross-section J is a spherical tensor, J b b ˆ 0 and from Eq. (38) 1 we obtain h 0 2 ˆ 0. The boundary-value problem (45) 1 and (45) 2 for the determination of H simpli es to ld R H k l graddivh ˆ Br in ; 2l gradh s k divh ^IŠN ˆ R2 2 BN N N; on : 51 For the bending vector b directed along a principal axis of inertia of a rectangular cross-section, the boundary-value problem (45) 1 and (45) 2 for H can also be somewhat simpli ed. 6. Conclusions We have found a second-order solution for the Saint-Venant problem for a straight, prismatic, homogeneous and transversely isotropic body made of a second-order piezoelectric material. The bar is stress and polarization free in the reference con guration. It is initially bent, stretched and electrically polarized by an in nitesimal amount and then deformed by loads and electric potential applied to its end faces. The displacements, in nitesimal rotations and the electric potential are assumed to vanish at the centroid of one end face to eliminate trivial solutions of the problem. It is found that there is a second-order e ect, not of the Saint-Venant type, which is quadratic in the bending vector b, electric eld x and the axial elongation and varies as r 2 where r is the distance of the point from the centroidal axis. The in-plane displacements represented by H in Eq. (49) 1 can not be characterized unless the plane elliptic problem de ned by Eq. (45) 1 and Eq. (45) 2 has been solved. For a prismatic circular bar subjected to bending moments only at the end faces, in addition to the second-order Poisson's e ect proportional to kbk 2, there is also a torsional e ect proportional to the square of the distance from the `clamped' face. The circular cross-section is deformed into an ellipse and the distortion of the cross-section is proportional to the square of the distance from the `clamped' end. The potential di erence between the end faces of a prebent bar is proportional to the cube of its length and is quadratic in b. When a bending moment and an electric charge are simultaneously applied to the end faces of a prismatic bar, then the curvature of its centroidal axis is altered by the electric eld. cknowledgements R.C. Batra's and S. Vidoli's work was partially supported by the NSF grant CMS and the RO grant DG to Virginia Polytechnic Institute and State University. F. dell'isola thanks Prof. N. Rizzi for having secured nancial support for his visit to Virginia Tech. Many of the algebraic operations were performed by using Mathematica.

14 34 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 ppendix Using the notations _E ˆ _ H _ H T =2; E ˆ _H T _H=2; _I 1 ˆ e _ Ee ; I 1 ˆ e Ee ; _I 2 ˆ tr _ H; I 2 ˆ tr E; _I 3 ˆ _W e; P 1 ˆ e _ E 2 e ; P 2 ˆ tr _ E 2 ; P 3 ˆ _W _W; P 4 ˆ e _ E _ W _ W _ Ee ; constitutive relations for second-order transversely isotropic material with the axis of transverse isotropy along the unit vector e are as follows: _T ˆ 2c 1 _I 1 c 3 _I 2 e 1 _I 3 e e 2c 2 _I 2 c 3 _I 1 e 2 _I 3 1 c 4 e Ee _ s 2c 5 E _ e3 e W ; _ T ˆ 2c 1 I 1 c 3 I 2 3k 1 _I 2 1 2k _ 3 I 1 _I 2 k 4 _I 2 2 k 5P 1 k 7 P 2 2m 1 _I 1 _I 3 m 2 _I 2 3 m 7 P 3 m 9 P 4 m 14 _I 2 _I 3 Še e 2c 2 I 2 c 3 I 1 3k 2 _I 2 2 k 3 _ I 2 1 2k 4 _ I 1 _I 2 k 6 P 1 k 8 P 2 2m 3 _I 2 _I 3 m 4 _I 2 3 m 8P 3 m 10 P 4 m 14 _I 1 _I 3 Š1 2c 4 e Ee _ s 2 k 5 _I 1 k 6 _I 2 m 5 _I 3 e Ee _ s 2c 5 E 2 k7 _I 1 k 8 _I 2 m 6 _I 3 _ E 2 m 9 _I 1 m 10 _I 2 m 11 _I 3 e _ W s 3k 9 _ E 2 m 12 _W _ W 2m 13 e _ E _ W _ W _ Ee s Hf 2c _ 1 _I 1 c 3 _I 2 e 1 _I 3 e e 2c 2 _I 2 c 3 _I 1 e 2 _I 3 1 c 4 e Ee _ s 2c 5 E _ e3 e W _ s g; _D ˆ 2 1 _I 3 e 1 _I 1 e 2 _I 2 e W _ 2e 3 Ee; _ D ˆ W _I 2 _H 2 E _ W _ 2 1 I 3 e 1 I 1 e 2 I 2 3l 1 _I 2 3 l 2P 3 m 1 _I 2 1 2m _ 2 I 3 _I 1 m 3 _I 2 2 2m 4 _I 3 _I 2 m 5 P 1 m 6 P 2 m 11 P 4 m 14 _I 1 _I 2 Še 2 l 2 _I 3 m 7 _I 1 m 8 _I 2 Š _ W 2e 3 Ee 2 m9 _I 1 m 10 _I 2 m 11 _I 3 _ Ee 2m 12 _ E _W 2m 13 E 2 e: Here c 1 ; c 2 ; :::; e 1 ; e 2 ; :::; k 1 ; k 2 ; :::; m 1 ; m 2 ; :::; 1 ; 2 ; :::; and l 1 ; l 2 ; ::: are material parameters. Expressions for v 1 ; v 2... and n 1 ; n 2 ;... in terms of these material parameteres are given below, and b^c equals b raised to the power c. v 1 ˆ e 1 2e 2 3e 3 ; v 2 ˆ 3k 2l e 2 e 3 = 2 k l c 3 ; v 3 ˆ 3k 2l e 3 = 2 k l ; v 4 ˆ ke 3 = 2 k l ; v 5 ˆ 3k 2l e 3 = 2 k l ;

15 v 6 ˆ 2k 3l 2c 1 4c 3 5c 4 =2; v 7 ˆ 1= 4 k l ^ 2c 3 e 2 6k ^ 3 4k ^ 2l 6kl ^ 2 4l ^ 3 8 k l ^ 2c 1 5k ^ c 4 11klc 4 6l ^ 2c 4 24l ^ 2k 2 8k ^ 2k 3 16klk 3 8l ^ 2k 3 16klk 4 16l ^ 2k 4 8k ^ 2k 6 16klk 6 8l ^ 2k 6 8k ^ 2k 7 8klk 7 12k ^ 2k 8 8klk 8 8l ^ 2k 8 6k ^ 2k 9 2 k l c 3 2 k l e 1 ke 2 4ke 3 4le 3 4lm 3 2km 6 4km 10 4lm 10 2km 14 2km 14 ; v 8 ˆ 1= 4 k l ^ 2 6k ^ 3 4k ^ 2l 6kl ^ 2 4l ^ 3 8 k l ^ 2c 1 2 k ^ 2 3kl 2l ^ 2 c 3 5k ^ 2c 4 11klc 4 6l ^ 2c 4 24l ^ 2k 2 8k ^ 2k 3 16klk 3 8l ^ 2k 3 16klk 4 16l ^ 2k 4 8k ^ 2k 6 16klk 6 8l ^ 2k 6 8k ^ 2k 7 8klk 7 12k ^ 2k 8 8klk 8 8l ^ 2k 8 6k ^ 2k 9 ; v 9 ˆ k 2k 2l 2c 3 ˆ c 4 = 4 k l ; v 10 ˆ 1= 4 k l ^ 2e 2 e 2 6k ^ 3 4k ^ 2l 6kl ^ 2 4l ^ 3 8 k l ^ 2c 1 5k ^ 2c 4 11klc 4 6l ^ 2c 4 24l ^ 2k 2 8k ^ 2k 3 16klk 3 8l ^ 2k 3 16klk 4 16l ^ 2k 4 8k ^ 2k 6 16klk 6 8l ^ 2k 6 8k ^ 2k 7 8klk 7 12k ^ 2k 8 8l ^ 2k 8 6k ^ 2k 9 ke 2 4ke 3 4le 3 4lm 3 2km 6 4km 10 4lm 10 2km 14 2lm 14 ; v 11 ˆ 3k 2l 2l c 4 e 2 = 4 k l c 3 ; v 12 ˆ 4 k l c 3 3k 2l 2l c 4 = 4 k l ; v 13 ˆ k 2l c 4 = 4 k l ; v 14 ˆ 3k 2l 2l c 4 = 4 k l ; v 15 ˆ 2l; v 16 ˆ 2k 2l c 3 ; S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 35 v 17 ˆ 1= 2 k l ^ 2c 3 e 2 e 2 2 3k ^ 3 5k ^ 2l 2kl ^ 2 12l ^ 2k 2 4k ^ 2k 3 8klk 3 4l ^ 2k 3 8klk 4 8l ^ 2k 4 4k ^ 2k 6 8klk 6 4l ^ 2k 6 4k ^ 2k 7 4klk 7 6k ^ 2k 8 4klk 8 4l ^ 2k 8 3k ^ 2k 9 2 k l ^ 2c m 4 2m 8 2 k l c 3 e 2 k l e 2 2 2lm 3 km 6 2km 10 2lm 10 km 14 lm 14 ;

16 36 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 v 18 ˆ 1= 4 k l ^ 2c 2 3 e2 2 3k ^ 3 5k ^ 2l 2kl ^ 2 12l ^ 2k 2 4k ^ 2k 3 8klk 3 4l ^ 2k 3 8klk 4 8l ^ 2k 4 4k ^ 2k 6 8klk 6 4l ^ 2k 6 4klk 7 4klk 7 6k ^ 2k 8 4klk 8 4l ^ 2k 8 3k ^ 2k 9 2 k l ^ 2c m 4 2m 8 2 k l c 3 e 2 k l e 2 2 2lm 3 km 6 2km 10 2lm 10 km 14 lm 14 ; v 19 ˆ 1= 4 k l ^ 2e 2 2 e2 2 3k ^ 3 5k ^ 2l 2kl ^ 2 12l ^ 2k 2 4k ^ 2k 3 8klk 3 4l ^ 2k 3 8klk 4 8l ^ 2k 4 4k ^ 2k 6 8klk 6 4l ^ 2k 6 4k ^ 2k 7 4klk 7 6k ^ 2k 8 4klk 8 4l ^ 2k 8 3k ^ 2k 9 2 k l ^ 2c m 4 2m 8 2 k l c 3 e 2 k l e 2 2 2lm 3 km 6 2km 10 2lm 10 km 14 lm 14 ; v 20 ˆ 1= 2 k l ^ 2c 3 e 2 3k ^ 3 5k ^ 2l 2kl ^ 2 k ^ 2 3kl 2l ^ 2 c 3 12l ^ 2k 2 4 ^ 2k 3 8klk 3 4l ^ 2k 3 8klk 4 8l ^ 2k 4 4k ^ 2k 6 8klk 6 4l ^ 2k 6 4k ^ 2k 7 4klk 7 6k ^ 2k 8 4klk 8 4l ^ 2k 8 3k ^ 2k 9 2 k l c 3 2lm 3 km 6 2km 10 2lm 10 km 14 lm 14 ; v 21 ˆ 1= 2 k l ^ 2e 2 e 2 3k ^ 3 5k ^ 2l 2kl ^ 2 k ^ 2 3kl 2l ^ 2 c 3 12l ^ 2k 2 4 ^ 2k 3 8klk 3 4l ^ 2k 3 8klk 4 8l ^ 2k 4 4k ^ 2k 6 8klk 6 4l ^ 2k 6 4k ^ 2k 7 4klk 7 6k ^ 2k 8 4klk 8 4l ^ 2k 8 3k ^ 2k 9 2 k l c 3 2lm 3 km 6 2km 10 2lm 10 km 14 lm 14 ; v 22 ˆ 1= 4 k l ^ 2 3k ^ 3 5k ^ 2l 2kl ^ 2 2l k l c 3 12l ^ 2k 2 4k ^ 2k 3 8klk 3 4l ^ 2k 3 8klk 4 8l ^ 2k 4 4k ^ 2k 6 8klk 6 4l ^ 2k 6 4k ^ 2k 7 4klk 7 6k ^ 2k 8 4klk 8 4l ^ 2k 8 3k ^ 2k 9 ; v 23 ˆ k ^ 2= 4 k l ; v 25 ˆ e 1 2 e 2 e 3 ; v 26 ˆ k 2l c 4 = 4 k l ; v 27 ˆ 6kl 4l ^ 2 8 k l c 1 4 k 2l c 3 5kc 4 6lc 4 = 4 k l ; v 28 ˆ 2c 1 3c 3 2 k l c 4 ; v 29 ˆ 1= 4 k l e 2 6kl 4l ^ 2 8 k l c 1 5kc 4 6lc 4 e 2 4c 3 k l e 1 le 2 2ke 3 2le 3 ;

17 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 37 v 30 ˆ 1= 4 k l c 3 6kl 4l ^ 2 8 k l c 1 5kc 4 6lc 4 e 2 4c 3 k l e 1 le 2 2ke 3 2le 3 ; v 31 ˆ 1=4 4k 4l 3kl = k l 4c 1 6c 3 4c 4 3kc 4 = 2 k l ; v 32 ˆ 1= 8 k l 8k ^ 2 10kl 4l ^ 2 16 k l c 1 4 4k 5l c 3 7kc 4 10lc 4 ; v 33 ˆ 1= 8 k l e 2 6kl 4l ^ 2 8 k l c 1 kc 4 2lc 4 e 2 4c 3 k l e 1 le 2 2ke 3 2le 3 ; v 34 ˆ 1= 8 k l c 3 6kl 4l ^ 2 8 kl c 1 kc 4 2lc 4 e 2 4c 3 k l e 1 le 2 2ke 3 2le 3 ; v 35 ˆ 2kl 2l ^ 2 4 k l c 1 2 k 2l c 3 2kc 4 3lc 4 = 4 k l ; v 36 ˆ 1= 8 k l e 2 6kl 4l ^ 2 8 k l c 1 5kc 4 6lc 4 e 2 4c 3 k l e 1 le 2 2ke 3 2le 3 ; v 37 ˆ 1= 8 k l c 3 6kl 4l ^ 2 8 k l c 1 5kc 4 6lc 4 e 2 4c 3 k l e 1 le 2 2ke 3 2le 3 ; v 38 ˆ e 1 2 e 2 e 3 ; v 39 ˆ 1= 4e 2 2 k l ^ 2 12c2 3 k l ^ 2 l 1 l 2 4c 3 e 2 k l k 2 3m 11 2m 12 2m 2 2m 7 l 1 3m 11 2m 12 2m 2 2m 4 2m 7 2m 8 e 2 2 3e 2k ^ 2 4e 3 k ^ 2 4e 2 kl 8e 3 kl 2e 2 l ^ 2 4e 3 l ^ 2 2e 1 k l ^ 2 4k ^ 2m 1 8kmm 1 4l ^ 2m 1 4klm 10 4l ^ 2m 10 8k ^ 2m 13 16klm 13 8l ^ 2m 13 4klm 14 4l ^ 2m 14 4l ^ 2m 3 4k ^ 2m 5 8klm 5 4l ^ 2m 5 6k ^ 2m 6 8klm 6 4l ^ 2m 6 4k ^ 2m 9 8kxlm 9 4l ^ 2m 9 ; v 40 ˆ 1= 4c 2 3 k l ^ 2 12c2 3 k l ^ 2 l 1 l 2 4c 3 e 2 k l k 2 3m 11 2m 12 2m 2 2m 7 l 1 3m 11 2m 12 2m 2 2m 4 2m 7 2m 8 e 2 2 3e 2k ^ 2 4e 3 k ^ 2 4e 2 kl 8e 3 kl 2e 2 l ^ 2 4e 3 l ^ 2 2e 1 k l ^ 2 4k ^ 2m 1 8kmm 1 4l ^ 2m 1 4klm 10 4l ^ 2m 10 8k ^ 2m 13 16klm 13 8l ^ 2m 13 4klm 14 4l ^ 2m 14 4l ^ 2m 3 4k ^ 2m 5 8klm 5 4l ^ 2m 5 6k ^ 2m 6 8klm 6 4l ^ 2m 6 4k ^ 2m 9 8klm 9 4l ^ 2m 9 ; v 41 ˆ 1= 2c 3 e 2 k l ^ 2 12c 2 3 k l ^ 2 l 1 l 2 4c 3 e 2 k l k 2 3m 11 2m 12 2m 2 2m 7 l 1 3m 11 2m 12 2m 2 2m 4 2m 7 2m 8 4l ^ 2k 8 3k ^ 2k 9 e 2 2 3e 2k ^ 2 4e 3 k ^ 2 4e 2 kl 8e 3 kl 2e 2 l ^ 2 4e 3 l ^ 2 2e 1 k l ^ 2 4k ^ 2m 1 8kmm 1 4l ^ 2m 1 4klm 10 4l ^ 2m 10 8k ^ 2m 13 16klm 13 8l ^ 2m 13 4klm 14 4l ^ 2m 14 4l ^ 2m 3 4k ^ 2m 5 8klm 5 4l ^ 2m 5 6k ^ 2m 6 8klm 6 4l ^ 2m 6 4k ^ 2m 9 8klm 9 4l ^ 2m 9 ; v 42 ˆ e 2 k ^ 2 = 4 k l ^ 2 ;

18 38 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 v 43 ˆ e 1 =2 e 3 1=4e 2 2 k ^ 2= k l ^ 2 m 1 m 10 km 10 = k l 2m 13 m 14 km 14 = k l m 3 k ^ 2m3 = k l ^ 2 2km 3 = k l m 5 m 6 k ^ 2m 6 = 2 k l ^ 2 m 9 ; v 44 ˆ 2c 1 3c 3 2 c 4 k l ; v 45 ˆ 1= 4e 2 k l e 2 5c 4 k 6c 4 l 6kl 4l ^ 2 8c 1 k l 4c 3 2e 3 k e 2 l 2e 3 l e 1 k l ; v 46 ˆ 1= 4c 3 k l e 2 5c 4 k 6c 4 l 6kl 4l ^ 2 8c 1 k l 4c 3 2e 3 k e 2 l 2e 3 l e 1 k l ; v 47 ˆ 1= 4e 2 2 k l ^ 2 e2 2 12c 4k ^ 2 3k ^ 3 12k ^ 2k 1 4k ^ 2k 3 12k ^ 2k 5 4k ^ 2k 6 14k ^ 2k 7 6k ^ 2k 8 12k ^ 2k 9 24c 4 kl 20k ^ 2l 24kk 1 l 16kk 3 l 8kk 4 l 24kk 5 l 16kk 6 l 24kk 7 l 16kk 8 l 24kk 9 l 12c 4 l ^ 2 30kl ^ 2 12k 1 l ^ 2 12k 2 l ^ 2 12k 3 l ^ 2 12k 4 l ^ 2 12k 5 l ^ 2 12k 6 l ^ 2 12k 7 l ^ 2 12k 8 l ^ 2 12k 9 l ^ 2 12l ^ 3 12c 1 k l ^ 2 2c 2 3 k l ^ 1 4e 1 4e 2 4m 11 2m 12 2m 2 2m 4 2m 7 2m 8 c 3 e 2 e 2 5k ^ 2 16kl 12l ^ 2 4 k l 2km 1 2lm 1 2km 10 4lm 10 4km 13 4lm 13 km 14 2lm 14 2lm 3 2km 5 2lm 5 2km 6 2lm 6 4km 9 4lm 9 ; v 48 ˆ 1= 4c 2 3 k l ^ 2 e2 2 12c 4k ^ 2 3k ^ 3 12k ^ 2k 1 4k ^ 2k 3 12k ^ 2k 5 4k ^ 2k 6 14k ^ 2k 7 6k ^ 2k 8 12k ^ 2k 9 24c 4 kl 20k ^ 2l 24kk 1 l 16kk 3 l 8kk 4 l 24kk 5 l 16kk 6 l 24kk 7 l 16kk 8 l 24kk 9 l 12c 4 l ^ 2 30kl ^ 2 12k 1 l ^ 2 12k 2 l ^ 2 12k 3 l ^ 2 12k 4 l ^ 2 12k 5 l ^ 2 12k 6 l ^ 2 12k 7 l ^ 2 12k 8 l ^ 2 12k 9 l ^ 2 12l ^ 3 12c 1 k l ^ 2 2c 2 3 k l ^ 1 4e 1 4e 2 4m 11 2m 12 2m 2 2m 4 2m 7 2m 8 c 3 e 2 e 2 5k ^ 2 16kl 12l ^ 2 4 k l 2km 1 2lm 1 2km 10 4lm 10 4km 13 4lm 13 km 14 2lm 14 2lm 3 2km 5 2lm 5 2km 6 2lm 6 4km 9 4lm 9 ; v 49 ˆ 1= 2c 3 e 2 k l ^ 2 e c 4k ^ 2 3k ^ 3 12k ^ 2k 1 4k ^ 2k 3 12k ^ 2k 5 4k ^ 2k 6 14k ^ 2k 7 6k ^ 2k 8 12k ^ 2k 9 24c 4 kl 20k ^ 2l 24kk 1 l 16kk 3 l 8kk 4 l 24kk 5 l 16kk 6 l 24kk 7 l 16kk 8 l 24kk 9 l 12c 4 l ^ 2 30kl ^ 2 12k 1 l ^ 2 12k 2 l ^ 2 12k 3 l ^ 2 12k 4 l ^ 2 12k 5 l ^ 2 12k 6 l ^ 2 12k 7 l ^ 2 12k 8 l ^ 2 12k 9 l ^ 2 12l ^ 3 12c 1 k l ^ 2 2c 2 3 k l ^ 1 4e 1 4e 2 4m 11 2m 12 2m 2 2m 4 2m 7 2m 8 c 3 e 2 e 2 5k ^ 2 16kl 12l ^ 2 4 k l 2km 1 2lm 1 2km 10 4lm 10 4km 13 4lm 13 km 14 2lm 14 2lm 3 2km 5 2lm 5 2km 6 2lm 6 4km 9 4lm 9 ; v 50 ˆ k ^ 2 c 3 k = 4 k l ^ 2 ;

19 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 39 v 51 ˆ 1= 4 k l ^ 2 12c 4 k ^ 2 3k ^ 3 12k ^ 2k 1 4k ^ 2k 3 12k ^ 2k 5 4k ^ 2k 6 14k ^ 2k 7 6k ^ 2k 8 12k ^ 2k 9 24c 4 kl 20k ^ 2l 24kk 1 l 16kk 3 l 8kk 4 l 24kk 5 l 16kk 6 l 24kk 7 l 16kk 8 24kk 9 l 12c 4 l ^ 2 30kl ^ 2 12k 1 l ^ 2 12k 2 l ^ 2 12k 3 l ^ 2 12k 4 l ^ 2 12k 5 l ^ 2 12k 6 l ^ 2 12k 7 l ^ 2 12k 8 l ^ 2 12k 9 l ^ 2 12l ^ 3 12c 1 k l ^ 2 c 3 9k ^ 2 20kl 12l ^ 2 ; v 52 ˆ1= 4e 2 k l e 2 5c 4 k 6c 4 l 6kl 4l ^ 2 8c 1 k l 4c 3 2e 3 k e 2 l 2e 3 l e 1 k l ; v 53 ˆ1= 4c 3 k l e 2 5c 4 k 6c 4 l 6kl 4l ^ 2 8c 1 k l 4c 3 2e 3 k e 2 l 2e 3 l e 1 k l ; v 54 ˆ 2c 4 k 3c 4 l 2kl 2l ^ 2 4c 1 k l 2c 3 k 2l = 4 k l ; v 55 ˆ 1= 4e 2 k l ^ 2 12c 1 e 2 k l ^ 2 e 2 12c 4 k ^ 2 3k ^ 3 12k ^ 2k 1 4k ^ 2k 3 12k ^ 2k 5 4k ^ 2k 6 14k ^ 2k 7 6k ^ 2k 8 12k ^ 2k 9 24c 4 kl 20k ^ 2l 24kk 1 l 16kk 3 l 8kk 4 24kk 5 l 16kk 6 l 24kk 7 l 16kk 8 l 24kk 9 l 12c 4 l ^ 2 30kl ^ 2 12k 1 l ^ 2 12k 2 l ^ 2 12k 3 l ^ 2 12k 4 l ^ 2 12k 5 l ^ 2 12k 6 l ^ 2 12k 7 l ^ 2 12k 8 l ^ 2 12k 9 l ^ 2 12l ^ 3 c 3 7e 2 k ^ 2 18e 2 kl 12e 2 l ^ 2 4k ^ 2m 1 8klm 1 4l ^ 2m 1 4k ^ 2m 10 12klm 10 8l ^ 2m 10 8k ^ 2m 13 16klm 13 8l ^ 2m 13 2l ^ 2m 14 6klm 14 4l ^ 2m 14 4klm 3 4l ^ 2m 3 4k ^ 2m 5 8klm 5 4l ^ 2m 5 4k ^ 2m 6 8klm 6 4l ^ 2m 6 8k ^ 2m 9 16klm 9 8l ^ 2m 9 ; v 56 ˆ 1= 4c 3 k l ^ 2 12c 1 e 2 k l ^ 2 e 2 12c 4 k ^ 2 3k ^ 3 12k ^ 2k 1 4k ^ 2k 3 12k ^ 2k 5 4k ^ 2k 6 14k ^ 2k 7 6k ^ 2k 8 12k ^ 2k 9 24c 4 kl 20k ^ 2l 24kk 1 l 16kk 3 l 8kk 4 24kk 5 l 16kk 6 l 24kk 7 l 16kk 8 l 24kk 9 l 12c 4 l ^ 2 30kl ^ 2 12k 1 l ^ 22 12k 2 l ^ 2 12k 3 l ^ 12k 4 l ^ 2 12k 5 l ^ 2 12k 6 l ^ 2 12k 7 l ^ 2 12k 8 l ^ 2 12k 9 l ^ 2 12l ^ 3 c 3 7e 2 k ^ 2 18e 2 kl 12e 2 l ^ 2 4k ^ 2m 1 8klm 1 4l ^ 2m 1 4k ^ 2m 10 12klm 10 8l ^ 2m 10 8k ^ 2m 13 16klm 13 8l ^ 2m 13 2l ^ 2m 14 6klm 14 4l ^ 2m 14 4klm 3 4l ^ 2m 3 4k ^ 2m 5 8klm 5 4l ^ 2m 5 4k ^ 2m 6 8klm 6 4l ^ 2m 6 8k ^ 2m 9 16klm 9 8l ^ 2m 9 ; n 1 ˆ c 3 k 2 k l ; n 2 ˆ c 3 3k 2l ; 2 k l n 3 ˆ c 2 3 c 4 e 1 e 2 5e 2 2 2e 2e 3 5k 10 1 k 10 2 k 4l 8 1 l 8 2 l

20 40 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 2 2c 1 e 2 2 2c 1e 2 e 3 2c 1 k 4 1 c 1 k 4 2 c 1 k e 2 1 k 5e 1e 3 k 6e 2 3 k 2c 1l 4 1 c 1 l 4 2 c 1 l e 2 1 l 3e 1e 2 l 4e 2 2 l 4e 1 e 3 l 4e 2 e 3 l 4e 2 3 l 4kl 8 1l 8 2 kl 2l l l 2 c c 4 2 2e 1 e 2 e 2 2 e 1e 3 4e 2 e 3 2e 2 3 k 2 1k 2 2 k 2l 4 1 l 4 2 l = c 2 3 c 3 c c c 4 4e 1 e 2 2e 1 e 3 10e 2 e 3 4e 2 3 6l 12 1l 12 2 l c 4 e 1 e 2 5e 2 2 2e 2e 3 5k 10 1 k 10 2 k 4l 8 1 l 8 2 l 2 c 1 e 2 2 2c 1e 2 e 3 2c 1 k 4 1 c 1 k 4 2 c 1 k e 2 1 k 5e 1e 3 k 6e 2 3 2c 1l 4 1 c 1 l 4 2 c 1 l e 2 1 l 3e 1e 2 l 4e 2 2 l 4e 1e 3 l 4e 2 e 3 l 4e 2 3 l 4kl 8 1 kl 8 2 kl 2l l l 2 ; n 4 ˆ 2c 3 c 3 e 2 e 3 3e 3 k e 2 l 2e 3 l e 1 k l = c 2 3 c 3 c c c 4 4e 1 e 2 2e 1 e 3 10e 2 e 3 4e 2 3 6l 12 1l 12 2 l c 4 e 1 e 2 5e 2 2 2e 2e 3 5k±10 1 k 10 2 k 4l 8 1 l 8 2 l 2 2c 1 e 2 2 2c 1e 2 e 3 2c 1 k 4 1 c 1 k 4 2 c 1 k e 2 1 k 5e 1e 3 k 6e 2 3 k 2c 1l 4 1 c 1 l 4 2 c 1 l e 2 1 l 3e 1e 2 l 4e 2 2 l 4e 1e 3 l 4e 2 e 3 l 4e 2 3 l 4kl 8 1kl 8 2 kl 2l l l 2 ; n 5 ˆ c 3 3 c c 4 2 2e 1 e 2 e 1 e 3 5e 2 e 3 2e 2 3 2k 4 1k 4 2 k 2l 4 1 l 4 2 l c 3 c 4 e 1 e 2 5e 2 2 2e 2e 3 6k 12 1 k 12 2 k 4l 8 1 l 8 2 l 2 2c 1 e 2 2 2c 1e 2 e 3 2c 1 k 4 1 c 1 k 4 2 c 1 k e 2 1 k 3e 1e 2 k e 2 2 k 6e 1e 3 k 7e 2 e 3 k 8e 2 3 k k2 2 2 k 2 2c 1 l 4 1 c 1 l 4 2 c 1 l e 2 1 l 2e 1e 2 l 3e 2 2 l 4e 1 e 3 l 2e 2 e 3 l 4e 2 3 l 6kl 12 1kl 12 2 kl 2l l l 2 k c 4 e 1 e 2 5e 2 2 2e 2e 3 5k 10 1 k 10 2 k 4l 8 1 l 8 2 l 2 2c 1 e 2 2 2c 1e 2 e 3 2c 1 k 4 1 c 1 k 4 2 c 1 k e 2 1 k 5e 1e 3 l 6e 2 3 k 2c 1l 4 1 c 1 l 4 2 c 1 l e 2 1 l 3e 1e 2 l 4e 2 2 l 4e 1 e 3 l 4e 2 e 3 l 4e 2 3 l 4kl 8 1kl 2 kl 2l l l 2 = 2 k l c 2 3 c 4 e 1 e 2 5e 2 2 2e 2e 3 5k 10 1 k 10 2 k 4l 8 1 l 8 2 l 2 2c 1 e 2 2 2c 1e 2 e 3 2c 1 k 4 1 c 1 k 4 2 c 1 k e 2 1 k 5e 1e 3 k 6e 2 3 k 2c 1l 4 1 c 1 l e 2 1 l 3e 1e 2 l 4e 2 2 l 4e 1e 3 l 4e 2 e 3 l 4kl 8 1 kl 8 2 kl 2l l l 2 c c 4 2 2e 1 e 2 e 1 e 3 5e 2 e 3 2e 2 3 3l 6 1l 6 2 l ;

21 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 41 n 6 ˆ 4c c 2 3 2c 4e 2 3 2c 4e 2 e 3 2c 4 k 4 1 c 4 k 4 2 c 4 k e 2 1 k 5e 1e 3 k 6e 2 3 k 2c 4l 4 1 c 4 l 4 2 c 4 l e 2 1 l 2e 1e 2 l 3e 2 2 l 4e 1e 3 l 2e 2 e 3 l 4e 2 3 l 3kl 6 1kl 6 2 kl 2l l l 2 c 3 5e 2 e 3 2e 2 3 e 1 2e 2 e 3 2l 4 1 l 4 2 l 2c 1 e 2 2 e 2e 3 k 2 1 k 2 2 k l 2 1 l 2 2 l = c 2 3 c 3 c 4 c 3 c c c 4 4e 1 e 2 2e 1 e 3 10e 2 e 3 4e 2 3 6l 12 1 l 12 2 l c 4 e 1 e 2 5e 2 2 2e 2e 3 5k 10 1 k 10 2 k 4l 8 1 l 8 2 l 2 2c 1 e 2 2 2c 1e 2 e 3 2c 1 k 4 1 c 1 k 4 2 c 1 k e 2 1 k 5e 1 e 3 k 6e 2 3 k 2c 1l 4 1 c 1 l 4 2 c 1 l e 2 1 l 3e 1e 2 l 4e 2 2 l 4e 1 e 3 l 4e 2 e 3 l 4e 2 3 l 4kl 8 1kl 8 2 kl 2l l l 2 ; n 7 ˆ 4c 3 e c 3 e 1 e 2 e 2 2 2e 2e 3 k 2 1 k 2 2 k = c 2 3 c 3 c c c 4 4e 1 e 2 2e 1 e 3 10e 2 e 3 4e 2 3 6l 12 1l 12 2 l c 4 e 1 e 2 5e 2 2 2e 2e 3 5k 10 1 k 10 2 k 4l 8 1 l 8 2 l 2 2c 1 e 2 2 2c 1e 2 e 3 2c 1 k 4 1 c 1 k 4 2 c 1 k e 2 1 k 5e 1e 3 k 6e 2 3 2c 1l 4 1 c 1 l 4 2 c 1 l e 2 1 l 3e 1e 2 l 4e 2 2 l 4e 3 1 l 4e 2e 3 l 4e 2 3 l 4kl 8 1kl 8 2 kl 2l l l 2 ; n 8 ˆ e 2 3k 2l 1 2 c 4 2 e l 2c 3 k l 1 2 c 4 2 e 2 3 l ; 2l n 9 ˆ 3k 2l 1 2 c 4 2 e l 2 k l 1 2 c 4 2 e 2 3 l ; 2l n 10 ˆ c 3 2k 1 2 c 4 2 e l 4 k l 1 2 c 4 2 e 2 3 l ; 2l n 11 ˆ c3 1 2 c 4 2 e k l 4 k l 1 2 c 4 2 e 2 3 l ; 2l n 12 ˆ 2l c 4 2 2l c 4 2e l c 4 2 c 4 2 l e 2 3 n 5; e 2 e 3 c 4 2l 3k 2l n 13 ˆ c 3 k l c 4 2 c 4 2 e 2 3 l 2l ;

22 42 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 e 3 c 4 2l 3k 2l n 14 ˆ k l c 4 2 c 4 2 e 2 3 l 2l ; e 3 c 3 2k c 4 2l n 15 ˆ 2 k l 1 2 c 4 2 e 2 3 l 2l ; c 3 e 3 c 4 2k n 16 ˆ 2 k l 1 2 c 4 2 e 2 3 l 2l ; 2l c 4 e 3 n 17 ˆ c 4 2 2l c 4 2 l e 2 3 n 5; 1 k l 3k 2l 2 k l 2c 3 c 4 e 2 2l c 4 2 2l c 4 2e 2 3 n 18 ˆ 4k l 2 c 3 c 4 2 2l c 4 2 l e k l 3k 2l 2l c 4 e 2 e 3 e 2 e 3 c 4 2 2l c 4 2 l e 2 3 e 2 8 k l 2 c 1 5k 2 11kl 6l 2 c 4 2 3k 3 2k 2 l 3kl 2 2l 3 12l 2 k 2 4k 2 k 3 8klk 3 4l 2 k 3 8klk 4 8l 2 k 4 4k 2 k 6 8klk 6 4l 2 k 6 4k 2 k 7 4klk 7 6k 2 k 8 4klk 8 4l 2 k 8 3k 2 k 9 2 k l c 3 2 k l e 1 ke 2 4ke 3 4le 3 4lm 3 2km 6 4km 10 4lm 10 2km 14 lm 14 ; 1 k l 3k 2l 2 k l 2c 3 c 4 2l c 4 2 2l c 4 2e 2 3 n 19 ˆ 4k l 2 c 3 c 4 2 2l c 4 2 l e k l 3k 2l 2l c 4 e 2 e 3 e 2 e 3 c 4 2 2l c 4 2 l e e 2 e 2 6k 3 4k 2 l 6kl 2 4l 3 8 k l 2 c 1 5k 2 c 4 11klc 4 6l 2 c 4 24l 2 k 2 8k 2 k 3 16klk 3 8l 2 k 3 16klk 4 16l 2 k 4 8l 2 k 4 8k 2 k 6 16klk 6 8l 2 k 6 8k 2 k 7 8klk 7 12k 2 k 8 8klk 8 8l 2 k 8 6k 2 k 9 2 k l c 3 2 k l e 1 ke 2 4ke 3 4le 3 4lm 3 2km 6 4km 10 4lm 10 2km 14 lm 14 ; 1 2 k l 3k 2l 2l c 4 e 2 2 n 20 ˆ e 3 2 k l 2 c 3 c 4 e 2 2l c 4 2 l e 2 3 k l 3k 2l k c 3 e 2 1 e 2 c 4 2 l 1 2 e 2 3 c 4 2 2l c 4 2 l e 2 3 e 2 3k 3 5k 2 l 2kl 2 k 2 3kl 2l 2 c 3 12l 2 k 2 4k 2 k 3 8klk 3 4l 2 k 3 8klk 4 8l 2 k 4 4k 2 k 6 8klk 6 4l 2 k 6 4k 2 k 7 4klk 7 6k 2 k 8 4klk 8 4l 2 k 8 3k 2 k 9 2 k l c 3 2lm 3 km 6 k l 2m 10 m 14 ;

23 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21± k l 3k 2l 2l c 4 e 2 e 3 n 21 ˆ 2 k l 2 c 4 2 2l c 4 2 l e 2 3 k l 3k 2l k c c 4 2 l 1 2 e 2 3 c 4 2 2l c 4 2 l e e 2 e 2 3k 3 5k 2 l 2kl 2 k 2 3kl 2l 2 c 3 12l 2 k 2 4k 2 k 3 8klk 3 4l 2 k 3 8klk 4 8l 2 k 4 4k 2 k 6 8klk 6 4l 2 k 6 4k 2 k 7 4klk 7 6k 2 k 8 4klk 8 4l 2 k 8! 3k 2 k 9 2 k l c 3 2lm 3 km 6 2km 10 2lm 10 km 14 lm 14 ; n 22 ˆ2 c 1 k=2 c 3 c 4 l c 3 k c 4 =2 l c 3 k = k l ; n 23 ˆ e 2 e 3 c 3 k = k l e 1 e 2 2e 3 ; n 24 ˆ k c 3 2l c 4 ; 2 k l n 25 ˆ k c 3 e 3 k l ; n 26 ˆ c 4 2 2l c 4 2 l e 2 3 ; 2e 3 n 27 ˆ c 4 2 2l c 4 2 l e 2 3 ; 2l c 4 n 28 ˆ c 4 2 2l c 4 2 l e 2 3 ; n 29 ˆ k l 2 k l 1 2 k l 2 e 2 2 = 3kl 2l2 2kc 1 2lc 1 kc 3 2lc 3 2kc 4 2lc kl 2l 2 2kc 1 2lc 1 kc 3 2lc 3 2kc 4 2lc kl 2l 2 2kc 1 2lc 1 kc 3 2lc 3 2kc 4 2lc 4 ke 2 1 le2 1 2le 1e 2 c 3 e 1 e 2 3le 2 2 2c 1e 2 2 c 3e 2 2 2c 4e 2 2 4ke 1e 3 4le 1 e 3 4le 2 e 3 2c 3 e 2 e 3 4ke 2 3 4le2 3 ; n 30 ˆ k l e 1 le 2 2 k l e 3 = 3kl 2l 2 2kc 1 2lc 1 kc 3 2lc 3 2kc 4 2lc kl 2l 2 2kc 1 2lc 1 kc 3 2lc 3 2kc 4 2lc kl 2l 2 2kc 1 2lc 1 kc 3 2lc 3 2kc 4 2lc 4 ke 2 1 le2 1 2le 1e 2 c 3 e 1 e 2 3le 2 2 2c 1e 2 2 c 3e 2 2 2c 4e 2 2 4ke 1e 3 4le 1 e 3 4le 2 e 3 2c 3 e 2 e 3 4ke 2 3 4le2 3 ;

24 44 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 n 31 ˆ 3kl 2l 2 2 k l c 1 k 2l c 3 2kc 4 2lc 4 = 3kl 2l 2 2kc 1 2lc 1 kc 3 2lc 3 2kc 4 2lc kl 2l 2 2 k l c 1 k 2l c 3 2kc 4 2lc kl 2l 2 2 k l c 1 k 2l c 3 2kc 4 2lc 4 ke 2 1 le2 1 2le 1e 2 c 3 e 1 e 2 3le 2 2 2c 1e 2 2 c 3e 2 2 2c 4e 2 2 4ke 1e 3 4le 1 e 3 4le 2 e 3 2c 3 e 2 e 3 4ke 2 3 4le2 3 ; ~E ˆ 3kl 2l2 2 k l c 1 k 2l c 3 2kc 4 2lc 4 ; 2 k l n 32 ˆ 2 kn 19 c 3 n 19 2kv 55 2lv 55 k 3k 2l 2c 1 4c 3 2c 4 ; n 33 ˆ 2 kn 18 c 3 n 18 2kv 56 2lv 56 k 3k 2l 2c 1 4c 3 2c 4 ; 2 k l v n 34 ˆ 41 ; k 2k 1 2k 2 ke 1 3ke 2 4le 2 2ke 3 2 k l e 2 2 n 35 ˆ v 39 kc 2 3 2k 1c 2 3 2k 2c 2 3 ke 1e 2 2 3ke3 2 4le3 2 2ke2 2 e ; 3 2 k l c 2 3 n 36 ˆ v 40 kc 2 3 e 1 3kc 2 3 e 2 4lc 2 3 e 2 ke 2 2 2k 1e 2 2 2k 2e 2 2 2kc2 3 e ; 3 n 38 ˆ 2 k l e 2 e 1 n 11 e 2 n 11 2e 3 n 11 e 1 n 12 e 2 n 12 2e 3 n 12 n n n 16 n n n 17 v 42 = kc 3 2k 1 c 3 2k 2 c 3 ke 1 e 2 3ke 2 2 4le2 2 2ke 2e 3 ; n 39 ˆ 2 k l e 2 e 1 n 10 e 2 n 11 2e 3 n 10 e 1 n 12 e 2 n 12 2e 3 n 12 n n n 15 n n n 17 v 43 = kc 3 2k 1 c 3 2k 2 c 3 ke 1 e 2 3ke 2 2 4le2 2 2ke 2e 3 : References [1].J.C.B Saint-Venant, Memoire sur la torsion des prismes, Memoires des Savants etrangers 14 (1856) 233. [2].J.C.B. Saint-Venant, Memoire sur la exion des prismes, J. de Mathematiques de Liouville, Ser. II 1 (1956) 89. [3] D. Iesan, Saint-Venant's problem for inhomogeneous and anisotropic elastic bodies, J. Elasticity 6 (1976) 277±294. [4] D. Iesan, On Saint-Venant's problem for elastic dielectrics, J. Elasticity 21 (1989) 101. [5] D. Iesan, Saint-Venant's problem, Springer, New York, [6] D. Iesan, L. Nappa, Saint-Venant's problem for microstretch elastic solids, Int. J. Engng.Sci. 32 (1994) 229±236. [7] F. dell'isola, L. Rosa, Saint-Venant problem in Linear Piezoelectricity. In: V.V. Varadhan (ed.), Mathematics and Control in Smart Structures, SPIE, vol. 2715, pp. 399±409, [8] F. dell'isola, L. Rosa, lmansi-type boundary conditions for electric potential inducing exure in linear piezoelectric beams, Cont. Mechs. and Thermodynamics 9 (1997) 115±125. [9] F. Davi, Saint-Venant's problem for linear piezoelectric bodies, J. Elasticity 43 (1996) 227±245. [10] F. dell'isola, R.C. Batra, Saint-Venant's problem for porous linear elastic materials, J. Elasticity 47 (1997) 73±81. [11] R.C. Batra, J.S. Yang, Saint-Venant's principle in linear piezoelectricity, J. Elasticity 38 (1995) 209±218. [12] R.. Toupin, Saint-Venant's principle, rch. Rational Mechanics nal 18 (1965) 83±96. [13] R.S. Rivlin, The solution of problems in second order elasticity theory, J. Rational Mechs. nalysis 2 (1953) 53±81.

25 S. Vidoli et al. / International Journal of Engineering Science 38 (2000) 21±45 45 [14] J.H. Poynting, On pressure perpendicular to the shear-planes in nite pure shears and on the lengthening of loaded wires when twisted, Proc. Roy. Soc. London 82 (1909) 546±549. [15]. Signorini, Sulle deformazioni termoelastiche nite, Proc. 3rd Int. Congr. ppl. Mechs. 2 (1930) 80±89. [16] C.. Truesdell, W. Noll, S. Flugge (Ed.), The nonlinear eld theories of mechanics, Handbuch der Physik, vol. III/ 3, Springer, Berlin, [17].E. Green, J.E. dkins, Large Elastic Deformations and Nonlinear Continuum Mechanics, Claredon Press, Oxford, [18].E. Green, R.T. Shield, Finite extension and torsion of cylinder, Proc. Roy. Soc. London 244 (1951) 47±86. [19] F. dell'isola, G.C. Ruta, R.C. Batra, second-order solution of Saint-Venant's problem for an elastic pretwisted bar using Signorini's perturbation method, J. Elasticity 49 (1998) 113±127. [20] F. dell'isola, G.C. Ruta, R.C. Batra, Generalized poynting e ects in predeformed-prismatic bars, J. Elasticity 50 (1998) 181±196. [21] R.C. Batra, F. dell'isola, S. Vidoli, second-order solution of Saint-Venant's problem for a piezoelectric circular bar using Signorini's perturbation method, J. Elasticity (in press). [22] J.S. Yang, R.C. Batra, second-order theory of piezoelectric materials, J. coustic Soc. merica 97 (1995) 280± 288. [23].C. Eringen, G.. Maugin, Electrodynamics of Continua, Springer, New York, 1989.