Evaluation of coherence factor for high Q data
|
|
|
- Ella Simon
- 5 years ago
- Views:
Transcription
1 Evaluation of coherence factor for high Q data M. Sutton February 19, 19 This is a calculation based on a formula in Pusey s review article[1]. The version I use is from the chapter in Mill s book[]. Here the wavelength of the x-rays is λ with spread λ, its wavevector is k = π/λ, c is the speed of light and Q = k f k i, the difference between the final and incident wavevectors. 1 β( κ) = V E i e i κ ( r r 1 ) V V Γ(, r r 1 Q, ( r r 1 ) ) d r ck 1 d r. (1) This gives the speckle shape, κ specifies the displacement between two positions of the x-ray detector (or between two detectors). The form of the mutual coherence function is (also in the chapter): (x x 1 ) (z z 1 ); Γ(x 1, z 1, x, z, t) = V E i e h e v e t /τ, () where h and v are the transverse coherence lengths in the horizontal and vertical directions. For an unfocused beam h = λ R sample /(πσ h ) and v = λ R sample /(πσ v ) where R sample is source to sample distance and σ h, σ v are the horizontal and vertical source sizes (RMS). The longitudinal coherence length is l = cτ = λ /(π λ) = λ/(k λ). This is the form used in Ref. [3, 4] (see Appendix I). The contrast of an intensity distribution I is typically defined as (I(max) I(min))/(I(max) + I(min)). The value β = β() and is related to the contrast squared of the speckle pattern and will be called the coherence factor. Sometimes this coherence factor is loosely referred to as the contrast. First we will calculate the coherence factor and then estimate the speckle sizes. 1
2 Figure 1: Coordinate system to define angles 1 Calculation of the coherence factor The coherence factor is given by the integral β = V V (x x 1 ) (y y 1 ) e h e v e t/τ. (3) Note that t = Q ( r r 1 )/ck. First we duplicate the calculations presented in Ref. [3] Using the coordinate system shown in Fig. 1, we can write the incident wavevector, the out-going wavevector and therefore the diffraction vector as: ki = k (, 1, ) kf = k (sin θ cos ϕ, cos θ, sin θ sin ϕ) Q = k sin θ (cos θ cos ϕ, sin θ, cos θ sin ϕ). (4) We also note that we have k = k i = k f and Q = Q = k sin θ. Thus, Q ( r r 1 ) = k sin θ(cos θ cos ϕ(x x 1 ) sin θ(y y 1 )+cos θ sin ϕ(z z 1 )). (5) This simplifies for Q in either horizontal or vertical diffraction to be: k sin θ cos θ x k sin θ y k sin θ cos θ z k sin θ y ϕ = (horizontal) ϕ = 9 (vertical).
3 Using the above form for τ (with ϕ = ), Q t/τ = ( r r 1 ) ck = k λ = λ λ Q k c λ λ λ sin θ((x x 1 ) cos θ (y y 1 ) sin θ) 1 Q 4k x λ Q y (6) λ k for ϕ = and using sin θ equals Q/(k ) and cos θ = 1 (Q/(k )). We now define A and B so t/τ = (A x + B y)/. Explicitly, A = k λ λ B = 4k λ λ cos θ sin θ = λ λ Q 1 Q 4k sin θ = λ Q = Q λ k l k l Q k For ϕ = 9 we simply replace x by z. Also note that B = A tan θ. Now we must specify the volume over which to integrate, i.e. the scattering volume. We chose a volume which respects the x, y and z directions of the coordinates systems and is of height M (along z) and width L (along x) and depth W (along y). With this symmetry, and specializing to ϕ =, the integral in Eqn. 3 factorizes into a two dimensional integral in z 1 and z and into a four dimensional in x 1, x, y 1 and y. We write this as β=β z β r. We first evaluate β z = 1 (z z 1 ) M dz 1 dz e v. (7) Using appendix II to evaluate this integral gives β z = 1 M = v M z dz(m z) e v [ M M M πerf( ) + e v 1 v v ] (8) Evaluating β r is similar, β r = 1 L (W L) L W W dx 1 dx dy 1 (x x 1 ) dy e h e A(x x 1 )+B(y y 1 ) 3
4 = = 1 L (W L) 1 (W L) ( e x h L L W dx 1 dx dx(l x) W (x x 1 ) ( dy(w y)e h e A(x x 1 )+By dy(w y) [ e Ax+By + e Ax By + e Ax+By + e Ax By ]) + e A(x x 1 ) By) ) = L W x [ (W L) dx(l x) dy(w y)e h e Ax+By + e Ax By ]. (9) This can be straight forwardly evaluated numerically. A few comments are worth making about the longitudinal coherence. 1. The longitudinal coherence is determined by the frequency resolution of the incident beam. In Goodman[5] an explicit formula is given for the longitudinal coherence in terms of the spectrum.. For a single bounce monochromator the typical spectrum will have 1/δQ tails and an exponential coherence time distribution (a Lorentzian spectrum) makes sense. 3. In Ref. [3] it was pointed out that for the first harmonic of an undulator spectrum (pink beam), a calculation using the formula in Goodman, gives a coherence length which agrees with that from the Lorentzian spectrum used above. 4. To contrast to the long tails of a Lorentzian spectrum, it is interesting to compare calculations to a Gaussian spectrum (exp( t ) which is τ more compact. The formula for β r then becomes L W x ] (W L) dx(l x) dy(w y)e h [e (Ax+By) 4 + e (Ax By) 4. (1) Note that τ is related to the half width of a Lorentzian spectrum but is related to the standard deviation for the Gaussian spectrum, so some factor should be used when comparing them. This spectrum was used in Abernathy et al[6]. 5. A two bounce monochromator (or multi-bounce) will have reduced tails in the frequency spectrum and this should give larger longitudinal coherence lengths than estimated by a Lorentzian spectrum. 4
5 Y W γ 11 1 L y=w+tan( γ )x t γ y=tan( )x X x rays Figure : Definition of angle for the scattering region. We will now generalize the calculation to have the sample at an angle γ as shown in Fig.. We will use a parallelepiped for the scattering volume. Such a geometry will directly apply to measuring a thin crystalline film whose planar dimensions are much larger than the beam dimensions. For reflection, one could imagine that the aborption length could be treated as the thickness for the sample. This changes the limits of integration for β r in Eqn. 9 by replacing the lower limits of y i (i=1,) from to x i tan γ and the upper limits from W to W + x i tan γ. Defining u i = y i x i tan γ and changing the variables of integration from y i to u i allows the integrals to be performed in a very similar way to Eqn. 9. In the end we obtain the result that a simple redefinition of A will handle this situation. Explicitly, β r = = 1 L (W L) 1 (W L) L L x1 tan γ+w dx 1 dx x 1 tan γ L W W dx 1 dx du 1 dy 1 x tan γ+w x tan γ (x x 1 ) dy e h e A(x x 1 )+B(y y 1 ) (x x 1 ) du e h e A(x x 1 )+B(u +x tan γ u 1 x 1 tan γ) 5
6 = = 1 L (W L) (W L) L L W W dx 1 dx du 1 dx(l x) W x dy(w y)e h (x x 1 ) du e h e (A+B tan γ)(x x 1 )+B(u u 1 ) [ e (A+B tan γ)x+by + e (A+B tan γ)x By ]. (11) So if A is replaced by A = A+B tan γ, this reduces to the previous formula. It is worth specializing to three standard diffraction geometries. For SAXS, conventionally γ = and this is the case first worked out (A = A). For reflection, one rotates the sample with Q and γ = 9 θ (θ is half of θ). Using the definitions of A and B and since tan(9 θ) = 1/ tan θ, A = A + B tan(9 θ) = A A tan θ/ tan θ =. A rotation is also done for diffraction in transmission but has an extra 9 offset, so γ = θ and A = A + B tan( θ) = A + B /A or A = A/ cos θ. Finally, one needs to relate W to the thickness of the film t. It is easy to see the W = t/ cos γ = t/ sin θ for reflection and W = t/ sin(θ 9) = t/ cos θ for transmission. Although varying γ with Q is good for comparing contrast factors and speckle sizes versus Q, most experiments are done with a fixed incident angle. In this case γ = 9 θ incident for reflection and γ = θ incident for transmission. Also W is the distance along the incident beam path, this can be set to the shortest of W = 1/µ, where µ is the absorption or to W = t/ cos γ for a sample of thickness t. For reflection, Eqn 9 can be analytically evaluated to give: β r = = (W L) [ L x W dx(l x)e h B W 1 + e B W ( B W ) ] h L dy(w y) [e By ] [ L L L ] πerf( ) + e h 1 (1). h h Remember that B W = W l Q k and so β r is the product of a function in W/ l and one in L/ h. Fig 3 compares the coherence factor for the three geometries (in the horizontal). For this and succeeding figures, the reference parameters are M = 1. µm, L = 5. µm, W = 1. µm, λ = 1.65 Å and λ/λ = The source to sample distance is 55 meters, and the source size is 345. by 45. µm (HxV) giving coherence lengths of h = 4. µm by v = 3. µm. These are typical parameters for Undulator A at the Advanced Photon Source. 6
7 .8 SAXS Reflection Transmission.6 β Q(Å 1 ) Figure 3: Comparison of three standard geometries. Figure 3 suggests that transmission geometry is better than reflection geometry. Reducing the thickness of the sample increases the contrast of the reflection geometry more than the others so that at a thickness of 5. µm all three are comparable and for smaller thicknesses reflection geometry dominates. Figure 4 compares horizontal diffraction to vertical diffraction. It plots for both 5x1 and 1x5 slits in each configuration for transmission geometry. I don t understand the large effect of difference between the black and blue curves yet. A similar set of curves exist for reflection geometry except by Eqn 1 simultaneously exchanging L and h and M and v gives identical coherence factors. Figure 5 shows the effect of varying the dimensions of the scattering volume. Each dimension is varied separately with the others left at the values given above. Note how the sample thickness in reflection matches the sample width in transmission. Equation 9 mixs one transverse and the longitudinal coherence effects. This probably explains the difference between the black and blue curves above. The coherence factor is further reduced if the detector area is larger than the speckle size. We leave a discussion of this effect until after the discussion 7
8 .8 1.,3. in plane (V) 5.,3. in plane (V) 1.,4. in plane (H) 5.,4. in plane (H).6 β Q(Å 1 ) Figure 4: Comparison of horizontal and vertial diffraction. The curves are labeled by their slit size, coherence length and orientation of their scattering plane, 8
9 .6.4 β. 5 1 L,M,W(µm) Figure 5: Effects of sample dimensions on coherence factor at Q = 1Å 1. The red curves are for reflection and the blue curves are for transmission. The solid lines are for varying L, the dashed for W and the dotted curve for L. 9
10 of speckle sizes in the next session. 1
11 Calculation of the speckle sizes We can estimate the speckle sizes by calculating the second moment of Eqn. 1 with respect to κ. This is twice the coefficient of the κ term in the expansion of Eqn 1. The second moment δ can be considered the variance of a Gaussian approximation for the shape of a speckle (e κ /(δ ) ) or the just the first term of an expansion in κ. 1 As for β, it makes sense to choose ϕ = to simplify the integral. From the form of the convolution integral, it can be seen that an odd function integrates to zero. Thus, we only need consider the three diagonal parts of the second moment, z z, x x and y y. Also, we can factor the resulting integrals into z-terms and r-terms with one term simply being one of the β i integrals above. We get: δ zz = = = 1 M β z M 1 β z M 4 v β z M dz 1 dz (z z 1 ) (z z 1 ) e v dzz z (M z) e v [ M M M πerf( ) + e v 1 v v ], (13) δ xx = = 1 L β r (W L) β r (W L) L L W W dx 1 dx dy 1 dx(l x) W x dy(w y)x e h (x x 1 ) dy (x x 1 ) e h e A (x x 1 )+B(y y 1 ) [ e A x+by + e A x By ] (14) and a similar term with x replaced by y for δ yy. Appendix III has yorick programs to calculate these three values. To calculate the speckle size in the plane of the detector select κ perpendicular to k f. For horizontal diffraction, δ zz is then the speckle size for the out of scattering plane direction. To get the speckle size in the scattering plane we use the parameterization of an ellipse given by r(ψ) = ab (b cos(ψ)) + (a sin(ψ)). 1 Use: where a is the value for κ = ( ) d ae κ dκ δ κ= = a δ 11
12 For us a = δ yy and b = δ xx and then the line perpendicular to k o cuts the center of the ellipse at ψ = θ + 9. This gives δ rr = sin (θ) δ yy 1 + cos (θ) δ xx and δ rr is the speckle width in the scattering plane (radial). For area detectors, θ would be the angle by which the plane of the detector is tilted around ẑ. Finally, one must consider the effect of the finite detector area. If its area is bigger than the speckle size, the measured coherence factor of the speckle pattern will be reduced and the speckle widths will be increased. A reasonable approximation is to assume the effect is the same as would be obtained by convolving a Gaussian representing the detector response with a Gaussian representing the speckle shape. Thus the speckle width is the sum in quadrature, of the speckle size estimated above to the size of a pixel in reciprocal angstroms. An estimate of the detector contribution is k U/(R det α) where U is the pixel size, R det is detector sample distance and the factor α converts the pixel size into a standard deviation (rms). In the calculations of appendix A of Ref [4] suitable for SAXS, that is for square pixels, α = 6 =.45. Explicitly the measured speckle sizes i are: ( ) i = δii + k U ( ) k U = δ ii 1 +. (15) αr det δ ii αr det The convolution of two Gaussians leads to the measured coherence factor being: 1 1 β = β ( ) ( ). (16) 1 + k U δ zzαr det 1 + k U δ rrαr det Figure 6 compares transmission and reflection geometries for the case of horizontal diffraction. A detector pixel size of µm at 1 m is used for convoluting with δ ii (α = 6). The curves for SAXS geometries are not plotted but they match quite well the transmission geometies as they did for β above. Figures 7 and 8 compares horizontal and vertical diffraction geometries. Figures 9 and 1 compares scattering volume dimensions for horizontal diffraction in both reflection and transmission geometries. (REDO to use 1m det distance). Finally, the effect of finite detector area on the contrast factor is presented in Fig 11. 1
13 .7 (1 4 Å 1 ) Q(Å 1 ) Figure 6: Comparison of speckle widths for reflection (red) and transmission geometry (blue). Horizontal diffraction is plotted, the dashed lines are for vertical widths and solid lines for horizontal widths. 13
14 .7 (1 4 Å 1 ) Q(Å 1 ) (1 4 Å 1 ).5 Figure 7: Comparison of speckle widths for horizontal and vertical geometries in reflection. Solid lines are for widths in the scattering plane and dashed lines are outof-plane widths. Black lines are for the 5 µm slit in plane horizontal (short coherence length direction). Blue lines are for a 1 µm in plane horizontal. Green lines are for the 5 µ slit in a vertical scattering plane and blue lines are for the 1 µm direction in the vertical scattering plane Q(Å 1 ) Figure 8: Comparison of speckle widths for horizontal and vertical geometries in transmission. Coloured lines have the same meaning as for Fig 7. 14
15 .6 1. (1 4 Å 1 ).5.4 (1 4 Å 1 ) L(µm).4 Figure 9: Comparison of speckle widths as scattering volume dimensions are changed, horizontal diffraction and reflection geometry. Solids lines for varying L, dashed for W and dotted for M. Red is for vertical direction and blue for horizontal. The horizontal green line is the width from the size of a pixel in the CCD. 4 L(µm) Figure 1: Comparison of speckle widths as scattering volume dimensions are changed, horizontal diffraction and transmission geometry. Line definitions are as for Fig 9. 15
16 1. β,frac Q(Å 1 ) Figure 11: Effect of detector size on the coherence factor. The coherence factors correspond to the widths in Fig 6. Reflection geometries are in red and transmission in blue. The dashed curves are the coherence factors, the dotted curves are the fraction by which the coherence factor is reduced and the solid lines are the resulting coherence factors. 16
17 Random points: for SAXS, with larger wavelength spreads (pink beam) the speckle are elongated in the radial directions (thus the nomenclature β r, for ϕ = and 9 radial is x and z directions). Should be able to handle asymmetric diffraction as well (giving elongated speckles). 17
18 Figure 1: Integration regions for doing the integral. Appendix I: Frequency spectrum The form of the temporal coherence is e iωt e t /τ. The frequency spectrum is then: S(ω) = e iωt e iωt e t /τ τ dt = 1 + τ (ω ω ) From this it can be seen that the width of the frequency spectrum is ω = 1/τ and it is the HWHM. Another form of the temporal coherence is e iωt e t τg, then: S(ω) = e iωt e iωt e t τg dt = πτg e τ g (ω ω ). Thus the sigma width is σ ω = 1/τ g. Converting both to FWHM gives δω = (.35) /τ FWHM = 5.5/τ FWHM Appendix II: Evaluation of correlation integrals We wish to evaluate integrals of the form: F (M) = dx dyf(y x), (17) 18
19 which often arise in correlation type calculations. From Fig. 1, we can divide the region of integration into two triangular regions, A and B. In region A, first integrate over x and in region B, over y. This gives F (M) = y x dy dxf(y x) + dx dyf(y x). (18) Change the variable of integration so u = y x. Then dx is du in the first and dy = du in the second. Changing limits of integration and relabelling an integration variable gives the following: F (M) = = = dx dx dy y y x duf(u) + duf( u) + dx dx x x duf( u) duf(u) dy {f(y) + f( y). (19) One integral can be done by intergration by parts. Defining g(x) = x dyf(y) and using the two parts u = g(y) and dv = dy to become v = y and du = g (y)dy = f(y)dy gives Thus, we find dy g(x) = g(m)m F (M) = = M dy f(y) Appendix III: Yorick programs dy y g (y) dy y f(y)). () dy (M y) {f(y) + f( y). (1) Here is a yorick file which calculates β and δ. To numerically evaluate Eqn 9, 11 and 14 we simply divide the region of integration into a by grid. This gives sufficient accuracy for typical parameters used at the APS. These and other yorick functions can be found at the URL mark/coherence/yorick/. // Using Pusey s formula modified f o r phi=9 and gam non 9. // // to avoid c o n f l i c t with beta ( ) d e f i n e d in gamma. i 19
20 func bbeta (Q, L,W, x i i p,m, xi op, k, d l o l, gam, gauss =,twobounce=) / DOCUMENT bbeta (Q, L,W, x i i p,m, xi op, k, d l o l, gam, gauss =,, twobounce=) C a l c u l a t e beta f o r given Q s. L,M are s l i t s s i z e s ( in plane (H) x out of plane (V) ), W i s along beam d i r e c t i o n, W=t h i c k n e s s / cos (gam) f o r thin f i l m = 1/(mu) f o r a b s o r p t i on dominated. x i i p, x i o p are coherence l e n g t h s ( in plane x out of plane ). k i s pi /lambda. d l o l i s d e l t a lambda over lambda (HWHM). gam i s angle o f s u r f a c e and normal to i n c i d e n t beam ( r a d i a n s ) gam= f o r SAXS gam=pi/ t h e t a i n c i d e n t f o r r e f l e c t i o n ( or pi/ tth / ). gam= t h e t a i n c i d e n t f o r t r a n s m i s s i o n ( or tth / ). gam= pi/ tth / gauss=1 or twobounce=1 w i l l chose a d i f f e r e n t frequency spectrum from the d e f a u l t which i s Lorenztion ( r e s p e c t i v e l y Gaussian and a double bounce mono ). In plane and out of plane r e f e r to the s c a t t e r i n g plane. Note : t h i s was designed f o r h o r i z o n t a l d i f f r a c t i o n at a synchrotron as t y p i c a l l y i s done f o r COSAXS at 8ID I. / //NOTE: changed order o f eta and x i Dec/4 { extern tth, AA, BB; i=dimsof (Q) ( ) ; tth= asin (Q// k ) ; i f (numberof(gam)==1) gam=array (gam, i ) ; i f (numberof(w)==1) W=array (W, i ) ; z=array (., i ) ; BB=AA=z ; NUM=; // use a x g r i d f o r i n t e g r a l, should be good to 1% for ( j =1; j<=i ; j++) { // loop over Q s z ( j )= betar ( tth ( j ), gam( j ),L,W( j ), x i i p, k, d l o l, gauss=gauss, twobounce=twobounce ) ; AA( j )=A; BB( j )=B; z = betaz (M, x i o p ) ; return ( z ) ; func betaz (M, x i ) { / DOCUMENT betaz (M, x i )
21 c a l c u l a t e s the beta f o r the d i r e c t i o n p e r p e n d i c u l a r to the s c a t t e r i n g plane. x i=coherence sigma=lambda Rsource /( pi sigma ( source ) ). M i s the s i z e. Gaussian coherence. / require, gamma. i ; x=m/ x i ; t = ( x sqrt ( pi ) (1. e r f c ( x))+exp( x ˆ) 1.)/ x ˆ ; return ( t ) ; require, gamma. i ; func betar ( tth, gam, L,W, xi, k, d l o l, gauss =,twobounce=) { / DOCUMENT betar ( tth, gam, L,W, xi,q, k, d l o l ) c a l c u l a t e betar in s c a t t e r i n g plane by brute f o r c e. L i s t r a n s v e r s e dimension, W i s sample t h i c k n e s s. x i i s coherence length ( in microns ), Q i s wavevector and k i s pi /lambda ( angstroms ˆ 1) and d l o l i s d e l t a lambda over lambda (HWHM). keywords : gauss =, twobounce= / extern NUM; // l o c a l A,B, x, y extern A, B, x, y // need to automate mapping from d l o l (FWHM) to c o r r e c t f a c t o r //W=min ( 1.,W/ cos (gam ) ) ; //W=W/ cos (gam ) ; //Now handled in c a l l i n g r o u t i n e Q= k sin ( tth /. ) ; //A = d l o l Q 1 e4 s q r t (1. (Q/( k ) ) ˆ ) ; // convert Q to micronsˆ 1 //B = d l o l 1 e4 Qˆ/ k ; A = d l o l Q 1 e4 sqrt (1. (Q/( k ) ) ˆ ) ; // convert Q to micronsˆ 1 B = d l o l 1 e4 Qˆ/ k ; A = A + B tan (gam ) ; x=span (., L,NUM)( :1:NUM, ) ; y=span (.,W,NUM) (, : 1 :NUM) ; t =. (L x ) (W y ) / ( ( L W)ˆ) exp( ((x/ x i ) ˆ ) ) ; i f (! is void ( gauss ) ) { // c o r r e c t f o r h a l f widths A = // Gaussian B = // s q r t ( l o g ( ) ), convert HWHM t = exp(.5 (A x+b y)ˆ)+exp(.5 (A x B y ) ˆ ) ; else i f (! is void ( twobounce ) ) {//CHECK t h i s //A = // Lorentzian squared //B = // s q r t ( s q r t (.) 1.) t = (1.+ abs (A x+b y )/)ˆ exp( abs (A x+b y))+ 1
22 ( 1. + abs (A x B y )/)ˆ exp( abs (A x B y ) ) ; else { t = exp( abs (A x+b y ) ) + exp( abs (A x B y ) ) ; // Lorentzian return (sum( x ( 1, ) y (, 1 ) t ) ) ; func betarg (Q, L,W, xi, k, d l o l ) { / DOCUMENT betarg (Q, L,W, xi, k, d l o l ) c a l c u l a t e s the betar f o r r e f l e c t i o n geometry using a n a l y t i c form. L i s t r a n s v e r s e dimension, W i s sample t h i c k n e s s. x i i s coherence length ( in microns ), Q i s wavevector and k i s pi /lambda ( angstroms ˆ 1) and d l o l i s d e l t a lambda over lambda (HWHM). / require, gamma. i ; x=l/ x i ; t = ( x sqrt ( pi ) (1. e r f c ( x))+exp( x ˆ) 1.)/ x ˆ ; B = abs ( d l o l 1 e4 Qˆ/ k ) ; // note l a c k o f minus s i g n tth= asin (Q// k ) ; gam = pi /. tth /. ; //W=min ( 1.,W/ cos (gam ) ) ; //W=W/ cos (gam ) ; //Now handled in c a l l i n g r o u t i n e t = ( B W 1+exp( B W) ) / / (B W)ˆ return ( t ) ; func betargauss (A, B, x i i p, L,W) { zz =.5 x i i p /L/ sqrt (1.+(A x i i p )ˆ+4. (W B) ˆ ) ; return ( zz ) ; And here are some yorick functions for calculating speckle widths. Note that the function also returns the coherence factor as the integrals needed for it are calculated along the way. // Using Pusey s formula modified f o r phi=9 and omega non 9. // func d e l t a v (Q, L,W, x i i p,m, xi op, k, d l o l, gam, gauss =,twobounce=) / DOCUMENT d e l t a v (Q, L,W, x i i p,m, xi op, k, d l o l, gauss =,omega=,twobounce=) C a l c u l a t e 1/ d e l t a ˆ ( and betas ) f o r given Q s. L,M are s l i t s s i z e s ( in plane (H) x out of plane (V) ), W i s along beam d i r e c t i o n, W=t h i c k n e s s / cos (gam) f o r thin f i l m
23 = 1/(mu) f o r a b s o r p t i on dominated. x i i p, x i o p are coherence l e n g t h s ( in plane x out of plane ). k i s pi /lambda. d l o l i s d e l t a lambda over lambda (HWHM). gam i s angle o f s u r f a c e and normal to i n c i d e n t beam ( r a d i a n s ) gam= f o r SAXS gam=pi/ t h e t a i n c i d e n t f o r r e f l e c t i o n ( or pi/ tth / ). gam= t h e t a i n c i d e n t f o r t r a n s m i s s i o n ( or tth / ). gam= pi/ tth / gauss=1 or twobounce=1 w i l l chose a d i f f e r e n t frequency spectrum from the d e f a u l t which i s Lorenztion ( r e s p e c t i v e l y Gaussian and a double bounce mono ). In plane and out of plane r e f e r to the s c a t t e r i n g plane. Note : t h i s was designed f o r h o r i z o n t a l d i f f r a c t i o n at a synchrotron as t y p i c a l l y i s done f o r COSAXS at 8ID I. { NOTE: r e t u r n s a 4 by number o f Q matrix, f i r s t t h r e e rows are 1/ d e l t a i i ˆ ( inv angrstroms ), f o u r t h row i s beta. / extern tth, AA, BB; i=dimsof (Q) ( ) ; tth= asin (Q// k ) ; i f (numberof(gam)==1) gam=array (gam, i ) ; i f (numberof(w)==1) W=array (W, i ) ; z=array (., i ) ; d e l t a s=array (., 4, i ) ; NUM=; // note using i s good to 1% t =betaz (M, x i o p ) d =d e l t a z (M, x i o p ) s c a l e =1. e4 ; // convert to angstroms from microns for ( j =1; j<=i ; j++) { t= betar ( tth ( j ), gam( j ),L,W( j ), x i i p, k, d l o l, gauss=gauss, twobounce=twobounce ) ; // x, y d i r e c t i o n t1=d e l t a r ( tth ( j ), gam( j ),L,W( j ), x i i p, k, d l o l, 1.,., gauss=gauss, twobounce=twobounc t=d e l t a r ( tth ( j ), gam( j ),L,W( j ), x i i p, k, d l o l,., 1., gauss=gauss, twobounce=twobounc d e l t a s ( 1, j )= s c a l e ˆ t1 / t ; d e l t a s (, j )= s c a l e ˆ t / t ; d e l t a s ( 3, j )= s c a l e ˆ d/ t ; d e l t a s ( 4, j )=t t ; return ( d e l t a s ) ; func d e l t a z (M, x i ) 3
24 { / DOCUMENT d e l t a z (M, x i ) c a l c u l a t e s the 1/ d e l t a ˆ ( microns ˆ) f o r the d i r e c t i o n p e r p e n d i c u l a r to the s c a t t e r i n g plane. x i=coherence sigma=lambda Rsource /( pi sigma ( source ) ). M i s the s l i t s i z e. Gaussian coherence. / x=m/ x i ; t = x sqrt ( pi )/. (1. e r f c ( x))+exp( x ˆ) 1.; t = ( x i /x ) ˆ ; return ( t ) ; //1 e8 convert to inv angstroms ˆ func d e l t a r ( tth, gam, L,W, xi, k, d l o l, dx, dy, gauss =,twobounce=) { / DOCUMENT d e l t a r ( tth, gam, L,W, xi,q, k, d l o l ) c a l c u l a t e 1/ d e l t a r ˆ by brute f o r c e ( microns ˆ ). L i s t r a n s v e r s e dimension, W i s sample t h i c k n e s s. x i i s coherence length ( in microns ), Q i s wavevector and k i s pi /lambda ( angstroms ˆ 1) and d l o l i s d e l t a lambda over lambda (HWHM). keywords : gauss =, twobounce= / extern NUM; l o c a l A, B, x, y ; //W=min ( 1.,W/ cos (gam ) ) ; //W=W/ cos (gam ) ; //Now done in c a l l i n g r o u t i n e // c o r r e c t f o r h a l f widths Q= k sin ( tth /. ) ; A = d l o l Q 1 e4 sqrt (1. (Q/( k ) ) ˆ ) ; // convert Q to micronsˆ 1 B = d l o l 1 e4 Qˆ/ k ; A = A + B tan (gam ) ; x=span (., L,NUM)( :1:NUM, ) ; y=span (.,W,NUM) (, : 1 :NUM) ; // Should t h e r e be a?? t=(l x ) (W y ) / ( ( L W)ˆ) exp( ((x/ x i ) ˆ ) ) ; t =(dx x+dy y ) ˆ ; i f (! is void ( gauss ) ) { A = // Gaussian B = // s q r t ( l o g ( ) ), convert HWHM t = exp(.5 (A x+b y)ˆ)+exp(.5 (A x B y ) ˆ ) ; else i f (! is void ( twobounce ) ) { //CHECK THIS A = // Lorentzian squared B = // s q r t ( s q r t (.) 1.) t = (1.+ abs (A x+b y ))ˆ exp(. abs (A x+b y))+ ( 1. + abs (A x B y ))ˆ exp(. abs (A x B y ) ) ; 4
25 else { t = exp( abs (A x+b y))+exp( abs (A x B y ) ) ; // Lorentzian return ( sum( x ( 1, ) y (, 1 ) t ) ) ; 5
26 References [1] P. N. Pusey, Statistical Properties of Scattered Radiation, in Photon Correlation Spectroscopy and Velocimetry, Editors, H. Z. Cumming and E. R. Pike, (New York: Plenum) (1974). [] M. Sutton, Coherent X-ray Diffraction, Chapter in Third-Generation Hard X-ray Synchrotron Radiation Sources: Source Properties, Optics, and Experimental Techniques, edited by. Dennis M. Mills, John Wiley and Sons, Inc, New York, (). [3] A. R. Sandy, L. B. Lurio, S. G. J. Mochrie, A. Malik, G. B. Stephenson, J. F. Pelletier and M. Sutton, Design and Characterization of an Undulator Beamline Optimized for Small-Angle Coherent X-ray Scattering at the Advanced Photon Source, J. Synch. Rad., 6, 1174 (1999). [4] D. Lumma, L.B. Lurio, S.G.J. Mochrie and M. Sutton, Area detector based photon correlation in the regime of short data batches: data reduction for dynamic x-ray scattering, Rev. Sci. Inst. 71, (). [5] Goodman, J. W., Statistical Optics, John Wiley & Sons, New York, USA (1985). [6] D.L. Abernathy, S. Brauer, G. Grübel, I. McNulty, S.G.J. Mochrie, N. Mulders, A.R. Sandy, G.B. Stephenson, M. Sutton, Small-angle coherent x-ray scattering using undulator radiation at the ESRF. J. Synchrotron Rad., 5, (1998). 6
X-ray Intensity Fluctuation Spectroscopy. Mark Sutton McGill University
 X-ray Intensity Fluctuation Spectroscopy Mark Sutton McGill University McGill University Collaborators J-F. Pelletier K. Laaziri K. Hassani A. Fluerasu E. Dufresne G. Brown M. Grant Yale/MIT S. Mochrie
X-ray Intensity Fluctuation Spectroscopy Mark Sutton McGill University McGill University Collaborators J-F. Pelletier K. Laaziri K. Hassani A. Fluerasu E. Dufresne G. Brown M. Grant Yale/MIT S. Mochrie
How can x-ray intensity fluctuation spectroscopy push the frontiers of Materials Science. Mark Sutton McGill University
 How can x-ray intensity fluctuation spectroscopy push the frontiers of Materials Science Mark Sutton McGill University Coherent diffraction (001) Cu 3 Au peak Sutton et al., The Observation of Speckle
How can x-ray intensity fluctuation spectroscopy push the frontiers of Materials Science Mark Sutton McGill University Coherent diffraction (001) Cu 3 Au peak Sutton et al., The Observation of Speckle
Setting The motor that rotates the sample about an axis normal to the diffraction plane is called (or ).
 X-Ray Diffraction X-ray diffraction geometry A simple X-ray diffraction (XRD) experiment might be set up as shown below. We need a parallel X-ray source, which is usually an X-ray tube in a fixed position
X-Ray Diffraction X-ray diffraction geometry A simple X-ray diffraction (XRD) experiment might be set up as shown below. We need a parallel X-ray source, which is usually an X-ray tube in a fixed position
SUPPLEMENTARY INFORMATION. Demonstration of Feasibility of X-Ray Free Electron Laser Studies of Dynamics of Nanoparticles in Entangled Polymer Melts
 SUPPLEMENTARY INFORMATION Demonstration of Feasibility of X-Ray Free Electron Laser Studies of Dynamics of Nanoparticles in Entangled Polymer Melts Jerome Carnis 1, Wonsuk Cha 1, James Wingert 2, Jinback
SUPPLEMENTARY INFORMATION Demonstration of Feasibility of X-Ray Free Electron Laser Studies of Dynamics of Nanoparticles in Entangled Polymer Melts Jerome Carnis 1, Wonsuk Cha 1, James Wingert 2, Jinback
Fourier Approach to Wave Propagation
 Phys 531 Lecture 15 13 October 005 Fourier Approach to Wave Propagation Last time, reviewed Fourier transform Write any function of space/time = sum of harmonic functions e i(k r ωt) Actual waves: harmonic
Phys 531 Lecture 15 13 October 005 Fourier Approach to Wave Propagation Last time, reviewed Fourier transform Write any function of space/time = sum of harmonic functions e i(k r ωt) Actual waves: harmonic
Coherent X-ray Scattering and X-ray Photon Correlation Spectroscopy
 Coherent X-ray Scattering and X-ray Photon Correlation Spectroscopy Laurence Lurio Department of Physics Northern Illinois University http://www.niu.edu/~llurio/coherence/ Outline Theory of X-ray Photon
Coherent X-ray Scattering and X-ray Photon Correlation Spectroscopy Laurence Lurio Department of Physics Northern Illinois University http://www.niu.edu/~llurio/coherence/ Outline Theory of X-ray Photon
Two-Stage Chirped-Beam SASE-FEL for High Power Femtosecond X-Ray Pulse Generation
 Two-Stage Chirped-Beam SASE-FEL for High ower Femtosecond X-Ray ulse Generation C. Schroeder*, J. Arthur^,. Emma^, S. Reiche*, and C. ellegrini* ^ Stanford Linear Accelerator Center * UCLA 12-10-2001 LCLS-TAC
Two-Stage Chirped-Beam SASE-FEL for High ower Femtosecond X-Ray ulse Generation C. Schroeder*, J. Arthur^,. Emma^, S. Reiche*, and C. ellegrini* ^ Stanford Linear Accelerator Center * UCLA 12-10-2001 LCLS-TAC
Spatial coherence measurement
 Spatial coherence measurement David Paterson Argonne National Laboratory A Laboratory Operated by The University of Chicago Motivation Third generation synchrotrons produce very bright, partially coherent
Spatial coherence measurement David Paterson Argonne National Laboratory A Laboratory Operated by The University of Chicago Motivation Third generation synchrotrons produce very bright, partially coherent
Instrumental Resolution
 Instrumental Resolution MLZ Triple-Axis Workshop T. Weber Technische Universität München, Physikdepartment E21 April 3 4, 2017 Contents General formalism Minimal example Monte-Carlo method Time-of-flight
Instrumental Resolution MLZ Triple-Axis Workshop T. Weber Technische Universität München, Physikdepartment E21 April 3 4, 2017 Contents General formalism Minimal example Monte-Carlo method Time-of-flight
Multiple Integrals and Vector Calculus: Synopsis
 Multiple Integrals and Vector Calculus: Synopsis Hilary Term 28: 14 lectures. Steve Rawlings. 1. Vectors - recap of basic principles. Things which are (and are not) vectors. Differentiation and integration
Multiple Integrals and Vector Calculus: Synopsis Hilary Term 28: 14 lectures. Steve Rawlings. 1. Vectors - recap of basic principles. Things which are (and are not) vectors. Differentiation and integration
Multiple Integrals and Vector Calculus (Oxford Physics) Synopsis and Problem Sets; Hilary 2015
 Multiple Integrals and Vector Calculus (Oxford Physics) Ramin Golestanian Synopsis and Problem Sets; Hilary 215 The outline of the material, which will be covered in 14 lectures, is as follows: 1. Introduction
Multiple Integrals and Vector Calculus (Oxford Physics) Ramin Golestanian Synopsis and Problem Sets; Hilary 215 The outline of the material, which will be covered in 14 lectures, is as follows: 1. Introduction
4. CONTINUOUS RANDOM VARIABLES
 IA Probability Lent Term 4 CONTINUOUS RANDOM VARIABLES 4 Introduction Up to now we have restricted consideration to sample spaces Ω which are finite, or countable; we will now relax that assumption We
IA Probability Lent Term 4 CONTINUOUS RANDOM VARIABLES 4 Introduction Up to now we have restricted consideration to sample spaces Ω which are finite, or countable; we will now relax that assumption We
International Distinguished Lecturer Program
 U 005-006 International Distinguished Lecturer Program Ken-ya Hashimoto Chiba University Sponsored by The Institute of Electrical and Electronics Engineers (IEEE) Ultrasonics, Ferroelectrics and Frequency
U 005-006 International Distinguished Lecturer Program Ken-ya Hashimoto Chiba University Sponsored by The Institute of Electrical and Electronics Engineers (IEEE) Ultrasonics, Ferroelectrics and Frequency
X-ray diffraction geometry
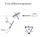 X-ray diffraction geometry Setting controls sample orientation in the diffraction plane. most important for single-crystal diffraction For any poly- (or nano-) crystalline specimen, we usually set: 1 X-ray
X-ray diffraction geometry Setting controls sample orientation in the diffraction plane. most important for single-crystal diffraction For any poly- (or nano-) crystalline specimen, we usually set: 1 X-ray
Lecture 19 Optical MEMS (1)
 EEL6935 Advanced MEMS (Spring 5) Instructor: Dr. Huikai Xie Lecture 19 Optical MEMS (1) Agenda: Optics Review EEL6935 Advanced MEMS 5 H. Xie 3/8/5 1 Optics Review Nature of Light Reflection and Refraction
EEL6935 Advanced MEMS (Spring 5) Instructor: Dr. Huikai Xie Lecture 19 Optical MEMS (1) Agenda: Optics Review EEL6935 Advanced MEMS 5 H. Xie 3/8/5 1 Optics Review Nature of Light Reflection and Refraction
GBS765 Electron microscopy
 GBS765 Electron microscopy Lecture 1 Waves and Fourier transforms 10/14/14 9:05 AM Some fundamental concepts: Periodicity! If there is some a, for a function f(x), such that f(x) = f(x + na) then function
GBS765 Electron microscopy Lecture 1 Waves and Fourier transforms 10/14/14 9:05 AM Some fundamental concepts: Periodicity! If there is some a, for a function f(x), such that f(x) = f(x + na) then function
Linac Based Photon Sources: XFELS. Coherence Properties. J. B. Hastings. Stanford Linear Accelerator Center
 Linac Based Photon Sources: XFELS Coherence Properties J. B. Hastings Stanford Linear Accelerator Center Coherent Synchrotron Radiation Coherent Synchrotron Radiation coherent power N 6 10 9 incoherent
Linac Based Photon Sources: XFELS Coherence Properties J. B. Hastings Stanford Linear Accelerator Center Coherent Synchrotron Radiation Coherent Synchrotron Radiation coherent power N 6 10 9 incoherent
Chapter 2 Radiation of an Accelerated Charge
 Chapter 2 Radiation of an Accelerated Charge Whatever the energy source and whatever the object, (but with the notable exception of neutrino emission that we will not consider further, and that of gravitational
Chapter 2 Radiation of an Accelerated Charge Whatever the energy source and whatever the object, (but with the notable exception of neutrino emission that we will not consider further, and that of gravitational
Lecture 5 Notes, Electromagnetic Theory II Dr. Christopher S. Baird, faculty.uml.edu/cbaird University of Massachusetts Lowell
 Lecture 5 Notes, Electromagnetic Theory II Dr. Christopher S. Baird, faculty.uml.edu/cbaird University of Massachusetts Lowell 1. Waveguides Continued - In the previous lecture we made the assumption that
Lecture 5 Notes, Electromagnetic Theory II Dr. Christopher S. Baird, faculty.uml.edu/cbaird University of Massachusetts Lowell 1. Waveguides Continued - In the previous lecture we made the assumption that
VARIABLE GAP UNDULATOR FOR KEV FREE ELECTRON LASER AT LINAC COHERENT LIGHT SOURCE
 LCLS-TN-10-1, January, 2010 VARIABLE GAP UNDULATOR FOR 1.5-48 KEV FREE ELECTRON LASER AT LINAC COHERENT LIGHT SOURCE C. Pellegrini, UCLA, Los Angeles, CA, USA J. Wu, SLAC, Menlo Park, CA, USA We study
LCLS-TN-10-1, January, 2010 VARIABLE GAP UNDULATOR FOR 1.5-48 KEV FREE ELECTRON LASER AT LINAC COHERENT LIGHT SOURCE C. Pellegrini, UCLA, Los Angeles, CA, USA J. Wu, SLAC, Menlo Park, CA, USA We study
The structure of laser pulses
 1 The structure of laser pulses 2 The structure of laser pulses Pulse characteristics Temporal and spectral representation Fourier transforms Temporal and spectral widths Instantaneous frequency Chirped
1 The structure of laser pulses 2 The structure of laser pulses Pulse characteristics Temporal and spectral representation Fourier transforms Temporal and spectral widths Instantaneous frequency Chirped
Toward a single mode Free Electron Laser for coherent hard X-ray experiments
 SLAC-PUB-15661 Toward a single mode Free Electron Laser for coherent hard X-ray experiments Sooheyong Lee 1,2,, Zhirong Huang 1, Yuantao Ding 1, Paul Emma 1, Wojciech Roseker 2, Gerhard Grübel 2 and Aymeric
SLAC-PUB-15661 Toward a single mode Free Electron Laser for coherent hard X-ray experiments Sooheyong Lee 1,2,, Zhirong Huang 1, Yuantao Ding 1, Paul Emma 1, Wojciech Roseker 2, Gerhard Grübel 2 and Aymeric
More On Carbon Monoxide
 More On Carbon Monoxide E = 0.25 ± 0.05 ev Electron beam results Jerry Gilfoyle The Configurations of CO 1 / 26 More On Carbon Monoxide E = 0.25 ± 0.05 ev Electron beam results Jerry Gilfoyle The Configurations
More On Carbon Monoxide E = 0.25 ± 0.05 ev Electron beam results Jerry Gilfoyle The Configurations of CO 1 / 26 More On Carbon Monoxide E = 0.25 ± 0.05 ev Electron beam results Jerry Gilfoyle The Configurations
Transverse Coherence Properties of the LCLS X-ray Beam
 LCLS-TN-06-13 Transverse Coherence Properties of the LCLS X-ray Beam S. Reiche, UCLA, Los Angeles, CA 90095, USA October 31, 2006 Abstract Self-amplifying spontaneous radiation free-electron lasers, such
LCLS-TN-06-13 Transverse Coherence Properties of the LCLS X-ray Beam S. Reiche, UCLA, Los Angeles, CA 90095, USA October 31, 2006 Abstract Self-amplifying spontaneous radiation free-electron lasers, such
Physics 505 Homework No. 12 Solutions S12-1
 Physics 55 Homework No. 1 s S1-1 1. 1D ionization. This problem is from the January, 7, prelims. Consider a nonrelativistic mass m particle with coordinate x in one dimension that is subject to an attractive
Physics 55 Homework No. 1 s S1-1 1. 1D ionization. This problem is from the January, 7, prelims. Consider a nonrelativistic mass m particle with coordinate x in one dimension that is subject to an attractive
sample-specific X-ray speckle contrast variation at absorption edges $ & ~ 0
 . 1. Introduction X-ray speckle contrast variation at absorption edges sample-specific Cornelia C. Retsch, Yuxin Wang, Sean P. Frigo, G. Brian Stephenson, Ian McNdty Argonne National Laboratory 9700 South
. 1. Introduction X-ray speckle contrast variation at absorption edges sample-specific Cornelia C. Retsch, Yuxin Wang, Sean P. Frigo, G. Brian Stephenson, Ian McNdty Argonne National Laboratory 9700 South
Statistics for scientists and engineers
 Statistics for scientists and engineers February 0, 006 Contents Introduction. Motivation - why study statistics?................................... Examples..................................................3
Statistics for scientists and engineers February 0, 006 Contents Introduction. Motivation - why study statistics?................................... Examples..................................................3
RADIATION SOURCES AT SIBERIA-2 STORAGE RING
 RADIATION SOURCES AT SIBERIA-2 STORAGE RING V.N. Korchuganov, N.Yu. Svechnikov, N.V. Smolyakov, S.I. Tomin RRC «Kurchatov Institute», Moscow, Russia Kurchatov Center Synchrotron Radiation undulator undulator
RADIATION SOURCES AT SIBERIA-2 STORAGE RING V.N. Korchuganov, N.Yu. Svechnikov, N.V. Smolyakov, S.I. Tomin RRC «Kurchatov Institute», Moscow, Russia Kurchatov Center Synchrotron Radiation undulator undulator
Methoden moderner Röntgenphysik I. Coherence based techniques II. Christian Gutt DESY, Hamburg
 Methoden moderner Röntgenphysik I Coherence based techniques II Christian Gutt DESY Hamburg christian.gutt@desy.de 8. January 009 Outline 18.1. 008 Introduction to Coherence 8.01. 009 Structure determination
Methoden moderner Röntgenphysik I Coherence based techniques II Christian Gutt DESY Hamburg christian.gutt@desy.de 8. January 009 Outline 18.1. 008 Introduction to Coherence 8.01. 009 Structure determination
AOL Spring Wavefront Sensing. Figure 1: Principle of operation of the Shack-Hartmann wavefront sensor
 AOL Spring Wavefront Sensing The Shack Hartmann Wavefront Sensor system provides accurate, high-speed measurements of the wavefront shape and intensity distribution of beams by analyzing the location and
AOL Spring Wavefront Sensing The Shack Hartmann Wavefront Sensor system provides accurate, high-speed measurements of the wavefront shape and intensity distribution of beams by analyzing the location and
Good Diffraction Practice Webinar Series
 Good Diffraction Practice Webinar Series High Resolution X-ray Diffractometry (1) Mar 24, 2011 www.bruker-webinars.com Welcome Heiko Ress Global Marketing Manager Bruker AXS Inc. Madison, Wisconsin, USA
Good Diffraction Practice Webinar Series High Resolution X-ray Diffractometry (1) Mar 24, 2011 www.bruker-webinars.com Welcome Heiko Ress Global Marketing Manager Bruker AXS Inc. Madison, Wisconsin, USA
2. Passage of Radiation Through Matter
 2. Passage of Radiation Through Matter Passage of Radiation Through Matter: Contents Energy Loss of Heavy Charged Particles by Atomic Collision (addendum) Cherenkov Radiation Energy loss of Electrons and
2. Passage of Radiation Through Matter Passage of Radiation Through Matter: Contents Energy Loss of Heavy Charged Particles by Atomic Collision (addendum) Cherenkov Radiation Energy loss of Electrons and
Small-Angle X-ray Scattering (SAXS) SPring-8/JASRI Naoto Yagi
 Small-Angle X-ray Scattering (SAXS) SPring-8/JASRI Naoto Yagi 1 Wikipedia Small-angle X-ray scattering (SAXS) is a small-angle scattering (SAS) technique where the elastic scattering of X-rays (wavelength
Small-Angle X-ray Scattering (SAXS) SPring-8/JASRI Naoto Yagi 1 Wikipedia Small-angle X-ray scattering (SAXS) is a small-angle scattering (SAS) technique where the elastic scattering of X-rays (wavelength
Which of the following can be used to calculate the resistive force acting on the brick? D (Total for Question = 1 mark)
 1 A brick of mass 5.0 kg falls through water with an acceleration of 0.90 m s 2. Which of the following can be used to calculate the resistive force acting on the brick? A 5.0 (0.90 9.81) B 5.0 (0.90 +
1 A brick of mass 5.0 kg falls through water with an acceleration of 0.90 m s 2. Which of the following can be used to calculate the resistive force acting on the brick? A 5.0 (0.90 9.81) B 5.0 (0.90 +
Detection of X-Rays. Solid state detectors Proportional counters Microcalorimeters Detector characteristics
 Detection of X-Rays Solid state detectors Proportional counters Microcalorimeters Detector characteristics Solid State X-ray Detectors X-ray interacts in material to produce photoelectrons which are collected
Detection of X-Rays Solid state detectors Proportional counters Microcalorimeters Detector characteristics Solid State X-ray Detectors X-ray interacts in material to produce photoelectrons which are collected
Short Wire Antennas: A Simplified Approach Part I: Scaling Arguments. Dan Dobkin version 1.0 July 8, 2005
 Short Wire Antennas: A Simplified Approach Part I: Scaling Arguments Dan Dobkin version 1.0 July 8, 2005 0. Introduction: How does a wire dipole antenna work? How do we find the resistance and the reactance?
Short Wire Antennas: A Simplified Approach Part I: Scaling Arguments Dan Dobkin version 1.0 July 8, 2005 0. Introduction: How does a wire dipole antenna work? How do we find the resistance and the reactance?
Time-Dependent Perturbation Theory. Absorption and Emission of Radiation. Band Shapes and Convolution
 Lecture 1 Perturbation Theory Lecture 2 Time-Dependent Perturbation Theory Lecture 3 Absorption and Emission of Radiation Lecture 4 Raman Scattering Workshop Band Shapes and Convolution Lecture 1 Perturbation
Lecture 1 Perturbation Theory Lecture 2 Time-Dependent Perturbation Theory Lecture 3 Absorption and Emission of Radiation Lecture 4 Raman Scattering Workshop Band Shapes and Convolution Lecture 1 Perturbation
Physics 217 Problem Set 1 Due: Friday, Aug 29th, 2008
 Problem Set 1 Due: Friday, Aug 29th, 2008 Course page: http://www.physics.wustl.edu/~alford/p217/ Review of complex numbers. See appendix K of the textbook. 1. Consider complex numbers z = 1.5 + 0.5i and
Problem Set 1 Due: Friday, Aug 29th, 2008 Course page: http://www.physics.wustl.edu/~alford/p217/ Review of complex numbers. See appendix K of the textbook. 1. Consider complex numbers z = 1.5 + 0.5i and
A6523 Signal Modeling, Statistical Inference and Data Mining in Astrophysics Spring 2011
 A6523 Signal Modeling, Statistical Inference and Data Mining in Astrophysics Spring 2011 Reading Chapter 5 (continued) Lecture 8 Key points in probability CLT CLT examples Prior vs Likelihood Box & Tiao
A6523 Signal Modeling, Statistical Inference and Data Mining in Astrophysics Spring 2011 Reading Chapter 5 (continued) Lecture 8 Key points in probability CLT CLT examples Prior vs Likelihood Box & Tiao
Coherence. Tsuneaki Miyahara, Japan Women s Univ.
 Coherence Tsuneaki Miyahara, Japan Women s Univ. 1) Description of light in the phase space First-order spatial coherence: Experiments First order temporal coherence Description of light in the 6-dimensional
Coherence Tsuneaki Miyahara, Japan Women s Univ. 1) Description of light in the phase space First-order spatial coherence: Experiments First order temporal coherence Description of light in the 6-dimensional
ME FINITE ELEMENT ANALYSIS FORMULAS
 ME 2353 - FINITE ELEMENT ANALYSIS FORMULAS UNIT I FINITE ELEMENT FORMULATION OF BOUNDARY VALUE PROBLEMS 01. Global Equation for Force Vector, {F} = [K] {u} {F} = Global Force Vector [K] = Global Stiffness
ME 2353 - FINITE ELEMENT ANALYSIS FORMULAS UNIT I FINITE ELEMENT FORMULATION OF BOUNDARY VALUE PROBLEMS 01. Global Equation for Force Vector, {F} = [K] {u} {F} = Global Force Vector [K] = Global Stiffness
Scattering Techniques and Geometries How to choose a beamline. Christopher J. Tassone
 Scattering Techniques and Geometries How to choose a beamline Christopher J. Tassone Why Care About Geometries? How do you decide which beamline you want to use? Questions you should be asking Do I want
Scattering Techniques and Geometries How to choose a beamline Christopher J. Tassone Why Care About Geometries? How do you decide which beamline you want to use? Questions you should be asking Do I want
CERN Accelerator School. Intermediate Accelerator Physics Course Chios, Greece, September Low Emittance Rings
 CERN Accelerator School Intermediate Accelerator Physics Course Chios, Greece, September 2011 Low Emittance Rings Part 1: Beam Dynamics with Synchrotron Radiation Andy Wolski The Cockcroft Institute, and
CERN Accelerator School Intermediate Accelerator Physics Course Chios, Greece, September 2011 Low Emittance Rings Part 1: Beam Dynamics with Synchrotron Radiation Andy Wolski The Cockcroft Institute, and
Perhaps the simplest way of modeling two (discrete) random variables is by means of a joint PMF, defined as follows.
 Chapter 5 Two Random Variables In a practical engineering problem, there is almost always causal relationship between different events. Some relationships are determined by physical laws, e.g., voltage
Chapter 5 Two Random Variables In a practical engineering problem, there is almost always causal relationship between different events. Some relationships are determined by physical laws, e.g., voltage
ELECTRON DYNAMICS WITH SYNCHROTRON RADIATION
 ELECTRON DYNAMICS WITH SYNCHROTRON RADIATION Lenny Rivkin Ecole Polythechnique Federale de Lausanne (EPFL) and Paul Scherrer Institute (PSI), Switzerland CERN Accelerator School: Introduction to Accelerator
ELECTRON DYNAMICS WITH SYNCHROTRON RADIATION Lenny Rivkin Ecole Polythechnique Federale de Lausanne (EPFL) and Paul Scherrer Institute (PSI), Switzerland CERN Accelerator School: Introduction to Accelerator
Simulation of Optics Correction for ERLs. V. Sajaev, ANL
 Simulation of Optics Correction for ERLs V. Sajaev, ANL Introduction Minimization of particle losses in ERL arcs requires use of sextupoles As in storage rings, trajectory errors in the presence of sextupoles
Simulation of Optics Correction for ERLs V. Sajaev, ANL Introduction Minimization of particle losses in ERL arcs requires use of sextupoles As in storage rings, trajectory errors in the presence of sextupoles
I. Rayleigh Scattering. EE Lecture 4. II. Dipole interpretation
 I. Rayleigh Scattering 1. Rayleigh scattering 2. Dipole interpretation 3. Cross sections 4. Other approximations EE 816 - Lecture 4 Rayleigh scattering is an approximation used to predict scattering from
I. Rayleigh Scattering 1. Rayleigh scattering 2. Dipole interpretation 3. Cross sections 4. Other approximations EE 816 - Lecture 4 Rayleigh scattering is an approximation used to predict scattering from
Accelerator Physics Final Exam pts.
 Accelerator Physics Final Exam - 170 pts. S. M. Lund and Y. Hao Graders: C. Richard and C. Y. Wong June 14, 2018 Problem 1 P052 Emittance Evolution 40 pts. a) 5 pts: Consider a coasting beam composed of
Accelerator Physics Final Exam - 170 pts. S. M. Lund and Y. Hao Graders: C. Richard and C. Y. Wong June 14, 2018 Problem 1 P052 Emittance Evolution 40 pts. a) 5 pts: Consider a coasting beam composed of
Coherent X-Ray Sources: Synchrotron, ERL, XFEL
 Coherent X-Ray Sources: Synchrotron, ERL, XFEL John Arthur SSRL/SLAC Energy Recovery Linac Science Workshop Cornell University 2 December 2000 Supported by the US Dept. of Energy, Office of Basic Energy
Coherent X-Ray Sources: Synchrotron, ERL, XFEL John Arthur SSRL/SLAC Energy Recovery Linac Science Workshop Cornell University 2 December 2000 Supported by the US Dept. of Energy, Office of Basic Energy
Geometry of Crystal Lattice
 0 Geometry of Crystal Lattice 0.1 Translational Symmetry The crystalline state of substances is different from other states (gaseous, liquid, amorphous) in that the atoms are in an ordered and symmetrical
0 Geometry of Crystal Lattice 0.1 Translational Symmetry The crystalline state of substances is different from other states (gaseous, liquid, amorphous) in that the atoms are in an ordered and symmetrical
1 Introduction Goal of calculating the analytical model of the instrument Basic method Parameters out of optimization...
 Contents 1 Introduction 3 1.1 Goal of calculating the analytical model of the instrument...................... 3 1.2 Basic method............................................... 3 1.3 Parameters out of
Contents 1 Introduction 3 1.1 Goal of calculating the analytical model of the instrument...................... 3 1.2 Basic method............................................... 3 1.3 Parameters out of
Review of Fundamental Equations Supplementary notes on Section 1.2 and 1.3
 Review of Fundamental Equations Supplementary notes on Section. and.3 Introduction of the velocity potential: irrotational motion: ω = u = identity in the vector analysis: ϕ u = ϕ Basic conservation principles:
Review of Fundamental Equations Supplementary notes on Section. and.3 Introduction of the velocity potential: irrotational motion: ω = u = identity in the vector analysis: ϕ u = ϕ Basic conservation principles:
EXAM # AM PM, Wednesday March 14. Write your name and ID number at the top of this page and on pages 2-5.
 NAME: SOLUTIONS Student ID: Score: Physics 322 Winter 2018 EXAM # 3 1030 AM - 1220 PM, Wednesday March 14 Write your name and ID number at the top of this page and on pages 2-5. Clearly show all your reasoning.
NAME: SOLUTIONS Student ID: Score: Physics 322 Winter 2018 EXAM # 3 1030 AM - 1220 PM, Wednesday March 14 Write your name and ID number at the top of this page and on pages 2-5. Clearly show all your reasoning.
X-ray Diffraction. Diffraction. X-ray Generation. X-ray Generation. X-ray Generation. X-ray Spectrum from Tube
 X-ray Diffraction Mineral identification Mode analysis Structure Studies X-ray Generation X-ray tube (sealed) Pure metal target (Cu) Electrons remover inner-shell electrons from target. Other electrons
X-ray Diffraction Mineral identification Mode analysis Structure Studies X-ray Generation X-ray tube (sealed) Pure metal target (Cu) Electrons remover inner-shell electrons from target. Other electrons
Particle Accelerators: Transverse Beam Dynamics
 Particle Accelerators: Transverse Beam Dynamics Volker Ziemann Department of Physics and Astronomy Uppsala University Research Training course in Detector Technology Stockholm, Sept. 8, 2008 080908 V.
Particle Accelerators: Transverse Beam Dynamics Volker Ziemann Department of Physics and Astronomy Uppsala University Research Training course in Detector Technology Stockholm, Sept. 8, 2008 080908 V.
Scattering of Electromagnetic Radiation. References:
 Scattering of Electromagnetic Radiation References: Plasma Diagnostics: Chapter by Kunze Methods of experimental physics, 9a, chapter by Alan Desilva and George Goldenbaum, Edited by Loveberg and Griem.
Scattering of Electromagnetic Radiation References: Plasma Diagnostics: Chapter by Kunze Methods of experimental physics, 9a, chapter by Alan Desilva and George Goldenbaum, Edited by Loveberg and Griem.
Classical Mechanics. Luis Anchordoqui
 1 Rigid Body Motion Inertia Tensor Rotational Kinetic Energy Principal Axes of Rotation Steiner s Theorem Euler s Equations for a Rigid Body Eulerian Angles Review of Fundamental Equations 2 Rigid body
1 Rigid Body Motion Inertia Tensor Rotational Kinetic Energy Principal Axes of Rotation Steiner s Theorem Euler s Equations for a Rigid Body Eulerian Angles Review of Fundamental Equations 2 Rigid body
Radiation Damping. 1 Introduction to the Abraham-Lorentz equation
 Radiation Damping Lecture 18 1 Introduction to the Abraham-Lorentz equation Classically, a charged particle radiates energy if it is accelerated. We have previously obtained the Larmor expression for the
Radiation Damping Lecture 18 1 Introduction to the Abraham-Lorentz equation Classically, a charged particle radiates energy if it is accelerated. We have previously obtained the Larmor expression for the
Wave Mechanics in One Dimension
 Wave Mechanics in One Dimension Wave-Particle Duality The wave-like nature of light had been experimentally demonstrated by Thomas Young in 1820, by observing interference through both thin slit diffraction
Wave Mechanics in One Dimension Wave-Particle Duality The wave-like nature of light had been experimentally demonstrated by Thomas Young in 1820, by observing interference through both thin slit diffraction
CONCEPTUAL STUDY OF A SELF-SEEDING SCHEME AT FLASH2
 CONCEPTUAL STUDY OF A SELF-SEEDING SCHEME AT FLASH2 T. Plath, L. L. Lazzarino, Universität Hamburg, Hamburg, Germany K. E. Hacker, T.U. Dortmund, Dortmund, Germany Abstract We present a conceptual study
CONCEPTUAL STUDY OF A SELF-SEEDING SCHEME AT FLASH2 T. Plath, L. L. Lazzarino, Universität Hamburg, Hamburg, Germany K. E. Hacker, T.U. Dortmund, Dortmund, Germany Abstract We present a conceptual study
The ideal fiber pattern exhibits 4-quadrant symmetry. In the ideal pattern the fiber axis is called the meridian, the perpendicular direction is
 Fiber diffraction is a method used to determine the structural information of a molecule by using scattering data from X-rays. Rosalind Franklin used this technique in discovering structural information
Fiber diffraction is a method used to determine the structural information of a molecule by using scattering data from X-rays. Rosalind Franklin used this technique in discovering structural information
Lecture 9: Introduction to Diffraction of Light
 Lecture 9: Introduction to Diffraction of Light Lecture aims to explain: 1. Diffraction of waves in everyday life and applications 2. Interference of two one dimensional electromagnetic waves 3. Typical
Lecture 9: Introduction to Diffraction of Light Lecture aims to explain: 1. Diffraction of waves in everyday life and applications 2. Interference of two one dimensional electromagnetic waves 3. Typical
Physics 411: Homework 3
 Physics 411: Homework 3 Because of the cancellation of class on January 28, this homework is a double-length homework covering two week s material, and you have two weeks to do it. It is due in class onthursday,
Physics 411: Homework 3 Because of the cancellation of class on January 28, this homework is a double-length homework covering two week s material, and you have two weeks to do it. It is due in class onthursday,
A Brief Introduction to Medical Imaging. Outline
 A Brief Introduction to Medical Imaging Outline General Goals Linear Imaging Systems An Example, The Pin Hole Camera Radiations and Their Interactions with Matter Coherent vs. Incoherent Imaging Length
A Brief Introduction to Medical Imaging Outline General Goals Linear Imaging Systems An Example, The Pin Hole Camera Radiations and Their Interactions with Matter Coherent vs. Incoherent Imaging Length
Analysis of Coherence Properties of 3-rd Generation Synchrotron Sources and Free-Electron Lasers
 Analysis of Coherence Properties of 3-rd Generation Synchrotron Sources and Free-Electron Lasers arxiv:0907.4009v1 [physics.optics] 23 Jul 2009 I.A. Vartanyants and A. Singer HASYLAB at DESY, Notkestr.
Analysis of Coherence Properties of 3-rd Generation Synchrotron Sources and Free-Electron Lasers arxiv:0907.4009v1 [physics.optics] 23 Jul 2009 I.A. Vartanyants and A. Singer HASYLAB at DESY, Notkestr.
worked out from first principles by parameterizing the path, etc. If however C is a A path C is a simple closed path if and only if the starting point
 III.c Green s Theorem As mentioned repeatedly, if F is not a gradient field then F dr must be worked out from first principles by parameterizing the path, etc. If however is a simple closed path in the
III.c Green s Theorem As mentioned repeatedly, if F is not a gradient field then F dr must be worked out from first principles by parameterizing the path, etc. If however is a simple closed path in the
Brightness and Coherence of Synchrotron Radiation and Free Electron Lasers. Zhirong Huang SLAC, Stanford University May 13, 2013
 Brightness and Coherence of Synchrotron Radiation and Free Electron Lasers Zhirong Huang SLAC, Stanford University May 13, 2013 Introduction GE synchrotron (1946) opened a new era of accelerator-based
Brightness and Coherence of Synchrotron Radiation and Free Electron Lasers Zhirong Huang SLAC, Stanford University May 13, 2013 Introduction GE synchrotron (1946) opened a new era of accelerator-based
Short Wavelength SASE FELs: Experiments vs. Theory. Jörg Rossbach University of Hamburg & DESY
 Short Wavelength SASE FELs: Experiments vs. Theory Jörg Rossbach University of Hamburg & DESY Contents INPUT (electrons) OUTPUT (photons) Momentum Momentum spread/chirp Slice emittance/ phase space distribution
Short Wavelength SASE FELs: Experiments vs. Theory Jörg Rossbach University of Hamburg & DESY Contents INPUT (electrons) OUTPUT (photons) Momentum Momentum spread/chirp Slice emittance/ phase space distribution
X-ray diffraction is a non-invasive method for determining many types of
 Chapter X-ray Diffraction.1 Introduction X-ray diffraction is a non-invasive method for determining many types of structural features in both crystalline and amorphous materials. In the case of single
Chapter X-ray Diffraction.1 Introduction X-ray diffraction is a non-invasive method for determining many types of structural features in both crystalline and amorphous materials. In the case of single
Check the LCLS Project website to verify 2 of 6 that this is the correct version prior to use.
 1. Introduction The XTOD Offset Systems are designed to spatially separate the useful FEL radiation from high-energy spontaneous radiation and Bremsstrahlung γ-rays. These unwanted radiations are generated
1. Introduction The XTOD Offset Systems are designed to spatially separate the useful FEL radiation from high-energy spontaneous radiation and Bremsstrahlung γ-rays. These unwanted radiations are generated
X-ray Photon Correlation Spectroscopy (XPCS) at Synchrotron and FEL sources
 X-ray Photon Correlation Spectroscopy (XPCS) at Synchrotron and FEL sources Christian Gutt Department of Physics, University ofsiegen, Germany gutt@physik.uni-siegen.de Outline How to measure dynamics
X-ray Photon Correlation Spectroscopy (XPCS) at Synchrotron and FEL sources Christian Gutt Department of Physics, University ofsiegen, Germany gutt@physik.uni-siegen.de Outline How to measure dynamics
MANIPAL INSTITUTE OF TECHNOLOGY
 SCHEME OF EVAUATION MANIPA INSTITUTE OF TECHNOOGY MANIPA UNIVERSITY, MANIPA SECOND SEMESTER B.Tech. END-SEMESTER EXAMINATION - MAY SUBJECT: ENGINEERING PHYSICS (PHY/) Time: 3 Hrs. Max. Marks: 5 Note: Answer
SCHEME OF EVAUATION MANIPA INSTITUTE OF TECHNOOGY MANIPA UNIVERSITY, MANIPA SECOND SEMESTER B.Tech. END-SEMESTER EXAMINATION - MAY SUBJECT: ENGINEERING PHYSICS (PHY/) Time: 3 Hrs. Max. Marks: 5 Note: Answer
Department of Physics, Korea University Page 1 of 8
 Name: Department: Student ID #: Notice +2 ( 1) points per correct (incorrect) answer No penalty for an unanswered question Fill the blank ( ) with ( ) if the statement is correct (incorrect) : corrections
Name: Department: Student ID #: Notice +2 ( 1) points per correct (incorrect) answer No penalty for an unanswered question Fill the blank ( ) with ( ) if the statement is correct (incorrect) : corrections
Simplified Collector Performance Model
 Simplified Collector Performance Model Prediction of the thermal output of various solar collectors: The quantity of thermal energy produced by any solar collector can be described by the energy balance
Simplified Collector Performance Model Prediction of the thermal output of various solar collectors: The quantity of thermal energy produced by any solar collector can be described by the energy balance
Quantum Condensed Matter Physics Lecture 5
 Quantum Condensed Matter Physics Lecture 5 detector sample X-ray source monochromator David Ritchie http://www.sp.phy.cam.ac.uk/drp2/home QCMP Lent/Easter 2019 5.1 Quantum Condensed Matter Physics 1. Classical
Quantum Condensed Matter Physics Lecture 5 detector sample X-ray source monochromator David Ritchie http://www.sp.phy.cam.ac.uk/drp2/home QCMP Lent/Easter 2019 5.1 Quantum Condensed Matter Physics 1. Classical
Fiber Optics. Equivalently θ < θ max = cos 1 (n 0 /n 1 ). This is geometrical optics. Needs λ a. Two kinds of fibers:
 Waves can be guided not only by conductors, but by dielectrics. Fiber optics cable of silica has nr varying with radius. Simplest: core radius a with n = n 1, surrounded radius b with n = n 0 < n 1. Total
Waves can be guided not only by conductors, but by dielectrics. Fiber optics cable of silica has nr varying with radius. Simplest: core radius a with n = n 1, surrounded radius b with n = n 0 < n 1. Total
EE485 Introduction to Photonics
 Pattern formed by fluorescence of quantum dots EE485 Introduction to Photonics Photon and Laser Basics 1. Photon properties 2. Laser basics 3. Characteristics of laser beams Reading: Pedrotti 3, Sec. 1.2,
Pattern formed by fluorescence of quantum dots EE485 Introduction to Photonics Photon and Laser Basics 1. Photon properties 2. Laser basics 3. Characteristics of laser beams Reading: Pedrotti 3, Sec. 1.2,
Introduction to Condensed Matter Physics
 Introduction to Condensed Matter Physics Diffraction I Basic Physics M.P. Vaughan Diffraction Electromagnetic waves Geometric wavefront The Principle of Linear Superposition Diffraction regimes Single
Introduction to Condensed Matter Physics Diffraction I Basic Physics M.P. Vaughan Diffraction Electromagnetic waves Geometric wavefront The Principle of Linear Superposition Diffraction regimes Single
Detecting high energy photons. Interactions of photons with matter Properties of detectors (with examples)
 Detecting high energy photons Interactions of photons with matter Properties of detectors (with examples) Interactions of high energy photons with matter Cross section/attenution length/optical depth Photoelectric
Detecting high energy photons Interactions of photons with matter Properties of detectors (with examples) Interactions of high energy photons with matter Cross section/attenution length/optical depth Photoelectric
where r n = dn+1 x(t)
 Random Variables Overview Probability Random variables Transforms of pdfs Moments and cumulants Useful distributions Random vectors Linear transformations of random vectors The multivariate normal distribution
Random Variables Overview Probability Random variables Transforms of pdfs Moments and cumulants Useful distributions Random vectors Linear transformations of random vectors The multivariate normal distribution
Roger Johnson Structure and Dynamics: X-ray Diffraction Lecture 6
 6.1. Summary In this Lecture we cover the theory of x-ray diffraction, which gives direct information about the atomic structure of crystals. In these experiments, the wavelength of the incident beam must
6.1. Summary In this Lecture we cover the theory of x-ray diffraction, which gives direct information about the atomic structure of crystals. In these experiments, the wavelength of the incident beam must
PRINCIPLES OF PHYSICAL OPTICS
 PRINCIPLES OF PHYSICAL OPTICS C. A. Bennett University of North Carolina At Asheville WILEY- INTERSCIENCE A JOHN WILEY & SONS, INC., PUBLICATION CONTENTS Preface 1 The Physics of Waves 1 1.1 Introduction
PRINCIPLES OF PHYSICAL OPTICS C. A. Bennett University of North Carolina At Asheville WILEY- INTERSCIENCE A JOHN WILEY & SONS, INC., PUBLICATION CONTENTS Preface 1 The Physics of Waves 1 1.1 Introduction
Introduction to Classical and Quantum FEL Theory R. Bonifacio University of Milano and INFN LNF
 Introduction to Classical and Quantum FEL Theory R. Bonifacio University of Milano and INFN LNF Natal 2016 1 1 OUTLINE Classical SASE and spiking Semi-classical FEL theory: quantum purification Fully quantum
Introduction to Classical and Quantum FEL Theory R. Bonifacio University of Milano and INFN LNF Natal 2016 1 1 OUTLINE Classical SASE and spiking Semi-classical FEL theory: quantum purification Fully quantum
4. The interaction of light with matter
 4. The interaction of light with matter The propagation of light through chemical materials is described by a wave equation similar to the one that describes light travel in a vacuum (free space). Again,
4. The interaction of light with matter The propagation of light through chemical materials is described by a wave equation similar to the one that describes light travel in a vacuum (free space). Again,
INVESTIGATIONS OF THE DISTRIBUTION IN VERY SHORT ELECTRON BUNCHES LONGITUDINAL CHARGE
 INVESTIGATIONS OF THE LONGITUDINAL CHARGE DISTRIBUTION IN VERY SHORT ELECTRON BUNCHES Markus Hüning III. Physikalisches Institut RWTH Aachen IIIa and DESY Invited talk at the DIPAC 2001 Methods to obtain
INVESTIGATIONS OF THE LONGITUDINAL CHARGE DISTRIBUTION IN VERY SHORT ELECTRON BUNCHES Markus Hüning III. Physikalisches Institut RWTH Aachen IIIa and DESY Invited talk at the DIPAC 2001 Methods to obtain
Problem Set 5: Solutions
 University of Alabama Department of Physics and Astronomy Department of Electrical and Computer Engineering PH 495/ECE 493 LeClair & Kung Spring 011 Problem Set 5: Solutions 1. Bekefi & Barrett 8.; Hecht
University of Alabama Department of Physics and Astronomy Department of Electrical and Computer Engineering PH 495/ECE 493 LeClair & Kung Spring 011 Problem Set 5: Solutions 1. Bekefi & Barrett 8.; Hecht
Laser Optics-II. ME 677: Laser Material Processing Instructor: Ramesh Singh 1
 Laser Optics-II 1 Outline Absorption Modes Irradiance Reflectivity/Absorption Absorption coefficient will vary with the same effects as the reflectivity For opaque materials: reflectivity = 1 - absorptivity
Laser Optics-II 1 Outline Absorption Modes Irradiance Reflectivity/Absorption Absorption coefficient will vary with the same effects as the reflectivity For opaque materials: reflectivity = 1 - absorptivity
EM radiation - Lecture 14
 EM radiation - Lecture 14 1 Review Begin with a review of the potentials, fields, and Poynting vector for a point charge in accelerated motion. The retarded potential forms are given below. The source
EM radiation - Lecture 14 1 Review Begin with a review of the potentials, fields, and Poynting vector for a point charge in accelerated motion. The retarded potential forms are given below. The source
High-Resolution. Transmission. Electron Microscopy
 Part 4 High-Resolution Transmission Electron Microscopy 186 Significance high-resolution transmission electron microscopy (HRTEM): resolve object details smaller than 1nm (10 9 m) image the interior of
Part 4 High-Resolution Transmission Electron Microscopy 186 Significance high-resolution transmission electron microscopy (HRTEM): resolve object details smaller than 1nm (10 9 m) image the interior of
Use of Crab Cavities for Short X-ray Pulse Production in Rings
 Use of Crab Cavities for Short X-ray Pulse Production in Rings Michael Borland Argonne National Laboratory March 2010 The submitted manuscript has been created by UChicago Argonne, LLC, Operator of Argonne
Use of Crab Cavities for Short X-ray Pulse Production in Rings Michael Borland Argonne National Laboratory March 2010 The submitted manuscript has been created by UChicago Argonne, LLC, Operator of Argonne
Ternary blend polymer solar cells with enhanced power conversion efficiency
 Ternary blend polymer solar cells with enhanced power conversion efficiency Luyao Lu 1, Tao Xu 1, Wei Chen 2,3, Erik S. Landry 2,3, Luping Yu 1 * 1. Department of Chemistry and The James Franck Institute,
Ternary blend polymer solar cells with enhanced power conversion efficiency Luyao Lu 1, Tao Xu 1, Wei Chen 2,3, Erik S. Landry 2,3, Luping Yu 1 * 1. Department of Chemistry and The James Franck Institute,
Classical electric dipole radiation
 B Classical electric dipole radiation In Chapter a classical model was used to describe the scattering of X-rays by electrons. The equation relating the strength of the radiated to incident X-ray electric
B Classical electric dipole radiation In Chapter a classical model was used to describe the scattering of X-rays by electrons. The equation relating the strength of the radiated to incident X-ray electric
Introduction to electron and photon beam physics. Zhirong Huang SLAC and Stanford University
 Introduction to electron and photon beam physics Zhirong Huang SLAC and Stanford University August 03, 2015 Lecture Plan Electron beams (1.5 hrs) Photon or radiation beams (1 hr) References: 1. J. D. Jackson,
Introduction to electron and photon beam physics Zhirong Huang SLAC and Stanford University August 03, 2015 Lecture Plan Electron beams (1.5 hrs) Photon or radiation beams (1 hr) References: 1. J. D. Jackson,
2) Measure sample and empties. 3) Measure transmissions of sample and empties. 4) Normalize to exposure time and transmission. 5) Subtract the empties
 1) Measure calibrants and direct beam to do Angular Integrations (transforms 2D into 1D) Need the distance SD Need center of beam Need to calculate q-vector 2) Measure sample and empties 3) Measure transmissions
1) Measure calibrants and direct beam to do Angular Integrations (transforms 2D into 1D) Need the distance SD Need center of beam Need to calculate q-vector 2) Measure sample and empties 3) Measure transmissions
Light as a Transverse Wave.
 Waves and Superposition (Keating Chapter 21) The ray model for light (i.e. light travels in straight lines) can be used to explain a lot of phenomena (like basic object and image formation and even aberrations)
Waves and Superposition (Keating Chapter 21) The ray model for light (i.e. light travels in straight lines) can be used to explain a lot of phenomena (like basic object and image formation and even aberrations)
(c) n (d) n 2. (a) (b) (c) (d) (a) Null set (b) {P} (c) {P, Q, R} (d) {Q, R} (a) 2k (b) 7 (c) 2 (d) K (a) 1 (b) 3 (c) 3xyz (d) 27xyz
 318 NDA Mathematics Practice Set 1. (1001)2 (101)2 (110)2 (100)2 2. z 1/z 2z z/2 3. The multiplication of the number (10101)2 by (1101)2 yields which one of the following? (100011001)2 (100010001)2 (110010011)2
318 NDA Mathematics Practice Set 1. (1001)2 (101)2 (110)2 (100)2 2. z 1/z 2z z/2 3. The multiplication of the number (10101)2 by (1101)2 yields which one of the following? (100011001)2 (100010001)2 (110010011)2
Lecture 11: Introduction to diffraction of light
 Lecture 11: Introduction to diffraction of light Diffraction of waves in everyday life and applications Diffraction in everyday life Diffraction in applications Spectroscopy: physics, chemistry, medicine,
Lecture 11: Introduction to diffraction of light Diffraction of waves in everyday life and applications Diffraction in everyday life Diffraction in applications Spectroscopy: physics, chemistry, medicine,
Methoden moderner Röntgenphysik II: Streuung und Abbildung
 . Methoden moderner Röntgenphysik II: Streuung und Abbildung Lecture 10 Vorlesung zum Haupt/Masterstudiengang Physik SS 2014 G. Grübel, M. Martins, E. Weckert Location: Hörs AP, Physik, Jungiusstrasse
. Methoden moderner Röntgenphysik II: Streuung und Abbildung Lecture 10 Vorlesung zum Haupt/Masterstudiengang Physik SS 2014 G. Grübel, M. Martins, E. Weckert Location: Hörs AP, Physik, Jungiusstrasse
In this chapter we study elliptical PDEs. That is, PDEs of the form. 2 u = lots,
 Chapter 8 Elliptic PDEs In this chapter we study elliptical PDEs. That is, PDEs of the form 2 u = lots, where lots means lower-order terms (u x, u y,..., u, f). Here are some ways to think about the physical
Chapter 8 Elliptic PDEs In this chapter we study elliptical PDEs. That is, PDEs of the form 2 u = lots, where lots means lower-order terms (u x, u y,..., u, f). Here are some ways to think about the physical
1. Consider the biconvex thick lens shown in the figure below, made from transparent material with index n and thickness L.
 Optical Science and Engineering 2013 Advanced Optics Exam Answer all questions. Begin each question on a new blank page. Put your banner ID at the top of each page. Please staple all pages for each individual
Optical Science and Engineering 2013 Advanced Optics Exam Answer all questions. Begin each question on a new blank page. Put your banner ID at the top of each page. Please staple all pages for each individual
