Sufficiency 1. Sufficiency. Math Stat II
|
|
|
- Myrtle Foster
- 5 years ago
- Views:
Transcription
1 Sufficiency 1 Sufficiency
2 Sufficiency 2 Outline for Sufficiency 1. Measures of Quality of Estimators 2. A sufficient Statistic for a Parameter 3. Properties of a Sufficient Statistic 4. Completeness and Uniqueness 5. The Exponential Class of Distributions 6. Functions of a Parameter 7. Sufficiency, Completeness and Independence
3 Sufficiency 3 To present some optimal point estimates Recall Let X 1,,X n be a random sample from a distribution with pdf f(x; θ) and let Y n = u(x 1,,X n ) be the point estimator. Then 1. Consistent estimator: Y n P θ 2. Unbiased estimator: E(Y n )=θ
4 Sufficiency 4 Optimal estimator 1. Unbiased (or consistent) estimator 2. Efficient estimator: the one with the smaller variance ** Does MLE satisfy both?
5 Sufficiency 5 1 Measures of Quality of Estimators
6 Sufficiency 6 Definition 1.1 Y = u(x 1,X 2,,X n ) will be called a minimum variance unbiased estimator, (MVUE),of the parameter θ, ify is unbiased, that is, E(Y )=θ, and if the variance of Y is less than or equal to the variance of every other unbiased estimator of θ.
7 Sufficiency 7 Example 1.1 As an illustration, let X 1,X 2,,X 9 denote a random sample from a distribution that is N(θ,σ 2 ),where < θ <. Then compare X 1 and X = 1 9 (X 1 + +X 9 ) as estimators. (sol) Both are unbiased but var( X) is σ2 9 while var(x 1) is σ 2.Thatis, var( X) var(x), which indicates X is a better estimator for θ.
8 Sufficiency 8 Generalization of MVUE Let Y = u(x 1,X 2, ) be a statistic on which we wish to base a point estimate of the parameter θ. Decision rule (function), δ( ): the function of the observed value of Y and it decides the point estimate of θ. Decision, δ(y): one value of the decision function L(θ,δ) : loss function a measure of the seriousness of the difference between θ and the point estimate R(θ,δ) : risk function R(θ; δ) =E{L[θ,δ(y)]} = L[θ,δ(y)]f Y (y; θ)dy ** It would be desirable to select a decision function that minimizes the risk R(θ,δ) for all θ where θ Ω. However, it is not always possible. ** MVUE is an estimator which minimizes the risk function of L(θ,δ) =(θ δ) 2 among unbiased estimators.
9 Sufficiency 9 Alternative choices 1. Minimax principle: one principle of selecting a best decision function, δ 0 max θ R(θ,δ 0 ) max θ R(θ,δ) for any decision function δ 2. Minimum mean-squared-error estimator (MMSE), δ 0 E(θ δ 0 ) 2 E(θ δ) 2 for any decision function δ ** With the resriction E[δ(Y )] = θ and the loss function L(θ,δ)=[θ δ(y)] 2, the decision function that minimizes the risk function yields an unbiased estimator with minimum variance.
10 Sufficiency 10 Example 1.2 Let X 1,X 2,,X 25 be a random sample from a distribution that is N(θ,1), for <θ <.LetY = X, the mean of the random sample, and let L[θ,δ(y)] = [θ δ(y)] 2. When δ 1 (y) =y, When δ 2 (y) =0, R(θ,δ 1 )=E[(θ Y ) 2 ]= 1 25 R(θ,δ 2 )=E[(θ 0) 2 ]=θ 2 ** Thus R(θ,δ 2 )<R(θ,δ 1 ) if 1 < θ < R(θ,δ 2 ) R(θ,δ 1 ). However and otherwise By itself the decision function means the MMSE estimator. The linear MMSE estimator means the dicision function achieving MMSE among all estimator of the linear form. If only unbiased estimators are considered, then the decision function is the MVUE. ** Loss function can be either asymmetric or symmetric.
11 Sufficiency 11 Likelihood principle In the inference about θ, all relevant experimental information is contained in the likelihood function for the observed random samples. Two likelihood functions contain the same information about θ if they are proportional to each other.
12 Sufficiency 12 Example Let Y B(n, θ) where n = 10 and Y = 1. Then, L(θ Y )=10θ(1 θ) 9, ˆθmle = Y n = 1 10, E(ˆθ mle )=θ 2. Let Z Geo(θ) where Z = 10. Then, L(θ Z) =θ(1 θ) 9, ˆθmle = 1 Z = 1 10, E(ˆθ mle )= z=1 Do we have to adjust the bias of the MLE for geometric distribution? 1 z (1 θ)z 1 θ > θ ** Because L 1 (θ) L 2 (θ), the likelihood principle states tat we should make the same inference for both cases, and believers in the likelihood principle would not adjust the second estimator to make it unbiased.
13 Sufficiency 13 2 A Sufficient Statistics for a Parameter
14 Sufficiency 14 Sufficient Statistic 1. Sufficient statistic: Y = T (X 1,,X n ) 2. Example The idea of sufficiency is that if we observe a random varible X (usingasamplex 1,,X n,orx) whose distribution depends on θ, oftenx can be reduced via a function, without losing any informaion about θ If we have random samples, X 1,,X n,fromn(θ,1), we can estimate θ with X. Then other than X, can we get additional information about θ from X 1,,X n?
15 Sufficiency How to find: f(x; θ)=h(x)g(y ; θ) If Y is given, then does f(x Y ; θ) depend on θ? 4. If X Y does not depend on θ, we can conclude that Y exhausts all the informaion about θ.
16 Sufficiency 16 Example 2.1 Motivating example Original experiment: observe (X 1,X 2 ) independently where X i Bernoulli(θ), i = 1, 2 obs (0,0) (0,1) (1,0) (1,1) prob (1 θ) 2 (1 θ)θ θ(1 θ) θ 2 Probability structure for X 1 + X 2 X 1 + X prob (1 θ) 2 2(1 θ)θ θ 2 Conditional prob of (X 1,X 2 ) given X 1 + X 2 X 1 + X prob 1 for (0, 0) 0.5 for both (0, 1), (1, 0) 1 for (1, 1) *** X 1 + X 2 has all information for θ!!!
17 Sufficiency 17 Example 2.2 Let X 1,X 2,,X n denote a random sample from the distribution that has pmf f(x; θ)= θ x (1 θ) 1 x x = 0, 1; 0 < θ < 1 0 elsewhere. The statistic Y 1 = X 1 + X 2 + +X n has the pmf f Y1 (y 1 ; θ)= ( n y 1 )θ y 1 (1 θ) n y 1 y 1 = 0, 1,,n 0 elsewhere What is the conditional probability P (X 1 = x 1,X 2 = x 2,,X n = x n Y 1 = y 1 )=P (A B), say, where y 1 = 0, 1, 2,,n?
18 Sufficiency 18 (sol) If y 1 n i=1, itis0. If y 1 = n i=1, n i=1 {θ x i (1 θ) 1 x i } ( n y 1 )θ y 1 (1 θ) n y 1 = 1 ( n x i )
19 Sufficiency 19 Definition 2.1 Let X 1,X 2,,X n denote a random sample of size n from a distribution that has pdf or pmf f(x; θ), θ Ω. Let Y 1 = u 1 (X 1,X 2,,X n ) be a statistic whose pdf or pmf is f Y1 (y 1 ; θ). Then Y 1 is a sufficient statistic for θ if and only if f(x 1,x 2,, ; θ) f Y1 [u 1 (x 1,x 2,,x n ); θ] = H(x 1,x 2,,x n ), where H(x 1,x 2,,x n ) does not depend upon θ Ω.
20 Sufficiency 20 Example 2.3 Let X 1,X 2,,X n be a random sample from a gamma distriburion with α = 2 and β = θ > 0. ThenisY 1 = n i=1 X i sufficient statistics? (sol) X i iid G(2,θ) Y 1 = n i=1 X i G(2n, θ) Thus, f X1,,X n Y 1 (x 1,,x n y) = [ = n i=1 { x2 1 i e x i/θ } Γ(2)θ 2 n 1 / Γ(2n)θ ( 2n x i ) 2n 1 e n i=1 xi/θ ] Γ(2n) Γ(2) n Y 1 = n i=1 X i is a sufficient statistic. i=1 n i=1 x i ( n i=1 x i ) 2n 1
21 Sufficiency 21 Example 2.4 Let Y 1 < Y 2 < <Y n denote the order statistics of a random sample of size n from the distribution with pdf f(x; θ)=e (x θ) I (θ, ) (x). Then Y 1 is a sufficient statistic for θ? (sol) F X1 (x) =1 e (x θ) f Y1 (y) = θ F Y 1 (y) = θ [1 (1 F X 1 (y)) n ] = ne n(y θ) I (θ, ) (y) Thus, f X1,,Xn Y 1 (x 1,,xn y) = n {e (x i θ) I (θ, ) (x i )} i=1 /{ne (y θ) I (θ, ) (y)} = e (x 1 + +x n) ne n min x i Y 1 = min i=1,,n X i is a sufficient statistic.
22 Sufficiency 22 Theorem 2.1 Let f X1,,X n (x 1,,x n ; θ) be the pdf for X 1,X 2,,X n.theny 1 = u 1 (X 1,,X n ) is a sufficient statistic for θ if and only if f X1,,X n (x 1,,x n ; θ)=k 1 [u 1 (x 1,x 2,,x n ); θ]k 2 (x 1,x 2,,x n ), where k 2 (x 1,x 2,,x n ) does not depend upon θ.
23 Proof) We let X =(X 1,,Xn) and x =(x 1,,xn) (i) For discrete rv, P θ {X = x u 1 (X) =y 1 } = = = P θ {X = x,u 1 (X) =y 1 } P θ {u 1 (X) =y 1 } k 1 (u 1 (x);θ)k 2 (x) z u1 (z)=y k 1 1 (u 1 (z);θ)k 2 (z), if u 1 (x) =y 1 0 o.w. k 2 (x) z;u1 (z)=y k 1 2 (z), if u 1 (x) =y 1 0 o.w. (ii) For continuous rv, to make the one-to-one transformation, let y 1 = u 1 (X),y 2 = u 2 (X),,yn = un(x). Because there exists the inverse function, we can have x 1 = w 1 (Y),,xn = wn(y). f Y1 (y 1 ; θ) = k 1 (y 1 ; θ) J k 2 (w 1,,w n)dy 2 dyn = k 1 (y 1 ; θ) J k 2 (w 1,,w n)dy 2 dyn = c k 1 (y 1 ; θ) P θ {X = x u 1 (X) =y} = k 1 (u 1 (x); θ)k 2 (x) c k 1 (y 1 ; θ) = k 2 (x) c 22-1
24 If we let g(θ) f X (x u 1 (X)), by the definition of sufficiency we have g(θ) =f X (x u 1 (X) =y 1 ; θ) = f X (x u 1 (X) = y 1 ; θ )=g(θ ) for any θ θ which indicates g(θ) =c(x) that does not depend on θ. Thus, f X (x) = f X,u1 (X) (x,u 1 (x); θ) = f X (x u 1 (X)) f u1 (X) (u 1 (x); θ) = c(x) k 1 (u 1 (x); θ) 22-2
25 Sufficiency 23 Example 2.5 Let X 1,X 2,,X n denote a random sample from a distribution that N(θ,σ 2 ), < θ <, where the variance σ 2 > 0 is known. If X = n 1 X i /n, then X is a sufficient statistic for θ. (sol) Because n i=1(x i θ) 2 = n i=1(x i x) 2 + n( x θ) 2, 1 f X1,,X n (x 1,,x n ) = ( σ (2π) )n exp { 1 2σ 2 1 = ( σ (2π) )n exp { 1 2σ 2 n i=1 n i=1 (x i θ) 2 } (x i x) 2 } exp { n( x θ) 2 } X is a sufficient statistic.
26 Sufficiency 24 Example 2.6 Let X 1,X 2,,X n denote a random sample from a distribution with pdf f(x; θ)= θx θ 1 0 < x < 1 0 elsewhere, where 0 < θ. Then n i=1 X i is a sufficient statisti for θ. (sol) f X1,,X n (x 1,,x n ) = θ n ( n i=1 X i is a sufficient statistic. = {θ n ( n x i ) θ 1 i=1 n i=1 x i ) θ 1 }{ n } i=1 x i
27 Sufficiency 25 Example 2.7 In Example 2.3 with f(x; θ)=e (x θ) I (θ, ) (x), we have random samples, X 1,X 2,X 3.ThenX (1) = min X i is the sufficient statistic for θ but X (3) = max X i is not a sufficient statistic. (sol) f X1,X 2,X 3 (x 1,x 2,x 3 ) = e (x 1+x 2 +x 3 3θ) I (θ, ) (x 1,x 2,x 3 ) = e (x 1+x 2 +x 3 )+3x (3) e 3x (3) +3θ I (θ, ) (x (1) ) X (3) is not a sufficient statistic because of I (θ, ) (x (1) ). X (1) is a sufficient statistic because f X1,X 2,X 3 (x 1,x 2,x 3 )=e 3x (3) e (x 1+x 2 +x 3 )+3x (3) e 3θ I (θ, ) (x (1) )
28 Sufficiency 26 Example 2.8 Let X 1,,X n be a random sample from the Poisson distribution with θ (0, ). f(x i,θ)= θx i e θ. x i! n i=1 X i is a sufficient statistic for θ. (X 1,,X n ) is a sufficient statistic for θ. (X 1 + X 2,X 3 + +X n ) is a sufficient statistic for θ. (sol) n f X1,,X n (x 1,,x n )= θ i=1 x i e nθ n i=1 x i! 1. k 1 (u, θ) =θ u e nθ, u = n i=1 x i 2. k 1 ((x 1,,x n ),θ)=θ n i=1 x i e nθ 3. k 1 ((u 1,u 2 ),θ)=θ u 1+u 2 e nθ, u 1 = x 1 + x 2,u 2 = n i=3 x i
29 Sufficiency 27 Example 2.9 Let X 1,,X n be a random sample from the Gamma distribution: f(x i,α,β)= xα 1 i e x i/β Γ(α)β. α n i=1 X i is a sufficient statistic for α. ( n i=1 X i, n i=1 X i ) is a sufficient statistic for (α, β). ( n i=1 X i + n i=1 X i, n i=1 X i ) is a sufficient statistic for (α, β). (sol) 1. k 1 (u, α) = f X1,,X n (x 1,,x n )= u α 1 Γ(α) n β nα, u = n i=1 x i ( n i=1 x i ) α 1 e n i=1 x i/β Γ(α) n β nα 2. k 1 ((u 1,u 2 ), (α, β)) = uα 1 1 e u 2 /β, u Γ(α) n β nα 1 = n i=1 x i, u 2 = n i=1 x i 3. k 1 ((u 1,u 2 ), (α, β)) = (u 1 u 2 ) α 1 e u 2 /β Γ(α) n β nα, u 1 = n i=1 x i + n i=1 x i, u 2 = n i=1 x i
30 Sufficiency 28 Minimal Sufficient statistic X 1,,X n : r.s. from a distribution that has pdf f(x; θ), θ Ω, and Y 1 = u(x 1,,X n ): statistics. Y 1 : minimal sufficient for θ Ω Y 1 is a function of any other sufficient statistics for θ Ω. Example X 1,X 2,X 3 :r.s.fromn(θ,1), < θ < Sufficient statistics for θ: (X 1,X 2,X 3 ), (X 1 + X 2,X3), (X 1 + X 2 + X 3 )
31 Sufficiency 29 3 Properties of a Sufficient Statistic
32 Sufficiency 30 Theorem 3.1 (Rao-Backwell) Let X 1,X 2,,X n denote a random sample from a distribution that has pdf f(x; θ), θ Ω. Let Y 1 = u 1 (X 1,X 2,,X n ) be a sufficient statistic for θ, andlet Y 2 = u 2 (X 1,X 2,,X n ),notafunctionofy 1 alone, be an unbiased estimator of θ. Ifweletρ(y 1 )=E(Y 2 Y 1 = y 1 ),then This statistic ρ(y 1 ) is a function of the sufficient statistic for θ. It is an unbiased estimator of θ. Its variance is less than that of Y 2.
33 Sufficiency 31 Theorem Unique MLE of θ is a function of sufficient statistic for θ 2. One to one function of a sufficient statistic for θ Ω is also sufficient statistic for θ Ω. X 1,,X n : r.s. from N(μ, σ 2 ), < μ <, σ 2 > 0 ( n i=1 X i, n i=1 Xi 2 ): sufficient statistic ( X, n i=1(x i X) 2 ): sufficient statistic
34 Proofof1) Let Y 1 be sufficient statistic ˆθ mle = argmax θ Ω L(θ,x) = argmax θ Ω {k 1 (u(x),θ)g 2 (x)} = argmax θ Ω k 1 (u(x),θ) = argmax θ Ω k 1 (Y 1,θ)=g 1 (Y 1 ) 31-1
35 Sufficiency 32 Example 3.1 Let X 1,X 2,,X n be iid with pdf f(x; θ)= θe θx 0 < x < 0 elsewhere, Find an unbiased estimator, Y 1,forθ(using MLE), sufficient statistic, Y 2,andE(Y 1 Y 2 ). (sol) because X i G(1,θ 1 ) X G(n, (nθ) 1 ) E( 1 X )= nθ n 1 ˆθ UE = n 1 n X E(W k )= 0 x k xα 1 e x/β Γ(α)β α dx = 0 β k Γ(α + k) Γ(α) x α+k 1 e x/β β k (α + k 1)! dx = Γ(α + k)βα+k (α 1)! if W G(α, β). Thus, n i=1 x i is a sufficient statistic. f X1,,Xn (x 1,,x n)=θ n e θ n i=1 x i
36 Sufficiency 33 Therefore, the conditional expectation is E( n 1 n n X n 1 n X i )=E( i=1 n i=1 X X i )= i i=1 n 1 n i=1 X i = n 1 n X
37 Sufficiency 34 Remark 3.1 Let Y 1 = u 1 (X 1,,X n ) and Y 2 = u 2 (X 1,,X n ). 1. If E(Y 1 )=θ, E(E(Y 1 Y 2 )) = E(Y 1 )=θ 2. Because var(y 1 )=var(e(y 1 Y 2 )) + E(var(Y 1 Y 2 ), var(y 1 ) var(e(y 1 Y 2 )) ** However, if Y 2 is not a sufficient statistic, then E(Y 1 Y 2 ) depends on θ anditisnotastatistic. ** By (1) and (2), if Y 2 is a sufficient statistic, is E(Y 1 Y 2 ) a MVUE?
38 Sufficiency 35 Example 3.2 Let X 1,X 2,X 3 be a random sample from an exponential distribution with mean θ > 0, so that the joint pdf is i=1,2,3, zero elsewhere. (sol) ( 1 θ ) 3 e (x 1+x 2 +x 3 )/θ, 0 < x <, Y 1 /3 = X: a function of a sufficient statistic and an unbiased estimator for θ Let Y 3 = X 3 and ρ(y 3 )=E(Y 1 /3 Y 3 ).ThenE(ρ(Y 3 )) = θ but ρ(y 3 ) involves θ X i G(1,θ) X 1 + X 2 + X 3 G(3,θ) E(Y 1 )=E(X 1 + X 2 + X 3 )=3θ Y 1 3 unbiased estimator E(Y 1 /3 Y 3 )=E( 1 3 (X 1 + X 2 + X 3 ) X 3 )= 2θ + X 3 3 not a statistic Thus, Y 3 has to be a sufficient statistic for θ.
39 Sufficiency 36 4 Completeness and Uniqueness
40 Sufficiency 37 Definition 4.1 For pdf Z (z) {h(z; θ) θ Ω}, {h(z; θ) θ Ω}: a complete family If E(u(Z)) = 0 for θ Ω, then P θ (u(z)=0)=1. In other words, suppose that h(z; θ) is a statistic constructed from Z that is being used as an estimator of 0 (thought of as a function of θ). The completeness condition means that the only such unbiased estimator is the statistic that is 0 with probability 1.
41 Sufficiency 38 Why do we need the completeness? Our interest is to find the MVUE. 1. We can always find some sufficient statistics Z i for our parameter θ. 2. By the Rao-Blackwellization, for any unbiased estimator, Y i, E{E(Y i Z i )} = E(Y i ) var{e(y i Z i )} var(y i ) If E(Y i Z i ) is always same for any Y i and Z i (in other words, it is unique), then E(Y i Z i ) is MVUE E(Y i Z i )=E(Y j Z j ) a.s. for any θ E(Y i Y i ) E(Y j Z j )=0 a.s. for any θ ˆ0 UE = 0 a.s. for any θ Ω completeness
42 Sufficiency 39 Note 4.1 Are these families complete? {Bin(n, θ) 0 θ 1} {Bin(2,θ) θ = 1 4 or 3 4 } (sol) For any u(x), we assume that 0 = 0 E(u(Y )) = 0 = n u(i)( n i=0 i )( n u(i)( n i=0 i )θi (1 θ) n i θ 1 θ )i for any θ (0, 1) n u(i)( n i=0 i )λi for any λ > 0 u(i) =0: complete 0 E(u(Y )) = 0 = 3 u(i)( 3 i=0 i )( 0 = 3 u(i)( 3 i=0 i )θi (1 θ) 3 i θ 1 θ )i for any θ (0, 1) 3 u(i)( 3 i=0 i )λi for λ = 3of1/3 If u(0) =1,u(1) = 5 3 and u(2) =1,E(u(Y )) = 0: not complete
43 Sufficiency 40 When X 1,,X n statistic and If E θ (u(y 1 )) 0, then iid Poisson(θ) andθ > 0, then Y 1 = n i=1 X i :sufficient g Y1 (y 1 ; θ) = (nθ) y 1 e nθ y 1! y 1 = 0, 1, 0 o.w. 0 = E(u(Y 1 )) = u(k) (nθ)k e nθ k=0 k! = e nθ (u(0)+u(1) nθ 1! Therefore, u(0)+u(1) nθ (nθ)2 + u(2) 1! 2! + u(2) (nθ)2 2! + =0 + ) and u(0) =u(1) = =0. That is, P θ (u(z) =0) =1 for any θ > 0and {g Y1 (y 1 ; θ) 0 < θ} is complete.
44 Sufficiency 41 Note 4.2 We assume that f(z) and (z) are piece-wise continuous. Uniqueness of power series If f(z) = n=0 a n (z z 0 ) n and g(z) = n=0 b n (z z 0 ) n,then f(z) = g(z) for any z <ɛ a n = b n a.s. Also, f(z) = 0 for any z <ɛ a n = 0 a.s. Uniqueness of Laplace transformation If F (t) = 0 f(x)e tx dx and G(t) = 0 g(x)e tx dx, for some ɛ > 0 we have F (t) = G(t) for any t (0,ɛ) f(x) =g(x) a.s. Also, F (t) = 0 for any t (0,ɛ) f(x) =0 a.s. Uniqueness of Bilateral Laplace transformation If F (t) = f(x)e tx dx and G(t) = g(x)e tx dx, for some ɛ > 0 we have F (t) =G(t) for t <ɛ f(x) =g(x) a.s.
45 Sufficiency 42 Example 4.1 Consider the family of pdfs {h(z; θ) 0 < θ < }. Suppose Z has a pdf in this family given by h(z; θ)= 1 θ e z/θ 0 < z < 0 elsewhere. Is the family complete? (sol) If E[u(Z)] = 0 for every θ > 0, then {h(z; θ) 0 < θ < }is complete because 1 θ u(z)e z/θ dz = 0forθ > 0, 0 0 u(z)e zθ dz = 0forθ = 1 θ > 0 By the uniquness of Laplace transformation, u(z) =0 and it is complete.
46 Sufficiency 43 Theorem 4.1 If Y 1 = u(x 1,,X n ) is sufficient for θ, {f Y1 (y 1 ; θ) θ Ω} is complete and E(ϕ(Y 1 )) = a(θ), thenϕ(y 1 ) is an unique MVUE for a(θ).
47 Proof) Uniqueness If we assume that there are another unbiased estimator, Y 3,thenlet By definition, u(y 1 ) E(Y 2 Y 1 ) E(Y 3 Y 1 ). E(u(Y 1 )) = E[E(Y 2 Y 1 )] E[E(Y 3 Y 1 )] = 0. Because {f Y1 (y 1 ; θ) θ Ω} is complete, P (u(y 1 )=0) =1. That is, MVUE P {E(Y 2 Y 1 )=E(Y 3 Y 1 )} = 1. By Rao-Blackwell theorem, E(Y 2 Y 1 )=ϕ(y 1 ) and for any other unbiased estimator Y 3 we have var(ϕ(y 1 )) = var(e(y 2 Y 1 )) = var(e(y 3 Y 1 )) var(y 3 ) 43-1
48 Sufficiency 44 Three requirements for MVUE 1. Rao-Blackwell : provides smaller variance for any given unbiased estimator 2. Sufficiency : provides estimator independent with any parameters. 3. Completeness : uniqueness
49 Sufficiency 45 5 The Exponential Class of Distributions
50 Sufficiency 46 Exponential family {f(x; θ) θ Ω} exponential family f(x; θ)= exp{p(θ)k(x)+s(x)+q(θ)} x S 0 o.w. For the exponential family, η = p(θ) is called natural parameter.
51 Sufficiency 47 Definition 5.1 (Regular exponential family) The exponential family is called regular exponential family if 1. S = supp(x) does not depend on θ. 2. p(θ) is a continuous function of θ Ω 3. If X: continuous, each of K (x) 0 and S(x) is continuous for x.
52 Sufficiency 48 Family: {f(x; θ) 0 < θ < } If f(x; θ)= 1 exp ( 1 2φθ 2θ x2 ), then it is exponential family. If f(x; θ)= 1 I(x (0,θ)), it is not a regular exponential family. θ If X 1,,X n denote a random sample from a distribution that represents a regular case of the exponential class, then Y 1 = n i=1 K(X i ) is a sufficient statistic for θ.
53 Sufficiency 49 Theorem 5.1 X 1,,X n : random sample from a distribution, pdf Xi (x) {f(x; θ),θ Ω} regular exponential family. Then 1. if η = p(θ), thenq(θ)= A(η) for some function A. 2. There exist some ɛ > 0 such that M K(X1 )(t)=exp{a(η + t) A(t)} for any t <ɛ 3. E(K(X 1 )) = η A(η)= q (θ) p (θ) and var(k(x 1 )) = 2 η 2 A(η)= 1 p (θ) 3 {p (θ)q (θ) q (θ)p (θ)}
54 Proof) We only consider continuous case. We can have f(x; θ)dx = 1, f(x, θ) = exp{p(θ)k(x)+ S(x)+ q(θ)} exp( q(θ)) = q(θ) = log ( exp{p(θ)k(x)+s(x)}dx exp{p(θ)k(x)+s(x)) = A(p(θ)) M K(X1 )(t) = E{exp(tK(X 1 ))} = = = exp(tk(x 1 ))f(x; η)dx, η = p(θ) exp{(η + t)k(x)+s(x) A(η)}dx exp{(η + t)k(x)+s(x) A(η + t)}dx exp{a(η + t) A(η)} = exp{a(η + t) A(η)} 49-1
55 Sufficiency 50 Example 5.1 Let X 1,,X n be a random sample from the Poisson distribution with θ (0, ). Then f(x, θ)=e θ θ x x! = exp{(log θ)x + log(1/x!)+( θ)}. (sol) Regular exponential family: Y 1 = n i=1 X i : sufficient statistic p(θ) =logθ, q(θ) = nθ E(Y 1 )= q (θ) p (θ) = nθ var(y 1 )= 1 p (θ) 3 [p (θ)q (θ) q (θ)p (θ)] = nθ
56 Sufficiency 51 Y 1 : complete sufficient statistic Y 1 is sufficient for θ and {f Y1 (y 1 ; θ) θ Ω} is complete. Theorem 5.2 X 1,,X n : random sample from a population with pdf f(x; θ) where γ < θ < δ and {f(x; θ) γ < θ < δ} is regular exponential family. Then, it satisfies f(x; θ)= exp{p(θ)k(x)+s(x)+q(θ)} x S 0 o.w.. Then, Y 1 = n i=1 K(X i ) is complete sufficient statistics.
57 Proof) Y 1 :sufficient n n f X1,,X n (x 1,,x n ) = exp {p(θ) K(x i )+ S(x i )+nq(θ)} i=1 i=1 n n = exp {p(θ) K(x i )+nq(θ)} exp { S(x i )} i=1 i=1 Thus, Y 1 is sufficient. {f Y1 (y 1 ; θ γ < θ < δ}: complete By theorem 7.5.1, f Y1 (y 1 ; θ) =R(y 1 ) exp{p(θ)y 1 + nq(θ)}, y 1 S Y1. Thus E(u(Y 1 )) = SY1 u(y 1 )R(y 1 ) exp{p(θ)y 1 + nq(θ)}dy 1 = exp{nq(θ)} SY1 u(y 1 )R(y 1 ) exp{p(θ)y 1 }dy 1. As a result, if E(u(Y 1 )) = 0, then SY1 u(y 1 )R(y 1 ) exp{p(θ)y 1 }dy 1 =
58 By the uniqueness of Laplace transformation, u(y 1 )R(y 1 )=0. However if y 1 S Y1, R(y 1 )>0andu(y 1 )=0. As a result, P (u(y 1 )=0) =1 51-2
59 Sufficiency 52 Example 5.2 X 1,,X n is random sample from Poisson(θ) and f Xi (x; θ)= e θ θ x x! Then X is a unique MVUE. (sol) n i=1 X i :CSS f X1,,X n (x 1,,x n )= e nθ θ n i=1 x i n i=1 x i! E( X) =θ X: unbiased estimator ˆθ MV UE = E( X n i=1 X i )=E( 1 n n X i=1 n i=1 X i )= 1 n n X = X i=1
60 Sufficiency 53 Example 5.3 X 1,,X n is random sample from N(θ,σ 2 ), σ 2 : known and f Xi (x; θ)= Then X is a unique MVUE. (sol) 1 σ 2π exp { 1 2σ 2 (x θ)2 } f X1,,X n (x 1,,x n ) = 1 ( σ 2π )n exp { 1 n 2σ 2 (x i θ) 2 } i=1 = 1 ( σ 2π )n exp { 1 n 2σ ( 2 x 2 n i θ x i + nθ 2 )} i=1 i=1 n i=1 X i :CSS E( X) =θ X: unbiased estimator ˆθ MV UE = E( X n i=1 X i )=E( 1 n n X i=1 n i=1 X i )= 1 n n X = X i=1
61 Sufficiency 54 6 Functions of a Parameter
62 Sufficiency 55 How can we find MVUE? 1. Find a complete sufficient statistic (CSS). 2. Find the unbiased estimator. Check the expectation of CSS. Check the expectation of MLE. Use the indicator function for unbiased estimator of some probability.
63 Sufficiency 56 Example 6.1 Let X 1,X 2,,X n be a random sample of size n > 1 from a distribution that is b(1,θ), 0 < θ < 1. IfY = n 1 X i,then MVUEs of θ and θ(1 θ) are Y n and n (n 1) Y n (1 Y n ) respectively. (sol) n i=1 X i :CSS f X1,,X n (x 1,,x n )=θ n i=1 x i (1 θ) n n i=1 x i ˆθ MLE = X E( X) =θ X unbiased estimator ˆθ MV UE = E( X n i=1 X i )=E( 1 n n X i=1 n i=1 X i )= 1 n n X = X i=1 θ(1 θ) MLE = X(1 X) E( X(1 X)) = θ 1 E(Y 2 )= n 1 n 2 n n X(1 X): UE n 1 ˆθ MV UE = n n 1 E( X(1 X) n X i )= i=1 n n 1 X(1 X) θ(1 θ)
64 Sufficiency 57 Example 6.2 Let X 1,X 2,,X n be a random sample of size n > 1 from a distribution that is N(θ,1). For any fixed c, find a MVUE for c 1 P (X c)= e (x θ)2 /2 dx = Φ(c θ). 2π (sol) f X1,,X n (x 1,,x n ) = 1 ( σ 2π )n exp { 1 n 2σ 2 (x i θ) 2 } i=1 = 1 ( σ 2π )n exp { 1 n 2σ ( 2 x 2 n i θ x i + nθ 2 )} i=1 i=1 n i=1 X i CSS X: CSS E(I (,c) (X 1 )) = P (X 1 c) I (,c) (X 1 ) unbiased estimator P (X c) MV UE = E(I (,c) (X 1 ) X) ( X,X 1 ): bivariate normal dist E( X) =E(X 1 )=θ
65 Sufficiency 58 var( X) = 1 n,var(x 1)=1, cov( X,X 1 )= 1 n X 1 X N(μ X1 + σ X 1 X σ X X ( X μ X),σ X1 X 1 σ2 X 1 X σ X X ) = N(θ +( X θ), 1 n 2 n 1 )=N( X,1 1 n ) E(I (,c) (X 1 ) X) = P (X 1 c X) =P (Z c θ (n 1)/n ) n = Φ( (c θ)) n 1
66 Sufficiency 59 Remark 6.1 Let X have a Poisson distribuion with parameter θ, 0 < θ <. MVUE of e 2θ MLE of e 2θ ê 2θ MV UE =( 1) X ê 2θ MLE = e 2X Which estimator is better? Can we say that MVUE is always better than MLE? The MVUE for e 2θ is always either 1 or 1, which indicates that MVUE can be worse than MLE. The best estimator can be different, depending on the situation and it should be carefully chosen.
67 Sufficiency 52 7 Sufficiency, Completeness and Independence
68 Sufficiency 53 Note 7.1 Let X 1,X 2,,X n be a random sample from a population with pdf f(x; θ). Then the statistic Y = v(x 1,,X n ) is called ancillary if its distribution is free of θ.
69 Sufficiency 54 Example 7.1 Consider a location model given by X i = θ + W i where W 1,W 2,,W n are iid with the common pdf f(w) and common continuous cdf F(w). From Example 7.5, we know that the order statistics Y 1 < Y 2 < <Y n are a set of complete and sufficient statistics for this situation. Can we obtain a smaller set of minimal sufficient statistics? When f W (w) = 1 2π exp( 1 2 w2 ) When f W (w) =exp( w), w > 0 When f W (w) = exp( w) (1+exp( w)) 2 (logistic pdf) When f W (w) = 1 2 exp( w ) (Laplace pdf)
70 Sufficiency 55 Example 7.2 (Location Invariant Statistics) Consider a location model given by X i = θ + W i, i= 1,,n, where < θ < is a parameter and W 1,W 2,,W n are iid random variables with the pdf f(w) which does not depend on θ. Then any statistic, u(x 1,,X n ), that satisfies u(x 1 + d, x 2 + d,,x n + d)=u(x 1,x 2,,x n ) for any real d, is ancially statistic.
71 Sufficiency 56 Note 7.2 Examples of location invariant statistics: if X 1,,X n : iid with pdf f(x θ), then 1. S 2 = 1 n 1 n i=1(x i X) 2 2. max X i min X i 3. 1 n n i=1 X i med(x i ) 4. X 1 + X 2 X 3 X 4
72 Sufficiency 57 Example 7.3 (Scale Invariant Statistics) Consider a random sample X 1,X 2,,X n which follows a scale model; i.e., a model of the form X i = θw i, i= 1,,n, where θ > 0 and W 1,W 2,,W n are iid random variables with pdf f(w) which does not depend on θ. If the statistic u(x 1,,X n ) satisfies u(cx 1,,cx n )=u(x 1,,x n ), then it is ancillary and we say that u(x 1,,X n ) is a scale-invariante statistic.
73 Sufficiency 58 Note 7.3 Examples of location and scale invariant statistics: if 1 X 1,,X n : iid with pdf θ 2 f( x θ ),then X 1 X 1 +X 2 X 2 i n i=1 X2 i min(x i ) max(x i )
74 Sufficiency 59 Example 7.4 (Location and Scale Invariant Statistics) Finally, consider a random sample X 1,X 2,,X n which follows a location and scale model as in Example 7.5. That is, X i = θ 1 + θ 2 W i, i= 1,,n, where W i are iid with the common pdf f(t) which is free of θ 1 and θ 2. Consider the statistic u(x 1,,X n ) where u(cx 1 + d,,cx n + d)=u(x 1,,x n ). Then u(x 1,,X n ) is ancillary statistic, and is called location and scale invariant statistics.
75 Sufficiency 60 Note 7.4 Examples of location and scale invariant statistics: if 1 X 1,,X n : iid with pdf θ 2 f( x θ 1 θ 2 ),then max(x i ) min(x i ) S n i=1 X i X S X i X j S (X i+1 X i ) 2 S 2
76 Sufficiency 61 Theorem 7.1 (Basu s theorem) Let X 1,X 2,,X n denote a random sample from a distribution having a pdf f(x; θ), θ Ω. If Y = u(x 1,,X n ) is CSS and Z = v(x 1,,X n ) is ancially statistics, then Y and Z is independent.
77 Proof) we will prove that P θ (Z A Y )=P θ (Z A) for any A and θ Ω. Then, g(y ) P θ (Z A Y ) P θ (Z A) E θ [g(y )] = E θ [P θ (Z A Y ) P θ (Z A)] = E θ [P θ (Z A Y ) P (Z A)] = P θ (Z A) P (Z A) = 0 Because g(y ) is complete, P θ (Z A Y )=P θ (Z A) and it is proven. 61-1
78 Sufficiency 62 Example 7.5 Let X 1,X 2,,X n be a random sample of size n from a distribution that is N(μ, σ 2 ).Then X and S 2 = 1 n 1 n i=1(x i X) 2 are independent.
79 Sufficiency 63 Example 7.6 Let X 1,X 2,,X n be a random sample of size n from a distribution having pdf f(x; θ)= e (x θ), θ < x <, < θ <, 0 elsewhere Then Y 1 = min(x i ) is independent with any location-invariant statistic, u(x 1,,X n ), that enjoys u(x 1 + d, x 2 + d,,x n + d)=u(x 1,,x n ).
80 Sufficiency 64 Example 7.7 Let X 1,X 2 be a random sample from a distribution with pdf f(x; θ)= 1 θ e (x/θ) 0 < x <, 0 < θ <, 0 elsewhere Then X 1 + X 2 is independent of any scale-invariant statistic u(x 1,X 2 ) with the property u(cx 1,cx 2 )=u(x 1,x 2 ).
81 Sufficiency 65 Example 7.8 Let X 1,X 2,,X n denote a random sample from a distribution that is N(θ 1,θ 2 ), < θ 1 <, < θ 2 <. Consider the statistic Z = n 1 1 (X i+1 X i ) 2 n 1 (X i X) 2 = u(x 1,X 2,,X n ), which satisfies the property that u(cx 1 + d,,cx n + d)=u(x 1,,x n ). That is, the ancillary statistic Z is independent of both X and S 2.
82 Sufficiency 66 Note 7.5 t-distribution Definition T = Z V /v Z N(0, 1) V χ 2 (df = v) Z and V are independent. In practice, if we let X 1,,X n be random sample from N(μ, σ 2 ), H 0 μ = μ 0 vs H 1 μ μ 0 t = ( X μ 0 )/(σ/ n) 1 σ 2 n i=1(x i X) 2 /(n 1) = X μ 0 1 n 1 n i=1(x i X) 2 /n t(n 1)
March 10, 2017 THE EXPONENTIAL CLASS OF DISTRIBUTIONS
 March 10, 2017 THE EXPONENTIAL CLASS OF DISTRIBUTIONS Abstract. We will introduce a class of distributions that will contain many of the discrete and continuous we are familiar with. This class will help
March 10, 2017 THE EXPONENTIAL CLASS OF DISTRIBUTIONS Abstract. We will introduce a class of distributions that will contain many of the discrete and continuous we are familiar with. This class will help
Theory of Statistical Tests
 Ch 9. Theory of Statistical Tests 9.1 Certain Best Tests How to construct good testing. For simple hypothesis H 0 : θ = θ, H 1 : θ = θ, Page 1 of 100 where Θ = {θ, θ } 1. Define the best test for H 0 H
Ch 9. Theory of Statistical Tests 9.1 Certain Best Tests How to construct good testing. For simple hypothesis H 0 : θ = θ, H 1 : θ = θ, Page 1 of 100 where Θ = {θ, θ } 1. Define the best test for H 0 H
Chapter 8.8.1: A factorization theorem
 LECTURE 14 Chapter 8.8.1: A factorization theorem The characterization of a sufficient statistic in terms of the conditional distribution of the data given the statistic can be difficult to work with.
LECTURE 14 Chapter 8.8.1: A factorization theorem The characterization of a sufficient statistic in terms of the conditional distribution of the data given the statistic can be difficult to work with.
Mathematical statistics
 October 4 th, 2018 Lecture 12: Information Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation Chapter
October 4 th, 2018 Lecture 12: Information Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation Chapter
Unbiased Estimation. Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others.
 Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
STAT 512 sp 2018 Summary Sheet
 STAT 5 sp 08 Summary Sheet Karl B. Gregory Spring 08. Transformations of a random variable Let X be a rv with support X and let g be a function mapping X to Y with inverse mapping g (A = {x X : g(x A}
STAT 5 sp 08 Summary Sheet Karl B. Gregory Spring 08. Transformations of a random variable Let X be a rv with support X and let g be a function mapping X to Y with inverse mapping g (A = {x X : g(x A}
STA 260: Statistics and Probability II
 Al Nosedal. University of Toronto. Winter 2017 1 Properties of Point Estimators and Methods of Estimation 2 3 If you can t explain it simply, you don t understand it well enough Albert Einstein. Definition
Al Nosedal. University of Toronto. Winter 2017 1 Properties of Point Estimators and Methods of Estimation 2 3 If you can t explain it simply, you don t understand it well enough Albert Einstein. Definition
Math 494: Mathematical Statistics
 Math 494: Mathematical Statistics Instructor: Jimin Ding jmding@wustl.edu Department of Mathematics Washington University in St. Louis Class materials are available on course website (www.math.wustl.edu/
Math 494: Mathematical Statistics Instructor: Jimin Ding jmding@wustl.edu Department of Mathematics Washington University in St. Louis Class materials are available on course website (www.math.wustl.edu/
1. Fisher Information
 1. Fisher Information Let f(x θ) be a density function with the property that log f(x θ) is differentiable in θ throughout the open p-dimensional parameter set Θ R p ; then the score statistic (or score
1. Fisher Information Let f(x θ) be a density function with the property that log f(x θ) is differentiable in θ throughout the open p-dimensional parameter set Θ R p ; then the score statistic (or score
Spring 2012 Math 541A Exam 1. X i, S 2 = 1 n. n 1. X i I(X i < c), T n =
 Spring 2012 Math 541A Exam 1 1. (a) Let Z i be independent N(0, 1), i = 1, 2,, n. Are Z = 1 n n Z i and S 2 Z = 1 n 1 n (Z i Z) 2 independent? Prove your claim. (b) Let X 1, X 2,, X n be independent identically
Spring 2012 Math 541A Exam 1 1. (a) Let Z i be independent N(0, 1), i = 1, 2,, n. Are Z = 1 n n Z i and S 2 Z = 1 n 1 n (Z i Z) 2 independent? Prove your claim. (b) Let X 1, X 2,, X n be independent identically
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003
 Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Statistics Ph.D. Qualifying Exam: Part I October 18, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Unbiased Estimation. Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others.
 Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
1. (Regular) Exponential Family
 1. (Regular) Exponential Family The density function of a regular exponential family is: [ ] Example. Poisson(θ) [ ] Example. Normal. (both unknown). ) [ ] [ ] [ ] [ ] 2. Theorem (Exponential family &
1. (Regular) Exponential Family The density function of a regular exponential family is: [ ] Example. Poisson(θ) [ ] Example. Normal. (both unknown). ) [ ] [ ] [ ] [ ] 2. Theorem (Exponential family &
MAS223 Statistical Inference and Modelling Exercises
 MAS223 Statistical Inference and Modelling Exercises The exercises are grouped into sections, corresponding to chapters of the lecture notes Within each section exercises are divided into warm-up questions,
MAS223 Statistical Inference and Modelling Exercises The exercises are grouped into sections, corresponding to chapters of the lecture notes Within each section exercises are divided into warm-up questions,
A Very Brief Summary of Statistical Inference, and Examples
 A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2009 Prof. Gesine Reinert Our standard situation is that we have data x = x 1, x 2,..., x n, which we view as realisations of random
A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2009 Prof. Gesine Reinert Our standard situation is that we have data x = x 1, x 2,..., x n, which we view as realisations of random
A Very Brief Summary of Statistical Inference, and Examples
 A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2008 Prof. Gesine Reinert 1 Data x = x 1, x 2,..., x n, realisations of random variables X 1, X 2,..., X n with distribution (model)
A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2008 Prof. Gesine Reinert 1 Data x = x 1, x 2,..., x n, realisations of random variables X 1, X 2,..., X n with distribution (model)
Principles of Statistics
 Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 81 Paper 4, Section II 28K Let g : R R be an unknown function, twice continuously differentiable with g (x) M for
Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 81 Paper 4, Section II 28K Let g : R R be an unknown function, twice continuously differentiable with g (x) M for
February 26, 2017 COMPLETENESS AND THE LEHMANN-SCHEFFE THEOREM
 February 26, 2017 COMPLETENESS AND THE LEHMANN-SCHEFFE THEOREM Abstract. The Rao-Blacwell theorem told us how to improve an estimator. We will discuss conditions on when the Rao-Blacwellization of an estimator
February 26, 2017 COMPLETENESS AND THE LEHMANN-SCHEFFE THEOREM Abstract. The Rao-Blacwell theorem told us how to improve an estimator. We will discuss conditions on when the Rao-Blacwellization of an estimator
SOLUTIONS TO MATH68181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH68181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question A1 a) The marginal cdfs of F X,Y (x, y) = [1 + exp( x) + exp( y) + (1 α) exp( x y)] 1 are F X (x) = F X,Y (x, ) = [1
SOLUTIONS TO MATH68181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question A1 a) The marginal cdfs of F X,Y (x, y) = [1 + exp( x) + exp( y) + (1 α) exp( x y)] 1 are F X (x) = F X,Y (x, ) = [1
Chapters 9. Properties of Point Estimators
 Chapters 9. Properties of Point Estimators Recap Target parameter, or population parameter θ. Population distribution f(x; θ). { probability function, discrete case f(x; θ) = density, continuous case The
Chapters 9. Properties of Point Estimators Recap Target parameter, or population parameter θ. Population distribution f(x; θ). { probability function, discrete case f(x; θ) = density, continuous case The
Mathematical Statistics
 Mathematical Statistics Chapter Three. Point Estimation 3.4 Uniformly Minimum Variance Unbiased Estimator(UMVUE) Criteria for Best Estimators MSE Criterion Let F = {p(x; θ) : θ Θ} be a parametric distribution
Mathematical Statistics Chapter Three. Point Estimation 3.4 Uniformly Minimum Variance Unbiased Estimator(UMVUE) Criteria for Best Estimators MSE Criterion Let F = {p(x; θ) : θ Θ} be a parametric distribution
Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017
 Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Let X 1, X 2,, X n be a sequence of i.i.d. observations from a
Ph.D. Qualifying Exam Friday Saturday, January 6 7, 2017 Put your solution to each problem on a separate sheet of paper. Problem 1. (5106) Let X 1, X 2,, X n be a sequence of i.i.d. observations from a
t x 1 e t dt, and simplify the answer when possible (for example, when r is a positive even number). In particular, confirm that EX 4 = 3.
 Mathematical Statistics: Homewor problems General guideline. While woring outside the classroom, use any help you want, including people, computer algebra systems, Internet, and solution manuals, but mae
Mathematical Statistics: Homewor problems General guideline. While woring outside the classroom, use any help you want, including people, computer algebra systems, Internet, and solution manuals, but mae
Master s Written Examination
 Master s Written Examination Option: Statistics and Probability Spring 016 Full points may be obtained for correct answers to eight questions. Each numbered question which may have several parts is worth
Master s Written Examination Option: Statistics and Probability Spring 016 Full points may be obtained for correct answers to eight questions. Each numbered question which may have several parts is worth
Statistics GIDP Ph.D. Qualifying Exam Theory Jan 11, 2016, 9:00am-1:00pm
 Statistics GIDP Ph.D. Qualifying Exam Theory Jan, 06, 9:00am-:00pm Instructions: Provide answers on the supplied pads of paper; write on only one side of each sheet. Complete exactly 5 of the 6 problems.
Statistics GIDP Ph.D. Qualifying Exam Theory Jan, 06, 9:00am-:00pm Instructions: Provide answers on the supplied pads of paper; write on only one side of each sheet. Complete exactly 5 of the 6 problems.
Lecture 1: August 28
 36-705: Intermediate Statistics Fall 2017 Lecturer: Siva Balakrishnan Lecture 1: August 28 Our broad goal for the first few lectures is to try to understand the behaviour of sums of independent random
36-705: Intermediate Statistics Fall 2017 Lecturer: Siva Balakrishnan Lecture 1: August 28 Our broad goal for the first few lectures is to try to understand the behaviour of sums of independent random
Statistics 3858 : Maximum Likelihood Estimators
 Statistics 3858 : Maximum Likelihood Estimators 1 Method of Maximum Likelihood In this method we construct the so called likelihood function, that is L(θ) = L(θ; X 1, X 2,..., X n ) = f n (X 1, X 2,...,
Statistics 3858 : Maximum Likelihood Estimators 1 Method of Maximum Likelihood In this method we construct the so called likelihood function, that is L(θ) = L(θ; X 1, X 2,..., X n ) = f n (X 1, X 2,...,
Partial Solutions for h4/2014s: Sampling Distributions
 27 Partial Solutions for h4/24s: Sampling Distributions ( Let X and X 2 be two independent random variables, each with the same probability distribution given as follows. f(x 2 e x/2, x (a Compute the
27 Partial Solutions for h4/24s: Sampling Distributions ( Let X and X 2 be two independent random variables, each with the same probability distribution given as follows. f(x 2 e x/2, x (a Compute the
STAT 730 Chapter 4: Estimation
 STAT 730 Chapter 4: Estimation Timothy Hanson Department of Statistics, University of South Carolina Stat 730: Multivariate Analysis 1 / 23 The likelihood We have iid data, at least initially. Each datum
STAT 730 Chapter 4: Estimation Timothy Hanson Department of Statistics, University of South Carolina Stat 730: Multivariate Analysis 1 / 23 The likelihood We have iid data, at least initially. Each datum
Methods of evaluating estimators and best unbiased estimators Hamid R. Rabiee
 Stochastic Processes Methods of evaluating estimators and best unbiased estimators Hamid R. Rabiee 1 Outline Methods of Mean Squared Error Bias and Unbiasedness Best Unbiased Estimators CR-Bound for variance
Stochastic Processes Methods of evaluating estimators and best unbiased estimators Hamid R. Rabiee 1 Outline Methods of Mean Squared Error Bias and Unbiasedness Best Unbiased Estimators CR-Bound for variance
Chapter 4 HOMEWORK ASSIGNMENTS. 4.1 Homework #1
 Chapter 4 HOMEWORK ASSIGNMENTS These homeworks may be modified as the semester progresses. It is your responsibility to keep up to date with the correctly assigned homeworks. There may be some errors in
Chapter 4 HOMEWORK ASSIGNMENTS These homeworks may be modified as the semester progresses. It is your responsibility to keep up to date with the correctly assigned homeworks. There may be some errors in
Statistical Methods for Handling Incomplete Data Chapter 2: Likelihood-based approach
 Statistical Methods for Handling Incomplete Data Chapter 2: Likelihood-based approach Jae-Kwang Kim Department of Statistics, Iowa State University Outline 1 Introduction 2 Observed likelihood 3 Mean Score
Statistical Methods for Handling Incomplete Data Chapter 2: Likelihood-based approach Jae-Kwang Kim Department of Statistics, Iowa State University Outline 1 Introduction 2 Observed likelihood 3 Mean Score
ECE531 Lecture 8: Non-Random Parameter Estimation
 ECE531 Lecture 8: Non-Random Parameter Estimation D. Richard Brown III Worcester Polytechnic Institute 19-March-2009 Worcester Polytechnic Institute D. Richard Brown III 19-March-2009 1 / 25 Introduction
ECE531 Lecture 8: Non-Random Parameter Estimation D. Richard Brown III Worcester Polytechnic Institute 19-March-2009 Worcester Polytechnic Institute D. Richard Brown III 19-March-2009 1 / 25 Introduction
ST5215: Advanced Statistical Theory
 Department of Statistics & Applied Probability Wednesday, October 19, 2011 Lecture 17: UMVUE and the first method of derivation Estimable parameters Let ϑ be a parameter in the family P. If there exists
Department of Statistics & Applied Probability Wednesday, October 19, 2011 Lecture 17: UMVUE and the first method of derivation Estimable parameters Let ϑ be a parameter in the family P. If there exists
Recall that in order to prove Theorem 8.8, we argued that under certain regularity conditions, the following facts are true under H 0 : 1 n
 Chapter 9 Hypothesis Testing 9.1 Wald, Rao, and Likelihood Ratio Tests Suppose we wish to test H 0 : θ = θ 0 against H 1 : θ θ 0. The likelihood-based results of Chapter 8 give rise to several possible
Chapter 9 Hypothesis Testing 9.1 Wald, Rao, and Likelihood Ratio Tests Suppose we wish to test H 0 : θ = θ 0 against H 1 : θ θ 0. The likelihood-based results of Chapter 8 give rise to several possible
1 Complete Statistics
 Complete Statistics February 4, 2016 Debdeep Pati 1 Complete Statistics Suppose X P θ, θ Θ. Let (X (1),..., X (n) ) denote the order statistics. Definition 1. A statistic T = T (X) is complete if E θ g(t
Complete Statistics February 4, 2016 Debdeep Pati 1 Complete Statistics Suppose X P θ, θ Θ. Let (X (1),..., X (n) ) denote the order statistics. Definition 1. A statistic T = T (X) is complete if E θ g(t
Final Examination a. STA 532: Statistical Inference. Wednesday, 2015 Apr 29, 7:00 10:00pm. Thisisaclosed bookexam books&phonesonthefloor.
 Final Examination a STA 532: Statistical Inference Wednesday, 2015 Apr 29, 7:00 10:00pm Thisisaclosed bookexam books&phonesonthefloor Youmayuseacalculatorandtwo pagesofyourownnotes Do not share calculators
Final Examination a STA 532: Statistical Inference Wednesday, 2015 Apr 29, 7:00 10:00pm Thisisaclosed bookexam books&phonesonthefloor Youmayuseacalculatorandtwo pagesofyourownnotes Do not share calculators
ECE534, Spring 2018: Solutions for Problem Set #3
 ECE534, Spring 08: Solutions for Problem Set #3 Jointly Gaussian Random Variables and MMSE Estimation Suppose that X, Y are jointly Gaussian random variables with µ X = µ Y = 0 and σ X = σ Y = Let their
ECE534, Spring 08: Solutions for Problem Set #3 Jointly Gaussian Random Variables and MMSE Estimation Suppose that X, Y are jointly Gaussian random variables with µ X = µ Y = 0 and σ X = σ Y = Let their
Qualifying Exam in Probability and Statistics. https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf
 Part : Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Part : Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Statistics. Statistics
 The main aims of statistics 1 1 Choosing a model 2 Estimating its parameter(s) 1 point estimates 2 interval estimates 3 Testing hypotheses Distributions used in statistics: χ 2 n-distribution 2 Let X 1,
The main aims of statistics 1 1 Choosing a model 2 Estimating its parameter(s) 1 point estimates 2 interval estimates 3 Testing hypotheses Distributions used in statistics: χ 2 n-distribution 2 Let X 1,
Theory of Statistics.
 Theory of Statistics. Homework V February 5, 00. MT 8.7.c When σ is known, ˆµ = X is an unbiased estimator for µ. If you can show that its variance attains the Cramer-Rao lower bound, then no other unbiased
Theory of Statistics. Homework V February 5, 00. MT 8.7.c When σ is known, ˆµ = X is an unbiased estimator for µ. If you can show that its variance attains the Cramer-Rao lower bound, then no other unbiased
Final Exam. 1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given.
 1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given. (a) If X and Y are independent, Corr(X, Y ) = 0. (b) (c) (d) (e) A consistent estimator must be asymptotically
1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given. (a) If X and Y are independent, Corr(X, Y ) = 0. (b) (c) (d) (e) A consistent estimator must be asymptotically
Mathematical statistics
 October 18 th, 2018 Lecture 16: Midterm review Countdown to mid-term exam: 7 days Week 1 Chapter 1: Probability review Week 2 Week 4 Week 7 Chapter 6: Statistics Chapter 7: Point Estimation Chapter 8:
October 18 th, 2018 Lecture 16: Midterm review Countdown to mid-term exam: 7 days Week 1 Chapter 1: Probability review Week 2 Week 4 Week 7 Chapter 6: Statistics Chapter 7: Point Estimation Chapter 8:
General Bayesian Inference I
 General Bayesian Inference I Outline: Basic concepts, One-parameter models, Noninformative priors. Reading: Chapters 10 and 11 in Kay-I. (Occasional) Simplified Notation. When there is no potential for
General Bayesian Inference I Outline: Basic concepts, One-parameter models, Noninformative priors. Reading: Chapters 10 and 11 in Kay-I. (Occasional) Simplified Notation. When there is no potential for
IIT JAM : MATHEMATICAL STATISTICS (MS) 2013
 IIT JAM : MATHEMATICAL STATISTICS (MS 2013 Question Paper with Answer Keys Ctanujit Classes Of Mathematics, Statistics & Economics Visit our website for more: www.ctanujit.in IMPORTANT NOTE FOR CANDIDATES
IIT JAM : MATHEMATICAL STATISTICS (MS 2013 Question Paper with Answer Keys Ctanujit Classes Of Mathematics, Statistics & Economics Visit our website for more: www.ctanujit.in IMPORTANT NOTE FOR CANDIDATES
Distributions of Functions of Random Variables. 5.1 Functions of One Random Variable
 Distributions of Functions of Random Variables 5.1 Functions of One Random Variable 5.2 Transformations of Two Random Variables 5.3 Several Random Variables 5.4 The Moment-Generating Function Technique
Distributions of Functions of Random Variables 5.1 Functions of One Random Variable 5.2 Transformations of Two Random Variables 5.3 Several Random Variables 5.4 The Moment-Generating Function Technique
This exam is closed book and closed notes. (You will have access to a copy of the Table of Common Distributions given in the back of the text.
 TEST #3 STA 5326 December 4, 214 Name: Please read the following directions. DO NOT TURN THE PAGE UNTIL INSTRUCTED TO DO SO Directions This exam is closed book and closed notes. (You will have access to
TEST #3 STA 5326 December 4, 214 Name: Please read the following directions. DO NOT TURN THE PAGE UNTIL INSTRUCTED TO DO SO Directions This exam is closed book and closed notes. (You will have access to
p y (1 p) 1 y, y = 0, 1 p Y (y p) = 0, otherwise.
 1. Suppose Y 1, Y 2,..., Y n is an iid sample from a Bernoulli(p) population distribution, where 0 < p < 1 is unknown. The population pmf is p y (1 p) 1 y, y = 0, 1 p Y (y p) = (a) Prove that Y is the
1. Suppose Y 1, Y 2,..., Y n is an iid sample from a Bernoulli(p) population distribution, where 0 < p < 1 is unknown. The population pmf is p y (1 p) 1 y, y = 0, 1 p Y (y p) = (a) Prove that Y is the
Math 362, Problem set 1
 Math 6, roblem set Due //. (4..8) Determine the mean variance of the mean X of a rom sample of size 9 from a distribution having pdf f(x) = 4x, < x
Math 6, roblem set Due //. (4..8) Determine the mean variance of the mean X of a rom sample of size 9 from a distribution having pdf f(x) = 4x, < x
 2018 2019 1 9 sei@mistiu-tokyoacjp http://wwwstattu-tokyoacjp/~sei/lec-jhtml 11 552 3 0 1 2 3 4 5 6 7 13 14 33 4 1 4 4 2 1 1 2 2 1 1 12 13 R?boxplot boxplotstats which does the computation?boxplotstats
2018 2019 1 9 sei@mistiu-tokyoacjp http://wwwstattu-tokyoacjp/~sei/lec-jhtml 11 552 3 0 1 2 3 4 5 6 7 13 14 33 4 1 4 4 2 1 1 2 2 1 1 12 13 R?boxplot boxplotstats which does the computation?boxplotstats
INTRODUCTION TO BAYESIAN METHODS II
 INTRODUCTION TO BAYESIAN METHODS II Abstract. We will revisit point estimation and hypothesis testing from the Bayesian perspective.. Bayes estimators Let X = (X,..., X n ) be a random sample from the
INTRODUCTION TO BAYESIAN METHODS II Abstract. We will revisit point estimation and hypothesis testing from the Bayesian perspective.. Bayes estimators Let X = (X,..., X n ) be a random sample from the
6. MAXIMUM LIKELIHOOD ESTIMATION
 6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
Brief Review on Estimation Theory
 Brief Review on Estimation Theory K. Abed-Meraim ENST PARIS, Signal and Image Processing Dept. abed@tsi.enst.fr This presentation is essentially based on the course BASTA by E. Moulines Brief review on
Brief Review on Estimation Theory K. Abed-Meraim ENST PARIS, Signal and Image Processing Dept. abed@tsi.enst.fr This presentation is essentially based on the course BASTA by E. Moulines Brief review on
Math 3215 Intro. Probability & Statistics Summer 14. Homework 5: Due 7/3/14
 Math 325 Intro. Probability & Statistics Summer Homework 5: Due 7/3/. Let X and Y be continuous random variables with joint/marginal p.d.f. s f(x, y) 2, x y, f (x) 2( x), x, f 2 (y) 2y, y. Find the conditional
Math 325 Intro. Probability & Statistics Summer Homework 5: Due 7/3/. Let X and Y be continuous random variables with joint/marginal p.d.f. s f(x, y) 2, x y, f (x) 2( x), x, f 2 (y) 2y, y. Find the conditional
A Few Notes on Fisher Information (WIP)
 A Few Notes on Fisher Information (WIP) David Meyer dmm@{-4-5.net,uoregon.edu} Last update: April 30, 208 Definitions There are so many interesting things about Fisher Information and its theoretical properties
A Few Notes on Fisher Information (WIP) David Meyer dmm@{-4-5.net,uoregon.edu} Last update: April 30, 208 Definitions There are so many interesting things about Fisher Information and its theoretical properties
Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic
 Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic Unbiased estimation Unbiased or asymptotically unbiased estimation plays an important role in
Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic Unbiased estimation Unbiased or asymptotically unbiased estimation plays an important role in
MIT Spring 2016
 Dr. Kempthorne Spring 2016 1 Outline Building 1 Building 2 Definition Building Let X be a random variable/vector with sample space X R q and probability model P θ. The class of probability models P = {P
Dr. Kempthorne Spring 2016 1 Outline Building 1 Building 2 Definition Building Let X be a random variable/vector with sample space X R q and probability model P θ. The class of probability models P = {P
Elements of statistics (MATH0487-1)
 Elements of statistics (MATH0487-1) Prof. Dr. Dr. K. Van Steen University of Liège, Belgium November 12, 2012 Introduction to Statistics Basic Probability Revisited Sampling Exploratory Data Analysis -
Elements of statistics (MATH0487-1) Prof. Dr. Dr. K. Van Steen University of Liège, Belgium November 12, 2012 Introduction to Statistics Basic Probability Revisited Sampling Exploratory Data Analysis -
Parametric Inference
 Parametric Inference Moulinath Banerjee University of Michigan April 14, 2004 1 General Discussion The object of statistical inference is to glean information about an underlying population based on a
Parametric Inference Moulinath Banerjee University of Michigan April 14, 2004 1 General Discussion The object of statistical inference is to glean information about an underlying population based on a
Master s Written Examination
 Master s Written Examination Option: Statistics and Probability Spring 05 Full points may be obtained for correct answers to eight questions Each numbered question (which may have several parts) is worth
Master s Written Examination Option: Statistics and Probability Spring 05 Full points may be obtained for correct answers to eight questions Each numbered question (which may have several parts) is worth
Statistics Masters Comprehensive Exam March 21, 2003
 Statistics Masters Comprehensive Exam March 21, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Statistics Masters Comprehensive Exam March 21, 2003 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your answer
Three hours. To be supplied by the Examinations Office: Mathematical Formula Tables and Statistical Tables THE UNIVERSITY OF MANCHESTER.
 Three hours To be supplied by the Examinations Office: Mathematical Formula Tables and Statistical Tables THE UNIVERSITY OF MANCHESTER EXTREME VALUES AND FINANCIAL RISK Examiner: Answer QUESTION 1, QUESTION
Three hours To be supplied by the Examinations Office: Mathematical Formula Tables and Statistical Tables THE UNIVERSITY OF MANCHESTER EXTREME VALUES AND FINANCIAL RISK Examiner: Answer QUESTION 1, QUESTION
Sampling Distributions
 In statistics, a random sample is a collection of independent and identically distributed (iid) random variables, and a sampling distribution is the distribution of a function of random sample. For example,
In statistics, a random sample is a collection of independent and identically distributed (iid) random variables, and a sampling distribution is the distribution of a function of random sample. For example,
Summary. Ancillary Statistics What is an ancillary statistic for θ? .2 Can an ancillary statistic be a sufficient statistic?
 Biostatistics 62 - Statistical Inference Lecture 5 Hyun Min Kang 1 What is an ancillary statistic for θ? 2 Can an ancillary statistic be a sufficient statistic? 3 What are the location parameter and the
Biostatistics 62 - Statistical Inference Lecture 5 Hyun Min Kang 1 What is an ancillary statistic for θ? 2 Can an ancillary statistic be a sufficient statistic? 3 What are the location parameter and the
Exercises and Answers to Chapter 1
 Exercises and Answers to Chapter The continuous type of random variable X has the following density function: a x, if < x < a, f (x), otherwise. Answer the following questions. () Find a. () Obtain mean
Exercises and Answers to Chapter The continuous type of random variable X has the following density function: a x, if < x < a, f (x), otherwise. Answer the following questions. () Find a. () Obtain mean
Generalized Linear Models Introduction
 Generalized Linear Models Introduction Statistics 135 Autumn 2005 Copyright c 2005 by Mark E. Irwin Generalized Linear Models For many problems, standard linear regression approaches don t work. Sometimes,
Generalized Linear Models Introduction Statistics 135 Autumn 2005 Copyright c 2005 by Mark E. Irwin Generalized Linear Models For many problems, standard linear regression approaches don t work. Sometimes,
Solution. (i) Find a minimal sufficient statistic for (θ, β) and give your justification. X i=1. By the factorization theorem, ( n
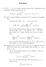 Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Central Limit Theorem ( 5.3)
 Central Limit Theorem ( 5.3) Let X 1, X 2,... be a sequence of independent random variables, each having n mean µ and variance σ 2. Then the distribution of the partial sum S n = X i i=1 becomes approximately
Central Limit Theorem ( 5.3) Let X 1, X 2,... be a sequence of independent random variables, each having n mean µ and variance σ 2. Then the distribution of the partial sum S n = X i i=1 becomes approximately
Statistics - Lecture One. Outline. Charlotte Wickham 1. Basic ideas about estimation
 Statistics - Lecture One Charlotte Wickham wickham@stat.berkeley.edu http://www.stat.berkeley.edu/~wickham/ Outline 1. Basic ideas about estimation 2. Method of Moments 3. Maximum Likelihood 4. Confidence
Statistics - Lecture One Charlotte Wickham wickham@stat.berkeley.edu http://www.stat.berkeley.edu/~wickham/ Outline 1. Basic ideas about estimation 2. Method of Moments 3. Maximum Likelihood 4. Confidence
conditional cdf, conditional pdf, total probability theorem?
 6 Multiple Random Variables 6.0 INTRODUCTION scalar vs. random variable cdf, pdf transformation of a random variable conditional cdf, conditional pdf, total probability theorem expectation of a random
6 Multiple Random Variables 6.0 INTRODUCTION scalar vs. random variable cdf, pdf transformation of a random variable conditional cdf, conditional pdf, total probability theorem expectation of a random
4. Distributions of Functions of Random Variables
 4. Distributions of Functions of Random Variables Setup: Consider as given the joint distribution of X 1,..., X n (i.e. consider as given f X1,...,X n and F X1,...,X n ) Consider k functions g 1 : R n
4. Distributions of Functions of Random Variables Setup: Consider as given the joint distribution of X 1,..., X n (i.e. consider as given f X1,...,X n and F X1,...,X n ) Consider k functions g 1 : R n
Evaluating the Performance of Estimators (Section 7.3)
 Evaluating the Performance of Estimators (Section 7.3) Example: Suppose we observe X 1,..., X n iid N(θ, σ 2 0 ), with σ2 0 known, and wish to estimate θ. Two possible estimators are: ˆθ = X sample mean
Evaluating the Performance of Estimators (Section 7.3) Example: Suppose we observe X 1,..., X n iid N(θ, σ 2 0 ), with σ2 0 known, and wish to estimate θ. Two possible estimators are: ˆθ = X sample mean
BMIR Lecture Series on Probability and Statistics Fall 2015 Discrete RVs
 Lecture #7 BMIR Lecture Series on Probability and Statistics Fall 2015 Department of Biomedical Engineering and Environmental Sciences National Tsing Hua University 7.1 Function of Single Variable Theorem
Lecture #7 BMIR Lecture Series on Probability and Statistics Fall 2015 Department of Biomedical Engineering and Environmental Sciences National Tsing Hua University 7.1 Function of Single Variable Theorem
Chapter 5 continued. Chapter 5 sections
 Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
ECE 275B Homework # 1 Solutions Winter 2018
 ECE 275B Homework # 1 Solutions Winter 2018 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2 < < x n Thus,
ECE 275B Homework # 1 Solutions Winter 2018 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2 < < x n Thus,
ECE 275B Homework # 1 Solutions Version Winter 2015
 ECE 275B Homework # 1 Solutions Version Winter 2015 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2
ECE 275B Homework # 1 Solutions Version Winter 2015 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2
Qualifying Exam in Probability and Statistics. https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf
 Part 1: Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Part 1: Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
MATH c UNIVERSITY OF LEEDS Examination for the Module MATH2715 (January 2015) STATISTICAL METHODS. Time allowed: 2 hours
 MATH2750 This question paper consists of 8 printed pages, each of which is identified by the reference MATH275. All calculators must carry an approval sticker issued by the School of Mathematics. c UNIVERSITY
MATH2750 This question paper consists of 8 printed pages, each of which is identified by the reference MATH275. All calculators must carry an approval sticker issued by the School of Mathematics. c UNIVERSITY
Practice Problems Section Problems
 Practice Problems Section 4-4-3 4-4 4-5 4-6 4-7 4-8 4-10 Supplemental Problems 4-1 to 4-9 4-13, 14, 15, 17, 19, 0 4-3, 34, 36, 38 4-47, 49, 5, 54, 55 4-59, 60, 63 4-66, 68, 69, 70, 74 4-79, 81, 84 4-85,
Practice Problems Section 4-4-3 4-4 4-5 4-6 4-7 4-8 4-10 Supplemental Problems 4-1 to 4-9 4-13, 14, 15, 17, 19, 0 4-3, 34, 36, 38 4-47, 49, 5, 54, 55 4-59, 60, 63 4-66, 68, 69, 70, 74 4-79, 81, 84 4-85,
Probability and Distributions
 Probability and Distributions What is a statistical model? A statistical model is a set of assumptions by which the hypothetical population distribution of data is inferred. It is typically postulated
Probability and Distributions What is a statistical model? A statistical model is a set of assumptions by which the hypothetical population distribution of data is inferred. It is typically postulated
Course: ESO-209 Home Work: 1 Instructor: Debasis Kundu
 Home Work: 1 1. Describe the sample space when a coin is tossed (a) once, (b) three times, (c) n times, (d) an infinite number of times. 2. A coin is tossed until for the first time the same result appear
Home Work: 1 1. Describe the sample space when a coin is tossed (a) once, (b) three times, (c) n times, (d) an infinite number of times. 2. A coin is tossed until for the first time the same result appear
Mathematical statistics
 October 1 st, 2018 Lecture 11: Sufficient statistic Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation
October 1 st, 2018 Lecture 11: Sufficient statistic Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation
Statistics and Econometrics I
 Statistics and Econometrics I Point Estimation Shiu-Sheng Chen Department of Economics National Taiwan University September 13, 2016 Shiu-Sheng Chen (NTU Econ) Statistics and Econometrics I September 13,
Statistics and Econometrics I Point Estimation Shiu-Sheng Chen Department of Economics National Taiwan University September 13, 2016 Shiu-Sheng Chen (NTU Econ) Statistics and Econometrics I September 13,
f(y θ) = g(t (y) θ)h(y)
 EXAM3, FINAL REVIEW (and a review for some of the QUAL problems): No notes will be allowed, but you may bring a calculator. Memorize the pmf or pdf f, E(Y ) and V(Y ) for the following RVs: 1) beta(δ,
EXAM3, FINAL REVIEW (and a review for some of the QUAL problems): No notes will be allowed, but you may bring a calculator. Memorize the pmf or pdf f, E(Y ) and V(Y ) for the following RVs: 1) beta(δ,
Probability and Statistics qualifying exam, May 2015
 Probability and Statistics qualifying exam, May 2015 Name: Instructions: 1. The exam is divided into 3 sections: Linear Models, Mathematical Statistics and Probability. You must pass each section to pass
Probability and Statistics qualifying exam, May 2015 Name: Instructions: 1. The exam is divided into 3 sections: Linear Models, Mathematical Statistics and Probability. You must pass each section to pass
Miscellaneous Errors in the Chapter 6 Solutions
 Miscellaneous Errors in the Chapter 6 Solutions 3.30(b In this problem, early printings of the second edition use the beta(a, b distribution, but later versions use the Poisson(λ distribution. If your
Miscellaneous Errors in the Chapter 6 Solutions 3.30(b In this problem, early printings of the second edition use the beta(a, b distribution, but later versions use the Poisson(λ distribution. If your
Lecture 4: UMVUE and unbiased estimators of 0
 Lecture 4: UMVUE and unbiased estimators of Problems of approach 1. Approach 1 has the following two main shortcomings. Even if Theorem 7.3.9 or its extension is applicable, there is no guarantee that
Lecture 4: UMVUE and unbiased estimators of Problems of approach 1. Approach 1 has the following two main shortcomings. Even if Theorem 7.3.9 or its extension is applicable, there is no guarantee that
Foundations of Statistical Inference
 Foundations of Statistical Inference Jonathan Marchini Department of Statistics University of Oxford MT 2013 Jonathan Marchini (University of Oxford) BS2a MT 2013 1 / 27 Course arrangements Lectures M.2
Foundations of Statistical Inference Jonathan Marchini Department of Statistics University of Oxford MT 2013 Jonathan Marchini (University of Oxford) BS2a MT 2013 1 / 27 Course arrangements Lectures M.2
Testing Hypothesis. Maura Mezzetti. Department of Economics and Finance Università Tor Vergata
 Maura Department of Economics and Finance Università Tor Vergata Hypothesis Testing Outline It is a mistake to confound strangeness with mystery Sherlock Holmes A Study in Scarlet Outline 1 The Power Function
Maura Department of Economics and Finance Università Tor Vergata Hypothesis Testing Outline It is a mistake to confound strangeness with mystery Sherlock Holmes A Study in Scarlet Outline 1 The Power Function
Introduction to Estimation Methods for Time Series models Lecture 2
 Introduction to Estimation Methods for Time Series models Lecture 2 Fulvio Corsi SNS Pisa Fulvio Corsi Introduction to Estimation () Methods for Time Series models Lecture 2 SNS Pisa 1 / 21 Estimators:
Introduction to Estimation Methods for Time Series models Lecture 2 Fulvio Corsi SNS Pisa Fulvio Corsi Introduction to Estimation () Methods for Time Series models Lecture 2 SNS Pisa 1 / 21 Estimators:
4 Invariant Statistical Decision Problems
 4 Invariant Statistical Decision Problems 4.1 Invariant decision problems Let G be a group of measurable transformations from the sample space X into itself. The group operation is composition. Note that
4 Invariant Statistical Decision Problems 4.1 Invariant decision problems Let G be a group of measurable transformations from the sample space X into itself. The group operation is composition. Note that
Estimation theory. Parametric estimation. Properties of estimators. Minimum variance estimator. Cramer-Rao bound. Maximum likelihood estimators
 Estimation theory Parametric estimation Properties of estimators Minimum variance estimator Cramer-Rao bound Maximum likelihood estimators Confidence intervals Bayesian estimation 1 Random Variables Let
Estimation theory Parametric estimation Properties of estimators Minimum variance estimator Cramer-Rao bound Maximum likelihood estimators Confidence intervals Bayesian estimation 1 Random Variables Let
Statistics Ph.D. Qualifying Exam: Part II November 9, 2002
 Statistics Ph.D. Qualifying Exam: Part II November 9, 2002 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your
Statistics Ph.D. Qualifying Exam: Part II November 9, 2002 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. 1 2 3 4 5 6 7 8 9 10 11 12 2. Write your
Hypothesis Testing. 1 Definitions of test statistics. CB: chapter 8; section 10.3
 Hypothesis Testing CB: chapter 8; section 0.3 Hypothesis: statement about an unknown population parameter Examples: The average age of males in Sweden is 7. (statement about population mean) The lowest
Hypothesis Testing CB: chapter 8; section 0.3 Hypothesis: statement about an unknown population parameter Examples: The average age of males in Sweden is 7. (statement about population mean) The lowest
Course arrangements. Foundations of Statistical Inference
 Course arrangements Foundations of Statistical Inference Jonathan Marchini Department of Statistics University of Oxford MT 013 Lectures M. and Th.10 SPR1 weeks 1-8 Classes Weeks 3-8 Friday 1-1, 4-5, 5-6
Course arrangements Foundations of Statistical Inference Jonathan Marchini Department of Statistics University of Oxford MT 013 Lectures M. and Th.10 SPR1 weeks 1-8 Classes Weeks 3-8 Friday 1-1, 4-5, 5-6
Siegel s formula via Stein s identities
 Siegel s formula via Stein s identities Jun S. Liu Department of Statistics Harvard University Abstract Inspired by a surprising formula in Siegel (1993), we find it convenient to compute covariances,
Siegel s formula via Stein s identities Jun S. Liu Department of Statistics Harvard University Abstract Inspired by a surprising formula in Siegel (1993), we find it convenient to compute covariances,
SOLUTION FOR HOMEWORK 6, STAT 6331
 SOLUTION FOR HOMEWORK 6, STAT 633. Exerc.7.. It is given that X,...,X n is a sample from N(θ, σ ), and the Bayesian approach is used with Θ N(µ, τ ). The parameters σ, µ and τ are given. (a) Find the joinf
SOLUTION FOR HOMEWORK 6, STAT 633. Exerc.7.. It is given that X,...,X n is a sample from N(θ, σ ), and the Bayesian approach is used with Θ N(µ, τ ). The parameters σ, µ and τ are given. (a) Find the joinf
Two hours. To be supplied by the Examinations Office: Mathematical Formula Tables and Statistical Tables THE UNIVERSITY OF MANCHESTER.
 Two hours MATH38181 To be supplied by the Examinations Office: Mathematical Formula Tables and Statistical Tables THE UNIVERSITY OF MANCHESTER EXTREME VALUES AND FINANCIAL RISK Examiner: Answer any FOUR
Two hours MATH38181 To be supplied by the Examinations Office: Mathematical Formula Tables and Statistical Tables THE UNIVERSITY OF MANCHESTER EXTREME VALUES AND FINANCIAL RISK Examiner: Answer any FOUR
Patterns of Scalable Bayesian Inference Background (Session 1)
 Patterns of Scalable Bayesian Inference Background (Session 1) Jerónimo Arenas-García Universidad Carlos III de Madrid jeronimo.arenas@gmail.com June 14, 2017 1 / 15 Motivation. Bayesian Learning principles
Patterns of Scalable Bayesian Inference Background (Session 1) Jerónimo Arenas-García Universidad Carlos III de Madrid jeronimo.arenas@gmail.com June 14, 2017 1 / 15 Motivation. Bayesian Learning principles
Formulas for probability theory and linear models SF2941
 Formulas for probability theory and linear models SF2941 These pages + Appendix 2 of Gut) are permitted as assistance at the exam. 11 maj 2008 Selected formulae of probability Bivariate probability Transforms
Formulas for probability theory and linear models SF2941 These pages + Appendix 2 of Gut) are permitted as assistance at the exam. 11 maj 2008 Selected formulae of probability Bivariate probability Transforms
