Splay Trees. Splay Trees. Splay Trees. Splay Trees
|
|
|
- Suzanna Hicks
- 5 years ago
- Views:
Transcription
1 Slay Trees Slay Trees isadvantae of balanced search trees: worst case; no advantae for easy inuts additional memory required comlicated imlementation Slay Trees: + after access, an element is moved to the root; slay() reeated accesses are faster find() search for accordin to a search tree let be last element on search-ath slay( ) only amortized uarantee read-oerations chane the tree Ernst Mayr, Harald Räcke 16 Ernst Mayr, Harald Räcke 163 Slay Trees Slay Trees insert() search for ; is last visited element durin search (successer or redecessor of ) slay( ) moves to the root insert as new root delete() search for ; slay(); remove search larest element in slay( ) (on subtree ) connect root of as riht child of The illustration shows the case when is the redecessor of. Ernst Mayr, Harald Räcke 164 Ernst Mayr, Harald Räcke 165
2 Move to Root Slay: Zi ase How to brin element to root? one (bad) otion: movetoroot() iteratively do rotation around arent of until is root better otion slay(): zi case: if is child of root do left rotation or riht rotation around arent if is left child do riht rotation otw. left rotation Note that movetoroot() does the same. Ernst Mayr, Harald Räcke 166 Ernst Mayr, Harald Räcke 167 Slay: Ziza ase ouble Rotations z better otion slay(): LeftRotate(y) y RihtRotate() ziza case: if is riht child and arent of is left child z (or left child arent of riht child) y y do double riht rotation around rand-arent (res. double left rotation) z oublerihtrotate() Note that movetoroot() does the same. Ernst Mayr, Harald Räcke 168
3 Slay: Zizi ase This case is different between movetoroot() and slay(). Slay vs. Move to Root a b H e d E c F G better otion slay(): zizi case: if is left child and arent of is left child (or f riht child, arent of riht child) do riht roation around rand-arent followed by riht rotation around arent (res. left rotations) Inut tree on which slay() and movetoroot() is eecuted. Ernst Mayr, Harald Räcke 170 Ernst Mayr, Harald Räcke 171 Slay vs. Move to Root Slay vs. Move to Root a b b H d a c G f c G H e d E F e E F f Result after movetoroot(). Result after slay(). Ernst Mayr, Harald Räcke 171 Ernst Mayr, Harald Räcke 17
4 Static Otimality ynamic Otimality Suose we have a sequence of m find-oerations. find() aears h times in this sequence. The cost of a static search tree T is: Let S be a sequence with m find-oerations. Let be a data-structure based on a search tree: the cost for accessin element is 1 + deth(); cost(t ) = m + h deth T () after accessin the tree may be re-arraned throuh rotations; The total cost for rocessin the sequence on a slay-tree is O(cost(T min )), where T min is an otimal static search tree. onjecture: slay tree that only contains elements from S has cost O(cost(, S)), for rocessin S. deth T () is the number of edes on a ath from the root of T to. Theorem iven without roof. Ernst Mayr, Harald Räcke 173 Ernst Mayr, Harald Räcke 174 mortized nalysis Lemma 1 Slay Trees have an amortized runnin time of O(lo n) for all oerations. efinition data structure with oerations o 1 (),..., o k () has amortized runnin times t 1,..., t k for these oerations if the followin holds. Suose you are iven a sequence of oerations (startin with an emty data-structure) that oerate on at most n elements, and let k i denote the number of occurences of o i () within this sequence. Then the actual runnin time must be at most i k i t i (n). Ernst Mayr, Harald Räcke 175 Ernst Mayr, Harald Räcke 176
5 Potential Method Introduce a otential for the data structure. Φ( i ) is the otential after the i-th oeration. mortized cost of the i-th oeration is Show that Φ( i ) Φ( 0 ). Then k c i i=1 ĉ i = c i + Φ( i ) Φ( i 1 ). k c i + Φ( k ) Φ( 0 ) = i=1 This means the amortized costs can be used to derive a bound on the total cost. k i=1 ĉ i Eamle: Stack Stack S. ush() S. o() S. multio(k): removes k items from the stack. If the stack currently contains less than k items it emties the stack. The user has to ensure that o and multio do not enerate an underflow. ctual cost: S. ush(): cost 1. S. o(): cost 1. S. multio(k): cost min{size, k} = k. Ernst Mayr, Harald Räcke 177 Ernst Mayr, Harald Räcke 178 Eamle: Stack Use otential function Φ(S) = number of elements on the stack. mortized cost: S. ush(): cost S. o(): cost Ĉ ush = ush + Φ = Ĉ o = o + Φ = S. multio(k): cost Note that the analysis becomes wron if o() or multio() are called on an emty stack. Ĉ m = m + Φ = min{size, k} min{size, k} 0. Eamle: inary ounter Incrementin a binary counter: onsider a comutational model where each bit-oeration costs one time-unit. Incrementin an n-bit binary counter may require to eamine n-bits, and maybe chane them. ctual cost: hanin bit from 0 to 1: cost 1. hanin bit from 1 to 0: cost 1. Increment: cost is k + 1, where k is the number of consecutive ones in the least sinificant bit-ositions (e., has k = 1). Ernst Mayr, Harald Räcke 179 Ernst Mayr, Harald Räcke 180
6 Eamle: inary ounter hoose otential function Φ() = k, where k denotes the number of ones in the binary reresentation of. mortized cost: hanin bit from 0 to 1: Ĉ 0 1 = Φ = Slay Trees otential function for slay trees: size s() = T rank r() = lo (s()) Φ(T ) = v T r (v) hanin bit from 1 to 0: amortized cost = real cost + otential chane Ĉ 1 0 = Φ = Increment: Let k denotes the number of consecutive ones in the least sinificant bit-ositions. n increment involves k (1 0)-oerations, and one (0 1)-oeration. The cost is essentially the cost of the slay-oeration, which is 1 lus the number of rotations. Hence, the amortized cost is kĉ Ĉ 0 1. Ernst Mayr, Harald Räcke 18 Slay: Zi ase Slay: Zizi ase Last inequality follows from net slide. Φ = r () + r () r () r () = r () r () r () r () cost zi 1 + 3(r () r ()) Φ = r () + r () + r () r () r () r () = r () + r () r () r () r () + r () r () r () = r () + r () + r () 3r () + 3r () r () r () = r () + r () + r () + 3(r () r ()) Ernst Mayr, Harald Räcke (r () r ()) cost zizi 3(r () r ())
7 Slay: Zizi ase The last inequality holds because lo is a concave function. Slay: Ziza ase 1( ) r () + r () r () = 1 ( ) lo(s()) + lo(s ()) lo(s ()) = 1 ( s() ) lo + 1 ( s lo () ) ( 1 lo s () s () s() s () + 1 s () ) ( 1 s lo = 1 () ) Φ = r () + r () + r () r () r () r () = r () + r () r () r () r () + r () r () r () = r () + r () r () + r () r () + (r () r ()) cost ziza 3(r () r ()) Ernst Mayr, Harald Räcke 185 Slay: Ziza ase 1( ) r () + r () r () = 1 ( ) lo(s ()) + lo(s ()) lo(s ()) ( 1 s () lo s () + 1 s () ) ( 1 s lo = 1 () ) mortized cost of the whole slay oeration: stes t = + r (root) r 0 () O(lo n) 3(r t () r t 1 ()) The first one is added due to the fact that so far for each ste of a slay-oeration we have only counted the number of rotations, but the cost is 1+#rotations. The second one comes from the zi-oeration. Note that we have at most one zi-oeration durin a slay. Ernst Mayr, Harald Räcke 185 Ernst Mayr, Harald Räcke 186
8 Slay Trees ibliorahy?????????????????????????????????????? Ernst Mayr, Harald Räcke 187
Part III. Data Structures. Abstract Data Type. Dynamic Set Operations. Dynamic Set Operations
 Abstract Data Type Part III Data Structures An abstract data type (ADT) is defined by an interface of operations or methods that can be performed and that have a defined behavior. The data types in this
Abstract Data Type Part III Data Structures An abstract data type (ADT) is defined by an interface of operations or methods that can be performed and that have a defined behavior. The data types in this
7.3 AVL-Trees. Definition 15. Lemma 16. AVL-trees are binary search trees that fulfill the following balance condition.
 Definition 15 AVL-trees are binary search trees that fulfill the following balance condition. F eery node height(left sub-tree()) height(right sub-tree()) 1. Lemma 16 An AVL-tree of height h contains at
Definition 15 AVL-trees are binary search trees that fulfill the following balance condition. F eery node height(left sub-tree()) height(right sub-tree()) 1. Lemma 16 An AVL-tree of height h contains at
16. Binary Search Trees
 Dictionary imlementation 16. Binary Search Trees [Ottman/Widmayer, Ka..1, Cormen et al, Ka. 1.1-1.] Hashing: imlementation of dictionaries with exected very fast access times. Disadvantages of hashing:
Dictionary imlementation 16. Binary Search Trees [Ottman/Widmayer, Ka..1, Cormen et al, Ka. 1.1-1.] Hashing: imlementation of dictionaries with exected very fast access times. Disadvantages of hashing:
16. Binary Search Trees
 Dictionary imlementation 16. Binary Search Trees [Ottman/Widmayer, Ka..1, Cormen et al, Ka. 12.1-12.] Hashing: imlementation of dictionaries with exected very fast access times. Disadvantages of hashing:
Dictionary imlementation 16. Binary Search Trees [Ottman/Widmayer, Ka..1, Cormen et al, Ka. 12.1-12.] Hashing: imlementation of dictionaries with exected very fast access times. Disadvantages of hashing:
7 Dictionary. Ernst Mayr, Harald Räcke 126
 7 Dictionary Dictionary: S. insert(x): Insert an element x. S. delete(x): Delete the element pointed to by x. S. search(k): Return a pointer to an element e with key[e] = k in S if it exists; otherwise
7 Dictionary Dictionary: S. insert(x): Insert an element x. S. delete(x): Delete the element pointed to by x. S. search(k): Return a pointer to an element e with key[e] = k in S if it exists; otherwise
Each internal node v with d(v) children stores d 1 keys. k i 1 < key in i-th sub-tree k i, where we use k 0 = and k d =.
 7.5 (a, b)-trees 7.5 (a, b)-trees Definition For b a an (a, b)-tree is a search tree with the following properties. all leaves have the same distance to the root. every internal non-root vertex v has at
7.5 (a, b)-trees 7.5 (a, b)-trees Definition For b a an (a, b)-tree is a search tree with the following properties. all leaves have the same distance to the root. every internal non-root vertex v has at
CS 5321: Advanced Algorithms Amortized Analysis of Data Structures. Motivations. Motivation cont d
 CS 5321: Advanced Algorithms Amortized Analysis of Data Structures Ali Ebnenasir Department of Computer Science Michigan Technological University Motivations Why amortized analysis and when? Suppose you
CS 5321: Advanced Algorithms Amortized Analysis of Data Structures Ali Ebnenasir Department of Computer Science Michigan Technological University Motivations Why amortized analysis and when? Suppose you
8: Splay Trees. Move-to-Front Heuristic. Splaying. Splay(12) CSE326 Spring April 16, Search for Pebbles: Move found item to front of list
 : Splay Trees SE Spring 00 pril, 00 Move-to-Front Heuristic Search for ebbles: Fred Wilma ebbles ino Fred Wilma ino ebbles Move found item to front of list Frequently searched items will move to start
: Splay Trees SE Spring 00 pril, 00 Move-to-Front Heuristic Search for ebbles: Fred Wilma ebbles ino Fred Wilma ino ebbles Move found item to front of list Frequently searched items will move to start
Lecture Notes for Chapter 17: Amortized Analysis
 Lecture Notes for Chapter 17: Amortized Analysis Chapter 17 overview Amortized analysis Analyze a sequence of operations on a data structure. Goal: Show that although some individual operations may be
Lecture Notes for Chapter 17: Amortized Analysis Chapter 17 overview Amortized analysis Analyze a sequence of operations on a data structure. Goal: Show that although some individual operations may be
Lecture 7: Amortized analysis
 Lecture 7: Amortized analysis In many applications we want to minimize the time for a sequence of operations. To sum worst-case times for single operations can be overly pessimistic, since it ignores correlation
Lecture 7: Amortized analysis In many applications we want to minimize the time for a sequence of operations. To sum worst-case times for single operations can be overly pessimistic, since it ignores correlation
Another way of saying this is that amortized analysis guarantees the average case performance of each operation in the worst case.
 Amortized Analysis: CLRS Chapter 17 Last revised: August 30, 2006 1 In amortized analysis we try to analyze the time required by a sequence of operations. There are many situations in which, even though
Amortized Analysis: CLRS Chapter 17 Last revised: August 30, 2006 1 In amortized analysis we try to analyze the time required by a sequence of operations. There are many situations in which, even though
Amortized analysis. Amortized analysis
 In amortized analysis the goal is to bound the worst case time of a sequence of operations on a data-structure. If n operations take T (n) time (worst case), the amortized cost of an operation is T (n)/n.
In amortized analysis the goal is to bound the worst case time of a sequence of operations on a data-structure. If n operations take T (n) time (worst case), the amortized cost of an operation is T (n)/n.
Graduate Analysis of Algorithms Dr. Haim Levkowitz
 UMass Lowell Computer Science 9.53 Graduate Analysis of Algorithms Dr. Haim Levkowitz Fall 27 Lecture 5 Tuesday, 2 Oct 27 Amortized Analysis Overview Amortize: To pay off a debt, usually by periodic payments
UMass Lowell Computer Science 9.53 Graduate Analysis of Algorithms Dr. Haim Levkowitz Fall 27 Lecture 5 Tuesday, 2 Oct 27 Amortized Analysis Overview Amortize: To pay off a debt, usually by periodic payments
The null-pointers in a binary search tree are replaced by pointers to special null-vertices, that do not carry any object-data
 Definition 1 A red black tree is a balanced binary search tree in which each internal node has two children. Each internal node has a color, such that 1. The root is black. 2. All leaf nodes are black.
Definition 1 A red black tree is a balanced binary search tree in which each internal node has two children. Each internal node has a color, such that 1. The root is black. 2. All leaf nodes are black.
Amortized Analysis (chap. 17)
 Amortized Analysis (chap. 17) Not just consider one operation, but a sequence of operations on a given data structure. Average cost over a sequence of operations. Probabilistic analysis: Average case running
Amortized Analysis (chap. 17) Not just consider one operation, but a sequence of operations on a given data structure. Average cost over a sequence of operations. Probabilistic analysis: Average case running
So far we have implemented the search for a key by carefully choosing split-elements.
 7.7 Hashing Dictionary: S. insert(x): Insert an element x. S. delete(x): Delete the element pointed to by x. S. search(k): Return a pointer to an element e with key[e] = k in S if it exists; otherwise
7.7 Hashing Dictionary: S. insert(x): Insert an element x. S. delete(x): Delete the element pointed to by x. S. search(k): Return a pointer to an element e with key[e] = k in S if it exists; otherwise
Topic: Lower Bounds on Randomized Algorithms Date: September 22, 2004 Scribe: Srinath Sridhar
 15-859(M): Randomized Algorithms Lecturer: Anuam Guta Toic: Lower Bounds on Randomized Algorithms Date: Setember 22, 2004 Scribe: Srinath Sridhar 4.1 Introduction In this lecture, we will first consider
15-859(M): Randomized Algorithms Lecturer: Anuam Guta Toic: Lower Bounds on Randomized Algorithms Date: Setember 22, 2004 Scribe: Srinath Sridhar 4.1 Introduction In this lecture, we will first consider
Outline. CS21 Decidability and Tractability. Regular expressions and FA. Regular expressions and FA. Regular expressions and FA
 Outline CS21 Decidability and Tractability Lecture 4 January 14, 2019 FA and Regular Exressions Non-regular languages: Puming Lemma Pushdown Automata Context-Free Grammars and Languages January 14, 2019
Outline CS21 Decidability and Tractability Lecture 4 January 14, 2019 FA and Regular Exressions Non-regular languages: Puming Lemma Pushdown Automata Context-Free Grammars and Languages January 14, 2019
8 Priority Queues. 8 Priority Queues. Prim s Minimum Spanning Tree Algorithm. Dijkstra s Shortest Path Algorithm
 8 Priority Queues 8 Priority Queues A Priority Queue S is a dynamic set data structure that supports the following operations: S. build(x 1,..., x n ): Creates a data-structure that contains just the elements
8 Priority Queues 8 Priority Queues A Priority Queue S is a dynamic set data structure that supports the following operations: S. build(x 1,..., x n ): Creates a data-structure that contains just the elements
Today: Amortized Analysis
 Today: Amortized Analysis COSC 581, Algorithms March 6, 2014 Many of these slides are adapted from several online sources Today s class: Chapter 17 Reading Assignments Reading assignment for next class:
Today: Amortized Analysis COSC 581, Algorithms March 6, 2014 Many of these slides are adapted from several online sources Today s class: Chapter 17 Reading Assignments Reading assignment for next class:
Chapter 6. Self-Adjusting Data Structures
 Chapter 6 Self-Adjusting Data Structures Chapter 5 describes a data structure that is able to achieve an epected quer time that is proportional to the entrop of the quer distribution. The most interesting
Chapter 6 Self-Adjusting Data Structures Chapter 5 describes a data structure that is able to achieve an epected quer time that is proportional to the entrop of the quer distribution. The most interesting
UPPAAL tutorial What s inside UPPAAL The UPPAAL input languages
 UPPAAL tutorial What s inside UPPAAL The UPPAAL inut languages 1 UPPAAL tool Develoed jointly by Usala & Aalborg University >>8,000 downloads since 1999 1 UPPAAL Tool Simulation Modeling Verification 3
UPPAAL tutorial What s inside UPPAAL The UPPAAL inut languages 1 UPPAAL tool Develoed jointly by Usala & Aalborg University >>8,000 downloads since 1999 1 UPPAAL Tool Simulation Modeling Verification 3
AMORTIZED ANALYSIS. binary counter multipop stack dynamic table. Lecture slides by Kevin Wayne. Last updated on 1/24/17 11:31 AM
 AMORTIZED ANALYSIS binary counter multipop stack dynamic table Lecture slides by Kevin Wayne http://www.cs.princeton.edu/~wayne/kleinberg-tardos Last updated on 1/24/17 11:31 AM Amortized analysis Worst-case
AMORTIZED ANALYSIS binary counter multipop stack dynamic table Lecture slides by Kevin Wayne http://www.cs.princeton.edu/~wayne/kleinberg-tardos Last updated on 1/24/17 11:31 AM Amortized analysis Worst-case
Illinois Institute of Technology Department of Computer Science. Splay Trees. CS 535 Design and Analysis of Algorithms Fall Semester, 2018
 Illinois Institute of Technolog epartment of omputer Science Spla Trees S 535 esign and nalsis of lgorithms Fall Semester, 2018 Spla trees are a powerful form of (leicographic) balanced binar trees devised
Illinois Institute of Technolog epartment of omputer Science Spla Trees S 535 esign and nalsis of lgorithms Fall Semester, 2018 Spla trees are a powerful form of (leicographic) balanced binar trees devised
past balancing schemes require maintenance of balance info at all times, are aggresive use work of searches to pay for work of rebalancing
 1 Splay Trees Sleator and Tarjan, Self Adjusting Binary Search Trees JACM 32(3) 1985 The claim planning ahead. But matches previous idea of being lazy, letting potential build up, using it to pay for expensive
1 Splay Trees Sleator and Tarjan, Self Adjusting Binary Search Trees JACM 32(3) 1985 The claim planning ahead. But matches previous idea of being lazy, letting potential build up, using it to pay for expensive
Cmpt 250 Unsigned Numbers January 11, 2008
 Cmt 25 Unsined Numbers Januar, 28 These notes serve two uroses in the contet of Cmt 25: as we develo the basic desin of an inteer ALU, we ll review the basics of number reresentation and combinational
Cmt 25 Unsined Numbers Januar, 28 These notes serve two uroses in the contet of Cmt 25: as we develo the basic desin of an inteer ALU, we ll review the basics of number reresentation and combinational
Computer arithmetic. Intensive Computation. Annalisa Massini 2017/2018
 Comuter arithmetic Intensive Comutation Annalisa Massini 7/8 Intensive Comutation - 7/8 References Comuter Architecture - A Quantitative Aroach Hennessy Patterson Aendix J Intensive Comutation - 7/8 3
Comuter arithmetic Intensive Comutation Annalisa Massini 7/8 Intensive Comutation - 7/8 References Comuter Architecture - A Quantitative Aroach Hennessy Patterson Aendix J Intensive Comutation - 7/8 3
10 van Emde Boas Trees
 Dynamic Set Data Structure S: S. insert(x) S. delete(x) S. search(x) S. min() S. max() S. succ(x) S. pred(x) Ernst Mayr, Harald Räcke 389 For this chapter we ignore the problem of storing satellite data:
Dynamic Set Data Structure S: S. insert(x) S. delete(x) S. search(x) S. min() S. max() S. succ(x) S. pred(x) Ernst Mayr, Harald Räcke 389 For this chapter we ignore the problem of storing satellite data:
Chapter 5 Data Structures Algorithm Theory WS 2017/18 Fabian Kuhn
 Chapter 5 Data Structures Algorithm Theory WS 2017/18 Fabian Kuhn Priority Queue / Heap Stores (key,data) pairs (like dictionary) But, different set of operations: Initialize-Heap: creates new empty heap
Chapter 5 Data Structures Algorithm Theory WS 2017/18 Fabian Kuhn Priority Queue / Heap Stores (key,data) pairs (like dictionary) But, different set of operations: Initialize-Heap: creates new empty heap
Data Structures and Algorithm. Xiaoqing Zheng
 Data Structures and Algorithm Xiaoqing Zheng zhengxq@fudan.edu.cn MULTIPOP top[s] = 6 top[s] = 2 3 2 8 5 6 5 S MULTIPOP(S, x). while not STACK-EMPTY(S) and k 0 2. do POP(S) 3. k k MULTIPOP(S, 4) Analysis
Data Structures and Algorithm Xiaoqing Zheng zhengxq@fudan.edu.cn MULTIPOP top[s] = 6 top[s] = 2 3 2 8 5 6 5 S MULTIPOP(S, x). while not STACK-EMPTY(S) and k 0 2. do POP(S) 3. k k MULTIPOP(S, 4) Analysis
On the Chvatál-Complexity of Knapsack Problems
 R u t c o r Research R e o r t On the Chvatál-Comlexity of Knasack Problems Gergely Kovács a Béla Vizvári b RRR 5-08, October 008 RUTCOR Rutgers Center for Oerations Research Rutgers University 640 Bartholomew
R u t c o r Research R e o r t On the Chvatál-Comlexity of Knasack Problems Gergely Kovács a Béla Vizvári b RRR 5-08, October 008 RUTCOR Rutgers Center for Oerations Research Rutgers University 640 Bartholomew
9 Union Find. 9 Union Find. List Implementation. 9 Union Find. Union Find Data Structure P: Maintains a partition of disjoint sets over elements.
 Union Find Data Structure P: Maintains a partition of disjoint sets over elements. P. makeset(x): Given an element x, adds x to the data-structure and creates a singleton set that contains only this element.
Union Find Data Structure P: Maintains a partition of disjoint sets over elements. P. makeset(x): Given an element x, adds x to the data-structure and creates a singleton set that contains only this element.
Outline. EECS150 - Digital Design Lecture 26 Error Correction Codes, Linear Feedback Shift Registers (LFSRs) Simple Error Detection Coding
 Outline EECS150 - Digital Design Lecture 26 Error Correction Codes, Linear Feedback Shift Registers (LFSRs) Error detection using arity Hamming code for error detection/correction Linear Feedback Shift
Outline EECS150 - Digital Design Lecture 26 Error Correction Codes, Linear Feedback Shift Registers (LFSRs) Error detection using arity Hamming code for error detection/correction Linear Feedback Shift
CSC165H, Mathematical expression and reasoning for computer science week 12
 CSC165H, Mathematical exression and reasoning for comuter science week 1 nd December 005 Gary Baumgartner and Danny Hea hea@cs.toronto.edu SF4306A 416-978-5899 htt//www.cs.toronto.edu/~hea/165/s005/index.shtml
CSC165H, Mathematical exression and reasoning for comuter science week 1 nd December 005 Gary Baumgartner and Danny Hea hea@cs.toronto.edu SF4306A 416-978-5899 htt//www.cs.toronto.edu/~hea/165/s005/index.shtml
Splay trees (Sleator, Tarjan 1983)
 Splay trees (Sleator, Tarjan 1983) 1 Main idea Try to arrange so frequently used items are near the root We shall assume that there is an item in every node including internal nodes. We can change this
Splay trees (Sleator, Tarjan 1983) 1 Main idea Try to arrange so frequently used items are near the root We shall assume that there is an item in every node including internal nodes. We can change this
Outline for Today. Static Optimality. Splay Trees. Properties of Splay Trees. Dynamic Optimality (ITA) Balanced BSTs aren't necessarily optimal!
 Splay Trees Outline for Today Static Optimality alanced STs aren't necessarily optimal! Splay Trees self-adjusting binary search tree. Properties of Splay Trees Why is splaying worthwhile? ynamic Optimality
Splay Trees Outline for Today Static Optimality alanced STs aren't necessarily optimal! Splay Trees self-adjusting binary search tree. Properties of Splay Trees Why is splaying worthwhile? ynamic Optimality
Amortized Analysis. DistributeMoney(n, k) 1 Each of n people gets $1. 2 for i = 1to k 3 do Give a dollar to a random person
 Amortized Analysis DistributeMoney(n, k) 1 Each of n people gets $1. 2 for i = 1to k 3 do Give a dollar to a random person What is the maximum amount of money I can receive? Amortized Analysis DistributeMoney(n,
Amortized Analysis DistributeMoney(n, k) 1 Each of n people gets $1. 2 for i = 1to k 3 do Give a dollar to a random person What is the maximum amount of money I can receive? Amortized Analysis DistributeMoney(n,
PCFG estimation with EM. The Inside-Outside Algorithm
 PCFG estiation with EM The Inside-Outside Alorith Presentation order l otation l Calculatin inside robabilities l Calculatin outside robabilities l General schea or EM aloriths l The inside-outside alorith
PCFG estiation with EM The Inside-Outside Alorith Presentation order l otation l Calculatin inside robabilities l Calculatin outside robabilities l General schea or EM aloriths l The inside-outside alorith
Advanced Implementations of Tables: Balanced Search Trees and Hashing
 Advanced Implementations of Tables: Balanced Search Trees and Hashing Balanced Search Trees Binary search tree operations such as insert, delete, retrieve, etc. depend on the length of the path to the
Advanced Implementations of Tables: Balanced Search Trees and Hashing Balanced Search Trees Binary search tree operations such as insert, delete, retrieve, etc. depend on the length of the path to the
Round-off Errors and Computer Arithmetic - (1.2)
 Round-off Errors and Comuter Arithmetic - (.). Round-off Errors: Round-off errors is roduced when a calculator or comuter is used to erform real number calculations. That is because the arithmetic erformed
Round-off Errors and Comuter Arithmetic - (.). Round-off Errors: Round-off errors is roduced when a calculator or comuter is used to erform real number calculations. That is because the arithmetic erformed
Convex Analysis and Economic Theory Winter 2018
 Division of the Humanities and Social Sciences Ec 181 KC Border Conve Analysis and Economic Theory Winter 2018 Toic 16: Fenchel conjugates 16.1 Conjugate functions Recall from Proosition 14.1.1 that is
Division of the Humanities and Social Sciences Ec 181 KC Border Conve Analysis and Economic Theory Winter 2018 Toic 16: Fenchel conjugates 16.1 Conjugate functions Recall from Proosition 14.1.1 that is
7 Dictionary. 7.1 Binary Search Trees. Binary Search Trees: Searching. 7.1 Binary Search Trees
 7 Dictionary Dictionary: S.insert(): Insert an element. S.delete(): Delete the element pointed to by. 7.1 Binary Search Trees An (internal) binary search tree stores the elements in a binary tree. Each
7 Dictionary Dictionary: S.insert(): Insert an element. S.delete(): Delete the element pointed to by. 7.1 Binary Search Trees An (internal) binary search tree stores the elements in a binary tree. Each
SAT based Abstraction-Refinement using ILP and Machine Learning Techniques
 SAT based Abstraction-Refinement using ILP and Machine Learning Techniques 1 SAT based Abstraction-Refinement using ILP and Machine Learning Techniques Edmund Clarke James Kukula Anubhav Guta Ofer Strichman
SAT based Abstraction-Refinement using ILP and Machine Learning Techniques 1 SAT based Abstraction-Refinement using ILP and Machine Learning Techniques Edmund Clarke James Kukula Anubhav Guta Ofer Strichman
MAP Estimation Algorithms in Computer Vision - Part II
 MAP Estimation Algorithms in Comuter Vision - Part II M. Pawan Kumar, University of Oford Pushmeet Kohli, Microsoft Research Eamle: Image Segmentation E() = c i i + c ij i (1- j ) i i,j E: {0,1} n R 0
MAP Estimation Algorithms in Comuter Vision - Part II M. Pawan Kumar, University of Oford Pushmeet Kohli, Microsoft Research Eamle: Image Segmentation E() = c i i + c ij i (1- j ) i i,j E: {0,1} n R 0
where x i is the ith coordinate of x R N. 1. Show that the following upper bound holds for the growth function of H:
 Mehryar Mohri Foundations of Machine Learning Courant Institute of Mathematical Sciences Homework assignment 2 October 25, 2017 Due: November 08, 2017 A. Growth function Growth function of stum functions.
Mehryar Mohri Foundations of Machine Learning Courant Institute of Mathematical Sciences Homework assignment 2 October 25, 2017 Due: November 08, 2017 A. Growth function Growth function of stum functions.
Data selection. Lower complexity bound for sorting
 Data selection. Lower complexity bound for sorting Lecturer: Georgy Gimel farb COMPSCI 220 Algorithms and Data Structures 1 / 12 1 Data selection: Quickselect 2 Lower complexity bound for sorting 3 The
Data selection. Lower complexity bound for sorting Lecturer: Georgy Gimel farb COMPSCI 220 Algorithms and Data Structures 1 / 12 1 Data selection: Quickselect 2 Lower complexity bound for sorting 3 The
7 Dictionary. EADS c Ernst Mayr, Harald Räcke 109
 7 Dictionary Dictionary: S.insert(x): Insert an element x. S.delete(x): Delete the element pointed to by x. S.search(k): Return a pointer to an element e with key[e] = k in S if it exists; otherwise return
7 Dictionary Dictionary: S.insert(x): Insert an element x. S.delete(x): Delete the element pointed to by x. S.search(k): Return a pointer to an element e with key[e] = k in S if it exists; otherwise return
An Introduction To Range Searching
 An Introduction To Range Searching Jan Vahrenhold eartment of Comuter Science Westfälische Wilhelms-Universität Münster, Germany. Overview 1. Introduction: Problem Statement, Lower Bounds 2. Range Searching
An Introduction To Range Searching Jan Vahrenhold eartment of Comuter Science Westfälische Wilhelms-Universität Münster, Germany. Overview 1. Introduction: Problem Statement, Lower Bounds 2. Range Searching
CHAPTER 16. Basic Concepts. Basic Concepts. The Equilibrium Constant. Reaction Quotient & Equilibrium Constant. Chemical Equilibrium
 Proerties of an Equilibrium System CHAPTER 6 Chemial Equilibrium Equilibrium systems are DYNAMIC (in onstant motion) REVERSIBLE an be aroahed from either diretion Pink to blue Co(H O) 6 Cl ---> > Co(H
Proerties of an Equilibrium System CHAPTER 6 Chemial Equilibrium Equilibrium systems are DYNAMIC (in onstant motion) REVERSIBLE an be aroahed from either diretion Pink to blue Co(H O) 6 Cl ---> > Co(H
Fundamental Algorithms
 Fundamental Algithms Chapter 4: AVL Trees Jan Křetínský Winter 2016/17 Chapter 4: AVL Trees, Winter 2016/17 1 Part I AVL Trees (Adelson-Velsky and Landis, 1962) Chapter 4: AVL Trees, Winter 2016/17 2 Binary
Fundamental Algithms Chapter 4: AVL Trees Jan Křetínský Winter 2016/17 Chapter 4: AVL Trees, Winter 2016/17 1 Part I AVL Trees (Adelson-Velsky and Landis, 1962) Chapter 4: AVL Trees, Winter 2016/17 2 Binary
4.3. Solving Friction Problems. Static Friction Problems. Tutorial 1 Static Friction Acting on Several Objects. Sample Problem 1.
 Solvin Friction Problems Sometimes friction is desirable and we want to increase the coefficient of friction to help keep objects at rest. For example, a runnin shoe is typically desined to have a lare
Solvin Friction Problems Sometimes friction is desirable and we want to increase the coefficient of friction to help keep objects at rest. For example, a runnin shoe is typically desined to have a lare
Problem. Problem Given a dictionary and a word. Which page (if any) contains the given word? 3 / 26
 Binary Search Introduction Problem Problem Given a dictionary and a word. Which page (if any) contains the given word? 3 / 26 Strategy 1: Random Search Randomly select a page until the page containing
Binary Search Introduction Problem Problem Given a dictionary and a word. Which page (if any) contains the given word? 3 / 26 Strategy 1: Random Search Randomly select a page until the page containing
Lecture 8: Pesudorandom Generators (II) 1 Pseudorandom Generators for Bounded Computation
 Expander Graphs in Computer Science WS 2010/2011 Lecture 8: Pesudorandom Generators (II) Lecturer: He Sun 1 Pseudorandom Generators for Bounded Computation Definition 8.1 Let M be a randomized TM that
Expander Graphs in Computer Science WS 2010/2011 Lecture 8: Pesudorandom Generators (II) Lecturer: He Sun 1 Pseudorandom Generators for Bounded Computation Definition 8.1 Let M be a randomized TM that
Part V. Matchings. Matching. 19 Augmenting Paths for Matchings. 18 Bipartite Matching via Flows
 Matching Input: undirected graph G = (V, E). M E is a matching if each node appears in at most one Part V edge in M. Maximum Matching: find a matching of maximum cardinality Matchings Ernst Mayr, Harald
Matching Input: undirected graph G = (V, E). M E is a matching if each node appears in at most one Part V edge in M. Maximum Matching: find a matching of maximum cardinality Matchings Ernst Mayr, Harald
The homework problem (pucks_on_ice) illustrates several important points:
 Ekman laers, friction & eostrohic flow The homework roblem (ucks_on_ice) illustrates several imortant oints: 1. Particles move erendicular to the alied force, to the riht in the northern hemishere, to
Ekman laers, friction & eostrohic flow The homework roblem (ucks_on_ice) illustrates several imortant oints: 1. Particles move erendicular to the alied force, to the riht in the northern hemishere, to
Data Structures and Algorithms " Search Trees!!
 Data Structures and Algorithms " Search Trees!! Outline" Binary Search Trees! AVL Trees! (2,4) Trees! 2 Binary Search Trees! "! < 6 2 > 1 4 = 8 9 Ordered Dictionaries" Keys are assumed to come from a total
Data Structures and Algorithms " Search Trees!! Outline" Binary Search Trees! AVL Trees! (2,4) Trees! 2 Binary Search Trees! "! < 6 2 > 1 4 = 8 9 Ordered Dictionaries" Keys are assumed to come from a total
Unit 1 - Computer Arithmetic
 FIXD-POINT (FX) ARITHMTIC Unit 1 - Comuter Arithmetic INTGR NUMBRS n bit number: b n 1 b n 2 b 0 Decimal Value Range of values UNSIGND n 1 SIGND D = b i 2 i D = 2 n 1 b n 1 + b i 2 i n 2 i=0 i=0 [0, 2
FIXD-POINT (FX) ARITHMTIC Unit 1 - Comuter Arithmetic INTGR NUMBRS n bit number: b n 1 b n 2 b 0 Decimal Value Range of values UNSIGND n 1 SIGND D = b i 2 i D = 2 n 1 b n 1 + b i 2 i n 2 i=0 i=0 [0, 2
RANDOM WALKS AND PERCOLATION: AN ANALYSIS OF CURRENT RESEARCH ON MODELING NATURAL PROCESSES
 RANDOM WALKS AND PERCOLATION: AN ANALYSIS OF CURRENT RESEARCH ON MODELING NATURAL PROCESSES AARON ZWIEBACH Abstract. In this aer we will analyze research that has been recently done in the field of discrete
RANDOM WALKS AND PERCOLATION: AN ANALYSIS OF CURRENT RESEARCH ON MODELING NATURAL PROCESSES AARON ZWIEBACH Abstract. In this aer we will analyze research that has been recently done in the field of discrete
Inorder traversal of splay trees
 Electronic Notes in Theoretical omuter Science 74 (2003) URL: htt://www.elsevier.nl/locate/entcs/volume74.html 24 ages Inorder traversal of sla trees olm ÓDúnlaing 1 Mathematics, Trinit ollege, Dublin
Electronic Notes in Theoretical omuter Science 74 (2003) URL: htt://www.elsevier.nl/locate/entcs/volume74.html 24 ages Inorder traversal of sla trees olm ÓDúnlaing 1 Mathematics, Trinit ollege, Dublin
MATH 2710: NOTES FOR ANALYSIS
 MATH 270: NOTES FOR ANALYSIS The main ideas we will learn from analysis center around the idea of a limit. Limits occurs in several settings. We will start with finite limits of sequences, then cover infinite
MATH 270: NOTES FOR ANALYSIS The main ideas we will learn from analysis center around the idea of a limit. Limits occurs in several settings. We will start with finite limits of sequences, then cover infinite
6 Mole Concept. g mol. g mol. g mol ) + 1( g : mol ratios are the units of molar mass. It does not matter which unit is on the
 What is a e? 6 Mole Concept The nature of chemistry is to chane one ecule into one or more new ecules in order to create new substances such as paints, fertilizers, food additives, medicines, etc. When
What is a e? 6 Mole Concept The nature of chemistry is to chane one ecule into one or more new ecules in order to create new substances such as paints, fertilizers, food additives, medicines, etc. When
Ordered Dictionary & Binary Search Tree
 Ordered Dictionary & Binary Search Tree Finite map from keys to values, assuming keys are comparable (). insert(k, v) lookup(k) aka find: the associated value if any delete(k) (Ordered set: No values;
Ordered Dictionary & Binary Search Tree Finite map from keys to values, assuming keys are comparable (). insert(k, v) lookup(k) aka find: the associated value if any delete(k) (Ordered set: No values;
Search Trees. Chapter 10. CSE 2011 Prof. J. Elder Last Updated: :52 AM
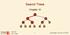 Search Trees Chapter 1 < 6 2 > 1 4 = 8 9-1 - Outline Ø Binary Search Trees Ø AVL Trees Ø Splay Trees - 2 - Outline Ø Binary Search Trees Ø AVL Trees Ø Splay Trees - 3 - Binary Search Trees Ø A binary search
Search Trees Chapter 1 < 6 2 > 1 4 = 8 9-1 - Outline Ø Binary Search Trees Ø AVL Trees Ø Splay Trees - 2 - Outline Ø Binary Search Trees Ø AVL Trees Ø Splay Trees - 3 - Binary Search Trees Ø A binary search
Maximum Cardinality Matchings on Trees by Randomized Local Search
 Maximum Cardinality Matchings on Trees by Randomized Local Search ABSTRACT Oliver Giel Fachbereich Informatik, Lehrstuhl 2 Universität Dortmund 44221 Dortmund, Germany oliver.giel@cs.uni-dortmund.de To
Maximum Cardinality Matchings on Trees by Randomized Local Search ABSTRACT Oliver Giel Fachbereich Informatik, Lehrstuhl 2 Universität Dortmund 44221 Dortmund, Germany oliver.giel@cs.uni-dortmund.de To
Lecture 5: Splay Trees
 15-750: Graduate Algorithms February 3, 2016 Lecture 5: Splay Trees Lecturer: Gary Miller Scribe: Jiayi Li, Tianyi Yang 1 Introduction Recall from previous lecture that balanced binary search trees (BST)
15-750: Graduate Algorithms February 3, 2016 Lecture 5: Splay Trees Lecturer: Gary Miller Scribe: Jiayi Li, Tianyi Yang 1 Introduction Recall from previous lecture that balanced binary search trees (BST)
Lecture VI AMORTIZATION
 1. Potential Framework Lecture VI Page 1 Lecture VI AMORTIZATION Many algorithms amount to a sequence of operations on a data structure. For instance, the well-known heapsort algorithm is a sequence of
1. Potential Framework Lecture VI Page 1 Lecture VI AMORTIZATION Many algorithms amount to a sequence of operations on a data structure. For instance, the well-known heapsort algorithm is a sequence of
Inference for Empirical Wasserstein Distances on Finite Spaces: Supplementary Material
 Inference for Emirical Wasserstein Distances on Finite Saces: Sulementary Material Max Sommerfeld Axel Munk Keywords: otimal transort, Wasserstein distance, central limit theorem, directional Hadamard
Inference for Emirical Wasserstein Distances on Finite Saces: Sulementary Material Max Sommerfeld Axel Munk Keywords: otimal transort, Wasserstein distance, central limit theorem, directional Hadamard
CSE 5311 Notes 5: Trees. (Last updated 6/4/13 4:12 PM)
 SE 511 Notes 5: Trees (Last updated 6//1 :1 PM) What is the optimal wa to organie a static tree for searching? n optimal (static) binar search tree is significantl more complicated to construct than an
SE 511 Notes 5: Trees (Last updated 6//1 :1 PM) What is the optimal wa to organie a static tree for searching? n optimal (static) binar search tree is significantl more complicated to construct than an
Convex Optimization methods for Computing Channel Capacity
 Convex Otimization methods for Comuting Channel Caacity Abhishek Sinha Laboratory for Information and Decision Systems (LIDS), MIT sinhaa@mit.edu May 15, 2014 We consider a classical comutational roblem
Convex Otimization methods for Comuting Channel Caacity Abhishek Sinha Laboratory for Information and Decision Systems (LIDS), MIT sinhaa@mit.edu May 15, 2014 We consider a classical comutational roblem
A randomized sorting algorithm on the BSP model
 A randomized sorting algorithm on the BSP model Alexandros V. Gerbessiotis a, Constantinos J. Siniolakis b a CS Deartment, New Jersey Institute of Technology, Newark, NJ 07102, USA b The American College
A randomized sorting algorithm on the BSP model Alexandros V. Gerbessiotis a, Constantinos J. Siniolakis b a CS Deartment, New Jersey Institute of Technology, Newark, NJ 07102, USA b The American College
Biased Quantiles. Flip Korn Graham Cormode S. Muthukrishnan
 Biased Quantiles Graham Cormode cormode@bell-labs.com S. Muthukrishnan muthu@cs.rutgers.edu Flip Korn flip@research.att.com Divesh Srivastava divesh@research.att.com Quantiles Quantiles summarize data
Biased Quantiles Graham Cormode cormode@bell-labs.com S. Muthukrishnan muthu@cs.rutgers.edu Flip Korn flip@research.att.com Divesh Srivastava divesh@research.att.com Quantiles Quantiles summarize data
The Knuth-Yao Quadrangle-Inequality Speedup is a Consequence of Total-Monotonicity
 The Knuth-Yao Quadrangle-Ineuality Seedu is a Conseuence of Total-Monotonicity Wolfgang W. Bein Mordecai J. Golin Lawrence L. Larmore Yan Zhang Abstract There exist several general techniues in the literature
The Knuth-Yao Quadrangle-Ineuality Seedu is a Conseuence of Total-Monotonicity Wolfgang W. Bein Mordecai J. Golin Lawrence L. Larmore Yan Zhang Abstract There exist several general techniues in the literature
Amortized Complexity Main Idea
 omp2711 S1 2006 Amortized Complexity Example 1 Amortized Complexity Main Idea Worst case analysis of run time complexity is often too pessimistic. Average case analysis may be difficult because (i) it
omp2711 S1 2006 Amortized Complexity Example 1 Amortized Complexity Main Idea Worst case analysis of run time complexity is often too pessimistic. Average case analysis may be difficult because (i) it
A Deterministic Algorithm for Summarizing Asynchronous Streams over a Sliding Window
 A Deterministic Algorithm for Summarizing Asynchronous Streams over a Sliding Window Costas Busch 1 and Srikanta Tirthapura 2 1 Department of Computer Science Rensselaer Polytechnic Institute, Troy, NY
A Deterministic Algorithm for Summarizing Asynchronous Streams over a Sliding Window Costas Busch 1 and Srikanta Tirthapura 2 1 Department of Computer Science Rensselaer Polytechnic Institute, Troy, NY
EE 457 HW 2 Arithmetic Designs Redekopp Puvvada Name: Due: See Website
 EE 457 HW 2 rithmetic Desins Redeko uvvada Name: Due: ee Website core: lease ost any questions reardin HW roblems on iazza. Refer to your class notes Unit on Fast ddition. In this class we will count the
EE 457 HW 2 rithmetic Desins Redeko uvvada Name: Due: ee Website core: lease ost any questions reardin HW roblems on iazza. Refer to your class notes Unit on Fast ddition. In this class we will count the
, αβ, > 0 is strictly quasi-concave on
 John Riley 8 Setember 9 Econ Diagnostic Test Time allowed: 9 minutes. Attemt all three questions. Note that the last two arts of questions and 3 are marked with an asterisk (). These do not carry many
John Riley 8 Setember 9 Econ Diagnostic Test Time allowed: 9 minutes. Attemt all three questions. Note that the last two arts of questions and 3 are marked with an asterisk (). These do not carry many
CSCB63 Winter Week 11 Bloom Filters. Anna Bretscher. March 30, / 13
 CSCB63 Winter 2019 Week 11 Bloom Filters Anna Bretscher March 30, 2019 1 / 13 Today Bloom Filters Definition Expected Complexity Applications 2 / 13 Bloom Filters (Specification) A bloom filter is a probabilistic
CSCB63 Winter 2019 Week 11 Bloom Filters Anna Bretscher March 30, 2019 1 / 13 Today Bloom Filters Definition Expected Complexity Applications 2 / 13 Bloom Filters (Specification) A bloom filter is a probabilistic
Analysis of Algorithms. Outline 1 Introduction Basic Definitions Ordered Trees. Fibonacci Heaps. Andres Mendez-Vazquez. October 29, Notes.
 Analysis of Algorithms Fibonacci Heaps Andres Mendez-Vazquez October 29, 2015 1 / 119 Outline 1 Introduction Basic Definitions Ordered Trees 2 Binomial Trees Example 3 Fibonacci Heap Operations Fibonacci
Analysis of Algorithms Fibonacci Heaps Andres Mendez-Vazquez October 29, 2015 1 / 119 Outline 1 Introduction Basic Definitions Ordered Trees 2 Binomial Trees Example 3 Fibonacci Heap Operations Fibonacci
arxiv: v2 [math.co] 6 Jul 2017
![arxiv: v2 [math.co] 6 Jul 2017 arxiv: v2 [math.co] 6 Jul 2017](/thumbs/94/118054097.jpg) COUNTING WORDS SATISFYING THE RHYTHMIC ODDITY PROPERTY FRANCK JEDRZEJEWSKI arxiv:1607.07175v2 [math.co] 6 Jul 2017 Abstract. This aer describes an enumeration of all words having a combinatoric roerty
COUNTING WORDS SATISFYING THE RHYTHMIC ODDITY PROPERTY FRANCK JEDRZEJEWSKI arxiv:1607.07175v2 [math.co] 6 Jul 2017 Abstract. This aer describes an enumeration of all words having a combinatoric roerty
4 Scheduling. Outline of the chapter. 4.1 Preliminaries
 4 Scheduling In this section, e consider so-called Scheduling roblems I.e., if there are altogether M machines or resources for each machine, a roduction sequence of all N jobs has to be found as ell as
4 Scheduling In this section, e consider so-called Scheduling roblems I.e., if there are altogether M machines or resources for each machine, a roduction sequence of all N jobs has to be found as ell as
Conical Pendulum: Part 2 A Detailed Theoretical and Computational Analysis of the Period, Tension and Centripetal Forces
 European J of Physics Education Volume 8 Issue 1 1309-70 Dean onical Pendulum: Part A Detailed heoretical and omputational Analysis of the Period, ension and entripetal orces Kevin Dean Physics Department,
European J of Physics Education Volume 8 Issue 1 1309-70 Dean onical Pendulum: Part A Detailed heoretical and omputational Analysis of the Period, ension and entripetal orces Kevin Dean Physics Department,
Computing Connected Components Given a graph G = (V; E) compute the connected components of G. Connected-Components(G) 1 for each vertex v 2 V [G] 2 d
![Computing Connected Components Given a graph G = (V; E) compute the connected components of G. Connected-Components(G) 1 for each vertex v 2 V [G] 2 d Computing Connected Components Given a graph G = (V; E) compute the connected components of G. Connected-Components(G) 1 for each vertex v 2 V [G] 2 d](/thumbs/87/96051759.jpg) Data Structures for Disjoint Sets Maintain a Dynamic collection of disjoint sets. Each set has a unique representative (an arbitrary member of the set). x. Make-Set(x) - Create a new set with one member
Data Structures for Disjoint Sets Maintain a Dynamic collection of disjoint sets. Each set has a unique representative (an arbitrary member of the set). x. Make-Set(x) - Create a new set with one member
CS 6260 Some number theory. Groups
 Let Z = {..., 2, 1, 0, 1, 2,...} denote the set of integers. Let Z+ = {1, 2,...} denote the set of ositive integers and = {0, 1, 2,...} the set of non-negative integers. If a, are integers with > 0 then
Let Z = {..., 2, 1, 0, 1, 2,...} denote the set of integers. Let Z+ = {1, 2,...} denote the set of ositive integers and = {0, 1, 2,...} the set of non-negative integers. If a, are integers with > 0 then
Sorting. CMPS 2200 Fall Carola Wenk Slides courtesy of Charles Leiserson with changes and additions by Carola Wenk
 CMPS 2200 Fall 2017 Sorting Carola Wenk Slides courtesy of Charles Leiserson with changes and additions by Carola Wenk 11/17/17 CMPS 2200 Intro. to Algorithms 1 How fast can we sort? All the sorting algorithms
CMPS 2200 Fall 2017 Sorting Carola Wenk Slides courtesy of Charles Leiserson with changes and additions by Carola Wenk 11/17/17 CMPS 2200 Intro. to Algorithms 1 How fast can we sort? All the sorting algorithms
Outline for Today. Static Optimality. Splay Trees. Properties of Splay Trees. Dynamic Optimality (ITA) Balanced BSTs aren't necessarily optimal!
 Splay Trees Outline for Today Static Optimality Balanced BSTs aren't necessarily optimal! Splay Trees A self-adjusting binary search tree. Properties of Splay Trees Why is splaying worthwhile? Dynamic
Splay Trees Outline for Today Static Optimality Balanced BSTs aren't necessarily optimal! Splay Trees A self-adjusting binary search tree. Properties of Splay Trees Why is splaying worthwhile? Dynamic
CS 310 Advanced Data Structures and Algorithms
 CS 310 Advanced Data Structures and Algorithms Runtime Analysis May 31, 2017 Tong Wang UMass Boston CS 310 May 31, 2017 1 / 37 Topics Weiss chapter 5 What is algorithm analysis Big O, big, big notations
CS 310 Advanced Data Structures and Algorithms Runtime Analysis May 31, 2017 Tong Wang UMass Boston CS 310 May 31, 2017 1 / 37 Topics Weiss chapter 5 What is algorithm analysis Big O, big, big notations
Model checking, verification of CTL. One must verify or expel... doubts, and convert them into the certainty of YES [Thomas Carlyle]
![Model checking, verification of CTL. One must verify or expel... doubts, and convert them into the certainty of YES [Thomas Carlyle] Model checking, verification of CTL. One must verify or expel... doubts, and convert them into the certainty of YES [Thomas Carlyle]](/thumbs/81/83711762.jpg) Chater 5 Model checking, verification of CTL One must verify or exel... doubts, and convert them into the certainty of YES or NO. [Thomas Carlyle] 5. The verification setting Page 66 We introduce linear
Chater 5 Model checking, verification of CTL One must verify or exel... doubts, and convert them into the certainty of YES or NO. [Thomas Carlyle] 5. The verification setting Page 66 We introduce linear
Part II. Foundations. Ernst Mayr, Harald Räcke 16
 Part II Foundations Ernst Mayr, Harald Räcke 16 Vocabularies a b a times b a multiplied by b a into b a b a divided by b a by b a over b a b (a: numerator (Zähler), b: denominator (Nenner)) a raised to
Part II Foundations Ernst Mayr, Harald Räcke 16 Vocabularies a b a times b a multiplied by b a into b a b a divided by b a by b a over b a b (a: numerator (Zähler), b: denominator (Nenner)) a raised to
Lecture 1 : Data Compression and Entropy
 CPS290: Algorithmic Foundations of Data Science January 8, 207 Lecture : Data Compression and Entropy Lecturer: Kamesh Munagala Scribe: Kamesh Munagala In this lecture, we will study a simple model for
CPS290: Algorithmic Foundations of Data Science January 8, 207 Lecture : Data Compression and Entropy Lecturer: Kamesh Munagala Scribe: Kamesh Munagala In this lecture, we will study a simple model for
Fibonacci Heaps These lecture slides are adapted from CLRS, Chapter 20.
 Fibonacci Heaps These lecture slides are adapted from CLRS, Chapter 20. Princeton University COS 4 Theory of Algorithms Spring 2002 Kevin Wayne Priority Queues Operation mae-heap insert find- delete- union
Fibonacci Heaps These lecture slides are adapted from CLRS, Chapter 20. Princeton University COS 4 Theory of Algorithms Spring 2002 Kevin Wayne Priority Queues Operation mae-heap insert find- delete- union
Search Trees. EECS 2011 Prof. J. Elder Last Updated: 24 March 2015
 Search Trees < 6 2 > 1 4 = 8 9-1 - Outline Ø Binary Search Trees Ø AVL Trees Ø Splay Trees - 2 - Learning Outcomes Ø From this lecture, you should be able to: q Define the properties of a binary search
Search Trees < 6 2 > 1 4 = 8 9-1 - Outline Ø Binary Search Trees Ø AVL Trees Ø Splay Trees - 2 - Learning Outcomes Ø From this lecture, you should be able to: q Define the properties of a binary search
Introduction to Randomized Algorithms III
 Introduction to Randomized Algorithms III Joaquim Madeira Version 0.1 November 2017 U. Aveiro, November 2017 1 Overview Probabilistic counters Counting with probability 1 / 2 Counting with probability
Introduction to Randomized Algorithms III Joaquim Madeira Version 0.1 November 2017 U. Aveiro, November 2017 1 Overview Probabilistic counters Counting with probability 1 / 2 Counting with probability
Nearly Tight Linear Programming Bounds for Demand Matching in Bipartite Graphs
 Nearly Tight Linear Programming Bounds for Demand Matching in Biartite Grahs Mohit Singh Hehui Wu Setember 23, 212 Abstract We consider the demand matching roblem which is a generalization of the maximum
Nearly Tight Linear Programming Bounds for Demand Matching in Biartite Grahs Mohit Singh Hehui Wu Setember 23, 212 Abstract We consider the demand matching roblem which is a generalization of the maximum
A Social Welfare Optimal Sequential Allocation Procedure
 A Social Welfare Otimal Sequential Allocation Procedure Thomas Kalinowsi Universität Rostoc, Germany Nina Narodytsa and Toby Walsh NICTA and UNSW, Australia May 2, 201 Abstract We consider a simle sequential
A Social Welfare Otimal Sequential Allocation Procedure Thomas Kalinowsi Universität Rostoc, Germany Nina Narodytsa and Toby Walsh NICTA and UNSW, Australia May 2, 201 Abstract We consider a simle sequential
Graphical Models (Lecture 1 - Introduction)
 Grahical Models Lecture - Introduction Tibério Caetano tiberiocaetano.com Statistical Machine Learning Grou NICTA Canberra LLSS Canberra 009 Tibério Caetano: Grahical Models Lecture - Introduction / 7
Grahical Models Lecture - Introduction Tibério Caetano tiberiocaetano.com Statistical Machine Learning Grou NICTA Canberra LLSS Canberra 009 Tibério Caetano: Grahical Models Lecture - Introduction / 7
Oblivious Transfer based on Key Exchange
 Oblivious Transfer based on Key Echane bhishek Parakh bstract: Key-echane rotocols have been overlooked as a ossible means for imlementin oblivious transfer (OT) In this aer we resent a rotocol for mutual
Oblivious Transfer based on Key Echane bhishek Parakh bstract: Key-echane rotocols have been overlooked as a ossible means for imlementin oblivious transfer (OT) In this aer we resent a rotocol for mutual
Static Dictionaries on AC 0 RAMs: Query time ( log n= log log n) is necessary and sufficient
 q Static Dictionaries on AC 0 RAMs: Query time ( = log ) is necessary and sufficient Arne Andersson Lund University arne@dna.lth.se Peter Bro Miltersen y University of Toronto bmilter@cs.toronto.edu Søren
q Static Dictionaries on AC 0 RAMs: Query time ( = log ) is necessary and sufficient Arne Andersson Lund University arne@dna.lth.se Peter Bro Miltersen y University of Toronto bmilter@cs.toronto.edu Søren
Chapter #7: Sequential Logic Case Studies Contemporary Logic Design
 hapter #7: Sequential Logic ase Studies ontemporary Logic Design No. 7- Storage egister Group of storage elements read/written as a unit 4-bit register constructed from 4 D FFs Shared clock and clear lines
hapter #7: Sequential Logic ase Studies ontemporary Logic Design No. 7- Storage egister Group of storage elements read/written as a unit 4-bit register constructed from 4 D FFs Shared clock and clear lines
15-451/651: Design & Analysis of Algorithms October 23, 2018 Lecture #17: Prediction from Expert Advice last changed: October 25, 2018
 5-45/65: Design & Analysis of Algorithms October 23, 208 Lecture #7: Prediction from Exert Advice last changed: October 25, 208 Prediction with Exert Advice Today we ll study the roblem of making redictions
5-45/65: Design & Analysis of Algorithms October 23, 208 Lecture #7: Prediction from Exert Advice last changed: October 25, 208 Prediction with Exert Advice Today we ll study the roblem of making redictions
Parallelism and Locality in Priority Queues. A. Ranade S. Cheng E. Deprit J. Jones S. Shih. University of California. Berkeley, CA 94720
 Parallelism and Locality in Priority Queues A. Ranade S. Cheng E. Derit J. Jones S. Shih Comuter Science Division University of California Berkeley, CA 94720 Abstract We exlore two ways of incororating
Parallelism and Locality in Priority Queues A. Ranade S. Cheng E. Derit J. Jones S. Shih Comuter Science Division University of California Berkeley, CA 94720 Abstract We exlore two ways of incororating
