1 Review and Overview
|
|
|
- Aron Wilkerson
- 5 years ago
- Views:
Transcription
1 DRAFT a final version will be posted shortly CS229T/STATS231: Statistical Learning Theory Lecturer: Tengyu Ma Lecture # 16 Scribe: Chris Cundy, Ananya Kumar November 14, Review and Overview Last time, we discussed how the Follow the Leader algorithm does not perform very well as an online convex optimization algorithm, and how we could introduce the Follow the Regularized Leader algorithm to fix some of the shortcomings of FTL. In this lecture we will show the rates of FTRL on the concrete examples we discussed earlier to build some intuition. To use FTRL on the expert problem we will introduce the entropic regularizer, a useful regularizer when we have to make actions that are probability distributions. Recall that on each timestep FTRL chooses ω t = argmin f i (ω) + 1 ω Ω η l(ω), (1) }{{} s.c where ω is in the set of actions the algorithm can take, and l is strongly convex with respect to some norm. (Good to expand what each term is here) Now last time we proved that the regret at time t, R t is bounded as follows: R t D T η + η f t (ω t ) 2, (2) where is the dual norm of the norm that l is strongly convex with respect to and the parameter D is given by the range of values that the regularizer ϕ can output: D = max x Ω ϕ(x) min ϕ(x). (3) x Ω So if we can show that the dual norm of the gradient is bounded, i.e. f t (ω) G for all t and ω Ω, we can find the value of η which gives the tightest bound. This is η = D/T G 2 and substituting in we see R t D ( η + ηt G2 O G ) T D. (4) Today we will show concretely the values of D, G, etc on the problems we motivated our discussion of online learning with, and investigate which regularizers we might want to use. 2 Online Regression We are given data points {x R d : x 2 1} and a label y t [ 1, 1]. We can output a weight vector in Ω = {ω : ω 2 1}. This is a bit more concrete than when we introduced the problem last time, as we didn t have the norm-constraints on the variables.
2 We receive (x t, y t ) and have f t (ω) = 1 2 ( ω, x t y t ) 2. We choose the regularizer as ϕ(ω) = 1 2 ω 2 2 which is 1-strongly convex with respect to the l 2-norm since applying the definition of strongly convex, 1 2 ω ω What is G? We will show that G = 2 in this case, using the fact that the dual norm of the l 2 -norm is the l 2 -norm: f t (ω t ) 2 = x( ω t, x t y t ) 2 = ω t, x t y t x }{{} t 2 2 Now D is max ϕ(ω) min ϕ(ω). So D 1/2 0 = 1/2. This gives us a bound on the regret: ( ) R T O T (6) Recall the batch to online reduction : we can convert a batch algorithm to an online one by feeding each data point sequentially to the online algorithm. This involves running the online system for T timesteps, getting average loss R T /T. For our regression case, this gives us an O ( n 1/2) rate for the loss, which is a reasonable rate. This is typically the best rate we can hope for without some special knowledge on the problem (such as realizability, etc). The fact that we get a reasonable rate should be an indication that we haven t made a big mistake along the way. 3 Expert Problem Recall the expert problem, where we have N experts. At each timestep we output a probability distribution, describing a stochastic policy of the form choose expert 1 with probability p 1, expert 2 with probability p 2, etc. We represent that choice of stochastic policy with a vector p which lies in the N-simplex (N), i.e. we have an action space { Ω = (N) = p : } p = 1, 0 p 1. (7) We receive a loss f t (p) = l t, p where l t is the loss vector l t [0, 1] N, i.e. l t quantifies how well each of the experts performed at step t. We will apply FTRL with two choices of the regularizer: the simple choice of the l 2 -norm, and the more problem-specific entropic regularizer. We will see that the second choice of the regularizer gives a better bound on the regret. 3.1 l 2 -regularized If we use the l 2 -norm with a regularizer ϕ(p) = 1 2 p 2 2 then as before this is strongly convex wrt the l 2 -norm. Computing D, we see D = sup ϕ(p) inf ϕ(p) 2. sup p (N) 1 (5) 2 p , (8) as the sup over a simplex has to be at the vertices, and p 2 p 1. Turning to G, we see that f t (p t ) 2 = l t 2 N (as p R d, p i 1). (9) 2
3 Plugging into equation 4, we achieve a rate of O( NT ). As discussed above, this is likely a good rate with respect to T. However, it is not a great rate in N. It isn t immediately clear why N is a bad rate in N, but we will show soon that we are able to get log N dependence on N if we use a different regularizer. In some sense the worse rate that we achieve is because we use a regularizer that isn t very compatible with the actions. We can hope to do better by choosing a regularizer that fits with the constraint on p to lie in the N-simplex. 3.2 Entropic Regularization Since p is a probability distribution, we might aim for a regularizer with an informationtheoretic basis. We want to penalize p that are too certain, concentrating probability around a small number of experts. A natural choice is to penalize p if the entropy of p is too low. ϕ(p) = H(p) = p(i) log p(i). (10) Now we can show that ϕ( ) is 1-strongly convex with respect to the l 1 -norm: we want to show that First note that ϕ(p) ϕ(q) ϕ(q), p q p q 2 1. (11) ϕ(q) = So we can re-arrange equation 11 to get log q i + 1. log q N + 1. (12) p i log p i q i log q i. (log q i + 1) (p i q i ) p q 2 1 (13) We can make further simplifications, as the q i log q i cancels on both sides, and we know that 1 (pi q i ) = 0 since p, q are probability distributions. Finally we see that convexity of the entropic regularizer is equivalent to the following statement: which is true from the Pinsker inequality. All that remains is to compute D and G: p i log p i 1 q 2 p q 2 1, (14) i }{{}}{{} TV(p,q) KL(p q) 3
4 D = sup ϕ(p) }{{} 0 as ϕ 0 inf ϕ(p) log N, (15) because H(p) log N. Then for G we need to bound the gradient under the dual norm: f t (ω t ) 2 = l t 1, (so G = 1). (16) Here we see that using the l -norm was useful as it allowed us to remove any N from G. Plugging in, we see that R t O(G T D) = O( T log N). (17) It s interesting that we can get regret that s logarithmic in N, but why is this algorithm able to work, while the unregularized follow the leader algorithm doesn t work? In the following section we will gain some intuition for the behaviour of FTRL by calculating the updates in the expert problem. 4 Computing the Updates for FTRL Let s take a look at what the FTRL algorithm with entropic regularization is actually doing. We begin by deriving a closed form for p t, the probability distribution over experts that we select at the t th step. p t = argmin = argmin = argmin f i (p) + 1 η ϕ(p) l i, p + 1 η ϕ(p) l i, p + 1 η ϕ(p) = argmin η = argmax η l i, p H(p) l i, p + H(p) In homework 0 we dervied the closed form to this using Lagrange multipliers. That is, p t = softmax( η l i). An alternative way we can do this is using Gibbs variational principle. Gibbs variational principle is as follows, where µ and γ are probability distributions: [ ] log E x µ e g(x) = sup γ E [g(x)] KL(γ µ) x γ 4
5 And the supremum is achieved when γ(x) µ(x)e f(x). To apply this to our problem, select µ to be the uniform distribution over [N] and γ = p. Define g(j) = η( l i) j. Then, we have, [ ] η l i, p = E η( l i ) j. j p Additionally, we have, KL(γ µ) = = p i log p i q i p i log p i 1/N = log N + p i log p i = H(p) + log N. Finally, we can compute the desired result, where µ and g are defined above: argmax [ ] η l i, p + H(p) ( ) = argsup E [g(x)] KL(p µ) + log N p x p So by Gibbs variational result, the argsup is achieved when p j exp[ η( l i) j ], which is precisely the softmax. This can be viewed as a multiplicative weights update. We begin with a uniform weight over all the experts. Whenever an expert makes a mistake, and incures loss 1, we divide the weight of that expert by a factor of exp(η) and re-normalize p. This is a very common procedure that is used in many algorithms in machine learning (e.g. boosting) and other fields. 5 The Convex to Linear Reduction We will now tackle the more general problem of online convex optimization. Let Ω be a set of parameters. Let G Ω be a set of linear functions on Ω. By linear, we mean that for all g G Ω there exists a s.t. g(w) = a, w for all w Ω. Suppose we have an online learning algorithm A that achieves regret upper bounded by R(T ) on G Ω. Now, suppose we have a set F of differentiable convex functions on Ω such that for all f F and all w Ω, f(w) G Ω. We will show that we can achieve regret upper bounded by R(T ) on F. Our high level approach will be to reduce this online convex setting to the online linear setting, by taking linear approximations. We will then upper bound the regret by the regret in the online linear setting. To refresh our memories about convex functions, we begin with a simple result on convex functions that we will use. From the first order characterization of convex functions, With some manipulation, this gives us, f(y) f(x) + f(x), (y x) f(x) f(y) f(x), (x y) 5
6 In other words, we can upper bound the difference between function values using the gradient. This will allow us to bound the regret. We now give the online convex optimization algorithm that has regret R(T ). On each iteration t [T ]: 1. Ask online linear algorithm A to pick action w t. 2. Obtain a loss function f t F. 3. As usual in the online setting, we incur loss f t (w t ). 4. Construct a linear approximation to the loss g t (w) = f t (w t ), w. 5. Give g t as the loss function to A. We can now prove that the regret of this algorithm is bounded by R(T ), beginning from the definition of regret. max w T f t (w t ) f t (w) max w = T f t (w t ), (w t w) T g t (w t ) g t (w) R(T ) Where the first step used the warm up result above on convex functions. If our regularization function ϕ(w) = w 2, then this algorithm becomes online gradient descent. This is because, w t = argmin w Ω f i (w i ), w + 1 η w 2 We can show that the solution to this is: w t = ( ) η f i (w i ) Ω where Π Ω projects the input to Ω (the projection is in l 2 norm). This can be viewed as doing gradient descent, starting from w = 0, and then finally projecting the result onto Ω. Since we project after applying all the updates, this is known as lazy projection. This is in contrast to what we do in standard projected gradient descent, for example, where we project the parameters back into the constraint set at each step. That is known as eager projection. 6
Lecture 16: FTRL and Online Mirror Descent
 Lecture 6: FTRL and Online Mirror Descent Akshay Krishnamurthy akshay@cs.umass.edu November, 07 Recap Last time we saw two online learning algorithms. First we saw the Weighted Majority algorithm, which
Lecture 6: FTRL and Online Mirror Descent Akshay Krishnamurthy akshay@cs.umass.edu November, 07 Recap Last time we saw two online learning algorithms. First we saw the Weighted Majority algorithm, which
Exponentiated Gradient Descent
 CSE599s, Spring 01, Online Learning Lecture 10-04/6/01 Lecturer: Ofer Dekel Exponentiated Gradient Descent Scribe: Albert Yu 1 Introduction In this lecture we review norms, dual norms, strong convexity,
CSE599s, Spring 01, Online Learning Lecture 10-04/6/01 Lecturer: Ofer Dekel Exponentiated Gradient Descent Scribe: Albert Yu 1 Introduction In this lecture we review norms, dual norms, strong convexity,
Online Learning and Online Convex Optimization
 Online Learning and Online Convex Optimization Nicolò Cesa-Bianchi Università degli Studi di Milano N. Cesa-Bianchi (UNIMI) Online Learning 1 / 49 Summary 1 My beautiful regret 2 A supposedly fun game
Online Learning and Online Convex Optimization Nicolò Cesa-Bianchi Università degli Studi di Milano N. Cesa-Bianchi (UNIMI) Online Learning 1 / 49 Summary 1 My beautiful regret 2 A supposedly fun game
Classification: Logistic Regression from Data
 Classification: Logistic Regression from Data Machine Learning: Jordan Boyd-Graber University of Colorado Boulder LECTURE 3 Slides adapted from Emily Fox Machine Learning: Jordan Boyd-Graber Boulder Classification:
Classification: Logistic Regression from Data Machine Learning: Jordan Boyd-Graber University of Colorado Boulder LECTURE 3 Slides adapted from Emily Fox Machine Learning: Jordan Boyd-Graber Boulder Classification:
The FTRL Algorithm with Strongly Convex Regularizers
 CSE599s, Spring 202, Online Learning Lecture 8-04/9/202 The FTRL Algorithm with Strongly Convex Regularizers Lecturer: Brandan McMahan Scribe: Tamara Bonaci Introduction In the last lecture, we talked
CSE599s, Spring 202, Online Learning Lecture 8-04/9/202 The FTRL Algorithm with Strongly Convex Regularizers Lecturer: Brandan McMahan Scribe: Tamara Bonaci Introduction In the last lecture, we talked
Online Learning with Experts & Multiplicative Weights Algorithms
 Online Learning with Experts & Multiplicative Weights Algorithms CS 159 lecture #2 Stephan Zheng April 1, 2016 Caltech Table of contents 1. Online Learning with Experts With a perfect expert Without perfect
Online Learning with Experts & Multiplicative Weights Algorithms CS 159 lecture #2 Stephan Zheng April 1, 2016 Caltech Table of contents 1. Online Learning with Experts With a perfect expert Without perfect
15-859E: Advanced Algorithms CMU, Spring 2015 Lecture #16: Gradient Descent February 18, 2015
 5-859E: Advanced Algorithms CMU, Spring 205 Lecture #6: Gradient Descent February 8, 205 Lecturer: Anupam Gupta Scribe: Guru Guruganesh In this lecture, we will study the gradient descent algorithm and
5-859E: Advanced Algorithms CMU, Spring 205 Lecture #6: Gradient Descent February 8, 205 Lecturer: Anupam Gupta Scribe: Guru Guruganesh In this lecture, we will study the gradient descent algorithm and
Bregman Divergence and Mirror Descent
 Bregman Divergence and Mirror Descent Bregman Divergence Motivation Generalize squared Euclidean distance to a class of distances that all share similar properties Lots of applications in machine learning,
Bregman Divergence and Mirror Descent Bregman Divergence Motivation Generalize squared Euclidean distance to a class of distances that all share similar properties Lots of applications in machine learning,
Online Convex Optimization
 Advanced Course in Machine Learning Spring 2010 Online Convex Optimization Handouts are jointly prepared by Shie Mannor and Shai Shalev-Shwartz A convex repeated game is a two players game that is performed
Advanced Course in Machine Learning Spring 2010 Online Convex Optimization Handouts are jointly prepared by Shie Mannor and Shai Shalev-Shwartz A convex repeated game is a two players game that is performed
Lecture 23: Online convex optimization Online convex optimization: generalization of several algorithms
 EECS 598-005: heoretical Foundations of Machine Learning Fall 2015 Lecture 23: Online convex optimization Lecturer: Jacob Abernethy Scribes: Vikas Dhiman Disclaimer: hese notes have not been subjected
EECS 598-005: heoretical Foundations of Machine Learning Fall 2015 Lecture 23: Online convex optimization Lecturer: Jacob Abernethy Scribes: Vikas Dhiman Disclaimer: hese notes have not been subjected
Online Convex Optimization. Gautam Goel, Milan Cvitkovic, and Ellen Feldman CS 159 4/5/2016
 Online Convex Optimization Gautam Goel, Milan Cvitkovic, and Ellen Feldman CS 159 4/5/2016 The General Setting The General Setting (Cover) Given only the above, learning isn't always possible Some Natural
Online Convex Optimization Gautam Goel, Milan Cvitkovic, and Ellen Feldman CS 159 4/5/2016 The General Setting The General Setting (Cover) Given only the above, learning isn't always possible Some Natural
Constrained Optimization and Lagrangian Duality
 CIS 520: Machine Learning Oct 02, 2017 Constrained Optimization and Lagrangian Duality Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may
CIS 520: Machine Learning Oct 02, 2017 Constrained Optimization and Lagrangian Duality Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may
ICS-E4030 Kernel Methods in Machine Learning
 ICS-E4030 Kernel Methods in Machine Learning Lecture 3: Convex optimization and duality Juho Rousu 28. September, 2016 Juho Rousu 28. September, 2016 1 / 38 Convex optimization Convex optimisation This
ICS-E4030 Kernel Methods in Machine Learning Lecture 3: Convex optimization and duality Juho Rousu 28. September, 2016 Juho Rousu 28. September, 2016 1 / 38 Convex optimization Convex optimisation This
18.657: Mathematics of Machine Learning
 8.657: Mathematics of Machine Learning Lecturer: Philippe Rigollet Lecture 3 Scribe: Mina Karzand Oct., 05 Previously, we analyzed the convergence of the projected gradient descent algorithm. We proved
8.657: Mathematics of Machine Learning Lecturer: Philippe Rigollet Lecture 3 Scribe: Mina Karzand Oct., 05 Previously, we analyzed the convergence of the projected gradient descent algorithm. We proved
Advanced computational methods X Selected Topics: SGD
 Advanced computational methods X071521-Selected Topics: SGD. In this lecture, we look at the stochastic gradient descent (SGD) method 1 An illustrating example The MNIST is a simple dataset of variety
Advanced computational methods X071521-Selected Topics: SGD. In this lecture, we look at the stochastic gradient descent (SGD) method 1 An illustrating example The MNIST is a simple dataset of variety
Introduction to Logistic Regression and Support Vector Machine
 Introduction to Logistic Regression and Support Vector Machine guest lecturer: Ming-Wei Chang CS 446 Fall, 2009 () / 25 Fall, 2009 / 25 Before we start () 2 / 25 Fall, 2009 2 / 25 Before we start Feel
Introduction to Logistic Regression and Support Vector Machine guest lecturer: Ming-Wei Chang CS 446 Fall, 2009 () / 25 Fall, 2009 / 25 Before we start () 2 / 25 Fall, 2009 2 / 25 Before we start Feel
Lecture 14 : Online Learning, Stochastic Gradient Descent, Perceptron
 CS446: Machine Learning, Fall 2017 Lecture 14 : Online Learning, Stochastic Gradient Descent, Perceptron Lecturer: Sanmi Koyejo Scribe: Ke Wang, Oct. 24th, 2017 Agenda Recap: SVM and Hinge loss, Representer
CS446: Machine Learning, Fall 2017 Lecture 14 : Online Learning, Stochastic Gradient Descent, Perceptron Lecturer: Sanmi Koyejo Scribe: Ke Wang, Oct. 24th, 2017 Agenda Recap: SVM and Hinge loss, Representer
Notes on AdaGrad. Joseph Perla 2014
 Notes on AdaGrad Joseph Perla 2014 1 Introduction Stochastic Gradient Descent (SGD) is a common online learning algorithm for optimizing convex (and often non-convex) functions in machine learning today.
Notes on AdaGrad Joseph Perla 2014 1 Introduction Stochastic Gradient Descent (SGD) is a common online learning algorithm for optimizing convex (and often non-convex) functions in machine learning today.
CPSC 540: Machine Learning
 CPSC 540: Machine Learning Proximal-Gradient Mark Schmidt University of British Columbia Winter 2018 Admin Auditting/registration forms: Pick up after class today. Assignment 1: 2 late days to hand in
CPSC 540: Machine Learning Proximal-Gradient Mark Schmidt University of British Columbia Winter 2018 Admin Auditting/registration forms: Pick up after class today. Assignment 1: 2 late days to hand in
Conditional Gradient (Frank-Wolfe) Method
 Conditional Gradient (Frank-Wolfe) Method Lecturer: Aarti Singh Co-instructor: Pradeep Ravikumar Convex Optimization 10-725/36-725 1 Outline Today: Conditional gradient method Convergence analysis Properties
Conditional Gradient (Frank-Wolfe) Method Lecturer: Aarti Singh Co-instructor: Pradeep Ravikumar Convex Optimization 10-725/36-725 1 Outline Today: Conditional gradient method Convergence analysis Properties
Lecture 21: Minimax Theory
 Lecture : Minimax Theory Akshay Krishnamurthy akshay@cs.umass.edu November 8, 07 Recap In the first part of the course, we spent the majority of our time studying risk minimization. We found many ways
Lecture : Minimax Theory Akshay Krishnamurthy akshay@cs.umass.edu November 8, 07 Recap In the first part of the course, we spent the majority of our time studying risk minimization. We found many ways
0.1 Motivating example: weighted majority algorithm
 princeton univ. F 16 cos 521: Advanced Algorithm Design Lecture 8: Decision-making under total uncertainty: the multiplicative weight algorithm Lecturer: Sanjeev Arora Scribe: Sanjeev Arora (Today s notes
princeton univ. F 16 cos 521: Advanced Algorithm Design Lecture 8: Decision-making under total uncertainty: the multiplicative weight algorithm Lecturer: Sanjeev Arora Scribe: Sanjeev Arora (Today s notes
Classification: Logistic Regression from Data
 Classification: Logistic Regression from Data Machine Learning: Alvin Grissom II University of Colorado Boulder Slides adapted from Emily Fox Machine Learning: Alvin Grissom II Boulder Classification:
Classification: Logistic Regression from Data Machine Learning: Alvin Grissom II University of Colorado Boulder Slides adapted from Emily Fox Machine Learning: Alvin Grissom II Boulder Classification:
CS229T/STATS231: Statistical Learning Theory. Lecturer: Tengyu Ma Lecture 11 Scribe: Jongho Kim, Jamie Kang October 29th, 2018
 CS229T/STATS231: Statistical Learning Theory Lecturer: Tengyu Ma Lecture 11 Scribe: Jongho Kim, Jamie Kang October 29th, 2018 1 Overview This lecture mainly covers Recall the statistical theory of GANs
CS229T/STATS231: Statistical Learning Theory Lecturer: Tengyu Ma Lecture 11 Scribe: Jongho Kim, Jamie Kang October 29th, 2018 1 Overview This lecture mainly covers Recall the statistical theory of GANs
1. Implement AdaBoost with boosting stumps and apply the algorithm to the. Solution:
 Mehryar Mohri Foundations of Machine Learning Courant Institute of Mathematical Sciences Homework assignment 3 October 31, 2016 Due: A. November 11, 2016; B. November 22, 2016 A. Boosting 1. Implement
Mehryar Mohri Foundations of Machine Learning Courant Institute of Mathematical Sciences Homework assignment 3 October 31, 2016 Due: A. November 11, 2016; B. November 22, 2016 A. Boosting 1. Implement
CS-E4830 Kernel Methods in Machine Learning
 CS-E4830 Kernel Methods in Machine Learning Lecture 3: Convex optimization and duality Juho Rousu 27. September, 2017 Juho Rousu 27. September, 2017 1 / 45 Convex optimization Convex optimisation This
CS-E4830 Kernel Methods in Machine Learning Lecture 3: Convex optimization and duality Juho Rousu 27. September, 2017 Juho Rousu 27. September, 2017 1 / 45 Convex optimization Convex optimisation This
Machine Learning: Chenhao Tan University of Colorado Boulder LECTURE 5
 Machine Learning: Chenhao Tan University of Colorado Boulder LECTURE 5 Slides adapted from Jordan Boyd-Graber, Tom Mitchell, Ziv Bar-Joseph Machine Learning: Chenhao Tan Boulder 1 of 27 Quiz question For
Machine Learning: Chenhao Tan University of Colorado Boulder LECTURE 5 Slides adapted from Jordan Boyd-Graber, Tom Mitchell, Ziv Bar-Joseph Machine Learning: Chenhao Tan Boulder 1 of 27 Quiz question For
Machine Learning for NLP
 Machine Learning for NLP Linear Models Joakim Nivre Uppsala University Department of Linguistics and Philology Slides adapted from Ryan McDonald, Google Research Machine Learning for NLP 1(26) Outline
Machine Learning for NLP Linear Models Joakim Nivre Uppsala University Department of Linguistics and Philology Slides adapted from Ryan McDonald, Google Research Machine Learning for NLP 1(26) Outline
Introduction to Machine Learning
 Introduction to Machine Learning Machine Learning: Jordan Boyd-Graber University of Maryland LOGISTIC REGRESSION FROM TEXT Slides adapted from Emily Fox Machine Learning: Jordan Boyd-Graber UMD Introduction
Introduction to Machine Learning Machine Learning: Jordan Boyd-Graber University of Maryland LOGISTIC REGRESSION FROM TEXT Slides adapted from Emily Fox Machine Learning: Jordan Boyd-Graber UMD Introduction
Online Kernel PCA with Entropic Matrix Updates
 Online Kernel PCA with Entropic Matrix Updates Dima Kuzmin Manfred K. Warmuth University of California - Santa Cruz ICML 2007, Corvallis, Oregon April 23, 2008 D. Kuzmin, M. Warmuth (UCSC) Online Kernel
Online Kernel PCA with Entropic Matrix Updates Dima Kuzmin Manfred K. Warmuth University of California - Santa Cruz ICML 2007, Corvallis, Oregon April 23, 2008 D. Kuzmin, M. Warmuth (UCSC) Online Kernel
Learning Methods for Online Prediction Problems. Peter Bartlett Statistics and EECS UC Berkeley
 Learning Methods for Online Prediction Problems Peter Bartlett Statistics and EECS UC Berkeley Course Synopsis A finite comparison class: A = {1,..., m}. 1. Prediction with expert advice. 2. With perfect
Learning Methods for Online Prediction Problems Peter Bartlett Statistics and EECS UC Berkeley Course Synopsis A finite comparison class: A = {1,..., m}. 1. Prediction with expert advice. 2. With perfect
Ad Placement Strategies
 Case Study : Estimating Click Probabilities Intro Logistic Regression Gradient Descent + SGD AdaGrad Machine Learning for Big Data CSE547/STAT548, University of Washington Emily Fox January 7 th, 04 Ad
Case Study : Estimating Click Probabilities Intro Logistic Regression Gradient Descent + SGD AdaGrad Machine Learning for Big Data CSE547/STAT548, University of Washington Emily Fox January 7 th, 04 Ad
Logistic Regression. COMP 527 Danushka Bollegala
 Logistic Regression COMP 527 Danushka Bollegala Binary Classification Given an instance x we must classify it to either positive (1) or negative (0) class We can use {1,-1} instead of {1,0} but we will
Logistic Regression COMP 527 Danushka Bollegala Binary Classification Given an instance x we must classify it to either positive (1) or negative (0) class We can use {1,-1} instead of {1,0} but we will
CS261: A Second Course in Algorithms Lecture #11: Online Learning and the Multiplicative Weights Algorithm
 CS61: A Second Course in Algorithms Lecture #11: Online Learning and the Multiplicative Weights Algorithm Tim Roughgarden February 9, 016 1 Online Algorithms This lecture begins the third module of the
CS61: A Second Course in Algorithms Lecture #11: Online Learning and the Multiplicative Weights Algorithm Tim Roughgarden February 9, 016 1 Online Algorithms This lecture begins the third module of the
Frank-Wolfe Method. Ryan Tibshirani Convex Optimization
 Frank-Wolfe Method Ryan Tibshirani Convex Optimization 10-725 Last time: ADMM For the problem min x,z f(x) + g(z) subject to Ax + Bz = c we form augmented Lagrangian (scaled form): L ρ (x, z, w) = f(x)
Frank-Wolfe Method Ryan Tibshirani Convex Optimization 10-725 Last time: ADMM For the problem min x,z f(x) + g(z) subject to Ax + Bz = c we form augmented Lagrangian (scaled form): L ρ (x, z, w) = f(x)
Logarithmic Regret Algorithms for Strongly Convex Repeated Games
 Logarithmic Regret Algorithms for Strongly Convex Repeated Games Shai Shalev-Shwartz 1 and Yoram Singer 1,2 1 School of Computer Sci & Eng, The Hebrew University, Jerusalem 91904, Israel 2 Google Inc 1600
Logarithmic Regret Algorithms for Strongly Convex Repeated Games Shai Shalev-Shwartz 1 and Yoram Singer 1,2 1 School of Computer Sci & Eng, The Hebrew University, Jerusalem 91904, Israel 2 Google Inc 1600
Least Mean Squares Regression
 Least Mean Squares Regression Machine Learning Spring 2018 The slides are mainly from Vivek Srikumar 1 Lecture Overview Linear classifiers What functions do linear classifiers express? Least Squares Method
Least Mean Squares Regression Machine Learning Spring 2018 The slides are mainly from Vivek Srikumar 1 Lecture Overview Linear classifiers What functions do linear classifiers express? Least Squares Method
Linear Models for Regression
 Linear Models for Regression CSE 4309 Machine Learning Vassilis Athitsos Computer Science and Engineering Department University of Texas at Arlington 1 The Regression Problem Training data: A set of input-output
Linear Models for Regression CSE 4309 Machine Learning Vassilis Athitsos Computer Science and Engineering Department University of Texas at Arlington 1 The Regression Problem Training data: A set of input-output
Warm up. Regrade requests submitted directly in Gradescope, do not instructors.
 Warm up Regrade requests submitted directly in Gradescope, do not email instructors. 1 float in NumPy = 8 bytes 10 6 2 20 bytes = 1 MB 10 9 2 30 bytes = 1 GB For each block compute the memory required
Warm up Regrade requests submitted directly in Gradescope, do not email instructors. 1 float in NumPy = 8 bytes 10 6 2 20 bytes = 1 MB 10 9 2 30 bytes = 1 GB For each block compute the memory required
Statistical Machine Learning II Spring 2017, Learning Theory, Lecture 4
 Statistical Machine Learning II Spring 07, Learning Theory, Lecture 4 Jean Honorio jhonorio@purdue.edu Deterministic Optimization For brevity, everywhere differentiable functions will be called smooth.
Statistical Machine Learning II Spring 07, Learning Theory, Lecture 4 Jean Honorio jhonorio@purdue.edu Deterministic Optimization For brevity, everywhere differentiable functions will be called smooth.
Online Passive-Aggressive Algorithms
 Online Passive-Aggressive Algorithms Koby Crammer Ofer Dekel Shai Shalev-Shwartz Yoram Singer School of Computer Science & Engineering The Hebrew University, Jerusalem 91904, Israel {kobics,oferd,shais,singer}@cs.huji.ac.il
Online Passive-Aggressive Algorithms Koby Crammer Ofer Dekel Shai Shalev-Shwartz Yoram Singer School of Computer Science & Engineering The Hebrew University, Jerusalem 91904, Israel {kobics,oferd,shais,singer}@cs.huji.ac.il
On the interior of the simplex, we have the Hessian of d(x), Hd(x) is diagonal with ith. µd(w) + w T c. minimize. subject to w T 1 = 1,
 Math 30 Winter 05 Solution to Homework 3. Recognizing the convexity of g(x) := x log x, from Jensen s inequality we get d(x) n x + + x n n log x + + x n n where the equality is attained only at x = (/n,...,
Math 30 Winter 05 Solution to Homework 3. Recognizing the convexity of g(x) := x log x, from Jensen s inequality we get d(x) n x + + x n n log x + + x n n where the equality is attained only at x = (/n,...,
Portfolio Optimization
 Statistical Techniques in Robotics (16-831, F12) Lecture#12 (Monday October 8) Portfolio Optimization Lecturer: Drew Bagnell Scribe: Ji Zhang 1 1 Portfolio Optimization - No Regret Portfolio We want to
Statistical Techniques in Robotics (16-831, F12) Lecture#12 (Monday October 8) Portfolio Optimization Lecturer: Drew Bagnell Scribe: Ji Zhang 1 1 Portfolio Optimization - No Regret Portfolio We want to
1 Overview. 2 Learning from Experts. 2.1 Defining a meaningful benchmark. AM 221: Advanced Optimization Spring 2016
 AM 1: Advanced Optimization Spring 016 Prof. Yaron Singer Lecture 11 March 3rd 1 Overview In this lecture we will introduce the notion of online convex optimization. This is an extremely useful framework
AM 1: Advanced Optimization Spring 016 Prof. Yaron Singer Lecture 11 March 3rd 1 Overview In this lecture we will introduce the notion of online convex optimization. This is an extremely useful framework
Case Study 1: Estimating Click Probabilities. Kakade Announcements: Project Proposals: due this Friday!
 Case Study 1: Estimating Click Probabilities Intro Logistic Regression Gradient Descent + SGD Machine Learning for Big Data CSE547/STAT548, University of Washington Sham Kakade April 4, 017 1 Announcements:
Case Study 1: Estimating Click Probabilities Intro Logistic Regression Gradient Descent + SGD Machine Learning for Big Data CSE547/STAT548, University of Washington Sham Kakade April 4, 017 1 Announcements:
ECE521 lecture 4: 19 January Optimization, MLE, regularization
 ECE521 lecture 4: 19 January 2017 Optimization, MLE, regularization First four lectures Lectures 1 and 2: Intro to ML Probability review Types of loss functions and algorithms Lecture 3: KNN Convexity
ECE521 lecture 4: 19 January 2017 Optimization, MLE, regularization First four lectures Lectures 1 and 2: Intro to ML Probability review Types of loss functions and algorithms Lecture 3: KNN Convexity
Online Passive-Aggressive Algorithms
 Online Passive-Aggressive Algorithms Koby Crammer Ofer Dekel Shai Shalev-Shwartz Yoram Singer School of Computer Science & Engineering The Hebrew University, Jerusalem 91904, Israel {kobics,oferd,shais,singer}@cs.huji.ac.il
Online Passive-Aggressive Algorithms Koby Crammer Ofer Dekel Shai Shalev-Shwartz Yoram Singer School of Computer Science & Engineering The Hebrew University, Jerusalem 91904, Israel {kobics,oferd,shais,singer}@cs.huji.ac.il
Introduction to Optimization
 Introduction to Optimization Konstantin Tretyakov (kt@ut.ee) MTAT.03.227 Machine Learning So far Machine learning is important and interesting The general concept: Fitting models to data So far Machine
Introduction to Optimization Konstantin Tretyakov (kt@ut.ee) MTAT.03.227 Machine Learning So far Machine learning is important and interesting The general concept: Fitting models to data So far Machine
Machine Learning for NLP
 Machine Learning for NLP Uppsala University Department of Linguistics and Philology Slides borrowed from Ryan McDonald, Google Research Machine Learning for NLP 1(50) Introduction Linear Classifiers Classifiers
Machine Learning for NLP Uppsala University Department of Linguistics and Philology Slides borrowed from Ryan McDonald, Google Research Machine Learning for NLP 1(50) Introduction Linear Classifiers Classifiers
i=1 cosn (x 2 i y2 i ) over RN R N. cos y sin x
 Mehryar Mohri Foundations of Machine Learning Courant Institute of Mathematical Sciences Homework assignment 3 November 16, 017 Due: Dec 01, 017 A. Kernels Show that the following kernels K are PDS: 1.
Mehryar Mohri Foundations of Machine Learning Courant Institute of Mathematical Sciences Homework assignment 3 November 16, 017 Due: Dec 01, 017 A. Kernels Show that the following kernels K are PDS: 1.
1 Sparsity and l 1 relaxation
 6.883 Learning with Combinatorial Structure Note for Lecture 2 Author: Chiyuan Zhang Sparsity and l relaxation Last time we talked about sparsity and characterized when an l relaxation could recover the
6.883 Learning with Combinatorial Structure Note for Lecture 2 Author: Chiyuan Zhang Sparsity and l relaxation Last time we talked about sparsity and characterized when an l relaxation could recover the
Full-information Online Learning
 Introduction Expert Advice OCO LM A DA NANJING UNIVERSITY Full-information Lijun Zhang Nanjing University, China June 2, 2017 Outline Introduction Expert Advice OCO 1 Introduction Definitions Regret 2
Introduction Expert Advice OCO LM A DA NANJING UNIVERSITY Full-information Lijun Zhang Nanjing University, China June 2, 2017 Outline Introduction Expert Advice OCO 1 Introduction Definitions Regret 2
Tutorial: PART 1. Online Convex Optimization, A Game- Theoretic Approach to Learning.
 Tutorial: PART 1 Online Convex Optimization, A Game- Theoretic Approach to Learning http://www.cs.princeton.edu/~ehazan/tutorial/tutorial.htm Elad Hazan Princeton University Satyen Kale Yahoo Research
Tutorial: PART 1 Online Convex Optimization, A Game- Theoretic Approach to Learning http://www.cs.princeton.edu/~ehazan/tutorial/tutorial.htm Elad Hazan Princeton University Satyen Kale Yahoo Research
Warm up: risk prediction with logistic regression
 Warm up: risk prediction with logistic regression Boss gives you a bunch of data on loans defaulting or not: {(x i,y i )} n i= x i 2 R d, y i 2 {, } You model the data as: P (Y = y x, w) = + exp( yw T
Warm up: risk prediction with logistic regression Boss gives you a bunch of data on loans defaulting or not: {(x i,y i )} n i= x i 2 R d, y i 2 {, } You model the data as: P (Y = y x, w) = + exp( yw T
Max Margin-Classifier
 Max Margin-Classifier Oliver Schulte - CMPT 726 Bishop PRML Ch. 7 Outline Maximum Margin Criterion Math Maximizing the Margin Non-Separable Data Kernels and Non-linear Mappings Where does the maximization
Max Margin-Classifier Oliver Schulte - CMPT 726 Bishop PRML Ch. 7 Outline Maximum Margin Criterion Math Maximizing the Margin Non-Separable Data Kernels and Non-linear Mappings Where does the maximization
Bregman Divergences for Data Mining Meta-Algorithms
 p.1/?? Bregman Divergences for Data Mining Meta-Algorithms Joydeep Ghosh University of Texas at Austin ghosh@ece.utexas.edu Reflects joint work with Arindam Banerjee, Srujana Merugu, Inderjit Dhillon,
p.1/?? Bregman Divergences for Data Mining Meta-Algorithms Joydeep Ghosh University of Texas at Austin ghosh@ece.utexas.edu Reflects joint work with Arindam Banerjee, Srujana Merugu, Inderjit Dhillon,
Lecture 4: Training a Classifier
 Lecture 4: Training a Classifier Roger Grosse 1 Introduction Now that we ve defined what binary classification is, let s actually train a classifier. We ll approach this problem in much the same way as
Lecture 4: Training a Classifier Roger Grosse 1 Introduction Now that we ve defined what binary classification is, let s actually train a classifier. We ll approach this problem in much the same way as
Error Functions & Linear Regression (1)
 Error Functions & Linear Regression (1) John Kelleher & Brian Mac Namee Machine Learning @ DIT Overview 1 Introduction Overview 2 Univariate Linear Regression Linear Regression Analytical Solution Gradient
Error Functions & Linear Regression (1) John Kelleher & Brian Mac Namee Machine Learning @ DIT Overview 1 Introduction Overview 2 Univariate Linear Regression Linear Regression Analytical Solution Gradient
Neural Network Training
 Neural Network Training Sargur Srihari Topics in Network Training 0. Neural network parameters Probabilistic problem formulation Specifying the activation and error functions for Regression Binary classification
Neural Network Training Sargur Srihari Topics in Network Training 0. Neural network parameters Probabilistic problem formulation Specifying the activation and error functions for Regression Binary classification
Classification CE-717: Machine Learning Sharif University of Technology. M. Soleymani Fall 2012
 Classification CE-717: Machine Learning Sharif University of Technology M. Soleymani Fall 2012 Topics Discriminant functions Logistic regression Perceptron Generative models Generative vs. discriminative
Classification CE-717: Machine Learning Sharif University of Technology M. Soleymani Fall 2012 Topics Discriminant functions Logistic regression Perceptron Generative models Generative vs. discriminative
Lecture 8: Decision-making under total uncertainty: the multiplicative weight algorithm. Lecturer: Sanjeev Arora
 princeton univ. F 13 cos 521: Advanced Algorithm Design Lecture 8: Decision-making under total uncertainty: the multiplicative weight algorithm Lecturer: Sanjeev Arora Scribe: (Today s notes below are
princeton univ. F 13 cos 521: Advanced Algorithm Design Lecture 8: Decision-making under total uncertainty: the multiplicative weight algorithm Lecturer: Sanjeev Arora Scribe: (Today s notes below are
U Logo Use Guidelines
 Information Theory Lecture 3: Applications to Machine Learning U Logo Use Guidelines Mark Reid logo is a contemporary n of our heritage. presents our name, d and our motto: arn the nature of things. authenticity
Information Theory Lecture 3: Applications to Machine Learning U Logo Use Guidelines Mark Reid logo is a contemporary n of our heritage. presents our name, d and our motto: arn the nature of things. authenticity
Gradient Descent. Ryan Tibshirani Convex Optimization /36-725
 Gradient Descent Ryan Tibshirani Convex Optimization 10-725/36-725 Last time: canonical convex programs Linear program (LP): takes the form min x subject to c T x Gx h Ax = b Quadratic program (QP): like
Gradient Descent Ryan Tibshirani Convex Optimization 10-725/36-725 Last time: canonical convex programs Linear program (LP): takes the form min x subject to c T x Gx h Ax = b Quadratic program (QP): like
Course Notes for EE227C (Spring 2018): Convex Optimization and Approximation
 Course Notes for EE227C (Spring 2018): Convex Optiization and Approxiation Instructor: Moritz Hardt Eail: hardt+ee227c@berkeley.edu Graduate Instructor: Max Sichowitz Eail: sichow+ee227c@berkeley.edu October
Course Notes for EE227C (Spring 2018): Convex Optiization and Approxiation Instructor: Moritz Hardt Eail: hardt+ee227c@berkeley.edu Graduate Instructor: Max Sichowitz Eail: sichow+ee227c@berkeley.edu October
(Kernels +) Support Vector Machines
 (Kernels +) Support Vector Machines Machine Learning Torsten Möller Reading Chapter 5 of Machine Learning An Algorithmic Perspective by Marsland Chapter 6+7 of Pattern Recognition and Machine Learning
(Kernels +) Support Vector Machines Machine Learning Torsten Möller Reading Chapter 5 of Machine Learning An Algorithmic Perspective by Marsland Chapter 6+7 of Pattern Recognition and Machine Learning
Neural Networks and Deep Learning
 Neural Networks and Deep Learning Professor Ameet Talwalkar November 12, 2015 Professor Ameet Talwalkar Neural Networks and Deep Learning November 12, 2015 1 / 16 Outline 1 Review of last lecture AdaBoost
Neural Networks and Deep Learning Professor Ameet Talwalkar November 12, 2015 Professor Ameet Talwalkar Neural Networks and Deep Learning November 12, 2015 1 / 16 Outline 1 Review of last lecture AdaBoost
Value Function Methods. CS : Deep Reinforcement Learning Sergey Levine
 Value Function Methods CS 294-112: Deep Reinforcement Learning Sergey Levine Class Notes 1. Homework 2 is due in one week 2. Remember to start forming final project groups and writing your proposal! Proposal
Value Function Methods CS 294-112: Deep Reinforcement Learning Sergey Levine Class Notes 1. Homework 2 is due in one week 2. Remember to start forming final project groups and writing your proposal! Proposal
Neural Networks in Structured Prediction. November 17, 2015
 Neural Networks in Structured Prediction November 17, 2015 HWs and Paper Last homework is going to be posted soon Neural net NER tagging model This is a new structured model Paper - Thursday after Thanksgiving
Neural Networks in Structured Prediction November 17, 2015 HWs and Paper Last homework is going to be posted soon Neural net NER tagging model This is a new structured model Paper - Thursday after Thanksgiving
Selected Topics in Optimization. Some slides borrowed from
 Selected Topics in Optimization Some slides borrowed from http://www.stat.cmu.edu/~ryantibs/convexopt/ Overview Optimization problems are almost everywhere in statistics and machine learning. Input Model
Selected Topics in Optimization Some slides borrowed from http://www.stat.cmu.edu/~ryantibs/convexopt/ Overview Optimization problems are almost everywhere in statistics and machine learning. Input Model
Multiclass Logistic Regression
 Multiclass Logistic Regression Sargur. Srihari University at Buffalo, State University of ew York USA Machine Learning Srihari Topics in Linear Classification using Probabilistic Discriminative Models
Multiclass Logistic Regression Sargur. Srihari University at Buffalo, State University of ew York USA Machine Learning Srihari Topics in Linear Classification using Probabilistic Discriminative Models
Convex Optimization Lecture 16
 Convex Optimization Lecture 16 Today: Projected Gradient Descent Conditional Gradient Descent Stochastic Gradient Descent Random Coordinate Descent Recall: Gradient Descent (Steepest Descent w.r.t Euclidean
Convex Optimization Lecture 16 Today: Projected Gradient Descent Conditional Gradient Descent Stochastic Gradient Descent Random Coordinate Descent Recall: Gradient Descent (Steepest Descent w.r.t Euclidean
Stochastic and online algorithms
 Stochastic and online algorithms stochastic gradient method online optimization and dual averaging method minimizing finite average Stochastic and online optimization 6 1 Stochastic optimization problem
Stochastic and online algorithms stochastic gradient method online optimization and dual averaging method minimizing finite average Stochastic and online optimization 6 1 Stochastic optimization problem
Homework 4. Convex Optimization /36-725
 Homework 4 Convex Optimization 10-725/36-725 Due Friday November 4 at 5:30pm submitted to Christoph Dann in Gates 8013 (Remember to a submit separate writeup for each problem, with your name at the top)
Homework 4 Convex Optimization 10-725/36-725 Due Friday November 4 at 5:30pm submitted to Christoph Dann in Gates 8013 (Remember to a submit separate writeup for each problem, with your name at the top)
Relative Loss Bounds for Multidimensional Regression Problems
 Relative Loss Bounds for Multidimensional Regression Problems Jyrki Kivinen and Manfred Warmuth Presented by: Arindam Banerjee A Single Neuron For a training example (x, y), x R d, y [0, 1] learning solves
Relative Loss Bounds for Multidimensional Regression Problems Jyrki Kivinen and Manfred Warmuth Presented by: Arindam Banerjee A Single Neuron For a training example (x, y), x R d, y [0, 1] learning solves
Adaptive Gradient Methods AdaGrad / Adam. Machine Learning for Big Data CSE547/STAT548, University of Washington Sham Kakade
 Adaptive Gradient Methods AdaGrad / Adam Machine Learning for Big Data CSE547/STAT548, University of Washington Sham Kakade 1 Announcements: HW3 posted Dual coordinate ascent (some review of SGD and random
Adaptive Gradient Methods AdaGrad / Adam Machine Learning for Big Data CSE547/STAT548, University of Washington Sham Kakade 1 Announcements: HW3 posted Dual coordinate ascent (some review of SGD and random
ML (cont.): SUPPORT VECTOR MACHINES
 ML (cont.): SUPPORT VECTOR MACHINES CS540 Bryan R Gibson University of Wisconsin-Madison Slides adapted from those used by Prof. Jerry Zhu, CS540-1 1 / 40 Support Vector Machines (SVMs) The No-Math Version
ML (cont.): SUPPORT VECTOR MACHINES CS540 Bryan R Gibson University of Wisconsin-Madison Slides adapted from those used by Prof. Jerry Zhu, CS540-1 1 / 40 Support Vector Machines (SVMs) The No-Math Version
1 Review of Winnow Algorithm
 COS 511: Theoretical Machine Learning Lecturer: Rob Schapire Lecture # 17 Scribe: Xingyuan Fang, Ethan April 9th, 2013 1 Review of Winnow Algorithm We have studied Winnow algorithm in Algorithm 1. Algorithm
COS 511: Theoretical Machine Learning Lecturer: Rob Schapire Lecture # 17 Scribe: Xingyuan Fang, Ethan April 9th, 2013 1 Review of Winnow Algorithm We have studied Winnow algorithm in Algorithm 1. Algorithm
Homework 5. Convex Optimization /36-725
 Homework 5 Convex Optimization 10-725/36-725 Due Tuesday November 22 at 5:30pm submitted to Christoph Dann in Gates 8013 (Remember to a submit separate writeup for each problem, with your name at the top)
Homework 5 Convex Optimization 10-725/36-725 Due Tuesday November 22 at 5:30pm submitted to Christoph Dann in Gates 8013 (Remember to a submit separate writeup for each problem, with your name at the top)
CPSC 340: Machine Learning and Data Mining. Stochastic Gradient Fall 2017
 CPSC 340: Machine Learning and Data Mining Stochastic Gradient Fall 2017 Assignment 3: Admin Check update thread on Piazza for correct definition of trainndx. This could make your cross-validation code
CPSC 340: Machine Learning and Data Mining Stochastic Gradient Fall 2017 Assignment 3: Admin Check update thread on Piazza for correct definition of trainndx. This could make your cross-validation code
Lecture 4 Lebesgue spaces and inequalities
 Lecture 4: Lebesgue spaces and inequalities 1 of 10 Course: Theory of Probability I Term: Fall 2013 Instructor: Gordan Zitkovic Lecture 4 Lebesgue spaces and inequalities Lebesgue spaces We have seen how
Lecture 4: Lebesgue spaces and inequalities 1 of 10 Course: Theory of Probability I Term: Fall 2013 Instructor: Gordan Zitkovic Lecture 4 Lebesgue spaces and inequalities Lebesgue spaces We have seen how
Applications of Linear Programming
 Applications of Linear Programming lecturer: András London University of Szeged Institute of Informatics Department of Computational Optimization Lecture 9 Non-linear programming In case of LP, the goal
Applications of Linear Programming lecturer: András London University of Szeged Institute of Informatics Department of Computational Optimization Lecture 9 Non-linear programming In case of LP, the goal
Gradient descent. Barnabas Poczos & Ryan Tibshirani Convex Optimization /36-725
 Gradient descent Barnabas Poczos & Ryan Tibshirani Convex Optimization 10-725/36-725 1 Gradient descent First consider unconstrained minimization of f : R n R, convex and differentiable. We want to solve
Gradient descent Barnabas Poczos & Ryan Tibshirani Convex Optimization 10-725/36-725 1 Gradient descent First consider unconstrained minimization of f : R n R, convex and differentiable. We want to solve
Linear & nonlinear classifiers
 Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1394 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1394 1 / 34 Table
Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1394 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1394 1 / 34 Table
The Online Approach to Machine Learning
 The Online Approach to Machine Learning Nicolò Cesa-Bianchi Università degli Studi di Milano N. Cesa-Bianchi (UNIMI) Online Approach to ML 1 / 53 Summary 1 My beautiful regret 2 A supposedly fun game I
The Online Approach to Machine Learning Nicolò Cesa-Bianchi Università degli Studi di Milano N. Cesa-Bianchi (UNIMI) Online Approach to ML 1 / 53 Summary 1 My beautiful regret 2 A supposedly fun game I
The Blessing and the Curse
 The Blessing and the Curse of the Multiplicative Updates Manfred K. Warmuth University of California, Santa Cruz CMPS 272, Feb 31, 2012 Thanks to David Ilstrup and Anindya Sen for helping with the slides
The Blessing and the Curse of the Multiplicative Updates Manfred K. Warmuth University of California, Santa Cruz CMPS 272, Feb 31, 2012 Thanks to David Ilstrup and Anindya Sen for helping with the slides
Regret bounded by gradual variation for online convex optimization
 Noname manuscript No. will be inserted by the editor Regret bounded by gradual variation for online convex optimization Tianbao Yang Mehrdad Mahdavi Rong Jin Shenghuo Zhu Received: date / Accepted: date
Noname manuscript No. will be inserted by the editor Regret bounded by gradual variation for online convex optimization Tianbao Yang Mehrdad Mahdavi Rong Jin Shenghuo Zhu Received: date / Accepted: date
Support vector machines Lecture 4
 Support vector machines Lecture 4 David Sontag New York University Slides adapted from Luke Zettlemoyer, Vibhav Gogate, and Carlos Guestrin Q: What does the Perceptron mistake bound tell us? Theorem: The
Support vector machines Lecture 4 David Sontag New York University Slides adapted from Luke Zettlemoyer, Vibhav Gogate, and Carlos Guestrin Q: What does the Perceptron mistake bound tell us? Theorem: The
On Acceleration with Noise-Corrupted Gradients. + m k 1 (x). By the definition of Bregman divergence:
 A Omitted Proofs from Section 3 Proof of Lemma 3 Let m x) = a i On Acceleration with Noise-Corrupted Gradients fxi ), u x i D ψ u, x 0 ) denote the function under the minimum in the lower bound By Proposition
A Omitted Proofs from Section 3 Proof of Lemma 3 Let m x) = a i On Acceleration with Noise-Corrupted Gradients fxi ), u x i D ψ u, x 0 ) denote the function under the minimum in the lower bound By Proposition
Coordinate Descent and Ascent Methods
 Coordinate Descent and Ascent Methods Julie Nutini Machine Learning Reading Group November 3 rd, 2015 1 / 22 Projected-Gradient Methods Motivation Rewrite non-smooth problem as smooth constrained problem:
Coordinate Descent and Ascent Methods Julie Nutini Machine Learning Reading Group November 3 rd, 2015 1 / 22 Projected-Gradient Methods Motivation Rewrite non-smooth problem as smooth constrained problem:
CSC321 Lecture 4: Learning a Classifier
 CSC321 Lecture 4: Learning a Classifier Roger Grosse Roger Grosse CSC321 Lecture 4: Learning a Classifier 1 / 28 Overview Last time: binary classification, perceptron algorithm Limitations of the perceptron
CSC321 Lecture 4: Learning a Classifier Roger Grosse Roger Grosse CSC321 Lecture 4: Learning a Classifier 1 / 28 Overview Last time: binary classification, perceptron algorithm Limitations of the perceptron
Lecture 4: Training a Classifier
 Lecture 4: Training a Classifier Roger Grosse 1 Introduction Now that we ve defined what binary classification is, let s actually train a classifier. We ll approach this problem in much the same way as
Lecture 4: Training a Classifier Roger Grosse 1 Introduction Now that we ve defined what binary classification is, let s actually train a classifier. We ll approach this problem in much the same way as
Composite Objective Mirror Descent
 Composite Objective Mirror Descent John C. Duchi 1,3 Shai Shalev-Shwartz 2 Yoram Singer 3 Ambuj Tewari 4 1 University of California, Berkeley 2 Hebrew University of Jerusalem, Israel 3 Google Research
Composite Objective Mirror Descent John C. Duchi 1,3 Shai Shalev-Shwartz 2 Yoram Singer 3 Ambuj Tewari 4 1 University of California, Berkeley 2 Hebrew University of Jerusalem, Israel 3 Google Research
Course Notes for EE227C (Spring 2018): Convex Optimization and Approximation
 Course Notes for EE7C (Spring 08): Convex Optimization and Approximation Instructor: Moritz Hardt Email: hardt+ee7c@berkeley.edu Graduate Instructor: Max Simchowitz Email: msimchow+ee7c@berkeley.edu October
Course Notes for EE7C (Spring 08): Convex Optimization and Approximation Instructor: Moritz Hardt Email: hardt+ee7c@berkeley.edu Graduate Instructor: Max Simchowitz Email: msimchow+ee7c@berkeley.edu October
CSC 411 Lecture 17: Support Vector Machine
 CSC 411 Lecture 17: Support Vector Machine Ethan Fetaya, James Lucas and Emad Andrews University of Toronto CSC411 Lec17 1 / 1 Today Max-margin classification SVM Hard SVM Duality Soft SVM CSC411 Lec17
CSC 411 Lecture 17: Support Vector Machine Ethan Fetaya, James Lucas and Emad Andrews University of Toronto CSC411 Lec17 1 / 1 Today Max-margin classification SVM Hard SVM Duality Soft SVM CSC411 Lec17
Lecture 25: November 27
 10-725: Optimization Fall 2012 Lecture 25: November 27 Lecturer: Ryan Tibshirani Scribes: Matt Wytock, Supreeth Achar Note: LaTeX template courtesy of UC Berkeley EECS dept. Disclaimer: These notes have
10-725: Optimization Fall 2012 Lecture 25: November 27 Lecturer: Ryan Tibshirani Scribes: Matt Wytock, Supreeth Achar Note: LaTeX template courtesy of UC Berkeley EECS dept. Disclaimer: These notes have
ECE G: Special Topics in Signal Processing: Sparsity, Structure, and Inference
 ECE 18-898G: Special Topics in Signal Processing: Sparsity, Structure, and Inference Sparse Recovery using L1 minimization - algorithms Yuejie Chi Department of Electrical and Computer Engineering Spring
ECE 18-898G: Special Topics in Signal Processing: Sparsity, Structure, and Inference Sparse Recovery using L1 minimization - algorithms Yuejie Chi Department of Electrical and Computer Engineering Spring
Online Kernel PCA with Entropic Matrix Updates
 Dima Kuzmin Manfred K. Warmuth Computer Science Department, University of California - Santa Cruz dima@cse.ucsc.edu manfred@cse.ucsc.edu Abstract A number of updates for density matrices have been developed
Dima Kuzmin Manfred K. Warmuth Computer Science Department, University of California - Santa Cruz dima@cse.ucsc.edu manfred@cse.ucsc.edu Abstract A number of updates for density matrices have been developed
Linear smoother. ŷ = S y. where s ij = s ij (x) e.g. s ij = diag(l i (x))
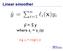 Linear smoother ŷ = S y where s ij = s ij (x) e.g. s ij = diag(l i (x)) 2 Online Learning: LMS and Perceptrons Partially adapted from slides by Ryan Gabbard and Mitch Marcus (and lots original slides by
Linear smoother ŷ = S y where s ij = s ij (x) e.g. s ij = diag(l i (x)) 2 Online Learning: LMS and Perceptrons Partially adapted from slides by Ryan Gabbard and Mitch Marcus (and lots original slides by
Tutorial: PART 2. Online Convex Optimization, A Game- Theoretic Approach to Learning
 Tutorial: PART 2 Online Convex Optimization, A Game- Theoretic Approach to Learning Elad Hazan Princeton University Satyen Kale Yahoo Research Exploiting curvature: logarithmic regret Logarithmic regret
Tutorial: PART 2 Online Convex Optimization, A Game- Theoretic Approach to Learning Elad Hazan Princeton University Satyen Kale Yahoo Research Exploiting curvature: logarithmic regret Logarithmic regret
Convex Optimization. Ofer Meshi. Lecture 6: Lower Bounds Constrained Optimization
 Convex Optimization Ofer Meshi Lecture 6: Lower Bounds Constrained Optimization Lower Bounds Some upper bounds: #iter μ 2 M #iter 2 M #iter L L μ 2 Oracle/ops GD κ log 1/ε M x # ε L # x # L # ε # με f
Convex Optimization Ofer Meshi Lecture 6: Lower Bounds Constrained Optimization Lower Bounds Some upper bounds: #iter μ 2 M #iter 2 M #iter L L μ 2 Oracle/ops GD κ log 1/ε M x # ε L # x # L # ε # με f
