Radon Transform An Introduction
|
|
|
- Ira Rice
- 5 years ago
- Views:
Transcription
1 Radon Transform An Introduction Yi-Hsuan Lin The Radon transform is widely applicable to tomography, the creation of an image from the scattering data associated to crosssectional scans of an object. If a function Œ represents an unknown density, then the Radon transform represents the scattering data obtained as the output of a tomographic scan. Hence the inverse of the Radon transform can be used to reconstruct the original density from the scattering data, and thus it forms the mathematical underpinning for tomographic reconstruction. The Radon transform data is often called a sinogram because the Radon transform of a Dirac delta function is a distribution supported on the graph of a sine wave. Consequently the Radon transform of a number of small objects appears graphically as a number of blurred sine waves with dierent amplitudes and phases. The Radon transform is useful in computed axial tomography (CAT scan), electron microscopy of macromolecular assemblies like viruses and protein complexes, reection seismology and in the solution of hyperbolic partial dierential equations. [wikipedia] Denition 1. Given a function f(x), Radon transform produces the value of f(x)dx along all the lines L. Dene Rf(L) = f(x)dx. If we rewrite the L L lines L in coordinates, that is, L = {x x ω = s}, then we have Rf(ω, s) = f(x)dx, where (ω, s) x ω=s S1 R The Radon transform has the following properties: 1. Evenness Rf(ω, s) = Rf( ω, s), we can identify the two points (ω, s) to 1
2 ( ω, s). g = Rf is dened on the Mobius strip: S 1 R/ 2. Shift invariance Let (T a f)(x) = f(x + a), and (t p g)(ω, s) = g(ω, s + p) Then R(T a f)(ω, s) = t a ω Rf = Rf(ω, s + a ω). 3. Rotation invariace A is a rotation operator in R 2, then R(f(Ax))(ω, s) = Rf(Aω, s). Corollary 2. Fourier transform methods might be useful. Denition 3. We call Q is a ridge function if Q can be written as the following form: Q(x) = q(x ω). Proposition 4. Q is a ridge function, i.e. Q(x) = q(x ω). Then we have the following identity: f(x)q(x)dx = Rf(ω, s)q(s)ds. R R 2 Proof. For Q(x) = e ix ξ = e iσω x, where σ = x, and ω = (cosθ, sinθ), then we can get the above identity. Theorem 5. (Projection-Slice formula or Fourier-Slice formula) Let ˆf be the Fourier transform of f, and ĝ(ω, σ) be the Fourier transform of g w.r.t. the parameter s. Then we have ˆf(σω) = 1 ĝ(ω, σ), where g = Rf is the Radon transform of f. Dual Radon Transform Denition 6. R : f Rf(ω, s) is a Radon transform, we call R # : g(ω, s) R # g(x) is a dual Radon transform, such that Rf(ω, s)g(ω, s)dωds = f(x)r # g(x)dx. Lemma 7. We have the formula R # g(x) = S 1 g(ω, x ω)dω, where S 1 is the unit circle in R 1. Remark 8. We call R # is the backprojection operator. The line with normal coordinates (ω, x ω) are passing through x. This explains the name backprojection operator. 2
3 Theorem 9. (L 2 continuity) Let Ω be the unit disc on the plane, f supported inside, then we have the estimate Rf L 2 1 k f (C, 1 s 2 ) L 2. where Rf 2 L 2 1 = Rf(ω, 1 (C, 1 s 2 ) C s) 2 dωds, k is a constant 1 s 2 and C is a cylinder with C = S 1 R. Remark 10. In R n (n > 2), one can take d dimesional Radon transform fo any 1 d < n: f(x) H f(x)dx, where H is a d dimensional subsapce. Example 11. In R 3 : 1. d = 2, Radon transform x ω=s f(x)dx 2. d = 1, X-ray transform f(x + tω)dt. Fourier inversion Projection-slice formula gives an inversion procedure: f(x) = Rf(ω, s) = Rf(ω, σ) = f(σω) = IF T denotes the inverse Fourier transform. f(x), where IFT Fourier inversion in polar coordinates Let's elaborate on Fourier inversion, denoting g = Rf: f(x) = 1 1 eix ξ f(ξ)dξ = e iσω x 1 f(σω) σ dσdω ω =1 0 = ω =1 4π = 1 ω =1 4π dω( 1 eiσω x ĝ(ω, σ) σ dσ), here we need to use the projectionslice formula to change the function f into g. Moreover, by using Hilbert 1 transform, we have that eiσω x ĝ(ω, σ) σ dσ = (H dg )(ω, x ω), where ds H is the Hilbert transform and (Hg)(s) = 1 π v.p. g(τ) dτ, then we can s τ write the above identities as f(x) = 1 4π R# (H d ds g)(x) = 1 4π R# H d ds g(x). Note that Ĥ dg (ω, σ) = σ ĝ(ω, σ). ds 3
4 Theorem 12. (FBP inversion) f(x) = 1 4π R# H d ds Rf, where H d ds is a ltration, R# is a backprojection. Remark 13. Radon transform is not invertible. It is just left invertible. Left inverse operators are not unique. Range Q: Is a given function g(ω, s) Radon transform for some f? (appropriate function classes assumed) Ex: If g(ω, s) C (S 1 [ 1, 1]), can we nd some f such that g = Rf? A: Let g = Rf. 1. g(ω, s) = g( ω, s) 2. consider kth moment G k (ω) = R sk g(ω, s)ds - function on the unit sphere. G k (ω) = sk ds f(x)dx = R (x ω) k f(x)dx homogeneous x ω=s 2 polynomial of degree k in ω. Theorem 14. A function g S(C), where S(C) is the Schwartz space over C = S 1 R. g = Rf for some f S(R 2 ) if and only if it satises the following range condtions: 1. Evenness. g(ω, s) = g( ω, s) 2. Moment condtions. For any k = 0, 1, 2,..., G k (ω) extends to a homogeneous polynomial of degree k of ω R 2. Remark 15. g(ω, s) ĝ(ω, σ) f(σω) = cĝ(ω, σ) f(x), since polar coordinate is not a nice coordinate. Note that σω = ( σ)( ω), if we want the identity f(σω) = cĝ(ω, σ) is well-dened, we need the evenness condition. Range revisited in Fourier domain Consider 1D FT ĝ(ω, σ) of g = Rf. Get 2D FT of f along radial lines: f(σω) = cĝ(ω, σ). Notice the role of evenness! Function h(σω) = ĝ(ω, σ) is smooth everywhere, possibly except the origin. 4
5 Stability of inversion Stability: Small variations in data lead to small changes in the result. Theorem 16. (Stability estimate for Radon transform in 2D) D is a disk in R 2, f H s 0(D), (i.e. f(ξ) 2 (1+ ξ 2 ) s < ), C 1 Rf H s+1/2 f H s C 2 Rf H s+1/2. Conclusion: X-ray transform smoothes functions by 1/2 derivatives. Same with the dual. Thus, two of them add a derivative, which must be removed during inversion. (remember the lter H d ds?) More generally, d-plane transform adds 2 d derivatives need to be removed by ltration. Instability of inverting smoothing operators Rule of thumb: derivatives, thus in FBP d If an operator A increases smoothness of functions, its inversion is unstable. More smoothing leads to more instability. The extreme cases are when A turns non-smooth functions into C or even worse, analytic functions. Incomplete data What if the values of Rf(ω, s) are known for a set of points (ω, s) only? 1. Is the reconstruction possible (uniqueness)? 2. Reconstruction procedures. 3. Stability. 4. Any resulting image deterioration? 5
6 Limited angle Theorem 17. (Data known for an open set of ωs and all s ) Any compactly supported function is uniquely reconstructed. Remark 18. Reconstruction is unstable. 6
Mathematical Methods of Computed Tomography
 Mathematical Methods of Computed Tomography Peter Kuchment Dedicated to the memory of Leon Ehrenpreis, Larry Shepp and Iosif Shneiberg friends, great mathematicians and human beings Young Researchers School
Mathematical Methods of Computed Tomography Peter Kuchment Dedicated to the memory of Leon Ehrenpreis, Larry Shepp and Iosif Shneiberg friends, great mathematicians and human beings Young Researchers School
Microlocal Methods in X-ray Tomography
 Microlocal Methods in X-ray Tomography Plamen Stefanov Purdue University Lecture I: Euclidean X-ray tomography Mini Course, Fields Institute, 2012 Plamen Stefanov (Purdue University ) Microlocal Methods
Microlocal Methods in X-ray Tomography Plamen Stefanov Purdue University Lecture I: Euclidean X-ray tomography Mini Course, Fields Institute, 2012 Plamen Stefanov (Purdue University ) Microlocal Methods
1 Radon Transform and X-Ray CT
 Radon Transform and X-Ray CT In this section we look at an important class of imaging problems, the inverse Radon transform. We have seen that X-ray CT (Computerized Tomography) involves the reconstruction
Radon Transform and X-Ray CT In this section we look at an important class of imaging problems, the inverse Radon transform. We have seen that X-ray CT (Computerized Tomography) involves the reconstruction
Lecture 9 February 2, 2016
 MATH 262/CME 372: Applied Fourier Analysis and Winter 26 Elements of Modern Signal Processing Lecture 9 February 2, 26 Prof. Emmanuel Candes Scribe: Carlos A. Sing-Long, Edited by E. Bates Outline Agenda:
MATH 262/CME 372: Applied Fourier Analysis and Winter 26 Elements of Modern Signal Processing Lecture 9 February 2, 26 Prof. Emmanuel Candes Scribe: Carlos A. Sing-Long, Edited by E. Bates Outline Agenda:
On stable inversion of the attenuated Radon transform with half data Jan Boman. We shall consider weighted Radon transforms of the form
 On stable inversion of the attenuated Radon transform with half data Jan Boman We shall consider weighted Radon transforms of the form R ρ f(l) = f(x)ρ(x, L)ds, L where ρ is a given smooth, positive weight
On stable inversion of the attenuated Radon transform with half data Jan Boman We shall consider weighted Radon transforms of the form R ρ f(l) = f(x)ρ(x, L)ds, L where ρ is a given smooth, positive weight
LECTURES ON MICROLOCAL CHARACTERIZATIONS IN LIMITED-ANGLE
 LECTURES ON MICROLOCAL CHARACTERIZATIONS IN LIMITED-ANGLE TOMOGRAPHY Jürgen Frikel 4 LECTURES 1 Today: Introduction to the mathematics of computerized tomography 2 Mathematics of computerized tomography
LECTURES ON MICROLOCAL CHARACTERIZATIONS IN LIMITED-ANGLE TOMOGRAPHY Jürgen Frikel 4 LECTURES 1 Today: Introduction to the mathematics of computerized tomography 2 Mathematics of computerized tomography
EE 4372 Tomography. Carlos E. Davila, Dept. of Electrical Engineering Southern Methodist University
 EE 4372 Tomography Carlos E. Davila, Dept. of Electrical Engineering Southern Methodist University EE 4372, SMU Department of Electrical Engineering 86 Tomography: Background 1-D Fourier Transform: F(
EE 4372 Tomography Carlos E. Davila, Dept. of Electrical Engineering Southern Methodist University EE 4372, SMU Department of Electrical Engineering 86 Tomography: Background 1-D Fourier Transform: F(
Hamburger Beiträge zur Angewandten Mathematik
 Hamburger Beiträge zur Angewandten Mathematik Error Estimates for Filtered Back Projection Matthias Beckmann and Armin Iske Nr. 2015-03 January 2015 Error Estimates for Filtered Back Projection Matthias
Hamburger Beiträge zur Angewandten Mathematik Error Estimates for Filtered Back Projection Matthias Beckmann and Armin Iske Nr. 2015-03 January 2015 Error Estimates for Filtered Back Projection Matthias
Quadrature Formula for Computed Tomography
 Quadrature Formula for Computed Tomography orislav ojanov, Guergana Petrova August 13, 009 Abstract We give a bivariate analog of the Micchelli-Rivlin quadrature for computing the integral of a function
Quadrature Formula for Computed Tomography orislav ojanov, Guergana Petrova August 13, 009 Abstract We give a bivariate analog of the Micchelli-Rivlin quadrature for computing the integral of a function
Interpolation procedure in filtered backprojection algorithm for the limited-angle tomography
 Interpolation procedure in filtered backprojection algorithm for the limited-angle tomography Aleksander Denisiuk 1 Abstract A new data completion procedure for the limited-angle tomography is proposed.
Interpolation procedure in filtered backprojection algorithm for the limited-angle tomography Aleksander Denisiuk 1 Abstract A new data completion procedure for the limited-angle tomography is proposed.
Efficient Solution Methods for Inverse Problems with Application to Tomography Radon Transform and Friends
 Efficient Solution Methods for Inverse Problems with Application to Tomography Radon Transform and Friends Alfred K. Louis Institut für Angewandte Mathematik Universität des Saarlandes 66041 Saarbrücken
Efficient Solution Methods for Inverse Problems with Application to Tomography Radon Transform and Friends Alfred K. Louis Institut für Angewandte Mathematik Universität des Saarlandes 66041 Saarbrücken
A review: The Laplacian and the d Alembertian. j=1
 Chapter One A review: The Laplacian and the d Alembertian 1.1 THE LAPLACIAN One of the main goals of this course is to understand well the solution of wave equation both in Euclidean space and on manifolds
Chapter One A review: The Laplacian and the d Alembertian 1.1 THE LAPLACIAN One of the main goals of this course is to understand well the solution of wave equation both in Euclidean space and on manifolds
Reminder Notes for the Course on Distribution Theory
 Reminder Notes for the Course on Distribution Theory T. C. Dorlas Dublin Institute for Advanced Studies School of Theoretical Physics 10 Burlington Road, Dublin 4, Ireland. Email: dorlas@stp.dias.ie March
Reminder Notes for the Course on Distribution Theory T. C. Dorlas Dublin Institute for Advanced Studies School of Theoretical Physics 10 Burlington Road, Dublin 4, Ireland. Email: dorlas@stp.dias.ie March
u xx + u yy = 0. (5.1)
 Chapter 5 Laplace Equation The following equation is called Laplace equation in two independent variables x, y: The non-homogeneous problem u xx + u yy =. (5.1) u xx + u yy = F, (5.) where F is a function
Chapter 5 Laplace Equation The following equation is called Laplace equation in two independent variables x, y: The non-homogeneous problem u xx + u yy =. (5.1) u xx + u yy = F, (5.) where F is a function
Heisenberg's inequality for Fourier transform
 Heisenberg's inequality for Fourier transform Riccardo Pascuzzo Abstract In this paper, we prove the Heisenberg's inequality using the Fourier transform. Then we show that the equality holds for the Gaussian
Heisenberg's inequality for Fourier transform Riccardo Pascuzzo Abstract In this paper, we prove the Heisenberg's inequality using the Fourier transform. Then we show that the equality holds for the Gaussian
I. Introduction. A New Method for Inverting Integrals Attenuated Radon Transform (SPECT) D to N map for Moving Boundary Value Problems
 I. Introduction A New Method for Inverting Integrals Attenuated Radon Transform (SPECT) D to N map for Moving Boundary Value Problems F(k) = T 0 e k2 t+ikl(t) f (t)dt, k C. Integrable Nonlinear PDEs in
I. Introduction A New Method for Inverting Integrals Attenuated Radon Transform (SPECT) D to N map for Moving Boundary Value Problems F(k) = T 0 e k2 t+ikl(t) f (t)dt, k C. Integrable Nonlinear PDEs in
SPHERICAL RADON TRANSFORMS AND MATHEMATICAL PROBLEMS OF THERMOACOUSTIC TOMOGRAPHY. A Dissertation GAIK AMBARTSOUMIAN
 SPHERICAL RADON TRANSFORMS AND MATHEMATICAL PROBLEMS OF THERMOACOUSTIC TOMOGRAPHY A Dissertation by GAIK AMBARTSOUMIAN Submitted to the Office of Graduate Studies of Texas A&M University in partial fulfillment
SPHERICAL RADON TRANSFORMS AND MATHEMATICAL PROBLEMS OF THERMOACOUSTIC TOMOGRAPHY A Dissertation by GAIK AMBARTSOUMIAN Submitted to the Office of Graduate Studies of Texas A&M University in partial fulfillment
be the set of complex valued 2π-periodic functions f on R such that
 . Fourier series. Definition.. Given a real number P, we say a complex valued function f on R is P -periodic if f(x + P ) f(x) for all x R. We let be the set of complex valued -periodic functions f on
. Fourier series. Definition.. Given a real number P, we say a complex valued function f on R is P -periodic if f(x + P ) f(x) for all x R. We let be the set of complex valued -periodic functions f on
f(x) cos dx L L f(x) sin L + b n sin a n cos
 Chapter Fourier Series and Transforms. Fourier Series et f(x be an integrable functin on [, ]. Then the fourier co-ecients are dened as a n b n f(x cos f(x sin The claim is that the function f then can
Chapter Fourier Series and Transforms. Fourier Series et f(x be an integrable functin on [, ]. Then the fourier co-ecients are dened as a n b n f(x cos f(x sin The claim is that the function f then can
Medical Imaging. Transmission Measurement
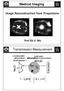 Medical Imaging Image Recontruction from Projection Prof Ed X. Wu Tranmiion Meaurement ( meaurable unknown attenuation, aborption cro-ection hadowgram ) I(ϕ,ξ) µ(x,) I = I o exp A(x, )dl L X-ra ource X-Ra
Medical Imaging Image Recontruction from Projection Prof Ed X. Wu Tranmiion Meaurement ( meaurable unknown attenuation, aborption cro-ection hadowgram ) I(ϕ,ξ) µ(x,) I = I o exp A(x, )dl L X-ra ource X-Ra
2D X-Ray Tomographic Reconstruction From Few Projections
 2D X-Ray Tomographic Reconstruction From Few Projections Application of Compressed Sensing Theory CEA-LID, Thalès, UJF 6 octobre 2009 Introduction Plan 1 Introduction 2 Overview of Compressed Sensing Theory
2D X-Ray Tomographic Reconstruction From Few Projections Application of Compressed Sensing Theory CEA-LID, Thalès, UJF 6 octobre 2009 Introduction Plan 1 Introduction 2 Overview of Compressed Sensing Theory
Chapter III Beyond L 2 : Fourier transform of distributions
 Chapter III Beyond L 2 : Fourier transform of distributions 113 1 Basic definitions and first examples In this section we generalize the theory of the Fourier transform developed in Section 1 to distributions.
Chapter III Beyond L 2 : Fourier transform of distributions 113 1 Basic definitions and first examples In this section we generalize the theory of the Fourier transform developed in Section 1 to distributions.
Generalized Transforms of Radon Type and Their Applications
 Proceedings of Symposia in Applied Mathematics Generalized Transforms of Radon Type and Their Applications Peter Kuchment Abstract. These notes represent an extended version of the contents of the third
Proceedings of Symposia in Applied Mathematics Generalized Transforms of Radon Type and Their Applications Peter Kuchment Abstract. These notes represent an extended version of the contents of the third
ψ( ) k (r) which take the asymtotic form far away from the scattering center: k (r) = E kψ (±) φ k (r) = e ikr
 Scattering Theory Consider scattering of two particles in the center of mass frame, or equivalently scattering of a single particle from a potential V (r), which becomes zero suciently fast as r. The initial
Scattering Theory Consider scattering of two particles in the center of mass frame, or equivalently scattering of a single particle from a potential V (r), which becomes zero suciently fast as r. The initial
RKHS, Mercer s theorem, Unbounded domains, Frames and Wavelets Class 22, 2004 Tomaso Poggio and Sayan Mukherjee
 RKHS, Mercer s theorem, Unbounded domains, Frames and Wavelets 9.520 Class 22, 2004 Tomaso Poggio and Sayan Mukherjee About this class Goal To introduce an alternate perspective of RKHS via integral operators
RKHS, Mercer s theorem, Unbounded domains, Frames and Wavelets 9.520 Class 22, 2004 Tomaso Poggio and Sayan Mukherjee About this class Goal To introduce an alternate perspective of RKHS via integral operators
1 Vectors and 3-Dimensional Geometry
 Calculus III (part ): Vectors and 3-Dimensional Geometry (by Evan Dummit, 07, v..55) Contents Vectors and 3-Dimensional Geometry. Functions of Several Variables and 3-Space..................................
Calculus III (part ): Vectors and 3-Dimensional Geometry (by Evan Dummit, 07, v..55) Contents Vectors and 3-Dimensional Geometry. Functions of Several Variables and 3-Space..................................
Nonlinear Radon and Fourier Transforms
 Nonlinear Radon and Fourier Transforms François Rouvière Université de Nice Laboratoire Dieudonné, UMR 7351 May 16, 2015 Abstract In this note we explain a generalization, due to Leon Ehrenpreis, of the
Nonlinear Radon and Fourier Transforms François Rouvière Université de Nice Laboratoire Dieudonné, UMR 7351 May 16, 2015 Abstract In this note we explain a generalization, due to Leon Ehrenpreis, of the
EXAMINATION: MATHEMATICAL TECHNIQUES FOR IMAGE ANALYSIS
 EXAMINATION: MATHEMATICAL TECHNIQUES FOR IMAGE ANALYSIS Course code: 8D Date: Thursday April 8 th, Time: 4h 7h Place: AUD 3 Read this first! Write your name and student identification number on each paper
EXAMINATION: MATHEMATICAL TECHNIQUES FOR IMAGE ANALYSIS Course code: 8D Date: Thursday April 8 th, Time: 4h 7h Place: AUD 3 Read this first! Write your name and student identification number on each paper
ON RADON TRANSFORMS AND THE KAPPA OPERATOR. François Rouvière (Université de Nice) Bruxelles, November 24, 2006
 ON RADON TRANSFORMS AND THE KAPPA OPERATOR François Rouvière (Université de Nice) Bruxelles, November 24, 2006 1. Introduction In 1917 Johann Radon solved the following problem : nd a function f on the
ON RADON TRANSFORMS AND THE KAPPA OPERATOR François Rouvière (Université de Nice) Bruxelles, November 24, 2006 1. Introduction In 1917 Johann Radon solved the following problem : nd a function f on the
18 Green s function for the Poisson equation
 8 Green s function for the Poisson equation Now we have some experience working with Green s functions in dimension, therefore, we are ready to see how Green s functions can be obtained in dimensions 2
8 Green s function for the Poisson equation Now we have some experience working with Green s functions in dimension, therefore, we are ready to see how Green s functions can be obtained in dimensions 2
Overview I. Approaches to Reconstruction in Photoacoustic Tomography. Bell and the Photoacoustic Effect I. Overview II
 I Introduction Photoacoustic Tomography Approaches to Reconstruction in Photoacoustic Tomography March 9, 2011 Photoacoustic tomography (PAT) and the related thermoacoustic tomography (TAT) are important
I Introduction Photoacoustic Tomography Approaches to Reconstruction in Photoacoustic Tomography March 9, 2011 Photoacoustic tomography (PAT) and the related thermoacoustic tomography (TAT) are important
BioE Exam 1 10/9/2018 Answer Sheet - Correct answer is A for all questions. 1. The sagittal plane
 BioE 1330 - Exam 1 10/9/2018 Answer Sheet - Correct answer is A for all questions 1. The sagittal plane A. is perpendicular to the coronal plane. B. is parallel to the top of the head. C. represents a
BioE 1330 - Exam 1 10/9/2018 Answer Sheet - Correct answer is A for all questions 1. The sagittal plane A. is perpendicular to the coronal plane. B. is parallel to the top of the head. C. represents a
Numerical Harmonic Analysis on the Hyperbolic Plane
 Numerical Harmonic Analysis on the Hyperbolic Plane Buma Fridman, Peter Kuchment, Kirk Lancaster, Serguei Lissianoi, Mila Mogilevsky, Daowei Ma, Igor Ponomarev, and Vassilis Papanicolaou Mathematics and
Numerical Harmonic Analysis on the Hyperbolic Plane Buma Fridman, Peter Kuchment, Kirk Lancaster, Serguei Lissianoi, Mila Mogilevsky, Daowei Ma, Igor Ponomarev, and Vassilis Papanicolaou Mathematics and
Garrett: `Bernstein's analytic continuation of complex powers' 2 Let f be a polynomial in x 1 ; : : : ; x n with real coecients. For complex s, let f
 1 Bernstein's analytic continuation of complex powers c1995, Paul Garrett, garrettmath.umn.edu version January 27, 1998 Analytic continuation of distributions Statement of the theorems on analytic continuation
1 Bernstein's analytic continuation of complex powers c1995, Paul Garrett, garrettmath.umn.edu version January 27, 1998 Analytic continuation of distributions Statement of the theorems on analytic continuation
Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information
 1 Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information Emmanuel Candès, California Institute of Technology International Conference on Computational Harmonic
1 Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information Emmanuel Candès, California Institute of Technology International Conference on Computational Harmonic
Part 2 Introduction to Microlocal Analysis
 Part 2 Introduction to Microlocal Analysis Birsen Yazıcı & Venky Krishnan Rensselaer Polytechnic Institute Electrical, Computer and Systems Engineering August 2 nd, 2010 Outline PART II Pseudodifferential
Part 2 Introduction to Microlocal Analysis Birsen Yazıcı & Venky Krishnan Rensselaer Polytechnic Institute Electrical, Computer and Systems Engineering August 2 nd, 2010 Outline PART II Pseudodifferential
Inverse problems in statistics
 Inverse problems in statistics Laurent Cavalier (Université Aix-Marseille 1, France) YES, Eurandom, 10 October 2011 p. 1/27 Table of contents YES, Eurandom, 10 October 2011 p. 2/27 Table of contents 1)
Inverse problems in statistics Laurent Cavalier (Université Aix-Marseille 1, France) YES, Eurandom, 10 October 2011 p. 1/27 Table of contents YES, Eurandom, 10 October 2011 p. 2/27 Table of contents 1)
Fourier transform of tempered distributions
 Fourier transform of tempered distributions 1 Test functions and distributions As we have seen before, many functions are not classical in the sense that they cannot be evaluated at any point. For eample,
Fourier transform of tempered distributions 1 Test functions and distributions As we have seen before, many functions are not classical in the sense that they cannot be evaluated at any point. For eample,
Aero III/IV Conformal Mapping
 Aero III/IV Conformal Mapping View complex function as a mapping Unlike a real function, a complex function w = f(z) cannot be represented by a curve. Instead it is useful to view it as a mapping. Write
Aero III/IV Conformal Mapping View complex function as a mapping Unlike a real function, a complex function w = f(z) cannot be represented by a curve. Instead it is useful to view it as a mapping. Write
Phys 622 Problems Chapter 6
 1 Problem 1 Elastic scattering Phys 622 Problems Chapter 6 A heavy scatterer interacts with a fast electron with a potential V (r) = V e r/r. (a) Find the differential cross section dσ dω = f(θ) 2 in the
1 Problem 1 Elastic scattering Phys 622 Problems Chapter 6 A heavy scatterer interacts with a fast electron with a potential V (r) = V e r/r. (a) Find the differential cross section dσ dω = f(θ) 2 in the
8 Singular Integral Operators and L p -Regularity Theory
 8 Singular Integral Operators and L p -Regularity Theory 8. Motivation See hand-written notes! 8.2 Mikhlin Multiplier Theorem Recall that the Fourier transformation F and the inverse Fourier transformation
8 Singular Integral Operators and L p -Regularity Theory 8. Motivation See hand-written notes! 8.2 Mikhlin Multiplier Theorem Recall that the Fourier transformation F and the inverse Fourier transformation
Jim Lambers ENERGY 281 Spring Quarter Lecture 3 Notes
 Jim Lambers ENERGY 8 Spring Quarter 7-8 Lecture 3 Notes These notes are based on Rosalind Archer s PE8 lecture notes, with some revisions by Jim Lambers. Introduction The Fourier transform is an integral
Jim Lambers ENERGY 8 Spring Quarter 7-8 Lecture 3 Notes These notes are based on Rosalind Archer s PE8 lecture notes, with some revisions by Jim Lambers. Introduction The Fourier transform is an integral
Fourier Series Example
 Fourier Series Example Let us compute the Fourier series for the function on the interval [ π,π]. f(x) = x f is an odd function, so the a n are zero, and thus the Fourier series will be of the form f(x)
Fourier Series Example Let us compute the Fourier series for the function on the interval [ π,π]. f(x) = x f is an odd function, so the a n are zero, and thus the Fourier series will be of the form f(x)
Separation of Variables in Polar and Spherical Coordinates
 Separation of Variables in Polar and Spherical Coordinates Polar Coordinates Suppose we are given the potential on the inside surface of an infinitely long cylindrical cavity, and we want to find the potential
Separation of Variables in Polar and Spherical Coordinates Polar Coordinates Suppose we are given the potential on the inside surface of an infinitely long cylindrical cavity, and we want to find the potential
Kernel-based Image Reconstruction from scattered Radon data by (anisotropic) positive definite functions
 Kernel-based Image Reconstruction from scattered Radon data by (anisotropic) positive definite functions Stefano De Marchi 1 February 5, 2016 1 Joint work with A. Iske (Hamburg, D), A. Sironi (Lousanne,
Kernel-based Image Reconstruction from scattered Radon data by (anisotropic) positive definite functions Stefano De Marchi 1 February 5, 2016 1 Joint work with A. Iske (Hamburg, D), A. Sironi (Lousanne,
Numerical Methods for geodesic X-ray transforms and applications to open theoretical questions
 Numerical Methods for geodesic X-ray transforms and applications to open theoretical questions François Monard Department of Mathematics, University of Washington. Nov. 13, 2014 UW Numerical Analysis Research
Numerical Methods for geodesic X-ray transforms and applications to open theoretical questions François Monard Department of Mathematics, University of Washington. Nov. 13, 2014 UW Numerical Analysis Research
Compactness in Product Spaces
 Pure Mathematical Sciences, Vol. 1, 2012, no. 3, 107-113 Compactness in Product Spaces WonSok Yoo Department of Applied Mathematics Kumoh National Institute of Technology Kumi 730-701, Korea wsyoo@kumoh.ac.kr
Pure Mathematical Sciences, Vol. 1, 2012, no. 3, 107-113 Compactness in Product Spaces WonSok Yoo Department of Applied Mathematics Kumoh National Institute of Technology Kumi 730-701, Korea wsyoo@kumoh.ac.kr
ON A CLASS OF GENERALIZED RADON TRANSFORMS AND ITS APPLICATION IN IMAGING SCIENCE
 ON A CLASS OF GENERALIZED RADON TRANSFORMS AND ITS APPLICATION IN IMAGING SCIENCE T.T. TRUONG 1 AND M.K. NGUYEN 2 1 University of Cergy-Pontoise, LPTM CNRS UMR 889, F-9532, France e-mail: truong@u-cergy.fr
ON A CLASS OF GENERALIZED RADON TRANSFORMS AND ITS APPLICATION IN IMAGING SCIENCE T.T. TRUONG 1 AND M.K. NGUYEN 2 1 University of Cergy-Pontoise, LPTM CNRS UMR 889, F-9532, France e-mail: truong@u-cergy.fr
About the primer To review concepts in functional analysis that Goal briey used throughout the course. The following be will concepts will be describe
 Camp 1: Functional analysis Math Mukherjee + Alessandro Verri Sayan About the primer To review concepts in functional analysis that Goal briey used throughout the course. The following be will concepts
Camp 1: Functional analysis Math Mukherjee + Alessandro Verri Sayan About the primer To review concepts in functional analysis that Goal briey used throughout the course. The following be will concepts
Partial Differential Equations Summary
 Partial Differential Equations Summary 1. The heat equation Many physical processes are governed by partial differential equations. temperature of a rod. In this chapter, we will examine exactly that.
Partial Differential Equations Summary 1. The heat equation Many physical processes are governed by partial differential equations. temperature of a rod. In this chapter, we will examine exactly that.
The spherical mean value operator with centers on a sphere
 The spherical mean value operator with centers on a sphere David Finch Department of Mathematics Oregon State University Corvallis, OR 9733-465 Email: finch@math.oregonstate.edu Rakesh Department of Mathematics
The spherical mean value operator with centers on a sphere David Finch Department of Mathematics Oregon State University Corvallis, OR 9733-465 Email: finch@math.oregonstate.edu Rakesh Department of Mathematics
Generalized Functions Theory and Technique Second Edition
 Ram P. Kanwal Generalized Functions Theory and Technique Second Edition Birkhauser Boston Basel Berlin Contents Preface to the Second Edition x Chapter 1. The Dirac Delta Function and Delta Sequences 1
Ram P. Kanwal Generalized Functions Theory and Technique Second Edition Birkhauser Boston Basel Berlin Contents Preface to the Second Edition x Chapter 1. The Dirac Delta Function and Delta Sequences 1
QM1 - Tutorial 1 The Bohr Atom and Mathematical Introduction
 QM - Tutorial The Bohr Atom and Mathematical Introduction 26 October 207 Contents Bohr Atom. Energy of a Photon - The Photo Electric Eect.................................2 The Discrete Energy Spectrum
QM - Tutorial The Bohr Atom and Mathematical Introduction 26 October 207 Contents Bohr Atom. Energy of a Photon - The Photo Electric Eect.................................2 The Discrete Energy Spectrum
Today s lecture. The Fourier transform. Sampling, aliasing, interpolation The Fast Fourier Transform (FFT) algorithm
 Today s lecture The Fourier transform What is it? What is it useful for? What are its properties? Sampling, aliasing, interpolation The Fast Fourier Transform (FFT) algorithm Jean Baptiste Joseph Fourier
Today s lecture The Fourier transform What is it? What is it useful for? What are its properties? Sampling, aliasing, interpolation The Fast Fourier Transform (FFT) algorithm Jean Baptiste Joseph Fourier
Fourier Transform & Sobolev Spaces
 Fourier Transform & Sobolev Spaces Michael Reiter, Arthur Schuster Summer Term 2008 Abstract We introduce the concept of weak derivative that allows us to define new interesting Hilbert spaces the Sobolev
Fourier Transform & Sobolev Spaces Michael Reiter, Arthur Schuster Summer Term 2008 Abstract We introduce the concept of weak derivative that allows us to define new interesting Hilbert spaces the Sobolev
The mathematics behind Computertomography
 Radon transforms The mathematics behind Computertomography PD Dr. Swanhild Bernstein, Institute of Applied Analysis, Freiberg University of Mining and Technology, International Summer academic course 2008,
Radon transforms The mathematics behind Computertomography PD Dr. Swanhild Bernstein, Institute of Applied Analysis, Freiberg University of Mining and Technology, International Summer academic course 2008,
Part II: Magnetic Resonance Imaging (MRI)
 Part II: Magnetic Resonance Imaging (MRI) Contents Magnetic Field Gradients Selective Excitation Spatially Resolved Reception k-space Gradient Echo Sequence Spin Echo Sequence Magnetic Resonance Imaging
Part II: Magnetic Resonance Imaging (MRI) Contents Magnetic Field Gradients Selective Excitation Spatially Resolved Reception k-space Gradient Echo Sequence Spin Echo Sequence Magnetic Resonance Imaging
UNIVERSITY OF MARYLAND Department of Physics College Park, Maryland. PHYSICS Ph.D. QUALIFYING EXAMINATION PART II
 UNIVERSITY OF MARYLAND Department of Physics College Park, Maryland PHYSICS Ph.D. QUALIFYING EXAMINATION PART II August 23, 208 9:00 a.m. :00 p.m. Do any four problems. Each problem is worth 25 points.
UNIVERSITY OF MARYLAND Department of Physics College Park, Maryland PHYSICS Ph.D. QUALIFYING EXAMINATION PART II August 23, 208 9:00 a.m. :00 p.m. Do any four problems. Each problem is worth 25 points.
LECTURES ON MICROLOCAL CHARACTERIZATIONS IN LIMITED-ANGLE
 LECTURES ON MICROLOCAL CHARACTERIZATIONS IN LIMITED-ANGLE TOMOGRAPHY Jürgen Frikel 4 LECTURES 1 Nov. 11: Introduction to the mathematics of computerized tomography 2 Today: Introduction to the basic concepts
LECTURES ON MICROLOCAL CHARACTERIZATIONS IN LIMITED-ANGLE TOMOGRAPHY Jürgen Frikel 4 LECTURES 1 Nov. 11: Introduction to the mathematics of computerized tomography 2 Today: Introduction to the basic concepts
CONVEXIFICATION OF COEFFICIENT INVERSE PROBLEMS
 CONVEXIFICATION OF COEFFICIENT INVERSE PROBLEMS Michael V. Klibanov Department of Mathematics and Statistics University of North Carolina at Charlotte Charlotte, NC 28223, USA THE MOST RECENT RESULT PDE-based
CONVEXIFICATION OF COEFFICIENT INVERSE PROBLEMS Michael V. Klibanov Department of Mathematics and Statistics University of North Carolina at Charlotte Charlotte, NC 28223, USA THE MOST RECENT RESULT PDE-based
MB-JASS D Reconstruction. Hannes Hofmann March 2006
 MB-JASS 2006 2-D Reconstruction Hannes Hofmann 19 29 March 2006 Outline Projections Radon Transform Fourier-Slice-Theorem Filtered Backprojection Ramp Filter 19 29 Mar 2006 Hannes Hofmann 2 Parallel Projections
MB-JASS 2006 2-D Reconstruction Hannes Hofmann 19 29 March 2006 Outline Projections Radon Transform Fourier-Slice-Theorem Filtered Backprojection Ramp Filter 19 29 Mar 2006 Hannes Hofmann 2 Parallel Projections
Part 2 Introduction to Microlocal Analysis
 Part 2 Introduction to Microlocal Analysis Birsen Yazıcı& Venky Krishnan Rensselaer Polytechnic Institute Electrical, Computer and Systems Engineering March 15 th, 2010 Outline PART II Pseudodifferential(ψDOs)
Part 2 Introduction to Microlocal Analysis Birsen Yazıcı& Venky Krishnan Rensselaer Polytechnic Institute Electrical, Computer and Systems Engineering March 15 th, 2010 Outline PART II Pseudodifferential(ψDOs)
EXPOSITORY NOTES ON DISTRIBUTION THEORY, FALL 2018
 EXPOSITORY NOTES ON DISTRIBUTION THEORY, FALL 2018 While these notes are under construction, I expect there will be many typos. The main reference for this is volume 1 of Hörmander, The analysis of liner
EXPOSITORY NOTES ON DISTRIBUTION THEORY, FALL 2018 While these notes are under construction, I expect there will be many typos. The main reference for this is volume 1 of Hörmander, The analysis of liner
The Radon Transform and the Mathematics of Medical Imaging
 Colby College Digital Commons @ Colby Honors Theses Student Research 2012 The Radon Transform and the Mathematics of Medical Imaging Jen Beatty Colby College Follow this and additional works at: http://digitalcommons.colby.edu/honorstheses
Colby College Digital Commons @ Colby Honors Theses Student Research 2012 The Radon Transform and the Mathematics of Medical Imaging Jen Beatty Colby College Follow this and additional works at: http://digitalcommons.colby.edu/honorstheses
Lecture 4: Fourier Transforms.
 1 Definition. Lecture 4: Fourier Transforms. We now come to Fourier transforms, which we give in the form of a definition. First we define the spaces L 1 () and L 2 (). Definition 1.1 The space L 1 ()
1 Definition. Lecture 4: Fourier Transforms. We now come to Fourier transforms, which we give in the form of a definition. First we define the spaces L 1 () and L 2 (). Definition 1.1 The space L 1 ()
Convolution and Linear Systems
 CS 450: Introduction to Digital Signal and Image Processing Bryan Morse BYU Computer Science Introduction Analyzing Systems Goal: analyze a device that turns one signal into another. Notation: f (t) g(t)
CS 450: Introduction to Digital Signal and Image Processing Bryan Morse BYU Computer Science Introduction Analyzing Systems Goal: analyze a device that turns one signal into another. Notation: f (t) g(t)
Math 251 December 14, 2005 Answer Key to Final Exam. 1 18pt 2 16pt 3 12pt 4 14pt 5 12pt 6 14pt 7 14pt 8 16pt 9 20pt 10 14pt Total 150pt
 Name Section Math 51 December 14, 5 Answer Key to Final Exam There are 1 questions on this exam. Many of them have multiple parts. The point value of each question is indicated either at the beginning
Name Section Math 51 December 14, 5 Answer Key to Final Exam There are 1 questions on this exam. Many of them have multiple parts. The point value of each question is indicated either at the beginning
Fourier-like Transforms
 L 2 (R) Solutions of Dilation Equations and Fourier-like Transforms David Malone December 6, 2000 Abstract We state a novel construction of the Fourier transform on L 2 (R) based on translation and dilation
L 2 (R) Solutions of Dilation Equations and Fourier-like Transforms David Malone December 6, 2000 Abstract We state a novel construction of the Fourier transform on L 2 (R) based on translation and dilation
A Spherical Harmonic Expansion of the Hilbert Transform on S 2. Oliver Fleischmann Cognitive Systems Group Kiel University.
 A Spherical Harmonic Expansion of the Hilbert Transform on S 2 Oliver Fleischmann Cognitive Systems Group Kiel University München 2010 Motivation Goal: Extract local structural information from signals
A Spherical Harmonic Expansion of the Hilbert Transform on S 2 Oliver Fleischmann Cognitive Systems Group Kiel University München 2010 Motivation Goal: Extract local structural information from signals
2 J. BRACHO, L. MONTEJANO, AND D. OLIVEROS Observe as an example, that the circle yields a Zindler carrousel with n chairs, because we can inscribe in
 A CLASSIFICATION THEOREM FOR ZINDLER CARROUSELS J. BRACHO, L. MONTEJANO, AND D. OLIVEROS Abstract. The purpose of this paper is to give a complete classication of Zindler Carrousels with ve chairs. This
A CLASSIFICATION THEOREM FOR ZINDLER CARROUSELS J. BRACHO, L. MONTEJANO, AND D. OLIVEROS Abstract. The purpose of this paper is to give a complete classication of Zindler Carrousels with ve chairs. This
MAC2313 Final A. (5 pts) 1. How many of the following are necessarily true? i. The vector field F = 2x + 3y, 3x 5y is conservative.
 MAC2313 Final A (5 pts) 1. How many of the following are necessarily true? i. The vector field F = 2x + 3y, 3x 5y is conservative. ii. The vector field F = 5(x 2 + y 2 ) 3/2 x, y is radial. iii. All constant
MAC2313 Final A (5 pts) 1. How many of the following are necessarily true? i. The vector field F = 2x + 3y, 3x 5y is conservative. ii. The vector field F = 5(x 2 + y 2 ) 3/2 x, y is radial. iii. All constant
f (t) K(t, u) d t. f (t) K 1 (t, u) d u. Integral Transform Inverse Fourier Transform
 Integral Transforms Massoud Malek An integral transform maps an equation from its original domain into another domain, where it might be manipulated and solved much more easily than in the original domain.
Integral Transforms Massoud Malek An integral transform maps an equation from its original domain into another domain, where it might be manipulated and solved much more easily than in the original domain.
Our goal is to solve a general constant coecient linear second order. this way but that will not always happen). Once we have y 1, it will always
 October 5 Relevant reading: Section 2.1, 2.2, 2.3 and 2.4 Our goal is to solve a general constant coecient linear second order ODE a d2 y dt + bdy + cy = g (t) 2 dt where a, b, c are constants and a 0.
October 5 Relevant reading: Section 2.1, 2.2, 2.3 and 2.4 Our goal is to solve a general constant coecient linear second order ODE a d2 y dt + bdy + cy = g (t) 2 dt where a, b, c are constants and a 0.
Math Camp Notes: Everything Else
 Math Camp Notes: Everything Else Systems of Dierential Equations Consider the general two-equation system of dierential equations: Steady States ẋ = f(x, y ẏ = g(x, y Just as before, we can nd the steady
Math Camp Notes: Everything Else Systems of Dierential Equations Consider the general two-equation system of dierential equations: Steady States ẋ = f(x, y ẏ = g(x, y Just as before, we can nd the steady
Math 234 Exam 3 Review Sheet
 Math 234 Exam 3 Review Sheet Jim Brunner LIST OF TOPIS TO KNOW Vector Fields lairaut s Theorem & onservative Vector Fields url Divergence Area & Volume Integrals Using oordinate Transforms hanging the
Math 234 Exam 3 Review Sheet Jim Brunner LIST OF TOPIS TO KNOW Vector Fields lairaut s Theorem & onservative Vector Fields url Divergence Area & Volume Integrals Using oordinate Transforms hanging the
Motivation: X.Ji, PRL 78, 61 (1997): DVCS, GPDs, ~J q,! GPDs are interesting physical observable! But do GPDs have a simple physical interpretation?
 Geometric Interpretation of Generalized Parton Distributions or: what DVCS has to do with the distribution of partons in the transverse plane PRD 62, 7153 (2). M.Burkardt New Mexico State Univ. & TU Munchen
Geometric Interpretation of Generalized Parton Distributions or: what DVCS has to do with the distribution of partons in the transverse plane PRD 62, 7153 (2). M.Burkardt New Mexico State Univ. & TU Munchen
Gaussian Measure of Sections of convex bodies
 Gaussian Measure of Sections of convex bodies A. Zvavitch Department of Mathematics, University of Missouri, Columbia, MO 652, USA Abstract In this paper we study properties of sections of convex bodies
Gaussian Measure of Sections of convex bodies A. Zvavitch Department of Mathematics, University of Missouri, Columbia, MO 652, USA Abstract In this paper we study properties of sections of convex bodies
Math 46, Applied Math (Spring 2009): Final
 Math 46, Applied Math (Spring 2009): Final 3 hours, 80 points total, 9 questions worth varying numbers of points 1. [8 points] Find an approximate solution to the following initial-value problem which
Math 46, Applied Math (Spring 2009): Final 3 hours, 80 points total, 9 questions worth varying numbers of points 1. [8 points] Find an approximate solution to the following initial-value problem which
Chapter 4. Adjoint-state methods
 Chapter 4 Adjoint-state methods As explained in section (3.4), the adjoint F of the linearized forward (modeling) operator F plays an important role in the formula of the functional gradient δj of the
Chapter 4 Adjoint-state methods As explained in section (3.4), the adjoint F of the linearized forward (modeling) operator F plays an important role in the formula of the functional gradient δj of the
PROBLEMS IN UNBOUNDED CYLINDRICAL DOMAINS
 PROBLEMS IN UNBOUNDED CYLINDRICAL DOMAINS PATRICK GUIDOTTI Mathematics Department, University of California, Patrick Guidotti, 103 Multipurpose Science and Technology Bldg, Irvine, CA 92697, USA 1. Introduction
PROBLEMS IN UNBOUNDED CYLINDRICAL DOMAINS PATRICK GUIDOTTI Mathematics Department, University of California, Patrick Guidotti, 103 Multipurpose Science and Technology Bldg, Irvine, CA 92697, USA 1. Introduction
9 Radon-Nikodym theorem and conditioning
 Tel Aviv University, 2015 Functions of real variables 93 9 Radon-Nikodym theorem and conditioning 9a Borel-Kolmogorov paradox............. 93 9b Radon-Nikodym theorem.............. 94 9c Conditioning.....................
Tel Aviv University, 2015 Functions of real variables 93 9 Radon-Nikodym theorem and conditioning 9a Borel-Kolmogorov paradox............. 93 9b Radon-Nikodym theorem.............. 94 9c Conditioning.....................
APPLIED PARTIM DIFFERENTIAL EQUATIONS with Fourier Series and Boundary Value Problems
 APPLIED PARTIM DIFFERENTIAL EQUATIONS with Fourier Series and Boundary Value Problems Fourth Edition Richard Haberman Department of Mathematics Southern Methodist University PEARSON Prentice Hall PEARSON
APPLIED PARTIM DIFFERENTIAL EQUATIONS with Fourier Series and Boundary Value Problems Fourth Edition Richard Haberman Department of Mathematics Southern Methodist University PEARSON Prentice Hall PEARSON
Error estimation for Quasi Monte Carlo Methods
 Error estimation for Quasi Monte Carlo Methods Introduction of an algorithm for integration relying on the fast transform coecients decay Lluís Antoni Jiménez Rugama July 11, 2013 Index 1 Introduction
Error estimation for Quasi Monte Carlo Methods Introduction of an algorithm for integration relying on the fast transform coecients decay Lluís Antoni Jiménez Rugama July 11, 2013 Index 1 Introduction
Fourier Series. ,..., e ixn ). Conversely, each 2π-periodic function φ : R n C induces a unique φ : T n C for which φ(e ix 1
 Fourier Series Let {e j : 1 j n} be the standard basis in R n. We say f : R n C is π-periodic in each variable if f(x + πe j ) = f(x) x R n, 1 j n. We can identify π-periodic functions with functions on
Fourier Series Let {e j : 1 j n} be the standard basis in R n. We say f : R n C is π-periodic in each variable if f(x + πe j ) = f(x) x R n, 1 j n. We can identify π-periodic functions with functions on
The Radon transform. Chris Stolk. December 18, 2014
 The Radon transform Chris Stolk December 18, 2014 1 Introduction In two dimensions the Radon transform is an integral transform that maps a function to its integrals over lines. Let θ S 1 and s R then
The Radon transform Chris Stolk December 18, 2014 1 Introduction In two dimensions the Radon transform is an integral transform that maps a function to its integrals over lines. Let θ S 1 and s R then
UNIVERSITY of LIMERICK OLLSCOIL LUIMNIGH
 UNIVERSITY of LIMERICK OLLSCOIL LUIMNIGH Faculty of Science and Engineering Department of Mathematics and Statistics END OF SEMESTER ASSESSMENT PAPER MODULE CODE: MA4006 SEMESTER: Spring 2011 MODULE TITLE:
UNIVERSITY of LIMERICK OLLSCOIL LUIMNIGH Faculty of Science and Engineering Department of Mathematics and Statistics END OF SEMESTER ASSESSMENT PAPER MODULE CODE: MA4006 SEMESTER: Spring 2011 MODULE TITLE:
Inverse problems Total Variation Regularization Mark van Kraaij Casa seminar 23 May 2007 Technische Universiteit Eindh ove n University of Technology
 Inverse problems Total Variation Regularization Mark van Kraaij Casa seminar 23 May 27 Introduction Fredholm first kind integral equation of convolution type in one space dimension: g(x) = 1 k(x x )f(x
Inverse problems Total Variation Regularization Mark van Kraaij Casa seminar 23 May 27 Introduction Fredholm first kind integral equation of convolution type in one space dimension: g(x) = 1 k(x x )f(x
LECTURE 3 Functional spaces on manifolds
 LECTURE 3 Functional spaces on manifolds The aim of this section is to introduce Sobolev spaces on manifolds (or on vector bundles over manifolds). These will be the Banach spaces of sections we were after
LECTURE 3 Functional spaces on manifolds The aim of this section is to introduce Sobolev spaces on manifolds (or on vector bundles over manifolds). These will be the Banach spaces of sections we were after
THE RESTRICTION PROBLEM AND THE TOMAS-STEIN THEOREM
 THE RESTRICTION PROBLEM AND THE TOMAS-STEIN THEOREM DENNIS KRIVENTSOV Abstract. E. M. Stein s restriction problem for Fourier transforms is a deep and only partially solved conjecture in harmonic analysis.
THE RESTRICTION PROBLEM AND THE TOMAS-STEIN THEOREM DENNIS KRIVENTSOV Abstract. E. M. Stein s restriction problem for Fourier transforms is a deep and only partially solved conjecture in harmonic analysis.
Average theorem, Restriction theorem and Strichartz estimates
 Average theorem, Restriction theorem and trichartz estimates 2 August 27 Abstract We provide the details of the proof of the average theorem and the restriction theorem. Emphasis has been placed on the
Average theorem, Restriction theorem and trichartz estimates 2 August 27 Abstract We provide the details of the proof of the average theorem and the restriction theorem. Emphasis has been placed on the
MATH 52 FINAL EXAM DECEMBER 7, 2009
 MATH 52 FINAL EXAM DECEMBER 7, 2009 THIS IS A CLOSED BOOK, CLOSED NOTES EXAM. NO CALCULATORS OR OTHER ELECTRONIC DEVICES ARE PERMITTED. IF YOU NEED EXTRA SPACE, PLEASE USE THE BACK OF THE PREVIOUS PROB-
MATH 52 FINAL EXAM DECEMBER 7, 2009 THIS IS A CLOSED BOOK, CLOSED NOTES EXAM. NO CALCULATORS OR OTHER ELECTRONIC DEVICES ARE PERMITTED. IF YOU NEED EXTRA SPACE, PLEASE USE THE BACK OF THE PREVIOUS PROB-
AN INVERSE PROBLEM FOR THE WAVE EQUATION WITH A TIME DEPENDENT COEFFICIENT
 AN INVERSE PROBLEM FOR THE WAVE EQUATION WITH A TIME DEPENDENT COEFFICIENT Rakesh Department of Mathematics University of Delaware Newark, DE 19716 A.G.Ramm Department of Mathematics Kansas State University
AN INVERSE PROBLEM FOR THE WAVE EQUATION WITH A TIME DEPENDENT COEFFICIENT Rakesh Department of Mathematics University of Delaware Newark, DE 19716 A.G.Ramm Department of Mathematics Kansas State University
Even and odd functions
 Connexions module: m15279 1 Even and odd functions Sunil Kumar Singh This work is produced by The Connexions Project and licensed under the Creative Commons Attribution License Even and odd functions are
Connexions module: m15279 1 Even and odd functions Sunil Kumar Singh This work is produced by The Connexions Project and licensed under the Creative Commons Attribution License Even and odd functions are
GBS765 Electron microscopy
 GBS765 Electron microscopy Lecture 1 Waves and Fourier transforms 10/14/14 9:05 AM Some fundamental concepts: Periodicity! If there is some a, for a function f(x), such that f(x) = f(x + na) then function
GBS765 Electron microscopy Lecture 1 Waves and Fourier transforms 10/14/14 9:05 AM Some fundamental concepts: Periodicity! If there is some a, for a function f(x), such that f(x) = f(x + na) then function
Final Examination Solutions
 Math. 42 Fulling) 4 December 25 Final Examination Solutions Calculators may be used for simple arithmetic operations only! Laplacian operator in polar coordinates: Some possibly useful information 2 u
Math. 42 Fulling) 4 December 25 Final Examination Solutions Calculators may be used for simple arithmetic operations only! Laplacian operator in polar coordinates: Some possibly useful information 2 u
Chapter One. The Calderón-Zygmund Theory I: Ellipticity
 Chapter One The Calderón-Zygmund Theory I: Ellipticity Our story begins with a classical situation: convolution with homogeneous, Calderón- Zygmund ( kernels on R n. Let S n 1 R n denote the unit sphere
Chapter One The Calderón-Zygmund Theory I: Ellipticity Our story begins with a classical situation: convolution with homogeneous, Calderón- Zygmund ( kernels on R n. Let S n 1 R n denote the unit sphere
Feature Reconstruction in Tomography
 Feature Reconstruction in Tomography Alfred K. Louis Institut für Angewandte Mathematik Universität des Saarlandes 66041 Saarbrücken http://www.num.uni-sb.de louis@num.uni-sb.de Wien, July 20, 2009 Images
Feature Reconstruction in Tomography Alfred K. Louis Institut für Angewandte Mathematik Universität des Saarlandes 66041 Saarbrücken http://www.num.uni-sb.de louis@num.uni-sb.de Wien, July 20, 2009 Images
Tomography and Sampling Theory
 Tomography and Sampling Theory Adel Faridani Department of Mathematics Oregon State University January 11, 2006 Tomography and Sampling Theory p. 1/34 The Divergent Beam X-Ray Transform D z f(ω) = 0 f(z
Tomography and Sampling Theory Adel Faridani Department of Mathematics Oregon State University January 11, 2006 Tomography and Sampling Theory p. 1/34 The Divergent Beam X-Ray Transform D z f(ω) = 0 f(z
Stability of optimization problems with stochastic dominance constraints
 Stability of optimization problems with stochastic dominance constraints D. Dentcheva and W. Römisch Stevens Institute of Technology, Hoboken Humboldt-University Berlin www.math.hu-berlin.de/~romisch SIAM
Stability of optimization problems with stochastic dominance constraints D. Dentcheva and W. Römisch Stevens Institute of Technology, Hoboken Humboldt-University Berlin www.math.hu-berlin.de/~romisch SIAM
Continuous Frames and Sampling
 NuHAG University of Vienna, Faculty for Mathematics Marie Curie Fellow within the European network HASSIP HPRN-CT-2002-285 SampTA05, Samsun July 2005 Joint work with Massimo Fornasier Overview 1 Continuous
NuHAG University of Vienna, Faculty for Mathematics Marie Curie Fellow within the European network HASSIP HPRN-CT-2002-285 SampTA05, Samsun July 2005 Joint work with Massimo Fornasier Overview 1 Continuous
