2 J. BRACHO, L. MONTEJANO, AND D. OLIVEROS Observe as an example, that the circle yields a Zindler carrousel with n chairs, because we can inscribe in
|
|
|
- Augusta Charles
- 6 years ago
- Views:
Transcription
1 A CLASSIFICATION THEOREM FOR ZINDLER CARROUSELS J. BRACHO, L. MONTEJANO, AND D. OLIVEROS Abstract. The purpose of this paper is to give a complete classication of Zindler Carrousels with ve chairs. This classication theorem gives enough evidence to show the non existence of gures, dierent from the disk, that oat in equilibrium in every position for the corresponding perimetral densities. 1. Introduction and Carrousels Zindler Carrousels are analytic dynamical systems. The initial motivation for their study was the following. Auerbach [1] proved that Zindler curves bound gures, dierent from the disk, that oat in equilibrium in every position for the density 1/2. In general, for gures that oat in equilibrium in every position some remarkable facts follow, namely, that the oating chords have constant length that the curve of their midpoints has the corresponding chords as tangents, and that these chords divide the perimeter in a xed ratio (the perimetral density). Suppose that is rational. Then, for every point p in the boundary of one of this gures, we have an inscribed equilateral n-gon which moves, as a linkage with rigid rods, as p moves along the boundary, in such a way that the midpoints of the sides move parallel to them. So, this is the main motivation for the following denition. A Carrousel (with n chairs) is a system which consists of n smooth (not necessarily closed) curves f 1 (t) 2 (t) ::: n (t)g in R 2 satisfying the following properties for every t 2 R and for all i = 1 ::: n where i+n (t) = i (t): 1) The length of the interval with end points i (t) and i+1 (t), j i+1 (t) ; i (t)j, is a non-zero constant 2) The curve of midpoints, m i (t) = i(t)+ i+1 (t), of the segments from 2 i (t) to i+1 (t), has tangent vector, m 0 i(t), parallel to i+1 (t) ; i (t). A carrousel with n chairs f 1 (t) ::: n (t)g is a Zindler carrousel if all the curves i (t) are reparametrizations of the same closed curve. Date: April,
2 2 J. BRACHO, L. MONTEJANO, AND D. OLIVEROS Observe as an example, that the circle yields a Zindler carrousel with n chairs, because we can inscribe in it an equilateral n-gon such that, when rotating, its vertices describe the original circle and the midpoints of its sides describe a smaller concentric circle. Zindler curves studied in [8] are essentially Zindler carrousels with two chairs, which, according to [], are in one to one correspondence with curves of constant width. The purpose of this paper is to give a complete classication of Zindler Carrousels with ve chairs. This classication theorem gives enough evidence to show the non existence of gures, dierent from the disk, that oat in equilibrium in every position for perimetral densities 1 and 2. Although the main properties of carrousels were studied in [4], for completeness we summarize them, in this section, without proofs. Denition 1. Let be a gure (region bounded by a simple closed curve). A chord system fc(p)g for is a continuous selection of an oriented chord C(p), starting at p, for every point p in the boundary of. There are three natural kinds of chord systems for a gure : 1) The system fc a (p)g of chords which divide the area in a xed ratio. 2) The system fc p (p)g of chords which divide the perimeter in a xed ratio : 3) The system fc l (p)g of chords of constant length. Note that for non-convex gures the chord system fc a (p)g is not necessarily well dened, for all. Let be a gure of area A and let us suppose that the chord system which divides the area of in a xed ratio, fc a (p)g, is well dened. Let G be the mass center of and g(p) the mass center of the regions of, bounded by C a (p), of area A. Then, according to Archimedes Law, we have the following denition Denition 2. We say that the gure oats in equilibrium in a given position p, if the line through G and G(p) is orthogonal to C(p). A gure that oats in equilibrium in every position will be called an Auerbach gure. In 1938 Auerbach [1] proved the following theorem THEOREM 1. A gure is an Auerbach gure if and only if the system of chords fc a (p)g is well dened and it is also of the type fc l (p)g of constant length.
3 ZINDLER CARROUSELS 3 For the prove he used the following facts which will be used later: A) If a system of interior non-concurrent chords, fc i (p)g, is of any of the two types i 2 fa p l g, then it is also of the third type. B) The area A(p), of the region of a gure, left to the right by the chord C(p) of a chord system fc(p)g, is constant if and only if every chord C(p) is tangent to the curve described by the midpoints of C(p). This motivates the following denition. Denition 3. If is an Auerbach gure for the density we say that has perimetral density if the chord system which divides the area of in the ratio fc a (p)g is well dened and divides the perimeter of in a xed ratio : In what follows, when studying Auerbach gures, we will classify them according with their perimetral density. Denition 4. Let 2 R 0 < < 1. We say that a gure is an ;Zindler curve, if the system of chords fc p (p)g, which divides the perimeter in a xed ratio, is also a fc l (p)g system of xed length. Observe, that the classic Zindler curves [8] are 1 -Zindler. The next 2 two theorems relates -Zindler curves, Zindler Carrousels and Auerbach gures. THEOREM 2. f 1 ::: n g is a Zindler Carrousel with n chairs if and only if there exists an = q=n (with q=n an irreducible fraction ), for some q 2 Z 1 q n 2, such that each i(t) is an ;Zindler curve. THEOREM 3. Let be a closed smooth curve such that the system of chords of xed perimeter is interior. Then is an ;Zindler curve if and only if the gure bounded by the curve is an Auerbach curve for some density. Note now that the existence of Zindler carrousels with interior chords give rise to 2-dimensional bodies that oat in equilibrium in every position. Given a carrousel f 1 (t) ::: n (t)g, by the rst carrousel law [4], 0 i+1(t) is a reection of 0 i(t) along the line generated by i+1 (t); i (t). So we may assume that all the curves i (t) are parametrized by arc length and furthermore that j i+1 (t) ; i (t)j = 2. Let i (t) denote the angle between the vectors 0 i(t) and i+1 (t) ; i (t), and let i (t) be the angle between the x-axis and the vector i+1 (t) ; i (t), then by the second carrousel law [4], 0 i(t) = sin ( i (t)).
4 4 J. BRACHO, L. MONTEJANO, AND D. OLIVEROS Next theorem exhibits the dierential equations of carrousels, where x i (t) denotes the angle between the vectors i+1 (t); i (t) and i;1(t); i (t). THEOREM 4. Let f 1 (t) ::: n (t)g be a carrousel with n-chairs. Then, the interior angles x i (t), i = 1 ::: n, satisfy the following system of constrained dierential equations (1) If n is odd then x 0 i(t) = sin( i;1(t)) ; sin( i (t)) (2) i (t) = x i+2 (t) + x i+4 (t) + ::: + x i+(n;1)(t) ; ( k ; 1 P ) 2 n where k is the integer number such that x i=1 i(0) = k. Conversely, if n is odd and we have functions x i (t), i = 1 ::: n, satisfying the system of dierential equations (1) (2) and such that the initial conditions (x 1 (0) ::: x n (0)) are the interior angles of an equilateral n-gon with sides of length 2. Then, there exists a carrousel of n chairs f 1 (t) ::: n (t)g, with the property that x i (t) is the angle between i+1 (t) ; i (t) and i;1(t) ; i (t). The following two corollaries will be used in the next section. COROLLARY 1. Let X(0) be an n-gon with interior angles (x 1 (0) ::: x n (0)) n odd. Then there exist a unique carrousel f 1 (t) ::: n (t)g up to orientation, with initial condition X(0). COROLLARY 2. Let f 1 (t) ::: n (t)g be a carrousel with n-chairs, n odd. If there exists t 0 2 R such that x i (t 0 ) = x i+1 (0) (i = 1 : : : n), then the curves 1 (t),..., n (t) are congruent. An interesting propertie of carrousels is given by the following theorem THEOREM. Let f 1 (t) ::: n (t)g be a carrousel with n-chairs, n odd. Let X(t) be the n-gon with vertices f 1 (t) ::: n (t)g. Then, the area A(t) of X(t) is constant and the mass center H(t) of X(t) is a xed point. 2. Carrousels with Five Chairs For the study of the carrousel with chairs, we shall consider the space, P, of all equilateral pentagons in the plane, one of whose sides
5 ZINDLER CARROUSELS is the distinguished interval [(;1 0) (1 0)], and all the other sides have length two. If X 2 P is a pentagon, we can write it as X = (z 1 ::: z ), where z j = e ix j is a complex number and the ve real numbers (x 1 ::: x ) are the interior angles of the equilateral pentagon X. Clearly, the x i 's satisfy the following equation: where u() = (cos sin ): u(0) + u( ; x 2 ) + u(2 ; (x 2 + x 3 )) + :::+ +u(4 ; (x 2 + x 3 + x 4 + x )) = 0: We know [6] that P is an oriented surface of genus 4, embedded in S 1 S 1 S 1 S 1 S 1 where S 1 is the sphere of dimension 1. So, we can think of Euclidean space R as the covering space of S 1 S 1 S 1 S 1 S 1 with its natural projection P : R! S 1 S 1 S 1 S 1 S 1 which sends (x 1 ::: x ) to the corresponding (z 1 ::: z ). It is clear that ~ P = P ;1 (P ) is also a surface, and (x 1 ::: x ) is a member of ~ P if it satises the following three equations: a) P i=1 x i = 3 + 2k where k is an integer. b) cos(x 1 ) + cos(x 2 ) ; cos(x 2 + x 3 ) ; cos(x 1 + x ) = 1. c) sin(x 1 ) ; sin(x 2 ) + sin(x 2 + x 3 ) ; sin(x 1 + x ) = 0. Now, consider the function ~f : ~ P R! R which determines the area of a pentagon. ~f(x 1 ::: x ) = sin(x 1 ) + sin(x 2 ) ; sin(x 1 + x 2 ) + sin(x 4 ) and at the same time let us call f the corresponding area function f : P! R: LEMMA 1. The area function f : P! R has 14 non-degenerate critical points: 2 maxima (which correspond to the area of the positively oriented regular convex pentagon and the negatively oriented regular pentagram), 2 minima (which correspond to the area of the negatively oriented regular convex pentagon and the positively oriented regular pentagram) and 10 saddle points. Proof. Let us take the following function F = (f 1 f 2 f 3 f 4 ) : R ;! R 4
6 6 J. BRACHO, L. MONTEJANO, AND D. OLIVEROS where f 1 (x 1 : : : x ) := x 1 + x 2 + x 3 + x 4 + x : f 2 (x 1 : : : x ) := cos(x 1 ) + cos(x 2 ) ; cos(x 2 + x 3 ) ; cos(x 1 + x ): f 3 (x 1 : : : x ) := sin(x 1 ) ; sin(x 2 ) + sin(x 2 + x 3 ) ; sin(x 1 + x ): f 4 (x 1 : : : x ) := sin(x 1 ) + sin(x 2 ) ; sin(x 1 + x 2 ) + sin(x 4 ): By calculating the determinants of all the 4 4 sub matrices of the matrix df p and taking the restriction to P ~ we obtain the following system of equations, whose solution give us the set of critical points of the area function f ~ : P ~! R. (2.1) 8 >< >: sin(x 3 + x ) ; sin(x 2 + x 4 ) = 0 sin(x 4 + x 1 ) ; sin(x 3 + x ) = 0 sin(x + x 2 ) ; sin(x 4 + x 1 ) = 0 sin(x 1 + x 3 ) ; sin(x + x 2 ) = 0 sin(x 2 + x 4 ) ; sin(x 1 + x 3 ) = 0 Since P : ~ P! P is a covering space and the map ~ f : ~ P! R is a lift of f : P! R, then the critical points of f can be obtained by projecting the critical points of ~ f. So, we obtain that the pentagons with interior angles (x 1 ::: x ) which solve the system of equations (2.1) are precisely the two regular convex pentagons, oriented and unoriented, X 1 and X ~ 1, respectively, with interior angles of the form 3 + 2k, k an integer the regular pentagrams, X 2 and X ~ 2 with interior angles of the form + 2k, k an integer, and 10 pentagons which are like a triangle, with interior angles of the form: x i = x i+1 = x i+2 = =3 + 2k 1, x i+3 = 2k 2 and x i+4 = 2k 3, k 1 k 2 k 3 integers and i = 1 ::: (i + = i). 9 >= > Then the function f : P! R has 14 non-degenerate critical points, 2 local maxima, given by X 1 and X ~ 2 2 local minima given by X 2 and X ~ 1 and 10 more critical points, that by the Euler characteristic, are saddle points and are given by the 10 pentagons which look like a triangle. Next, we shall study the Morse Theory of the area function f : P! R. First note that it has the following 6 critical values: f;m ;b ;n n b mg, where m is the area of the oriented regular pentagon X 1, n is the area of the regular oriented pentagram X 2 and b is the area of the pentagons which look like a triangle. The set, Po, of oriented pentagons without intersections on their sides is given by
7 ZINDLER CARROUSELS 7 f ;1 ((b m]), which is a connected surface with only one critical point, a maxima, and hence topologically homeomorphic to an open disc. Similarly, the set, P u, of unoriented pentagons without intersections on their sides is given by f ;1 ([;m ;b)), which is a connected surface with only one critical point, a minima, and hence topologically homeomorphic to an open disc. f ;1 ((;b b)) is an open surface that consists of three connected components: the set, R, of all pentagons with exactly one intersection on their sides, the set, Q o, of oriented pentagrams (with intersections) and the set, Q u, of unoriented pentagrams. Since there are only two critical points in f ;1 ((;b b)), then Q o and Q u are homeomorphic to open discs and R is homeomorphic to an open cylinder. Finally, we summarize the situation of the bers as follows: a) if x 2 (;m ;b) [ (;n n) [ (b m), then f ;1 (x) consists of a simple closed curve, b) if x 2 (;b ;n) [ (n b), then f ;1 (x) consists of two simple closed curves, c) if x 2 f;m ;n n m g, then f ;1 (x) consists of a single point, and d) if x 2 f;b bg, then f ;1 (x), consists of a chain of simple closed curves in which two consecutive curves have one point in common. Each one of these closed curves represents pentagons in which two consecutive sides coincide. Note that for the area function ~ f : ~ P! R, the kernel Ker(dF p ) = Ker(d ~ f p ), coincides with the system of constrained dierential equations given in Theorem 1.4, for n =. Hence, Ker(df p ) is the set of tangent vectors to the curves f ;1 (A). For a pentagon in (z 1 ::: z ) 2 Po P u Q o Q u R, respectively, we identify (z 1 ::: z ) with (x 1 ::: x ) 2 P ~ P, where z j = e ix j and x i=1 i = 3 7, 9, respectively. Furthermore, f ;1 (A) is parametrized by (x 1 (t),...,x (t)), satisfying the system of dierential equations (1),(2), with initial conditions (x 1 (0) ::: x (0)) 2 Po P u Q o Q u R, respectively, which are the interior angles P of an equilateral pentagon with sides of length 2, area A and x i=1 i(0) = 3 7 9, respectively. Moreover, for every one of this curves, there exists a carrousel of n chairs f 1 (t) ::: n (t)g, with the property that x i (t) is the angle between i+1 (t) ; i (t) and i;1(t) ; i (t). Consequently, carrousels are classied, by real numbers in [;m m]. Our next purpose is to study P0. First of all, observe that for every A 2 (b m), there exists t A in R such that, for every t, x i (t + t A ) = x i+1 (t), because f ;1 (A) consists of a simple closed curve and if (x 1 (0) x 2 (0) x 3 (0) x 4 (0) x (0)) is in the curve f ;1 (A) then,
8 8 J. BRACHO, L. MONTEJANO, AND D. OLIVEROS (x 2 (0) x 3 (0) x 4 (0) x (0) x 1 (0)) is also in f ;1 (A). By Corollary 1.6, for the corresponding carrousel f 1 (t) ::: n (t)g, we conclude that the curve i (t + t A ) is congruent to i+1 (t). LEMMA 2. Let A 2 (b m) and suppose the curve f ;1 (A) is parametrized by (x 1 (t) ::: x (t)), satisfying the system of constrained dierential equations (1) (2). Let t A A 2 R, be the minimum positive numbers such that for every t 2 R, Then, x i (t + t A ) = x i+1 (t) and x i (t + A ) = x i (t): t A = 2 A : Proof. Observe that in Po = f ;1 ((b m)), which by convention can be thought as a subset of R, the projection to the rst two coordinates is one to one because these equilateral pentagons are determined by two of their angles. Let g A R 2 be the simple closed curve which is the projection of f ;1 (A) in R 2. First of all we can see that g A is a simple closed curve symmetric with respect to the line x = y, because if the pentagon (x 1 x 2 x 3 x 4 x ) is in f ;1 (A) then, the symmetric one, (x 2 x 1 x x 4 x 3 ), is also in f ;1 (A). Therefore, g A intersects the line x = y in exactly two points, lets say (d d) and (a a). Then there exists a pentagon P 1 of the form (a a b c b)) 2 f ;1 (A). Let P 2 = (a b c b a) P 3 = (b c b a a) P 4 = (c b a a b) and P = (b a a b c). They are also in f ;1 (A). Hence, the projection of these ve points, q 1 = (a a) q 2 = (a b) q 3 = (b c) q 4 = (c b) and q = (b a) belong to g A. Again, since the curve g A is a simple closed symmetric curve and since for pentagons of the form (a a b c b) in these region we have that if a b then c a and if b a, then a c, we have that there exist only two possibilities for the cyclic order of the points fq i g in the curve g A. Either fq 1 q 2 q 4 q 3 q g or fq 1 q 4 q 2 q q 3 g. We shall now prove that the rst cyclic order is not possible. Suppose the curve f ;1 (A) is parametrized by P (t) = (x 1 (t) ::: x (t)), where the fx i (t)g 1 satisfy the system of constrained dierential equations (1), (2). Suppose, without loss of generality, that P (0) = P 1 = (x 1 (0) ::: x (0)). Hence P (it A ) = P i+1 = (x 1 (it A ) ::: x (it A )), i = If the cyclic order of the points fq i g in the curve g A is fq 1 q 2 q 4 q 3 q g, then the cyclic order of the points fp i g in the curve f ;1 (A) is fp (0) P (t A ), P (3t A ) P (2t A ) P (4t A )g, which implies that
9 ZINDLER CARROUSELS 9 there exists s 0 2 R, t A < s 0 < 2t A such that P (2t A + s 0 ) = P (4t A ). Thus, P (s 0 ) = P (2t A ), which is impossible because t A is the minimum positive number such that, for every t, x i (t + t A ) = x i+1 (t): If the cyclic order of the points fp i g in the curve f ;1 (A) is fp (0) P (3t A ), P (t A ) P (4t A ) P (2t A )g, then there exists 0 < A < t A such that x i (t + A ) = x i+3 (t) for every t 2 R. Then, x i (t + A ) = x i (t + A ) and x i (t + 10 A ) = x i (t + t A ) = x i (t + 2 A ). Consequently t A = 2 A and 2 A = t A. From now on, let 0 < A < t A be the minimum real number such that x i (t + A ) = x i+3 (t), for every t 2 R. Note that 2 A = t A. Remark. The corresponding result for A 2 (n b) and f ;1 (A) Q o is that t A = A : 3. The Classification In this section we shall classify Zindler carrousels for n =. So we need to study rst some parameters associated to carrousels, and the small pieces of curves that describe them. Let us do the case in which A 2 (b m) and suppose the curve f ;1 (A) is parametrized by (x 1 (t) ::: x (t)), satisfying the system of constrained dierential equations (1), (2) with initial conditions (x 1 (0) ::: x (0)) 2 Po, which are the interior P angles of an equilateral pentagon with sides of length 2, area A and x i=1 i(0) = 3. By theorem 1.4, there exists a carrousel f 1 (t) ::: n (t)g, with the property that x i (t) is the angle between i+1 (t); i (t) and i;1(t); i (t) and, by Lemma 2.2, such that x i (t+ A ) = x i+3 (t), for every t 2 R, where 2 A = t A : Consequently, the curves i (t + A ) and i+3 (t) are congruent. Furthermore, by Theorem 1.7, assume that the mass center of the pentagons is the origin. Hence, there exists a rotation R A of an angle A such that, for every t 2 R, i (t + A ) = R A i+3 (t): Let us call A, the basic angle of this carrousel. That is, for every t 2 R, A = 3 (t + A ) ; 1 (t): where i (t) denotes the angle between the x-axes and the vector i+1 (t) ; i (t):
10 10 J. BRACHO, L. MONTEJANO, AND D. OLIVEROS We shall classify Zindler carrousels in terms of their basic angles, which in turn, depend on the area A of the carrousel. For that purpose the following denitions are important. The period, A, of the carrousel is the minimum real positive number such that x i (t + A ) = x i (t), for every t 2 R and i = 1 :::. Note that the pentagons at the time 0 and A are congruent. So we dene the rotational angle, A, of the carrousel as the angle between them, that is: A = i ( A ) ; i (0) i = 1 ::: : Remember that 0 i(t) = ; sin(x i+2 (t) + x i+4 (t)), hence Z A A = ; sin(x 2 (t) + x (t))dt : 0 The next Lemma relates the value of the basic angle A rotational angle A of a carrousel. LEMMA 3. Let A 2 (b m). Then, A ; 4 = A : and the Proof. Using the fact that 3 (t) ; 1 (t) = 2 ; (x 2 (t) + x 3 (t)), and that for i = , A = 3 ((i + 1) A ) ; 1 (i A ) = Z (i+1)a = ; sin(x (t) + x 2 (t))dt + ( 3 (i A ) ; 1 (i A )) i A we obtain, adding this ve equalities, we obtain the result. Denition. Let us call the i;track of the carrousel, the curve segment f i (s)j0 s A g, i = 1 :::. LEMMA 4. It is possible to reconstruct the curves i (t), t 2 R, by pasting one after the other, the ve i;tracks. Proof. Let us take some t 2 R, then we can write t = m A +, where m 2 Z and 0 < < A. So i (t) = i (m A + ) = R m A k () where k i + 3m mod(). Besides, we are interested in nding the index of Zindler carrousels around the mass center, because if the index of the curve has absolute value greater than one, then the curve intersects itself and therefore it
11 ZINDLER CARROUSELS 11 is not a gure which oats in equilibrium with perimetral density 1. For that purpose we need to know the angular length of the i;tracks. Denition 6. Let us suppose that the mass center of the pentagons is in the origin. Then we dene the angular length of the i;track as follows and we call C i := the angle between i (0) and i ( A ) i := the angle between i (0) and i+1 (0): The following theorem classies 1 -Zindler carrousels THEOREM 6. Any 1 -Zindler carrousel of index d has basic angle A = r2, with m = s + 2, s a natural number, and 1 < r < m, m satisfying for some K the integer equation (3s r) mk = d and conversely, if a carrousel with area A 2 (b m) has basic angle A satisfying the above integer equation, then it is a 1 -Zindler carrousel. Proof. Let us suppose we have a Zindler Carrousel. So, after a certain time, the curve i reaches and follows the curve i+1. That is, i (t + ) = i+1 (t), for every t 2 R. So x i (t+) = x i+1 (t), which implies that = m A, where m = s + 2, for s a natural number. Let 0 < < A, so we have i (m A + ) = R m A i+1 () = i+1 (). Therefore, R m A must be the identity and hence A = r2, for 1 < r < m. m Since R A sends the 4-track to the set f 1 ( A + t)j0 < t < A g, then A = C 1 + 2l for some integer l. We already know that A must be of the form r2, with m m = s + 2, therefore, C 1 must be of the form for some k 1 2 Z. Similarly C 1 = ( r m + k 1)2 C i = i + i+1 + i+2 + ( r m + k i)2: Then, C i + C i+3 + ::: + C i+3(m;1) = i + (3s + 1)2 + r2 + (k i + k i+3 + :::+k i+3(m;1))2 where C i + C i+3 + :::+C i+3(m;1) is the angular length of the curve f i (t)j0 < t < m A g.
12 12 J. BRACHO, L. MONTEJANO, AND D. OLIVEROS For a Zindler carrousel with index d we have that that is X i=1 where K = P i=1 k i. (C i + C i+3 + ::: + C i+3(m;1)) = 2d (3s r) + mk = d ; 1 Therefore, the integer solutions of the preceding equation with 1 < r < m give rise all the possible angles A for 1 -Zindler carrousels with index d and, by construction, if a carrousel with ve chairs has basic angle determined by this equation, then it is a 1 -Zindler carrousel. With this discussion we have nished the proof. COROLLARY 3. Any 1 -Zindler carrousel of index 1 has basic angle of the form 4s+2 for s > 0 a natural number and conversely, if a s+2 carrousel with area A 2 (b m) has basic angle A = 4s+2 for s > 0 a s+2 natural number, then it is a 1 -Zindler carrousel. Proof. The natural solutions of the equation (3s r) + mk = 0 with m = s + 2 and 1 < r < m are precisely the natural numbers for which 2r = 4s+2. m s+2 Figure 1 and 2 shows carrousels with basic angles 6 10 and respectively, the basic angles 4s+2 tends to 4, when s tends to innity, 7 12 s+2 which correspond to the basic angle of the carrousel shown in Figure 4. Figure 3 corresponds to the carrousel of area zero whose center of mass is at innity. THEOREM 7. A 1 -Zindler carrousel with index 1 and interior chords must have a period A < 2:4002: Proof. Let us suppose we have a 1 -Zindler carrousel parametrized by (x 1 (t) ::: x (t)), satisfying the system of constrained dierential equations (1), (2) with initial conditions (x 1 (0) ::: x (0)) 2 Po, which are the interior angles of an equilateral pentagon of area A 2 (b m), and P x i=1 i(0) = 3. Let us assume that our carrousel has basic angle A = 4s+2, with s a natural number greater than zero. Suppose that s+2 all chords are interior. Then for 0 < t < (s + 2) A, we have that 0 < 1 (t) < 2 (0). Writing 1 ( A ) in terms of A = 3 ( A ), we obtain: 3 ( A ) + x 1 (0) + x (0) = 1 ( A )
13 ZINDLER CARROUSELS ( A ) + x 1 (0) + x (0) + x 4 (0) + x 3 (0) = 1 (2 A ) 3 3 ( A ) + x 1 (0) + x (0) + x 4 (0) + x 3 (0) + x 2 (0) + x 1 (0) = 1 (3 A ) and so on. Therefore, taking A = 4s+2 = s+2 3( A ), we have that x 1 (0) + x (0) > 6s+2, x s+2 2(0) < 3s+2 and x s+2 1(0) > 3s. Since this s+2 follows for every initial condition, we have the following inequalities: x i (t) + x i+1 (t) > 6s + 2 s + 2 and 3s s + 2 < x i(t) < 3s + 2 s + 2 which in turn give rise to the following inequality, for s 2 6s ; sin( s + 2 ) < ;(sin(x i(t) + x i+2 (t))) < ; sin( 6s + 4 s + 2 ): Using now Lemma 3.1, we obtain, for s 3, the following bound for A, 2sec s+2 s+2 ) (s + 2) < A < s;2 2sec( ) s+2 < 2:4002: (s + 2) Finally, the carrousels with basic angle 6 10 and are shown in the 7 12 gures 1 and 2, respectively. In both of them their chords are not interior. The case 2 can be studied in a similar way. One proves that, for A 2 (n b), A ; 6 = A. It is also possible to obtain a classication of 2- Zindler carrousels of index d. In particular, we have the corresponding theorem. THEOREM 8. Any 2 -Zindler carrousel of index 1 has basic angle of the form 6s+4, for s a natural number. s+3 COROLLARY 4. A 2 -Zindler carrousel with index 1 must have a period A < 2:: Proof. Is easy to see that for X = (x 1 ::: x ) 2 Q o, we have sin(x 3 + x ) sin(4 arcsin( 1 )) :847214, which implies that, for any A 2 (n b), 4 the rotational angle of a carrousel is A :847 A. Therefore, a 2- Zindler carrousel with basic angle A = 6s+4, must have a period s+3 A < 2:.
14 14 J. BRACHO, L. MONTEJANO, AND D. OLIVEROS 4. Some Consequences of the Theory Using the fact that f ;1 (m) where f : P! R is an isolated singular point of the vector eld and a non-degenerate center, that is, the linear part of the vector eld has eigenvalues i!! > 0, we may prove, using the Classical Poincare-Lyapunov Center Theorem [2],[7], that the limit of the period function : (b m)! R when A! m is 2=! which, after the corresponding calculations, gives (m) = 2=! 2:4002. CONJECTURE 1. The period function : (b m)! R is an decreasing function. In fact, (A) (m) for every A 2 (b m): There is clear evidence of this fact given by the computer. The graph 1(a) shows the values, obtained with a computer, for A and A. Note that A < 2:9132 and A > 2:4002, for every A 2 (b m). In [4] it was proved that there are no gures that oat in equilibrium in every position with perimetral density 1 and 1 although there are 3 4 with perimetral density 1 : This time we show that there are no gures 2 that oat in equilibrium in every position with perimetral density 1 and, dierent from the circle. 2 To see this, let us suppose that there exist a gure that oat in equilibrium in every position with perimetral density 1 which give rise to a 1-Zindler carrousel. If the index is 1, by Theorem 3., A < 2:4002 which is a contradiction. The same ideas can be analogously applied to study 1 -Zindler carrousels of index ;1 to conclude that there are no gures that oat in equilibrium in every position with perimetral density 1 : Furthermore, by Corollary 3.7, a 2 -Zindler carrousel of index 1 must have a period A < 2:. It is possible to verify, using the previous discussion of the Poincare-Lyapunov Center Theorem and graph 1(b), that the period of any carrousel with area A 2 (n b) is greater than 2.. Therefore, there are no 2 -Zindler carrousels of index 1 and an analogous discussion shows the same for index ;1:. Acknowledgments The authors acknowledge and thank A. Davidov for his many helpful suggestions.
15 ZINDLER CARROUSELS 1 References [1] Auerbach, H.,\Sur un probleme de M. Ulam concernant l' equilibre des corps ottant", Studia Math. 7 (1938) [2] Lyapunov, A.M., Stability of Motion, Math. SciEngrg. 30. Academic Press, London-New York. (1966). [3] Mauldin, R.D., The Scottish Book, Mathematics from the Scottish Cafe, Birkhauser, Boston. (1981). [4] Bracho J, Montejano, L. and Oliveros D.,\Carrousels, Zindler curves and the oating body problem". Preprint [] Oliveros, D., \Los Volantines: Sistemas Dinamicos asociados al problema de la otacion de los cuerpos", Ph.D. Thesis. Faculty of Science, National University of Mexico. (1997). [6] Oliveros D., \The space of pentagons and the otation problem", Aportaciones Matematicas. Serie Comunicaciones 2 (1999), [7] Poincare H., Memoire sur le courbes denies par une equation dierentielle, J. Math. Pures Appl.(3) 37. (1881) [8] Zindler,K.,\ Uber Konvexe Gebilde II", Monatsh. Math. Phys. 31 (1921)
16 16 J. BRACHO, L. MONTEJANO, AND D. OLIVEROS Figure 1 The Zindler Carrousel with basic angle 6=7
17 ZINDLER CARROUSELS 17 Figure 2 The Zindler carrousel with basic angle 10=6
18 18 J. BRACHO, L. MONTEJANO, AND D. OLIVEROS Figure 3 The unique carrousel of area zero and center of mass at innity
19 ZINDLER CARROUSELS 19. Figure 4 Carrousel with area and basic angle 4=
20 20 J. BRACHO, L. MONTEJANO, AND D. OLIVEROS
MORE ON THE PEDAL PROPERTY OF THE ELLIPSE
 INTERNATIONAL JOURNAL OF GEOMETRY Vol. 3 (2014), No. 1, 5-11 MORE ON THE PEDAL PROPERTY OF THE ELLIPSE I. GONZÁLEZ-GARCÍA and J. JERÓNIMO-CASTRO Abstract. In this note we prove that if a convex body in
INTERNATIONAL JOURNAL OF GEOMETRY Vol. 3 (2014), No. 1, 5-11 MORE ON THE PEDAL PROPERTY OF THE ELLIPSE I. GONZÁLEZ-GARCÍA and J. JERÓNIMO-CASTRO Abstract. In this note we prove that if a convex body in
Convex bodies with many elliptic sections
 Convex bodies with many elliptic sections arxiv:1408.5647v1 [math.mg] 25 Aug 2014 Isaac Arelio Luis Montejano Abstract We show in this paper that two normal elliptic sections through every point of the
Convex bodies with many elliptic sections arxiv:1408.5647v1 [math.mg] 25 Aug 2014 Isaac Arelio Luis Montejano Abstract We show in this paper that two normal elliptic sections through every point of the
SOLUTIONS FOR 2011 APMO PROBLEMS
 SOLUTIONS FOR 2011 APMO PROBLEMS Problem 1. Solution: Suppose all of the 3 numbers a 2 + b + c, b 2 + c + a and c 2 + a + b are perfect squares. Then from the fact that a 2 + b + c is a perfect square
SOLUTIONS FOR 2011 APMO PROBLEMS Problem 1. Solution: Suppose all of the 3 numbers a 2 + b + c, b 2 + c + a and c 2 + a + b are perfect squares. Then from the fact that a 2 + b + c is a perfect square
CLASSIFICATION OF FIRST-ORDER FLEXIBLE REGULAR BICYCLE POLYGONS
 CLASSIFICATION OF FIRST-ORDER FLEXIBLE REGULAR BICYCLE POLYGONS ROBERT CONNELLY AND BALÁZS CSIKÓS Abstract. A bicycle (n, k)-gon is an equilateral n-gon whose k-diagonals are equal. S. Tabachnikov proved
CLASSIFICATION OF FIRST-ORDER FLEXIBLE REGULAR BICYCLE POLYGONS ROBERT CONNELLY AND BALÁZS CSIKÓS Abstract. A bicycle (n, k)-gon is an equilateral n-gon whose k-diagonals are equal. S. Tabachnikov proved
Malfatti s problems 165. Malfatti s problems. Emil Kostadinov Mathematics High School Acad. S. Korolov, 11 grade Blagoevgrad, Bulgaria.
 Malfatti s problems 165 Malfatti s problems Emil Kostadinov Mathematics High School Acad. S. Korolov, 11 grade Blagoevgrad, Bulgaria Abstract The purpose of the present project is to consider the original
Malfatti s problems 165 Malfatti s problems Emil Kostadinov Mathematics High School Acad. S. Korolov, 11 grade Blagoevgrad, Bulgaria Abstract The purpose of the present project is to consider the original
Course 212: Academic Year Section 1: Metric Spaces
 Course 212: Academic Year 1991-2 Section 1: Metric Spaces D. R. Wilkins Contents 1 Metric Spaces 3 1.1 Distance Functions and Metric Spaces............. 3 1.2 Convergence and Continuity in Metric Spaces.........
Course 212: Academic Year 1991-2 Section 1: Metric Spaces D. R. Wilkins Contents 1 Metric Spaces 3 1.1 Distance Functions and Metric Spaces............. 3 1.2 Convergence and Continuity in Metric Spaces.........
Integrated Math II. IM2.1.2 Interpret given situations as functions in graphs, formulas, and words.
 Standard 1: Algebra and Functions Students graph linear inequalities in two variables and quadratics. They model data with linear equations. IM2.1.1 Graph a linear inequality in two variables. IM2.1.2
Standard 1: Algebra and Functions Students graph linear inequalities in two variables and quadratics. They model data with linear equations. IM2.1.1 Graph a linear inequality in two variables. IM2.1.2
Math 1270 Honors ODE I Fall, 2008 Class notes # 14. x 0 = F (x; y) y 0 = G (x; y) u 0 = au + bv = cu + dv
 Math 1270 Honors ODE I Fall, 2008 Class notes # 1 We have learned how to study nonlinear systems x 0 = F (x; y) y 0 = G (x; y) (1) by linearizing around equilibrium points. If (x 0 ; y 0 ) is an equilibrium
Math 1270 Honors ODE I Fall, 2008 Class notes # 1 We have learned how to study nonlinear systems x 0 = F (x; y) y 0 = G (x; y) (1) by linearizing around equilibrium points. If (x 0 ; y 0 ) is an equilibrium
BROUWER FIXED POINT THEOREM. Contents 1. Introduction 1 2. Preliminaries 1 3. Brouwer fixed point theorem 3 Acknowledgments 8 References 8
 BROUWER FIXED POINT THEOREM DANIELE CARATELLI Abstract. This paper aims at proving the Brouwer fixed point theorem for smooth maps. The theorem states that any continuous (smooth in our proof) function
BROUWER FIXED POINT THEOREM DANIELE CARATELLI Abstract. This paper aims at proving the Brouwer fixed point theorem for smooth maps. The theorem states that any continuous (smooth in our proof) function
Numerical Integration for Multivariable. October Abstract. We consider the numerical integration of functions with point singularities over
 Numerical Integration for Multivariable Functions with Point Singularities Yaun Yang and Kendall E. Atkinson y October 199 Abstract We consider the numerical integration of functions with point singularities
Numerical Integration for Multivariable Functions with Point Singularities Yaun Yang and Kendall E. Atkinson y October 199 Abstract We consider the numerical integration of functions with point singularities
Handlebody Decomposition of a Manifold
 Handlebody Decomposition of a Manifold Mahuya Datta Statistics and Mathematics Unit Indian Statistical Institute, Kolkata mahuya@isical.ac.in January 12, 2012 contents Introduction What is a handlebody
Handlebody Decomposition of a Manifold Mahuya Datta Statistics and Mathematics Unit Indian Statistical Institute, Kolkata mahuya@isical.ac.in January 12, 2012 contents Introduction What is a handlebody
ON THE RELATIVE LENGTHS OF SIDES OF CONVEX POLYGONS. Zsolt Lángi
 ON THE RELATIVE LENGTHS OF SIDES OF CONVEX POLYGONS Zsolt Lángi Abstract. Let C be a convex body. By the relative distance of points p and q we mean the ratio of the Euclidean distance of p and q to the
ON THE RELATIVE LENGTHS OF SIDES OF CONVEX POLYGONS Zsolt Lángi Abstract. Let C be a convex body. By the relative distance of points p and q we mean the ratio of the Euclidean distance of p and q to the
Minimal Surfaces. December 13, Alex Verzea. MATH 580: Partial Dierential Equations 1. Professor: Gantumur Tsogtgerel
 Minimal Surfaces December 13, 2012 Alex Verzea 260324472 MATH 580: Partial Dierential Equations 1 Professor: Gantumur Tsogtgerel 1 Intuitively, a Minimal Surface is a surface that has minimal area, locally.
Minimal Surfaces December 13, 2012 Alex Verzea 260324472 MATH 580: Partial Dierential Equations 1 Professor: Gantumur Tsogtgerel 1 Intuitively, a Minimal Surface is a surface that has minimal area, locally.
2017 Harvard-MIT Mathematics Tournament
 Team Round 1 Let P(x), Q(x) be nonconstant polynomials with real number coefficients. Prove that if P(y) = Q(y) for all real numbers y, then P(x) = Q(x) for all real numbers x. 2 Does there exist a two-variable
Team Round 1 Let P(x), Q(x) be nonconstant polynomials with real number coefficients. Prove that if P(y) = Q(y) for all real numbers y, then P(x) = Q(x) for all real numbers x. 2 Does there exist a two-variable
Minimum and maximum values *
 OpenStax-CNX module: m17417 1 Minimum and maximum values * Sunil Kumar Singh This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 2.0 In general context, a
OpenStax-CNX module: m17417 1 Minimum and maximum values * Sunil Kumar Singh This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 2.0 In general context, a
1966 IMO Shortlist. IMO Shortlist 1966
 IMO Shortlist 1966 1 Given n > 3 points in the plane such that no three of the points are collinear. Does there exist a circle passing through (at least) 3 of the given points and not containing any other
IMO Shortlist 1966 1 Given n > 3 points in the plane such that no three of the points are collinear. Does there exist a circle passing through (at least) 3 of the given points and not containing any other
A Mathematical Trivium
 A Mathematical Trivium V.I. Arnold 1991 1. Sketch the graph of the derivative and the graph of the integral of a function given by a freehand graph. 2. Find the limit lim x 0 sin tan x tan sin x arcsin
A Mathematical Trivium V.I. Arnold 1991 1. Sketch the graph of the derivative and the graph of the integral of a function given by a freehand graph. 2. Find the limit lim x 0 sin tan x tan sin x arcsin
(x 1, y 1 ) = (x 2, y 2 ) if and only if x 1 = x 2 and y 1 = y 2.
 1. Complex numbers A complex number z is defined as an ordered pair z = (x, y), where x and y are a pair of real numbers. In usual notation, we write z = x + iy, where i is a symbol. The operations of
1. Complex numbers A complex number z is defined as an ordered pair z = (x, y), where x and y are a pair of real numbers. In usual notation, we write z = x + iy, where i is a symbol. The operations of
SYMPLECTIC LEFSCHETZ FIBRATIONS ALEXANDER CAVIEDES CASTRO
 SYMPLECTIC LEFSCHETZ FIBRATIONS ALEXANDER CAVIEDES CASTRO. Introduction A Lefschetz pencil is a construction that comes from algebraic geometry, but it is closely related with symplectic geometry. Indeed,
SYMPLECTIC LEFSCHETZ FIBRATIONS ALEXANDER CAVIEDES CASTRO. Introduction A Lefschetz pencil is a construction that comes from algebraic geometry, but it is closely related with symplectic geometry. Indeed,
This class will demonstrate the use of bijections to solve certain combinatorial problems simply and effectively.
 . Induction This class will demonstrate the fundamental problem solving technique of mathematical induction. Example Problem: Prove that for every positive integer n there exists an n-digit number divisible
. Induction This class will demonstrate the fundamental problem solving technique of mathematical induction. Example Problem: Prove that for every positive integer n there exists an n-digit number divisible
3. Which of these numbers does not belong to the set of solutions of the inequality 4
 Math Field Day Exam 08 Page. The number is equal to b) c) d) e). Consider the equation 0. The slope of this line is / b) / c) / d) / e) None listed.. Which of these numbers does not belong to the set of
Math Field Day Exam 08 Page. The number is equal to b) c) d) e). Consider the equation 0. The slope of this line is / b) / c) / d) / e) None listed.. Which of these numbers does not belong to the set of
Part II. Algebraic Topology. Year
 Part II Year 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2017 Paper 3, Section II 18I The n-torus is the product of n circles: 5 T n = } S 1. {{.. S } 1. n times For all n 1 and 0
Part II Year 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2017 Paper 3, Section II 18I The n-torus is the product of n circles: 5 T n = } S 1. {{.. S } 1. n times For all n 1 and 0
Def. A topological space X is disconnected if it admits a non-trivial splitting: (We ll abbreviate disjoint union of two subsets A and B meaning A B =
 CONNECTEDNESS-Notes Def. A topological space X is disconnected if it admits a non-trivial splitting: X = A B, A B =, A, B open in X, and non-empty. (We ll abbreviate disjoint union of two subsets A and
CONNECTEDNESS-Notes Def. A topological space X is disconnected if it admits a non-trivial splitting: X = A B, A B =, A, B open in X, and non-empty. (We ll abbreviate disjoint union of two subsets A and
using the Hamiltonian constellations from the packing theory, i.e., the optimal sphere packing points. However, in [11] it is shown that the upper bou
![using the Hamiltonian constellations from the packing theory, i.e., the optimal sphere packing points. However, in [11] it is shown that the upper bou using the Hamiltonian constellations from the packing theory, i.e., the optimal sphere packing points. However, in [11] it is shown that the upper bou](/thumbs/72/66917214.jpg) Some 2 2 Unitary Space-Time Codes from Sphere Packing Theory with Optimal Diversity Product of Code Size 6 Haiquan Wang Genyuan Wang Xiang-Gen Xia Abstract In this correspondence, we propose some new designs
Some 2 2 Unitary Space-Time Codes from Sphere Packing Theory with Optimal Diversity Product of Code Size 6 Haiquan Wang Genyuan Wang Xiang-Gen Xia Abstract In this correspondence, we propose some new designs
2 G. D. DASKALOPOULOS AND R. A. WENTWORTH general, is not true. Thus, unlike the case of divisors, there are situations where k?1 0 and W k?1 = ;. r;d
 ON THE BRILL-NOETHER PROBLEM FOR VECTOR BUNDLES GEORGIOS D. DASKALOPOULOS AND RICHARD A. WENTWORTH Abstract. On an arbitrary compact Riemann surface, necessary and sucient conditions are found for the
ON THE BRILL-NOETHER PROBLEM FOR VECTOR BUNDLES GEORGIOS D. DASKALOPOULOS AND RICHARD A. WENTWORTH Abstract. On an arbitrary compact Riemann surface, necessary and sucient conditions are found for the
Changing coordinates to adapt to a map of constant rank
 Introduction to Submanifolds Most manifolds of interest appear as submanifolds of others e.g. of R n. For instance S 2 is a submanifold of R 3. It can be obtained in two ways: 1 as the image of a map into
Introduction to Submanifolds Most manifolds of interest appear as submanifolds of others e.g. of R n. For instance S 2 is a submanifold of R 3. It can be obtained in two ways: 1 as the image of a map into
Lectures 15: Parallel Transport. Table of contents
 Lectures 15: Parallel Transport Disclaimer. As we have a textbook, this lecture note is for guidance and supplement only. It should not be relied on when preparing for exams. In this lecture we study the
Lectures 15: Parallel Transport Disclaimer. As we have a textbook, this lecture note is for guidance and supplement only. It should not be relied on when preparing for exams. In this lecture we study the
GRE Math Subject Test #5 Solutions.
 GRE Math Subject Test #5 Solutions. 1. E (Calculus) Apply L Hôpital s Rule two times: cos(3x) 1 3 sin(3x) 9 cos(3x) lim x 0 = lim x 2 x 0 = lim 2x x 0 = 9. 2 2 2. C (Geometry) Note that a line segment
GRE Math Subject Test #5 Solutions. 1. E (Calculus) Apply L Hôpital s Rule two times: cos(3x) 1 3 sin(3x) 9 cos(3x) lim x 0 = lim x 2 x 0 = lim 2x x 0 = 9. 2 2 2. C (Geometry) Note that a line segment
SIMPLE MULTIVARIATE OPTIMIZATION
 SIMPLE MULTIVARIATE OPTIMIZATION 1. DEFINITION OF LOCAL MAXIMA AND LOCAL MINIMA 1.1. Functions of variables. Let f(, x ) be defined on a region D in R containing the point (a, b). Then a: f(a, b) is a
SIMPLE MULTIVARIATE OPTIMIZATION 1. DEFINITION OF LOCAL MAXIMA AND LOCAL MINIMA 1.1. Functions of variables. Let f(, x ) be defined on a region D in R containing the point (a, b). Then a: f(a, b) is a
DESK Secondary Math II
 Mathematical Practices The Standards for Mathematical Practice in Secondary Mathematics I describe mathematical habits of mind that teachers should seek to develop in their students. Students become mathematically
Mathematical Practices The Standards for Mathematical Practice in Secondary Mathematics I describe mathematical habits of mind that teachers should seek to develop in their students. Students become mathematically
3.1 Basic properties of real numbers - continuation Inmum and supremum of a set of real numbers
 Chapter 3 Real numbers The notion of real number was introduced in section 1.3 where the axiomatic denition of the set of all real numbers was done and some basic properties of the set of all real numbers
Chapter 3 Real numbers The notion of real number was introduced in section 1.3 where the axiomatic denition of the set of all real numbers was done and some basic properties of the set of all real numbers
Math 147, Homework 1 Solutions Due: April 10, 2012
 1. For what values of a is the set: Math 147, Homework 1 Solutions Due: April 10, 2012 M a = { (x, y, z) : x 2 + y 2 z 2 = a } a smooth manifold? Give explicit parametrizations for open sets covering M
1. For what values of a is the set: Math 147, Homework 1 Solutions Due: April 10, 2012 M a = { (x, y, z) : x 2 + y 2 z 2 = a } a smooth manifold? Give explicit parametrizations for open sets covering M
Contents. 2 Partial Derivatives. 2.1 Limits and Continuity. Calculus III (part 2): Partial Derivatives (by Evan Dummit, 2017, v. 2.
 Calculus III (part 2): Partial Derivatives (by Evan Dummit, 2017, v 260) Contents 2 Partial Derivatives 1 21 Limits and Continuity 1 22 Partial Derivatives 5 23 Directional Derivatives and the Gradient
Calculus III (part 2): Partial Derivatives (by Evan Dummit, 2017, v 260) Contents 2 Partial Derivatives 1 21 Limits and Continuity 1 22 Partial Derivatives 5 23 Directional Derivatives and the Gradient
40th International Mathematical Olympiad
 40th International Mathematical Olympiad Bucharest, Romania, July 999 Determine all finite sets S of at least three points in the plane which satisfy the following condition: for any two distinct points
40th International Mathematical Olympiad Bucharest, Romania, July 999 Determine all finite sets S of at least three points in the plane which satisfy the following condition: for any two distinct points
Thinnest Covering of a Circle by Eight, Nine, or Ten Congruent Circles
 Combinatorial Computational Geometry MSRI Publications Volume 5, 005 Thinnest Covering of a Circle by Eight, Nine, or Ten Congruent Circles Abstract. Let r n be the maximum radius of a circular disc that
Combinatorial Computational Geometry MSRI Publications Volume 5, 005 Thinnest Covering of a Circle by Eight, Nine, or Ten Congruent Circles Abstract. Let r n be the maximum radius of a circular disc that
Congurations of periodic orbits for equations with delayed positive feedback
 Congurations of periodic orbits for equations with delayed positive feedback Dedicated to Professor Tibor Krisztin on the occasion of his 60th birthday Gabriella Vas 1 MTA-SZTE Analysis and Stochastics
Congurations of periodic orbits for equations with delayed positive feedback Dedicated to Professor Tibor Krisztin on the occasion of his 60th birthday Gabriella Vas 1 MTA-SZTE Analysis and Stochastics
Vectors, dot product, and cross product
 MTH 201 Multivariable calculus and differential equations Practice problems Vectors, dot product, and cross product 1. Find the component form and length of vector P Q with the following initial point
MTH 201 Multivariable calculus and differential equations Practice problems Vectors, dot product, and cross product 1. Find the component form and length of vector P Q with the following initial point
USAC Colloquium. Bending Polyhedra. Andrejs Treibergs. September 4, Figure 1: A Rigid Polyhedron. University of Utah
 USAC Colloquium Bending Polyhedra Andrejs Treibergs University of Utah September 4, 2013 Figure 1: A Rigid Polyhedron. 2. USAC Lecture: Bending Polyhedra The URL for these Beamer Slides: BendingPolyhedra
USAC Colloquium Bending Polyhedra Andrejs Treibergs University of Utah September 4, 2013 Figure 1: A Rigid Polyhedron. 2. USAC Lecture: Bending Polyhedra The URL for these Beamer Slides: BendingPolyhedra
1 2n. i=1. 2m+1 i = m, while. 2m + 1 = 1. is the best possible for any odd n.
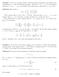 Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
Problem 1. Let n be a positive integer. Find the largest nonnegative real number f(n) (depending on n) with the following property: whenever a 1, a,..., a n are real numbers such that a 1 + a + + a n is
MATH II CCR MATH STANDARDS
 RELATIONSHIPS BETWEEN QUANTITIES M.2HS.1 M.2HS.2 M.2HS.3 M.2HS.4 M.2HS.5 M.2HS.6 Explain how the definition of the meaning of rational exponents follows from extending the properties of integer exponents
RELATIONSHIPS BETWEEN QUANTITIES M.2HS.1 M.2HS.2 M.2HS.3 M.2HS.4 M.2HS.5 M.2HS.6 Explain how the definition of the meaning of rational exponents follows from extending the properties of integer exponents
Research Projects
 SUMMER@ICERM 2012 Research Projects The document contains a list of possible research problems for the 2012 SUMMER@ICERM undergraduate research program. Contents 1 Billiards and related systems 2 1.1 Polygonal
SUMMER@ICERM 2012 Research Projects The document contains a list of possible research problems for the 2012 SUMMER@ICERM undergraduate research program. Contents 1 Billiards and related systems 2 1.1 Polygonal
arxiv: v1 [math.mg] 28 Dec 2018
![arxiv: v1 [math.mg] 28 Dec 2018 arxiv: v1 [math.mg] 28 Dec 2018](/thumbs/92/111014126.jpg) NEIGHBORING MAPPING POINTS THEOREM ANDREI V. MALYUTIN AND OLEG R. MUSIN arxiv:1812.10895v1 [math.mg] 28 Dec 2018 Abstract. Let f: X M be a continuous map of metric spaces. We say that points in a subset
NEIGHBORING MAPPING POINTS THEOREM ANDREI V. MALYUTIN AND OLEG R. MUSIN arxiv:1812.10895v1 [math.mg] 28 Dec 2018 Abstract. Let f: X M be a continuous map of metric spaces. We say that points in a subset
1 + lim. n n+1. f(x) = x + 1, x 1. and we check that f is increasing, instead. Using the quotient rule, we easily find that. 1 (x + 1) 1 x (x + 1) 2 =
 Chapter 5 Sequences and series 5. Sequences Definition 5. (Sequence). A sequence is a function which is defined on the set N of natural numbers. Since such a function is uniquely determined by its values
Chapter 5 Sequences and series 5. Sequences Definition 5. (Sequence). A sequence is a function which is defined on the set N of natural numbers. Since such a function is uniquely determined by its values
Practice Problems for the Final Exam
 Math 114 Spring 2017 Practice Problems for the Final Exam 1. The planes 3x + 2y + z = 6 and x + y = 2 intersect in a line l. Find the distance from the origin to l. (Answer: 24 3 ) 2. Find the area of
Math 114 Spring 2017 Practice Problems for the Final Exam 1. The planes 3x + 2y + z = 6 and x + y = 2 intersect in a line l. Find the distance from the origin to l. (Answer: 24 3 ) 2. Find the area of
Analysis-3 lecture schemes
 Analysis-3 lecture schemes (with Homeworks) 1 Csörgő István November, 2015 1 A jegyzet az ELTE Informatikai Kar 2015. évi Jegyzetpályázatának támogatásával készült Contents 1. Lesson 1 4 1.1. The Space
Analysis-3 lecture schemes (with Homeworks) 1 Csörgő István November, 2015 1 A jegyzet az ELTE Informatikai Kar 2015. évi Jegyzetpályázatának támogatásával készült Contents 1. Lesson 1 4 1.1. The Space
Topological Classification of Morse Functions and Generalisations of Hilbert s 16-th Problem
 Math Phys Anal Geom (2007) 10:227 236 DOI 10.1007/s11040-007-9029-0 Topological Classification of Morse Functions and Generalisations of Hilbert s 16-th Problem Vladimir I. Arnold Received: 30 August 2007
Math Phys Anal Geom (2007) 10:227 236 DOI 10.1007/s11040-007-9029-0 Topological Classification of Morse Functions and Generalisations of Hilbert s 16-th Problem Vladimir I. Arnold Received: 30 August 2007
Evgeniy V. Martyushev RESEARCH STATEMENT
 Evgeniy V. Martyushev RESEARCH STATEMENT My research interests lie in the fields of topology of manifolds, algebraic topology, representation theory, and geometry. Specifically, my work explores various
Evgeniy V. Martyushev RESEARCH STATEMENT My research interests lie in the fields of topology of manifolds, algebraic topology, representation theory, and geometry. Specifically, my work explores various
STABILITY OF INVARIANT SUBSPACES OF COMMUTING MATRICES We obtain some further results for pairs of commuting matrices. We show that a pair of commutin
 On the stability of invariant subspaces of commuting matrices Tomaz Kosir and Bor Plestenjak September 18, 001 Abstract We study the stability of (joint) invariant subspaces of a nite set of commuting
On the stability of invariant subspaces of commuting matrices Tomaz Kosir and Bor Plestenjak September 18, 001 Abstract We study the stability of (joint) invariant subspaces of a nite set of commuting
Notes on Complex Analysis
 Michael Papadimitrakis Notes on Complex Analysis Department of Mathematics University of Crete Contents The complex plane.. The complex plane...................................2 Argument and polar representation.........................
Michael Papadimitrakis Notes on Complex Analysis Department of Mathematics University of Crete Contents The complex plane.. The complex plane...................................2 Argument and polar representation.........................
Part IB Geometry. Theorems. Based on lectures by A. G. Kovalev Notes taken by Dexter Chua. Lent 2016
 Part IB Geometry Theorems Based on lectures by A. G. Kovalev Notes taken by Dexter Chua Lent 2016 These notes are not endorsed by the lecturers, and I have modified them (often significantly) after lectures.
Part IB Geometry Theorems Based on lectures by A. G. Kovalev Notes taken by Dexter Chua Lent 2016 These notes are not endorsed by the lecturers, and I have modified them (often significantly) after lectures.
Deviation Measures and Normals of Convex Bodies
 Beiträge zur Algebra und Geometrie Contributions to Algebra Geometry Volume 45 (2004), No. 1, 155-167. Deviation Measures Normals of Convex Bodies Dedicated to Professor August Florian on the occasion
Beiträge zur Algebra und Geometrie Contributions to Algebra Geometry Volume 45 (2004), No. 1, 155-167. Deviation Measures Normals of Convex Bodies Dedicated to Professor August Florian on the occasion
INVERSION IN THE PLANE BERKELEY MATH CIRCLE
 INVERSION IN THE PLANE BERKELEY MATH CIRCLE ZVEZDELINA STANKOVA MILLS COLLEGE/UC BERKELEY SEPTEMBER 26TH 2004 Contents 1. Definition of Inversion in the Plane 1 Properties of Inversion 2 Problems 2 2.
INVERSION IN THE PLANE BERKELEY MATH CIRCLE ZVEZDELINA STANKOVA MILLS COLLEGE/UC BERKELEY SEPTEMBER 26TH 2004 Contents 1. Definition of Inversion in the Plane 1 Properties of Inversion 2 Problems 2 2.
Devil s Staircase Rotation Number of Outer Billiard with Polygonal Invariant Curves
 Devil s Staircase Rotation Number of Outer Billiard with Polygonal Invariant Curves Zijian Yao February 10, 2014 Abstract In this paper, we discuss rotation number on the invariant curve of a one parameter
Devil s Staircase Rotation Number of Outer Billiard with Polygonal Invariant Curves Zijian Yao February 10, 2014 Abstract In this paper, we discuss rotation number on the invariant curve of a one parameter
Part IB GEOMETRY (Lent 2016): Example Sheet 1
 Part IB GEOMETRY (Lent 2016): Example Sheet 1 (a.g.kovalev@dpmms.cam.ac.uk) 1. Suppose that H is a hyperplane in Euclidean n-space R n defined by u x = c for some unit vector u and constant c. The reflection
Part IB GEOMETRY (Lent 2016): Example Sheet 1 (a.g.kovalev@dpmms.cam.ac.uk) 1. Suppose that H is a hyperplane in Euclidean n-space R n defined by u x = c for some unit vector u and constant c. The reflection
Course 212: Academic Year Section 9: Winding Numbers
 Course 212: Academic Year 1991-2 Section 9: Winding Numbers D. R. Wilkins Contents 9 Winding Numbers 71 9.1 Winding Numbers of Closed Curves in the Plane........ 71 9.2 Winding Numbers and Contour Integrals............
Course 212: Academic Year 1991-2 Section 9: Winding Numbers D. R. Wilkins Contents 9 Winding Numbers 71 9.1 Winding Numbers of Closed Curves in the Plane........ 71 9.2 Winding Numbers and Contour Integrals............
TEACHER CERTIFICATION EXAM 1.0 KNOWLEDGE OF ALGEBRA Identify graphs of linear inequalities on a number line...1
 TABLE OF CONTENTS COMPETENCY/SKILL PG # 1.0 KNOWLEDGE OF ALGEBRA...1 1.1. Identify graphs of linear inequalities on a number line...1 1.2. Identify graphs of linear equations and inequalities in the coordinate
TABLE OF CONTENTS COMPETENCY/SKILL PG # 1.0 KNOWLEDGE OF ALGEBRA...1 1.1. Identify graphs of linear inequalities on a number line...1 1.2. Identify graphs of linear equations and inequalities in the coordinate
MAXIMA AND MINIMA CHAPTER 7.1 INTRODUCTION 7.2 CONCEPT OF LOCAL MAXIMA AND LOCAL MINIMA
 CHAPTER 7 MAXIMA AND MINIMA 7.1 INTRODUCTION The notion of optimizing functions is one of the most important application of calculus used in almost every sphere of life including geometry, business, trade,
CHAPTER 7 MAXIMA AND MINIMA 7.1 INTRODUCTION The notion of optimizing functions is one of the most important application of calculus used in almost every sphere of life including geometry, business, trade,
On the classication of algebras
 Technische Universität Carolo-Wilhelmina Braunschweig Institut Computational Mathematics On the classication of algebras Morten Wesche September 19, 2016 Introduction Higman (1950) published the papers
Technische Universität Carolo-Wilhelmina Braunschweig Institut Computational Mathematics On the classication of algebras Morten Wesche September 19, 2016 Introduction Higman (1950) published the papers
Economics Noncooperative Game Theory Lectures 3. October 15, 1997 Lecture 3
 Economics 8117-8 Noncooperative Game Theory October 15, 1997 Lecture 3 Professor Andrew McLennan Nash Equilibrium I. Introduction A. Philosophy 1. Repeated framework a. One plays against dierent opponents
Economics 8117-8 Noncooperative Game Theory October 15, 1997 Lecture 3 Professor Andrew McLennan Nash Equilibrium I. Introduction A. Philosophy 1. Repeated framework a. One plays against dierent opponents
The Minimal Element Theorem
 The Minimal Element Theorem The CMC Dynamics Theorem deals with describing all of the periodic or repeated geometric behavior of a properly embedded CMC surface with bounded second fundamental form in
The Minimal Element Theorem The CMC Dynamics Theorem deals with describing all of the periodic or repeated geometric behavior of a properly embedded CMC surface with bounded second fundamental form in
Faculty of Engineering, Mathematics and Science School of Mathematics
 Faculty of Engineering, Mathematics and Science School of Mathematics GROUPS Trinity Term 06 MA3: Advanced Calculus SAMPLE EXAM, Solutions DAY PLACE TIME Prof. Larry Rolen Instructions to Candidates: Attempt
Faculty of Engineering, Mathematics and Science School of Mathematics GROUPS Trinity Term 06 MA3: Advanced Calculus SAMPLE EXAM, Solutions DAY PLACE TIME Prof. Larry Rolen Instructions to Candidates: Attempt
REGULAR TRIPLETS IN COMPACT SYMMETRIC SPACES
 REGULAR TRIPLETS IN COMPACT SYMMETRIC SPACES MAKIKO SUMI TANAKA 1. Introduction This article is based on the collaboration with Tadashi Nagano. In the first part of this article we briefly review basic
REGULAR TRIPLETS IN COMPACT SYMMETRIC SPACES MAKIKO SUMI TANAKA 1. Introduction This article is based on the collaboration with Tadashi Nagano. In the first part of this article we briefly review basic
UNC Charlotte Super Competition - Comprehensive test March 2, 2015
 March 2, 2015 1. triangle is inscribed in a semi-circle of radius r as shown in the figure: θ The area of the triangle is () r 2 sin 2θ () πr 2 sin θ () r sin θ cos θ () πr 2 /4 (E) πr 2 /2 2. triangle
March 2, 2015 1. triangle is inscribed in a semi-circle of radius r as shown in the figure: θ The area of the triangle is () r 2 sin 2θ () πr 2 sin θ () r sin θ cos θ () πr 2 /4 (E) πr 2 /2 2. triangle
Calculus 221 worksheet
 Calculus 221 worksheet Graphing A function has a global maximum at some a in its domain if f(x) f(a) for all other x in the domain of f. Global maxima are sometimes also called absolute maxima. A function
Calculus 221 worksheet Graphing A function has a global maximum at some a in its domain if f(x) f(a) for all other x in the domain of f. Global maxima are sometimes also called absolute maxima. A function
Covering the Convex Quadrilaterals of Point Sets
 Covering the Convex Quadrilaterals of Point Sets Toshinori Sakai, Jorge Urrutia 2 Research Institute of Educational Development, Tokai University, 2-28-4 Tomigaya, Shibuyaku, Tokyo 5-8677, Japan 2 Instituto
Covering the Convex Quadrilaterals of Point Sets Toshinori Sakai, Jorge Urrutia 2 Research Institute of Educational Development, Tokai University, 2-28-4 Tomigaya, Shibuyaku, Tokyo 5-8677, Japan 2 Instituto
HOMOGENEITY DEGREE OF SOME SYMMETRIC PRODUCTS
 HOMOGENEITY DEGREE OF SOME SYMMETRIC PRODUCTS RODRIGO HERNÁNDEZ-GUTIÉRREZ AND VERÓNICA MARTÍNEZ-DE-LA-VEGA Abstract. For a metric continuum X, we consider the n th -symmetric product F n(x) defined as
HOMOGENEITY DEGREE OF SOME SYMMETRIC PRODUCTS RODRIGO HERNÁNDEZ-GUTIÉRREZ AND VERÓNICA MARTÍNEZ-DE-LA-VEGA Abstract. For a metric continuum X, we consider the n th -symmetric product F n(x) defined as
Our rst result is the direct analogue of the main theorem of [5], and can be roughly stated as follows: Theorem. Let R be a complex reection of order
![Our rst result is the direct analogue of the main theorem of [5], and can be roughly stated as follows: Theorem. Let R be a complex reection of order Our rst result is the direct analogue of the main theorem of [5], and can be roughly stated as follows: Theorem. Let R be a complex reection of order](/thumbs/80/80698440.jpg) Unfaithful complex hyperbolic triangle groups II: Higher order reections John R. Parker Department of Mathematical Sciences, University of Durham, South Road, Durham DH LE, England. e-mail: j.r.parker@durham.ac.uk
Unfaithful complex hyperbolic triangle groups II: Higher order reections John R. Parker Department of Mathematical Sciences, University of Durham, South Road, Durham DH LE, England. e-mail: j.r.parker@durham.ac.uk
How well do I know the content? (scale 1 5)
 Page 1 I. Number and Quantity, Algebra, Functions, and Calculus (68%) A. Number and Quantity 1. Understand the properties of exponents of s I will a. perform operations involving exponents, including negative
Page 1 I. Number and Quantity, Algebra, Functions, and Calculus (68%) A. Number and Quantity 1. Understand the properties of exponents of s I will a. perform operations involving exponents, including negative
Math 46 Final Exam Review Packet
 Math 46 Final Exam Review Packet Question 1. Perform the indicated operation. Simplify if possible. 7 x x 2 2x + 3 2 x Question 2. The sum of a number and its square is 72. Find the number. Question 3.
Math 46 Final Exam Review Packet Question 1. Perform the indicated operation. Simplify if possible. 7 x x 2 2x + 3 2 x Question 2. The sum of a number and its square is 72. Find the number. Question 3.
EASY PUTNAM PROBLEMS
 EASY PUTNAM PROBLEMS (Last updated: December 11, 2017) Remark. The problems in the Putnam Competition are usually very hard, but practically every session contains at least one problem very easy to solve
EASY PUTNAM PROBLEMS (Last updated: December 11, 2017) Remark. The problems in the Putnam Competition are usually very hard, but practically every session contains at least one problem very easy to solve
MATH Max-min Theory Fall 2016
 MATH 20550 Max-min Theory Fall 2016 1. Definitions and main theorems Max-min theory starts with a function f of a vector variable x and a subset D of the domain of f. So far when we have worked with functions
MATH 20550 Max-min Theory Fall 2016 1. Definitions and main theorems Max-min theory starts with a function f of a vector variable x and a subset D of the domain of f. So far when we have worked with functions
Abstract. Jacobi curves are far going generalizations of the spaces of \Jacobi
 Principal Invariants of Jacobi Curves Andrei Agrachev 1 and Igor Zelenko 2 1 S.I.S.S.A., Via Beirut 2-4, 34013 Trieste, Italy and Steklov Mathematical Institute, ul. Gubkina 8, 117966 Moscow, Russia; email:
Principal Invariants of Jacobi Curves Andrei Agrachev 1 and Igor Zelenko 2 1 S.I.S.S.A., Via Beirut 2-4, 34013 Trieste, Italy and Steklov Mathematical Institute, ul. Gubkina 8, 117966 Moscow, Russia; email:
Math 42, Discrete Mathematics
 c Fall 2018 last updated 12/05/2018 at 15:47:21 For use by students in this class only; all rights reserved. Note: some prose & some tables are taken directly from Kenneth R. Rosen, and Its Applications,
c Fall 2018 last updated 12/05/2018 at 15:47:21 For use by students in this class only; all rights reserved. Note: some prose & some tables are taken directly from Kenneth R. Rosen, and Its Applications,
Exhaustion: From Eudoxus to Archimedes
 Exhaustion: From Eudoxus to Archimedes Franz Lemmermeyer April 22, 2005 Abstract Disclaimer: Eventually, I plan to polish this and use my own diagrams; so far, most of it is lifted from the web. Exhaustion
Exhaustion: From Eudoxus to Archimedes Franz Lemmermeyer April 22, 2005 Abstract Disclaimer: Eventually, I plan to polish this and use my own diagrams; so far, most of it is lifted from the web. Exhaustion
MIDTERM EXAMINATION. Spring MTH301- Calculus II (Session - 3)
 ASSALAM O ALAIKUM All Dear fellows ALL IN ONE MTH3 Calculus II Midterm solved papers Created BY Ali Shah From Sahiwal BSCS th semester alaoudin.bukhari@gmail.com Remember me in your prayers MIDTERM EXAMINATION
ASSALAM O ALAIKUM All Dear fellows ALL IN ONE MTH3 Calculus II Midterm solved papers Created BY Ali Shah From Sahiwal BSCS th semester alaoudin.bukhari@gmail.com Remember me in your prayers MIDTERM EXAMINATION
14.7: Maxima and Minima
 14.7: Maxima and Minima Marius Ionescu October 29, 2012 Marius Ionescu () 14.7: Maxima and Minima October 29, 2012 1 / 13 Local Maximum and Local Minimum Denition Marius Ionescu () 14.7: Maxima and Minima
14.7: Maxima and Minima Marius Ionescu October 29, 2012 Marius Ionescu () 14.7: Maxima and Minima October 29, 2012 1 / 13 Local Maximum and Local Minimum Denition Marius Ionescu () 14.7: Maxima and Minima
1 Lagrange Multiplier Method
 1 Lagrange Multiplier Method Near a maximum the decrements on both sides are in the beginning only imperceptible. J. Kepler When a quantity is greatest or least, at that moment its flow neither increases
1 Lagrange Multiplier Method Near a maximum the decrements on both sides are in the beginning only imperceptible. J. Kepler When a quantity is greatest or least, at that moment its flow neither increases
A note on integral Menger curvature for curves
 A note on integral Menger curvature for curves Simon Blatt August 26, 20 For continuously dierentiable embedded curves γ, we will give a necessary and sucient condition for the boundedness of integral
A note on integral Menger curvature for curves Simon Blatt August 26, 20 For continuously dierentiable embedded curves γ, we will give a necessary and sucient condition for the boundedness of integral
Math Maximum and Minimum Values, I
 Math 213 - Maximum and Minimum Values, I Peter A. Perry University of Kentucky October 8, 218 Homework Re-read section 14.7, pp. 959 965; read carefully pp. 965 967 Begin homework on section 14.7, problems
Math 213 - Maximum and Minimum Values, I Peter A. Perry University of Kentucky October 8, 218 Homework Re-read section 14.7, pp. 959 965; read carefully pp. 965 967 Begin homework on section 14.7, problems
Topology Proceedings. COPYRIGHT c by Topology Proceedings. All rights reserved.
 Topology Proceedings Web: http://topology.auburn.edu/tp/ Mail: Topology Proceedings Department of Mathematics & Statistics Auburn University, Alabama 36849, USA E-mail: topolog@auburn.edu ISSN: 0146-4124
Topology Proceedings Web: http://topology.auburn.edu/tp/ Mail: Topology Proceedings Department of Mathematics & Statistics Auburn University, Alabama 36849, USA E-mail: topolog@auburn.edu ISSN: 0146-4124
THE BORSUK-ULAM THEOREM FOR GENERAL SPACES
 THE BORSUK-ULAM THEOREM FOR GENERAL SPACES PEDRO L. Q. PERGHER, DENISE DE MATTOS, AND EDIVALDO L. DOS SANTOS Abstract. Let X, Y be topological spaces and T : X X a free involution. In this context, a question
THE BORSUK-ULAM THEOREM FOR GENERAL SPACES PEDRO L. Q. PERGHER, DENISE DE MATTOS, AND EDIVALDO L. DOS SANTOS Abstract. Let X, Y be topological spaces and T : X X a free involution. In this context, a question
On bisectors in Minkowski normed space.
 On bisectors in Minkowski normed space. Á.G.Horváth Department of Geometry, Technical University of Budapest, H-1521 Budapest, Hungary November 6, 1997 Abstract In this paper we discuss the concept of
On bisectors in Minkowski normed space. Á.G.Horváth Department of Geometry, Technical University of Budapest, H-1521 Budapest, Hungary November 6, 1997 Abstract In this paper we discuss the concept of
COURSE STRUCTURE CLASS IX Maths
 COURSE STRUCTURE CLASS IX Maths Units Unit Name Marks I NUMBER SYSTEMS 08 II ALGEBRA 17 III COORDINATE GEOMETRY 04 IV GEOMETRY 28 V MENSURATION 13 VI STATISTICS & PROBABILITY 10 Total 80 UNIT I: NUMBER
COURSE STRUCTURE CLASS IX Maths Units Unit Name Marks I NUMBER SYSTEMS 08 II ALGEBRA 17 III COORDINATE GEOMETRY 04 IV GEOMETRY 28 V MENSURATION 13 VI STATISTICS & PROBABILITY 10 Total 80 UNIT I: NUMBER
SOME SPECIAL KLEINIAN GROUPS AND THEIR ORBIFOLDS
 Proyecciones Vol. 21, N o 1, pp. 21-50, May 2002. Universidad Católica del Norte Antofagasta - Chile SOME SPECIAL KLEINIAN GROUPS AND THEIR ORBIFOLDS RUBÉN HIDALGO Universidad Técnica Federico Santa María
Proyecciones Vol. 21, N o 1, pp. 21-50, May 2002. Universidad Católica del Norte Antofagasta - Chile SOME SPECIAL KLEINIAN GROUPS AND THEIR ORBIFOLDS RUBÉN HIDALGO Universidad Técnica Federico Santa María
Name: GEOMETRY: EXAM (A) A B C D E F G H D E. 1. How many non collinear points determine a plane?
 GMTRY: XM () Name: 1. How many non collinear points determine a plane? ) none ) one ) two ) three 2. How many edges does a heagonal prism have? ) 6 ) 12 ) 18 ) 2. Name the intersection of planes Q and
GMTRY: XM () Name: 1. How many non collinear points determine a plane? ) none ) one ) two ) three 2. How many edges does a heagonal prism have? ) 6 ) 12 ) 18 ) 2. Name the intersection of planes Q and
Ramsey Theory. May 24, 2015
 Ramsey Theory May 24, 2015 1 König s Lemma König s Lemma is a basic tool to move between finite and infinite combinatorics. To be concise, we use the notation [k] = {1, 2,..., k}, and [X] r will denote
Ramsey Theory May 24, 2015 1 König s Lemma König s Lemma is a basic tool to move between finite and infinite combinatorics. To be concise, we use the notation [k] = {1, 2,..., k}, and [X] r will denote
V. Graph Sketching and Max-Min Problems
 V. Graph Sketching and Max-Min Problems The signs of the first and second derivatives of a function tell us something about the shape of its graph. In this chapter we learn how to find that information.
V. Graph Sketching and Max-Min Problems The signs of the first and second derivatives of a function tell us something about the shape of its graph. In this chapter we learn how to find that information.
12-neighbour packings of unit balls in E 3
 12-neighbour packings of unit balls in E 3 Károly Böröczky Department of Geometry Eötvös Loránd University Pázmány Péter sétány 1/c H-1117 Budapest Hungary László Szabó Institute of Informatics and Economics
12-neighbour packings of unit balls in E 3 Károly Böröczky Department of Geometry Eötvös Loránd University Pázmány Péter sétány 1/c H-1117 Budapest Hungary László Szabó Institute of Informatics and Economics
Organization Team Team ID#
 1. [4] A random number generator will always output 7. Sam uses this random number generator once. What is the expected value of the output? 2. [4] Let A, B, C, D, E, F be 6 points on a circle in that
1. [4] A random number generator will always output 7. Sam uses this random number generator once. What is the expected value of the output? 2. [4] Let A, B, C, D, E, F be 6 points on a circle in that
MTH301 Calculus II Glossary For Final Term Exam Preparation
 MTH301 Calculus II Glossary For Final Term Exam Preparation Glossary Absolute maximum : The output value of the highest point on a graph over a given input interval or over all possible input values. An
MTH301 Calculus II Glossary For Final Term Exam Preparation Glossary Absolute maximum : The output value of the highest point on a graph over a given input interval or over all possible input values. An
1. The sides of a triangle are in the ratio 3 : 5 : 9. Which of the following words best describes the triangle?
 UNIVERSITY OF NORTH CAROLINA CHARLOTTE 999 HIGH SCHOOL MATHEMATICS CONTEST March 8, 999 The sides of a triangle are in the ratio : 5 : 9 Which of the following words best describes the triangle? (A) obtuse
UNIVERSITY OF NORTH CAROLINA CHARLOTTE 999 HIGH SCHOOL MATHEMATICS CONTEST March 8, 999 The sides of a triangle are in the ratio : 5 : 9 Which of the following words best describes the triangle? (A) obtuse
MATH 18.01, FALL PROBLEM SET # 6 SOLUTIONS
 MATH 181, FALL 17 - PROBLEM SET # 6 SOLUTIONS Part II (5 points) 1 (Thurs, Oct 6; Second Fundamental Theorem; + + + + + = 16 points) Let sinc(x) denote the sinc function { 1 if x =, sinc(x) = sin x if
MATH 181, FALL 17 - PROBLEM SET # 6 SOLUTIONS Part II (5 points) 1 (Thurs, Oct 6; Second Fundamental Theorem; + + + + + = 16 points) Let sinc(x) denote the sinc function { 1 if x =, sinc(x) = sin x if
Theorem 1.2 (Converse of Pythagoras theorem). If the lengths of the sides of ABC satisfy a 2 + b 2 = c 2, then the triangle has a right angle at C.
 hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a + b = c. roof. b a a 3 b b 4 b a b 4 1 a a 3
hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a + b = c. roof. b a a 3 b b 4 b a b 4 1 a a 3
MATH 434 Fall 2016 Homework 1, due on Wednesday August 31
 Homework 1, due on Wednesday August 31 Problem 1. Let z = 2 i and z = 3 + 4i. Write the product zz and the quotient z z in the form a + ib, with a, b R. Problem 2. Let z C be a complex number, and let
Homework 1, due on Wednesday August 31 Problem 1. Let z = 2 i and z = 3 + 4i. Write the product zz and the quotient z z in the form a + ib, with a, b R. Problem 2. Let z C be a complex number, and let
Topological properties
 CHAPTER 4 Topological properties 1. Connectedness Definitions and examples Basic properties Connected components Connected versus path connected, again 2. Compactness Definition and first examples Topological
CHAPTER 4 Topological properties 1. Connectedness Definitions and examples Basic properties Connected components Connected versus path connected, again 2. Compactness Definition and first examples Topological
(1.) For any subset P S we denote by L(P ) the abelian group of integral relations between elements of P, i.e. L(P ) := ker Z P! span Z P S S : For ea
 Torsion of dierentials on toric varieties Klaus Altmann Institut fur reine Mathematik, Humboldt-Universitat zu Berlin Ziegelstr. 13a, D-10099 Berlin, Germany. E-mail: altmann@mathematik.hu-berlin.de Abstract
Torsion of dierentials on toric varieties Klaus Altmann Institut fur reine Mathematik, Humboldt-Universitat zu Berlin Ziegelstr. 13a, D-10099 Berlin, Germany. E-mail: altmann@mathematik.hu-berlin.de Abstract
B 1 = {B(x, r) x = (x 1, x 2 ) H, 0 < r < x 2 }. (a) Show that B = B 1 B 2 is a basis for a topology on X.
 Math 6342/7350: Topology and Geometry Sample Preliminary Exam Questions 1. For each of the following topological spaces X i, determine whether X i and X i X i are homeomorphic. (a) X 1 = [0, 1] (b) X 2
Math 6342/7350: Topology and Geometry Sample Preliminary Exam Questions 1. For each of the following topological spaces X i, determine whether X i and X i X i are homeomorphic. (a) X 1 = [0, 1] (b) X 2
Math 302 Outcome Statements Winter 2013
 Math 302 Outcome Statements Winter 2013 1 Rectangular Space Coordinates; Vectors in the Three-Dimensional Space (a) Cartesian coordinates of a point (b) sphere (c) symmetry about a point, a line, and a
Math 302 Outcome Statements Winter 2013 1 Rectangular Space Coordinates; Vectors in the Three-Dimensional Space (a) Cartesian coordinates of a point (b) sphere (c) symmetry about a point, a line, and a
Iowa State University. Instructor: Alex Roitershtein Summer Homework #5. Solutions
 Math 50 Iowa State University Introduction to Real Analysis Department of Mathematics Instructor: Alex Roitershtein Summer 205 Homework #5 Solutions. Let α and c be real numbers, c > 0, and f is defined
Math 50 Iowa State University Introduction to Real Analysis Department of Mathematics Instructor: Alex Roitershtein Summer 205 Homework #5 Solutions. Let α and c be real numbers, c > 0, and f is defined
The Common Core Georgia Performance Standards (CCGPS) for Grades K-12 Mathematics may be accessed on-line at:
 FORMAT FOR CORRELATION TO THE COMMON CORE GEORGIA PERFORMANCE STANDARDS (CCGPS) Subject Area: Mathematics Textbook Title: State-Funded Course: 27.09720 Analytic Geometry,, I Publisher: Agile Mind Standard
FORMAT FOR CORRELATION TO THE COMMON CORE GEORGIA PERFORMANCE STANDARDS (CCGPS) Subject Area: Mathematics Textbook Title: State-Funded Course: 27.09720 Analytic Geometry,, I Publisher: Agile Mind Standard
