The Radon Transform and the Mathematics of Medical Imaging
|
|
|
- Alexander Atkinson
- 6 years ago
- Views:
Transcription
1 Colby College Digital Colby Honors Theses Student Research 2012 The Radon Transform and the Mathematics of Medical Imaging Jen Beatty Colby College Follow this and additional works at: Part of the Analytical, Diagnostic and Therapeutic Techniques and Equipment Commons, and the Applied Mathematics Commons Colby College theses are protected by copyright. They may be viewed or downloaded from this site for the purposes of research and scholarship. Reproduction or distribution for commercial purposes is prohibited without written permission of the author. Recommended Citation Beatty, Jen, "The Radon Transform and the Mathematics of Medical Imaging" (2012). Honors Theses. Paper This Honors Thesis (Open Access) is brought to you for free and open access by the Student Research at Digital Colby. It has been accepted for inclusion in Honors Theses by an authorized administrator of Digital Colby. For more information, please contact enrhodes@colby.edu.
2 THE RADON TRANSFORM AND THE MATHEMATICS OF MEDICAL IMAGING JEN BEATTY 1
3 2 JEN BEATTY Table of Contents 1. Introduction 3 2. A Mathematical Model for X-Ray Tomography 6 3. Geometry of Medical Imaging 8 4. The Radon Transform The Fourier Transform The Central Slice Theorem The Backprojection Convolution and Low Pass Filters Discrete Version Conclusion Acknowledgements 26 References 26
4 THE RADON TRANSFORM AND THE MATHEMATICS OF MEDICAL IMAGING 3 Abstract. Tomography is the mathematical process of imaging an object via a set of finite slices. In medical imaging, these slices are defined by multiple parallel X-ray beams shot through the object at varying angles. The initial and final intensity of each beam is recorded, and the original image is recreated using this data for multiple slices. I will discuss the central role of the Radon transform and its inversion formula in this recovery process. 1. Introduction Tomography is a means of imaging a two- or three- dimensional object from many onedimensional slices of the object. In a CT (computerized tomography) scan, these slices are defined by multiple parallel X-ray beams that are perpendicular to the object. This idea is shown in Figure 1, where a slice is defined by the dark band surrounding the patient s head. A CT scanner makes two measurements: the initial intensity of each X-ray beam, I 0, at the radiation source, and the final intensity of each beam, I 1, at the radiation detector. The changes in intensity for a single beam are dependent on the internal density of the object along the line the X-ray passes through (we shall go into more detail about exactly how this process works later in this section). By changing the orientation of the source and detector we are able to gain more information about the internal density of a single slice by looking at the corresponding intensity changes. The motivating question for this discussion is: how do we use the information measured by a CT scanner (the changes in density) to accurately create a picture of the varying densities along a single slice of our object? If we are able to recreate a single slice, we can then use multiple slices to get an idea about the internal structure of our entire object. As a starting point for our discussion, we will consider a single X-ray beam. Figure 1. CT Example
5 4 JEN BEATTY X-rays are a type of electromagnetic radiation, a form of energy that is dependent on charged particles traveling through space. X-rays have wavelengths between 0.01 to 0.1 nm (1nm = 10 9 m) and corresponding frequencies in the range of 3 x Hz - 3 x Hz. We will not focus on the physical properties of X-rays all that much, most important to our discussion is actually the changes in the intensity of a single beam as it comes in contact with a solid object. When an X-ray is shot through an object it looses some of its energy to the surrounding medium. This loss corresponds to a decrease in the intensity of the beam. Intensity is energy flux averaged over the period of the wave and is dependent on both the speed of the wave and the energy density (energy/ unit volume) of the wave. By measuring the initial and final intensities of a single beam, we gain some knowledge about the density of the medium through which it passed. Intuitively it makes sense that a denser object (such as bone) would cause a greater change in the intensity of the beam than would a less dense object (such as human tissue). Figure 2. Parallel X-Ray Beam Geometry What about more complex objects, however? In a CT scan a single X-ray beam cross through many different materials such as blood, bone, tissue, etc. This causes the density of the object to vary over the length of the beam and measuring the initial and final intensities of a single beam in one direction does not give us any information about the changing densities along the path of the beam, only the overall loss in intensity. The idea behind tomography is that by measuring the changes in intensity of X-ray beams in many different directions we might be able to compile enough information to determine the different densities of our initial medium. To make these varying measurements, we shall assume a parallel beam geometry. This idea is demonstrated in Figure 2, where we have multiple parallel beams creating two different slices; first the beams are perpendicular to the x-axis, then they are rotated through by an angle θ. By changing the angle θ the beams travel along, we are able to create a new slice. There are other beam geometries
6 THE RADON TRANSFORM AND THE MATHEMATICS OF MEDICAL IMAGING 5 Figure 3. Shepp Logan Phantom and Sinogram used in modern CT scanners such as a fan beam or cone geometry, however we shall limit this discussion to parallel X-ray beams. The corresponding losses in intensity are given a grayscale value between 0 (black) and 1 (white). A value of 0 corresponds to zero change in intensity and a value of 1 corresponds to the beam being completely absorbed by the medium. The compilation of these varying values creates what is known as a sinogram (Figure 3). A sinogram is a graphical representation of the intensity losses measured by the CT scanner where the vertical axis represents the distance various beams are from the origin and the horizontal axis represents the angle at which the slice is measured. Therefore, a single point in the sinogram represents our measured change in intensity for a given distance and angle. From the information given in a sinogram we are able to recreate the structure of the original object. In Figure 3 we see an example of a sinogram created from a phantom image. A phantom image is an object created from predetermined data (i.e., it is a fake image). Phantom images are generally used in the testing process for various reconstruction algorithms to determine that any errors in the outcome are due to errors in the algorithm itself and not errors in the data gathering process The Shepp Logan phantom shown in Figure 3 is the most common phantom used in medical imaging reconstruction. In order to reconstruct our starting image, however, we need some method of deriving detailed information about the internal density of the medium from the initial and final densities of our various x-ray beams. It is nearly impossible to determine the starting densities of the object merely by inspecting the information shown in the sinogram. Finding a meaningful and useful solution to this problem will be the point of this paper. In order to solve this, however, we will need to make several simplifying (but not highly unreasonable) assumptions about X-ray beams.
7 6 JEN BEATTY (i) (ii) (iii) All X-ray beams are monochromatic (each photon in the wave propagates at the same frequency and with the same energy level E). All X-ray beams have zero width. X-ray beams are not subject to refraction (they do not scatter when they come into contact with a surface) or diffraction (they do not bend when they come into contact with a surface). While these assumptions are not entirely accurate, they are close enough to reality so that, for our purposes, we can take them as fact. Actual CT scanners use corrective algorithms to deal with the refraction and diffraction of some particles in the beam. The amount of energy lost by an X-ray beam as it travels through a medium is specific to that medium and in particular depends on the density of the medium. We wish to be able to somehow classify the density of the medium in terms of the amount of energy it causes an X-ray beam to lose. This characteristic of a medium is known as it s attenuation coefficient. As hinted at earlier in our discussion of the changes in intensity through bone versus tissue, denser objects have a higher attenuation coefficient than less dense objects. In objects of uniform density, the attenuation coefficient is constant for all points P = (x, y). Most interesting objects, however, are not of a uniform density and therefore have a varying attenuation coefficient over a range of P values. Therefore, what we really desire is a means of determining an equation for A(P ) which accounts for the varying densities of our medium. This thesis describes one solution to the inverse problem of solving for the attenuation coefficient in medical imaging. In Section 2 we offer a mathematical model for X-ray tomography and in Sections 3 and 4 we discuss the Radon transform and a parametrization method which presents us with a link between our measured data and the attenuation coefficient we wish to solve for. In Section 5 we introduce the Fourier transform which is a necessary part of the inversion process because of the key role it plays in the Central Slice Theorem discussed in Section 6. Sections 7 and 8 discuss an inversion process known as the backprojection formula and a means of increasing the accuracy of inversion, while Section 9 addresses the discretization of the formulas used previously to make them applicable to real world data. 2. A Mathematical Model for X-Ray Tomography Now that we have an idea of the physical model for CT scans, we shall take a closer look at the mathematical model we will use to determine the attenuation coefficient of our object. In order to do that, however, we will need more mathematical rigorous definitions for the intensity and attenuation coefficient of an object.
8 THE RADON TRANSFORM AND THE MATHEMATICS OF MEDICAL IMAGING 7 Definition 2.1. For a given energy level E of an X-ray beam and a rate of photon propagation N(x), the intensity of the beam, I(x), at a distance x from the origin is defined as I(x) = N(x) E. (2.1) Definition 2.2. The proportion of photons absorbed per millimeter of substance at a distance x from the origin is known as the attenuation coefficient, A(x), of the medium. We know the initial and final intensities, I 0 and I 1, of a single beam. What we want is to be able to use these intensities to determine the attenuation coefficient over the path of the beam. Fortunately, we are find a relationship between these two values in the Beer-Lambert Law. Definition 2.3. The Beer-Lambert Law states that for a monochromatic, non-refractive, zero-width X-ray beam that transverses a homogenous material along a distance x from the origin, the intensity I(x) is given by I(x) = e A(x)x. (2.2) As it stands, this equation is not all that useful to us. It gives the attenuation coefficient at a certain point in relation to the intensity at that point, but we only know the value of the intensity at points outside our object. What we really want is to be able to find some relationship between the attenuation coefficient inside our object and the change in intensity of the beam. To do this, we shall manipulate equation (2.1) slightly. Differentiating (2.1) we see: di dx = A(x)I(x). Let I(x 0 ) = I 0 be the initial intensity at x 0 and I(x 1 ) = I 1 be the final intensity at x 1. We therefore are able to see that which, after integration, yields x1 x 0 ln di x1 I(x) = A(x)dx, x 0 ( I1 I 0 ) x1 = A(x)dx. x 0 When multiplied by -1 this gives us a very nice final equation relating the initial and final intensities with the attenuation coefficient
9 8 JEN BEATTY ln ( I0 I 1 ) = x1 x 0 A(x)dx. (2.3) Therefore, what CT scan algorithms actually solve for is not the density function of the material but rather its attenuation coefficient. Logically this is not altogether surprising because it seems reasonable that there is a strong relationship between the density of an object and the proportion of photons it attenuates. From now on we shall not concern ourselves with the difference between the density function and the attenuation coefficient of a material and shall discuss them interchangeably. 3. Geometry of Medical Imaging Before going into further analysis of solving equation (2.2) it will be useful for us to spend some time describing the coordinate system that we will be using. The problem with a Cartesian coordinate system is that it is unable to handle vertical lines with an infinite slope (and we certainly do not want to exclude all vertical lines from our CT scan), and a polar coordinate system does not easily lend itself to systems dependent on parallel lines. Therefore we adopt a point normal parameterization for a line. We are all familiar with the idea that a line l in R 2 can be represented by the equation ax + by = c where a, b, c R and a 2 + b 2 0. One could say that a, b, and c parameterize l. Knowing a 2 + b 2 0, we can rewrite the standard equation of a line in the following format a a 2 + b 2 x + ( We now define ω = (ω 1, ω 2 ) = unit circle S 1, for a, a 2 +b 2 b a 2 + b 2 y = c a 2 + b 2. b a 2 +b 2 ) which we can see is a point lying on the ( ) a 2 ( ) b 2 + = 1. a 2 + b 2 a 2 + b 2 ( This furthermore implies that ω = (cos θ, sin θ) for some θ [0, 2π). Letting t = c a ), 2 +b 2 we see that we can rewrite l using the inner product z, ω where z = (x, y) R 2. In other words, we have shown that: z, ω = xω 1 + yω 2 = a a 2 + b 2 x + = x cos θ + y sin θ = t b a 2 + b 2 y = c a 2 + b 2
10 THE RADON TRANSFORM AND THE MATHEMATICS OF MEDICAL IMAGING 9 Note that in the above equations t and θ are fixed and determine a specific line l in the plane. We therefore can say that t and θ parameterize a line l t,θ and that z determines specific points on the line l. In other words: l t,θ = { z R 2 : z, (cos θ, sin θ) = t }. (3.1) Figure 4. Parameterized line l t,θ Figure 4 offers a visual of what we have done to parameterize the space of all lines We can imagine that the combination of θ and t define a point (t cos θ, t sin θ) in space and that as z varies we travel up and down our desired line l t,θ. The line l t,θ is the line that is perpendicular to the vector t cos θ, t sin θ through the point (t cos θ, t sin θ). We now offer an alternative definition for a specific point on the line l t,θ (although this may seem a bit redundant now, this additional notation will become useful in future derivations). To do this, we note that sin θ, cos θ is perpendicular to cos θ, sin θ. Therefore we can describe a particular point (x, y) on l t,θ in terms of a real number s as follows: (x(s), y(s)) = t cos θ, t sin θ + s sin θ, s cos θ, for s R.
11 10 JEN BEATTY In the above equation, each t and θ determine a particular line l. This leads to an alternative definition for the set of points that make up a line l t,θ : l t,θ = (x(s), y(s)) = {(t cos θ s sin θ, t sin θ + s cos θ) : s R}. (3.2) 4. The Radon Transform We are ready to introduce some mathematical tools that will be central to solving for the attenuation coefficient in equation (2.3). Definition 4.1. For a function f(t, θ) defined on R 2 with compact support the Radon transform of f, denoted by Rf, is defined for t R and θ (0, 2π] as Rf(t, θ) = f(x(s), y(s))ds. (4.1) A function with compact support is one that takes the value zero everywhere outside of a compact set. This is a reasonable requirement for a medical imaging problem because we are only dealing with finite areas (or slices) of some object. Recall that our goal is to determine the attenuation coefficient of our object which is related to the object s density. Therefore, since we are only dealing with finite slices, there will be some finite region outside of which the attenuation coefficient must equal zero. The Radon transform offers a means of determining the total density of a certain function f along a given line l. This line l is determined by an angle θ from the x-axis and a distance t from the origin as described in equation (3.1). As shown in Figure 5 if we take the Radon transform along multiple lines at varying angles (here θ 1 and θ 2 ), we are able to determine multiple density functions for our object. Intuitively we can interpret the Radon transform as a smeared version of our initial object. Suppose the blob like region represented in Figure 5 were an ink blot; if we were to smear this blot along varying lines in the direction θ 1, we can expect that the wider regions of the ink blot would correspond to a larger region than smaller regions, which is exactly what we see. The integral Rf(t, θ) represents the right half of equation (2.3). Recall that in this equation A(x) is unknown and ln( I 0 I 1 ) is measured information. In other words, ln( I 0 I 1 ) is the Radon transform, and therefore the Radon transform represents known, measured data.
12 THE RADON TRANSFORM AND THE MATHEMATICS OF MEDICAL IMAGING 11 Figure 5. Radon Transform for θ 1 and θ 2 The goal now is to find some type of inversion formula for the Radon transform that will allow us to recover our starting function f (or, in the context of medical imaging, A(x)). To do this, it will be useful to note several properties of the Radon transform. Properties 4.2. For real constants α, β, and continuous functions f and g on R 2 with compact support: (i) (ii) R(αf + βg) = αrf + βrg Rf(t, θ) = Rf( t, θ) (iii) Rf(t, θ) = f(x(s), y(s))ds = f(t cos θ s sin θ, t sin θ + s cos θ)ds Property (i) tells us that the Radon transform is linear, (ii) that it is even, and (iii) utilizes the equivalent geometric expressions used in the previous section to create different expressions for the same transform which we will use interchangeably depending on which best suits our needs. We furthermore define the natural domain of the Radon transform as the set of functions f on R 2 such that f(x(s), y(s)) ds <. That is, we restrict our domain to the set of absolutely integrable functions.
13 12 JEN BEATTY We have now devised a new way of stating our initial problem of solving for the attenuation coefficient function A(x) in a mathematical framework. The Radon transform is the mathematical name for equation (2.3). Therefore to recover A(x), we need to find an inversion formula for the Radon transform. Unfortunately, there is no single straightforward answer to this solution. To get an actual inversion formula we will have to delve into some more advanced mathematics. 5. The Fourier Transform Definition 5.1. For a given absolutely integrable function f on R the Fourier Transform of f, denoted by Ff is defined for every real number ξ as Ff(ξ) = f(x)e 2πixξ dx. (5.1) Although it might not seem relevant at the present, we will make extensive use of the Fourier transform and its inverse formula in our search for a solution to our medical imaging problem. The Fourier transform is used frequently in signal analysis and offers a means of changing a function of time into a function of frequency, the variable x represents time in seconds and the variable ξ represents the frequency of the function in Hertz. There exists an alternate definition that uses the angular frequency, ω, where ω = 2πξ, giving us Ff(ω) = f(x)e iωx dx. (5.2) We will primarily deal with this second definition of the Fourier transform throughout our discussion as it is the form more commonly used in engineering and medical imaging. We now note that compactly supported functions are a subset of a larger space of functions, the Schwartz Space (S(R n )), which consists of all infinitely differentiable functions on R n such that for all k, l 0: l sup xk x l f(x) < x R n These functions are also known as rapidly decreasing functions. Henceforth we shall assume that S denotes the two dimensional Schwartz space (S(R 2 )) since that is the dimension we are interested in for our attenuation problem. We limit our discussion to functions within S because there are several nice properties about this domain. The first is that within this domain there exists a bijective relationship between the Fourier transform and its inverse; the second is that the Fourier transform of a Schwartz function is still a Schwartz function; and the third is that we are allowed to change the order of integration for multiple integrals if f S.
14 THE RADON TRANSFORM AND THE MATHEMATICS OF MEDICAL IMAGING 13 As we did with the Radon transform, we shall list several properties of the Fourier transform. Properties 5.2. For real constants α and β and absolutely integrable functions f and g: (i) (ii) F(αf + βg) = αf(f) + βf(g) Ff(ω) < As was hinted at earlier, we will also make use of the inverse Fourier transform. Definition 5.3. For an absolutely integrable function f we define the inverse Fourier transform of f, denoted by F 1 f, evaluated at x as F 1 f(x) = 1 2π This immediately leads us to the following theorem. f(ω)e iωx dω. Theorem 5.4. For a function f S the Fourier Inversion Theorem states that, for all x: F 1 (Ff)(x) = f(x). So far, we have only addressed the Fourier transform in one dimension. There exist corresponding definitions in higher dimensions, although for our purposes we will only utilize the two dimensional analogs. Definition 5.5. For an absolutely integrable function g defined on R 2, the 2 dimensional Fourier transform of g, denoted by F 2 g, is defined for all (X, Y ) R 2 as F 2 g(x, Y ) = We similarly define the inverse Fourier transform on R 2. g(x, y)e i(xx+yy ) dxdy. (5.3) Definition 5.6. For an absolutely integrable function g defined on R 2 the 2 dimensional inverse Fourier transform at a point (x, y), denoted by F 1 g(x, y) is given as F2 1 1 g(x, y) = 4π 2 6. The Central Slice Theorem 2 g(x, Y )e i(xx+yy ) dxdy. (5.4) There is just one more big theorem we need to discuss before we can begin the actual process of inverting the Radon transform and recovering our attenuation coefficient. The central slice theorem gives us a remarkable relationship between the two dimensional Fourier transform and the one dimensional Fourier transform of the Radon transform.
15 14 JEN BEATTY Theorem 6.1. For an absolutely integrable function f defined on R 2 and all S R and θ [0, 2π), F 2 f(s cos θ, S sin θ) = F(Rf)(S, θ). Proof. We first recall that the two dimensional Fourier transform of f(x, y) is given by: F 2 f(x, y) = f(x, y)e is(x cos θ+y sin θ) dxdy (6.1) We now implement a change of variables here according to the coordinate system we defined in section 3. Recall that when we parameterized the line l t,θ we discovered that we could say the following for s R: x(s) = t cos θ s sin θ, y(s) = t sin θ + s cos θ, t = x cos θ + y cos θ Looking at the determinant of the Jacobian for x(s) and y(s): det x t y t x s y s = 1 we see that we can say that dsdt = dxdy. We therefore rewrite the right half of equation (6.1) in terms of the variables s, t f(t cos θ s sin θ, t sin θ + s cos θ)e ist dsdt. Because e ist has no dependence on s, we are able to rearrange the above integral as follows: ( ) f(t cos θ s sin θ, t sin θ + s cos θ)ds e ist dt. This inner integral is exactly the Radon transform of f(t, θ), implying that (Rf(t, θ))e ist dt. Which in turn is the Fourier transform of Rf(S, θ), and we conclude our proof.
16 THE RADON TRANSFORM AND THE MATHEMATICS OF MEDICAL IMAGING 15 The central slice theorem (also known as the Fourier slice theorem or the slice projection theorem) is a link between the one and two dimensional Fourier transforms. The theorem tells us that the one dimensional Fourier transform of a projected function (the Radon transform) is equal to the two dimensional Fourier transform of the original function taken on the slice through the origin parallel to the line we projected our function on. This idea is demonstrated in Figure 3. In the left part of the figure we start with a function F (x, y) and apply the Radon transform to get a projection g to which we then apply the Fourier transform, receiving the orange G function at the top of the figure. In the right half we take the 2 dimensional Fourier transform of the orange slice of F (x, y) parallel to the projection line. This 2 dimensional Fourier transform also equals the orange G function depicted at the top of the image. Figure 6. Central Slice Theorem This theory can also be extended to higher dimensions, but for our purposes in solving the inverse problem of finding the attenuation coefficient the two dimensional interpretation will suffice. 7. The Backprojection We are now finally ready to make a first attempt at recovering our attenuation coefficient function. Recall that, physically speaking, the Radon transform Rf(t, θ) gives us the total density of the object f along a line l t,θ. We have determined this density by measuring the initial and final intensities of an X-ray beam shot through the object along this line. By doing this along multiple different lines, we are able to create a single slice of our starting object and by varying the angle θ of these X-rays we are able to define many slices.
17 16 JEN BEATTY If we are somehow able to backproject these densities onto the plane, perhaps we will be able to recreate our starting object. Intuitively we can think of this process as taking the sinogram data and unsmearing it back onto the plane. Definition 7.1. Let h = h(t, θ). We define the backprojection, Bh, at a point (x, y) as Bh(x, y) = 1 π π 0 h(x cos θ + y sin θ, θ)dθ. Applying this backprojection formula to the Radon transform, we receive the following: BRf(x, y) = 1 π π 0 Rf(x cos θ + y sin θ, θ)dθ. (7.1) In the context of medical imaging, f represents our attenuation coefficient function. We are able to backproject over the slices we have measured. As demonstrated in Figure 7, backprojecting in only a few directions θ is an incredibly inaccurate way of recreating even a simple object. However, even if we significantly increase the number of backprojections we use (say to 1000 directions), there is still a large amount of noise blurring our recreated image. As it turns out, no matter how many directions we try to backproject in, we will still not be able to perfectly recreate our image using the backprojection formula of equation (7.1). For this process to be at all useful, we will need to derive a way to filter out some of the noise the backprojection formula seems to create in our picture and get a smoother representation of our object. To this end, we define a filtered backprojection formula. Theorem 7.2. For an absolutely integrable function f defined on R 2 f(x, y) = 1 2 B { F 1 [ S F(Rf)(S, θ)] } (x, y). (7.2) Proof. We first note the fact that, for the 2 dimensional Fourier transform and its inverse: f(x, y) = F2 1 F 2f(x, y) = 1 4π 2 F 2 f(x, Y )e i(xx+yy ) dxdy. (7.3) We now will use a change of variables from Cartesian (X, Y ) to polar coordinates (S, θ) where X = S cos θ and Y = S sin θ with S R and θ [0, π]. This gives the following Jacobian determinant:
18 THE RADON TRANSFORM AND THE MATHEMATICS OF MEDICAL IMAGING 17 Figure 7. Backprojection of a Square in 5, 25, 100, and 1000 Directions det X S Y S X θ Y θ = S Which tells us that dxdy = S dsdθ. Incorporating this new change of variables equation (7.2) becomes: 1 π 4π 2 F 2 f(s cos θ, S sin θ)e is(x cos θ+y sin θ) S dsdθ. 0 And using the central slice theorem we see that the above equation is in fact equal to 1 π 4π 2 F(Rf(S, θ))e is(x cos θ+y sin θ) S dsdθ. (7.4) 0 Now let us take a closer look at the inner integral of equation (7.4) and note the following:
19 18 JEN BEATTY =2π F(Rf(S, θ)e is(x cos θ+y sin θ) S ds ( 1 2π ) F(Rf(S, θ))e is(x cos θ+y sin θ) S ds =2πF 1 [ S F(Rf)(S, θ)] (x cos θ + y sin θ, θ) That is, the inner integral of equation (7.4) is 2π times the inverse of the Fourier transform of S F(Rf)(S, θ) at the point (x cos θ + y sin θ, θ). We are then able to see that (7.4) in fact equals 1 π F 1 [ S F(Rf)(S, θ)] (x cos θ + y sin θ, θ)dθ. 2π 0 Finally we see that the above integral is 1 2 the backprojection given in definition (7.1) for F 1 [ S F(Rf)(S, θ)]. We therefore simplify the above equation to 1 2 B { F 1[ S F(Rf(S, θ)] } (x, y). Which leads us to our desired conclusion that f(x, y) = 1 2 B { F 1 [ S F(Rf)(S, θ)] } (x, y). The important factor in this formula is the S multiplier that occurs between the Fourier transform and its inverse. Without this factor these two terms would cancel each other out and we would be left with the standard backprojection formula for the Radon transform we encountered earlier which, as we saw, does not directly give us back f(x, y). We call this additional S a filter to the Radon transform, giving us the name for the filtered backprojection formula. 8. Convolution and Low Pass Filters Here we shall examine the role of the filtering factor S in the filtered backprojection formula given in equation (7.2). In order to do that, however, we must first introduce the notion of the convolution of two functions. Definition 8.1. For two integrable functions f, g defined on R we define the convolution of f and g, denoted by f g, as
20 THE RADON TRANSFORM AND THE MATHEMATICS OF MEDICAL IMAGING 19 where x R. (f g)(x) = f(t)g(x t)dt We can easily extend this definition to 2 dimensional space. For polar functions, we only take the integral over the radial variable while for Cartesian functions we integrate over both variables. Explicit definitions are given as follows: Definition 8.2. For integrable polar functions f(t, θ) and g(t, θ) we define the convolution of f and g as (f g)(t, θ) = f(s, θ) g(t s, θ)ds For integrable functions F, G on R 2, we define the convolution of F and G as (F G)(x, y) = F (s, t) G(x s, y t)dsdt. Convolution is a mathematical method of averaging one function, f, with the shifting of another function, g. In the convolution f g, the function g is translated across the function f and the resulting function is dependent on the area of overlap during this translation. In a sense we can view g as a filter we are using to average f over a certain interval. The filtering function acts as a smoother for the noisy data given by the original function. Properties 8.3. For integrable functions f, g, h on R and constants α, β R: (i) f g = g f (ii) f (αg + βh) = α(f g) + β(f h) (iii) Ff Fg = F(f g) (iv) (Bg f)(x, Y ) = B(g Rf)(X, Y ). We now reconsider the filtered backprojection formula from theorem (7.2): f(x, y) = 1 2 B { F 1 [ S F(Rf)(S, θ)] } (x, y). This is, admittedly, a rather ugly equation to deal with. Fully expanded it would include several infinite integrals, which is problematic since we are only dealing with a finite set of data. It would be nice if we could somehow further simplify this to a more useful form. To that end, we shall make a seemingly odd assumption. Suppose that there was some function, call it φ(t), whose Fourier transform equaled our filtering factor S. That is, suppose we had a function φ(t) such that Fφ(S) = S. More simply put, suppose we knew of a function whose Fourier transform equaled the absolute value function. Then we would be able to rewrite the backprojection as
21 20 JEN BEATTY f(x, y) = 1 2 B { F 1 [Fφ F(Rf)(S, θ)] } (x, y). (8.1) However the right half of equation (8.1) contains a product of Fourier transforms, which we know to be equal to the convolution of the functions being transformed as shown in property (iii). We therefore have f(x, y) = 1 2 B { F 1 [F(φ Rf)(S, θ)] } (x, y). But this is merely the inverse Fourier transform of the Fourier transform, which we know returns our starting function. This leads us to the much simpler filtered backprojection formula f(x, y) = 1 B(φ Rf)(x, y). (8.2) 2 Equation (8.2) looks much nicer than our original filtered backprojection formula and doesn t seem that difficult to apply. Physically speaking, Rf is our measured data and (8.2) only requires us to filter it with our new function φ and then apply the backprojection formula which is a relatively straightforward integral. Unfortunately, there is no such function φ whose Fourier transform is exactly equal to the absolute value. Consider the function Fφ: Fφ(ω) = φ(x)e iωx dx We can see that, as ω, Fφ(ω) 0 (note the negative exponential). However, for the absolute value function, ω, as ω, ω. Therefore we, are unable to find a function φ such that for all ω, Fφ(ω) = ω. All our previous work was not in waste, however. Let us consider what type of functions we have restricted our interest to. We are only looking at our function on a finite interval and are in fact assuming it to be zero outside of that interval. If we extend this idea to the Fourier transform, we find that we want to focus our attention on band limited functions. Definition 8.4. A function φ is said to be a band limited function if, for some real number L > 0: Fφ(ω) = φ(x)e iωx dx = 0 for all ω / [ L, L] (8.3) The filtering factor S serves to magnify the F(Rf) term in the original filtered backprojection formula (7.2). In practice F(Rf) is very sensitive to high frequencies. By focusing
22 THE RADON TRANSFORM AND THE MATHEMATICS OF MEDICAL IMAGING 21 our attention on the lower frequencies via a band limited function φ, we are able to avoid this issue. Our goal will be to replace S with what is known as a low pass filter (denoted by S ) which takes into account the affects of lower frequencies but attenuates higher frequencies. This function S needs to have compact support and be of the form S = Fφ (on a compact interval). The cost of using this S (ω) is that we no longer have the equality shown in equation (8.2). Rather, we receive the following: f(x, y) 1 2 B(F 1 S Rf)(x, y). (8.4) Generally speaking, most low pass filters are of the form S (ω) = ω F (ω) L (ω) where L > 0 defines the region we are filtering over. Different functions for F determine the precise characteristics of the filer, and L (ω) is defined as follows: { 1 if ω L L (ω) = 0 if ω > L We shall introduce two common filters used in digital imaging and signal processing, the Ram-Lak filter and Hann filter. The Ram-Lak filter: S (ω) = ω L (ω) = { ω if ω L 0 if ω > L The Ram-Lak filter is the basis for many of the other filters used in signal analysis for it is simply replaces the F (ω) function with the constant 1 function. Other filters, such as the Hann filter, generally consist of multiples of sin or cos to filter out unwanted noise. The Hann filter: S (ω) = ω 1 ( 1 + cos 2πω ) L (ω) 2 L The Hann filter uses the Hann function ( 1 + cos 2πω ) L as its F (ω) and its effectiveness is demonstrated in the sinogram and backprojection of Johann Radon shown in Figure 5. Figure 8. Sinogram and Hann Filter Backprojection for 10, 100, and 1000 Backprojections
23 22 JEN BEATTY 9. Discrete Version Thus far we have been dealing almost exclusively with continuous integrals for the Radon transform, Fourier transform, and backprojection formulas. In practice, however, we only have a finite set of data to work with Therefore we will need to form discrete versions of all the formulas we have used in our filtered backprojection. A discrete function is one that is only defined on a countable set. For our purposes, we shall be looking at discrete functions defined on finite sets (the set being composed of the lines we took our intensity measurements on). Let g n denote the discrete function g at the value n. Because we know this discrete function at a finite set of points, say N, we can say that g = g n : 0 n N 1. If we wish to extend this definition to all integers, we can simply repeat our function over and over again; that is, we can make it periodic with period N. This extension will be useful for some of the discrete formulas we will encounter. Suppose we are taking measurements at P different angles θ and that for each angle have 2 M + 1 beams spaced a distance d apart. Then we can define particular values θ k and t j as { } kπ θ k = P : 0 k P 1, t j = {j d : M j M}. Which allows us to define particular line as l tj,θ k. We therefore define the discrete Radon transform as follows: Definition 9.1. For an absolutely integrable function f and 0 k P and M j M, (P, M > 0), we define the discrete Radon transform of f, denoted R D f, as R D f j,k = Rf(t j, θ k ). (9.1) To implement the filtered backprojection formula (8.4), we shall also need to define the convolution of two discrete functions. Definition 9.2. For two N-periodic discrete functions f and g, we define the discrete convolution of f and g, denoted f g, as (f g) m = N 1 j=0 Clearly, we shall also need the discrete Fourier transform. f j g (m j), for m Z (9.2)
24 THE RADON TRANSFORM AND THE MATHEMATICS OF MEDICAL IMAGING 23 Definition 9.3. Given an N-periodic discrete function f we define the discrete Fourier transform of f, denoted F D f, as (F D f) j = N 1 k=0 f k e i2πkj/n for j = 0, 1,..., (N 1). (9.3) It is worth noting that the N-periodicity of f allows us to replace the bounds in the summation by any set of integers of length (N 1). Given the above definition, it should not come as a surprise that we define the discrete inverse Fourier transform as follows: Definition 9.4. Given an N-periodic discrete function g the discrete inverse Fourier transform of g, denoted F 1 D g, is defined as (F 1 D g) n = 1 N 1 g k e i2πkn/n, for n = 0, 1,..., (N 1). (9.4) N k=0 We note that several of the same properties of the Fourier transform we defined in the continuous setting also apply to the discrete case with slight modifications: Properties 9.5. For N-periodic discrete functions f and g: (i) F D (f g) = (F D f) (F D g) (ii) F D (f g) = 1 N (F Df) (F D g) (iii) F 1 D (F Df n ) = f n for all n Z We are now ready to attack the discretization of the backprojection formula itself. Recall that the backprojection formula was defined as an integral from 0 to π over dθ. In the discrete case we have replaced this continuous dθ with kπ/p for 0 k (P 1). This leads to the following definition for the discrete backprojection: Definition 9.6. Given a discrete function h we define the discrete backprojection of h, denoted B D h, as ( ) N 1 1 B D h(x, y) = h(x cos kπ kπ + y sin, kπ/n). (9.5) N N N k=0 Recall our final form for the filtered backprojection formula in equation (8.4) f(x, y) 1 2 B(F 1 S Rf)(x, y). To form the discrete version of this equation, we see that we need to apply the following formula:
25 24 JEN BEATTY f(x, y) 1 2 B D(F 1 D S R D f)(x, y). And now, we run into a slight problem. R D f is measured data based on the initial and final intensities of a single X-ray beam. We defined the locations of different beams (and therefore different slices) using a coordinate system perpendicular to polar coordinates based on discrete angles θ and distances t. Looking at equation (9.5), however, we see that we will need to sum over h at various points (x, y) in the Cartesian coordinate system to create a rectangular grayscale grid that represents our original object. The polar and Cartesian coordinate systems do not necessarily match up as nicely as we wish them to, and therefore we must interpolate the missing data points. Interpolation is the process of making a continuous (or at a minimum piecewise continuous) function out of a discrete set of values. There are many different ways to interpolate a function (cubic spline, Lagrange, etc.), each with it s own set of gains and drawbacks. For our purposes we shall define a general type of interpolation based on a weighting function W which determines how we shall choose our interpolated points. We will not define a particular weighting function, W, since the details of how the values are interpolated is not as important to us as is the knowledge that we are able to fill in the gaps in our data. Definition 9.7. For a given weighting function W and an N-periodic discrete function g, the W -interpolation of g is defined as I W (g)(x) = ( x ) g(n) W d n, for < x <. (9.6) n Now that we have covered all the various parts of equation (8.2) in a discrete setting and dealt with the interpolation issue, we are able to give a discrete reconstruction algorithm to solve for the attenuation coefficient using a discrete set of data. Here we are interpolating the function (F 1 D S ) (R D f)(jd, kπ/n) (that is, are filling in the gaps after filtering the Radon transform). Let us define this interpolated function as I. This leads to the following reconstruction formula: f(x m, y n ) 1 2 B D ( (F 1 D S ) (R D f) ) (jd, kπ/n) 1 2 B DI(x m, y n ) = 1 N 1 I 2N k=0 ( x m cos kπ N + y n sin kπ N, kπ ). (9.7) N Equation (9.7) accounts for the discrete nature of our real world data and addresses the issues (such as not enough data) that arise from only having a finite number of measurements.
26 THE RADON TRANSFORM AND THE MATHEMATICS OF MEDICAL IMAGING 25 We therefore offer the following completed algorithm for solving the inverse problem of CT scan medical imaging using the Radon transform. (1) Given a set 2 M + 1 X-ray beams each spaced a distance d apart, measure the initial and final intensities, (I 0, I 1 ), of each beam. (2) Repeat this process for P different angles θ. (3) Choose a filter function F 1 D S. (4) Choose a weighting function for interpolation, I W (g)(x) (5) Apply the reconstruction formula described in equation (9.7) 10. Conclusion We have shown the mathematical background for the images created by CT scans and explained the central role of the Radon (and consequently Fourier) transform in this process. While the algorithm described here is not the only method for reconstructing a threedimensional image from projected two-dimensional slices, it did serve as a starting point for research into the field of medical imaging. In particular, there are reconstruction methods based on a specific function which mimics the backprojection formula [4] or there are recent numerical algorithms which are much more efficient in reconstruction [1], although, as in our method derived here, every option has it s own strengths and weaknesses.
27 26 JEN BEATTY 11. Acknowledgements I would like to thank my thesis advisor, Alan Von Herrmann, for his guidance during my thesis research and my second reader, Fernando Gouvêa, for his invaluable help during my research. References [1] Bal, G., Moireau, P. Fast numerical inversion of the attenuated Radon transform with full and partial measurements, Inverse Problems, Institute of Physics Publishing, 20(2004), pp [2] Freeman, T.G., The Mathematics of Medical Imaging, Springer Undergraduate Texts in Mathematics and Technology, [3] Smith, S., The Scientist and Engineer s Guide to Signal Processing, California Technical Publishing, [4] Nievergelt, Y. Elementary Inversion of Radon s Transform, SIAM Review, 28(1986), pp [5] Tianhu, L. Statistics of Medical Imaging, Taylor and Franics Group, 2012.
Hamburger Beiträge zur Angewandten Mathematik
 Hamburger Beiträge zur Angewandten Mathematik Error Estimates for Filtered Back Projection Matthias Beckmann and Armin Iske Nr. 2015-03 January 2015 Error Estimates for Filtered Back Projection Matthias
Hamburger Beiträge zur Angewandten Mathematik Error Estimates for Filtered Back Projection Matthias Beckmann and Armin Iske Nr. 2015-03 January 2015 Error Estimates for Filtered Back Projection Matthias
Lecture 9 February 2, 2016
 MATH 262/CME 372: Applied Fourier Analysis and Winter 26 Elements of Modern Signal Processing Lecture 9 February 2, 26 Prof. Emmanuel Candes Scribe: Carlos A. Sing-Long, Edited by E. Bates Outline Agenda:
MATH 262/CME 372: Applied Fourier Analysis and Winter 26 Elements of Modern Signal Processing Lecture 9 February 2, 26 Prof. Emmanuel Candes Scribe: Carlos A. Sing-Long, Edited by E. Bates Outline Agenda:
The mathematics behind Computertomography
 Radon transforms The mathematics behind Computertomography PD Dr. Swanhild Bernstein, Institute of Applied Analysis, Freiberg University of Mining and Technology, International Summer academic course 2008,
Radon transforms The mathematics behind Computertomography PD Dr. Swanhild Bernstein, Institute of Applied Analysis, Freiberg University of Mining and Technology, International Summer academic course 2008,
Microlocal Methods in X-ray Tomography
 Microlocal Methods in X-ray Tomography Plamen Stefanov Purdue University Lecture I: Euclidean X-ray tomography Mini Course, Fields Institute, 2012 Plamen Stefanov (Purdue University ) Microlocal Methods
Microlocal Methods in X-ray Tomography Plamen Stefanov Purdue University Lecture I: Euclidean X-ray tomography Mini Course, Fields Institute, 2012 Plamen Stefanov (Purdue University ) Microlocal Methods
EE 4372 Tomography. Carlos E. Davila, Dept. of Electrical Engineering Southern Methodist University
 EE 4372 Tomography Carlos E. Davila, Dept. of Electrical Engineering Southern Methodist University EE 4372, SMU Department of Electrical Engineering 86 Tomography: Background 1-D Fourier Transform: F(
EE 4372 Tomography Carlos E. Davila, Dept. of Electrical Engineering Southern Methodist University EE 4372, SMU Department of Electrical Engineering 86 Tomography: Background 1-D Fourier Transform: F(
MATH 353 LECTURE NOTES: WEEK 1 FIRST ORDER ODES
 MATH 353 LECTURE NOTES: WEEK 1 FIRST ORDER ODES J. WONG (FALL 2017) What did we cover this week? Basic definitions: DEs, linear operators, homogeneous (linear) ODEs. Solution techniques for some classes
MATH 353 LECTURE NOTES: WEEK 1 FIRST ORDER ODES J. WONG (FALL 2017) What did we cover this week? Basic definitions: DEs, linear operators, homogeneous (linear) ODEs. Solution techniques for some classes
Maximal Entropy for Reconstruction of Back Projection Images
 Maximal Entropy for Reconstruction of Back Projection Images Tryphon Georgiou Department of Electrical and Computer Engineering University of Minnesota Minneapolis, MN 5545 Peter J Olver Department of
Maximal Entropy for Reconstruction of Back Projection Images Tryphon Georgiou Department of Electrical and Computer Engineering University of Minnesota Minneapolis, MN 5545 Peter J Olver Department of
6 The Fourier transform
 6 The Fourier transform In this presentation we assume that the reader is already familiar with the Fourier transform. This means that we will not make a complete overview of its properties and applications.
6 The Fourier transform In this presentation we assume that the reader is already familiar with the Fourier transform. This means that we will not make a complete overview of its properties and applications.
Kernel-based Image Reconstruction from scattered Radon data by (anisotropic) positive definite functions
 Kernel-based Image Reconstruction from scattered Radon data by (anisotropic) positive definite functions Stefano De Marchi 1 February 5, 2016 1 Joint work with A. Iske (Hamburg, D), A. Sironi (Lousanne,
Kernel-based Image Reconstruction from scattered Radon data by (anisotropic) positive definite functions Stefano De Marchi 1 February 5, 2016 1 Joint work with A. Iske (Hamburg, D), A. Sironi (Lousanne,
1 Radon Transform and X-Ray CT
 Radon Transform and X-Ray CT In this section we look at an important class of imaging problems, the inverse Radon transform. We have seen that X-ray CT (Computerized Tomography) involves the reconstruction
Radon Transform and X-Ray CT In this section we look at an important class of imaging problems, the inverse Radon transform. We have seen that X-ray CT (Computerized Tomography) involves the reconstruction
A Brief Introduction to Medical Imaging. Outline
 A Brief Introduction to Medical Imaging Outline General Goals Linear Imaging Systems An Example, The Pin Hole Camera Radiations and Their Interactions with Matter Coherent vs. Incoherent Imaging Length
A Brief Introduction to Medical Imaging Outline General Goals Linear Imaging Systems An Example, The Pin Hole Camera Radiations and Their Interactions with Matter Coherent vs. Incoherent Imaging Length
LECTURES ON MICROLOCAL CHARACTERIZATIONS IN LIMITED-ANGLE
 LECTURES ON MICROLOCAL CHARACTERIZATIONS IN LIMITED-ANGLE TOMOGRAPHY Jürgen Frikel 4 LECTURES 1 Today: Introduction to the mathematics of computerized tomography 2 Mathematics of computerized tomography
LECTURES ON MICROLOCAL CHARACTERIZATIONS IN LIMITED-ANGLE TOMOGRAPHY Jürgen Frikel 4 LECTURES 1 Today: Introduction to the mathematics of computerized tomography 2 Mathematics of computerized tomography
Taylor series. Chapter Introduction From geometric series to Taylor polynomials
 Chapter 2 Taylor series 2. Introduction The topic of this chapter is find approximations of functions in terms of power series, also called Taylor series. Such series can be described informally as infinite
Chapter 2 Taylor series 2. Introduction The topic of this chapter is find approximations of functions in terms of power series, also called Taylor series. Such series can be described informally as infinite
Math 265H: Calculus III Practice Midterm II: Fall 2014
 Name: Section #: Math 65H: alculus III Practice Midterm II: Fall 14 Instructions: This exam has 7 problems. The number of points awarded for each question is indicated in the problem. Answer each question
Name: Section #: Math 65H: alculus III Practice Midterm II: Fall 14 Instructions: This exam has 7 problems. The number of points awarded for each question is indicated in the problem. Answer each question
Math 345: Applied Mathematics VIII: The Wobble Problem
 Math 345: Applied Mathematics VIII: The Wobble Problem Marcus Pendergrass November 12, 2008 Old audio recordings often suffer from so-called wow and flutter distortion. On a tape player, for instance,
Math 345: Applied Mathematics VIII: The Wobble Problem Marcus Pendergrass November 12, 2008 Old audio recordings often suffer from so-called wow and flutter distortion. On a tape player, for instance,
PHY 475/375. Lecture 5. (April 9, 2012)
 PHY 475/375 Lecture 5 (April 9, 2012) Describing Curvature (contd.) So far, we have studied homogenous and isotropic surfaces in 2-dimensions. The results can be extended easily to three dimensions. As
PHY 475/375 Lecture 5 (April 9, 2012) Describing Curvature (contd.) So far, we have studied homogenous and isotropic surfaces in 2-dimensions. The results can be extended easily to three dimensions. As
Error Estimates and Convergence Rates for Filtered Back Projection Reconstructions
 Universität Hamburg Dissertation Error Estimates and Convergence ates for Filtered Back Projection econstructions Dissertation zur Erlangung des Doktorgrades an der Fakultät für Mathematik, Informatik
Universität Hamburg Dissertation Error Estimates and Convergence ates for Filtered Back Projection econstructions Dissertation zur Erlangung des Doktorgrades an der Fakultät für Mathematik, Informatik
01 Harmonic Oscillations
 Utah State University DigitalCommons@USU Foundations of Wave Phenomena Library Digital Monographs 8-2014 01 Harmonic Oscillations Charles G. Torre Department of Physics, Utah State University, Charles.Torre@usu.edu
Utah State University DigitalCommons@USU Foundations of Wave Phenomena Library Digital Monographs 8-2014 01 Harmonic Oscillations Charles G. Torre Department of Physics, Utah State University, Charles.Torre@usu.edu
Topics. EM spectrum. X-Rays Computed Tomography Direct Inverse and Iterative Inverse Backprojection Projection Theorem Filtered Backprojection
 Bioengineering 28A Principles of Biomedical Imaging Fall Quarter 24 X-Rays/CT Lecture Topics X-Rays Computed Tomography Direct Inverse and Iterative Inverse Backprojection Projection Theorem Filtered Backprojection
Bioengineering 28A Principles of Biomedical Imaging Fall Quarter 24 X-Rays/CT Lecture Topics X-Rays Computed Tomography Direct Inverse and Iterative Inverse Backprojection Projection Theorem Filtered Backprojection
Discrete Fourier Transform
 Last lecture I introduced the idea that any function defined on x 0,..., N 1 could be written a sum of sines and cosines. There are two different reasons why this is useful. The first is a general one,
Last lecture I introduced the idea that any function defined on x 0,..., N 1 could be written a sum of sines and cosines. There are two different reasons why this is useful. The first is a general one,
Topics. EM spectrum. X-Rays Computed Tomography Direct Inverse and Iterative Inverse Backprojection Projection Theorem Filtered Backprojection
 Bioengineering 28A Principles of Biomedical Imaging Fall Quarter 25 X-Rays/CT Lecture Topics X-Rays Computed Tomography Direct Inverse and Iterative Inverse Backprojection Projection Theorem Filtered Backprojection
Bioengineering 28A Principles of Biomedical Imaging Fall Quarter 25 X-Rays/CT Lecture Topics X-Rays Computed Tomography Direct Inverse and Iterative Inverse Backprojection Projection Theorem Filtered Backprojection
What is Image Deblurring?
 What is Image Deblurring? When we use a camera, we want the recorded image to be a faithful representation of the scene that we see but every image is more or less blurry, depending on the circumstances.
What is Image Deblurring? When we use a camera, we want the recorded image to be a faithful representation of the scene that we see but every image is more or less blurry, depending on the circumstances.
Bioengineering 280A Principles of Biomedical Imaging. Fall Quarter 2005 X-Rays/CT Lecture 1. Topics
 Bioengineering 28A Principles of Biomedical Imaging Fall Quarter 25 X-Rays/CT Lecture Topics X-Rays Computed Tomography Direct Inverse and Iterative Inverse Backprojection Projection Theorem Filtered Backprojection
Bioengineering 28A Principles of Biomedical Imaging Fall Quarter 25 X-Rays/CT Lecture Topics X-Rays Computed Tomography Direct Inverse and Iterative Inverse Backprojection Projection Theorem Filtered Backprojection
BioE Exam 1 10/9/2018 Answer Sheet - Correct answer is A for all questions. 1. The sagittal plane
 BioE 1330 - Exam 1 10/9/2018 Answer Sheet - Correct answer is A for all questions 1. The sagittal plane A. is perpendicular to the coronal plane. B. is parallel to the top of the head. C. represents a
BioE 1330 - Exam 1 10/9/2018 Answer Sheet - Correct answer is A for all questions 1. The sagittal plane A. is perpendicular to the coronal plane. B. is parallel to the top of the head. C. represents a
Numerical Methods for geodesic X-ray transforms and applications to open theoretical questions
 Numerical Methods for geodesic X-ray transforms and applications to open theoretical questions François Monard Department of Mathematics, University of Washington. Nov. 13, 2014 UW Numerical Analysis Research
Numerical Methods for geodesic X-ray transforms and applications to open theoretical questions François Monard Department of Mathematics, University of Washington. Nov. 13, 2014 UW Numerical Analysis Research
Midterm 1 Review. Distance = (x 1 x 0 ) 2 + (y 1 y 0 ) 2.
 Midterm 1 Review Comments about the midterm The midterm will consist of five questions and will test on material from the first seven lectures the material given below. No calculus either single variable
Midterm 1 Review Comments about the midterm The midterm will consist of five questions and will test on material from the first seven lectures the material given below. No calculus either single variable
7.5 Partial Fractions and Integration
 650 CHPTER 7. DVNCED INTEGRTION TECHNIQUES 7.5 Partial Fractions and Integration In this section we are interested in techniques for computing integrals of the form P(x) dx, (7.49) Q(x) where P(x) and
650 CHPTER 7. DVNCED INTEGRTION TECHNIQUES 7.5 Partial Fractions and Integration In this section we are interested in techniques for computing integrals of the form P(x) dx, (7.49) Q(x) where P(x) and
Efficient Solution Methods for Inverse Problems with Application to Tomography Radon Transform and Friends
 Efficient Solution Methods for Inverse Problems with Application to Tomography Radon Transform and Friends Alfred K. Louis Institut für Angewandte Mathematik Universität des Saarlandes 66041 Saarbrücken
Efficient Solution Methods for Inverse Problems with Application to Tomography Radon Transform and Friends Alfred K. Louis Institut für Angewandte Mathematik Universität des Saarlandes 66041 Saarbrücken
MATH 114 Calculus Notes on Chapter 2 (Limits) (pages 60-? in Stewart)
 Still under construction. MATH 114 Calculus Notes on Chapter 2 (Limits) (pages 60-? in Stewart) As seen in A Preview of Calculus, the concept of it underlies the various branches of calculus. Hence we
Still under construction. MATH 114 Calculus Notes on Chapter 2 (Limits) (pages 60-? in Stewart) As seen in A Preview of Calculus, the concept of it underlies the various branches of calculus. Hence we
Feature Reconstruction in Tomography
 Feature Reconstruction in Tomography Alfred K. Louis Institut für Angewandte Mathematik Universität des Saarlandes 66041 Saarbrücken http://www.num.uni-sb.de louis@num.uni-sb.de Wien, July 20, 2009 Images
Feature Reconstruction in Tomography Alfred K. Louis Institut für Angewandte Mathematik Universität des Saarlandes 66041 Saarbrücken http://www.num.uni-sb.de louis@num.uni-sb.de Wien, July 20, 2009 Images
Image Reconstruction from Projection
 Image Reconstruction from Projection Reconstruct an image from a series of projections X-ray computed tomography (CT) Computed tomography is a medical imaging method employing tomography where digital
Image Reconstruction from Projection Reconstruct an image from a series of projections X-ray computed tomography (CT) Computed tomography is a medical imaging method employing tomography where digital
Unit 4 Parent Guide: Waves. What is a wave?
 Unit 4 Parent Guide: Waves What is a wave? A wave is a disturbance or vibration that carries energy from one location to another. Some waves require a medium to transmit the energy whereas others can travel
Unit 4 Parent Guide: Waves What is a wave? A wave is a disturbance or vibration that carries energy from one location to another. Some waves require a medium to transmit the energy whereas others can travel
f (t) K(t, u) d t. f (t) K 1 (t, u) d u. Integral Transform Inverse Fourier Transform
 Integral Transforms Massoud Malek An integral transform maps an equation from its original domain into another domain, where it might be manipulated and solved much more easily than in the original domain.
Integral Transforms Massoud Malek An integral transform maps an equation from its original domain into another domain, where it might be manipulated and solved much more easily than in the original domain.
ter. on Can we get a still better result? Yes, by making the rectangles still smaller. As we make the rectangles smaller and smaller, the
 Area and Tangent Problem Calculus is motivated by two main problems. The first is the area problem. It is a well known result that the area of a rectangle with length l and width w is given by A = wl.
Area and Tangent Problem Calculus is motivated by two main problems. The first is the area problem. It is a well known result that the area of a rectangle with length l and width w is given by A = wl.
3.4 Introduction to power series
 3.4 Introduction to power series Definition 3.4.. A polynomial in the variable x is an expression of the form n a i x i = a 0 + a x + a 2 x 2 + + a n x n + a n x n i=0 or a n x n + a n x n + + a 2 x 2
3.4 Introduction to power series Definition 3.4.. A polynomial in the variable x is an expression of the form n a i x i = a 0 + a x + a 2 x 2 + + a n x n + a n x n i=0 or a n x n + a n x n + + a 2 x 2
AP Calculus Chapter 9: Infinite Series
 AP Calculus Chapter 9: Infinite Series 9. Sequences a, a 2, a 3, a 4, a 5,... Sequence: A function whose domain is the set of positive integers n = 2 3 4 a n = a a 2 a 3 a 4 terms of the sequence Begin
AP Calculus Chapter 9: Infinite Series 9. Sequences a, a 2, a 3, a 4, a 5,... Sequence: A function whose domain is the set of positive integers n = 2 3 4 a n = a a 2 a 3 a 4 terms of the sequence Begin
MB-JASS D Reconstruction. Hannes Hofmann March 2006
 MB-JASS 2006 2-D Reconstruction Hannes Hofmann 19 29 March 2006 Outline Projections Radon Transform Fourier-Slice-Theorem Filtered Backprojection Ramp Filter 19 29 Mar 2006 Hannes Hofmann 2 Parallel Projections
MB-JASS 2006 2-D Reconstruction Hannes Hofmann 19 29 March 2006 Outline Projections Radon Transform Fourier-Slice-Theorem Filtered Backprojection Ramp Filter 19 29 Mar 2006 Hannes Hofmann 2 Parallel Projections
Metric spaces and metrizability
 1 Motivation Metric spaces and metrizability By this point in the course, this section should not need much in the way of motivation. From the very beginning, we have talked about R n usual and how relatively
1 Motivation Metric spaces and metrizability By this point in the course, this section should not need much in the way of motivation. From the very beginning, we have talked about R n usual and how relatively
Uncertainty Principle Applied to Focused Fields and the Angular Spectrum Representation
 Uncertainty Principle Applied to Focused Fields and the Angular Spectrum Representation Manuel Guizar, Chris Todd Abstract There are several forms by which the transverse spot size and angular spread of
Uncertainty Principle Applied to Focused Fields and the Angular Spectrum Representation Manuel Guizar, Chris Todd Abstract There are several forms by which the transverse spot size and angular spread of
Designing Information Devices and Systems I Fall 2018 Lecture Notes Note Introduction to Linear Algebra the EECS Way
 EECS 16A Designing Information Devices and Systems I Fall 018 Lecture Notes Note 1 1.1 Introduction to Linear Algebra the EECS Way In this note, we will teach the basics of linear algebra and relate it
EECS 16A Designing Information Devices and Systems I Fall 018 Lecture Notes Note 1 1.1 Introduction to Linear Algebra the EECS Way In this note, we will teach the basics of linear algebra and relate it
ROI Reconstruction in CT
 Reconstruction in CT From Tomo reconstruction in the 21st centery, IEEE Sig. Proc. Magazine (R.Clackdoyle M.Defrise) L. Desbat TIMC-IMAG September 10, 2013 L. Desbat Reconstruction in CT Outline 1 CT Radiology
Reconstruction in CT From Tomo reconstruction in the 21st centery, IEEE Sig. Proc. Magazine (R.Clackdoyle M.Defrise) L. Desbat TIMC-IMAG September 10, 2013 L. Desbat Reconstruction in CT Outline 1 CT Radiology
n=0 ( 1)n /(n + 1) converges, but not
 Math 07H Topics for the third exam (and beyond) (Technically, everything covered on the first two exams plus...) Absolute convergence and alternating series A series a n converges absolutely if a n converges.
Math 07H Topics for the third exam (and beyond) (Technically, everything covered on the first two exams plus...) Absolute convergence and alternating series A series a n converges absolutely if a n converges.
Exercises to Applied Functional Analysis
 Exercises to Applied Functional Analysis Exercises to Lecture 1 Here are some exercises about metric spaces. Some of the solutions can be found in my own additional lecture notes on Blackboard, as the
Exercises to Applied Functional Analysis Exercises to Lecture 1 Here are some exercises about metric spaces. Some of the solutions can be found in my own additional lecture notes on Blackboard, as the
Tomography and Reconstruction
 Tomography and Reconstruction Lecture Overview Applications Background/history of tomography Radon Transform Fourier Slice Theorem Filtered Back Projection Algebraic techniques Measurement of Projection
Tomography and Reconstruction Lecture Overview Applications Background/history of tomography Radon Transform Fourier Slice Theorem Filtered Back Projection Algebraic techniques Measurement of Projection
Connectedness. Proposition 2.2. The following are equivalent for a topological space (X, T ).
 Connectedness 1 Motivation Connectedness is the sort of topological property that students love. Its definition is intuitive and easy to understand, and it is a powerful tool in proofs of well-known results.
Connectedness 1 Motivation Connectedness is the sort of topological property that students love. Its definition is intuitive and easy to understand, and it is a powerful tool in proofs of well-known results.
Medical Imaging. Transmission Measurement
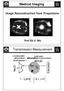 Medical Imaging Image Recontruction from Projection Prof Ed X. Wu Tranmiion Meaurement ( meaurable unknown attenuation, aborption cro-ection hadowgram ) I(ϕ,ξ) µ(x,) I = I o exp A(x, )dl L X-ra ource X-Ra
Medical Imaging Image Recontruction from Projection Prof Ed X. Wu Tranmiion Meaurement ( meaurable unknown attenuation, aborption cro-ection hadowgram ) I(ϕ,ξ) µ(x,) I = I o exp A(x, )dl L X-ra ource X-Ra
UMASS AMHERST MATH 300 SP 05, F. HAJIR HOMEWORK 8: (EQUIVALENCE) RELATIONS AND PARTITIONS
 UMASS AMHERST MATH 300 SP 05, F. HAJIR HOMEWORK 8: (EQUIVALENCE) RELATIONS AND PARTITIONS 1. Relations Recall the concept of a function f from a source set X to a target set Y. It is a rule for mapping
UMASS AMHERST MATH 300 SP 05, F. HAJIR HOMEWORK 8: (EQUIVALENCE) RELATIONS AND PARTITIONS 1. Relations Recall the concept of a function f from a source set X to a target set Y. It is a rule for mapping
The Integers. Peter J. Kahn
 Math 3040: Spring 2009 The Integers Peter J. Kahn Contents 1. The Basic Construction 1 2. Adding integers 6 3. Ordering integers 16 4. Multiplying integers 18 Before we begin the mathematics of this section,
Math 3040: Spring 2009 The Integers Peter J. Kahn Contents 1. The Basic Construction 1 2. Adding integers 6 3. Ordering integers 16 4. Multiplying integers 18 Before we begin the mathematics of this section,
Slope Fields: Graphing Solutions Without the Solutions
 8 Slope Fields: Graphing Solutions Without the Solutions Up to now, our efforts have been directed mainly towards finding formulas or equations describing solutions to given differential equations. Then,
8 Slope Fields: Graphing Solutions Without the Solutions Up to now, our efforts have been directed mainly towards finding formulas or equations describing solutions to given differential equations. Then,
Math 234 Exam 3 Review Sheet
 Math 234 Exam 3 Review Sheet Jim Brunner LIST OF TOPIS TO KNOW Vector Fields lairaut s Theorem & onservative Vector Fields url Divergence Area & Volume Integrals Using oordinate Transforms hanging the
Math 234 Exam 3 Review Sheet Jim Brunner LIST OF TOPIS TO KNOW Vector Fields lairaut s Theorem & onservative Vector Fields url Divergence Area & Volume Integrals Using oordinate Transforms hanging the
2. Signal Space Concepts
 2. Signal Space Concepts R.G. Gallager The signal-space viewpoint is one of the foundations of modern digital communications. Credit for popularizing this viewpoint is often given to the classic text of
2. Signal Space Concepts R.G. Gallager The signal-space viewpoint is one of the foundations of modern digital communications. Credit for popularizing this viewpoint is often given to the classic text of
Solutions to Tutorial for Week 4
 The University of Sydney School of Mathematics and Statistics Solutions to Tutorial for Week 4 MATH191/1931: Calculus of One Variable (Advanced) Semester 1, 018 Web Page: sydneyeduau/science/maths/u/ug/jm/math191/
The University of Sydney School of Mathematics and Statistics Solutions to Tutorial for Week 4 MATH191/1931: Calculus of One Variable (Advanced) Semester 1, 018 Web Page: sydneyeduau/science/maths/u/ug/jm/math191/
CS711008Z Algorithm Design and Analysis
 CS711008Z Algorithm Design and Analysis Lecture 5 FFT and Divide and Conquer Dongbo Bu Institute of Computing Technology Chinese Academy of Sciences, Beijing, China 1 / 56 Outline DFT: evaluate a polynomial
CS711008Z Algorithm Design and Analysis Lecture 5 FFT and Divide and Conquer Dongbo Bu Institute of Computing Technology Chinese Academy of Sciences, Beijing, China 1 / 56 Outline DFT: evaluate a polynomial
Introduction to the Mathematics of Medical Imaging
 Introduction to the Mathematics of Medical Imaging Second Edition Charles L. Epstein University of Pennsylvania Philadelphia, Pennsylvania EiaJTL Society for Industrial and Applied Mathematics Philadelphia
Introduction to the Mathematics of Medical Imaging Second Edition Charles L. Epstein University of Pennsylvania Philadelphia, Pennsylvania EiaJTL Society for Industrial and Applied Mathematics Philadelphia
Algebraic Topology Homework 4 Solutions
 Algebraic Topology Homework 4 Solutions Here are a few solutions to some of the trickier problems... Recall: Let X be a topological space, A X a subspace of X. Suppose f, g : X X are maps restricting to
Algebraic Topology Homework 4 Solutions Here are a few solutions to some of the trickier problems... Recall: Let X be a topological space, A X a subspace of X. Suppose f, g : X X are maps restricting to
Chirp Transform for FFT
 Chirp Transform for FFT Since the FFT is an implementation of the DFT, it provides a frequency resolution of 2π/N, where N is the length of the input sequence. If this resolution is not sufficient in a
Chirp Transform for FFT Since the FFT is an implementation of the DFT, it provides a frequency resolution of 2π/N, where N is the length of the input sequence. If this resolution is not sufficient in a
FXA UNIT G485 Module X-Rays. Candidates should be able to : I = I 0 e -μx
 1 Candidates should be able to : HISTORY Describe the nature of X-rays. Describe in simple terms how X-rays are produced. X-rays were discovered by Wilhelm Röntgen in 1865, when he found that a fluorescent
1 Candidates should be able to : HISTORY Describe the nature of X-rays. Describe in simple terms how X-rays are produced. X-rays were discovered by Wilhelm Röntgen in 1865, when he found that a fluorescent
The Integers. Math 3040: Spring Contents 1. The Basic Construction 1 2. Adding integers 4 3. Ordering integers Multiplying integers 12
 Math 3040: Spring 2011 The Integers Contents 1. The Basic Construction 1 2. Adding integers 4 3. Ordering integers 11 4. Multiplying integers 12 Before we begin the mathematics of this section, it is worth
Math 3040: Spring 2011 The Integers Contents 1. The Basic Construction 1 2. Adding integers 4 3. Ordering integers 11 4. Multiplying integers 12 Before we begin the mathematics of this section, it is worth
Eigenvectors and Hermitian Operators
 7 71 Eigenvalues and Eigenvectors Basic Definitions Let L be a linear operator on some given vector space V A scalar λ and a nonzero vector v are referred to, respectively, as an eigenvalue and corresponding
7 71 Eigenvalues and Eigenvectors Basic Definitions Let L be a linear operator on some given vector space V A scalar λ and a nonzero vector v are referred to, respectively, as an eigenvalue and corresponding
3 rd class Mech. Eng. Dept. hamdiahmed.weebly.com Fourier Series
 Definition 1 Fourier Series A function f is said to be piecewise continuous on [a, b] if there exists finitely many points a = x 1 < x 2
Definition 1 Fourier Series A function f is said to be piecewise continuous on [a, b] if there exists finitely many points a = x 1 < x 2
MTH Linear Algebra. Study Guide. Dr. Tony Yee Department of Mathematics and Information Technology The Hong Kong Institute of Education
 MTH 3 Linear Algebra Study Guide Dr. Tony Yee Department of Mathematics and Information Technology The Hong Kong Institute of Education June 3, ii Contents Table of Contents iii Matrix Algebra. Real Life
MTH 3 Linear Algebra Study Guide Dr. Tony Yee Department of Mathematics and Information Technology The Hong Kong Institute of Education June 3, ii Contents Table of Contents iii Matrix Algebra. Real Life
CS168: The Modern Algorithmic Toolbox Lecture #11: The Fourier Transform and Convolution
 CS168: The Modern Algorithmic Toolbox Lecture #11: The Fourier Transform and Convolution Tim Roughgarden & Gregory Valiant May 8, 2015 1 Intro Thus far, we have seen a number of different approaches to
CS168: The Modern Algorithmic Toolbox Lecture #11: The Fourier Transform and Convolution Tim Roughgarden & Gregory Valiant May 8, 2015 1 Intro Thus far, we have seen a number of different approaches to
Introduction and some preliminaries
 1 Partial differential equations Introduction and some preliminaries A partial differential equation (PDE) is a relationship among partial derivatives of a function (or functions) of more than one variable.
1 Partial differential equations Introduction and some preliminaries A partial differential equation (PDE) is a relationship among partial derivatives of a function (or functions) of more than one variable.
Superiorized Inversion of the Radon Transform
 Superiorized Inversion of the Radon Transform Gabor T. Herman Graduate Center, City University of New York March 28, 2017 The Radon Transform in 2D For a function f of two real variables, a real number
Superiorized Inversion of the Radon Transform Gabor T. Herman Graduate Center, City University of New York March 28, 2017 The Radon Transform in 2D For a function f of two real variables, a real number
POL502: Foundations. Kosuke Imai Department of Politics, Princeton University. October 10, 2005
 POL502: Foundations Kosuke Imai Department of Politics, Princeton University October 10, 2005 Our first task is to develop the foundations that are necessary for the materials covered in this course. 1
POL502: Foundations Kosuke Imai Department of Politics, Princeton University October 10, 2005 Our first task is to develop the foundations that are necessary for the materials covered in this course. 1
Ideas from Vector Calculus Kurt Bryan
 Ideas from Vector Calculus Kurt Bryan Most of the facts I state below are for functions of two or three variables, but with noted exceptions all are true for functions of n variables..1 Tangent Line Approximation
Ideas from Vector Calculus Kurt Bryan Most of the facts I state below are for functions of two or three variables, but with noted exceptions all are true for functions of n variables..1 Tangent Line Approximation
1.5 Approximate Identities
 38 1 The Fourier Transform on L 1 (R) which are dense subspaces of L p (R). On these domains, P : D P L p (R) and M : D M L p (R). Show, however, that P and M are unbounded even when restricted to these
38 1 The Fourier Transform on L 1 (R) which are dense subspaces of L p (R). On these domains, P : D P L p (R) and M : D M L p (R). Show, however, that P and M are unbounded even when restricted to these
Lecture 13 - Wednesday April 29th
 Lecture 13 - Wednesday April 29th jacques@ucsdedu Key words: Systems of equations, Implicit differentiation Know how to do implicit differentiation, how to use implicit and inverse function theorems 131
Lecture 13 - Wednesday April 29th jacques@ucsdedu Key words: Systems of equations, Implicit differentiation Know how to do implicit differentiation, how to use implicit and inverse function theorems 131
1.1 Simple functions and equations Polynomials and polynomial equations
 1 Preliminary algebra This opening chapter reviews the basic algebra of which a working knowledge is presumed in the rest of the book. Many students will be familiar with much, if not all, of it, but recent
1 Preliminary algebra This opening chapter reviews the basic algebra of which a working knowledge is presumed in the rest of the book. Many students will be familiar with much, if not all, of it, but recent
Fourier Series Example
 Fourier Series Example Let us compute the Fourier series for the function on the interval [ π,π]. f(x) = x f is an odd function, so the a n are zero, and thus the Fourier series will be of the form f(x)
Fourier Series Example Let us compute the Fourier series for the function on the interval [ π,π]. f(x) = x f is an odd function, so the a n are zero, and thus the Fourier series will be of the form f(x)
22.56J Noninvasive Imaging in Biology and Medicine Instructor: Prof. Alan Jasanoff Fall 2005, TTh 1-2:30
 22.56J Noninvasive Imaging in Biology and Medicine Instructor: Prof. Alan Jasanoff Fall 2005, TTh 1-2:30 Sample problems HW1 1. Look up (e.g. in the CRC Manual of Chemistry and Physics www.hbcpnetbase.com)
22.56J Noninvasive Imaging in Biology and Medicine Instructor: Prof. Alan Jasanoff Fall 2005, TTh 1-2:30 Sample problems HW1 1. Look up (e.g. in the CRC Manual of Chemistry and Physics www.hbcpnetbase.com)
Math Final Exam Review
 Math - Final Exam Review. Find dx x + 6x +. Name: Solution: We complete the square to see if this function has a nice form. Note we have: x + 6x + (x + + dx x + 6x + dx (x + + Note that this looks a lot
Math - Final Exam Review. Find dx x + 6x +. Name: Solution: We complete the square to see if this function has a nice form. Note we have: x + 6x + (x + + dx x + 6x + dx (x + + Note that this looks a lot
EXAMINATION: MATHEMATICAL TECHNIQUES FOR IMAGE ANALYSIS
 EXAMINATION: MATHEMATICAL TECHNIQUES FOR IMAGE ANALYSIS Course code: 8D Date: Thursday April 8 th, Time: 4h 7h Place: AUD 3 Read this first! Write your name and student identification number on each paper
EXAMINATION: MATHEMATICAL TECHNIQUES FOR IMAGE ANALYSIS Course code: 8D Date: Thursday April 8 th, Time: 4h 7h Place: AUD 3 Read this first! Write your name and student identification number on each paper
MATH 1130 Exam 1 Review Sheet
 MATH 1130 Exam 1 Review Sheet The Cartesian Coordinate Plane The Cartesian Coordinate Plane is a visual representation of the collection of all ordered pairs (x, y) where x and y are real numbers. This
MATH 1130 Exam 1 Review Sheet The Cartesian Coordinate Plane The Cartesian Coordinate Plane is a visual representation of the collection of all ordered pairs (x, y) where x and y are real numbers. This
MAT100 OVERVIEW OF CONTENTS AND SAMPLE PROBLEMS
 MAT100 OVERVIEW OF CONTENTS AND SAMPLE PROBLEMS MAT100 is a fast-paced and thorough tour of precalculus mathematics, where the choice of topics is primarily motivated by the conceptual and technical knowledge
MAT100 OVERVIEW OF CONTENTS AND SAMPLE PROBLEMS MAT100 is a fast-paced and thorough tour of precalculus mathematics, where the choice of topics is primarily motivated by the conceptual and technical knowledge
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER / Functions
 ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER 1 2017/2018 DR. ANTHONY BROWN 4. Functions 4.1. What is a Function: Domain, Codomain and Rule. In the course so far, we
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER 1 2017/2018 DR. ANTHONY BROWN 4. Functions 4.1. What is a Function: Domain, Codomain and Rule. In the course so far, we
Differential Topology Solution Set #2
 Differential Topology Solution Set #2 Select Solutions 1. Show that X compact implies that any smooth map f : X Y is proper. Recall that a space is called compact if, for every cover {U } by open sets
Differential Topology Solution Set #2 Select Solutions 1. Show that X compact implies that any smooth map f : X Y is proper. Recall that a space is called compact if, for every cover {U } by open sets
APPENDIX A. Background Mathematics. A.1 Linear Algebra. Vector algebra. Let x denote the n-dimensional column vector with components x 1 x 2.
 APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
A Method for Reducing Ill-Conditioning of Polynomial Root Finding Using a Change of Basis
 Portland State University PDXScholar University Honors Theses University Honors College 2014 A Method for Reducing Ill-Conditioning of Polynomial Root Finding Using a Change of Basis Edison Tsai Portland
Portland State University PDXScholar University Honors Theses University Honors College 2014 A Method for Reducing Ill-Conditioning of Polynomial Root Finding Using a Change of Basis Edison Tsai Portland
Filters in Analysis and Topology
 Filters in Analysis and Topology David MacIver July 1, 2004 Abstract The study of filters is a very natural way to talk about convergence in an arbitrary topological space, and carries over nicely into
Filters in Analysis and Topology David MacIver July 1, 2004 Abstract The study of filters is a very natural way to talk about convergence in an arbitrary topological space, and carries over nicely into
Technical University of Denmark
 Technical University of Denmark Page 1 of 11 pages Written test, 9 December 2010 Course name: Introduction to medical imaging Course no. 31540 Aids allowed: none. "Weighting": All problems weight equally.
Technical University of Denmark Page 1 of 11 pages Written test, 9 December 2010 Course name: Introduction to medical imaging Course no. 31540 Aids allowed: none. "Weighting": All problems weight equally.
Continuum Limit and Fourier Series
 Chapter 6 Continuum Limit and Fourier Series Continuous is in the eye of the beholder Most systems that we think of as continuous are actually made up of discrete pieces In this chapter, we show that a
Chapter 6 Continuum Limit and Fourier Series Continuous is in the eye of the beholder Most systems that we think of as continuous are actually made up of discrete pieces In this chapter, we show that a
1 Differentiable manifolds and smooth maps
 1 Differentiable manifolds and smooth maps Last updated: April 14, 2011. 1.1 Examples and definitions Roughly, manifolds are sets where one can introduce coordinates. An n-dimensional manifold is a set
1 Differentiable manifolds and smooth maps Last updated: April 14, 2011. 1.1 Examples and definitions Roughly, manifolds are sets where one can introduce coordinates. An n-dimensional manifold is a set
Designing Information Devices and Systems I Spring 2019 Lecture Notes Note 2
 EECS 6A Designing Information Devices and Systems I Spring 9 Lecture Notes Note Vectors and Matrices In the previous note, we introduced vectors and matrices as a way of writing systems of linear equations
EECS 6A Designing Information Devices and Systems I Spring 9 Lecture Notes Note Vectors and Matrices In the previous note, we introduced vectors and matrices as a way of writing systems of linear equations
Designing Information Devices and Systems I Spring 2018 Lecture Notes Note Introduction to Linear Algebra the EECS Way
 EECS 16A Designing Information Devices and Systems I Spring 018 Lecture Notes Note 1 1.1 Introduction to Linear Algebra the EECS Way In this note, we will teach the basics of linear algebra and relate
EECS 16A Designing Information Devices and Systems I Spring 018 Lecture Notes Note 1 1.1 Introduction to Linear Algebra the EECS Way In this note, we will teach the basics of linear algebra and relate
Implicit Functions, Curves and Surfaces
 Chapter 11 Implicit Functions, Curves and Surfaces 11.1 Implicit Function Theorem Motivation. In many problems, objects or quantities of interest can only be described indirectly or implicitly. It is then
Chapter 11 Implicit Functions, Curves and Surfaces 11.1 Implicit Function Theorem Motivation. In many problems, objects or quantities of interest can only be described indirectly or implicitly. It is then
We denote the space of distributions on Ω by D ( Ω) 2.
 Sep. 1 0, 008 Distributions Distributions are generalized functions. Some familiarity with the theory of distributions helps understanding of various function spaces which play important roles in the study
Sep. 1 0, 008 Distributions Distributions are generalized functions. Some familiarity with the theory of distributions helps understanding of various function spaces which play important roles in the study
Designing Information Devices and Systems I Fall 2017 Official Lecture Notes Note 2
 EECS 6A Designing Information Devices and Systems I Fall 07 Official Lecture Notes Note Introduction Previously, we introduced vectors and matrices as a way of writing systems of linear equations more
EECS 6A Designing Information Devices and Systems I Fall 07 Official Lecture Notes Note Introduction Previously, we introduced vectors and matrices as a way of writing systems of linear equations more
Lecture 34. Fourier Transforms
 Lecture 34 Fourier Transforms In this section, we introduce the Fourier transform, a method of analyzing the frequency content of functions that are no longer τ-periodic, but which are defined over the
Lecture 34 Fourier Transforms In this section, we introduce the Fourier transform, a method of analyzing the frequency content of functions that are no longer τ-periodic, but which are defined over the
Chapter 3. Introducing Groups
 Chapter 3 Introducing Groups We need a super-mathematics in which the operations are as unknown as the quantities they operate on, and a super-mathematician who does not know what he is doing when he performs
Chapter 3 Introducing Groups We need a super-mathematics in which the operations are as unknown as the quantities they operate on, and a super-mathematician who does not know what he is doing when he performs
Theorem 5.3. Let E/F, E = F (u), be a simple field extension. Then u is algebraic if and only if E/F is finite. In this case, [E : F ] = deg f u.
![Theorem 5.3. Let E/F, E = F (u), be a simple field extension. Then u is algebraic if and only if E/F is finite. In this case, [E : F ] = deg f u. Theorem 5.3. Let E/F, E = F (u), be a simple field extension. Then u is algebraic if and only if E/F is finite. In this case, [E : F ] = deg f u.](/thumbs/81/83685479.jpg) 5. Fields 5.1. Field extensions. Let F E be a subfield of the field E. We also describe this situation by saying that E is an extension field of F, and we write E/F to express this fact. If E/F is a field
5. Fields 5.1. Field extensions. Let F E be a subfield of the field E. We also describe this situation by saying that E is an extension field of F, and we write E/F to express this fact. If E/F is a field
MATHEMATICS COURSE SYLLABUS
 Course Title: Algebra 1 Honors Department: Mathematics MATHEMATICS COURSE SYLLABUS Primary Course Materials: Big Ideas Math Algebra I Book Authors: Ron Larson & Laurie Boswell Algebra I Student Workbooks
Course Title: Algebra 1 Honors Department: Mathematics MATHEMATICS COURSE SYLLABUS Primary Course Materials: Big Ideas Math Algebra I Book Authors: Ron Larson & Laurie Boswell Algebra I Student Workbooks
Continuum Probability and Sets of Measure Zero
 Chapter 3 Continuum Probability and Sets of Measure Zero In this chapter, we provide a motivation for using measure theory as a foundation for probability. It uses the example of random coin tossing to
Chapter 3 Continuum Probability and Sets of Measure Zero In this chapter, we provide a motivation for using measure theory as a foundation for probability. It uses the example of random coin tossing to
Volume in n Dimensions
 Volume in n Dimensions MA 305 Kurt Bryan Introduction You ve seen that if we have two vectors v and w in two dimensions then the area spanned by these vectors can be computed as v w = v 1 w 2 v 2 w 1 (where
Volume in n Dimensions MA 305 Kurt Bryan Introduction You ve seen that if we have two vectors v and w in two dimensions then the area spanned by these vectors can be computed as v w = v 1 w 2 v 2 w 1 (where
Electro Magnetic Field Dr. Harishankar Ramachandran Department of Electrical Engineering Indian Institute of Technology Madras
 Electro Magnetic Field Dr. Harishankar Ramachandran Department of Electrical Engineering Indian Institute of Technology Madras Lecture - 7 Gauss s Law Good morning. Today, I want to discuss two or three
Electro Magnetic Field Dr. Harishankar Ramachandran Department of Electrical Engineering Indian Institute of Technology Madras Lecture - 7 Gauss s Law Good morning. Today, I want to discuss two or three
ELLIPTIC CURVES BJORN POONEN
 ELLIPTIC CURVES BJORN POONEN 1. Introduction The theme of this lecture is to show how geometry can be used to understand the rational number solutions to a polynomial equation. We will illustrate this
ELLIPTIC CURVES BJORN POONEN 1. Introduction The theme of this lecture is to show how geometry can be used to understand the rational number solutions to a polynomial equation. We will illustrate this
2. FUNCTIONS AND ALGEBRA
 2. FUNCTIONS AND ALGEBRA You might think of this chapter as an icebreaker. Functions are the primary participants in the game of calculus, so before we play the game we ought to get to know a few functions.
2. FUNCTIONS AND ALGEBRA You might think of this chapter as an icebreaker. Functions are the primary participants in the game of calculus, so before we play the game we ought to get to know a few functions.
Math (P)Review Part II:
 Math (P)Review Part II: Vector Calculus Computer Graphics Assignment 0.5 (Out today!) Same story as last homework; second part on vector calculus. Slightly fewer questions Last Time: Linear Algebra Touched
Math (P)Review Part II: Vector Calculus Computer Graphics Assignment 0.5 (Out today!) Same story as last homework; second part on vector calculus. Slightly fewer questions Last Time: Linear Algebra Touched
(1) Consider the space S consisting of all continuous real-valued functions on the closed interval [0, 1]. For f, g S, define
![(1) Consider the space S consisting of all continuous real-valued functions on the closed interval [0, 1]. For f, g S, define (1) Consider the space S consisting of all continuous real-valued functions on the closed interval [0, 1]. For f, g S, define](/thumbs/88/116259117.jpg) Homework, Real Analysis I, Fall, 2010. (1) Consider the space S consisting of all continuous real-valued functions on the closed interval [0, 1]. For f, g S, define ρ(f, g) = 1 0 f(x) g(x) dx. Show that
Homework, Real Analysis I, Fall, 2010. (1) Consider the space S consisting of all continuous real-valued functions on the closed interval [0, 1]. For f, g S, define ρ(f, g) = 1 0 f(x) g(x) dx. Show that
For those of you who are taking Calculus AB concurrently with AP Physics, I have developed a
 AP Physics C: Mechanics Greetings, For those of you who are taking Calculus AB concurrently with AP Physics, I have developed a brief introduction to Calculus that gives you an operational knowledge of
AP Physics C: Mechanics Greetings, For those of you who are taking Calculus AB concurrently with AP Physics, I have developed a brief introduction to Calculus that gives you an operational knowledge of
