I. Introduction. A New Method for Inverting Integrals Attenuated Radon Transform (SPECT) D to N map for Moving Boundary Value Problems

Transcription

1 I. Introduction A New Method for Inverting Integrals Attenuated Radon Transform (SPECT) D to N map for Moving Boundary Value Problems F(k) = T 0 e k2 t+ikl(t) f (t)dt, k C. Integrable Nonlinear PDEs in and DS and KP type generalizations.

2 Novemb er 2005, Volume 52, Number 10 Feature Article Generalized Fourier Transforms, Their Nonlinearization and the Imaging of the Brain A. S. Fokas and L.- Y. Sung

3 II.Inversion of Integrals-Imaging Ablowitz-F, Beals and Coifman (1982) µ x 1 + iσ 3 µ x 2 k[σ 3, µ] = Qµ, k C, (x 1, x 2 ) R 2, σ 3 = ( ), Q = Nonlinear FT in 2D via the formalism F-Gelfand (1992) Novel derivation of 2D FT via ( 0 q(x 1, x 2 ) q(x 1, x 2 ) 0 ( x1 + i x2 k)µ(x 1, x 2, k) = q(x 1, x 2 ) )

4 F-Novikov (1992) [ ( 1 k + 1 ) x1 + 1 ( k 1 ) ] x2 µ(x 1, x 2, k) = f (x 1, x 2 ) 2 k 2i k Novel derivation of Radon transform Novikov (2003), F (2004) [ ( 1 k k ) x i Derivation of attenuated Radon transform ( k 1 ) ] x2 µ(x 1, x 2, k) k +f (x 1, x 2 )µ(x 1, x 2, k) = g(x 1, x 2 )

5 II.1 RADON TRANSFORM Reconstruct f from its line integrals. (x, x ) 1 2 τ ρ θ x 1 =τ cosθ ρ sinθ x 2 =τ sin θ+ρ cosθ τ =x 1 cosθ+x 2 sin θ ρ= x 1 sinθ+x 2 cosθ

6 Direct Radon transform F(τ, ρ, θ) = f (τ cosθ ρ sin θ, τ sin θ + ρ cosθ). ˆf (ρ, θ) = F(τ, ρ, θ)dτ. Inverse Radon transform(filter Back Projection) f (x 1,x 2 )= 1 4π ( x 1 i x2 ) H(θ, ρ) = 1 ˆf (ρ, θ) iπ ρ ρ dρ, 2π 0 e iθ H(θ, x 1 sinθ + x 2 cosθ)dθ.

7 The reconstruction of the phantoms before the filtering procedure.

8

9 II.2 MATHEMATICS OF SPECT Reconstruct g from its weighted line integrals I = e R L(x) fds gdτ. Direct Attenuated Radon transform ĝ f (ρ, θ) = Inverse Attenuated Radon transform L P ± g(ρ) = ± g(ρ) 2 e R τ F(s,ρ,θ)ds G(τ, ρ, θ)dτ + 1 2iπ g(ρ ) ρ ρ dρ

10 H(θ, τ, ρ)=e R τ F(s,ρ,θ)ds{ e P ˆf (ρ,θ) P e P ˆf (ρ,θ) + +e P+ˆf (ρ,θ) P + e P+ˆf (ρ,θ) }ĝ f (ρ, θ), g(x 1, x 2 ) = 1 4π ( x 1 i x2 ) 2π 0 e iθ H(θ, x 1 cosθ + x 2 sin θ, x 2 cosθ x 1 sin θ)dθ.

11 Spectral analysis of a SINGLE equation Analytic inversion of integrals j 1 k + 1 «x1 + 1 k 1 ff «x2 µ(x 1,x 2, k)=f (x 1,x 2) 2 k 2i k k C, (x 1,x 2) R 2, f (x) S(R 2 ) (i) Solve for µ in terms of f for ALL k C z 1 ( k 1 ) x 1 1 ( k + 1 ) x 2 2i k 2 k ( ) 1 1 µ 2i k 2 k 2 z = f (x 1, x 2 ), (x 1, x 2 ) R 2 Impose: µ = O ( 1 z ), z.

12 µ(x 1,x 2,k)= 1 sgn 1 R k 2 2πi k 2 f (x R 2 1,x 2 )dx 1 dx 2 z z, k =1 (ii) Solve for µ in terms of ˆf ( µ ± = P ˆf ) F(ρ, s, θ)ds, τ (ρ, τ) R 2, θ (0, 2π) complex k-plane : µ(x 1,x 2,k)= 1 R 2π e iθ 2iπ 2 0 e iθ k H ˆf (ρ,θ)dρ ρ (x 2 cos θ x 1 dθ sin θ)

13 NCAT phantom gaussian blur, σ = (GP collimator), noise free, R=28cm, 200 projections Original FBP, no attenuation correction IART, no deblurring IART, with deblurring

14 III. Inverting Integrals: The D to N Map q t = q xx, 0 < x <, 0 < t < T. q(x, 0) = 0, q x (0, t) = g 1 (t). q(0, t) = 1 t g 1 (s) ds, 0 < t < T. π t s 0 q t + q xxx = 0, 0 < x <, 0 < t < T. q(x, 0) = 0, q xx (0, t) = g 2 (t). t g 2 (s) q(0, t) = c 1 ds, (t s) t g 2 (s) q x (0, t) = c 2 ds (t s) 2 3 0

15 The Global Relation and Lax pairs [ [ ] e ikx+k2t q(x, t) ]t e ikx+k2t (q x (x, t) + ikq(x, t)) = 0, x k C D e ikx+k2t [q(x, t)dx + (q x (x, t) + ikq(x, t))dt] = 0, k C.

16 0 < x < x T t T 0 e k2s [q x (0, s) + ikq(0, s)]ds = e ikx q(x, 0)dx e k2 T 0 0 e ikx q(x, T)dx, Imk 0

17 e k2t : T e k2 s 0 [ q x (0, s) + ikq(0, s)]ds = e k2 T 0 e ikx q(x, T)dx, Imk 0 µ x + ikµ = q µ t + k 2 µ = q x + ikq

18 l(t) < x < T 0 l(t) > 0, 0 < t < T, l(0) = 0 [ ] e k2 s ikl(s) q x (l(s), s) + ( l(s) + ik)g 0 (s) ds = ˆq 0 (k) e k2 T l(t) e ikx q(x, T)dx.

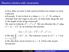
19 (F, Pelloni, JMP 2007) (Delillo, F, Inverse Problems 2007) F(k) = T 0 e k2 s ikl(s) f (s)ds, k C. ( ) µ t (t, k) + k 2 ik l(t) µ(k, t) = kf (t), k C, 0 < t < T.

20 3 4 f (t) = 1 t ke k2t+ikl(t) F(k)dk + f (s)k(s, t)ds, 0 < t < T, 2πi Γ(t) 0 { Γ(t) : } k = k R + ik I, kr 2 k2 I + k I l(t) = 0; < kr <, k I < 0; 0 < t < T, Figure: The curve Γ(t)

21 K(s, t) = 1 2π 0 1 i ν 2 ν 2 l(s)ν ν 2 l(s)ν + B(ν, s, t) dν, ν ( ) ν 2 l(s)ν [ + iν exp ν( l(s) ϑ(t, s))(s t) B(ν, s, t) = ] +i ν 2 l(s)ν (2ν ϑ(t, s))(s t), ϑ(t, s) = l(t) l(s). t s

22 µ(t, k) = µ j (t, k), k Ω j (t), 0 < t < T, j = 1, 2, 3 Figure: The domains Ω 1(t) and Ω 2(t).

23 } } Ω 1 (t) : {k I > 0, kr 2 k2 I + k I l(0) > 0 {k I < 0, kr 2 k2 I + k I l(t) > 0, Ω 2 (t) : { } { } k I > 0, kr 2 k2 I + k I l(t) < 0 k I < 0, kr 2 k2 I + k I l(t) < 0. } Γ + 12 {k (t) : R 2 ki 2 + k I l(t) = 0, ki > 0.

24 t µ j (t, k) = k e k 2 (s t) ik(l(s) l(t)) f (s)ds, 0 < t < T, k Ω j, j = 1, 2, 3. t j t 1 = 0, t 2 = T, t 3 = S(k R, k I ), k 2 R k 2 I + k I l(t) = 0, 0 < t < T, ki > 0, < k R < : t = S(k R, k I ). µ j = O ( ) 1, k, k Ω j, j = 1, 2, 3. k

25 µ(t, k, k) = 1 jump 2πi Γ(t) λ k dλ 1 π Ω(t) 0 < t < T, k C µ(t, λ, λ) dλ R dλ I λ λ k

26 Above inversion and global relation imply: 3 4 g 1(t) = 1 2 π 1 t t + g 1 (s)k(s, t)ds, 0 0 e (l(t) x)2 4t t q 0 (x)dx 0 0 < t < T e (l(t) l(s))2 4(t s) t s ġ 0 (s)ds

27 IV. Nonlinear PDEs in 4+2 and 3+1 (F, PRL, May 2006) µ x + σ µ 3 ȳ k[σ 3, µ] + Qµ = 0, ( ) x = 1 2 (ξ + η), y = 1 2 (ξ η), k = k 1 + ik 2, ξ = ξ 1 + iξ 2, η = η 1 + iη 2 σ 3 = ( ), Q = ( ) 0 q 1 (ξ 1, ξ 2, η 1, η 2 ) q 2 (ξ 1, ξ 2, η 1, η 2 ) 0

28 Nonlinear FT in 4D {q 1, q 2 } {f 1, f 2 } f 1 (k 1, k 2, λ 1, λ 2 ) = c e 4i(k2ξ1 k1ξ2+λ2η1 λ1η2) q 1 µ 22 dξ 1 dξ 2 dη 1 dη 2, R 4 f 2 (k 1, k 2, λ 1, λ 2 ) = c e 4i( λ2ξ1+λ1ξ2 k2η1+k1η2) q 2 µ 11 dξ 1 dξ 2 dη 1 dη 2, R 4 c = (2/π) 3. µ(ξ 1, ξ 2, η 1, η 2, k 1, k 2 ) is determined in terms of {q j (ξ 1, ξ 2, η 1, η 2 )} 2 1 by ( ) with µ I as ξ ξ η η 2 2

29 {f 1, f 2 } {q 1, q 2 } q 1 (ξ 1, ξ 2, η 1, η 2 ) = e 4i(k2ξ1 k1ξ2+λ2η1 λ1η2) f 1 µ 11 dk 1 dk 2 dλ 1 dλ 2 R 4 q 2 (ξ 1, ξ 2, η 1, η 2 ) = e 4i( λ2ξ1+λ1ξ2 k2η1+k1η2) f 2 µ 22 dk 1 dk 2 dλ 1 dλ 2, R 4

30 µ is determined in terms of {f j (k 1, k 2, λ 1, λ 2 )} 2 1 by µ(k 1, k 2 ) = µ(λ 1, λ 2 ) k R 2 0 e 4i(k2ξ1 k1ξ2+λ2η1 λ1η2) f 1 e 4i( λ2ξ1+λ1ξ2 k2η1+k1η2) f 2 0 dλ 1 dλ 2, µ I + O( 1 k ), k

31 Integrable PDEs in 4+2 { } 2 { } 2 q (0) j (ξ 1, ξ 2, η 1, η 2 ) f (0) j (k 1, k 2, λ 1, λ 2 ) 1 1 { f (0) 1 E, f (0) 2 E 1} {q j (ξ 1, ξ 2, η 1, η 2, t 1, t 2 )} 2 1 Then, E = e 4i(λ1λ2+k1k2)t2 2i(λ2 1 λ2 2 +k2 1 k2 2 )t1 ( 1) j tq j ( 2 ξ + 2 η )q j q j 1 (q ξ 1 q 2 ) η = 0, j = 1, 2, 1 q = 1 q(ξ 1, ξ 2 ) ξ π R ξ ξ dξ 1 dξ 2. 2

32 Implicit Reductions to 3+1 independence of t 1 λ 1 λ 2 + k 1 k 2 = 0 Linear limit: 2 q + 2 q = 0. ξ 1 ξ 2 η 1 η 2 KP type q t = 1 3 q 4 x q q x q 4 1 x ȳ 2 independence of t 2 k1 3 λ λ 1λ 2 2 3k 1k2 2 = 0

33 Explicit Reductions to 3+1 Potential KdV q t = 1 4 q x x x 3 4 q2 x, t = t 1 + it 2, x = x 1 + ix 2, (1) To preserve reality: q t = 1 4 q xxx 3 4 q2 x. (2) (q t) t = (q t ) t : ( q x x x 3q x 2 ) t = ( q xxx 3qx 2 ) t.

34 Use x = 1 2 ( x 1 + i x2 ) : (1)± (2): ( q)( q x2 ) = 0, = 2 x x 2. q t1 = 1 ( 3 16 x1 3 x1 x 2 ) 3 ( 2 q q 2 8 x1 qx 2 ) 2, (3) q t2 = 1 ( 3 16 x2 + 3 x2 x 2 ) 3 1 q 4 q x 1 q x2. (4)

35 q t1 = 1 4 qx 1x 1 x `q2 x1 q 2 x 2, q = 0, (5) q t2 = 1 4 qx 2x 2 x qx 1q x2, q = 0. (6) Claim : q t1 = q t2 = 0 Let q(x 1, x 2, 0) = q 0 (x 1, x 2 ) be a harmonic function. Then q(x 1, x 2, t 1 ) and q(x 1, x 2, t 2 ) satisfy the integrable systems (5) and (6) respectively. If q 0 is real, then q remains real.

36 Potential KP where q t = 1 4 q x x x 3 4 q2 x Lq, y = y 1 + iy 2, L = 1 x 2 y, x 1 f = 1 f (x 1 π, x 2 )dx 1 dx 2 R x x. 2 ( q)( q x2 ) + q x Lq x q x Lqx ( Lq x Lq 2 x ) = 0. q = q xy = 0, q = 0, q y2 = 1 x 1 q x2y 1

37 q t1 = 1 4 qx 1x 1 x `q2 x1 q 2 x x 1 q y1 y 1, q = 0, q t2 = 1 4 qx 2x 2 x qx 1q x x 2 q y1 y 1, q = 0. = 2 x x 2

38 Example: < x 1 <, x 2 > 0. q(x 1, 0, y 1, 0) = Q 0 (x 1, y 1 ). q x2 (x 1, 0, y 1, t) = Hq x1 (x 1, 0, y 1, t) q(x 1, 0, y 1, t) = Q(x 1, y 1, t) Q t1 = 1 4 Q x 1x 1x 1 3 [ Q 2 8 x1 (HQ x1 ) 2] x 1 Q y1y 1, Q(x 1, y 1, 0) = Q 0 (x 1, y 1 ). Laplace s equation with q(x 1, 0, y 1, t) = Q(x 1, y 1, t), yields q(x 1, x 2, y, t)