Two Posts to Fill On School Board
|
|
|
- Reynard White
- 3 years ago
- Views:
Transcription
1 Y Y qz 86 x : ( ) z Y x 4 z z x x Y 5 x q x 8 Y 8 x x : 6 ; : 5 x ; 4 ( z ; ( ) ) x ; z 94 ; x ; ; ; ; 3 x : 5 89 q ; ; x ; x ; ; x : ; ; ; ; ; ; 87 47% : () : / : 83 ; ;»4 & 8 ; 44 6 : 3 85 : : q x Z Y } : : q : : ; ; ; q ; ) x ; x» ( 3? > 876 x] > 4 q x? 8 > x 43»» q (4) 6 9 x 4 7 : x x ; z 35 q 99 5 ( ; z 85 4 ; 7358 ; 4 ; ; q x 4 z 3 ; ;(x z» x x x : 6: 5 : x 887 x 5: q 3 x 75 ] 6 9 [ Q q 8»? ) x 6 6 ( ) 8578 x ( ) 4 x 4 x 8 8 x x 4 6:3 4 x > x ) x q x q : q x Q q Y X x ; q x ; x 56 x ; 5 ; 87 z q 7 Y q q z x 8 ~ 7? x : Z» 6 x Q 4 6 [ Q 3586 x Q #
2 Y / : \ / ( ) 4 96 Y»» 93 97; < <» Y Y 65? 6 q 8 : Y: q x z 3 ( 8» ) 4 47 ; < Z 5: 8 8 x # 49 z x z Y : / x x Y Y # z z q // q 5 q 8 Y z 963 Y x Y ; ( ) x z 8 Z Y 4 z q x z q : z 8 z ( ; 8 Y < q 8 ;?? 4:8 ( x 8 : 7 8 ><<? ; & Y ( ) 9 : z Y z q x Y Y z x z Z ; z z? # q z? z x» ; z 8 x x q? Z ; z x z q / x»\ q z 5 x ( ) x q x z z» ; ; z z q 6 z ( x 886 x 6 69 x 7 q x ; / 6 / 6 / Y q [ ] Y 6 Y 5 x q Q 58 X 75 :3 7: 64 Q & 7 6 Q q 5 66 ; x x x ] q : ; q ; x; 3 ; z » Q 5:3 6: 6 Y [ q 43 Y z q % ? Y / z q 5 8 q z x Z 7 3 Q 9 9 x 5 3 x q Z / Y x z 4 Y 6 5 9: : % Y 6 6 x x z X Y x () () Y z q Y x 4 z & X Q Y»4 Y Y Y x 389 % 94 X z Q ( ; : x ; 6 Y» 3> ; 94» ( 8 Y < 94 Y : 8 : Q Y q q Y 8 94 Y : 8: 6: 3: 5 94 Y
3 X Y Y ; ( x ( ( ) z 4 Y 94» ( 4787 x Q : 8 : (3) & q (9) ; :? # (4) q x (8) : ; () : 7 94 x x : ; 4 q 3 84 z q > < >» >4 } >: >? ) 8 < # = z x 94 :3 ; q # q : ( ) q () q ( ) q 8 4 ) < / (8 3) (45) q x ( ) q (3) q ( z ( ) q () (5%) 4 (3) ( 9 ) (5) x qx x 3 94 x x : : q x 4 Q ;» ; < : : ; ;» x» > x : z ) Q x () 8 9 : \ : 8» 4 ( : q ( ) ( ( ) ) 8 : x 5 Y ; Y : q : Q () z Q ( ) 5 ( 7) (4) ( 7 ) 94 () : : 8 3 Y 6 7 # 5 Y Y Y x Q > Y Y Y Y Y 94 ; 3 x : x Z :5? Y 55 6 xx Y Y 3 q Y 6 98 ( \ q x x Y? x 3 ( 9? 6 xx Y z 5 8 Y 4 94 x x x x Z ; z 5 x z x > x : % z X Y z 6 x ( ) z x Y q z ( x ) : 4 x 4 < ( ; ( ) 8 ; > 8 5 Y x z :?? 7 5 :? z? z 8? x x 3 x q & z 4 x : z x 47? Y 4 9 9: :3 x z z ? : ; / Y Y Y z 3 ) Y 6:45 5 7:3 7:45 x 7 4 )
4 5 \ Y X> Y 6 ( ) Y ( ) 94 ) 8? 9 q Y» z z Y z 8[) z z: Y / z ; z x : Y x Y? z x 8 x : [ ; ; ; : z ; } Z» Q 8 x 8 9 q» x < # / x : 8 x / <? 8 >? > z / 8 :> /< < 8 88 x q :» ~ Y 8 <>< ( 4) < ] Y? x x x Y 8 q > x \ > Y x X ~8 : (5 9) 8 ~? 4% \» 7 4% 69 3/4 44? z Z / % ; 8 7 Y zz Y x 5 5 ( ) # q 7 56 ( ) : ( x x & 3 5 :? ( ) 7 x q x 85 8 ; 3 x : Q 8 % 9 8 Q» 9 ] z? 3? 5 [ 4? x 5 7 x x [»» ( 7) ( q 3 YY x 4 6 z 7» 5 Z 8 x Y 4 > ( 8) [ x x 3 3 x < z ( (94) z x x 94 [ Y Qz Q ( 6) <> 5 Y Y % Y 65 Y 69 Z & : 3: ;3 : X) x 4 :45 Z : : 678 7:5 Y 8: Z 8: : : Y 6:45 X Y 7:45 : 7:45 : Y 8: x : : x z : : Y : () : X ( )» 6 Z 87 3% x q# 9 9 x ( ) :3 x 8:4? 3 x ( 4:3) : z z Y x 8 : z 35 3 : z 94 (9 Q ) ( 57 6 ( 9:): ) ; x z q z 5 : z : 95): 6 z :5 :5 Y 845 Y x :3 x :3 : : : z Y : (»? 4 : 7:3 5 8: Y Y 53 8 q Y q { z ~ 5 5 7:45 ( : 5 x : 8 & z Y x x 3 x x : q 4 ): Y 48 q x x 8:3 : x : :5 4 Y x :3 : x z : ; 47 q :3 :8 7:8 : ] 3 8:3 5 < 35 5 x» 6 () Y 5 : 8 & : x ( 8 8 x ; Y 6 Y Y zz /? [ Y? Y 5 8 q q ( q z) 48 7
5 7 Y q & 9 > & & q & 7 \\ 8z & & 4 q x 3 7 x 3 x & 7 Q \ & 9 5 4z XY x Y 6 5 q» () ( ) ( )» > Y Q Q x Y Y Y Y 6? x) z z 4: ( )?? Y Z x x \ z ] z ( 7 6? : 85 ; 5 ; x 788 x 9648 Y Z & x 98: »>» & : 56 x x 7: :8 7% 6 z \ > : : Y Y Y ( Y z Y 4 Y z : Y 5% 8 q Q q Z : ; ; x 5 Y ; x 4 ; 5 : Y 8 / % 386 : ; x q z Q 6 z x z ; 3 q [ 7 7 : 76 q : : z z Y Y ; 4479 : ; Y z 34
A DARK GREY P O N T, with a Switch Tail, and a small Star on the Forehead. Any
Y Y Y X X «/ YY Y Y ««Y x ) & \ & & } # Y \#$& / Y Y X» \\ / X X X x & Y Y X «q «z \x» = q Y # % \ & [ & Z \ & { + % ) / / «q zy» / & / / / & x x X / % % ) Y x X Y $ Z % Y Y x x } / % «] «] # z» & Y X»
' Liberty and Umou Ono and Inseparablo "
3 5? #< q 8 2 / / ) 9 ) 2 ) > < _ / ] > ) 2 ) ) 5 > x > [ < > < ) > _ ] ]? <
County Council Named for Kent
\ Y Y 8 9 69 6» > 69 ««] 6 : 8 «V z 9 8 x 9 8 8 8?? 9 V q» :: q;; 8 x () «; 8 x ( z x 9 7 ; x >«\ 8 8 ; 7 z x [ q z «z : > ; ; ; ( 76 x ; x z «7 8 z ; 89 9 z > q _ x 9 : ; 6? ; ( 9 [ ) 89 _ ;»» «; x V
OWELL WEEKLY JOURNAL
Y \»< - } Y Y Y & #»»» q ] q»»»>) & - - - } ) x ( - { Y» & ( x - (» & )< - Y X - & Q Q» 3 - x Q Y 6 \Y > Y Y X 3 3-9 33 x - - / - -»- --
A. H. Hall, 33, 35 &37, Lendoi
7 X x > - z Z - ----»»x - % x x» [> Q - ) < % - - 7»- -Q 9 Q # 5 - z -> Q x > z»- ~» - x " < z Q q»» > X»? Q ~ - - % % < - < - - 7 - x -X - -- 6 97 9
LOWELL WEEKLY JOURNAL
Y -» $ 5 Y 7 Y Y -Y- Q x Q» 75»»/ q } # ]»\ - - $ { Q» / X x»»- 3 q $ 9 ) Y q - 5 5 3 3 3 7 Q q - - Q _»»/Q Y - 9 - - - )- [ X 7» -» - )»? / /? Q Y»» # X Q» - -?» Q ) Q \ Q - - - 3? 7» -? #»»» 7 - / Q
LOWELL WEEKLY JOURNAL
G $ G 2 G ««2 ««q ) q «\ { q «««/ 6 «««««q «] «q 6 ««Z q «««Q \ Q «q «X ««G X G ««? G Q / Q Q X ««/«X X «««Q X\ «q «X \ / X G XX «««X «x «X «x X G X 29 2 ««Q G G «) 22 G XXX GG G G G G G X «x G Q «) «G
Educjatipnal. L a d ie s * COBNWALILI.S H IG H SCHOOL. I F O R G IR L S A n B k i n d e r g a r t e n.
- - - 0 x ] - ) ) -? - Q - - z 0 x 8 - #? ) 80 0 0 Q ) - 8-8 - ) x ) - ) -] ) Q x?- x - - / - - x - - - x / /- Q ] 8 Q x / / - 0-0 0 x 8 ] ) / - - /- - / /? x ) x x Q ) 8 x q q q )- 8-0 0? - Q - - x?-
LOWELL WEEKLY JOURNAL
Y G y G Y 87 y Y 8 Y - $ X ; ; y y q 8 y $8 $ $ $ G 8 q < 8 6 4 y 8 7 4 8 8 < < y 6 $ q - - y G y G - Y y y 8 y y y Y Y 7-7- G - y y y ) y - y y y y - - y - y 87 7-7- G G < G y G y y 6 X y G y y y 87 G
P A L A C E P IE R, S T. L E O N A R D S. R a n n o w, q u a r r y. W WALTER CR O TC H, Esq., Local Chairman. E. CO O PER EVANS, Esq.,.
? ( # [ ( 8? [ > 3 Q [ ««> » 9 Q { «33 Q> 8 \ \ 3 3 3> Q»«9 Q ««« 3 8 3 8 X \ [ 3 ( ( Z ( Z 3( 9 9 > < < > >? 8 98 ««3 ( 98 < # # Q 3 98? 98 > > 3 8 9 9 ««««> 3 «>
a s*:?:; -A: le London Dyers ^CleanefSt * S^d. per Y ard. -P W ..n 1 0, , c t o b e e d n e sd *B A J IllW6fAi>,EB. E D U ^ T IG r?
? 9 > 25? < ( x x 52 ) < x ( ) ( { 2 2 8 { 28 ] ( 297 «2 ) «2 2 97 () > Q ««5 > «? 2797 x 7 82 2797 Q z Q (
LOWELL WEEKLY JOURNAL. ^Jberxy and (Jmott Oao M d Ccmsparftble. %m >ai ruv GEEAT INDUSTRIES
? (») /»» 9 F ( ) / ) /»F»»»»»# F??»»» Q ( ( »»» < 3»» /» > > } > Q ( Q > Z F 5
W i n t e r r e m e m b e r t h e W O O L L E N S. W rite to the M anageress RIDGE LAUNDRY, ST. H E LE N S. A uction Sale.
> 7? 8 «> ««0? [ -! ««! > - ««>« ------------ - 7 7 7 = - Q9 8 7 ) [ } Q ««
7 ( - ( - < Q & > & ) r/lt.i Ml s." ifcr ' W ATI II. The fnncrnl.icniccs of Mr*. John We mil uppn our tcpiiblicnn rcprc Died.
$ / / - (\ \ - ) # -/ ( - ( [ & - - - - \ - - ( - - - - & - ( ( / - ( \) Q & - - { Q ( - & - ( & q \ ( - ) Q - - # & - - - & - - - $ - 6 - & # - - - & -- - - - & 9 & q - / \ / - - - -)- - ( - - 9 - - -
9 Q - - LOWHLL #WEEKLY JOURNAL.
# F 7 F --) 2 9 Q - Q - - F - x $ 2 F? F \ F q - x q - - - - )< - -? - F - - Q z 2 Q - x -- - - - 3 - % 3 3 - - ) F x - \ - - - - - q - q - - - - -z- < F 7-7- - Q F 2 F - F \x -? - - - - - z - x z F -
oenofc : COXT&IBCTOEU. AU skaacst sftwer thsa4 aafcekr will be ehat«s«ai Bi. C. W. JUBSSOS. PERFECT THBOUGH SDFFEBISG. our
x V - --- < x x 35 V? 3?/ -V 3 - ) - - [ Z8 - & Z - - - - - x 0-35 - 3 75 3 33 09 33 5 \ - - 300 0 ( -? 9 { - - - -- - < - V 3 < < - - Z 7 - z 3 - [ } & _ 3 < 3 ( 5 7< ( % --- /? - / 4-4 - & - % 4 V 2
..«W- tn^zmxmmrrx/- NEW STORE. Popular Goods at Popular D. E. SPRING, Mas just opened a large fdo.k of DRY GOODS & GROCERIES,
B y «X }() z zxx/ X y y y y )3 y «y
«4 [< « PanHomc'r I'rui;* :".>r '.a'' W"»' I'fltolt. 'j'l :. r... Jnfii<on. Kslaiaaac. <.T i.. %.. 1 >
5 28 (x / &» )»(»»» Q ( 3 Q» (» ( (3 5» ( q 2 5 q 2 5 5 8) 5 2 2 ) ~ ( / x {» /»»»»» (»»» ( 3 ) / & Q ) X ] Q & X X X x» 8 ( &» 2 & % X ) 8 x & X ( #»»q 3 ( ) & X 3 / Q X»»» %» ( z 22 (»» 2» }» / & 2 X
MANY BILLS OF CONCERN TO PUBLIC
- 6 8 9-6 8 9 6 9 XXX 4 > -? - 8 9 x 4 z ) - -! x - x - - X - - - - - x 00 - - - - - x z - - - x x - x - - - - - ) x - - - - - - 0 > - 000-90 - - 4 0 x 00 - -? z 8 & x - - 8? > 9 - - - - 64 49 9 x - -
A L T O SOLO LOWCLL. MICHIGAN, THURSDAY. DECEMBER 10,1931. ritt. Mich., to T h e Heights. Bos" l u T H I S COMMl'NiTY IN Wilcox
G 093 < 87 G 9 G 4 4 / - G G 3 -!! - # -G G G : 49 q» - 43 8 40 - q - z 4 >» «9 0-9 - - q 00! - - q q!! ) 5 / : \ 0 5 - Z : 9 [ -?! : ) 5 - - > - 8 70 / q - - - X!! - [ 48 - -!
Y G q G Y Y 29 8 $ 29 G 6 q ) L bor y nnd Union One nnd Inseparable. LOW I'LL, MICHIGAN. WLDNHSDA Y. JULY ), I8T. liuwkll NATIdiNAI, liank
G k y $5 y / >/ k «««# ) /% < # «/» Y»««««?# «< >«>» y k»» «k F 5 8 Y Y F G k F >«y y
Q SON,' (ESTABLISHED 1879L
( < 5(? Q 5 9 7 00 9 0 < 6 z 97 ( # ) $ x 6 < ( ) ( ( 6( ( ) ( $ z 0 z z 0 ) { ( % 69% ( ) x 7 97 z ) 7 ) ( ) 6 0 0 97 )( 0 x 7 97 5 6 ( ) 0 6 ) 5 ) 0 ) 9%5 z» 0 97 «6 6» 96? 0 96 5 0 ( ) ( ) 0 x 6 0
LOWELL WEEKLY JOURNAL.
Y $ Y Y 7 27 Y 2» x 7»» 2» q» ~ [ } q q $ $ 6 2 2 2 2 2 2 7 q > Y» Y >» / Y» ) Y» < Y»» _»» < Y > Y Y < )»» >» > ) >» >> >Y x x )»» > Y Y >>»» }> ) Y < >» /» Y x» > / x /»»»»» >» >» >»» > > >» < Y /~ >
Governor Green Triumphs Over Mudslinging
; XXX 6 928 - x 22 5 Q 0 x 2- Q- & & x 30 - x 93000000 95000000 50 000 x 0:30 7 7 2 x q 9 0 0:30 2;00 7:30 9 ( 9 & ( ( - ( - 225000 x ( ( 800 ) - 70000 200000 - x ; 200-0: 3333 0850; 778: 5-38 090; 002;
ACCEPTS HUGE FLORAL KEY TO LOWELL. Mrs, Walter Laid to Rest Yesterday
$ j < < < > XXX Y 928 23 Y Y 4% Y 6 -- Q 5 9 2 5 Z 48 25 )»-- [ Y Y Y & 4 j q - Y & Y 7 - -- - j \ -2 -- j j -2 - - - - [ - - / - ) ) - - / j Y 72 - ) 85 88 - / X - j ) \ 7 9 Y Y 2 3» - ««> Y 2 5 35 Y
LOWELL WEEKLY JOURNAL
: Y J G V $ 5 V V G Y 2 25 Y 2» 5 X # VG q q q 6 6 X J 6 $3 ( 6 2 6 2 6 25 3 2 6 Y q 2 25: JJ JJ < X Q V J J Y J Q V (» Y V X Y? G # V Y J J J G J»Y ) J J / J Y Y X ({ G #? J Y ~» 9? ) < ( J VY Y J G (
Neatest and Promptest Manner. E d i t u r ami rul)lihher. FOIt THE CIIILDIIES'. Trifles.
» ~ $ ) 7 x X ) / ( 8 2 X 39 ««x» ««! «! / x? \» «({? «» q «(? (?? x! «? 8? ( z x x q? ) «q q q ) x z x 69 7( X X ( 3»«! ( ~«x ««x ) (» «8 4 X «4 «4 «8 X «x «(» X) ()»» «X «97 X X X 4 ( 86) x) ( ) z z
LOWELL. MICHIGAN, OCTOBER morning for Owen J. Howard, M last Friday in Blodpett hospital.
G GG Y G 9 Y- Y 77 8 Q / x -! -} 77 - - # - - - - 0 G? x? x - - V - x - -? : : - q -8 : : - 8 - q x V - - - )?- X - - 87 X - ::! x - - -- - - x -- - - - )0 0 0 7 - - 0 q - V -
V o l u m e 5, N u m b e r 5 2, 1 6 P a g e s. Gold B e U ClUt Stamps Double Stamp D a y E v e r y Wednesday
1 6 5 J 9 6 " " z k ; k x k k k z z k j " " ( k " " k 8 1959 " " x k j 5 25 ; ; k k qz ; x 13 x k * k ( ) k k : qz 13 k k k j ; q k x ; x 615 26 ( : k z 113 99751 z k k q ; 15 k k k j q " " k j x x ( *»
LOWELL WEEKLY JOURNAL
KY Y 872 K & q $ < 9 2 q 4 8 «7 K K K «> 2 26 8 5 4 4 7»» 2 & K q 4 [«5 «$6 q X «K «8K K88 K 7 ««$25 K Q ««q 8 K K Y & 7K /> Y 8«#»«Y 87 8 Y 4 KY «7««X & Y» K ) K K 5 KK K > K» Y Y 8 «KK > /» >» 8 K X
II&Ij <Md Tmlaiiiiiit, aad once in Ihe y a w Teataa m i, the vmb thatalmta oot Uiaapirit world. into as abode or wotld by them- CooTBOtioa
382 4 7 q X
LOWELL WEEKLY JOURNAL.
Y 5 ; ) : Y 3 7 22 2 F $ 7 2 F Q 3 q q 6 2 3 6 2 5 25 2 2 3 $2 25: 75 5 $6 Y q 7 Y Y # \ x Y : { Y Y Y : ( \ _ Y ( ( Y F [ F F ; x Y : ( : G ( ; ( ~ x F G Y ; \ Q ) ( F \ Q / F F \ Y () ( \ G Y ( ) \F
THE I Establiifrad June, 1893
89 : 8 Y Y 2 96 6 - - : - 2 q - 26 6 - - q 2 2 2 4 6 4«4 ' V () 8 () 6 64-4 '2" () 6 ( ) * 'V ( 4 ) 94-4 q ( / ) K ( x- 6% j 9*V 2'%" 222 27 q - - K 79-29 - K x 2 2 j - -% K 4% 2% 6% ' K - 2 47 x - - j
d A L. T O S O U LOWELL, MICHIGAN. THURSDAY, DECEMBER 5, 1929 Cadillac, Nov. 20. Indignation
) - 5 929 XXX - $ 83 25 5 25 $ ( 2 2 z 52 $9285)9 7 - - 2 72 - - 2 3 zz - 9 86 - - - - 88 - q 2 882 q 88 - - - - - - ( 89 < - Q - 857-888 - - - & - - q - { q 7 - - - - q - - - - - - q - - - - 929 93 q
LOWELL WEEKI.Y JOURINAL
/ $ 8) 2 {!»!» X ( (!!!?! () ~ x 8» x /»!! $?» 8! ) ( ) 8 X x /! / x 9 ( 2 2! z»!!»! ) / x»! ( (»»!» [ ~!! 8 X / Q X x» ( (!»! Q ) X x X!! (? ( ()» 9 X»/ Q ( (X )!» / )! X» x / 6!»! }? ( q ( ) / X! 8 x»
( ) y 2! 4. ( )( y! 2)
1. Dividing: 4x3! 8x 2 + 6x 2x 5.7 Division of Polynomials = 4x3 2x! 8x2 2x + 6x 2x = 2x2! 4 3. Dividing: 1x4 + 15x 3! 2x 2!5x 2 = 1x4!5x 2 + 15x3!5x 2! 2x2!5x 2 =!2x2! 3x + 4 5. Dividing: 8y5 + 1y 3!
A b r i l l i a n t young chemist, T h u r e Wagelius of N e w Y o r k, ac. himself with eth
6 6 0 x J 8 0 J 0 z (0 8 z x x J x 6 000 X j x "" "" " " x " " " x " " " J " " " " " " " " x : 0 z j ; J K 0 J K q 8 K K J x 0 j " " > J x J j z ; j J q J 0 0 8 K J 60 : K 6 x 8 K J :? 0 J J K 0 6% 8 0
Chapter 2: Heat Conduction Equation
-1 General Relation for Fourier s Law of Heat Conduction - Heat Conduction Equation -3 Boundary Conditions and Initial Conditions -1 General Relation for Fourier s Law of Heat Conduction (1) The rate of
' '-'in.-i 1 'iritt in \ rrivfi pr' 1 p. ru
V X X Y Y 7 VY Y Y F # < F V 6 7»< V q q $ $» q & V 7» Q F Y Q 6 Q Y F & Q &» & V V» Y V Y [ & Y V» & VV & F > V } & F Q \ Q \» Y / 7 F F V 7 7 x» > QX < #» > X >» < F & V F» > > # < q V 6 & Y Y q < &
A Memorial. Death Crash Branch Out. Symbol The. at Crossing Flaming Poppy. in Belding
- G Y Y 8 9 XXX G - Y - Q 5 8 G Y G Y - - * Y G G G G 9 - G - - : - G - - ) G G- Y G G q G G : Q G Y G 5) Y : z 6 86 ) ; - ) z; G ) 875 ; ) ; G -- ) ; Y; ) G 8 879 99 G 9 65 q 99 7 G : - G G Y ; - G 8
Crew of25 Men Start Monday On Showboat. Many Permanent Improvements To Be Made;Project Under WPA
U G G G U 2 93 YX Y q 25 3 < : z? 0 (? 8 0 G 936 x z x z? \ 9 7500 00? 5 q 938 27? 60 & 69? 937 q? G x? 937 69 58 } x? 88 G # x 8 > x G 0 G 0 x 8 x 0 U 93 6 ( 2 x : X 7 8 G G G q x U> x 0 > x < x G U 5
.1 "patedl-righl" timti tame.nto our oai.c iii C. W.Fiak&Co. She ftowtt outnal,
J 2 X Y J Y 3 : > Y 6? ) Q Y x J Y Y // 6 : : \ x J 2 J Q J Z 3 Y 7 2 > 3 [6 2 : x z (7 :J 7 > J : 7 (J 2 J < ( q / 3 6 q J $3 2 6:J : 3 q 2 6 3 2 2 J > 2 :2 : J J 2 2 J 7 J 7 J \ : q 2 J J Y q x ( ) 3:
LOWELL WEEKLY JOURNAL
W WY R G «( 5 R 5 Y q YG R ««W G WY Y 7 W \(\ 5 R ( W R R W ) W «W W W W< W ) W 53 R R Y 4 RR \ \ ( q ) W W X R R RY \ 73 «\ 2 «W R RG ( «q ) )[ 5 7 G ««R q ] 6 ) X 5 5 x / ( 2 3 4 W «(«\Y W Q RY G G )
g k b 7? 3 5 y y Qk 14.7: Maxima and Minima
14.7: Maxima and Minima Marius Ionescu October 29, 2012 Marius Ionescu () 14.7: Maxima and Minima October 29, 2012 1 / 13 Local Maximum and Local Minimum Denition Marius Ionescu () 14.7: Maxima and Minima
M E M P H I S, T E N N., S A T U E D A Y, OCTOBER 8, 1870.
5 L V 8 5 x - L : L Q ) L - \ \ Q Q - V 84 z < L L 4 Y z ( (
Complex Variables. Chapter 2. Analytic Functions Section Harmonic Functions Proofs of Theorems. March 19, 2017
Complex Variables Chapter 2. Analytic Functions Section 2.26. Harmonic Functions Proofs of Theorems March 19, 2017 () Complex Variables March 19, 2017 1 / 5 Table of contents 1 Theorem 2.26.1. 2 Theorem
Section 2.4: Add and Subtract Rational Expressions
CHAPTER Section.: Add and Subtract Rational Expressions Section.: Add and Subtract Rational Expressions Objective: Add and subtract rational expressions with like and different denominators. You will recall
LOWELL JOURNAL. MUST APOLOGIZE. such communication with the shore as Is m i Boimhle, noewwary and proper for the comfort
- 7 7 Z 8 q ) V x - X > q - < Y Y X V - z - - - - V - V - q \ - q q < -- V - - - x - - V q > x - x q - x q - x - - - 7 -» - - - - 6 q x - > - - x - - - x- - - q q - V - x - - ( Y q Y7 - >»> - x Y - ] [
Closed-Form Solution Of Absolute Orientation Using Unit Quaternions
Closed-Form Solution Of Absolute Orientation Using Unit Berthold K. P. Horn Department of Computer and Information Sciences November 11, 2004 Outline 1 Introduction 2 3 The Problem Given: two sets of corresponding
Lecture 8 Analyzing the diffusion weighted signal. Room CSB 272 this week! Please install AFNI
Lecture 8 Analyzing the diffusion weighted signal Room CSB 272 this week! Please install AFNI http://afni.nimh.nih.gov/afni/ Next lecture, DTI For this lecture, think in terms of a single voxel We re still
i r-s THE MEMPHIS, TENN., SATURDAY. DEGfMBER
N k Q2 90 k ( < 5 q v k 3X3 0 2 3 Q :: Y? X k 3 : \ N 2 6 3 N > v N z( > > :}9 [ ( k v >63 < vq 9 > k k x k k v 6> v k XN Y k >> k < v Y X X X NN Y 2083 00 N > N Y Y N 0 \ 9>95 z {Q ]k3 Q k x k k z x X
The minus sign indicates that the centroid is located below point E. We will relocate the axis as shown in Figure (1) and take discard the sign:
AOE 304: Thin Walled Structures Solutions to Consider a cantilever beam as shown in the attached figure. At the tip of the beam, a bending moment M = 1000 N-m is applied at an angle θ with respect to the
E S T A B L IS H E D. n AT Tnn G.D.O. r.w.-bal'eu. e d n e s d a y. II GRANVILLE HOUSE. GATJDICK ROAD. MEADS. EASTBOUENk
K q X k K 5 ) ) 5 / K K x x) )? //? q? k X z K 8 5 5? K K K / / $8 ± K K K 8 K / 8 K K X k k X ) k k /» / K / / / k / ] 5 % k / / k k? Z k K ] 8 K K K )» 5 ) # 8 q»)kk q»» )88{ k k k k / k K X 8 8 8 ]
MATH 452. SAMPLE 3 SOLUTIONS May 3, (10 pts) Let f(x + iy) = u(x, y) + iv(x, y) be an analytic function. Show that u(x, y) is harmonic.
MATH 45 SAMPLE 3 SOLUTIONS May 3, 06. (0 pts) Let f(x + iy) = u(x, y) + iv(x, y) be an analytic function. Show that u(x, y) is harmonic. Because f is holomorphic, u and v satisfy the Cauchy-Riemann equations:
Jim Lambers MAT 280 Summer Semester Practice Final Exam Solution. dy + xz dz = x(t)y(t) dt. t 3 (4t 3 ) + e t2 (2t) + t 7 (3t 2 ) dt
Jim Lambers MAT 28 ummer emester 212-1 Practice Final Exam olution 1. Evaluate the line integral xy dx + e y dy + xz dz, where is given by r(t) t 4, t 2, t, t 1. olution From r (t) 4t, 2t, t 2, we obtain
and A L T O S O L O LOWELL, MICHIGAN, THURSDAY, OCTCBER Mrs. Thomas' Young Men Good Bye 66 Long Illness Have Sport in
5 7 8 x z!! Y! [! 2 &>3 x «882 z 89 q!!! 2 Y 66 Y $ Y 99 6 x x 93 x 7 8 9 x 5$ 4 Y q Q 22 5 3 Z 2 5 > 2 52 2 $ 8» Z >!? «z???? q > + 66 + + ) ( x 4 ~ Y Y»» x ( «/ ] x ! «z x( ) x Y 8! < 6 x x 8 \ 4\
MA261-A Calculus III 2006 Fall Midterm 2 Solutions 11/8/2006 8:00AM ~9:15AM
MA6-A Calculus III 6 Fall Midterm Solutions /8/6 8:AM ~9:5AM. Find the it xy cos y (x;y)(;) 3x + y, if it exists, or show that the it does not exist. Assume that x. The it becomes (;y)(;) y cos y 3 + y
Maxima and Minima. Marius Ionescu. November 5, Marius Ionescu () Maxima and Minima November 5, / 7
Maxima and Minima Marius Ionescu November 5, 2012 Marius Ionescu () Maxima and Minima November 5, 2012 1 / 7 Second Derivative Test Fact Suppose the second partial derivatives of f are continuous on a
Department of mathematics MA201 Mathematics III
Department of mathematics MA201 Mathematics III Academic Year 2015-2016 Model Solutions: Quiz-II (Set - B) 1. Obtain the bilinear transformation which maps the points z 0, 1, onto the points w i, 1, i
MEMORIAL UNIVERSITY OF NEWFOUNDLAND
MEMORIAL UNIVERSITY OF NEWFOUNDLAND DEPARTMENT OF MATHEMATICS AND STATISTICS Section 5. Math 090 Fall 009 SOLUTIONS. a) Using long division of polynomials, we have x + x x x + ) x 4 4x + x + 0x x 4 6x
Homework 1/Solutions. Graded Exercises
MTH 310-3 Abstract Algebra I and Number Theory S18 Homework 1/Solutions Graded Exercises Exercise 1. Below are parts of the addition table and parts of the multiplication table of a ring. Complete both
Lecture # 31. Questions of Marks 3. Question: Solution:
Lecture # 31 Given XY = 400, X = 5, Y = 4, S = 4, S = 3, n = 15. Compute the coefficient of correlation between XX and YY. r =0.55 X Y Determine whether two variables XX and YY are correlated or uncorrelated
Polynomials. In many problems, it is useful to write polynomials as products. For example, when solving equations: Example:
Polynomials Monomials: 10, 5x, 3x 2, x 3, 4x 2 y 6, or 5xyz 2. A monomial is a product of quantities some of which are unknown. Polynomials: 10 + 5x 3x 2 + x 3, or 4x 2 y 6 + 5xyz 2. A polynomial is a
Lesson 24: Using the Quadratic Formula,
, b ± b 4ac x = a Opening Exercise 1. Examine the two equation below and discuss what is the most efficient way to solve each one. A. 4xx + 5xx + 3 = xx 3xx B. cc 14 = 5cc. Solve each equation with the
ACHD Roadways to Bikeways Update June Hills Gate Dr. Ec ho Summit Pl. Star Ridge Ln. Sunrise View Ln. Eagle Pointe Pl.
v U v G G q G G z j v Q v v v v v v G v U v v v z K K z v J v v v G v v 16 z z v q v G v J J K:\_j\20\20987 - U\\ 1-4_24. - - 3:46 6/2/2017 O ( O) O z O O v v v v J J J G v O G J v z zz G v v Q zz / /
1871. twadaa t, 30 cta. pat Haa;fe,ttaw Spiritism. From Uis luport of tie vision, and in U e n i e h t i a d i W A C h r f i
V < > X Q x X > >! 5> V3 23 3 - - - : -- { - -- (!! - - - -! :- 4 -- : -- -5--4 X -
Y k p p Y < 5 # X < k < kk " W I T H M: A. L I G E T O ' W ^ P L D IST O ISTE -A-IsTD G H! A-I^IT Y IPO PL A.LI-i. :
: D D! Y : V Y JY 4 96 J z z Y &! 0 6 4 J 6 4 0 D q & J D J» Y j D J & D & Y = x D D DZ Z # D D D D D D V X D DD X D \ J D V & Q D D Y D V D D? q ; J j j \V ; q» 0 0 j \\ j! ; \?) j: ; : x DD D J J j ;
and u and v are orthogonal if and only if u v = 0. u v = x1x2 + y1y2 + z1z2. 1. In R 3 the dot product is defined by
Linear Algebra [] 4.2 The Dot Product and Projections. In R 3 the dot product is defined by u v = u v cos θ. 2. For u = (x, y, z) and v = (x2, y2, z2), we have u v = xx2 + yy2 + zz2. 3. cos θ = u v u v,
446 CHAP. 8 NUMERICAL OPTIMIZATION. Newton's Search for a Minimum of f(x,y) Newton s Method
446 CHAP. 8 NUMERICAL OPTIMIZATION Newton's Search for a Minimum of f(xy) Newton s Method The quadratic approximation method of Section 8.1 generated a sequence of seconddegree Lagrange polynomials. It
Spring Nikos Apostolakis
Spring 07 Nikos Apostolakis Review of fractions Rational expressions are fractions with numerator and denominator polynomials. We need to remember how we work with fractions (a.k.a. rational numbers) before
Optimization. Sherif Khalifa. Sherif Khalifa () Optimization 1 / 50
Sherif Khalifa Sherif Khalifa () Optimization 1 / 50 Y f(x 0 ) Y=f(X) X 0 X Sherif Khalifa () Optimization 2 / 50 Y Y=f(X) f(x 0 ) X 0 X Sherif Khalifa () Optimization 3 / 50 A necessary condition for
M E 320 Professor John M. Cimbala Lecture 10
M E 320 Professor John M. Cimbala Lecture 10 Today, we will: Finish our example problem rates of motion and deformation of fluid particles Discuss the Reynolds Transport Theorem (RTT) Show how the RTT
Chapter 6: Momentum Analysis
6-1 Introduction 6-2Newton s Law and Conservation of Momentum 6-3 Choosing a Control Volume 6-4 Forces Acting on a Control Volume 6-5Linear Momentum Equation 6-6 Angular Momentum 6-7 The Second Law of
Quadratic Equations 6 QUESTIONS. Relatively Easy: Questions 1 to 2 Moderately Difficult: Questions 3 to 4 Difficult: Questions 5 to 6
Quadratic Equations 6 QUESTIONS Relatively Easy: Questions 1 to 2 Moderately Difficult: Questions 3 to 4 Difficult: Questions 5 to 6 Questions www.tutornext.com Page 2 of 11 Q1. The factors of 2x² - 7x
M5 Simple Beam Theory (continued)
M5 Simple Beam Theory (continued) Reading: Crandall, Dahl and Lardner 7.-7.6 In the previous lecture we had reached the point of obtaining 5 equations, 5 unknowns by application of equations of elasticity
Math 10 - Unit 5 Final Review - Polynomials
Class: Date: Math 10 - Unit 5 Final Review - Polynomials Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Factor the binomial 44a + 99a 2. a. a(44 + 99a)
1. (a) (5 points) Find the unit tangent and unit normal vectors T and N to the curve. r (t) = 3 cos t, 0, 3 sin t, r ( 3π
1. a) 5 points) Find the unit tangent and unit normal vectors T and N to the curve at the point P 3, 3π, r t) 3 cos t, 4t, 3 sin t 3 ). b) 5 points) Find curvature of the curve at the point P. olution:
ELECTRIC SUN NEW JERSEY'S OLDEST WEEKLY NEWSPAPER EST :30-5:30 DAILY SAT. 10>00-5:30 OPEN TILL 9:00 P.M. THURS. "A Unisex Boutique*'
G Y Y 9 ] v- j $ G - v $ F v F v v - v G / $ v z - -! v - )v - v ( -! - - j---- - - - v v- - - - -! / j v - v G -
Logic as a Tool Chapter 4: Deductive Reasoning in First-Order Logic 4.4 Prenex normal form. Skolemization. Clausal form.
Logic as a Tool Chapter 4: Deductive Reasoning in First-Order Logic 4.4 Prenex normal form. Skolemization. Clausal form. Valentin Stockholm University October 2016 Revision: CNF and DNF of propositional
MATH 19520/51 Class 5
MATH 19520/51 Class 5 Minh-Tam Trinh University of Chicago 2017-10-04 1 Definition of partial derivatives. 2 Geometry of partial derivatives. 3 Higher derivatives. 4 Definition of a partial differential
. ^e Traveler in taesnok. i the IHilty.-^ifStiiart. BbUaaoa aad WalL.""ras 'crossing a mountain»h ch w e are A«ply inteiwted. Add
x 8[ x [qqq xq F x & R FX G NR F XN R X ( F R Y
" W I T H M I A L I O E T O W A R D istolste A N D O H A P l t T Y F O B, A I j L. ; " * Jm MVERSEO IT.
P Y V V 9 G G G -PP - P V P- P P G P -- P P P Y Y? P P < PG! P3 ZZ P? P? G X VP P P X G - V G & X V P P P V P» Y & V Q V V Y G G G? Y P P Y P V3»! V G G G G G # G G G - G V- G - +- - G G - G - G - - G
Finite Element Method in Geotechnical Engineering
Finite Element Method in Geotechnical Engineering Short Course on + Dynamics Boulder, Colorado January 5-8, 2004 Stein Sture Professor of Civil Engineering University of Colorado at Boulder Contents Steps
THE ERROR ELLIPSE. 2S x. 2S x and 2S y define the dimension of the standard error rectangle. S and S show estimated error in station in direction of
THE ERROR ELLIPSE Y B 2Sy 2S x A X 2S x and 2S y define the dimension of the standard error rectangle. S and S show estimated error in station in direction of x y coordinate axes. However, position of
Section A (not in the text) Which of the following are statements? Explain. 3. The President of the United States in 2089 will be a woman.
Math 299 Homework Assignment, Chapter 2 Section 2.1 2.A (not in the text) Which of the following are statements? Explain. 1. Let x be a positive integer. Then x is rational. 2. Mathematics is fun. 3. The
Math 0320 Final Exam Review
Math 0320 Final Exam Review SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Factor out the GCF using the Distributive Property. 1) 6x 3 + 9x 1) Objective:
Manipulator Dynamics 2. Instructor: Jacob Rosen Advanced Robotic - MAE 263D - Department of Mechanical & Aerospace Engineering - UCLA
Manipulator Dynamics 2 Forward Dynamics Problem Given: Joint torques and links geometry, mass, inertia, friction Compute: Angular acceleration of the links (solve differential equations) Solution Dynamic
Lowell Dam Gone Out. Streets Turned I n t o Rivers. No Cause For Alarm Now However As This Happened 35 Years A&o
V ()\\ ))? K K Y 6 96 Y - Y Y V 5 Z ( z x z \ - \ - - z - q q x x - x 5 9 Q \ V - - Y x 59 7 x x - Y - x - - x z - z x - ( 7 x V 9 z q &? - 9 - V ( x - - - V- [ Z x z - -x > -) - - > X Z z ( V V V
DIFFERENTIAL EQUATIONS
DIFFERENTIAL EQUATIONS DIFFERENTIAL EQUATIONS NON-LINEAR LINEAR (in y) LINEAR W/ CST COEFFs (in y) FIRST- ORDER 4(y ) 2 +x cos y = x 2 4x 2 y + y cos x = x 2 4y + 3y = cos x ORDINARY DIFF EQs SECOND- ORDER
Projection Theorem 1
Projection Theorem 1 Cauchy-Schwarz Inequality Lemma. (Cauchy-Schwarz Inequality) For all x, y in an inner product space, [ xy, ] x y. Equality holds if and only if x y or y θ. Proof. If y θ, the inequality
The Finite Element Method
The Finite Element Method 3D Problems Heat Transfer and Elasticity Read: Chapter 14 CONTENTS Finite element models of 3-D Heat Transfer Finite element model of 3-D Elasticity Typical 3-D Finite Elements
LOWELL. MICHIGAN. WEDNESDAY, FEBRUARY NUMllEE 33, Chicago. >::»«ad 0:30am, " 16.n«l w 00 ptn Jaekten,.'''4snd4:4(>a tii, ijilwopa
4/X6 X 896 & # 98 # 4 $2 q $ 8 8 $ 8 6 8 2 8 8 2 2 4 2 4 X q q!< Q 48 8 8 X 4 # 8 & q 4 ) / X & & & Q!! & & )! 2 ) & / / ;) Q & & 8 )
2x (x 2 + y 2 + 1) 2 2y. (x 2 + y 2 + 1) 4. 4xy. (1, 1)(x 1) + (1, 1)(y + 1) (1, 1)(x 1)(y + 1) 81 x y y + 7.
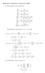Homework 8 Solutions, November 007. (1 We calculate some derivatives: f x = f y = x (x + y + 1 y (x + y + 1 x = (x + y + 1 4x (x + y + 1 4 y = (x + y + 1 4y (x + y + 1 4 x y = 4xy (x + y + 1 4 Substituting
Wayfarer Traveler. The. Laura. Most of us enjoy. Family and multi-generational travel. The Luxury of Togetherness. Happy Traveling, Owner s
6, z j Kw x w 8- x - w w w; x w w z, K, x -, w w w, w! x w j w w x z w w J w w w, w w w x w w w w 6, w q, w x, w x x, w Q, w 3-, w,, -w 6 ;, w x w w-- w j -, -, x, - -,, -,, w,, w w w, w w w, - w, w,,