A Rewrite Approach for Pattern Containment
|
|
|
- Ashley Sharp
- 5 years ago
- Views:
Transcription
1 A Rewrite Approh or Pttern Continment Brr Kory LIFO - Université Orléns, Frne Astrt. In this pper we introue n pproh tht llows to hnle the ontinment prolem or the rgment XP(/,//,[ ], ) o XPth. Using rewriting tehniques we eine neessry n suiient onition or pttern ontinment. This rewrite view is then pte to query evlution on XML ouments, n remins vli even i the ouments re given in ompresse orm, s gs. 1 Introution The ous in this pper is on the ontinment prolem ([1,2]) or the rgment XP(/,//,[ ], ) o XPth. XPth ([3]) is the min lnguge or nvigting n seleting noes in XML ouments. The segment XP(/,//,[ ], ) eines lss o Core XPth queries expressing esennt reltionships etween noes, possily ontining ilters, n llowing to use the on t re (or wilr) symol. The queries o this rgment n e moele y ptterns: tree like grphs hving two types o eges hil n esennt. Every XML oument t is n unrnke tree t = (Noes t, Eges t ), n n lso e seen s pttern. For ny two ptterns P n Q, we sy tht P is ontine in Q (P Q), i the query represente y Q is more generl thn the one represente y P. For exmple, / is ontine in //, sine hil (/) is prtiulr se o esennt (//). The ig interest in the query ontinment prolem ([1,2,4,5]) is motivte y its pplitions. Using the notion o pttern ontinment we n eine queries whih re equivlent, i.e., tht on ny XML oument, selet the sme set o noes. The query equivlene prolem is losely linke to the query minimiztion prolem, whih is essentil or t se reserhers. Sine the time require or the evlution o given query Q is liner with respet to the size o Q ([6]), the minimiztion possiility o repling Q y n equivlent query o smller size is o interest rom the point o view o omplexity ([7,8,9,10]). We propose to hnle the ontinment prolem using rewrite pproh. We eine set o rewrite rules se on the semntis o XP(/,//,[ ], ) query ontinment, n show tht or ny two ptterns P n Q, P is ontine in Q i n only i we n rewrite P to Q using these rules. This provies hrteriztion o the ontinment prolem using lgeri tehniques, whih ws missing in the literture. Suh rewrite view gives us uniorm rmework to tret lso other prolems, or instne query evlution. We exten our pproh on ompresse ouments enoe s strightline regulr grmmrs, n pply The originl pulition is ville t:
2 our rewrite tehnique in orer to evlute XP(/,//,[ ], ) queries on ompresse or unole (roresent) XML ouments. This pper is orgnize s ollows: In Setion 2 we introue terminology n nottion, n rell some results on the pttern ontinment prolem. Our rewrite metho is presente in Setion 3. Finlly, in Setion 4 we show how to pt this rewrite pproh to the query evlution prolem. 2 The Pttern Continment Prolem Let Σ e n lphet ontining the element nmes o ll XML ouments onsiere. In this work we onsier the rgment XP(/,//,[ ], ) o XPth, whih onsists o: noe tests (symols rom Σ { }), hil xis (/), esennt xis (//), n quliiers lso lle ilters ([...]). Any element o XP(/,//,[ ], ) is query tht n e represente s roote tree struture grph over Σ { }, lle unry pttern, hving: eges o two types: simple or hil, n oule or esennt, noes lele y the symols rom Σ { }, one istinguishe noe mrke with speil seletion symol s representing the output inormtion (lote t the en o the min pth in the query onsiere). For instne, the unry pttern in Figure 1 represents the XP(/,//,[ ], ) query ///[.///]/[./ //]. The notion o unry ptterns is esily extene to s Fig. 1. Unry pttern representing query ///[.///]/[./ //] tht o n ry ptterns, where we hve n istinguishe noes, tht moel n ry queries seleting n tuples o noes. Miklu n Suiu show in [1] tht, or the purpose o the ontinment prolem, it is suiient to onsier only the ptterns o rity zero, lle oolen, where there re no istinguishe noes. Thus, ll ptterns onsiere in the sequel will e oolen, n they will e simply lle ptterns. For given pttern P, we enote y Noes P the set o ll its noes. For ny u Noes P, nme P (u) stns or the element o Σ { } leling the noe u. By Eges (P ) n Eges (P ) we men respetively the set o hil n esennt 2
3 eges o P. We eine the size o P (enote y P ) to e the numer o ll eges in P. Deinition 1. An XML tree t is moel o pttern P i there exists n emeing rom P to t; i.e., untion e: Noes P Noes t, stisying the ollowing onitions: 1. e preserves the root: e(root P ) = root t ; 2. e preserves the nmes: u Noes P, nme P (u) =, or nme P (u) = nme t (e(u)); 3. e preserves the reltion hil: (u, v) Eges (P ), (e(u), e(v)) Eges t ; 4. e preserves the reltion esennt: (u, v) Eges (P ), (e(u), e(v)) (Eges t ) +, where (Eges t ) + is the trnsitive losure o the reltion Eges t. The notion o moel is illustrte in Figure 2. P e t Fig. 2. Pttern P, its moel t, n emeing e rom P to t Deinition 2. Given two ptterns P n Q, we sy tht P is ontine in Q (P Q) i every moel o P is lso moel o Q. The ptterns P n Q re equivlent (P Q) i P Q n Q P. Figure 3 represents two ptterns whih re esily seen to e equivlent. P Q Fig. 3. Equivlent ptterns P n Q Miklu n Suiu prove in [1] tht the ontinment prolem or XP(/,//,[ ], ) is CoNP omplete. They lso give suiient ut not neessry onition or pttern ontinment. For tht purpose, they exten the notion o emeing to pttern homomorphism: 3
4 Deinition 3. Given two ptterns P n Q, homomorphism rom Q to P is untion ϕ: Noes Q Noes P, whih is: root n nme preserving; hil preserving: (u, v) Eges (Q), (ϕ(u), ϕ(v)) Eges (P ); esennt preserving: (u, v) Eges (Q), (ϕ(u), ϕ(v)) (Eges (P ) Eges (P )) +. The uthors o [1] prove tht i there exists homomorphism rom Q to P, then P is ontine in Q. They give n lgorithm whih or two given ptterns P n Q veriies, in time O( P Q ), whether there exists homomorphism rom Q to P. Figure 4 shows the ptterns P n Q, n the homomorphism ϕ rom Q to P proving tht P Q. Nevertheless, the existene o homomorphism rom Q P Q P ϕ ϕ Q Fig. 4. Homomorphism ϕ rom Q to P proving tht P Q to P is not neessry onition or P Q (s is esily heke or the ptterns P n Q given in Figure 3, whih re equivlent, ut there is no homomorphism neither rom Q to P, nor rom P to Q). In the ollowing exmple we show wy to prove the ontinment P Q, i there is no homomorphism rom Q to P. Exmple 1. In Figure 5 we hve presente two ptterns P n Q (orrowe rom [1]) stisying P Q, suh tht there is no homomorphism rom Q to P. Here, P Q Fig. 5. Ptterns s.t. P Q, ut no homomorphism rom Q to P to show the ontinment P Q, we hve to reson y ses. Let t e moel o P, n onsier the mile ege // o pttern P. This ege n e relize on t: either y the hil ege / (s in Figure 6), 4
5 P t e e Q e e Fig. 6. Moel o P (n Q), where // is relize y / P e t e Q e e Fig. 7. Moel o P (n Q), where // is relize y // or y pth / /... /, hving length 2 (s in Figure 7). Suh n nlysis shows tht ny moel o P is lso moel o Q, thus P Q. However, it is impossile to eine one generl homomorphism rom Q to P, s the right rnh //// // o Q orrespons in eh se to ierent rnh o P. 3 Pttern Continment vi rewriting We propose to hnle the pttern ontinment prolem using n pproh se on rewriting tehniques. A key ie is tht heking ontinment requires se nlysis in generl, n this n e enoe s rewriting (s we illustrte in Exmple 2 elow). We onstrut rewrite system R tht permits to eine neessry n suiient onition (see Theorem 1) or pttern ontinment on the rgment XP(/,//,[ ], ). We strt y giving orml einition o pttern, lterntive to tht use in the previous setions. Deinition 4. We eine ptterns over n lphet Σ s the expressions P erive rom the grmmr o Tle 1, where n stn respetively or hil n esennt, ω Σ { }, n is the on t re symol o XPth tht n reple ny σ o Σ. This grmmr proues preisely the ptterns s eine in [7,1]. For instne, the grph P in Figure 8 orrespons to the expression P = { {, }, } 5
6 M : ε ω ω MM // pth S : {MS} S S // set o siling unroote terms P : ωms // ptterns Tle 1. Grmmr or ptterns erive rom the grmmr o Tle 1. P Fig. 8. Pttern By term we men ny expression o the type M, S or P erive rom the grmmr o Tle 1, s well s ny inite isjuntion P 1 P 2 P n o ptterns. The terms o the type M orrespon to the liner pths without rnhing, they strt y mol symol ξ {, }; those o the type S represent set o terms hving ommon prent noe; n those o the type P re ptterns. The terms in P re roote (they strt y symol rom Σ { }), those in M n S re unroote. To simpliy, we will oten ientiy the singleton {M S} with the term MS. Given ptterns P n P i, or 1 i n, the terms o the orm ε, P, or P 1 P n, will lso e lle ptterns. A tree t is moel o pttern P 1 P n i t is moel o t lest one pttern P i, or 1 i n. Deinition 2 o pttern ontinment is extene in nturl wy to pttern ontinment. A isjuntive pttern will e use in se nlysis to represent ierent moels o given pttern with unique term, s in the ollowing exmple. Exmple 2. Consier the ptterns P = n Q = given in Figure 3. We know tht P Q, thus in prtiulr P Q, ut there is no homomorphism whih proves it. Using the rules o our system R eine elow we will e le to rewrite P to Q, n prove the ontinment P Q. The ie is tht every esennt is either hil or hs epth 2; thus, the ege o P n e relize either y the hil ege, or y pth hving t lest one itionl noe etween n, tht we n enote y. 6
7 We will then rewrite the pttern P to the pttern epiting the two ses mentione. The two pttern omponents o this pttern will then e rewritten in prllel. A hil, s well s esennt o epth 2 re prtiulr ses o esennt. As onsequene, the ege will e rewritten to, iem or the pth. This will give us the ollowing term:, whih will e inlly rewritten to Q, sine eh pttern omposing this pttern is extly the pttern Q. To ormlize the ie employe in the exmples ove, we introue set R o rules tht serve to rewrite roote n unroote terms. Let M, S (possily with primes, susripts) e s in the grmmr o Tle 1; ξ, ξ {, }, σ Σ, n ω, ω Σ { }: 1. S, M ε //ut; 2. MσS M S //reple ny symol o Σ y the o XPth; 3. ωs ωs //every hil is lso esennt; 4. ξωξ ω S ω S //ignore n intermeite noe; 5. M{S 1, S 2 } {MS 1, MS 2 } //let istriutivity; 6. S S S, where S S // new silings; 7. S S 1 S S 1, i S S //rewrite some o the silings; 8. ωs ( ωs) ( ωs) //se nlysis: esennt is either hil or hs epth 2; 9. ωs ( ωs) ( ωs) //iem. By ontext pttern we men ny pttern hving speil itionl hole symol tht reples one o its unroote su terms. Let us onsier ontext pttern C n n unroote term X. We eine the ill in o C with X (enote s C X) to e the pttern otine rom C y repling its hole symol with the term X; e.g. or the ontext pttern C = {, {, }, }, n the unroote term X = x{ y, z}, we get the ill in: C X = {, { x{ y, z}, }, }. We lso suppose tht or ny ontext pttern C n unroote terms X n X, the nottion C (X X ) stns or the isjuntive pttern C X C X. To rewrite ptterns with the rules o R given ove, we use suix rewriting: Deinition 5. Given pttern P n pttern or pttern Q, we sy tht P n e rewritten to Q in one step using suix rewriting, i there exist ontext pttern C n two unroote terms X n X, suh tht: P = C X, Q = C X, n X X is n instne o rule in R. Moreover, isjuntive terms n e rewritten using the ollowing itionl two rules, where P is pttern, n D, D 1, D 2 stn or ptterns: 7
8 10. D 1 D D 2 D, i D 1 n e rewritten to D 2 //se rewriting; 11. P P D P D //onsier ny given se only one. Rules 10 n 11 re use s ollows: i pttern L is n instne (moulo ommuttivity) o the LHS o rule 10 or 11, n pttern R is n instne (moulo ommuttivity) o the RHS o the sme rule, then L n e rewritten to R. We will enote y A R B the t tht pttern or pttern A is rewritten in one step to pttern or pttern B, y using the rules o R. The min result o our work is the ollowing: Theorem 1. For ny two ptterns P n Q, P is ontine in Q i n only i P R Q, i.e., P n e rewritten to Q using the rules o R in zero or initely mny steps. Proo. The semntis o the rules in R gurntee tht P R Q implies P Q. Inee, i X X is n instne o one o the rules 1 9, then or every ontext pttern C, we hve C X C X ; i L R is n instne o rule 10 or 11, we oviously hve L R. To show the onverse, we strt with the ollowing lemm: Lemm 1. For ny ptterns P n Q, i there exists homomorphism rom Q to P, then P R Q. Proo. Given homomorphism ϕ rom Q to P, we onstrut pttern P, suh tht P R P R Q, s ollows: () or every noe u o Q, we onstrut orresponing noe u o P, n we set nme P (u ) = nme P (ϕ(u)); () we onstrut hil ege (u, v ) Eges (P ), i n only i (u, v) Eges (Q); () we onstrut esennt ege (u, v ) Eges (P ), i n only i (u, v) Eges (Q). The ost o suh onstrution is liner with respet to the size o Q. The pttern P n e rewritten to the pttern Q using rule 2 o R. Inee, the strutures (noes, simple n oule eges) o P n Q re the sme, ut the nmes o some u Noes Q n the orresponing noe u Noes P my e ierent. Conition () implies tht: either nme Q (u) = nme P (u ) = nme P (ϕ(u)), or nme Q (u) nme P (u ) = nme P (ϕ(u)). In the seon se we hve (see Deinition 3): nme Q (u) =, n nme P (u ) Σ, thus to rewrite P to Q we hve to use rule 2. It remins to e shown tht P n e rewritten to P : using rules 1 n 7 (with S = ), we n ignore ll su rnhes o P whih o not ontin the noes imges uner ϕ; i some noe w o P is n imge o m istint noes u 1,..., u m o Q, then we rewrite the unique noe w o P to m noes u 1,..., u m o P, y using rule 6 (with S = S) n/or rule 5; 8
9 se when ege (u, v ) is in Eges (P ): rom onition () we know tht (u, v) Eges (Q), thus y Deinition 3 we hve (ϕ(u), ϕ(v)) Eges (P ) (we hve nothing to o with the ege (ϕ(u), ϕ(v)) when rewriting P to P ); se when ege (u, v ) is in Eges (P ): rom onition () n Deinition 3 we n eue tht there exist k 1 n w 0,... w k Noes P, suh tht: w 0 = ϕ(u), w k = ϕ(v), n i {0,..., k 1} we hve (w i, w i+1 ) Eges (P ) Eges (P ). I k = 1 n (ϕ(u), ϕ(v)) Eges (P ), then we n rewrite P to P using rule 3. I k 2, then we use (k 1 times) rule 4 to ignore the noes w 1,... w k 1 while rewriting P to P. Finlly, we otin P R P R Q. Note tht i P is tree, we lso hve the onverse o Lemm 1. Inee, it is suiient to remrk tht i P R Q n P is tree, then one n rewrite P to Q y using only rules 1 7; i X X is n instne o one o those rules, then or every ontext pttern C, there exists homomorphism rom C X to C X. O ourse, in the se when P is tree, homomorphism rom Q to P is n emeing rom the pttern Q to the tree P. The ove onsiertions give us the ollowing hrteriztion: Remrk 1. A tree t is moel o pttern Q i t R Q. By homomorphism rom pttern Q to pttern D = P 1 P n, we men untion whih is homomorphism rom Q to P i, or every 1 i n. Thus, using Lemm 1, we otin the ollowing orollry: Corollry 1. For ny given pttern Q n pttern D, i there exists homomorphism rom Q to D, then D R Q. Proo. It suies to remrk tht rules 10 n 11 imply tht pttern P 1 P n n e rewritten to pttern Q i n only i, or every 1 i n, we hve P i R Q. To inish the proo o Theorem 1, we use the ollowing proposition: Proposition 1. For two ptterns P n Q, i P Q, then one n onstrut pttern D veriying P R D, suh tht there exists homomorphism rom Q to D. Proo. From the result o Miklu n Suiu ([1]) we know tht it is possile to hek i there exists homomorphism rom Q to P. I it is the se, the pttern D stisying the proposition is equl to P (see Lemm 1). I not, isjuntive pttern D stisying the proposition n e onstrute y using rules 8 n 9 initely mny times. We know tht every moel o P is lso moel o Q. The ie is to represent ll moels o P y n equivlent pttern D = P 1 P n representing se nlysis, suh tht or every 1 i n, there exists homomorphism rom Q to P i. This termintes the proo o Theorem 1. 9
10 The rewrite system R is non eterministi; nevertheless i P n Q re given, there exists well eine, gol irete strtegy or rewriting P to Q. The ie is to use only those rules mong 1 11 tht permit to onverge to Q. We illustrte this strtegy in the ollowing exmple: Exmple 3. Let P n Q e the ptterns represente in Figure 5. We show how to rewrite P to Q, n thus prove the ontinment P Q. The pttern P = { {, }, } n e seen s the ill in { {, }, }. Using rule 8 or the unerline term, we enoe the ses epite in Exmple 1: { {, }, } { {, }, }. We otin the pttern { {, }, } { {, }, }, whih n e seen uner the orm { {, }, } { {, }, }. We rewrite it using rule 10. We ut (rule 1) the unerline prts, n get { { }, } { {, }}. The pttern tht we hve otine is then ientiie with {, } {, }. Its irst omponent is equl to the pttern Q. To the seon one, seen s the ill in {, }, we pply rule 4, n get the term {, } = {, }. Thus we otin the pttern {, } {, } = Q Q, tht is inlly rewritten to Q using rule 11. Remrk 2. Our pproh is no longer vli, i it is not se on suix rewriting; e.g. or P = n Q =, we hve P Q (P R Q using rules 9, 1), ut P = is not ontine in Q = : or instne, the tree t = g is moel o, ut not o. 10
11 4 Applitions The ojetive o this setion is to show tht our rewrite pproh remins vli even i the moels o ptterns re given in ompresse orm (s gs), n tht it n e pte or query evlution on XML ouments. 4.1 Cse o Compresse Douments To moel ompresse ouments we use roote gs inste o trees (s in [11,12,13,14]). Figure 9 represents three ormts o the sme oument: tree, ully n prtilly ompresse ormt (see [11] or orml einitions). In the Tree Fully ompresse Prtilly ompresse Fig. 9. Tree, ully ompresse ormt, prtilly ompresse ormt sequel, y t we will enote ny given representtion (tree or g) o the oument onsiere. To istinguish etween ierent ormts o the sme oument we use regulr tree grmmrs. Given oument t, we ll normlize grmmr or t regulr tree grmmr G t : whih reognizes only t, where every noe o t is represente y extly one non terminl, the inexes o non terminls or hilren noes re greter then the inexes o non terminls or prent noes. Suh normlize grmmrs re strightline in the sense eine in [15], i.e., there is no yle on their epeneny grph. For this reson we will reer to them s SLR grmmrs. Exmple 4. The SLR grmmrs or the three gs rom Figure 9 re respetively: X 0 (X 1, X 2, X 3, X 4 ) Y 0 (Y 1, Y 1, Y 2, Y 1 ) Z 0 (Z 1, Z 1, Z 2, Z 3 ) X 1 Y 1 Z 1 X 2 Y 2 Z 2 X 3 Z 3. X 4 We exten the notion o SLR grmmr to ptterns. To eine normlize grmmr G P or pttern P, it is suiient tht every non terminl X i ppering 11
12 on the right hn sie o ny proution o G P, is preee y mol symol or, orresponing to the type o ege pointing to the noe represente y X i on P. In orer to hve uniorm nottion tht overs ptterns s well s ouments, we will o the sme on the normlize grmmr G t, or ny oument t: every non terminl X i ppering on the right hn sie o some proution in G t, will e preee y. For instne, the grmmrs G P n G t respetively or the pttern P n the tree t o Figure 11, re given in Figure 10. P 0 ( P 1, P 2) X 0 ( X 2, X 1) P 1 X 1 ( X 2) P 2 X 2. Fig. 10. SLR grmmrs G P n G t or P n t rom Figure 11 To eine n emeing e rom pttern P to g t, we reple the onitions 3 n 4 o Deinition 1 respetively y: 3. u, v Noes P, suh tht (u, v) Eges (P ), there exists n ege going orm e(u) to e(v) on t; 4. u, v Noes P, suh tht (u, v) Eges (P ), there exists pth going rom e(u) to e(v) in (Eges t ) +. The notion o (g) moel o pttern n the pttern ontinment prolem re eine in the sme wy s in the se o tree moels. Figure 11 shows pttern P, its ompresse moel t, n n emeing rom P to t. P t Fig. 11. Pttern P, its ompresse moel t, n emeing rom P to t SLR grmmrs n e use in our rewrite pproh. To prove tht given g t is moel o pttern P, it is suiient (oring to Remrk 1) to rewrite the grmmr G t representing t to the grmmr G P representing P. We illustrte this ie in the ollowing exmple. 12
13 Exmple 5. Consier the grmmrs G P n G t given in Figure 10. We show how to rewrite G t to G P using rules o R: X 0 ( X 2, X 1 ) 2 X 0 ( X 2, X 1 ) X 1 ( X 2 ) X 1 ( X 2 ) 1 1 X 0 ( X 2 ) X 2 X 2 X 2 6 The irst proution o G t is irst rewritten using rule 2; then we ut rnh represente y X 1 (rule 1). At the sme time, we n eliminte rom G t the proution X 1 ( X 2 ), sine it hs eome unproutive (there is no more proution hving X 1 on their right hn sies). X 0 ( X 2, X 2) 3 X 0 ( X 2, X 2) P 0 ( P 1, P 2 ) X 2 X 2 P 1 X 2 X 2 P 2. Then, using rule 6 we oule the numer o hilren o X 0 ; we introue new non terminl X 2, whih proues the sme su pttern s X 2. Finlly, y Rule 3, we get grmmr whih is equl, up to non terminl renming, to G P. 4.2 Query Evlution SLR grmmrs help us to pt the rewrite pproh o Setion 3 to XP(/,//,[ ], ) query evlution on (ompresse) ouments. To represent unry queries, we use unry ptterns (see Setion 2). Let us onsier the unry pttern P rep- P: P 0 t: X 0 P 1 X 1 X 2 P 2 P 3 s X 3 X 4 X 5 P 4 X 6 Fig. 12. Unry pttern P n its ompresse moel t resenting the query P = / //[./]//[./], n the ompresse oument t, given in Figure 12. The orresponing SLR grmmrs G P n G t re respe- 13
14 tively: P 0 ( P 1 ) X 0 ( X 1, X 2 ) P 1 ( P 2, P 3 ) X 2 ( X 6 ) P 2 X 1 ( X 6, X 3 ) P 3 (s) ( P 4 ) X 3 ( X 4, X 5 ) P 4 X 4 ( X 6 ) X 5 ( X 6 ) X 6. The non terminl P 3 o G P is mrke s, sine it represents the output noe o P. To in n nswer or P on t, we rewrite the grmmr G t to the grmmr G P, using the rules o R. The non terminl o G t whih will e rewritten to the seleting non terminl P 3 o G P, will represent n nswer or P on t. We illustrte this resoning elow: X 0 ( X 1, X 2 ) X 2 ( X 6 ) X 1 ( X 6, X 3 ) 1 X 0 ( X 1 ) 2 X 0 ( X 1 ) 1 X 1 ( X 3 ) X 1 ( X 3 ) X 3 ( X 4, X 5 ) X 3 ( X 4, X 5 ) X 4 ( X 6 ) 4 3 X 3 ( X 4, X 5 ) 1 X 4 X 4 X 5 ( X 6 ) X 5 ( X 6 ) X 5 ( X 6 ) X 6 X 6 X 6 X 0 ( X 3 ) P 0 ( P 1 ) X 3 ( X 4, X 5 ) P 1 ( P 2, P 3 ) X 4 P 2 X 5 ( X 6 ) P 3 (s) ( P 4 ) X 6 P 4, We hve otine n SLR grmmr, whih is (up to non terminl renming) the SLR grmmr G P or P. The non terminl X 5 o G t hs een rewritten to the non terminl P 3, thus the noe represente y X 5 is n nswer or P on t. Note tht, s ny query P o the rgment XP(/,//,[ ], ) is purely esennt, the nswer or P on oument t oes not epen on the orm uner whih t is given (tree or g); this is no longer vli or queries ontining sennt xes (.[11]). Remrk lso tht our rewrite pproh n e extene to ny n ry query o XP(/,//,[ ], ); n n ry query selets set o n tuples o noes ([16]), n is esily represente s n n ry pttern. 14
15 5 Conlusion We hve presente n pproh se on rewrite tehniques, tht llows to hnle the prolem o query ontinment or the segment XP(/,//,[ ], ) o XPth. Suh rewrite view is lso pproprite or ompresse ouments moele s gs, n n e pte to (unry s well s n ry) query evlution on (ompresse) ouments. Strightline regulr tree grmmrs n provie n exponentil spe ompression. Nevertheless there exist more eiient ompression tehniques, like those se on stightline ontext ree grmmrs (SLCF, [15]), giving etter (up to ouly exponentil) ompression rtes. Currently we re stuying the possiility o extening our rewrite pproh to suh more eiient ompressions. We lso hope to pt our results to lrger rgments o XPth, ontining queries moele y more generl ptterns, hving oth esennt n sennt eges. Reerenes 1. Miklu, G., Suiu, D.: Continment n Equivlene or Frgment o XPth. J. ACM 51(1) (2004) Neven, F., Shwentik, T.: XPth Continment in the Presene o Disjuntion, DTDs, n Vriles. In Clvnese, D., Lenzerini, M., Motwni, R., es.: ICDT 03. Volume 2572 o LNCS., Springer (2003) W3C: XML Pth Lnguge. (1999) 4. Woo, P.T.: On the Equivlene o XML Ptterns. In Lloy, J.W., Dhl, V., Furh, U., Kerer, M., Lu, K.K., Plmiessi, C., Pereir, L.M., Sgiv, Y., Stukey, P.J., es.: CL 00. Volume 1861 o LNCS., Lonon, UK, Springer (2000) Shwentik, T.: XPth Query Continment. SIGMOD Re. 33(1) (2004) Gottlo, G., Koh, C., Pihler, R.: Eiient Algorithms or Proessing XPth Queries. ACM Trns. Dtse Syst. 30(2) (2005) Fles, S., Furro, F., Msiri, E.: On the Minimiztion o XPth Queries. J. ACM 55(1) (2008) 8. Amer-Yhi, S., Cho, S., Lkshmnn, L.V.S., Srivstv, D.: Tree Pttern Query Minimiztion. VLDB J. 11(4) (2002) Kimelel, B., Sgiv, Y.: Revisiting Reunny n Minimiztion in n XPth Frgment. In: EDBT 08: Proeeings o the 11th Interntionl Conerene on Extening Dtse Tehnology, New York, USA, ACM (2008) Rmnn, P.: Eiient Algorithms or Minimizing Tree Pttern Queries. In: SIG- MOD 02: Proeeings o the 2002 ACM SIGMOD Interntionl Conerene on Mngement o Dt, New York, USA, ACM (2002) Fil, B., Annthrmn, S.: Automt or Positive Core XPth Queries on Compresse Douments. In Hermn, M., Voronkov, A., es.: LPAR 06. Volume 4246 o LNAI., Springer (2006) Bunemn, P., Grohe, M., Koh, C.: Pth Queries on Compresse XML. In: VLDB 03, Morgn Kumnn (2003) Mrx, M.: XPth n Mol Logis o Finite DAG s. In Cile-Myer, M., Pirri, F., es.: TABLEAUX 03. Volume 2796 o LNAI., Springer (2003)
16 14. Frik, M., Grohe, M., Koh, C.: Query Evlution on Compresse Trees (Extene Astrt). In: LICS 03: Proeeings o the 18th Annul IEEE Symposium on Logi in Computer Siene, Wshington, DC, USA, IEEE Computer Soiety (2003) Bustto, G., Lohrey, M., Mneth, S.: Eiient Memory Representtion o XML Doument Trees. In. Syst. 33(4-5) (2008) Niehren, J., Plnque, L., Tlot, J.M., Tison, S.: N ry Queries y Tree Automt. In Biermn, G.M., Koh, C., es.: DPL 05. Volume 3774 o LNCS., Springer (2005)
Lecture 6: Coding theory
 Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
Data Structures LECTURE 10. Huffman coding. Example. Coding: problem definition
 Dt Strutures, Spring 24 L. Joskowiz Dt Strutures LEURE Humn oing Motivtion Uniquel eipherle oes Prei oes Humn oe onstrution Etensions n pplitions hpter 6.3 pp 385 392 in tetook Motivtion Suppose we wnt
Dt Strutures, Spring 24 L. Joskowiz Dt Strutures LEURE Humn oing Motivtion Uniquel eipherle oes Prei oes Humn oe onstrution Etensions n pplitions hpter 6.3 pp 385 392 in tetook Motivtion Suppose we wnt
CS 491G Combinatorial Optimization Lecture Notes
 CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
Compression vs Queryability - A Case Study
 Compression vs Queryility - A Cse Stuy Siv Annthrmn To ite this version: Siv Annthrmn. Compression vs Queryility - A Cse Stuy. Dgstuhl Seminr 08621, Jun 2008, Dgstuhl, Germny. http://rops.gstuhl.e/opus/volltexte/2008/1676,
Compression vs Queryility - A Cse Stuy Siv Annthrmn To ite this version: Siv Annthrmn. Compression vs Queryility - A Cse Stuy. Dgstuhl Seminr 08621, Jun 2008, Dgstuhl, Germny. http://rops.gstuhl.e/opus/volltexte/2008/1676,
CIT 596 Theory of Computation 1. Graphs and Digraphs
 CIT 596 Theory of Computtion 1 A grph G = (V (G), E(G)) onsists of two finite sets: V (G), the vertex set of the grph, often enote y just V, whih is nonempty set of elements lle verties, n E(G), the ege
CIT 596 Theory of Computtion 1 A grph G = (V (G), E(G)) onsists of two finite sets: V (G), the vertex set of the grph, often enote y just V, whih is nonempty set of elements lle verties, n E(G), the ege
Compression of Palindromes and Regularity.
 Compression of Plinromes n Regulrity. Kyoko Shikishim-Tsuji Center for Lierl Arts Eution n Reserh Tenri University 1 Introution In [1], property of likstrem t t view of tse is isusse n it is shown tht
Compression of Plinromes n Regulrity. Kyoko Shikishim-Tsuji Center for Lierl Arts Eution n Reserh Tenri University 1 Introution In [1], property of likstrem t t view of tse is isusse n it is shown tht
CS311 Computational Structures Regular Languages and Regular Grammars. Lecture 6
 CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
Necessary and sucient conditions for some two. Abstract. Further we show that the necessary conditions for the existence of an OD(44 s 1 s 2 )
 Neessry n suient onitions for some two vrile orthogonl esigns in orer 44 C. Koukouvinos, M. Mitrouli y, n Jennifer Seerry z Deite to Professor Anne Penfol Street Astrt We give new lgorithm whih llows us
Neessry n suient onitions for some two vrile orthogonl esigns in orer 44 C. Koukouvinos, M. Mitrouli y, n Jennifer Seerry z Deite to Professor Anne Penfol Street Astrt We give new lgorithm whih llows us
Lecture 11 Binary Decision Diagrams (BDDs)
 C 474A/57A Computer-Aie Logi Design Leture Binry Deision Digrms (BDDs) C 474/575 Susn Lyseky o 3 Boolen Logi untions Representtions untion n e represente in ierent wys ruth tle, eqution, K-mp, iruit, et
C 474A/57A Computer-Aie Logi Design Leture Binry Deision Digrms (BDDs) C 474/575 Susn Lyseky o 3 Boolen Logi untions Representtions untion n e represente in ierent wys ruth tle, eqution, K-mp, iruit, et
Counting Paths Between Vertices. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs
 Isomorphism of Grphs Definition The simple grphs G 1 = (V 1, E 1 ) n G = (V, E ) re isomorphi if there is ijetion (n oneto-one n onto funtion) f from V 1 to V with the property tht n re jent in G 1 if
Isomorphism of Grphs Definition The simple grphs G 1 = (V 1, E 1 ) n G = (V, E ) re isomorphi if there is ijetion (n oneto-one n onto funtion) f from V 1 to V with the property tht n re jent in G 1 if
2.4 Theoretical Foundations
 2 Progrmming Lnguge Syntx 2.4 Theoretil Fountions As note in the min text, snners n prsers re se on the finite utomt n pushown utomt tht form the ottom two levels of the Chomsky lnguge hierrhy. At eh level
2 Progrmming Lnguge Syntx 2.4 Theoretil Fountions As note in the min text, snners n prsers re se on the finite utomt n pushown utomt tht form the ottom two levels of the Chomsky lnguge hierrhy. At eh level
XML and Databases. Exam Preperation Discuss Answers to last year s exam. Sebastian Maneth NICTA and UNSW
 XML n Dtses Exm Prepertion Disuss Answers to lst yer s exm Sestin Mneth NICTA n UNSW CSE@UNSW -- Semester 1, 2008 (1) For eh of the following, explin why it is not well-forme XML (is WFC or the XML grmmr
XML n Dtses Exm Prepertion Disuss Answers to lst yer s exm Sestin Mneth NICTA n UNSW CSE@UNSW -- Semester 1, 2008 (1) For eh of the following, explin why it is not well-forme XML (is WFC or the XML grmmr
Solutions to Problem Set #1
 CSE 233 Spring, 2016 Solutions to Prolem Set #1 1. The movie tse onsists of the following two reltions movie: title, iretor, tor sheule: theter, title The first reltion provies titles, iretors, n tors
CSE 233 Spring, 2016 Solutions to Prolem Set #1 1. The movie tse onsists of the following two reltions movie: title, iretor, tor sheule: theter, title The first reltion provies titles, iretors, n tors
Solutions for HW9. Bipartite: put the red vertices in V 1 and the black in V 2. Not bipartite!
 Solutions for HW9 Exerise 28. () Drw C 6, W 6 K 6, n K 5,3. C 6 : W 6 : K 6 : K 5,3 : () Whih of the following re iprtite? Justify your nswer. Biprtite: put the re verties in V 1 n the lk in V 2. Biprtite:
Solutions for HW9 Exerise 28. () Drw C 6, W 6 K 6, n K 5,3. C 6 : W 6 : K 6 : K 5,3 : () Whih of the following re iprtite? Justify your nswer. Biprtite: put the re verties in V 1 n the lk in V 2. Biprtite:
Technische Universität München Winter term 2009/10 I7 Prof. J. Esparza / J. Křetínský / M. Luttenberger 11. Februar Solution
 Tehnishe Universität Münhen Winter term 29/ I7 Prof. J. Esprz / J. Křetínský / M. Luttenerger. Ferur 2 Solution Automt nd Forml Lnguges Homework 2 Due 5..29. Exerise 2. Let A e the following finite utomton:
Tehnishe Universität Münhen Winter term 29/ I7 Prof. J. Esprz / J. Křetínský / M. Luttenerger. Ferur 2 Solution Automt nd Forml Lnguges Homework 2 Due 5..29. Exerise 2. Let A e the following finite utomton:
CS 573 Automata Theory and Formal Languages
 Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Parse trees, ambiguity, and Chomsky normal form
 Prse trees, miguity, nd Chomsky norml form In this lecture we will discuss few importnt notions connected with contextfree grmmrs, including prse trees, miguity, nd specil form for context-free grmmrs
Prse trees, miguity, nd Chomsky norml form In this lecture we will discuss few importnt notions connected with contextfree grmmrs, including prse trees, miguity, nd specil form for context-free grmmrs
Finite State Automata and Determinisation
 Finite Stte Automt nd Deterministion Tim Dworn Jnury, 2016 Lnguges fs nf re df Deterministion 2 Outline 1 Lnguges 2 Finite Stte Automt (fs) 3 Non-deterministi Finite Stte Automt (nf) 4 Regulr Expressions
Finite Stte Automt nd Deterministion Tim Dworn Jnury, 2016 Lnguges fs nf re df Deterministion 2 Outline 1 Lnguges 2 Finite Stte Automt (fs) 3 Non-deterministi Finite Stte Automt (nf) 4 Regulr Expressions
I 3 2 = I I 4 = 2A
 ECE 210 Eletril Ciruit Anlysis University of llinois t Chigo 2.13 We re ske to use KCL to fin urrents 1 4. The key point in pplying KCL in this prolem is to strt with noe where only one of the urrents
ECE 210 Eletril Ciruit Anlysis University of llinois t Chigo 2.13 We re ske to use KCL to fin urrents 1 4. The key point in pplying KCL in this prolem is to strt with noe where only one of the urrents
Lecture 8: Abstract Algebra
 Mth 94 Professor: Pri Brtlett Leture 8: Astrt Alger Week 8 UCSB 2015 This is the eighth week of the Mthemtis Sujet Test GRE prep ourse; here, we run very rough-n-tumle review of strt lger! As lwys, this
Mth 94 Professor: Pri Brtlett Leture 8: Astrt Alger Week 8 UCSB 2015 This is the eighth week of the Mthemtis Sujet Test GRE prep ourse; here, we run very rough-n-tumle review of strt lger! As lwys, this
The DOACROSS statement
 The DOACROSS sttement Is prllel loop similr to DOALL, ut it llows prouer-onsumer type of synhroniztion. Synhroniztion is llowe from lower to higher itertions sine it is ssume tht lower itertions re selete
The DOACROSS sttement Is prllel loop similr to DOALL, ut it llows prouer-onsumer type of synhroniztion. Synhroniztion is llowe from lower to higher itertions sine it is ssume tht lower itertions re selete
Minimal DFA. minimal DFA for L starting from any other
 Miniml DFA Among the mny DFAs ccepting the sme regulr lnguge L, there is exctly one (up to renming of sttes) which hs the smllest possile numer of sttes. Moreover, it is possile to otin tht miniml DFA
Miniml DFA Among the mny DFAs ccepting the sme regulr lnguge L, there is exctly one (up to renming of sttes) which hs the smllest possile numer of sttes. Moreover, it is possile to otin tht miniml DFA
Mid-Term Examination - Spring 2014 Mathematical Programming with Applications to Economics Total Score: 45; Time: 3 hours
 Mi-Term Exmintion - Spring 0 Mthemtil Progrmming with Applitions to Eonomis Totl Sore: 5; Time: hours. Let G = (N, E) e irete grph. Define the inegree of vertex i N s the numer of eges tht re oming into
Mi-Term Exmintion - Spring 0 Mthemtil Progrmming with Applitions to Eonomis Totl Sore: 5; Time: hours. Let G = (N, E) e irete grph. Define the inegree of vertex i N s the numer of eges tht re oming into
Nondeterministic Automata vs Deterministic Automata
 Nondeterministi Automt vs Deterministi Automt We lerned tht NFA is onvenient model for showing the reltionships mong regulr grmmrs, FA, nd regulr expressions, nd designing them. However, we know tht n
Nondeterministi Automt vs Deterministi Automt We lerned tht NFA is onvenient model for showing the reltionships mong regulr grmmrs, FA, nd regulr expressions, nd designing them. However, we know tht n
Graph Algorithms. Vertex set = { a,b,c,d } Edge set = { {a,c}, {b,c}, {c,d}, {b,d}} Figure 1: An example for a simple graph
 Inin Institute of Informtion Tehnology Design n Mnufturing, Knheepurm, Chenni 00, Ini An Autonomous Institute uner MHRD, Govt of Ini http://www.iiitm..in COM 0T Design n Anlysis of Algorithms -Leture Notes
Inin Institute of Informtion Tehnology Design n Mnufturing, Knheepurm, Chenni 00, Ini An Autonomous Institute uner MHRD, Govt of Ini http://www.iiitm..in COM 0T Design n Anlysis of Algorithms -Leture Notes
Formal Languages and Automata
 Moile Computing nd Softwre Engineering p. 1/5 Forml Lnguges nd Automt Chpter 2 Finite Automt Chun-Ming Liu cmliu@csie.ntut.edu.tw Deprtment of Computer Science nd Informtion Engineering Ntionl Tipei University
Moile Computing nd Softwre Engineering p. 1/5 Forml Lnguges nd Automt Chpter 2 Finite Automt Chun-Ming Liu cmliu@csie.ntut.edu.tw Deprtment of Computer Science nd Informtion Engineering Ntionl Tipei University
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
Introduction to Olympiad Inequalities
 Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Assignment 1 Automata, Languages, and Computability. 1 Finite State Automata and Regular Languages
 Deprtment of Computer Science, Austrlin Ntionl University COMP2600 Forml Methods for Softwre Engineering Semester 2, 206 Assignment Automt, Lnguges, nd Computility Smple Solutions Finite Stte Automt nd
Deprtment of Computer Science, Austrlin Ntionl University COMP2600 Forml Methods for Softwre Engineering Semester 2, 206 Assignment Automt, Lnguges, nd Computility Smple Solutions Finite Stte Automt nd
Project 6: Minigoals Towards Simplifying and Rewriting Expressions
 MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
Grammar. Languages. Content 5/10/16. Automata and Languages. Regular Languages. Regular Languages
 5//6 Grmmr Automt nd Lnguges Regulr Grmmr Context-free Grmmr Context-sensitive Grmmr Prof. Mohmed Hmd Softwre Engineering L. The University of Aizu Jpn Regulr Lnguges Context Free Lnguges Context Sensitive
5//6 Grmmr Automt nd Lnguges Regulr Grmmr Context-free Grmmr Context-sensitive Grmmr Prof. Mohmed Hmd Softwre Engineering L. The University of Aizu Jpn Regulr Lnguges Context Free Lnguges Context Sensitive
Laboratory for Foundations of Computer Science. An Unfolding Approach. University of Edinburgh. Model Checking. Javier Esparza
 An Unfoling Approh to Moel Cheking Jvier Esprz Lbortory for Fountions of Computer Siene University of Einburgh Conurrent progrms Progrm: tuple P T 1 T n of finite lbelle trnsition systems T i A i S i i
An Unfoling Approh to Moel Cheking Jvier Esprz Lbortory for Fountions of Computer Siene University of Einburgh Conurrent progrms Progrm: tuple P T 1 T n of finite lbelle trnsition systems T i A i S i i
XML and Databases. Outline. 1. Top-Down Evaluation of Simple Paths. 1. Top-Down Evaluation of Simple Paths. 1. Top-Down Evaluation of Simple Paths
 Outline Leture Effiient XPth Evlution XML n Dtses. Top-Down Evlution of simple pths. Noe Sets only: Core XPth. Bottom-Up Evlution of Core XPth. Polynomil Time Evlution of Full XPth Sestin Mneth NICTA n
Outline Leture Effiient XPth Evlution XML n Dtses. Top-Down Evlution of simple pths. Noe Sets only: Core XPth. Bottom-Up Evlution of Core XPth. Polynomil Time Evlution of Full XPth Sestin Mneth NICTA n
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
MAT 403 NOTES 4. f + f =
 MAT 403 NOTES 4 1. Fundmentl Theorem o Clulus We will proo more generl version o the FTC thn the textook. But just like the textook, we strt with the ollowing proposition. Let R[, ] e the set o Riemnn
MAT 403 NOTES 4 1. Fundmentl Theorem o Clulus We will proo more generl version o the FTC thn the textook. But just like the textook, we strt with the ollowing proposition. Let R[, ] e the set o Riemnn
Automata and Regular Languages
 Chpter 9 Automt n Regulr Lnguges 9. Introution This hpter looks t mthemtil moels of omputtion n lnguges tht esrie them. The moel-lnguge reltionship hs multiple levels. We shll explore the simplest level,
Chpter 9 Automt n Regulr Lnguges 9. Introution This hpter looks t mthemtil moels of omputtion n lnguges tht esrie them. The moel-lnguge reltionship hs multiple levels. We shll explore the simplest level,
Coalgebra, Lecture 15: Equations for Deterministic Automata
 Colger, Lecture 15: Equtions for Deterministic Automt Julin Slmnc (nd Jurrin Rot) Decemer 19, 2016 In this lecture, we will study the concept of equtions for deterministic utomt. The notes re self contined
Colger, Lecture 15: Equtions for Deterministic Automt Julin Slmnc (nd Jurrin Rot) Decemer 19, 2016 In this lecture, we will study the concept of equtions for deterministic utomt. The notes re self contined
Lecture 08: Feb. 08, 2019
 4CS4-6:Theory of Computtion(Closure on Reg. Lngs., regex to NDFA, DFA to regex) Prof. K.R. Chowdhry Lecture 08: Fe. 08, 2019 : Professor of CS Disclimer: These notes hve not een sujected to the usul scrutiny
4CS4-6:Theory of Computtion(Closure on Reg. Lngs., regex to NDFA, DFA to regex) Prof. K.R. Chowdhry Lecture 08: Fe. 08, 2019 : Professor of CS Disclimer: These notes hve not een sujected to the usul scrutiny
NON-DETERMINISTIC FSA
 Tw o types of non-determinism: NON-DETERMINISTIC FS () Multiple strt-sttes; strt-sttes S Q. The lnguge L(M) ={x:x tkes M from some strt-stte to some finl-stte nd ll of x is proessed}. The string x = is
Tw o types of non-determinism: NON-DETERMINISTIC FS () Multiple strt-sttes; strt-sttes S Q. The lnguge L(M) ={x:x tkes M from some strt-stte to some finl-stte nd ll of x is proessed}. The string x = is
On a Class of Planar Graphs with Straight-Line Grid Drawings on Linear Area
 Journl of Grph Algorithms n Applitions http://jg.info/ vol. 13, no. 2, pp. 153 177 (2009) On Clss of Plnr Grphs with Stright-Line Gri Drwings on Liner Are M. Rezul Krim 1,2 M. Siur Rhmn 1 1 Deprtment of
Journl of Grph Algorithms n Applitions http://jg.info/ vol. 13, no. 2, pp. 153 177 (2009) On Clss of Plnr Grphs with Stright-Line Gri Drwings on Liner Are M. Rezul Krim 1,2 M. Siur Rhmn 1 1 Deprtment of
22: Union Find. CS 473u - Algorithms - Spring April 14, We want to maintain a collection of sets, under the operations of:
 22: Union Fin CS 473u - Algorithms - Spring 2005 April 14, 2005 1 Union-Fin We wnt to mintin olletion of sets, uner the opertions of: 1. MkeSet(x) - rete set tht ontins the single element x. 2. Fin(x)
22: Union Fin CS 473u - Algorithms - Spring 2005 April 14, 2005 1 Union-Fin We wnt to mintin olletion of sets, uner the opertions of: 1. MkeSet(x) - rete set tht ontins the single element x. 2. Fin(x)
On the Spectra of Bipartite Directed Subgraphs of K 4
 On the Spetr of Biprtite Direte Sugrphs of K 4 R. C. Bunge, 1 S. I. El-Znti, 1, H. J. Fry, 1 K. S. Kruss, 2 D. P. Roerts, 3 C. A. Sullivn, 4 A. A. Unsiker, 5 N. E. Witt 6 1 Illinois Stte University, Norml,
On the Spetr of Biprtite Direte Sugrphs of K 4 R. C. Bunge, 1 S. I. El-Znti, 1, H. J. Fry, 1 K. S. Kruss, 2 D. P. Roerts, 3 C. A. Sullivn, 4 A. A. Unsiker, 5 N. E. Witt 6 1 Illinois Stte University, Norml,
Chapter 3. Vector Spaces. 3.1 Images and Image Arithmetic
 Chpter 3 Vetor Spes In Chpter 2, we sw tht the set of imges possessed numer of onvenient properties. It turns out tht ny set tht possesses similr onvenient properties n e nlyzed in similr wy. In liner
Chpter 3 Vetor Spes In Chpter 2, we sw tht the set of imges possessed numer of onvenient properties. It turns out tht ny set tht possesses similr onvenient properties n e nlyzed in similr wy. In liner
Proportions: A ratio is the quotient of two numbers. For example, 2 3
 Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx
![for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx](/thumbs/74/70408252.jpg) Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
Implication Graphs and Logic Testing
 Implition Grphs n Logi Testing Vishwni D. Agrwl Jmes J. Dnher Professor Dept. of ECE, Auurn University Auurn, AL 36849 vgrwl@eng.uurn.eu www.eng.uurn.eu/~vgrwl Joint reserh with: K. K. Dve, ATI Reserh,
Implition Grphs n Logi Testing Vishwni D. Agrwl Jmes J. Dnher Professor Dept. of ECE, Auurn University Auurn, AL 36849 vgrwl@eng.uurn.eu www.eng.uurn.eu/~vgrwl Joint reserh with: K. K. Dve, ATI Reserh,
The University of Nottingham SCHOOL OF COMPUTER SCIENCE A LEVEL 2 MODULE, SPRING SEMESTER MACHINES AND THEIR LANGUAGES ANSWERS
 The University of ottinghm SCHOOL OF COMPUTR SCIC A LVL 2 MODUL, SPRIG SMSTR 2015 2016 MACHIS AD THIR LAGUAGS ASWRS Time llowed TWO hours Cndidtes my omplete the front over of their nswer ook nd sign their
The University of ottinghm SCHOOL OF COMPUTR SCIC A LVL 2 MODUL, SPRIG SMSTR 2015 2016 MACHIS AD THIR LAGUAGS ASWRS Time llowed TWO hours Cndidtes my omplete the front over of their nswer ook nd sign their
Chapter 4 State-Space Planning
 Leture slides for Automted Plnning: Theory nd Prtie Chpter 4 Stte-Spe Plnning Dn S. Nu CMSC 722, AI Plnning University of Mrylnd, Spring 2008 1 Motivtion Nerly ll plnning proedures re serh proedures Different
Leture slides for Automted Plnning: Theory nd Prtie Chpter 4 Stte-Spe Plnning Dn S. Nu CMSC 722, AI Plnning University of Mrylnd, Spring 2008 1 Motivtion Nerly ll plnning proedures re serh proedures Different
Maximum size of a minimum watching system and the graphs achieving the bound
 Mximum size of minimum wthing system n the grphs hieving the oun Tille mximum un système e ontrôle minimum et les grphes tteignnt l orne Dvi Auger Irène Chron Olivier Hury Antoine Lostein 00D0 Mrs 00 Déprtement
Mximum size of minimum wthing system n the grphs hieving the oun Tille mximum un système e ontrôle minimum et les grphes tteignnt l orne Dvi Auger Irène Chron Olivier Hury Antoine Lostein 00D0 Mrs 00 Déprtement
1 Nondeterministic Finite Automata
 1 Nondeterministic Finite Automt Suppose in life, whenever you hd choice, you could try oth possiilities nd live your life. At the end, you would go ck nd choose the one tht worked out the est. Then you
1 Nondeterministic Finite Automt Suppose in life, whenever you hd choice, you could try oth possiilities nd live your life. At the end, you would go ck nd choose the one tht worked out the est. Then you
Factorising FACTORISING.
 Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
CS 330 Formal Methods and Models
 CS 330 Forml Methods nd Models Dn Richrds, George Mson University, Spring 2017 Quiz Solutions Quiz 1, Propositionl Logic Dte: Ferury 2 1. Prove ((( p q) q) p) is tutology () (3pts) y truth tle. p q p q
CS 330 Forml Methods nd Models Dn Richrds, George Mson University, Spring 2017 Quiz Solutions Quiz 1, Propositionl Logic Dte: Ferury 2 1. Prove ((( p q) q) p) is tutology () (3pts) y truth tle. p q p q
arxiv: v2 [math.co] 31 Oct 2016
![arxiv: v2 [math.co] 31 Oct 2016 arxiv: v2 [math.co] 31 Oct 2016](/thumbs/96/127000397.jpg) On exlue minors of onnetivity 2 for the lss of frme mtrois rxiv:1502.06896v2 [mth.co] 31 Ot 2016 Mtt DeVos Dryl Funk Irene Pivotto Astrt We investigte the set of exlue minors of onnetivity 2 for the lss
On exlue minors of onnetivity 2 for the lss of frme mtrois rxiv:1502.06896v2 [mth.co] 31 Ot 2016 Mtt DeVos Dryl Funk Irene Pivotto Astrt We investigte the set of exlue minors of onnetivity 2 for the lss
Tree Pattern Aggregation for Scalable XML Data Dissemination
 Tree Pttern Aggregtion or Slle XML Dt Dissemintion Chee-Yong Chn, Wenei Fn, Psl Feler, Minos Grolkis, Rjeev Rstogi Bell Ls, Luent Tehnologies yhn,wenei,minos,rstogi @reserh.ell-ls.om, Psl.Feler@eureom.r
Tree Pttern Aggregtion or Slle XML Dt Dissemintion Chee-Yong Chn, Wenei Fn, Psl Feler, Minos Grolkis, Rjeev Rstogi Bell Ls, Luent Tehnologies yhn,wenei,minos,rstogi @reserh.ell-ls.om, Psl.Feler@eureom.r
Graph Theory. Simple Graph G = (V, E). V={a,b,c,d,e,f,g,h,k} E={(a,b),(a,g),( a,h),(a,k),(b,c),(b,k),...,(h,k)}
 Grph Theory Simple Grph G = (V, E). V ={verties}, E={eges}. h k g f e V={,,,,e,f,g,h,k} E={(,),(,g),(,h),(,k),(,),(,k),...,(h,k)} E =16. 1 Grph or Multi-Grph We llow loops n multiple eges. G = (V, E.ψ)
Grph Theory Simple Grph G = (V, E). V ={verties}, E={eges}. h k g f e V={,,,,e,f,g,h,k} E={(,),(,g),(,h),(,k),(,),(,k),...,(h,k)} E =16. 1 Grph or Multi-Grph We llow loops n multiple eges. G = (V, E.ψ)
Linear Inequalities. Work Sheet 1
 Work Sheet 1 Liner Inequlities Rent--Hep, cr rentl compny,chrges $ 15 per week plus $ 0.0 per mile to rent one of their crs. Suppose you re limited y how much money you cn spend for the week : You cn spend
Work Sheet 1 Liner Inequlities Rent--Hep, cr rentl compny,chrges $ 15 per week plus $ 0.0 per mile to rent one of their crs. Suppose you re limited y how much money you cn spend for the week : You cn spend
p-adic Egyptian Fractions
 p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
POSITIVE IMPLICATIVE AND ASSOCIATIVE FILTERS OF LATTICE IMPLICATION ALGEBRAS
 Bull. Koren Mth. So. 35 (998), No., pp. 53 6 POSITIVE IMPLICATIVE AND ASSOCIATIVE FILTERS OF LATTICE IMPLICATION ALGEBRAS YOUNG BAE JUN*, YANG XU AND KEYUN QIN ABSTRACT. We introue the onepts of positive
Bull. Koren Mth. So. 35 (998), No., pp. 53 6 POSITIVE IMPLICATIVE AND ASSOCIATIVE FILTERS OF LATTICE IMPLICATION ALGEBRAS YOUNG BAE JUN*, YANG XU AND KEYUN QIN ABSTRACT. We introue the onepts of positive
Regular expressions, Finite Automata, transition graphs are all the same!!
 CSI 3104 /Winter 2011: Introduction to Forml Lnguges Chpter 7: Kleene s Theorem Chpter 7: Kleene s Theorem Regulr expressions, Finite Automt, trnsition grphs re ll the sme!! Dr. Neji Zgui CSI3104-W11 1
CSI 3104 /Winter 2011: Introduction to Forml Lnguges Chpter 7: Kleene s Theorem Chpter 7: Kleene s Theorem Regulr expressions, Finite Automt, trnsition grphs re ll the sme!! Dr. Neji Zgui CSI3104-W11 1
Common intervals of genomes. Mathieu Raffinot CNRS LIAFA
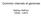 Common intervls of genomes Mthieu Rffinot CNRS LIF Context: omprtive genomis. set of genomes prtilly/totlly nnotte Informtive group of genes or omins? Ex: COG tse Mny iffiulties! iology Wht re two similr
Common intervls of genomes Mthieu Rffinot CNRS LIF Context: omprtive genomis. set of genomes prtilly/totlly nnotte Informtive group of genes or omins? Ex: COG tse Mny iffiulties! iology Wht re two similr
CSC2542 State-Space Planning
 CSC2542 Stte-Spe Plnning Sheil MIlrith Deprtment of Computer Siene University of Toronto Fll 2010 1 Aknowlegements Some the slies use in this ourse re moifitions of Dn Nu s leture slies for the textook
CSC2542 Stte-Spe Plnning Sheil MIlrith Deprtment of Computer Siene University of Toronto Fll 2010 1 Aknowlegements Some the slies use in this ourse re moifitions of Dn Nu s leture slies for the textook
Determinants. x 1 y 2 z 3 + x 2 y 3 z 1 + x 3 y 1 z 2 x 1 y 3 z 2 + x 2 y 1 z 3 + x 3 y 2 z 1 = 0,
 6 Determinnts One person s onstnt is nother person s vrile. Susn Gerhrt While the previous hpters h their ous on the explortion o the logi n struturl properties o projetive plnes this hpter will ous on
6 Determinnts One person s onstnt is nother person s vrile. Susn Gerhrt While the previous hpters h their ous on the explortion o the logi n struturl properties o projetive plnes this hpter will ous on
6.5 Improper integrals
 Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Chapter 2 Finite Automata
 Chpter 2 Finite Automt 28 2.1 Introduction Finite utomt: first model of the notion of effective procedure. (They lso hve mny other pplictions). The concept of finite utomton cn e derived y exmining wht
Chpter 2 Finite Automt 28 2.1 Introduction Finite utomt: first model of the notion of effective procedure. (They lso hve mny other pplictions). The concept of finite utomton cn e derived y exmining wht
CS 360 Exam 2 Fall 2014 Name
 CS 360 Exm 2 Fll 2014 Nme 1. The lsses shown elow efine singly-linke list n stk. Write three ifferent O(n)-time versions of the reverse_print metho s speifie elow. Eh version of the metho shoul output
CS 360 Exm 2 Fll 2014 Nme 1. The lsses shown elow efine singly-linke list n stk. Write three ifferent O(n)-time versions of the reverse_print metho s speifie elow. Eh version of the metho shoul output
Nondeterministic Finite Automata
 Nondeterministi Finite utomt The Power of Guessing Tuesdy, Otoer 4, 2 Reding: Sipser.2 (first prt); Stoughton 3.3 3.5 S235 Lnguges nd utomt eprtment of omputer Siene Wellesley ollege Finite utomton (F)
Nondeterministi Finite utomt The Power of Guessing Tuesdy, Otoer 4, 2 Reding: Sipser.2 (first prt); Stoughton 3.3 3.5 S235 Lnguges nd utomt eprtment of omputer Siene Wellesley ollege Finite utomton (F)
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018
 Finite Automt Theory nd Forml Lnguges TMV027/DIT321 LP4 2018 Lecture 10 An Bove April 23rd 2018 Recp: Regulr Lnguges We cn convert between FA nd RE; Hence both FA nd RE ccept/generte regulr lnguges; More
Finite Automt Theory nd Forml Lnguges TMV027/DIT321 LP4 2018 Lecture 10 An Bove April 23rd 2018 Recp: Regulr Lnguges We cn convert between FA nd RE; Hence both FA nd RE ccept/generte regulr lnguges; More
Separable discrete functions: recognition and sufficient conditions
 Seprle isrete funtions: reognition n suffiient onitions Enre Boros Onřej Čepek Vlimir Gurvih Novemer 21, 217 rxiv:1711.6772v1 [mth.co] 17 Nov 217 Astrt A isrete funtion of n vriles is mpping g : X 1...
Seprle isrete funtions: reognition n suffiient onitions Enre Boros Onřej Čepek Vlimir Gurvih Novemer 21, 217 rxiv:1711.6772v1 [mth.co] 17 Nov 217 Astrt A isrete funtion of n vriles is mpping g : X 1...
Boolean Algebra cont. The digital abstraction
 Boolen Alger ont The igitl strtion Theorem: Asorption Lw For every pir o elements B. + =. ( + ) = Proo: () Ientity Distriutivity Commuttivity Theorem: For ny B + = Ientity () ulity. Theorem: Assoitive
Boolen Alger ont The igitl strtion Theorem: Asorption Lw For every pir o elements B. + =. ( + ) = Proo: () Ientity Distriutivity Commuttivity Theorem: For ny B + = Ientity () ulity. Theorem: Assoitive
= state, a = reading and q j
 4 Finite Automt CHAPTER 2 Finite Automt (FA) (i) Derterministi Finite Automt (DFA) A DFA, M Q, q,, F, Where, Q = set of sttes (finite) q Q = the strt/initil stte = input lphet (finite) (use only those
4 Finite Automt CHAPTER 2 Finite Automt (FA) (i) Derterministi Finite Automt (DFA) A DFA, M Q, q,, F, Where, Q = set of sttes (finite) q Q = the strt/initil stte = input lphet (finite) (use only those
GNFA GNFA GNFA GNFA GNFA
 DFA RE NFA DFA -NFA REX GNFA Definition GNFA A generlize noneterministic finite utomton (GNFA) is grph whose eges re lele y regulr expressions, with unique strt stte with in-egree, n unique finl stte with
DFA RE NFA DFA -NFA REX GNFA Definition GNFA A generlize noneterministic finite utomton (GNFA) is grph whose eges re lele y regulr expressions, with unique strt stte with in-egree, n unique finl stte with
F / x everywhere in some domain containing R. Then, + ). (10.4.1)
 0.4 Green's theorem in the plne Double integrls over plne region my be trnsforme into line integrls over the bounry of the region n onversely. This is of prtil interest beuse it my simplify the evlution
0.4 Green's theorem in the plne Double integrls over plne region my be trnsforme into line integrls over the bounry of the region n onversely. This is of prtil interest beuse it my simplify the evlution
Farey Fractions. Rickard Fernström. U.U.D.M. Project Report 2017:24. Department of Mathematics Uppsala University
 U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
Answers and Solutions to (Some Even Numbered) Suggested Exercises in Chapter 11 of Grimaldi s Discrete and Combinatorial Mathematics
 Answers n Solutions to (Some Even Numere) Suggeste Exercises in Chpter 11 o Grimli s Discrete n Comintoril Mthemtics Section 11.1 11.1.4. κ(g) = 2. Let V e = {v : v hs even numer o 1 s} n V o = {v : v
Answers n Solutions to (Some Even Numere) Suggeste Exercises in Chpter 11 o Grimli s Discrete n Comintoril Mthemtics Section 11.1 11.1.4. κ(g) = 2. Let V e = {v : v hs even numer o 1 s} n V o = {v : v
#A42 INTEGERS 11 (2011) ON THE CONDITIONED BINOMIAL COEFFICIENTS
 #A42 INTEGERS 11 (2011 ON THE CONDITIONED BINOMIAL COEFFICIENTS Liqun To Shool of Mthemtil Sienes, Luoyng Norml University, Luoyng, Chin lqto@lynuedun Reeived: 12/24/10, Revised: 5/11/11, Aepted: 5/16/11,
#A42 INTEGERS 11 (2011 ON THE CONDITIONED BINOMIAL COEFFICIENTS Liqun To Shool of Mthemtil Sienes, Luoyng Norml University, Luoyng, Chin lqto@lynuedun Reeived: 12/24/10, Revised: 5/11/11, Aepted: 5/16/11,
System Validation (IN4387) November 2, 2012, 14:00-17:00
 System Vlidtion (IN4387) Novemer 2, 2012, 14:00-17:00 Importnt Notes. The exmintion omprises 5 question in 4 pges. Give omplete explntion nd do not onfine yourself to giving the finl nswer. Good luk! Exerise
System Vlidtion (IN4387) Novemer 2, 2012, 14:00-17:00 Importnt Notes. The exmintion omprises 5 question in 4 pges. Give omplete explntion nd do not onfine yourself to giving the finl nswer. Good luk! Exerise
Model Reduction of Finite State Machines by Contraction
 Model Reduction of Finite Stte Mchines y Contrction Alessndro Giu Dip. di Ingegneri Elettric ed Elettronic, Università di Cgliri, Pizz d Armi, 09123 Cgliri, Itly Phone: +39-070-675-5892 Fx: +39-070-675-5900
Model Reduction of Finite Stte Mchines y Contrction Alessndro Giu Dip. di Ingegneri Elettric ed Elettronic, Università di Cgliri, Pizz d Armi, 09123 Cgliri, Itly Phone: +39-070-675-5892 Fx: +39-070-675-5900
Automata for Analyzing and Querying Compressed Documents Barbara FILA, LIFO, Orl eans (Fr.) Siva ANANTHARAMAN, LIFO, Orl eans (Fr.) Rapport No
 Automt for Anlyzing nd Querying Compressed Documents Brr FILA, LIFO, Orléns (Fr.) Siv ANANTHARAMAN, LIFO, Orléns (Fr.) Rpport N o 2006-03 Automt for Anlyzing nd Querying Compressed Documents Brr Fil, Siv
Automt for Anlyzing nd Querying Compressed Documents Brr FILA, LIFO, Orléns (Fr.) Siv ANANTHARAMAN, LIFO, Orléns (Fr.) Rpport N o 2006-03 Automt for Anlyzing nd Querying Compressed Documents Brr Fil, Siv
A Study on the Properties of Rational Triangles
 Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Section 2.3. Matrix Inverses
 Mtri lger Mtri nverses Setion.. Mtri nverses hree si opertions on mtries, ition, multiplition, n sutrtion, re nlogues for mtries of the sme opertions for numers. n this setion we introue the mtri nlogue
Mtri lger Mtri nverses Setion.. Mtri nverses hree si opertions on mtries, ition, multiplition, n sutrtion, re nlogues for mtries of the sme opertions for numers. n this setion we introue the mtri nlogue
CS 310 (sec 20) - Winter Final Exam (solutions) SOLUTIONS
 CS 310 (sec 20) - Winter 2003 - Finl Exm (solutions) SOLUTIONS 1. (Logic) Use truth tles to prove the following logicl equivlences: () p q (p p) (q q) () p q (p q) (p q) () p q p q p p q q (q q) (p p)
CS 310 (sec 20) - Winter 2003 - Finl Exm (solutions) SOLUTIONS 1. (Logic) Use truth tles to prove the following logicl equivlences: () p q (p p) (q q) () p q (p q) (p q) () p q p q p p q q (q q) (p p)
A Lower Bound for the Length of a Partial Transversal in a Latin Square, Revised Version
 A Lower Bound for the Length of Prtil Trnsversl in Ltin Squre, Revised Version Pooy Htmi nd Peter W. Shor Deprtment of Mthemtil Sienes, Shrif University of Tehnology, P.O.Bo 11365-9415, Tehrn, Irn Deprtment
A Lower Bound for the Length of Prtil Trnsversl in Ltin Squre, Revised Version Pooy Htmi nd Peter W. Shor Deprtment of Mthemtil Sienes, Shrif University of Tehnology, P.O.Bo 11365-9415, Tehrn, Irn Deprtment
18.06 Problem Set 4 Due Wednesday, Oct. 11, 2006 at 4:00 p.m. in 2-106
 8. Problem Set Due Wenesy, Ot., t : p.m. in - Problem Mony / Consier the eight vetors 5, 5, 5,..., () List ll of the one-element, linerly epenent sets forme from these. (b) Wht re the two-element, linerly
8. Problem Set Due Wenesy, Ot., t : p.m. in - Problem Mony / Consier the eight vetors 5, 5, 5,..., () List ll of the one-element, linerly epenent sets forme from these. (b) Wht re the two-element, linerly
Homework 3 Solutions
 CS 341: Foundtions of Computer Science II Prof. Mrvin Nkym Homework 3 Solutions 1. Give NFAs with the specified numer of sttes recognizing ech of the following lnguges. In ll cses, the lphet is Σ = {,1}.
CS 341: Foundtions of Computer Science II Prof. Mrvin Nkym Homework 3 Solutions 1. Give NFAs with the specified numer of sttes recognizing ech of the following lnguges. In ll cses, the lphet is Σ = {,1}.
MA10207B: ANALYSIS SECOND SEMESTER OUTLINE NOTES
 MA10207B: ANALYSIS SECOND SEMESTER OUTLINE NOTES CHARLIE COLLIER UNIVERSITY OF BATH These notes hve been typeset by Chrlie Collier nd re bsed on the leture notes by Adrin Hill nd Thoms Cottrell. These
MA10207B: ANALYSIS SECOND SEMESTER OUTLINE NOTES CHARLIE COLLIER UNIVERSITY OF BATH These notes hve been typeset by Chrlie Collier nd re bsed on the leture notes by Adrin Hill nd Thoms Cottrell. These
INTRODUCTION TO AUTOMATA THEORY
 Chpter 3 INTRODUCTION TO AUTOMATA THEORY In this hpter we stuy the most si strt moel of omputtion. This moel els with mhines tht hve finite memory pity. Setion 3. els with mhines tht operte eterministilly
Chpter 3 INTRODUCTION TO AUTOMATA THEORY In this hpter we stuy the most si strt moel of omputtion. This moel els with mhines tht hve finite memory pity. Setion 3. els with mhines tht operte eterministilly
Algorithms & Data Structures Homework 8 HS 18 Exercise Class (Room & TA): Submitted by: Peer Feedback by: Points:
 Eidgenössishe Tehnishe Hohshule Zürih Eole polytehnique fédérle de Zurih Politenio federle di Zurigo Federl Institute of Tehnology t Zurih Deprtement of Computer Siene. Novemer 0 Mrkus Püshel, Dvid Steurer
Eidgenössishe Tehnishe Hohshule Zürih Eole polytehnique fédérle de Zurih Politenio federle di Zurigo Federl Institute of Tehnology t Zurih Deprtement of Computer Siene. Novemer 0 Mrkus Püshel, Dvid Steurer
CSE 332. Sorting. Data Abstractions. CSE 332: Data Abstractions. QuickSort Cutoff 1. Where We Are 2. Bounding The MAXIMUM Problem 4
 Am Blnk Leture 13 Winter 2016 CSE 332 CSE 332: Dt Astrtions Sorting Dt Astrtions QuikSort Cutoff 1 Where We Are 2 For smll n, the reursion is wste. The onstnts on quik/merge sort re higher thn the ones
Am Blnk Leture 13 Winter 2016 CSE 332 CSE 332: Dt Astrtions Sorting Dt Astrtions QuikSort Cutoff 1 Where We Are 2 For smll n, the reursion is wste. The onstnts on quik/merge sort re higher thn the ones
Symmetrical Components 1
 Symmetril Components. Introdution These notes should e red together with Setion. of your text. When performing stedy-stte nlysis of high voltge trnsmission systems, we mke use of the per-phse equivlent
Symmetril Components. Introdution These notes should e red together with Setion. of your text. When performing stedy-stte nlysis of high voltge trnsmission systems, we mke use of the per-phse equivlent
1. For each of the following theorems, give a two or three sentence sketch of how the proof goes or why it is not true.
 York University CSE 2 Unit 3. DFA Clsses Converting etween DFA, NFA, Regulr Expressions, nd Extended Regulr Expressions Instructor: Jeff Edmonds Don t chet y looking t these nswers premturely.. For ech
York University CSE 2 Unit 3. DFA Clsses Converting etween DFA, NFA, Regulr Expressions, nd Extended Regulr Expressions Instructor: Jeff Edmonds Don t chet y looking t these nswers premturely.. For ech
Eigenvectors and Eigenvalues
 MTB 050 1 ORIGIN 1 Eigenvets n Eigenvlues This wksheet esries the lger use to lulte "prinipl" "hrteristi" iretions lle Eigenvets n the "prinipl" "hrteristi" vlues lle Eigenvlues ssoite with these iretions.
MTB 050 1 ORIGIN 1 Eigenvets n Eigenvlues This wksheet esries the lger use to lulte "prinipl" "hrteristi" iretions lle Eigenvets n the "prinipl" "hrteristi" vlues lle Eigenvlues ssoite with these iretions.
Linear Algebra Introduction
 Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
First Midterm Examination
 24-25 Fll Semester First Midterm Exmintion ) Give the stte digrm of DFA tht recognizes the lnguge A over lphet Σ = {, } where A = {w w contins or } 2) The following DFA recognizes the lnguge B over lphet
24-25 Fll Semester First Midterm Exmintion ) Give the stte digrm of DFA tht recognizes the lnguge A over lphet Σ = {, } where A = {w w contins or } 2) The following DFA recognizes the lnguge B over lphet
6.1 Definition of the Riemann Integral
 6 The Riemnn Integrl 6. Deinition o the Riemnn Integrl Deinition 6.. Given n intervl [, b] with < b, prtition P o [, b] is inite set o points {x, x,..., x n } [, b], lled grid points, suh tht x =, x n
6 The Riemnn Integrl 6. Deinition o the Riemnn Integrl Deinition 6.. Given n intervl [, b] with < b, prtition P o [, b] is inite set o points {x, x,..., x n } [, b], lled grid points, suh tht x =, x n
Logic, Set Theory and Computability [M. Coppenbarger]
![Logic, Set Theory and Computability [M. Coppenbarger] Logic, Set Theory and Computability [M. Coppenbarger]](/thumbs/90/103901048.jpg) 14 Orer (Hnout) Definition 7-11: A reltion is qusi-orering (or preorer) if it is reflexive n trnsitive. A quisi-orering tht is symmetri is n equivlene reltion. A qusi-orering tht is nti-symmetri is n orer
14 Orer (Hnout) Definition 7-11: A reltion is qusi-orering (or preorer) if it is reflexive n trnsitive. A quisi-orering tht is symmetri is n equivlene reltion. A qusi-orering tht is nti-symmetri is n orer
Foundations of XML Types: Tree Automata
 1 / 43 Foundtions of XML Types: Tree Automt Pierre Genevès CNRS (slides mostly sed on slides y W. Mrtens nd T. Schwentick) University of Grenole Alpes, 2017 2018 2 / 43 Why Tree Automt? Foundtions of XML
1 / 43 Foundtions of XML Types: Tree Automt Pierre Genevès CNRS (slides mostly sed on slides y W. Mrtens nd T. Schwentick) University of Grenole Alpes, 2017 2018 2 / 43 Why Tree Automt? Foundtions of XML
On Determinisation of History-Deterministic Automata.
 On Deterministion of History-Deterministic Automt. Denis Kupererg Mich l Skrzypczk University of Wrsw YR-ICALP 2014 Copenhgen Introduction Deterministic utomt re centrl tool in utomt theory: Polynomil
On Deterministion of History-Deterministic Automt. Denis Kupererg Mich l Skrzypczk University of Wrsw YR-ICALP 2014 Copenhgen Introduction Deterministic utomt re centrl tool in utomt theory: Polynomil
Analysis of Temporal Interactions with Link Streams and Stream Graphs
 Anlysis of Temporl Intertions with n Strem Grphs, Tiphine Vir, Clémene Mgnien http:// ltpy@ LIP6 CNRS n Soronne Université Pris, Frne 1/23 intertions over time 0 2 4 6 8,,, n for 10 time units time 2/23
Anlysis of Temporl Intertions with n Strem Grphs, Tiphine Vir, Clémene Mgnien http:// ltpy@ LIP6 CNRS n Soronne Université Pris, Frne 1/23 intertions over time 0 2 4 6 8,,, n for 10 time units time 2/23
CS 2204 DIGITAL LOGIC & STATE MACHINE DESIGN SPRING 2014
 S 224 DIGITAL LOGI & STATE MAHINE DESIGN SPRING 214 DUE : Mrh 27, 214 HOMEWORK III READ : Relte portions of hpters VII n VIII ASSIGNMENT : There re three questions. Solve ll homework n exm prolems s shown
S 224 DIGITAL LOGI & STATE MAHINE DESIGN SPRING 214 DUE : Mrh 27, 214 HOMEWORK III READ : Relte portions of hpters VII n VIII ASSIGNMENT : There re three questions. Solve ll homework n exm prolems s shown
Connectivity in Graphs. CS311H: Discrete Mathematics. Graph Theory II. Example. Paths. Connectedness. Example
 Connetiit in Grphs CSH: Disrete Mthemtis Grph Theor II Instrtor: Işıl Dillig Tpil qestion: Is it possile to get from some noe to nother noe? Emple: Trin netork if there is pth from to, possile to tke trin
Connetiit in Grphs CSH: Disrete Mthemtis Grph Theor II Instrtor: Işıl Dillig Tpil qestion: Is it possile to get from some noe to nother noe? Emple: Trin netork if there is pth from to, possile to tke trin
