Robotics. Islam S. M. Khalil. September 19, German University in Cairo
|
|
|
- Isabella Curtis
- 5 years ago
- Views:
Transcription
1 Robotics German University in Cairo September 19, 2016
2 Angular Velocity Let b l, b 2, and b 3 form a right-handed set of mutually perpendicular unit vectors fixed in a rigid body B moving in a reference frame A. The angular velocity of B in A, denoted by A ω B, is defined as A ω B b 1 A db 2 b 3 + b 2 A db 3 b 1 + b 3 A db 1 b 2 (1) One task facilitated by the use of angular velocity vectors is the time-differentiation of vectors fixed in a rigid body, for it enables one to obtain the first time-derivative of such a vector by performing a cross-multiplication. Specifically, if β is any vector fixed in B, then A dβ A ω B β (2)
3 Angular Velocity A ω B b 1 A db 2 A db 3 db 1 b 3 + b 2 b 1 + b 3 b 2 (3) A dβ A ω B β (4) Figure: Angular velocity of B with respect to A.
4 Angular Velocity Derivation Using dots to denote time-differentiation in A, one can rewrite (1) A ω B b 1 ḃ 2 b 3 + b 2 ḃ 3 b 1 + b 3 ḃ 1 b 2 (5) and cross-multiplication of (5) with b 1 gives We also know that A ω B b 1 b 2 b 1 ḃ 3 b 1 + b 3 b 1 ḃ 1 b 2 (6) b 2 b 3 b 1 b 3 b 1 b 2 (7) Substitution of (7) in (6) yields A ω B b 1 b 3 ḃ 3 b 1 + b 2 ḃ 1 b 2 (8)
5 Angular Velocity Derivation Moreover, time-differentiation of the equations b 1 b 1 1 and b 3 b 1 0 yields rewrite (8) ḃ 1 b 1 ḃ 3 b 1 ḃ 1 b 3 (9) A ω B b 1 b 1 ḃ 1 b 1 + b 2 ḃ 1 b 2 + b 3 ḃ 1 b 3 (10) But the right-hand member of this equation is simply a way of writing ḃ 1. A ω B b 1 ḃ1 (11) Similarly, A ω B b 2 ḃ 2 A ω B b 3 ḃ 3 (12) and, after expressing any vector β fixed in B as β β 1 b 1 + β 2 b 2 + β 3 b 3 (13)
6 Angular Velocity Derivation where β 1, β 2, and β 3 are constants, so that β β 1 ḃ 1 + β 2 ḃ 2 + β 3 ḃ 3 (14) Therefore, β β A 1 ω B b 1 + β A 2 ω B b 2 + β A 3 ω B b 3 (15) Finally we obtain β A ω B (β 1 b 1 + β 2 b 2 + β 3 b 3 ) A ω B β (16) Auxiliary Reference Frames β A ω B β (17)
7 Angular Velocity Example. Here B represents a door supported by hinges in a room A. Mutually perpendicular unit vectors a 1, a 2, and a 3 are fixed in A, with a 3 parallel to the axis of the hinges, and mutually perpendicular unit vectors b 1, b 2, and b 3 are fixed in B, with b 3 a 3.
8 Angular Velocity If θ is the radian measure of the angle between a 1 and b 1 as shown below, then a 1, a 2, and a 3 and b 1, b 2, and b 3 are related to each other as indicated in the table below b 1 b 2 b 3 a 1 cos θ -sin θ 0 a 2 sin θ cos θ 0 a The angular velocity of B in A, A ω B is given by A ω B θb 3 (18) The second time-derivative in A of the position vector from the point O to the point P, that is, of the vector β given by A β t β L 1 b 1 L 3 b 3 (19) The derivative of β in A is given by θb 3 ( L 1 b 1 L 3 b 3 ) L 1 θb 2 (20)
9 Angular Velocity A 2 β t 2 L 1 θb 2 L 1 θ A b 2 t Since b 2 is a vector fixed in B, its time-derivative in A can be found as follows: (21) A b 2 t A ω B b 2 θb 1 (22) Therefore, A 2 β ( t 2 L θ2 1 b 1 θb ) 2 (23) In more complex situations, that is, when the motion of B in A is more complicated than that of a door B in a room A, the use of the angular velocity vector as an operator which, through cross-multiplication, produces time-derivatives, is all the more advantageous.
10 Differentiation in Two Reference Frames If A and B are any two reference frames, the first time-derivatives of any vector v in A and in B are related to each other as follows: A dv B dv + A ω B v (24) where A ω B is the angular velocity of B in A. Derivation. Let us define a vector v in B so that 3 v v i b i (25) i1 The time-derivative of v in A is A dv 3 dv i b i + i1 B dv + 3 i1 v i A db i (26) 3 v A i ω B b i (27) i1
11 Differentiation in Two Reference Frames A dv 3 i1 B dv B dv B dv dv i b i i1 v i A db i (28) 3 v A i ω B b i (29) i1 + A ω B Differentiation in Two Reference Frames A dv B dv 3 v i b i (30) i1 + A ω B v (31) + A ω B v (32)
12 Auxiliary Reference Frames The angular velocity of a rigid body B in a reference frame A can be expressed in the following form involving n auxiliary reference frames A 1,..., A n : Auxiliary Reference Frames A ω B A ω A 1 + A 1 ω A A n 1 ω An + An ω B (33) The reference frames A 1,..., A n may or may not correspond to actual rigid bodies. Frequently, such reference frames are introduced as aids in analysis, but have no physical counterparts. Derivation. For any vector β fixed in B A dβ A ω B β A 1 dβ A 1 ω B β (34) A dβ A 1 dβ + A ω A 1 β (35)
13 Auxiliary Reference Frames Therefore, A ω B β A 1 ω B β + A ω A 1 β (36) Since this equation is satisfied by every β fixed in B, it implies that A ω B A 1 ω B + A ω A 1 (37) Proceeding similarly, one can verify that Auxiliary Reference Frames A ω B A ω A 1 + A 1 ω A A n 1 ω An + An ω B (38)
14 Angular Acceleration The angular acceleration A α B of a rigid body B in a reference frame A is defined as the first time-derivative in A of the angular velocity of B in A A α B A d A ω B (39) We also know that A dv B dv + A ω B v (40) A α B A d A ω B B d A ω B + A ω B A ω B B d A ω B (41) The angular velocity of B in A can always be expressed as A ω B ωk ω, where k ω is a unit vector parallel to A ω B ; similarly A α B can always be expressed as A α B αk α, where k α is a unit vector parallel to A α B. In general, k ω differs from k α.
15 Velocity and Acceleration Let p denote the position vector from any point O fixed in a reference frame A to a point P moving in A. The velocity of P in A and the acceleration of P in A, denoted by A v P and A a P 9 respectively, are defined as and A v P A dp A a P A d A v P (42) (43)
16 Velocity and Acceleration Example P 1 and P 2 designate two points connected by a line of length L and free to move in a plane B that is rotating at a constant rate ω about a line Y fixed both in B and in a reference frame A. The velocities A v P 1 and A v P 2 of P 1 and P 2 in A are to be expressed in terms of the quantities q 1, q 2, q 3 their time-derivatives q 1, q 2, q 3, and the mutually perpendicular unit vectors e x, e y, e z. Figure: Velocity.
17 Velocity and Acceleration Example The point O is fixed in A, and the position vector p 1 from O from P 1 is p 1 q 1 b x + q 2 b y (44) A v P 1 where A dp 1 B dp 1 + A ω B p 1 A dp 1 q 1 b x + q 2 b y A ω B p 1 ωb y (q 1 b x + q 2 b y ) ωq 1 b z Therefore, A v P 1 q 1 b x + q 2 b y ωq 1 b z (45) Figure: Velocity.
18 Velocity and Acceleration Example The unit vectors b x,y,z are related to the unit vectors e x,y,z e x e y e z b through x cos q 3 -sin q 3 0 b y sin q 3 cos q 3 0 b z A v P 1 ( q 1 cos q 3 + q 2 sin q 3 )e x +( q 1 sin q 3 + q 2 cos q 3 )e y ωq 1 e z which is the desired expression for the velocity of P 1 in A. Proceeding similary, one can determine the velocity of P 2 in A. Figure: Velocity.
19 Thank You Thank You! Questions please
Robotics. Islam S. M. Khalil. September 18, German University in Cairo
 Robotics German University in Cairo September 18, 2016 Vector Functions A vector v in a reference frame A depends on a scalar verifiable q. We can say that v is a vector function of q in A. Otherwise,
Robotics German University in Cairo September 18, 2016 Vector Functions A vector v in a reference frame A depends on a scalar verifiable q. We can say that v is a vector function of q in A. Otherwise,
Handout 6: Rotational motion and moment of inertia. Angular velocity and angular acceleration
 1 Handout 6: Rotational motion and moment of inertia Angular velocity and angular acceleration In Figure 1, a particle b is rotating about an axis along a circular path with radius r. The radius sweeps
1 Handout 6: Rotational motion and moment of inertia Angular velocity and angular acceleration In Figure 1, a particle b is rotating about an axis along a circular path with radius r. The radius sweeps
Dynamics 12e. Copyright 2010 Pearson Education South Asia Pte Ltd. Chapter 20 3D Kinematics of a Rigid Body
 Engineering Mechanics: Dynamics 12e Chapter 20 3D Kinematics of a Rigid Body Chapter Objectives Kinematics of a body subjected to rotation about a fixed axis and general plane motion. Relative-motion analysis
Engineering Mechanics: Dynamics 12e Chapter 20 3D Kinematics of a Rigid Body Chapter Objectives Kinematics of a body subjected to rotation about a fixed axis and general plane motion. Relative-motion analysis
Chapter 6: Vector Analysis
 Chapter 6: Vector Analysis We use derivatives and various products of vectors in all areas of physics. For example, Newton s 2nd law is F = m d2 r. In electricity dt 2 and magnetism, we need surface and
Chapter 6: Vector Analysis We use derivatives and various products of vectors in all areas of physics. For example, Newton s 2nd law is F = m d2 r. In electricity dt 2 and magnetism, we need surface and
The Cross Product. MATH 311, Calculus III. J. Robert Buchanan. Fall Department of Mathematics. J. Robert Buchanan The Cross Product
 The Cross Product MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Introduction Recall: the dot product of two vectors is a scalar. There is another binary operation on vectors
The Cross Product MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Introduction Recall: the dot product of two vectors is a scalar. There is another binary operation on vectors
!T = 2# T = 2! " The velocity and acceleration of the object are found by taking the first and second derivative of the position:
 A pendulum swinging back and forth or a mass oscillating on a spring are two examples of (SHM.) SHM occurs any time the position of an object as a function of time can be represented by a sine wave. We
A pendulum swinging back and forth or a mass oscillating on a spring are two examples of (SHM.) SHM occurs any time the position of an object as a function of time can be represented by a sine wave. We
9 Kinetics of 3D rigid bodies - rotating frames
 9 Kinetics of 3D rigid bodies - rotating frames 9. Consider the two gears depicted in the figure. The gear B of radius R B is fixed to the ground, while the gear A of mass m A and radius R A turns freely
9 Kinetics of 3D rigid bodies - rotating frames 9. Consider the two gears depicted in the figure. The gear B of radius R B is fixed to the ground, while the gear A of mass m A and radius R A turns freely
CBE 6333, R. Levicky 1. Orthogonal Curvilinear Coordinates
 CBE 6333, R. Levicky 1 Orthogonal Curvilinear Coordinates Introduction. Rectangular Cartesian coordinates are convenient when solving problems in which the geometry of a problem is well described by the
CBE 6333, R. Levicky 1 Orthogonal Curvilinear Coordinates Introduction. Rectangular Cartesian coordinates are convenient when solving problems in which the geometry of a problem is well described by the
RIGID BODY MOTION (Section 16.1)
 RIGID BODY MOTION (Section 16.1) There are cases where an object cannot be treated as a particle. In these cases the size or shape of the body must be considered. Rotation of the body about its center
RIGID BODY MOTION (Section 16.1) There are cases where an object cannot be treated as a particle. In these cases the size or shape of the body must be considered. Rotation of the body about its center
Lecture II: Rigid-Body Physics
 Rigid-Body Motion Previously: Point dimensionless objects moving through a trajectory. Today: Objects with dimensions, moving as one piece. 2 Rigid-Body Kinematics Objects as sets of points. Relative distances
Rigid-Body Motion Previously: Point dimensionless objects moving through a trajectory. Today: Objects with dimensions, moving as one piece. 2 Rigid-Body Kinematics Objects as sets of points. Relative distances
Rotational Motion and Torque
 Rotational Motion and Torque Introduction to Angular Quantities Sections 8- to 8-2 Introduction Rotational motion deals with spinning objects, or objects rotating around some point. Rotational motion is
Rotational Motion and Torque Introduction to Angular Quantities Sections 8- to 8-2 Introduction Rotational motion deals with spinning objects, or objects rotating around some point. Rotational motion is
REVIEW - Vectors. Vectors. Vector Algebra. Multiplication by a scalar
 J. Peraire Dynamics 16.07 Fall 2004 Version 1.1 REVIEW - Vectors By using vectors and defining appropriate operations between them, physical laws can often be written in a simple form. Since we will making
J. Peraire Dynamics 16.07 Fall 2004 Version 1.1 REVIEW - Vectors By using vectors and defining appropriate operations between them, physical laws can often be written in a simple form. Since we will making
CIRCULAR MOTION AND ROTATION
 1. UNIFORM CIRCULAR MOTION So far we have learned a great deal about linear motion. This section addresses rotational motion. The simplest kind of rotational motion is an object moving in a perfect circle
1. UNIFORM CIRCULAR MOTION So far we have learned a great deal about linear motion. This section addresses rotational motion. The simplest kind of rotational motion is an object moving in a perfect circle
General Definition of Torque, final. Lever Arm. General Definition of Torque 7/29/2010. Units of Chapter 10
 Units of Chapter 10 Determining Moments of Inertia Rotational Kinetic Energy Rotational Plus Translational Motion; Rolling Why Does a Rolling Sphere Slow Down? General Definition of Torque, final Taking
Units of Chapter 10 Determining Moments of Inertia Rotational Kinetic Energy Rotational Plus Translational Motion; Rolling Why Does a Rolling Sphere Slow Down? General Definition of Torque, final Taking
Kinematics. Professor Sanjay Sarma. September 12, 2007
 Kinematics Professor Sanjay Sarma September 12, 2007 1.0 What is Dynamics? The goal of the field of dynamics is to understand how mechanical systems move under the effect of forces. There are 3 components
Kinematics Professor Sanjay Sarma September 12, 2007 1.0 What is Dynamics? The goal of the field of dynamics is to understand how mechanical systems move under the effect of forces. There are 3 components
Karlstads University Faculty of Technology and Science Physics. Rolling constraints. Author: Henrik Jackman. Classical mechanics
 Karlstads University Faculty of Technology and Science Physics Rolling constraints Author: Henrik Jackman Classical mechanics 008-01-08 Introduction Rolling constraints are so called non-holonomic constraints.
Karlstads University Faculty of Technology and Science Physics Rolling constraints Author: Henrik Jackman Classical mechanics 008-01-08 Introduction Rolling constraints are so called non-holonomic constraints.
Lecture D16-2D Rigid Body Kinematics
 J. Peraire 16.07 Dynamics Fall 2004 Version 1.2 Lecture D16-2D Rigid Body Kinematics In this lecture, we will start from the general relative motion concepts introduced in lectures D11 and D12, and then
J. Peraire 16.07 Dynamics Fall 2004 Version 1.2 Lecture D16-2D Rigid Body Kinematics In this lecture, we will start from the general relative motion concepts introduced in lectures D11 and D12, and then
University of California, Berkeley Department of Mechanical Engineering ME 104, Fall Midterm Exam 1 Solutions
 University of California, Berkeley Department of Mechanical Engineering ME 104, Fall 2013 Midterm Exam 1 Solutions 1. (20 points) (a) For a particle undergoing a rectilinear motion, the position, velocity,
University of California, Berkeley Department of Mechanical Engineering ME 104, Fall 2013 Midterm Exam 1 Solutions 1. (20 points) (a) For a particle undergoing a rectilinear motion, the position, velocity,
Rotational Motion. Lecture 17. Chapter 10. Physics I Department of Physics and Applied Physics
 Lecture 17 Chapter 10 Physics I 04.0.014 otational Motion Torque Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi Lecture Capture: http://echo360.uml.edu/danylov013/physics1spring.html
Lecture 17 Chapter 10 Physics I 04.0.014 otational Motion Torque Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi Lecture Capture: http://echo360.uml.edu/danylov013/physics1spring.html
Robotics I. Figure 1: Initial placement of a rigid thin rod of length L in an absolute reference frame.
 Robotics I September, 7 Exercise Consider the rigid body in Fig., a thin rod of length L. The rod will be rotated by an angle α around the z axis, then by an angle β around the resulting x axis, and finally
Robotics I September, 7 Exercise Consider the rigid body in Fig., a thin rod of length L. The rod will be rotated by an angle α around the z axis, then by an angle β around the resulting x axis, and finally
Cross Product Angular Momentum
 Lecture 21 Chapter 12 Physics I Cross Product Angular Momentum Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi IN THIS CHAPTER, you will continue discussing rotational dynamics
Lecture 21 Chapter 12 Physics I Cross Product Angular Momentum Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi IN THIS CHAPTER, you will continue discussing rotational dynamics
Rotation of Rigid Objects
 Notes 12 Rotation and Extended Objects Page 1 Rotation of Rigid Objects Real objects have "extent". The mass is spread out over discrete or continuous positions. THERE IS A DISTRIBUTION OF MASS TO "AN
Notes 12 Rotation and Extended Objects Page 1 Rotation of Rigid Objects Real objects have "extent". The mass is spread out over discrete or continuous positions. THERE IS A DISTRIBUTION OF MASS TO "AN
1 DIFFERENTIATION OF VECTORS
 1 DIFFERENTIATION OF VECTORS The discipline of dynamics deals with changes of various kinds, such as changes in the position of a particle in a reference frame and changes in the configuration of a mechanical
1 DIFFERENTIATION OF VECTORS The discipline of dynamics deals with changes of various kinds, such as changes in the position of a particle in a reference frame and changes in the configuration of a mechanical
DEVIL PHYSICS BADDEST CLASS ON CAMPUS IB PHYSICS
 DEVIL PHYSICS BADDEST CLASS ON CAMPUS IB PHYSICS OPTION B-1A: ROTATIONAL DYNAMICS Essential Idea: The basic laws of mechanics have an extension when equivalent principles are applied to rotation. Actual
DEVIL PHYSICS BADDEST CLASS ON CAMPUS IB PHYSICS OPTION B-1A: ROTATIONAL DYNAMICS Essential Idea: The basic laws of mechanics have an extension when equivalent principles are applied to rotation. Actual
Rigid Object. Chapter 10. Angular Position. Angular Position. A rigid object is one that is nondeformable
 Rigid Object Chapter 10 Rotation of a Rigid Object about a Fixed Axis A rigid object is one that is nondeformable The relative locations of all particles making up the object remain constant All real objects
Rigid Object Chapter 10 Rotation of a Rigid Object about a Fixed Axis A rigid object is one that is nondeformable The relative locations of all particles making up the object remain constant All real objects
Vectors. J.R. Wilson. September 28, 2017
 Vectors J.R. Wilson September 28, 2017 This chapter introduces vectors that are used in many areas of physics (needed for classical physics this year). One complication is that a number of different forms
Vectors J.R. Wilson September 28, 2017 This chapter introduces vectors that are used in many areas of physics (needed for classical physics this year). One complication is that a number of different forms
For the instant shown, a) determine the angular velocity of link OA. b) determine the speed of D. c) determine the angular acceleration of link OA.
 ME 74 Fall 008 PROBLEM NO. 1 Given: mechanism is made up of lins O, B and BD, with all three lins joined at pin. Lin O is pinned to ground at end O, end D of D is constrained to vertical motion only, and
ME 74 Fall 008 PROBLEM NO. 1 Given: mechanism is made up of lins O, B and BD, with all three lins joined at pin. Lin O is pinned to ground at end O, end D of D is constrained to vertical motion only, and
Phys101 Lectures 19, 20 Rotational Motion
 Phys101 Lectures 19, 20 Rotational Motion Key points: Angular and Linear Quantities Rotational Dynamics; Torque and Moment of Inertia Rotational Kinetic Energy Ref: 10-1,2,3,4,5,6,8,9. Page 1 Angular Quantities
Phys101 Lectures 19, 20 Rotational Motion Key points: Angular and Linear Quantities Rotational Dynamics; Torque and Moment of Inertia Rotational Kinetic Energy Ref: 10-1,2,3,4,5,6,8,9. Page 1 Angular Quantities
Rotational Motion. Lecture 17. Chapter 10. Physics I Department of Physics and Applied Physics
 Lecture 17 Chapter 10 Physics I 11.13.2013 otational Motion Torque Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi Lecture Capture: http://echo360.uml.edu/danylov2013/physics1fall.html
Lecture 17 Chapter 10 Physics I 11.13.2013 otational Motion Torque Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi Lecture Capture: http://echo360.uml.edu/danylov2013/physics1fall.html
3 Space curvilinear motion, motion in non-inertial frames
 3 Space curvilinear motion, motion in non-inertial frames 3.1 In-class problem A rocket of initial mass m i is fired vertically up from earth and accelerates until its fuel is exhausted. The residual mass
3 Space curvilinear motion, motion in non-inertial frames 3.1 In-class problem A rocket of initial mass m i is fired vertically up from earth and accelerates until its fuel is exhausted. The residual mass
Angular momentum Vector product.
 Lecture 19 Chapter 11 Physics I 11.20.2013 Angular momentum Vector product. Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi Lecture Capture: http://echo360.uml.edu/danylov2013/physics1fall.html
Lecture 19 Chapter 11 Physics I 11.20.2013 Angular momentum Vector product. Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi Lecture Capture: http://echo360.uml.edu/danylov2013/physics1fall.html
5. Plane Kinetics of Rigid Bodies
 5. Plane Kinetics of Rigid Bodies 5.1 Mass moments of inertia 5.2 General equations of motion 5.3 Translation 5.4 Fixed axis rotation 5.5 General plane motion 5.6 Work and energy relations 5.7 Impulse
5. Plane Kinetics of Rigid Bodies 5.1 Mass moments of inertia 5.2 General equations of motion 5.3 Translation 5.4 Fixed axis rotation 5.5 General plane motion 5.6 Work and energy relations 5.7 Impulse
Lecture PowerPoints. Chapter 8 Physics: Principles with Applications, 6 th edition Giancoli
 Lecture PowerPoints Chapter 8 Physics: Principles with Applications, 6 th edition Giancoli 2005 Pearson Prentice Hall This work is protected by United States copyright laws and is provided solely for the
Lecture PowerPoints Chapter 8 Physics: Principles with Applications, 6 th edition Giancoli 2005 Pearson Prentice Hall This work is protected by United States copyright laws and is provided solely for the
Dynamics. Basilio Bona. Semester 1, DAUIN Politecnico di Torino. B. Bona (DAUIN) Dynamics Semester 1, / 18
 Dynamics Basilio Bona DAUIN Politecnico di Torino Semester 1, 2016-17 B. Bona (DAUIN) Dynamics Semester 1, 2016-17 1 / 18 Dynamics Dynamics studies the relations between the 3D space generalized forces
Dynamics Basilio Bona DAUIN Politecnico di Torino Semester 1, 2016-17 B. Bona (DAUIN) Dynamics Semester 1, 2016-17 1 / 18 Dynamics Dynamics studies the relations between the 3D space generalized forces
Rotation. Rotational Variables
 Rotation Rigid Bodies Rotation variables Constant angular acceleration Rotational KE Rotational Inertia Rotational Variables Rotation of a rigid body About a fixed rotation axis. Rigid Body an object that
Rotation Rigid Bodies Rotation variables Constant angular acceleration Rotational KE Rotational Inertia Rotational Variables Rotation of a rigid body About a fixed rotation axis. Rigid Body an object that
Rotation of Rigid Objects
 Notes 12 Rotation and Extended Objects Page 1 Rotation of Rigid Objects Real objects have "extent". The mass is spread out over discrete or continuous positions. THERE IS A DISTRIBUTION OF MASS TO "AN
Notes 12 Rotation and Extended Objects Page 1 Rotation of Rigid Objects Real objects have "extent". The mass is spread out over discrete or continuous positions. THERE IS A DISTRIBUTION OF MASS TO "AN
6. 3D Kinematics DE2-EA 2.1: M4DE. Dr Connor Myant
 DE2-EA 2.1: M4DE Dr Connor Myant 6. 3D Kinematics Comments and corrections to connor.myant@imperial.ac.uk Lecture resources may be found on Blackboard and at http://connormyant.com Contents Three-Dimensional
DE2-EA 2.1: M4DE Dr Connor Myant 6. 3D Kinematics Comments and corrections to connor.myant@imperial.ac.uk Lecture resources may be found on Blackboard and at http://connormyant.com Contents Three-Dimensional
Interactive work with Computer Algebra Systems when solving problems on physics
 1 Interactive work with Computer Algebra Systems when solving problems on physics Leon Magiera, Grażyna Mulak Institute of Physics Wrocław University of Technology, POLAND Leon.Magiera@pwr.wroc.pl Abstract
1 Interactive work with Computer Algebra Systems when solving problems on physics Leon Magiera, Grażyna Mulak Institute of Physics Wrocław University of Technology, POLAND Leon.Magiera@pwr.wroc.pl Abstract
Laws of gyroscopes / cardanic gyroscope
 Principle If the axis of rotation of the force-free gyroscope is displaced slightly, a nutation is produced. The relationship between precession frequency or nutation frequency and gyrofrequency is examined
Principle If the axis of rotation of the force-free gyroscope is displaced slightly, a nutation is produced. The relationship between precession frequency or nutation frequency and gyrofrequency is examined
Physics 141 Rotational Motion 1 Page 1. Rotational Motion 1. We're going to turn this team around 360 degrees.! Jason Kidd
 Physics 141 Rotational Motion 1 Page 1 Rotational Motion 1 We're going to turn this team around 360 degrees.! Jason Kidd Rigid bodies To a good approximation, a solid object behaves like a perfectly rigid
Physics 141 Rotational Motion 1 Page 1 Rotational Motion 1 We're going to turn this team around 360 degrees.! Jason Kidd Rigid bodies To a good approximation, a solid object behaves like a perfectly rigid
Rotational Kinetic Energy
 Lecture 17, Chapter 10: Rotational Energy and Angular Momentum 1 Rotational Kinetic Energy Consider a rigid body rotating with an angular velocity ω about an axis. Clearly every point in the rigid body
Lecture 17, Chapter 10: Rotational Energy and Angular Momentum 1 Rotational Kinetic Energy Consider a rigid body rotating with an angular velocity ω about an axis. Clearly every point in the rigid body
Chapter 11. Angular Momentum
 Chapter 11 Angular Momentum Angular Momentum Angular momentum plays a key role in rotational dynamics. There is a principle of conservation of angular momentum. In analogy to the principle of conservation
Chapter 11 Angular Momentum Angular Momentum Angular momentum plays a key role in rotational dynamics. There is a principle of conservation of angular momentum. In analogy to the principle of conservation
Mechanics 2 Aide Memoire. Work done = or Fx for a constant force, F over a distance, x. = or Pt for constant power, P over t seconds
 Mechanics 2 Aide Memoire Work done measured in Joules Energy lost due to overcoming a force (no work done if force acts perpendicular to the direction of motion) Work done = or Fx for a constant force,
Mechanics 2 Aide Memoire Work done measured in Joules Energy lost due to overcoming a force (no work done if force acts perpendicular to the direction of motion) Work done = or Fx for a constant force,
Vectors. J.R. Wilson. September 27, 2018
 Vectors J.R. Wilson September 27, 2018 This chapter introduces vectors that are used in many areas of physics (needed for classical physics this year). One complication is that a number of different forms
Vectors J.R. Wilson September 27, 2018 This chapter introduces vectors that are used in many areas of physics (needed for classical physics this year). One complication is that a number of different forms
LAWS OF GYROSCOPES / CARDANIC GYROSCOPE
 LAWS OF GYROSCOPES / CARDANC GYROSCOPE PRNCPLE f the axis of rotation of the force-free gyroscope is displaced slightly, a nutation is produced. The relationship between precession frequency or nutation
LAWS OF GYROSCOPES / CARDANC GYROSCOPE PRNCPLE f the axis of rotation of the force-free gyroscope is displaced slightly, a nutation is produced. The relationship between precession frequency or nutation
2/28/2006 Statics ( F.Robilliard) 1
 2/28/2006 Statics (.Robilliard) 1 Extended Bodies: In our discussion so far, we have considered essentially only point masses, under the action of forces. We now broaden our considerations to extended
2/28/2006 Statics (.Robilliard) 1 Extended Bodies: In our discussion so far, we have considered essentially only point masses, under the action of forces. We now broaden our considerations to extended
14. Rotational Kinematics and Moment of Inertia
 14. Rotational Kinematics and Moment of nertia A) Overview n this unit we will introduce rotational motion. n particular, we will introduce the angular kinematic variables that are used to describe the
14. Rotational Kinematics and Moment of nertia A) Overview n this unit we will introduce rotational motion. n particular, we will introduce the angular kinematic variables that are used to describe the
We define angular displacement, θ, and angular velocity, ω. What's a radian?
 We define angular displacement, θ, and angular velocity, ω Units: θ = rad ω = rad/s What's a radian? Radian is the ratio between the length of an arc and its radius note: counterclockwise is + clockwise
We define angular displacement, θ, and angular velocity, ω Units: θ = rad ω = rad/s What's a radian? Radian is the ratio between the length of an arc and its radius note: counterclockwise is + clockwise
Rotational N.2 nd Law
 Lecture 19 Chapter 12 Rotational N.2 nd Law Torque Newton 2 nd Law again!? That s it. He crossed the line! Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi IN THIS CHAPTER, you will
Lecture 19 Chapter 12 Rotational N.2 nd Law Torque Newton 2 nd Law again!? That s it. He crossed the line! Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi IN THIS CHAPTER, you will
Rigid Body Motion. Greg Hager Simon Leonard
 Rigid ody Motion Greg Hager Simon Leonard Overview Different spaces used in robotics and why we need to get from one space to the other Focus on Cartesian space Transformation between two Cartesian coordinate
Rigid ody Motion Greg Hager Simon Leonard Overview Different spaces used in robotics and why we need to get from one space to the other Focus on Cartesian space Transformation between two Cartesian coordinate
For a rigid body that is constrained to rotate about a fixed axis, the gravitational torque about the axis is
 Experiment 14 The Physical Pendulum The period of oscillation of a physical pendulum is found to a high degree of accuracy by two methods: theory and experiment. The values are then compared. Theory For
Experiment 14 The Physical Pendulum The period of oscillation of a physical pendulum is found to a high degree of accuracy by two methods: theory and experiment. The values are then compared. Theory For
AP Pd 3 Rotational Dynamics.notebook. May 08, 2014
 1 Rotational Dynamics Why do objects spin? Objects can travel in different ways: Translation all points on the body travel in parallel paths Rotation all points on the body move around a fixed point An
1 Rotational Dynamics Why do objects spin? Objects can travel in different ways: Translation all points on the body travel in parallel paths Rotation all points on the body move around a fixed point An
Recap. The bigger the exhaust speed, ve, the higher the gain in velocity of the rocket.
 Recap Classical rocket propulsion works because of momentum conservation. Exhaust gas ejected from a rocket pushes the rocket forwards, i.e. accelerates it. The bigger the exhaust speed, ve, the higher
Recap Classical rocket propulsion works because of momentum conservation. Exhaust gas ejected from a rocket pushes the rocket forwards, i.e. accelerates it. The bigger the exhaust speed, ve, the higher
Rotational & Rigid-Body Mechanics. Lectures 3+4
 Rotational & Rigid-Body Mechanics Lectures 3+4 Rotational Motion So far: point objects moving through a trajectory. Next: moving actual dimensional objects and rotating them. 2 Circular Motion - Definitions
Rotational & Rigid-Body Mechanics Lectures 3+4 Rotational Motion So far: point objects moving through a trajectory. Next: moving actual dimensional objects and rotating them. 2 Circular Motion - Definitions
Angular momentum Vector product.
 Lecture 19 Chapter 11 Physics I 04.09.2014 Angular momentum Vector product. Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi Lecture Capture: http://echo360.uml.edu/danylov2013/physics1spring.html
Lecture 19 Chapter 11 Physics I 04.09.2014 Angular momentum Vector product. Course website: http://faculty.uml.edu/andriy_danylov/teaching/physicsi Lecture Capture: http://echo360.uml.edu/danylov2013/physics1spring.html
Chapter 6: Momentum Analysis
 6-1 Introduction 6-2Newton s Law and Conservation of Momentum 6-3 Choosing a Control Volume 6-4 Forces Acting on a Control Volume 6-5Linear Momentum Equation 6-6 Angular Momentum 6-7 The Second Law of
6-1 Introduction 6-2Newton s Law and Conservation of Momentum 6-3 Choosing a Control Volume 6-4 Forces Acting on a Control Volume 6-5Linear Momentum Equation 6-6 Angular Momentum 6-7 The Second Law of
Motion Of An Extended Object. Physics 201, Lecture 17. Translational Motion And Rotational Motion. Motion of Rigid Object: Translation + Rotation
 Physics 01, Lecture 17 Today s Topics q Rotation of Rigid Object About A Fixed Axis (Chap. 10.1-10.4) n Motion of Extend Object n Rotational Kinematics: n Angular Velocity n Angular Acceleration q Kinetic
Physics 01, Lecture 17 Today s Topics q Rotation of Rigid Object About A Fixed Axis (Chap. 10.1-10.4) n Motion of Extend Object n Rotational Kinematics: n Angular Velocity n Angular Acceleration q Kinetic
26. Directional Derivatives & The Gradient
 26. Directional Derivatives & The Gradient Given a multivariable function z = f(x, y) and a point on the xy-plane P 0 = (x 0, y 0 ) at which f is differentiable (i.e. it is smooth with no discontinuities,
26. Directional Derivatives & The Gradient Given a multivariable function z = f(x, y) and a point on the xy-plane P 0 = (x 0, y 0 ) at which f is differentiable (i.e. it is smooth with no discontinuities,
Differential Kinematics
 Differential Kinematics Relations between motion (velocity) in joint space and motion (linear/angular velocity) in task space (e.g., Cartesian space) Instantaneous velocity mappings can be obtained through
Differential Kinematics Relations between motion (velocity) in joint space and motion (linear/angular velocity) in task space (e.g., Cartesian space) Instantaneous velocity mappings can be obtained through
1 Kalman Filter Introduction
 1 Kalman Filter Introduction You should first read Chapter 1 of Stochastic models, estimation, and control: Volume 1 by Peter S. Maybec (available here). 1.1 Explanation of Equations (1-3) and (1-4) Equation
1 Kalman Filter Introduction You should first read Chapter 1 of Stochastic models, estimation, and control: Volume 1 by Peter S. Maybec (available here). 1.1 Explanation of Equations (1-3) and (1-4) Equation
Handout 7: Torque, angular momentum, rotational kinetic energy and rolling motion. Torque and angular momentum
 Handout 7: Torque, angular momentum, rotational kinetic energy and rolling motion Torque and angular momentum In Figure, in order to turn a rod about a fixed hinge at one end, a force F is applied at a
Handout 7: Torque, angular momentum, rotational kinetic energy and rolling motion Torque and angular momentum In Figure, in order to turn a rod about a fixed hinge at one end, a force F is applied at a
16. Rotational Dynamics
 6. Rotational Dynamics A Overview In this unit we will address examples that combine both translational and rotational motion. We will find that we will need both Newton s second law and the rotational
6. Rotational Dynamics A Overview In this unit we will address examples that combine both translational and rotational motion. We will find that we will need both Newton s second law and the rotational
EE 565: Position, Navigation and Timing
 EE 565: Position, Navigation and Timing Navigation Mathematics: Angular and Linear Velocity Kevin Wedeward Aly El-Osery Electrical Engineering Department New Mexico Tech Socorro, New Mexico, USA In Collaboration
EE 565: Position, Navigation and Timing Navigation Mathematics: Angular and Linear Velocity Kevin Wedeward Aly El-Osery Electrical Engineering Department New Mexico Tech Socorro, New Mexico, USA In Collaboration
Fundamentals Physics. Chapter 10 Rotation
 Fundamentals Physics Tenth Edition Halliday Chapter 10 Rotation 10-1 Rotational Variables (1 of 15) Learning Objectives 10.01 Identify that if all parts of a body rotate around a fixed axis locked together,
Fundamentals Physics Tenth Edition Halliday Chapter 10 Rotation 10-1 Rotational Variables (1 of 15) Learning Objectives 10.01 Identify that if all parts of a body rotate around a fixed axis locked together,
Torque and Rotation Lecture 7
 Torque and Rotation Lecture 7 ˆ In this lecture we finally move beyond a simple particle in our mechanical analysis of motion. ˆ Now we consider the so-called rigid body. Essentially, a particle with extension
Torque and Rotation Lecture 7 ˆ In this lecture we finally move beyond a simple particle in our mechanical analysis of motion. ˆ Now we consider the so-called rigid body. Essentially, a particle with extension
RELATIVE MOTION ANALYSIS: VELOCITY (Section 16.5)
 RELATIVE MOTION ANALYSIS: VELOCITY (Section 16.5) Today s Objectives: Students will be able to: a) Describe the velocity of a rigid body in terms of translation and rotation components. b) Perform a relative-motion
RELATIVE MOTION ANALYSIS: VELOCITY (Section 16.5) Today s Objectives: Students will be able to: a) Describe the velocity of a rigid body in terms of translation and rotation components. b) Perform a relative-motion
PLANAR KINETIC EQUATIONS OF MOTION (Section 17.2)
 PLANAR KINETIC EQUATIONS OF MOTION (Section 17.2) We will limit our study of planar kinetics to rigid bodies that are symmetric with respect to a fixed reference plane. As discussed in Chapter 16, when
PLANAR KINETIC EQUATIONS OF MOTION (Section 17.2) We will limit our study of planar kinetics to rigid bodies that are symmetric with respect to a fixed reference plane. As discussed in Chapter 16, when
Physics 218 Lecture 21
 Physics 218 Lecture 21 Dr. David Toback Physics 218, Lecture XXI 1 Checklist for Today Things due Yesterday Chapters 12 & 13 in WebCT Things that are due for today Read Chapters 14-16 Things that are due
Physics 218 Lecture 21 Dr. David Toback Physics 218, Lecture XXI 1 Checklist for Today Things due Yesterday Chapters 12 & 13 in WebCT Things that are due for today Read Chapters 14-16 Things that are due
Lecture 13 REVIEW. Physics 106 Spring What should we know? What should we know? Newton s Laws
 Lecture 13 REVIEW Physics 106 Spring 2006 http://web.njit.edu/~sirenko/ What should we know? Vectors addition, subtraction, scalar and vector multiplication Trigonometric functions sinθ, cos θ, tan θ,
Lecture 13 REVIEW Physics 106 Spring 2006 http://web.njit.edu/~sirenko/ What should we know? Vectors addition, subtraction, scalar and vector multiplication Trigonometric functions sinθ, cos θ, tan θ,
Review of Engineering Dynamics
 Review of Engineering Dynamics Part 1: Kinematics of Particles and Rigid Bodies by James Doane, PhD, PE Contents 1.0 Course Overview... 4.0 Basic Introductory Concepts... 4.1 Introduction... 4.1.1 Vectors
Review of Engineering Dynamics Part 1: Kinematics of Particles and Rigid Bodies by James Doane, PhD, PE Contents 1.0 Course Overview... 4.0 Basic Introductory Concepts... 4.1 Introduction... 4.1.1 Vectors
Dealing with Rotating Coordinate Systems Physics 321. (Eq.1)
 Dealing with Rotating Coordinate Systems Physics 321 The treatment of rotating coordinate frames can be very confusing because there are two different sets of aes, and one set of aes is not constant in
Dealing with Rotating Coordinate Systems Physics 321 The treatment of rotating coordinate frames can be very confusing because there are two different sets of aes, and one set of aes is not constant in
Prof. Rupak Mahapatra. Physics 218, Chapter 15 & 16
 Physics 218 Chap 14 & 15 Prof. Rupak Mahapatra Physics 218, Chapter 15 & 16 1 Angular Quantities Position Angle θ Velocity Angular Velocity ω Acceleration Angular Acceleration α Moving forward: Force Mass
Physics 218 Chap 14 & 15 Prof. Rupak Mahapatra Physics 218, Chapter 15 & 16 1 Angular Quantities Position Angle θ Velocity Angular Velocity ω Acceleration Angular Acceleration α Moving forward: Force Mass
Physics 1C. Lecture 12B
 Physics 1C Lecture 12B SHM: Mathematical Model! Equations of motion for SHM:! Remember, simple harmonic motion is not uniformly accelerated motion SHM: Mathematical Model! The maximum values of velocity
Physics 1C Lecture 12B SHM: Mathematical Model! Equations of motion for SHM:! Remember, simple harmonic motion is not uniformly accelerated motion SHM: Mathematical Model! The maximum values of velocity
Rigid Body Kinetics :: Force/Mass/Acc
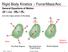 Rigid Body Kinetics :: Force/Mass/Acc General Equations of Motion G is the mass center of the body Action Dynamic Response 1 Rigid Body Kinetics :: Force/Mass/Acc Fixed Axis Rotation All points in body
Rigid Body Kinetics :: Force/Mass/Acc General Equations of Motion G is the mass center of the body Action Dynamic Response 1 Rigid Body Kinetics :: Force/Mass/Acc Fixed Axis Rotation All points in body
Conservation of Angular Momentum
 Physics 101 Section 3 March 3 rd : Ch. 10 Announcements: Monday s Review Posted (in Plummer s section (4) Today start Ch. 10. Next Quiz will be next week Test# (Ch. 7-9) will be at 6 PM, March 3, Lockett-6
Physics 101 Section 3 March 3 rd : Ch. 10 Announcements: Monday s Review Posted (in Plummer s section (4) Today start Ch. 10. Next Quiz will be next week Test# (Ch. 7-9) will be at 6 PM, March 3, Lockett-6
Lecture Note 5: Velocity of a Rigid Body
 ECE5463: Introduction to Robotics Lecture Note 5: Velocity of a Rigid Body Prof. Wei Zhang Department of Electrical and Computer Engineering Ohio State University Columbus, Ohio, USA Spring 2018 Lecture
ECE5463: Introduction to Robotics Lecture Note 5: Velocity of a Rigid Body Prof. Wei Zhang Department of Electrical and Computer Engineering Ohio State University Columbus, Ohio, USA Spring 2018 Lecture
Induction and Inductance
 Welcome Back to Physics 1308 Induction and Inductance Michael Faraday 22 September 1791 25 August 1867 Announcements Assignments for Tuesday, November 6th: - Reading: Chapter 30.6-30.8 - Watch Videos:
Welcome Back to Physics 1308 Induction and Inductance Michael Faraday 22 September 1791 25 August 1867 Announcements Assignments for Tuesday, November 6th: - Reading: Chapter 30.6-30.8 - Watch Videos:
Rotational Motion Rotational Kinematics
 Rotational Motion Rotational Kinematics Lana Sheridan De Anza College Nov 16, 2017 Last time 3D center of mass example systems of many particles deforming systems Overview rotation relating rotational
Rotational Motion Rotational Kinematics Lana Sheridan De Anza College Nov 16, 2017 Last time 3D center of mass example systems of many particles deforming systems Overview rotation relating rotational
8 Rotational motion of solid objects
 8 Rotational motion of solid objects Kinematics of rotations PHY166 Fall 005 In this Lecture we call solid objects such extended objects that are rigid (nondeformable) and thus retain their shape. In contrast
8 Rotational motion of solid objects Kinematics of rotations PHY166 Fall 005 In this Lecture we call solid objects such extended objects that are rigid (nondeformable) and thus retain their shape. In contrast
EOS 352 Continuum Dynamics Conservation of angular momentum
 EOS 352 Continuum Dynamics Conservation of angular momentum c Christian Schoof. Not to be copied, used, or revised without explicit written permission from the copyright owner The copyright owner explicitly
EOS 352 Continuum Dynamics Conservation of angular momentum c Christian Schoof. Not to be copied, used, or revised without explicit written permission from the copyright owner The copyright owner explicitly
V (r,t) = i ˆ u( x, y,z,t) + ˆ j v( x, y,z,t) + k ˆ w( x, y, z,t)
 IV. DIFFERENTIAL RELATIONS FOR A FLUID PARTICLE This chapter presents the development and application of the basic differential equations of fluid motion. Simplifications in the general equations and common
IV. DIFFERENTIAL RELATIONS FOR A FLUID PARTICLE This chapter presents the development and application of the basic differential equations of fluid motion. Simplifications in the general equations and common
Massachusetts Institute of Technology Physics Department
 Massachusetts Institute of Technology Physics Department Physics 8.0 IAP 005 Introduction to Special Relativity Midterm Exam Solutions. (a). The laws of physics should take the same form in all inertial
Massachusetts Institute of Technology Physics Department Physics 8.0 IAP 005 Introduction to Special Relativity Midterm Exam Solutions. (a). The laws of physics should take the same form in all inertial
Answers to selected problems from Essential Physics, Chapter 10
 Answers to selected problems from Essential Physics, Chapter 10 1. (a) The red ones have the same speed as one another. The blue ones also have the same speed as one another, with a value twice the speed
Answers to selected problems from Essential Physics, Chapter 10 1. (a) The red ones have the same speed as one another. The blue ones also have the same speed as one another, with a value twice the speed
APPLIED MATHEMATICS ADVANCED LEVEL
 APPLIED MATHEMATICS ADVANCED LEVEL INTRODUCTION This syllabus serves to examine candidates knowledge and skills in introductory mathematical and statistical methods, and their applications. For applications
APPLIED MATHEMATICS ADVANCED LEVEL INTRODUCTION This syllabus serves to examine candidates knowledge and skills in introductory mathematical and statistical methods, and their applications. For applications
Chapter One Introduction to Oscillations
 Chapter One Introduction to Oscillations This chapter discusses simple oscillations. This chapter also discusses simple functions to model oscillations like the sine and cosine functions. Part One Sine
Chapter One Introduction to Oscillations This chapter discusses simple oscillations. This chapter also discusses simple functions to model oscillations like the sine and cosine functions. Part One Sine
PLANAR RIGID BODY MOTION: TRANSLATION &
 PLANAR RIGID BODY MOTION: TRANSLATION & Today s Objectives : ROTATION Students will be able to: 1. Analyze the kinematics of a rigid body undergoing planar translation or rotation about a fixed axis. In-Class
PLANAR RIGID BODY MOTION: TRANSLATION & Today s Objectives : ROTATION Students will be able to: 1. Analyze the kinematics of a rigid body undergoing planar translation or rotation about a fixed axis. In-Class
Chapter 10: Rotation. Chapter 10: Rotation
 Chapter 10: Rotation Change in Syllabus: Only Chapter 10 problems (CH10: 04, 27, 67) are due on Thursday, Oct. 14. The Chapter 11 problems (Ch11: 06, 37, 50) will be due on Thursday, Oct. 21 in addition
Chapter 10: Rotation Change in Syllabus: Only Chapter 10 problems (CH10: 04, 27, 67) are due on Thursday, Oct. 14. The Chapter 11 problems (Ch11: 06, 37, 50) will be due on Thursday, Oct. 21 in addition
Rotational Kinematics and Dynamics. UCVTS AIT Physics
 Rotational Kinematics and Dynamics UCVTS AIT Physics Angular Position Axis of rotation is the center of the disc Choose a fixed reference line Point P is at a fixed distance r from the origin Angular Position,
Rotational Kinematics and Dynamics UCVTS AIT Physics Angular Position Axis of rotation is the center of the disc Choose a fixed reference line Point P is at a fixed distance r from the origin Angular Position,
Planar Rigid Body Kinematics Homework
 Chapter 2: Planar Rigid ody Kinematics Homework Chapter 2 Planar Rigid ody Kinematics Homework Freeform c 2018 2-1 Chapter 2: Planar Rigid ody Kinematics Homework 2-2 Freeform c 2018 Chapter 2: Planar
Chapter 2: Planar Rigid ody Kinematics Homework Chapter 2 Planar Rigid ody Kinematics Homework Freeform c 2018 2-1 Chapter 2: Planar Rigid ody Kinematics Homework 2-2 Freeform c 2018 Chapter 2: Planar
Rotation Angular Momentum
 Rotation Angular Momentum Lana Sheridan De Anza College Nov 28, 2017 Last time rolling motion Overview Definition of angular momentum relation to Newton s 2nd law angular impulse angular momentum of rigid
Rotation Angular Momentum Lana Sheridan De Anza College Nov 28, 2017 Last time rolling motion Overview Definition of angular momentum relation to Newton s 2nd law angular impulse angular momentum of rigid
Robotics. Islam S. M. Khalil. September 6, German University in Cairo
 Robotics German University in Cairo September 6, 2016 Outline Motivation Agenda Generalized pseudoinverse Over- and under-determined systems Motivation Autonomous Robotic Systems Controller, power source,
Robotics German University in Cairo September 6, 2016 Outline Motivation Agenda Generalized pseudoinverse Over- and under-determined systems Motivation Autonomous Robotic Systems Controller, power source,
AP Physics QUIZ Chapters 10
 Name: 1. Torque is the rotational analogue of (A) Kinetic Energy (B) Linear Momentum (C) Acceleration (D) Force (E) Mass A 5-kilogram sphere is connected to a 10-kilogram sphere by a rigid rod of negligible
Name: 1. Torque is the rotational analogue of (A) Kinetic Energy (B) Linear Momentum (C) Acceleration (D) Force (E) Mass A 5-kilogram sphere is connected to a 10-kilogram sphere by a rigid rod of negligible
Lecture Notes Multibody Dynamics B, wb1413
 Lecture Notes Multibody Dynamics B, wb1413 A. L. Schwab & Guido M.J. Delhaes Laboratory for Engineering Mechanics Mechanical Engineering Delft University of Technolgy The Netherlands June 9, 29 Contents
Lecture Notes Multibody Dynamics B, wb1413 A. L. Schwab & Guido M.J. Delhaes Laboratory for Engineering Mechanics Mechanical Engineering Delft University of Technolgy The Netherlands June 9, 29 Contents
3D Coordinate Transformations. Tuesday September 8 th 2015
 3D Coordinate Transformations Tuesday September 8 th 25 CS 4 Ross Beveridge & Bruce Draper Questions / Practice (from last week I messed up!) Write a matrix to rotate a set of 2D points about the origin
3D Coordinate Transformations Tuesday September 8 th 25 CS 4 Ross Beveridge & Bruce Draper Questions / Practice (from last week I messed up!) Write a matrix to rotate a set of 2D points about the origin
Classical Mechanics Lecture 15
 Classical Mechanics Lecture 5 Today s Concepts: a) Parallel Axis Theorem b) Torque & Angular Acceleration Mechanics Lecture 5, Slide Unit 4 Main Points Mechanics Lecture 4, Slide Unit 4 Main Points Mechanics
Classical Mechanics Lecture 5 Today s Concepts: a) Parallel Axis Theorem b) Torque & Angular Acceleration Mechanics Lecture 5, Slide Unit 4 Main Points Mechanics Lecture 4, Slide Unit 4 Main Points Mechanics
Lecture 6. Circular Motion. Pre-reading: KJF 6.1 and 6.2. Please take a clicker CIRCULAR MOTION KJF
 Lecture 6 Circular Motion Pre-reading: KJF 6.1 and 6.2 Please take a clicker CIRCULAR MOTION KJF 6.1 6.4 Angular position If an object moves in a circle of radius r, then after travelling a distance s
Lecture 6 Circular Motion Pre-reading: KJF 6.1 and 6.2 Please take a clicker CIRCULAR MOTION KJF 6.1 6.4 Angular position If an object moves in a circle of radius r, then after travelling a distance s
Advanced Higher Physics. Rotational Motion
 Wallace Hall Academy Physics Department Advanced Higher Physics Rotational Motion Solutions AH Physics: Rotational Motion Problems Solutions Page 1 013 TUTORIAL 1.0 Equations of motion 1. (a) v = ds, ds
Wallace Hall Academy Physics Department Advanced Higher Physics Rotational Motion Solutions AH Physics: Rotational Motion Problems Solutions Page 1 013 TUTORIAL 1.0 Equations of motion 1. (a) v = ds, ds
CHAPTER 12 OSCILLATORY MOTION
 CHAPTER 1 OSCILLATORY MOTION Before starting the discussion of the chapter s concepts it is worth to define some terms we will use frequently in this chapter: 1. The period of the motion, T, is the time
CHAPTER 1 OSCILLATORY MOTION Before starting the discussion of the chapter s concepts it is worth to define some terms we will use frequently in this chapter: 1. The period of the motion, T, is the time
Artificial Intelligence & Neuro Cognitive Systems Fakultät für Informatik. Robot Dynamics. Dr.-Ing. John Nassour J.
 Artificial Intelligence & Neuro Cognitive Systems Fakultät für Informatik Robot Dynamics Dr.-Ing. John Nassour 25.1.218 J.Nassour 1 Introduction Dynamics concerns the motion of bodies Includes Kinematics
Artificial Intelligence & Neuro Cognitive Systems Fakultät für Informatik Robot Dynamics Dr.-Ing. John Nassour 25.1.218 J.Nassour 1 Introduction Dynamics concerns the motion of bodies Includes Kinematics
Central to this is two linear transformations: the Fourier Transform and the Laplace Transform. Both will be considered in later lectures.
 In this second lecture, I will be considering signals from the frequency perspective. This is a complementary view of signals, that in the frequency domain, and is fundamental to the subject of signal
In this second lecture, I will be considering signals from the frequency perspective. This is a complementary view of signals, that in the frequency domain, and is fundamental to the subject of signal
