US01CMTH02 UNIT-3. exists, then it is called the partial derivative of f with respect to y at (a, b) and is denoted by f. f(a, b + b) f(a, b) lim
|
|
|
- Branden Butler
- 5 years ago
- Views:
Transcription
1 Study material of BSc(Semester - I US01CMTH02 (Partial Derivatives Prepared by Nilesh Y Patel Head,Mathematics Department,VPand RPTPScience College 1 Partial derivatives US01CMTH02 UNIT-3 The concept of partial derivative plays a vital role in differential calculus The different ways of limit discussed in the previous section, yields different type of partial derivatives of a function 11 Definitions Consider a real valued function z = f(, y defined on E R 2 such that E contains a neighbourhood of (a, b R 2 Let a be a change in a If the limit, f(a + a, b f(a, b lim a 0 a eists, then it is called the partial derivative of f with respect to at (a, b and is denoted by f or f (a, b or z (a, b Similarly, let b be a change in b If the limit, (a,b f(a, b + b f(a, b lim b 0 b eists, then it is called the partial derivative of f with respect to y at (a, b and is denoted by f or f y (a, b or z y (a, b (a,b Notations If the partial derivatives f and f y eist at each point of E, then they are also the real valued functions on E Further, we can obtain the partial derivatives of these functions, if they are differentiable In these cases, we fi up the following notations f = 2 f 2 = f y = 2 f = ( f ( f, f yy = 2 f = ( f 2 ; and f y = 2 f =, ( f The notations of derivatives of order greater than two should be clear from the above pattern 12 Remark As we have seen in the above eample, in general, f y and f y need not be equal, even if they eist The following proposition gives a sufficient condition for them to be equal We accept it without proof However, we shall be dealing only with the functions f for which these two are equal 1
2 2 13 Proposition Consider a real valued function z = f(, y defined on E R 2 such that E contains a neighbourhood of (a, b R 2 If f y and f y eist and are continuous, then f y = f y Throughout this chapter our blanket assumption will be that the operation of taking partial derivatives is commutative That is, for our function f of two variables, f y = f y In general, we may assume that the second derivatives of functions eists and are continuous, so that, the Proposition 13 ensures our requirement 14 Eample For u = 3 3y 2, prove that 2 u + 2 u 2 2 Solution Here u = 3 3y 2 u = 32 3y 2 ; u = 6y; 2 u 2 = 6; = 0 Also prove that 2 u = 2 u 2 u = 6y = 2 u 2 u 2 = 6 2 u + 2 u 2 = 6 6 = 0 and 2 u 2 = 2 u 2 Homogeneous functions Let us observe the following epressions carefully (1 f 1 (, y = 2 y 4 3 y 3 + y 5 (2 f 2 (, y = 4 y 4 5 y y 2 The combined degree of and y in each term of the first epression is 6 and that in the second epression is 8 Can we determine whether the combined degree of and y in each term of the epression is same or not? It seems difficult to determine Let us develop 4 +y 4 the following tests Test 1: Let us take t = y Then and 2 y 4 3 y 3 + y 5 = 6 (t 4 t 3 + t 5 = 6 f(t 4 y 4 5 y y 2 = 8 (t 4 t 3 + t 2 = 8 g(t, where f and g are functions of one variable t Test 2: Now, let us replace by t and y by ty Then and f 1 (t, ty = (t 2 (ty 4 (t 3 (ty 3 + (t(ty 5 = t 6 f 1 (, y f 2 (t, ty = (t 4 (ty 4 (t 5 (ty 3 + (t 6 (ty 2 = t 8 f 2 (, y 21 Definitions A function z = f(, y is said to be a homogeneous function of degree r, if f(t, ty = t r f(, y for some real number r Otherwise, f is said to be a nonhomogeneous function
3 2 Homogeneous functions 3 22 Eample Let f : R 2 \ {(, y : y = } R defined by f(, y = y Then prove +y that f is a homogeneous function of degree 0 and f and f y eist at each point of the domain Solution Clearly, f(t, ty = f(, y = t 0 f(, y Thus f is a homogeneous function of degree 0 Now for any (, y R 2 with + y 0, we have, and f (, y = f y (, y = ( + y(1 ( y(1 ( + y 2 = 2y ( + y 2 ( + y( 1 ( y(1 ( + y 2 = 2 ( + y 2 23 Eample f : R 2 \ {(0, 0} R defined by f(, y = 5 5 y 3 +y 3 function of degree 14 5 is a homogeneous 24 Theorem (Euler s Theorem State and prove Euler s Theorem Statement : Let z = f(, y be a real valued function defined on E R 2 Suppose that f is a homogeneous function of degree n If f and f y eist on E, then + y = nz (241 Proof Since z = f(, y is a homogeneous function of, y of degree n, we can write ( y z = f(, y = n g (242 Differentiating (242 partially with respect to, we get, ( y ( y = nn 1 g + n g ( y 2 ( y ( y = nn g n 1 yg (243 Similarly, differentiating (242 partially with respect to y, we get, ( y 1 ( y = n g = n 1 g y ( y = yn 1 g (244 Adding (243 and (244 we get, + y ( y = nn g = nz This completes the proof We note that the converse of Euler s Theorem also holds That is, if a function z = f(, y satisfies (241, on a certain domain, then it must be homogeneous on that domain
4 4 25 Remark Now onwards we shall not mention the domain of the functions under discussion Also, whenever we use the derivatives of functions under discussion, we assume them to be sufficiently many times differentiable 26 Corollary Let z = f(, y be a real valued function defined on E R 2 Suppose that f is a homogeneous function of degree n and that all the second order partial derivatives of f eist and are continuous Then prove that 2 2 z + 2y 2 z z y2 = n(n 1z 2 Proof Since z = f(, y is a homogeneous function of, y of degree n, by Euler s Theorem, + y = nz (261 Differentiating (261 partially with respect to, we have, which, on multiplication by, gives 2 z y 2 z = n, 2 2 z y 2 z 2 2 z 2 + y 2 z = n = (n 1 (262 Similarly, differentiating (261 partially with respect to y and then multiplying the result by y, we get, Since 2 z = 2 z, we get, y 2 2 z 2 + y 2 z y 2 2 z 2 + y 2 z By adding (262 and (263 we have, = (n 1y = (n 1y ( z + 2y 2 z z y2 = (n 1( 2 + y = n(n 1z This completes the proof 27 Corollary Let u = u(, y be a nonhomogeneous real valued function defined on E R 2 and z = φ(u be homogeneous function of degree n Then prove that provided φ (u 0 for any (, y E u + y u = n φ(u φ (u,
5 2 Homogeneous functions 5 Proof Since z = φ(u is a homogeneous function of, y of degree n, by Euler s Theorem we have, + y = nz = nφ(u ( φ (u u ( + y φ (u u = nφ(u ( u + y ( u = n φ(u φ (u 28 Corollary (Only statementlet u = u(, y be a nonhomogeneous real valued function defined on E R 2 and z = φ(u be homogeneous function of degree n Then prove that 2 2 u 2 + 2y 2 u + y2 2 u 2 = ψ(u[ψ (u 1], where ψ(u = n φ(u φ (u, provided φ (u 0 for any (, y E 29 Eample For the following functions, verify Euler s Theorem and find 2 2 z + 2y 2 z + 2 y2 2 z 2 (1 z = n log ( y (2 z = sin 1 ( + y tan 1 ( y Solution (1 Clearly, z is a homogeneous function of degree n ( y = nn 1 log + n ( y ( y = n n 1 log y n 1 2 ( y = nn log n Also, ( ( 1 = n = n y y y = n + y ( y = nn log = nz Thus Euler s Theorem is verified By the Corollary 26, 2 2 z + 2y 2 z z y2 = n(n 1z 2 (2 Replacing by t and y by ty, f(t, ty = sin 1 ( + y tan 1 ( y = t0 f(, y Thus z = f(, y is a homogeneous function of degree 0 Now, ( = ( y 1 = 1 y y2 2 y 2 2 y2 y y 2 = y2 2 y 2 + y 2
6 6 Also, ( = 1 1 y 2 2 y 2 y = y2 2 + Thus Euler s Theorem is verified By the Corollary 26, as n = y2 2 y 2 + y 2 ( 1 = + y = 0 y y z + 2y 2 z z y2 = n(n 1z = 0, Eample If u = sin 1 ( 2 y 2, then prove the following +y (1 u + y u = 3 tan u (2 2 2 u 2 + 2y 2 u + y2 2 u 2 = 3 tan u(3 sec 2 u y 2 Solution Here u = sin 1 ( 2 y 2 is not a homogeneous function of, y Writing the given +y equation differently, we have sin u = 2 y 2, which is +y Let z = φ(u = sin u Then z = 2 y 2 +y homogeneous of degree 3 Hence by Corollary 27, u + y u = 3 φ(u = 3 sin u φ (u cos u which proves (1 Also, by Corollary 28, we have, 2 2 u 2 + 2y 2 u + y2 2 u 2 = 3 tan u[3 sec2 u 1] 3 Theorem on total differentials = 3 tan u, Throughout this section we consider only those functions of two variables that admit continuous partial derivatives on their domain of definition That is, if we are discussing about a function z = f(, y, then f, f y eist and are continuous on the domain of f 31 Theorem ( Only statement Let z = f(, y be defined on E Then dz = d + dy 4 Differentiation of composite functions In this section we shall study the differentiation of composite functions Let z = f(, y be function defined on E R 2 In turn one can have = ϕ(t and y = ψ(t, t F R This makes f a function of one independent variable t That is, t F (ϕ(t, ψ(t E f(ϕ(t, ψ(t The following theorem describes the differentiation of f with respect to t in this situation
7 5 Change of variables 7 41 Theorem ( Only statement Let z = f(, y be function defined on E R 2 and = ϕ(t, y = ψ(t, t F R Then prove that df = f d + f dy dt dt dt To etend Theorem 41 for functions of three variables, let u = f(, y, z be a function of three variables with = (t, y = y(t and z = z(t Then 5 Change of variables du dt = u d dt + u dy dt + u dz dt Like the composite functions we can also consider the following situation Let z = f(, y be function defined on E R 2 and let there be another domain F R 2 such that for each (, y E, = ϕ(u, v, y = ψ(u, v, (u, v F R 2 This is nothing but the change of variable In this case, the following theorem describes the partial derivatives of f with respect to u and v Now we prove Euler s Theorem for three variables The homogeneous functions of more than two variables are defined as in Definition 21 More eplicitly, a function H = f( 1, 2,, n of n variables is called homogeneous if there eists r R such that for f(t 1, t 2,, t n = t r f( 1, 2,, n for all t R In this case, the degree of homogeneity of H is r 51 Theorem (Euler s Theorem for Three variables Let H = f(, y, z be a real valued homogeneous function of three variables, y, z of degree n defined on E R 3 If f, f y, f z eist on E, then prove that H + y H + z H Proof Since H = f(, y, z is homogeneous function of degree n, ( y H = n φ, z = n φ(u, v, = nh (511 where u = y and v = z [ H φ = nn 1 φ(u, v + n u u + φ ] v v [ = n n 1 φ(u, v + n y φ 2 u z ] φ 2 v = n n 1 φ(u, v n 2 y φ u n 2 z φ v H = nn φ(u, v n 1 y φ u n 1 z φ v (512 Now, H = n [ φ u u + φ ] v v [ ] 1 = n φ u + 0 φ n 1 φ = v u y H = n 1 y φ u (513
8 8 Similarly, z H = n 1 z φ v (514 Adding (512, (513 and (514 we have, H + y H + z H = nn φ(u, v = nh This completes the proof As noted in case of the functions of two variables, here also we recall that the converse of Euler s Theorem also holds That is, if a function z = f(, y satisfies (511, on a certain domain, then it must be homogeneous on that domain 52 Eample Find dz dt when z = sin 1 ( y, = 3t, y = 4t 3 Also verify by the direct substitution Solution dz dt = d dt + dy dt 1 = ( y 2 1 ( y 2 12t2 = 3(1 4t2 1 ( y 2 = = = 3(1 4t 2 1 (3t 4t3 2 3(1 4t 2 (1 3t + 4t3 (1 + 3t 4t 3 3(1 4t 2 (1 t2 (1 4t 2 = t 2 On the other hand, verifying directly by putting the values of and y in z, we have z = sin 1 (3t 4t 3 dz dt = (3 12t 2 1 (3t 4t3 2 = 3(1 4t 2 1 (3t 4t3 2 = 3 1 t 2 53 Eample If z = f(, y, = r cos θ, y = r sin θ, then prove that [ ] 2 [ ] 2 [ ] 2 + = + 1 [ ] 2 r r 2 θ Solution Here, y are functions of r, θ Hence z is a composite function of r, θ Thus, r = r + = cos θ + sin θ r [ ] 2 [ ] 2 = cos 2 θ + 2 sin θ cos θ [ ] 2 r + sin2 θ (531
9 5 Change of variables 9 Also, θ = θ + = r sin θ + r cos θ θ [ ] 2 [ ] 2 = r 2 sin 2 θ 2r 2 sin θ cos θ [ ] 2 θ + r2 cos 2 θ 1 [ ] 2 [ ] 2 = sin 2 θ 2 sin θ cos θ [ ] 2 r 2 θ + cos2 θ (532 Adding (531 and (532 we get, [ ] r r 2 [ ] 2 = θ [ ] 2 + [ ] 2 54 Eample If H = f(2 3y, 3y 4z, 4z 2, then prove that 1 H H H 4 = 0 Solution Let u = 2 3y, v = 3y 4z, w = 4z 2 Then H = f(u, v, w Hence H is a composite function of, y, z Therefore, H = H u u + H v v + H w w = 2 H u + 0 H v 2 H w = 2 H u 2 H w (541 Also, H = H u u + H v v + H w w = 3 H u + 3 H v + 0 H w = 3 H u + 3 H v (542 Finally, H = H u u + H v v + H w w = 0 H u 4 H v + 4 H w = 4 H v + 4 H w (543 1 H H H 4 = H u H w H u + H v H v + H w = 0 55 Eample If z = f(, y and u = e cos y, v = e sin y Then prove that f u f + v f u v Solution u = e cos y, v = e sin y Also, u 2 + v 2 = e 2 e = u 2 + v 2 = 1 2 log (u2 + v 2 v u = tan y y = tan 1 ( v u Thus, y are functions of u, v, and so, z is a composite function of u, v Now, f u = f u + f u = f [ u u 2 + v 2 ] + f [ v u 2 + v 2 ] =
10 10 Similarly, u f [ u = u 2 u 2 + v 2 v f [ v = ] [ f v 2 u 2 + v 2 uv u 2 + v 2 ] [ f + Adding (551 and (552 we get, u f u + v f v = f 6 Differentiation of implicit functions ] f (551 uv u 2 + v 2 ] f (552 Many a times we are given an epression f(, y = c, where c R is a constant Note here that, and y are associated by a rule however we may not be able to write y as a function of In this case, we say that y is a function of, implicitly described by f(, y = c or y is an implicit function of We obtain the method of calculating dy and d d 2 y d 2 using the tools of partial derivatives 61 Theorem Let a function y of be implicitly described by f(, y = c Then prove that (1 dy d = f f y (2 d2 y d 2 = f (f y 2 2f y f f y + f yy (f 2 (f y 3 Proof We know that f is a function of and y Also, y is an implicit function of So, f is a composite function of differentiating the equation f(, y = c with respect to, we get, This proves (1 Now we prove (2 f d d + f dy d = 0 f + f dy d = 0 dy d 2 y d = d 2 d = d d ( dy d ( f f y = f y d (f d d f (f d y (f y 2 ( f y (f + (f dy d = f ( d = f f = f f y (f y + (f y dy d (f y 2 ( ( f y f + f y ( f f y f f y + f yy ( f f y = (f y 2 = f (f y 2 f y f f y f f y f y + f yy (f 2 (f y 3
11 6 Implicit functions 11 = f (f y 2 2f f y f y + f yy (f 2 (f y 3 62 Eample Find dy d when (1 sin( y ( + y = 0 (2 y = y Proof (1 Let f(, y = sin( y (+y Since f(, y = 0, by the previous theorem, we have, dy d = f cos( y + sin( y 1 = f y cos( y( 1 1 cos( y + sin( y 1 = cos( y + 1 (2 Let f(, y = y y Since f(, y = 0, by the previous theorem, we have, dy d = f f y = yy 1 y log y y log y 1 = y log y y y 1 y log y 1 63 Eample If z = yf( y and z is constant, then show that f ( y dy [y + = y[y dy f( y Solution Let F (, y = yf( y Then F (, y = z, z is constant Thus y is an implicit function of So, F + F dy = 0 (631 d Now differentiating F (, y with respect to, we get, F ( = yf(y + yf ( y y = yf( y y2 2 f ( y = y [ f( y yf ( y ] Similarly, d ] d ] F = f(y + yf ( y ( 1 = f(y + yf ( y Putting these values in (631, we have, y [ f( y yf ( y ] + f( y + yf ( y dy d = 0 [ y + dy ] f( y d = y [ y dy ] f ( y d f ( y [ ] f( y = y + dy d y y dy d
12 12 64 Eample If A, B and C are angles of a ABC such that sin 2 A + sin 2 B + sin 2 C = K, a constant, then prove that db tan C tan A = dc tan A tan B Solution Clearly, A + B + C = π So, A = π (B + C Therefore, sin A = sin(b + C Let f(b, C = sin 2 (B + C + sin 2 B + sin 2 C K Hence f(b, C = 0, ie, B is an implicit function of C So, db = f C dc f B Also, Similarly, we get, f B = f B = 2 sin(b + C cos(b + C + 2 sin B cos B db dc = sin 2(B + C + sin 2B = sin(2π 2A + sin 2B = sin 2A + sin 2B = 2 cos(b + A sin(b A = 2 cos(π C sin(b A = 2 cos C sin(b A = 2 cos C sin(a B Dividing by cos A cos B cos C, we get, db tan A tan C tan C tan A = = dc tan A tan B tan A tan B f C = 2 cos B sin(a C B sin(a C = cos cos C sin(a B cos B(sin A cos C cos A sin C = cos C(sin A cos B cos A sin B sin A cos B cos C cos A cos B sin C = sin A cos B cos C cos A sin B cos C
Dr. P.K. Srivastava Assistant Professor of Mathematics Galgotia College of Engineering & Technology Greater Noida (U.P.)
 Engineering Mathematics-III Dr. P.K. Srivastava Assistant Professor of Mathematics Galgotia College of Engineering & Technology Greater Noida (U.P.) (An ISO 9001:008 Certified Company) Vayu Education of
Engineering Mathematics-III Dr. P.K. Srivastava Assistant Professor of Mathematics Galgotia College of Engineering & Technology Greater Noida (U.P.) (An ISO 9001:008 Certified Company) Vayu Education of
Answer Key 1973 BC 1969 BC 24. A 14. A 24. C 25. A 26. C 27. C 28. D 29. C 30. D 31. C 13. C 12. D 12. E 3. A 32. B 27. E 34. C 14. D 25. B 26.
 Answer Key 969 BC 97 BC. C. E. B. D 5. E 6. B 7. D 8. C 9. D. A. B. E. C. D 5. B 6. B 7. B 8. E 9. C. A. B. E. D. C 5. A 6. C 7. C 8. D 9. C. D. C. B. A. D 5. A 6. B 7. D 8. A 9. D. E. D. B. E. E 5. E.
Answer Key 969 BC 97 BC. C. E. B. D 5. E 6. B 7. D 8. C 9. D. A. B. E. C. D 5. B 6. B 7. B 8. E 9. C. A. B. E. D. C 5. A 6. C 7. C 8. D 9. C. D. C. B. A. D 5. A 6. B 7. D 8. A 9. D. E. D. B. E. E 5. E.
4. Integration. Type - I Integration of a proper algebraic rational function r(x) = p(x), with nonrepeated real linear factors in the denominator.
 4. Integration The process of determining an integral of a function is called integration and the function to be integrated is called integrand. The stu of integral calculus consists in developing techniques
4. Integration The process of determining an integral of a function is called integration and the function to be integrated is called integrand. The stu of integral calculus consists in developing techniques
Name: Date: Period: Calculus Honors: 4-2 The Product Rule
 Name: Date: Period: Calculus Honors: 4- The Product Rule Warm Up: 1. Factor and simplify. 9 10 0 5 5 10 5 5. Find ' f if f How did you go about finding the derivative? Let s Eplore how to differentiate
Name: Date: Period: Calculus Honors: 4- The Product Rule Warm Up: 1. Factor and simplify. 9 10 0 5 5 10 5 5. Find ' f if f How did you go about finding the derivative? Let s Eplore how to differentiate
1. The following problems are not related: (a) (15 pts, 5 pts ea.) Find the following limits or show that they do not exist: arcsin(x)
 APPM 5 Final Eam (5 pts) Fall. The following problems are not related: (a) (5 pts, 5 pts ea.) Find the following limits or show that they do not eist: (i) lim e (ii) lim arcsin() (b) (5 pts) Find and classify
APPM 5 Final Eam (5 pts) Fall. The following problems are not related: (a) (5 pts, 5 pts ea.) Find the following limits or show that they do not eist: (i) lim e (ii) lim arcsin() (b) (5 pts) Find and classify
Chapter 2: First Order DE 2.4 Linear vs. Nonlinear DEs
 Chapter 2: First Order DE 2.4 Linear vs. Nonlinear DEs First Order DE 2.4 Linear vs. Nonlinear DE We recall the general form of the First Oreder DEs (FODE): dy = f(t, y) (1) dt where f(t, y) is a function
Chapter 2: First Order DE 2.4 Linear vs. Nonlinear DEs First Order DE 2.4 Linear vs. Nonlinear DE We recall the general form of the First Oreder DEs (FODE): dy = f(t, y) (1) dt where f(t, y) is a function
Lecture Notes in Mathematics. Arkansas Tech University Department of Mathematics
 Lecture Notes in Mathematics Arkansas Tech University Department of Mathematics Introductory Notes in Ordinary Differential Equations for Physical Sciences and Engineering Marcel B. Finan c All Rights
Lecture Notes in Mathematics Arkansas Tech University Department of Mathematics Introductory Notes in Ordinary Differential Equations for Physical Sciences and Engineering Marcel B. Finan c All Rights
CONTINUITY AND DIFFERENTIABILITY
 5. Introduction The whole of science is nothing more than a refinement of everyday thinking. ALBERT EINSTEIN This chapter is essentially a continuation of our stu of differentiation of functions in Class
5. Introduction The whole of science is nothing more than a refinement of everyday thinking. ALBERT EINSTEIN This chapter is essentially a continuation of our stu of differentiation of functions in Class
Trig Identities, Solving Trig Equations Answer Section
 Trig Identities, Solving Trig Equations Answer Section MULTIPLE CHOICE. ANS: B PTS: REF: Knowledge and Understanding OBJ: 7. - Compound Angle Formulas. ANS: A PTS: REF: Knowledge and Understanding OBJ:
Trig Identities, Solving Trig Equations Answer Section MULTIPLE CHOICE. ANS: B PTS: REF: Knowledge and Understanding OBJ: 7. - Compound Angle Formulas. ANS: A PTS: REF: Knowledge and Understanding OBJ:
Contents PART II. Foreword
 Contents PART II Foreword v Preface vii 7. Integrals 87 7. Introduction 88 7. Integration as an Inverse Process of Differentiation 88 7. Methods of Integration 00 7.4 Integrals of some Particular Functions
Contents PART II Foreword v Preface vii 7. Integrals 87 7. Introduction 88 7. Integration as an Inverse Process of Differentiation 88 7. Methods of Integration 00 7.4 Integrals of some Particular Functions
Review for the Final Exam
 Math 171 Review for the Final Exam 1 Find the limits (4 points each) (a) lim 4x 2 3; x x (b) lim ( x 2 x x 1 )x ; (c) lim( 1 1 ); x 1 ln x x 1 sin (x 2) (d) lim x 2 x 2 4 Solutions (a) The limit lim 4x
Math 171 Review for the Final Exam 1 Find the limits (4 points each) (a) lim 4x 2 3; x x (b) lim ( x 2 x x 1 )x ; (c) lim( 1 1 ); x 1 ln x x 1 sin (x 2) (d) lim x 2 x 2 4 Solutions (a) The limit lim 4x
DIFFERENTIATION RULES
 3 DIFFERENTIATION RULES DIFFERENTIATION RULES 3.6 Derivatives of Logarithmic Functions In this section, we: use implicit differentiation to find the derivatives of the logarithmic functions and, in particular,
3 DIFFERENTIATION RULES DIFFERENTIATION RULES 3.6 Derivatives of Logarithmic Functions In this section, we: use implicit differentiation to find the derivatives of the logarithmic functions and, in particular,
Chapter 2 Section 3. Partial Derivatives
 Chapter Section 3 Partial Derivatives Deinition. Let be a unction o two variables and. The partial derivative o with respect to is the unction, denoted b D1 1 such that its value at an point (,) in the
Chapter Section 3 Partial Derivatives Deinition. Let be a unction o two variables and. The partial derivative o with respect to is the unction, denoted b D1 1 such that its value at an point (,) in the
Math 1000 Final Exam Review Solutions. (x + 3)(x 2) = lim. = lim x 2 = 3 2 = 5. (x + 1) 1 x( x ) = lim. = lim. f f(1 + h) f(1) (1) = lim
 Math Final Eam Review Solutions { + 3 if < Consider f() Find the following limits: (a) lim f() + + (b) lim f() + 3 3 (c) lim f() does not eist Find each of the following limits: + 6 (a) lim 3 + 3 (b) lim
Math Final Eam Review Solutions { + 3 if < Consider f() Find the following limits: (a) lim f() + + (b) lim f() + 3 3 (c) lim f() does not eist Find each of the following limits: + 6 (a) lim 3 + 3 (b) lim
THE INVERSE FUNCTION THEOREM
 THE INVERSE FUNCTION THEOREM W. PATRICK HOOPER The implicit function theorem is the following result: Theorem 1. Let f be a C 1 function from a neighborhood of a point a R n into R n. Suppose A = Df(a)
THE INVERSE FUNCTION THEOREM W. PATRICK HOOPER The implicit function theorem is the following result: Theorem 1. Let f be a C 1 function from a neighborhood of a point a R n into R n. Suppose A = Df(a)
Rolle s Theorem, the Mean Value Theorem, and L Hôpital s Rule
 Rolle s Theorem, the Mean Value Theorem, and L Hôpital s Rule 5. Rolle s Theorem In the following problems (a) Verify that the three conditions of Rolle s theorem have been met. (b) Find all values z that
Rolle s Theorem, the Mean Value Theorem, and L Hôpital s Rule 5. Rolle s Theorem In the following problems (a) Verify that the three conditions of Rolle s theorem have been met. (b) Find all values z that
National University of Singapore Department of Mathematics
 National University of Singapore Department of Mathematics Semester I, 2002/2003 MA505 Math I Suggested Solutions to T. 2. Let f() be a real function defined as follows: sin(a) if
National University of Singapore Department of Mathematics Semester I, 2002/2003 MA505 Math I Suggested Solutions to T. 2. Let f() be a real function defined as follows: sin(a) if
Solutions to Math 53 First Exam April 20, 2010
 Solutions to Math 53 First Exam April 0, 00. (5 points) Match the direction fields below with their differential equations. Also indicate which two equations do not have matches. No justification is necessary.
Solutions to Math 53 First Exam April 0, 00. (5 points) Match the direction fields below with their differential equations. Also indicate which two equations do not have matches. No justification is necessary.
2nd-Order Linear Equations
 4 2nd-Order Linear Equations 4.1 Linear Independence of Functions In linear algebra the notion of linear independence arises frequently in the context of vector spaces. If V is a vector space over the
4 2nd-Order Linear Equations 4.1 Linear Independence of Functions In linear algebra the notion of linear independence arises frequently in the context of vector spaces. If V is a vector space over the
EXACT EQUATIONS AND INTEGRATING FACTORS
 MAP- EXACT EQUATIONS AND INTEGRATING FACTORS First-order Differential Equations for Which We Can Find Eact Solutions Stu the patterns carefully. The first step of any solution is correct identification
MAP- EXACT EQUATIONS AND INTEGRATING FACTORS First-order Differential Equations for Which We Can Find Eact Solutions Stu the patterns carefully. The first step of any solution is correct identification
Find the indicated derivative. 1) Find y(4) if y = 3 sin x. A) y(4) = 3 cos x B) y(4) = 3 sin x C) y(4) = - 3 cos x D) y(4) = - 3 sin x
 Assignment 5 Name Find the indicated derivative. ) Find y(4) if y = sin x. ) A) y(4) = cos x B) y(4) = sin x y(4) = - cos x y(4) = - sin x ) y = (csc x + cot x)(csc x - cot x) ) A) y = 0 B) y = y = - csc
Assignment 5 Name Find the indicated derivative. ) Find y(4) if y = sin x. ) A) y(4) = cos x B) y(4) = sin x y(4) = - cos x y(4) = - sin x ) y = (csc x + cot x)(csc x - cot x) ) A) y = 0 B) y = y = - csc
Calculus I Review Solutions
 Calculus I Review Solutions. Compare and contrast the three Value Theorems of the course. When you would typically use each. The three value theorems are the Intermediate, Mean and Extreme value theorems.
Calculus I Review Solutions. Compare and contrast the three Value Theorems of the course. When you would typically use each. The three value theorems are the Intermediate, Mean and Extreme value theorems.
CHAPTER 2 First Order Equations
 CHAPTER 2 First Order Equations IN THIS CHAPTER we study first order equations for which there are general methods of solution. SECTION 2.1 deals with linear equations, the simplest kind of first order
CHAPTER 2 First Order Equations IN THIS CHAPTER we study first order equations for which there are general methods of solution. SECTION 2.1 deals with linear equations, the simplest kind of first order
Calculus 1: A Large and In Charge Review Solutions
 Calculus : A Large and n Charge Review Solutions use the symbol which is shorthand for the phrase there eists.. We use the formula that Average Rate of Change is given by f(b) f(a) b a (a) (b) 5 = 3 =
Calculus : A Large and n Charge Review Solutions use the symbol which is shorthand for the phrase there eists.. We use the formula that Average Rate of Change is given by f(b) f(a) b a (a) (b) 5 = 3 =
Exercises given in lecture on the day in parantheses.
 A.Miller M22 Fall 23 Exercises given in lecture on the day in parantheses. The ɛ δ game. lim x a f(x) = L iff Hero has a winning strategy in the following game: Devil plays: ɛ > Hero plays: δ > Devil plays:
A.Miller M22 Fall 23 Exercises given in lecture on the day in parantheses. The ɛ δ game. lim x a f(x) = L iff Hero has a winning strategy in the following game: Devil plays: ɛ > Hero plays: δ > Devil plays:
4 Inverse function theorem
 Tel Aviv University, 2014/15 Analysis-III,IV 71 4 Inverse function theorem 4a What is the problem................ 71 4b Simple observations before the theorem..... 72 4c The theorem.....................
Tel Aviv University, 2014/15 Analysis-III,IV 71 4 Inverse function theorem 4a What is the problem................ 71 4b Simple observations before the theorem..... 72 4c The theorem.....................
Problem 1 In each of the following problems find the general solution of the given differential
 VI Problem 1 dt + 2dy 3y = 0; dt 9dy + 9y = 0. Problem 2 dt + dy 2y = 0, y(0) = 1, y (0) = 1; dt 2 y = 0, y( 2) = 1, y ( 2) = Problem 3 Find the solution of the initial value problem 2 d2 y dt 2 3dy dt
VI Problem 1 dt + 2dy 3y = 0; dt 9dy + 9y = 0. Problem 2 dt + dy 2y = 0, y(0) = 1, y (0) = 1; dt 2 y = 0, y( 2) = 1, y ( 2) = Problem 3 Find the solution of the initial value problem 2 d2 y dt 2 3dy dt
Math 1B Final Exam, Solution. Prof. Mina Aganagic Lecture 2, Spring (6 points) Use substitution and integration by parts to find:
 Math B Final Eam, Solution Prof. Mina Aganagic Lecture 2, Spring 20 The eam is closed book, apart from a sheet of notes 8. Calculators are not allowed. It is your responsibility to write your answers clearly..
Math B Final Eam, Solution Prof. Mina Aganagic Lecture 2, Spring 20 The eam is closed book, apart from a sheet of notes 8. Calculators are not allowed. It is your responsibility to write your answers clearly..
First Order ODEs, Part I
 Craig J. Sutton craig.j.sutton@dartmouth.edu Department of Mathematics Dartmouth College Math 23 Differential Equations Winter 2013 Outline 1 2 in General 3 The Definition & Technique Example Test for
Craig J. Sutton craig.j.sutton@dartmouth.edu Department of Mathematics Dartmouth College Math 23 Differential Equations Winter 2013 Outline 1 2 in General 3 The Definition & Technique Example Test for
MATH section 3.1 Maximum and Minimum Values Page 1 of 7
 MATH section. Maimum and Minimum Values Page of 7 Definition : Let c be a number in the domain D of a function f. Then c ) is the Absolute maimum value of f on D if ) c f() for all in D. Absolute minimum
MATH section. Maimum and Minimum Values Page of 7 Definition : Let c be a number in the domain D of a function f. Then c ) is the Absolute maimum value of f on D if ) c f() for all in D. Absolute minimum
Recapitulation of Mathematics
 Unit I Recapitulation of Mathematics Basics of Differentiation Rolle s an Lagrange s Theorem Tangent an Normal Inefinite an Definite Integral Engineering Mathematics I Basics of Differentiation CHAPTER
Unit I Recapitulation of Mathematics Basics of Differentiation Rolle s an Lagrange s Theorem Tangent an Normal Inefinite an Definite Integral Engineering Mathematics I Basics of Differentiation CHAPTER
Boundary-Value Problems
 46 We are now switching back to problems involving solitary differential equations. For the most part, these differential equations will be linear and second order. And, for various reasons, we will switch
46 We are now switching back to problems involving solitary differential equations. For the most part, these differential equations will be linear and second order. And, for various reasons, we will switch
a x a y = a x+y a x a = y ax y (a x ) r = a rx and log a (xy) = log a (x) + log a (y) log a ( x y ) = log a(x) log a (y) log a (x r ) = r log a (x).
 You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
10. Linear Systems of ODEs, Matrix multiplication, superposition principle (parts of sections )
 c Dr. Igor Zelenko, Fall 2017 1 10. Linear Systems of ODEs, Matrix multiplication, superposition principle (parts of sections 7.2-7.4) 1. When each of the functions F 1, F 2,..., F n in right-hand side
c Dr. Igor Zelenko, Fall 2017 1 10. Linear Systems of ODEs, Matrix multiplication, superposition principle (parts of sections 7.2-7.4) 1. When each of the functions F 1, F 2,..., F n in right-hand side
CALCULUS III THE CHAIN RULE, DIRECTIONAL DERIVATIVES, AND GRADIENT
 CALCULUS III THE CHAIN RULE, DIRECTIONAL DERIVATIVES, AND GRADIENT MATH 20300 DD & ST2 prepared by Antony Foster Department of Mathematics (office: NAC 6-273) The City College of The City University of
CALCULUS III THE CHAIN RULE, DIRECTIONAL DERIVATIVES, AND GRADIENT MATH 20300 DD & ST2 prepared by Antony Foster Department of Mathematics (office: NAC 6-273) The City College of The City University of
Solutions to Math 41 Exam 2 November 10, 2011
 Solutions to Math 41 Eam November 10, 011 1. (1 points) Find each of the following its, with justification. If the it does not eist, eplain why. If there is an infinite it, then eplain whether it is or.
Solutions to Math 41 Eam November 10, 011 1. (1 points) Find each of the following its, with justification. If the it does not eist, eplain why. If there is an infinite it, then eplain whether it is or.
Daily Lessons and Assessments for AP* Calculus AB, A Complete Course Page 584 Mark Sparks 2012
 The Second Fundamental Theorem of Calculus Functions Defined by Integrals Given the functions, f(t), below, use F( ) f ( t) dt to find F() and F () in terms of.. f(t) = 4t t. f(t) = cos t Given the functions,
The Second Fundamental Theorem of Calculus Functions Defined by Integrals Given the functions, f(t), below, use F( ) f ( t) dt to find F() and F () in terms of.. f(t) = 4t t. f(t) = cos t Given the functions,
Calculus IV - HW 3. Due 7/ Give the general solution to the following differential equations: y = c 1 e 5t + c 2 e 5t. y = c 1 e 2t + c 2 e 4t.
 Calculus IV - HW 3 Due 7/13 Section 3.1 1. Give the general solution to the following differential equations: a y 25y = 0 Solution: The characteristic equation is r 2 25 = r 5r + 5. It follows that the
Calculus IV - HW 3 Due 7/13 Section 3.1 1. Give the general solution to the following differential equations: a y 25y = 0 Solution: The characteristic equation is r 2 25 = r 5r + 5. It follows that the
MAC 2311 Final Exam Review Fall Private-Appointment, one-on-one tutoring at Broward Hall
 Fall 2016 This review, produced by the CLAS Teaching Center, contains a collection of questions which are representative of the type you may encounter on the eam. Other resources made available by the
Fall 2016 This review, produced by the CLAS Teaching Center, contains a collection of questions which are representative of the type you may encounter on the eam. Other resources made available by the
Economics 205 Exercises
 Economics 05 Eercises Prof. Watson, Fall 006 (Includes eaminations through Fall 003) Part 1: Basic Analysis 1. Using ε and δ, write in formal terms the meaning of lim a f() = c, where f : R R.. Write the
Economics 05 Eercises Prof. Watson, Fall 006 (Includes eaminations through Fall 003) Part 1: Basic Analysis 1. Using ε and δ, write in formal terms the meaning of lim a f() = c, where f : R R.. Write the
3.1 Functions. We will deal with functions for which both domain and the range are the set (or subset) of real numbers
 3.1 Functions A relation is a set of ordered pairs (, y). Eample: The set {(1,a), (1, b), (,b), (3,c), (3, a), (4,a)} is a relation A function is a relation (so, it is the set of ordered pairs) that does
3.1 Functions A relation is a set of ordered pairs (, y). Eample: The set {(1,a), (1, b), (,b), (3,c), (3, a), (4,a)} is a relation A function is a relation (so, it is the set of ordered pairs) that does
Integrals of the form. Notes by G.J.O. Jameson. I f (x) = x. f(t) cos t dt, S f (x) = x
 Integrals of the form f(t)eit dt Notes by G.J.O. Jameson Basic results We consider integrals of the form with real and imaginary parts I f () = f(t)e it dt, C f () = f(t) cos t dt, S f () = f(t) sin t
Integrals of the form f(t)eit dt Notes by G.J.O. Jameson Basic results We consider integrals of the form with real and imaginary parts I f () = f(t)e it dt, C f () = f(t) cos t dt, S f () = f(t) sin t
The Chain Rule. This is a generalization of the (general) power rule which we have already met in the form: then f (x) = r [g(x)] r 1 g (x).
![The Chain Rule. This is a generalization of the (general) power rule which we have already met in the form: then f (x) = r [g(x)] r 1 g (x). The Chain Rule. This is a generalization of the (general) power rule which we have already met in the form: then f (x) = r [g(x)] r 1 g (x).](/thumbs/78/77820746.jpg) The Chain Rule This is a generalization of the general) power rule which we have already met in the form: If f) = g)] r then f ) = r g)] r g ). Here, g) is any differentiable function and r is any real
The Chain Rule This is a generalization of the general) power rule which we have already met in the form: If f) = g)] r then f ) = r g)] r g ). Here, g) is any differentiable function and r is any real
±. Then. . x. lim g( x) = lim. cos x 1 sin x. and (ii) lim
 MATH 36 L'H ˆ o pital s Rule Si of the indeterminate forms of its may be algebraically determined using L H ˆ o pital's Rule. This rule is only stated for the / and ± /± indeterminate forms, but four other
MATH 36 L'H ˆ o pital s Rule Si of the indeterminate forms of its may be algebraically determined using L H ˆ o pital's Rule. This rule is only stated for the / and ± /± indeterminate forms, but four other
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. D) g (x) = - 2 x2 ; g (- 2) = C) 21 4
 Cal 1: Test review Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question Calculate the derivative of the function. Then find the value of the derivative
Cal 1: Test review Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question Calculate the derivative of the function. Then find the value of the derivative
Name Class. 5. Find the particular solution to given the general solution y C cos x and the. x 2 y
 10 Differential Equations Test Form A 1. Find the general solution to the first order differential equation: y 1 yy 0. 1 (a) (b) ln y 1 y ln y 1 C y y C y 1 C y 1 y C. Find the general solution to the
10 Differential Equations Test Form A 1. Find the general solution to the first order differential equation: y 1 yy 0. 1 (a) (b) ln y 1 y ln y 1 C y y C y 1 C y 1 y C. Find the general solution to the
Solutions to Problem Sheet for Week 6
 THE UNIVERSITY OF SYDNEY SCHOOL OF MATHEMATICS AND STATISTICS Solutions to Problem Sheet for Week 6 MATH90: Differential Calculus (Advanced) Semester, 07 Web Page: sydney.edu.au/science/maths/u/ug/jm/math90/
THE UNIVERSITY OF SYDNEY SCHOOL OF MATHEMATICS AND STATISTICS Solutions to Problem Sheet for Week 6 MATH90: Differential Calculus (Advanced) Semester, 07 Web Page: sydney.edu.au/science/maths/u/ug/jm/math90/
Math 240 Calculus III
 Line Math 114 Calculus III Summer 2013, Session II Monday, July 1, 2013 Agenda Line 1.,, and 2. Line vector Line Definition Let f : X R 3 R be a differentiable scalar function on a region of 3-dimensional
Line Math 114 Calculus III Summer 2013, Session II Monday, July 1, 2013 Agenda Line 1.,, and 2. Line vector Line Definition Let f : X R 3 R be a differentiable scalar function on a region of 3-dimensional
2 nd ORDER O.D.E.s SUBSTITUTIONS
 nd ORDER O.D.E.s SUBSTITUTIONS Question 1 (***+) d y y 8y + 16y = d d d, y 0, Find the general solution of the above differential equation by using the transformation equation t = y. Give the answer in
nd ORDER O.D.E.s SUBSTITUTIONS Question 1 (***+) d y y 8y + 16y = d d d, y 0, Find the general solution of the above differential equation by using the transformation equation t = y. Give the answer in
C3 Revision Questions. (using questions from January 2006, January 2007, January 2008 and January 2009)
 C3 Revision Questions (using questions from January 2006, January 2007, January 2008 and January 2009) 1 2 1. f(x) = 1 3 x 2 + 3, x 2. 2 ( x 2) (a) 2 x x 1 Show that f(x) =, x 2. 2 ( x 2) (4) (b) Show
C3 Revision Questions (using questions from January 2006, January 2007, January 2008 and January 2009) 1 2 1. f(x) = 1 3 x 2 + 3, x 2. 2 ( x 2) (a) 2 x x 1 Show that f(x) =, x 2. 2 ( x 2) (4) (b) Show
CHAPTER 2 DIFFERENTIATION 2.1 FIRST ORDER DIFFERENTIATION. What is Differentiation?
 BA01 ENGINEERING MATHEMATICS 01 CHAPTER DIFFERENTIATION.1 FIRST ORDER DIFFERENTIATION What is Differentiation? Differentiation is all about finding rates of change of one quantity compared to another.
BA01 ENGINEERING MATHEMATICS 01 CHAPTER DIFFERENTIATION.1 FIRST ORDER DIFFERENTIATION What is Differentiation? Differentiation is all about finding rates of change of one quantity compared to another.
Review: A Cross Section of the Midterm. MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Review: A Cross Section of the Midterm Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the limit, if it eists. 4 + ) lim - - ) A) - B) -
Review: A Cross Section of the Midterm Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the limit, if it eists. 4 + ) lim - - ) A) - B) -
Department of Mathematical x 1 x 2 1
 Contents Limits. Basic Factoring Eample....................................... One-Sided Limit........................................... 3.3 Squeeze Theorem.......................................... 4.4
Contents Limits. Basic Factoring Eample....................................... One-Sided Limit........................................... 3.3 Squeeze Theorem.......................................... 4.4
Chapter 2: The Derivative
 Chapter 2: The Derivative Summary: Chapter 2 builds upon the ideas of limits and continuity discussed in the previous chapter. By using limits, the instantaneous rate at which a function changes with respect
Chapter 2: The Derivative Summary: Chapter 2 builds upon the ideas of limits and continuity discussed in the previous chapter. By using limits, the instantaneous rate at which a function changes with respect
Section: I. u 4 du. (9x + 1) + C, 3
 EXAM 3 MAT 168 Calculus II Fall 18 Name: Section: I All answers must include either supporting work or an eplanation of your reasoning. MPORTANT: These elements are considered main part of the answer and
EXAM 3 MAT 168 Calculus II Fall 18 Name: Section: I All answers must include either supporting work or an eplanation of your reasoning. MPORTANT: These elements are considered main part of the answer and
Problem Set 9 Solutions
 8.4 Problem Set 9 Solutions Total: 4 points Problem : Integrate (a) (b) d. ( 4 + 4)( 4 + 5) d 4. Solution (4 points) (a) We use the method of partial fractions to write A B (C + D) = + +. ( ) ( 4 + 5)
8.4 Problem Set 9 Solutions Total: 4 points Problem : Integrate (a) (b) d. ( 4 + 4)( 4 + 5) d 4. Solution (4 points) (a) We use the method of partial fractions to write A B (C + D) = + +. ( ) ( 4 + 5)
First-Order ODEs. Chapter Separable Equations. We consider in this chapter differential equations of the form dy (1.1)
 Chapter 1 First-Order ODEs We consider in this chapter differential equations of the form dy (1.1) = F (t, y), where F (t, y) is a known smooth function. We wish to solve for y(t). Equation (1.1) is called
Chapter 1 First-Order ODEs We consider in this chapter differential equations of the form dy (1.1) = F (t, y), where F (t, y) is a known smooth function. We wish to solve for y(t). Equation (1.1) is called
First Order Differential Equations Lecture 3
 First Order Differential Equations Lecture 3 Dibyajyoti Deb 3.1. Outline of Lecture Differences Between Linear and Nonlinear Equations Exact Equations and Integrating Factors 3.. Differences between Linear
First Order Differential Equations Lecture 3 Dibyajyoti Deb 3.1. Outline of Lecture Differences Between Linear and Nonlinear Equations Exact Equations and Integrating Factors 3.. Differences between Linear
Solutions to Homework Assignment #2
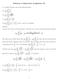 Solutions to Homework Assignment #. [4 marks] Evaluate each of the following limits. n i a lim n. b lim c lim d lim n i. sin πi n. a i n + b, where a and b are constants. n a There are ways to do this
Solutions to Homework Assignment #. [4 marks] Evaluate each of the following limits. n i a lim n. b lim c lim d lim n i. sin πi n. a i n + b, where a and b are constants. n a There are ways to do this
171, Calculus 1. Summer 1, CRN 50248, Section 001. Time: MTWR, 6:30 p.m. 8:30 p.m. Room: BR-43. CRN 50248, Section 002
 171, Calculus 1 Summer 1, 018 CRN 5048, Section 001 Time: MTWR, 6:0 p.m. 8:0 p.m. Room: BR-4 CRN 5048, Section 00 Time: MTWR, 11:0 a.m. 1:0 p.m. Room: BR-4 CONTENTS Syllabus Reviews for tests 1 Review
171, Calculus 1 Summer 1, 018 CRN 5048, Section 001 Time: MTWR, 6:0 p.m. 8:0 p.m. Room: BR-4 CRN 5048, Section 00 Time: MTWR, 11:0 a.m. 1:0 p.m. Room: BR-4 CONTENTS Syllabus Reviews for tests 1 Review
Math 181, Exam 2, Fall 2014 Problem 1 Solution. sin 3 (x) cos(x) dx.
 Math 8, Eam 2, Fall 24 Problem Solution. Integrals, Part I (Trigonometric integrals: 6 points). Evaluate the integral: sin 3 () cos() d. Solution: We begin by rewriting sin 3 () as Then, after using the
Math 8, Eam 2, Fall 24 Problem Solution. Integrals, Part I (Trigonometric integrals: 6 points). Evaluate the integral: sin 3 () cos() d. Solution: We begin by rewriting sin 3 () as Then, after using the
Functions. Chapter Continuous Functions
 Chapter 3 Functions 3.1 Continuous Functions A function f is determined by the domain of f: dom(f) R, the set on which f is defined, and the rule specifying the value f(x) of f at each x dom(f). If f is
Chapter 3 Functions 3.1 Continuous Functions A function f is determined by the domain of f: dom(f) R, the set on which f is defined, and the rule specifying the value f(x) of f at each x dom(f). If f is
Calculus with business applications, Lehigh U, Lecture 05 notes Summer
 Calculus with business applications, Lehigh U, Lecture 0 notes Summer 0 Trigonometric functions. Trigonometric functions often arise in physical applications with periodic motion. They do not arise often
Calculus with business applications, Lehigh U, Lecture 0 notes Summer 0 Trigonometric functions. Trigonometric functions often arise in physical applications with periodic motion. They do not arise often
VARIATIONAL PRINCIPLES
 CHAPTER - II VARIATIONAL PRINCIPLES Unit : Euler-Lagranges s Differential Equations: Introduction: We have seen that co-ordinates are the tools in the hands of a mathematician. With the help of these co-ordinates
CHAPTER - II VARIATIONAL PRINCIPLES Unit : Euler-Lagranges s Differential Equations: Introduction: We have seen that co-ordinates are the tools in the hands of a mathematician. With the help of these co-ordinates
4. Higher Order Linear DEs
 4. Higher Order Linear DEs Department of Mathematics & Statistics ASU Outline of Chapter 4 1 General Theory of nth Order Linear Equations 2 Homogeneous Equations with Constant Coecients 3 The Method of
4. Higher Order Linear DEs Department of Mathematics & Statistics ASU Outline of Chapter 4 1 General Theory of nth Order Linear Equations 2 Homogeneous Equations with Constant Coecients 3 The Method of
Calculus Problem Sheet Prof Paul Sutcliffe. 2. State the domain and range of each of the following functions
 f( 8 6 4 8 6-3 - - 3 4 5 6 f(.9.8.7.6.5.4.3.. -4-3 - - 3 f( 7 6 5 4 3-3 - - Calculus Problem Sheet Prof Paul Sutcliffe. By applying the vertical line test, or otherwise, determine whether each of the following
f( 8 6 4 8 6-3 - - 3 4 5 6 f(.9.8.7.6.5.4.3.. -4-3 - - 3 f( 7 6 5 4 3-3 - - Calculus Problem Sheet Prof Paul Sutcliffe. By applying the vertical line test, or otherwise, determine whether each of the following
Section 3.7. Rolle s Theorem and the Mean Value Theorem
 Section.7 Rolle s Theorem and the Mean Value Theorem The two theorems which are at the heart of this section draw connections between the instantaneous rate of change and the average rate of change of
Section.7 Rolle s Theorem and the Mean Value Theorem The two theorems which are at the heart of this section draw connections between the instantaneous rate of change and the average rate of change of
Some commonly encountered sets and their notations
 NATIONAL UNIVERSITY OF SINGAPORE DEPARTMENT OF MATHEMATICS (This notes are based on the book Introductory Mathematics by Ng Wee Seng ) LECTURE SETS & FUNCTIONS Some commonly encountered sets and their
NATIONAL UNIVERSITY OF SINGAPORE DEPARTMENT OF MATHEMATICS (This notes are based on the book Introductory Mathematics by Ng Wee Seng ) LECTURE SETS & FUNCTIONS Some commonly encountered sets and their
PROBLEMS In each of Problems 1 through 12:
 6.5 Impulse Functions 33 which is the formal solution of the given problem. It is also possible to write y in the form 0, t < 5, y = 5 e (t 5/ sin 5 (t 5, t 5. ( The graph of Eq. ( is shown in Figure 6.5.3.
6.5 Impulse Functions 33 which is the formal solution of the given problem. It is also possible to write y in the form 0, t < 5, y = 5 e (t 5/ sin 5 (t 5, t 5. ( The graph of Eq. ( is shown in Figure 6.5.3.
CLEP Calculus. Time 60 Minutes 45 Questions. For each question below, choose the best answer from the choices given. 2. If f(x) = 3x, then f (x) =
 CLEP Calculus Time 60 Minutes 5 Questions For each question below, choose the best answer from the choices given. 7. lim 5 + 5 is (A) 7 0 (C) 7 0 (D) 7 (E) Noneistent. If f(), then f () (A) (C) (D) (E)
CLEP Calculus Time 60 Minutes 5 Questions For each question below, choose the best answer from the choices given. 7. lim 5 + 5 is (A) 7 0 (C) 7 0 (D) 7 (E) Noneistent. If f(), then f () (A) (C) (D) (E)
Lecture 2. Classification of Differential Equations and Method of Integrating Factors
 Math 245 - Mathematics of Physics and Engineering I Lecture 2. Classification of Differential Equations and Method of Integrating Factors January 11, 2012 Konstantin Zuev (USC) Math 245, Lecture 2 January
Math 245 - Mathematics of Physics and Engineering I Lecture 2. Classification of Differential Equations and Method of Integrating Factors January 11, 2012 Konstantin Zuev (USC) Math 245, Lecture 2 January
Chapter 8: Taylor s theorem and L Hospital s rule
 Chapter 8: Taylor s theorem and L Hospital s rule Theorem: [Inverse Mapping Theorem] Suppose that a < b and f : [a, b] R. Given that f (x) > 0 for all x (a, b) then f 1 is differentiable on (f(a), f(b))
Chapter 8: Taylor s theorem and L Hospital s rule Theorem: [Inverse Mapping Theorem] Suppose that a < b and f : [a, b] R. Given that f (x) > 0 for all x (a, b) then f 1 is differentiable on (f(a), f(b))
Introduction to Differential Equations
 Math0 Lecture # Introduction to Differential Equations Basic definitions Definition : (What is a DE?) A differential equation (DE) is an equation that involves some of the derivatives (or differentials)
Math0 Lecture # Introduction to Differential Equations Basic definitions Definition : (What is a DE?) A differential equation (DE) is an equation that involves some of the derivatives (or differentials)
Solutions to the Exercises of Chapter 8
 8A Domains of Functions Solutions to the Eercises of Chapter 8 1 For 7 to make sense, we need 7 0or7 So the domain of f() is{ 7} For + 5 to make sense, +5 0 So the domain of g() is{ 5} For h() to make
8A Domains of Functions Solutions to the Eercises of Chapter 8 1 For 7 to make sense, we need 7 0or7 So the domain of f() is{ 7} For + 5 to make sense, +5 0 So the domain of g() is{ 5} For h() to make
Chapter 2 Notes, Kohler & Johnson 2e
 Contents 2 First Order Differential Equations 2 2.1 First Order Equations - Existence and Uniqueness Theorems......... 2 2.2 Linear First Order Differential Equations.................... 5 2.2.1 First
Contents 2 First Order Differential Equations 2 2.1 First Order Equations - Existence and Uniqueness Theorems......... 2 2.2 Linear First Order Differential Equations.................... 5 2.2.1 First
PHYS 705: Classical Mechanics. Calculus of Variations I
 1 PHYS 705: Classical Mechanics Calculus of Variations I Calculus of Variations: The Problem Determine the function y() such that the following integral is min(ma)imized. Comments: I F y( ), y'( ); d 1.
1 PHYS 705: Classical Mechanics Calculus of Variations I Calculus of Variations: The Problem Determine the function y() such that the following integral is min(ma)imized. Comments: I F y( ), y'( ); d 1.
Multiple Choice. Circle the best answer. No work needed. No partial credit available. is continuous.
 Multiple Choice. Circle the best answer. No work needed. No partial credit available. + +. Evaluate lim + (a (b (c (d 0 (e None of the above.. Evaluate lim (a (b (c (d 0 (e + + None of the above.. Find
Multiple Choice. Circle the best answer. No work needed. No partial credit available. + +. Evaluate lim + (a (b (c (d 0 (e None of the above.. Evaluate lim (a (b (c (d 0 (e + + None of the above.. Find
term from the numerator yields 2
 APPM 1350 Eam 2 Fall 2013 1. The following parts are not related: (a) (12 pts) Find y given: (i) y = (ii) y = sec( 2 1) tan() (iii) ( 2 + y 2 ) 2 = 2 2 2y 2 1 (b) (8 pts) Let f() be a function such that
APPM 1350 Eam 2 Fall 2013 1. The following parts are not related: (a) (12 pts) Find y given: (i) y = (ii) y = sec( 2 1) tan() (iii) ( 2 + y 2 ) 2 = 2 2 2y 2 1 (b) (8 pts) Let f() be a function such that
UCLA Math 135, Winter 2015 Ordinary Differential Equations
 UCLA Math 135, Winter 2015 Ordinary Differential Equations C. David Levermore Department of Mathematics University of Maryland January 5, 2015 Contents 1.1. Normal Forms and Solutions 1.2. Initial-Value
UCLA Math 135, Winter 2015 Ordinary Differential Equations C. David Levermore Department of Mathematics University of Maryland January 5, 2015 Contents 1.1. Normal Forms and Solutions 1.2. Initial-Value
6.5 Trigonometric Equations
 6. Trigonometric Equations In this section, we discuss conditional trigonometric equations, that is, equations involving trigonometric functions that are satisfied only by some values of the variable (or
6. Trigonometric Equations In this section, we discuss conditional trigonometric equations, that is, equations involving trigonometric functions that are satisfied only by some values of the variable (or
Fundamental Theorem of Calculus
 Fundamental Theorem of Calculus MATH 6 Calculus I J. Robert Buchanan Department of Mathematics Summer 208 Remarks The Fundamental Theorem of Calculus (FTC) will make the evaluation of definite integrals
Fundamental Theorem of Calculus MATH 6 Calculus I J. Robert Buchanan Department of Mathematics Summer 208 Remarks The Fundamental Theorem of Calculus (FTC) will make the evaluation of definite integrals
Regent College Maths Department. Core Mathematics 4 Trapezium Rule. C4 Integration Page 1
 Regent College Maths Department Core Mathematics Trapezium Rule C Integration Page Integration It might appear to be a bit obvious but you must remember all of your C work on differentiation if you are
Regent College Maths Department Core Mathematics Trapezium Rule C Integration Page Integration It might appear to be a bit obvious but you must remember all of your C work on differentiation if you are
Ordinary Differential Equation Theory
 Part I Ordinary Differential Equation Theory 1 Introductory Theory An n th order ODE for y = y(t) has the form Usually it can be written F (t, y, y,.., y (n) ) = y (n) = f(t, y, y,.., y (n 1) ) (Implicit
Part I Ordinary Differential Equation Theory 1 Introductory Theory An n th order ODE for y = y(t) has the form Usually it can be written F (t, y, y,.., y (n) ) = y (n) = f(t, y, y,.., y (n 1) ) (Implicit
Partial Fractions. dx dx x sec tan d 1 4 tan 2. 2 csc d. csc cot C. 2x 5. 2 ln. 2 x 2 5x 6 C. 2 ln. 2 ln x
 460_080.qd //04 :08 PM Page CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8. Partial Fractions Understand the concept of a partial fraction decomposition. Use partial
460_080.qd //04 :08 PM Page CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8. Partial Fractions Understand the concept of a partial fraction decomposition. Use partial
Calculus - II Multivariable Calculus. M.Thamban Nair. Department of Mathematics Indian Institute of Technology Madras
 Calculus - II Multivariable Calculus M.Thamban Nair epartment of Mathematics Indian Institute of Technology Madras February 27 Revised: January 29 Contents Preface v 1 Functions of everal Variables 1 1.1
Calculus - II Multivariable Calculus M.Thamban Nair epartment of Mathematics Indian Institute of Technology Madras February 27 Revised: January 29 Contents Preface v 1 Functions of everal Variables 1 1.1
Homework #12 corrections
 Homework #2 corrections April 25, 205 (284) Let f() = 2 sin for 0 and f(0) = 0 (a) Use Theorems 283 and 284 to show f is differentiable at each a 0 and calculate f (a) Use, without proof, the fact that
Homework #2 corrections April 25, 205 (284) Let f() = 2 sin for 0 and f(0) = 0 (a) Use Theorems 283 and 284 to show f is differentiable at each a 0 and calculate f (a) Use, without proof, the fact that
Definition of Tangent Line with Slope m: If f is defined on an open interval containing x, and if the limit y f( c x) f( c) f( c x) f( c) lim lim lim
 Derivatives and the Tangent Line Problem Objective: Find the slope of the tangent line to a curve at a point. Use the limit definition to find the derivative of a function. Understand the relationship
Derivatives and the Tangent Line Problem Objective: Find the slope of the tangent line to a curve at a point. Use the limit definition to find the derivative of a function. Understand the relationship
2413 Exam 3 Review. 14t 2 Ë. dt. t 6 1 dt. 3z 2 12z 9 z 4 8 Ë. n 7 4,4. Short Answer. 1. Find the indefinite integral 9t 2 ˆ
 3 Eam 3 Review Short Answer. Find the indefinite integral 9t ˆ t dt.. Find the indefinite integral of the following function and check the result by differentiation. 6t 5 t 6 dt 3. Find the indefinite
3 Eam 3 Review Short Answer. Find the indefinite integral 9t ˆ t dt.. Find the indefinite integral of the following function and check the result by differentiation. 6t 5 t 6 dt 3. Find the indefinite
The answers below are not comprehensive and are meant to indicate the correct way to solve the problem. sin
 Math : Practice Final Answer Key Name: The answers below are not comprehensive and are meant to indicate the correct way to solve the problem. Problem : Consider the definite integral I = 5 sin ( ) d.
Math : Practice Final Answer Key Name: The answers below are not comprehensive and are meant to indicate the correct way to solve the problem. Problem : Consider the definite integral I = 5 sin ( ) d.
dx dx x sec tan d 1 4 tan 2 2 csc d 2 ln 2 x 2 5x 6 C 2 ln 2 ln x ln x 3 x 2 C Now, suppose you had observed that x 3
 CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8. Partial Fractions Understand the concept of a partial fraction decomposition. Use partial fraction decomposition with
CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8. Partial Fractions Understand the concept of a partial fraction decomposition. Use partial fraction decomposition with
Course 212: Academic Year Section 1: Metric Spaces
 Course 212: Academic Year 1991-2 Section 1: Metric Spaces D. R. Wilkins Contents 1 Metric Spaces 3 1.1 Distance Functions and Metric Spaces............. 3 1.2 Convergence and Continuity in Metric Spaces.........
Course 212: Academic Year 1991-2 Section 1: Metric Spaces D. R. Wilkins Contents 1 Metric Spaces 3 1.1 Distance Functions and Metric Spaces............. 3 1.2 Convergence and Continuity in Metric Spaces.........
Limits and Continuous Functions. 2.2 Introduction to Limits. We first interpret limits loosely. We write. lim f(x) = L
 2 Limits and Continuous Functions 2.2 Introduction to Limits We first interpret limits loosel. We write lim f() = L and sa the limit of f() as approaches c, equals L if we can make the values of f() arbitraril
2 Limits and Continuous Functions 2.2 Introduction to Limits We first interpret limits loosel. We write lim f() = L and sa the limit of f() as approaches c, equals L if we can make the values of f() arbitraril
25. Chain Rule. Now, f is a function of t only. Expand by multiplication:
 25. Chain Rule The Chain Rule is present in all differentiation. If z = f(x, y) represents a two-variable function, then it is plausible to consider the cases when x and y may be functions of other variable(s).
25. Chain Rule The Chain Rule is present in all differentiation. If z = f(x, y) represents a two-variable function, then it is plausible to consider the cases when x and y may be functions of other variable(s).
for any C, including C = 0, because y = 0 is also a solution: dy
 Math 3200-001 Fall 2014 Practice exam 1 solutions 2/16/2014 Each problem is worth 0 to 4 points: 4=correct, 3=small error, 2=good progress, 1=some progress 0=nothing relevant. If the result is correct,
Math 3200-001 Fall 2014 Practice exam 1 solutions 2/16/2014 Each problem is worth 0 to 4 points: 4=correct, 3=small error, 2=good progress, 1=some progress 0=nothing relevant. If the result is correct,
MATH 1010E University Mathematics Lecture Notes (week 8) Martin Li
 MATH 1010E University Mathematics Lecture Notes (week 8) Martin Li 1 L Hospital s Rule Another useful application of mean value theorems is L Hospital s Rule. It helps us to evaluate its of indeterminate
MATH 1010E University Mathematics Lecture Notes (week 8) Martin Li 1 L Hospital s Rule Another useful application of mean value theorems is L Hospital s Rule. It helps us to evaluate its of indeterminate
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals 8. Basic Integration Rules In this section we will review various integration strategies. Strategies: I. Separate
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals 8. Basic Integration Rules In this section we will review various integration strategies. Strategies: I. Separate
Spherical trigonometry
 Spherical trigonometry 1 The spherical Pythagorean theorem Proposition 1.1 On a sphere of radius, any right triangle AC with C being the right angle satisfies cos(c/) = cos(a/) cos(b/). (1) Proof: Let
Spherical trigonometry 1 The spherical Pythagorean theorem Proposition 1.1 On a sphere of radius, any right triangle AC with C being the right angle satisfies cos(c/) = cos(a/) cos(b/). (1) Proof: Let
Review sheet Final Exam Math 140 Calculus I Fall 2015 UMass Boston
 Review sheet Final Eam Math Calculus I Fall 5 UMass Boston The eam is closed tetbook NO CALCULATORS OR ELECTRONIC DEVICES ARE ALLOWED DURING THE EXAM The final eam will contain problems of types similar
Review sheet Final Eam Math Calculus I Fall 5 UMass Boston The eam is closed tetbook NO CALCULATORS OR ELECTRONIC DEVICES ARE ALLOWED DURING THE EXAM The final eam will contain problems of types similar
M151B Practice Problems for Final Exam
 M5B Practice Problems for Final Eam Calculators will not be allowed on the eam. Unjustified answers will not receive credit. On the eam you will be given the following identities: n k = n(n + ) ; n k =
M5B Practice Problems for Final Eam Calculators will not be allowed on the eam. Unjustified answers will not receive credit. On the eam you will be given the following identities: n k = n(n + ) ; n k =
7.1. Calculus of inverse functions. Text Section 7.1 Exercise:
 Contents 7. Inverse functions 1 7.1. Calculus of inverse functions 2 7.2. Derivatives of exponential function 4 7.3. Logarithmic function 6 7.4. Derivatives of logarithmic functions 7 7.5. Exponential
Contents 7. Inverse functions 1 7.1. Calculus of inverse functions 2 7.2. Derivatives of exponential function 4 7.3. Logarithmic function 6 7.4. Derivatives of logarithmic functions 7 7.5. Exponential
