Mathematical Proofs Table of Contents
|
|
|
- Harvey Gregory
- 5 years ago
- Views:
Transcription
1 Mthemtil Proofs Tle of Contents Proof Stnr Pge(s) Are of Trpezoi 7MG. Geometry 8.0 Are of Cirle 6MG., 9 6MG. 7MG. Geometry 8.0 Volume of Right Cirulr Cyliner 6MG. 4 7MG. Geometry 8.0 Volume of Sphere Geometry Algeri Ientities Alger I 0.0 6, 7, 8, 7 Irrtionlity of 7NS.4 9, 0, Alger I.0 Alger I 5.0 Division y 0 NS.6 Diviing y Frtion 6NS. 7NS. Slope of Line is Constnt 7AF. Alger I 6.0 Prout Property of Rils Alger I Squre Roots Alger I.0 5 Pythgoren Theorem n Converse 7MG. 6, 7 Geometry 4.0 Definition of pi 6MG. 8 6MG. Cirumferene of Cirle 6MG. 8 6MG. Zero Prout Rule 7AF. Alger I.0 9 N is irrtionl if N is positive integer tht 7NS.4 0 is not perfet squre Alger I. Density A Property of Rtionl Numers Alger I. Squre n Tringulr Numers 7NS.0 4 Alger I. Multiplition of Negtive Numers 6NS. 5 7NS. Zero Property of Multiplition 7 NS.0 6 Alger I. Commuttive, Assoitive, n Distriutive 7NS.0 8 Properties Alger I 5.0 Terminting Deimls 7NS.5 0
2 Are of Trpezoi Proof of A h Trpezoi Region h Region h Region x x The proof of the re formul flls into ple s follows: The re of tringle Region : xh A l eft trin gle The re of retngle Region : h A retngle The re of tringle Region : A xh right tringle The omine re of the three Regions: A Trpezoi xh h xh Aing the three regions ATrpezoi xh h h h xh ATrpezoi h h h Aition Property ATrpezoi h h Simplify ATrpezoi h Q.E.D. Are of Cirle
3 Using the onept of the Are of Tringle to show tht Are of Cirle = r. r If we ut the irles long the rius of the isk n let them fn out to eome stright lines, we get tringle (euse the rtio of the irumferene of the irles to their imeters is onstnt). The se length of the resulting tringle is equl to the irumferene of the originl irle, n its height is equl to the rius of this irle. Thus, the re of irle is equl to hlf of the prout of the rius n the irumferene. A Tringle re of se height Sine, A re of se height A Tringle Tringle r r r r whih equls to the re of the DISK or CIRCLE. Volume of Right Cirulr Cyliner
4 Volume = (Are of Bse)(Height) V r h If you en retngulr sheet of pper, ringing two opposite sies together, you will get n open tue. r h h This is lle n open yliner. The surfe re of this open yliner is the re of its urve surfe given y the prout of the istne roun the rim n the height. rh r h If the top n ottom of the yliner re overe, we will hve lose yliner. Thus, the formul for volume of prism or yliner is given y V = Volume = (Are of Bse)(Height) V r h 4
5 Volumes Cvlieri s Priniple: Solis with the sme height n with ross-setions of equl re hve the sme volume; in prtiulr, prisms or yliners with equl ses n heights hve the sme volume. Volume of Sphere An Experimentl Approh: If we uil yliner with height r n the imeter r n fill the yliner with wter n then remove the sphere from the yliner, the wter will only tke up of the yliner. Thus, the volume of the sphere is the volume of the yliner hving the sme imeter s the sphere n height equl to the imeter. r r Volume of the Cyliner: V r h. Proven erlier Eqution h r. Given V r r. Sustitution So, V r. Simplify Eqution We know from the experiment tht: Volume of the Sphere the Volume of Cyliner Volume of the Sphere r Volume of the Sphere = 4 r Q.E.D. 5
6 Algeri Ientities Algeri mnipultion very often n e expline with the i of geometril figures. Ojetive : To show tht The figure on the right is squre me up of four Regions: I, II, III & IV. I A II Eh sie of the squre hs length units. III IV Are of the squre is: squre units. A A Are Region I: A squre units Are Region II: Are Region III: A squre units A squre units Are Region IV: A squre units Are of the Squre = Are Region I + Are Region II + Are Region III + Are Region IV, whih is Sum of the res in the lrge squre ( ) Equte the two expressions for the re 6
7 Ojetive : To show tht (see n lternte proof on pge 7) - I IV The figure on the left is me up of four Regions: I, II, III, n IV. II III Regions: I, II, III mke up SQUARE, whih hs n AREA of squre units. Region IV hs n re of units. squre Are Region I: A squre units Are Region II: A squre units Are Region III: A squre units Are Region IV: A squre units Are Regions I & IV: A squre units We know Region I + Region II + Region III = ( ) ( ) Sum of res in the squre Isolting ( ) ( ) ( ) ( ) Distriutive Property ( ) Assoitive n Commuttive Properties 7
8 Ojetive : To show tht II I II I Figure Figure A smll squre (in re), re squre units is remove from igger squre of re squre units s shown in the Figure ove. Thus, the re of regions I n II is squre units. In Figure, the two remining regions, I n II, re rerrnge to form the retngle shown. The re of the newly forme retngle is equl to Hene, Further justifition: Totl Are of Figure : Totl Are of Figure : squre units 8
9 Proof is irrtionl The Greeks isovere tht the igonl of squre whose sie is unit long hs igonl whose length nnot e rtionl. By the Pythgoren Theorem, the length of the igonl equls the squre root of. So the squre root of is irrtionl! The following proof is lssi exmple of proof y ontrition: We wnt to show tht A is true, so we ssume it's not, n ome to ontrition. Thus A must e true sine there re no ontritions in mthemtis! Proof: Suppose is rtionl. Tht mens n e written s the rtio of two integers p n q, where q 0. p Eqution # q Where we my ssume tht p n q hve no ommon ftors. (If there re ny ommon ftors we nel them in the numertor n enomintor.) Then, p Squring oth sies of Eq. # q This implies p q Isolting Thus, p p is even. This mens tht p itself must e even. woul lso e o. (An o numer times n o numer is lwys o.) So p is n even numer. Then p is times some other whole numer, or p k, where k is this other numer. We on't nee to know extly wht k is; it oesn't mtter. Soon we will get our ontrition: Why? Beuse if p ws o, then p p Then Hene p = 4k. So 4k = q, hene q = k. q is even n therefore q itself must e even. So p n q re BOTH even. They oth hve ommon ftor of. This ontrits our ssumption tht p n q hve no ommon ftors. The squre root of is NOT rtionl. 9
10 The Irrtionlity of Prove tht is n irrtionl numer. Solution: The numer,, is irrtionl, ie., it nnot e expresse s rtio of integers n. To prove tht this sttement is true, let us ssume tht is rtionl so tht we my write = /. for n = ny two integers. To show tht is irrtionl, we must show tht no two suh integers n e foun. We egin y squring oth sies of eq. : = /. or =. From eq., we must onlue tht (n, therefore, ) is even; (n, therefore, ) my e even or o. If is even, the rtio / my e immeitely reue y neling ommon ftor of. If is o, it is possile tht the rtio / is lrey reue to smllest possile terms. We ssume tht (n, therefore, ) is o. Now, we set = m, n = n +, n require tht m n n e integers (to ensure integer vlues of n ). Then = 4m. n = 4n + 4n + 4. Sustituting these expressions into eq., we otin (4n + 4n + ) = 4m 5. or 4n + 4n + = m 6. The L.H.S. of eq. 6 is n o integer. The R.H.S., on the other hn, is n even integer. There re no solutions for eq. 6. Therefore, integer vlues of n whih stisfy the reltionship = / nnot e foun. We re fore to onlue tht is irrtionl. 0
11 Division y 0 is Meningless Sine ivision is efine in terms of multiplition, the rules for the sign of prout le iretly to the orresponing rules for the sign of quotient, whih re given elow: Symols 0 ; Divisor n ivien Both Positive Both Negtive One Positive One Negtive Divien 0 Divisor not 0 Quotient Positive Positive Negtive 0 Note: For 0, in the quotient 0 Q You must hve Q 0 Sine the prout Q Cn e 0 only if one of the ftors is 0. Therefore, 0 0 Also, for 0, if you h Q, 0 Then it woul follow tht But this is impossile, sine 0 0Q n 0Q 0 For exmple, suppose you wishe to fin the quotient Q in: Q 0 You woul hve to fin numer Q suh tht Q 0. But tht is impossile euse you hve lrey seen tht the prout of 0 n ny numer must e 0. Thus, we n onlue tht ivision y 0 is meningless.
12 Diviing y Frtion If n re rtionl numers with,, n 0, then. Let Q, where 0, 0, n 0 (you shoul orinrily sustitute prtiulr numers for,,, n ) Fining the quotient Q mens fining the missing ftor Q in Q Sine, Q n nme the sme numer The prout of this numer n n e written either s Q or s Tht is, Q Therefore, Q Assoitively Q Q Q.E.D.
13 Slope of Line is Constnt Prove tht the slope of nonvertil line oes not epen on whih two points re use to lulte it. Conept: Slope of line is CONSTANT n it oes NOT epen on whih two points re use to lulte it. Proof: Let A, B, C, D e ny four points on the line. Prove tht the slope otine using A n B equls the slope otine using C n D. D C x run y rise B A y rise x run Stuy Tip: If two figures re similr, then the rtios of the lengths of orresponing sies re equl. y y x Definition of similr tringles x y x x y Cross prout property of equlity y x x y xx x x Divie oth sies y x x y y x x Simplify Slope using points A n B = Slope using points C n D Q.E.D.
14 Prout Property of Rils Prove: Proof: n Definition of ue root Sustitution, Commuttivity, Assoitivity Definition of ue root Sustitution or trnsitive property of equlity Uniqueness of the rel ue root of numer Q.E.D. Prove:, 0 Proof: n Definition of ue root Definition. If 0, then Sustitution Definition of ue root n Sustitution or trnsitive property of equlity Uniqueness of the rel ue root of numer Q.E.D. n n 4
15 Squre Roots Prove: Any positive rel numer hs POSITIVE rel numer s squre root The re of SQUARE is otine y squring the length of sie. The sie of squre with n re of squre units must hve length whose squre is. Tht is, the sie hs length. Figure on the right shows squres with AREAS,,, n 4 n sies mesuring,,, n, respetively. Figure These squres show tht ny positive rel numer k hs POSITIVE rel numer s one of its squre roots. Speifilly, the squre whose re is equl to k squre units hs sie whose length is equl to the positive squre root of k. Sine every rel numer hs n itive inverse, n sine every positive rel numer lerly hs negtive squre root s well. Thus the sttement for eh rel numer, is onsequene of our efinition tht k, k 0, shll nme only nonnegtive numer. We lso hve the sttement This sttement simply resserts the efinition of k. This ie is of importne in lter mthemtis ourses when, for exmple, stuents re ske to solve equtions suh s: x 4. 5
16 Pythgoren Theorem Consier Figure, squre whose sie hs length +. As inite, there re four ientil right tringles n n interior qurilterl. The legs of eh tringle hve lengths n. The hypotenuse of eh tringle is. The mesures of the two ute ngles of eh tringle hve sum of 90. Now look t the point P. Sine the two ute ngles t tht point hve sum of 90, the interior ngle of the qurilterl must hve mesure of 90. The sme is true for eh of the other verties of the interior qurilterl. An the four sies of the interior qurilterl ll hve length. Thus the interior qurilterl is squre. Hene, the re of the lrge squre = the sum of the res of the 4 tringles plus the re of the interior squre 4 4. But the lrge squre n lso split into two squres n 4 tringles, s shown in Figure. The re of Figure is 4. These two expressions for the re of the lrge squre must e equl. Hene, = Figure Figure 6
17 Converse of Pythgoren Theorem Consier tringle ABC with sies of length,, n respetively. In the figure, ngle C is unknown. We ssume tht + =, n we wnt to prove tht ngle C is right ngle. Now onsier tringle A B C. As inite, this is right tringle with the right ngle t C n legs of length n. Sine we know tht + = n tringle A B C is right tringle, it follows tht the length of its hypotenuse must e. Thus in the two tringles, the three pirs of orresponing sies re equl in length. Hene these tringles must e ongruent y the Sie-Sie-Sie theorem of ongruent tringles. Hene their orresponing ngles re equl. Sine ngle C is right ngle, so is ngle C. B B? C A C A 7
18 Definition of π The numer π is efine to e the length of the perimeter (usully lle the irumferene) of irle whose imeter is unit. Its vlue is irrtionl ut is pproximtely equl to.459. Cirumferene of Cirle Notie tht ny two irles re similr to eh other. In similr geometri figures, the lengths of orresponing mesures re proportionl. Now onsier the two irles elow, with rii of ½ n r. Cll the imeter n irumferene of the seon irle n C respetively. Sine these irles re similr, the rtio of the irumferene of the first irle to its imeter is equl to the rtio of the irumferene of the seon irle to its imeter. This mens tht π/ = C/. When we simplify this eqution, we get C = π, or equivlently, sine = r, we hve C = πr. / C r 8
19 Are of Cirle Consier the following figure. The irle ontins n insrie regulr hexgon. As inite, the length of eh sie of the hexgon is s n the pothem (the istne of the perpeniulr segment from the enter of the irle to the sie of the hexgon) is. Notie tht the hexgon n e split into six ongruent tringles. Then the re of one of these tringles is (/)s. Hene the re of the entire hexgon is 6(/)s = (/)(6s) = (/) times the perimeter of the hexgon times the pothem. Now suppose inste of n insrie regulr hexgon, we hve n insrie regulr polygon with sies. Using the sme symols s ove, the re of this polygon is (/) times the perimeter of the polygon times the pothem. We n lso see tht the re of the polygon is loser to the re of the irle thn the re of the hexgon. Clerly, s the numer of sies of the polygon inreses, the re of the polygon gets loser n loser to the re of the irle. The formul for the re of this polygon is gin (/) times its perimeter times the pothem. Finlly, notie tht s the numer of sies inreses, the perimeter of the polygon pprohes the irumferene of the irle, πr, n the pothem pprohes the rius of the irle r. Thus the re of the irle is this limiting vlue, (/) times πr times r. When simplifie, this is just πr. S Zero Prout Rule: If = 0, then either = 0 or = 0. Suppose tht the prout is equl to zero. Suppose lso tht is not zero. Then the multiplitive inverse of, -, exists. So we hve: = 0 ( - ) = ( - )0 Multiply oth sies y - ( - ) = 0 Assoitivity of multiplition = 0 Definition of multiplitive inverse = 0 Definition of multiplitive ientity 9
20 A proof tht N is irrtionl if N is positive integer tht is not perfet squre The proof tht we re out to rener is epenent on the well orering priniple for positive integers. This priniple sttes tht ny nonempty set of positive integers ontins smllest positive integer. As in the usul proof tht the is irrtionl, we will proee y ontrition. Thus ssume tht the N is rtionl. Hene there re positive integers k n l with l 0 suh tht k N. Consier the set l k S { l : N for some positive integers k n l}. l The set S is nonempty set of positive integers; therefore, it ontins smllest positive integer y the well orering priniple. Denote the smllest positive integer in S y n. Thus there is positive m integer m suh tht N. Now ivie the integer m y the integer n to otin quotient q n n reminer r stisfying m nq r, where 0 r n; note tht the reminer r is greter thn zero sine the numer N is not perfet squre. Now from the eqution m nq r N n n we otin the eqution ( nq r) n q nqr r N. n n Hene Nn n q nqr r. Now rewrite this eqution to otin the equtions ( N q ) n nqr r ( N q ) n nqr nqr r n[( N q ) n qr] r( nq r) Now we otin the frtions ( N q ) n qr nq r N. r n Sine r n N re positive integers, we onlue tht the numertor ( N q ) n qr is positive integer. Therefore the positive integer r is in the set S. But r is stritly less thn n; thus we hve otine ontrition to the ft tht the integer n is the smllest positive integer in the set S. 0
21 A seon proof tht is irrtionl The proof tht we re out to rener is epenent on the well orering priniple for positive integers. This priniple sttes tht ny nonempty set of positive integers ontins smllest positive integer. As in the usul proof tht the is irrtionl, we will proee y ontrition. Thus ssume tht the is rtionl. Hene there re positive integers k n l with l 0 suh tht k. Consier the set l k S { l : for some positive integers k n l}. l The set S is nonempty set of positive integers; therefore, it ontins smllest positive integer y the well orering priniple. Denote the smllest positive integer in S y n. Thus there is positive m integer m suh tht. Sine, the integer m stisfies m n. Thus there is positive n integer k suh tht m n k. Furthermore, sine n k m n n ( n k) we onlue tht the positive integer k stisfies the inequlity k n. Now. Hene n n kn k n. Rewrite the previous eqution to otin the eqution n kn kn k. Therefore, n( n k) k( n k). Finlly we otin the eqution n k n k. k n The integer n k is positive integer sine k n. This inequlity together with the previous eqution shows tht the integer k is in the set S. But the positive integer k is less thn the integer n. We hve estlishe ontrition.
22 Density A Property of Rtionl Numers The set of rtionl numers hs the property tht etween ny two ifferent rtionl numers there re infinitely more rtionl numers. This property is referre to s ensity. One wy "etween ny two rel numers n there exists rtionl numer r suh tht r " then the proof is s follows: We first nee the Arhimeen Property: If x > 0 n y > 0 re rel numers, then there exists positive integer n suh tht n x y. This tells us tht even if is quite smll n is quite lrge, some integer multiple of will exee. Another wy to think of this is, "given enough time, one n empty swimming pool with te spoon." We nee to show tht given rel numers n we n onstrut m n n. We n ssume tht n > 0 without loss of generlity. If our frtion m n e the negtive numer. m for some integers n is to e negtive, just let m Sine n > 0 we n multiply everything y n n we on't hve to worry out flipping the inequlity. Thus we nee n m n. Sine we hve 0n so, y the Arhimeen property, there exists positive integer n suh tht n( ) (pik x n y in the sttement of the Arhimeen property ove; we n o this sine n re oth greter thn zero). Sine n n it is firly evient tht there is n integer m etween n n n. Does this mke sense? If the ifferene etween two numers is greter thn one unit (i.e., if two numers re more thn one unit prt), there must e n integer etween them, sine the integers re spe extly one unit prt. If this isn't ler, try to pik two numers tht re more thn one unit prt suh tht there isn't n integer etween them. I think you'll fin yourself unle to o so. Thus there exist integers m n n suh tht n m n, whih implies m whih ws to e shown. n Notie tht this proof oesn't tell us how to fin m n. All it oes is show tht m n exists. Suh proofs re very ommon in higher mthemtis.
23 Note: One wy of ientifying numer etween two given numers is to fin their verge. Tht the verge of two numers lies extly hlfwy etween them n e proven riefly s follows: if n re rtionl numers suh tht, ssume tht their verge,, oes not lie extly hlfwy etween them. Then Sine the lst sttement is flse, the ssumption is lso flse, n n, where. oes lie miwy etween
24 Squre n Tringulr Numers To ompute squre of given numer = 4, = 9, 4 = 6, n so on. Why is the opertion of multiplying numer y itself lle squring? The reson is est grspe from the following piture. A squre with sie of length n n e visulize s omprising gri of n n smller squres of size. Tringulr numers owe their nme to similr onstrution, now of tringles. Atully we lrey use tringulr numers in the proof of Lemm ove. Tringulr numers re in the form,, 6, nn ( ) 0, 5,... The generl formul is tht for every n the numer N is tringulr n esries the numer of points rrnge in tringulr shpe with n points on sie s shown elow. Of ourse it nees to e proven tht the totl numer of rosses rrnge s in the igrm is given nn ( ) y the formul N. However, we n oserve tht the numer of rosses in every tringle equls the sum n, where n is the numer of rosses on the sie of the tringle. Thus, long the wy, we re going to prove tht n = n(n+)/. Another igrm will mke this sttement ovious Inee, two tringles, eh with n rosses on the sie, together form n nn retngle. You my question whether pointing to the igrm proves nything. No, of ourse y itself the igrm oes not prove nything. But it oes help to visulize n perhps isern the proof. Inee, we seek formul for the sum of integers from through n. This sum represents the numer of rosses in tringle. Two tringles of whih one is rotte 80 o form retngle, i.e. shpe in whih ll rows hve the sme numer of rosses. Rows in the first tringle ount rosses,,... in the inresing orer wheres in the seon we hve rows with n, n-,... rosses in the eresing orer. Let us mimi this proeure in n lgeri mnner. First tke two sums (one in inresing, nother in eresing orer) ( n) + (n ). Now, regroup the terms y omining first terms in oth sums, then seon terms n so on: Quite rigorously. Q.E.D. [+n] + [+(n-)] + [+(n-)] [(n-)+] + [n+] = n(n+) It is ovious tht ll Euli's perfet numers re tringulr. 4
25 Multiplition of Negtive Numers: (-)(-) = We know the ssoitive property of ition n the istriutive property of multiplition over ition. We lso know the ommuttive properties of ition n multiplition of rel numers. We know the ientity properties of ition n multiplition: 0 0 n for ll rel numers. Finlly, we know the inverse property of ition: For eh rel numer there is rel numer ( ) suh tht ( ) ( ) 0. Using these si rithmeti properties we re le to prove tht ( )( ). We hve lrey estlishe tht 00for ll rel numers ; thus ( ) 0 0. Also ( ) ( ) 0. So pplying the multiplitive ientity property n the istriutive property we otin the eqution ( ) ( )( ) ( ) ( )( ) ( ) ( ) ( ) 0 0. So we hve shown tht ( ) ( )( ) 0. Now to oth sies of the ove eqution to otin [ ( ) ( )( ) ] 0 To this ltter eqution pply the ssoitive property of ition to otin ( )( ) 0 ( )( ) [ ( ) ] ( )( ) [ ( ) ( )( ) ]. 5
26 Zero Property of Multiplition: 0 = 0 = 0 for ll rel numers We know the ssoitive property of ition n the istriutive property of multiplition over ition. We lso know the ommuttive properties of ition n multiplition of rel numers. We know the ientity properties of ition n multiplition: 0 0 n for ll rel numers. Finlly, we know the inverse property of ition: For eh rel numer there is rel numer ( ) suh tht ( ) ( ) 0. Using these si rithmeti properties we re le to prove tht for ll rel numers. Let e n ritrry rel numer. Then using the ientity n istriutive properties we otin the eqution () 0 (0 0) 0 0 By the inverse property for ition, there is rel numer ( 0) suh tht So from eqution () we otin 0 ( 0) ( 0) 0 0. [ ] 0 ( 0) 0 0 ( 0). Applying the ssoitive property of ition, we otin the eqution [ ] 0 ( 0) 0 0 ( 0) Applying the inverse property of ition, we otin the eqution We onlue tht 0 0. Sine multiplition is ommuttive we lso hve tht
27 To show tht (n lternte pproh see pge 7) No hrm is one if we ssume tht. - The figure on the right is squre me up of four Regions: I, II, III & IV. - I A II Eh sie of the lrge squre hs length units. III IV Are of the lrge squre, ompose of the four regions is squre units. A ( ) squre units Are Region I: Are Region II: A squre units Are Region III: A squre units Are Region IV: A squre units A A Are of the Squre = Are Region I + Are Region II + Are Region III + Are Region IV Therefore we otin the eqution ( ) ( ) ( ). Now simplify this eqution using ssoitive n ommuttive properties of ition to otin the eqution ( ). We n now solve for ( ) to otin ( ). 7
28 Use the ommuttive, ssoitive n istriutive properties n the four opertions to justify eh step of the following lultion: [ (4 7) + ( (4 ) + 8)] [( (( + 8) + 4) (7 )] = [ (4 7) + ( (4 ) + 8)] [( ((8 + ) + 4) (7 )] Commuttive Property = [ (4 7) + ( (4 ) + 8)] [( (8 + ( + 4)) (7 )] Assoitive Property = [ (4 7) + ( (4 ) + 8)] [( (8 + 7) (7 )] Aition = [[( 4) ( 7)] + ( (4 ) + 8)] [( (8 + 7) (7 )] Distriutive Property = [([( 4) ( 7)] + (4 )) + 8] [( (8 + 7) (7 )] Assoitive Property = [([( 4) ( 7)] + (4 )) + 8] [(( 8) + ( 7)) (7 )] Distriutive Property = [([ ] + (4 )) + 8] [(6 + 4) (7 )] Multiplition = [( 9 + (4 )) + 8] [(6 + 4) 4] Sutrtion = [( (4 )) + 8] [(6 + 4) 4] Division = [( 9 + [(4 4) (4 )]) + 8] [(6 + 4) 4] Distriutive Property = [([(4 4) (4 )] + (-9)) + 8] [(6 + 4) 4] Commuttive Property = [[(4 4) (4 )] + ((-9) + 8)] [(6 + 4) 4] Assoitive Property = [[6 8] + ((-9) + 8)] [(6 + 4) 4] Multiplition = [[6 8] + ((-9) + 8)] [(4 + 6) 4] Commuttive Property = [8 + ((-9) + 8)] [(4 + 6) 4] Sutrtion = [8 + ((-9) + 8)] [0 4] Aition = [8 + (-)] [0 4] Aition = [8 + (-)] [5/] Division = 7 [5/] Aition = ½ Sutrtion 8
29 Prove tht multiplition is ommuttive y showing s typil exmple tht 9 58 = Use only the multiplition lgorithm, expne form, ftoring, n the istriutive property. Proof = [0 + 9] 58 Expne form = [0 58] + [9 58] Distriutive property = [0 58] + [9 (50 + 8)] Expne form = [0 58] + [9 50] + [9 8] Distriutive property n ftoring = [0 (50 + 8)] + [9 50] + [9 8] Expne form = [0 50] + [0 8] + [9 5 0] + 7 Distriutive property, ftoring, n multiplition = [0 5 0] + [0 6] + [45 0] + 7 Multiplition n ftoring = [0 0 0] Multiplition = Multiplition = 68 Aition 58 9 = [50 + 8] 9 Expne form = [50 9] + [8 9] Distriutive property = [50 9] + [8 (0 + 9)] Expne form = [0 5 9] + [8 0] + [8 9] Distriutive Property n ftoring = [0 5 (0 + 9)] + [8 0] + [8 9] Expne form = [0 5 0] + [0 5 9] + [8 0] + 7 Distriutive Property, ftoring, n multiplition = [0 5 0] + [0 45] + [6 0] + 7 Multiplition n ftoring = [0 0 0] Multiplition = Multiplition = 68 Aition Sine oth prouts re equl to 68, they must e equl to eh other. Thus multiplition is ommuttive in this exmple. But sine there ws nothing speil out this exmple, we n onlue tht multiplition is lwys ommuttive. 9
30 Prove tht eiml is terminting eiml if n only if it is equivlent to frtion whose enomintor ontins no prime ftors other thn n 5. Proof. Suppose the enomintor of frtion ontins only the ftors, 5 or oth of them. Then we n multiply tht enomintor y itionl s n 5s so tht there is n equl numer of s n 5s. We lso multiply the numertor of the frtion y the sme numer of s n 5s. This proues frtion equivlent to the originl one whose enomintor onsists of n equl numer of s n 5s. But this mens tht the enomintor is power of 0. A frtion whose enomintor is power of 0 orrespons to terminting eiml. Thus, if the frtion with enomintor tht is power of 0 is the frtion. n /0 n, then the eiml tht is equivlent to this frtion is the terminting eiml 0.. n. Now suppose tht we egin with terminting eiml, sy 0.. n. Then this eiml is equivlent to the frtion. n /0 n. The enomintor of this frtion ontins only the prime ftors n 5. 0
Numbers and indices. 1.1 Fractions. GCSE C Example 1. Handy hint. Key point
 GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
Proportions: A ratio is the quotient of two numbers. For example, 2 3
 Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Surds and Indices. Surds and Indices. Curriculum Ready ACMNA: 233,
 Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
CS 491G Combinatorial Optimization Lecture Notes
 CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
Factorising FACTORISING.
 Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
Lecture 8: Abstract Algebra
 Mth 94 Professor: Pri Brtlett Leture 8: Astrt Alger Week 8 UCSB 2015 This is the eighth week of the Mthemtis Sujet Test GRE prep ourse; here, we run very rough-n-tumle review of strt lger! As lwys, this
Mth 94 Professor: Pri Brtlett Leture 8: Astrt Alger Week 8 UCSB 2015 This is the eighth week of the Mthemtis Sujet Test GRE prep ourse; here, we run very rough-n-tumle review of strt lger! As lwys, this
Intermediate Math Circles Wednesday 17 October 2012 Geometry II: Side Lengths
 Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Comparing the Pre-image and Image of a Dilation
 hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
Section 2.1 Special Right Triangles
 Se..1 Speil Rigt Tringles 49 Te --90 Tringle Setion.1 Speil Rigt Tringles Te --90 tringle (or just 0-60-90) is so nme euse of its ngle mesures. Te lengts of te sies, toug, ve very speifi pttern to tem
Se..1 Speil Rigt Tringles 49 Te --90 Tringle Setion.1 Speil Rigt Tringles Te --90 tringle (or just 0-60-90) is so nme euse of its ngle mesures. Te lengts of te sies, toug, ve very speifi pttern to tem
Lecture 6: Coding theory
 Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
Mid-Term Examination - Spring 2014 Mathematical Programming with Applications to Economics Total Score: 45; Time: 3 hours
 Mi-Term Exmintion - Spring 0 Mthemtil Progrmming with Applitions to Eonomis Totl Sore: 5; Time: hours. Let G = (N, E) e irete grph. Define the inegree of vertex i N s the numer of eges tht re oming into
Mi-Term Exmintion - Spring 0 Mthemtil Progrmming with Applitions to Eonomis Totl Sore: 5; Time: hours. Let G = (N, E) e irete grph. Define the inegree of vertex i N s the numer of eges tht re oming into
Section 1.3 Triangles
 Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
THE PYTHAGOREAN THEOREM
 THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
p-adic Egyptian Fractions
 p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
HS Pre-Algebra Notes Unit 9: Roots, Real Numbers and The Pythagorean Theorem
 HS Pre-Alger Notes Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Roots nd Cue Roots Syllus Ojetive 5.4: The student will find or pproximte squre roots of numers to 4. CCSS 8.EE.-: Evlute squre roots
HS Pre-Alger Notes Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Roots nd Cue Roots Syllus Ojetive 5.4: The student will find or pproximte squre roots of numers to 4. CCSS 8.EE.-: Evlute squre roots
Solutions for HW9. Bipartite: put the red vertices in V 1 and the black in V 2. Not bipartite!
 Solutions for HW9 Exerise 28. () Drw C 6, W 6 K 6, n K 5,3. C 6 : W 6 : K 6 : K 5,3 : () Whih of the following re iprtite? Justify your nswer. Biprtite: put the re verties in V 1 n the lk in V 2. Biprtite:
Solutions for HW9 Exerise 28. () Drw C 6, W 6 K 6, n K 5,3. C 6 : W 6 : K 6 : K 5,3 : () Whih of the following re iprtite? Justify your nswer. Biprtite: put the re verties in V 1 n the lk in V 2. Biprtite:
Algebra 2 Semester 1 Practice Final
 Alger 2 Semester Prtie Finl Multiple Choie Ientify the hoie tht est ompletes the sttement or nswers the question. To whih set of numers oes the numer elong?. 2 5 integers rtionl numers irrtionl numers
Alger 2 Semester Prtie Finl Multiple Choie Ientify the hoie tht est ompletes the sttement or nswers the question. To whih set of numers oes the numer elong?. 2 5 integers rtionl numers irrtionl numers
for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx
![for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx](/thumbs/74/70408252.jpg) Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
Project 6: Minigoals Towards Simplifying and Rewriting Expressions
 MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
Section 2.3. Matrix Inverses
 Mtri lger Mtri nverses Setion.. Mtri nverses hree si opertions on mtries, ition, multiplition, n sutrtion, re nlogues for mtries of the sme opertions for numers. n this setion we introue the mtri nlogue
Mtri lger Mtri nverses Setion.. Mtri nverses hree si opertions on mtries, ition, multiplition, n sutrtion, re nlogues for mtries of the sme opertions for numers. n this setion we introue the mtri nlogue
A Study on the Properties of Rational Triangles
 Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
MCH T 111 Handout Triangle Review Page 1 of 3
 Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Introduction to Olympiad Inequalities
 Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
6.5 Improper integrals
 Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
18.06 Problem Set 4 Due Wednesday, Oct. 11, 2006 at 4:00 p.m. in 2-106
 8. Problem Set Due Wenesy, Ot., t : p.m. in - Problem Mony / Consier the eight vetors 5, 5, 5,..., () List ll of the one-element, linerly epenent sets forme from these. (b) Wht re the two-element, linerly
8. Problem Set Due Wenesy, Ot., t : p.m. in - Problem Mony / Consier the eight vetors 5, 5, 5,..., () List ll of the one-element, linerly epenent sets forme from these. (b) Wht re the two-element, linerly
APPENDIX. Precalculus Review D.1. Real Numbers and the Real Number Line
 APPENDIX D Preclculus Review APPENDIX D.1 Rel Numers n the Rel Numer Line Rel Numers n the Rel Numer Line Orer n Inequlities Asolute Vlue n Distnce Rel Numers n the Rel Numer Line Rel numers cn e represente
APPENDIX D Preclculus Review APPENDIX D.1 Rel Numers n the Rel Numer Line Rel Numers n the Rel Numer Line Orer n Inequlities Asolute Vlue n Distnce Rel Numers n the Rel Numer Line Rel numers cn e represente
Now we must transform the original model so we can use the new parameters. = S max. Recruits
 MODEL FOR VARIABLE RECRUITMENT (ontinue) Alterntive Prmeteriztions of the pwner-reruit Moels We n write ny moel in numerous ifferent ut equivlent forms. Uner ertin irumstnes it is onvenient to work with
MODEL FOR VARIABLE RECRUITMENT (ontinue) Alterntive Prmeteriztions of the pwner-reruit Moels We n write ny moel in numerous ifferent ut equivlent forms. Uner ertin irumstnes it is onvenient to work with
Farey Fractions. Rickard Fernström. U.U.D.M. Project Report 2017:24. Department of Mathematics Uppsala University
 U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
I 3 2 = I I 4 = 2A
 ECE 210 Eletril Ciruit Anlysis University of llinois t Chigo 2.13 We re ske to use KCL to fin urrents 1 4. The key point in pplying KCL in this prolem is to strt with noe where only one of the urrents
ECE 210 Eletril Ciruit Anlysis University of llinois t Chigo 2.13 We re ske to use KCL to fin urrents 1 4. The key point in pplying KCL in this prolem is to strt with noe where only one of the urrents
Identifying and Classifying 2-D Shapes
 Ientifying n Clssifying -D Shpes Wht is your sign? The shpe n olour of trffi signs let motorists know importnt informtion suh s: when to stop onstrution res. Some si shpes use in trffi signs re illustrte
Ientifying n Clssifying -D Shpes Wht is your sign? The shpe n olour of trffi signs let motorists know importnt informtion suh s: when to stop onstrution res. Some si shpes use in trffi signs re illustrte
50 AMC Lectures Problem Book 2 (36) Substitution Method
 0 AMC Letures Prolem Book Sustitution Metho PROBLEMS Prolem : Solve for rel : 9 + 99 + 9 = Prolem : Solve for rel : 0 9 8 8 Prolem : Show tht if 8 Prolem : Show tht + + if rel numers,, n stisf + + = Prolem
0 AMC Letures Prolem Book Sustitution Metho PROBLEMS Prolem : Solve for rel : 9 + 99 + 9 = Prolem : Solve for rel : 0 9 8 8 Prolem : Show tht if 8 Prolem : Show tht + + if rel numers,, n stisf + + = Prolem
LESSON 11: TRIANGLE FORMULAE
 . THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
. THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
Counting Paths Between Vertices. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs
 Isomorphism of Grphs Definition The simple grphs G 1 = (V 1, E 1 ) n G = (V, E ) re isomorphi if there is ijetion (n oneto-one n onto funtion) f from V 1 to V with the property tht n re jent in G 1 if
Isomorphism of Grphs Definition The simple grphs G 1 = (V 1, E 1 ) n G = (V, E ) re isomorphi if there is ijetion (n oneto-one n onto funtion) f from V 1 to V with the property tht n re jent in G 1 if
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
 PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
If the numbering is a,b,c,d 1,2,3,4, then the matrix representation is as follows:
 Reltions. Solutions 1. ) true; ) true; ) flse; ) true; e) flse; f) true; g) flse; h) true; 2. 2 A B 3. Consier ll reltions tht o not inlue the given pir s n element. Oviously, the rest of the reltions
Reltions. Solutions 1. ) true; ) true; ) flse; ) true; e) flse; f) true; g) flse; h) true; 2. 2 A B 3. Consier ll reltions tht o not inlue the given pir s n element. Oviously, the rest of the reltions
Linear Algebra Introduction
 Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
GM1 Consolidation Worksheet
 Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Maintaining Mathematical Proficiency
 Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Solids of Revolution
 Solis of Revolution Solis of revolution re rete tking n re n revolving it roun n is of rottion. There re two methos to etermine the volume of the soli of revolution: the isk metho n the shell metho. Disk
Solis of Revolution Solis of revolution re rete tking n re n revolving it roun n is of rottion. There re two methos to etermine the volume of the soli of revolution: the isk metho n the shell metho. Disk
Part I: Study the theorem statement.
 Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
5. Every rational number have either terminating or repeating (recurring) decimal representation.
 CHAPTER NUMBER SYSTEMS Points to Rememer :. Numer used for ounting,,,,... re known s Nturl numers.. All nturl numers together with zero i.e. 0,,,,,... re known s whole numers.. All nturl numers, zero nd
CHAPTER NUMBER SYSTEMS Points to Rememer :. Numer used for ounting,,,,... re known s Nturl numers.. All nturl numers together with zero i.e. 0,,,,,... re known s whole numers.. All nturl numers, zero nd
Lecture 2: Cayley Graphs
 Mth 137B Professor: Pri Brtlett Leture 2: Cyley Grphs Week 3 UCSB 2014 (Relevnt soure mteril: Setion VIII.1 of Bollos s Moern Grph Theory; 3.7 of Gosil n Royle s Algeri Grph Theory; vrious ppers I ve re
Mth 137B Professor: Pri Brtlett Leture 2: Cyley Grphs Week 3 UCSB 2014 (Relevnt soure mteril: Setion VIII.1 of Bollos s Moern Grph Theory; 3.7 of Gosil n Royle s Algeri Grph Theory; vrious ppers I ve re
SEMI-EXCIRCLE OF QUADRILATERAL
 JP Journl of Mthemtil Sienes Volume 5, Issue &, 05, Pges - 05 Ishn Pulishing House This pper is ville online t http://wwwiphsiom SEMI-EXCIRCLE OF QUADRILATERAL MASHADI, SRI GEMAWATI, HASRIATI AND HESY
JP Journl of Mthemtil Sienes Volume 5, Issue &, 05, Pges - 05 Ishn Pulishing House This pper is ville online t http://wwwiphsiom SEMI-EXCIRCLE OF QUADRILATERAL MASHADI, SRI GEMAWATI, HASRIATI AND HESY
Chapter 8 Roots and Radicals
 Chpter 8 Roots nd Rdils 7 ROOTS AND RADICALS 8 Figure 8. Grphene is n inredily strong nd flexile mteril mde from ron. It n lso ondut eletriity. Notie the hexgonl grid pttern. (redit: AlexnderAIUS / Wikimedi
Chpter 8 Roots nd Rdils 7 ROOTS AND RADICALS 8 Figure 8. Grphene is n inredily strong nd flexile mteril mde from ron. It n lso ondut eletriity. Notie the hexgonl grid pttern. (redit: AlexnderAIUS / Wikimedi
03. Early Greeks & Aristotle
 03. Erly Greeks & Aristotle I. Erly Greeks Topis I. Erly Greeks II. The Method of Exhustion III. Aristotle. Anximnder (. 60 B.C.) to peiron - the unlimited, unounded - fundmentl sustne of relity - underlying
03. Erly Greeks & Aristotle I. Erly Greeks Topis I. Erly Greeks II. The Method of Exhustion III. Aristotle. Anximnder (. 60 B.C.) to peiron - the unlimited, unounded - fundmentl sustne of relity - underlying
2.4 Linear Inequalities and Interval Notation
 .4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
.4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
 PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
Discrete Structures Lecture 11
 Introdution Good morning. In this setion we study funtions. A funtion is mpping from one set to nother set or, perhps, from one set to itself. We study the properties of funtions. A mpping my not e funtion.
Introdution Good morning. In this setion we study funtions. A funtion is mpping from one set to nother set or, perhps, from one set to itself. We study the properties of funtions. A mpping my not e funtion.
CARLETON UNIVERSITY. 1.0 Problems and Most Solutions, Sect B, 2005
 RLETON UNIVERSIT eprtment of Eletronis ELE 2607 Swithing iruits erury 28, 05; 0 pm.0 Prolems n Most Solutions, Set, 2005 Jn. 2, #8 n #0; Simplify, Prove Prolem. #8 Simplify + + + Reue to four letters (literls).
RLETON UNIVERSIT eprtment of Eletronis ELE 2607 Swithing iruits erury 28, 05; 0 pm.0 Prolems n Most Solutions, Set, 2005 Jn. 2, #8 n #0; Simplify, Prove Prolem. #8 Simplify + + + Reue to four letters (literls).
Proving the Pythagorean Theorem
 Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
QUADRATIC EQUATION. Contents
 QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
(e) if x = y + z and a divides any two of the integers x, y, or z, then a divides the remaining integer
 Divisibility In this note we introduce the notion of divisibility for two integers nd b then we discuss the division lgorithm. First we give forml definition nd note some properties of the division opertion.
Divisibility In this note we introduce the notion of divisibility for two integers nd b then we discuss the division lgorithm. First we give forml definition nd note some properties of the division opertion.
APPROXIMATION AND ESTIMATION MATHEMATICAL LANGUAGE THE FUNDAMENTAL THEOREM OF ARITHMETIC LAWS OF ALGEBRA ORDER OF OPERATIONS
 TOPIC 2: MATHEMATICAL LANGUAGE NUMBER AND ALGEBRA You shoul unerstn these mthemtil terms, n e le to use them ppropritely: ² ition, sutrtion, multiplition, ivision ² sum, ifferene, prout, quotient ² inex
TOPIC 2: MATHEMATICAL LANGUAGE NUMBER AND ALGEBRA You shoul unerstn these mthemtil terms, n e le to use them ppropritely: ² ition, sutrtion, multiplition, ivision ² sum, ifferene, prout, quotient ² inex
STRAND I: Geometry and Trigonometry. UNIT 32 Angles, Circles and Tangents: Student Text Contents. Section Compass Bearings
 ME Jmi: STR I UIT 32 ngles, irles n Tngents: Stuent Tet ontents STR I: Geometry n Trigonometry Unit 32 ngles, irles n Tngents Stuent Tet ontents Setion 32.1 ompss erings 32.2 ngles n irles 1 32.3 ngles
ME Jmi: STR I UIT 32 ngles, irles n Tngents: Stuent Tet ontents STR I: Geometry n Trigonometry Unit 32 ngles, irles n Tngents Stuent Tet ontents Setion 32.1 ompss erings 32.2 ngles n irles 1 32.3 ngles
Green s Theorem. (2x e y ) da. (2x e y ) dx dy. x 2 xe y. (1 e y ) dy. y=1. = y e y. y=0. = 2 e
 Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
Bases for Vector Spaces
 Bses for Vector Spces 2-26-25 A set is independent if, roughly speking, there is no redundncy in the set: You cn t uild ny vector in the set s liner comintion of the others A set spns if you cn uild everything
Bses for Vector Spces 2-26-25 A set is independent if, roughly speking, there is no redundncy in the set: You cn t uild ny vector in the set s liner comintion of the others A set spns if you cn uild everything
Algebra Basics. Algebra Basics. Curriculum Ready ACMNA: 133, 175, 176, 177, 179.
 Curriulum Redy ACMNA: 33 75 76 77 79 www.mthletis.om Fill in the spes with nything you lredy know out Alger Creer Opportunities: Arhitets eletriins plumers et. use it to do importnt lultions. Give this
Curriulum Redy ACMNA: 33 75 76 77 79 www.mthletis.om Fill in the spes with nything you lredy know out Alger Creer Opportunities: Arhitets eletriins plumers et. use it to do importnt lultions. Give this
9.1 Day 1 Warm Up. Solve the equation = x x 2 = March 1, 2017 Geometry 9.1 The Pythagorean Theorem 1
 9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
Activities. 4.1 Pythagoras' Theorem 4.2 Spirals 4.3 Clinometers 4.4 Radar 4.5 Posting Parcels 4.6 Interlocking Pipes 4.7 Sine Rule Notes and Solutions
 MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
Lesson 55 - Inverse of Matrices & Determinants
 // () Review Lesson - nverse of Mtries & Determinnts Mth Honors - Sntowski - t this stge of stuying mtries, we know how to, subtrt n multiply mtries i.e. if Then evlute: () + B (b) - () B () B (e) B n
// () Review Lesson - nverse of Mtries & Determinnts Mth Honors - Sntowski - t this stge of stuying mtries, we know how to, subtrt n multiply mtries i.e. if Then evlute: () + B (b) - () B () B (e) B n
CIT 596 Theory of Computation 1. Graphs and Digraphs
 CIT 596 Theory of Computtion 1 A grph G = (V (G), E(G)) onsists of two finite sets: V (G), the vertex set of the grph, often enote y just V, whih is nonempty set of elements lle verties, n E(G), the ege
CIT 596 Theory of Computtion 1 A grph G = (V (G), E(G)) onsists of two finite sets: V (G), the vertex set of the grph, often enote y just V, whih is nonempty set of elements lle verties, n E(G), the ege
Trigonometry Revision Sheet Q5 of Paper 2
 Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
2.4 Theoretical Foundations
 2 Progrmming Lnguge Syntx 2.4 Theoretil Fountions As note in the min text, snners n prsers re se on the finite utomt n pushown utomt tht form the ottom two levels of the Chomsky lnguge hierrhy. At eh level
2 Progrmming Lnguge Syntx 2.4 Theoretil Fountions As note in the min text, snners n prsers re se on the finite utomt n pushown utomt tht form the ottom two levels of the Chomsky lnguge hierrhy. At eh level
= x x 2 = 25 2
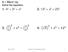 9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
Equivalent fractions have the same value but they have different denominators. This means they have been divided into a different number of parts.
 Frtions equivlent frtions Equivlent frtions hve the sme vlue ut they hve ifferent enomintors. This mens they hve een ivie into ifferent numer of prts. Use the wll to fin the equivlent frtions: Wht frtions
Frtions equivlent frtions Equivlent frtions hve the sme vlue ut they hve ifferent enomintors. This mens they hve een ivie into ifferent numer of prts. Use the wll to fin the equivlent frtions: Wht frtions
How do we solve these things, especially when they get complicated? How do we know when a system has a solution, and when is it unique?
 XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
Matrix- System of rows and columns each position in a matrix has a purpose. 5 Ex: 5. Ex:
 Mtries Prelulus Mtri- Sstem of rows n olumns eh position in mtri hs purpose. Element- Eh vlue in the mtri mens the element in the n row, r olumn Dimensions- How mn rows b number of olumns Ientif the element:
Mtries Prelulus Mtri- Sstem of rows n olumns eh position in mtri hs purpose. Element- Eh vlue in the mtri mens the element in the n row, r olumn Dimensions- How mn rows b number of olumns Ientif the element:
UNCORRECTED SAMPLE PAGES. surds NUMBER AND ALGEBRA
 Chpter Wht you will lern A Irrtionl numers n surs (0A) B Aing n sutrting surs (0A) C Multiplying n iviing surs (0A) D Binomil prouts (0A) E Rtionlising the enomintor (0A) F Review of inex lws (Consoliting)
Chpter Wht you will lern A Irrtionl numers n surs (0A) B Aing n sutrting surs (0A) C Multiplying n iviing surs (0A) D Binomil prouts (0A) E Rtionlising the enomintor (0A) F Review of inex lws (Consoliting)
12.4 Similarity in Right Triangles
 Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Polynomials. Polynomials. Curriculum Ready ACMNA:
 Polynomils Polynomils Curriulum Redy ACMNA: 66 www.mthletis.om Polynomils POLYNOMIALS A polynomil is mthemtil expression with one vrile whose powers re neither negtive nor frtions. The power in eh expression
Polynomils Polynomils Curriulum Redy ACMNA: 66 www.mthletis.om Polynomils POLYNOMIALS A polynomil is mthemtil expression with one vrile whose powers re neither negtive nor frtions. The power in eh expression
Lesson 2.1 Inductive Reasoning
 Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Lesson 2: The Pythagorean Theorem and Similar Triangles. A Brief Review of the Pythagorean Theorem.
 27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
Math 4310 Solutions to homework 1 Due 9/1/16
 Mth 4310 Solutions to homework 1 Due 9/1/16 1. Use the Eucliden lgorithm to find the following gretest common divisors. () gcd(252, 180) = 36 (b) gcd(513, 187) = 1 (c) gcd(7684, 4148) = 68 252 = 180 1
Mth 4310 Solutions to homework 1 Due 9/1/16 1. Use the Eucliden lgorithm to find the following gretest common divisors. () gcd(252, 180) = 36 (b) gcd(513, 187) = 1 (c) gcd(7684, 4148) = 68 252 = 180 1
Lesson 2.1 Inductive Reasoning
 Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Trigonometry and Constructive Geometry
 Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
CHENG Chun Chor Litwin The Hong Kong Institute of Education
 PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
I1 = I2 I1 = I2 + I3 I1 + I2 = I3 + I4 I 3
 2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.
 Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
set is not closed under matrix [ multiplication, ] and does not form a group.
![set is not closed under matrix [ multiplication, ] and does not form a group. set is not closed under matrix [ multiplication, ] and does not form a group.](/thumbs/78/78412113.jpg) Prolem 2.3: Which of the following collections of 2 2 mtrices with rel entries form groups under [ mtrix ] multipliction? i) Those of the form for which c d 2 Answer: The set of such mtrices is not closed
Prolem 2.3: Which of the following collections of 2 2 mtrices with rel entries form groups under [ mtrix ] multipliction? i) Those of the form for which c d 2 Answer: The set of such mtrices is not closed
Geodesics on Regular Polyhedra with Endpoints at the Vertices
 Arnol Mth J (2016) 2:201 211 DOI 101007/s40598-016-0040-z RESEARCH CONTRIBUTION Geoesis on Regulr Polyher with Enpoints t the Verties Dmitry Fuhs 1 To Sergei Thnikov on the osion of his 60th irthy Reeive:
Arnol Mth J (2016) 2:201 211 DOI 101007/s40598-016-0040-z RESEARCH CONTRIBUTION Geoesis on Regulr Polyher with Enpoints t the Verties Dmitry Fuhs 1 To Sergei Thnikov on the osion of his 60th irthy Reeive:
Exam 1 Study Guide. Differentiation and Anti-differentiation Rules from Calculus I
 Exm Stuy Guie Mth 26 - Clulus II, Fll 205 The following is list of importnt onepts from eh setion tht will be teste on exm. This is not omplete list of the mteril tht you shoul know for the ourse, but
Exm Stuy Guie Mth 26 - Clulus II, Fll 205 The following is list of importnt onepts from eh setion tht will be teste on exm. This is not omplete list of the mteril tht you shoul know for the ourse, but
Probability. b a b. a b 32.
 Proility If n event n hppen in '' wys nd fil in '' wys, nd eh of these wys is eqully likely, then proility or the hne, or its hppening is, nd tht of its filing is eg, If in lottery there re prizes nd lnks,
Proility If n event n hppen in '' wys nd fil in '' wys, nd eh of these wys is eqully likely, then proility or the hne, or its hppening is, nd tht of its filing is eg, If in lottery there re prizes nd lnks,
Preliminary preparation
 Preliminry preprtion Syllus prerequisite: Preliminry preprtion This topi provies the si knowlege, skills n unerstnings require in Yer. Outomes Simplify n lgeri expression. Estlish n pply inex lws in lgeri
Preliminry preprtion Syllus prerequisite: Preliminry preprtion This topi provies the si knowlege, skills n unerstnings require in Yer. Outomes Simplify n lgeri expression. Estlish n pply inex lws in lgeri
Geometry of the Circle - Chords and Angles. Geometry of the Circle. Chord and Angles. Curriculum Ready ACMMG: 272.
 Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Something found at a salad bar
 Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Bridging the gap: GCSE AS Level
 Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
Pythagoras theorem and surds
 HPTER Mesurement nd Geometry Pythgors theorem nd surds In IE-EM Mthemtis Yer 8, you lernt out the remrkle reltionship etween the lengths of the sides of right-ngled tringle. This result is known s Pythgors
HPTER Mesurement nd Geometry Pythgors theorem nd surds In IE-EM Mthemtis Yer 8, you lernt out the remrkle reltionship etween the lengths of the sides of right-ngled tringle. This result is known s Pythgors
Necessary and sucient conditions for some two. Abstract. Further we show that the necessary conditions for the existence of an OD(44 s 1 s 2 )
 Neessry n suient onitions for some two vrile orthogonl esigns in orer 44 C. Koukouvinos, M. Mitrouli y, n Jennifer Seerry z Deite to Professor Anne Penfol Street Astrt We give new lgorithm whih llows us
Neessry n suient onitions for some two vrile orthogonl esigns in orer 44 C. Koukouvinos, M. Mitrouli y, n Jennifer Seerry z Deite to Professor Anne Penfol Street Astrt We give new lgorithm whih llows us
This enables us to also express rational numbers other than natural numbers, for example:
 Overview Study Mteril Business Mthemtis 05-06 Alger The Rel Numers The si numers re,,3,4, these numers re nturl numers nd lso lled positive integers. The positive integers, together with the negtive integers
Overview Study Mteril Business Mthemtis 05-06 Alger The Rel Numers The si numers re,,3,4, these numers re nturl numers nd lso lled positive integers. The positive integers, together with the negtive integers
1 ELEMENTARY ALGEBRA and GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE
 ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
22: Union Find. CS 473u - Algorithms - Spring April 14, We want to maintain a collection of sets, under the operations of:
 22: Union Fin CS 473u - Algorithms - Spring 2005 April 14, 2005 1 Union-Fin We wnt to mintin olletion of sets, uner the opertions of: 1. MkeSet(x) - rete set tht ontins the single element x. 2. Fin(x)
22: Union Fin CS 473u - Algorithms - Spring 2005 April 14, 2005 1 Union-Fin We wnt to mintin olletion of sets, uner the opertions of: 1. MkeSet(x) - rete set tht ontins the single element x. 2. Fin(x)
Polynomials and Division Theory
 Higher Checklist (Unit ) Higher Checklist (Unit ) Polynomils nd Division Theory Skill Achieved? Know tht polynomil (expression) is of the form: n x + n x n + n x n + + n x + x + 0 where the i R re the
Higher Checklist (Unit ) Higher Checklist (Unit ) Polynomils nd Division Theory Skill Achieved? Know tht polynomil (expression) is of the form: n x + n x n + n x n + + n x + x + 0 where the i R re the
MATHEMATICS AND STATISTICS 1.6
 MTHMTIS N STTISTIS 1.6 pply geometri resoning in solving prolems ternlly ssessed 4 redits S 91031 inding unknown ngles When finding the size of unknown ngles in figure, t lest two steps of resoning will
MTHMTIS N STTISTIS 1.6 pply geometri resoning in solving prolems ternlly ssessed 4 redits S 91031 inding unknown ngles When finding the size of unknown ngles in figure, t lest two steps of resoning will
Math 154B Elementary Algebra-2 nd Half Spring 2015
 Mth 154B Elementry Alger- nd Hlf Spring 015 Study Guide for Exm 4, Chpter 9 Exm 4 is scheduled for Thursdy, April rd. You my use " x 5" note crd (oth sides) nd scientific clcultor. You re expected to know
Mth 154B Elementry Alger- nd Hlf Spring 015 Study Guide for Exm 4, Chpter 9 Exm 4 is scheduled for Thursdy, April rd. You my use " x 5" note crd (oth sides) nd scientific clcultor. You re expected to know
Chapter 3. Vector Spaces. 3.1 Images and Image Arithmetic
 Chpter 3 Vetor Spes In Chpter 2, we sw tht the set of imges possessed numer of onvenient properties. It turns out tht ny set tht possesses similr onvenient properties n e nlyzed in similr wy. In liner
Chpter 3 Vetor Spes In Chpter 2, we sw tht the set of imges possessed numer of onvenient properties. It turns out tht ny set tht possesses similr onvenient properties n e nlyzed in similr wy. In liner
QUADRATIC EQUATION EXERCISE - 01 CHECK YOUR GRASP
 QUADRATIC EQUATION EXERCISE - 0 CHECK YOUR GRASP. Sine sum of oeffiients 0. Hint : It's one root is nd other root is 8 nd 5 5. tn other root 9. q 4p 0 q p q p, q 4 p,,, 4 Hene 7 vlues of (p, q) 7 equtions
QUADRATIC EQUATION EXERCISE - 0 CHECK YOUR GRASP. Sine sum of oeffiients 0. Hint : It's one root is nd other root is 8 nd 5 5. tn other root 9. q 4p 0 q p q p, q 4 p,,, 4 Hene 7 vlues of (p, q) 7 equtions
GRUPOS NANTEL BERGERON
 Drft of Septemer 8, 2017 GRUPOS NANTEL BERGERON Astrt. 1. Quik Introution In this mini ourse we will see how to ount severl ttriute relte to symmetries of n ojet. For exmple, how mny ifferent ies with
Drft of Septemer 8, 2017 GRUPOS NANTEL BERGERON Astrt. 1. Quik Introution In this mini ourse we will see how to ount severl ttriute relte to symmetries of n ojet. For exmple, how mny ifferent ies with
Computing data with spreadsheets. Enter the following into the corresponding cells: A1: n B1: triangle C1: sqrt
 Computing dt with spredsheets Exmple: Computing tringulr numers nd their squre roots. Rell, we showed 1 ` 2 ` `n npn ` 1q{2. Enter the following into the orresponding ells: A1: n B1: tringle C1: sqrt A2:
Computing dt with spredsheets Exmple: Computing tringulr numers nd their squre roots. Rell, we showed 1 ` 2 ` `n npn ` 1q{2. Enter the following into the orresponding ells: A1: n B1: tringle C1: sqrt A2:
