Merge Sort. Outline and Reading. Divide-and-Conquer. Divide-and-conquer paradigm ( 4.1.1) Merge-sort ( 4.1.1)

Data Structures Lecture 9

Fall 2017 Fag Yu Software Security Lab. Dept. Maagemet Iformatio Systems, Natioal Chegchi Uiversity Data Structures Lecture 9 Midterm o Dec. 7 (9:10-12:00am, 106) Lec 1-9, TextBook Ch1-8, 11,12 How to

Similar idea to multiplication in N, C. Divide and conquer approach provides unexpected improvements. Naïve matrix multiplication

Next. Covered bsics of simple desig techique (Divided-coquer) Ch. of the text.. Next, Strsse s lgorithm. Lter: more desig d coquer lgorithms: MergeSort. Solvig recurreces d the Mster Theorem. Similr ide

5. Solving recurrences

5. Solvig recurreces Time Complexity Alysis of Merge Sort T( ) 0 if 1 2T ( / 2) otherwise sortig oth hlves mergig Q. How to prove tht the ru-time of merge sort is O( )? A. 2 Time Complexity Alysis of Merge

Lecture 4 Recursive Algorithm Analysis. Merge Sort Solving Recurrences The Master Theorem

Lecture 4 Recursive Algorithm Alysis Merge Sort Solvig Recurreces The Mster Theorem Merge Sort MergeSortA, left, right) { if left < right) { mid = floorleft + right) / 2); MergeSortA, left, mid); MergeSortA,

Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, Divide-and-Conquer

Presettio for use with the textook, Algorithm Desig d Applictios, y M. T. Goodrich d R. Tmssi, Wiley, 25 Divide-d-Coquer Divide-d-Coquer Divide-d coquer is geerl lgorithm desig prdigm: Divide: divide the

Lecture 4 Recursive Algorithm Analysis. Merge Sort Solving Recurrences The Master Theorem

Lecture 4 Recursive Algorithm Alysis Merge Sort Solvig Recurreces The Mster Theorem Merge Sort MergeSortA, left, right) { if left < right) { mid floorleft right) / 2); MergeSortA, left, mid); MergeSortA,

Divide-and-Conquer. Divide-and-Conquer 1

Divide-d-Coquer 7 9 4 4 7 9 7 7 9 4 4 9 7 7 9 9 4 4 Divide-d-Coquer 1 Outie d Redig Divide-d-coquer prdigm 5. Review Merge-sort 4.1.1 Recurrece Equtios 5..1 tertive sustitutio Recursio trees Guess-d-test

Merge and Quick Sort

Merge ad Quick Sort Merge Sort Merge Sort Tree Implemetatio Quick Sort Pivot Item Radomized Quick Sort Adapted from: Goodrich ad Tamassia, Data Structures ad Algorithms i Java, Joh Wiley & So (1998). Ruig

Recurrece reltio & Recursio 9 Chpter 3 Recurrece reltio & Recursio Recurrece reltio : A recurrece is equtio or iequlity tht describes fuctio i term of itself with its smller iputs. T T The problem of size

This Lecture. Divide and Conquer. Merge Sort: Algorithm. Merge Sort Algorithm. MergeSort (Example) - 1. MergeSort (Example) - 2

This Lecture Divide-ad-coquer techique for algorithm desig. Example the merge sort. Writig ad solvig recurreces Divide ad Coquer Divide-ad-coquer method for algorithm desig: Divide: If the iput size is

CS 331 Design and Analysis of Algorithms. -- Divide and Conquer. Dr. Daisy Tang

CS 33 Desig d Alysis of Algorithms -- Divide d Coquer Dr. Disy Tg Divide-Ad-Coquer Geerl ide: Divide problem ito subproblems of the sme id; solve subproblems usig the sme pproh, d ombie prtil solutios,

Section IV.6: The Master Method and Applications

Sectio IV.6: The Mster Method d Applictios Defiitio IV.6.1: A fuctio f is symptoticlly positive if d oly if there exists rel umer such tht f(x) > for ll x >. A cosequece of this defiitio is tht fuctio

Sorting Algorithms. Algorithms Kyuseok Shim SoEECS, SNU.

Sortig Algorithms Algorithms Kyuseo Shim SoEECS, SNU. Desigig Algorithms Icremetal approaches Divide-ad-Coquer approaches Dyamic programmig approaches Greedy approaches Radomized approaches You are ot

Relation of BSTs to Quicksort, Analysis of Random BST. Lecture 9

Reltio o BSTs to Quicsort, Alysis o Rdom BST Lecture 9 Biry-serch-tree sort T Crete empty BST or i = to do TREE-INSERT(T, A[i]) Perorm iorder tree wl o T. Emple: 3 A = [3 8 2 6 7 5] 8 Tree-wl time = O(),

Review of the Riemann Integral

Chpter 1 Review of the Riem Itegrl This chpter provides quick review of the bsic properties of the Riem itegrl. 1.0 Itegrls d Riem Sums Defiitio 1.0.1. Let [, b] be fiite, closed itervl. A prtitio P of

CS583 Lecture 02. Jana Kosecka. some materials here are based on E. Demaine, D. Luebke slides

CS583 Lecture 02 Jaa Kosecka some materials here are based o E. Demaie, D. Luebke slides Previously Sample algorithms Exact ruig time, pseudo-code Approximate ruig time Worst case aalysis Best case aalysis

Classification of problem & problem solving strategies. classification of time complexities (linear, logarithmic etc)

Classificatio of problem & problem solvig strategies classificatio of time complexities (liear, arithmic etc) Problem subdivisio Divide ad Coquer strategy. Asymptotic otatios, lower boud ad upper boud:

Introduction to Algorithms 6.046J/18.401J

Itrodutio to Algorithms.04J/8.40J The divide-d-oquer desig prdigm. Divide the problem (iste) ito subproblems.. Coquer the subproblems by solvig them reursively. 3. Combie subproblem solutios. Leture 3

CS 332: Algorithms. Quicksort

CS 33: Aorithms Quicsort David Luebe //03 Homewor Assiged today, due ext Wedesday Will be o web page shortly after class Go over ow David Luebe //03 Review: Quicsort Sorts i place Sorts O( ) i the average

) 2 2(2. Assume that

lg lg W W W W W W W Assume tht lg log. 0. with for, W W W For ot power of, W 0 W W W for hrd to lyze this cse exctly ecuse of the floors d ceiligs. usig iductio rgumet lie the oe i Ex B.5 i Appedix B,

Matriculation number: You have 90 minutes to complete the exam of InformatikIIb. The following rules apply:

Departmet of Iformatics Prof. Dr. Michael Böhle Bizmühlestrasse 14 8050 Zurich Phoe: +41 44 635 4333 Email: boehle@ifi.uzh.ch AlgoDat Midterm1 Sprig 016 08.04.016 Name: Matriculatio umber: Advice You have

CSED233: Data Structures (2018F) Lecture13: Sorting and Selection

(018F) Lecture13: Sortig ad Selectio Daiji Kim CSE, POSECH dkim@postech.ac.kr Divide-ad-Coquer Divide-ad coquer a geeral algorithm desig paradigm: Divide: divide the iput data S i two djoit susets S 1

1.3 Continuous Functions and Riemann Sums

mth riem sums, prt 0 Cotiuous Fuctios d Riem Sums I Exmple we sw tht lim Lower() = lim Upper() for the fuctio!! f (x) = + x o [0, ] This is o ccidet It is exmple of the followig theorem THEOREM Let f be

CS 270 Algorithms. Oliver Kullmann. Growth of Functions. Divide-and- Conquer Min-Max- Problem. Tutorial. Reading from CLRS for week 2

Geeral remarks Week 2 1 Divide ad First we cosider a importat tool for the aalysis of algorithms: Big-Oh. The we itroduce a importat algorithmic paradigm:. We coclude by presetig ad aalysig two examples.

Design and Analysis of Algorithms

Desig ad Aalysis of Algorithms CSE 53 Lecture 9 Media ad Order Statistics Juzhou Huag, Ph.D. Departmet of Computer Sciece ad Egieerig Dept. CSE, UT Arligto CSE53 Desig ad Aalysis of Algorithms Medias ad

A recurrence equation is just a recursive function definition. It defines a function at one input in terms of its value on smaller inputs.

CS23 Algorithms Hadout #6 Prof Ly Turbak September 8, 200 Wellesley College RECURRENCES This hadout summarizes highlights of CLRS Chapter 4 ad Appedix A (CLR Chapters 3 & 4) Two-Step Strategy for Aalyzig

Advanced Algorithmic Problem Solving Le 6 Math and Search

Advced Algorithmic Prolem Solvig Le Mth d Serch Fredrik Heitz Dept of Computer d Iformtio Sciece Liköpig Uiversity Outlie Arithmetic (l. d.) Solvig lier equtio systems (l. d.) Chiese remider theorem (l.5

Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, Divide-and-Conquer

Presettio or use wit te textook, Agoritm Desig Appictios, y M. T. Gooric R. Tmssi, Wiey, 015 Divie--Coquer 015 Gooric Tmssi Divie--Coquer 1 Appictio: Mxim Sets We c visuize te vrious tre-os or optimizig

0 otherwise. sin( nx)sin( kx) 0 otherwise. cos( nx) sin( kx) dx 0 for all integers n, k.

. Computtio of Fourier Series I this sectio, we compute the Fourier coefficiets, f ( x) cos( x) b si( x) d b, i the Fourier series To do this, we eed the followig result o the orthogolity of the trigoometric

CSE 4095/5095 Topics in Big Data Analytics Spring 2017; Homework 1 Solutions

CSE 09/09 Topics i ig Data Aalytics Sprig 2017; Homework 1 Solutios Note: Solutios to problems,, ad 6 are due to Marius Nicolae. 1. Cosider the followig algorithm: for i := 1 to α log e do Pick a radom

Fast Fourier Transform 1) Legendre s Interpolation 2) Vandermonde Matrix 3) Roots of Unity 4) Polynomial Evaluation

Algorithm Desig d Alsis Victor Admchi CS 5-45 Sprig 4 Lecture 3 J 7, 4 Cregie Mello Uiversit Outlie Fst Fourier Trsform ) Legedre s Iterpoltio ) Vdermode Mtri 3) Roots of Uit 4) Polomil Evlutio Guss (777

2 DD2458 Popup HT Solution: Choose the activity which ends first and does not conflict with earlier chosen activities.

DD2458, Problem Solvig ad Programmig Uder Pressure Lecture 1: Greedy algorithms ad dyamic programmig Date: 2008-09-01 Scribe(s: Marti Wedi ad Nilas Wagre Lecturer: Douglas Wiström This lecture cotais basic

COMP26120: More on the Complexity of Recursive Programs (2018/19) Lucas Cordeiro

COMP26120: More o the Complexity of Recursive Programs (2018/19) Lucas Cordeiro lucas.cordeiro@machester.ac.uk Divide-ad-Coquer (Recurrece) Textbook: Algorithm Desig ad Applicatios, Goodrich, Michael T.

Data Structures and Algorithms

Data Structures ad Algorithms Autum 2017-2018 Outlie 1 Sortig Algorithms (cotd) Outlie Sortig Algorithms (cotd) 1 Sortig Algorithms (cotd) Heapsort Sortig Algorithms (cotd) Have see that we ca build a

Algorithms. Elementary Sorting. Dong Kyue Kim Hanyang University

Algorithms Elemetary Sortig Dog Kyue Kim Hayag Uiversity dqkim@hayag.a.kr Cotets Sortig problem Elemetary sortig algorithms Isertio sort Merge sort Seletio sort Bubble sort Sortig problem Iput A sequee

Discrete Mathematics I Tutorial 12

Discrete Mthemtics I Tutoril Refer to Chpter 4., 4., 4.4. For ech of these sequeces fid recurrece reltio stisfied by this sequece. (The swers re ot uique becuse there re ifiitely my differet recurrece

PROGRESSIONS AND SERIES

PROGRESSIONS AND SERIES A sequece is lso clled progressio. We ow study three importt types of sequeces: () The Arithmetic Progressio, () The Geometric Progressio, () The Hrmoic Progressio. Arithmetic Progressio.

CIS 121 Data Structures and Algorithms with Java Spring Code Snippets and Recurrences Monday, February 4/Tuesday, February 5

CIS 11 Data Structures ad Algorithms with Java Sprig 019 Code Sippets ad Recurreces Moday, February 4/Tuesday, February 5 Learig Goals Practice provig asymptotic bouds with code sippets Practice solvig

CS 332: Algorithms. Linear-Time Sorting. Order statistics. Slide credit: David Luebke (Virginia)

1 CS 332: Algorithms Liear-Time Sortig. Order statistics. Slide credit: David Luebke (Virgiia) Quicksort: Partitio I Words Partitio(A, p, r): Select a elemet to act as the pivot (which?) Grow two regios,

Divide & Conquer. Divide-and-conquer algorithms. Conventional product of polynomials. Conventional product of polynomials.

Divide-ad-coquer algorithms Divide & Coquer Strategy: Divide the problem ito smaller subproblems of the same type of problem Solve the subproblems recursively Combie the aswers to solve the origial problem

) n. ALG 1.3 Deterministic Selection and Sorting: Problem P size n. Examples: 1st lecture's mult M(n) = 3 M ( È

Algorithms Professor Joh Reif ALG 1.3 Determiistic Selectio ad Sortig: (a) Selectio Algorithms ad Lower Bouds (b) Sortig Algorithms ad Lower Bouds Problem P size fi divide ito subproblems size 1,..., k

Stalnaker s Argument

Stlker s Argumet (This is supplemet to Coutble Additiviy, Dutch Books d the Sleepig Beuty roblem ) Stlker (008) suggests rgumet tht c be stted thus: Let t be the time t which Beuty wkes o Mody morig. Upo

MAS221 Analysis, Semester 2 Exercises

MAS22 Alysis, Semester 2 Exercises Srh Whitehouse (Exercises lbelled * my be more demdig.) Chpter Problems: Revisio Questio () Stte the defiitio of covergece of sequece of rel umbers, ( ), to limit. (b)

Numbers (Part I) -- Solutions

Ley College -- For AMATYC SML Mth Competitio Cochig Sessios v.., [/7/00] sme s /6/009 versio, with presettio improvemets Numbers Prt I) -- Solutios. The equtio b c 008 hs solutio i which, b, c re distict

SOLUTION OF SYSTEM OF LINEAR EQUATIONS. Lecture 4: (a) Jacobi's method. method (general). (b) Gauss Seidel method.

SOLUTION OF SYSTEM OF LINEAR EQUATIONS Lecture 4: () Jcobi's method. method (geerl). (b) Guss Seidel method. Jcobi s Method: Crl Gustv Jcob Jcobi (804-85) gve idirect method for fidig the solutio of system

Error-free compression

Error-free compressio Useful i pplictio where o loss of iformtio is tolerble. This mybe due to ccurcy requiremets, legl requiremets, or less th perfect qulity of origil imge. Compressio c be chieved by

Section 6.3: Geometric Sequences

40 Chpter 6 Sectio 6.: Geometric Sequeces My jobs offer ul cost-of-livig icrese to keep slries cosistet with ifltio. Suppose, for exmple, recet college grdute fids positio s sles mger erig ul slry of $6,000.

Fundamental Algorithms

Fudametal Algorithms Chapter 2b: Recurreces Michael Bader Witer 2014/15 Chapter 2b: Recurreces, Witer 2014/15 1 Recurreces Defiitio A recurrece is a (i-equality that defies (or characterizes a fuctio i

CSI 5163 (95.573) ALGORITHM ANALYSIS AND DESIGN

CSI 5163 (95.573) ALGORITHM ANALYSIS AND DESIGN CSI 5163 (95.5703) ALGORITHM ANALYSIS AND DESIGN (3 cr.) (T) Topics of curret iterest i the desig ad aalysis of computer algorithms for graphtheoretical

Algorithms and Data Structures Lecture IV

Algorithms ad Data Structures Lecture IV Simoas Šalteis Aalborg Uiversity simas@cs.auc.dk September 5, 00 1 This Lecture Aalyzig the ruig time of recursive algorithms (such as divide-ad-coquer) Writig

Skip Lists. Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 S 3 S S 1

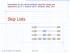Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Skip Lists S 3 15 15 23 10 15 23 36 Skip Lists 1 What is a Skip List A skip list for

,... are the terms of the sequence. If the domain consists of the first n positive integers only, the sequence is a finite sequence.

Chpter 9 & 0 FITZGERALD MAT 50/5 SECTION 9. Sequece Defiitio A ifiite sequece is fuctio whose domi is the set of positive itegers. The fuctio vlues,,, 4,...,,... re the terms of the sequece. If the domi

MA123, Chapter 9: Computing some integrals (pp )

MA13, Chpter 9: Computig some itegrls (pp. 189-05) Dte: Chpter Gols: Uderstd how to use bsic summtio formuls to evlute more complex sums. Uderstd how to compute its of rtiol fuctios t ifiity. Uderstd how

Model of Computation and Runtime Analysis

Model of Computatio ad Rutime Aalysis Model of Computatio Model of Computatio Specifies Set of operatios Cost of operatios (ot ecessarily time) Examples Turig Machie Radom Access Machie (RAM) PRAM Map

Chapter 7 Infinite Series

MA Ifiite Series Asst.Prof.Dr.Supree Liswdi Chpter 7 Ifiite Series Sectio 7. Sequece A sequece c be thought of s list of umbers writte i defiite order:,,...,,... 2 The umber is clled the first term, 2

is an ordered list of numbers. Each number in a sequence is a term of a sequence. n-1 term

Mthemticl Ptters. Arithmetic Sequeces. Arithmetic Series. To idetify mthemticl ptters foud sequece. To use formul to fid the th term of sequece. To defie, idetify, d pply rithmetic sequeces. To defie rithmetic

Chapter 5. The Riemann Integral. 5.1 The Riemann integral Partitions and lower and upper integrals. Note: 1.5 lectures

Chpter 5 The Riem Itegrl 5.1 The Riem itegrl Note: 1.5 lectures We ow get to the fudmetl cocept of itegrtio. There is ofte cofusio mog studets of clculus betwee itegrl d tiderivtive. The itegrl is (iformlly)

4.3 Growth Rates of Solutions to Recurrences

4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.

Divide and Conquer II

Algorithms Divide ad Coquer II Divide ad Coquer II Desig ad Aalsis of Algorithms Adrei Bulatov Algorithms Divide ad Coquer II 6- Closest Pair: The Problem The Closest Pair Problem Istace: poits i the plae

ICS141: Discrete Mathematics for Computer Science I

ICS4: Discrete Mthemtics for Computer Sciece I Dept. Iformtio & Computer Sci., J Stelovsky sed o slides y Dr. Bek d Dr. Still Origils y Dr. M. P. Frk d Dr. J.L. Gross Provided y McGrw-Hill 3- Quiz. gcd(84,96).

Examples: data compression, path-finding, game-playing, scheduling, bin packing

Algorithms - Basic Cocepts Algorithms so what is a algorithm, ayway? The dictioary defiitio: A algorithm is a well-defied computatioal procedure that takes iput ad produces output. This class will deal

Definite Integral. The Left and Right Sums

Clculus Li Vs Defiite Itegrl. The Left d Right Sums The defiite itegrl rises from the questio of fidig the re betwee give curve d x-xis o itervl. The re uder curve c be esily clculted if the curve is give

f(bx) dx = f dx = dx l dx f(0) log b x a + l log b a 2ɛ log b a.

Eercise 5 For y < A < B, we hve B A f fb B d = = A B A f d f d For y ɛ >, there re N > δ >, such tht d The for y < A < δ d B > N, we hve ba f d f A bb f d l By ba A A B A bb ba fb d f d = ba < m{, b}δ

Mathacle. PSet Stats, Concepts In Statistics Level Number Name: Date:

APPENDEX I. THE RAW ALGEBRA IN STATISTICS A I-1. THE INEQUALITY Exmple A I-1.1. Solve ech iequlity. Write the solutio i the itervl ottio..) 2 p - 6 p -8.) 2x- 3 < 5 Solutio:.). - 4 p -8 p³ 2 or pî[2, +

Week 13 Notes: 1) Riemann Sum. Aim: Compute Area Under a Graph. Suppose we want to find out the area of a graph, like the one on the right:

Week 1 Notes: 1) Riem Sum Aim: Compute Are Uder Grph Suppose we wt to fid out the re of grph, like the oe o the right: We wt to kow the re of the red re. Here re some wys to pproximte the re: We cut the

INFINITE SERIES. ,... having infinite number of terms is called infinite sequence and its indicated sum, i.e., a 1

Appedix A.. Itroductio As discussed i the Chpter 9 o Sequeces d Series, sequece,,...,,... hvig ifiite umber of terms is clled ifiite sequece d its idicted sum, i.e., + + +... + +... is clled ifite series

=> PARALLEL INTERCONNECTION. Basic Properties LTI Systems. The Commutative Property. Convolution. The Commutative Property. The Distributive Property

Lier Time-Ivrit Bsic Properties LTI The Commuttive Property The Distributive Property The Associtive Property Ti -6.4 / Chpter Covolutio y ] x ] ] x ]* ] x ] ] y] y ( t ) + x( τ ) h( t τ ) dτ x( t) * h(

1. (25 points) Use the limit definition of the definite integral and the sum formulas to compute. [1 x + x2

Mth 3, Clculus II Fil Exm Solutios. (5 poits) Use the limit defiitio of the defiite itegrl d the sum formuls to compute 3 x + x. Check your swer by usig the Fudmetl Theorem of Clculus. Solutio: The limit

COMP285 Midterm Exam Department of Mathematics

COMP85 Midterm Exam Departmet of Mathematics Fall 010/011 - November 8, 010 Name: Studet Number: Please fiish withi 90 miutes. All poits above 100 are cosidered as bous poit. You ca reach maximal 1 poits.

Data Structures and Algorithms CMPSC 465

Dt Structures nd Algorithms CMPSC 465 LECTURE 10 Solving recurrences Mster theorem Adm Smith S. Rskhodnikov nd A. Smith; bsed on slides by E. Demine nd C. Leiserson Review questions Guess the solution

POWER SERIES R. E. SHOWALTER

POWER SERIES R. E. SHOWALTER. sequeces We deote by lim = tht the limit of the sequece { } is the umber. By this we me tht for y ε > 0 there is iteger N such tht < ε for ll itegers N. This mkes precise

Divide and Conquer. 1 Overview. 2 Multiplying Bit Strings. COMPSCI 330: Design and Analysis of Algorithms 1/19/2016 and 1/21/2016

COMPSCI 330: Desig ad Aalysis of Algorithms 1/19/2016 ad 1/21/2016 Lecturer: Debmalya Paigrahi Divide ad Coquer Scribe: Tiaqi Sog 1 Overview I this lecture, a importat algorithm desig techique called divide-ad-coquer

The Weierstrass Approximation Theorem

The Weierstrss Approximtio Theorem Jmes K. Peterso Deprtmet of Biologicl Scieces d Deprtmet of Mthemticl Scieces Clemso Uiversity Februry 26, 2018 Outlie The Wierstrss Approximtio Theorem MtLb Implemettio

MTH 146 Class 16 Notes

MTH 46 Clss 6 Notes 0.4- Cotiued Motivtio: We ow cosider the rc legth of polr curve. Suppose we wish to fid the legth of polr curve curve i terms of prmetric equtios s: r f where b. We c view the cos si

Vectors. Vectors in Plane ( 2

Vectors Vectors i Ple ( ) The ide bout vector is to represet directiol force Tht mes tht every vector should hve two compoets directio (directiol slope) d mgitude (the legth) I the ple we preset vector

Department of Informatics Prof. Dr. Michael Böhlen Binzmühlestrasse Zurich Phone:

Departmet of Iformatics Prof. Dr. Michael Böhle Bizmühlestrasse 14 8050 Zurich Phoe: +41 44 635 4333 Email: boehle@ifi.uzh.ch Iformatik II Midterm1 Sprig 018 3.03.018 Advice You have 90 miutes to complete

( a n ) converges or diverges.

Chpter Ifiite Series Pge of Sectio E Rtio Test Chpter : Ifiite Series By the ed of this sectio you will be ble to uderstd the proof of the rtio test test series for covergece by pplyig the rtio test pprecite

A GENERAL METHOD FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS: THE FROBENIUS (OR SERIES) METHOD

Diol Bgoo () A GENERAL METHOD FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS: THE FROBENIUS (OR SERIES) METHOD I. Itroductio The first seprtio of vribles (see pplictios to Newto s equtios) is ver useful method

Fig. 1. I a. V ag I c. I n. V cg. Z n Z Y. I b. V bg

ymmetricl Compoets equece impedces Although the followig focuses o lods, the results pply eqully well to lies, or lies d lods. Red these otes together with sectios.6 d.9 of text. Cosider the -coected lced

Math 104: Final exam solutions

Mth 14: Fil exm solutios 1. Suppose tht (s ) is icresig sequece with coverget subsequece. Prove tht (s ) is coverget sequece. Aswer: Let the coverget subsequece be (s k ) tht coverges to limit s. The there

CSE 332. Data Structures and Parallelism

Aam Blak Lecture 6a Witer 2017 CSE 332 Data Structures a Parallelism CSE 332: Data Structures a Parallelism More Recurreces T () T (/2) T (/2) T (/4) T (/4) T (/4) T (/4) P1 De-Brief 1 You i somethig substatial!

Model of Computation and Runtime Analysis

Model of Computatio ad Rutime Aalysis Model of Computatio Model of Computatio Specifies Set of operatios Cost of operatios (ot ecessarily time) Examples Turig Machie Radom Access Machie (RAM) PRAM Map

8.3 Sequences & Series: Convergence & Divergence

8.3 Sequeces & Series: Covergece & Divergece A sequece is simply list of thigs geerted by rule More formlly, sequece is fuctio whose domi is the set of positive itegers, or turl umbers,,,3,. The rge of

Data Structures and Algorithm. Xiaoqing Zheng

Data Structures ad Algorithm Xiaoqig Zheg zhegxq@fudaeduc What are algorithms? A sequece of computatioal steps that trasform the iput ito the output Sortig problem: Iput: A sequece of umbers

Taylor Polynomials. The Tangent Line. (a, f (a)) and has the same slope as the curve y = f (x) at that point. It is the best

Tylor Polyomils Let f () = e d let p() = 1 + + 1 + 1 6 3 Without usig clcultor, evlute f (1) d p(1) Ok, I m still witig With little effort it is possible to evlute p(1) = 1 + 1 + 1 (144) + 6 1 (178) =

Laws of Integral Indices

A Lws of Itegrl Idices A. Positive Itegrl Idices I, is clled the se, is clled the idex lso clled the expoet. mes times.... Exmple Simplify 5 6 c Solutio 8 5 6 c 6 Exmple Simplify Solutio The results i

We will begin by supplying the proof to (a).

(The solutios of problem re mostly from Jeffrey Mudrock s HWs) Problem 1. There re three sttemet from Exmple 5.4 i the textbook for which we will supply proofs. The sttemets re the followig: () The spce

Introduction to Algorithms 6.046J/18.401J LECTURE 3 Divide and conquer Binary search Powering a number Fibonacci numbers Matrix multiplication

Itroductio to Algorithms 6.046J/8.40J LECTURE 3 Divide ad coquer Biary search Powerig a umber Fiboacci umbers Matrix multiplicatio Strasse s algorithm VLSI tree layout Prof. Charles E. Leiserso The divide-ad-coquer

10.5 Power Series. In this section, we are going to start talking about power series. A power series is a series of the form

0.5 Power Series I the lst three sectios, we ve spet most of tht time tlkig bout how to determie if series is coverget or ot. Now it is time to strt lookig t some specific kids of series d we will evetully

Introduction to Computational Molecular Biology. Suffix Trees

18.417 Itroductio to Computtiol Moleculr Biology Lecture 11: October 14, 004 Scribe: Athich Muthitchroe Lecturer: Ross Lippert Editor: Toy Scelfo Suffix Trees This is oe of the most complicted dt structures

Recursive Algorithms. Recurrences. Recursive Algorithms Analysis

Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects

Applied Databases. Sebastian Maneth. Lecture 16 Suffix Array, Burrows-Wheeler Transform. University of Edinburgh - March 10th, 2016

Applied Dtbses Lecture 16 Suffix Arry, Burrows-Wheeler Trsform Sebsti Meth Uiversity of Ediburgh - Mrch 10th, 2016 2 Outlie 1. Suffix Arry 2. Burrows-Wheeler Trsform 3 Olie Strig-Mtchig how c we do Horspool

: : 8.2. Test About a Population Mean. STT 351 Hypotheses Testing Case I: A Normal Population with Known. - null hypothesis states 0

8.2. Test About Popultio Me. Cse I: A Norml Popultio with Kow. H - ull hypothesis sttes. X1, X 2,..., X - rdom smple of size from the orml popultio. The the smple me X N, / X X Whe H is true. X 8.2.1.

Remarks: (a) The Dirac delta is the function zero on the domain R {0}.

Sectio Objective(s): The Dirc s Delt. Mi Properties. Applictios. The Impulse Respose Fuctio. 4.4.. The Dirc Delt. 4.4. Geerlized Sources Defiitio 4.4.. The Dirc delt geerlized fuctio is the limit δ(t)

ALGEBRA II CHAPTER 7 NOTES. Name

ALGEBRA II CHAPTER 7 NOTES Ne Algebr II 7. th Roots d Rtiol Expoets Tody I evlutig th roots of rel ubers usig both rdicl d rtiol expoet ottio. I successful tody whe I c evlute th roots. It is iportt for

Analysis of Algorithms -Quicksort-

Aalysis of Algorithms -- Adreas Ermedahl MRTC (Mälardales Real-Time Research Ceter) adreas.ermedahl@mdh.se Autum 2004 Proposed by C.A.R. Hoare i 962 Worst- case ruig time: Θ( 2 ) Expected ruig time: Θ(

Lecture 3: Asymptotic Analysis + Recurrences

Lecture 3: Asymptotic Aalysis + Recurreces Data Structures ad Algorithms CSE 373 SU 18 BEN JONES 1 Warmup Write a model ad fid Big-O for (it i = 0; i < ; i++) { for (it j = 0; j < i; j++) { System.out.pritl(

Improving XOR-Dominated Circuits by Exploiting Dependencies between Operands. Ajay K. Verma and Paolo Ienne. csda

Improvig XOR-Domited Circuits y Exploitig Depedecies etwee Operds Ajy K. Verm d Polo Iee csd Processor Architecture Lortory LAP & Cetre for Advced Digitl Systems CSDA Ecole Polytechique Fédérle de Luse

Riemann Integration. Chapter 1

Mesure, Itegrtio & Rel Alysis. Prelimiry editio. 8 July 2018. 2018 Sheldo Axler 1 Chpter 1 Riem Itegrtio This chpter reviews Riem itegrtio. Riem itegrtio uses rectgles to pproximte res uder grphs. This

INTEGRATION IN THEORY

CHATER 5 INTEGRATION IN THEORY 5.1 AREA AROXIMATION 5.1.1 SUMMATION NOTATION Fibocci Sequece First, exmple of fmous sequece of umbers. This is commoly ttributed to the mthemtici Fibocci of is, lthough