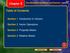
Vectors. chapter. Figure 3.1 Designation of points in a Cartesian coordinate system. Every point is labeled with coordinates (x, y).

Transcription

1 chapter 3 Vectors 3.1 Coordinate stems 3.2 Vector and calar Qantities 3.3 ome Properties of Vectors 3.4 Components of a Vector and Unit Vectors In or std of phsics, we often need to work with phsical qantities that have both nmerical and directional properties. s noted in ection 2.1, qantities of this natre are vector qantities. This chapter is primaril concerned with general properties of vector qantities. We discss the addition and sbtraction of vector qantities, together with some common applications to phsical sitations. Vector qantities are sed throghot this tet. Therefore, it is imperative that o master the techniqes discssed in this chapter. signpost in Westport, New Zealand shows the distance and direction to several cities. Qantities that are defined b both a magnitde and a direction are called vector qantities. ( lan Chant) 10 (, ) 3.1 Coordinate stems Man aspects of phsics involve a description of a location in space. In Chapter 2, for eample, we saw that the mathematical description of an object s motion reqires a method for describing the object s position at varios times. In two dimensions, this description is accomplished with the se of the Cartesian coordinate sstem, in which perpendiclar aes intersect at a point defined as the origin (Fig. 3.1). Cartesian coordinates are also called rectanglar coordinates. Q 5 P ( 3, 4) (5, 3) O 5 10 Figre 3.1 Designation of points in a Cartesian coordinate sstem. Ever point is labeled with coordinates (, ). 55

2 56 CHPTER 3 Vectors (, ) r sin = r cos = r r O tan = a b CTIVE FIGURE 3.2 (a) The plane polar coordinates of a point are represented b the distance r and the angle, where is measred conterclockwise from the positive ais. (b) The right triangle sed to relate (, ) to (r, ). ometimes it is more convenient to represent a point in a plane b its plane polar coordinates (r, ) as shown in ctive Figre 3.2a. In this polar coordinate sstem, r is the distance from the origin to the point having Cartesian coordinates (, ) and is the angle between a fied ais and a line drawn from the origin to the point. The fied ais is often the positive ais, and is sall measred conterclockwise from it. From the right triangle in ctive Figre 3.2b, we find that sin /r and that cos /r. ( review of trigonometric fnctions is given in ppendi B.4.) Therefore, starting with the plane polar coordinates of an point, we can obtain the Cartesian coordinates b sing the eqations 5 r cos (3.1) 5 r sin (3.2) Frthermore, if we know the Cartesian coordinates, the definitions of trigonometr tell s that tan 5 (3.3) r 5 " (3.4) Eqation 3.4 is the familiar Pthagorean theorem. These for epressions relating the coordinates (, ) to the coordinates (r, ) appl onl when is defined as shown in ctive Figre 3.2a in other words, when positive is an angle measred conterclockwise from the positive ais. (ome scientific calclators perform conversions between Cartesian and polar coordinates based on these standard conventions.) If the reference ais for the polar angle is chosen to be one other than the positive ais or if the sense of increasing is chosen differentl, the epressions relating the two sets of coordinates will change. Eample 3.1 Polar Coordinates The Cartesian coordinates of a point in the plane are (, ) ( 3.50, 2.50) m as shown in ctive Figre 3.3. Find the polar coordinates of this point. OLUTION (m) Conceptalize The drawing in ctive Figre 3.3 helps s conceptalize the problem. Categorize Based on the statement of the problem and the Conceptalize step, we recognize that we are simpl converting from Cartesian coordinates to polar coordinates. We therefore categorize this eample as a sb- CTIVE FIGURE 3.3 (Eample 3.1) Finding polar coordinates when Cartesian coordinates are given. r ( 3.50, 2.50) (m)

3 3.2 Vector and calar Qantities 57 stittion problem. bstittion problems generall do not have an etensive nalze step other than the sbstittion of nmbers into a given eqation. imilarl, the Finalize step consists primaril of checking the nits and making sre that the answer is reasonable. Therefore, for sbstittion problems, we will not label nalze or Finalize steps. Use Eqation 3.4 to find r : Use Eqation 3.3 to find : r 5 " " m m m tan m m Notice that o mst se the signs of and to find that the point lies in the third qadrant of the coordinate sstem. That is, 216, not 35.5, whose tangent is also Vector and calar Qantities We now formall describe the difference between scalar qantities and vector qantities. When o want to know the temperatre otside so that o will know how to dress, the onl information o need is a nmber and the nit degrees C or degrees F. Temperatre is therefore an eample of a scalar qantit: scalar qantit is completel specified b a single vale with an appropriate nit and has no direction. Other eamples of scalar qantities are volme, mass, speed, and time intervals. ome scalars are alwas positive, sch as mass and speed. Others, sch as temperatre, can have either positive or negative vales. The rles of ordinar arithmetic are sed to maniplate scalar qantities. If o are preparing to pilot a small plane and need to know the wind velocit, o mst know both the speed of the wind and its direction. Becase direction is important for its complete specification, velocit is a vector qantit: vector qantit is completel specified b a nmber with an appropriate nit pls a direction. nother eample of a vector qantit is displacement, as o know from Chapter 2. ppose a particle moves from some point to some point along a straight path as shown in Figre 3.4. We represent this displacement b drawing an arrow from to, with the tip of the arrow pointing awa from the starting point. The direction of the arrowhead represents the direction of the displacement, and the length of the arrow represents the magnitde of the displacement. If the particle travels along some other path from to sch as shown b the broken line in Figre 3.4, its displacement is still the arrow drawn from to. Displacement depends onl on the initial and final positions, so the displacement vector is independent of the path taken b the particle between these two points. In this tet, we se a boldface letter with an arrow over the letter, sch as, to represent a vector. nother common notation for vectors with which o shold be familiar is a simple boldface character:. The magnitde of the vector is written either or 0 0. The magnitde of a vector has phsical nits, sch as meters for displacement or meters per second for velocit. The magnitde of a vector is alwas a positive nmber. Figre 3.4 s a particle moves from to along an arbitrar path represented b the broken line, its displacement is a vector qantit shown b the arrow drawn from to. Qick Qiz 3.1 Which of the following are vector qantities and which are scalar qantities? (a) or age (b) acceleration (c) velocit (d) speed (e) mass

4 58 CHPTER 3 Vectors O Figre 3.5 These for vectors are eqal becase the have eqal lengths and point in the same direction. Pitfall Prevention 3.1 Vector ddition Verss calar ddition Notice that 1 B 5 C is ver different from B C. The first eqation is a vector sm, which mst be handled carefll, sch as with the graphical method. The second eqation is a simple algebraic addition of nmbers that is handled with the normal rles of arithmetic. Commtative law of addition 3.3 ome Properties of Vectors In this section, we shall investigate general properties of vectors representing phsical qantities. We also discss how to add and sbtract vectors sing both algebraic and geometric methods. Eqalit of Two Vectors For man prposes, two vectors and B ma be defined to be eqal if the have the same magnitde and if the point in the same direction. That is, 5 B onl if B and if and B point in the same direction along parallel lines. For eample, all the vectors in Figre 3.5 are eqal even thogh the have different starting points. This propert allows s to move a vector to a position parallel to itself in a diagram withot affecting the vector. dding Vectors The rles for adding vectors are convenientl described b a graphical method. To add vector B to vector, first draw vector on graph paper, with its magnitde represented b a convenient length scale, and then draw vector B to the same scale, with its tail starting from the tip of, as shown in ctive Figre 3.6. The resltant vector R 5 1 B is the vector drawn from the tail of to the tip of B. geometric constrction can also be sed to add more than two vectors as shown in Figre 3.7 for the case of for vectors. The resltant vector R 5 1 B 1 C 1 D is the vector that completes the polgon. In other words, R is the vector drawn from the tail of the first vector to the tip of the last vector. This techniqe for adding vectors is often called the head to tail method. When two vectors are added, the sm is independent of the order of the addition. (This fact ma seem trivial, bt as o will see in Chapter 11, the order is important when vectors are mltiplied. Procedres for mltipling vectors are discssed in Chapters 7 and 11.) This propert, which can be seen from the geometric constrction in Figre 3.8, is known as the commtative law of addition: 1 B 5 B 1 (3.5) When three or more vectors are added, their sm is independent of the wa in which the individal vectors are groped together. geometric proof of this rle B Draw, then add. R B CTIVE FIGURE 3.6 B When vector B is added to vector, the resltant R is the vector that rns from the tail of to the tip of B. D B C Figre 3.7 Geometric constrction for smming for vectors. The resltant vector R is b definition the one that completes the polgon. D B C B R B B B Draw, then add B. Figre 3.8 This constrction shows that 1 B 5 B 1 or, in other words, that vector addition is commtative.

5 3.3 ome Properties of Vectors 59 B dd and C ; dd and ; then add the then add C to reslt to. the reslt. B Figre 3.9 Geometric constrctions for verifing the associative law of addition. ( B C ) B C C B ( ) B C B C B for three vectors is given in Figre 3.9. This propert is called the associative law of addition: 1 1B 1 C B2 1 C (3.6) In smmar, a vector qantit has both magnitde and direction and also obes the laws of vector addition as described in ctive Figre 3.6 and Figres 3.7 to 3.9. When two or more vectors are added together, the mst all have the same nits and the mst all be the same tpe of qantit. It wold be meaningless to add a velocit vector (for eample, 60 km/h to the east) to a displacement vector (for eample, 200 km to the north) becase these vectors represent different phsical qantities. The same rle also applies to scalars. For eample, it wold be meaningless to add time intervals to temperatres. ssociative law of addition Negative of a Vector The negative of the vector is defined as the vector that when added to gives zero for the vector sm. That is, The vectors and 2 have the same magnitde bt point in opposite directions. btracting Vectors The operation of vector sbtraction makes se of the definition of the negative of a vector. We define the operation 2 B as vector 2B added to vector : 2 B B2 (3.7) The geometric constrction for sbtracting two vectors in this wa is illstrated in Figre 3.10a. nother wa of looking at vector sbtraction is to notice that the difference 2 B between two vectors and B is what o have to add to the second vector to obtain the first. In this case, as Figre 3.10b shows, the vector 2 B points from the tip of the second vector to the tip of the first. wold draw We B here if we were adding it to. B Vector C B is the vector we mst add to to obtain. B C a B B dding to is eqivalent to sbtracting B from. B b B C B Figre 3.10 (a) btracting vector B from vector. The vector 2B is eqal in magnitde to vector B and points in the opposite direction. (b) second wa of looking at vector sbtraction.

6 60 CHPTER 3 Vectors Mltipling a Vector b a calar If vector is mltiplied b a positive scalar qantit m, the prodct m is a vector that has the same direction as and magnitde m. If vector is mltiplied b a negative scalar qantit m, the prodct 2m is directed opposite. For eample, the vector 5 is five times as long as and points in the same direction as ; the vector is one-third the length of and points in the direction opposite. Qick Qiz 3.2 The magnitdes of two vectors and B are 12 nits and B 8 nits. Which pair of nmbers represents the largest and smallest possible vales for the magnitde of the resltant vector R 5 1 B? (a) 14.4 nits, 4 nits (b) 12 nits, 8 nits (c) 20 nits, 4 nits (d) none of these answers Qick Qiz 3.3 If vector B is added to vector, which two of the following choices mst be tre for the resltant vector to be eqal to zero? (a) and B are parallel and in the same direction. (b) and B are parallel and in opposite directions. (c) and B have the same magnitde. (d) and B are perpendiclar. Eample 3.2 Vacation Trip car travels 20.0 km de north and then 35.0 km in a direction 60.0 west of north as shown in Figre 3.11a. Find the magnitde and direction of the car s resltant displacement. OLUTION Conceptalize The vectors and B drawn in Figre 3.11a help s conceptalize the problem. Categorize We can categorize this eample as a simple analsis problem in vector addition. The displacement R is the resltant when the two individal displacements and B are added. We can frther categorize it as a problem abot the analsis of triangles, so we appeal to or epertise in geometr and trigonometr. nalze In this eample, we show two was to analze the problem of finding the resltant of two vectors. The first wa is to solve the problem geometricall, sing graph paper and a protractor to measre the magnitde of R and its direction in Figre 3.11a. (In fact, even when o know o are going to be carring ot a calclation, o shold sketch the vectors to check or reslts.) With an ordinar rler and protractor, a large diagram tpicall gives answers to two-digit bt not to three-digit precision. Tr sing these tools on R in Figre 3.11a! The second wa to solve the problem is to analze it algebraicall. The magnitde of R can be obtained from the law of cosines as applied to the triangle in Figre 3.11a (see ppendi B.4). R B 20 a (km) b W N (km) E B R 20 b (km) b (km) Figre 3.11 (Eample 3.2) (a) Graphical method for finding the resltant displacement vector R 5 1 B. (b) dding the vectors in reverse order 1B 1 2 gives the same reslt for R. Use R 2 2 B 2 2B cos from the law of cosines to find R: R 5 " 2 1 B 2 2 2B cos bstitte nmerical vales, noting that : R 5 "120.0 km km km km2 cos km

7 3.4 Components of a Vector and Unit Vectors 61 Use the law of sines (ppendi B.4) to find the direction of R measred from the northerl direction: sin b B 5 sin R sin b 5 B R b sin km 48.2 km sin The resltant displacement of the car is 48.2 km in a direction 38.9 west of north. Finalize Does the angle b that we calclated agree with an estimate made b looking at Figre 3.11a or with an actal angle measred from the diagram sing the graphical method? Is it reasonable that the magnitde of R is larger than that of both and B? re the nits of R correct? lthogh the head to tail method of adding vectors works well, it sffers from two disadvantages. First, some people find sing the laws of cosines and sines to be awkward. econd, a triangle onl reslts if o are adding two vectors. If o are adding three or more vectors, the reslting geometric shape is sall not a triangle. In ection 3.4, we eplore a new method of adding vectors that will address both of these disadvantages. WHT IF? ppose the trip were taken with the two vectors in reverse order: 35.0 km at 60.0 west of north first and then 20.0 km de north. How wold the magnitde and the direction of the resltant vector change? nswer The wold not change. The commtative law for vector addition tells s that the order of vectors in an addition is irrelevant. Graphicall, Figre 3.11b shows that the vectors added in the reverse order give s the same resltant vector. 3.4 Components of a Vector and Unit Vectors The graphical method of adding vectors is not recommended whenever high accrac is reqired or in three-dimensional problems. In this section, we describe a method of adding vectors that makes se of the projections of vectors along coordinate aes. These projections are called the components of the vector or its rectanglar components. n vector can be completel described b its components. Consider a vector ling in the plane and making an arbitrar angle with the positive ais as shown in Figre 3.12a. This vector can be epressed as the sm of two other component vectors, which is parallel to the ais, and, which is parallel to the ais. From Figre 3.12b, we see that the three vectors form a right triangle and that 5 1. We shall often refer to the components of a vector, written and (withot the boldface notation). The component represents the projection of along the ais, and the component represents the projection of along the ais. These components can be positive or negative. The component is positive if the component vector points in the positive direction and is negative if points in the negative direction. similar statement is made for the component. From Figre 3.12 and the definition of sine and cosine, we see that cos / and that sin /. Hence, the components of are 5 cos (3.8) 5 sin (3.9) Pitfall Prevention 3.2 and Components Eqations 3.8 and 3.9 associate the cosine of the angle with the component and the sine of the angle with the component. This association is tre onl becase we measred the angle with respect to the ais, so do not memorize these eqations. If is measred with respect to the ais (as in some problems), these eqations will be incorrect. Think abot which side of the triangle containing the components is adjacent to the angle and which side is opposite and then assign the cosine and sine accordingl. Components of the vector O a O b Figre 3.12 (a) vector ling in the plane can be represented b its component vectors and. (b) The component vector can be moved to the right so that it adds to. The vector sm of the component vectors is. These three vectors form a right triangle.

8 62 CHPTER 3 Vectors The magnitdes of these components are the lengths of the two sides of a right triangle with a hpotense of length. Therefore, the magnitde and direction of are related to its components throgh the epressions 5 " (3.10) points left and is points p and is points left and is points down and is points right and is points p and is points right and is points down and is Figre 3.13 The signs of the components of a vector depend on the qadrant in which the vector is located. 5tan 21 a b (3.11) Notice that the signs of the components and depend on the angle. For eample, if 120, is negative and is positive. If 225, both and are negative. Figre 3.13 smmarizes the signs of the components when lies in the varios qadrants. When solving problems, o can specif a vector either with its components and or with its magnitde and direction and. ppose o are working a phsics problem that reqires resolving a vector into its components. In man applications, it is convenient to epress the components in a coordinate sstem having aes that are not horizontal and vertical bt that are still perpendiclar to each other. For eample, we will consider the motion of objects sliding down inclined planes. For these eamples, it is often convenient to orient the ais parallel to the plane and the ais perpendiclar to the plane. Qick Qiz 3.4 Choose the correct response to make the sentence tre: component of a vector is (a) alwas, (b) never, or (c) sometimes larger than the magnitde of the vector. Unit Vectors Vector qantities often are epressed in terms of nit vectors. nit vector is a dimensionless vector having a magnitde of eactl 1. Unit vectors are sed to specif a given direction and have no other phsical significance. The are sed solel as a bookkeeping convenience in describing a direction in space. We shall se the smbols i^, j^, and k^ to represent nit vectors pointing in the positive,, and z directions, respectivel. (The hats, or circmflees, on the smbols are a standard notation for nit vectors.) The nit vectors i^, j^, and k^ form a set of mtall perpendiclar vectors in a right-handed coordinate sstem as shown in ctive Figre 3.14a. The magnitde of each nit vector eqals 1; that is, 0 i^ j^ k^ Consider a vector ling in the plane as shown in ctive Figre 3.14b. The prodct of the component and the nit vector i^ is the component vector 5 i^, which lies on the ais and has magnitde 0 0. Likewise, 5 j is the component vector of magnitde 0 0 ling on the ais. Therefore, the nit-vector notation for the vector is 5 i^ 1 j^ (3.12) CTIVE FIGURE 3.14 (a) The nit vectors i^, j^, and k^ are directed along the,, and z aes, respectivel. (b) Vector 5 i^ 1 j^ ling in the plane has components and. a ĵ ˆk î z b ĵ î

9 3.4 Components of a Vector and Unit Vectors 63 For eample, consider a point ling in the plane and having Cartesian coordinates (, ) as in Figre The point can be specified b the position vector r, which in nit-vector form is given b r 5 i^ 1 j^ (3.13) This notation tells s that the components of r are the coordinates and. Now let s see how to se components to add vectors when the graphical method is not sfficientl accrate. ppose we wish to add vector B to vector in Eqation 3.12, where vector B has components B and B. Becase of the bookkeeping convenience of the nit vectors, all we do is add the and components separatel. The resltant vector R 5 1 B is or R 5 1 i^ 1 j^ 2 1 1B i^ 1 B j^ 2 R B 2 i^ B 2 j^ (3.14) Becase R 5 R i^ 1 R j^, we see that the components of the resltant vector are R 5 1 B (3.15) R 5 1 B Therefore, we see that in the component method of adding vectors, we add all the components together to find the component of the resltant vector and se the same process for the components. We can check this addition b components with a geometric constrction as shown in Figre The magnitde of R and the angle it makes with the ais are obtained from its components sing the relationships R 5 "R 2 1 R 2 5 "1 1 B B 2 2 (3.16) tan 5 R 5 1 B (3.17) R 1 B t times, we need to consider sitations involving motion in three component directions. The etension of or methods to three-dimensional vectors is straightforward. If and B both have,, and z components, the can be epressed in the form 5 i^ 1 j^ 1 z k^ (3.18) B 5 B i^ 1 B j^ 1 B z k^ (3.19) The sm of and B is R B 2 i^ B 2 j^ 1 1 z 1 B z 2 k^ (3.20) Notice that Eqation 3.20 differs from Eqation 3.14: in Eqation 3.20, the resltant vector also has a z component R z z B z. If a vector R has,, and z components, the magnitde of the vector is R 5!R 2 1 R 2 1 R 2 z. The angle that R makes with the ais is fond from the epression cos R /R, with similar epressions for the angles with respect to the and z aes. The etension of or method to adding more than two vectors is also straightforward. For eample, 1 B 1 C B 1 C 2 i^ B 1 C 2 j^ 1 1 z 1 B z 1 C z 2 k^. We have described adding displacement vectors in this section becase these tpes of vectors are eas to visalize. We can also add other tpes of vectors, sch as velocit, force, and electric field vectors, which we will do in later chapters. O r î (, ) ĵ Figre 3.15 The point whose Cartesian coordinates are (, ) can be represented b the position vector r 5 i^ 1 j^. R B R B Figre 3.16 This geometric constrction for the sm of two vectors shows the relationship between the components of the resltant R and the components of the individal vectors. Pitfall Prevention 3.3 Tangents on Calclators Eqation 3.17 involves the calclation of an angle b means of a tangent fnction. Generall, the inverse tangent fnction on calclators provides an angle between 90 and 90. s a conseqence, if the vector o are stding lies in the second or third qadrant, the angle measred from the positive ais will be the angle or calclator retrns pls 180. R B Qick Qiz 3.5 For which of the following vectors is the magnitde of the vector eqal to one of the components of the vector? (a) 5 2 i^ 1 5 j^ (b) B 523 j^ (c) C 515 k^

10 64 CHPTER 3 Vectors Eample 3.3 The m of Two Vectors Find the sm of two displacement vectors and B ling in the plane and given b i^ j^ 2 m and B i^ j^ 2 m OLUTION Conceptalize Yo can conceptalize the sitation b drawing the vectors on graph paper. Categorize We categorize this eample as a simple sbstittion problem. Comparing this epression for with the general epression 5 i^ 1 j^ 1 z k^, we see that 2.0 m, 2.0 m, and z 0. Likewise, B 2.0 m, B 4.0 m, and B z 0. We can se a two-dimensional approach becase there are no z components. Use Eqation 3.14 to obtain the resltant vector R : R 5 1 B i^ m j^ m Evalate the components of R : R m R m Use Eqation 3.16 to find the magnitde of R : Find the direction of R from Eqation 3.17: R 5 "R 2 1 R 2 5 "14.0 m m2 2 5 "20 m m tan 5 R m R 4.0 m Yor calclator likel gives the answer 27 for tan 1 ( 0.50). This answer is correct if we interpret it to mean 27 clockwise from the ais. Or standard form has been to qote the angles measred conterclockwise from the ais, and that angle for this vector is 333. Eample 3.4 The Resltant Displacement particle ndergoes three consective displacements: D r i^ 1 30 j^ 1 12 k^ 2 cm, D r i^ 2 14 j^ k^ 2 cm, and D r i^ 1 15 j^ 2 cm. Find nit-vector notation for the resltant displacement and its magnitde. OLUTION Conceptalize lthogh is sfficient to locate a point in one dimension, we need a vector r to locate a point in two or three dimensions. The notation D r is a generalization of the one-dimensional displacement in Eqation 2.1. Three-dimensional displacements are more difficlt to conceptalize than those in two dimensions becase the latter can be drawn on paper. For this problem, let s imagine that o start with or pencil at the origin of a piece of graph paper on which o have drawn and aes. Move or pencil 15 cm to the right along the ais, then 30 cm pward along the ais, and then 12 cm perpendiclarl toward o awa from the graph paper. This procedre provides the displacement described b D r 1. From this point, move or pencil 23 cm to the right parallel to the ais, then 14 cm parallel to the graph paper in the direction, and then 5.0 cm perpendiclarl awa from o toward the graph paper. Yo are now at the displacement from the origin described b D r 1 1Dr 2. From this point, move or pencil 13 cm to the left in the direction, and (finall!) 15 cm parallel to the graph paper along the ais. Yor final position is at a displacement D r 1 1Dr 2 1Dr 3 from the origin. Categorize Despite the difficlt in conceptalizing in three dimensions, we can categorize this problem as a sbstittion problem becase of the carefl bookkeeping methods that we have developed for vectors. The mathematical maniplation keeps track of this motion along the three perpendiclar aes in an organized, compact wa, as we see below. To find the resltant displacement, add the three vectors: Find the magnitde of the resltant vector: D r 5Dr 1 1Dr 2 1Dr i^ cm j^ cm k^ cm i^ 1 31 j^ k^ 2 cm R 5 "R 2 1 R R z 5 "125 cm cm cm cm

11 3.4 Components of a Vector and Unit Vectors 65 Eample 3.5 Taking a Hike hiker begins a trip b first walking 25.0 km sotheast from her car. he stops and sets p her tent for the night. On the second da, she walks 40.0 km in a direction 60.0 north of east, at which point she discovers a forest ranger s tower. () Determine the components of the hiker s displacement for each da. OLUTION Conceptalize We conceptalize the problem b drawing a sketch as in Figre If we denote the displacement vectors on the first and second das b and B, respectivel, and se the car as the origin of coordinates, we obtain the vectors shown in Figre Categorize Drawing the resltant R, we can now categorize this problem as one we ve solved before: an addition of two vectors. Yo shold now have a hint of the power of categorization in that man new problems are ver similar to problems we have alread solved if we are carefl to conceptalize them. Once we have drawn the displacement vectors and categorized the problem, this problem is no longer abot a hiker, a walk, a car, a tent, or a tower. It is a problem abot vector addition, one that we have alread solved. (km) Car W R Tent N E 60.0 B Tower (km) Figre 3.17 (Eample 3.5) The total displacement of the hiker is the vector R 5 1 B. nalze Displacement has a magnitde of 25.0 km and is directed 45.0 below the positive ais. Find the components of sing Eqations 3.8 and 3.9: 5 cos km km 5 sin km km The negative vale of indicates that the hiker walks in the negative direction on the first da. The signs of and also are evident from Figre Find the components of B sing Eqations 3.8 and 3.9: B 5 B cos km km B 5 B sin km km (B) Determine the components of the hiker s resltant displacement R for the trip. Find an epression for R in terms of nit vectors. OLUTION Use Eqation 3.15 to find the components of the resltant displacement R 5 1 B : R 5 1 B km km km R 5 1 B km km km Write the total displacement in nit-vector form: R i^ j^ 2 km Finalize Looking at the graphical representation in Figre 3.17, we estimate the position of the tower to be abot (38 km, 17 km), which is consistent with the components of R in or reslt for the final position of the hiker. lso, both components of R are positive, ptting the final position in the first qadrant of the coordinate sstem, which is also consistent with Figre WHT IF? fter reaching the tower, the hiker wishes to retrn to her car along a single straight line. What are the components of the vector representing this hike? What shold the direction of the hike be? nswer The desired vector R car is the negative of vector R : R car 52R i^ j^ 2 km The direction is fond b calclating the angle that the vector makes with the ais: tan 5 R car, km 5 R car, km which gives an angle of 204.2, or 24.2 soth of west.

12 66 CHPTER 3 Vectors Definitions mmar calar qantities are those that have onl a nmerical vale and no associated direction. Vector qantities have both magnitde and direction and obe the laws of vector addition. The magnitde of a vector is alwas a positive nmber. Concepts and Principles When two or more vectors are added together, the mst all have the same nits and the all mst be the same tpe of qantit. We can add two vectors and B graphicall. In this method (ctive Fig. 3.6), the resltant vector R 5 1 B rns from the tail of to the tip of B. second method of adding vectors involves components of the vectors. The component of the vector is eqal to the projection of along the ais of a coordinate sstem, where cos. The component of is the projection of along the ais, where sin. If a vector has an component and a component, the vector can be epressed in nit-vector form as 5 i^ 1 j^. In this notation, i^ is a nit vector pointing in the positive direction and j^ is a nit vector pointing in the positive direction. Becase i^ and j^ are nit vectors, 0 i^ j^ We can find the resltant of two or more vectors b resolving all vectors into their and components, adding their resltant and components, and then sing the Pthagorean theorem to find the magnitde of the resltant vector. We can find the angle that the resltant vector makes with respect to the ais b sing a sitable trigonometric fnction. Objective Qestions 1. Yes or no: Is each of the following qantities a vector? (a) force (b) temperatre (c) the volme of water in a can (d) the ratings of a TV show (e) the height of a bilding (f) the velocit of a sports car (g) the age of the Universe 2. sbmarine dives from the water srface at an angle of 30 below the horizontal, following a straight path 50 m long. How far is the sbmarine then below the water srface? (a) 50 m (b) (50 m)/sin 30 (c) (50 m) sin 30 (d) (50 m) cos 30 (e) none of those answers 3. Figre OQ3.3 shows two vectors D 1 and D 2. Which of the possibilities (a) throgh (d) is the vector D 2 2 2D 1, or (e) is it none of them? D 1 D 2 a b c d Figre OQ3.3 denotes answer available in tdent oltions Manal/td Gide 4. The ctting tool on a lathe is given two displacements, one of magnitde 4 cm and one of magnitde 3 cm, in each one of five sitations (a) throgh (e) diagrammed in Figre OQ3.4. Rank these sitations according to the magnitde of the total displacement of the tool, ptting the sitation with the greatest resltant magnitde first. If the total displacement is the same size in two sitations, give those letters eqal ranks. a b c d e Figre OQ vector points from the origin into the second qadrant of the plane. What can o conclde abot its components? (a) Both components are positive. (b) The component is positive, and the component is negative. (c) The

13 Problems 67 component is negative, and the component is positive. (d) Both components are negative. (e) More than one answer is possible. 6. Let vector point from the origin into the second qadrant of the plane and vector B point from the origin into the forth qadrant. The vector B 2 mst be in which qadrant, (a) the first, (b) the second, (c) the third, or (d) the forth, or (e) is more than one answer possible? 7. What is the magnitde of the vector 110 i^ 2 10 k^ 2 m/s? (a) 0 (b) 10 m/s (c) 10 m/s (d) 10 (e) 14.1 m/s 8. What is the component of the vector 13 i^ 2 8 k^ 2 m/s? (a) 3 m/s (b) 8 m/s (c) 0 (d) 8 m/s (e) none of those answers 9. What is the component of the vector shown in Figre OQ3.9? (a) 3 cm (b) 6 cm (c) 4 cm (d) 6 cm (e) none of those answers (cm) What is the component of the vector shown in Figre OQ3.9? (a) 3 cm (b) 6 cm (c) 4 cm (d) 6 cm (e) none of those answers 11. Vector lies in the plane. Both of its components will be negative if it points from the origin into which qadrant? (a) the first qadrant (b) the second qadrant (c) the third qadrant (d) the forth qadrant (e) the second or forth qadrants 12. vector ling in the plane has components of opposite sign. The vector mst lie in which qadrant? (a) the first qadrant (b) the second qadrant (c) the third qadrant (d) the forth qadrant (e) either the second or the forth qadrant 13. The magnitde of vector is 8 km, and the magnitde of B is 6 km. Which of the following are possible vales for the magnitde of 1 B? Choose all possible answers. (a) 10 km (b) 8 km (c) 2 km (d) 0 (e) 2 km (cm) Figre OQ3.9 Objective Qestions 9 and 10. Conceptal Qestions 1. book is moved once arond the perimeter of a tabletop with the dimensions 1.0 m b 2.0 m. The book ends p at its initial position. (a) What is its displacement? (b) What is the distance traveled? 2. If the component of vector along the direction of vector B is zero, what can o conclde abot the two vectors? 3. Is it possible to add a vector qantit to a scalar qantit? Eplain. denotes answer available in tdent oltions Manal/td Gide 4. Can the magnitde of a vector have a negative vale? Eplain. 5. On a certain calclator, the inverse tangent fnction retrns a vale between 90 and 90. In what cases will this vale correctl state the direction of a vector in the plane, b giving its angle measred conterclockwise from the positive ais? In what cases will it be incorrect? Problems The problems fond in this chapter ma be assigned online in Enhanced Webssign 1. denotes straightforward problem; 2. denotes intermediate problem; 3. denotes challenging problem 1. fll soltion available in the tdent oltions Manal/td Gide 1. denotes problems most often assigned in Enhanced Webssign; these provide stdents with targeted feedback and either a Master It ttorial or a Watch It soltion video. ection 3.1 Coordinate stems 1. The polar coordinates of a point are r 5.50 m and 240. What are the Cartesian coordinates of this point? 2. Two points in a plane have polar coordinates (2.50 m, 30.0 ) and (3.80 m, ). Determine (a) the Cartesian coordinates of these points and (b) the distance between them. denotes asking for qantitative and conceptal reasoning denotes smbolic reasoning problem denotes Master It ttorial available in Enhanced Webssign denotes gided problem shaded denotes paired problems that develop reasoning with smbols and nmerical vales 3. fl lands on one wall of a room. The lower-left corner of the wall is selected as the origin of a two-dimensional Cartesian coordinate sstem. If the fl is located at the point having coordinates (2.00, 1.00) m, (a) how far is it from the origin? (b) What is its location in polar coordinates? 4. The rectanglar coordinates of a point are given b (2, ), and its polar coordinates are (r, 30 ). Determine (a) the vale of and (b) the vale of r.

14 68 CHPTER 3 Vectors 5. The polar coordinates of a certain point are (r 4.30 cm, 214 ). (a) Find its Cartesian coordinates and. Find the polar coordinates of the points with Cartesian coordinates (b) (, ), (c) ( 2, 2), and (d) (3, 3). 6. Let the polar coordinates of the point (, ) be (r, ). Determine the polar coordinates for the points (a) (, ), (b) ( 2, 2), and (c) (3, 3). ection 3.2 Vector and calar Qantities ection 3.3 ome Properties of Vectors 7. srveor measres the distance across a straight river b the following method (Fig. P3.7). tarting directl across from a tree on the opposite bank, she walks d 100 m along the riverbank to establish a baseline. Then she sights across to the tree. The angle from her baseline to the tree is How wide is the river? d Figre P Vector has a magnitde of 29 nits and points in the positive direction. When vector B is added to, the resltant vector 1 B points in the negative direction with a magnitde of 14 nits. Find the magnitde and direction of B. 9. Wh is the following sitation impossible? skater glides along a circlar path. he defines a certain point on the circle as her origin. Later on, she passes throgh a point at which the distance she has traveled along the path from the origin is smaller than the magnitde of her displacement vector from the origin. 10. force F 1 of magnitde 6.00 nits acts on an object at the origin in a direction 30.0 above the positive ais (Fig. P3.10). second force F 2 of magnitde 5.00 nits acts on the object in the direction of the positive ais. Find graphicall the magnitde and direction of the resltant force F 1 1 F The displacement vectors and B shown in Figre P3.11 both have magnitdes of 3.00 m. The direction of vector is Find graphicall (a) 1 B, (b) 2 B, (c) B 2, and (d) 2 2B. (Report all angles conterclockwise from the positive ais.) Figre P Three displacements are Problems 11 and m de soth, B 250 m de west, and C 150 m at 30.0 east of north. F 2 O B F 1 Figre P3.10 (a) Constrct a separate diagram for each of the following possible was of adding these vectors: R B 1 C ; R 2 5 B 1 C 1 ; R 3 5 C 1 B 1. (b) Eplain what o can conclde from comparing the diagrams. 13. roller-coaster car moves 200 ft horizontall and then rises 135 ft at an angle of 30.0 above the horizontal. It net travels 135 ft at an angle of 40.0 downward. What is its displacement from its starting point? Use graphical techniqes. ection 3.4 Components of a Vector and Unit Vectors 14. Vector has a magnitde of 35.0 nits and points in the direction 325 conterclockwise from the positive ais. Calclate the and components of this vector. 15. vector has an component of 25.0 nits and a component of 40.0 nits. Find the magnitde and direction of this vector. 16. person walks 25.0 north of east for 3.10 km. How far wold she have to walk de north and de east to arrive at the same location? 17. minivan travels straight north in the right lane of a divided highwa at 28.0 m/s. camper passes the minivan and then changes from the left lane into the right lane. s it does so, the camper s path on the road is a straight displacement at 8.50 east of north. To avoid ctting off the minivan, the north soth distance between the camper s back bmper and the minivan s front bmper shold not decrease. (a) Can the camper be driven to satisf this reqirement? (b) Eplain or answer. 18. girl delivering newspapers covers her rote b traveling 3.00 blocks west, 4.00 blocks north, and then 6.00 blocks east. (a) What is her resltant displacement? (b) What is the total distance she travels? 19. Obtain epressions in component form for the position vectors having the polar coordinates (a) 12.8 m, 150 ; (b) 3.30 cm, 60.0 ; and (c) 22.0 in., Use the component method to add the vectors and B shown in Figre P3.11. Both vectors have magnitdes of 3.00 m and vector makes an angle of with the ais. Epress the resltant 1 B in nit-vector notation. 21. While eploring a cave, a spelnker starts at the entrance and moves the following distances in a horizontal plane. he goes 75.0 m north, 250 m east, 125 m at an angle 30.0 north of east, and 150 m soth. Find her resltant displacement from the cave entrance. Figre P3.21 sggests the sitation bt is not drawn to scale. Cave entrance W N E Figre P3.21 Final position 22. map sggests that tlanta is 730 miles in a direction of 5.00 north of east from Dallas. The same map shows that Chicago is 560 miles in a direction of 21.0 west of north

15 Problems 69 from tlanta. Figre P3.22 shows the locations of these three cities. Modeling the Earth as flat, se this information to find the displacement from Dallas to Chicago. Dallas Chicago 560 mi 730 mi tlanta Figre P Consider the two vectors 5 3 i^ 2 2 j^ and B 5 2 i^ 2 4 j^. Calclate (a) 1 B, (b) 2 B, (c) 0 1 B 0, (d) 0 2 B 0, and (e) the directions of 1 B and 2 B. 24. Given the vectors i^ j^ and B i^ j^, (a) draw the vector sm C 5 1 B and the vector difference D 5 2 B. (b) Calclate C and D, in terms of nit vectors. (c) Calclate C and D in terms of polar coordinates, with angles measred with respect to the positive ais. 25. Yor dog is rnning arond the grass in or back ard. He ndergoes sccessive displacements 3.50 m soth, 8.20 m northeast, and 15.0 m west. What is the resltant displacement? 26. snow-covered ski slope makes an angle of 35.0 with the horizontal. When a ski jmper plmmets onto the hill, a parcel of splashed snow is thrown p to a maimm displacement of 1.50 m at 16.0 from the vertical in the phill direction as shown in Figre P3.26. Find the components of its maimm displacement (a) parallel to the srface and (b) perpendiclar to the srface Figre P novice golfer on the green takes three strokes to sink the ball. The sccessive displacements of the ball are 4.00 m to the north, 2.00 m northeast, and 1.00 m at 30.0 west of soth (Fig. P3.27). tarting at the same initial point, an epert golfer cold make the hole in what single displacement? 35.0 W N 2.00 m E 4.00 m 30.0 Figre P m 28. In a game of merican football, a qarterback takes the ball from the line of scrimmage, rns backward a distance of 10.0 ards, and then rns sidewas parallel to the line of scrimmage for 15.0 ards. t this point, he throws a forward pass downfield 50.0 ards perpendiclar to the line of scrimmage. What is the magnitde of the football s resltant displacement? 29. The helicopter view in Fig. P3.29 shows two people plling on a stbborn mle. The person on the right plls with a force F 1 of magnitde 120 N and direction of The person on the left plls with a force F 2 of magnitde 80.0 N and direction of Find (a) the single force that is eqivalent to the two forces shown and (b) the force that a third person wold have to eert on the mle to make the resltant force eqal to zero. The forces are measred in nits of newtons (smbolized N). F F 1 Figre P Vector has and components of 8.70 cm and 15.0 cm, respectivel; vector B has and components of 13.2 cm and 6.60 cm, respectivel. If 2 B 1 3C 5 0, what are the components of C? 31. Consider the three displacement vectors 5 13 i^ 2 3 j^ 2 m, B 5 1i^ 2 4 j^ 2 m, and C i^ 1 5 j^ 2 m. Use the component method to determine (a) the magnitde and direction of the vector D 5 1 B 1 C and (b) the magnitde and direction of E 52 2 B 1 C. 32. Given the displacement vectors 5 13 i^ 2 4 j^ 1 4 k^ 2 m and B 5 12 i^ 1 3 j^ 2 7 k^ 2 m, find the magnitdes of the following vectors and epress each in terms of its rectanglar components. (a) C 5 1 B (b) D B 33. The vector has,, and z components of 8.00, 12.0, and 4.00 nits, respectivel. (a) Write a vector epression for in nit-vector notation. (b) Obtain a nit-vector epression for a vector B one-forth the length of pointing in the same direction as. (c) Obtain a nit-vector epression for a vector C three times the length of pointing in the direction opposite the direction of. 34. Vector B has,, and z components of 4.00, 6.00, and 3.00 nits, respectivel. Calclate (a) the magnitde of B and (b) the angle that B makes with each coordinate ais. 35. Vector has a negative component 3.00 nits in length and a positive component 2.00 nits in length. (a) Determine an epression for in nit-vector notation. (b) Determine the magnitde and direction of. (c) What vector B when added to gives a resltant vector with no

16 70 CHPTER 3 Vectors component and a negative component 4.00 nits in length? 36. Three displacement vectors of a cro - qet ball are shown in Figre P3.36, where nits, 0 B nits, and 0 C nits. Find (a) the resltant in nit-vector notation and (b) the magnitde and direction of the resltant displacement. 37. (a) Taking i^ j^ 2 nits, B i^ j^ 2 nits, and C i^ j^ 2 nits, determine a and b sch that a 1 b B 1 C 5 0. (b) stdent has learned that a single eqation cannot be solved to determine vales for more than one nknown in it. How wold o eplain to him that both a and b can be determined from the single eqation sed in part (a)? 38. Figre P3.38 illstrates tpical proportions of male (m) and female (f) anatomies. The displacements d 1m and d 1f from the soles of the feet to the navel have magnitdes of 104 cm and 84.0 cm, respectivel. The displacements d 2m and d 2f from the navel to otstretched fingertips have magnitdes of 100 cm and 86.0 cm, respectivel. Find the vector sm of these displacements d 3 5 d 1 1 d 2 for both people d 2m O C B Figre P d 2f epression for the displacement of the hrricane dring the first 3.00 h? (d) What is the nit-vector epression for the displacement of the hrricane dring the latter 1.50 h? (e) How far from Grand Bahama is the ee 4.50 h after it passes over the island? 42. In an assembl operation illstrated in Figre P3.42, a robot moves an object first straight pward and then also to the east, arond an arc forming one-qarter of a circle of radis 4.80 cm that lies in an east west vertical plane. The robot then moves the object pward and to the north, throgh one-qarter Figre P3.42 of a circle of radis 3.70 cm that lies in a north soth vertical plane. Find (a) the magnitde of the total displacement of the object and (b) the angle the total displacement makes with the vertical. North 43. Review. Yo are standing on the grond at the origin of a coordinate sstem. n airplane flies over o with constant velocit parallel to the ais and at a fied height of m. t time t 0, the airplane is directl above o so that the vector leading from o to it is P j^ m. t t 30.0 s, the position vector leading from o to the airplane is P i^ j^ 2 m as sggested in Figre P3.43. Determine the magnitde and orientation of the airplane s position vector at t 45.0 s. East d 1m d 1f P 0 P 30 Figre P man pshing a mop across a floor cases it to ndergo two displacements. The first has a magnitde of 150 cm and makes an angle of 120 with the positive ais. The resltant displacement has a magnitde of 140 cm and is directed at an angle of 35.0 to the positive ais. Find the magnitde and direction of the second displacement. 40. Wh is the following sitation impossible? shopper pshing a cart throgh a market follows directions to the canned goods and moves throgh a displacement 8.00 i^ m down one aisle. He then makes a 90.0 trn and moves 3.00 m along the ais. He then makes another 90.0 trn and moves 4.00 m along the ais. Ever shopper who follows these directions correctl ends p 5.00 m from the starting point. 41. Review. s it passes over Grand Bahama Island, the ee of a hrricane is moving in a direction north of west with a speed of 41.0 km/h. (a) What is the nit-vector epression for the velocit of the hrricane? It maintains this velocit for 3.00 h, at which time the corse of the hrricane sddenl shifts de north, and its speed slows to a constant 25.0 km/h. This new velocit is maintained for 1.50 h. (b) What is the nit-vector epression for the new velocit of the hrricane? (c) What is the nit-vector Figre P radar station locates a sinking ship at range 17.3 km and bearing 136 clockwise from north. From the same station, a resce plane is at horizontal range 19.6 km, 153 clockwise from north, with elevation 2.20 km. (a) Write the position vector for the ship relative to the plane, letting i^ represent east, j^ north, and k^ p. (b) How far apart are the plane and ship? 45. Epress in nit-vector notation the following vectors, each of which has magnitde 17.0 cm. (a) Vector E is directed 27.0 conterclockwise from the positive (16, 12) ais. (b) Vector F is directed 27.0 conterclockwise from the positive ais. (c) Vector G is directed (5, 3) 27.0 clockwise from the negative O ais. 46. In Figre P3.46, the line segment represents a path from the point with position vector 15 i^ 1 3 j^ 2 m to the point with loca- Figre P3.46 Point is a fraction f of the distance from the initial point (5, 3) to the final point (16, 12).