2.5 CONTINUITY. a x. Notice that Definition l implicitly requires three things if f is continuous at a:
|
|
|
- Erick Allison
- 5 years ago
- Views:
Transcription
1 SECTION.5 CONTINUITY 9.5 CONTINUITY We noticed in Section.3 that the it of a function as approaches a can often be found simpl b calculating the value of the function at a. Functions with this propert are called continuous at a. We will see that the mathematical definition of continuit corresponds closel with the meaning of the word continuit in everda language. (A continuous process is one that takes place graduall, without interruption or abrupt change.) DEFINITION A function f is continuous at a number a if f f a la N As illustrated in Figure, if f is continuous, then the points, f on the graph of f approach the point a, f a on the graph. So there is no gap in the curve. ƒ approaches f(a). FIGURE f(a) =ƒ a As approaches a, FIGURE Notice that Definition l implicitl requires three things if f is continuous at a:. f a is defined (that is, a is in the domain of f ). f eists 3. la f f a la The definition sas that f is continuous at a if f approaches f a as approaches a. Thus a continuous function f has the propert that a small change in produces onl a small change in f. In fact, the change in f can be kept as small as we please b keeping the change in sufficientl small. If f is defined near a (in other words, f is defined on an open interval containing a, ecept perhaps at a), we sa that f is discontinuous at a (or f has a discontinuit at a) if f is not continuous at a. Phsical phenomena are usuall continuous. For instance, the displacement or velocit of a vehicle varies continuousl with time, as does a person s height. But discontinuities do occur in such situations as electric currents. [See Eample 6 in Section., where the Heaviside function is discontinuous at because t l H t does not eist.] Geometricall, ou can think of a function that is continuous at ever number in an interval as a function whose graph has no break in it. The graph can be drawn without removing our pen from the paper. EXAPLE Figure shows the graph of a function f. At which numbers is f discontinuous? Wh? SOLUTION It looks as if there is a discontinuit when a because the graph has a break there. The official reason that f is discontinuous at is that f is not defined. The graph also has a break when a 3, but the reason for the discontinuit is different. Here, f 3 is defined, but l3 f does not eist (because the left right its are different). So f is discontinuous at 3. What about a 5? Here, f 5 is defined l5 f eists (because the left right its are the same). But f f 5 l 5 So f is discontinuous at 5. Now let s see how to detect discontinuities when a function is defined b a formula.
2 CHAPTER LIITS AND DERIVATIVES V EXAPLE Where are each of the following functions discontinuous? (a) f (c) f if if SOLUTION (a) Notice that f is not defined, so f is discontinuous at. Later we ll see wh f is continuous at all other numbers. (b) Here f is defined but does not eist. (See Eample 8 in Section..) So f is discontinuous at. (c) Here f is defined eists. But so f is not continuous at. (d) The greatest integer function f has discontinuities at all of the integers because ln does not eist if n is an integer. (See Eample Eercise 49 in Section.3.) Figure 3 shows the graphs of the functions in Eample. In each case the graph can t be drawn without lifting the pen from the paper because a hole or break or jump occurs in the graph. The kind of discontinuit illustrated in parts (a) (c) is called removable because we could remove the discontinuit b redefining f at just the single number. [The function t is continuous.] The discontinuit in part (b) is called an infinite discontinuit. The discontinuities in part (d) are called jump discontinuities because the function jumps from one value to another. (b) (d) f l l f f l f if f if f 3 l l l l 3 (a) ƒ= -- - (b) ƒ= if if = (c) ƒ= -- if - if = (d) ƒ=[] FIGURE 3 Graphs of the functions in Eample
3 SECTION.5 CONTINUITY DEFINITION A function f is continuous from the right at a number a if f is continuous from the left at a if f f a la f f a la EXAPLE 3 At each integer n, the function f [see Figure 3(d)] is continuous from the right but discontinuous from the left because ln f n f n ln but ln f n f n ln 3 DEFINITION A function f is continuous on an interval if it is continuous at ever number in the interval. (If f is defined onl on one side of an endpoint of the interval, we underst continuous at the endpoint to mean continuous from the right or continuous from the left.) EXAPLE 4 Show that the function f s is continuous on the interval,. SOLUTION If a, then using the Limit Laws, we have f ( s ) s s s a f a (b Laws 7) (b ) (b, 7, 9) ƒ=-œ - Thus, b Definition l, f is continuous at a if a. Similar calculations show that f f l f f l - so f is continuous from the right at continuous from the left at. Therefore, according to Definition 3, f is continuous on,. The graph of f is sketched in Figure 4. It is the lower half of the circle FIGURE 4 Instead of alwas using Definitions,, 3 to verif the continuit of a function as we did in Eample 4, it is often convenient to use the net theorem, which shows how to build up complicated continuous functions from simple ones.
4 CHAPTER LIITS AND DERIVATIVES 4 THEORE If f t are continuous at a c is a constant, then the following functions are also continuous at a:. f t. f t 3. cf f 4. ft 5. if t a t PROOF Each of the five parts of this theorem follows from the corresponding Limit Law in Section.3. For instance, we give the proof of part. Since f t are continuous at a, we have f f a t t a Therefore f t f t f a t a f t a f t (b Law ) This shows that f t is continuous at a. It follows from Theorem 4 Definition 3 that if f t are continuous on an interval, then so are the functions f t, f t, cf, ft, (if t is never ) f t. The following theorem was stated in Section.3 as the Direct Substitution Propert. 5 THEORE (a) An polnomial is continuous everwhere; that is, it is continuous on,. (b) An rational function is continuous wherever it is defined; that is, it is continuous on its domain. PROOF (a) A polnomial is a function of the form P c n n c n n c c where c, c,..., c n are constants. We know that c c (b Law 7) m a m m,,..., n (b 9) This equation is precisel the statement that the function f m is a continuous function. Thus, b part 3 of Theorem 4, the function t c m is continuous. Since P is a sum of functions of this form a constant function, it follows from part of Theorem 4 that P is continuous.
5 SECTION.5 CONTINUITY 3 (b) A rational function is a function of the form f P Q where P Q are polnomials. The domain of f is D Q. We know from part (a) that P Q are continuous everwhere. Thus, b part 5 of Theorem 4, f is continuous at ever number in D. As an illustration of Theorem 5, observe that the volume of a sphere varies continuousl with its radius because the formula V r 4 3 r 3 shows that V is a polnomial function of r. Likewise, if a ball is thrown verticall into the air with a velocit of 5 ft s, then the height of the ball in feet t seconds later is given b the formula h 5t 6t. Again this is a polnomial function, so the height is a continuous function of the elapsed time. Knowledge of which functions are continuous enables us to evaluate some its ver quickl, as the following eample shows. Compare it with Eample (b) in Section.3. 3 EXAPLE 5 Find. l 5 3 SOLUTION The function f is rational, so b Theorem 5 it is continuous on its domain, which is. Therefore 3 f f l 5 3 l { 5 3} FIGURE 5 P(cos, sin ) (, ) It turns out that most of the familiar functions are continuous at ever number in their domains. For instance, Limit Law (page ) is eactl the statement that root functions are continuous. From the appearance of the graphs of the sine cosine functions (Figure 8 in Section.), we would certainl guess that the are continuous. We know from the definitions of sin cos that the coordinates of the point P in Figure 5 are cos, sin. As, we see that P approaches the point, so cos l sin l. Thus l 6 cos sin l l N Another wa to establish the its in (6) is to use the Squeeze Theorem with the inequalit sin (for ), which is proved in Section 3.3. Since cos sin, the equations in (6) assert that the cosine sine functions are continuous at. The addition formulas for cosine sine can then be used to deduce that these functions are continuous everwhere (see Eercises 56 57). It follows from part 5 of Theorem 4 that tan sin cos
6 4 CHAPTER LIITS AND DERIVATIVES _ 3π _π FIGURE 6 π _ =tan π π 3π is continuous ecept where cos. This happens when is an odd integer multiple of, so tan has infinite discontinuities when, 3, 5, so on (see Figure 6). The inverse function of an continuous one-to-one function is also continuous. (This fact is proved in Appendi F, but our geometric intuition makes it seem plausible: The graph of f is obtained b reflecting the graph of f about the line. So if the graph of f has no break in it, neither does the graph of f.) Thus the inverse trigonometric functions are continuous. In Section.5 we defined the eponential function a so as to fill in the holes in the graph of a where is rational. In other words, the ver definition of a makes it a continuous function on. Therefore its inverse function log a is continuous on,. N The inverse trigonometric functions are reviewed in Section.6. 7 THEORE their domains: The following tpes of functions are continuous at ever number in polnomials rational functions root functions trigonometric functions eponential functions inverse trigonometric functions logarithmic functions EXAPLE 6 Where is the function continuous? SOLUTION We know from Theorem 7 that the function ln is continuous for tan is continuous on. Thus, b part of Theorem 4, ln tan is continuous on,. The denominator,, is a polnomial, so it is continuous everwhere. Therefore, b part 5 of Theorem 4, f is continuous at all positive numbers ecept where. So f is continuous on the intervals,,. sin EXAPLE 7 Evaluate. l cos f ln tan SOLUTION Theorem 7 tells us that sin is continuous. The function in the denominator, cos, is the sum of two continuous functions is therefore continuous. Notice that this function is never because cos for all so cos everwhere. Thus the ratio f sin cos is continuous everwhere. Hence, b definition of a continuous function, sin l cos f f sin l cos Another wa of combining continuous functions f t to get a new continuous function is to form the composite function f t. This fact is a consequence of the following theorem.
7 SECTION.5 CONTINUITY 5 N This theorem sas that a it smbol can be moved through a function smbol if the function is continuous the it eists. In other words, the order of these two smbols can be reversed. 8 THEORE If f is continuous at b t b, then la In other words, f t f ( t ) f t f b. la Intuitivel, Theorem 8 is reasonable because if is close to a, then t is close to b, since f is continuous at b, if t is close to b, then f t is close to f b. A proof of Theorem 8 is given in Appendi F. s EXAPLE 8 Evaluate arcsin. l SOLUTION Because arcsin is a continuous function, we can appl Theorem 8: s s arcsin arcsin l l s arcsin l ( s ) ( s ) arcsin l s arcsin Let s now appl Theorem 8 in the special case where f s n, with n being a positive integer. Then f t s n t 6 f ( t ) s n t If we put these epressions into Theorem 8, we get t s sn n t so Limit Law has now been proved. (We assume that the roots eist.) 9 THEORE If t is continuous at a f is continuous at t a, then the composite function f t given b f t f t is continuous at a. This theorem is often epressed informall b saing a continuous function of a continuous function is a continuous function. PROOF Since t is continuous at a, we have t t a Since f is continuous at b t a, we can appl Theorem 8 to obtain f t f t a
8 6 CHAPTER LIITS AND DERIVATIVES which is precisel the statement that the function h f t is continuous at a; that is, f t is continuous at a. V EXAPLE 9 Where are the following functions continuous? (a) h sin (b) F ln cos SOLUTION (a) We have h f t, where t f sin _ FIGURE 7 =ln(+cos ) _6 Now t is continuous on since it is a polnomial, f is also continuous everwhere. Thus h f t is continuous on b Theorem 9. (b) We know from Theorem 7 that f ln is continuous t cos is continuous (because both cos are continuous). Therefore, b Theorem 9, F f t is continuous wherever it is defined. Now ln cos is defined when cos. So it is undefined when cos, this happens when, 3,.... Thus F has discontinuities when is an odd multiple of is continuous on the intervals between these values (see Figure 7). An important propert of continuous functions is epressed b the following theorem, whose proof is found in more advanced books on calculus. THE INTEREDIATE VALUE THEORE Suppose that f is continuous on the closed interval a, b let N be an number between f a f b, where f a f b. Then there eists a number c in a, b such that f c N. The Intermediate Value Theorem states that a continuous function takes on ever intermediate value between the function values f a f b. It is illustrated b Figure 8. Note that the value N can be taken on once [as in part (a)] or more than once [as in part (b)]. f(b) N f(b) N =ƒ f(a) =ƒ f(a) a c b a c c c b FIGURE 8 f(a) =ƒ N =N f(b) a b FIGURE 9 (a) If we think of a continuous function as a function whose graph has no hole or break, then it is eas to believe that the Intermediate Value Theorem is true. In geometric terms it sas that if an horizontal line N is given between f a f b as in Figure 9, then the graph of f can t jump over the line. It must intersect N somewhere. It is important that the function f in Theorem be continuous. The Intermediate Value Theorem is not true in general for discontinuous functions (see Eercise 44). One use of the Intermediate Value Theorem is in locating roots of equations as in the following eample. (b)
9 SECTION.5 CONTINUITY 7 V EXAPLE Show that there is a root of the equation between. SOLUTION Let f We are looking for a solution of the given equation, that is, a number c between such that f c. Therefore, we take a, b, N in Theorem. We have f f Thus f f ; that is, N is a number between f f. Now f is continuous since it is a polnomial, so the Intermediate Value Theorem sas there is a number c between such that f c. In other words, the equation has at least one root c in the interval,. In fact, we can locate a root more precisel b using the Intermediate Value Theorem again. Since f..8 f a root must lie between..3. A calculator gives, b trial error, f..78 f so a root lies in the interval.,.3. We can use a graphing calculator or computer to illustrate the use of the Intermediate Value Theorem in Eample. Figure shows the graph of f in the viewing rectangle, 3 b 3, 3 ou can see that the graph crosses the -ais between. Figure shows the result of zooming in to the viewing rectangle.,.3 b.,.. 3. _ 3..3 FIGURE _3 _. FIGURE In fact, the Intermediate Value Theorem plas a role in the ver wa these graphing devices work. A computer calculates a finite number of points on the graph turns on the piels that contain these calculated points. It assumes that the function is continuous takes on all the intermediate values between two consecutive points. The computer therefore connects the piels b turning on the intermediate piels.
10 8 CHAPTER LIITS AND DERIVATIVES.5 EXERCISES. Write an equation that epresses the fact that a function is continuous at the number 4.. If f is continuous on,, what can ou sa about its graph? 3. (a) From the graph of f, state the numbers at which f is discontinuous eplain wh. (b) For each of the numbers stated in part (a), determine whether f is continuous from the right, or from the left, or neither. f (d) The cost of a tai ride as a function of the distance traveled (e) The current in the circuit for the lights in a room as a function of time 9. If f t are continuous functions with f 3 5 l 3 f t 4, find t 3. Use the definition of continuit the properties of its to show that the function is continuous at the given number a.. f s7,. f 3 4, t 3t. h t, t 3 a a a 4 _4 _ From the graph of t, state the intervals on which t is continuous. _4 _ Use the definition of continuit the properties of its to show that the function is continuous on the given interval f, 4. t s3, 5 Eplain wh the function is discontinuous at the given number a. Sketch the graph of the function. 5. f ln 6. f,, 3 if if a a 5. Sketch the graph of a function that is continuous everwhere ecept at 3 is continuous from the left at Sketch the graph of a function that has a jump discontinuit at a removable discontinuit at 4, but is continuous elsewhere. 7. A parking lot charges $3 for the first hour (or part of an hour) $ for each succeeding hour (or part), up to a dail maimum of $. (a) Sketch a graph of the cost of parking at this lot as a function of the time parked there. (b) Discuss the discontinuities of this function their significance to someone who parks in the lot. 8. Eplain wh each function is continuous or discontinuous. (a) The temperature at a specific location as a function of time (b) The temperature at a specific time as a function of the distance due west from New York Cit (c) The altitude above sea level as a function of the distance due west from New York Cit f e if if f f cos if if if if if f if 3 if 3 a a a a 3 8 Eplain, using Theorems 4, 5, 7, 9, wh the function is continuous at ever number in its domain. State the domain.. F. G s
11 SECTION.5 CONTINUITY 9 3. R s L t e 5t cos t G t ln t 4 8. h sin F sin H cos(e s ) 4. For what value of the constant c is the function f continuous on,? f c 3 c if if ; 9 3 Locate the discontinuities of the function illustrate b graphing Use continuit to evaluate the it Show that f is continuous on, Find the numbers at which f is discontinuous. At which of these numbers is f continuous from the right, from the left, or neither? Sketch the graph of f l e e 5 s l4 s5 f if s if f sin if 4 cos if 4 f f s 3 f e 4. The gravitational force eerted b the earth on a unit mass at a distance r from the center of the planet is F r Gr R 3 G r 3. if if if if if 3 if 3 if if if ln tan sin sin l arctan 4 l 3 6 if r R if r R where is the mass of the earth, R is its radius, G is the gravitational constant. Is F a continuous function of r? 4. Find the values of a b that make f continuous everwhere. 43. Which of the following functions f has a removable discontinuit at a? If the discontinuit is removable, find a function t that agrees with f for a is continuous at a. (a) f 4, (b) f 3, (c) f sin, 44. Suppose that a function f is continuous on [, ] ecept at.5 that f f 3. Let N. Sketch two possible graphs of f, one showing that f might not satisf the conclusion of the Intermediate Value Theorem one showing that f might still satisf the conclusion of the Intermediate Value Theorem (even though it doesn t satisf the hpothesis). 45. If f sin, show that there is a number c such that f c. 46. Suppose f is continuous on, 5 the onl solutions of the equation f 6 are 4. If f 8, eplain wh f Use the Intermediate Value Theorem to show that there is a root of the given equation in the specified interval ,, 48. s 3, 49. cos,, 5. ln e, 5 5 (a) Prove that the equation has at least one real root. (b) Use our calculator to find an interval of length. that contains a root. 5. cos 3 5. ln 3 ; (a) Prove that the equation has at least one real root. (b) Use our graphing device to find the root correct to three decimal places. 53. f e. 4 a b 3 a b a a a if if 3 if 3, 54. arctan,
12 3 CHAPTER LIITS AND DERIVATIVES 55. Prove that f is continuous at a if onl if 56. To prove that sine is continuous, we need to show that sin sin a for ever real number a. B Eercise 55 an equivalent statement is that Use (6) to show that this is true. 57. Prove that cosine is a continuous function. 58. (a) Prove Theorem 4, part 3. (b) Prove Theorem 4, part For what values of is f continuous? 6. For what values of is t continuous? 6. f a h f a h l sin a h sin a h l f t if is rational if is irrational if is rational if is irrational Is there a number that is eactl more than its cube? 6. If a b are positive numbers, prove that the equation has at least one solution in the interval,. 63. Show that the function a 3 b 3 f 4 sin is continuous on,. if if F 64. (a) Show that the absolute value function is continuous everwhere. (b) Prove that if f is a continuous function on an interval, then so is f. (c) Is the converse of the statement in part (b) also true? In other words, if f is continuous, does it follow that f is continuous? If so, prove it. If not, find a countereample. 65. A Tibetan monk leaves the monaster at 7: A takes his usual path to the top of the mountain, arriving at 7: P. The following morning, he starts at 7: A at the top takes the same path back, arriving at the monaster at 7: P. Use the Intermediate Value Theorem to show that there is a point on the path that the monk will cross at eactl the same time of da on both das f FIGURE LIITS AT INFINITY; HORIZONTAL ASYPTOTES In Sections..4 we investigated infinite its vertical asmptotes. There we let approach a number the result was that the values of became arbitraril large (positive or negative). In this section we let become arbitraril large (positive or negative) see what happens to. Let s begin b investigating the behavior of the function f defined b f as becomes large. The table at the left gives values of this function correct to si decimal places, the graph of f has been drawn b a computer in Figure. As grows larger larger ou can see that the values of f get closer closer to. In fact, it seems that we can make the values of f as close as we like to b taking sufficientl large. This situation is epressed smbolicall b writing = l = - +
In everyday speech, a continuous. Limits and Continuity. Critical Thinking Exercises
 062 Chapter Introduction to Calculus Critical Thinking Eercises Make Sense? In Eercises 74 77, determine whether each statement makes sense or does not make sense, and eplain our reasoning. 74. I evaluated
062 Chapter Introduction to Calculus Critical Thinking Eercises Make Sense? In Eercises 74 77, determine whether each statement makes sense or does not make sense, and eplain our reasoning. 74. I evaluated
x c x c This suggests the following definition.
 110 Chapter 1 / Limits and Continuit 1.5 CONTINUITY A thrown baseball cannot vanish at some point and reappear someplace else to continue its motion. Thus, we perceive the path of the ball as an unbroken
110 Chapter 1 / Limits and Continuit 1.5 CONTINUITY A thrown baseball cannot vanish at some point and reappear someplace else to continue its motion. Thus, we perceive the path of the ball as an unbroken
1.6 CONTINUITY OF TRIGONOMETRIC, EXPONENTIAL, AND INVERSE FUNCTIONS
 .6 Continuit of Trigonometric, Eponential, and Inverse Functions.6 CONTINUITY OF TRIGONOMETRIC, EXPONENTIAL, AND INVERSE FUNCTIONS In this section we will discuss the continuit properties of trigonometric
.6 Continuit of Trigonometric, Eponential, and Inverse Functions.6 CONTINUITY OF TRIGONOMETRIC, EXPONENTIAL, AND INVERSE FUNCTIONS In this section we will discuss the continuit properties of trigonometric
1.3 LIMITS AT INFINITY; END BEHAVIOR OF A FUNCTION
 . Limits at Infinit; End Behavior of a Function 89. LIMITS AT INFINITY; END BEHAVIOR OF A FUNCTION Up to now we have been concerned with its that describe the behavior of a function f) as approaches some
. Limits at Infinit; End Behavior of a Function 89. LIMITS AT INFINITY; END BEHAVIOR OF A FUNCTION Up to now we have been concerned with its that describe the behavior of a function f) as approaches some
2.5. Infinite Limits and Vertical Asymptotes. Infinite Limits
 . Infinite Limits and Vertical Asmptotes. Infinite Limits and Vertical Asmptotes In this section we etend the concept of it to infinite its, which are not its as before, but rather an entirel new use of
. Infinite Limits and Vertical Asmptotes. Infinite Limits and Vertical Asmptotes In this section we etend the concept of it to infinite its, which are not its as before, but rather an entirel new use of
2.1 Rates of Change and Limits AP Calculus
 . Rates of Change and Limits AP Calculus. RATES OF CHANGE AND LIMITS Limits Limits are what separate Calculus from pre calculus. Using a it is also the foundational principle behind the two most important
. Rates of Change and Limits AP Calculus. RATES OF CHANGE AND LIMITS Limits Limits are what separate Calculus from pre calculus. Using a it is also the foundational principle behind the two most important
1.2 Functions and Their Properties PreCalculus
 1. Functions and Their Properties PreCalculus 1. FUNCTIONS AND THEIR PROPERTIES Learning Targets for 1. 1. Determine whether a set of numbers or a graph is a function. Find the domain of a function given
1. Functions and Their Properties PreCalculus 1. FUNCTIONS AND THEIR PROPERTIES Learning Targets for 1. 1. Determine whether a set of numbers or a graph is a function. Find the domain of a function given
Limits and Continuous Functions. 2.2 Introduction to Limits. We first interpret limits loosely. We write. lim f(x) = L
 2 Limits and Continuous Functions 2.2 Introduction to Limits We first interpret limits loosel. We write lim f() = L and sa the limit of f() as approaches c, equals L if we can make the values of f() arbitraril
2 Limits and Continuous Functions 2.2 Introduction to Limits We first interpret limits loosel. We write lim f() = L and sa the limit of f() as approaches c, equals L if we can make the values of f() arbitraril
1. d = 1. or Use Only in Pilot Program F Review Exercises 131
 or Use Onl in Pilot Program F 0 0 Review Eercises. Limit proof Suppose f is defined for all values of near a, ecept possibl at a. Assume for an integer N 7 0, there is another integer M 7 0 such that f
or Use Onl in Pilot Program F 0 0 Review Eercises. Limit proof Suppose f is defined for all values of near a, ecept possibl at a. Assume for an integer N 7 0, there is another integer M 7 0 such that f
Limits 4: Continuity
 Limits 4: Continuit 55 Limits 4: Continuit Model : Continuit I. II. III. IV. z V. VI. z a VII. VIII. IX. Construct Your Understanding Questions (to do in class). Which is the correct value of f (a) in
Limits 4: Continuit 55 Limits 4: Continuit Model : Continuit I. II. III. IV. z V. VI. z a VII. VIII. IX. Construct Your Understanding Questions (to do in class). Which is the correct value of f (a) in
Properties of Limits
 33460_003qd //04 :3 PM Page 59 SECTION 3 Evaluating Limits Analticall 59 Section 3 Evaluating Limits Analticall Evaluate a it using properties of its Develop and use a strateg for finding its Evaluate
33460_003qd //04 :3 PM Page 59 SECTION 3 Evaluating Limits Analticall 59 Section 3 Evaluating Limits Analticall Evaluate a it using properties of its Develop and use a strateg for finding its Evaluate
We have examined power functions like f (x) = x 2. Interchanging x
 CHAPTER 5 Eponential and Logarithmic Functions We have eamined power functions like f =. Interchanging and ields a different function f =. This new function is radicall different from a power function
CHAPTER 5 Eponential and Logarithmic Functions We have eamined power functions like f =. Interchanging and ields a different function f =. This new function is radicall different from a power function
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval................... 0 Section. Rolle s Theorem and the Mean Value Theorem...... 0 Section. Increasing and Decreasing Functions and
CHAPTER Applications of Differentiation Section. Etrema on an Interval................... 0 Section. Rolle s Theorem and the Mean Value Theorem...... 0 Section. Increasing and Decreasing Functions and
Section 1.2: A Catalog of Functions
 Section 1.: A Catalog of Functions As we discussed in the last section, in the sciences, we often tr to find an equation which models some given phenomenon in the real world - for eample, temperature as
Section 1.: A Catalog of Functions As we discussed in the last section, in the sciences, we often tr to find an equation which models some given phenomenon in the real world - for eample, temperature as
Rolle s Theorem. THEOREM 3 Rolle s Theorem. x x. then there is at least one number c in (a, b) at which ƒ scd = 0.
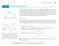 4.2 The Mean Value Theorem 255 4.2 The Mean Value Theorem f '(c) 0 f() We know that constant functions have zero derivatives, ut could there e a complicated function, with man terms, the derivatives of
4.2 The Mean Value Theorem 255 4.2 The Mean Value Theorem f '(c) 0 f() We know that constant functions have zero derivatives, ut could there e a complicated function, with man terms, the derivatives of
3.5 Continuity of a Function One Sided Continuity Intermediate Value Theorem... 23
 Chapter 3 Limit and Continuity Contents 3. Definition of Limit 3 3.2 Basic Limit Theorems 8 3.3 One sided Limit 4 3.4 Infinite Limit, Limit at infinity and Asymptotes 5 3.4. Infinite Limit and Vertical
Chapter 3 Limit and Continuity Contents 3. Definition of Limit 3 3.2 Basic Limit Theorems 8 3.3 One sided Limit 4 3.4 Infinite Limit, Limit at infinity and Asymptotes 5 3.4. Infinite Limit and Vertical
A function from a set D to a set R is a rule that assigns a unique element in R to each element in D.
 1.2 Functions and Their Properties PreCalculus 1.2 FUNCTIONS AND THEIR PROPERTIES Learning Targets for 1.2 1. Determine whether a set of numbers or a graph is a function 2. Find the domain of a function
1.2 Functions and Their Properties PreCalculus 1.2 FUNCTIONS AND THEIR PROPERTIES Learning Targets for 1.2 1. Determine whether a set of numbers or a graph is a function 2. Find the domain of a function
Infinite Limits. Let f be the function given by. f x 3 x 2.
 0_005.qd //0 :07 PM Page 8 SECTION.5 Infinite Limits 8, as Section.5, as + f() = f increases and decreases without bound as approaches. Figure.9 Infinite Limits Determine infinite its from the left and
0_005.qd //0 :07 PM Page 8 SECTION.5 Infinite Limits 8, as Section.5, as + f() = f increases and decreases without bound as approaches. Figure.9 Infinite Limits Determine infinite its from the left and
v t t t t a t v t d dt t t t t t 23.61
 SECTION 4. MAXIMUM AND MINIMUM VALUES 285 The values of f at the endpoints are f 0 0 and f 2 2 6.28 Comparing these four numbers and using the Closed Interval Method, we see that the absolute minimum value
SECTION 4. MAXIMUM AND MINIMUM VALUES 285 The values of f at the endpoints are f 0 0 and f 2 2 6.28 Comparing these four numbers and using the Closed Interval Method, we see that the absolute minimum value
Math 123 Summary of Important Algebra & Trigonometry Concepts Chapter 1 & Appendix D, Stewart, Calculus Early Transcendentals
 Math Summar of Important Algebra & Trigonometr Concepts Chapter & Appendi D, Stewart, Calculus Earl Transcendentals Function a rule that assigns to each element in a set D eactl one element, called f (
Math Summar of Important Algebra & Trigonometr Concepts Chapter & Appendi D, Stewart, Calculus Earl Transcendentals Function a rule that assigns to each element in a set D eactl one element, called f (
Review Topics for MATH 1400 Elements of Calculus Table of Contents
 Math 1400 - Mano Table of Contents - Review - page 1 of 2 Review Topics for MATH 1400 Elements of Calculus Table of Contents MATH 1400 Elements of Calculus is one of the Marquette Core Courses for Mathematical
Math 1400 - Mano Table of Contents - Review - page 1 of 2 Review Topics for MATH 1400 Elements of Calculus Table of Contents MATH 1400 Elements of Calculus is one of the Marquette Core Courses for Mathematical
Continuity, End Behavior, and Limits. Unit 1 Lesson 3
 Unit Lesson 3 Students will be able to: Interpret ke features of graphs and tables in terms of the quantities, and sketch graphs showing ke features given a verbal description of the relationship. Ke Vocabular:
Unit Lesson 3 Students will be able to: Interpret ke features of graphs and tables in terms of the quantities, and sketch graphs showing ke features given a verbal description of the relationship. Ke Vocabular:
1.1 Exercises. (b) For what values of x is f x t x?
 CHAPTER FUNCTIONS AND MODELS. Eercises. The graph of a function f is given. (a) State the value of f. Estimate the value of f. (c) For what values of is f? (d) Estimate the values of such that f. (e) State
CHAPTER FUNCTIONS AND MODELS. Eercises. The graph of a function f is given. (a) State the value of f. Estimate the value of f. (c) For what values of is f? (d) Estimate the values of such that f. (e) State
1.2 Functions and Their Properties PreCalculus
 1. Functions and Their Properties PreCalculus 1. FUNCTIONS AND THEIR PROPERTIES Learning Targets for 1. 1. Determine whether a set of numbers or a graph is a function. Find the domain of a function given
1. Functions and Their Properties PreCalculus 1. FUNCTIONS AND THEIR PROPERTIES Learning Targets for 1. 1. Determine whether a set of numbers or a graph is a function. Find the domain of a function given
Limits and Continuity
 Limits and Continuity Philippe B. Laval Kennesaw State University January 2, 2005 Contents Abstract Notes and practice problems on its and continuity. Limits 2. Introduction... 2.2 Theory:... 2.2. GraphicalMethod...
Limits and Continuity Philippe B. Laval Kennesaw State University January 2, 2005 Contents Abstract Notes and practice problems on its and continuity. Limits 2. Introduction... 2.2 Theory:... 2.2. GraphicalMethod...
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 0 Section. Rolle s Theorem and the Mean Value Theorem. 07 Section. Increasing and Decreasing Functions and the First
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 0 Section. Rolle s Theorem and the Mean Value Theorem. 07 Section. Increasing and Decreasing Functions and the First
Limits. or Use Only in Pilot Program F The Idea of Limits 2.2 Definitions of Limits 2.3 Techniques for Computing.
 Limits or Use Onl in Pilot Program F 03 04. he Idea of Limits. Definitions of Limits.3 echniques for Computing Limits.4 Infinite Limits.5 Limits at Infinit.6 Continuit.7 Precise Definitions of Limits Biologists
Limits or Use Onl in Pilot Program F 03 04. he Idea of Limits. Definitions of Limits.3 echniques for Computing Limits.4 Infinite Limits.5 Limits at Infinit.6 Continuit.7 Precise Definitions of Limits Biologists
Chapter 3: Three faces of the derivative. Overview
 Overview We alread saw an algebraic wa of thinking about a derivative. Geometric: zooming into a line Analtic: continuit and rational functions Computational: approimations with computers 3. The geometric
Overview We alread saw an algebraic wa of thinking about a derivative. Geometric: zooming into a line Analtic: continuit and rational functions Computational: approimations with computers 3. The geometric
KEY IDEAS. Chapter 1 Function Transformations. 1.1 Horizontal and Vertical Translations Pre-Calculus 12 Student Workbook MHR 1
 Chapter Function Transformations. Horizontal and Vertical Translations A translation can move the graph of a function up or down (vertical translation) and right or left (horizontal translation). A translation
Chapter Function Transformations. Horizontal and Vertical Translations A translation can move the graph of a function up or down (vertical translation) and right or left (horizontal translation). A translation
4.3 Exercises. local maximum or minimum. The second derivative is. e 1 x 2x 1. f x x 2 e 1 x 1 x 2 e 1 x 2x x 4
 SECTION 4.3 HOW DERIVATIVES AFFECT THE SHAPE OF A GRAPH 297 local maimum or minimum. The second derivative is f 2 e 2 e 2 4 e 2 4 Since e and 4, we have f when and when 2 f. So the curve is concave downward
SECTION 4.3 HOW DERIVATIVES AFFECT THE SHAPE OF A GRAPH 297 local maimum or minimum. The second derivative is f 2 e 2 e 2 4 e 2 4 Since e and 4, we have f when and when 2 f. So the curve is concave downward
Answer Explanations. The SAT Subject Tests. Mathematics Level 1 & 2 TO PRACTICE QUESTIONS FROM THE SAT SUBJECT TESTS STUDENT GUIDE
 The SAT Subject Tests Answer Eplanations TO PRACTICE QUESTIONS FROM THE SAT SUBJECT TESTS STUDENT GUIDE Mathematics Level & Visit sat.org/stpractice to get more practice and stud tips for the Subject Test
The SAT Subject Tests Answer Eplanations TO PRACTICE QUESTIONS FROM THE SAT SUBJECT TESTS STUDENT GUIDE Mathematics Level & Visit sat.org/stpractice to get more practice and stud tips for the Subject Test
Algebra/Pre-calc Review
 Algebra/Pre-calc Review The following pages contain various algebra and pre-calculus topics that are used in the stud of calculus. These pages were designed so that students can refresh their knowledge
Algebra/Pre-calc Review The following pages contain various algebra and pre-calculus topics that are used in the stud of calculus. These pages were designed so that students can refresh their knowledge
f x, y x 2 y 2 2x 6y 14. Then
 SECTION 11.7 MAXIMUM AND MINIMUM VALUES 645 absolute minimum FIGURE 1 local maimum local minimum absolute maimum Look at the hills and valles in the graph of f shown in Figure 1. There are two points a,
SECTION 11.7 MAXIMUM AND MINIMUM VALUES 645 absolute minimum FIGURE 1 local maimum local minimum absolute maimum Look at the hills and valles in the graph of f shown in Figure 1. There are two points a,
APPENDIXES. B Coordinate Geometry and Lines C. D Trigonometry E F. G The Logarithm Defined as an Integral H Complex Numbers I
 APPENDIXES A Numbers, Inequalities, and Absolute Values B Coordinate Geometr and Lines C Graphs of Second-Degree Equations D Trigonometr E F Sigma Notation Proofs of Theorems G The Logarithm Defined as
APPENDIXES A Numbers, Inequalities, and Absolute Values B Coordinate Geometr and Lines C Graphs of Second-Degree Equations D Trigonometr E F Sigma Notation Proofs of Theorems G The Logarithm Defined as
7.7. Inverse Trigonometric Functions. Defining the Inverses
 7.7 Inverse Trigonometric Functions 57 7.7 Inverse Trigonometric Functions Inverse trigonometric functions arise when we want to calculate angles from side measurements in triangles. The also provide useful
7.7 Inverse Trigonometric Functions 57 7.7 Inverse Trigonometric Functions Inverse trigonometric functions arise when we want to calculate angles from side measurements in triangles. The also provide useful
4.3 Mean-Value Theorem and Monotonicity
 .3 Mean-Value Theorem and Monotonicit 1. Mean Value Theorem Theorem: Suppose that f is continuous on the interval a, b and differentiable on the interval a, b. Then there eists a number c in a, b such
.3 Mean-Value Theorem and Monotonicit 1. Mean Value Theorem Theorem: Suppose that f is continuous on the interval a, b and differentiable on the interval a, b. Then there eists a number c in a, b such
Unit 3 NOTES Honors Common Core Math 2 1. Day 1: Properties of Exponents
 Unit NOTES Honors Common Core Math Da : Properties of Eponents Warm-Up: Before we begin toda s lesson, how much do ou remember about eponents? Use epanded form to write the rules for the eponents. OBJECTIVE
Unit NOTES Honors Common Core Math Da : Properties of Eponents Warm-Up: Before we begin toda s lesson, how much do ou remember about eponents? Use epanded form to write the rules for the eponents. OBJECTIVE
5.6 RATIOnAl FUnCTIOnS. Using Arrow notation. learning ObjeCTIveS
 CHAPTER PolNomiAl ANd rational functions learning ObjeCTIveS In this section, ou will: Use arrow notation. Solve applied problems involving rational functions. Find the domains of rational functions. Identif
CHAPTER PolNomiAl ANd rational functions learning ObjeCTIveS In this section, ou will: Use arrow notation. Solve applied problems involving rational functions. Find the domains of rational functions. Identif
Math Review Packet #5 Algebra II (Part 2) Notes
 SCIE 0, Spring 0 Miller Math Review Packet #5 Algebra II (Part ) Notes Quadratic Functions (cont.) So far, we have onl looked at quadratic functions in which the term is squared. A more general form of
SCIE 0, Spring 0 Miller Math Review Packet #5 Algebra II (Part ) Notes Quadratic Functions (cont.) So far, we have onl looked at quadratic functions in which the term is squared. A more general form of
2.1 Rates of Change and Limits AP Calculus
 .1 Rates of Change and Limits AP Calculus.1 RATES OF CHANGE AND LIMITS Limits Limits are what separate Calculus from pre calculus. Using a it is also the foundational principle behind the two most important
.1 Rates of Change and Limits AP Calculus.1 RATES OF CHANGE AND LIMITS Limits Limits are what separate Calculus from pre calculus. Using a it is also the foundational principle behind the two most important
Exponential, Logistic, and Logarithmic Functions
 CHAPTER 3 Eponential, Logistic, and Logarithmic Functions 3.1 Eponential and Logistic Functions 3.2 Eponential and Logistic Modeling 3.3 Logarithmic Functions and Their Graphs 3.4 Properties of Logarithmic
CHAPTER 3 Eponential, Logistic, and Logarithmic Functions 3.1 Eponential and Logistic Functions 3.2 Eponential and Logistic Modeling 3.3 Logarithmic Functions and Their Graphs 3.4 Properties of Logarithmic
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. Section. Rolle s Theorem and the Mean Value Theorem. 7 Section. Increasing and Decreasing Functions and the First Derivative
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. Section. Rolle s Theorem and the Mean Value Theorem. 7 Section. Increasing and Decreasing Functions and the First Derivative
FIRST- AND SECOND-ORDER IVPS The problem given in (1) is also called an nth-order initial-value problem. For example, Solve: Solve:
 .2 INITIAL-VALUE PROBLEMS 3.2 INITIAL-VALUE PROBLEMS REVIEW MATERIAL Normal form of a DE Solution of a DE Famil of solutions INTRODUCTION We are often interested in problems in which we seek a solution
.2 INITIAL-VALUE PROBLEMS 3.2 INITIAL-VALUE PROBLEMS REVIEW MATERIAL Normal form of a DE Solution of a DE Famil of solutions INTRODUCTION We are often interested in problems in which we seek a solution
2.1 Limits, Rates of Change, and Tangent Lines. Preliminary Questions 1. Average velocity is defined as a ratio of which two quantities?
 LIMITS. Limits, Rates of Change, and Tangent Lines Preinar Questions. Average velocit is defined as a ratio of which two quantities? Average velocit is defined as the ratio of distance traveled to time
LIMITS. Limits, Rates of Change, and Tangent Lines Preinar Questions. Average velocit is defined as a ratio of which two quantities? Average velocit is defined as the ratio of distance traveled to time
3.1 Graphing Quadratic Functions. Quadratic functions are of the form.
 3.1 Graphing Quadratic Functions A. Quadratic Functions Completing the Square Quadratic functions are of the form. 3. It is easiest to graph quadratic functions when the are in the form using transformations.
3.1 Graphing Quadratic Functions A. Quadratic Functions Completing the Square Quadratic functions are of the form. 3. It is easiest to graph quadratic functions when the are in the form using transformations.
6.4 graphs OF logarithmic FUnCTIOnS
 SECTION 6. graphs of logarithmic functions 9 9 learning ObjeCTIveS In this section, ou will: Identif the domain of a logarithmic function. Graph logarithmic functions. 6. graphs OF logarithmic FUnCTIOnS
SECTION 6. graphs of logarithmic functions 9 9 learning ObjeCTIveS In this section, ou will: Identif the domain of a logarithmic function. Graph logarithmic functions. 6. graphs OF logarithmic FUnCTIOnS
L 8.6 L 10.6 L 13.3 L Psud = u 3-4u 2 + 5u; [1, 2]
![L 8.6 L 10.6 L 13.3 L Psud = u 3-4u 2 + 5u; [1, 2] L 8.6 L 10.6 L 13.3 L Psud = u 3-4u 2 + 5u; [1, 2]](/thumbs/80/82149634.jpg) . Rates of Change and Tangents to Curves 6 p Q (5, ) (, ) (5, ) (, 65) Slope of PQ p/ t (flies/ da) - 5 5 - - 5 - - 5 5-65 - 5 - L 8.6 L.6 L. L 6. Number of flies 5 B(5, 5) Q(5, ) 5 5 P(, 5) 5 5 A(, )
. Rates of Change and Tangents to Curves 6 p Q (5, ) (, ) (5, ) (, 65) Slope of PQ p/ t (flies/ da) - 5 5 - - 5 - - 5 5-65 - 5 - L 8.6 L.6 L. L 6. Number of flies 5 B(5, 5) Q(5, ) 5 5 P(, 5) 5 5 A(, )
1.5 Inverse Trigonometric Functions
 1.5 Inverse Trigonometric Functions Remember that only one-to-one functions have inverses. So, in order to find the inverse functions for sine, cosine, and tangent, we must restrict their domains to intervals
1.5 Inverse Trigonometric Functions Remember that only one-to-one functions have inverses. So, in order to find the inverse functions for sine, cosine, and tangent, we must restrict their domains to intervals
Chapter One. Chapter One
 Chapter One Chapter One CHAPTER ONE Hughes Hallett et al c 005, John Wile & Sons ConcepTests and Answers and Comments for Section.. Which of the following functions has its domain identical with its range?
Chapter One Chapter One CHAPTER ONE Hughes Hallett et al c 005, John Wile & Sons ConcepTests and Answers and Comments for Section.. Which of the following functions has its domain identical with its range?
b. Create a graph that gives a more complete representation of f.
 or Use Onl in Pilot Program F 96 Chapter Limits 6 7. Steep secant lines a. Given the graph of f in the following figures, find the slope of the secant line that passes through, and h, f h in terms of h,
or Use Onl in Pilot Program F 96 Chapter Limits 6 7. Steep secant lines a. Given the graph of f in the following figures, find the slope of the secant line that passes through, and h, f h in terms of h,
Polynomial and Rational Functions
 Polnomial and Rational Functions Figure -mm film, once the standard for capturing photographic images, has been made largel obsolete b digital photograph. (credit film : modification of work b Horia Varlan;
Polnomial and Rational Functions Figure -mm film, once the standard for capturing photographic images, has been made largel obsolete b digital photograph. (credit film : modification of work b Horia Varlan;
Higher. Functions and Graphs. Functions and Graphs 15
 Higher Mathematics UNIT UTCME Functions and Graphs Contents Functions and Graphs 5 Set Theor 5 Functions 6 Inverse Functions 9 4 Eponential Functions 0 5 Introduction to Logarithms 0 6 Radians 7 Eact Values
Higher Mathematics UNIT UTCME Functions and Graphs Contents Functions and Graphs 5 Set Theor 5 Functions 6 Inverse Functions 9 4 Eponential Functions 0 5 Introduction to Logarithms 0 6 Radians 7 Eact Values
Set 3: Limits of functions:
 Set 3: Limits of functions: A. The intuitive approach (.): 1. Watch the video at: https://www.khanacademy.org/math/differential-calculus/it-basics-dc/formal-definition-of-its-dc/v/itintuition-review. 3.
Set 3: Limits of functions: A. The intuitive approach (.): 1. Watch the video at: https://www.khanacademy.org/math/differential-calculus/it-basics-dc/formal-definition-of-its-dc/v/itintuition-review. 3.
LESSON #48 - INTEGER EXPONENTS COMMON CORE ALGEBRA II
 LESSON #8 - INTEGER EXPONENTS COMMON CORE ALGEBRA II We just finished our review of linear functions. Linear functions are those that grow b equal differences for equal intervals. In this unit we will
LESSON #8 - INTEGER EXPONENTS COMMON CORE ALGEBRA II We just finished our review of linear functions. Linear functions are those that grow b equal differences for equal intervals. In this unit we will
6 = 1 2. The right endpoints of the subintervals are then 2 5, 3, 7 2, 4, 2 9, 5, while the left endpoints are 2, 5 2, 3, 7 2, 4, 9 2.
 5 THE ITEGRAL 5. Approimating and Computing Area Preliminar Questions. What are the right and left endpoints if [, 5] is divided into si subintervals? If the interval [, 5] is divided into si subintervals,
5 THE ITEGRAL 5. Approimating and Computing Area Preliminar Questions. What are the right and left endpoints if [, 5] is divided into si subintervals? If the interval [, 5] is divided into si subintervals,
McKinney High School AP Calculus Summer Packet
 McKinne High School AP Calculus Summer Packet (for students entering AP Calculus AB or AP Calculus BC) Name:. This packet is to be handed in to our Calculus teacher the first week of school.. ALL work
McKinne High School AP Calculus Summer Packet (for students entering AP Calculus AB or AP Calculus BC) Name:. This packet is to be handed in to our Calculus teacher the first week of school.. ALL work
Limits and Their Properties
 Chapter 1 Limits and Their Properties Course Number Section 1.1 A Preview of Calculus Objective: In this lesson you learned how calculus compares with precalculus. I. What is Calculus? (Pages 42 44) Calculus
Chapter 1 Limits and Their Properties Course Number Section 1.1 A Preview of Calculus Objective: In this lesson you learned how calculus compares with precalculus. I. What is Calculus? (Pages 42 44) Calculus
Review: Limits of Functions - 10/7/16
 Review: Limits of Functions - 10/7/16 1 Right and Left Hand Limits Definition 1.0.1 We write lim a f() = L to mean that the function f() approaches L as approaches a from the left. We call this the left
Review: Limits of Functions - 10/7/16 1 Right and Left Hand Limits Definition 1.0.1 We write lim a f() = L to mean that the function f() approaches L as approaches a from the left. We call this the left
Solutions to Math 41 Final Exam December 9, 2013
 Solutions to Math 4 Final Eam December 9,. points In each part below, use the method of your choice, but show the steps in your computations. a Find f if: f = arctane csc 5 + log 5 points Using the Chain
Solutions to Math 4 Final Eam December 9,. points In each part below, use the method of your choice, but show the steps in your computations. a Find f if: f = arctane csc 5 + log 5 points Using the Chain
Section 3.1. ; X = (0, 1]. (i) f : R R R, f (x, y) = x y
![Section 3.1. ; X = (0, 1]. (i) f : R R R, f (x, y) = x y Section 3.1. ; X = (0, 1]. (i) f : R R R, f (x, y) = x y](/thumbs/83/88503328.jpg) Paul J. Bruillard MATH 0.970 Problem Set 6 An Introduction to Abstract Mathematics R. Bond and W. Keane Section 3.1: 3b,c,e,i, 4bd, 6, 9, 15, 16, 18c,e, 19a, 0, 1b Section 3.: 1f,i, e, 6, 1e,f,h, 13e,
Paul J. Bruillard MATH 0.970 Problem Set 6 An Introduction to Abstract Mathematics R. Bond and W. Keane Section 3.1: 3b,c,e,i, 4bd, 6, 9, 15, 16, 18c,e, 19a, 0, 1b Section 3.: 1f,i, e, 6, 1e,f,h, 13e,
4.7. Newton s Method. Procedure for Newton s Method HISTORICAL BIOGRAPHY
 4. Newton s Method 99 4. Newton s Method HISTORICAL BIOGRAPHY Niels Henrik Abel (18 189) One of the basic problems of mathematics is solving equations. Using the quadratic root formula, we know how to
4. Newton s Method 99 4. Newton s Method HISTORICAL BIOGRAPHY Niels Henrik Abel (18 189) One of the basic problems of mathematics is solving equations. Using the quadratic root formula, we know how to
AP Calculus AB Summer Assignment
 AP Calculus AB Summer Assignment Name: When you come back to school, it is my epectation that you will have this packet completed. You will be way behind at the beginning of the year if you haven t attempted
AP Calculus AB Summer Assignment Name: When you come back to school, it is my epectation that you will have this packet completed. You will be way behind at the beginning of the year if you haven t attempted
Quick Review 4.1 (For help, go to Sections 1.2, 2.1, 3.5, and 3.6.)
 Section 4. Etreme Values of Functions 93 EXPLORATION Finding Etreme Values Let f,.. Determine graphicall the etreme values of f and where the occur. Find f at these values of.. Graph f and f or NDER f,,
Section 4. Etreme Values of Functions 93 EXPLORATION Finding Etreme Values Let f,.. Determine graphicall the etreme values of f and where the occur. Find f at these values of.. Graph f and f or NDER f,,
INTRODUCTION TO DIFFERENTIAL EQUATIONS
 INTRODUCTION TO DIFFERENTIAL EQUATIONS. Definitions and Terminolog. Initial-Value Problems.3 Differential Equations as Mathematical Models CHAPTER IN REVIEW The words differential and equations certainl
INTRODUCTION TO DIFFERENTIAL EQUATIONS. Definitions and Terminolog. Initial-Value Problems.3 Differential Equations as Mathematical Models CHAPTER IN REVIEW The words differential and equations certainl
UNIVERSIDAD CARLOS III DE MADRID MATHEMATICS II EXERCISES (SOLUTIONS )
 UNIVERSIDAD CARLOS III DE MADRID MATHEMATICS II EXERCISES (SOLUTIONS ) CHAPTER : Limits and continuit of functions in R n. -. Sketch the following subsets of R. Sketch their boundar and the interior. Stud
UNIVERSIDAD CARLOS III DE MADRID MATHEMATICS II EXERCISES (SOLUTIONS ) CHAPTER : Limits and continuit of functions in R n. -. Sketch the following subsets of R. Sketch their boundar and the interior. Stud
Polynomial and Rational Functions
 Name Date Chapter Polnomial and Rational Functions Section.1 Quadratic Functions Objective: In this lesson ou learned how to sketch and analze graphs of quadratic functions. Important Vocabular Define
Name Date Chapter Polnomial and Rational Functions Section.1 Quadratic Functions Objective: In this lesson ou learned how to sketch and analze graphs of quadratic functions. Important Vocabular Define
LESSON #42 - INVERSES OF FUNCTIONS AND FUNCTION NOTATION PART 2 COMMON CORE ALGEBRA II
 LESSON #4 - INVERSES OF FUNCTIONS AND FUNCTION NOTATION PART COMMON CORE ALGEBRA II You will recall from unit 1 that in order to find the inverse of a function, ou must switch and and solve for. Also,
LESSON #4 - INVERSES OF FUNCTIONS AND FUNCTION NOTATION PART COMMON CORE ALGEBRA II You will recall from unit 1 that in order to find the inverse of a function, ou must switch and and solve for. Also,
3 Polynomial and Rational Functions
 3 Polnomial and Rational Functions 3.1 Quadratic Functions and Models 3.2 Polnomial Functions and Their Graphs 3.3 Dividing Polnomials 3.4 Real Zeros of Polnomials 3.5 Comple Zeros and the Fundamental
3 Polnomial and Rational Functions 3.1 Quadratic Functions and Models 3.2 Polnomial Functions and Their Graphs 3.3 Dividing Polnomials 3.4 Real Zeros of Polnomials 3.5 Comple Zeros and the Fundamental
1.5. Analyzing Graphs of Functions. The Graph of a Function. What you should learn. Why you should learn it. 54 Chapter 1 Functions and Their Graphs
 0_005.qd /7/05 8: AM Page 5 5 Chapter Functions and Their Graphs.5 Analzing Graphs of Functions What ou should learn Use the Vertical Line Test for functions. Find the zeros of functions. Determine intervals
0_005.qd /7/05 8: AM Page 5 5 Chapter Functions and Their Graphs.5 Analzing Graphs of Functions What ou should learn Use the Vertical Line Test for functions. Find the zeros of functions. Determine intervals
MAT 1275: Introduction to Mathematical Analysis. Graphs and Simplest Equations for Basic Trigonometric Functions. y=sin( x) Function
 MAT 275: Introduction to Mathematical Analsis Dr. A. Rozenblum Graphs and Simplest Equations for Basic Trigonometric Functions We consider here three basic functions: sine, cosine and tangent. For them,
MAT 275: Introduction to Mathematical Analsis Dr. A. Rozenblum Graphs and Simplest Equations for Basic Trigonometric Functions We consider here three basic functions: sine, cosine and tangent. For them,
14.1 FUNCTIONS OF SEVERAL VARIABLES. In this section we study functions of two or more variables from four points of view:
 4 PARTIAL DERIVATIVES Functions of two variables can be visualied b means of level curves, which connect points where the function takes on a given value. Atmospheric pressure at a given time is a function
4 PARTIAL DERIVATIVES Functions of two variables can be visualied b means of level curves, which connect points where the function takes on a given value. Atmospheric pressure at a given time is a function
Solutions to Problem Sheet for Week 6
 THE UNIVERSITY OF SYDNEY SCHOOL OF MATHEMATICS AND STATISTICS Solutions to Problem Sheet for Week 6 MATH90: Differential Calculus (Advanced) Semester, 07 Web Page: sydney.edu.au/science/maths/u/ug/jm/math90/
THE UNIVERSITY OF SYDNEY SCHOOL OF MATHEMATICS AND STATISTICS Solutions to Problem Sheet for Week 6 MATH90: Differential Calculus (Advanced) Semester, 07 Web Page: sydney.edu.au/science/maths/u/ug/jm/math90/
Table of Contents. Module 1
 Table of Contents Module 1 11 Order of Operations 16 Signed Numbers 1 Factorization of Integers 17 Further Signed Numbers 13 Fractions 18 Power Laws 14 Fractions and Decimals 19 Introduction to Algebra
Table of Contents Module 1 11 Order of Operations 16 Signed Numbers 1 Factorization of Integers 17 Further Signed Numbers 13 Fractions 18 Power Laws 14 Fractions and Decimals 19 Introduction to Algebra
Section 1.5 Formal definitions of limits
 Section.5 Formal definitions of limits (3/908) Overview: The definitions of the various tpes of limits in previous sections involve phrases such as arbitraril close, sufficientl close, arbitraril large,
Section.5 Formal definitions of limits (3/908) Overview: The definitions of the various tpes of limits in previous sections involve phrases such as arbitraril close, sufficientl close, arbitraril large,
A.5. Complex Numbers AP-12. The Development of the Real Numbers
 AP- A.5 Comple Numbers Comple numbers are epressions of the form a + ib, where a and b are real numbers and i is a smbol for -. Unfortunatel, the words real and imaginar have connotations that somehow
AP- A.5 Comple Numbers Comple numbers are epressions of the form a + ib, where a and b are real numbers and i is a smbol for -. Unfortunatel, the words real and imaginar have connotations that somehow
CHAPTER 2 Polynomial and Rational Functions
 CHAPTER Polnomial and Rational Functions Section. Quadratic Functions..................... 9 Section. Polnomial Functions of Higher Degree.......... Section. Real Zeros of Polnomial Functions............
CHAPTER Polnomial and Rational Functions Section. Quadratic Functions..................... 9 Section. Polnomial Functions of Higher Degree.......... Section. Real Zeros of Polnomial Functions............
Differentiation and applications
 FS O PA G E PR O U N C O R R EC TE D Differentiation and applications. Kick off with CAS. Limits, continuit and differentiabilit. Derivatives of power functions.4 C oordinate geometr applications of differentiation.5
FS O PA G E PR O U N C O R R EC TE D Differentiation and applications. Kick off with CAS. Limits, continuit and differentiabilit. Derivatives of power functions.4 C oordinate geometr applications of differentiation.5
67. (a) Use a computer algebra system to find the partial fraction CAS. 68. (a) Find the partial fraction decomposition of the function CAS
 SECTION 7.5 STRATEGY FOR INTEGRATION 483 6. 2 sin 2 2 cos CAS 67. (a) Use a computer algebra sstem to find the partial fraction decomposition of the function 62 63 Find the area of the region under the
SECTION 7.5 STRATEGY FOR INTEGRATION 483 6. 2 sin 2 2 cos CAS 67. (a) Use a computer algebra sstem to find the partial fraction decomposition of the function 62 63 Find the area of the region under the
Coordinate geometry. + bx + c. Vertical asymptote. Sketch graphs of hyperbolas (including asymptotic behaviour) from the general
 A Sketch graphs of = a m b n c where m = or and n = or B Reciprocal graphs C Graphs of circles and ellipses D Graphs of hperbolas E Partial fractions F Sketch graphs using partial fractions Coordinate
A Sketch graphs of = a m b n c where m = or and n = or B Reciprocal graphs C Graphs of circles and ellipses D Graphs of hperbolas E Partial fractions F Sketch graphs using partial fractions Coordinate
Chapter 11 Exponential and Logarithmic Function
 Chapter Eponential and Logarithmic Function - Page 69.. Real Eponents. a m a n a mn. (a m ) n a mn. a b m a b m m, when b 0 Graphing Calculator Eploration Page 700 Check for Understanding. The quantities
Chapter Eponential and Logarithmic Function - Page 69.. Real Eponents. a m a n a mn. (a m ) n a mn. a b m a b m m, when b 0 Graphing Calculator Eploration Page 700 Check for Understanding. The quantities
4 The Cartesian Coordinate System- Pictures of Equations
 The Cartesian Coordinate Sstem- Pictures of Equations Concepts: The Cartesian Coordinate Sstem Graphs of Equations in Two Variables -intercepts and -intercepts Distance in Two Dimensions and the Pthagorean
The Cartesian Coordinate Sstem- Pictures of Equations Concepts: The Cartesian Coordinate Sstem Graphs of Equations in Two Variables -intercepts and -intercepts Distance in Two Dimensions and the Pthagorean
Summer Review Packet for Students Entering AP Calculus BC. Complex Fractions
 Summer Review Packet for Students Entering AP Calculus BC Comple Fractions When simplifying comple fractions, multiply by a fraction equal to 1 which has a numerator and denominator composed of the common
Summer Review Packet for Students Entering AP Calculus BC Comple Fractions When simplifying comple fractions, multiply by a fraction equal to 1 which has a numerator and denominator composed of the common
STANDARD FORM is a QUADRATIC FUNCTION and its graph is a PARABOLA. The domain of a quadratic function is the set of all real numbers.
 EXERCISE 2-3 Things to remember: 1. QUADRATIC FUNCTION If a, b, and c are real numbers with a 0, then the function f() = a 2 + b + c STANDARD FORM is a QUADRATIC FUNCTION and its graph is a PARABOLA. The
EXERCISE 2-3 Things to remember: 1. QUADRATIC FUNCTION If a, b, and c are real numbers with a 0, then the function f() = a 2 + b + c STANDARD FORM is a QUADRATIC FUNCTION and its graph is a PARABOLA. The
Review of Essential Skills and Knowledge
 Review of Essential Skills and Knowledge R Eponent Laws...50 R Epanding and Simplifing Polnomial Epressions...5 R 3 Factoring Polnomial Epressions...5 R Working with Rational Epressions...55 R 5 Slope
Review of Essential Skills and Knowledge R Eponent Laws...50 R Epanding and Simplifing Polnomial Epressions...5 R 3 Factoring Polnomial Epressions...5 R Working with Rational Epressions...55 R 5 Slope
STUDY KNOWHOW PROGRAM STUDY AND LEARNING CENTRE. Functions & Graphs
 STUDY KNOWHOW PROGRAM STUDY AND LEARNING CENTRE Functions & Graphs Contents Functions and Relations... 1 Interval Notation... 3 Graphs: Linear Functions... 5 Lines and Gradients... 7 Graphs: Quadratic
STUDY KNOWHOW PROGRAM STUDY AND LEARNING CENTRE Functions & Graphs Contents Functions and Relations... 1 Interval Notation... 3 Graphs: Linear Functions... 5 Lines and Gradients... 7 Graphs: Quadratic
Continuity at a Point
 Continuity at a Point When we eplored the limit of f() as approaches c, the emphasis was on the function values close to = c rather than what happens to the function at = c. We will now consider the following
Continuity at a Point When we eplored the limit of f() as approaches c, the emphasis was on the function values close to = c rather than what happens to the function at = c. We will now consider the following
CHAPTER 1 Limits and Their Properties
 CHAPTER Limits and Their Properties Section. A Preview of Calculus................... 305 Section. Finding Limits Graphically and Numerically....... 305 Section.3 Evaluating Limits Analytically...............
CHAPTER Limits and Their Properties Section. A Preview of Calculus................... 305 Section. Finding Limits Graphically and Numerically....... 305 Section.3 Evaluating Limits Analytically...............
8.1 Exponents and Roots
 Section 8. Eponents and Roots 75 8. Eponents and Roots Before defining the net famil of functions, the eponential functions, we will need to discuss eponent notation in detail. As we shall see, eponents
Section 8. Eponents and Roots 75 8. Eponents and Roots Before defining the net famil of functions, the eponential functions, we will need to discuss eponent notation in detail. As we shall see, eponents
Exponential and Logarithmic Functions
 Eponential and Logarithmic Functions 6 Figure Electron micrograph of E. Coli bacteria (credit: Mattosaurus, Wikimedia Commons) CHAPTER OUTLINE 6. Eponential Functions 6. Logarithmic Properties 6. Graphs
Eponential and Logarithmic Functions 6 Figure Electron micrograph of E. Coli bacteria (credit: Mattosaurus, Wikimedia Commons) CHAPTER OUTLINE 6. Eponential Functions 6. Logarithmic Properties 6. Graphs
Tangent Lines. Limits 1
 Limits Tangent Lines The concept of the tangent line to a circle dates back at least to the earl das of Greek geometr, that is, at least 5 ears. The tangent line to a circle with centre O at a point A
Limits Tangent Lines The concept of the tangent line to a circle dates back at least to the earl das of Greek geometr, that is, at least 5 ears. The tangent line to a circle with centre O at a point A
10.2 The Unit Circle: Cosine and Sine
 0. The Unit Circle: Cosine and Sine 77 0. The Unit Circle: Cosine and Sine In Section 0.., we introduced circular motion and derived a formula which describes the linear velocit of an object moving on
0. The Unit Circle: Cosine and Sine 77 0. The Unit Circle: Cosine and Sine In Section 0.., we introduced circular motion and derived a formula which describes the linear velocit of an object moving on
Law of Sines, Law of Cosines, Heron s Formula:
 PreAP Math Analsis nd Semester Review Law of Sines, Law of Cosines, Heron s Formula:. Determine how man solutions the triangle has and eplain our reasoning. (FIND YOUR FLOW CHART) a. A = 4, a = 4 ards,
PreAP Math Analsis nd Semester Review Law of Sines, Law of Cosines, Heron s Formula:. Determine how man solutions the triangle has and eplain our reasoning. (FIND YOUR FLOW CHART) a. A = 4, a = 4 ards,
(2) Find the domain of f (x) = 2x3 5 x 2 + x 6
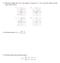 CHAPTER FUNCTIONS AND MODELS () Determine whether the curve is the graph of a function of. If it is state the domain and the range of the function. 5 8 Determine whether the curve is the graph of a function
CHAPTER FUNCTIONS AND MODELS () Determine whether the curve is the graph of a function of. If it is state the domain and the range of the function. 5 8 Determine whether the curve is the graph of a function
SEE and DISCUSS the pictures on pages in your text. Key picture:
 Math 6 Notes 1.1 A PREVIEW OF CALCULUS There are main problems in calculus: 1. Finding a tangent line to a curve though a point on the curve.. Finding the area under a curve on some interval. SEE and DISCUSS
Math 6 Notes 1.1 A PREVIEW OF CALCULUS There are main problems in calculus: 1. Finding a tangent line to a curve though a point on the curve.. Finding the area under a curve on some interval. SEE and DISCUSS
Derivatives of Multivariable Functions
 Chapter 0 Derivatives of Multivariable Functions 0. Limits Motivating Questions In this section, we strive to understand the ideas generated b the following important questions: What do we mean b the limit
Chapter 0 Derivatives of Multivariable Functions 0. Limits Motivating Questions In this section, we strive to understand the ideas generated b the following important questions: What do we mean b the limit
11.4 Polar Coordinates
 11. Polar Coordinates 917 11. Polar Coordinates In Section 1.1, we introduced the Cartesian coordinates of a point in the plane as a means of assigning ordered pairs of numbers to points in the plane.
11. Polar Coordinates 917 11. Polar Coordinates In Section 1.1, we introduced the Cartesian coordinates of a point in the plane as a means of assigning ordered pairs of numbers to points in the plane.
Limits and Their Properties
 Limits and Their Properties The it of a function is the primar concept that distinguishes calculus from algebra and analtic geometr. The notion of a it is fundamental to the stud of calculus. Thus, it
Limits and Their Properties The it of a function is the primar concept that distinguishes calculus from algebra and analtic geometr. The notion of a it is fundamental to the stud of calculus. Thus, it
Answers to Some Sample Problems
 Answers to Some Sample Problems. Use rules of differentiation to evaluate the derivatives of the following functions of : cos( 3 ) ln(5 7 sin(3)) 3 5 +9 8 3 e 3 h 3 e i sin( 3 )3 +[ ln ] cos( 3 ) [ln(5)
Answers to Some Sample Problems. Use rules of differentiation to evaluate the derivatives of the following functions of : cos( 3 ) ln(5 7 sin(3)) 3 5 +9 8 3 e 3 h 3 e i sin( 3 )3 +[ ln ] cos( 3 ) [ln(5)
PACKET Unit 4 Honors ICM Functions and Limits 1
 PACKET Unit 4 Honors ICM Functions and Limits 1 Day 1 Homework For each of the rational functions find: a. domain b. -intercept(s) c. y-intercept Graph #8 and #10 with at least 5 EXACT points. 1. f 6.
PACKET Unit 4 Honors ICM Functions and Limits 1 Day 1 Homework For each of the rational functions find: a. domain b. -intercept(s) c. y-intercept Graph #8 and #10 with at least 5 EXACT points. 1. f 6.
Homework Assignments Math /02 Spring 2015
 Homework Assignments Math 1-01/0 Spring 015 Assignment 1 Due date : Frida, Januar Section 5.1, Page 159: #1-, 10, 11, 1; Section 5., Page 16: Find the slope and -intercept, and then plot the line in problems:
Homework Assignments Math 1-01/0 Spring 015 Assignment 1 Due date : Frida, Januar Section 5.1, Page 159: #1-, 10, 11, 1; Section 5., Page 16: Find the slope and -intercept, and then plot the line in problems:
