( ) ( ) CHAPTER 8. Lai et al, Introduction to Continuum Mechanics. Copyright 2010, Elsevier Inc 8-1
|
|
|
- Poppy Bruce
- 5 years ago
- Views:
Transcription
1 CHAPER 8 81 Shw ha f an incmpessible Newnian fluid in Cuee flw he pessue a he ue cylinde ( R ) is always lage han ha a he inne cylinde ha is bain R i Ri ρ ω R R d B Ans In Cuee flw v vz and vθ A+ [see Eq (6154) and (6157)] hus dvθ vθ θθ zz p z θ z and θ μ funcin f nly d 1 z hus he -equain f min θ θθ θ z ρ ω becmes: R R ρω Nw d ρ ω d Ri hus Ri ρ ω R R d R i he igh hand side f his las equain is always R i psiive 8 Shw ha he cnsiuive equain τ τ1+ τ + τ wih τn + n τ n / μnd n 1 is equivalen τ + a1 τ / + a τ / + a τ / bd+ b1 D/ + b D/ whee a + + a + + a b b ( μ μ μ ) b μ ( ) μ ( ) μ ( ) ( μ μ μ ) Ans τ τ j τ j i i j i i i 1 i 1 τ j 1 i 1 j 1 i 1 j 1 τ τ i j τ j i + i ( μid τ i) + i i 1 i 1 j 1 i 1 i 1 j 1 j i j i τ j D μi τ i i D μi τ + i 1 i 1 i 1 j 1 i 1 i 1 j 1 j i j i i + ha is τ j 8-1 Cpyigh 1 Elsevie Inc
2 τ τ τ τ1 τ τ1 τ i D μi i 1 τ (i) i 1 Nex we have + + τ / + + τ / τ / ( 1 1) ( 1 1) 1 ( 1 1) ( ) ( ) ( ) + τ / + ( + ) τ / + τ / 1 1 τ / 1 1 τ1/ τ1/ 1 τ / ie ( ) τ / μ1( + ) + μ( 1+ ) + μ( + 1) D / + τ / + τ / + τ / + τ / + τ / τ / + Finally we have τ τ1 τ τ D τ1 D τ D τ μ1 + 1 μ + 1 μ D D D τ τ τ 1 μ + μ + μ 1 ha is 1 τ μ D 1 μ D 1 1 μ D τ τ 1 τ (iii) hus (i) + (ii)+ (iii) gives τ τ / τ / + τ / ( 1 ) ( 1 1) 1 D( μ1 μ μ) μ1( ) μ( 1 ) μ( 1) ( μ μ μ ) D D/ / ha is τ τ τ D D τ + a1 + a + a b D + b1 + b whee a + + a + + a b b ( μ μ μ ) b μ ( ) μ ( ) μ ( ) ( μ μ μ ) Obain he fce-displacemen elainship f he Kelvin-Vig slid which cnsiss f a dashp (wih damping cefficien η ) and a sping (wih sping cnsan G ) cnneced in paallel Als bain is elaxain funcin Ans Since he sping and he dashp ae cnneced in paallel heefe he al fce is given by: S Ssp + Sdash and he al displacemen ε is given by ε εsp εdash Nw (ii) 8- Cpyigh 1 Elsevie Inc
3 dε dε Ssp Gε and Sdash η heefe S Gε + η find he elaxain funcin we le d d ε ε H () whee H is he Heaviside funcin hen S GεH() + ηεδ () hus he elaxain funcin is S / ε GH + ηδ 84 (a) Obain he fce-displacemen elainship f a dashp (damping cefficien η ) and a Kelvin-Vig slid (damping cefficien η and sping cnsan G see he pevius pblem) cnneced in seies (b) Obain is elaxain funcin Ans (a) Le Sv and Sd be he fce ansmied by he Kelvin-Vigh elemen and he dashp especively and le εv and εd be he elngain f he Kelvin-Vigh elemen and he dashp especively hen we have he al fce is given by S Sd Sv (i) and he al displacemen dεd dεv is given by ε εd + εv(ii) whee Sd η S Sv Gεv + η (iii) Fm (ii) and d d dε dεd dεv S 1 S S G (iii) we have + + ( S Gε v ) + ( ε εd ) (iv) hus d d d η η η η η d ε η η + ds G dε G dεd ηη d ε ( η + η ) ds dε + η + S d ηη d η d η d G d G d d hus he fce-displacemen elainship is given by: ( η + η ) ds dε ηη d ε S + η + (v) G d d G d (b) Le ε ε H () whee H is Heaviside funcin hen Eq (v) gives ds G G () d + S ε η δ + ε ηη δ (vi) d η + η η + η η + η d whee () hus δ is he Diac funcin he inegain fac f his ODE is exp G / ( η + η ) G G G d η G d Se + η εη η η εηη η η δ e δ () e d ( η η) + + ( η η) + and + + d G G G η + η G η η η η () + δ + η η ( η η) εη εηη dδ d Se e d e d εη G εηη G/( η η) / () G G η η e δ δe d ( η η) ( η η) η + η ha is G G G G G G Se η + η εη εηη e () e () η + η εη εηη δ η + η + + δ η + η η + η η + η η + η η + η G + S η G η η ηη hus he elaxain funcin is e + δ () ε ( η + η ) ( η + η) 8- Cpyigh 1 Elsevie Inc
4 85 A linea Maxwell fluid defined by Eq (81) is beween w paallel plaes which ae ne uni apa Saing fm es a ime he p plae is given a displacemen u v while he bm plae emains fixed Neglec ineia effecs bain he shea sess hisy Ans he velciy field f he fluid in his min is given by (ineia negleced) v1 vh() x v v whee H is he Heaviside Funcin he nly nn-ze ae f defmain cmpnen is D1 v H / hus fm he cnsiuive equain f he linea ds1 d Maxwell fluid we bain S1 + μvh() hus / / 1 v S e μ e H () ha is d d / v / v / v / / S1e μ e μ H() d e μ d e μv ( e 1) hus he shea sess hisy is: 1 ( 1 / S μv e ) 86 Obain Eq (81) ie ' ' ' / φ( ) ( ) d whee φ ( μ / ) e S D by slving ds he linea nn-hmgeneus dinay diffeenial equain S+ μd d exp / ha is he equain can be wien as; Ans he inegain fac f his ODE is [ ] d d ( e ) μ / / / / S e D hus S ( / ) D / / ( μ / ) ( ' )/ S e e D d ha is e μ e d φ S μ e ' d' ' ' d' D D 87 Shw ha f he linea Maxwell fluid defined by Eq (81) φ whee φ () is he elaxain funcin and J is he ceep cmpliance funcin ' J ' d' S S H be applied he p plae f a channel f uni deph in which is he linea Ans Le 1 Maxwell fluid [ H is he uni sep funcin ie Heaviside funcin] Neglecing ineia he velciy field is v( x ) v x v is he velciy f he p plae hen fm he whee cnsiuive equain d / d μ S+ S D we bain S + S δ μd μ v / μdu / d 1 du S whee u is he displacemen f he p plae Fm Sδ () d μ + μ we bain du S S S d d Sδ () u S ( ) d μ μ hus he ceep cmpliance μ μ μ funcin is: J () u / S ( + )/ μ / Since he elaxain funcin is φ() ( μ / ) e heefe 8-4 Cpyigh 1 Elsevie Inc
5 ( ) ( ) ( )/ ( )/ e d + (1 / ) e ( ) d ( )/ ( ) ' / Nw ' / / φ J d ( μ / ) e ( + )/ μd (1/ ) e ( + ) d e d [ e ] and 1 ' ' ' φ J d + + ( )/ / / / ' e d ( de )( ) d e e d hus 88 Obain he sage mdulus and lss mdulus f he linea Maxwell fluid wih a H ( ) / cninuus elaxain specum defined by Eq (841) ie φ () e d Ans Le he shea sain be: γ1 γe iω F his sain hisy he ae f defmain hisy is dγ1 given by D1 i e i ω ωγ hus fm he cnsiuive equain d φ d S D d i e i ω φ ωγ φ d S D we have 1 1 / Wih φ () H / e d we have / H ( )/ iω H e / iω S1 i e e d d i e e dd ' Nw / iω ( 1 + i ω) / e e d e d e ( 1 + i ω ) / hus 1+ iω 1 i S ω H i e d G e i ω ω ( ) γ whee G iω d + iω ( + iω) ωγ ωγ H 1 1 is he cmplex mdulus Nw H iω H G iω d iω d 1+ iω 1+ iω 1iω ( 1 ) ( iω+ ω ) H ω H ωh d d + i d (1 + ω) (1 + ω) (1 + ω) ωh ωh hus G d G d (1 + ω ) (1 + ω ) 89 Shw ha he viscsiy μ f a linea Maxwell fluid define by φ ( ) is elaed he elaxain funcin φ and he memy funcin f ( s) by he elain φ( s) ds sf ( s) ds μ S D d 8-5 Cpyigh 1 Elsevie Inc
6 S φ D d φ s D s ds φ s D s ds Ans s s F simple sheaing flw v 1 x v v D1 s ha S 1 φ( s ) ds μ S 1 / φ( s ) ds s Nw he memy funcin s elaxain funcin φ ( s) by he elain dφ ( s) / ds f( s) hus dφ() s μ φ( s) ds sφ( s) s ds sf ( s) ds ds f s is elaed he 81 Shw ha he elaxain funcin f he Jeffey mdel [Eq (87)] wih a is given by [ne: Refeence Eq(87) is missing in he pblem saemen in he ex] S1 b b1 a / b 1 1 φ() 1 e + δ() δ() Diac Funcin γ a1 ba1 b Ans Le he shea sain γ 1 be given by γ1 γ H () hen D1 dγ1 / d γδ whee δ () is Diac funcin Fm he cnsiuive equain we have S1 γ γ δ S1 1 γ b b1 δ S1 + a1 b δ + b1 + S1 δ + a1 a1 a1 a / 1 a / b 1 b1 δ ( S1e ) e γ δ + a1 a1 S1 a / b 1 a / b 1 1 a / dδ () e e δ d e 1 d γ a + 1 a 1 d b b1 a / b a / b 1 b1 a / b e δ() δ() e d + e δ() a 1 a 1 a 1 a1 a1 a1 a1 hus he elaxain funcin is: S1 b b () / a b1 b b 1 () / a b 1 φ 1 e + δ 1 e + δ () γ a1 ab 1 a1 a1 ab 1 b v1 v v x1 v Obain (a) he paicle pahline equains using he cuen ime as he efeence ime (b) he elaive igh Cauchy- Geen defmain ens and (c) he Rivlin-Eicsen enss using he equain C I+ τ - A1+ τ - A / + (d) he Rivlin-Eicsen ens A using he ecusive 811 Given he fllwing velciy field: equain [ ] [ D / D] + [ ][ ] + [ ] [ ] A A1 A1 v v A 1 ec Ans (a) Le x xi e ibe he psiin a ime τ f he paicle which is a x xieia ime hen x x x x x τ gives he pahline equain hus i i 1 dx1 dx dx v1 (i) v v( x1 ) (ii) (iii) dτ dτ dτ 8-6 Cpyigh 1 Elsevie Inc
7 wih he iniial cndiins: xi xi ( x1 x x ) Eq (i) gives x1 f ( x1 x x) x1 dx gives x g( x x x ) x Eq (ii) becmes v( x ) x v( x ) τ h( x x x ) Eq (iii) dτ x ' v x1 + h x1 x x h x1 x x x v x1 x x + v( x1)( τ ) hus x1 x1 x x + v( x1)( τ ) x x 1 1 (b) [ F] [ x ] ( dv / dx1)( τ ) 1 ( τ ) 1 dv / dx ( τ ) 1 1+ ( τ ) ( τ ) [ C] [ F] [ F] 1 ( τ ) 1 ( τ ) ( τ ) 1 + ( τ ) + 1 dv (c) [ A1] [ A ] dx1 DA1 (d) [ A] + [ 1][ ] + [ ] [ 1] D A v v A whee [ A 1] hus DA ( 1) 1 A1 DA1 A1 A + [ 1][ ] + v + D A v D x [ A1][ v] [ v] [ A 1] hus [ A] [ A1][ v] + [ v] [ A 1] 81 Given he fllwing velciy field: v 1 x 1 v x v Obain (a) he paicle pahline equains using he cuen ime as he efeence ime (b) he elaive igh Cauchy- Geen defmain ens and (c) he Rivlin-Eicsen enss using he equain C I+ τ - A1+ τ - A / + (d) he Rivlin-Eicsen ens A and A using he ecusive equain [ ] [ D / D] + [ ][ ] + [ ] [ ] A A1 A1 v v A 1 ec 8-7 Cpyigh 1 Elsevie Inc
8 Ans (a) (a) Le x hen x x ( x x x τ ) i i x ie ibe he psiin a ime τ f he paicle which is a i i gives he pahline equain hus 1 dx1 dx dx v1 x1 (i) v x (ii) (iii) dτ dτ dτ wih he iniial cndiins: xi xi ( x1 x x ) Nw dx1 x ' 1 ln x1 τ + g ( x1 x x) g ( x1 x x) ln x1+ dτ ln ln ln ln ( τ x τ + x + x x x x e ) ( τ ) dx Similaly ( τ ) dτ hus ( τ) ( τ x xe x x e ) x x x x xe and x f ( x1 x x) x 1 1 ( τ) ( e τ e ) ( τ) ( τ F ) x e [ C] [ F] [ F ] e 1 1 (b) [ ] [ ] x x e a ime m Since ( τ ) 4 8 e 1m ( τ ) + ( τ ) m ( τ ) + heefe! 4 8 ( τ ) ( τ ) [ C ] [] I + ( τ ) ! (d) wih v 1 x 1 v x v [ v] [ 1] A DA ( 1) 1 A1 DA1 A1 A + [ 1][ ] + v + D A v D x (c) [ A ] [ A ] [ A ] [ A ] [ A ][ v] + [ v] [ A ] Nex 8-8 Cpyigh 1 Elsevie Inc
9 4 4 [ A ][ v ] hus [ A] [ ] + [ A][ v] + [ v] [ A ] 8 81 Given he fllwing velciy field: v 1 x 1 v x v x Obain (a) he paicle pahline equains using he cuen ime as he efeence ime (b) he elaive igh Cauchy-Geen defmain ens and (c) he Rivlin-Eicsen enss using he equain C I+ τ - A1+ τ - A / + (d) he Rivlin-Eicsen ens A and A using he ecusive equain [ ] [ D / D] + [ ][ ] + [ ] [ ] A A1 A1 v v A 1 ec Ans (a) Le x xi e ibe he psiin a ime τ f he paicle which is a x xieia ime hen x x x x τ gives he pahline equain hus i 1 dx1 dx dx v1 x1 (i) v x (ii) x (iii) dτ dτ dτ wih he iniial cndiins: xi xi ( x1 x x ) Nw dx1 x1 ln x1 τ + g ( x1 x x) g ( x1 x x) lnx1 dτ ln ln ln ln ( x τ x x x x xe τ + ) ( τ ) dx Similaly ( τ x ) x xe and ( τ x ) xe hus dτ ( x ) 1 xe τ 1 x xe τ x xe τ (b) ( τ) ( e τ e ) [ ] ' τ τ F x e [ C] [ F] [ F ] e ( τ) 4 ( τ e e ) Since ( τ ) 4 8 e 1+ ( τ ) + ( τ ) + ( τ ) +! 4( τ ) e 14 ( τ ) + ( τ ) ( τ ) +! C I heefe [ ] [] 8-9 Cpyigh 1 Elsevie Inc
10 4 8 ( τ ) ( τ ) + ( τ ) ! (c) [ A1] [ A] 4 [ A ] (d) wih v 1 x 1 v x v x [ v] [ 1] A 4 DA ( 1) 1 A1 DA1 A1 A + [ 1][ ] + v + D A v D x [ A ] [ A ][ v] + [ v] [ A ] Nex 4 4 [ A ][ v ] hus [ A] [ ] + [ A][ v] + [ v] [ A ] 8 Ec Given he fllwing velciy field: v 1 x v x 1 v Obain (a) he paicle pahline equains using he cuen ime as he efeence ime (b) he elaive igh Cauchy- Geen defmain ens and (c) he Rivlin-Eicsen enss using he equain C I+ τ - A1+ τ - A / + (d) he Rivlin-Eicsen ens A and A using he ecusive equain [ ] [ D / D] + [ ][ ] + [ ] [ ] A A1 A1 v v A 1 ec Ans (a) Le x xi e ibe he psiin a ime τ f he paicle which is a x xieia ime hen x x x x x τ gives he pahline equain hus i i 1 dx1 dx dx v1 x (i) v x1 (ii) (iii) dτ dτ dτ 8-1 Cpyigh 1 Elsevie Inc
11 wih he iniial cndiins: x x ( x x x ) i i 1 Nw dx1 d x1 dx d x1 (i) x x 1 x 1 dτ dτ dτ dτ x1 Asinh τ + Bcsh τ x1 Asinh + Bcsh (iv) 1 dx1 (ii) x Acsh τ + Bsinh τ x Acsh + Bsinh (v) dτ (iv) and (v) gives A x1sinh + xcsh B x1csh xsinh x x csh csh τ sinh sinh τ + x csh sinh τ sinh csh τ ( csh sinh τ sinh csh τ) ( csh csh τ sinh sinh τ) 1 1 x x1 + x ha is x1 x1csh ( τ ) + xsinh ( τ ) x x1sinh ( τ ) + xcsh ( τ ) x x (b) Since [ F ] [ x ] ( τ ) ( τ ) ( τ ) ( τ ) csh sinh sinh csh 1 csh x+ sinh x csh xsinh x [ C ] [ F ] [ F ] csh xsinh x sinh x+ csh x x ( τ ) 1 4 x 5 x cshx 1+ + O( x ) sinhx x+ + O( x ) x 5 csh x 1+ x + O( x ) sinh x x + O( x ) sinh xcsh x x+ + O( x ) 4 1+ x + x+ x + 4 [ C ] x + x + 1+ x + [] I + ( τ ) ( τ ) ( τ ) hus (c) [ A ] [ A ] [ A ] 4 8 ec 8-11 Cpyigh 1 Elsevie Inc
12 (d) wih v 1 x v x 1 v [ v] [ 1] A DA ( 1) 1 A1 DA1 A1 A + [ 1][ ] + v + D A v D x [ A ] [ A ][ v] + [ v] [ A ] [ A ][ v] [ A ] Nex [ A ][ v ] hus [ A] [ ] + [ A][ v] + [ v] [ A ] 8 θ z bain he secnd Rivlin-Eicsen enss A N N using he ecusive fmula dv Ans [ v] [ A ] [ ] [ ] 1 v + v d 815 Given he velciy field in cylindical cdinaes: v v v v Since ( A 1) cnsan independen f ime and space heefe DA A A v [ ] D Cpyigh 1 Elsevie Inc
13 [ ] ( ) + ( ) A A1 v v A1 + [ A ] A v + v A + hus A N N Using he equains given in Appendix 81 f cylindical cdinaes veify ha he θ cmpnen f he hid de ens is given by: 1 θ + θ ( ) θ θ Ans Fm he equains ( ) hm + qjγ qmi + iqγqmj n sum n m sum n q m xm and h 1 h h 1; Γ 1 Γ 1 all he Γ θ z θθ θθ we have ( ) h q q q q θ + Γ θ + Γ θ + θ Γ θθ + θ θγθθ hus θ θ 1 θ + θ ( ) + ( 1) ( 1 ) ( ) θ θ + θ θ θ θ 817 Using he equains given in Appendix 81 f cylindical cdinaes veify ha he θθ cmpnen f he hid de ens is given by: 1 θ θθ ( ) + θθ θ Ans Fm he equains ( ) hm + qjγ qmi + iqγqmj n sum n m sum n q m xm and h 1 h h 1; Γ 1 Γ 1 all he Γ we have θ z θθ θθ 8-1 Cpyigh 1 Elsevie Inc
14 θ θ ( ) h + Γ + Γ ( ) h + Γ + Γ θθ θ θθ θ θ 1 θ θθ ( ) + ( 1) ( 1 ) ( ) θθ θθ + + θ θθ θ θ qθ qθ q qθθ θ θθ θθ θθ 818 Using he equains given in Appendix 81 f spheical cdinaes veify ha he φ cmpnen f he hid de ens is given by: ( φ + φ ) 1 ( ) φ sinθ φ Ans Fm he equains ( ) hm + qjγ qmi + iqγqmj n sum n m sum n q m xm and h 1 hθ hφ sin θ; Γ θθ 1 Γ φφ sin θ Γ φφ sin θ Γ φφθ cs θ Γ θθ 1 Γ θφφ cs θ all he Γ we have ( ) h + Γ + Γ ( ) h + φ φ φ φ Γ + Γ ( ) ( sin θ) + ( sin ) ( sin ) φ φ θ + φ θ φ 1 φ + φ ( ) φ sinθ φ φ q qφ q qφ φ φ φφ φ φφ 819 Using he equains given in Appendix 81 f spheical cdinaes veify ha he φφφ cmpnen f he hid de ens is given by: ( φ + φ) ( θφ + φθ )c 1 φφ θ + + sinθ φ Ans Fm he equains ( ) hm + qjγ qmi + iqγqmj n sum n m sum n q m xm h 1 hθ hφ sin θ; Γ θθ 1 Γ φφ sin θ Γ sin θ Γ cs θ Γ 1 Γ cs θ all he Γ φφ φφθ θθ θφφ we have 8-14 Cpyigh 1 Elsevie Inc
15 φφ ( ) hφ + qφγ qφφ + φqγ φφφ qφφ φ φφ ( ) hφ + φ Γ φφ + θφ Γ θφφ + φ Γ φφ + φθ Γ φφφ θφφ φ φφ ( ) hφ + ( φ + φ) Γ φφ + ( θφ + φθ ) Γ φφφ θφφ φ φφ + ( φ + φ)( sinθ) + ( θφ + φθ ) csθ φ 1 φφ ( φ + φ) ( θφ + φθ ) cθ ( ) + + φφφ sin θ φ v vθ v vz bain (a) he fis Rivlin-Eicsen ens A 1 (b) A 1 (c) he secnd Rivlin-Eicsen enss A using he ecusive fmula v 1 v v v v () θ θ z v θ 1 vθ v θ dv Ans [ v] v + θ z d v 1 z vz v z θ z dv v() [ A1] [ v] + [ v] d DA1 A 1 ( 1) v D + A ( A1) v ( 1) v ( 1) v θ θ A θθ θ A zθ θ ( A1) v ( 1) v ( 1) v ( 1) v A θ θ θ A θθθ θ A θ zθ θ ( A1) v z θ ( A1) v z θ ( A1) v θ θθ zzθ θ A can be bained fm Appendix 81 as: 8 Given he velciy field in cylindical cdinaes: he cmpnens f he hid de ens 1 1 A A + A 1 Aθ A Aθθ 1 θ θ 1 + θθ θ 1 Az Aθ z A 1 zθ θ 1 Aθ A Aθθ 1 Aθ z Az A 1 + ( A ) θθ 1 ( A ) θ θθθ 1 + θzθ θ θ θ ( A ) ( A ) 8-15 Cpyigh 1 Elsevie Inc
16 1 Az Azθ 1 Azθ Az 1 Azz ( A 1) zθ ( A 1) + θ zθθ ( A 1) θ zzθ θ / v/ DA1 hus v / θ v/ D v/ dv / d [ A1][ v] dv / d v / [ v] [ A ] 1 dv / d dv / d v ()/ v/ ( ) dv/ d v/ DA1 A [ 1][ ] [ ] [ 1] D + A v + v A D N 81 Deive Eq (811) ie N+ 1 A A N N D + A v + v A Ans We had {see Eq (8117)} N ( N+ 1 D D ) ( Ddx DAN Ddx ds dx A N Ndx ds N 1 ) ANdx+ dx dx+ dx A + N ha is D D D D D N + 1 DAN ( ) N N ( ) D ds v dx A dx+ dx dx+ dx A v dx N + 1 D D DAN dx ( v) ANdx+ dx AN ( v) dx+ dx dx D DAN dx ( v) A N +AN ( v ) + d d N+ 1d D x x A x D N hus N+ 1 A A N N D + A v + v A 8 Le S D/ D+ WW whee is an bjecive ens and W is he spin ens shw ha S is bjecive ie () () S Q SQ Ans Since is bjecive heefe () () W dq/ d Q () + Q() WQ () heefe Q Q and fm Eq (811) 8-16 Cpyigh 1 Elsevie Inc
17 S D + W -W D dq D dq dq Q + Q Q + Q + QQ Q + QQ QWQ d D d d dq Q QQ QWQ Q () Q () d dq dq Nw Q() Q () I Q () Q () heefe he abve equain becmes d d dq D dq dq S Q + Q Q + Q Q + QWQ d D d d dq () Q d QWQ ha is D S Q() + W W () () () D Q Q SQ 8 Obain he viscsiy funcin and he w nmal sess funcin f he nnlinea 1 viscelasic fluid defined by S f () s s I C ds Ans F v 1 x v v we have [see Secin 89 Eq(891)] 1 ( τ ) 1+ ( τ ) ( τ ) [ ] 1 C τ τ τ + 1 C ( τ) ( τ ) s s s s 1 ( s) 1 C s 1 hus IC ( s) s 1 S S sf s ds sf s ds 1 μ S11 S s f( s) ds σ S S S s f s ds S S σ 84 Deive he fllwing ansfmain laws [Eqs(818) and Eq (811)] unde a change f fame ( τ) ( τ) and ( τ) V Q VQ R Q R Q 8-17 Cpyigh 1 Elsevie Inc
18 Ans Since FVR and F VR heefe fm ( τ) ( τ) ( τ) V R Q( τ) VR Q Q( τ) VQ ( τ) Q( τ) RQ whee ( τ ) ( τ ) symmey ens and ( τ ) F Q F Q we ge Q VQ is a Q R Q is an hgnal ens heefe he uniqueness f he pla decmpsiin leads V Q( τ) VQ ( τ) and R Q( τ) RQ L DJ τ 85 Fm ( DF τ and v shw ha Dτ Dτ τ τ ( + D+D [ne mispin in he pblem in ex] Ans Fm JL ( τ ) F ( τ) ( τ) F ( τ) we have D J L( τ ) D ( τ) D ( τ) D ( τ) F ( τ) F( τ) + F ( τ) F( τ) + F ( τ) ( τ) F Dτ Dτ Dτ Dτ DJL( τ ) D hus ( v) + + () v [Ne () () F F I] Dτ D τ Nw vd+w heefe DJL( τ ) D D + D + W + D + W + D + D + W + W Dτ D D τ D + D + D + ( W W ) + D + D D 86 Cnside 1 J τ F ( τ) ( τ) F 1 ( τ) Shw ha (a) J ( τ) U D U / Dτ τ and (b) D D U ( τ) / Dτ τ Dτ J v v D+D is bjecive Ans (a) Given J ( τ ) F ( τ) ( τ)( F ) ( τ) and ( τ ) ( τ) ( τ)( ) ( τ) U J F F U In a change f fame (see Secin 81 Eq(816) ( τ) ( τ) ( τ) F Q F Q s ha ( τ) ( τ) ( τ) and ( ) ( τ) ( τ)( ) ( τ) F Q F Q F Q F Q Als () Q() () Q () hus 1 1 ( τ) ( τ) ( τ) τ τ τ ( τ) ( τ) JU Q F Q Q Q Q F Q 1 1 () ( τ) τ ( τ) Q F F Q ha is J ( τ) Q J ( τ) Q and U U ( U ) () N N N N D JU τ / Dτ Q D J τ / Dτ Q hus 8-18 Cpyigh 1 Elsevie Inc
19 N U τ D J τ U () () N D J Q Q N N Dτ Dτ τ 1 1 (b) + [ ] + () τ DJU τ / Dτ DF / Dτ D/ Dτ D / Dτ τ τ τ F F τ F τ I DF / Dτ F τ + F τ DF / Dτ DF ( τ) / Dτ F [ DF / Dτ] F () [ DF / Dτ] ( ) ( τ ) τ v F ( v) hus D D D U ( τ) / Dτ τ D J v v D D W D+W ha is he uppe cnveced deivaive f can be wien: ˆ DJU ( τ ) D + W W ( D + D) ( D + D ) Dτ D τ Nw [ ] τ τ τ τ 87 Given he velciy field f a plane Cuee flw: v 1 v x 1 (a) F a Newnian fluid find he sess field [ ] and he c-ainal sess ae (b) Cnside a change f fame (change f bseve) descibed by: x 1 csω sinω x1 csω sinω [ ] x sinω csω x Q sinω csω Find and v v D W (c) Find he c-ainal sess ae f he saed fame (d) Veify ha he w sess aes ae elaed by he bjecive ensial elain Ans / / (a) [ v ] [ ] [ ] D / W / hus sess ens is [ p / p μ ] + μ p / μ p p μ / / p μ μ [ W] [ W ] μ p / / μ p μ D μ μ C-ainal sess ae is: D + μ μ (b) Fm Eq (5561) f Chape 5 we have [ v( x) ] [ Qv ] + ( d / d) [ ] ( d / d) Q x Qv + Q Q x hus v 1 csω sinω sinω csω csω sinω x 1 ω sin cs v v ω ω + csω sinω sinω csω Since x 8-19 Cpyigh 1 Elsevie Inc
20 x1 csω sinω x1 x 1 csωx1 sinωx v ( csωx1 sinωx) x + + sinω csω x heefe v 1 vsin 1 x csωsinωx 1 1 sin ωx ω + x ω ω v v csω x ( cs ωx1 + sinω csωx) x1 fm which we ge ( sin ω) / sin ω 1 ( v ) + ω cs ω ( sin ω) / 1 ( sin ω) / ( cs ω) / [ D ] [ ( cs ω) / ( sin ω) / W 1/ 1 ] + ω 1/ 1 (c) F he Newnian fluid he sess field in he saed-fame is: pμ( sin ω) μcs ω [ ] μ( cs ω) p+ μ( sin ω) whee he indeeminae pessue p is ime independen hus D ( cs ω) ( sin ω) D μω and ( sin ω) ( cs ω) μcs ω p+ μsin ω μcs ω p+ μsin ω W + ω p+ μ( sin ω) μcs ω p + μsin ω μcsω μcs ω pμsin ω μcs ω pμsin ω W + ω p μsin ω μcsω pμsin ω μcs ω hus μcs ω μsin ω cs ω sin ω W W + μω μsin ω μcs ω sin ω csω cs ω sin ω hus D / D+ W W μ sin ω csω (d) [ Q] [ Q ] csω sinω μ csω sinω csω sin ω μ sinω csω μ sinω csω sin ω csω hus we have [ Q] [ Q ] 88 Given he velciy field: v 1 x 1 v x v Obain (a) he sess field f a secnd-de fluid (b) he c-ainal deivaive f he sess ens Cpyigh 1 Elsevie Inc
21 v D W Ans (a) [ ] [ ] [ ] [ ] 4 4 [ A ] [ D] [ A ] 1 1 [ ] D / D+ ( ) + ( ) ( ) + ( ) A A1 A1 v v A1 A1 v v A he secnd-de fluid is defined by Eq(8186): pi+ μ A + μ A + μ A [ ] [ I] p + μ 1 + μ 4 + μ 4 11 μ1 4( μ μ) μ1 4( μ μ) p + + p+ + + p bain he pessue p we fis calculae he acceleain: x1 x 1 [ a] [ v/ ] + [ v][ v ] x x Equains f min ρai hen give x ρ x1 ρ x 1 ρ ( 1 )/ j p p p hus x x x p x + x +C (b) he c-ainal deivaive f : D/ D+ W-W Since W 1 D p p v1 v v1 v 1 D + x1 x x1 x p p x1 x 1 ρ x1 x 1 ρ v v1 x1 x + I 1 1 [] 8-1 Cpyigh 1 Elsevie Inc
22 ( 89 Shw ha he Lwe Cnveced deivaive f A 1 is A ie A1 A Ans Fm Eq(819) ( A A + A D+ DA DA / D+ A W WA + A D+ DA DA1 D A1 W D D W A1 DA1 D A1 v v A 1 A / / he Reine-Rivlin fluid is defined by he cnsiuive equain: φ pi+s S φ1 I I D+ I I D whee Ii ae he scala invaians f D Obain he sess cmpnens f his fluid in a simple sheaing flw Ans In a simple sheaing flw v 1 x v v / /4 [ ] / D D /4 I I 4 / /4 [ ] p[ I ] + φ1( /4 ) / + φ( /4) /4 81 he expnenial f a ens A is defined as: exp [ ] ens is exp [ A ] als bjecive? Ans Yes Because () () () () () () () () N N ( A ) Q() A Q () A Q AQ A Q AQ Q AQ Q A Q N 1 n A I+ A If A is an bjecive n! ha is ( A ) N is bjecive f all N As a cnsequence exp [ A] is bjecive 8 Why is i ha he fllwing cnsiuive equain is n accepable: pi+s S α v whee v is velciy and α is a cnsan Ans Because v is n bjecive 1 8- Cpyigh 1 Elsevie Inc
23 8 Le da and da dene he diffeenial aea vecs a ime τ and ime especively F an incmpessible fluid shw ha N N N 1 N D da / Dτ da D C / Dτ da da MNdA τ τ whee da is he magniude f da and he enss MN ae nwn as he Whie-Mezne enss - Ans Fm Eq (71) we have [ne hee da is he efeence aea and da is he aea a he 1 unning ime τ ] d ( de ) d a F F da F an incmpessible fluid ( de F ) 1 s ha a F da ha is 1 A C 1 da da F da F da da F F da da F F da da d da hus N N 1 N 1 D da D C D C d d d Nd whee N A N A A M A M N N Dτ Dτ Dτ τ τ τ 84 (a) Veify ha Oldyd's lwe cnveced deivaives f he ideniy ens I ae he Rivlin-Eicsen ens A N (b) Veify ha Oldyd uppe deivaives f he ideniy ens ae he negaive Whie-Mezne enss [see Pb 8 f he definiin f Whie-Mezne ens] Ans (a) he Nh lwe cnveced deivaive f is given by N N D JL / Dτ whee JL( τ) F ( τ) ( τ) F ( τ ) F I τ ( τ ) N N D J L D C JL τ F ( τ) F( τ) C ( τ) hus N A N Dτ Dτ τ τ (b) he Nh uppe cnveced deivaive f is given by N N 1 1 D JU / Dτ whee JU ( τ) F ( τ) ( τ)( F ) ( τ ) F I τ N N D J U D C JU ( τ ) F ( τ)( F ) ( τ) C ( τ) hus N M N N Dτ Dτ τ τ N 1 ( τ ) ( 85 Obain he equain D/ D+ v+ ( v) whee ( is he lwe cnveced deivaive f Ans By definiin he lwe cnveced deivaive is DJ L ( τ) / Dτ whee τ JL τ F ( τ) ( τ) F ( τ) hus D L( τ) / D τ D / D τ J F ( ) F ( ) τ τ + F ()[ τ] F () + F () () F Nw F F ( F ) ( v ) [see Eq(81)] and D / D D / D τ τ τ D τ / Dτ D / D D / D τ heefe F I 8- Cpyigh 1 Elsevie Inc
24 ( τ ) ( DJL D + v+ ( v) Dτ D τ 86 Cnside he fllwing cnsiuive equain: ( D / D) whee ( D / D) + S+ S μd S S α DS+SD and S is c-ainal deivaive f S Obain he shea sess funcin and he w nmal sess funcins f his fluid Ans Wih v 1 x v v he ae f defmain ens and spin ens ae: / / [ ] / [ ] / S D W Since he flw is seady he c-ainal deivaive is f symmeic S: + [ ] [ ] S SW WS SW SW Nw S1 S11 S1 S S SW S S 1 S11 S1 S 1 SW S S1 S1 S11 S S S S S 11 S S 1 1 [ ] [ ] S1 S11 + S S SD + DS S S 11 S S S S1 S S1 hus D S/ D S + α ( DS+SD ) gives ( α 1) ( 1+ α) + ( α 1) ( α 1) D S ( 1+ α) + ( α 1) ( 1+ α) ( 1+ α) D ( α 1) S ( 1+ α) S S1 S11 S S S11 S S1 S1 1 D S heefe S+ μd D S11 + ( α 1) S1 (i) S1 + ( 1 + α) S11 + ( α 1 ) S μ (ii) S1 + ( α 1) S (iii) S + ( 1+ α) S1 (iv) S + ( 1+ α ) S1 (v) S (vi) Nw (iii) (v) and (vi) give S1 S S S 1 α S Eq(iv) gives ( 1 α) ( α )( ) S + S hus wih 1 A 1+ 1 we have Eq (i) gives ( ) 11 1 S1 μ / A( ) S11 μ 1 α / A( ) S μ 1 + α / A( ) he shea sess funcin is S1 μ / A( ) he nmal sess funcins ae: 1 11 σ S S μ / A( ) σ S S μ 1 + α / A( ) 8-4 Cpyigh 1 Elsevie Inc
25 87 Obain he appaen viscsiy and he nmal sess funcins f he Oldyd -cnsan fluid [see (C) f Secin 8] Ans F he simple sheaing flw / / [ D] / [ ] / W S1 S11 S S S [ ] + [ SW] [ WS ] ( / ) S11 S S1 S 1 S S1 S1 S11 + S S [ SD ] + [ DS ] ( / ) S11 S S1 S + 1 S S1 4S1 S S SS ˆ ( SD+DS ) ( / ) S S / 1 D [ ] + [ DW] [ WD ] / DD 1 4 μ μ ˆ DD D ( ˆ μ D+ D ) μ S11 1S1 S1 1S S1 1S S+ ˆ 1S S1 1S S S S1 1S S S S+ Sˆ μ D+ Dˆ 1 ( ) S11 1S1 S1 1S S1 1S μ μ S S S S μ 1 1 S1 1S S S hus S S S S S μ S S μ s ha we have μ 11 μ ( 1 ) all he S S S he appaen viscsiy is η S1 / μ σ1 11 μ 1 σ1 8-5 Cpyigh 1 Elsevie Inc
26 88 Obain he appaen viscsiy and he nmal sess funcins f he Oldyd 4-cnsan fluid [see (D) f Secin 8] Ans F he simple sheaing flw / / S1 S11 S S [ ] / [ ] / D W S S11 S S1 S 1 S S1 4S1 S S SS ˆ ( SD+DS ) ( / ) S S / 1 D [ ] + [ DW] [ WD ] / DD ˆ DD D 1 1 / μ ( S)[ D ] μ ( S11 + S + S ) / 1 ( ) ( ˆ ) S+ Sˆ + μ S D μ D+ D S S S S + μ S + S + S / S S S1 1S + μ( S11 + S + S )/ S S S1 1S S S μ μ μ hus S S S S1 S11 1S1 μ S1 + μs11 / μ Fm which we ge wih B( ) (1 + μ ) 1 ( ) ( + ) 11 μ 1 / 1 μ 1 μ / S B S B hus he appaen viscsiy is: η μ μ S / (1 + )/ B( ) ( 1 )/ B( ) Nmal sess funcins ae: σ μ σ 8-6 Cpyigh 1 Elsevie Inc
27 1 1 { n } 89 Given [ Q] 1 and [ N] 1 and i 1 and { n } A N+N A N N (a) Veify ha QA Q A and QA Q A (b) Fm i 1 1 pi+f( A1 A) and ( Qf A1 A Q f QA1Q QAQ ) shw ha Q( ) Q ( ) and (c) Fm he esuls f pa (b) shw ha he viscmeic funcins have he ppeies: S( ) S ( ) σ1( ) σ1( ) σ( ) σ( ) 1 Ans (a) [ A1] ( N+N ) and 1 A 1 1 QA1Q 1 1 [ A 1] QAQ 1 1 [ A ] 1 1 (b) Q( ) Q Q pi+f( A1 A) Q pi+qf( A1 A) Q pi+f( QAQ 1 QAQ ) pi+f( A1( ) A( ) ) A A and A A hus Nw 1 1 Q( ) Q pi + f ( A1( ) A( ) ) and ( ) p 1( ) ( ) ha is Q( ) Q ( ) and Q( ) Q ( ) (c) [ ] Q Q I + f A A Q Q ( ) ( ) 11 ( ) 11 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) S( ) S( ) Q Q hus σ1 σ1 σ σ [Ne in viscmeic flw 1 ] 84 F he velciy field given in example 81 ie v vθ vz v he sess cmpnens in ems f he shea sess funcin S( ) and he nmal sess funcins σ ( ) and σ ( ) whee dv/ d (b) bain he fllwing velciy disibuin f he 1 (a) bain 8-7 Cpyigh 1 Elsevie Inc
28 Piseuille flw unde a pessue gadien f ( f ): v γ ( f /) d whee γ is he invese shea sess funcin and (c)bain he elain γ π Rf / 1/( R f ) f Q / f Ans (a) In example 81 we see ha he velciy field v vθ vz v descibes a viscmeic flw wih he nnze Rivlin-Eicsen enss given by [ A1] [ A ] n i whee n1 ez n e n e θ and dv / d (see Example 81 bu ne he diffeences in he de f bases) hus he sess cmpnens wih espec he basis { n i } ae given by (See secin 8): Sz τ( ) Szz S σ1( ) S Sθθ σ( ) Szθ Sθ (b) Wih S depending nly n he equains f min becme: S S Sθθ p p 1 p + ( i) (ii) ( Sz ) ( iii) θ z p p p Eq (i) gives z Eq (ii) gives θ z and Eq (iii) gives z z hus p / z a cnsan f Eq (iii) becmes 1 f C ( Sz ) f ( Sz ) f Sz + Since S z mus be finie a hus C and S f / Nw S τ ( ) whee τ ( ) is he shea sess funcin and dv/ d z z hus τ ( ) f / Inveing his equain we have τ ( f /) γ ( f /) n i R 1 Since τ ( ) is an dd funcin f heefe γ is als an dd funcin f s ha γ f / dv/ d γ f / dv γ f / d R R hus v( R) v γ ( f /) d Since v( R ) heefe γ ( /) R (c) he vlume dischage is given by Q v π d heefe v f d R R R dv R dv R Q v d v d d f d π π π π γ ( /) d d R hus Q/ π γ ( f /) d Le f / s d ds / f and 4 s / f hen R R f / R f / s s Q / π γ f / d 8 s / f γ sds f Q / π 8 sγ sds Diffeeniaing he las equain wih espec f we bain 1 f Q Rf Rf Rf R Rf Rf Rf 8 γ 8 γ R f γ π f f Rf 1 ( f Q) hus γ π R f f 8-8 Cpyigh 1 Elsevie Inc
29 8-9 Cpyigh 1 Elsevie Inc
11. HAFAT İş-Enerji Power of a force: Power in the ability of a force to do work
 MÜHENDİSLİK MEKNİĞİ. HFT İş-Eneji Pwe f a fce: Pwe in he abiliy f a fce d wk F: The fce applied n paicle Q P = F v = Fv cs( θ ) F Q v θ Pah f Q v: The velciy f Q ÖRNEK: İŞ-ENERJİ ω µ k v Calculae he pwe
MÜHENDİSLİK MEKNİĞİ. HFT İş-Eneji Pwe f a fce: Pwe in he abiliy f a fce d wk F: The fce applied n paicle Q P = F v = Fv cs( θ ) F Q v θ Pah f Q v: The velciy f Q ÖRNEK: İŞ-ENERJİ ω µ k v Calculae he pwe
10.7 Temperature-dependent Viscoelastic Materials
 Secin.7.7 Temperaure-dependen Viscelasic Maerials Many maerials, fr example plymeric maerials, have a respnse which is srngly emperaure-dependen. Temperaure effecs can be incrpraed in he hery discussed
Secin.7.7 Temperaure-dependen Viscelasic Maerials Many maerials, fr example plymeric maerials, have a respnse which is srngly emperaure-dependen. Temperaure effecs can be incrpraed in he hery discussed
MEAN GRAVITY ALONG PLUMBLINE. University of New Brunswick, Department of Geodesy and Geomatics Engineering, Fredericton, N.B.
 MEA GRAVITY ALG PLUMBLIE Beh-Anne Main 1, Chis MacPhee, Rbe Tenze 1, Pe Vaníek 1 and Macel Sans 1 1. Inducin 1 Univesiy f ew Bunswick, Depamen f Gedesy and Gemaics Engineeing, Fedeicn,.B., E3B 5A3, Canada
MEA GRAVITY ALG PLUMBLIE Beh-Anne Main 1, Chis MacPhee, Rbe Tenze 1, Pe Vaníek 1 and Macel Sans 1 1. Inducin 1 Univesiy f ew Bunswick, Depamen f Gedesy and Gemaics Engineeing, Fedeicn,.B., E3B 5A3, Canada
2. The units in which the rate of a chemical reaction in solution is measured are (could be); 4rate. sec L.sec
 Kineic Pblem Fm Ramnd F. X. Williams. Accding he equain, NO(g + B (g NOB(g In a ceain eacin miue he ae f fmain f NOB(g was fund be 4.50 0-4 ml L - s -. Wha is he ae f cnsumpin f B (g, als in ml L - s -?
Kineic Pblem Fm Ramnd F. X. Williams. Accding he equain, NO(g + B (g NOB(g In a ceain eacin miue he ae f fmain f NOB(g was fund be 4.50 0-4 ml L - s -. Wha is he ae f cnsumpin f B (g, als in ml L - s -?
( t) Steady Shear Flow Material Functions. Material function definitions. How do we predict material functions?
 Rle f aeial Funins in Rhelgial Analysis Rle f aeial Funins in Rhelgial Analysis QUALIY CONROL QUALIAIVE ANALYSIS QUALIY CONROL QUALIAIVE ANALYSIS mpae wih he in-huse daa n qualiaive basis unknwn maeial
Rle f aeial Funins in Rhelgial Analysis Rle f aeial Funins in Rhelgial Analysis QUALIY CONROL QUALIAIVE ANALYSIS QUALIY CONROL QUALIAIVE ANALYSIS mpae wih he in-huse daa n qualiaive basis unknwn maeial
MEEN 617 Handout #11 MODAL ANALYSIS OF MDOF Systems with VISCOUS DAMPING
 MEEN 67 Handou # MODAL ANALYSIS OF MDOF Sysems wih VISCOS DAMPING ^ Symmeic Moion of a n-dof linea sysem is descibed by he second ode diffeenial equaions M+C+K=F whee () and F () ae n ows vecos of displacemens
MEEN 67 Handou # MODAL ANALYSIS OF MDOF Sysems wih VISCOS DAMPING ^ Symmeic Moion of a n-dof linea sysem is descibed by he second ode diffeenial equaions M+C+K=F whee () and F () ae n ows vecos of displacemens
Maxwell Equations. Dr. Ray Kwok sjsu
 Maxwell quains. Ray Kwk sjsu eeence: lecmagneic Fields and Waves, Lain & Csn (Feeman) Inducin lecdynamics,.. Giihs (Penice Hall) Fundamenals ngineeing lecmagneics,.k. Cheng (Addisn Wesley) Maxwell quains.
Maxwell quains. Ray Kwk sjsu eeence: lecmagneic Fields and Waves, Lain & Csn (Feeman) Inducin lecdynamics,.. Giihs (Penice Hall) Fundamenals ngineeing lecmagneics,.k. Cheng (Addisn Wesley) Maxwell quains.
Lecture 3. Electrostatics
 Lecue lecsics In his lecue yu will len: Thee wys slve pblems in elecsics: ) Applicin f he Supepsiin Pinciple (SP) b) Applicin f Guss Lw in Inegl Fm (GLIF) c) Applicin f Guss Lw in Diffeenil Fm (GLDF) C
Lecue lecsics In his lecue yu will len: Thee wys slve pblems in elecsics: ) Applicin f he Supepsiin Pinciple (SP) b) Applicin f Guss Lw in Inegl Fm (GLIF) c) Applicin f Guss Lw in Diffeenil Fm (GLDF) C
Visco-elastic Layers
 Visc-elasic Layers Visc-elasic Sluins Sluins are bained by elasic viscelasic crrespndence principle by applying laplace ransfrm remve he ime variable Tw mehds f characerising viscelasic maerials: Mechanical
Visc-elasic Layers Visc-elasic Sluins Sluins are bained by elasic viscelasic crrespndence principle by applying laplace ransfrm remve he ime variable Tw mehds f characerising viscelasic maerials: Mechanical
Lecture 17: Kinetics of Phase Growth in a Two-component System:
 Lecue 17: Kineics of Phase Gowh in a Two-componen Sysem: descipion of diffusion flux acoss he α/ ineface Today s opics Majo asks of oday s Lecue: how o deive he diffusion flux of aoms. Once an incipien
Lecue 17: Kineics of Phase Gowh in a Two-componen Sysem: descipion of diffusion flux acoss he α/ ineface Today s opics Majo asks of oday s Lecue: how o deive he diffusion flux of aoms. Once an incipien
Brace-Gatarek-Musiela model
 Chaper 34 Brace-Gaarek-Musiela mdel 34. Review f HJM under risk-neural IP where f ( T Frward rae a ime fr brrwing a ime T df ( T ( T ( T d + ( T dw ( ( T The ineres rae is r( f (. The bnd prices saisfy
Chaper 34 Brace-Gaarek-Musiela mdel 34. Review f HJM under risk-neural IP where f ( T Frward rae a ime fr brrwing a ime T df ( T ( T ( T d + ( T dw ( ( T The ineres rae is r( f (. The bnd prices saisfy
Part 2 KINEMATICS Motion in One and Two Dimensions Projectile Motion Circular Motion Kinematics Problems
 Pa 2 KINEMATICS Min in One and Tw Dimensins Pjecile Min Cicula Min Kinemaics Pblems KINEMATICS The Descipin f Min Physics is much me han jus he descipin f min. Bu being able descibe he min f an bjec mahemaically
Pa 2 KINEMATICS Min in One and Tw Dimensins Pjecile Min Cicula Min Kinemaics Pblems KINEMATICS The Descipin f Min Physics is much me han jus he descipin f min. Bu being able descibe he min f an bjec mahemaically
CHAPTER 24 GAUSS LAW
 CHAPTR 4 GAUSS LAW LCTRIC FLUX lectic flux is a measue f the numbe f electic filed lines penetating sme suface in a diectin pependicula t that suface. Φ = A = A csθ with θ is the angle between the and
CHAPTR 4 GAUSS LAW LCTRIC FLUX lectic flux is a measue f the numbe f electic filed lines penetating sme suface in a diectin pependicula t that suface. Φ = A = A csθ with θ is the angle between the and
EN221 - Fall HW # 7 Solutions
 EN221 - Fall2008 - HW # 7 Soluions Pof. Vivek Shenoy 1.) Show ha he fomulae φ v ( φ + φ L)v (1) u v ( u + u L)v (2) can be pu ino he alenaive foms φ φ v v + φv na (3) u u v v + u(v n)a (4) (a) Using v
EN221 - Fall2008 - HW # 7 Soluions Pof. Vivek Shenoy 1.) Show ha he fomulae φ v ( φ + φ L)v (1) u v ( u + u L)v (2) can be pu ino he alenaive foms φ φ v v + φv na (3) u u v v + u(v n)a (4) (a) Using v
Kinematics Review Outline
 Kinemaics Review Ouline 1.1.0 Vecrs and Scalars 1.1 One Dimensinal Kinemaics Vecrs have magniude and direcin lacemen; velciy; accelerain sign indicaes direcin + is nrh; eas; up; he righ - is suh; wes;
Kinemaics Review Ouline 1.1.0 Vecrs and Scalars 1.1 One Dimensinal Kinemaics Vecrs have magniude and direcin lacemen; velciy; accelerain sign indicaes direcin + is nrh; eas; up; he righ - is suh; wes;
General Non-Arbitrage Model. I. Partial Differential Equation for Pricing A. Traded Underlying Security
 1 Geneal Non-Abiage Model I. Paial Diffeenial Equaion fo Picing A. aded Undelying Secuiy 1. Dynamics of he Asse Given by: a. ds = µ (S, )d + σ (S, )dz b. he asse can be eihe a sock, o a cuency, an index,
1 Geneal Non-Abiage Model I. Paial Diffeenial Equaion fo Picing A. aded Undelying Secuiy 1. Dynamics of he Asse Given by: a. ds = µ (S, )d + σ (S, )dz b. he asse can be eihe a sock, o a cuency, an index,
AP Physics 1 MC Practice Kinematics 1D
 AP Physics 1 MC Pracice Kinemaics 1D Quesins 1 3 relae w bjecs ha sar a x = 0 a = 0 and mve in ne dimensin independenly f ne anher. Graphs, f he velciy f each bjec versus ime are shwn belw Objec A Objec
AP Physics 1 MC Pracice Kinemaics 1D Quesins 1 3 relae w bjecs ha sar a x = 0 a = 0 and mve in ne dimensin independenly f ne anher. Graphs, f he velciy f each bjec versus ime are shwn belw Objec A Objec
The Components of Vector B. The Components of Vector B. Vector Components. Component Method of Vector Addition. Vector Components
 Upcming eens in PY05 Due ASAP: PY05 prees n WebCT. Submiing i ges yu pin ward yur 5-pin Lecure grade. Please ake i seriusly, bu wha cuns is wheher r n yu submi i, n wheher yu ge hings righ r wrng. Due
Upcming eens in PY05 Due ASAP: PY05 prees n WebCT. Submiing i ges yu pin ward yur 5-pin Lecure grade. Please ake i seriusly, bu wha cuns is wheher r n yu submi i, n wheher yu ge hings righ r wrng. Due
Differential Equations
 Mah 21 (Fall 29) Differenial Equaions Soluion #3 1. Find he paricular soluion of he following differenial equaion by variaion of parameer (a) y + y = csc (b) 2 y + y y = ln, > Soluion: (a) The corresponding
Mah 21 (Fall 29) Differenial Equaions Soluion #3 1. Find he paricular soluion of he following differenial equaion by variaion of parameer (a) y + y = csc (b) 2 y + y y = ln, > Soluion: (a) The corresponding
Orthotropic Materials
 Kapiel 2 Ohoopic Maeials 2. Elasic Sain maix Elasic sains ae elaed o sesses by Hooke's law, as saed below. The sesssain elaionship is in each maeial poin fomulaed in he local caesian coodinae sysem. ε
Kapiel 2 Ohoopic Maeials 2. Elasic Sain maix Elasic sains ae elaed o sesses by Hooke's law, as saed below. The sesssain elaionship is in each maeial poin fomulaed in he local caesian coodinae sysem. ε
7 Wave Equation in Higher Dimensions
 7 Wave Equaion in Highe Dimensions We now conside he iniial-value poblem fo he wave equaion in n dimensions, u c u x R n u(x, φ(x u (x, ψ(x whee u n i u x i x i. (7. 7. Mehod of Spheical Means Ref: Evans,
7 Wave Equaion in Highe Dimensions We now conside he iniial-value poblem fo he wave equaion in n dimensions, u c u x R n u(x, φ(x u (x, ψ(x whee u n i u x i x i. (7. 7. Mehod of Spheical Means Ref: Evans,
Transient Radial Flow Toward a Well Aquifer Equation, based on assumptions becomes a 1D PDE for h(r,t) : Transient Radial Flow Toward a Well
 ansien Radial Flw wad a Well Aqife Eqain, based n assmpins becmes a D PDE f h(,) : -ansien flw in a hmgenes, ispic aqife -flly peneaing pmping well & infinie, hiznal, cnfined aqife f nifm hickness, hs
ansien Radial Flw wad a Well Aqife Eqain, based n assmpins becmes a D PDE f h(,) : -ansien flw in a hmgenes, ispic aqife -flly peneaing pmping well & infinie, hiznal, cnfined aqife f nifm hickness, hs
Notes on Inductance and Circuit Transients Joe Wolfe, Physics UNSW. Circuits with R and C. τ = RC = time constant
 Nes n Inducance and cu Tansens Je Wlfe, Physcs UNSW cus wh and - Wha happens when yu clse he swch? (clse swch a 0) - uen flws ff capac, s d Acss capac: Acss ess: c d s d d ln + cns. 0, ln cns. ln ln ln
Nes n Inducance and cu Tansens Je Wlfe, Physcs UNSW cus wh and - Wha happens when yu clse he swch? (clse swch a 0) - uen flws ff capac, s d Acss capac: Acss ess: c d s d d ln + cns. 0, ln cns. ln ln ln
β A Constant-G m Biasing
 p 2002 EE 532 Anal IC Des II Pae 73 Cnsan-G Bas ecall ha us a PTAT cuen efeence (see p f p. 66 he nes) bas a bpla anss pes cnsan anscnucance e epeaue (an als epenen f supply lae an pcess). Hw h we achee
p 2002 EE 532 Anal IC Des II Pae 73 Cnsan-G Bas ecall ha us a PTAT cuen efeence (see p f p. 66 he nes) bas a bpla anss pes cnsan anscnucance e epeaue (an als epenen f supply lae an pcess). Hw h we achee
Lecture 4 ( ) Some points of vertical motion: Here we assumed t 0 =0 and the y axis to be vertical.
 Sme pins f erical min: Here we assumed and he y axis be erical. ( ) y g g y y y y g dwnwards 9.8 m/s g Lecure 4 Accelerain The aerage accelerain is defined by he change f elciy wih ime: a ; In analgy,
Sme pins f erical min: Here we assumed and he y axis be erical. ( ) y g g y y y y g dwnwards 9.8 m/s g Lecure 4 Accelerain The aerage accelerain is defined by he change f elciy wih ime: a ; In analgy,
Physics Courseware Physics I Constant Acceleration
 Physics Curseware Physics I Cnsan Accelerain Equains fr cnsan accelerain in dimensin x + a + a + ax + x Prblem.- In he 00-m race an ahlee acceleraes unifrmly frm res his p speed f 0m/s in he firs x5m as
Physics Curseware Physics I Cnsan Accelerain Equains fr cnsan accelerain in dimensin x + a + a + ax + x Prblem.- In he 00-m race an ahlee acceleraes unifrmly frm res his p speed f 0m/s in he firs x5m as
Today - Lecture 13. Today s lecture continue with rotations, torque, Note that chapters 11, 12, 13 all involve rotations
 Today - Lecue 13 Today s lecue coninue wih oaions, oque, Noe ha chapes 11, 1, 13 all inole oaions slide 1 eiew Roaions Chapes 11 & 1 Viewed fom aboe (+z) Roaional, o angula elociy, gies angenial elociy
Today - Lecue 13 Today s lecue coninue wih oaions, oque, Noe ha chapes 11, 1, 13 all inole oaions slide 1 eiew Roaions Chapes 11 & 1 Viewed fom aboe (+z) Roaional, o angula elociy, gies angenial elociy
Lecture 3: Resistive forces, and Energy
 Lecure 3: Resisive frces, and Energy Las ie we fund he velciy f a prjecile ving wih air resisance: g g vx ( ) = vx, e vy ( ) = + v + e One re inegrain gives us he psiin as a funcin f ie: dx dy g g = vx,
Lecure 3: Resisive frces, and Energy Las ie we fund he velciy f a prjecile ving wih air resisance: g g vx ( ) = vx, e vy ( ) = + v + e One re inegrain gives us he psiin as a funcin f ie: dx dy g g = vx,
Stress, Cauchy s equation and the Navier-Stokes equations
 Chapte 3 Stess, Cauchy s equation and the Navie-Stokes equations 3. The concept of taction/stess Conside the volume of fluid shown in the left half of Fig. 3.. The volume of fluid is subjected to distibuted
Chapte 3 Stess, Cauchy s equation and the Navie-Stokes equations 3. The concept of taction/stess Conside the volume of fluid shown in the left half of Fig. 3.. The volume of fluid is subjected to distibuted
CHAPTER GAUSS'S LAW
 lutins--ch 14 (Gauss's Law CHAPTE 14 -- GAU' LAW 141 This pblem is ticky An electic field line that flws int, then ut f the cap (see Figue I pduces a negative flux when enteing and an equal psitive flux
lutins--ch 14 (Gauss's Law CHAPTE 14 -- GAU' LAW 141 This pblem is ticky An electic field line that flws int, then ut f the cap (see Figue I pduces a negative flux when enteing and an equal psitive flux
Heat transfer between shell and rigid body through the thin heat-conducting layer taking into account mechanical contact
 Advanced Cmpuainal Meds in Hea Tansfe X 8 Hea ansfe beween sell and igid bdy ug e in ea-cnducing laye aking in accun mecanical cnac V. V. Zzulya Cen de Invesigación Cienífica de Yucaán, Méida, Yucaán,
Advanced Cmpuainal Meds in Hea Tansfe X 8 Hea ansfe beween sell and igid bdy ug e in ea-cnducing laye aking in accun mecanical cnac V. V. Zzulya Cen de Invesigación Cienífica de Yucaán, Méida, Yucaán,
Lecture-V Stochastic Processes and the Basic Term-Structure Equation 1 Stochastic Processes Any variable whose value changes over time in an uncertain
 Lecue-V Sochasic Pocesses and he Basic Tem-Sucue Equaion 1 Sochasic Pocesses Any vaiable whose value changes ove ime in an unceain way is called a Sochasic Pocess. Sochasic Pocesses can be classied as
Lecue-V Sochasic Pocesses and he Basic Tem-Sucue Equaion 1 Sochasic Pocesses Any vaiable whose value changes ove ime in an unceain way is called a Sochasic Pocess. Sochasic Pocesses can be classied as
Total Deformation and its Role in Heavy Precipitation Events Associated with Deformation-Dominant Flow Patterns
 ADVANCES IN ATMOSPHERIC SCIENCES VOL. 25 NO. 1 2008 11 23 Tal Defmain and is Rle in Heavy Pecipiain Evens Assciaed wih Defmain-Dminan Flw Paens GAO Shuing 1 (påë) YANG Shuai 12 (fl R) XUE Ming 3 (Å ) and
ADVANCES IN ATMOSPHERIC SCIENCES VOL. 25 NO. 1 2008 11 23 Tal Defmain and is Rle in Heavy Pecipiain Evens Assciaed wih Defmain-Dminan Flw Paens GAO Shuing 1 (påë) YANG Shuai 12 (fl R) XUE Ming 3 (Å ) and
ELECTRIC & MAGNETIC FIELDS I (STATIC FIELDS) ELC 205A
 LCTRIC & MAGNTIC FILDS I (STATIC FILDS) LC 05A D. Hanna A. Kils Assciate Pfess lectnics & Cmmnicatins ngineeing Depatment Faclty f ngineeing Cai Univesity Fall 0 f Static lecticity lectic & Magnetic Fields
LCTRIC & MAGNTIC FILDS I (STATIC FILDS) LC 05A D. Hanna A. Kils Assciate Pfess lectnics & Cmmnicatins ngineeing Depatment Faclty f ngineeing Cai Univesity Fall 0 f Static lecticity lectic & Magnetic Fields
A) (0.46 î ) N B) (0.17 î ) N
 Phys10 Secnd Maj-14 Ze Vesin Cdinat: xyz Thusday, Apil 3, 015 Page: 1 Q1. Thee chages, 1 = =.0 μc and Q = 4.0 μc, ae fixed in thei places as shwn in Figue 1. Find the net electstatic fce n Q due t 1 and.
Phys10 Secnd Maj-14 Ze Vesin Cdinat: xyz Thusday, Apil 3, 015 Page: 1 Q1. Thee chages, 1 = =.0 μc and Q = 4.0 μc, ae fixed in thei places as shwn in Figue 1. Find the net electstatic fce n Q due t 1 and.
Note: Please use the actual date you accessed this material in your citation.
 MIT OpenCuseWae hp://cw.m.edu 6.03/ESD.03J Elecmagnecs and Applcans, Fall 005 Please use he fllwng can fma: Makus Zahn, Ech Ippen, and Davd Saeln, 6.03/ESD.03J Elecmagnecs and Applcans, Fall 005. (Massachuses
MIT OpenCuseWae hp://cw.m.edu 6.03/ESD.03J Elecmagnecs and Applcans, Fall 005 Please use he fllwng can fma: Makus Zahn, Ech Ippen, and Davd Saeln, 6.03/ESD.03J Elecmagnecs and Applcans, Fall 005. (Massachuses
( ) ( ) if t = t. It must satisfy the identity. So, bulkiness of the unit impulse (hyper)function is equal to 1. The defining characteristic is
 UNIT IMPULSE RESPONSE, UNIT STEP RESPONSE, STABILITY. Uni impulse funcion (Dirac dela funcion, dela funcion) rigorously defined is no sricly a funcion, bu disribuion (or measure), precise reamen requires
UNIT IMPULSE RESPONSE, UNIT STEP RESPONSE, STABILITY. Uni impulse funcion (Dirac dela funcion, dela funcion) rigorously defined is no sricly a funcion, bu disribuion (or measure), precise reamen requires
3.3.1 Expanded forms of the Continuity Equation. θ (ρv θ)+ z (ρv z)=0. θ (ρv θ sin θ)+ 1
 Ke Equations 58 3.3 Ke Equations 3.3.1 Epanded foms of the Continuit Equation Rectangula coodinates: t (v (v z (v z0 Clindical coodinates: t 1 Spheical coodinates: (v 1 t 1 2 (2 v 1 θ (v θ z (v z0 θ (v
Ke Equations 58 3.3 Ke Equations 3.3.1 Epanded foms of the Continuit Equation Rectangula coodinates: t (v (v z (v z0 Clindical coodinates: t 1 Spheical coodinates: (v 1 t 1 2 (2 v 1 θ (v θ z (v z0 θ (v
Electric Charge. Electric charge is quantized. Electric charge is conserved
 lectstatics lectic Chage lectic chage is uantized Chage cmes in incements f the elementay chage e = ne, whee n is an intege, and e =.6 x 0-9 C lectic chage is cnseved Chage (electns) can be mved fm ne
lectstatics lectic Chage lectic chage is uantized Chage cmes in incements f the elementay chage e = ne, whee n is an intege, and e =.6 x 0-9 C lectic chage is cnseved Chage (electns) can be mved fm ne
(V 1. (T i. )- FrC p. ))= 0 = FrC p (T 1. (T 1s. )+ UA(T os. (T is
 . Yu are repnible fr a reacr in which an exhermic liqui-phae reacin ccur. The fee mu be preheae he hrehl acivain emperaure f he caaly, bu he pruc ream mu be cle. T reuce uiliy c, yu are cniering inalling
. Yu are repnible fr a reacr in which an exhermic liqui-phae reacin ccur. The fee mu be preheae he hrehl acivain emperaure f he caaly, bu he pruc ream mu be cle. T reuce uiliy c, yu are cniering inalling
Circuit Variables. AP 1.1 Use a product of ratios to convert two-thirds the speed of light from meters per second to miles per second: 1 ft 12 in
 Circui Variables 1 Assessmen Problems AP 1.1 Use a produc of raios o conver wo-hirds he speed of ligh from meers per second o miles per second: ( ) 2 3 1 8 m 3 1 s 1 cm 1 m 1 in 2.54 cm 1 f 12 in 1 mile
Circui Variables 1 Assessmen Problems AP 1.1 Use a produc of raios o conver wo-hirds he speed of ligh from meers per second o miles per second: ( ) 2 3 1 8 m 3 1 s 1 cm 1 m 1 in 2.54 cm 1 f 12 in 1 mile
Application of Fractional Calculus in Food Rheology E. Vozáry, Gy. Csima, L. Csapó, F. Mohos
 Applicain f Facinal Calculus in F Rhelgy Szen Isán Uniesiy, Depamen f Physics an Cnl Vzay.sze@ek.szie.hu Keyws: facinal calculus, iscelasic, f, ceep, ecey Absac. In facinal calculus he e (β) f iffeeniain
Applicain f Facinal Calculus in F Rhelgy Szen Isán Uniesiy, Depamen f Physics an Cnl Vzay.sze@ek.szie.hu Keyws: facinal calculus, iscelasic, f, ceep, ecey Absac. In facinal calculus he e (β) f iffeeniain
Field due to a collection of N discrete point charges: r is in the direction from
 Physcs 46 Fomula Shee Exam Coulomb s Law qq Felec = k ˆ (Fo example, f F s he elecc foce ha q exes on q, hen ˆ s a un veco n he decon fom q o q.) Elecc Feld elaed o he elecc foce by: Felec = qe (elecc
Physcs 46 Fomula Shee Exam Coulomb s Law qq Felec = k ˆ (Fo example, f F s he elecc foce ha q exes on q, hen ˆ s a un veco n he decon fom q o q.) Elecc Feld elaed o he elecc foce by: Felec = qe (elecc
Chapter Finite Difference Method for Ordinary Differential Equations
 Chape 8.7 Finie Diffeence Mehod fo Odinay Diffeenial Eqaions Afe eading his chape, yo shold be able o. Undesand wha he finie diffeence mehod is and how o se i o solve poblems. Wha is he finie diffeence
Chape 8.7 Finie Diffeence Mehod fo Odinay Diffeenial Eqaions Afe eading his chape, yo shold be able o. Undesand wha he finie diffeence mehod is and how o se i o solve poblems. Wha is he finie diffeence
Laplace Transforms. Examples. Is this equation differential? y 2 2y + 1 = 0, y 2 2y + 1 = 0, (y ) 2 2y + 1 = cos x,
 Laplace Transforms Definiion. An ordinary differenial equaion is an equaion ha conains one or several derivaives of an unknown funcion which we call y and which we wan o deermine from he equaion. The equaion
Laplace Transforms Definiion. An ordinary differenial equaion is an equaion ha conains one or several derivaives of an unknown funcion which we call y and which we wan o deermine from he equaion. The equaion
Work, Energy, and Power. AP Physics C
 k, Eneg, and Pwe AP Phsics C Thee ae man diffeent TYPES f Eneg. Eneg is expessed in JOULES (J) 4.19 J = 1 calie Eneg can be expessed me specificall b using the tem ORK() k = The Scala Dt Pduct between
k, Eneg, and Pwe AP Phsics C Thee ae man diffeent TYPES f Eneg. Eneg is expessed in JOULES (J) 4.19 J = 1 calie Eneg can be expessed me specificall b using the tem ORK() k = The Scala Dt Pduct between
Mass Linear Momentum Moment of Momentum Energy Putting it all together!
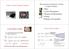 inie Cnrl lue nalsis vin fr a Sse a inie Cnrl lue a Linear enu en f enu Ener Puin i all eer! D Cnservain f a B = Tal aun f a in e e b = a er uni a = DB ˆ b b n ˆ n ˆ equain Bu D / =! Cninui Equain a leavin
inie Cnrl lue nalsis vin fr a Sse a inie Cnrl lue a Linear enu en f enu Ener Puin i all eer! D Cnservain f a B = Tal aun f a in e e b = a er uni a = DB ˆ b b n ˆ n ˆ equain Bu D / =! Cninui Equain a leavin
a. (1) Assume T = 20 ºC = 293 K. Apply Equation 2.22 to find the resistivity of the brass in the disk with
 Aignmen #5 EE7 / Fall 0 / Aignmen Sluin.7 hermal cnducin Cnider bra ally wih an X amic fracin f Zn. Since Zn addiin increae he number f cnducin elecrn, we have cale he final ally reiiviy calculaed frm
Aignmen #5 EE7 / Fall 0 / Aignmen Sluin.7 hermal cnducin Cnider bra ally wih an X amic fracin f Zn. Since Zn addiin increae he number f cnducin elecrn, we have cale he final ally reiiviy calculaed frm
Stochastic Modelling in Finance - Solutions to sheet 8
 Sochasic Modelling in Finance - Soluions o shee 8 8.1 The price of a defaulable asse can be modeled as ds S = µ d + σ dw dn where µ, σ are consans, (W ) is a sandard Brownian moion and (N ) is a one jump
Sochasic Modelling in Finance - Soluions o shee 8 8.1 The price of a defaulable asse can be modeled as ds S = µ d + σ dw dn where µ, σ are consans, (W ) is a sandard Brownian moion and (N ) is a one jump
PHYS PRACTICE EXAM 2
 PHYS 1800 PRACTICE EXAM Pa I Muliple Choice Quesions [ ps each] Diecions: Cicle he one alenaive ha bes complees he saemen o answes he quesion. Unless ohewise saed, assume ideal condiions (no ai esisance,
PHYS 1800 PRACTICE EXAM Pa I Muliple Choice Quesions [ ps each] Diecions: Cicle he one alenaive ha bes complees he saemen o answes he quesion. Unless ohewise saed, assume ideal condiions (no ai esisance,
Fig. 1S. The antenna construction: (a) main geometrical parameters, (b) the wire support pillar and (c) the console link between wire and coaxial
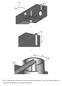 a b c Fig. S. The anenna consucion: (a) ain geoeical paaees, (b) he wie suppo pilla and (c) he console link beween wie and coaial pobe. Fig. S. The anenna coss-secion in he y-z plane. Accoding o [], he
a b c Fig. S. The anenna consucion: (a) ain geoeical paaees, (b) he wie suppo pilla and (c) he console link beween wie and coaial pobe. Fig. S. The anenna coss-secion in he y-z plane. Accoding o [], he
Circular Motion. Radians. One revolution is equivalent to which is also equivalent to 2π radians. Therefore we can.
 1 Cicula Moion Radians One evoluion is equivalen o 360 0 which is also equivalen o 2π adians. Theefoe we can say ha 360 = 2π adians, 180 = π adians, 90 = π 2 adians. Hence 1 adian = 360 2π Convesions Rule
1 Cicula Moion Radians One evoluion is equivalen o 360 0 which is also equivalen o 2π adians. Theefoe we can say ha 360 = 2π adians, 180 = π adians, 90 = π 2 adians. Hence 1 adian = 360 2π Convesions Rule
Lecture 5. Chapter 3. Electromagnetic Theory, Photons, and Light
 Lecue 5 Chape 3 lecomagneic Theo, Phoons, and Ligh Gauss s Gauss s Faada s Ampèe- Mawell s + Loen foce: S C ds ds S C F dl dl q Mawell equaions d d qv A q A J ds ds In mae fields ae defined hough ineacion
Lecue 5 Chape 3 lecomagneic Theo, Phoons, and Ligh Gauss s Gauss s Faada s Ampèe- Mawell s + Loen foce: S C ds ds S C F dl dl q Mawell equaions d d qv A q A J ds ds In mae fields ae defined hough ineacion
Lecture 18: Kinetics of Phase Growth in a Two-component System: general kinetics analysis based on the dilute-solution approximation
 Lecue 8: Kineics of Phase Gowh in a Two-componen Sysem: geneal kineics analysis based on he dilue-soluion appoximaion Today s opics: In he las Lecues, we leaned hee diffeen ways o descibe he diffusion
Lecue 8: Kineics of Phase Gowh in a Two-componen Sysem: geneal kineics analysis based on he dilue-soluion appoximaion Today s opics: In he las Lecues, we leaned hee diffeen ways o descibe he diffusion
ECE 2100 Circuit Analysis
 ECE 1 Circui Analysis Lesson 35 Chaper 8: Second Order Circuis Daniel M. Liynski, Ph.D. ECE 1 Circui Analysis Lesson 3-34 Chaper 7: Firs Order Circuis (Naural response RC & RL circuis, Singulariy funcions,
ECE 1 Circui Analysis Lesson 35 Chaper 8: Second Order Circuis Daniel M. Liynski, Ph.D. ECE 1 Circui Analysis Lesson 3-34 Chaper 7: Firs Order Circuis (Naural response RC & RL circuis, Singulariy funcions,
The shortest path between two truths in the real domain passes through the complex domain. J. Hadamard
 Complex Analysis R.G. Halbud R.Halbud@ucl.ac.uk Depamen of Mahemaics Univesiy College London 202 The shoes pah beween wo uhs in he eal domain passes hough he complex domain. J. Hadamad Chape The fis fundamenal
Complex Analysis R.G. Halbud R.Halbud@ucl.ac.uk Depamen of Mahemaics Univesiy College London 202 The shoes pah beween wo uhs in he eal domain passes hough he complex domain. J. Hadamad Chape The fis fundamenal
Control Volume Derivation
 School of eospace Engineeing Conol Volume -1 Copyigh 1 by Jey M. Seizman. ll ighs esee. Conol Volume Deiaion How o cone ou elaionships fo a close sysem (conol mass) o an open sysem (conol olume) Fo mass
School of eospace Engineeing Conol Volume -1 Copyigh 1 by Jey M. Seizman. ll ighs esee. Conol Volume Deiaion How o cone ou elaionships fo a close sysem (conol mass) o an open sysem (conol olume) Fo mass
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.265/15.070J Fall 2013 Lecture 15 10/30/2013. Ito integral for simple processes
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.65/15.7J Fall 13 Lecure 15 1/3/13 I inegral fr simple prcesses Cnen. 1. Simple prcesses. I ismery. Firs 3 seps in cnsrucing I inegral fr general prcesses 1 I inegral
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.65/15.7J Fall 13 Lecure 15 1/3/13 I inegral fr simple prcesses Cnen. 1. Simple prcesses. I ismery. Firs 3 seps in cnsrucing I inegral fr general prcesses 1 I inegral
MA 214 Calculus IV (Spring 2016) Section 2. Homework Assignment 1 Solutions
 MA 14 Calculus IV (Spring 016) Secion Homework Assignmen 1 Soluions 1 Boyce and DiPrima, p 40, Problem 10 (c) Soluion: In sandard form he given firs-order linear ODE is: An inegraing facor is given by
MA 14 Calculus IV (Spring 016) Secion Homework Assignmen 1 Soluions 1 Boyce and DiPrima, p 40, Problem 10 (c) Soluion: In sandard form he given firs-order linear ODE is: An inegraing facor is given by
5/20/2011. HITT An electron moves from point i to point f, in the direction of a uniform electric field. During this displacement:
 5/0/011 Chapte 5 In the last lectue: CapacitanceII we calculated the capacitance C f a system f tw islated cnducts. We als calculated the capacitance f sme simple gemeties. In this chapte we will cve the
5/0/011 Chapte 5 In the last lectue: CapacitanceII we calculated the capacitance C f a system f tw islated cnducts. We als calculated the capacitance f sme simple gemeties. In this chapte we will cve the
Ch.1. Group Work Units. Continuum Mechanics Course (MMC) - ETSECCPB - UPC
 Ch.. Group Work Unis Coninuum Mechanics Course (MMC) - ETSECCPB - UPC Uni 2 Jusify wheher he following saemens are rue or false: a) Two sreamlines, corresponding o a same insan of ime, can never inersec
Ch.. Group Work Unis Coninuum Mechanics Course (MMC) - ETSECCPB - UPC Uni 2 Jusify wheher he following saemens are rue or false: a) Two sreamlines, corresponding o a same insan of ime, can never inersec
$ i. !((( dv vol. Physics 8.02 Quiz One Equations Fall q 1 q 2 r 2 C = 2 C! V 2 = Q 2 2C F = 4!" or. r ˆ = points from source q to observer
 Physics 8.0 Quiz One Equations Fall 006 F = 1 4" o q 1 q = q q ˆ 3 4" o = E 4" o ˆ = points fom souce q to obseve 1 dq E = # ˆ 4" 0 V "## E "d A = Q inside closed suface o d A points fom inside to V =
Physics 8.0 Quiz One Equations Fall 006 F = 1 4" o q 1 q = q q ˆ 3 4" o = E 4" o ˆ = points fom souce q to obseve 1 dq E = # ˆ 4" 0 V "## E "d A = Q inside closed suface o d A points fom inside to V =
The Buck Resonant Converter
 EE646 Pwer Elecrnics Chaper 6 ecure Dr. Sam Abdel-Rahman The Buck Resnan Cnverer Replacg he swich by he resnan-ype swich, ba a quasi-resnan PWM buck cnverer can be shwn ha here are fur mdes f pera under
EE646 Pwer Elecrnics Chaper 6 ecure Dr. Sam Abdel-Rahman The Buck Resnan Cnverer Replacg he swich by he resnan-ype swich, ba a quasi-resnan PWM buck cnverer can be shwn ha here are fur mdes f pera under
5.1 Angles and Their Measure
 5. Angles and Their Measure Secin 5. Nes Page This secin will cver hw angles are drawn and als arc lengh and rains. We will use (hea) represen an angle s measuremen. In he figure belw i describes hw yu
5. Angles and Their Measure Secin 5. Nes Page This secin will cver hw angles are drawn and als arc lengh and rains. We will use (hea) represen an angle s measuremen. In he figure belw i describes hw yu
ANTENNAS. Vector and Scalar Potentials. Maxwell's Equations. D = εe. For a linear, homogeneous, isotropic medium µ and ε are contant.
 ANTNNAS Vecto and Scala Potentials Maxwell's quations jωb J + jωd D ρ B (M) (M) (M3) (M4) D ε B Fo a linea, homogeneous, isotopic medium and ε ae contant. Since B, thee exists a vecto A such that B A and
ANTNNAS Vecto and Scala Potentials Maxwell's quations jωb J + jωd D ρ B (M) (M) (M3) (M4) D ε B Fo a linea, homogeneous, isotopic medium and ε ae contant. Since B, thee exists a vecto A such that B A and
ANSWER KEY. Page 1 Page 2 cake key pie boat glue cat sled pig fox sun dog fish zebra. Page 3. Page 7. Page 6
 P 1 P 2 y sd fx s d fsh z ys P 3 P 4 my, ms, m, m, m, m P 6 d d P 7 m y P 5 m m s P 10 y y y P 8 P 9 s sh, s, ss, sd sds, s, sh sv s s P 11 s P 12,, m, m, m,, dd P 13 m f m P 18 h m s P 22 f fx f fsh fm
P 1 P 2 y sd fx s d fsh z ys P 3 P 4 my, ms, m, m, m, m P 6 d d P 7 m y P 5 m m s P 10 y y y P 8 P 9 s sh, s, ss, sd sds, s, sh sv s s P 11 s P 12,, m, m, m,, dd P 13 m f m P 18 h m s P 22 f fx f fsh fm
[Griffiths Ch.1-3] 2008/11/18, 10:10am 12:00am, 1. (6%, 7%, 7%) Suppose the potential at the surface of a hollow hemisphere is specified, as shown
![[Griffiths Ch.1-3] 2008/11/18, 10:10am 12:00am, 1. (6%, 7%, 7%) Suppose the potential at the surface of a hollow hemisphere is specified, as shown [Griffiths Ch.1-3] 2008/11/18, 10:10am 12:00am, 1. (6%, 7%, 7%) Suppose the potential at the surface of a hollow hemisphere is specified, as shown](/thumbs/80/81190242.jpg) [Giffiths Ch.-] 8//8, :am :am, Useful fomulas V ˆ ˆ V V V = + θ+ φ ˆ and v = ( v ) + (sin θvθ ) + v θ sinθ φ sinθ θ sinθ φ φ. (6%, 7%, 7%) Suppose the potential at the suface of a hollow hemisphee is specified,
[Giffiths Ch.-] 8//8, :am :am, Useful fomulas V ˆ ˆ V V V = + θ+ φ ˆ and v = ( v ) + (sin θvθ ) + v θ sinθ φ sinθ θ sinθ φ φ. (6%, 7%, 7%) Suppose the potential at the suface of a hollow hemisphee is specified,
Physics 2212 GH Quiz #2 Solutions Spring 2016
 Physics 2212 GH Quiz #2 Solutions Sping 216 I. 17 points) Thee point chages, each caying a chage Q = +6. nc, ae placed on an equilateal tiangle of side length = 3. mm. An additional point chage, caying
Physics 2212 GH Quiz #2 Solutions Sping 216 I. 17 points) Thee point chages, each caying a chage Q = +6. nc, ae placed on an equilateal tiangle of side length = 3. mm. An additional point chage, caying
Structural Dynamics and Earthquake Engineering
 Srucural Dynamics and Earhquae Engineering Course 1 Inroducion. Single degree of freedom sysems: Equaions of moion, problem saemen, soluion mehods. Course noes are available for download a hp://www.c.up.ro/users/aurelsraan/
Srucural Dynamics and Earhquae Engineering Course 1 Inroducion. Single degree of freedom sysems: Equaions of moion, problem saemen, soluion mehods. Course noes are available for download a hp://www.c.up.ro/users/aurelsraan/
ECE Spring Prof. David R. Jackson ECE Dept. Notes 5
 ECE 6345 Sping 15 Pof. David R. Jackson ECE Dept. Notes 5 1 Oveview This set of notes discusses impoved models of the pobe inductance of a coaxially-fed patch (accuate fo thicke substates). A paallel-plate
ECE 6345 Sping 15 Pof. David R. Jackson ECE Dept. Notes 5 1 Oveview This set of notes discusses impoved models of the pobe inductance of a coaxially-fed patch (accuate fo thicke substates). A paallel-plate
21.9 Magnetic Materials
 21.9 Magneic Maerials The inrinsic spin and rbial min f elecrns gives rise he magneic prperies f maerials è elecrn spin and rbis ac as iny curren lps. In ferrmagneic maerials grups f 10 16-10 19 neighbring
21.9 Magneic Maerials The inrinsic spin and rbial min f elecrns gives rise he magneic prperies f maerials è elecrn spin and rbis ac as iny curren lps. In ferrmagneic maerials grups f 10 16-10 19 neighbring
ψ(t) = V x (0)V x (t)
 .93 Home Work Se No. (Professor Sow-Hsin Chen Spring Term 5. Due March 7, 5. This problem concerns calculaions of analyical expressions for he self-inermediae scaering funcion (ISF of he es paricle in
.93 Home Work Se No. (Professor Sow-Hsin Chen Spring Term 5. Due March 7, 5. This problem concerns calculaions of analyical expressions for he self-inermediae scaering funcion (ISF of he es paricle in
Homework-8(1) P8.3-1, 3, 8, 10, 17, 21, 24, 28,29 P8.4-1, 2, 5
 Homework-8() P8.3-, 3, 8, 0, 7, 2, 24, 28,29 P8.4-, 2, 5 Secion 8.3: The Response of a Firs Order Circui o a Consan Inpu P 8.3- The circui shown in Figure P 8.3- is a seady sae before he swich closes a
Homework-8() P8.3-, 3, 8, 0, 7, 2, 24, 28,29 P8.4-, 2, 5 Secion 8.3: The Response of a Firs Order Circui o a Consan Inpu P 8.3- The circui shown in Figure P 8.3- is a seady sae before he swich closes a
3 ) = 10(1-3t)e -3t A
 haper 6, Sluin. d i ( e 6 e ) 0( - )e - A p i 0(-)e - e - 0( - )e -6 W haper 6, Sluin. w w (40)(80 (40)(0) ) ( ) w w w 0 0 80 60 kw haper 6, Sluin. i d 80 60 40x0 480 ma haper 6, Sluin 4. i (0) 6sin 4-0.7
haper 6, Sluin. d i ( e 6 e ) 0( - )e - A p i 0(-)e - e - 0( - )e -6 W haper 6, Sluin. w w (40)(80 (40)(0) ) ( ) w w w 0 0 80 60 kw haper 6, Sluin. i d 80 60 40x0 480 ma haper 6, Sluin 4. i (0) 6sin 4-0.7
Motion Along a Straight Line
 PH 1-3A Fall 010 Min Alng a Sraigh Line Lecure Chaper (Halliday/Resnick/Walker, Fundamenals f Physics 8 h ediin) Min alng a sraigh line Sudies he min f bdies Deals wih frce as he cause f changes in min
PH 1-3A Fall 010 Min Alng a Sraigh Line Lecure Chaper (Halliday/Resnick/Walker, Fundamenals f Physics 8 h ediin) Min alng a sraigh line Sudies he min f bdies Deals wih frce as he cause f changes in min
SMKA NAIM LILBANAT KOTA BHARU KELANTAN. SEKOLAH BERPRESTASI TINGGI. Kertas soalan ini mengandungi 7 halaman bercetak.
 Name : Frm :. SMKA NAIM LILBANAT 55 KOTA BHARU KELANTAN. SEKOLAH BERPRESTASI TINGGI PEPERIKSAAN PERCUBAAN SPM / ADDITIONAL MATHEMATICS Keras ½ Jam ½ Jam Unuk Kegunaan Pemeriksa Arahan:. This quesin paper
Name : Frm :. SMKA NAIM LILBANAT 55 KOTA BHARU KELANTAN. SEKOLAH BERPRESTASI TINGGI PEPERIKSAAN PERCUBAAN SPM / ADDITIONAL MATHEMATICS Keras ½ Jam ½ Jam Unuk Kegunaan Pemeriksa Arahan:. This quesin paper
Homework # 3 Solution Key
 PHYSICS 631: Geneal Relativity Homewok # 3 Solution Key 1. You e on you hono not to do this one by hand. I ealize you can use a compute o simply look it up. Please don t. In a flat space, the metic in
PHYSICS 631: Geneal Relativity Homewok # 3 Solution Key 1. You e on you hono not to do this one by hand. I ealize you can use a compute o simply look it up. Please don t. In a flat space, the metic in
Relative and Circular Motion
 Relaie and Cicula Moion a) Relaie moion b) Cenipeal acceleaion Mechanics Lecue 3 Slide 1 Mechanics Lecue 3 Slide 2 Time on Video Pelecue Looks like mosly eeyone hee has iewed enie pelecue GOOD! Thank you
Relaie and Cicula Moion a) Relaie moion b) Cenipeal acceleaion Mechanics Lecue 3 Slide 1 Mechanics Lecue 3 Slide 2 Time on Video Pelecue Looks like mosly eeyone hee has iewed enie pelecue GOOD! Thank you
Final Review of AerE 243 Class
 Final Review of AeE 4 Class Content of Aeodynamics I I Chapte : Review of Multivaiable Calculus Chapte : Review of Vectos Chapte : Review of Fluid Mechanics Chapte 4: Consevation Equations Chapte 5: Simplifications
Final Review of AeE 4 Class Content of Aeodynamics I I Chapte : Review of Multivaiable Calculus Chapte : Review of Vectos Chapte : Review of Fluid Mechanics Chapte 4: Consevation Equations Chapte 5: Simplifications
3. Electromagnetic Waves II
 Lectue 3 - Electomagnetic Waves II 9 3. Electomagnetic Waves II Last time, we discussed the following. 1. The popagation of an EM wave though a macoscopic media: We discussed how the wave inteacts with
Lectue 3 - Electomagnetic Waves II 9 3. Electomagnetic Waves II Last time, we discussed the following. 1. The popagation of an EM wave though a macoscopic media: We discussed how the wave inteacts with
Chem. 6C Midterm 1 Version B October 19, 2007
 hem. 6 Miderm Verin Ocber 9, 007 Name Suden Number ll wr mu be hwn n he exam fr parial credi. Pin will be aen ff fr incrrec r n uni. Nn graphing calcular and ne hand wrien 5 ne card are allwed. Prblem
hem. 6 Miderm Verin Ocber 9, 007 Name Suden Number ll wr mu be hwn n he exam fr parial credi. Pin will be aen ff fr incrrec r n uni. Nn graphing calcular and ne hand wrien 5 ne card are allwed. Prblem
The 37th International Physics Olympiad Singapore. Experimental Competition. Wednesday, 12 July, Sample Solution
 The 37h Inernainal Physics Olypiad Singapre Experienal Cpeiin Wednesday, July, 006 Saple Sluin Par a A skech f he experienal seup (n required) Receiver Raing able Gnieer Fixed ar Bea splier Gnieer Mvable
The 37h Inernainal Physics Olypiad Singapre Experienal Cpeiin Wednesday, July, 006 Saple Sluin Par a A skech f he experienal seup (n required) Receiver Raing able Gnieer Fixed ar Bea splier Gnieer Mvable
Chapter 2 Solutions. ψ 1 ψ. 16 t. ( z υt ), where υ is in the negative z direction. = 2 A. Chapter 2 Solutions = 32
 Chaper Soluions 1 Chaper Soluions.1 υ ( z+ υ) ψ υ( z+ υ) ψ υ I s a wice differeniable funcion of ( z υ ), where υ is in he negaive z direcion.. υ ψ ( y,) ( y 4) ( y 4 ) ψ ( y 4 ) ψ 3 Thus, υ 4, υ 16, and,
Chaper Soluions 1 Chaper Soluions.1 υ ( z+ υ) ψ υ( z+ υ) ψ υ I s a wice differeniable funcion of ( z υ ), where υ is in he negaive z direcion.. υ ψ ( y,) ( y 4) ( y 4 ) ψ ( y 4 ) ψ 3 Thus, υ 4, υ 16, and,
Physics 442. Electro-Magneto-Dynamics. M. Berrondo. Physics BYU
 Physis 44 Eleo-Magneo-Dynamis M. Beondo Physis BYU Paaveos Φ= V + Α Φ= V Α = = + J = + ρ J J ρ = J S = u + em S S = u em S Physis BYU Poenials Genealize E = V o he ime dependen E & B ase Podu of paaveos:
Physis 44 Eleo-Magneo-Dynamis M. Beondo Physis BYU Paaveos Φ= V + Α Φ= V Α = = + J = + ρ J J ρ = J S = u + em S S = u em S Physis BYU Poenials Genealize E = V o he ime dependen E & B ase Podu of paaveos:
 WORK POWER AND ENERGY Consevaive foce a) A foce is said o be consevaive if he wok done by i is independen of pah followed by he body b) Wok done by a consevaive foce fo a closed pah is zeo c) Wok done
WORK POWER AND ENERGY Consevaive foce a) A foce is said o be consevaive if he wok done by i is independen of pah followed by he body b) Wok done by a consevaive foce fo a closed pah is zeo c) Wok done
A 1. EN2210: Continuum Mechanics. Homework 7: Fluid Mechanics Solutions
 EN10: Continuum Mechanics Homewok 7: Fluid Mechanics Solutions School of Engineeing Bown Univesity 1. An ideal fluid with mass density ρ flows with velocity v 0 though a cylindical tube with cosssectional
EN10: Continuum Mechanics Homewok 7: Fluid Mechanics Solutions School of Engineeing Bown Univesity 1. An ideal fluid with mass density ρ flows with velocity v 0 though a cylindical tube with cosssectional
MEMS 0031 Electric Circuits
 MEMS 0031 Elecric Circuis Chaper 1 Circui variables Chaper/Lecure Learning Objecives A he end of his lecure and chaper, you should able o: Represen he curren and volage of an elecric circui elemen, paying
MEMS 0031 Elecric Circuis Chaper 1 Circui variables Chaper/Lecure Learning Objecives A he end of his lecure and chaper, you should able o: Represen he curren and volage of an elecric circui elemen, paying
r P + '% 2 r v(r) End pressures P 1 (high) and P 2 (low) P 1 , which must be independent of z, so # dz dz = P 2 " P 1 = " #P L L,
 Lecue 36 Pipe Flow and Low-eynolds numbe hydodynamics 36.1 eading fo Lecues 34-35: PKT Chape 12. Will y fo Monday?: new daa shee and daf fomula shee fo final exam. Ou saing poin fo hydodynamics ae wo equaions:
Lecue 36 Pipe Flow and Low-eynolds numbe hydodynamics 36.1 eading fo Lecues 34-35: PKT Chape 12. Will y fo Monday?: new daa shee and daf fomula shee fo final exam. Ou saing poin fo hydodynamics ae wo equaions:
The complex Fourier series has an important limiting form when the period approaches infinity, i.e., T 0. 0 since it is proportional to 1/L, but
 Fourier Transforms The complex Fourier series has an imporan limiing form when he period approaches infiniy, i.e., T or L. Suppose ha in his limi () k = nπ L remains large (ranging from o ) and (2) c n
Fourier Transforms The complex Fourier series has an imporan limiing form when he period approaches infiniy, i.e., T or L. Suppose ha in his limi () k = nπ L remains large (ranging from o ) and (2) c n
GEOID-QUASIGEOID CORRECTION IN FORMULATION OF THE FUNDAMENTAL FORMULA OF PHYSICAL GEODESY. Robert Tenzer 1 Petr Vaníček 2
 GEID-QUASIGEID CECTI I FMULATI F TE FUDAMETAL FMULA F PYSICAL GEDESY be Tenze 1 Pe Vaníček 1 Depamen f Gedesy and Gemaics Enineein Univesiy f ew Bunswick P Bx 4400 Fedeicn ew Bunswick Canada E3B 5A3; Tel
GEID-QUASIGEID CECTI I FMULATI F TE FUDAMETAL FMULA F PYSICAL GEDESY be Tenze 1 Pe Vaníček 1 Depamen f Gedesy and Gemaics Enineein Univesiy f ew Bunswick P Bx 4400 Fedeicn ew Bunswick Canada E3B 5A3; Tel
KINEMATICS OF RIGID BODIES
 KINEMTICS OF RIGID ODIES In igid body kinemaics, we use he elaionships govening he displacemen, velociy and acceleaion, bu mus also accoun fo he oaional moion of he body. Descipion of he moion of igid
KINEMTICS OF RIGID ODIES In igid body kinemaics, we use he elaionships govening he displacemen, velociy and acceleaion, bu mus also accoun fo he oaional moion of he body. Descipion of he moion of igid
Maximum Cross Section Reduction Ratio of Billet in a Single Wire Forming Pass Based on Unified Strength Theory. Xiaowei Li1,2, a
 Inenainal Fum n Enegy, Envinmen and Susainable evelpmen (IFEES 06 Maximum Css Sein Reduin Rai f Bille in a Single Wie Fming Pass Based n Unified Sengh They Xiawei Li,, a Shl f Civil Engineeing, Panzhihua
Inenainal Fum n Enegy, Envinmen and Susainable evelpmen (IFEES 06 Maximum Css Sein Reduin Rai f Bille in a Single Wie Fming Pass Based n Unified Sengh They Xiawei Li,, a Shl f Civil Engineeing, Panzhihua
ELECTRODYNAMICS: PHYS 30441
 ELETRODYNAMIS: PHYS 44. Electomagnetic Field Equations. Maxwell s Equations Analysis in space (vacuum). oulomb Bon June 4, 76 Angoulême, Fance Died August 2, 86 Pais, Fance In 785 oulomb pesented his thee
ELETRODYNAMIS: PHYS 44. Electomagnetic Field Equations. Maxwell s Equations Analysis in space (vacuum). oulomb Bon June 4, 76 Angoulême, Fance Died August 2, 86 Pais, Fance In 785 oulomb pesented his thee
Single Degree of Freedom System Forced Vibration
 Maa Kliah : Dinamia Srr & Penganar Reayasa Kegempaan Kde : TSP 3 SKS : 3 SKS Single Degree f Freedm Sysem Frced Vibrain Pereman - 3 TIU : Mahasiswa dapa menelasan enang eri dinamia srr. Mahasiswa dapa
Maa Kliah : Dinamia Srr & Penganar Reayasa Kegempaan Kde : TSP 3 SKS : 3 SKS Single Degree f Freedm Sysem Frced Vibrain Pereman - 3 TIU : Mahasiswa dapa menelasan enang eri dinamia srr. Mahasiswa dapa
A) N B) 0.0 N C) N D) N E) N
 Cdinat: H Bahluli Sunday, Nvembe, 015 Page: 1 Q1. Five identical pint chages each with chage =10 nc ae lcated at the cnes f a egula hexagn, as shwn in Figue 1. Find the magnitude f the net electic fce
Cdinat: H Bahluli Sunday, Nvembe, 015 Page: 1 Q1. Five identical pint chages each with chage =10 nc ae lcated at the cnes f a egula hexagn, as shwn in Figue 1. Find the magnitude f the net electic fce
Physics 1402: Lecture 22 Today s Agenda
 Physics 142: ecure 22 Today s Agenda Announcemens: R - RV - R circuis Homework 6: due nex Wednesday Inducion / A curren Inducion Self-Inducance, R ircuis X X X X X X X X X long solenoid Energy and energy
Physics 142: ecure 22 Today s Agenda Announcemens: R - RV - R circuis Homework 6: due nex Wednesday Inducion / A curren Inducion Self-Inducance, R ircuis X X X X X X X X X long solenoid Energy and energy
Department of Chemical Engineering University of Tennessee Prof. David Keffer. Course Lecture Notes SIXTEEN
 D. Keffe - ChE 40: Hea Tansfe and Fluid Flow Deamen of Chemical Enee Uniesi of Tennessee Pof. Daid Keffe Couse Lecue Noes SIXTEEN SECTION.6 DIFFERENTIL EQUTIONS OF CONTINUITY SECTION.7 DIFFERENTIL EQUTIONS
D. Keffe - ChE 40: Hea Tansfe and Fluid Flow Deamen of Chemical Enee Uniesi of Tennessee Pof. Daid Keffe Couse Lecue Noes SIXTEEN SECTION.6 DIFFERENTIL EQUTIONS OF CONTINUITY SECTION.7 DIFFERENTIL EQUTIONS
Do not turn over until you are told to do so by the Invigilator.
 UNIVERSITY OF EAST ANGLIA School of Mathematics Main Seies UG Examination 2015 16 FLUID DYNAMICS WITH ADVANCED TOPICS MTH-MD59 Time allowed: 3 Hous Attempt QUESTIONS 1 and 2, and THREE othe questions.
UNIVERSITY OF EAST ANGLIA School of Mathematics Main Seies UG Examination 2015 16 FLUID DYNAMICS WITH ADVANCED TOPICS MTH-MD59 Time allowed: 3 Hous Attempt QUESTIONS 1 and 2, and THREE othe questions.
( ) exp i ω b ( ) [ III-1 ] exp( i ω ab. exp( i ω ba
![( ) exp i ω b ( ) [ III-1 ] exp( i ω ab. exp( i ω ba ( ) exp i ω b ( ) [ III-1 ] exp( i ω ab. exp( i ω ba](/thumbs/83/87856399.jpg) THE INTEACTION OF ADIATION AND MATTE: SEMICLASSICAL THEOY PAGE 26 III. EVIEW OF BASIC QUANTUM MECHANICS : TWO -LEVEL QUANTUM SYSTEMS : The lieaue of quanum opics and lase specoscop abounds wih discussions
THE INTEACTION OF ADIATION AND MATTE: SEMICLASSICAL THEOY PAGE 26 III. EVIEW OF BASIC QUANTUM MECHANICS : TWO -LEVEL QUANTUM SYSTEMS : The lieaue of quanum opics and lase specoscop abounds wih discussions
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
