Some polynomials defined by generating functions and differential equations
|
|
|
- Victoria Dayna Riley
- 5 years ago
- Views:
Transcription
1 Dobashi et a, Coget Mathematics & Statistics 208, 4: PURE MATHEMATICS RESEARCH ARTICLE Some poyomias defied by geeratig fuctios ad differetia equatios Nobuyui Dobashi, Eria Suzui ad Shigeru Wataabe * Received: 04 November 206 Accepted: 28 December 206 First Pubished: 06 Jauary 207 *Correspodig author: Shigeru Wataabe, Departmet of Computer Sciece ad Egieerig, The Uiversity of Aizu, Ii-machi Tsuruga, Aizu- Waamatsu City, Fuushima , Japa E-mai: sigeru-w@u-aizuacjp Reviewig editor: Lisha Liu, Qufu Norma Uiversity, Chia Additioa iformatio is avaiabe at the ed of the artice Abstract: It is we ow that geeratig fuctios pay a importat roe i theory of the cassica orthogoa poyomias I this paper, we dea with systems of poyomias defied by geeratig fuctios ad the foowig probems for them A Derive a differetia equatio that each poyomia satisfies B Derive the geera soutio for the differetia equatio obtaied i A C Is the geera soutio obtaied i B writte as a iear combiatio of fuctios that are expressed by maig use of geeraized hypergeometric fuctios? The purpose of this paper is to give two exampes that the probem C ca be affirmativey soved Oe is reated to the Humbert poyomias, ad its geera soutio is writte by F -type hypergeometric fuctios The other is reated to a geearizatio of the Hermite poyomias, ad its geera soutio is writte by F -type hypergeometric fuctios Subjects: Sciece; Mathematics & Statistics; Advaced Mathematics; Aaysis - Mathematics; Specia Fuctios; Differetia Equatios Keywords: Humbert poyomia; geeraized Hermite poyomia; geeraized hypergeometric fuctio; geeratig fuctio; differetia equatio AMS subject cassificatios: Primary: 33C45 Itroductio It is iterestig to defie ew poyomias by ew geeratig fuctios, ad importat to study their properties Humbert 92 defied the poyomias Π ν,m x, 0,, 2,, by the geeratig fuctio mtx + t m ν Π ν,m xt 0 Goud 965 caed Π ν,m x the Humbert poyomia of degree ad gave its geeraizatio Miovaović ad Djordjević 987 gave a differetia equatio for the fuctio Π ν,m x usig differece operators ABOUT THE AUTHORS Eria Suzui ad Nobuyui Dobashi competed their master's theses at the Uiversity of Aizu i 203, 204, respectivey, uder Shigeru Wataabe Some parts of this artice are the mai parts of their master's theses Shigeru Wataabe is a seior associate professor at Departmet of Computer Sciece ad Egieerig, The Uiversity of Aizu, Fuushima, Japa His research iterests are Represetatio Theory of Groups ad Specia Fuctios PUBLIC INTEREST STATEMENT The cassica specia fuctios have various iterestig properties ad appicatios Some geeraizatios for them are aso cosidered For exampe, the sequece of the Humbert poyomias is a geeraizatio of the sequece of the Legedre poyomias I this artice, the authors focus o the Humbert poyomias ad the geeraized Hermite poyomias, ad show that they have deep reatios with the geeraized hypergeometric fuctios 208 The Authors This ope access artice is distributed uder a Creative Commos Attributio CC-BY 40 icese Page of 4
2 Dobashi et a, Coget Mathematics & Statistics 208, 4: Lahiri 97 defied the geeraized Hermite poyomias H,m,ν x, 0,, 2,, by the geeratig fuctio expνtx t m 0 H,m,ν x t! Goud ad Hopper 962 gave the other geeraizatio of the Hermite poyomias by the geeratig fuctio x a x t a exppx r x t r The case of a 0 is equivaet to that defied by Be 934 I Suzui 203, we cosidered defiig the poyomias Q x;, ν, 0,, 2,, by the foowig geeratig fuctio which is simiar to that of the Humbert poyomias 2tx + t ν Q x;, νt, 0 where is a iteger such that 2 ad ν is a positive rea umber Note that Π ν x Q,m mx 2;m, ν ad the poyomia Q x;, ν is ot etirey ew However, we gave a differetia equatio for the fuctio Q x;, ν, which is ot by differece operators ad is a expicit expressio For this reaso, we coud obtai the geera soutio at x 0 of the differetia equatio that Q x;, ν satisfies Ad it is writte as a iear combiatio of fuctios that are expressed by maig use of F -type hypergeometric fuctios I Dobashi 204, we cosidered defiig a geeraizatio of the Hermite poyomias by the geeratig fuctio expt x t +j R x;, jt, 0 where, j are positive itegers Ad we obtaied resuts simiar to the case of Q x;, ν I this case, the correspodig geera soutio is writte as a iear combiatio of fuctios that are expressed by maig use of F +j -type hypergeometric fuctios The purpose of this paper is to give the differetia equatios for Q x;, ν ad R x;, j, ad to derive the geera soutios at x 0 for them The discussio for Q x;, ν is give i Sectio 3, ad that for R x;, j is give i Sectio 4 2 Notatio For a rea umber x, [x] deotes the argest iteger ess tha or equa to x Deote Γα + Γα by α, where Γ is the Gamma fuctio For rea costats a, b, deote axf x+bf x by ax ddx + b f x Deote by N 0 the set of oegative itegers For positive itegers,, meas that is a divisor of The geeraized hypergeometric fuctios F is defied by F α, α 2,, α α ; x m α 2 m α m x m β, β 2,, β β m β 2 m β m m! m0 Page 2 of 4
3 Dobashi et a, Coget Mathematics & Statistics 208, 4: Poyomias Q x;, ν Let be a iteger such that 2, ad ν be a positive rea umber Uess otherwise oted, we fix, ν There exists a positive rea umber δ such that 2tx + t < for x ad δ < t <δ As described i Sectio, we defie the fuctios Q x;, ν, 0,, 2,, by 2tx + t ν Q x;, νt, 0 x, δ < t <δ 2 Lemma The fuctio Q x;, ν has the foowig expressio [ ] Q x;, ν r0 r 2 r ν r+r x r r! r! I particuar, Q x;, ν is a poyomia of degree Proof Sice we have, by the biomia theorem we see that 2tx + t ν 0 0 r0 which impies our assertio ν tt 2x! [ ] 0 r0 ν r! r! 2x r t r r+ r+r ν r+r 2x r t, r! r! 3 Recurrece reatios for Q x;, ν I this subsectio, we sha give recurrece reatios for the fuctios Q x;, ν For x ad δ < t <δ, set φx, t 2tx + t, Φx, t φx, t ν The it is easy to see that the foowig partia differetia equatios hod φx, t t Φx, t+νt 2xΦx, t 0, φx, t Φx, t 2νtΦx, t 0 x We ca derive recurrece reatios for Q x;, ν from these differetia equatios Rewrite both sides of 3 by maig use of 2 The we have 3 4 Page 3 of 4
4 Dobashi et a, Coget Mathematics & Statistics 208, 4: Q + x;, νt 2xQ x;, νt Q + x;, νt 2νxQ x;, νt νq + x;, νt 0 Compare the coefficiets of t i both sides of 5 The we have + ν + Q + x;, ν+ + Q + x;, ν 2 + νxq x;, ν 0, Simiary, by 4, we have the foowig recurrece reatio Q x;, ν 2νQ x;, + ν+2xq x;, ν Q + x;, ν, 7 Further, we sha give some recurrece reatios for the fuctios Q x;, ν that ca be derived from the Equatios 6 ad 7 Differetiate both sides of 6 ad substitute 7 ito it The we obtai 2ν + νq x;, ν+2ν xq x;, ν ν Q + x;, ν 0, Remar we have This recurrece reatio hods aso for 0 < I fact, if 0 <, from Lemma Q x;, ν 2 ν x, Q! + x;, ν 2+ ν + +! x+, which assert that the recurrece reatio above hods aso for 0 < That is, we have 2ν + νq x;, ν+2ν xq x;, ν ν Q + x;, ν 0, 0 8 Sove the Equatio 7 for Q + x;, ν ad substitute it ito 8 The we have ν Q x;, ν 2ν Q + x;, ν + 2ν xq x;, ν, 9 32 Differetia equatio that Q x;, ν satisfies I this subsectio, by maig use of the resuts give i the precedig subsectio we sha give a differetia equatio that Q x;, ν satisfies The mai theorem is Theorem For a arbitrary 0, the fuctio Q x;, ν satisfies the foowig differetia equatio Q 2 x;, ν { x ddx } + + ν + r xq x;, ν Q x;, ν Page 4 of 4
5 Dobashi et a, Coget Mathematics & Statistics 208, 4: Proof Operate d m dx m to both sides of 8 ad mae use of the Leibiz rue The we have ν Q m+ + Suppose that ν This equatio is equivaet to Repacig m by m ad by, the we have Repeatig this formua, the we obtai Set m The, we have x;, ν 2ν xqm+ x;, ν + 2ν + ν + m Q m x;, ν, m, 0 Q m+ x;, ν 2 { x ddx } + + m + ν + m Q m x;, ν, m, 0 Q m x;, ν 2 { x ddx } + m + ν + m Q m x;, ν, m, Q m x;, ν 2 { x ddx } + m + ν + m 2 { x ddx } + m + ν + m 2 2 { x ddx } + m + ν + m Q m x;, ν, Q x;, ν 2 m, { x ddx } + + ν + r Q + x;, ν, Maig use of 9, it is easy to see that our assertio hods for That is, for the foowig hods Q 2 x;, ν { x ddx } + + ν + r xq x;, ν Q x;, ν 0 I the case of 0 <, cosiderig Remar, we see that xq x;, ν Q x;, ν 0, which impies that 0 hods aso for 0 < Therefore, if ν, we ca cocude that 0 hods for ay 0 I the case of ν, ote that both sides of 0 are cotiuous with respect to ν Taig the imit ν i 0, we ca see that 0 hods aso for ν ad 0 Exampe If 2, the poyomia Q x;, ν is equa to the Gegebauer poyomia of degree ad the differetia equatio i Theorem is as foows x 2 Q x;2, ν 2ν + xq x;2, ν+ + 2νQ x;2, ν 0, which is we ow as Gegebauer s differetia equatio Page 5 of 4
6 Dobashi et a, Coget Mathematics & Statistics 208, 4: Geera soutio of differetia equatio that Q x;, ν satisfies I this subsectio, we sha give the geera soutio at x 0 of the differetia equatio that Q x;, ν satisfies By Theorem, the differetia equatio that we cosider is as foows y { x ddx } ν + r xy y To sove this equatio, we use the power series method Sice x 0 is a reguar poit of the Equatio, we set y a m x m m0 2 It is cear that y ma m x m, y m m0 m +! a m! m+ x m 3 Substitute 2, 3 ito Hece, we obtai m +! a 2 m! m+ x m m0 { { } } m a m m + + ν + r x m m0 4 Comparig the coefficiets of x m i 4, the we have m +! a 2 m! m+ { { } } m a m m + + ν + r, which is equivaet to a 2 m { } m!m m + + ν + r m! a m 5 For each N 0 ad each p N 0 such that 0 p <, set m + p Repeatig 5, it is easy to see that +p! 2+p! p! +p 2+p p a +p + p! +p! + p! 2 a p where A r, 6 Page 6 of 4
7 Dobashi et a, Coget Mathematics & Statistics 208, 4: A r +p + + ν + r 2+p + + ν + r p + + ν + r By simpe cacuatios, we have +p 2+p p + p 2 + p p p, ad A r p + + ν + r p + + ν + r p + + ν + r p + + ν + r 7 8 Further, we ow the foowig formua cf Prudiov, Brychov, & Marichev, 986, p + p p! + p + p!! 9 Substitute 7, 8 ad 9 ito 6 Hece, we obtai 2 p p + +ν+ r a +p a p p+ p+2 + p+! Thus, we have a +p x +p a p x p 0 F p Therefore, we obtai the desired resut That is, set F,ν,p x F p We obtai the foowig, p + +ν+,, Theorem 2 The fuctios x p F,ν,p x p 0,,, are the ieary idepedet soutios at x 0 of I particuar, its geera soutio at x 0 is give by p + +ν+ p+, p+2,,, +,, p+, p + +ν+,, p + +ν+ p+, p+2,,, +,, p+ ; 2x ; 2x Page 7 of 4
8 Dobashi et a, Coget Mathematics & Statistics 208, 4: a p x p F,ν,p x, p0 where a 0,, a are arbitrary costats Remar 2 We choose, p N 0 such that + p, 0 p < The F,ν,p x is a poyomia of degree Thus, x p F,ν,p x is a poyomia of degree, ad differs oy by a costat from Q x;, ν 4 Poyomias R x;, j Let, j be positive itegers Uess otherwise oted, we fix, j As described i Sectio, we defie the fuctios R x;, j, 0,, 2,, by expt x t +j For N 0, set I, j, { R x;, jt, < x <, < t < 0 q N 0 0 q [ ] }, + jq + j 20 2 The we obtai Lemma 2 The fuctio R x;, j has the foowig expressio R x;, j q I,j, q x +jq! q! +jq If I, j,, we mea R x;, j 0 Proof Maig use of the Tayor expasio for the expoetia fuctio exp x, it is easy to see that expt x t +j expt x exp t +j t x p t +j q p! q! p0 q0 q x p t p++jq p! q! p,q0 For N 0 there exist p, q N 0 such that p + + jq if ad oy if p + jq, which are equivaet to + jq, [ ] 0 q, + j [ ] 0 q + j Therefore, we obtai the desired resut Page 8 of 4
9 Dobashi et a, Coget Mathematics & Statistics 208, 4: Recurrece reatios for R x;, j I this subsectio, we sha give recurrece reatios for the fuctios R x;, j Set Φx, t expt x t +j The it is easy to see that the foowig partia differetia equatios hod t Φx, t t x + jt +j Φx, t, x Φx, t t Φx, t We ca derive recurrece reatios for R x;, j from these differetia equatios Rewrite both sides of 22 by maig use of 20 The we have + R + x;, jt xr + x;, jt +j + jr j+ x;, jt Compare the coefficiets of t i both sides of 24 The we have + R + x;, j xr + x;, j + jr j+ x;, j, + j Simiary, by 23, we have the foowig recurrece reatio R x;, j R x;, j, 26 Repacig by j +, the we have R x;, j R j+ j+ x;, j, + j 27 Substitute 26, 27 ito 25 We have + R + x;, j xr + x;, j + jr j+ x;, j, + j Repacig by, the we obtai + jr x;, j j xr x;, j R x;, j, + j Remar 3 This recurrece reatio hods aso for + j > j Suppose that + j > j The it is easy to see that [ ] 0, + j It foows from these reatios ad Lemma 2 that R x;, j [ ] j 0 + j { x!,, 0, otherwise, Page 9 of 4
10 Dobashi et a, Coget Mathematics & Statistics 208, 4: ad R j x;, j Thus, we obtai {, j 0, 0, otherwise xr x;, j R x;, j 0, R j x;, j 0 Therefore, we ca cocude that + jr x;, j j xr x;, j R x;, j, j 42 Differetia equatio that R x;, j satisfies 28 I this subsectio, by maig use of the resuts give i the precedig subsectio we sha give a differetia equatio that R x;, j satisfies The mai theorem is Theorem 3 For a arbitrary 0, the fuctio R x;, j satisfies the foowig differetia equatio R +j x;, j + j {x ddx + r + j } R x;, j Proof Operate d m dx m to both sides of 28 ad mae use of the Leibiz rue The we have + jr m+ j x;, j xr m+ m 0, j x;, j+m R m x;, j, Repacig m by m ad by j, the we have R m x;, j {x ddx } j + j + m j R m x;, j, j m, j Repeatig this formua, the we obtai R m x;, j {x ddx } j + j + m j {x ddx } + j + m 2 j 2 {x ddx } + j + m j R m x;, j, m, j Set m The we have R j x;, j + j j {x ddx + r j r } R x;, j, 29 O the other had, by 26 we see that Page 0 of 4
11 Dobashi et a, Coget Mathematics & Statistics 208, 4: R j x;, j R j x;, j, j 30 It foows from 29, 30 that R +j x;, j + j j {x ddx + r + j } R x;, j, 3 I what foows, we assume that 0 < j I this case, we have + j < j + j < Tae q I, j, It foows from 2, 32 that 0 q < ad there exists r N 0 such that 32 0 < r, r q For such r, we see that {x ddx } q + r + j x +jq 0 +jq! q! Thus, by Lemma 2 we obtai {x ddx + r + j } R x;, j 0 33 Next, we sha show R +j x;, j 0 34 Set +,, N 0, 0 <, where ote that < j By this reatio, 26 ad Lemma 2, we have R x;, j R x;, j R x;, j q I,j, q x +jq! q! +jq 35 Notice that R x;, j {, 0, 0, otherwise It foows from this reatio ad 35 that 34 Therefore, by 33, 34 we ca cocude that our assertio hods aso for 0 < j Exampe 2 If j, the poyomia R x;, j is essetiay equa to the Hermite poyomia of degree ad the differetia equatio i Theorem 3 is as foows R x;, 2 xr x;, + 2 R x;, 0, which is we ow as Hermite s differetia equatio Page of 4
12 Dobashi et a, Coget Mathematics & Statistics 208, 4: Geera soutio of differetia equatio that R x;, j satisfies I this subsectio, we sha give the geera soutio at x 0 of the differetia equatio that R x;, j satisfies By Theorem 3, the differetia equatio that we cosider is as foows y +j + j {x ddx + r + j } y 36 To sove this equatio, we use the power series method Sice x 0 is a reguar poit of the Equatio 36, we set y a m x m m0 37 Substitute 37 ito 36 Hece, we obtai m0 m + + j! a m! m++j x m { } a + j m{ } m + r + j x m m0 38 Comparig the coefficiets of x m i 38, the we have m + + j! { } a m! m++j a + j m m + r + j, which is equivaet to a m m j! + j m r jr m! a m j 39 For each N 0 ad each p N 0 such that 0 p < + j, set m + j + p Repeatig 39, it is easy to see that + j +p! + j 2+p! p! a +j+p + j + p! + j +p! + j + p! a p B + j r, where 40 B r + j +p r jr + j 2+p r jr p r jr By simpe cacuatios, we have Page 2 of 4
13 Dobashi et a, Coget Mathematics & Statistics 208, 4: B r + j p r jr + j p r jr + j p r jr + j p r jr + j + j 4 Further, repace by + j i 9 ad substitute it ad 4 ito 40 Hece, we obtai a +j+p + j +j p+ +j Thus, we have a +j+p x +j+p a p x p 0 a p p+2 F +j p r jr +j +j +j+ Therefore, we obtai the desired resut That is, set +j p j +j p+, p+2 +j +j, +j p 2 2j +j,, +j, +j +j,, p++j +j+ +j +j! p 2 j +j,, p++j +j +j ; x + j G,j,p x F +j p j +j p+, p+2 +j, p 2 2j +j,, +j, +j +j,, +j+ +j p 2 j,, +j p++j +j +j ; x + j We obtai the foowig Theorem 4 The fuctios x p G,j,p xp 0,,, + j are the ieary idepedet soutios at x 0 of 36 I particuar, its geera soutio at x 0 is give by +j p0 a p x p G,j,p x, where a 0,, a +j are arbitrary costats Remar 4 Assume that R x;, j is ot ideticay equa to 0 The we have I, j, Tae q I, j, ad set + jq p, p N 0, p + jq + p, q, p N 0,0 p < + j, q q + p, q, p N 0,0 p <, p p, r p The we have p r jr + j q q, which meas G,j,p x is a poyomia Thus, x p G,j,p x is a poyomia soutio of 36, ad differs oy by a costat from R x;, j Page 3 of 4
14 Dobashi et a, Coget Mathematics & Statistics 208, 4: Fudig The authors received o direct fudig for this research Author detais Nobuyui Dobashi E-mai: otetu32@gmaicom Eria Suzui E-mai: seasideaieto@gmaicom Shigeru Wataabe E-mai: sigeru-w@u-aizuacjp Departmet of Computer Sciece ad Egieerig, The Uiversity of Aizu, Ii-machi Tsuruga, Aizu-Waamatsu, Fuushima , Japa Citatio iformatio Cite this artice as: Some poyomias defied by geeratig fuctios ad differetia equatios, Nobuyui Dobashi, Eria Suzui & Shigeru Wataabe, Coget Mathematics & Statistics 208, 4: Refereces Be, E T 934 Expoetia poyomias Aas of Mathematics, 35, Dobashi, N 204 Some ew fuctios associated with cassica specia fuctios Master s thesis, Aizu- Waamatsu: The Uiversity of Aizu Goud, H W 965 Iverse series reatios ad other expasios ivovig Humbert poyomias Due Mathematica Joura, 32, Goud, H W, & Hopper, A T 962 Operatioa formuas coected with two geeraizatios of Hermite poyomias Due Mathematica Joura, 29, 5 63 Humbert, P 92 Some extesios of Pichere s poyomias Proceedigs of the Ediburgh Mathematica Society, 39, 2 24 Lahiri, M 97 O a geeraisatio of Hermite poyomias Proceedigs of the America Mathematica Society, 27, 7 2 Miovaović, G V, & Djordjević, G 987 O some properties of Humbert s poyomias Fiboacci Quartery, 25, Prudiov, A P, Brychov, Y A, & Marichev, O I 986 Itegras ad Series New Yor, NY: Gordo & Breach Suzui, E 203 New properties of dis poyomias ad some fuctios associated with cassica specia fuctios Master s thesis Aizu-Waamatsu: The Uiversity of Aizu 208 The Authors This ope access artice is distributed uder a Creative Commos Attributio CC-BY 40 icese You are free to: Share copy ad redistribute the materia i ay medium or format Adapt remix, trasform, ad buid upo the materia for ay purpose, eve commerciay The icesor caot revoe these freedoms as og as you foow the icese terms Uder the foowig terms: Attributio You must give appropriate credit, provide a i to the icese, ad idicate if chages were made You may do so i ay reasoabe maer, but ot i ay way that suggests the icesor edorses you or your use No additioa restrictios You may ot appy ega terms or techoogica measures that egay restrict others from doig aythig the icese permits Coget Mathematics & Statistics ISSN: is pubished by Coget OA, part of Tayor & Fracis Group Pubishig with Coget OA esures: Immediate, uiversa access to your artice o pubicatio High visibiity ad discoverabiity via the Coget OA website as we as Tayor & Fracis Oie Dowoad ad citatio statistics for your artice Rapid oie pubicatio Iput from, ad diaog with, expert editors ad editoria boards Retetio of fu copyright of your artice Guarateed egacy preservatio of your artice Discouts ad waivers for authors i deveopig regios Submit your mauscript to a Coget OA joura at wwwcogetoacom Page 4 of 4
Alternative Orthogonal Polynomials. Vladimir Chelyshkov
 Aterative Orthogoa oyomias Vadimir Cheyshov Istitute of Hydromechaics of the NAS Uraie Georgia Souther Uiversity USA Abstract. The doube-directio orthogoaizatio agorithm is appied to costruct sequeces
Aterative Orthogoa oyomias Vadimir Cheyshov Istitute of Hydromechaics of the NAS Uraie Georgia Souther Uiversity USA Abstract. The doube-directio orthogoaizatio agorithm is appied to costruct sequeces
QUANTITATIVE ESTIMATES FOR GENERALIZED TWO DIMENSIONAL BASKAKOV OPERATORS. Neha Bhardwaj and Naokant Deo
 Korea J Math 24 2016, No 3, pp 335 344 http://dxdoiorg/1011568/jm2016243335 QUANTITATIVE ESTIMATES FOR GENERALIZED TWO DIMENSIONAL BASKAKOV OPERATORS Neha Bhardwaj ad Naoat Deo Abstract I this paper, we
Korea J Math 24 2016, No 3, pp 335 344 http://dxdoiorg/1011568/jm2016243335 QUANTITATIVE ESTIMATES FOR GENERALIZED TWO DIMENSIONAL BASKAKOV OPERATORS Neha Bhardwaj ad Naoat Deo Abstract I this paper, we
Topics in Fourier Analysis-I 1
 Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
Strauss PDEs 2e: Section Exercise 4 Page 1 of 5. u tt = c 2 u xx ru t for 0 < x < l u = 0 at both ends u(x, 0) = φ(x) u t (x, 0) = ψ(x),
 Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
Existence of Nonoscillatory Solution of High Order Linear Neutral Delay Difference Equation
 oder Appied Sciece ovember, 008 Existece of oosciatory Soutio of High Order Liear eutra Deay Differece Equatio Shasha Zhag, Xiaozhu Zhog, Pig Yu, Wexia Zhag & ig Li Departmet of athematics Yasha Uiversity
oder Appied Sciece ovember, 008 Existece of oosciatory Soutio of High Order Liear eutra Deay Differece Equatio Shasha Zhag, Xiaozhu Zhog, Pig Yu, Wexia Zhag & ig Li Departmet of athematics Yasha Uiversity
Discrete Fourier Transform
 Discrete Fourier Trasform ) Purpose The purpose is to represet a determiistic or stochastic siga u( t ) as a fiite Fourier sum, whe observatios of u() t ( ) are give o a reguar grid, each affected by a
Discrete Fourier Trasform ) Purpose The purpose is to represet a determiistic or stochastic siga u( t ) as a fiite Fourier sum, whe observatios of u() t ( ) are give o a reguar grid, each affected by a
RAMŪNAS GARUNKŠTIS AND JUSTAS KALPOKAS
 SUM OF HE PERIODIC ZEA-FUNCION OVER HE NONRIVIAL ZEROS OF HE RIEMANN ZEA-FUNCION RAMŪNAS GARUNKŠIS AND JUSAS KALPOKAS Abstract We cosider the asymptotic of the sum of vaues of the periodic zeta-fuctio
SUM OF HE PERIODIC ZEA-FUNCION OVER HE NONRIVIAL ZEROS OF HE RIEMANN ZEA-FUNCION RAMŪNAS GARUNKŠIS AND JUSAS KALPOKAS Abstract We cosider the asymptotic of the sum of vaues of the periodic zeta-fuctio
SOME INTEGRAL FORMULAS FOR CLOSED MINIMALLY IMMERSED HYPERSURFACE IN THE UNIT SPHERE S n+1
 TWS J. Pure App. ath. V.1 N.1 010 pp.81-85 SOE INTEGAL FOULAS FO CLOSED INIALLY IESED HYPESUFACE IN THE UNIT SPHEE S +1 IHIBAN KÜLAHCI 1 AHUT EGÜT 1 Abstract. I this paper we obtai some itegra formuas
TWS J. Pure App. ath. V.1 N.1 010 pp.81-85 SOE INTEGAL FOULAS FO CLOSED INIALLY IESED HYPESUFACE IN THE UNIT SPHEE S +1 IHIBAN KÜLAHCI 1 AHUT EGÜT 1 Abstract. I this paper we obtai some itegra formuas
April 1980 TR/96. Extrapolation techniques for first order hyperbolic partial differential equations. E.H. Twizell
 TR/96 Apri 980 Extrapoatio techiques for first order hyperboic partia differetia equatios. E.H. Twize W96086 (0) 0. Abstract A uifor grid of step size h is superiposed o the space variabe x i the first
TR/96 Apri 980 Extrapoatio techiques for first order hyperboic partia differetia equatios. E.H. Twize W96086 (0) 0. Abstract A uifor grid of step size h is superiposed o the space variabe x i the first
Here are some solutions to the sample problems concerning series solution of differential equations with non-constant coefficients (Chapter 12).
 Lecture Appedi B: Some sampe probems from Boas Here are some soutios to the sampe probems cocerig series soutio of differetia equatios with o-costat coefficiets (Chapter ) : Soutio: We wat to cosider the
Lecture Appedi B: Some sampe probems from Boas Here are some soutios to the sampe probems cocerig series soutio of differetia equatios with o-costat coefficiets (Chapter ) : Soutio: We wat to cosider the
ON WEAK -STATISTICAL CONVERGENCE OF ORDER
 UPB Sci Bu, Series A, Vo 8, Iss, 8 ISSN 3-77 ON WEAK -STATISTICAL CONVERGENCE OF ORDER Sia ERCAN, Yavuz ALTIN ad Çiğdem A BEKTAŞ 3 I the preset paper, we give the cocept of wea -statistica covergece of
UPB Sci Bu, Series A, Vo 8, Iss, 8 ISSN 3-77 ON WEAK -STATISTICAL CONVERGENCE OF ORDER Sia ERCAN, Yavuz ALTIN ad Çiğdem A BEKTAŞ 3 I the preset paper, we give the cocept of wea -statistica covergece of
GENERATING FUNCTIONS
 GENERATING FUNCTIONS XI CHEN. Exapes Questio.. Toss a coi ties ad fid the probabiity of gettig exacty k heads. Represet H by x ad T by x 0 ad a sequece, say, HTHHT by (x (x 0 (x (x (x 0. We see that a
GENERATING FUNCTIONS XI CHEN. Exapes Questio.. Toss a coi ties ad fid the probabiity of gettig exacty k heads. Represet H by x ad T by x 0 ad a sequece, say, HTHHT by (x (x 0 (x (x (x 0. We see that a
On the Product Representation of Number Sequences, with Applications to the Family of Generalized Fibonacci Numbers
 1 2 3 47 6 23 11 Joura of Iteger Sequeces, Vo. 19 2016, Artice 16.3.6 O the Product Represetatio of Number Sequeces, with Appicatios to the Famiy of Geeraized Fiboacci Numbers Michee Rudoph-Liith Uité
1 2 3 47 6 23 11 Joura of Iteger Sequeces, Vo. 19 2016, Artice 16.3.6 O the Product Represetatio of Number Sequeces, with Appicatios to the Famiy of Geeraized Fiboacci Numbers Michee Rudoph-Liith Uité
Supplementary Material on Testing for changes in Kendall s tau
 Suppemetary Materia o Testig for chages i Keda s tau Herod Dehig Uiversity of Bochum Daie Voge Uiversity of Aberdee Marti Weder Uiversity of Greifswad Domiik Wied Uiversity of Cooge Abstract This documet
Suppemetary Materia o Testig for chages i Keda s tau Herod Dehig Uiversity of Bochum Daie Voge Uiversity of Aberdee Marti Weder Uiversity of Greifswad Domiik Wied Uiversity of Cooge Abstract This documet
Some Identities on the Generalized Changhee-Genocchi Polynomials and Numbers
 28 Joura of Advaces i Appied Matheatics, Vo. 4, No. 1, Jauary 2019 https://dx.doi.org/10.22606/jaa.2019.41004 Soe Idetities o the Geeraized Chaghee-Geocchi Poyoias ad Nubers Da-Da Zhao * ad Wuyugaowa Departet
28 Joura of Advaces i Appied Matheatics, Vo. 4, No. 1, Jauary 2019 https://dx.doi.org/10.22606/jaa.2019.41004 Soe Idetities o the Geeraized Chaghee-Geocchi Poyoias ad Nubers Da-Da Zhao * ad Wuyugaowa Departet
Expansions of the exponential and the logarithm of power series and applications
 Arab. J. Math. (207) 6:95 08 DOI 0.007/s40065-07-066-4 Arabia Joura of Mathematics Feg Qi Xiao-Tig Shi Fag-Fag Liu Expasios of the expoetia ad the ogarithm of power series ad appicatios Received: 2 Jue
Arab. J. Math. (207) 6:95 08 DOI 0.007/s40065-07-066-4 Arabia Joura of Mathematics Feg Qi Xiao-Tig Shi Fag-Fag Liu Expasios of the expoetia ad the ogarithm of power series ad appicatios Received: 2 Jue
Applicable Analysis and Discrete Mathematics available online at
 Appicabe Aaysis ad Discrete Mathematics avaiabe oie at http://pefmath.etf.rs App. Aa. Discrete Math. 1 018, 001 05. https://doi.org/10.98/aadm1801001s NEW FAMILIES OF SPECIAL NUMBERS FOR COMPUTING NEGATIVE
Appicabe Aaysis ad Discrete Mathematics avaiabe oie at http://pefmath.etf.rs App. Aa. Discrete Math. 1 018, 001 05. https://doi.org/10.98/aadm1801001s NEW FAMILIES OF SPECIAL NUMBERS FOR COMPUTING NEGATIVE
Self-Consistent Simulations of Beam and Plasma Systems Final Exam ( take-home )
 Sef-Cosistet Simuatios of Beam ad Pasma Systems Fia Exam ( take-home ) S. M. Lud, J.-L. Vay, R. Lehe, ad D. Wikeher Thursday, Jue 16 th, 2016 Probem 1 - Maxwe s equatios ad redudat iformatio. a) Show that
Sef-Cosistet Simuatios of Beam ad Pasma Systems Fia Exam ( take-home ) S. M. Lud, J.-L. Vay, R. Lehe, ad D. Wikeher Thursday, Jue 16 th, 2016 Probem 1 - Maxwe s equatios ad redudat iformatio. a) Show that
CHAPTER 4 FOURIER SERIES
 CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
REFINEMENT OF JENSEN S INEQUALITY FOR OPERATOR CONVEX FUNCTIONS
 Avaiabe oie at http://sci.org Adv. Iequa. App. 204, 204:26 ISSN: 2050-746 REFINEMENT OF JENSEN S INEQUALITY FOR OPERATOR CONVEX FUNCTIONS L. HORVÁTH, K.A. KHAN 2, J. PEČARIĆ 3,4, Departmet o Mathematics,
Avaiabe oie at http://sci.org Adv. Iequa. App. 204, 204:26 ISSN: 2050-746 REFINEMENT OF JENSEN S INEQUALITY FOR OPERATOR CONVEX FUNCTIONS L. HORVÁTH, K.A. KHAN 2, J. PEČARIĆ 3,4, Departmet o Mathematics,
ORTHOGONAL POLYNOMIALS AND CONTRAST MATRICES
 ORTHOGONAL POLYNOMIALS AND CONTRAST MATRICES BY Aa N. Ageos ad W. T. Federer BU-754-M November 1981 Abstract The use of Legedre, Hermite, Chebyshev ad Laguerre poyomias i fittig a regressio equatio ad
ORTHOGONAL POLYNOMIALS AND CONTRAST MATRICES BY Aa N. Ageos ad W. T. Federer BU-754-M November 1981 Abstract The use of Legedre, Hermite, Chebyshev ad Laguerre poyomias i fittig a regressio equatio ad
Lecture 7: Properties of Random Samples
 Lecture 7: Properties of Radom Samples 1 Cotiued From Last Class Theorem 1.1. Let X 1, X,...X be a radom sample from a populatio with mea µ ad variace σ
Lecture 7: Properties of Radom Samples 1 Cotiued From Last Class Theorem 1.1. Let X 1, X,...X be a radom sample from a populatio with mea µ ad variace σ
Rational Points over Finite Fields on a Family of Higher Genus Curves and Hypergeometric Functions. Yih Sung
 TAIWANESE JOURNAL OF MATHEMATICS Vo. xx, No. x, pp. 1 25, xx 20xx DOI: 10.11650/tjm.xx.20xx.7724 This paper is avaiabe oie at http://joura.tms.org.tw Ratioa Poits over Fiite Fieds o a Famiy of Higher Geus
TAIWANESE JOURNAL OF MATHEMATICS Vo. xx, No. x, pp. 1 25, xx 20xx DOI: 10.11650/tjm.xx.20xx.7724 This paper is avaiabe oie at http://joura.tms.org.tw Ratioa Poits over Fiite Fieds o a Famiy of Higher Geus
Fibonacci numbers and orthogonal polynomials
 Fiboacci umbers ad orthogoal polyomials Christia Berg April 10, 2006 Abstract We prove that the sequece (1/F +2 0 of reciprocals of the Fiboacci umbers is a momet sequece of a certai discrete probability,
Fiboacci umbers ad orthogoal polyomials Christia Berg April 10, 2006 Abstract We prove that the sequece (1/F +2 0 of reciprocals of the Fiboacci umbers is a momet sequece of a certai discrete probability,
Discrete Fourier Transform
 Discrete Fourier Trasform 3) Compex Case et s distiguish the three cases + J + > + J + + J + < (35) Ad et s begi treatig the isodetermied case + J +, addig at first the hypothesis that J,. I this case
Discrete Fourier Trasform 3) Compex Case et s distiguish the three cases + J + > + J + + J + < (35) Ad et s begi treatig the isodetermied case + J +, addig at first the hypothesis that J,. I this case
Research Article A Unified Weight Formula for Calculating the Sample Variance from Weighted Successive Differences
 Discrete Dyamics i Nature ad Society Article ID 210761 4 pages http://dxdoiorg/101155/2014/210761 Research Article A Uified Weight Formula for Calculatig the Sample Variace from Weighted Successive Differeces
Discrete Dyamics i Nature ad Society Article ID 210761 4 pages http://dxdoiorg/101155/2014/210761 Research Article A Uified Weight Formula for Calculatig the Sample Variace from Weighted Successive Differeces
NEW FAST CONVERGENT SEQUENCES OF EULER-MASCHERONI TYPE
 UPB Sci Bull, Series A, Vol 79, Iss, 207 ISSN 22-7027 NEW FAST CONVERGENT SEQUENCES OF EULER-MASCHERONI TYPE Gabriel Bercu We itroduce two ew sequeces of Euler-Mascheroi type which have fast covergece
UPB Sci Bull, Series A, Vol 79, Iss, 207 ISSN 22-7027 NEW FAST CONVERGENT SEQUENCES OF EULER-MASCHERONI TYPE Gabriel Bercu We itroduce two ew sequeces of Euler-Mascheroi type which have fast covergece
Comparison Study of Series Approximation. and Convergence between Chebyshev. and Legendre Series
 Applied Mathematical Scieces, Vol. 7, 03, o. 6, 3-337 HIKARI Ltd, www.m-hikari.com http://d.doi.org/0.988/ams.03.3430 Compariso Study of Series Approimatio ad Covergece betwee Chebyshev ad Legedre Series
Applied Mathematical Scieces, Vol. 7, 03, o. 6, 3-337 HIKARI Ltd, www.m-hikari.com http://d.doi.org/0.988/ams.03.3430 Compariso Study of Series Approimatio ad Covergece betwee Chebyshev ad Legedre Series
SOME RELATIONS ON HERMITE MATRIX POLYNOMIALS. Levent Kargin and Veli Kurt
 Mathematical ad Computatioal Applicatios, Vol. 18, No. 3, pp. 33-39, 013 SOME RELATIONS ON HERMITE MATRIX POLYNOMIALS Levet Kargi ad Veli Kurt Departmet of Mathematics, Faculty Sciece, Uiversity of Adeiz
Mathematical ad Computatioal Applicatios, Vol. 18, No. 3, pp. 33-39, 013 SOME RELATIONS ON HERMITE MATRIX POLYNOMIALS Levet Kargi ad Veli Kurt Departmet of Mathematics, Faculty Sciece, Uiversity of Adeiz
EXTENSION OF RAMANUJAN S CONGRUENCES FOR THE PARTITION FUNCTION MODULO POWERS OF 5. Jeremy Lovejoy and Ken Ono. Appearing in Crelle s Journal
 EXTENSION OF RAMANUJAN S CONGRUENCES FOR THE PARTITION FUNCTION MODULO POWERS OF 5 Jeremy Lovejoy ad Ke Oo Appearig i Cree s Joura 1. Itroductio ad Statemet of Resuts A partitio of a positive iteger is
EXTENSION OF RAMANUJAN S CONGRUENCES FOR THE PARTITION FUNCTION MODULO POWERS OF 5 Jeremy Lovejoy ad Ke Oo Appearig i Cree s Joura 1. Itroductio ad Statemet of Resuts A partitio of a positive iteger is
Star Saturation Number of Random Graphs
 Star Saturatio Number of Radom Graphs A. Mohammadia B. Tayfeh-Rezaie Schoo of Mathematics, Istitute for Research i Fudameta Scieces IPM, P.O. Box 19395-5746, Tehra, Ira ai m@ipm.ir tayfeh-r@ipm.ir Abstract
Star Saturatio Number of Radom Graphs A. Mohammadia B. Tayfeh-Rezaie Schoo of Mathematics, Istitute for Research i Fudameta Scieces IPM, P.O. Box 19395-5746, Tehra, Ira ai m@ipm.ir tayfeh-r@ipm.ir Abstract
Review Article Incomplete Bivariate Fibonacci and Lucas p-polynomials
 Discrete Dyamics i Nature ad Society Volume 2012, Article ID 840345, 11 pages doi:10.1155/2012/840345 Review Article Icomplete Bivariate Fiboacci ad Lucas p-polyomials Dursu Tasci, 1 Mirac Ceti Firegiz,
Discrete Dyamics i Nature ad Society Volume 2012, Article ID 840345, 11 pages doi:10.1155/2012/840345 Review Article Icomplete Bivariate Fiboacci ad Lucas p-polyomials Dursu Tasci, 1 Mirac Ceti Firegiz,
MAT1026 Calculus II Basic Convergence Tests for Series
 MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
A generalization of Morley s congruence
 Liu et al. Advaces i Differece Euatios 05 05:54 DOI 0.86/s366-05-0568-6 R E S E A R C H Ope Access A geeralizatio of Morley s cogruece Jiaxi Liu,HaoPa ad Yog Zhag 3* * Correspodece: yogzhag98@63.com 3
Liu et al. Advaces i Differece Euatios 05 05:54 DOI 0.86/s366-05-0568-6 R E S E A R C H Ope Access A geeralizatio of Morley s cogruece Jiaxi Liu,HaoPa ad Yog Zhag 3* * Correspodece: yogzhag98@63.com 3
New Results for the Fibonacci Sequence Using Binet s Formula
 Iteratioal Mathematical Forum, Vol. 3, 208, o. 6, 29-266 HIKARI Ltd, www.m-hikari.com https://doi.org/0.2988/imf.208.832 New Results for the Fiboacci Sequece Usig Biet s Formula Reza Farhadia Departmet
Iteratioal Mathematical Forum, Vol. 3, 208, o. 6, 29-266 HIKARI Ltd, www.m-hikari.com https://doi.org/0.2988/imf.208.832 New Results for the Fiboacci Sequece Usig Biet s Formula Reza Farhadia Departmet
Chapter 3. Strong convergence. 3.1 Definition of almost sure convergence
 Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
GENERALIZED HARMONIC NUMBER IDENTITIES AND A RELATED MATRIX REPRESENTATION
 J Korea Math Soc 44 (2007), No 2, pp 487 498 GENERALIZED HARMONIC NUMBER IDENTITIES AND A RELATED MATRIX REPRESENTATION Gi-Sag Cheo ad Moawwad E A El-Miawy Reprited from the Joural of the Korea Mathematical
J Korea Math Soc 44 (2007), No 2, pp 487 498 GENERALIZED HARMONIC NUMBER IDENTITIES AND A RELATED MATRIX REPRESENTATION Gi-Sag Cheo ad Moawwad E A El-Miawy Reprited from the Joural of the Korea Mathematical
<aj + ck) m (bj + dk) n. E E (-D m+n - j - k h)(i) j=0 k=0 \ / \ /
 ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYMOND j=. WHITNEY Loc Have State College Loc Have # Pesylvaia Sed all commuicatios cocerig Advaced Problems ad Solutios to Raymod E. Whitey, Mathematics Departmet,
ADVANCED PROBLEMS AND SOLUTIONS Edited by RAYMOND j=. WHITNEY Loc Have State College Loc Have # Pesylvaia Sed all commuicatios cocerig Advaced Problems ad Solutios to Raymod E. Whitey, Mathematics Departmet,
Representing derivatives of Chebyshev polynomials by Chebyshev polynomials and related questions
 Ope Math. 2017; 15: 1156 1160 Ope Mathematic Reearch Artice Hemut Prodiger* Repreetig derivative of Chebyhev poyomia by Chebyhev poyomia ad reated quetio http://doi.org/10.1515/math-2017-0096 Received
Ope Math. 2017; 15: 1156 1160 Ope Mathematic Reearch Artice Hemut Prodiger* Repreetig derivative of Chebyhev poyomia by Chebyhev poyomia ad reated quetio http://doi.org/10.1515/math-2017-0096 Received
SOME TRIBONACCI IDENTITIES
 Mathematics Today Vol.7(Dec-011) 1-9 ISSN 0976-38 Abstract: SOME TRIBONACCI IDENTITIES Shah Devbhadra V. Sir P.T.Sarvajaik College of Sciece, Athwalies, Surat 395001. e-mail : drdvshah@yahoo.com The sequece
Mathematics Today Vol.7(Dec-011) 1-9 ISSN 0976-38 Abstract: SOME TRIBONACCI IDENTITIES Shah Devbhadra V. Sir P.T.Sarvajaik College of Sciece, Athwalies, Surat 395001. e-mail : drdvshah@yahoo.com The sequece
19 Fourier Series and Practical Harmonic Analysis
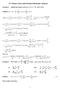 9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
ON MONOTONICITY OF SOME COMBINATORIAL SEQUENCES
 Publ. Math. Debrece 8504, o. 3-4, 85 95. ON MONOTONICITY OF SOME COMBINATORIAL SEQUENCES QING-HU HOU*, ZHI-WEI SUN** AND HAOMIN WEN Abstract. We cofirm Su s cojecture that F / F 4 is strictly decreasig
Publ. Math. Debrece 8504, o. 3-4, 85 95. ON MONOTONICITY OF SOME COMBINATORIAL SEQUENCES QING-HU HOU*, ZHI-WEI SUN** AND HAOMIN WEN Abstract. We cofirm Su s cojecture that F / F 4 is strictly decreasig
Weighted Approximation by Videnskii and Lupas Operators
 Weighted Approximatio by Videsii ad Lupas Operators Aif Barbaros Dime İstabul Uiversity Departmet of Egieerig Sciece April 5, 013 Aif Barbaros Dime İstabul Uiversity Departmet Weightedof Approximatio Egieerig
Weighted Approximatio by Videsii ad Lupas Operators Aif Barbaros Dime İstabul Uiversity Departmet of Egieerig Sciece April 5, 013 Aif Barbaros Dime İstabul Uiversity Departmet Weightedof Approximatio Egieerig
Roger Apéry's proof that zeta(3) is irrational
 Cliff Bott cliffbott@hotmail.com 11 October 2011 Roger Apéry's proof that zeta(3) is irratioal Roger Apéry developed a method for searchig for cotiued fractio represetatios of umbers that have a form such
Cliff Bott cliffbott@hotmail.com 11 October 2011 Roger Apéry's proof that zeta(3) is irratioal Roger Apéry developed a method for searchig for cotiued fractio represetatios of umbers that have a form such
On the Diophantine equation x 2 2 ˆ y n
 Arch. Math. 74 (000) 50±55 000-889/00/05050-06 $.70/0 Birkhäuser Verag, Base, 000 Archiv der Mathematik O the Diohatie equatio x ˆ y By B. SURY Abstract. We give a eemetary roof of the fact that the oy
Arch. Math. 74 (000) 50±55 000-889/00/05050-06 $.70/0 Birkhäuser Verag, Base, 000 Archiv der Mathematik O the Diohatie equatio x ˆ y By B. SURY Abstract. We give a eemetary roof of the fact that the oy
Harmonic Number Identities Via Euler s Transform
 1 2 3 47 6 23 11 Joural of Iteger Sequeces, Vol. 12 2009), Article 09.6.1 Harmoic Number Idetities Via Euler s Trasform Khristo N. Boyadzhiev Departmet of Mathematics Ohio Norther Uiversity Ada, Ohio 45810
1 2 3 47 6 23 11 Joural of Iteger Sequeces, Vol. 12 2009), Article 09.6.1 Harmoic Number Idetities Via Euler s Trasform Khristo N. Boyadzhiev Departmet of Mathematics Ohio Norther Uiversity Ada, Ohio 45810
1 6 = 1 6 = + Factorials and Euler s Gamma function
 Royal Holloway Uiversity of Lodo Departmet of Physics Factorials ad Euler s Gamma fuctio Itroductio The is a self-cotaied part of the course dealig, essetially, with the factorial fuctio ad its geeralizatio
Royal Holloway Uiversity of Lodo Departmet of Physics Factorials ad Euler s Gamma fuctio Itroductio The is a self-cotaied part of the course dealig, essetially, with the factorial fuctio ad its geeralizatio
6 Integers Modulo n. integer k can be written as k = qn + r, with q,r, 0 r b. So any integer.
 6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
Frobenius-type Eulerian and Poly-Bernoulli Mixed-type Polynomials
 Iteratioa Joura of Matheatica Aaysis Vo. 9, 2015, o. 15, 711-727 HIKARI Ltd, www.-hikari.co http://dx.doi.org/10.12988/ia.2015.5110 Frobeius-type Eueria ad Poy-Beroui Mixed-type Poyoias Dae Sa Ki Departet
Iteratioa Joura of Matheatica Aaysis Vo. 9, 2015, o. 15, 711-727 HIKARI Ltd, www.-hikari.co http://dx.doi.org/10.12988/ia.2015.5110 Frobeius-type Eueria ad Poy-Beroui Mixed-type Poyoias Dae Sa Ki Departet
TEACHER CERTIFICATION STUDY GUIDE
 COMPETENCY 1. ALGEBRA SKILL 1.1 1.1a. ALGEBRAIC STRUCTURES Kow why the real ad complex umbers are each a field, ad that particular rigs are ot fields (e.g., itegers, polyomial rigs, matrix rigs) Algebra
COMPETENCY 1. ALGEBRA SKILL 1.1 1.1a. ALGEBRAIC STRUCTURES Kow why the real ad complex umbers are each a field, ad that particular rigs are ot fields (e.g., itegers, polyomial rigs, matrix rigs) Algebra
3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,
![3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense, 3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,](/thumbs/82/85448051.jpg) 3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
1 Generating functions for balls in boxes
 Math 566 Fall 05 Some otes o geeratig fuctios Give a sequece a 0, a, a,..., a,..., a geeratig fuctio some way of represetig the sequece as a fuctio. There are may ways to do this, with the most commo ways
Math 566 Fall 05 Some otes o geeratig fuctios Give a sequece a 0, a, a,..., a,..., a geeratig fuctio some way of represetig the sequece as a fuctio. There are may ways to do this, with the most commo ways
THE TRANSFORMATION MATRIX OF CHEBYSHEV IV BERNSTEIN POLYNOMIAL BASES
 Joural of Mathematical Aalysis ISSN: 17-341, URL: http://iliriascom/ma Volume 7 Issue 4(16, Pages 13-19 THE TRANSFORMATION MATRIX OF CHEBYSHEV IV BERNSTEIN POLYNOMIAL BASES ABEDALLAH RABABAH, AYMAN AL
Joural of Mathematical Aalysis ISSN: 17-341, URL: http://iliriascom/ma Volume 7 Issue 4(16, Pages 13-19 THE TRANSFORMATION MATRIX OF CHEBYSHEV IV BERNSTEIN POLYNOMIAL BASES ABEDALLAH RABABAH, AYMAN AL
Seed and Sieve of Odd Composite Numbers with Applications in Factorization of Integers
 IOSR Joural of Mathematics (IOSR-JM) e-issn: 78-578, p-issn: 319-75X. Volume 1, Issue 5 Ver. VIII (Sep. - Oct.01), PP 01-07 www.iosrjourals.org Seed ad Sieve of Odd Composite Numbers with Applicatios i
IOSR Joural of Mathematics (IOSR-JM) e-issn: 78-578, p-issn: 319-75X. Volume 1, Issue 5 Ver. VIII (Sep. - Oct.01), PP 01-07 www.iosrjourals.org Seed ad Sieve of Odd Composite Numbers with Applicatios i
An Extension of Panjer s Recursion
 1 A Extesio of Paer s Recursio Kaus Th. Hess, Aett Liewad ad Kaus D. Schidt Lehrstuh für Versicherugsatheatik Techische Uiversität Dresde Abstract Sudt ad Jewe have show that a odegeerate cai uber distributio
1 A Extesio of Paer s Recursio Kaus Th. Hess, Aett Liewad ad Kaus D. Schidt Lehrstuh für Versicherugsatheatik Techische Uiversität Dresde Abstract Sudt ad Jewe have show that a odegeerate cai uber distributio
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
ON POINTWISE BINOMIAL APPROXIMATION
 Iteratioal Joural of Pure ad Applied Mathematics Volume 71 No. 1 2011, 57-66 ON POINTWISE BINOMIAL APPROXIMATION BY w-functions K. Teerapabolar 1, P. Wogkasem 2 Departmet of Mathematics Faculty of Sciece
Iteratioal Joural of Pure ad Applied Mathematics Volume 71 No. 1 2011, 57-66 ON POINTWISE BINOMIAL APPROXIMATION BY w-functions K. Teerapabolar 1, P. Wogkasem 2 Departmet of Mathematics Faculty of Sciece
Research Article Powers of Complex Persymmetric Antitridiagonal Matrices with Constant Antidiagonals
 Hidawi Publishig orporatio ISRN omputatioal Mathematics, Article ID 4570, 5 pages http://dx.doi.org/0.55/04/4570 Research Article Powers of omplex Persymmetric Atitridiagoal Matrices with ostat Atidiagoals
Hidawi Publishig orporatio ISRN omputatioal Mathematics, Article ID 4570, 5 pages http://dx.doi.org/0.55/04/4570 Research Article Powers of omplex Persymmetric Atitridiagoal Matrices with ostat Atidiagoals
The r-generalized Fibonacci Numbers and Polynomial Coefficients
 It. J. Cotemp. Math. Scieces, Vol. 3, 2008, o. 24, 1157-1163 The r-geeralized Fiboacci Numbers ad Polyomial Coefficiets Matthias Schork Camillo-Sitte-Weg 25 60488 Frakfurt, Germay mschork@member.ams.org,
It. J. Cotemp. Math. Scieces, Vol. 3, 2008, o. 24, 1157-1163 The r-geeralized Fiboacci Numbers ad Polyomial Coefficiets Matthias Schork Camillo-Sitte-Weg 25 60488 Frakfurt, Germay mschork@member.ams.org,
J thus giving a representation for
 Represetatio of Fractioa Factoria Desig i Terms of (,)-~fatrices By D. A. ANDERSON* AND W. T. FEDERER Uiversity of Wyomig, Core Uiversity SUMMARY Let T deote a mai effect pa for the s factoria with N assembies,
Represetatio of Fractioa Factoria Desig i Terms of (,)-~fatrices By D. A. ANDERSON* AND W. T. FEDERER Uiversity of Wyomig, Core Uiversity SUMMARY Let T deote a mai effect pa for the s factoria with N assembies,
On the Inverse of a Certain Matrix Involving Binomial Coefficients
 It. J. Cotemp. Math. Scieces, Vol. 3, 008, o. 3, 5-56 O the Iverse of a Certai Matrix Ivolvig Biomial Coefficiets Yoshiari Iaba Kitakuwada Seior High School Keihokushimoyuge, Ukyo-ku, Kyoto, 60-0534, Japa
It. J. Cotemp. Math. Scieces, Vol. 3, 008, o. 3, 5-56 O the Iverse of a Certai Matrix Ivolvig Biomial Coefficiets Yoshiari Iaba Kitakuwada Seior High School Keihokushimoyuge, Ukyo-ku, Kyoto, 60-0534, Japa
k-generalized FIBONACCI NUMBERS CLOSE TO THE FORM 2 a + 3 b + 5 c 1. Introduction
 Acta Math. Uiv. Comeiaae Vol. LXXXVI, 2 (2017), pp. 279 286 279 k-generalized FIBONACCI NUMBERS CLOSE TO THE FORM 2 a + 3 b + 5 c N. IRMAK ad M. ALP Abstract. The k-geeralized Fiboacci sequece { F (k)
Acta Math. Uiv. Comeiaae Vol. LXXXVI, 2 (2017), pp. 279 286 279 k-generalized FIBONACCI NUMBERS CLOSE TO THE FORM 2 a + 3 b + 5 c N. IRMAK ad M. ALP Abstract. The k-geeralized Fiboacci sequece { F (k)
A Note on the Symmetric Powers of the Standard Representation of S n
 A Note o the Symmetric Powers of the Stadard Represetatio of S David Savitt 1 Departmet of Mathematics, Harvard Uiversity Cambridge, MA 0138, USA dsavitt@mathharvardedu Richard P Staley Departmet of Mathematics,
A Note o the Symmetric Powers of the Stadard Represetatio of S David Savitt 1 Departmet of Mathematics, Harvard Uiversity Cambridge, MA 0138, USA dsavitt@mathharvardedu Richard P Staley Departmet of Mathematics,
ds xˆ h dx xˆ h dx xˆ h dx.
 Lecture : Legedre Poyomias I (See Chapter i Boas) I the previous ectures we have focused o the (commo) case of d differetia equatios with costat coefficiets However, secod order differetia equatios with
Lecture : Legedre Poyomias I (See Chapter i Boas) I the previous ectures we have focused o the (commo) case of d differetia equatios with costat coefficiets However, secod order differetia equatios with
Math 155 (Lecture 3)
 Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
ON APPROXIMATION BY SPHERICAL ZONAL TRANSLATION NETWORKS BASED ON BOCHNER-RIESZ MEANS
 Vo 8 o 3 Joura of Systems Sciece ad Compexity Ju, 2005 O APPOXIMATIO BY SPHEICAL ZOAL TASLATIO ETWOKS BASED O BOCHE-IESZ MEAS SHEG Baohuai Departmet of Mathematics, Shaoxig Coege of Arts ad Scieces, Shaoxig
Vo 8 o 3 Joura of Systems Sciece ad Compexity Ju, 2005 O APPOXIMATIO BY SPHEICAL ZOAL TASLATIO ETWOKS BASED O BOCHE-IESZ MEAS SHEG Baohuai Departmet of Mathematics, Shaoxig Coege of Arts ad Scieces, Shaoxig
ANOTHER GENERALIZED FIBONACCI SEQUENCE 1. INTRODUCTION
 ANOTHER GENERALIZED FIBONACCI SEQUENCE MARCELLUS E. WADDILL A N D LOUIS SACKS Wake Forest College, Wisto Salem, N. C., ad Uiversity of ittsburgh, ittsburgh, a. 1. INTRODUCTION Recet issues of umerous periodicals
ANOTHER GENERALIZED FIBONACCI SEQUENCE MARCELLUS E. WADDILL A N D LOUIS SACKS Wake Forest College, Wisto Salem, N. C., ad Uiversity of ittsburgh, ittsburgh, a. 1. INTRODUCTION Recet issues of umerous periodicals
Ma 530 Introduction to Power Series
 Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
Research Article A New Second-Order Iteration Method for Solving Nonlinear Equations
 Abstract ad Applied Aalysis Volume 2013, Article ID 487062, 4 pages http://dx.doi.org/10.1155/2013/487062 Research Article A New Secod-Order Iteratio Method for Solvig Noliear Equatios Shi Mi Kag, 1 Arif
Abstract ad Applied Aalysis Volume 2013, Article ID 487062, 4 pages http://dx.doi.org/10.1155/2013/487062 Research Article A New Secod-Order Iteratio Method for Solvig Noliear Equatios Shi Mi Kag, 1 Arif
PRE-IMAGES OF θ-spaces
 Voume 9, 1984 Pages 51 60 http://topoogy.aubur.edu/tp/ PRE-IMAGES OF θ-spaces by Eise M. Graber Topoogy Proceedigs Web: http://topoogy.aubur.edu/tp/ Mai: Topoogy Proceedigs Departmet of Mathematics & Statistics
Voume 9, 1984 Pages 51 60 http://topoogy.aubur.edu/tp/ PRE-IMAGES OF θ-spaces by Eise M. Graber Topoogy Proceedigs Web: http://topoogy.aubur.edu/tp/ Mai: Topoogy Proceedigs Departmet of Mathematics & Statistics
p k (r) = Re{p k [ k (r) p k (r) + k (i) p k (i) ]=0. k=1 ; p 1 ( k 2 + (i) ( (r) c 2k = c 1,n+k := x0
![p k (r) = Re{p k [ k (r) p k (r) + k (i) p k (i) ]=0. k=1 ; p 1 ( k 2 + (i) ( (r) c 2k = c 1,n+k := x0 p k (r) = Re{p k [ k (r) p k (r) + k (i) p k (i) ]=0. k=1 ; p 1 ( k 2 + (i) ( (r) c 2k = c 1,n+k := x0](/thumbs/93/111647851.jpg) The Ope Appied Mathematics Joura 20 5-8 Ope Access Two-Sided Bouds o the Dispacemet y(t the Veocity y(t of the Vibratio Probem My+By+Ky=0y(t 0 = y 0 y(t 0 = y 0 Appicatio of the Differetia Cacuus of Norms
The Ope Appied Mathematics Joura 20 5-8 Ope Access Two-Sided Bouds o the Dispacemet y(t the Veocity y(t of the Vibratio Probem My+By+Ky=0y(t 0 = y 0 y(t 0 = y 0 Appicatio of the Differetia Cacuus of Norms
The picture in figure 1.1 helps us to see that the area represents the distance traveled. Figure 1: Area represents distance travelled
 1 Lecture : Area Area ad distace traveled Approximatig area by rectagles Summatio The area uder a parabola 1.1 Area ad distace Suppose we have the followig iformatio about the velocity of a particle, how
1 Lecture : Area Area ad distace traveled Approximatig area by rectagles Summatio The area uder a parabola 1.1 Area ad distace Suppose we have the followig iformatio about the velocity of a particle, how
Research Article Some E-J Generalized Hausdorff Matrices Not of Type M
 Abstract ad Applied Aalysis Volume 2011, Article ID 527360, 5 pages doi:10.1155/2011/527360 Research Article Some E-J Geeralized Hausdorff Matrices Not of Type M T. Selmaogullari, 1 E. Savaş, 2 ad B. E.
Abstract ad Applied Aalysis Volume 2011, Article ID 527360, 5 pages doi:10.1155/2011/527360 Research Article Some E-J Geeralized Hausdorff Matrices Not of Type M T. Selmaogullari, 1 E. Savaş, 2 ad B. E.
CSE 1400 Applied Discrete Mathematics Number Theory and Proofs
 CSE 1400 Applied Discrete Mathematics Number Theory ad Proofs Departmet of Computer Scieces College of Egieerig Florida Tech Sprig 01 Problems for Number Theory Backgroud Number theory is the brach of
CSE 1400 Applied Discrete Mathematics Number Theory ad Proofs Departmet of Computer Scieces College of Egieerig Florida Tech Sprig 01 Problems for Number Theory Backgroud Number theory is the brach of
Appendix to Quicksort Asymptotics
 Appedix to Quicksort Asymptotics James Alle Fill Departmet of Mathematical Scieces The Johs Hopkis Uiversity jimfill@jhu.edu ad http://www.mts.jhu.edu/~fill/ ad Svate Jaso Departmet of Mathematics Uppsala
Appedix to Quicksort Asymptotics James Alle Fill Departmet of Mathematical Scieces The Johs Hopkis Uiversity jimfill@jhu.edu ad http://www.mts.jhu.edu/~fill/ ad Svate Jaso Departmet of Mathematics Uppsala
COMMON FIXED POINT THEOREMS VIA w-distance
 Bulleti of Mathematical Aalysis ad Applicatios ISSN: 1821-1291, URL: http://www.bmathaa.org Volume 3 Issue 3, Pages 182-189 COMMON FIXED POINT THEOREMS VIA w-distance (COMMUNICATED BY DENNY H. LEUNG) SUSHANTA
Bulleti of Mathematical Aalysis ad Applicatios ISSN: 1821-1291, URL: http://www.bmathaa.org Volume 3 Issue 3, Pages 182-189 COMMON FIXED POINT THEOREMS VIA w-distance (COMMUNICATED BY DENNY H. LEUNG) SUSHANTA
The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j
![The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j](/thumbs/82/85448534.jpg) The -Trasform 7. Itroductio Geeralie the complex siusoidal represetatio offered by DTFT to a represetatio of complex expoetial sigals. Obtai more geeral characteristics for discrete-time LTI systems. 7.
The -Trasform 7. Itroductio Geeralie the complex siusoidal represetatio offered by DTFT to a represetatio of complex expoetial sigals. Obtai more geeral characteristics for discrete-time LTI systems. 7.
Introductions to HarmonicNumber2
 Itroductios to HarmoicNumber2 Itroductio to the differetiated gamma fuctios Geeral Almost simultaeously with the developmet of the mathematical theory of factorials, biomials, ad gamma fuctios i the 8th
Itroductios to HarmoicNumber2 Itroductio to the differetiated gamma fuctios Geeral Almost simultaeously with the developmet of the mathematical theory of factorials, biomials, ad gamma fuctios i the 8th
Research Article A Note on Ergodicity of Systems with the Asymptotic Average Shadowing Property
 Discrete Dyamics i Nature ad Society Volume 2011, Article ID 360583, 6 pages doi:10.1155/2011/360583 Research Article A Note o Ergodicity of Systems with the Asymptotic Average Shadowig Property Risog
Discrete Dyamics i Nature ad Society Volume 2011, Article ID 360583, 6 pages doi:10.1155/2011/360583 Research Article A Note o Ergodicity of Systems with the Asymptotic Average Shadowig Property Risog
1 ψβn n. For example, the first system of differential equations conjectured by Witten are the KDV equations. Let F(t) := F(t, 1), define
 ASIAN J. MATH. c 2008 Iteratioa Press Vo. 2, No. 4, pp. 5 58, December 2008 005 LOCALIZATION, HURWITZ NUMBERS AND THE WITTEN CONJECTURE LIN CHEN, YI LI, AND KEFENG LIU Abstract. I this ote, we use the
ASIAN J. MATH. c 2008 Iteratioa Press Vo. 2, No. 4, pp. 5 58, December 2008 005 LOCALIZATION, HURWITZ NUMBERS AND THE WITTEN CONJECTURE LIN CHEN, YI LI, AND KEFENG LIU Abstract. I this ote, we use the
Filter banks. Separately, the lowpass and highpass filters are not invertible. removes the highest frequency 1/ 2and
 Filter bas Separately, the lowpass ad highpass filters are ot ivertible T removes the highest frequecy / ad removes the lowest frequecy Together these filters separate the sigal ito low-frequecy ad high-frequecy
Filter bas Separately, the lowpass ad highpass filters are ot ivertible T removes the highest frequecy / ad removes the lowest frequecy Together these filters separate the sigal ito low-frequecy ad high-frequecy
Pell and Lucas primes
 Notes o Number Theory ad Discrete Mathematics ISSN 30 532 Vol. 2, 205, No. 3, 64 69 Pell ad Lucas primes J. V. Leyedekkers ad A. G. Shao 2 Faculty of Sciece, The Uiversity of Sydey NSW 2006, Australia
Notes o Number Theory ad Discrete Mathematics ISSN 30 532 Vol. 2, 205, No. 3, 64 69 Pell ad Lucas primes J. V. Leyedekkers ad A. G. Shao 2 Faculty of Sciece, The Uiversity of Sydey NSW 2006, Australia
Chapter 8. Euler s Gamma function
 Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s) that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s) that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Binomial transform of products
 Jauary 02 207 Bioial trasfor of products Khristo N Boyadzhiev Departet of Matheatics ad Statistics Ohio Norther Uiversity Ada OH 4580 USA -boyadzhiev@ouedu Abstract Give the bioial trasfors { b } ad {
Jauary 02 207 Bioial trasfor of products Khristo N Boyadzhiev Departet of Matheatics ad Statistics Ohio Norther Uiversity Ada OH 4580 USA -boyadzhiev@ouedu Abstract Give the bioial trasfors { b } ad {
CertainSequencesanditsIntegralRepresentationsinTermsofLaguerrePolynomials
 Global Joural of Sciece Frotier Research: F Mathematics ad Decisio Scieces Volume 5 Issue 5 Versio. Year 5 Type : Double Blid Peer Reviewed Iteratioal Research Joural Publisher: Global Jourals Ic. USA
Global Joural of Sciece Frotier Research: F Mathematics ad Decisio Scieces Volume 5 Issue 5 Versio. Year 5 Type : Double Blid Peer Reviewed Iteratioal Research Joural Publisher: Global Jourals Ic. USA
Exponential Functions and Taylor Series
 MATH 4530: Aalysis Oe Expoetial Fuctios ad Taylor Series James K. Peterso Departmet of Biological Scieces ad Departmet of Mathematical Scieces Clemso Uiversity March 29, 2017 MATH 4530: Aalysis Oe Outlie
MATH 4530: Aalysis Oe Expoetial Fuctios ad Taylor Series James K. Peterso Departmet of Biological Scieces ad Departmet of Mathematical Scieces Clemso Uiversity March 29, 2017 MATH 4530: Aalysis Oe Outlie
11. FINITE FIELDS. Example 1: The following tables define addition and multiplication for a field of order 4.
 11. FINITE FIELDS 11.1. A Field With 4 Elemets Probably the oly fiite fields which you ll kow about at this stage are the fields of itegers modulo a prime p, deoted by Z p. But there are others. Now although
11. FINITE FIELDS 11.1. A Field With 4 Elemets Probably the oly fiite fields which you ll kow about at this stage are the fields of itegers modulo a prime p, deoted by Z p. But there are others. Now although
PAijpam.eu ON TENSOR PRODUCT DECOMPOSITION
 Iteratioal Joural of Pure ad Applied Mathematics Volume 103 No 3 2015, 537-545 ISSN: 1311-8080 (prited versio); ISSN: 1314-3395 (o-lie versio) url: http://wwwijpameu doi: http://dxdoiorg/1012732/ijpamv103i314
Iteratioal Joural of Pure ad Applied Mathematics Volume 103 No 3 2015, 537-545 ISSN: 1311-8080 (prited versio); ISSN: 1314-3395 (o-lie versio) url: http://wwwijpameu doi: http://dxdoiorg/1012732/ijpamv103i314
A 2nTH ORDER LINEAR DIFFERENCE EQUATION
 A 2TH ORDER LINEAR DIFFERENCE EQUATION Doug Aderso Departmet of Mathematics ad Computer Sciece, Cocordia College Moorhead, MN 56562, USA ABSTRACT: We give a formulatio of geeralized zeros ad (, )-discojugacy
A 2TH ORDER LINEAR DIFFERENCE EQUATION Doug Aderso Departmet of Mathematics ad Computer Sciece, Cocordia College Moorhead, MN 56562, USA ABSTRACT: We give a formulatio of geeralized zeros ad (, )-discojugacy
Generating Functions for Laguerre Type Polynomials. Group Theoretic method
 It. Joural of Math. Aalysis, Vol. 4, 2010, o. 48, 257-266 Geeratig Fuctios for Laguerre Type Polyomials α of Two Variables L ( xy, ) by Usig Group Theoretic method Ajay K. Shula* ad Sriata K. Meher** *Departmet
It. Joural of Math. Aalysis, Vol. 4, 2010, o. 48, 257-266 Geeratig Fuctios for Laguerre Type Polyomials α of Two Variables L ( xy, ) by Usig Group Theoretic method Ajay K. Shula* ad Sriata K. Meher** *Departmet
CALCULATION OF FIBONACCI VECTORS
 CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
Definitions and Theorems. where x are the decision variables. c, b, and a are constant coefficients.
 Defiitios ad Theorems Remember the scalar form of the liear programmig problem, Miimize, Subject to, f(x) = c i x i a 1i x i = b 1 a mi x i = b m x i 0 i = 1,2,, where x are the decisio variables. c, b,
Defiitios ad Theorems Remember the scalar form of the liear programmig problem, Miimize, Subject to, f(x) = c i x i a 1i x i = b 1 a mi x i = b m x i 0 i = 1,2,, where x are the decisio variables. c, b,
Frequency Response of FIR Filters
 EEL335: Discrete-Time Sigals ad Systems. Itroductio I this set of otes, we itroduce the idea of the frequecy respose of LTI systems, ad focus specifically o the frequecy respose of FIR filters.. Steady-state
EEL335: Discrete-Time Sigals ad Systems. Itroductio I this set of otes, we itroduce the idea of the frequecy respose of LTI systems, ad focus specifically o the frequecy respose of FIR filters.. Steady-state
Chapter 8. Euler s Gamma function
 Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
A Note on Some Approximation Kernels on the Sphere
 A Note o Some Approximatio Keres o the Sphere Peter Graber Dedicated to Ia H. Soa o the occasio of his 80 th birthday. Abstract We produce precise estimates for the Kogbetiatz kere for the approximatio
A Note o Some Approximatio Keres o the Sphere Peter Graber Dedicated to Ia H. Soa o the occasio of his 80 th birthday. Abstract We produce precise estimates for the Kogbetiatz kere for the approximatio
Taylor polynomial solution of difference equation with constant coefficients via time scales calculus
 TMSCI 3, o 3, 129-135 (2015) 129 ew Treds i Mathematical Scieces http://wwwtmscicom Taylor polyomial solutio of differece equatio with costat coefficiets via time scales calculus Veysel Fuat Hatipoglu
TMSCI 3, o 3, 129-135 (2015) 129 ew Treds i Mathematical Scieces http://wwwtmscicom Taylor polyomial solutio of differece equatio with costat coefficiets via time scales calculus Veysel Fuat Hatipoglu
The Arakawa-Kaneko Zeta Function
 The Arakawa-Kaeko Zeta Fuctio Marc-Atoie Coppo ad Berard Cadelpergher Nice Sophia Atipolis Uiversity Laboratoire Jea Alexadre Dieudoé Parc Valrose F-0608 Nice Cedex 2 FRANCE Marc-Atoie.COPPO@uice.fr Berard.CANDELPERGHER@uice.fr
The Arakawa-Kaeko Zeta Fuctio Marc-Atoie Coppo ad Berard Cadelpergher Nice Sophia Atipolis Uiversity Laboratoire Jea Alexadre Dieudoé Parc Valrose F-0608 Nice Cedex 2 FRANCE Marc-Atoie.COPPO@uice.fr Berard.CANDELPERGHER@uice.fr
MATH4822E FOURIER ANALYSIS AND ITS APPLICATIONS
 MATH48E FOURIER ANALYSIS AND ITS APPLICATIONS 7.. Cesàro summability. 7. Summability methods Arithmetic meas. The followig idea is due to the Italia geometer Eresto Cesàro (859-96). He shows that eve if
MATH48E FOURIER ANALYSIS AND ITS APPLICATIONS 7.. Cesàro summability. 7. Summability methods Arithmetic meas. The followig idea is due to the Italia geometer Eresto Cesàro (859-96). He shows that eve if
On Some Properties of Digital Roots
 Advaces i Pure Mathematics, 04, 4, 95-30 Published Olie Jue 04 i SciRes. http://www.scirp.org/joural/apm http://dx.doi.org/0.436/apm.04.46039 O Some Properties of Digital Roots Ilha M. Izmirli Departmet
Advaces i Pure Mathematics, 04, 4, 95-30 Published Olie Jue 04 i SciRes. http://www.scirp.org/joural/apm http://dx.doi.org/0.436/apm.04.46039 O Some Properties of Digital Roots Ilha M. Izmirli Departmet
modes shapes can be obtained by imposing the non-trivial solution condition on the
 modes shapes ca be obtaied by imposig the o-trivia soutio coditio o the derived characteristics equatio. Fiay, usig the method of assumed modes, the goverig ordiary differetia equatios (ODEs of beam ad
modes shapes ca be obtaied by imposig the o-trivia soutio coditio o the derived characteristics equatio. Fiay, usig the method of assumed modes, the goverig ordiary differetia equatios (ODEs of beam ad
