Topics in Fourier Analysis-I 1
|
|
|
- Eugene Kelley
- 5 years ago
- Views:
Transcription
1 Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio Fourier Series of -Periodic fuctios Fourier Series for Eve ad Odd Fuctios Sie ad Cosie Series Expasios Fourier Series of -Periodic Fuctios Fourier Series o Arbitrary Itervas Exercises Lectures for the course MA 68, Juy-November 14.
2 1 Fourier Series 1.1 Motivatio through heat equatio The cosideratio of Fourier Series ca be traced back to the situatio which Fourier ecoutered i the begiig of ast cetury whie sovig heat equatio: Cosider a thi metaic wire of egth. Suppose a iitia temperature is suppied to it, ad suppose the temperature at both the ed poits kept at. The oe woud ike to kow the temperature at each poit of the strig at a particuar time. Let us represet the strig as a iterva [, ]. Let u(x, t) be the temperature at the poit x [, ] at time t. It is kow that u(, ) satisfies the partia equatio u t = c u, < x <, (1.1) t where c > is the heat coductivity of the materia. Sice the temperature at both the ed poits kept at, we have u(, t) = = u(, t), t >. (1.) Let the iitia temperature at the poit x be f()x), i.e., u(x, ) = f(x), x. (1.3) Exercise 1.1. Equatio (1.1) satisfyig (1.) ad (1.3) caot have more tha oe soutio. I order to fid u(x, t), we use a procedure caed method of separatio of variabes. I this method, we assume first that u(x, t) is of the form: u(x, t) = φ(x)ψ(t). The we have Hece, from (1.1), Hece, Hece, u t = φ(x)ψ (t), u t = φ (x)ψ(t). φ(x)ψ (t) = c φ (x)ψ(t). ψ (t) c ψ(t) = φ (x) = K, cost. φ(x) ψ (t) = Kc ψ(t), φ (x) = Kφ(x). (1.4) Let us cosider differet cases: Case(i): K = : I this case, φ (x) = so that φ is of the form φ(x) = ax + b.
3 By (1.), φ()ψ(t) = = φ()ψ(t). bψ(t) = = (a + b)ψ(t). Thus, we arrive at either ψ = or φ =. Case(ii): K > : I this case, K = α for some α. The we have φ (x) α φ(x) = so that φ is of the form φ(x) = ae αx + be αx. Agai, by (1.), φ()ψ(t) = = φ()ψ(t) so that (a + b)ψ(t) = = (ae α + be α )ψ(t). This agai ead to u(x, t) =. Case(iii): K < : I this case, K = α for some α. The we have φ (x) + α φ(x) = so that φ is of the form φ(x) = a cos αx + b si αx. By (1.), φ()ψ(t) = = φ()ψ(t) so that if ψ, we obtai a = ad b si α =. Assumig b (otherwise φ = ), we have α =, Z. Thus, α / : Z}. Now, from (1.4), with α / : Z}. Hece, ψ (t) = α c ψ(t) ψ(t) = ae α c t, ad hece, u is of the form u(x, t) = ae α c t si αx, α / : Z}. Thus, for each Z, u (x, t) = a e λ ct si λ x, λ :=, with a R satisfies (1.1) ad (1.). But, this u eed ot satisfy (1.3), uess f(x) = a si(x/) for some Z. If f is of the form for some k N, the we see that k f(x) = a si(x/) (1.5) k u(x, t) := a e λ ct si(x/) 3
4 satisfies (1.1), (1.) ad (1.3). What ca we say if f is, i some sese, arbitrary? The cosideratio of the fuctios of the form i (1.5) suggests the foowig query: If f is of the form f(x) = a si(x/), ca we say that u(x, t) := a e λ ct si(x/) is a soutio of (1.1) satisfyig (1.) ad (1.3) with appropriate otio of covergece? As a first step, et us assume that f is of the form f(x) = a si( x ). (1.6) Assume further that, term by term itegratio of the above series is possibe. The, we have f(x) si( mx )dx = a si( x ) si(mx )dx. Sice ad we obtai si( x ) si(mx )dx = for m, si ( x )dx = a = 1 cos ( x Note that, if f has the form as i (1.6), the f is -periodic, i.e., ad f is a odd fuctio, i.e., If f is as i (1.6), we we may defie u(x, t) := ) dx =, f(x) si( x )dx. (1.7) f(x + ) = f(x) for a x R f( x) = f(x) for a x R. a e λ ct si(x/), λ := /. Assumig that the above series is coverget ad ca be differetiated term by term, we see that u(, ) is a soutio of (1.1) satisfyig (1.) ad (1.3). Exercise 1.. Show that each λ := / is a eigevaue of the operator eigevector si λ x. d dx wit correspodig 4
5 1. Fourier Series of -Periodic fuctios I the ast sectio, we assumed that the fuctio f ca be represeted as f(x) = If =, the the above series takes the form a si( mx ). f(x) = A si x, A := f(x) si xdx. The above series is a specia case of the Fourier series that we are goig to itroduce. Let us cosider a few defiitios. Defiitio 1.3. A fuctio of the form k c + (a cos x + b si x). where c, a, b R, is caed a trigoometric poyomia, ad a series of the form c + (a cos x + b si x) with c, a, b R is caed a trigoometric series. Note that a trigoometric poyomia is a specia case of a trigoometric series. We observe that trigoometric poyomias are -periodic o R, i.e., if f(x) is a trigoometric poyomia, the f(x + ) = f(x) x R. From this, we ca ifer that, if the trigoometric series c + (a cos x + b si x) coverges at a poit x R, the it has to coverge at x + as we; ad hece at x + for a itegers. This shows that we ca restrict the discussio of covergece of a trigoometric series to a iterva of egth. Hece, we caot expect to have a trigoometric series expasio for a fuctio f : R R if it is ot a -periodic fuctio. We kow that a coverget trigoometric series is -periodic. What about the coverse? Suppose that f is a -periodic fuctio. Is it possibe to represet f as a trigoometric series? 5
6 Suppose, for a momet, that we ca write f(x) = c + (a cos x + b si x) for a x R. The what shoud be the coefficiets c, a, b? To aswer this questio, et us further assume that f is itegrabe o [, ] ad the series ca be itegrated term by term. For istace if the above series is uiformy coverget to f i [, ], the term by term itegratio is possibe. By Weierstrass test,we have the foowig resut: If = ( a + b ) coverges, the c + (a cos x + b si x) is a domiated series o R ad hece it is uiformy coverget. For, m N }, we observe the foowig orthogoaity reatios: cos x cos mxdx = si x si mxdx = cos x si mxdx =., if m, if = m,, if = m =,, if m, if = m, Thus, uder the assumptio that f is itegrabe o [, ] ad the series ca be itegrated term by term, we obtai a = 1 c = 1 f(x)dx, f(x) cos xdx, b = 1 f(x) si xdx. Defiitio 1.4. The Fourier series of a -periodic fuctio f is the trigoometric series where a = 1 a (a cos x + b si x), f(x) cos xdx ad b = 1 f(x) si xdx ad this fact is writte as f(x) a (a cos x + b si x). The umbers a ad b are caed the Fourier coefficiets of f. 6
7 If f is a trigoometric poyomia, the its Fourier series is itsef. Writig cos x = 1 [eix + e ix ], si x = 1 i [eix e ix ], we have Thus, writig we have a cos x + b si x = a [eix + e ix ] + b i [eix e ix ] ( a = + b ) ( e ix a + i b ) e ix. i a + c := a + b i, c := a b i, (a cos x + b si x) = Z c e ix. Now, suppose f(x) = Z c e ix with c C, ad this series ca be itegrated term by term. The, we have But, Hece, f(x)e imx dx = Z e i( m) dx = c m, i.e., e i( m) dx = c e i( m)x dx. if m = m, if m m. c = 1 f(x)e ix dx, Z. The foowig theorem show that there is a arge cass of fuctios which ca be represeted by their Fourier series (see Bhatia [1]). We sha come back to this theorem at a ater stage. THEOREM 1.5. (Dirichet s theorem) Suppose f : R R is a -periodic fuctio which is piecewise differetiabe o (, ). The the Fourier series of f coverges, ad the imit fuctio f(x) is give by f(x) = f(x) if f is cotiuous at x, 1 [f(x ) + f(x+)] if f is ot cotiuous at x. I Theorem 1.5 we used the termioogy piecewise differetiabe as per the foowig defiitio. Defiitio 1.6. A fuctio f : [a, b] R is said to be piecewise differetiabe if f exists ad is piecewise cotiuous o [a, b] except possiby at a fiite umber of poits. 7
8 Remark 1.7. It is kow that there are cotiuous fuctios f defied o [, ] whose Fourier series does ot coverge poitwise to f. Its proof reies o UBP (see []). We sha cosider this at a ater occasio. Athough each term ad the partia sums of a Fourier series are ifiitey differetiabe, the sum fuctio eed ot be eve cotiuous at certai poits. This fact is iustrated by the foowig exampe., x, Exampe 1.8. Let f(x) = By Dirichet s theorem (Theorem 1.5), the Fourier 1, < x. series of f coverges to f(x) for every x, ad at the poit, the series coverges to 1/. Note that ad for N, b = 1 Thus, Fourier series of f is I particuar, for x = /, a = 1 cos xdx = 1, =,,, si xdx = 1 [ ] 1 cos = 1 [ ] 1 ( 1) = 1 = 1 + = 1 + which eads to the Madhava Niakaṅtha series = si[( + 1)/] ( + 1) si( + 1)x. ( + 1) = 1 + =, ( 1) ( + 1) odd,, eve. 4 = ( 1) ( + 1). = 1.3 Fourier Series for Eve ad Odd Fuctios The foowig ca be verified easiy: Suppose f is a eve fuctio, i.e., f( x) = f(x) x X. The f(x) cos x is a eve fuctio ad f(x) si x is a odd fuctio, so that a = 1 f(x) cos xdx = b = 1 f(x) si xdx. f(x) cos xdx, 8
9 Suppose f is a odd fuctio, i.e., f( x) = f(x) x X. The f(x) cos x is a odd fuctio ad f(x) si x is a eve fuctio, so that a = 1 f(x) cos xdx =, b = 1 f(x) si xdx = Thus, we have the foowig: f(x) si xdx. (1) Suppose f is a eve fuctio. The the Fourier series of f is I particuar, respectivey. a a cos x with a := f(x) cos xdx. f() = a a, f() = a ( 1) a, = () Suppose f is a odd fuctio. The the Fourier series of f is b si x with b := I particuar, f(/) = ( 1) b +1. Exampe 1.9. Cosider the fuctio f defied by = f(x) si xdx, f(x) = x, x [, ]. I this case, f is a eve fuctio. Hece, the Fourier series is with a a cos x, x [, ] a = x dx = ad for = 1,,..., a = x cos xdx = [ si x x = [ cos x ] = [ ( 1) ] 1 ] } si x dx 9
10 Thus, so that a =, a +1 = x 4 = Takig x = (usig Dirichet s theorem), we obtai Exampe 1.1. Let f(x) = x, series is with b = Thus the Fourier series is = 4, = 1,,... ( + 1) cos( + 1)x ( + 1), x [, ]. 8 = 1 ( + 1). = x [, ]. I this case, f is a odd fuctio. Hece, the Fourier b si x, x [, ] x si x dx = cos } [ x = ( 1)+1. ( 1) +1 si x. cos x ] + } cos x dx I particuar (usig Dirichet s theorem), with x = / we obtai the Madhava-Nīakaṅtha series 4 = ( 1) +1 si = = ( 1) + 1. Exampe Let f(x) = Fourier series is with Thus b = 1, x <, 1, x. b si x, I this case, f is a odd fuctio. Hece, the si x dx = (1 cos ) = [1 ( 1) ]. f(x) 4 = si( + 1)x. + 1 Takig x = /, agai we obtai the Madhava-Nīakaṅtha series 4 = ( 1) + 1. = 1
11 Exampe 1.1. Let f(x) = x, a x [, ]. Sice f is a eve fuctio, its Fourier series is a cos x, x [, ], a = It ca be see that a = /3, ad a = ( 1) 4/. Thus x ( 1) cos x, x [, ]. Takig x = ad x = (usig Dirichet s theorem), we have respectivey. 1 = ( 1) +1, 6 = 1 x cos x dx. 1.4 Sie ad Cosie Series Expasios Suppose a fuctio f is defied o [, ]. By extedig it to [, ] so that the exteded fuctio is a odd fuctio, we obtai Forier sie series of f, ad by extedig it to [, ] so that the exteded fuctio is a eve fuctio, we obtai Fourier cosie series of f. The odd extesio ad eve extesio of f, deoted by f odd ad f eve are defied by f odd (x) = f(x) if x <, f( x) if x <,, f eve (x) = f(x) if x <, f( x) if x <, respectivey. Therefore, f(x) = f odd (x) b si x, x [, ] ad f(x) = f eve (x) a a cos x, x [, ] with a = f(x) cos x dx, b = f(x) si x dx. Exampe Let f(x) = x, x [, ]. The eve extesio of f is itsef. Its odd extesio is: x, if x <, f odd (x) =, x, if x <. Hece, f(x) = f odd (x) b si x, x [, ], 11
12 with b = Note that [ cos x x [ cos x si x x dx = x Thus, x si x dx = [ cos x x ] ] cos = ] + = ( 1)+1, } cos x x dx. si x [ cos x ] dx = = [ ( 1) 1 b = [ ( 1)+1 ( 1) ]} 1 + = ( 1) [ ( 1) ] 1. ]. Exampe Let f(x) = x, x [, ]. Its odd extesio is itsef, ad f eve (x) = x, x [, ]. From Exampes 1.1 ad 1.9, we obtai ( 1) +1 x si x, x [, ] ad x 4 Exampe Let us fid the sie series expasio of the fuctio, if x < /, f(x) = 1, if / x <. The sie series of f is give by where Note that b 1 = b = / f(x) = cos( + 1)x ( + 1), x [, ]. b si x, si x dx = [ cos x ] ( 1) ad b = [( 1) 1] = x [, ], / = [ cos / cos if odd, if eve. ]. Thus, for x [, ], we have si x si x si 3x si 5x si(4 3)x f(x) si(4 )x si(4 1)x si(4 + 1)x
13 1.5 Fourier Series of -Periodic Fuctios Suppose f is a T -periodic fuctio. We may write T =. The we may cosider the chage of variabe t = x/ so that the fuctio f(x) := f(t/), as a fuctio of t is -periodic. Hece, its Fourier series is a (a cos t + b si t) where I particuar, a = 1 b = 1 ( t f ( t f ) cos tdt = 1 ) si tdt = 1 f eve = b = ad a = f odd = a = ad b = f(x) cos x dx, f(x) si x dx. f(x) cos x dx, f(x) si x dx. Exampe Let f(x) = 1 x, 1 x 1. Takig = 1, we have ad Now, Hece, Thus, 1 a = 1 x cos x dx = a = 1 1 (1 x ) cos x dx = b = (1 x ) si x dx =. (1 x ) cos x dx 1 [ si x cos x dx = =, [ ] 1 si x 1 si x [ cos x x dx = ] 1 (1 x ) cos x dx = [1 ( 1) ] = f(x) = 4 cos x. + 1 ] 1 = ( 1) 1., eve, 4/, odd. 13
14 1.6 Fourier Series o Arbitrary Itervas Suppose a fuctio f is defied i a iterva [a, b]. We ca obtai Fourier expasio of it o [a, b] as foows: Method 1: Let us cosider a chage of variabe as y = x a+b. Let ϕ(y) := f(x) = f(y + a + b ), where y with = (b a)/. We ca exted ϕ as a -periodic fuctio ad obtai its Fourier series as where Thus, where a = 1 a = 1 ϕ(y) a (a cos y + b si ) y ϕ(y) cos y dy, b = 1 ϕ(y) si y dy. f(x) a (a cos y + b si ) y with = (b a)/ ad y = x a+b. f(x) cos y dx, b = 1 f(x) si y dx Method : Cosiderig the chage of variabe as y = x a ad := b a, we defie ϕ(y) := f(x) = f(y + a) where y <. We ca exted ϕ as a -periodic fuctio i ay maer ad obtai its Fourier series. Here are two specific cases: (a) For y [, ], defie f e (y) = ϕf( y). Thus f e o [, ] is a eve fuctio. I this case, where = (b a)/ ad ϕ(y) a a cos y a = 1 ϕ(y) cos y dy. (b) For y [, ], defie f o (y) = ϕ( y). Thus f o o [, ] is a odd fuctio. I this case, where ϕ(y) b = 1 b si y ϕ(y) si y dy. From the series of ϕ we ca recover the correspodig series of f o [a, b] by writig y = x a. 14
15 1.7 Exercises The foowig are take from [3]. 1. Fid the Fourier series of the - period fuctio f such that: 1, (a) f(x) = x <, < x < 3. (b) f(x) = (c) f(x) = x, x, x < < x < x, x 1 x, x. (d) f(x) = x 4, x.. Usig the Fourier series i Exercise 1, fid the sum of the foowig series: (a) , (b) (c) , (d) si x, x 4 3. If f(x) = cos x, 4 x < f(x) 8 cos 4, the show that [ si x si 3x 5.7 ] si 1x Show that for < x < 1, x x = 8 [ ] si x si 3x si 5x Show that for < x <, 6. Show that for < x <, ad fid the sum of the series si x + si 3x 3 + si 5x = 4. x si x = 1 1 cos x cos x + cos 3x cos 4x +..., Show that for x, [ ] x( x) = cos x 6 cos 4x cos 6x , x( x) = 8 [ ] si x si 3x si 5x
16 8. Assumig that the Fourier series of f coverges uiformy o [, ), show that 9. Usig Exercises 7 ad 8 show that 1 (a) 4 = 4 9, (b) ( 1) 1 (c) 1 6 = (d) 1 [f(x)] dx = a (a + b ). = 1 ( 1) 1 ( 1) 3 = Write dow the Fourier series of f(x) = x for x [1, ) so that it coverges to 1/ at x = 1. Refereces [1] R. Bhatia, Fourier Series, TRIM series, [] Nair, M. T. () (Fourth Prit: 14): Fuctioa Aaysis: A First Course, New Dehi: Pritice-Ha of Idia. [3] Nair, M. T. (14): Cacuus of Oe Variabe, Ae Books, Pvt Ltd. [4] M.T. Nair, Measure ad Itegratio, Notes for the MSc. Course, Ja-may, 14. [5] R. Radha ad S. Thagaveu (13): Fourier Aaysis, NPTEL Notes, IIT Madras. 16
Notes: MA1102: Series and Matrices
 Notes: MA: Series ad Matrices M.T. Nair (IIT Madras) Jauary - May 8 April 3, 8 Cotets Sequeces 3. Defiitio ad examples............................. 3. Covergece ad divergece...........................
Notes: MA: Series ad Matrices M.T. Nair (IIT Madras) Jauary - May 8 April 3, 8 Cotets Sequeces 3. Defiitio ad examples............................. 3. Covergece ad divergece...........................
MATH4822E FOURIER ANALYSIS AND ITS APPLICATIONS
 MATH48E FOURIER ANALYSIS AND ITS APPLICATIONS 7.. Cesàro summability. 7. Summability methods Arithmetic meas. The followig idea is due to the Italia geometer Eresto Cesàro (859-96). He shows that eve if
MATH48E FOURIER ANALYSIS AND ITS APPLICATIONS 7.. Cesàro summability. 7. Summability methods Arithmetic meas. The followig idea is due to the Italia geometer Eresto Cesàro (859-96). He shows that eve if
Fourier Series and their Applications
 Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
Chapter 4. Fourier Series
 Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Chapter 6 Infinite Series
 Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Math 234 Test 1, Tuesday 27 September 2005, 4 pages, 30 points, 75 minutes.
 Math 34 Test 1, Tuesday 7 September 5, 4 pages, 3 poits, 75 miutes. The high score was 9 poits out of 3, achieved by two studets. The class average is 3.5 poits out of 3, or 77.5%, which ordiarily would
Math 34 Test 1, Tuesday 7 September 5, 4 pages, 3 poits, 75 miutes. The high score was 9 poits out of 3, achieved by two studets. The class average is 3.5 poits out of 3, or 77.5%, which ordiarily would
1.3 Convergence Theorems of Fourier Series. k k k k. N N k 1. With this in mind, we state (without proof) the convergence of Fourier series.
 .3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
.3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
Fourier Series and the Wave Equation
 Fourier Series ad the Wave Equatio We start with the oe-dimesioal wave equatio u u =, x u(, t) = u(, t) =, ux (,) = f( x), u ( x,) = This represets a vibratig strig, where u is the displacemet of the strig
Fourier Series ad the Wave Equatio We start with the oe-dimesioal wave equatio u u =, x u(, t) = u(, t) =, ux (,) = f( x), u ( x,) = This represets a vibratig strig, where u is the displacemet of the strig
19 Fourier Series and Practical Harmonic Analysis
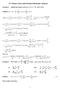 9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
Solutions to Final Exam Review Problems
 . Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
. Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
MAT1026 Calculus II Basic Convergence Tests for Series
 MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
Lecture 3: Convergence of Fourier Series
 Lecture 3: Covergece of Fourier Series Himashu Tyagi Let f be a absolutely itegrable fuctio o T : [ π,π], i.e., f L (T). For,,... defie ˆf() f(θ)e i θ dθ. π T The series ˆf()e i θ is called the Fourier
Lecture 3: Covergece of Fourier Series Himashu Tyagi Let f be a absolutely itegrable fuctio o T : [ π,π], i.e., f L (T). For,,... defie ˆf() f(θ)e i θ dθ. π T The series ˆf()e i θ is called the Fourier
Archimedes - numbers for counting, otherwise lengths, areas, etc. Kepler - geometry for planetary motion
 Topics i Aalysis 3460:589 Summer 007 Itroductio Ree descartes - aalysis (breaig dow) ad sythesis Sciece as models of ature : explaatory, parsimoious, predictive Most predictios require umerical values,
Topics i Aalysis 3460:589 Summer 007 Itroductio Ree descartes - aalysis (breaig dow) ad sythesis Sciece as models of ature : explaatory, parsimoious, predictive Most predictios require umerical values,
Measure and Measurable Functions
 3 Measure ad Measurable Fuctios 3.1 Measure o a Arbitrary σ-algebra Recall from Chapter 2 that the set M of all Lebesgue measurable sets has the followig properties: R M, E M implies E c M, E M for N implies
3 Measure ad Measurable Fuctios 3.1 Measure o a Arbitrary σ-algebra Recall from Chapter 2 that the set M of all Lebesgue measurable sets has the followig properties: R M, E M implies E c M, E M for N implies
Strauss PDEs 2e: Section Exercise 4 Page 1 of 5. u tt = c 2 u xx ru t for 0 < x < l u = 0 at both ends u(x, 0) = φ(x) u t (x, 0) = ψ(x),
 Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
Question 1: The magnetic case
 September 6, 018 Corell Uiversity, Departmet of Physics PHYS 337, Advace E&M, HW # 4, due: 9/19/018, 11:15 AM Questio 1: The magetic case I class, we skipped over some details, so here you are asked to
September 6, 018 Corell Uiversity, Departmet of Physics PHYS 337, Advace E&M, HW # 4, due: 9/19/018, 11:15 AM Questio 1: The magetic case I class, we skipped over some details, so here you are asked to
Alternative Orthogonal Polynomials. Vladimir Chelyshkov
 Aterative Orthogoa oyomias Vadimir Cheyshov Istitute of Hydromechaics of the NAS Uraie Georgia Souther Uiversity USA Abstract. The doube-directio orthogoaizatio agorithm is appied to costruct sequeces
Aterative Orthogoa oyomias Vadimir Cheyshov Istitute of Hydromechaics of the NAS Uraie Georgia Souther Uiversity USA Abstract. The doube-directio orthogoaizatio agorithm is appied to costruct sequeces
Ma 4121: Introduction to Lebesgue Integration Solutions to Homework Assignment 5
 Ma 42: Itroductio to Lebesgue Itegratio Solutios to Homework Assigmet 5 Prof. Wickerhauser Due Thursday, April th, 23 Please retur your solutios to the istructor by the ed of class o the due date. You
Ma 42: Itroductio to Lebesgue Itegratio Solutios to Homework Assigmet 5 Prof. Wickerhauser Due Thursday, April th, 23 Please retur your solutios to the istructor by the ed of class o the due date. You
LECTURE 21. DISCUSSION OF MIDTERM EXAM. θ [0, 2π). f(θ) = π θ 2
 LECTURE. DISCUSSION OF MIDTERM EXAM FOURIER ANALYSIS (.443) PROF. QIAO ZHANG Problem. Cosider the itegrable -periodic fuctio f(θ) = θ θ [, ). () Compute the Fourier series for f(θ). () Discuss the covergece
LECTURE. DISCUSSION OF MIDTERM EXAM FOURIER ANALYSIS (.443) PROF. QIAO ZHANG Problem. Cosider the itegrable -periodic fuctio f(θ) = θ θ [, ). () Compute the Fourier series for f(θ). () Discuss the covergece
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
Discrete Fourier Transform
 Discrete Fourier Trasform ) Purpose The purpose is to represet a determiistic or stochastic siga u( t ) as a fiite Fourier sum, whe observatios of u() t ( ) are give o a reguar grid, each affected by a
Discrete Fourier Trasform ) Purpose The purpose is to represet a determiistic or stochastic siga u( t ) as a fiite Fourier sum, whe observatios of u() t ( ) are give o a reguar grid, each affected by a
Sequences and Series of Functions
 Chapter 6 Sequeces ad Series of Fuctios 6.1. Covergece of a Sequece of Fuctios Poitwise Covergece. Defiitio 6.1. Let, for each N, fuctio f : A R be defied. If, for each x A, the sequece (f (x)) coverges
Chapter 6 Sequeces ad Series of Fuctios 6.1. Covergece of a Sequece of Fuctios Poitwise Covergece. Defiitio 6.1. Let, for each N, fuctio f : A R be defied. If, for each x A, the sequece (f (x)) coverges
A detailed proof of the irrationality of π
 Matthew Straugh Math 4 Midterm A detailed proof of the irratioality of The proof is due to Iva Nive (1947) ad essetial to the proof are Lemmas ad 3 due to Charles Hermite (18 s) First let us itroduce some
Matthew Straugh Math 4 Midterm A detailed proof of the irratioality of The proof is due to Iva Nive (1947) ad essetial to the proof are Lemmas ad 3 due to Charles Hermite (18 s) First let us itroduce some
radians A function f ( x ) is called periodic if it is defined for all real x and if there is some positive number P such that:
 Fourier Series. Graph of y Asix ad y Acos x Amplitude A ; period 36 radias. Harmoics y y six is the first harmoic y y six is the th harmoics 3. Periodic fuctio A fuctio f ( x ) is called periodic if it
Fourier Series. Graph of y Asix ad y Acos x Amplitude A ; period 36 radias. Harmoics y y six is the first harmoic y y six is the th harmoics 3. Periodic fuctio A fuctio f ( x ) is called periodic if it
Fall 2013 MTH431/531 Real analysis Section Notes
 Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
1 Approximating Integrals using Taylor Polynomials
 Seughee Ye Ma 8: Week 7 Nov Week 7 Summary This week, we will lear how we ca approximate itegrals usig Taylor series ad umerical methods. Topics Page Approximatig Itegrals usig Taylor Polyomials. Defiitios................................................
Seughee Ye Ma 8: Week 7 Nov Week 7 Summary This week, we will lear how we ca approximate itegrals usig Taylor series ad umerical methods. Topics Page Approximatig Itegrals usig Taylor Polyomials. Defiitios................................................
3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,
![3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense, 3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,](/thumbs/82/85448051.jpg) 3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
s = and t = with C ij = A i B j F. (i) Note that cs = M and so ca i µ(a i ) I E (cs) = = c a i µ(a i ) = ci E (s). (ii) Note that s + t = M and so
 3 From the otes we see that the parts of Theorem 4. that cocer us are: Let s ad t be two simple o-egative F-measurable fuctios o X, F, µ ad E, F F. The i I E cs ci E s for all c R, ii I E s + t I E s +
3 From the otes we see that the parts of Theorem 4. that cocer us are: Let s ad t be two simple o-egative F-measurable fuctios o X, F, µ ad E, F F. The i I E cs ci E s for all c R, ii I E s + t I E s +
MATH301 Real Analysis (2008 Fall) Tutorial Note #7. k=1 f k (x) converges pointwise to S(x) on E if and
 MATH01 Real Aalysis (2008 Fall) Tutorial Note #7 Sequece ad Series of fuctio 1: Poitwise Covergece ad Uiform Covergece Part I: Poitwise Covergece Defiitio of poitwise covergece: A sequece of fuctios f
MATH01 Real Aalysis (2008 Fall) Tutorial Note #7 Sequece ad Series of fuctio 1: Poitwise Covergece ad Uiform Covergece Part I: Poitwise Covergece Defiitio of poitwise covergece: A sequece of fuctios f
Indian Statistical Institute, Bangalore Centre Solution set of M.Math II Year, End-Sem Examination 2015 Fourier Analysis
 Idia Statistical Istitute, Bagalore Cetre Solutio set of M.Math II Year, Ed-Sem Examiatio 05 Fourier Aalysis Note: We use the followig otatios L () L ad L () L.. Prove that f, ˆf L the f L. Proof. Sice
Idia Statistical Istitute, Bagalore Cetre Solutio set of M.Math II Year, Ed-Sem Examiatio 05 Fourier Aalysis Note: We use the followig otatios L () L ad L () L.. Prove that f, ˆf L the f L. Proof. Sice
sin(n) + 2 cos(2n) n 3/2 3 sin(n) 2cos(2n) n 3/2 a n =
 60. Ratio ad root tests 60.1. Absolutely coverget series. Defiitio 13. (Absolute covergece) A series a is called absolutely coverget if the series of absolute values a is coverget. The absolute covergece
60. Ratio ad root tests 60.1. Absolutely coverget series. Defiitio 13. (Absolute covergece) A series a is called absolutely coverget if the series of absolute values a is coverget. The absolute covergece
ON WEAK -STATISTICAL CONVERGENCE OF ORDER
 UPB Sci Bu, Series A, Vo 8, Iss, 8 ISSN 3-77 ON WEAK -STATISTICAL CONVERGENCE OF ORDER Sia ERCAN, Yavuz ALTIN ad Çiğdem A BEKTAŞ 3 I the preset paper, we give the cocept of wea -statistica covergece of
UPB Sci Bu, Series A, Vo 8, Iss, 8 ISSN 3-77 ON WEAK -STATISTICAL CONVERGENCE OF ORDER Sia ERCAN, Yavuz ALTIN ad Çiğdem A BEKTAŞ 3 I the preset paper, we give the cocept of wea -statistica covergece of
Product measures, Tonelli s and Fubini s theorems For use in MAT3400/4400, autumn 2014 Nadia S. Larsen. Version of 13 October 2014.
 Product measures, Toelli s ad Fubii s theorems For use i MAT3400/4400, autum 2014 Nadia S. Larse Versio of 13 October 2014. 1. Costructio of the product measure The purpose of these otes is to preset the
Product measures, Toelli s ad Fubii s theorems For use i MAT3400/4400, autum 2014 Nadia S. Larse Versio of 13 October 2014. 1. Costructio of the product measure The purpose of these otes is to preset the
Math 132, Fall 2009 Exam 2: Solutions
 Math 3, Fall 009 Exam : Solutios () a) ( poits) Determie for which positive real umbers p, is the followig improper itegral coverget, ad for which it is diverget. Evaluate the itegral for each value of
Math 3, Fall 009 Exam : Solutios () a) ( poits) Determie for which positive real umbers p, is the followig improper itegral coverget, ad for which it is diverget. Evaluate the itegral for each value of
Self-Consistent Simulations of Beam and Plasma Systems Final Exam ( take-home )
 Sef-Cosistet Simuatios of Beam ad Pasma Systems Fia Exam ( take-home ) S. M. Lud, J.-L. Vay, R. Lehe, ad D. Wikeher Thursday, Jue 16 th, 2016 Probem 1 - Maxwe s equatios ad redudat iformatio. a) Show that
Sef-Cosistet Simuatios of Beam ad Pasma Systems Fia Exam ( take-home ) S. M. Lud, J.-L. Vay, R. Lehe, ad D. Wikeher Thursday, Jue 16 th, 2016 Probem 1 - Maxwe s equatios ad redudat iformatio. a) Show that
The natural exponential function
 The atural expoetial fuctio Attila Máté Brookly College of the City Uiversity of New York December, 205 Cotets The atural expoetial fuctio for real x. Beroulli s iequality.....................................2
The atural expoetial fuctio Attila Máté Brookly College of the City Uiversity of New York December, 205 Cotets The atural expoetial fuctio for real x. Beroulli s iequality.....................................2
INFINITE SEQUENCES AND SERIES
 11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES 11.4 The Compariso Tests I this sectio, we will lear: How to fid the value of a series by comparig it with a kow series. COMPARISON TESTS
11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES 11.4 The Compariso Tests I this sectio, we will lear: How to fid the value of a series by comparig it with a kow series. COMPARISON TESTS
ENGI Series Page 6-01
 ENGI 3425 6 Series Page 6-01 6. Series Cotets: 6.01 Sequeces; geeral term, limits, covergece 6.02 Series; summatio otatio, covergece, divergece test 6.03 Stadard Series; telescopig series, geometric series,
ENGI 3425 6 Series Page 6-01 6. Series Cotets: 6.01 Sequeces; geeral term, limits, covergece 6.02 Series; summatio otatio, covergece, divergece test 6.03 Stadard Series; telescopig series, geometric series,
Chapter 10: Power Series
 Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
MIDTERM 3 CALCULUS 2. Monday, December 3, :15 PM to 6:45 PM. Name PRACTICE EXAM SOLUTIONS
 MIDTERM 3 CALCULUS MATH 300 FALL 08 Moday, December 3, 08 5:5 PM to 6:45 PM Name PRACTICE EXAM S Please aswer all of the questios, ad show your work. You must explai your aswers to get credit. You will
MIDTERM 3 CALCULUS MATH 300 FALL 08 Moday, December 3, 08 5:5 PM to 6:45 PM Name PRACTICE EXAM S Please aswer all of the questios, ad show your work. You must explai your aswers to get credit. You will
Chapter 3. Strong convergence. 3.1 Definition of almost sure convergence
 Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Alternating Series. 1 n 0 2 n n THEOREM 9.14 Alternating Series Test Let a n > 0. The alternating series. 1 n a n.
 0_0905.qxd //0 :7 PM Page SECTION 9.5 Alteratig Series Sectio 9.5 Alteratig Series Use the Alteratig Series Test to determie whether a ifiite series coverges. Use the Alteratig Series Remaider to approximate
0_0905.qxd //0 :7 PM Page SECTION 9.5 Alteratig Series Sectio 9.5 Alteratig Series Use the Alteratig Series Test to determie whether a ifiite series coverges. Use the Alteratig Series Remaider to approximate
Additional Notes on Power Series
 Additioal Notes o Power Series Mauela Girotti MATH 37-0 Advaced Calculus of oe variable Cotets Quick recall 2 Abel s Theorem 2 3 Differetiatio ad Itegratio of Power series 4 Quick recall We recall here
Additioal Notes o Power Series Mauela Girotti MATH 37-0 Advaced Calculus of oe variable Cotets Quick recall 2 Abel s Theorem 2 3 Differetiatio ad Itegratio of Power series 4 Quick recall We recall here
Ma 530 Introduction to Power Series
 Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
2 Banach spaces and Hilbert spaces
 2 Baach spaces ad Hilbert spaces Tryig to do aalysis i the ratioal umbers is difficult for example cosider the set {x Q : x 2 2}. This set is o-empty ad bouded above but does ot have a least upper boud
2 Baach spaces ad Hilbert spaces Tryig to do aalysis i the ratioal umbers is difficult for example cosider the set {x Q : x 2 2}. This set is o-empty ad bouded above but does ot have a least upper boud
MA131 - Analysis 1. Workbook 3 Sequences II
 MA3 - Aalysis Workbook 3 Sequeces II Autum 2004 Cotets 2.8 Coverget Sequeces........................ 2.9 Algebra of Limits......................... 2 2.0 Further Useful Results........................
MA3 - Aalysis Workbook 3 Sequeces II Autum 2004 Cotets 2.8 Coverget Sequeces........................ 2.9 Algebra of Limits......................... 2 2.0 Further Useful Results........................
f(x)g(x) dx is an inner product on D.
 Ark9: Exercises for MAT2400 Fourier series The exercises o this sheet cover the sectios 4.9 to 4.13. They are iteded for the groups o Thursday, April 12 ad Friday, March 30 ad April 13. NB: No group o
Ark9: Exercises for MAT2400 Fourier series The exercises o this sheet cover the sectios 4.9 to 4.13. They are iteded for the groups o Thursday, April 12 ad Friday, March 30 ad April 13. NB: No group o
Mathematical Methods for Physics and Engineering
 Mathematical Methods for Physics ad Egieerig Lecture otes Sergei V. Shabaov Departmet of Mathematics, Uiversity of Florida, Gaiesville, FL 326 USA CHAPTER The theory of covergece. Numerical sequeces..
Mathematical Methods for Physics ad Egieerig Lecture otes Sergei V. Shabaov Departmet of Mathematics, Uiversity of Florida, Gaiesville, FL 326 USA CHAPTER The theory of covergece. Numerical sequeces..
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Math 113, Calculus II Winter 2007 Final Exam Solutions
 Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
Physics 116A Solutions to Homework Set #9 Winter 2012
 Physics 116A Solutios to Homework Set #9 Witer 1 1. Boas, problem 11.3 5. Simplify Γ( 1 )Γ(4)/Γ( 9 ). Usig xγ(x) Γ(x + 1) repeatedly, oe obtais Γ( 9) 7 Γ( 7) 7 5 Γ( 5 ), etc. util fially obtaiig Γ( 9)
Physics 116A Solutios to Homework Set #9 Witer 1 1. Boas, problem 11.3 5. Simplify Γ( 1 )Γ(4)/Γ( 9 ). Usig xγ(x) Γ(x + 1) repeatedly, oe obtais Γ( 9) 7 Γ( 7) 7 5 Γ( 5 ), etc. util fially obtaiig Γ( 9)
SCORE. Exam 2. MA 114 Exam 2 Fall 2017
 Exam Name: Sectio ad/or TA: Do ot remove this aswer page you will retur the whole exam. You will be allowed two hours to complete this test. No books or otes may be used. You may use a graphig calculator
Exam Name: Sectio ad/or TA: Do ot remove this aswer page you will retur the whole exam. You will be allowed two hours to complete this test. No books or otes may be used. You may use a graphig calculator
CHAPTER 4 FOURIER SERIES
 CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
Comparison Study of Series Approximation. and Convergence between Chebyshev. and Legendre Series
 Applied Mathematical Scieces, Vol. 7, 03, o. 6, 3-337 HIKARI Ltd, www.m-hikari.com http://d.doi.org/0.988/ams.03.3430 Compariso Study of Series Approimatio ad Covergece betwee Chebyshev ad Legedre Series
Applied Mathematical Scieces, Vol. 7, 03, o. 6, 3-337 HIKARI Ltd, www.m-hikari.com http://d.doi.org/0.988/ams.03.3430 Compariso Study of Series Approimatio ad Covergece betwee Chebyshev ad Legedre Series
2 n = n=1 a n is convergent and we let. i=1
 Lecture 3 : Series So far our defiitio of a sum of umbers applies oly to addig a fiite set of umbers. We ca exted this to a defiitio of a sum of a ifiite set of umbers i much the same way as we exteded
Lecture 3 : Series So far our defiitio of a sum of umbers applies oly to addig a fiite set of umbers. We ca exted this to a defiitio of a sum of a ifiite set of umbers i much the same way as we exteded
We are mainly going to be concerned with power series in x, such as. (x)} converges - that is, lims N n
 Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
x x x Using a second Taylor polynomial with remainder, find the best constant C so that for x 0,
 Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
Lecture 19: Convergence
 Lecture 19: Covergece Asymptotic approach I statistical aalysis or iferece, a key to the success of fidig a good procedure is beig able to fid some momets ad/or distributios of various statistics. I may
Lecture 19: Covergece Asymptotic approach I statistical aalysis or iferece, a key to the success of fidig a good procedure is beig able to fid some momets ad/or distributios of various statistics. I may
6 Integers Modulo n. integer k can be written as k = qn + r, with q,r, 0 r b. So any integer.
 6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
It is often useful to approximate complicated functions using simpler ones. We consider the task of approximating a function by a polynomial.
 Taylor Polyomials ad Taylor Series It is ofte useful to approximate complicated fuctios usig simpler oes We cosider the task of approximatig a fuctio by a polyomial If f is at least -times differetiable
Taylor Polyomials ad Taylor Series It is ofte useful to approximate complicated fuctios usig simpler oes We cosider the task of approximatig a fuctio by a polyomial If f is at least -times differetiable
A collocation method for singular integral equations with cosecant kernel via Semi-trigonometric interpolation
 Iteratioal Joural of Mathematics Research. ISSN 0976-5840 Volume 9 Number 1 (017) pp. 45-51 Iteratioal Research Publicatio House http://www.irphouse.com A collocatio method for sigular itegral equatios
Iteratioal Joural of Mathematics Research. ISSN 0976-5840 Volume 9 Number 1 (017) pp. 45-51 Iteratioal Research Publicatio House http://www.irphouse.com A collocatio method for sigular itegral equatios
SOLUTION SET VI FOR FALL [(n + 2)(n + 1)a n+2 a n 1 ]x n = 0,
![SOLUTION SET VI FOR FALL [(n + 2)(n + 1)a n+2 a n 1 ]x n = 0, SOLUTION SET VI FOR FALL [(n + 2)(n + 1)a n+2 a n 1 ]x n = 0,](/thumbs/94/119566625.jpg) 4. Series Solutios of Differetial Equatios:Special Fuctios 4.. Illustrative examples.. 5. Obtai the geeral solutio of each of the followig differetial equatios i terms of Maclauri series: d y (a dx = xy,
4. Series Solutios of Differetial Equatios:Special Fuctios 4.. Illustrative examples.. 5. Obtai the geeral solutio of each of the followig differetial equatios i terms of Maclauri series: d y (a dx = xy,
1 Lecture 2: Sequence, Series and power series (8/14/2012)
 Summer Jump-Start Program for Aalysis, 202 Sog-Yig Li Lecture 2: Sequece, Series ad power series (8/4/202). More o sequeces Example.. Let {x } ad {y } be two bouded sequeces. Show lim sup (x + y ) lim
Summer Jump-Start Program for Aalysis, 202 Sog-Yig Li Lecture 2: Sequece, Series ad power series (8/4/202). More o sequeces Example.. Let {x } ad {y } be two bouded sequeces. Show lim sup (x + y ) lim
lim za n n = z lim a n n.
 Lecture 6 Sequeces ad Series Defiitio 1 By a sequece i a set A, we mea a mappig f : N A. It is customary to deote a sequece f by {s } where, s := f(). A sequece {z } of (complex) umbers is said to be coverget
Lecture 6 Sequeces ad Series Defiitio 1 By a sequece i a set A, we mea a mappig f : N A. It is customary to deote a sequece f by {s } where, s := f(). A sequece {z } of (complex) umbers is said to be coverget
Lecture 7: Fourier Series and Complex Power Series
 Math 1d Istructor: Padraic Bartlett Lecture 7: Fourier Series ad Complex Power Series Week 7 Caltech 013 1 Fourier Series 1.1 Defiitios ad Motivatio Defiitio 1.1. A Fourier series is a series of fuctios
Math 1d Istructor: Padraic Bartlett Lecture 7: Fourier Series ad Complex Power Series Week 7 Caltech 013 1 Fourier Series 1.1 Defiitios ad Motivatio Defiitio 1.1. A Fourier series is a series of fuctios
AMS Mathematics Subject Classification : 40A05, 40A99, 42A10. Key words and phrases : Harmonic series, Fourier series. 1.
 J. Appl. Math. & Computig Vol. x 00y), No. z, pp. A RECURSION FOR ALERNAING HARMONIC SERIES ÁRPÁD BÉNYI Abstract. We preset a coveiet recursive formula for the sums of alteratig harmoic series of odd order.
J. Appl. Math. & Computig Vol. x 00y), No. z, pp. A RECURSION FOR ALERNAING HARMONIC SERIES ÁRPÁD BÉNYI Abstract. We preset a coveiet recursive formula for the sums of alteratig harmoic series of odd order.
Math 210A Homework 1
 Math 0A Homework Edward Burkard Exercise. a) State the defiitio of a aalytic fuctio. b) What are the relatioships betwee aalytic fuctios ad the Cauchy-Riema equatios? Solutio. a) A fuctio f : G C is called
Math 0A Homework Edward Burkard Exercise. a) State the defiitio of a aalytic fuctio. b) What are the relatioships betwee aalytic fuctios ad the Cauchy-Riema equatios? Solutio. a) A fuctio f : G C is called
Chapter 8. Uniform Convergence and Differentiation.
 Chapter 8 Uiform Covergece ad Differetiatio This chapter cotiues the study of the cosequece of uiform covergece of a series of fuctio I Chapter 7 we have observed that the uiform limit of a sequece of
Chapter 8 Uiform Covergece ad Differetiatio This chapter cotiues the study of the cosequece of uiform covergece of a series of fuctio I Chapter 7 we have observed that the uiform limit of a sequece of
Seunghee Ye Ma 8: Week 5 Oct 28
 Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
7 Sequences of real numbers
 40 7 Sequeces of real umbers 7. Defiitios ad examples Defiitio 7... A sequece of real umbers is a real fuctio whose domai is the set N of atural umbers. Let s : N R be a sequece. The the values of s are
40 7 Sequeces of real umbers 7. Defiitios ad examples Defiitio 7... A sequece of real umbers is a real fuctio whose domai is the set N of atural umbers. Let s : N R be a sequece. The the values of s are
Integrable Functions. { f n } is called a determining sequence for f. If f is integrable with respect to, then f d does exist as a finite real number
 MATH 532 Itegrable Fuctios Dr. Neal, WKU We ow shall defie what it meas for a measurable fuctio to be itegrable, show that all itegral properties of simple fuctios still hold, ad the give some coditios
MATH 532 Itegrable Fuctios Dr. Neal, WKU We ow shall defie what it meas for a measurable fuctio to be itegrable, show that all itegral properties of simple fuctios still hold, ad the give some coditios
A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Section 5.5. Infinite Series: The Ratio Test
 Differece Equatios to Differetial Equatios Sectio 5.5 Ifiite Series: The Ratio Test I the last sectio we saw that we could demostrate the covergece of a series a, where a 0 for all, by showig that a approaches
Differece Equatios to Differetial Equatios Sectio 5.5 Ifiite Series: The Ratio Test I the last sectio we saw that we could demostrate the covergece of a series a, where a 0 for all, by showig that a approaches
TR/46 OCTOBER THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION A. TALBOT
 TR/46 OCTOBER 974 THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION by A. TALBOT .. Itroductio. A problem i approximatio theory o which I have recetly worked [] required for its solutio a proof that the
TR/46 OCTOBER 974 THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION by A. TALBOT .. Itroductio. A problem i approximatio theory o which I have recetly worked [] required for its solutio a proof that the
MATH2007* Partial Answers to Review Exercises Fall 2004
 MATH27* Partial Aswers to Review Eercises Fall 24 Evaluate each of the followig itegrals:. Let u cos. The du si ad Hece si ( cos 2 )(si ) (u 2 ) du. si u 2 cos 7 u 7 du Please fiish this. 2. We use itegratio
MATH27* Partial Aswers to Review Eercises Fall 24 Evaluate each of the followig itegrals:. Let u cos. The du si ad Hece si ( cos 2 )(si ) (u 2 ) du. si u 2 cos 7 u 7 du Please fiish this. 2. We use itegratio
SUMMARY OF SEQUENCES AND SERIES
 SUMMARY OF SEQUENCES AND SERIES Importat Defiitios, Results ad Theorems for Sequeces ad Series Defiitio. A sequece {a } has a limit L ad we write lim a = L if for every ɛ > 0, there is a correspodig iteger
SUMMARY OF SEQUENCES AND SERIES Importat Defiitios, Results ad Theorems for Sequeces ad Series Defiitio. A sequece {a } has a limit L ad we write lim a = L if for every ɛ > 0, there is a correspodig iteger
LECTURES 5 AND 6: CONVERGENCE TESTS
 LECTURES 5 AND 6: CONVERGENCE TESTS I the previous lecture we saw a very basic test for covergece - the compariso test. Here we develop slightly more sophisticated machiery for determiig the covergece
LECTURES 5 AND 6: CONVERGENCE TESTS I the previous lecture we saw a very basic test for covergece - the compariso test. Here we develop slightly more sophisticated machiery for determiig the covergece
(A sequence also can be thought of as the list of function values attained for a function f :ℵ X, where f (n) = x n for n 1.) x 1 x N +k x N +4 x 3
 MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
Sequence and Series of Functions
 6 Sequece d Series of Fuctios 6. Sequece of Fuctios 6.. Poitwise Covergece d Uiform Covergece Let J be itervl i R. Defiitio 6. For ech N, suppose fuctio f : J R is give. The we sy tht sequece (f ) of fuctios
6 Sequece d Series of Fuctios 6. Sequece of Fuctios 6.. Poitwise Covergece d Uiform Covergece Let J be itervl i R. Defiitio 6. For ech N, suppose fuctio f : J R is give. The we sy tht sequece (f ) of fuctios
Math 113 Exam 3 Practice
 Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
Math 113 Exam 3 Practice
 Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
Math 341 Lecture #31 6.5: Power Series
 Math 341 Lecture #31 6.5: Power Series We ow tur our attetio to a particular kid of series of fuctios, amely, power series, f(x = a x = a 0 + a 1 x + a 2 x 2 + where a R for all N. I terms of a series
Math 341 Lecture #31 6.5: Power Series We ow tur our attetio to a particular kid of series of fuctios, amely, power series, f(x = a x = a 0 + a 1 x + a 2 x 2 + where a R for all N. I terms of a series
INFINITE SEQUENCES AND SERIES
 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES I geeral, it is difficult to fid the exact sum of a series. We were able to accomplish this for geometric series ad the series /[(+)]. This is
INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES I geeral, it is difficult to fid the exact sum of a series. We were able to accomplish this for geometric series ad the series /[(+)]. This is
Enumerative & Asymptotic Combinatorics
 C50 Eumerative & Asymptotic Combiatorics Stirlig ad Lagrage Sprig 2003 This sectio of the otes cotais proofs of Stirlig s formula ad the Lagrage Iversio Formula. Stirlig s formula Theorem 1 (Stirlig s
C50 Eumerative & Asymptotic Combiatorics Stirlig ad Lagrage Sprig 2003 This sectio of the otes cotais proofs of Stirlig s formula ad the Lagrage Iversio Formula. Stirlig s formula Theorem 1 (Stirlig s
7.1 Convergence of sequences of random variables
 Chapter 7 Limit Theorems Throughout this sectio we will assume a probability space (, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
Chapter 7 Limit Theorems Throughout this sectio we will assume a probability space (, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
PAPER : IIT-JAM 2010
 MATHEMATICS-MA (CODE A) Q.-Q.5: Oly oe optio is correct for each questio. Each questio carries (+6) marks for correct aswer ad ( ) marks for icorrect aswer.. Which of the followig coditios does NOT esure
MATHEMATICS-MA (CODE A) Q.-Q.5: Oly oe optio is correct for each questio. Each questio carries (+6) marks for correct aswer ad ( ) marks for icorrect aswer.. Which of the followig coditios does NOT esure
Sequences. A Sequence is a list of numbers written in order.
 Sequeces A Sequece is a list of umbers writte i order. {a, a 2, a 3,... } The sequece may be ifiite. The th term of the sequece is the th umber o the list. O the list above a = st term, a 2 = 2 d term,
Sequeces A Sequece is a list of umbers writte i order. {a, a 2, a 3,... } The sequece may be ifiite. The th term of the sequece is the th umber o the list. O the list above a = st term, a 2 = 2 d term,
THE INTEGRAL TEST AND ESTIMATES OF SUMS
 THE INTEGRAL TEST AND ESTIMATES OF SUMS. Itroductio Determiig the exact sum of a series is i geeral ot a easy task. I the case of the geometric series ad the telescoig series it was ossible to fid a simle
THE INTEGRAL TEST AND ESTIMATES OF SUMS. Itroductio Determiig the exact sum of a series is i geeral ot a easy task. I the case of the geometric series ad the telescoig series it was ossible to fid a simle
MATH 10550, EXAM 3 SOLUTIONS
 MATH 155, EXAM 3 SOLUTIONS 1. I fidig a approximate solutio to the equatio x 3 +x 4 = usig Newto s method with iitial approximatio x 1 = 1, what is x? Solutio. Recall that x +1 = x f(x ) f (x ). Hece,
MATH 155, EXAM 3 SOLUTIONS 1. I fidig a approximate solutio to the equatio x 3 +x 4 = usig Newto s method with iitial approximatio x 1 = 1, what is x? Solutio. Recall that x +1 = x f(x ) f (x ). Hece,
Convergence of random variables. (telegram style notes) P.J.C. Spreij
 Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
Math Solutions to homework 6
 Math 175 - Solutios to homework 6 Cédric De Groote November 16, 2017 Problem 1 (8.11 i the book): Let K be a compact Hermitia operator o a Hilbert space H ad let the kerel of K be {0}. Show that there
Math 175 - Solutios to homework 6 Cédric De Groote November 16, 2017 Problem 1 (8.11 i the book): Let K be a compact Hermitia operator o a Hilbert space H ad let the kerel of K be {0}. Show that there
MA131 - Analysis 1. Workbook 9 Series III
 MA3 - Aalysis Workbook 9 Series III Autum 004 Cotets 4.4 Series with Positive ad Negative Terms.............. 4.5 Alteratig Series.......................... 4.6 Geeral Series.............................
MA3 - Aalysis Workbook 9 Series III Autum 004 Cotets 4.4 Series with Positive ad Negative Terms.............. 4.5 Alteratig Series.......................... 4.6 Geeral Series.............................
PLEASE MARK YOUR ANSWERS WITH AN X, not a circle! 1. (a) (b) (c) (d) (e) 3. (a) (b) (c) (d) (e) 5. (a) (b) (c) (d) (e) 7. (a) (b) (c) (d) (e)
 Math 0560, Exam 3 November 6, 07 The Hoor Code is i effect for this examiatio. All work is to be your ow. No calculators. The exam lasts for hour ad 5 mi. Be sure that your ame is o every page i case pages
Math 0560, Exam 3 November 6, 07 The Hoor Code is i effect for this examiatio. All work is to be your ow. No calculators. The exam lasts for hour ad 5 mi. Be sure that your ame is o every page i case pages
C. Complex Numbers. x 6x + 2 = 0. This equation was known to have three real roots, given by simple combinations of the expressions
 C. Complex Numbers. Complex arithmetic. Most people thik that complex umbers arose from attempts to solve quadratic equatios, but actually it was i coectio with cubic equatios they first appeared. Everyoe
C. Complex Numbers. Complex arithmetic. Most people thik that complex umbers arose from attempts to solve quadratic equatios, but actually it was i coectio with cubic equatios they first appeared. Everyoe
The Riemann Zeta Function
 Physics 6A Witer 6 The Riema Zeta Fuctio I this ote, I will sketch some of the mai properties of the Riema zeta fuctio, ζ(x). For x >, we defie ζ(x) =, x >. () x = For x, this sum diverges. However, we
Physics 6A Witer 6 The Riema Zeta Fuctio I this ote, I will sketch some of the mai properties of the Riema zeta fuctio, ζ(x). For x >, we defie ζ(x) =, x >. () x = For x, this sum diverges. However, we
Math 113 Exam 4 Practice
 Math Exam 4 Practice Exam 4 will cover.-.. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for
Math Exam 4 Practice Exam 4 will cover.-.. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for
Løsningsførslag i 4M
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side 1 av 6 Løsigsførslag i 4M Oppgave 1 a) A sketch of the graph of the give f o the iterval [ 3, 3) is as follows: The Fourier
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side 1 av 6 Løsigsførslag i 4M Oppgave 1 a) A sketch of the graph of the give f o the iterval [ 3, 3) is as follows: The Fourier
Sequences A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
CHAPTER I: Vector Spaces
 CHAPTER I: Vector Spaces Sectio 1: Itroductio ad Examples This first chapter is largely a review of topics you probably saw i your liear algebra course. So why cover it? (1) Not everyoe remembers everythig
CHAPTER I: Vector Spaces Sectio 1: Itroductio ad Examples This first chapter is largely a review of topics you probably saw i your liear algebra course. So why cover it? (1) Not everyoe remembers everythig
62. Power series Definition 16. (Power series) Given a sequence {c n }, the series. c n x n = c 0 + c 1 x + c 2 x 2 + c 3 x 3 +
 62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
