Self-Consistent Simulations of Beam and Plasma Systems Final Exam ( take-home )
|
|
|
- Barrie Dennis
- 5 years ago
- Views:
Transcription
1 Sef-Cosistet Simuatios of Beam ad Pasma Systems Fia Exam ( take-home ) S. M. Lud, J.-L. Vay, R. Lehe, ad D. Wikeher Thursday, Jue 16 th, 2016 Probem 1 - Maxwe s equatios ad redudat iformatio. a) Show that the reativistic Vasov equatio { } t + v x + q [E + v B] f(x, p, t) = 0 p with v = impies coservatio of charge with where p γm = p/m [1 + p 2 /(mc) 2 ] 1/2 t ρ + x J = 0 ρ = q J = q d 3 p f d 3 p vf Hit 1: Use the same steps as i Moday s probem 3 a). Hit 2: You are permitted to do this o-reativisticay if you wat. The resut hods either way. b) The 3D Maxwe equatios are iear, 1 st -order-i-time, kiematic equatios for E(x, t), B(x, t) if ρ(x, t) ad J(x, t) are regarded as prescribed sources. 1) How may fied compoets are i E, B? 2) How may equatios are i the stadard set of Maxwe equatios? E = ρ ɛ 0 E = t B B = 0 B = µ 0 J + µ 0 ɛ 0 t E 1
2 3) What iitia (t = 0) vaues are required for E ad B to sove the Maxwe equatios for E(x, t) ad B(x, t) for a times t with ρ(x, t) ad J(x, t) specified? c) To better uderstad the situatio i b), show that the Maxwe equatios impy that where d) Show that ( E) c 2 t 2 E = µ 0 t J ( B) + 1 c 2 2 t 2 B = µ 0 J µ 0 ɛ 0 = 1 c d -order-i-time equatios for 6 fied compoets E, B. E = t B impies that t B = 0. Does this impy that B(x, t) = 0 for a times t if B(x, t = 0) = 0? e) Show that B = µ 0 J + µ 0 ɛ 0 t E ad t ρ + x J = 0 impy that t ( E ρ/ɛ 0) = 0. Does this impy that E = ρ/ɛ 0 for a times t if E = ρ/ɛ 0 at t = 0? f) Show that the Maxwe equatios B = µ 0 J + µ 0 ɛ 0 t E ad E = ρ ɛ 0 impy that t ρ + x J = 0. Does this impy that the Maxwe equatios shoud oy be appied to charge ρ ad curret sources J which ocay coserve charge? g) Based o a) - f), ca we sove Maxwe s equatios for E(x, t) ad B(x, t) for sources ρ ad J satisfyig t ρ + x J = 0 for a times t 0 by oy sovig the two Maxwe equatios provided that E = t B ad B = µ 0J + µ 0 ɛ 0 t E E = ρ ɛ 0 ad B = 0 are satisfied at time t = 0? If yes, does it matter if we use E = ρ/ɛ 0 ad B = 0? Why? 2
3 Probem 2 - Exteded-steci Maxwe sover Let us cosider the foowig scheme for the 1D Maxwe equatios i vacuum E x +1 E x +1/2 B y +1/2 B y 1/2 +1/2 = c 2 ( ) Ex = +1 E x z (1 α) B y +1/2 +1/2 B y +1/2 1/2 z + α B +1/2 y +3/2 B y +1/2 3/2 3 z where B y ad E x represet the fieds B y ad E x at time ad positio z. a) By performig a Tayor expasio of the B fied to order 2 i z (i.e. with a error term O( z 3 )), show that the expressio Is a approximatio of B z 2 i z. (1 α) B +1/2 y+1/2 B y +1/2 1/2 z + α B +1/2 y+3/2 B y +1/2 3/2 3 z at positio z (ad time ( + 1/2)) which is accurate to order +1/2 Hit: remember that B y +1/2 deotes the B y fied at positio z = (+1/2) z. I other words: +1/2 B y +1/2 = B y +1/2 +1/2 (( + 1/2) z) (with simiar expressios for B y 1/2, B y +1/2 +3/2, B y +1/2 3/2 ). The perform a Tayor expasio aroud z = z. b) By combiig the discrete Maxwe equatios, show that the correspodig discrete propagatio equatio for E x is of the form: E x E x + E x c 2 2 = E x+1 2E x + E x 1 z 2 (1) ad give the expressio of β as a fuctio of α. Hit: Start by evauatig the quatity 1 ( Ex +1 + β E x +2 4E x E x 4E x 1 + E x 2 z 2 (2) E x usig the secod Maxwe equatio from above. c) By assumig that E x is of the form E x E ) x 1 E x = E 0 e ik z iω Show that the discrete dispersio reatio is: ( ) 1 ω c 2 2 si2 = 1 ( ) k z 2 z 2 si2 4α ( ) k z 2 3 z 2 si4 2 3
4 d) For α < 3/8, show that the right-had side of the above equatio is a growig fuctio of k, for k [0, π/ z]. Ifer the maximum vaue that the right-had takes for k [0, π/ z], ad thus ifer that the Courat imit is CF L = z 1 c 1 4α 3 Remider for stadard formuas: si(x) = eix e ix 2i Probem 3 - Pytho ODE sover Write a pytho script to advace the momets 2 x x x 2 x x x 2 κ x (s) x 2 + d x 2 2κ x (s) x x + ds ỹ 2 = 2 ỹỹ ỹỹ ỹ 2 ỹ 2 κ y (s) ỹ 2 + 2κ y (s) ỹỹ + ( with κ x (s) = κ y (s) = ˆκ cos 2πs ad attice period L p = 0.5 m. L p ) Q x 2 1/2 2[ x 2 1/2 Q x x x 2 1/2 [ x2 1/2 Q ỹ 2 1/2 2[ x 2 1/2 Q ỹỹ ỹ 2 1/2 [ x2 1/2. Use a perveace of Q = , focus stregth ˆκ = 30 meter 2, a) Use a scietific pytho package with a ODE itegrator (e.g. scipy.itegrate.odeit) to evove the secod order momets from a (arbitrary) iitia coditio at s = 0. Hit: use scipy.itegrate.odeit? i ipytho for more iformatio. Ask for hep if you are stuck! b) Appy the resut i a) to advace from the iitia coditio x 2 = ỹ 2 = 1 4 mm2 x x = ỹỹ = 0 x 2 = ỹ 2 = 25 mrad 2 Use matpotib to pot a 2 d order momets o a axia mesh with at east 10 grid poits over 10 attice periods. c) Pot the combiatio of momets correspodig to rms x-emittace ɛ x,rms = x 2 x 2 x x 2 [mm-mrad] vs. s for 10 periods. Shoud you expect this vaue to be costat to umerica precisio? 4
5 d) Show that iitia coditios at s = 0 ca be foud for some vaues of x 2 ad ỹ 2 with iitia coditios x x = ỹỹ = 0 x 2 = ỹ 2 = 25 mrad 2 such that a momets repeat to umera precisio at s = L p. Is ɛ x,rms sti costat? Hit: Try umerica root fidig from iitia guess vaues of x 2 = ỹ 2. Probem 4 - Aterative partice pusher I order to itegrate the cotiuous equatios of motio dx dt = p ( dp γm dt = q E + p ) γm B (with γ = 1 + p 2 /(mc) 2 ) we choose to use the foowig staggered scheme x +1 x p +1/2 p 1/2 = p+1/2 γ +1/2 m ( ( ) ) = q E + 1 p +1/2 2 γ +1/2 m + p 1/2 γ 1/2 B m (3) (4) where the superscripts, +1/2 ad +1 idicates that the correspodig quatity is take at time, ( + 1/2) ad ( + 1), ad where γ +1/2 = 1 + (p +1/2 ) 2 /(mc) 2 ad γ 1/2 = 1 + (p 1/2 ) 2 /(mc) 2. Whie equatio (3) is easy to covert ito a update equatio (x +1 = x + p+1/2 ), it is γ +1/2 m more difficut to obtai p +1/2 from p 1/2, sice equatio (4) is impicit (i.e. it ivoves p +1/2 i both its right-had side ad eft-had side). The aim of this probem is to obtai the correspodig update equatio. a) Verify that the foowig scheme p = p 1/2 + qe + p 1/2 s s = qb 2γ 1/2 m p +1/2 = p + p +1/2 t t = qb 2γ +1/2 m (5) (6) satisfies equatio (4). Which oe of the two above equatios is impicit? b) By takig the vector product ad scaar product of (6) by t +, show that p +1/2 ca be extracted from this equatio ad reads p +1/2 = t 2 ( p + p t + (p t)t ) (7) Remider: For ay set of 3 vectors a, b, c, oe has (a b) c = (a c)b (b c)a 5
6 c) I fact, equatio (7) is sti ot expicit, sice the expressio of t (i equatio (3)) depeds o p +1/2, through γ +1/2. Thus, i order to extract p +1/2 expicity from equatio (7), take the foowig steps: From equatio (7), show that the expressio of (p +1/2 ) 2 is: (p +1/2 ) 2 = (p ) 2 + (p t) t 2 (8) Remider: For ay set of two vectors a, b, oe has (a b) (a b) = a 2 b 2 (a b) 2 Usig the otatio show that equatio (8) eads to τ = qb 2m = γ+1/2 t (9) (γ 2 ) 2 + [τ 2 (γ ) 2 ]γ 2 [(u ) 2 + τ 2 ] = 0 (10) where γ is a short-had otatio for γ +1/2 (i other words γ 2 = 1 + (p +1/2 ) 2 /(mc) 2 ) ad where the foowig otatios where used τ 2 = τ 2 u = p τ mc (γ ) 2 = 1 + (p ) 2 (mc) 2 (11) By remarkig that equatio (10) is a secod-order poyomia i γ 2, show that its soutio is: γ = 1 2 (γ ) 2 τ 2 + [(γ ) 2 τ 2 ] 2 + 4u 2 + 4τ 2 (12) d) Summig up a the previous step, i a actua agorithm (e.g. i Pytho) that computes p +1/2 from p 1/2, i which order shoud the foowig steps be executed? i) Compute γ +1/2 (aso deoted here as γ) usig equatio (12) ad equatio (11). ii) Compute s usig equatio (3), ad τ usig equatio (11) iii) Compute p +1/2 usig equatio (7) iv) Compute p from p 1/2 usig equatio (5) v) Compute t from τ ad γ +1/2 (usig equatio (9)) e) Dowoad the script partice_pusher.py from py This is a icompete script that impemets the sover cosidered here. Fid the ies tagged by ## ASSIGNEMENT ad compete them with the appropriate code. f) Ru the script (pytho partice_pusher.py). It itegrates the equatios of motio for a reativistic eectro (γ 100), i a magetic fied of 1 Tesa. What do you expect the motio to be? Are the resuts from the code quatitativey cosistet with the expected Larmor period of τ = 2πγme eb 0 (with B 0 = 1 T, m e = kg ad e = C)? 6
Strauss PDEs 2e: Section Exercise 4 Page 1 of 5. u tt = c 2 u xx ru t for 0 < x < l u = 0 at both ends u(x, 0) = φ(x) u t (x, 0) = ψ(x),
 Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
Topics in Fourier Analysis-I 1
 Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
Discrete Fourier Transform
 Discrete Fourier Trasform ) Purpose The purpose is to represet a determiistic or stochastic siga u( t ) as a fiite Fourier sum, whe observatios of u() t ( ) are give o a reguar grid, each affected by a
Discrete Fourier Trasform ) Purpose The purpose is to represet a determiistic or stochastic siga u( t ) as a fiite Fourier sum, whe observatios of u() t ( ) are give o a reguar grid, each affected by a
Here are some solutions to the sample problems concerning series solution of differential equations with non-constant coefficients (Chapter 12).
 Lecture Appedi B: Some sampe probems from Boas Here are some soutios to the sampe probems cocerig series soutio of differetia equatios with o-costat coefficiets (Chapter ) : Soutio: We wat to cosider the
Lecture Appedi B: Some sampe probems from Boas Here are some soutios to the sampe probems cocerig series soutio of differetia equatios with o-costat coefficiets (Chapter ) : Soutio: We wat to cosider the
Estimation for Complete Data
 Estimatio for Complete Data complete data: there is o loss of iformatio durig study. complete idividual complete data= grouped data A complete idividual data is the oe i which the complete iformatio of
Estimatio for Complete Data complete data: there is o loss of iformatio durig study. complete idividual complete data= grouped data A complete idividual data is the oe i which the complete iformatio of
Alternative Orthogonal Polynomials. Vladimir Chelyshkov
 Aterative Orthogoa oyomias Vadimir Cheyshov Istitute of Hydromechaics of the NAS Uraie Georgia Souther Uiversity USA Abstract. The doube-directio orthogoaizatio agorithm is appied to costruct sequeces
Aterative Orthogoa oyomias Vadimir Cheyshov Istitute of Hydromechaics of the NAS Uraie Georgia Souther Uiversity USA Abstract. The doube-directio orthogoaizatio agorithm is appied to costruct sequeces
MATH 10550, EXAM 3 SOLUTIONS
 MATH 155, EXAM 3 SOLUTIONS 1. I fidig a approximate solutio to the equatio x 3 +x 4 = usig Newto s method with iitial approximatio x 1 = 1, what is x? Solutio. Recall that x +1 = x f(x ) f (x ). Hece,
MATH 155, EXAM 3 SOLUTIONS 1. I fidig a approximate solutio to the equatio x 3 +x 4 = usig Newto s method with iitial approximatio x 1 = 1, what is x? Solutio. Recall that x +1 = x f(x ) f (x ). Hece,
Let us give one more example of MLE. Example 3. The uniform distribution U[0, θ] on the interval [0, θ] has p.d.f.
![Let us give one more example of MLE. Example 3. The uniform distribution U[0, θ] on the interval [0, θ] has p.d.f. Let us give one more example of MLE. Example 3. The uniform distribution U[0, θ] on the interval [0, θ] has p.d.f.](/thumbs/91/105380228.jpg) Lecture 5 Let us give oe more example of MLE. Example 3. The uiform distributio U[0, ] o the iterval [0, ] has p.d.f. { 1 f(x =, 0 x, 0, otherwise The likelihood fuctio ϕ( = f(x i = 1 I(X 1,..., X [0,
Lecture 5 Let us give oe more example of MLE. Example 3. The uiform distributio U[0, ] o the iterval [0, ] has p.d.f. { 1 f(x =, 0 x, 0, otherwise The likelihood fuctio ϕ( = f(x i = 1 I(X 1,..., X [0,
The picture in figure 1.1 helps us to see that the area represents the distance traveled. Figure 1: Area represents distance travelled
 1 Lecture : Area Area ad distace traveled Approximatig area by rectagles Summatio The area uder a parabola 1.1 Area ad distace Suppose we have the followig iformatio about the velocity of a particle, how
1 Lecture : Area Area ad distace traveled Approximatig area by rectagles Summatio The area uder a parabola 1.1 Area ad distace Suppose we have the followig iformatio about the velocity of a particle, how
Areas and Distances. We can easily find areas of certain geometric figures using well-known formulas:
 Areas ad Distaces We ca easily fid areas of certai geometric figures usig well-kow formulas: However, it is t easy to fid the area of a regio with curved sides: METHOD: To evaluate the area of the regio
Areas ad Distaces We ca easily fid areas of certai geometric figures usig well-kow formulas: However, it is t easy to fid the area of a regio with curved sides: METHOD: To evaluate the area of the regio
(4 pts.) (4 pts.) (4 pts.) b) y(x,t) = 1/(ax 2 +b) This function has no time dependence, so cannot be a wave.
 12. For each of the possible wave forms below, idicate which satisf the wave equatio, ad which represet reasoable waveforms for actual waves o a strig. For those which do represet waves, fid the speed
12. For each of the possible wave forms below, idicate which satisf the wave equatio, ad which represet reasoable waveforms for actual waves o a strig. For those which do represet waves, fid the speed
Math 257: Finite difference methods
 Math 257: Fiite differece methods 1 Fiite Differeces Remember the defiitio of a derivative f f(x + ) f(x) (x) = lim 0 Also recall Taylor s formula: (1) f(x + ) = f(x) + f (x) + 2 f (x) + 3 f (3) (x) +...
Math 257: Fiite differece methods 1 Fiite Differeces Remember the defiitio of a derivative f f(x + ) f(x) (x) = lim 0 Also recall Taylor s formula: (1) f(x + ) = f(x) + f (x) + 2 f (x) + 3 f (3) (x) +...
Phys 6303 Final Exam Solutions December 19, 2012
 Phys 633 Fial Exam s December 19, 212 You may NOT use ay book or otes other tha supplied with this test. You will have 3 hours to fiish. DO YOUR OWN WORK. Express your aswers clearly ad cocisely so that
Phys 633 Fial Exam s December 19, 212 You may NOT use ay book or otes other tha supplied with this test. You will have 3 hours to fiish. DO YOUR OWN WORK. Express your aswers clearly ad cocisely so that
Seunghee Ye Ma 8: Week 5 Oct 28
 Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Question 1: The magnetic case
 September 6, 018 Corell Uiversity, Departmet of Physics PHYS 337, Advace E&M, HW # 4, due: 9/19/018, 11:15 AM Questio 1: The magetic case I class, we skipped over some details, so here you are asked to
September 6, 018 Corell Uiversity, Departmet of Physics PHYS 337, Advace E&M, HW # 4, due: 9/19/018, 11:15 AM Questio 1: The magetic case I class, we skipped over some details, so here you are asked to
Lecture 19: Convergence
 Lecture 19: Covergece Asymptotic approach I statistical aalysis or iferece, a key to the success of fidig a good procedure is beig able to fid some momets ad/or distributios of various statistics. I may
Lecture 19: Covergece Asymptotic approach I statistical aalysis or iferece, a key to the success of fidig a good procedure is beig able to fid some momets ad/or distributios of various statistics. I may
Løsningsførslag i 4M
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side 1 av 6 Løsigsførslag i 4M Oppgave 1 a) A sketch of the graph of the give f o the iterval [ 3, 3) is as follows: The Fourier
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side 1 av 6 Løsigsførslag i 4M Oppgave 1 a) A sketch of the graph of the give f o the iterval [ 3, 3) is as follows: The Fourier
Chem 442 Review for Exam 1. Hamiltonian operator in 1 dimension: ˆ d first term is kinetic energy, second term is potential energy
 Chem 44 Review for Eam 1 Eergies are quatized Wave/partice duaity de Brogie waveegth: h p Eergy: E h mometum operator: pˆ positio operator: ˆ d i d potetia eergy operator: V ˆ( ) pˆ d kietic eergy operator
Chem 44 Review for Eam 1 Eergies are quatized Wave/partice duaity de Brogie waveegth: h p Eergy: E h mometum operator: pˆ positio operator: ˆ d i d potetia eergy operator: V ˆ( ) pˆ d kietic eergy operator
3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,
![3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense, 3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,](/thumbs/82/85448051.jpg) 3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
Appendix: The Laplace Transform
 Appedix: The Laplace Trasform The Laplace trasform is a powerful method that ca be used to solve differetial equatio, ad other mathematical problems. Its stregth lies i the fact that it allows the trasformatio
Appedix: The Laplace Trasform The Laplace trasform is a powerful method that ca be used to solve differetial equatio, ad other mathematical problems. Its stregth lies i the fact that it allows the trasformatio
CHAPTER 4 FOURIER SERIES
 CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
ECE507 - Plasma Physics and Applications
 ECE57 - Pasma Physics ad Appicatios Lecture 9 Prof. Jorge Rocca ad r. Ferado Tomase epartmet of Eectrica ad Computer Egieerig Low temperature pasmas Low temperature pasmas are a very iterestig subject
ECE57 - Pasma Physics ad Appicatios Lecture 9 Prof. Jorge Rocca ad r. Ferado Tomase epartmet of Eectrica ad Computer Egieerig Low temperature pasmas Low temperature pasmas are a very iterestig subject
Notes The Incremental Motion Model:
 The Icremetal Motio Model: The Jacobia Matrix I the forward kiematics model, we saw that it was possible to relate joit agles θ, to the cofiguratio of the robot ed effector T I this sectio, we will see
The Icremetal Motio Model: The Jacobia Matrix I the forward kiematics model, we saw that it was possible to relate joit agles θ, to the cofiguratio of the robot ed effector T I this sectio, we will see
Fluid Physics 8.292J/12.330J % (1)
 Fluid Physics 89J/133J Problem Set 5 Solutios 1 Cosider the flow of a Euler fluid i the x directio give by for y > d U = U y 1 d for y d U + y 1 d for y < This flow does ot vary i x or i z Determie the
Fluid Physics 89J/133J Problem Set 5 Solutios 1 Cosider the flow of a Euler fluid i the x directio give by for y > d U = U y 1 d for y d U + y 1 d for y < This flow does ot vary i x or i z Determie the
Numerical Methods for Ordinary Differential Equations
 Numerical Methods for Ordiary Differetial Equatios Braislav K. Nikolić Departmet of Physics ad Astroomy, Uiversity of Delaware, U.S.A. PHYS 460/660: Computatioal Methods of Physics http://www.physics.udel.edu/~bikolic/teachig/phys660/phys660.html
Numerical Methods for Ordiary Differetial Equatios Braislav K. Nikolić Departmet of Physics ad Astroomy, Uiversity of Delaware, U.S.A. PHYS 460/660: Computatioal Methods of Physics http://www.physics.udel.edu/~bikolic/teachig/phys660/phys660.html
Differentiation Techniques 1: Power, Constant Multiple, Sum and Difference Rules
 Differetiatio Teciques : Power, Costat Multiple, Sum ad Differece Rules 97 Differetiatio Teciques : Power, Costat Multiple, Sum ad Differece Rules Model : Fidig te Equatio of f '() from a Grap of f ()
Differetiatio Teciques : Power, Costat Multiple, Sum ad Differece Rules 97 Differetiatio Teciques : Power, Costat Multiple, Sum ad Differece Rules Model : Fidig te Equatio of f '() from a Grap of f ()
January 25, 2017 INTRODUCTION TO MATHEMATICAL STATISTICS
 Jauary 25, 207 INTRODUCTION TO MATHEMATICAL STATISTICS Abstract. A basic itroductio to statistics assumig kowledge of probability theory.. Probability I a typical udergraduate problem i probability, we
Jauary 25, 207 INTRODUCTION TO MATHEMATICAL STATISTICS Abstract. A basic itroductio to statistics assumig kowledge of probability theory.. Probability I a typical udergraduate problem i probability, we
Math 105: Review for Final Exam, Part II - SOLUTIONS
 Math 5: Review for Fial Exam, Part II - SOLUTIONS. Cosider the fuctio f(x) = x 3 lx o the iterval [/e, e ]. (a) Fid the x- ad y-coordiates of ay ad all local extrema ad classify each as a local maximum
Math 5: Review for Fial Exam, Part II - SOLUTIONS. Cosider the fuctio f(x) = x 3 lx o the iterval [/e, e ]. (a) Fid the x- ad y-coordiates of ay ad all local extrema ad classify each as a local maximum
19 Fourier Series and Practical Harmonic Analysis
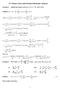 9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y
![1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y 1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y](/thumbs/95/125864248.jpg) Questio (a) A square matrix A= A is called positive defiite if the quadratic form waw > 0 for every o-zero vector w [Note: Here (.) deotes the traspose of a matrix or a vector]. Let 0 A = 0 = show that:
Questio (a) A square matrix A= A is called positive defiite if the quadratic form waw > 0 for every o-zero vector w [Note: Here (.) deotes the traspose of a matrix or a vector]. Let 0 A = 0 = show that:
Lecture 6: Integration and the Mean Value Theorem. slope =
 Math 8 Istructor: Padraic Bartlett Lecture 6: Itegratio ad the Mea Value Theorem Week 6 Caltech 202 The Mea Value Theorem The Mea Value Theorem abbreviated MVT is the followig result: Theorem. Suppose
Math 8 Istructor: Padraic Bartlett Lecture 6: Itegratio ad the Mea Value Theorem Week 6 Caltech 202 The Mea Value Theorem The Mea Value Theorem abbreviated MVT is the followig result: Theorem. Suppose
SOLUTIONS TO EXAM 3. Solution: Note that this defines two convergent geometric series with respective radii r 1 = 2/5 < 1 and r 2 = 1/5 < 1.
 SOLUTIONS TO EXAM 3 Problem Fid the sum of the followig series 2 + ( ) 5 5 2 5 3 25 2 2 This series diverges Solutio: Note that this defies two coverget geometric series with respective radii r 2/5 < ad
SOLUTIONS TO EXAM 3 Problem Fid the sum of the followig series 2 + ( ) 5 5 2 5 3 25 2 2 This series diverges Solutio: Note that this defies two coverget geometric series with respective radii r 2/5 < ad
Bayesian Methods: Introduction to Multi-parameter Models
 Bayesia Methods: Itroductio to Multi-parameter Models Parameter: θ = ( θ, θ) Give Likelihood p(y θ) ad prior p(θ ), the posterior p proportioal to p(y θ) x p(θ ) Margial posterior ( θ, θ y) is Iterested
Bayesia Methods: Itroductio to Multi-parameter Models Parameter: θ = ( θ, θ) Give Likelihood p(y θ) ad prior p(θ ), the posterior p proportioal to p(y θ) x p(θ ) Margial posterior ( θ, θ y) is Iterested
Math 113, Calculus II Winter 2007 Final Exam Solutions
 Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
18.01 Calculus Jason Starr Fall 2005
 Lecture 18. October 5, 005 Homework. Problem Set 5 Part I: (c). Practice Problems. Course Reader: 3G 1, 3G, 3G 4, 3G 5. 1. Approximatig Riema itegrals. Ofte, there is o simpler expressio for the atiderivative
Lecture 18. October 5, 005 Homework. Problem Set 5 Part I: (c). Practice Problems. Course Reader: 3G 1, 3G, 3G 4, 3G 5. 1. Approximatig Riema itegrals. Ofte, there is o simpler expressio for the atiderivative
CALCULUS AB SECTION I, Part A Time 60 minutes Number of questions 30 A CALCULATOR MAY NOT BE USED ON THIS PART OF THE EXAM.
 AP Calculus AB Portfolio Project Multiple Choice Practice Name: CALCULUS AB SECTION I, Part A Time 60 miutes Number of questios 30 A CALCULATOR MAY NOT BE USED ON THIS PART OF THE EXAM. Directios: Solve
AP Calculus AB Portfolio Project Multiple Choice Practice Name: CALCULUS AB SECTION I, Part A Time 60 miutes Number of questios 30 A CALCULATOR MAY NOT BE USED ON THIS PART OF THE EXAM. Directios: Solve
COMPUTING SUMS AND THE AVERAGE VALUE OF THE DIVISOR FUNCTION (x 1) + x = n = n.
 COMPUTING SUMS AND THE AVERAGE VALUE OF THE DIVISOR FUNCTION Abstract. We itroduce a method for computig sums of the form f( where f( is ice. We apply this method to study the average value of d(, where
COMPUTING SUMS AND THE AVERAGE VALUE OF THE DIVISOR FUNCTION Abstract. We itroduce a method for computig sums of the form f( where f( is ice. We apply this method to study the average value of d(, where
Most text will write ordinary derivatives using either Leibniz notation 2 3. y + 5y= e and y y. xx tt t
 Itroductio to Differetial Equatios Defiitios ad Termiolog Differetial Equatio: A equatio cotaiig the derivatives of oe or more depedet variables, with respect to oe or more idepedet variables, is said
Itroductio to Differetial Equatios Defiitios ad Termiolog Differetial Equatio: A equatio cotaiig the derivatives of oe or more depedet variables, with respect to oe or more idepedet variables, is said
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
Quantum Theory Assignment 3
 Quatum Theory Assigmet 3 Assigmet 3.1 1. Cosider a spi-1/ system i a magetic field i the z-directio. The Hamiltoia is give by: ) eb H = S z = ωs z. mc a) Fid the Heiseberg operators S x t), S y t), ad
Quatum Theory Assigmet 3 Assigmet 3.1 1. Cosider a spi-1/ system i a magetic field i the z-directio. The Hamiltoia is give by: ) eb H = S z = ωs z. mc a) Fid the Heiseberg operators S x t), S y t), ad
Simulation of Beam and Plasma Systems Homework 6
 Simulation of Beam and Plasma Systems Homework 6 D. Bruhwiler, S. M. Lund, J.-L. Vay, R. Lehe, and D. Winklehner Monday, Jan 22 nd, 2018 Problem 1 - Warp: parallel plates and Child-Langmuir law Let us
Simulation of Beam and Plasma Systems Homework 6 D. Bruhwiler, S. M. Lund, J.-L. Vay, R. Lehe, and D. Winklehner Monday, Jan 22 nd, 2018 Problem 1 - Warp: parallel plates and Child-Langmuir law Let us
4.3 Growth Rates of Solutions to Recurrences
 4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
Fourier Series and their Applications
 Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
Chapter 9 - CD companion 1. A Generic Implementation; The Common-Merge Amplifier. 1 τ is. ω ch. τ io
 Chapter 9 - CD compaio CHAPTER NINE CD-9.2 CD-9.2. Stages With Voltage ad Curret Gai A Geeric Implemetatio; The Commo-Merge Amplifier The advaced method preseted i the text for approximatig cutoff frequecies
Chapter 9 - CD compaio CHAPTER NINE CD-9.2 CD-9.2. Stages With Voltage ad Curret Gai A Geeric Implemetatio; The Commo-Merge Amplifier The advaced method preseted i the text for approximatig cutoff frequecies
mx bx kx F t. dt IR I LI V t, Q LQ RQ V t,
 Lecture 5 omplex Variables II (Applicatios i Physics) (See hapter i Boas) To see why complex variables are so useful cosider first the (liear) mechaics of a sigle particle described by Newto s equatio
Lecture 5 omplex Variables II (Applicatios i Physics) (See hapter i Boas) To see why complex variables are so useful cosider first the (liear) mechaics of a sigle particle described by Newto s equatio
1 Generating functions for balls in boxes
 Math 566 Fall 05 Some otes o geeratig fuctios Give a sequece a 0, a, a,..., a,..., a geeratig fuctio some way of represetig the sequece as a fuctio. There are may ways to do this, with the most commo ways
Math 566 Fall 05 Some otes o geeratig fuctios Give a sequece a 0, a, a,..., a,..., a geeratig fuctio some way of represetig the sequece as a fuctio. There are may ways to do this, with the most commo ways
Lecture 6 Chi Square Distribution (χ 2 ) and Least Squares Fitting
 Lecture 6 Chi Square Distributio (χ ) ad Least Squares Fittig Chi Square Distributio (χ ) Suppose: We have a set of measuremets {x 1, x, x }. We kow the true value of each x i (x t1, x t, x t ). We would
Lecture 6 Chi Square Distributio (χ ) ad Least Squares Fittig Chi Square Distributio (χ ) Suppose: We have a set of measuremets {x 1, x, x }. We kow the true value of each x i (x t1, x t, x t ). We would
Name: Math 10550, Final Exam: December 15, 2007
 Math 55, Fial Exam: December 5, 7 Name: Be sure that you have all pages of the test. No calculators are to be used. The exam lasts for two hours. Whe told to begi, remove this aswer sheet ad keep it uder
Math 55, Fial Exam: December 5, 7 Name: Be sure that you have all pages of the test. No calculators are to be used. The exam lasts for two hours. Whe told to begi, remove this aswer sheet ad keep it uder
MIDTERM 3 CALCULUS 2. Monday, December 3, :15 PM to 6:45 PM. Name PRACTICE EXAM SOLUTIONS
 MIDTERM 3 CALCULUS MATH 300 FALL 08 Moday, December 3, 08 5:5 PM to 6:45 PM Name PRACTICE EXAM S Please aswer all of the questios, ad show your work. You must explai your aswers to get credit. You will
MIDTERM 3 CALCULUS MATH 300 FALL 08 Moday, December 3, 08 5:5 PM to 6:45 PM Name PRACTICE EXAM S Please aswer all of the questios, ad show your work. You must explai your aswers to get credit. You will
Generalized Semi- Markov Processes (GSMP)
 Geeralized Semi- Markov Processes (GSMP) Summary Some Defiitios Markov ad Semi-Markov Processes The Poisso Process Properties of the Poisso Process Iterarrival times Memoryless property ad the residual
Geeralized Semi- Markov Processes (GSMP) Summary Some Defiitios Markov ad Semi-Markov Processes The Poisso Process Properties of the Poisso Process Iterarrival times Memoryless property ad the residual
Problem Cosider the curve give parametrically as x = si t ad y = + cos t for» t» ß: (a) Describe the path this traverses: Where does it start (whe t =
 Mathematics Summer Wilso Fial Exam August 8, ANSWERS Problem 1 (a) Fid the solutio to y +x y = e x x that satisfies y() = 5 : This is already i the form we used for a first order liear differetial equatio,
Mathematics Summer Wilso Fial Exam August 8, ANSWERS Problem 1 (a) Fid the solutio to y +x y = e x x that satisfies y() = 5 : This is already i the form we used for a first order liear differetial equatio,
Topic 9: Sampling Distributions of Estimators
 Topic 9: Samplig Distributios of Estimators Course 003, 2016 Page 0 Samplig distributios of estimators Sice our estimators are statistics (particular fuctios of radom variables), their distributio ca be
Topic 9: Samplig Distributios of Estimators Course 003, 2016 Page 0 Samplig distributios of estimators Sice our estimators are statistics (particular fuctios of radom variables), their distributio ca be
Stat 543 Exam 3 Spring 2016
 Stat 543 Exam 3 Sprig 06 I have either give or received uauthorized assistace o this exam. Name Siged Date Name Prited This exam cosists of parts. Do at east 8 of them. I wi score aswers at 0 poits apiece
Stat 543 Exam 3 Sprig 06 I have either give or received uauthorized assistace o this exam. Name Siged Date Name Prited This exam cosists of parts. Do at east 8 of them. I wi score aswers at 0 poits apiece
Chapter 8. Euler s Gamma function
 Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
10-701/ Machine Learning Mid-term Exam Solution
 0-70/5-78 Machie Learig Mid-term Exam Solutio Your Name: Your Adrew ID: True or False (Give oe setece explaatio) (20%). (F) For a cotiuous radom variable x ad its probability distributio fuctio p(x), it
0-70/5-78 Machie Learig Mid-term Exam Solutio Your Name: Your Adrew ID: True or False (Give oe setece explaatio) (20%). (F) For a cotiuous radom variable x ad its probability distributio fuctio p(x), it
CHAPTER 5. Theory and Solution Using Matrix Techniques
 A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
Chapter 8. Euler s Gamma function
 Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s) that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s) that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Lecture 6 Chi Square Distribution (χ 2 ) and Least Squares Fitting
 Lecture 6 Chi Square Distributio (χ ) ad Least Squares Fittig Chi Square Distributio (χ ) Suppose: We have a set of measuremets {x 1, x, x }. We kow the true value of each x i (x t1, x t, x t ). We would
Lecture 6 Chi Square Distributio (χ ) ad Least Squares Fittig Chi Square Distributio (χ ) Suppose: We have a set of measuremets {x 1, x, x }. We kow the true value of each x i (x t1, x t, x t ). We would
Time-Domain Representations of LTI Systems
 2.1 Itroductio Objectives: 1. Impulse resposes of LTI systems 2. Liear costat-coefficiets differetial or differece equatios of LTI systems 3. Bloc diagram represetatios of LTI systems 4. State-variable
2.1 Itroductio Objectives: 1. Impulse resposes of LTI systems 2. Liear costat-coefficiets differetial or differece equatios of LTI systems 3. Bloc diagram represetatios of LTI systems 4. State-variable
Discrete Mathematics for CS Spring 2007 Luca Trevisan Lecture 22
 CS 70 Discrete Mathematics for CS Sprig 2007 Luca Trevisa Lecture 22 Aother Importat Distributio The Geometric Distributio Questio: A biased coi with Heads probability p is tossed repeatedly util the first
CS 70 Discrete Mathematics for CS Sprig 2007 Luca Trevisa Lecture 22 Aother Importat Distributio The Geometric Distributio Questio: A biased coi with Heads probability p is tossed repeatedly util the first
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
April 1980 TR/96. Extrapolation techniques for first order hyperbolic partial differential equations. E.H. Twizell
 TR/96 Apri 980 Extrapoatio techiques for first order hyperboic partia differetia equatios. E.H. Twize W96086 (0) 0. Abstract A uifor grid of step size h is superiposed o the space variabe x i the first
TR/96 Apri 980 Extrapoatio techiques for first order hyperboic partia differetia equatios. E.H. Twize W96086 (0) 0. Abstract A uifor grid of step size h is superiposed o the space variabe x i the first
TMA4205 Numerical Linear Algebra. The Poisson problem in R 2 : diagonalization methods
 TMA4205 Numerical Liear Algebra The Poisso problem i R 2 : diagoalizatio methods September 3, 2007 c Eiar M Røquist Departmet of Mathematical Scieces NTNU, N-749 Trodheim, Norway All rights reserved A
TMA4205 Numerical Liear Algebra The Poisso problem i R 2 : diagoalizatio methods September 3, 2007 c Eiar M Røquist Departmet of Mathematical Scieces NTNU, N-749 Trodheim, Norway All rights reserved A
Exercise 4.3 Use the Continuity Theorem to prove the Cramér-Wold Theorem, Theorem. (1) φ a X(1).
 Assigmet 7 Exercise 4.3 Use the Cotiuity Theorem to prove the Cramér-Wold Theorem, Theorem 4.12. Hit: a X d a X implies that φ a X (1) φ a X(1). Sketch of solutio: As we poited out i class, the oly tricky
Assigmet 7 Exercise 4.3 Use the Cotiuity Theorem to prove the Cramér-Wold Theorem, Theorem 4.12. Hit: a X d a X implies that φ a X (1) φ a X(1). Sketch of solutio: As we poited out i class, the oly tricky
PROBLEMS AND SOLUTIONS 2
 PROBEMS AND SOUTIONS Problem 5.:1 Statemet. Fid the solutio of { u tt = a u xx, x, t R, u(x, ) = f(x), u t (x, ) = g(x), i the followig cases: (b) f(x) = e x, g(x) = axe x, (d) f(x) = 1, g(x) =, (f) f(x)
PROBEMS AND SOUTIONS Problem 5.:1 Statemet. Fid the solutio of { u tt = a u xx, x, t R, u(x, ) = f(x), u t (x, ) = g(x), i the followig cases: (b) f(x) = e x, g(x) = axe x, (d) f(x) = 1, g(x) =, (f) f(x)
Chapter 10: Power Series
 Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
We are mainly going to be concerned with power series in x, such as. (x)} converges - that is, lims N n
 Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Solutions to Final Exam Review Problems
 . Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
. Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
Assignment 2 Solutions SOLUTION. ϕ 1 Â = 3 ϕ 1 4i ϕ 2. The other case can be dealt with in a similar way. { ϕ 2 Â} χ = { 4i ϕ 1 3 ϕ 2 } χ.
 PHYSICS 34 QUANTUM PHYSICS II (25) Assigmet 2 Solutios 1. With respect to a pair of orthoormal vectors ϕ 1 ad ϕ 2 that spa the Hilbert space H of a certai system, the operator  is defied by its actio
PHYSICS 34 QUANTUM PHYSICS II (25) Assigmet 2 Solutios 1. With respect to a pair of orthoormal vectors ϕ 1 ad ϕ 2 that spa the Hilbert space H of a certai system, the operator  is defied by its actio
Ma 4121: Introduction to Lebesgue Integration Solutions to Homework Assignment 5
 Ma 42: Itroductio to Lebesgue Itegratio Solutios to Homework Assigmet 5 Prof. Wickerhauser Due Thursday, April th, 23 Please retur your solutios to the istructor by the ed of class o the due date. You
Ma 42: Itroductio to Lebesgue Itegratio Solutios to Homework Assigmet 5 Prof. Wickerhauser Due Thursday, April th, 23 Please retur your solutios to the istructor by the ed of class o the due date. You
Guiding-center transformation 1. δf = q ( c v f 0, (1) mc (v B 0) v f 0. (3)
 Guidig-ceter trasformatio 1 This is my otes whe readig Liu Che s book[1]. 1 Vlasov equatio The liearized Vlasov equatio is [ t + v x + q m E + v B c ] δf = q v m δe + v δb c v f, 1 where f ad δf are the
Guidig-ceter trasformatio 1 This is my otes whe readig Liu Che s book[1]. 1 Vlasov equatio The liearized Vlasov equatio is [ t + v x + q m E + v B c ] δf = q v m δe + v δb c v f, 1 where f ad δf are the
Numerical Methods in Fourier Series Applications
 Numerical Methods i Fourier Series Applicatios Recall that the basic relatios i usig the Trigoometric Fourier Series represetatio were give by f ( x) a o ( a x cos b x si ) () where the Fourier coefficiets
Numerical Methods i Fourier Series Applicatios Recall that the basic relatios i usig the Trigoometric Fourier Series represetatio were give by f ( x) a o ( a x cos b x si ) () where the Fourier coefficiets
Taylor expansion: Show that the TE of f(x)= sin(x) around. sin(x) = x - + 3! 5! L 7 & 8: MHD/ZAH
 Taylor epasio: Let ƒ() be a ifiitely differetiable real fuctio. A ay poit i the eighbourhood of 0, the fuctio ƒ() ca be represeted by a power series of the followig form: X 0 f(a) f() f() ( ) f( ) ( )
Taylor epasio: Let ƒ() be a ifiitely differetiable real fuctio. A ay poit i the eighbourhood of 0, the fuctio ƒ() ca be represeted by a power series of the followig form: X 0 f(a) f() f() ( ) f( ) ( )
Lecture III-2: Light propagation in nonmagnetic
 A. La Rosa Lecture Notes ALIED OTIC Lecture III2: Light propagatio i omagetic materials 2.1 urface ( ), volume ( ), ad curret ( j ) desities produced by arizatio charges The objective i this sectio is
A. La Rosa Lecture Notes ALIED OTIC Lecture III2: Light propagatio i omagetic materials 2.1 urface ( ), volume ( ), ad curret ( j ) desities produced by arizatio charges The objective i this sectio is
Lecture 7: Properties of Random Samples
 Lecture 7: Properties of Radom Samples 1 Cotiued From Last Class Theorem 1.1. Let X 1, X,...X be a radom sample from a populatio with mea µ ad variace σ
Lecture 7: Properties of Radom Samples 1 Cotiued From Last Class Theorem 1.1. Let X 1, X,...X be a radom sample from a populatio with mea µ ad variace σ
Math 132, Fall 2009 Exam 2: Solutions
 Math 3, Fall 009 Exam : Solutios () a) ( poits) Determie for which positive real umbers p, is the followig improper itegral coverget, ad for which it is diverget. Evaluate the itegral for each value of
Math 3, Fall 009 Exam : Solutios () a) ( poits) Determie for which positive real umbers p, is the followig improper itegral coverget, ad for which it is diverget. Evaluate the itegral for each value of
Properties and Hypothesis Testing
 Chapter 3 Properties ad Hypothesis Testig 3.1 Types of data The regressio techiques developed i previous chapters ca be applied to three differet kids of data. 1. Cross-sectioal data. 2. Time series data.
Chapter 3 Properties ad Hypothesis Testig 3.1 Types of data The regressio techiques developed i previous chapters ca be applied to three differet kids of data. 1. Cross-sectioal data. 2. Time series data.
x x x Using a second Taylor polynomial with remainder, find the best constant C so that for x 0,
 Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
Math 5C Discussion Problems 2 Selected Solutions
 Math 5 iscussio Problems 2 elected olutios Path Idepedece. Let be the striaght-lie path i 2 from the origi to (3, ). efie f(x, y) = xye xy. (a) Evaluate f dr. olutio. (b) Evaluate olutio. (c) Evaluate
Math 5 iscussio Problems 2 elected olutios Path Idepedece. Let be the striaght-lie path i 2 from the origi to (3, ). efie f(x, y) = xye xy. (a) Evaluate f dr. olutio. (b) Evaluate olutio. (c) Evaluate
Linear Regression Demystified
 Liear Regressio Demystified Liear regressio is a importat subject i statistics. I elemetary statistics courses, formulae related to liear regressio are ofte stated without derivatio. This ote iteds to
Liear Regressio Demystified Liear regressio is a importat subject i statistics. I elemetary statistics courses, formulae related to liear regressio are ofte stated without derivatio. This ote iteds to
First Year Quantitative Comp Exam Spring, Part I - 203A. f X (x) = 0 otherwise
 First Year Quatitative Comp Exam Sprig, 2012 Istructio: There are three parts. Aswer every questio i every part. Questio I-1 Part I - 203A A radom variable X is distributed with the margial desity: >
First Year Quatitative Comp Exam Sprig, 2012 Istructio: There are three parts. Aswer every questio i every part. Questio I-1 Part I - 203A A radom variable X is distributed with the margial desity: >
U8L1: Sec Equations of Lines in R 2
 MCVU U8L: Sec. 8.9. Equatios of Lies i R Review of Equatios of a Straight Lie (-D) Cosider the lie passig through A (-,) with slope, as show i the diagram below. I poit slope form, the equatio of the lie
MCVU U8L: Sec. 8.9. Equatios of Lies i R Review of Equatios of a Straight Lie (-D) Cosider the lie passig through A (-,) with slope, as show i the diagram below. I poit slope form, the equatio of the lie
Department of Mathematics
 Departmet of Mathematics Ma 3/103 KC Border Itroductio to Probability ad Statistics Witer 2017 Lecture 19: Estimatio II Relevat textbook passages: Larse Marx [1]: Sectios 5.2 5.7 19.1 The method of momets
Departmet of Mathematics Ma 3/103 KC Border Itroductio to Probability ad Statistics Witer 2017 Lecture 19: Estimatio II Relevat textbook passages: Larse Marx [1]: Sectios 5.2 5.7 19.1 The method of momets
Discrete Fourier Transform
 Discrete Fourier Trasform 3) Compex Case et s distiguish the three cases + J + > + J + + J + < (35) Ad et s begi treatig the isodetermied case + J +, addig at first the hypothesis that J,. I this case
Discrete Fourier Trasform 3) Compex Case et s distiguish the three cases + J + > + J + + J + < (35) Ad et s begi treatig the isodetermied case + J +, addig at first the hypothesis that J,. I this case
Chapter 2 The Monte Carlo Method
 Chapter 2 The Mote Carlo Method The Mote Carlo Method stads for a broad class of computatioal algorithms that rely o radom sampligs. It is ofte used i physical ad mathematical problems ad is most useful
Chapter 2 The Mote Carlo Method The Mote Carlo Method stads for a broad class of computatioal algorithms that rely o radom sampligs. It is ofte used i physical ad mathematical problems ad is most useful
EECS564 Estimation, Filtering, and Detection Hwk 2 Solns. Winter p θ (z) = (2θz + 1 θ), 0 z 1
 EECS564 Estimatio, Filterig, ad Detectio Hwk 2 Sols. Witer 25 4. Let Z be a sigle observatio havig desity fuctio where. p (z) = (2z + ), z (a) Assumig that is a oradom parameter, fid ad plot the maximum
EECS564 Estimatio, Filterig, ad Detectio Hwk 2 Sols. Witer 25 4. Let Z be a sigle observatio havig desity fuctio where. p (z) = (2z + ), z (a) Assumig that is a oradom parameter, fid ad plot the maximum
PLEASE MARK YOUR ANSWERS WITH AN X, not a circle! 1. (a) (b) (c) (d) (e) 3. (a) (b) (c) (d) (e) 5. (a) (b) (c) (d) (e) 7. (a) (b) (c) (d) (e)
 Math 0560, Exam 3 November 6, 07 The Hoor Code is i effect for this examiatio. All work is to be your ow. No calculators. The exam lasts for hour ad 5 mi. Be sure that your ame is o every page i case pages
Math 0560, Exam 3 November 6, 07 The Hoor Code is i effect for this examiatio. All work is to be your ow. No calculators. The exam lasts for hour ad 5 mi. Be sure that your ame is o every page i case pages
Electromagnetic wave propagation in Particle-In-Cell codes
 Electromagetic wave propagatio i Particle-I-Cell codes Remi Lehe Lawrece Berkeley Natioal Laboratory (LBNL) US Particle Accelerator School (USPAS) Summer Sessio Self-Cosistet Simulatios of Beam ad Plasma
Electromagetic wave propagatio i Particle-I-Cell codes Remi Lehe Lawrece Berkeley Natioal Laboratory (LBNL) US Particle Accelerator School (USPAS) Summer Sessio Self-Cosistet Simulatios of Beam ad Plasma
CEE 522 Autumn Uncertainty Concepts for Geotechnical Engineering
 CEE 5 Autum 005 Ucertaity Cocepts for Geotechical Egieerig Basic Termiology Set A set is a collectio of (mutually exclusive) objects or evets. The sample space is the (collectively exhaustive) collectio
CEE 5 Autum 005 Ucertaity Cocepts for Geotechical Egieerig Basic Termiology Set A set is a collectio of (mutually exclusive) objects or evets. The sample space is the (collectively exhaustive) collectio
Part I: Covers Sequence through Series Comparison Tests
 Part I: Covers Sequece through Series Compariso Tests. Give a example of each of the followig: (a) A geometric sequece: (b) A alteratig sequece: (c) A sequece that is bouded, but ot coverget: (d) A sequece
Part I: Covers Sequece through Series Compariso Tests. Give a example of each of the followig: (a) A geometric sequece: (b) A alteratig sequece: (c) A sequece that is bouded, but ot coverget: (d) A sequece
Symbolic computation 2: Linear recurrences
 Bachelor of Ecole Polytechique Computatioal Mathematics, year 2, semester Lecturer: Lucas Geri (sed mail) (mailto:lucas.geri@polytechique.edu) Symbolic computatio 2: Liear recurreces Table of cotets Warm-up
Bachelor of Ecole Polytechique Computatioal Mathematics, year 2, semester Lecturer: Lucas Geri (sed mail) (mailto:lucas.geri@polytechique.edu) Symbolic computatio 2: Liear recurreces Table of cotets Warm-up
INFINITE SEQUENCES AND SERIES
 11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES 11.4 The Compariso Tests I this sectio, we will lear: How to fid the value of a series by comparig it with a kow series. COMPARISON TESTS
11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES 11.4 The Compariso Tests I this sectio, we will lear: How to fid the value of a series by comparig it with a kow series. COMPARISON TESTS
Math 113 Exam 3 Practice
 Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
Worksheet on Generating Functions
 Worksheet o Geeratig Fuctios October 26, 205 This worksheet is adapted from otes/exercises by Nat Thiem. Derivatives of Geeratig Fuctios. If the sequece a 0, a, a 2,... has ordiary geeratig fuctio A(x,
Worksheet o Geeratig Fuctios October 26, 205 This worksheet is adapted from otes/exercises by Nat Thiem. Derivatives of Geeratig Fuctios. If the sequece a 0, a, a 2,... has ordiary geeratig fuctio A(x,
DEPARTMENT OF ACTUARIAL STUDIES RESEARCH PAPER SERIES
 DEPARTMENT OF ACTUARIAL STUDIES RESEARCH PAPER SERIES Icreasig ad Decreasig Auities ad Time Reversal by Jim Farmer Jim.Farmer@mq.edu.au Research Paper No. 2000/02 November 2000 Divisio of Ecoomic ad Fiacial
DEPARTMENT OF ACTUARIAL STUDIES RESEARCH PAPER SERIES Icreasig ad Decreasig Auities ad Time Reversal by Jim Farmer Jim.Farmer@mq.edu.au Research Paper No. 2000/02 November 2000 Divisio of Ecoomic ad Fiacial
f(x) dx as we do. 2x dx x also diverges. Solution: We compute 2x dx lim
 Math 3, Sectio 2. (25 poits) Why we defie f(x) dx as we do. (a) Show that the improper itegral diverges. Hece the improper itegral x 2 + x 2 + b also diverges. Solutio: We compute x 2 + = lim b x 2 + =
Math 3, Sectio 2. (25 poits) Why we defie f(x) dx as we do. (a) Show that the improper itegral diverges. Hece the improper itegral x 2 + x 2 + b also diverges. Solutio: We compute x 2 + = lim b x 2 + =
Existence of Nonoscillatory Solution of High Order Linear Neutral Delay Difference Equation
 oder Appied Sciece ovember, 008 Existece of oosciatory Soutio of High Order Liear eutra Deay Differece Equatio Shasha Zhag, Xiaozhu Zhog, Pig Yu, Wexia Zhag & ig Li Departmet of athematics Yasha Uiversity
oder Appied Sciece ovember, 008 Existece of oosciatory Soutio of High Order Liear eutra Deay Differece Equatio Shasha Zhag, Xiaozhu Zhog, Pig Yu, Wexia Zhag & ig Li Departmet of athematics Yasha Uiversity
L 5 & 6: RelHydro/Basel. f(x)= ( ) f( ) ( ) ( ) ( ) n! 1! 2! 3! If the TE of f(x)= sin(x) around x 0 is: sin(x) = x - 3! 5!
 aylor epasio: Let ƒ() be a ifiitely differetiable real fuctio. At ay poit i the eighbourhood of =0, the fuctio ca be represeted as a power series of the followig form: X 0 f(a) f() ƒ() f()= ( ) f( ) (
aylor epasio: Let ƒ() be a ifiitely differetiable real fuctio. At ay poit i the eighbourhood of =0, the fuctio ca be represeted as a power series of the followig form: X 0 f(a) f() ƒ() f()= ( ) f( ) (
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.265/15.070J Fall 2013 Lecture 2 9/9/2013. Large Deviations for i.i.d. Random Variables
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.265/15.070J Fall 2013 Lecture 2 9/9/2013 Large Deviatios for i.i.d. Radom Variables Cotet. Cheroff boud usig expoetial momet geeratig fuctios. Properties of a momet
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.265/15.070J Fall 2013 Lecture 2 9/9/2013 Large Deviatios for i.i.d. Radom Variables Cotet. Cheroff boud usig expoetial momet geeratig fuctios. Properties of a momet
Technical Proofs for Homogeneity Pursuit
 Techical Proofs for Homogeeity Pursuit bstract This is the supplemetal material for the article Homogeeity Pursuit, submitted for publicatio i Joural of the merica Statistical ssociatio. B Proofs B. Proof
Techical Proofs for Homogeeity Pursuit bstract This is the supplemetal material for the article Homogeeity Pursuit, submitted for publicatio i Joural of the merica Statistical ssociatio. B Proofs B. Proof
